A uniqueness criterion and a counterexample to regularity in an incompressible variational problem

Abstract

In this paper we consider the problem of minimizing functionals of the form $E(u)=\int _B f(x,\nabla u) \,dx$ in a suitably prepared class of incompressible, planar maps $u: B \rightarrow \mathbb {R}^2$. Here, B is the unit disk and $f(x,\xi )$ is quadratic and convex in $\xi$. It is shown that if u is a stationary point of E in a sense that is made clear in the paper, then u is a unique global minimizer of E(u) provided the gradient of the corresponding pressure satisfies a suitable smallness condition. We apply this result to construct a non-autonomous, uniformly convex functional $f(x,\xi )$, depending smoothly on $\xi$ but discontinuously on x, whose unique global minimizer is the so-called $N-$covering map, which is Lipschitz but not $C^1$.

1 Introduction

Let $B\subset \mathbb {R}^2$ be the unit ball. For any $u\in W^{1,2}(B,\mathbb {R}^2)$, define the energy E(u) by

$$\begin{aligned} E(u)=\int _B{f(x,\nabla u)\;dx}, \end{aligned}$$

(1.1)

where the integrand is quadratic in the gradient argument

$$\begin{aligned} f(x,\xi )=M(x)\xi \cdot \xi \;\;\text{ for } \text{ any }\; \;x\in B\;\;\text{ and }\; \;\xi \in \mathbb {R}^{2\times 2}, \end{aligned}$$

(1.2)

and where $M\in L^\infty (B,\mathbb {R}^{16})$ is symmetric, i.e. $M_{ijkl}=M_{klij}$ for all $i,j,k,l \in \{1,2\}.$

Furthermore, we require that there is a constant $\nu >0,$ s.t.

$$\begin{aligned} M(x)\xi \cdot \xi \ge \nu \, |\xi |^2 \;\;\text{ for } \text{ a.e. } \; x\in B \ \text {and all } \xi \in \mathbb {R}^{2\times 2},\end{aligned}$$

(1.3)

so that $f(x,\xi )$ is uniformly convex in $\xi$. Here $\nu$ plays the role of the well-known ellipticity constant.

Assume that g is the trace of a map $u_0 \in W^{1,2}(B,\mathbb {R}^2)$ that satisfies $\det \nabla u_0=1$ a.e. in B, so that the class

$$\begin{aligned} \mathcal {A}^g:=\{u\in W^{1,2}(B,\mathbb {R}^2): \det \nabla u=1 \;\;\text{ a.e. } \text{ in }\;\; B\; u_{|{\partial B}}=g\} \end{aligned}$$

(1.4)

is, in particular, nonempty. The constrained minimization problem that we study in this paper is then to find

$$\begin{aligned} \min \limits _{u\in \mathcal {A}^g} E(u) \end{aligned}$$

(1.5)

in $\mathcal {A}^g$. Concrete instances of g for which $\mathcal {A}^g$ is nonempty include:

• (a) $g(x):=Ax$, $x\in \partial B$, where A is any constant matrix in $SL^+(2,\mathbb {R})$, and

• (b) $g(\theta ):=\frac{1}{\sqrt{N}}e_R(N\theta )$, where $N\in \mathbb {N}\setminus \{0\}$ and $0 \le \theta \le 2\pi$.

Note that the latter is the trace of the so-called $N-$covering map

$$\begin{aligned} u_{_N}(R,\theta )=\frac{R}{\sqrt{N}}e_{R}(N\theta ), \end{aligned}$$

(1.6)

expressed in plane polar coordinates, and where we employ the notation $e_R(\theta )=(\cos \theta ,\sin \theta ),$ $e_\theta (\theta )=(-\sin \theta ,\cos \theta )$ for the basis vectors and $R:=|x|$ to denote the modulus of x.

Definition 1.1

(Stationary point) We say that $u\in \mathcal {A}^g$ is a stationary point of $E(\cdot )$ if there exists a function $\lambda$, which we shall henceforth refer to as a pressure, belonging to $L^2(B)$ and such that

$$\begin{aligned} \text {div}\;( \nabla _{\xi }f(x,\nabla u) + 2 \lambda (x) \, \text {cof}\;\nabla u) = 0 \quad \textrm{in} \ \mathcal {D}'(B). \end{aligned}$$

(1.7)

Here we recall that for any $2\times 2-$matrix A the cofactor is given by

$$\begin{aligned} \text {cof}\;A=\begin{pmatrix}a_{22} &{}-a_{21}\\ -a_{12} &{} a_{11} \end{pmatrix}. \end{aligned}$$

(1.8)

The first part of the paper is concerned with finding a criteria for a candidate to be a (unique) global minimizer. We will outline the idea first. Let $v, u \in \mathcal {A}^g$ and suppose that u is a stationary point of E in the sense of (1.7). To compare E(v) and E(u) we set $\eta =v-u$ and expand $E(v)=E(u+\eta )$ as

$$\begin{aligned} E(v)=E(u) + E(\eta ) + \int _B 2 M(x) \, \nabla u(x) \cdot \nabla \eta (x) \, dx. \end{aligned}$$

Our problem, as expressed in (1.5), is made more tractable by the observation made in [3] that the stationarity condition (1.7) allows us, at the expense of incorporating a pressure term, to rewrite the final, affine-in-$\nabla \eta$ term in the expansion above as a term that is quadratic in $\nabla \eta$, namely

$$\begin{aligned} \int _B M(x) \, \nabla u(x) \cdot \nabla \eta (x) \, dx = \int _B \lambda (x) \det \nabla \eta (x) \, dx. \end{aligned}$$

In particular,

$$\begin{aligned} E(v) = E(u) + E(\eta ) +\int _{B} 2\lambda \det \nabla \eta \,dx,\end{aligned}$$

(1.9)

which makes clear the role of the functional

$$\begin{aligned} F(\eta ):=E(\eta ) + \int _B 2\lambda \det \nabla \eta \,dx \quad \quad \eta \in W_0^{1,2}(B,\mathbb {R}^2) \end{aligned}$$

in determining the sign of $E(v)-E(u)$.

The precise condition that guarantees $F(\eta ) \ge 0$ for all $\eta$, and the first main result we obtain, shows that if u is a stationary point of the energy E whose corresponding pressure $\lambda$ satisfies, in addition, the assumption that

$$\begin{aligned} ||\nabla \lambda (x)|x|\Vert _{L^\infty (B,\mathbb {R}^2)}\le \frac{\sqrt{3}\nu }{2\sqrt{2}},\end{aligned}$$

(1.10)

then u is a global minimizer of E.¹

Theorem 1.2

(Uniqueness under small pressure) Let the energy functional E(u) be given by (1.1), and let $f(x,\xi )$ be given by (1.2), where $M\in L^{\infty }(B,\mathbb {R}^{16})$ is symmetric and satisfies (1.3) for some $\nu >0$. Let u be a stationary point of E in the sense of (1.7) and assume that the corresponding pressure $\lambda$ satisfies

$$\begin{aligned} \Vert \nabla \lambda (x)|x|\Vert _{L^\infty (B,\mathbb {R}^2)}\le \frac{\sqrt{3}\nu }{2\sqrt{2}}, \;\;\text{ for } \text{ a.e. }\;\; x\in B.\end{aligned}$$

(1.11)

Then u is a global minimizer of E in $\mathcal {A}^g$.

Moreover, if the inequality is strict, that is $|\nabla \lambda (x)|x||_{\infty }< \frac{\sqrt{3}\nu }{2\sqrt{2}}$ for every $x\in U,$ where $U \subset B$ is measurable and $\mathcal {L}^2(U)>0$, then u is the unique global minimizer of E in $\mathcal {A}^g$.

In our second main result we provide an explicit integrand $f(x,\xi )$ of the form (1.2) whose corresponding energy functional E is minimized in $\mathcal {A}^{g_N}$ by the $N-$covering map $u_{_N}$. Here, $g_N$ is the trace of $u_{_N}$ as defined in (1.6). For its construction we make use of Theorem 1.2. A novelty of our approach is that, in order to apply Theorem 1.2, we develop a method to compute the corresponding pressure explicitly.

Theorem 1.3

(Counterexample to regularity) Let $N\in \mathbb {N}\setminus \{1\}$ and let $a_N\in \left( N^2-N,N^2+N\right)$ be a constant. Let $g_N$ be the trace of the $N-$covering map $u_{_{N}}$, and define for $x \in B\setminus \{0\}$ and $\xi \in \mathbb {R}^{2 \times 2}$ the function

$$\begin{aligned}f_N(x,\xi )=\nu \left[ a_N(e_{R}^T\xi e_{R})^2+(e_{R}^T\xi e_{\theta })^2+a_N(e_{\theta }^T\xi e_{R})^2+(e_{\theta }^T\xi e_{\theta })^2\right] ,\end{aligned}$$

where $\nu >0$.

Then the following statements are true:

• (i) There exists $M_N\in L^\infty (B,\mathbb {R}^{16})$ such that

  $$\begin{aligned}f_N(x,\xi )=\nu M_N(x)\xi \cdot \xi \end{aligned}$$

  for any $x\in B\setminus \{0\},$ $\xi \in \mathbb {R}^{2\times 2}$ and where $M_N$ is of the explicit form

  $$\begin{aligned}M_N(x)=&a_N((e_R\otimes e_R)(e_R\otimes e_R))+((e_R\otimes e_\theta )(e_R\otimes e_\theta ))&\\&+a_N((e_\theta \otimes e_R)(e_\theta \otimes e_R))+((e_\theta \otimes e_\theta )(e_\theta \otimes e_\theta ))&\end{aligned}$$

  and satisfies $M_N(x) \ge \nu \text{ Id }$ for any $x\in B\setminus \{0\}.$²

• (ii) The maps $x\mapsto M_N(x)$ and $x\mapsto f_N(x,\xi ),$ for any $\xi \in \mathbb {R}^{2\times 2}\setminus \{0\},$ are discontinuous at 0.

• (iii) The maps $x\mapsto M_N(x)$ and $x\mapsto f_N(x,\xi ),$ for any $\xi \in \mathbb {R}^{2\times 2}\setminus \{0\},$ belong to

  $$\begin{aligned}W^{1,q}\setminus W^{1,2} \;\;\text{ for } \text{ any }\;\;1\le q<2\end{aligned}$$

  with the spaces $(B,\mathbb {R}^{16})$ and (B) respectively.

• (iv) The map

  $$\begin{aligned} u=u_{_N} \in C^{0,1}(B,\mathbb {R}^2)\setminus C^1(B,\mathbb {R}^2)\end{aligned}$$

  (1.12)

  is a stationary point of $E_N,$ as defined in (1.7), and the corresponding pressure $\lambda _N$ exists and satisfies $\lambda _N\in W^{1,q}(B) \;\;\text{ for } \text{ any }\;\;1\le q<2.$

• (v) Moreover, the map $u_{_N}$ is the unique global minimizer of $E_N$ in the class $\mathcal {A}^{g_N}.$

• (vi) The minimum energy is given by

  $$\begin{aligned}\min \limits _{v\in \mathcal {A}^{g_N}}E_N(v)=\frac{\nu \pi }{2}(1+a)\left( \frac{1}{N}+N\right) .\end{aligned}$$

The problem of studying a functional of the form E(u) is of interest not least because the regularity and/or uniqueness of minimizers of such incompressible problems cannot necessarily be determined a priori. Concerning uniqueness in the compressible setting, works including but not limited to John [11], Knops and Stuart [14], Sivaloganathan [20], Zhang [26], and Sivaloganathan and Spector [21] provide conditions under which the uniqueness of a global minimizer can be expected. By contrast, a striking example given by Spadaro [22] clearly demonstrates that global minimizers need not be unique, even under full displacement boundary conditions. When the domain of integration, or reference configuration, is an annulus, a number of papers, including those of John [11], Post and Sivaloganathan [16], Taheri [24], and Morris and Taheri [15, 25], address uniqueness. With the topology of the annulus at their disposal, a multiplicity of solutions/equilibria can be generated by working with certain homotopy classes. For example, Morris and Taheri [15, 25] consider functionals of the form $W(x,s,\xi )=F(|x|^2,|s|^2)|\xi |^2/2$, with $F\in C^2$, on the annulus A and admissible maps $\mathcal {A}=W_{\textrm{id}}^{1,2}(A,\mathbb {R}^2)$, and show that there are countably many solutions, with exactly one for each homotopy class.

In the homogeneous, incompressible elasticity setting, Knops and Stuart [14, Section 6] (see also [19]) show that the equilibirum solutions they consider are, when subject to affine displacement boundary conditions, global minimizers of the associated energy. Recent results [4] show that there are polyconvex energies with inhomogeneous integrands that, under pure displacement boundary conditions, possess countably many pairs of equal-energy stationary points. It is an open question whether the lowest-energy pair of such stationary points represent global minimizers.

The regularity of equilibrium solutions or mininimzers in incompressible variational problems is, like its compressible counterpart, a delicate matter. Ball [1, §2.6] points out that any minimizer of the Dirichlet energy in the class $W^{1,2}(B;\mathbb {R}^2)$, subject to the pointwise (incompressibility) constraint $\det \nabla u = 1$ a.e and boundary condition $u(1,\theta )=\frac{1}{\sqrt{2}}(\cos (2\theta ),\sin (2\theta ))$, must fail to be $C^1$. There is evidence to suggest that the double-covering map $u_{_2}$ (see (1.6)) itself may be the global minimizer in that particular problem [3, 5]. A partial regularity result for Lipschitz minimizers that are subject to a type of monotonicity condition was established in [10], and Karakhanyan [12, 13] proves that, in the case of the Dirichlet energy, bounds on the so-called dual pressure lead, by a sophisticated argument, to the conclusion that suitably defined equilibrium solutions must belong to the Hölder class $C_{\textrm{loc}}^{\frac{1}{2}}$. It is perhaps significant that Karakhanyan’s results, like ours, also depend on ‘pressure bounds’, but more significant still that the maps he deals with are measure-preserving. The double-covering map $u_2$ mentioned above, and indeed the $N-$covering maps which form the basis of the counterexample to regularity in Section 3 of this paper, do not preserve $\mathcal {L}^2-$measure in the sense of [23, Eq. (24)], for example, and so are less relevant to physically realistic models of elasticity.

It seems that pressure regimes can be used to divide the sorts of incompressible problems we consider into two classes. The double-covering problem introduced by Ball appears to lie in the ‘high pressure’ regime³, whereas the problem we focus on falls, by design, into the ‘low pressure’ regime, where we can say a bit more.

Plan of the paper: The main purpose of Sect. 2 will be to prove the uniqueness result, Theorem 1.2. We begin by giving two technical lemmas, the first of which enables us to decompose certain expressions in terms of Fourier modes. Section 2 concludes with the proof of Theorem 1.2, together with an argument which shows that the prefactor $3^{\frac{1}{2}}2^{-\frac{3}{2}} \simeq 0.6123$ appearing in (1.11) can be replaced by 1 when $\lambda$ depends on just one of the variables R, $\theta$. See Corollary 2.3. The focus of Sect. 3 is Theorem 1.3. In order to obtain this result we first develop a method to compute the pressure explicitly: this is done for a quite general situation in Lemma 3.1, and then more concretely in Lemmata 3.2-3.3.

Notation:. We define the matrix J via

$$\begin{aligned} J:=\begin{pmatrix}0 &{}-1\\ 1 &{} 0\end{pmatrix} \end{aligned}$$

and we later make use of the fact that for any $2 \times 2$ matrix A, the cofactor can be calculated by means of the identity $\text {cof}\;A = J^T A J$. When $\eta$ is suitably differentiable, we recall that in plane polar coordinates $(R,\theta )$, $\det \nabla \eta = \frac{1}{R}J \eta _{,R} \cdot \eta _{,\theta }$, where $\eta _{,R}$ and $\eta _{,\theta }$ are, respectively, the radial and angular derivatives of $\eta$. We let denote the integral average of a function f in $L^1(U)$ over a given (Lebesgue-)measurable, non-null set $U \subset \mathbb {R}^2$; that is,

where $\mathcal {L}^2$ is $2-$dimensional Lebesgue measure. All other notation is either standard or is defined when it is used.

2 Uniqueness in the small pressure regime

To prove Theorem 1.2 we need two technical lemmas. The first contains basic properties of functions in the class $W^{1,1}(B)$ that satisfy $\Vert \nabla \lambda (x)|x|\Vert _{L^\infty (B,\mathbb {R}^2)}<\infty ,$ and it relies on a standard Fourier decomposition which, when applied to $\eta \in C^\infty (B,\mathbb {R}^2)$, is given by:

$$\begin{aligned} \eta (x)=\sum \limits _{j\ge 0}\eta ^{(j)}(x),\;\;\text{ where }\;\;\eta ^{(0)}(x)=\frac{1}{2}A_0(R), \;A_0(R)=\frac{1}{2\pi }\int _{0}^{2\pi }{\eta (R,\theta )\;d\theta }\end{aligned}$$

and, for any $j\ge 1$,

$$\begin{aligned} \eta ^{(j)}(x)=A_j(R)\cos (j\theta )+B_j(R)\sin (j\theta ), \end{aligned}$$

where

$$\begin{aligned} A_j(R)=\frac{1}{2\pi }\int _{0}^{2\pi }{\eta (R,\theta )\cos (j\theta )\;d\theta }\;\;\text{ and }\;\; B_j(R)=\frac{1}{2\pi }\int _{0}^{2\pi }{\eta (R,\theta )\sin (j\theta )\;d\theta }. \end{aligned}$$

For later use, we set $\tilde{\eta }:=\eta -\eta ^{(0)}$.

With these notions at hand we can state the following technical result. Notice that the lemma is a generalisation of the results [3, Lem 3.2. and Prop 3.2]. Proofs are included for the convenience of the reader.

Lemma 2.1

Let $\lambda \in W^{1,1}(B)$ and assume that $\Vert \nabla \lambda (x)|x|\Vert _{L^\infty (B,\mathbb {R}^2)}<\infty .$

Then the following statements are true:

• i) $\lambda \in BMO(B).$

• ii) If $\varphi _n\rightarrow \varphi \in W^{1,2}(B,\mathbb {R}^2)$ then $\int _B{\lambda (x)\det \nabla \varphi _n\;dx}\rightarrow \int _B{\lambda (x)\det \nabla \varphi \;dx}.$

• iii) It holds $\int _B{|\nabla \varphi |^2\;dx}=\sum \limits _{j\ge 0}\int _B{|\nabla \varphi ^{(j)}|^2\;dx}$ for any $\varphi \in W^{1,2}(B,\mathbb {R}^2).$

• iv) $\det \nabla \varphi ^{(0)}=0$ for any $\varphi \in W^{1,2}(B,\mathbb {R}^2).$

• v) $\int _B{\lambda (x)\det \nabla \varphi \;dx}=-\frac{1}{2}\int _B{((\text {cof}\;\nabla \varphi )\nabla \lambda (x))\cdot \varphi \;dx}$ for any $\varphi \in W_0^{1,2}(B,\mathbb {R}^2).$

• vi) Moreover, for any $\varphi \in W_0^{1,2}(B,\mathbb {R}^2)$ it holds

  $$\begin{aligned}\int _B{\lambda (x)\det \nabla \varphi \;dx}=&-\frac{1}{2}\int _B{((\text {cof}\;\nabla \varphi ^{(0)})\nabla \lambda (x))\cdot \tilde{\varphi }\;dx}&\\&-\frac{1}{2}\int _B{((\text {cof}\;\nabla \varphi )\nabla \lambda (x))\cdot \tilde{\varphi }\;dx}.&\end{aligned}$$

Proof

• i) We begin by extending $\lambda$ outside B, as follows. Firstly, the hypothesis that $|y||\nabla \lambda (y)|$ is essentially bounded in B implies in particular that $|\nabla \lambda (y)|$ is essentially bounded on $B':=B\setminus B(0,\frac{1}{2})$, and hence, via Sobolev embedding, that $\lambda \in W^{1,\infty }(B')$. By employing a suitable extension operator E, say, (see [8, Section 5.4, Theorem 1], for instance), we extend $\lambda$ to a function $E\lambda$ belonging to $W^{1,\infty }(\mathbb {R}^2\setminus B(0,\frac{1}{2}))$ with $\text {spt}\,E\lambda \subset B(0,2)$, say. Finally, to simplify notation in what follows, we write $\lambda (y)=E\lambda (y)$ whenever $1\le |y|\le 2$, so that $\lambda \in W^{1,\infty }(\mathbb {R}^2\setminus B(0,\frac{1}{2}))$. Our assertion is then that $\lambda \in BMO$, which amounts to showing that

  

  (2.1)

  where, for any $x\in \mathbb {R}^2$ and $t>0$, we employ the notation

  

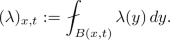
  Firstly, by Hölder’s inequality,

  

  (2.2)

  Then, by [9, Section 4.5.2, Theorem 2], we obtain

  

  (2.3)

  where the constants $C_1$ and $C_2$ do not depend on x or t. Putting (2.2) and (2.3) together gives

  

  (2.4)

  We claim that there is a constant M, which does not depend on x or t, such that the estimate

  

  (2.5)

  holds. To see (2.5), begin by noting that $B(x,t)\subset B(0,|x|+t)$, and hence

  $$\begin{aligned} \int _{B(x,t)}{|\nabla \lambda (y)|\;dy}&\le \int _{B(0,|x|+t)}{|\nabla \lambda (y)|\;dy} \\&= \int _{B(0,|x|+t)}{|\nabla \lambda (y)||y||y|^{-1}\;dy} \\&\le 2\pi M' (|x|+t), \end{aligned}$$

  where we have used the hypothesis that $|y||\nabla \lambda (y)|$ is essentially bounded by $M'$, say. Hence (2.5) holds with $M=2M'$. Finally, to see (2.1), we consider two cases. If $t > |x|/2$ then (2.5) implies that

  

  (2.6)

  If $t \le |x|/2$, any $y \in B(x,t)$ is such that $|y| \ge |x|/2$, and hence, again by using the essential boundedness of $|y||\nabla \lambda (y)|$, we obtain the estimate

  $$\begin{aligned} |\nabla \lambda (y)| \le \frac{2M'}{|x|}.\end{aligned}$$

  Therefore

  

  (2.7)

  Putting (2.6) and (2.7) together, it follows that the right-hand side of (2.4) is bounded above uniformly in x and t. Hence (2.1).

• ii) We give a sketch of the proof here. For more detail, see [3, Proposition 3.2 (ii)]. By part (i) and the well-known Fefferman-Stein duality [6], it is enough to show that if $\varphi _n\rightarrow \varphi \in W^{1,2}(B,\mathbb {R}^2)$ then $\det \nabla \varphi _n\rightarrow \det \nabla \varphi \in \mathcal {H}^{1}(\mathbb {R}^2).$ Firstly, we extend the functions $\varphi _n$ and $\varphi$ by setting them to zero outside B, and then apply the identity $2(\det \nabla \varphi _n-\det \nabla \varphi )=\text {cof}\;(\nabla \varphi _n+\nabla \varphi )\cdot (\nabla \varphi _n-\nabla \varphi )$, to whose right-hand side the div-curl lemma [7, Lemma II.1] applies. The result is that

  $$\begin{aligned}\Vert \det \nabla \varphi _n-\det \nabla \varphi \Vert _{\mathcal {H}^{1}}\le C\Vert \nabla \varphi _n+\nabla \varphi \Vert _{L^2}\Vert \nabla \varphi _n-\nabla \varphi \Vert _{L^2}\end{aligned}$$

  for some constant $C>0,$ and the convergence $\varphi _n \rightarrow \varphi$ in $W^{1,2}(B,\mathbb {R}^2)$ then yields the claim.

• iii) This is straightforward and exploits the $L^2$-orthogonality of the different Fourier modes. We omit the details.

• iv) Recall that $\varphi ^{(0)}(x)=\frac{1}{2}A_0(R)$ is just a function of R. Therefore $\nabla \varphi ^{(0)}(x)=\frac{1}{2}(A_0,_{R}(R))\otimes e_R(\theta )$, which is clearly a matrix of rank one. Hence the statement in part iv).

• v) Assuming $\varphi \in C_c^\infty (B,\mathbb {R}^2)$, a computation shows:

  $$\begin{aligned}\int _B{\lambda (x)\det \nabla \varphi \;dx}=&\int _B{\lambda (x)J\varphi ,_R\cdot \varphi ,_\theta \;\frac{dx}{R}}&\\ =&-\int _B{(\lambda (x)J\varphi ,_R),_\theta \cdot \varphi \;\frac{dx}{R}}&\\ =&-\int _B{\lambda (x),_\theta J\varphi ,_R\cdot \varphi \;\frac{dx}{R}}-\int _B{\lambda (x)J\varphi ,_{R\theta }\cdot \varphi \;\frac{dx}{R}}&\\ =&-\int _B{\lambda (x),_\theta J\varphi ,_R\cdot \varphi \;\frac{dx}{R}}+\int _B{\lambda (x),_RJ\varphi ,_{\theta }\cdot \varphi \;\frac{dx}{R}}&\\&+\int _B{(\lambda (x)J\varphi ,_{\theta })\cdot \varphi ,_R\;\frac{dx}{R}}&\\ =&-\int _B{((\text {cof}\;\nabla \varphi )\nabla \lambda (x))\cdot \varphi \;dx}-\int _B{(\lambda (x)J\varphi ,_{R})\cdot \varphi ,_\theta \;\frac{dx}{R}}&\end{aligned}$$

  The result follows by bringing the rightmost term to the left-hand side and dividing by two. Note, as a last step, that one needs to upgrade the above equation to hold not just for $\varphi \in C_c^\infty (B)$ but also for all $\varphi \in W_0^{1,2}(B).$ This is slightly delicate because of the weak spaces involved: for a proof, the argument in [3, Lem 3.2.(iv)] can be adapted.

• vi) This is a version of (v) in which we emphasise the way that the above expression depends on $\varphi ^{(0)}$. Again, we assume $\varphi \in C_c^\infty (B),$ and we start by noting $\varphi ,_\theta =\tilde{\varphi },_\theta$, so that we have

  $$\begin{aligned}\int _B{\lambda (x)\det \nabla \varphi \;dx}=&\int _B{\lambda (x)J\varphi ,_R\cdot \tilde{\varphi },_\theta \;\frac{dx}{R}}&\\ =&-\int _B{((\text {cof}\;\nabla \varphi )\nabla \lambda (x))\cdot \tilde{\varphi }\;dx}+\int _B{(\lambda (x)J\tilde{\varphi },_{\theta })\cdot \tilde{\varphi },_R\;\frac{dx}{R}}.&\end{aligned}$$

  Then the rightmost term is just

  $$\begin{aligned}\int _B{(\lambda (x)J\tilde{\varphi },_{\theta })\cdot \tilde{\varphi },_R\;\frac{dx}{R}}=&-\int _B{(\lambda (x)J\tilde{\varphi },_R)\cdot \tilde{\varphi },_{\theta }\;\frac{dx}{R}}&\\ =&\frac{1}{2}\int _B{((\text {cof}\;\nabla \tilde{\varphi })\nabla \lambda (x))\cdot \tilde{\varphi }\;dx}.&\end{aligned}$$

  Together with the above we get

  $$\begin{aligned}\int _B{\lambda (x)\det \nabla \varphi \;dx}=&-\frac{1}{2}\int _B{((\text {cof}\;\nabla \varphi ^{(0)})\nabla \lambda (x))\cdot \tilde{\varphi }\;dx}&\\&-\frac{1}{2}\int _B{((\text {cof}\;\nabla \varphi )\nabla \lambda (x))\cdot \tilde{\varphi }\;dx}.&\end{aligned}$$

$\square$

The uniqueness condition will be of the form $\Vert \nabla \lambda (x)|x|\Vert _{L^\infty (B,\mathbb {R}^2)}\le C$ for some constant $C>0$ and where $\lambda$ will be the corresponding pressure to some stationary point. A priori, the condition only guarantees the existence of $\nabla \lambda (x)|x|$ in a suitable space. In the next lemma we show that $\lambda$ and $\nabla \lambda$ themselves exist in a suitable space, which, in particular, allows one to make use of the technical lemma above.

Lemma 2.2

Let $\mu \in L^1_{\text {loc}}(B)$ be a weakly differentiable function satisfying

$$\begin{aligned}\Vert \nabla \mu (x)|x|\Vert _{L^\infty (B,\mathbb {R}^2)}<\infty .\end{aligned}$$

Then $\mu \in W^{1,p}(B,\mathbb {R}^2)$ for any $1\le p<2.$

Proof

The proof is straightforward. Indeed, it holds that

$$\begin{aligned}\int _B{|\nabla \mu |^p\;dx}\le \Vert \nabla \mu (x) |x|\Vert _{L^\infty (B,\mathbb {R}^2)}^p\int _B{R^{1-p}\;\frac{dx}{R}},\end{aligned}$$

where the latter integrand is integrable for all $1\le p<2.$ $\square$

We are now in a position to prove the main statement of this section.

Proof of Theorem 1.2

Let $u\in \mathcal {A}^g$ be a stationary point with pressure $\lambda$, let $v\in \mathcal {A}^g$ be arbitrary and set $\eta :=v-u\in W_0^{1,2}(B,\mathbb {R}^2).$

We start our argument by expanding the energy via

$$\begin{aligned}E(v)&=\int _B{M(x)\nabla v\cdot \nabla v\;dx}\\&=\int _B{M(x)\nabla u\cdot \nabla u\;dx}+\int _B{M(x)\nabla \eta \cdot \nabla \eta \;dx}+2\int _B{M(x)\nabla u\cdot \nabla \eta \;dx}\\&=E(u)+E(\eta )+H(u,\eta ),\end{aligned}$$

where

$$\begin{aligned}H(u,\eta ):=2\int _B{M(x)\nabla u\cdot \nabla \eta \;dx}\end{aligned}$$

denotes the mixed terms.

Expanding the Jacobian of $\eta$ and exploiting the fact that both u and v satisfy $\det \nabla u=\det \nabla v =1$ a.e. yields

$$\begin{aligned}\det \nabla \eta =-\text {cof}\;\nabla u \cdot \nabla \eta \;\;\text{ a.e. }\;\end{aligned}$$

By the latter identity and the fact that $(u,\lambda )$ satisfies (1.7), H can be written as

$$\begin{aligned} H(u,\eta )=2\int _B{\lambda (x)\det \nabla \eta \;dx}.\end{aligned}$$

(2.8)

By Lemma 2.1.(vi) we have

$$\begin{aligned} H(u,\eta ){} & {} =-\int _B{(\text {cof}\;\nabla \eta ^{(0)}\nabla \lambda (x))\cdot \tilde{\eta }\;dx}-\int _B{(\text {cof}\;\nabla \eta \nabla \lambda (x))\cdot \tilde{\eta }\;dx}\\{} & {} =:(I)+(II).\end{aligned}$$

Now by noting that the $0-$mode is only a function of R,  we get

$$\begin{aligned} (\text {cof}\;\nabla \eta ^{(0)}\nabla \lambda (x))\cdot \tilde{\eta }=\frac{\lambda ,_\theta }{R}(\eta _{1,R}^{(0)}\tilde{\eta }_2-\eta _{2,R}^{(0)}\tilde{\eta }_1). \end{aligned}$$

Instead of just $\lambda ,_\theta$ on the right hand side of the latter equation we would like to have the full gradient of $\lambda .$ This can be achieved by using the basic relations $e_\theta \cdot e_\theta =1$ and $e_R\cdot e_\theta =0$ to obtain

$$\begin{aligned} (\text {cof}\;\nabla \eta ^{(0)}\nabla \lambda (x))\cdot \tilde{\eta }=(\lambda ,_RR e_R+\lambda ,_\theta e_\theta )\cdot (\eta _{1,R}^{(0)}\tilde{\eta }_2-\eta _{2,R}^{(0)}\tilde{\eta }_1)\frac{e_\theta }{R}. \end{aligned}$$

Arguing similarly for (II), and a short computation shows

$$\begin{aligned} H(u,\eta )=&-\int _B(\lambda ,_RR e_R+\lambda ,_\theta e_\theta )\cdot \left[ (\tilde{\eta }_1\tilde{\eta }_{2,\theta }-\tilde{\eta }_2\tilde{\eta }_{1,\theta })\frac{e_R}{R}\right.&\nonumber \\&+\left. (\tilde{\eta }_2(\eta _{1,R}^{(0)}+\eta _{1,R})-\tilde{\eta }_1(\eta _{2,R}^{(0)}+\eta _{2,R}))e_\theta \right] \;\frac{dx}{R}.&\end{aligned}$$

(2.9)

By Hölder’s inequality we get⁴

$$\begin{aligned} H(u,\eta )\ge&-\Vert \nabla \lambda (x)R\Vert _{L^\infty (B,\mathbb {R}^2)}\int _B\left[ \left| \tilde{\eta }_1\tilde{\eta }_{2,\theta }-\tilde{\eta }_2\tilde{\eta }_{1,\theta }\right| \frac{1}{R}\right.&\\&+\left. \left| \tilde{\eta }_2(\eta _{1,R}^{(0)}+\eta _{1,R})-\tilde{\eta }_1(\eta _{2,R}^{(0)}+\eta _{2,R})\right| \right] \;\frac{dx}{R}.&\end{aligned}$$

By $\Vert \nabla \lambda (x) R\Vert _{L^\infty (B,\mathbb {R}^2)}\le \frac{\sqrt{3}\nu }{2\sqrt{2}}$ and a weighted Cauchy-Schwarz Inequality, we see⁵

$$\begin{aligned} H(u,\eta )\ge&-\frac{\nu \sqrt{3}}{4\sqrt{2}}\left[ 2a\Vert \tilde{\eta }_1\Vert _{L^2(dx/R^2)}^2+2a\Vert \tilde{\eta }_2\Vert _{L^2(dx/R^2)}^2\right.&\\&\left. +\frac{1}{a}\int _B{\left[ \frac{\tilde{\eta }_{2,\theta }^2}{R^2}+(\eta _{2,R}^{(0)}+\eta _{2,R})^2+(\eta _{1,R}^{(0)}+\eta _{1,R})^2+\frac{\tilde{\eta }_{1,\theta }^2}{R^2}\right] \;dx}\right] .&\end{aligned}$$

Next we recall an elementary Fourier estimate (see, for instance, [3, Proof of Proposition 3.3]), which states that for any $\phi \in C^\infty (B)$ it holds

$$\begin{aligned} \int _B{R^{-2}|\tilde{\phi }_{,\theta }|^2\;dx}\ge \int _B{R^{-2}|\tilde{\phi }|^2\;dx}.\end{aligned}$$

(2.10)

Applying the Cauchy-Schwarz inequality and (2.10), and then combining some of the norms yields

$$\begin{aligned} H(u,\eta )\ge&-\frac{\nu \sqrt{3}}{4\sqrt{2}}\left[ (2a+\frac{1}{a})\Vert \tilde{\eta }_1,_\theta \Vert _{L^2(dx/R^2)}^2+(2a+\frac{1}{a})\Vert \tilde{\eta }_2,_\theta \Vert _{L^2(dx/R^2)}^2 +\right.&\\&\left. +\frac{2}{a}\Vert \eta _1,_R^{(0)}\Vert _{L^2(dx)}^2+\frac{2}{a}\Vert \eta _1,_R\Vert _{L^2(dx)}^2\right.&\\&\left. +\frac{2}{a}\Vert \eta _2,_R^{(0)}\Vert _{L^2(dx)}^2+\frac{2}{a}\Vert \eta _2,_R\Vert _{L^2(dx)}^2\right]&\\ \ge&-\frac{\nu \sqrt{3}}{4\sqrt{2}}\left[ (2a+\frac{1}{a})\Vert \tilde{\eta },_\theta \Vert _{L^2(dx/R^2)}^2+\frac{2}{a}\Vert \eta ,_R^{(0)}\Vert _{L^2(dx)}^2\right.&\\&\left. +\frac{2}{a}\Vert \eta ,_R\Vert _{L^2(dx)}^2\right] .&\end{aligned}$$

Making use of $\tilde{\eta },_\theta =\eta ,_\theta ,$ which is true since the zero-mode does not depend on $\theta ,$ and $\Vert \eta ,_R^{(0)}\Vert _{L^2(dx)}^2\le \Vert \eta ,_R\Vert _{L^2(dx)}^2$ we obtain

$$\begin{aligned} H(u,\eta )\ge&-\frac{\nu \sqrt{3}}{4\sqrt{2}}\left[ (2a+\frac{1}{a})\Vert \eta ,_\theta \Vert _{L^2(dx/R^2)}^2+\frac{4}{a}\Vert \eta ,_R\Vert _{L^2(dx)}^2\right] .&\end{aligned}$$

Choosing $a=\frac{\sqrt{3}}{\sqrt{2}}$ and again combining norms gives

$$\begin{aligned} H(u,\eta )\ge&-\frac{\nu \sqrt{3}}{4\sqrt{2}}\left[ \frac{4\sqrt{2}}{\sqrt{3}}(\Vert \eta ,_\theta \Vert _{L^2(dx/R^2)}^2+\Vert \eta ,_R\Vert _{L^2(dx)}^2)\right]&\\ =&-\nu D(\eta ),&\end{aligned}$$

where $D(\eta ):=\Vert \nabla \eta \Vert _{L^2(dx)}^2$ denotes the Dirichlet energy. This yields

$$\begin{aligned}E(\eta )+H(u,\eta )\ge E(\eta )-\nu D(\eta )\ge 0,\end{aligned}$$

which, since $M\xi \cdot \xi \ge \nu |\xi |^2$ for all $\xi \in \mathbb {R}^2$, completes the proof. $\square$

The prefactor $\frac{\sqrt{3}}{2\sqrt{2}}$ in (1.11) is the best we have for general $\lambda$ at the moment. If, however, circumstances are such that $\lambda$ depends on only one of $R,\theta$ throughout B, then condition (1.11) can be replaced by the weaker assumption

$$\begin{aligned} \Vert \nabla \lambda (x)R\Vert _{L^\infty (B,\mathbb {R}^2)}\le \nu ,\end{aligned}$$

(2.11)

which is the content of the next result.

Corollary 2.3

Let the conditions of Theorem 1.2 be in force, but with (2.11) replacing (1.10), and assume that either $\lambda (x)=\lambda (R)$ or $\lambda (x)=\lambda (\theta )$ for all $x\in B$. Then the conclusions of Theorem 1.2 hold.

Proof

(i) ($\lambda (x)=\lambda (R)$.) This case is significantly simpler and one can argue more along the lines of the proof of [3, Prop.3.3]. The reason is that in this case it still holds that

$$\begin{aligned}H(v,\eta )=2\int _B{\lambda (R)\det \nabla \eta \;dx}=2\int _B{\lambda (R)\det \nabla \tilde{\eta }\;dx},\end{aligned}$$

where $\tilde{\eta }=\eta -\eta ^{(0)}$ eliminating the $0-$mode.

Then applying of [3, Lemma 3.2.(iv)] yields

$$\begin{aligned}H(v,\eta )=\int _B{\lambda '(R)R\tilde{\eta }\cdot J \tilde{\eta }_{,\theta }\;\frac{dx}{R^{2}}}.\end{aligned}$$

Using Hölder’s inequality, $\Vert \lambda '(R)R\Vert _{L^\infty (0,1)}\le \nu ,$ and Fourier estimate (2.10) we get

$$\begin{aligned} H(v,\eta )\ge&-\Vert \lambda '(R)R\Vert _{L^\infty (0,1)} \int _B{|\tilde{\eta }||\tilde{\eta }_{,\theta }|\;\frac{dx}{R^{2}}}&\\ \ge&-\nu \left( \int _B{|\tilde{\eta }|^2\;\frac{dx}{R^{2}}}\right) ^{1/2}\left( \int _B{|\tilde{\eta }_{,\theta }|^2\;\frac{dx}{R^{2}}}\right) ^{1/2}&\\ \ge&-\nu \int _B{|\tilde{\eta }_{,\theta }|^2\;\frac{dx}{R^{2}}}&\\ \ge&-\nu \int _B{|\nabla \eta |^2\;dx}.&\end{aligned}$$

Note, as before, that the $\sim$ could be dropped because $\int _B{|\nabla \tilde{\eta }|^2\;dx}\le \int _B{|\nabla \eta |^2\;dx}.$

(ii) ($\lambda (x)=\lambda (\theta ).$) Here we start with (2.9) which simplifies to

$$\begin{aligned} H(u,\eta )=&-\int _B{\lambda ,_\theta (\theta )[(\eta _2,_R^{(0)}+\eta _2,_R)\tilde{\eta }_1+(\eta _1,_R^{(0)}+\eta _1,_R)\tilde{\eta }_2]\;\frac{dx}{R}}&\end{aligned}$$

By Hölder’s inequality, Inequality (2.10) and $\Vert \lambda ,_\theta \Vert _{L^\infty (0,2\pi )}\le \nu$ we get

$$\begin{aligned} H(u,\eta )\ge&-\Vert \lambda ,_\theta \Vert _{L^\infty (0,2\pi )}\int _B{|(\eta _2,_R^{(0)}+\eta _2,_R)\tilde{\eta }_1+(\eta _1,_R^{(0)}+\eta _1,_R)\tilde{\eta }_2|\;\frac{dx}{R}}&\\ \ge&-\frac{\nu }{2}\left[ 2\Vert \tilde{\eta }_1,_\theta \Vert _{L^2(dx/R^2)}^2+2\Vert \tilde{\eta }_2,_\theta \Vert _{L^2(dx/R^2)}^2\right.&\\&+\left. \Vert \eta ,_R^{(0)}\Vert _{L^2(dx)}^2+\Vert \eta ,_R\Vert _{L^2(dx)}^2\right]&\end{aligned}$$

Using $\tilde{\eta },_\theta =\eta ,_\theta$ and $\Vert \eta ,_R^{(0)}\Vert _{L^2(dx)}^2\le \Vert \eta ,_R\Vert _{L^2(dx)}^2$ we get

$$\begin{aligned} H(u,\eta )\ge&-\frac{\nu }{2}[2\Vert \eta ,_\theta \Vert _{L^2(dx/R^2)}^2+2\Vert \eta ,_R\Vert _{L^2(dx)}^2]&\\ =&-\nu D(\eta ).&\end{aligned}$$

$\square$

Remark 2.4

(Relaxation of the assumptions) The result of Theorem 1.2 continues to hold if we assume that $f(x;\xi )=M(x)\xi \cdot \xi \ge \nu (|x|)|\xi |^2$ for some $\nu \in L^\infty (\mathbb {R}_{+})$, $\nu (R) \ge 0$, and all $\xi \in \mathbb {R}^{2\times 2}$. Here, $\nu (R)=0$ is allowed⁶ to be 0. The assumption $\nu =\nu (R)$ is needed because we do not know if the Fourier estimate (2.10) is still true if $\nu$ depends on both R and $\theta .$ In this case, the small pressure condition can be relaxed to a pointwise estimate:

$$\begin{aligned}|\nabla \lambda (x)R|\le \frac{\sqrt{3}\nu (R)}{2\sqrt{2}} \quad \mathrm {for \ a.e.} \ x \in B,\end{aligned}$$

with uniqueness if the inequality is strict on some non-null set.

3 A method for computing the pressure and a counterexample to regularity

In this section we construct an explicit functional E(u) of the form (1.1), where the integrand obeys (1.2) and (1.3), such that $u=u_{_N}$ is the global minimizer of E in $\mathcal {A}^{\textrm{tr}\,(u_{_{\small {N}}})}$. The strategy is as follows:

• (i) select a candidate trace function $g \in W^{k+1,p}(\mathbb {S}^1,\mathbb {R}^2)$ for $k \ge 1$ and $1 \le p \le \infty$ which obeys⁷$1=Jg(\theta )\cdot g'(\theta )$ for a.e. $\theta$ in $[0,2\pi )$⁸;

• (ii) extend g to a one-homogeneous function $u(R,\theta ):=R g(\theta )$, and compute, in Lemma 3.1, a PDE which must be satisfied by both u and an associated $\lambda$ in order that u is a stationary point of E in the sense of (1.7);

• (iii) fix $g=\textrm{tr}\,(u_{_{\small {N}}})$ and construct, in Lemma 3.2, a suitable $f(x,\xi )$ such that the PDE in step (ii) can be solved for $\lambda$, and

• (iv) verify that the small pressure condition stipulated in Corollary 2.3 is satisfied by $\lambda$, and hence that $u_{_{\small {N}}}$ is the unique global minimizer of the associated energy E.

In this section we will rely on the following notation:

Notation: Recall the notation for 2-dimensional polar coordinates

$$\begin{aligned}\{e_R,e_\theta \}:=\{(\cos \theta ,\sin \theta ),(-\sin \theta ,\cos \theta )\}.\end{aligned}$$

Additionally, we will use

$$\begin{aligned}\{e_{NR},e_{N\theta }\}:=\{(\cos (N\theta ),\sin (N\theta )),(-\sin (N\theta ),\cos (N\theta ))\}\end{aligned}$$

for any $N\in \mathbb {N}.$ Moreover, we will use the notation $M_{ijgk}=(M(e_i\otimes e_j))\cdot (g\otimes e_k)$ for any combination of $i,j,k\in \{R,\theta \}$ and any map $g \in \mathbb {R}^{2}.$ Especially, if $g=e_{Nl}$ for some $l\in \{R,\theta \}$ we will use $M_{ij(Nl)k}$ for short.

Lemma 3.1

(Representation of the pressure) Let $1\le p\le \infty ,$ $k\in \mathbb {N}\setminus \{0\}$ and assume $M\in (L^{\infty }\cap W^{k,p})(B,\mathbb {R}^{16}),$ $g \in W^{k+1,p}(\mathbb {S}^1,\mathbb {R}^2)$ where g obeys $Jg \cdot g'=1$ a.e. in $[0,2\pi ),$ and let $u=Rg(\theta ) \in \mathcal {A}^g$ be a stationary point of the energy E as defined in (1.7).

Then there exists a corresponding pressure $\lambda \in W^{k,p}(B,\mathbb {R})$ and it satisfies the following system of equations a.e. in B : 

$$\begin{aligned} \lambda (x),_\theta (Jg\cdot e_R)-\lambda (x),_RR(Jg'\cdot e_R)=&-[M_{R\theta (g+g'')\theta }&\nonumber \\&+((M,_\theta )_{R\theta g R}+(M,_\theta )_{R \theta g'\theta })&\nonumber \\&+ R((M,_R)_{R R g R}+(M,_R)_{R R g' \theta })]&\nonumber \\ =:&h_1(M,g)&\nonumber \\ \lambda (x),_\theta (Jg\cdot e_\theta )-\lambda (x),_RR(Jg'\cdot e_\theta )=&-[M_{\theta \theta (g+g'')\theta }&\nonumber \\&+((M,_\theta )_{\theta \theta g R}+(M,_\theta )_{\theta \theta g'\theta })&\nonumber \\&+ R((M,_R)_{\theta R g R}+(M,_R)_{\theta R g' \theta })]&\nonumber \\ =:&h_2(M,g)&\end{aligned}$$

(3.1)

Proof

Let $u=Rg(\theta )\in \mathcal {A}^g$ be a stationary point. If there exists a corresponding pressure $\lambda \in W^{1,p}$ then u is a solution of

$$\begin{aligned} \int _B{M(x)\nabla u\cdot \nabla \eta \;dx}=-\int _B{\lambda (x)\text {cof}\;\nabla u\cdot \nabla \eta \;dx}\;\;\text{ for } \text{ any }\; \eta \in C_c^\infty (B,\mathbb {R}^2).\qquad \end{aligned}$$

(3.2)

For now, let us assume that $\lambda \in W^{1,p}(B,\mathbb {R}).$ In order to derive the system of equations above, we enter the explicit form of u and the representation $\eta =(\eta \cdot e_R) e_R+(\eta \cdot e_{\theta }) e_{\theta }$ into the stationarity condition. By some further calculations, which are mainly integrations by parts, we obtain (3.1). In the last step of the proof we discuss the existence of $\lambda \in W^{1,p}.$

Step 1: Computation of left-hand side of (3.2):

The derivative and the cofactor of the map $u=Rg(\theta )$ are given by

$$\begin{aligned}\nabla u=g\otimes e_R+g'\otimes e_\theta ,\\\text {cof}\;\nabla u=Jg\otimes e_\theta -Jg'\otimes e_R.\end{aligned}$$

Plugging the above into the left-hand side of (3.2) and integrating by parts yields

$$\begin{aligned}(LHS)=&\int _B{M(x)(g\otimes e_R+g'\otimes e_\theta )\cdot \left( \eta ,_R\otimes e_R+\frac{1}{R}\eta ,_\theta \otimes e_\theta \right) \;dx}&\\ =&-\int _B{R(M(x),_R)(g\otimes e_R+g'\otimes e_\theta )\cdot (\eta \otimes e_R)\;\frac{dx}{R}}&\\&-\int _BM(x)((g+g'')\otimes e_\theta )\cdot (\eta \otimes e_\theta )\;\frac{dx}{R}&\\&-\int _BM(x),_\theta (g\otimes e_R+g'\otimes e_\theta )\cdot (\eta \otimes e_\theta )\;\frac{dx}{R}&\end{aligned}$$

Now by expanding $\eta =\alpha e_R+\beta e_{\theta }$ with $\alpha =(\eta \cdot e_R)$ and $\beta =(\eta \cdot e_{\theta })$ and the shorthand introduced above we get

$$\begin{aligned}(LHS)=&-\int _BR[(M,_R)_{RRgR}+(M,_R)_{RRg'\theta }]\alpha \;\frac{dx}{R}&\\&-\int _BR[(M,_R)_{\theta RgR}+(M,_R)_{\theta Rg'\theta }]\beta \;\frac{dx}{R}&\\&-\int _B{M_{R\theta (g+g'')\theta }\alpha +[(M,_\theta )_{R\theta gR}+(M,_\theta )_{R\theta g'\theta }]\alpha \;\frac{dx}{R}}&\\&-\int _B{M_{\theta \theta (g+g'')\theta }\beta +[(M,_\theta )_{\theta \theta gR}+(M,_\theta )_{\theta \theta g'\theta }]\beta \;\frac{dx}{R}}&\\ =&\int _B{h_1\alpha +h_2\beta \;\frac{dx}{R}}.&\end{aligned}$$

Step 2: Computation of right-hand side of (3.2):

Now by again using the explicit form of $\text {cof}\;\nabla u,$ and integration by parts we get

$$\begin{aligned} (RHS)=&-\int _B{(\lambda (x)(Jg\cdot \eta ,_\theta )-\lambda (x)R(Jg'\cdot \eta ,_R))\;\frac{dx}{R}}&\\ =&\int _B{\lambda ,_\theta (x)(Jg\cdot \eta )-\lambda ,_R(x)R(Jg'\cdot \eta )\;\frac{dx}{R}}.&\end{aligned}$$

Further, we use the expression $\eta =\alpha e_R+\beta e_{\theta }$ with the notation $\alpha =(\eta \cdot e_R)$ and $\beta =(\eta \cdot e_{\theta })$ to derive

$$\begin{aligned} (RHS)=&\int _B{(\lambda ,_\theta (x)(Jg\cdot e_R)-\lambda ,_R(x)R(Jg'\cdot e_R))\alpha }&\\&{+(\lambda ,_\theta (x)(Jg\cdot e_\theta )-\lambda ,_R(x)R(Jg'\cdot e_\theta ))\beta \;\frac{dx}{R}}.&\end{aligned}$$

Together with Step 1 and the realization that in the above $\alpha ,\beta \in C_c^\infty (B)$ are arbitrary, the claimed equations need to be true a.e. in B.

Step 3: Existence of the pressure $\lambda \in W^{1,p}(B,\mathbb {R}):$

The equations above can be rewritten as

$$\begin{aligned}\int _B{\text {div}\;(\lambda \, \text {cof}\;\nabla u)\cdot \eta \;dx}=\int _B{h(M,g)\cdot \eta \;\frac{dx}{R}},\end{aligned}$$

where $h=(h_1,h_2).$ We know that $\text {div}\;(\lambda \text {cof}\;\nabla u)\in L^p(dx)$ iff $h(M,g)\in L^p(\frac{dx}{R}),$ with obvious notation. Now consider $h_1(M,g)$ (the argument being similar for $h_2$) and define

$$\begin{aligned} h_{11}:=&-M_{R\theta (g+g'')\theta }&\\ h_{12}:=&[((M,_\theta )_{R\theta g R}+(M,_\theta )_{R \theta g'\theta })&\\&+ R((M,_R)_{R R g R}+(M,_R)_{R R g' \theta })].&\end{aligned}$$

Then for $h_{11}\in L^p(\frac{dx}{R})$ we need $M\in L^\infty (dx)$ and $g,g''\in L^p,$ which is true by assumption. Now, by Sobolev imbedding, we have $W^{2,p}\hookrightarrow W^{1,\infty }([0,2\pi ),\mathbb {R}^2),$ and hence, in order for $h_{12}\in L^p(\frac{dx}{R}),$ and bearing in mind that $g,g'\in L^\infty ,$ it is enough to require that $\nabla M\in L^{p}(dx).$ This is exactly how we chose the classes for M and g. This guarantees the existence of $\text {div}\;(\lambda \text {cof}\;\nabla u)=(\text {cof}\;\nabla u)\nabla \lambda \in L^p(dx).$ By further noting that $g,g'\in L^\infty$, it is immediate that $\nabla u\in L^\infty (dx),$ and since $\det \nabla u=1$ a.e. in B, we may write

$$\begin{aligned} \nabla \lambda =(\text {cof}\;\nabla u)^T \frac{h(M,g)}{R} \in L^p(dx). \end{aligned}$$

In particular, when M and g are specified, $\nabla \lambda$ is specified and it belongs to the class $L^p(B)$, reverting to the traditional notation.

If we want $\lambda$ to be in a better space, say, $\lambda \in W^{k,p}(dx),$ for some $k\in \mathbb {N},$ by the previous argument it is enough to show that $h(M,g)\in W^{k,p}(\frac{dx}{R}).$ For instance, we see by the product rule and the Sobolev imbedding above, that $h_{11}\in W^{k,p}(\frac{dx}{R})$ iff $M\in (L^\infty \cap W^{k,p})(dx)$ and $g\in W^{k+2,p}.$ Arguing similarly for the other components finishes the proof. $\square$

We now specify $g=\textrm{tr}\,(u_{_{\small {N}}})$ and compute the pressure under the assumptions that M depends only on $\theta$ and is diagonal with respect to the basis of polar coordinates.

Lemma 3.2

(Representation of the pressure, N-cover, M($\theta$)=diag) For $N\in \mathbb {N}\setminus \{1\}$ let $g=\frac{1}{\sqrt{N}}e_{NR}$ and assume $M\in (L^{\infty }\cap W^{k,p})(B,\mathbb {R}^{16})$ for some $1\le p\le \infty$ and $k\in \mathbb {N},$ where M is of the specific form

$$\begin{aligned}M(x)=diag(M_{R R R R},M_{R\theta R \theta },M_{\theta R \theta R},M_{\theta \theta \theta \theta })=diag(\alpha (\theta ),\beta (\theta ),\gamma (\theta ),\delta (\theta ))\end{aligned}$$

with $\nu >0$ and $\alpha ,\beta ,\gamma ,\delta \ge \nu$ for any $\theta \in [0,2\pi ).$ Furthermore, suppose $u=Rg(\theta )\in \mathcal {A}^g$ is a stationary point of the energy E,  as defined in (1.1).

Then there exists a corresponding pressure $\lambda \in W^{k,p}(B)$ and it satisfies the following system of equations a.e. in B : 

$$\begin{aligned}&-\lambda (x),_\theta \frac{1}{\sqrt{N}}\sin (\theta _{N-1})+\lambda (x),_RR\sqrt{N}\cos (\theta _{N-1})=\sqrt{N}\beta '\sin (\theta _{N-1})&\nonumber \\&\qquad +\left[ \sqrt{N}(N-1)\beta +\sqrt{N}\delta -\right. \left. \frac{\alpha }{\sqrt{N}}\right] \cos (\theta _{N-1})&\nonumber \\&\quad =:h_1 \end{aligned}$$

(3.3)

$$\begin{aligned}&\lambda (x),_\theta \frac{1}{\sqrt{N}}\cos (\theta _{N-1})+\lambda (x),_RR\sqrt{N}\sin (\theta _{N-1})=-\sqrt{N}\delta '\cos (\theta _{N-1})&\nonumber \\&\qquad +\left[ \sqrt{N}\beta +\sqrt{N}(N-1)\delta -\right. \left. \frac{\gamma }{\sqrt{N}} \right] \sin (\theta _{N-1})&\nonumber \\&\quad =:h_2 \end{aligned}$$

(3.4)

where we used the shorthand $\theta _{k}:=k\theta$ for any $k\in \mathbb {R}.$

Proof

By Lemma 3.1, we know that the pressure $\lambda$ exists and system (3.1) is satisfied. Now we just have to verify that (3.1) agrees with the claimed system given by (3.3) and (3.4). We start by verifying the first of the equations in the system (3.1).

Step 1:

That the left-hand side of (3.3) follows from the left-hand side of the first equation in system (3.1) is a straightforward calculation. Hence, we focus on the corresponding right-hand side, which we named $h_1.$ First note that, because M depends only on $\theta$, we are left with

$$\begin{aligned} h_1=-\left[ M_{R\theta (g+g'')\theta }+(M,_\theta )_{R\theta g R}+(M,_\theta )_{R \theta g'\theta }\right] .\end{aligned}$$

(3.5)

We have $g=\frac{1}{\sqrt{N}}e_{NR}, g'=\sqrt{N}e_{N\theta },g''=-N\sqrt{N}e_{NR}$, and hence

$$\begin{aligned}M_{R\theta (g+g'')\theta }=&\left( \frac{1}{\sqrt{N}}-\sqrt{N}N\right) M_{R\theta (NR)\theta }&\\=&\left( \frac{1}{\sqrt{N}}-\sqrt{N}N\right) (M_{R\theta R\theta }(e_{NR}\cdot e_R)+M_{R\theta \theta \theta }(e_{NR}\cdot e_\theta )).&\end{aligned}$$

Using that $M_{R\theta \theta \theta }=0$ and $M_{R\theta R\theta }=\beta$ yields

$$\begin{aligned}M_{R\theta (g+g'')\theta }=\left( \frac{1}{\sqrt{N}}-\sqrt{N}N\right) \beta \cos (\theta _{N-1}).\end{aligned}$$

For the second term of (3.5), consider

$$\begin{aligned}M_{R\theta g R,\theta }=(M,_\theta )_{R\theta g R}+M_{\theta \theta g R}-M_{R R g R}+M_{R\theta g' R}+M_{R\theta g \theta },\end{aligned}$$

which, after a short calculation, gives

$$\begin{aligned} (M,_\theta )_{R\theta g R}=&M_{R\theta g R,\theta }-M_{\theta \theta g R}+M_{R R g R}-M_{R\theta g' R}-M_{R\theta g \theta }&\\ =&\frac{1}{\sqrt{N}}[\alpha -\beta ]\cos (\theta _{N-1}).&\end{aligned}$$

Similarly, for the rightmost term of (3.5) we get

$$\begin{aligned} (M,_\theta )_{R\theta g' \theta }=&M_{R\theta g' \theta ,\theta }-M_{\theta \theta g' \theta }+M_{R R g' \theta }-M_{R\theta g'' \theta }+M_{R\theta g' R}&\\ =&-\sqrt{N}\beta '\sin (\theta _{N-1})+\sqrt{N}[\beta -\delta ]\cos (\theta _{N-1}).&\end{aligned}$$

Together,

$$\begin{aligned}h_1=\sqrt{N}\beta '\sin (\theta _{N-1})+\left[ \sqrt{N}\delta -\frac{\alpha }{\sqrt{N}}+\sqrt{N}(N-1)\beta \right] \cos (\theta _{N-1}).\end{aligned}$$

Step 2:

By arguing similarly, we find that

$$\begin{aligned}h_2=-\left[ M_{\theta \theta (g+g'')\theta }+(M,_\theta )_{\theta \theta g R}+(M,_\theta )_{\theta \theta g'\theta }\right] .\end{aligned}$$

Then

$$\begin{aligned} M_{\theta \theta (g+g'')\theta }=&\left( \frac{1}{\sqrt{N}}-\sqrt{N}N\right) \delta \sin (\theta _{N-1})&\\ (M,_\theta )_{\theta \theta g R}=&M_{\theta \theta g R,\theta }+M_{R \theta g R}+M_{\theta R g R}-M_{\theta \theta g' R}-M_{\theta \theta g \theta }&\\ =&\frac{1}{\sqrt{N}}[\gamma -\delta ]\sin (\theta _{N-1})&\\ (M,_\theta )_{\theta \theta g' \theta }=&M_{\theta \theta g' \theta ,\theta }+M_{R \theta g' \theta }+M_{\theta R g' \theta }-M_{\theta \theta g'' \theta }+M_{\theta \theta g' R}&\\ =&\sqrt{N}\delta '\cos (\theta _{N-1})+\sqrt{N}[\delta -\beta ]\sin (\theta _{N-1})&\end{aligned}$$

and finally

$$\begin{aligned}h_2=-\sqrt{N}\delta '\cos (\theta _{N-1})+\left[ \sqrt{N}\beta +\sqrt{N}(N-1)\delta -\frac{\gamma }{\sqrt{N}}\right] \sin (\theta _{N-1}),\end{aligned}$$

completing the proof.$\square$

Next, we compute the small pressure criteria in the same situation. Moreover, we will provide an explicit form of the pressure.

Lemma 3.3

(Small pressure condition, N-cover, M($\theta$)=diag) Let the assumptions be as above. For any $N\in \mathbb {N}\setminus \{1\},$ let $M=\text {diag}(a,1,a,1)\nu ,$ where we pick a to be constant and in the range

$$\begin{aligned}1\le N^2-N< a < N^2+N.\end{aligned}$$

Then for this M the corresponding pressure $\lambda$ is given by

$$\begin{aligned} \lambda (x)=c+\left[ N-\frac{a}{N}\right] \ln (R) \;\;\text{ for } \text{ any }\;\; x\in B \end{aligned}$$

for any real constant $c\in \mathbb {R},$ which is independent of R and $\theta .$ Moreover, $\lambda \in W^{1,q}(B) \;\;\text{ for } \text{ any }\;\;1\le q<2$ and $\lambda$ satisfies condition (1.11) strictly.

Proof

Define first

$$\begin{aligned}H_1=\left[ \sqrt{N}(N-1)\beta +\sqrt{N}\delta -\frac{\alpha }{\sqrt{N}}\right] ,\; H_2=\left[ \sqrt{N}\beta +\sqrt{N}(N-1)\delta -\frac{\gamma }{\sqrt{N}}\right] .\end{aligned}$$

By solving the system (3.3) and (3.4) we obtain

$$\begin{aligned} \lambda ,_RR=&(\beta '-\delta ')\frac{\sin (2\theta _{N-1})}{2}+\frac{1}{\sqrt{N}}(H_1\cos ^2(\theta _{N-1})+H_2\sin ^2(\theta _{N-1}))&\\ \lambda ,_\theta =&\sqrt{N}(H_2-H_1)\frac{\sin (2\theta _{N-1})}{2}-N(\beta '\sin ^2(\theta _{N-1})+\delta '\cos ^2(\theta _{N-1})).&\end{aligned}$$

For the specific case of $M=\text {diag}(a,1,a,1)\nu$ they become

$$\begin{aligned} \lambda ,_RR=\left[ N-\frac{a}{N}\right] \;\;\text{ and }\;\;\lambda ,_\theta =0 \end{aligned}$$

showing, in particular, that $\lambda$ depends only on R i.e. $\lambda (x)=\lambda (R).$ Indeed, the pressure is then given by

$$\begin{aligned} \lambda (x)=c+\left[ N-\frac{a}{N}\right] \ln (R) \;\;\text{ for } \text{ any }\;\; x\in B \end{aligned}$$

and for any real constant $c\in \mathbb {R},$ which is independent of R and $\theta .$ The small pressure condition of Corollary 2.3 can now be applied, giving

$$\begin{aligned} \left| N-\frac{a}{N}\right| <1. \end{aligned}$$

Solving this inequality by case distinction yields the claimed bounds on a. The integrability is then easily deduced, completing the proof.$\square$

To make it more accessible for the reader we collect what we have shown so far in the following.

Proof of Theorem 1.3

(i), (ii), and (vi) trivial.

• (iii) It is enough to show this point for M. Note, that M only depends on $\theta ,$ i.e. $M(x)=M(\theta ).$ Hence, the gradient is given by

  $$\begin{aligned} \nabla M=\frac{1}{R}\partial _\theta M(\theta )\otimes e_\theta \;\;\text{ for } \text{ any }\;\; x\in B\setminus \{0\}.\end{aligned}$$

  (3.6)

  First realise that the derivative with respect to $\theta$ only replaces $e_R$ with $e_\theta$ (up to sign) and vice versa, and therefore one can still bound the modulus of $\Vert \partial _\theta M(\theta )\Vert _{L^\infty (B,\mathbb {R}^{16})}\le C(a)$ via some real constant $C(a)>0$. Then, by integrating $|\nabla M|^q$ with respect to dx using (3.6) and by the latter discussion, the claim follows.

• (iv) As a consequence of $g\in C^\infty$ and point (iii), Lemma 3.2 guarantees that u is a stationary point and the existence of $\lambda$ in the right spaces.

• (v) By Lemma 3.3 we know that $\lambda$ satisfies the small pressure criteria strictly. Together with Theorem 1.2, this implies that $u=u_{_{\small {N}}}$ is indeed the unique global minimizer of the energy E. $\square$

Remark 3.4

(i) To summarize the foregoing analysis, we have shown that for the full ball $B\subset \mathbb {R}^2$ and smooth boundary conditions, albeit with a topological change, there is a uniformly convex functional, which depends discontinuously on x,  but smoothly on $\nabla u,$ such that the corresponding energy is uniquely globally minimised by a map that is Lipschitz but not $C^1(B)$.

(ii) One might also be interested in this counterexample on the scale of Sobolev spaces. With this in mind, note that for any $N\in \mathbb {N}\setminus \{1\}$ we have⁹

$$\begin{aligned}u=\frac{R}{\sqrt{N}}e_{NR}\in W^{2,q}(B,\mathbb {R}^2)\setminus W^{2,2}(B,\mathbb {R}^2) \;\;\text{ for } \text{ any }\;\;1\le q<2.\end{aligned}$$

Moreover, one might like to compare our result with the high-order regularity result, given in [2]. They showed that for the special case of the Dirichlet functional and $u\in W^{2,q}(B,\mathbb {R}^2)$ with $q>2$ being a stationary point satisfying $\det \nabla u=1$ a.e., then $u\in C^\infty (B,\mathbb {R}^2).$ It is possible that a similar result could be established, for a fairly general non-autonomous $p-$growth functional with the necessary changes in q. Assuming that such a result is indeed possible, this seems to leave a ‘gap’ at $q=2.$

(iii) The singular set $\Sigma$ in our example is, of course, just the origin $\Sigma =\{0\}.$ It remains an open question whether there can be other incompressible variational problems, including in incompressible elasticity, where the stationary points/minimizers possess a richer $\Sigma .$