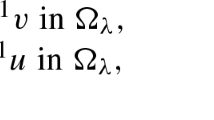Multiplicity results for Hamiltonian systems with Neumann-type boundary conditions

Abstract

We prove some multiplicity results for Neumann-type boundary value problems associated with a Hamiltonian system. Such a system can be seen as the weak coupling of two systems, the first of which has some periodicity properties in the Hamiltonian function, the second one presenting the existence of a well-ordered pair of lower/upper solutions.

1 Introduction

In the recent paper [12], the first author jointly with R. Ortega have obtained a multiplicity result for a two-point boundary value problem associated with a Hamiltonian system in ${\mathbb {R}}^{2N}$. For simplicity in the exposition, let us recall their result for a planar system

$$\begin{aligned} x'=\partial _{y}H(t,x,y),\qquad y'=-\partial _{x}H(t,x,y), \end{aligned}$$

(1)

with Neumann-type boundary conditions

$$\begin{aligned} y(a)=0=y(b). \end{aligned}$$

(2)

Theorem 1

(Fonda–Ortega [12]) Let $H:[a,b]\times {\mathbb {R}}^{2}\rightarrow {\mathbb {R}}$ be a continuous function with continuous partial derivatives with respect to x and y. Assume moreover that H is $\tau$-periodic with respect to x, for some $\tau >0$, and that all solutions of (1) starting with $y(a)=0$ are defined on [a, b]. Then, problem (1)-(2) has at least two geometrically distinct solutions.

Let us take a moment to explain what we mean by geometrically distinct solutions. In view of the $\tau$-periodicity of H in the x-variable, we can define an equivalence relation in $C^1([a,b])\times C^1([a,b])$ as follows:

$$\begin{aligned} (x,y)\sim ({{\hat{x}}},{{\hat{y}}})\quad \Leftrightarrow \quad x-{{\hat{x}}}\in \tau {\mathbb {Z}}. \end{aligned}$$

We say that two solutions (x, y) and $({{\hat{x}}},{{\hat{y}}})$ of (1) are geometrically distinct if they do not belong to the same equivalence class.

There are some similarities between Theorem 1 and the Poincaré–Birkhoff Theorem for the periodic problem associated with the Hamiltonian system (1). However, it is well known that the periodic problem requires an additional assumption, the so-called twist condition. Different versions of it have been proposed (see e.g. [16] for a deeper insight on this topic). Conversely, in the case of the Neumann-type boundary conditions (2), it has been shown in [12] that multiplicity results can be achieved without assuming any twist condition.

Although the Neumann problem for scalar second order equations has been widely studied, there are only few papers in the literature proving multiplicity results for Neumann-type problems associated with systems of ordinary differential equations. See, e.g., [2, 21].

We now consider a four-dimensional system of the form

$$\begin{aligned} {\left\{ \begin{array}{ll} x'=\partial _{y}H(t,x,y)+\varepsilon \partial _{y}P(t,x,y,u,v),\\ y'=-\partial _{x}H(t,x,y)-\varepsilon \partial _{x}P(t,x,y,u,v),\\ u'=f(t,\,v)+\varepsilon \partial _{v}P(t,x,y,u,v),\\ v'=g(t,\,u)-\varepsilon \partial _{u}P(t,x,y,u,v), \end{array}\right. } \end{aligned}$$

(3)

with Neumann-type boundary conditions

$$\begin{aligned} {\left\{ \begin{array}{ll} y(a)=0=y(b),\\ v(a)=0=v(b). \end{array}\right. } \end{aligned}$$

(4)

Here $H:[a,b]\times {\mathbb {R}}^{2}\rightarrow {\mathbb {R}}$ and $P:[a,b]\times {\mathbb {R}}^4\rightarrow {\mathbb {R}}$ are continuous functions, with continuous partial derivatives with respect to the variables x, y, u, v ; the functions $f:[a,b]\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ and $g:[a,b]\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ are continuous, and $\varepsilon$ is a small real parameter.

When $\varepsilon =0$, problem (3)–(4) decouples into two planar problems, the first one being (1)–(2), the second one being

$$\begin{aligned} u'=f(t,v),\qquad v'=g(t,u), \end{aligned}$$

(5)

with the boundary conditions

$$\begin{aligned} v(a)=0=v(b). \end{aligned}$$

(6)

Concerning problem (5)–(6), we will assume the existence of a pair of strict well-ordered lower/upper solutions, the definition of which will be recalled in Sect. 2.

Besides the regularity hypotheses stated above, here is the list of our assumptions.

(A1):

The function $H=H(t,x,y)$ is $\tau$-periodic in the variable x, for some $\tau >0$ .

(A2):

All solutions (x, y) of (1) starting with $y(a)=0$ are defined on [a, b] .

(A3):

The function $P=P(t,x,y,u,v)$ is $\tau$-periodic in the variable x .

(A4):

The function $P=P(t,x,y,u,v)$ has a bounded gradient with respect to $z=(x,y,u,v)$, i.e., there exists $C>0$ such that

$$\begin{aligned} |\nabla _{z} P(t,z)|\le C\quad \hbox {for every }\,(t,z)\in [a,b]\times {\mathbb {R}}^4. \end{aligned}$$

(A5):

There exist a strict lower solution $\alpha$ and a strict upper solution $\beta$ for problem (5)-(6) such that $\alpha \le \beta$ .

(A6):

The function f has continuous partial derivative with respect to the variable v and there exists $\lambda >0$ such that

$$\begin{aligned} \partial _{v}f(t,\,v)\ge \lambda ,\hbox { for every }(t,v)\in [a,b]\times {\mathbb {R}}. \end{aligned}$$

(A7):

$\partial _{v}P$ is independent of x and y, and locally Lipschitz continuous in v.

Let us state our main result.

Theorem 2

Let assumptions $(A1)-(A7)$ hold true. Then, there exists $\overline{\varepsilon }>0$ such that, when $|\varepsilon |\le \overline{\varepsilon }$, problem (3)–(4) has at least two solutions (x, y, u, v) with $\alpha \le u\le \beta$.

The proof is provided in Sect. 3. It relies on a Theorem by Szulkin [23], which can be seen as an infinite-dimensional extension of the classical Lusternik–Schnirelmann theory on the multiplicity of critical points.

Theorem 2 is the counterpart of the main result in [15] for the periodic problem associated with system (3). In that paper, a further twist condition was needed in order to apply an extension of the Poincaré–Birkhoff Theorem due to the first author and P. Gidoni [7]. Surprisingly enough, in Theorem 2, as for Theorem 1, no twist condition is needed.

In Sects. 4 and 5 we will extend Theorem 2 to higher dimensions. An analogue of system (3) will be considered in ${\mathbb {R}}^{2M}\times {\mathbb {R}}^{2L}$, assuming periodicity in the variables $x_1,\dots ,x_M$. We will obtain the existence of at least $M+1$ solutions to the related Neumann-type boundary value problem assuming either the existence of a pair of well-ordered vector valued lower/upper solutions (in Sect. 4), or a Hartman-type condition (in Sect. 5).

2 Lower and upper solutions

Let us recall the definitions of lower and upper solutions for planar systems (cf. [9, 13, 14]).

Definition 3

A $C^{1}$-function $\alpha :[a,b]\rightarrow {\mathbb {R}}$ is a lower solution for problem (5)–(6) if there exists a $C^{1}$-function $v_{\alpha }:[a,b]\rightarrow {\mathbb {R}}$ such that, for every $t\in [a,b]$,

$$\begin{aligned}{} & {} {\left\{ \begin{array}{ll} v<v_{\alpha }(t)\quad \Rightarrow \quad f(t,\,v)<\alpha '(t),\\ v>v_{\alpha }(t) \quad \Rightarrow \quad f(t,\,v)>\alpha ' (t), \end{array}\right. } \end{aligned}$$

(7)

$$\begin{aligned}{} & {} v_{\alpha }'(t) \ge g(t,\,\alpha (t)), \end{aligned}$$

(8)

and

$$\begin{aligned} v_{\alpha }(a)\ge 0\ge v_{\alpha }(b). \end{aligned}$$

The lower solution $\alpha$ is strict if the strict inequality holds in (8), for every $t\in [a,b]$.

Definition 4

A $C^{1}$-function $\beta :[a,b]\rightarrow {\mathbb {R}}$ is an upper solution for problem (5)–(6) if there exists a $C^{1}$-function $v_{\beta }:[a,b]\rightarrow {\mathbb {R}}$ such that, for every $t\in [a,b]$,

$$\begin{aligned}{} & {} {\left\{ \begin{array}{ll} v<v_{\beta }(t) \quad \Rightarrow \quad f(t,\,v)<\beta '(t),\\ v>v_{\beta }(t) \quad \Rightarrow \quad f(t,\,v)>\beta '(t), \end{array}\right. } \end{aligned}$$

(9)

$$\begin{aligned}{} & {} v_\beta '(t) \le g(t,\,\beta (t)), \end{aligned}$$

(10)

and

$$\begin{aligned} v_{\beta }(a)\le 0\le v_{\beta }(b). \end{aligned}$$

The upper solution $\beta$ is strict if the strict inequality holds in (10), for every $t\in [a,b]$.

We will consider the case when the pair of lower/upper solutions is well-ordered, i.e., such that $\alpha \le \beta$. For an intuitive meaning of the previous definitions, see Fig. 1.

Fig. 1

A visual illustration of hypotheses (7) and (9) from a dynamical point of view. Horizontal arrows represent the relative velocity $u'$ of solutions of system (5) compared with $\alpha '$ and $\beta '$. The trajectories enter or exit the grey regions through the vertical lines depending on the direction of the arrows. Notice that dashed lines may move in time

Let us recall the following consequence of [13, Corollary 10].

Theorem 5

Let assumption (A6) hold true. If $\alpha ,\beta$ is a well-ordered pair of lower/upper solutions for problem (5)–(6), then there exists a solution (u, v) of (5)–(6) such that $\alpha \le u\le \beta$.

Remark 6

As an immediate consequence of (7) and (9) we have, respectively,

$$\begin{aligned} f(t,v_{\alpha }(t))=\alpha '(t),\qquad f(t,v_{\beta }(t))=\beta '(t), \end{aligned}$$

(11)

for every $t\in [a,b]$. In view of Assumption (A6), these identities uniquely determine the functions $v_\alpha$ and $v_\beta$.

Remark 7

In the case when $f(t,v)=v$, problem (5)–(6) is equivalent to the Neumann problem

$$\begin{aligned} {\left\{ \begin{array}{ll} u''=g(t,u),\\ u'(a)=0=u'(b). \end{array}\right. } \end{aligned}$$

In such a case a lower solution $\alpha$ will satisfy the usual conditions

$$\begin{aligned} {\left\{ \begin{array}{ll} \alpha ''(t)\ge g(t,\alpha (t)),\\ \alpha '(a)\ge 0\ge \alpha '(b), \end{array}\right. } \end{aligned}$$

while for an upper solution $\beta$ we will have

$$\begin{aligned} {\left\{ \begin{array}{ll} \beta ''(t)\le g(t,\beta (t)),\\ \beta '(a)\le 0\le \beta '(b). \end{array}\right. } \end{aligned}$$

Indeed, in this case it is sufficient to choose $v_\alpha =\alpha '$ and $v_\beta =\beta '$. These are the classical definitions of lower/upper solutions dating back to the pioneering works [19, 20, 22] (for a historical account, see [3]).

3 The proof of Theorem 2

In this section we will prove Theorem 2. Precisely, in Sect. 3.1 we modify the problem and provide some useful lemmas. Then, in Sect. 3.2, we define the function spaces where the variational problem will be settled. In Sects. 3.3 and 3.4 we introduce the functional whose critical points correspond to the solutions of the modified problem, the existence of which will follow from the application of a theorem by Szulkin. Finally, we will show that such solutions are indeed solutions of the original problem.

Without loss of generality, from now on, we will assume $[a,b]=[0,\pi ]$. Moreover, it is not restrictive to look for $\overline{\varepsilon }$ in $\,]0,1]$.

3.1 Some preliminaries

In this section we provide some preliminary tools which will be useful for proving the main result. First of all we remark that, since the inequalities in (8) and (10) are assumed to be strict, by continuity there exists a ${{\bar{\delta }}}>0$ such that, if $0<\delta \le {{\bar{\delta }}}$, then $\alpha (t)+\delta$ and $\beta (t)-\delta$ are still a well-ordered pair of lower/upper solutions for problem (5)–(6), with the same associated functions $v_\alpha$ and $v_\beta$. In what follows we replace $\alpha (t)$ with $\alpha (t)+\delta$ and $\beta (t)$ with $\beta (t)-\delta$.

Before stating the next lemma, we recall that, by assumption (A7), the function $\partial _{v}P$ does not depend on x and y.

Lemma 8

For every $\varepsilon \in {\mathbb {R}}$ there exist some $C^1$-functions $\alpha _\varepsilon$ and $\beta _\varepsilon$ such that

(i):

$f(t,v_{\alpha }(t))+\varepsilon \partial _{v}P(t,\alpha _\varepsilon (t),v_\alpha (t))=\alpha _{\varepsilon }'(t)$ ,

(ii):

$f(t,v_{\beta }(t))+\varepsilon \partial _{v}P(t,\beta _\varepsilon (t),v_\beta (t))=\beta _{\varepsilon }^{'}(t)$ ,

(iii):

$|\alpha _{\varepsilon }(t)-\alpha (t)|<\varepsilon C\pi$, and $|\beta _{\varepsilon }(t)-\beta (t)|<\varepsilon C\pi$ ,

for every $t\in [0,\,\pi ]$, where the constant C is defined in assumption (A4).

Proof

Let $\Gamma :[0,\pi ]\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ be the continuous function defined by

$$\begin{aligned} \Gamma (t,w)=\partial _{v}P(t,\alpha (t)+w,v_\alpha (t)), \end{aligned}$$

and let $w_{\varepsilon }:[0,\pi ]\rightarrow {\mathbb {R}}$ be a solution of the Cauchy problem

$$\begin{aligned} {\left\{ \begin{array}{ll} w'=\varepsilon \,\Gamma (t,w),\\ w(0)=0. \end{array}\right. } \end{aligned}$$

Define

$$\begin{aligned} \alpha _{\varepsilon }(t)=\alpha (t)+w_{\varepsilon }(t). \end{aligned}$$

Then, recalling (11), we get

$$\begin{aligned} f(t,v_{\alpha }(t))+\varepsilon \partial _{v}P(t,\alpha _\varepsilon (t),v_\alpha (t))=\alpha '(t)+w_{\varepsilon }'(t)= \alpha _\varepsilon '(t), \end{aligned}$$

so that (i) is proved. Notice that

$$\begin{aligned} |\Gamma (t,w)|\le C,\quad \hbox { for every }(t,w)\in [0,\pi ]\times {\mathbb {R}}, \end{aligned}$$

with the constant C provided by (A4). Hence, $|w_{\varepsilon }(t)|\le \varepsilon C\pi$, for every $t\in [0,\pi ]$, thus proving the first part of (iii). An analogous argument applies for proving the existence of the function $\beta _\varepsilon$ satisfying (ii) and its property in (iii).

$\square$

Remark 9

Lemma 8 above is the analogue of [15, Lemma 3.1]. We observe however that in [15] a different approach was chosen, i.e., the functions $\alpha$ and $\beta$ were kept the same for every $\varepsilon$, while $v_\alpha$ and $v_\beta$ varied. Our approach here permits to avoid some regularity assumptions needed in [15].

Here after, we are going to modify system (3). Set

$$\begin{aligned} A=\min \alpha ,\qquad B=\max \beta , \end{aligned}$$

$$\begin{aligned} M=\max \{|g(t,s)|:\,t\in [0,\,\pi ],\,s\in [A-1,B+1] \}, \end{aligned}$$

(12)

and choose

$$\begin{aligned} d\ge \max \{(M+1)\pi ,\, ||v_{\alpha }||_{\infty },\,||v_{\beta }||_{\infty }\}+1. \end{aligned}$$

(13)

We define ${\tilde{f}}:[0,\,\pi ]\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ by

$$\begin{aligned} {\tilde{f}}(t,\,v)=f(t,\,\gamma (v))+v-\gamma (v), \end{aligned}$$

(14)

where

$$\begin{aligned} \gamma (v)={\left\{ \begin{array}{ll} -d,&{}\quad \hbox {if}\,\,v\le -d,\\ v,&{}\quad \hbox {if}\,\,|v|\le d,\\ d,&{}\quad \hbox {if}\,\,v\ge d, \end{array}\right. } \end{aligned}$$

and ${\tilde{g}}_{\varepsilon }:[0,\,\pi ]\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ by

$$\begin{aligned} {\tilde{g}}_{\varepsilon }(t,u)=g(t,\eta _{\varepsilon }(t,u))-\eta _{\varepsilon }(t,u)+u, \end{aligned}$$

where

$$\begin{aligned} \eta _{\varepsilon }(t,u)={\left\{ \begin{array}{ll} \alpha _{\varepsilon }(t),&{}\quad \hbox {if}\,\,u\le \alpha _{\varepsilon }(t),\\ u,&{}\quad \hbox {if}\,\,\alpha _{\varepsilon }(t)\le u\le \beta _{\varepsilon }(t),\\ \beta _{\varepsilon }(t),&{}\quad \hbox {if}\,\,u\ge \beta _{\varepsilon }(t). \end{array}\right. } \end{aligned}$$

In the above definition, $\alpha _\varepsilon$ and $\beta _\varepsilon$ are the functions introduced in Lemma 8.

Concerning the function H, by assumption (A2) there exists a constant $D>0$ such that every solution (x, y) of the system (1), starting with $y(0)=0$, satisfies

$$\begin{aligned} |y(t)|\le D,\quad \hbox {for every } t\in [0,\pi ], \end{aligned}$$

(15)

(see e.g. [5]). Let $\zeta :{\mathbb {R}}\rightarrow {\mathbb {R}}$ be a $C^{\infty }$-function such that

$$\begin{aligned} \zeta (y)={\left\{ \begin{array}{ll} 1,&{}\quad \hbox {if}\,\,|y|\le D+1,\\ 0,&{}\quad \hbox {if}\,\,|y|\ge D+2. \end{array}\right. } \end{aligned}$$

(16)

Then consider the function ${\widetilde{H}}:[0,\pi ]\times {\mathbb {R}}^{2}\rightarrow {\mathbb {R}}$ defined as

$$\begin{aligned} {\widetilde{H}}(t,x,y)=\zeta (y)H(t,x,y), \end{aligned}$$

so that the partial derivatives of ${\widetilde{H}}(t,x,y)$ with respect to x and y are bounded.

We can now introduce the modified system

$$\begin{aligned} {\left\{ \begin{array}{ll} x'=\partial _{y}{\widetilde{H}}(t,x,y)+\varepsilon \partial _{y}P(t,x,y,u,v),\\ y'=-\partial _{x}{\widetilde{H}}(t,x,y)-\varepsilon \partial _{x}P(t,x,y,u,v),\\ u'={\tilde{f}}(t,\,v)+\varepsilon \partial _{v}P(t,x,y,u,v),\\ v'={\tilde{g}}_{\varepsilon }(t,u)-\varepsilon \partial _{u}P(t,x,y,u,v), \end{array}\right. } \end{aligned}$$

(17)

which can also be written as

$$\begin{aligned} {\left\{ \begin{array}{ll} x'=\partial _{y}{\widetilde{K}}_\varepsilon (t,x,y,u,v),\\ y'=-\partial _{x}{\widetilde{K}}_\varepsilon (t,x,y,u,v),\\ u'=v + \partial _{v}{\widetilde{K}}_\varepsilon (t,x,y,u,v),\\ v'=u- \partial _{u}{\widetilde{K}}_\varepsilon (t,x,y,u,v), \end{array}\right. } \end{aligned}$$

(18)

where

$$\begin{aligned} {\widetilde{K}}_\varepsilon (t,x,y,u,v)&= {{\widetilde{H}}}(t,x,y) - G_\varepsilon (t,u) + F(t,v) +\varepsilon P(t,x,y,u,v) \,, \nonumber \\ \text {with } F(t,v)&=\int _0^v \big ({{\tilde{f}}}(t,s)-s \big )\, ds\,, \;G_\varepsilon (t,u)= \int _0^u \big ({{\tilde{g}}}_\varepsilon (t,\sigma )-\sigma \big )\, d\sigma \,. \end{aligned}$$

(19)

We will prove that, for $|\varepsilon |$ small enough, the modified problem (17)–(4) has at least two geometrically distinct solutions. These solutions will indeed be the solutions of the original problem (3)–(4) we are looking for. In order to show this, we first need to prove some preliminary lemmas.

Lemma 10

There exists $\overline{\varepsilon }>0$ such that, if (x, y, u, v) is a solution of problem (17)–(4), with $|\varepsilon |\le \overline{\varepsilon }$, then $|y(t)|\le D+1$, for every $t\in [0,\pi ]$.

Proof

Assume, by contradiction, that, for all $n\ge 1$, there exists a solution $(x_n,y_n,u_n,v_n)$ of problem (17)–(4), with $\varepsilon =1/n$, satisfying $\Vert y_n\Vert _\infty > D+1$.

By the periodicity of ${{\widetilde{H}}}$ and P in the variable x we can assume without loss of generality that $x_n(0)\in [0,\tau ]$ for every n. Moreover, since, ${{\widetilde{H}}}$ and P have bounded gradients, the sequences $(x_n)_n$ and $(y_n)_n$ are uniformly bounded, together with their derivatives, hence, by the Ascoli–Arzelà Theorem, they uniformly converge, up to a subsequence, to some functions $x_0$ and $y_0$, respectively. We can write

$$\begin{aligned} x_n(t){} & {} =x_n(0)+\int _0^t \Big ( \partial _{y}{\widetilde{H}}(s,x_n(s),y_n(s)) \\{} & {} \quad +\,\tfrac{1}{n} \partial _{y}P(s,x_n(s),y_n(s),u_n(s),v_n(s))\Big )\, ds\,, \end{aligned}$$

and

$$\begin{aligned} y_n(t)=\int _0^t \Big (-\partial _{x}{\widetilde{H}}(s,x_n(s),y_n(s))-\tfrac{1}{n} \partial _{x}P(s,x_n(s),y_n(s),u_n(s),v_n(s))\Big )\, ds\,. \end{aligned}$$

The functions in the integrals are bounded, hence by the dominated convergence theorem we can take the limits and obtain

$$\begin{aligned} x_0(t)&=x_0(0)+\int _0^t \partial _{y} {\widetilde{H}}(s,x_0(s),y_0(s))\, ds\,,\\ y_0(t)&=\int _0^t -\partial _{x}{\widetilde{H}}(s,x_0(s),y_0(s))\, ds\,. \end{aligned}$$

Therefore, $(x_0,y_0)$ is a solution of system (1), with H replaced by ${{\widetilde{H}}}$, starting with $y_0(0)=0$, satisfying $\Vert y_0\Vert _\infty \ge D+1$. Such a solution will solve the original system (1) on some maximal interval $[0,\omega ]\subseteq [0,\pi ]$. By the estimate in (15), it has to be $\omega =\pi$ and $\Vert y_0\Vert _\infty \le D$, a contradiction. $\square$

In what follows we will always assume $0< \overline{\varepsilon }\le \frac{1}{C\pi }$, where the constant C is the one introduced in assumption (A4).

Lemma 11

Reducing if necessary the constant $\overline{\varepsilon }$, if $|\varepsilon |\le \overline{\varepsilon }$, then,

$$\begin{aligned}{} & {} {\left\{ \begin{array}{ll} v<v_{\alpha }(t) \quad \Rightarrow \quad {\tilde{f}}(t,v)+\varepsilon \partial _{v}P(t,\alpha _\varepsilon (t),v)<\alpha _{\varepsilon }'(t),\\ v>v_{\alpha }(t) \quad \Rightarrow \quad {\tilde{f}}(t,v)+\varepsilon \partial _{v}P(t,\alpha _\varepsilon (t),v)>\alpha _{\varepsilon }'(t), \end{array}\right. } \end{aligned}$$

(20)

$$\begin{aligned}{} & {} {\left\{ \begin{array}{ll} v<v_{\beta }(t) \quad \Rightarrow \quad {\tilde{f}}(t,v)+\varepsilon \partial _{v}P(t,\beta _\varepsilon (t),v)<\beta _{\varepsilon }'(t),\\ v>v_{\beta }(t) \quad \Rightarrow \quad {\tilde{f}}(t,v)+\varepsilon \partial _{v}P(t,\beta _\varepsilon (t),v)>\beta _{\varepsilon }'(t), \end{array}\right. } \end{aligned}$$

(21)

$$\begin{aligned}{} & {} {\left\{ \begin{array}{ll} v_{\alpha }'(t)>{\tilde{g}}_{\varepsilon }(t,\alpha _{\varepsilon }(t))-\varepsilon \partial _{u}P(t,x,y,\alpha _{\varepsilon }(t),v_{\alpha }(t)),\\ v_{\beta }'(t)<{\tilde{g}}_{\varepsilon }(t,\beta _{\varepsilon }(t))-\varepsilon \partial _{u}P(t,x,y,\beta _{\varepsilon }(t),v_{\beta }(t)), \end{array}\right. } \end{aligned}$$

(22)

for every $(t,x,y,v)\in [0,\pi ]\times {\mathbb {R}}^{3}$.

Proof

We start by proving the second inequality in (20). Fix $t\in [0,\pi ]$, and assume $v>v_{\alpha }(t)$. We need to consider two cases: the first when $v_{\alpha }(t)<v<d$, and the second when $v\ge d$.

Case 1 : $v_{\alpha }(t)<v<d$. Using in the order (14), Lemma 8(i), assumptions (A6) and (A4), we get

$$\begin{aligned} {\tilde{f}}(t,v)&+\varepsilon \partial _{v}P(t,\alpha _\varepsilon (t),v)-\alpha _{\varepsilon }'(t)\\&=f(t,v)+\varepsilon \partial _{v}P(t,\alpha _\varepsilon (t),v)-\alpha _{\varepsilon }'(t)\\&=f(t,v)-f(t,v_\alpha (t))+\varepsilon [\partial _{v}P(t,\alpha _\varepsilon (t),v)-\partial _{v}P(t,\alpha _\varepsilon (t),v_\alpha (t))]\\&\ge \lambda (v-v_\alpha (t))-2C|\varepsilon |\,. \end{aligned}$$

If $v-v_{\alpha }(t)>\frac{2}{\lambda }\ge \frac{2C|\varepsilon |}{\lambda }$, then

$$\begin{aligned} \lambda (v-v_\alpha (t))-2C|\varepsilon | >0. \end{aligned}$$

Conversely, if $0<v-v_{\alpha }(t)\le \frac{2}{\lambda }$ , then by assumption (A7) we get

$$\begin{aligned} {\tilde{f}}(t,v)+\varepsilon \partial _{v}P(t,\alpha _\varepsilon (t),v)-\alpha _{\varepsilon }'(t)\ge \lambda (v-v_\alpha (t))-|\varepsilon |{\widetilde{C}}(v-v_{\alpha }(t)), \end{aligned}$$

where ${\widetilde{C}}$ is the Lipschitz constant such that

$$\begin{aligned} |\partial _{v}P(t,u,v)-\partial _{v}P(t,u,v_{\alpha }(t))|\le {\widetilde{C}}|v-v_{\alpha }(t)|, \end{aligned}$$

for every $(t,u)\in [0,\pi ]\times [A-1,B+1]$. Choosing $|\varepsilon |<\lambda /{\widetilde{C}}$, we get

$$\begin{aligned} f(t,v)+\varepsilon \partial _{v}P(t,\alpha _\varepsilon (t),v)-\alpha _{\varepsilon }'(t)>0. \end{aligned}$$

Case 2 : $v\ge d$. Similarly as above, if $|\varepsilon |$ is small enough, we get

$$\begin{aligned} {\tilde{f}}(t,v)&+\varepsilon \partial _{v}P(t,\alpha _\varepsilon (t),v)-\alpha _{\varepsilon }'(t)\\&=f(t,d)+(v-d)+\varepsilon \partial _{v}P(t,\alpha _\varepsilon (t),v)-\alpha _{\varepsilon }'(t)\\&\ge f(t,d)-f(t,v_\alpha (t))+\varepsilon [\partial _{v}P(t,\alpha _\varepsilon (t),v)-\partial _{v}P(t,\alpha _\varepsilon (t),v_\alpha (t))]\\&\ge \lambda (d-v_\alpha (t))-2C|\varepsilon |\ge \lambda -2C|\varepsilon |>0\,, \end{aligned}$$

completing the proof of the second inequality in (20).

The proofs of the first inequality in (20) and of the two inequalities in (21) are carried out similarly.

We now establish the first inequality in (22), a similar argument holding for the proof of the latter. Recalling (8) and the fact that $\alpha$ is a strict lower solution, let $\overline{e}>0$ be such that

$$\begin{aligned} v_{\alpha }'(t)-g(t,\alpha (t))> 2 \,\overline{e}> 0,\quad \,\hbox {for every }\,t\in [0,\pi ]. \end{aligned}$$

(23)

Reducing $\overline{\varepsilon }$ if necessary, recalling (iii) in Lemma 8, by the continuity of g we have

$$\begin{aligned} |g(t,\alpha (t))-{\tilde{g}}_{\varepsilon }(t,\alpha _{\varepsilon }(t))|=|g(t,\alpha (t))-g(t,\alpha _{\varepsilon }(t))|<\overline{e}, \end{aligned}$$

(24)

when $|\varepsilon |\le \overline{\varepsilon }$. Combining (23) and (24), we obtain

$$\begin{aligned} v_{\alpha }'(t)-{\tilde{g}}_{\varepsilon }(t,\alpha _{\varepsilon }(t))=v_{\alpha }'(t)-g(t,\alpha (t))+g(t,\alpha (t))-{\tilde{g}}_{\varepsilon }(t,\alpha (t))>\overline{e}, \end{aligned}$$

for all $t\in [0,\pi ]$. So, for $|\varepsilon |$ sufficiently small,

$$\begin{aligned} v_{\alpha }'(t)-{\tilde{g}}_{\varepsilon }(t,\alpha _{\varepsilon }(t))+\varepsilon \partial _{u}P(t,x,y,\alpha _{\varepsilon }(t),v_{\alpha }(t))> \overline{e} - |\varepsilon |C>0, \end{aligned}$$

thus completing the proof. $\square$

Let us fix now $\varepsilon$ satisfying $|\varepsilon |\le \overline{\varepsilon }$. We define some open sets in the space $[0,\,\pi ]\times {\mathbb {R}}^2$ and study some invariance properties of them with respect to the solutions of system (17). We set (see Fig. 2)

$$\begin{aligned} A_{NE}&=\lbrace (t,u,v):t\in [0,\pi ]\,,\quad u>\beta _{\varepsilon }(t)\,, v>v_{\beta }(t)\rbrace \,,\, \\ A_{SE}&=\lbrace (t,u,v):t\in [0,\pi ]\,,\quad u>\beta _{\varepsilon }(t),\,v<v_{\beta }(t)\rbrace \,,\\ A_{SW}&=\lbrace (t,u,v):t\in [0,\pi ]\,,\quad u<\alpha _{\varepsilon }(t),\, v<v_{\alpha }(t)\rbrace \,,\\ A_{NW}&=\lbrace (t,u,v):t\in [0,\pi ]\,,\quad u<\alpha _{\varepsilon }(t),\, v>v_{\alpha }(t)\rbrace \,. \end{aligned}$$

The following three lemmas are consequences of Lemma 11. We avoid giving the detailed proofs as they essentially follow the arguments in [13]; see also [8, 9, 15].

Lemma 12

Let (x, y, u, v) be a solution of (17) defined at a point $t_0\in [0,\pi ]$. We have:

(i):

if $(t_0,u(t_0),v(t_0))\in A_{NE}\,$, then $(t,u(t),v(t))\in A_{NE}$ for all $t>t_0;$

(ii):

if $(t_0,u(t_0),v(t_0))\in A_{SE}\,$, then $(t,u(t),v(t))\in A_{SE}$ for all $t<t_0;$

(iii):

if $(t_0,u(t_0),v(t_0))\in A_{SW\,}$, then $(t,u(t),v(t))\in A_{SW}$ for all $t>t_0;$

(iv):

if $(t_0,u(t_0),v(t_0))\in A_{NW}\,$, then $(t,u(t),v(t))\in A_{NW}$ for all $t<t_0$ .

Lemma 13

Let (x, y, u, v) be a solution of (17) defined at a point $t_0\in [0,\pi ]$. We have:

(i):

if $u(t_0)>\beta _\varepsilon (t_0)$ and $v(t_0)=v_\beta (t_0)$, then $v'(t_0)>v_\beta '(t_0)\,;$

(ii):

if $u(t_0)<\alpha _\varepsilon (t_0)$ and $v(t_0)=v_\alpha (t_0)$, then $v'(t_0)<v_\alpha '(t_0)$ .

Fig. 2

An illustrative picture of Lemmas 12 and 13. Trajectories of (17) enter or exit the regions depending on the direction of the arrows

Lemma 14

Let (x, y, u, v) be a solution of problem (17)-(4). Then, $\alpha _\varepsilon (t) \le u(t)\le \beta _\varepsilon (t)$, for every $t\in [0,\pi ]$.

By Lemma 10, the definition of M in (12), and the choice $\overline{\varepsilon }\le \frac{1}{C\pi }$, we can finally state the following a priori bound (Fig. 2).

Proposition 15

Let (x, y, u, v) be a solution of problem (17)–(4). Then,

$$\begin{aligned} \alpha _\varepsilon (t) \le u(t) \le \beta _\varepsilon (t),\qquad |v(t)|\le (M+1)\pi , \qquad |y(t)|\le D+1, \end{aligned}$$

for every $t\in [0,\pi ]$. As a consequence, (x, y, u, v) is also a solution of problem (3)–(4).

Recalling now the preliminary remark at the beginning of this subsection, going back to the original lower and upper solutions $\alpha$ and $\beta$, by (iii) in Lemma 8 we can conclude that, if $\varepsilon C\pi \le \delta$, then $\alpha \le u\le \beta$.

3.2 The function spaces

In this section we provide the functional spaces needed in our variational setting. We refer to [12] for a detailed exposition.

For any $\mu \in \,]0,1[$ , we define $X_{\mu }$ as the set of those real valued functions ${\tilde{x}}\in L^{2}(0,\pi )$ such that

$$\begin{aligned} {\tilde{x}}(t)\sim \sum \limits _{m=1}^{\infty }{\tilde{x}}_{m}\cos (mt), \end{aligned}$$

where $({\tilde{x}}_{m})_{m\ge 1}$ is a sequence in ${\mathbb {R}}$ satisfying

$$\begin{aligned} \sum \limits _{m=1}^{\infty }m^{2\mu }{\tilde{x}}_{m}^{2}<\infty . \end{aligned}$$

The space $X_{\mu }$ is endowed with the inner product and the norm

$$\begin{aligned} \langle {\tilde{x}},\, {\tilde{\eta }}\rangle _{X_{\mu }}=\sum \limits _{m=1}^{\infty }m^{2\mu }{\tilde{x}}_{m}{\tilde{\eta }}_{m}, \qquad ||{\tilde{x}}||_{X_{\mu }}=\sqrt{\sum \limits _{m=1}^{\infty }m^{2\mu }{\tilde{x}}_{m}^{2}}. \end{aligned}$$

We denote by ${{\widetilde{C}}}^1\left( [0,\pi ]\right)$ the set of $C^1$-functions having zero mean in $[0,\pi ]$.

Proposition 16

The space $X_\mu$ is continuously embedded in $L^2(0,\pi )$ and is made of functions with zero mean on $[0,\pi ]$. The set ${{\widetilde{C}}}^1([0,\pi ])$ is a dense subset of $X_\mu$.

For any $\nu \in \,]0,1[\,$, we define $Y_{\nu }$ as the set of those real valued functions $y\in L^{2}(0,\pi )$ such that

$$\begin{aligned} y(t)\sim \sum \limits _{m=1}^{\infty }y_{m}\sin (mt), \end{aligned}$$

where $(y_{m})_{m\ge 1}$ is a sequence in ${\mathbb {R}}$ satisfying

$$\begin{aligned} \sum \limits _{m=1}^{\infty }m^{2\nu }y_{m}^{2}<\infty . \end{aligned}$$

The space $Y_{\nu }$ is endowed with the inner product and the norm

$$\begin{aligned} \langle y,\, \rho \rangle _{Y_{\nu }}=\sum \limits _{m=1}^{\infty }m^{2\nu }y_{m}\rho _{m}, \qquad ||y||_{Y_{\nu }}=\sqrt{\sum \limits _{m=1}^{\infty }m^{2\nu }y_{m}^{2}}. \end{aligned}$$

We denote by $C^1_0([0,\pi ])$ the set of $C^1$-functions y satisfying $y(0)=0=y(\pi )$.

Proposition 17

The space $Y_\nu$ is continuously embedded in $L^2(0,\pi )$ and if $\nu >\tfrac{1}{2}$ it is continuously embedded in $C([0,\pi ])$. The set $C^1_0([0,\pi ])$ is a dense subset of $Y_\nu$.

We will look for solutions of problem (17)–(4) by decomposing them as

$$\begin{aligned} x(t)=\overline{x}+ {\tilde{x}}(t) , \quad \text {and}\quad u(t)=\overline{u}+{{\tilde{u}}}(t), \end{aligned}$$

where

$$\begin{aligned} \overline{x}=\frac{1}{\pi }\int \limits _{0}^{\pi }x(t)\,dt \quad \text {and}\quad \overline{u}=\frac{1}{\pi }\int \limits _{0}^{\pi }u(t)\,dt. \end{aligned}$$

We choose two positive numbers $\mu<\frac{1}{2}<\nu$ such that $\mu +\nu =1$, and consider the space $E=X_\mu \times Y_\nu \times ({\mathbb {R}}\times X_\mu )\times Y_\nu$. It is a separable Hilbert space endowed with the scalar product

$$\begin{aligned}{} & {} \langle ({\tilde{x}},y,\overline{u},{\tilde{u}},v),\,({\widetilde{X}},Y,\overline{U},{\widetilde{U}},V)\rangle _{E} \\{} & {} \quad =\langle {\tilde{x}},\,{\widetilde{X}}\rangle _{X_{\mu }}+\langle y,\,Y\rangle _{Y_{\nu }}+ \overline{u}\,\overline{U} +\langle {\tilde{u}},\,{\widetilde{U}}\rangle _{X_{\mu }}+\langle v,\,V\rangle _{Y_{\nu }} , \end{aligned}$$

and the corresponding norm

$$\begin{aligned} ||({\tilde{x}},y,\overline{u},{\tilde{u}},v)||_{E}=\sqrt{||{\tilde{x}}||^{2}_{X_{\mu }}+||y||^{2}_{Y_{\nu }}+\overline{u}^{2}+ ||{\tilde{u}}||^{2}_{X_{\mu }}+||v||^{2}_{Y_{\nu }}}. \end{aligned}$$

Recalling that the function ${{\widetilde{K}}}_\varepsilon$ in (19) is $\tau$-periodic in x, we can assume $\overline{x}\in S^1={\mathbb {R}}/(\tau {\mathbb {Z}})$ and look for critical points

$$\begin{aligned} \big ( z, \overline{x} \big ) = \big ( ({{\tilde{x}}},y , \overline{u}, {{\tilde{u}}}, v), \overline{x}\big ) \in E \times S^1 \end{aligned}$$

of a suitable functional $\varphi : E \times S^1\rightarrow {\mathbb {R}}$.

Let us briefly describe the rest of the proof of Theorem 2, to be carried out in the next sections. In Sect. 3.4 we will introduce a bounded selfadjoint invertible operator $L\in {{{\mathcal {L}}}}(E)$ so to define the functional

$$\begin{aligned} \varphi (z,\overline{x})=\frac{1}{2}\langle Lz,\,z\rangle +\psi (z,\overline{x}), \end{aligned}$$

(25)

where $\psi :E\times S^{1}\rightarrow {\mathbb {R}}$ is given by

$$\begin{aligned} \psi (z,\overline{x})&= \psi \big ( ({{\tilde{x}}}\,,y \,, \overline{u}\,, {{\tilde{u}}}, v)\,, \overline{x}\big )\nonumber \\&= \int _0^\pi {\widetilde{K}}_\varepsilon \big (t\,,\overline{x}+{{\tilde{x}}}(t)\,,y(t)\,,\overline{u}+{{\tilde{u}}}(t)\,,v(t)\big ) \,dt\,. \end{aligned}$$

(26)

In Sect. 3.3 we will prove that $d\psi (E\times S^{1})$ is relatively compact. Then, in Sect. 3.4 we will verify that the critical points of $\varphi$ are indeed solutions of problem (17)–(4). The existence of such critical points will be provided by the application of the following theorem, which is a particular case of [23, Theorem 3.8].

Theorem 18

(Szulkin) If $\varphi : E\times S^{1}\rightarrow {\mathbb {R}}$ is as in (25), where $d\psi (E\times S^{1})$ is relatively compact and $L:E\rightarrow E$ is a bounded selfadjoint invertible operator, then there exist at least two critical points of $\varphi$.

Finally, in view of Proposition 15, we will conclude that such solutions also solve problem (3)–(4), thus completing the proof of Theorem 2.

3.3 The functional $\psi$

With the aim of applying Szulkin’s Theorem, in this section we prove that the functional $\psi$ defined in (26) is continuously differentiable, with Fréchet differential $d\psi$, and the image $d\psi (E\times S^1)$ is relatively compact in the dual space ${\mathcal {L}}(E\times S^1,{\mathbb {R}})$. The proof essentially follows the arguments of [12, Section 2.2]. For sake of simplicity, in this section we replace $S^1$ with the linear space ${\mathbb {R}}$. The function $\psi$ is defined in the same way.

Proposition 19

The functional $\psi : E\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ is continuously differentiable.

Proof

Fix any point $(z_0,\overline{x}_0)=\big (({{\tilde{x}}}_0,y_0,\overline{u}_0,{{\tilde{u}}}_0,v_0),\overline{x}_0)\big ) \in E\times {\mathbb {R}}$. For every $(z,\overline{x})=\big (({{\tilde{x}}},y,\overline{u},{{\tilde{u}}},v),\overline{x}\big )\in E\times {\mathbb {R}}$ we compute the directional derivative

$$\begin{aligned} d_G&\psi (z_0,\overline{x}_0)(z,\overline{x}) =\lim _{s\rightarrow 0}\frac{1}{s}\big (\psi (z_0+sz,\overline{x}_0+s\overline{x})-\psi (z_0,\overline{x}_0)\big )\\ =&\int _0^\pi \Big ( \partial _x {{\widetilde{H}}}\big (t,\overline{x}_0 +{{\tilde{x}}}_0(t), y_0(t)\big ) \, \big (\overline{x}+{{\tilde{x}}}(t)\big ) +\partial _y {{\widetilde{H}}}\big (t,\overline{x}_0 +{{\tilde{x}}}_0(t), y_0(t) \big ) \, y(t) \Big ) \, dt \\&-\int _0^\pi \Big ( {{\tilde{g}}}_\varepsilon \big (t,\overline{u}_0 +{{\tilde{u}}}_0(t) \big ) - \big (\overline{u}_0 +{{\tilde{u}}}_0(t)\big ) \Big )\, \big (\overline{u}+ {{\tilde{u}}}(t)\big ) \, dt\\&+\int _0^\pi \Big ( {{\tilde{f}}}\big (t,v_0(t)\big ) - v_0(t) \Big ) \, v(t) \, dt\\&+\varepsilon \int _0^\pi \Big ( \partial _x P\big (t,\overline{x}_0 +{{\tilde{x}}}_0(t), y_0(t), \overline{u}_0 + {{\tilde{u}}}_0(t),v_0(t)\big ) \, \big (\overline{x}+{{\tilde{x}}}(t)\big ) \\&\qquad \qquad +\partial _y P\big (t,\overline{x}_0 +{{\tilde{x}}}_0(t), y_0(t), \overline{u}_0 + {{\tilde{u}}}_0(t),v_0(t)\big ) \, y(t) \\&\qquad \qquad + \partial _u P\big (t,\overline{x}_0 +{{\tilde{x}}}_0(t), y_0(t), \overline{u}_0 + {{\tilde{u}}}_0(t),v_0(t)\big ) \, \big (\overline{u}+{{\tilde{u}}}(t)\big )\\&\qquad \qquad +\partial _v P\big (t,\overline{x}_0 +{{\tilde{x}}}_0(t), y_0(t), \overline{u}_0 + {{\tilde{u}}}_0(t),v_0(t)\big ) \, v(t) \Big ) \, dt\,. \end{aligned}$$

(In the above computations, the dominated convergence theorem has been used, since all the quantities inside the integrals are uniformly bounded.) We verify now that the Gâteaux differential $d_G\psi : E\times {\mathbb {R}}\rightarrow {\mathcal {L}}(E\times {\mathbb {R}},{\mathbb {R}})$ is continuous at $(z_0,\overline{x}_0)$. The function ${\mathcal {T}}: E\times {\mathbb {R}}\rightarrow [L^2(0,\pi )]^4$, defined by

$$\begin{aligned} {\mathcal {T}}\big (({{\tilde{x}}}_0, y_0,\overline{u}_0,{{\tilde{u}}}_0,v_0),\overline{x}_0\big ) = (\overline{x}_0+{{\tilde{x}}}_0,y_0,\overline{u}_0 +{{\tilde{u}}}_0, v_0), \end{aligned}$$

is continuous, as the spaces $X_\mu$ and $Y_\nu$ are continuously embedded into $L^2(0,\pi )$. The Nemytskii operator ${\mathcal {N}}: [L^2(0,\pi )]^4 \rightarrow [L^2(0,\pi )]^4$, defined by

$$\begin{aligned}&{\mathcal {N}}(x_0,y_0,u_0,v_0) (t) \\&\quad =\Big (\partial _x {{\widetilde{H}}}\big (t,x_0(t), y_0(t)\big ) + \varepsilon \partial _x P\big (t,x_0(t), y_0(t), u_0(t), v_0(t)\big )\,,\\&\qquad \partial _y {{\widetilde{H}}}\big (t,x_0(t), y_0(t)\big ) + \varepsilon \partial _y P\big (t,x_0(t), y_0(t), u_0(t), v_0(t)\big )\,,\\&\quad - {{\tilde{g}}}_\varepsilon \big (t,u_0(t) \big )+u_0(t) + \varepsilon \partial _u P\big (t,x_0(t), y_0(t), u_0(t), v_0(t)\big )\,,\\&\qquad {\tilde{f}}\big (t,v_0(t) \big ) -v_0(t) + \varepsilon \partial _v P\big (t,x_0(t), y_0(t), u_0(t), v_0(t)\big ) \Big )\,, \end{aligned}$$

is continuous, since all the functions involved are continuous and bounded. Finally, the linear map $\Phi :[L^2(0,\pi )]^4 \rightarrow {\mathcal {L}}(E\times {\mathbb {R}},{\mathbb {R}})$, defined by

$$\begin{aligned}{} & {} \Phi (h_1,h_2,h_3,h_4)\big ((({{\tilde{x}}},y,\overline{u},{{\tilde{u}}},v),\overline{x})\big )\\{} & {} \quad = \int _0^\pi \Big ( h_1(t)\, \big (\overline{x}+{{\tilde{x}}}(t)\big ) + h_2(t)\, y(t) + h_3(t)\, \big (\overline{u}+{{\tilde{u}}}(t)\big ) + h_4(t)\, v(t) \Big )\, dt \end{aligned}$$

is bounded, hence continuous. As $d_G\psi =\Phi \circ {\mathcal {N}}\circ {\mathcal {T}}$, we conclude that $d_G\psi$ is continuous and $\psi$ is Fréchet differentiable, and $d\psi =d_G\psi$. $\square$

We verify now that the set $d\psi (E\times {\mathbb {R}})$ is relatively compact in ${\mathcal {L}}(E\times {\mathbb {R}},{\mathbb {R}})$. We need to recall the Hausdorff–Young-type inequality proved in [12, Proposition 2.2].

Proposition 20

Assume that $1<p\le 2 \le q$ verify $(1/p)+(1/q)=1$. Let ${{\widetilde{\Phi }}}\in L^p(0,\pi )$ be such that $\int _0^\pi {{\widetilde{\Phi }}}(t)\,dt=0$, with

$$\begin{aligned} {{\widetilde{\Phi }}}(t)\sim \sum _{m=1}^\infty \Phi _m \cos (mt). \end{aligned}$$

Then,

$$\begin{aligned} \sum _{m=1}^\infty |\Phi _m |^q \le \left( \frac{2}{\pi }\int _0^\pi |{{\widetilde{\Phi }}}(t)|^p\, dt \right) ^{\frac{q}{p}}. \end{aligned}$$

For all $m\ge 1$, we set

$$\begin{aligned}{} & {} {{{\tilde{e}}}_m}^\mu (t) = \frac{1}{m^\mu }\cos (mt), \qquad \qquad e_m^\nu (t) = \frac{1}{m^\nu }\sin (mt),\\{} & {} e_{[1],m}=({{{\tilde{e}}}_m}^\mu ,0,0,0,0,0), \quad e_{[2],m}=(0, e_m^\nu ,0,0,0,0), \quad e_{[3]}=(0,0,1,0,0,0),\\{} & {} e_{[4],m}=(0,0,0,{{{\tilde{e}}}_m}^\mu ,0,0), \quad e_{[5],m}=(0, 0,0,0, e_m^\nu ,0), \quad e_{[6]}=(0,0,0,0,0,1), \end{aligned}$$

and consider the orthonormal basis ${\mathcal {B}}$ in $E\times {\mathbb {R}}$ defined by

$$\begin{aligned} {\mathcal {B}}= \{e_{[1],m}, e_{[2],m}, e_{[3]}, e_{[4],m}, e_{[5],m}, e_{[6]}: m\ge 1\}. \end{aligned}$$

We need the following result.

Proposition 21

For all $\epsilon >0$ there exists $m_0\ge 1$ such that, for all $(z_0,\overline{x}_0)\in E\times {\mathbb {R}}$, we have

$$\begin{aligned}&\sum _{m=m_0}^\infty \Big ( |d\psi (z_0,\overline{x}_0)(e_{[1],m})|^2 + |d\psi (z_0,\overline{x}_0)(e_{[2],m})|^2+ |d\psi (z_0,\overline{x}_0)(e_{[4],m})|^2 \\&\quad + |d\psi (z_0,\overline{x}_0)(e_{[5],m})|^2 \Big ) <\epsilon \,. \end{aligned}$$

Proof

Let R be a constant satisfying, for every $(t,\sigma )\in [0,\pi ]\times {\mathbb R}$,

$$\begin{aligned} \Vert \nabla {{\widetilde{H}}}\Vert _\infty +\Vert \nabla P\Vert _\infty +\Vert {{\tilde{f}}}(t,\sigma )-\sigma \Vert + \Vert {{\tilde{g}}}_\varepsilon (t,\sigma )-\sigma \Vert \le R. \end{aligned}$$

(27)

Fix $(z_0,\overline{x}_0)\in E\times {\mathbb {R}}$ and expand the function

$$\begin{aligned} \Phi (t)= \partial _x {{\widetilde{H}}}\big (t,\overline{x}_0+{{\tilde{x}}}_0(t), y_0(t)\big ) + \varepsilon \partial _x P\big (t,\overline{x}_0+{{\tilde{x}}}_0(t), y_0(t), \overline{u}_0+{{\tilde{u}}}_0(t), v_0(t)\big ) \end{aligned}$$

in a Fourier series as $\Phi (t)\sim \Phi _0+\sum _{k=1}^\infty \Phi _k \cos (kt).$ We have

$$\begin{aligned} d\psi (z_0,\overline{x}_0)(e_{[1],m})=\int _0^\pi \Phi (t)\, {{{\tilde{e}}}_m}^\mu (t)\, dt = \frac{\pi }{2} \frac{1}{m^\mu }\Phi _m. \end{aligned}$$

Pick $\rho >2$ such that $2\mu \rho >1$ and set

$$\begin{aligned} S_{m_0}=\left( \sum _{m=m_0}^\infty \frac{1}{m^{2\mu \rho }}\right) ^{\frac{1}{\rho }}. \end{aligned}$$

Let $\rho '$ be the conjugate exponent of $\rho$, satisfying $1/\rho +1/\rho '=1$. By the Hölder inequality, we have

$$\begin{aligned} \sum _{m=m_0}^\infty \frac{1}{m^{2\mu }}\, \Phi _m^2 \le \left( \sum _{m=m_0}^\infty \frac{1}{m^{2\mu \rho }} \right) ^{\frac{1}{\rho }}\, \left( \sum _{m=m_0}^\infty | \Phi _m|^{2\rho '}\right) ^{\frac{1}{\rho '}}. \end{aligned}$$

In the following computation we apply the Hausdorff–Young inequality of Proposition 20 to ${{\widetilde{\Phi }}}(t)=\Phi (t)-\Phi _0$. Moreover, we observe that $|\Phi (t)-\Phi _0|\le 2R$, where R is the constant defined in (27). We get

$$\begin{aligned}&\sum _{m=m_0}^\infty |d\psi (z_0,\overline{x}_0)(e_{[1],m})|^2 =\frac{\pi ^2}{4}\sum _{m=m_0}^\infty \frac{1}{m^{2\mu }}\, \Phi _m^2 \le \frac{\pi ^2}{4} S_{m_0} \, \left( \sum _{m={m_0}}^\infty |\Phi _m|^{2\rho '}\right) ^{\frac{1}{\rho '}}\\&\quad \le \frac{\pi ^2}{4} S_{m_0} \, \left( \frac{2}{\pi }\int _0^\pi |\Phi (t)-\Phi _0|^{\frac{2\rho '}{2\rho '-1}}\, dt \right) ^{2\rho '-1} \le \frac{\pi ^2}{4} S_{m_0} \, 2^{4\rho '-1}\, R^{2\rho '}. \end{aligned}$$

Since $\displaystyle \lim _{{m_0}\rightarrow \infty } S_{m_0}=0$ we conclude that there exists ${m_0}$ such that

$$\begin{aligned} \sum _{m={m_0}}^\infty |d\psi (z_0,\overline{x}_0)(e_{[1],m})|^2 <\frac{\epsilon }{4}, \end{aligned}$$

for all $(z_0,\overline{x}_0)\in E\times {\mathbb {R}}$. Similar computations allow to take ${m_0}$ such that

$$\begin{aligned}&\sum _{m={m_0}}^\infty |d\psi (z_0,\overline{x}_0)(e_{[2],m})|^2<\frac{\epsilon }{4}, \quad \sum _{m={m_0}}^\infty |d\psi (z_0,\overline{x}_0)(e_{[4],m})|^2<\frac{\epsilon }{4},\\&\sum _{m={m_0}}^\infty |d\psi (z_0,\overline{x}_0)(e_{[5],m})|^2 <\frac{\epsilon }{4}, \end{aligned}$$

hence the claim is proved. $\square$

Proposition 22

The image $d\psi (E\times {\mathbb {R}})$ is relatively compact in ${\mathcal {L}}(E\times {\mathbb {R}},{\mathbb {R}})$.

Proof

To verify that $d\psi (E\times {\mathbb {R}})$ is bounded in ${\mathcal {L}}(E\times {\mathbb {R}},{\mathbb {R}})$, take any $(z,\overline{x})=({{\tilde{x}}}, y,\overline{u}, {{\tilde{u}}}, v, \overline{x})\in E\times {\mathbb {R}}$ with unitary norm and compute

$$\begin{aligned}&|d\psi (z_0,\overline{x}_0)(z,\overline{x})| \nonumber \\&\quad \le \Bigg ( \sum _{m=1}^\infty \Big ( |d\psi (z_0,\overline{x}_0)(e_{[1],m}) |^2 + |d\psi (z_0,\overline{x}_0)(e_{[2],m}) |^2+ |d\psi (z_0,\overline{x}_0)(e_{[4],m}) |^2 \nonumber \\&\qquad + |d\psi (z_0,\overline{x}_0)(e_{[5],m})|^2 \Big )+|d\psi (z_0,\overline{x}_0)(e_{[3]})|^2 + |d\psi (z_0,\overline{x}_0)(e_{[6]})|^2\Bigg )^\frac{1}{2}. \end{aligned}$$

(28)

We note that both

$$\begin{aligned} d\psi (z_0,\overline{x}_0)(e_{[3]}) =&\int _0^\pi \Big ( \partial _x {{\widetilde{H}}}\big (t,\overline{x}_0 +{{\tilde{x}}}_0(t), y_0(t)\big ) \, \\&\quad + \varepsilon \partial _x P\big (t,\overline{x}_0 +{{\tilde{x}}}_0(t), y_0(t), \overline{u}_0 + {{\tilde{u}}}_0(t),v_0(t)\big ) \Big ) \, dt \end{aligned}$$

and

$$\begin{aligned} d\psi (z_0,\overline{x}_0)(e_{[6]}) =&\int _0^\pi \Big ( - {{\tilde{g}}}_\varepsilon \big (t,\overline{u}_0 +{{\tilde{u}}}_0(t) \big ) - \big (\overline{u}_0 +{{\tilde{u}}}_0(t)\big ) \, \\&\quad + \varepsilon \partial _u P\big (t,\overline{x}_0 +{{\tilde{x}}}_0(t), y_0(t), \overline{u}_0 + {{\tilde{u}}}_0(t),v_0(t)\big ) \,\Big ) \, dt \end{aligned}$$

are uniformly bounded. Moreover, by Proposition 21, the series in the right-hand side of (28) is also uniformly bounded, hence we conclude that $d\psi (E\times {\mathbb {R}})$ is bounded.

To verify compactness, pick any sequence $\big (d\psi ( z_0^n,\overline{x}_0^n)\big )_n$ in $d\psi (E\times {\mathbb {R}})$, where $z_0^n = ({{\tilde{x}}}_0^n,y_0^n,\overline{u}_0^n,{{\tilde{u}}}_0^n,v_0^n)$. Since $d\psi (E\times {\mathbb {R}})$ is bounded, we may assume that the sequence weakly converges to some $h\in {\mathcal {L}}(E\times {\mathbb {R}},{\mathbb {R}})$. We aim to prove that the sequence strongly converges to h.

We set $h_{[1],m}= h(e_{[1],m})$, $h_{[2],m}= h(e_{[2],m})$, $h_{[3]}= h(e_{[3]})$, $h_{[4],m}= h(e_{[4],m})$, $h_{[5],m}= h(e_{[5],m})$ and $h_{[6]}= h(e_{[6]})$, so that,

$$\begin{aligned} \begin{aligned} \Vert h\Vert _{{\mathcal {L}}(E\times {\mathbb {R}},{\mathbb {R}})}^2&=\sum _{m=1}^\infty \Big ( h_{[1], m}^2 + h_{[2], m}^2 + h_{[4], m}^2 + h_{[5], m}^2 \Big ) + h_{[3]}^2 + h_{[6]}^2<\infty . \end{aligned} \end{aligned}$$

(29)

Fix $\epsilon >0$. By Proposition 21, there is $m_0>1$, such that, for all $(z_0,\overline{x}_0)\in E\times {\mathbb {R}}$, we have

$$\begin{aligned} \begin{aligned}&\sum _{m=m_0}^\infty \Big ( |d\psi (z_0,\overline{x}_0)(e_{[1],m})|^2 + |d\psi (z_0,\overline{x}_0)(e_{[2],m})|^2+ |d\psi (z_0,\overline{x}_0)(e_{[4],m})|^2 \\&\quad + |d\psi (z_0,\overline{x}_0)(e_{[5],m})|^2 \Big ) <\epsilon . \end{aligned} \end{aligned}$$

(30)

By (29), we may further assume that

$$\begin{aligned} \sum _{m=m_0}^\infty \Big ( h_{[1], m}^2 + h_{[2], m}^2 + h_{[4], m}^2 + h_{[5], m}^2 \Big ) <\epsilon . \end{aligned}$$

(31)

From the weak convergence of the sequence $\big (d\psi ( z_0^n,\overline{x}_0^n)\big )_n$, we can take $n_0\in {\mathbb {N}}$ large enough such that, for all $n\ge n_0$, for all $m\ge 1$, with $m\le m_0-1$, we have

$$\begin{aligned}{} & {} |d\psi (z_0^n,\overline{x}_0^n)(e_{[1],m})-h_{[1],m} |^2 + |d\psi (z_0^n,\overline{x}_0^n)(e_{[2],m})-h_{[2],m} |^2 \nonumber \\{} & {} \quad + |d\psi (z_0^n,\overline{x}_0^n)(e_{[4],m})-h_{[4],m}|^2 + |d\psi (z_0^n,\overline{x}_0^n)(e_{[5],m})-h_{[5],m})|^2 <\frac{\epsilon }{m_0-1}\nonumber \\ \end{aligned}$$

(32)

and furthermore

$$\begin{aligned} |d\psi (z_0^n,\overline{x}_0^n)(e_{[3]}) -h_{[3]} |^2 + |d\psi (z_0^n,\overline{x}_0^n)(e_{[6]}) -h_{[6]} |^2 <\epsilon . \end{aligned}$$

(33)

Then we compute, using (30), (31), (32), and (33),

$$\begin{aligned} \begin{aligned}&|d\psi (z_0^n,\overline{x}_0^n) (z,\overline{x}) - h(z,\overline{x})|^2\\&\quad \le \sum _{m=1}^{m_0-1} \Big ( |d\psi (z_0^n,\overline{x}_0^n)(e_{[1],m})-h_{[1],m} |^2 + |d\psi (z_0^n,\overline{x}_0^n)(e_{[2],m})-h_{[2],m} |^2\\&\qquad + |d\psi (z_0^n,\overline{x}_0^n)(e_{[4],m})-h_{[4],m}|^2 + |d\psi (z_0^n,\overline{x}_0^n)(e_{[5],m})-h_{[5],m})|^2 \Big )\\&\qquad +|d\psi (z_0^n,\overline{x}_0^n)(e_{[3]}) -h_{[3]} |^2 + |d\psi (z_0^n,\overline{x}_0^n)(e_{[6]}) -h_{[6]} |^2 \\&\qquad +\sum _{m=m_0}^{\infty } \Big ( |d\psi (z_0^n,\overline{x}_0^n)(e_{[1],m}) |^2 + |d\psi (z_0^n,\overline{x}_0^n)(e_{[2],m}) |^2\\&\qquad + |d\psi (z_0^n,\overline{x}_0^n)(e_{[4],m})|^2 + |d\psi (z_0^n,\overline{x}_0^n)(e_{[5],m})|^2 \Big )\\&\qquad +\sum _{m=m_0}^{\infty } \big ( h_{[1],m}^2 + h_{[2],m}^2+ h_{[4],m}^2+ h_{[5],m}^2 \big )\\&\quad \le \sum _{m=1}^{m_0-1} \frac{\epsilon }{m_0-1} +\epsilon + \epsilon +\epsilon =4\epsilon . \end{aligned} \end{aligned}$$

We just proved that the sequence $\big (d\psi ( z_0^n,\overline{x}_0^n)\big )_n$ strongly converges to h. This shows that the set $d\psi (E\times {\mathbb {R}})$ is relatively compact in ${\mathcal {L}}(E\times {\mathbb {R}},{\mathbb {R}})$. $\square$

3.4 The operator L

In this section we are going to introduce the operator L which is in force in the application of Theorem 18.

Let us first introduce a continuous symmetric bilinear form ${\mathcal {B}}: D \times D \rightarrow {\mathbb {R}}$, where

$$\begin{aligned} D={{\widetilde{C}}}^1([0,\pi ]) \times C^1_0([0,\pi ]) \times {\mathbb {R}}\times {{\widetilde{C}}}^1([0,\pi ]) \times C^1_0([0,\pi ]). \end{aligned}$$

Given $z=({{\tilde{x}}}, y, \overline{u}, {{\tilde{u}}}, v)$ and $Z=({{\widetilde{X}}}, Y, \overline{U}, {{\widetilde{U}}}, V)$ in D we define

$$\begin{aligned}{} & {} {\mathcal {B}}(z,Z)=\int _0^\pi \Big [ y'(t){{\widetilde{X}}}(t)+v'(t){{\widetilde{U}}}(t) -{{\tilde{x}}}'(t)Y(t)-{{\tilde{u}}}'(t)V(t)\\{} & {} \quad +\, v(t)V(t) -\big (\overline{u} + {{\tilde{u}}}(t)\big )\big (\overline{U} + {{\widetilde{U}}}(t)\big )\Big ] \,dt, \end{aligned}$$

which is equivalent to

$$\begin{aligned}{} & {} {\mathcal {B}}(z,Z)=\int _0^\pi \Big [ Y'(t){{\tilde{x}}}(t)+V'(t){{\tilde{u}}}(t) -{{\widetilde{X}}}'(t)y(t)-{{\widetilde{U}}}'(t)v(t)\\{} & {} \quad +\, V(t)v(t) -\big (\overline{U} + {{\widetilde{U}}}(t)\big )\big (\overline{u} + {{\tilde{u}}}(t)\big )\Big ] \,dt, \end{aligned}$$

recalling the boundary conditions $y(0)=0=y(\pi )$, $v(0)=0=v(\pi )$, $Y(0)=0=Y(\pi )$, and $V(0)=0=V(\pi )$.

Let us verify that the form ${\mathcal {B}}$ is continuous in $D\times D$ with the topology induced by the topology of $E\times E$. We can write

$$\begin{aligned} y=\sum _{m=1}^\infty y_m\, \sin (mt), \quad {{\widetilde{X}}}=\sum _{m=1}^\infty {{\widetilde{X}}}_m\, \cos (mt), \end{aligned}$$

and compute

$$\begin{aligned}{} & {} \left| \int _0^\pi y'(t)\, {{\widetilde{X}}}(t)\, dt\right| = \frac{\pi }{2}\left| \sum _{m=1}^\infty m\, y_m \, {{\widetilde{X}}}_m\right| = \frac{\pi }{2}\left| \sum _{m=1}^\infty m^\mu \, y_m \, m^\nu {{\widetilde{X}}}_m\right| \\{} & {} \quad \le \frac{\pi }{2}\Vert y\Vert _{Y\nu }\, \Vert {{\widetilde{X}}}\Vert _{X_\mu }. \end{aligned}$$

Similar inequalities hold for the other terms in the definition of ${\mathcal {B}}$. For example we compute, writing

$$\begin{aligned}{} & {} {{\tilde{u}}}=\sum _{m=1}^\infty {{\tilde{u}}}_m\, \cos (mt), \quad {{\widetilde{U}}}=\sum _{m=1}^\infty {{\widetilde{U}}}_m\, \cos (mt), \\{} & {} \left| \int _0^\pi \big (\overline{u} +{{\tilde{u}}}(t)\big )\, \big ( \overline{U}+{{\widetilde{U}}}(t)\big )\, dt\right| \le \pi \left| \overline{u}\, \overline{U} \right| + \frac{\pi }{2}\left| \sum _{m=1}^\infty {{\tilde{u}}}_m \, {{\widetilde{U}}}_m\right| \\{} & {} \quad \le \pi \left| \overline{u}\, \overline{U} \right| + \frac{\pi }{2}\left| \sum _{m=1}^\infty m^\mu {{\tilde{u}}}_m \, m^\mu {{\widetilde{U}}}_m\right| \le \pi \left| \overline{u}\, \overline{U} \right| + \frac{\pi }{2}\Vert {{\tilde{u}}}\Vert _{X\mu }\, \Vert {{\widetilde{U}}}\Vert _{X_\mu }. \end{aligned}$$

Therefore we have

$$\begin{aligned} \left| {\mathcal {B}}\Big (({{\tilde{x}}}, y, \overline{u}, {{\tilde{u}}}, v),({{\widetilde{X}}}, Y, \overline{U}, {{\widetilde{U}}}, V)\Big )\right| \le 4\pi \Vert ({{\tilde{x}}}, y, \overline{u}, {{\tilde{u}}}, v)\Vert _E\, \Vert ({{\widetilde{X}}}, Y, \overline{U}, {{\widetilde{U}}}, V)\Vert _E. \end{aligned}$$

Since D is a dense subspace of E (see Propositions 16 and 17 ) we can extend ${\mathcal {B}}$ to a continuous bilinear symmetric form ${\mathcal {B}}: E \times E \rightarrow {\mathbb {R}}$.

Now, we can introduce the bounded selfadjoint operator $L: E\rightarrow E$ generated by ${\mathcal {B}}$: we define L such that, for every $z,Z\in E$,

$$\begin{aligned} {\mathcal {B}}(z,Z) = \langle Lz,\, Z \rangle . \end{aligned}$$

Lemma 23

The operator L is invertible with continuous inverse.

Proof

At first notice that we can decompose ${\mathcal {B}}$ as follows

$$\begin{aligned} {\mathcal {B}}(z,Z) = {\mathcal {B}}_1\big (({{\tilde{x}}},y),({{\widetilde{X}}}, Y)\big ) + {\mathcal {B}}_2\big ((\overline{u}, {{\tilde{u}}}, v),(\overline{U}, {{\widetilde{U}}}, V)\big ), \end{aligned}$$

where

$$\begin{aligned} {\mathcal {B}}_1\big (({{\tilde{x}}},y),({{\widetilde{X}}}, Y)\big )=\int _0^\pi \big [ y'(t){{\widetilde{X}}}(t) - {{\tilde{x}}}'(t)Y(t)\big ] \,dt, \end{aligned}$$

and

$$\begin{aligned}{} & {} {\mathcal {B}}_2\big ((\overline{u}, {{\tilde{u}}}, v),(\overline{U}, {{\widetilde{U}}}, V)\big )=\int _0^\pi \Big [ v'(t){{\widetilde{U}}}(t) -{{\tilde{u}}}'(t)V(t)\\{} & {} \quad +\, v(t)V(t) -\big (\overline{u} + {{\tilde{u}}}(t)\big ) \big (\overline{U}+ {{\widetilde{U}}}(t)\big ) \Big ] \,dt. \end{aligned}$$

Consequently we will have

$$\begin{aligned} L({{\tilde{x}}}, y,\overline{u}, {{\tilde{u}}}, v)= \big ( L_1({{\tilde{x}}}, y), L_2 (\overline{u}, {{\tilde{u}}}, v) \big ), \end{aligned}$$

where

$$\begin{aligned} {\mathcal {B}}_1\big (({{\tilde{x}}},y),({{\widetilde{X}}}, Y)\big ) = \langle L_1({{\tilde{x}}},y),\, ({{\widetilde{X}}}, Y) \rangle , \end{aligned}$$

and

$$\begin{aligned} {\mathcal {B}}_2\big ((\overline{u}, {{\tilde{u}}}, v),(\overline{U}, {{\widetilde{U}}}, V)\big )= \langle L_2(\overline{u}, {{\tilde{u}}}, v),\, (\overline{U}, {{\widetilde{U}}}, V)\rangle . \end{aligned}$$

Arguing as in [12, Proposition 2.14] we can prove that

$$\begin{aligned} \Vert L_1({{\tilde{x}}},y)\Vert _{X_\mu \times Y_\nu } = \frac{\pi }{2} \Vert ({{\tilde{x}}},y)\Vert _{X_\mu \times Y_\nu }. \end{aligned}$$

(34)

Now, we are going to prove that there are two constants $c_1,c_2>0$ such that

$$\begin{aligned} c_1 \Vert (\overline{u}, {{\tilde{u}}}, v) \Vert _{{\mathbb {R}}\times X_\mu \times Y_\nu } \le \Vert L_2(\overline{u}, {{\tilde{u}}}, v)\Vert _{{\mathbb {R}}\times X_\mu \times Y_\nu } \le c_2 \Vert (\overline{u}, {{\tilde{u}}}, v) \Vert _{{\mathbb {R}}\times X_\mu \times Y_\nu }, \end{aligned}$$

(35)

for every $(\overline{u}, {{\tilde{u}}}, v)\in {{\mathbb {R}}\times X_\mu \times Y_\nu }$. To this aim, let $(\overline{p},{{\tilde{p}}},q)\in {\mathbb {R}}\times X_\mu \times Y_\nu$ be such that

$$\begin{aligned}{} & {} \langle L_2(\overline{u}, {{\tilde{u}}}, v), (\overline{U}, {{\widetilde{U}}}, V) \rangle _{{\mathbb {R}}\times X_\mu \times Y_\nu } \nonumber \\{} & {} \quad = {\mathcal {B}}_2\big ((\overline{u}, {{\tilde{u}}}, v), (\overline{U}, {{\widetilde{U}}}, V)\big ) = \langle (\overline{p}, {{\tilde{p}}}, q), (\overline{U}, {{\widetilde{U}}}, V)\rangle _{{\mathbb {R}}\times X_\mu \times Y_\nu }, \end{aligned}$$

(36)

for every $(\overline{U}, {{\widetilde{U}}}, V)\in {\mathbb {R}}\times X_\mu \times Y_\nu$. Setting

$$\begin{aligned} {{\tilde{p}}}&\sim \sum _{m=1}^\infty p_m \cos (mt)\,,&q&\sim \sum _{m=1}^\infty q_m \sin (mt)\,,\\ {{\tilde{u}}}&\sim \sum _{m=1}^\infty u_m \cos (mt)\,,&v&\sim \sum _{m=1}^\infty v_m \sin (mt)\,, \end{aligned}$$

and choosing in (36) at first $V=0$, and next $\overline{U} + {{\widetilde{U}}}=0$ we get the identities

$$\begin{aligned} {\left\{ \begin{array}{ll} \overline{p} = -\pi \overline{u},\\ p_m m^{2\mu } = \frac{\pi }{2} ( - u_m + m v_m),\\ q_m m^{2\nu } = \frac{\pi }{2} ( m u_m + v_m). \end{array}\right. } \end{aligned}$$

(37)

In particular

$$\begin{aligned} p_m m^{\mu } = \frac{\pi }{2} \left( - u_m m^{-\mu } + v_m m^\nu \right) , \qquad q_m m^{\nu } = \frac{\pi }{2} \left( u_m m^\mu + v_m m^{-\nu }\right) , \end{aligned}$$

so that, using the Young inequality,

$$\begin{aligned}&p_m^2 m^{2\mu } + q_m^2 m^{2\nu } = \frac{\pi ^2}{4}\Big [ u_m^2 m^{2\mu } (1+m^{-4\mu }) + v_m^2 m^{2\nu } (1+m^{-4\nu }) \nonumber \\&\quad - 2 (u_m m^{\mu }) (v_m m^{\nu }) ( m^{-2\mu } - m^{-2\nu }) \Big ]\nonumber \\&\quad \le \pi ^2 \Big [ u_m^2 m^{2\mu } + v_m^2 m^{2\nu } \Big ]\,. \end{aligned}$$

(38)

Hence, from the first identity in (37) we get

$$\begin{aligned} \Vert L_2(\overline{u}, {{\tilde{u}}}, v)\Vert ^2_{{\mathbb {R}}\times X_\mu \times Y_\nu }&= \overline{p}^2 +\Vert {{\tilde{p}}}\Vert _{X_\mu }^2 + \Vert q\Vert _{Y_\nu }^2\\&=\overline{p}^2 + \sum _{m=1}^\infty (p_m^2 m^{2\mu } + q_m^2 m^{2\nu })\\&\le \pi ^2 \bigg ( \overline{u}^2 + \sum _{m=1}^\infty (u_m^2 m^{2\mu } + v_m^2 m^{2\nu })\bigg ) \\&\le \pi ^2 \Vert (\overline{u}, {{\tilde{u}}}, v)\Vert ^2_{{\mathbb {R}}\times X_\mu \times Y_\nu }\,, \end{aligned}$$

so that we can choose $c_2=\pi$ in (35).

We now provide the value $c_1$. At first notice that (38) in the case $m=1$ reads as

$$\begin{aligned} p_1^2+q_1^2 = \frac{\pi ^2}{4}\cdot 2\, \left( u_1^2 + v_1^2 \right) . \end{aligned}$$

(39)

For $m\ge 2$, since $( m^{-2\mu } - m^{-2\nu })\le m^{-2\mu }\le \left( \tfrac{1}{2}\right) ^{2\mu }$, from (38) we get, using again the Young inequality,

$$\begin{aligned} p_m^2 m^{2\mu } + q_m^2 m^{2\nu }&\ge \frac{\pi ^2}{4}\Big [ u_m^2 m^{2\mu } + v_m^2 m^{2\nu } - 2 |u_m m^{\mu } v_m m^{\nu }| (\tfrac{1}{2})^{2\mu } \Big ]\\&\ge \frac{\pi ^2}{4} \left( 1- (\tfrac{1}{2})^{2\mu }\right) \Big [ u_m^2 m^{2\mu } + v_m^2 m^{2\nu } \Big ]\,. \end{aligned}$$

Finally we get, from the first estimate in (37) and (39),

$$\begin{aligned} \Vert L_2(\overline{u}, {{\tilde{u}}}, v)\Vert ^2_{{\mathbb {R}}\times X_\mu \times Y_\nu }&= \overline{p}^2 +\Vert {{\tilde{p}}}\Vert _{X_\mu }^2 + \Vert q\Vert _{Y_\nu }^2\\&\ge \frac{\pi ^2}{4} \left( 1- (\tfrac{1}{2})^{2\mu }\right) \bigg ( \overline{u}^2 + \sum _{m=1}^\infty (u_m^2 m^{2\mu } + v_m^2 m^{2\nu })\bigg ) \\&\ge \frac{\pi ^2}{4} \left( 1- \left( \tfrac{1}{2}\right) ^{2\mu }\right) \Vert (\overline{u}, {{\tilde{u}}}, v)\Vert ^2_{{\mathbb {R}}\times X_\mu \times Y_\nu }\,, \end{aligned}$$

providing the constant $c_1= \frac{\pi }{2} \sqrt{1- (\tfrac{1}{2})^{2\mu }}$. Hence, (35) holds.

Summing up, from (34) and (35), since $c_1\le \frac{\pi }{2} \le c_2$, we deduce that

$$\begin{aligned} c_1 \Vert z\Vert _E \le \Vert L(z)\Vert _E \le c_2 \Vert z\Vert _E , \end{aligned}$$

in particular L is continuous and $\ker L=\{0\}$. A classical reasoning (cf. [12, Proposition 2.14]) shows that the image of L is closed and, since L is selfadjoint, we conclude that it is bijective and admits a continuous inverse $L^{-1}:E\rightarrow E$.

$\square$

Proposition 24

If $\big ( ({{\tilde{x}}}_0\,,y_0 \,, \overline{u}_0\,, {{\tilde{u}}}_0, v_0)\,, \overline{x}_0\big )$ is a critical point of $\varphi$, then

$$\begin{aligned} (\overline{x}_0 + {{\tilde{x}}}_0,y_0 , \overline{u}_0+ {{\tilde{u}}}_0, v_0)\hbox { is a solution of problem}~(17)-(4). \end{aligned}$$

Proof

Let $\big ( z_0\,, \overline{x}_0\big )= \big ( ({{\tilde{x}}}_0\,,y_0 \,, \overline{u}_0\,, {{\tilde{u}}}_0, v_0)\,, \overline{x}_0\big )\in E\times {\mathbb {R}}$ be a critical point of $\varphi$. Then, for any $\big ( z\,, \overline{x} \big )=\big ( ({{\tilde{x}}}\,,y \,, \overline{u}\,, {{\tilde{u}}}, v)\,, \overline{x}\big )\in E\times {\mathbb {R}}$, we have

$$\begin{aligned} 0=d\varphi (z_0,\overline{x}_0)(z,\overline{x})={\mathcal {B}}\big (z_0,z\big )+ d\psi (z_0,\overline{x}_0)(z,\overline{x}). \end{aligned}$$

(40)

Let us consider $u\in C^1([0,\pi ])$ and write $u={{\tilde{u}}} + \overline{u}$, with $\overline{u} = \frac{1}{\pi } \int _0^\pi u(t)\, dt$. Choosing $\big ( z\,, \overline{x} \big )=\big ( (0\,,0 \,, \overline{u}\,,{{\tilde{u}}}, 0)\,, 0\big )$ in (40), we obtain

$$\begin{aligned} 0= \int _0^\pi \Big (-{{\tilde{u}}}'\, v_0 - (\overline{u}+{{\tilde{u}}})\, (\overline{u}_0+{{\tilde{u}}}_0) + \partial _{u}{\widetilde{K}}_\varepsilon (t,\overline{x}_0+{{\tilde{x}}}_0,y_0,\overline{u}_0+{{\tilde{u}}}_0,v_0)\, (\overline{u} + {{\tilde{u}}})\Big )\, dt, \end{aligned}$$

that is, as $u'={{\tilde{u}}}'$,

$$\begin{aligned} -\int _0^\pi u'\, v_0\, dt = \int _0^\pi \Big ( (\overline{u}_0+{{\tilde{u}}}_0) - \partial _{u}{\widetilde{K}}_\varepsilon (t,\overline{x}_0+{{\tilde{x}}}_0,y_0,\overline{u}_0+{{\tilde{u}}}_0,v_0)\Big )\, u\, dt. \end{aligned}$$

Therefore, in the sense of distributions, we have

$$\begin{aligned} v_0'= (\overline{u}_0+{{\tilde{u}}}_0) - \partial _{u}{\widetilde{K}}_\varepsilon (t,\overline{x}_0+{{\tilde{x}}}_0,y_0,\overline{u}_0+{{\tilde{u}}}_0,v_0), \end{aligned}$$

which is the fourth equation in (18). In particular, $v_0\in W^{1,2}(0,\pi )$ and therefore it is continuous. With a similar reasoning, choosing, respectively, $\big ( z\,, \overline{x} \big )=\big ( (0\,,y \,,0\,, 0\,, 0)\,, 0\big )$, $\big ( z\,, \overline{x} \big )=\big ( ({{\tilde{x}}}\,,0 \,, 0\,, 0 \,, 0)\,, 0\big )$ and $\big ( z, \overline{x} \big )=\big ( (0,0 , 0, 0,v), 0\big )$ in formula (40), we see that the functions $\overline{x}_0 +{{\tilde{x}}}_0$, $y_0$ and $\overline{u}_0 + {{\tilde{u}}}_0$ are continuous and, in the sense of distributions, satisfy the other three equations in (18). From the equations in (18), we also deduce that $(\overline{x}_0 + {{\tilde{x}}}_0\,,y_0 \,, \overline{u}_0+ {{\tilde{u}}}_0, v_0)\in C^1([0,\pi ])^4$, so that the equations are satisfied in the classical sense. Therefore $(\overline{x}_0 + {{\tilde{x}}}_0\,,y_0 \,, \overline{u}_0+ {{\tilde{u}}}_0, v_0)$ is a solution of problem (17). Since $y_0, v_0\in Y_\nu$, the boundary conditions (4) are also satisfied and the conclusion follows. $\square$

4 The higher dimensional case

For $z=(x,y,u,v)\in {\mathbb {R}}^{N}$, we write

$$\begin{aligned}&x=(x_1 , \dots , x_M) \in {\mathbb {R}}^{M}, \quad y=(y_1 , \dots , y_M)\in {\mathbb {R}}^{M},\\&u=(u_1 , \dots , u_L) \in {\mathbb {R}}^{L}, \quad v=(v_1 , \dots , v_L)\in {\mathbb {R}}^{L}. \end{aligned}$$

We now consider the higher dimensional system

$$\begin{aligned} {\left\{ \begin{array}{ll} x'= \nabla _{y} H(t,x,y)+\varepsilon \,\nabla _{y}P(t,x,y,u,v)\,,\\ y'= -\nabla _{x} H(t,x,y)-\varepsilon \,\nabla _{x}P(t,x,y,u,v), \\ \displaystyle {u'_{j}} = f_{j}(t,v_{j})+\varepsilon \, \partial _{v_j}P (t,x,y,u,v), \quad j= 1, \dots , L,\\ \displaystyle {v'_{j}}= g_{j}(t,u_{j} )-\varepsilon \, \partial _{u_j}P (t,x,y,u,v), \quad j= 1,\dots , L, \end{array}\right. } \end{aligned}$$

(41)

with Neumann-type boundary conditions

$$\begin{aligned} {\left\{ \begin{array}{ll} y(a)=0=y(b),\\ v(a)=0=v(b). \end{array}\right. } \end{aligned}$$

(42)

Here $H:[a,b]\times {\mathbb {R}}^{2M}\rightarrow {\mathbb {R}}$, $P:[a,b]\times {\mathbb {R}}^{2M+2L}\rightarrow {\mathbb {R}}$ and $f_j:[a,b]\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ are continuous functions, with continuous partial derivatives with respect to the variables x, y, u, v, for every $j=1,\dots ,L$ ; the functions $g_j:[a,b]\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ are continuous, and $\varepsilon$ is a small real parameter.

We recall the definition of lower and upper solution for the system

$$\begin{aligned} u'_{j} = f_{j}(t,v_{j}), \quad \quad v'_{j}= g_{j}(t,u_{j} ), \quad j= 1, \dots , L, \end{aligned}$$

(43)

with Neumann-type boundary conditions

$$\begin{aligned} v(a)=0=v(b). \end{aligned}$$

(44)

Definition 25

A $C^{1}$-function $\alpha :[a,b]\rightarrow {\mathbb {R}}^L$ is a lower solution for problem (43)-(44) if there exists a $C^{1}$-function $v_{\alpha }:[a,b]\rightarrow {\mathbb {R}}^L$ such that, for every $t\in [a,b]$ and $j=1, \dots , L$,

$$\begin{aligned} {\left\{ \begin{array}{ll} s< v_{\alpha ,j}(t) \quad \Rightarrow \quad f_{j}(t,s) <{\alpha '_{j}}(t),\\ s> v_{\alpha ,j}(t) \quad \Rightarrow \quad f_{j}(t,s) >{\alpha '_{j}}(t), \end{array}\right. } \end{aligned}$$

$$\begin{aligned} v'_{\alpha ,j}(t) \ge g_{j}(t,\alpha _{j}(t)) , \end{aligned}$$

(45)

and

$$\begin{aligned} v_{\alpha ,j}(a)\ge 0\ge v_{\alpha ,j}(b). \end{aligned}$$

The lower solution is strict if the strict inequalities in (45) hold, for every $t\in [a,b]$ and $j=1, \dots , L$.

Definition 26

A $C^1$-function $\beta :[a,b] \rightarrow {\mathbb {R}}^{L}$ is an upper solution for problem (43)–(44) if there exists a $C^1$-function $v_{\beta }:[a,b]\rightarrow {\mathbb {R}}^{L}$ such that, for every $t\in [a,b]$ and $j=1, \dots , L$,

$$\begin{aligned} {\left\{ \begin{array}{ll} s< v_{\beta ,j}(t) \quad \Rightarrow \quad f_{j}(t,s) <{\beta '_{j}}(t),\\ s> v_{\beta ,j}(t) \quad \Rightarrow \quad f_{j}(t,s) >{\beta '_{j}}(t), \end{array}\right. } \end{aligned}$$

$$\begin{aligned} v'_{\beta ,j}(t) \le g_{j}(t,\beta _{j}(t)) , \end{aligned}$$

(46)

and

$$\begin{aligned} v_{\beta ,j}(a)\le 0\le v_{\beta ,j}(b). \end{aligned}$$

The upper solution is strict if the strict inequalities in (46) hold, for every $t\in [a,b]$ and $j=1, \dots , L$.

In the sequel, inequalities of n-tuples will be meant component-wise. Here is the list of our assumptions.

$(A1')$:

The function $H=H(t,x,y)$ is $\tau _j$-periodic in the variable $x_j$, for some $\tau _j>0$, for every $j=1,\dots ,M$ .

$(A2')$:

All solutions (x, y) of system

$$\begin{aligned} x'= \nabla _{y} H(t,x,y), \qquad y'=- \nabla _{x} H(t,x,y) \end{aligned}$$

starting with $y(a)=0$ are defined on [a, b] .

$(A3')$:

The function $P=P(t,x,y,u,v)$ is $\tau _j$-periodic in the variable $x_j$, for every $j=1,\dots ,M$.

$(A4')$:

The function $P=P(t,x,y,u,v)$ has a bounded gradient with respect to $z=(x,y,u,v)$.

$(A5')$:

There exist a strict lower solution $\alpha$ and a strict upper solution $\beta$ for problem (43)–(44) such that $\alpha \le \beta$ .

$(A6')$:

There exists $\lambda >0$ such that $\partial _{s}f_j(t,\,s)\ge \lambda$, for every $(t,s)\in [a,b]\times {\mathbb {R}}$ and $j=1,\dots ,L$ .

$(A7')$:

For every $j=1,\dots ,L$, the partial derivative $\partial _{v_j} P$ depends only on t, u and $v_j$ and is locally Lipschitz continuous with respect to $v_j$.

Let us state our main theorem.

Theorem 27

Let assumptions $(A1')$–$(A7')$ hold true. Then, there exists $\overline{\varepsilon }>0$ such that, when $|\varepsilon |\le \overline{\varepsilon }$, problem (41)–(42) has at least $M+1$ solutions (x, y, u, v) with $\alpha \le u\le \beta$.

Proof

Arguing as in Lemma 8, for every $\varepsilon \in {\mathbb {R}}$ and $j=1,\dots ,L$ there exist some $C^1$-functions $\alpha _{\varepsilon ,j}:[a,b]\rightarrow {\mathbb {R}}$ and $\beta _{\varepsilon ,j}:[a,b]\rightarrow {\mathbb {R}}$ such that

$$\begin{aligned} \begin{aligned}&f_{j}(t,v_{\alpha ,j}(t))+\varepsilon \partial _{v_{j}}P(t,\alpha _{\varepsilon }(t),v_{\alpha }(t))=\alpha _{\varepsilon ,j}'(t),\\&f_{j}(t,v_{\beta ,j}(t))+\varepsilon \partial _{v_{j}}P(t,\beta _{\varepsilon }(t),v_{\beta }(t))=\beta _{\varepsilon ,j}^{'}(t),\\&|\alpha _{\varepsilon ,j}(t)-\alpha _{j}(t)|<\varepsilon C\pi , \hbox { and }\, |\beta _{\varepsilon ,j}(t)-\beta _{j}(t)|<\varepsilon C\pi , \end{aligned} \end{aligned}$$

for every $t\in [a,\,b]$, where $\Vert \nabla _z P\Vert _\infty \le C$, from assumption $(A4')$.

Proceeding with the same strategy as in Sect. 3.1, we get the following modified system associated with system (41),

$$\begin{aligned} {\left\{ \begin{array}{ll} x'=\nabla _{y}{\widetilde{H}}(t,x,y)+\varepsilon \nabla _{y}P(t,x,y,u,v),\\ y'=-\nabla _{x}{\widetilde{H}}(t,x,y)-\varepsilon \nabla _{x}P(t,x,y,u,v),\\ u_j'={\tilde{f}}_{j}(t,\,v_{j})+\varepsilon \partial _{v_{j}}P(t,x,y,u,v), \quad j= 1, \dots , L,\\ v_j'={\tilde{g}}_{\varepsilon ,j}(t,u_{j})-\varepsilon \partial _{u_{j}}P(t,x,y,u,v) \quad j= 1, \dots , L. \end{array}\right. } \end{aligned}$$

(47)

In system (47),

• for every $j=1,\dots ,L$, ${\tilde{f}}_{j}:[a,b]\times {\mathbb {R}}^{L}\rightarrow {\mathbb {R}}$ is defined by

  $$\begin{aligned} {\tilde{f}}_{j}(t,v_{j})={\left\{ \begin{array}{ll} f_{j}(t,-d_{j})+v_{j}+d_{j},&{}\quad \hbox {if}\,\,v_{j}\le -d_{j},\\ f_{j}(t,v_{j}),&{}\quad \hbox {if}\,\,|v_{j}|\le d_{j},\\ f_{j}(t,d_{j})+v_{j}-d_{j},&{}\quad \hbox {if}\,\,v_{j}\ge d_{j}, \end{array}\right. } \end{aligned}$$

  where $d=(d_{1},\dots ,d_{j})$ is defined similarly as in (13).

• for every $j=1,\dots ,L$, ${\tilde{g}}_{\varepsilon ,j}:[a,b]\times {\mathbb {R}}^{L}\rightarrow {\mathbb {R}}$ is defined by

  $$\begin{aligned} {\tilde{g}}_{\varepsilon ,j}(t,u_{j})={\left\{ \begin{array}{ll} g_{j}(t,\alpha _{\varepsilon ,j}(t))-\alpha _{\varepsilon ,j}(t)+u_{j},&{}\quad \hbox {if}\,\,u_{j}\le \alpha _{\varepsilon ,j}(t),\\ g_{j}(t,u_{j}),&{}\quad \hbox {if}\,\,\alpha _{\varepsilon ,j}(t)\le u_{j}\le \beta _{\varepsilon ,j}(t),\\ g_{j}(t,\beta _{\varepsilon ,j}(t))-\beta _{\varepsilon ,j}(t)+u_{j},&{}\quad \hbox {if}\,\,u_{j}\ge \beta _{\varepsilon ,j}(t). \end{array}\right. } \end{aligned}$$

• ${\widetilde{H}}:[a,b]\times {\mathbb {R}}^{2M}\rightarrow {\mathbb {R}}$ is defined by

  $$\begin{aligned} {\widetilde{H}}(t,x,y)=\zeta (|y|)H(t,x,y), \end{aligned}$$

  where $\zeta$ is given in (16).

System (47) can also be written as

$$\begin{aligned} {\left\{ \begin{array}{ll} x'=\nabla _{y}{\widetilde{K}}_\varepsilon (t,x,y,u,v),\\ y'=-\nabla _{x}{\widetilde{K}}_\varepsilon (t,x,y,u,v),\\ u_{j}'=v_{j} + \partial _{v_{j}}{\widetilde{K}}_\varepsilon (t,x,y,u,v), \quad j= 1, \dots , L,\\ v_{j}'=u_{j}- \partial _{u_{j}}{\widetilde{K}}_\varepsilon (t,x,y,u,v), \quad j= 1, \dots , L, \end{array}\right. } \end{aligned}$$

(48)

where

$$\begin{aligned} {\widetilde{K}}_{\varepsilon }(t,x,y,u,v)&= {{\widetilde{H}}}(t,x,y)+\varepsilon P(t,x,y,u,v) + \sum _{j=1}^L \big (F_{j}(t,v_{j}) - G_{\varepsilon ,j}(t,u_{j})\big )\,, \\ \text {with } F_{j}(t,v_{j})&=\int \limits _{0}^{v_{j}} \big ({{\tilde{f}}}_{j}(t,s)-s \big )\, ds\,, \quad G_{\varepsilon ,j}(t,u_{j})= \int _0^{u_{j}} \big ({{\tilde{g}}}_{\varepsilon ,j}(t,\sigma )-\sigma \big )\, d\sigma \,. \end{aligned}$$

Arguing as in Lemma 11, we can verify that $\alpha _\varepsilon$ and $\beta _\varepsilon$ are indeed lower and upper solutions for the modified problem.

We will consider functions x and y belonging to the spaces

$$\begin{aligned} X_{\mu }^{M}=X_{\mu }\times \dots \times X_{\mu },\quad Y_{\nu }^{M}=Y_{\nu }\times \dots \times Y_{\nu }. \end{aligned}$$

Propositions 16 and 17 which are taken from [12] hold here also.

The existence of $M+1$ solutions of problem (41) with Neumann boundary conditions (42) will be given through the application of the following theorem.

Theorem 28

(Szulkin) If $\varphi : E\times {\mathbb {T}}^{M}\rightarrow {\mathbb {R}}$ is as in (25), where $d\psi (E\times {\mathbb {T}}^{M})$ is relatively compact and $L:E\rightarrow E$ is a bounded selfadjoint invertible operator, then there exist at least $M+1$ critical points of $\varphi$.

In the above theorem, ${\mathbb {T}}^{M}$ denotes the torus

$$\begin{aligned} {\mathbb {T}}^{M}=({\mathbb {R}}/\tau _{1}{\mathbb {Z}})\times \dots \times ({\mathbb {R}}/\tau _{M}{\mathbb {Z}}). \end{aligned}$$

We will apply it with L defined with the same strategy adopted in Sect. 3.4, the functionals $\varphi$ and $\psi$ defined by (25) and (26), respectively. All the hypotheses of Szulkin’s theorem are verified, providing the existence of $M+1$ solutions of the modified problem.

The lemmas stated in Sect. 3.1 are also true for the higher dimensional situation. Specifically, Proposition 15 in the higher dimensional setting assures that all the $M+1$ distinct solutions of (47)–(42) are also solutions of problem (41)–(42). This completes the proof. $\square$

5 A further result in higher dimension

Finally we want to deal with a system of a different type, i.e.,

$$\begin{aligned} {\left\{ \begin{array}{ll} x'= \nabla _{y} H(t,x,y)+\varepsilon \,\nabla _{y}P(t,x,y,u)\,,\\ y'= -\nabla _{x} H(t,x,y)-\varepsilon \,\nabla _{x}P(t,x,y,u),\\ u'=v, \quad v'= \nabla _u G(t,u)-\varepsilon \, \nabla _{u}P (t,x,y,u), \end{array}\right. } \end{aligned}$$

(49)

with Neumann-type boundary conditions

$$\begin{aligned} {\left\{ \begin{array}{ll} y(a)=0=y(b),\\ v(a)=0=v(b). \end{array}\right. } \end{aligned}$$

(50)

Here $H:[a,b]\times {\mathbb {R}}^{2M}\rightarrow {\mathbb {R}}$, $P:[a,b]\times {\mathbb {R}}^{2M+L}\rightarrow {\mathbb {R}}$ and $G:[a,b]\times {\mathbb {R}}^L\rightarrow {\mathbb {R}}$ are continuous functions, with continuous partial derivatives with respect to the variables x, y, u. Here is our result.

Theorem 29

Let assumptions $(A1')$–$(A4')$ hold true. Moreover, let $R>0$ be such that

$$\begin{aligned} |u|=R\quad \Rightarrow \quad \langle \nabla _uG(t,u),u\rangle >0. \end{aligned}$$

(51)

Then, there exists $\overline{\varepsilon }>0$ such that, when $|\varepsilon |\le \overline{\varepsilon }$, problem (49)–(50) has at least $M+1$ solutions (x, y, u, v) with $|u(t)|\le R$, for every $t\in [a,b]$.

Proof

We modify the function H exactly as above. Moreover, we also modify G as follows. From the Hartman’s condition (51) and the continuity of the inner product, there exists ${{\bar{e}}}>0$ and $\lambda >0$ such that

$$\begin{aligned} R\le |u|\le R+{{\bar{e}}}\quad \Rightarrow \quad \langle \nabla _uG(t,u),u\rangle \ge \lambda . \end{aligned}$$

(52)

Without loss of generality we can assume that

$$\begin{aligned} R\le |u|\le R+{{\bar{e}}}\quad \Rightarrow \quad G(t,u)\le 0,\quad \hbox {for every }t\in [a,b]. \end{aligned}$$

(53)

Define the function ${\widetilde{G}}:[a,b]\times {\mathbb {R}}^{L}\rightarrow {\mathbb {R}}$ by

$$\begin{aligned} {\widetilde{G}}(t,u)=\eta (|u|)\,G(t,u)+\frac{1}{2}|u|^{2}(1-\eta (|u|)), \end{aligned}$$

(54)

where $\eta :{\mathbb {R}}\rightarrow {\mathbb {R}}$ is a $C^{\infty }$-function such that

$$\begin{aligned} \eta (r)= {\left\{ \begin{array}{ll} 1,\quad &{}\hbox {if }\,r\le R,\\ 0,\quad &{}\hbox {if }\,r\ge R+{{\bar{e}}}, \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} \eta '(r)\le 0,\quad \hbox {when } R\le r\le R+{{\bar{e}}}. \end{aligned}$$

(55)

We consider the modified system

$$\begin{aligned} {\left\{ \begin{array}{ll} x'= \nabla _{y} {\widetilde{H}}(t,x,y)+\varepsilon \,\nabla _{y}P(t,x,y,u),\\ y'= -\nabla _{x} {\widetilde{H}}(t,x,y)-\varepsilon \,\nabla _{x}P(t,x,y,u),\\ u'=v, \quad v'= \nabla _u {\widetilde{G}}(t,u)-\varepsilon \, \nabla _{u}P (t,x,y,u). \end{array}\right. } \end{aligned}$$

(56)

We are in force to apply Szulkin’s Theorem 28, which provides us at least $M+1$ solutions for problem (56)–(50).

We now need to show that the solutions of problem (56)–(50) satisfy

$$\begin{aligned} |u(t)|\le R,\quad \hbox {for every }\,t\in [a,b], \end{aligned}$$

so that they are also solutions of problem (49)–(50). In order to show this, we argue by contradiction. Suppose there is $t_0\in [a,b]$ such that

$$\begin{aligned} |u(t_0)|=\max \{|u(t)|:t\in [a,b]\}>R. \end{aligned}$$

Let $f(t)=|u(t)|^{2}$; we have $f'(t)=2\langle u(t),u'(t)\rangle$, and

$$\begin{aligned} \begin{aligned} f''(t)&=2\langle u'(t),u'(t)\rangle +2\langle u(t),u''(t)\rangle \\&=2|u'(t)|^{2}+2\langle u(t),v'(t)\rangle \\&=2|u'(t)|^{2}+2\langle u(t),\nabla _u {\widetilde{G}}(t,u(t))-\varepsilon \, \nabla _{u}P (t,x(t),y(t),u(t))\rangle . \end{aligned} \end{aligned}$$

(57)

Assume first that $t_0\in \,]a,b[$ . Then, since f(t) has a maximum point at $t=t_0$, we have

$$\begin{aligned} f'(t_0)=0\quad \hbox {and}\quad f''(t_0)\le 0. \end{aligned}$$

(58)

On the other hand, if $t_0=a$, then necessarily $f'(a)=2\langle u(a),v(a)\rangle =0$, hence also in this case it has to be $f''(a)\le 0$. The same if $t_0=b$; it will be $f'(b)=2\langle u(b),v(b)\rangle =0$, hence $f''(b)\le 0$. We thus conclude that (58) holds in any case of $t_0\in [a,b]$.

Let us now analyze two distinct cases.

The first case is when $|u(t_0)|\ge R+{{\bar{e}}}$. From (57) and (54), if we apply the Cauchy–Schwarz inequality and the fact that $|\nabla _{u}P(t,x(t),y(t),u(t))|\le C$, we get

$$\begin{aligned} f''(t_0)&\ge 2\langle u(t_0),u(t_0)-\varepsilon \, \nabla _{u}P (t_0,x(t_0),y(t_0),u(t_0))\rangle \\&\ge 2|u(t_0)|^{2}-2 |\varepsilon |\, |u(t_0)|\, |\nabla _{u}P (t_0,x(t_0),y(t_0),u(t_0))|\\&= 2|u(t_0)|\Big [|u(t_0)|- |\varepsilon |\, |\nabla _{u}P (t_0,x(t_0),y(t_0),u(t_0))|\Big ]\\&\ge 2R\big [R- |\varepsilon | C\big ]>0\,, \end{aligned}$$

when $|\varepsilon |$ is small, a contradiction.

The other case is when $R<|u(t_0)|<R+{{\bar{e}}}$. Then, we compute

$$\begin{aligned} f''(t_0)&\ge 2\Big \langle u(t_0),\eta '(|u(t_0)|)\frac{u(t_0)}{|u(t_0)|}G(t_0,u(t_0))\Big \rangle \\&\quad - 2\Big \langle u(t_0), \textstyle {\frac{1}{2}}u(t_0)|u(t_0)|\eta '(|u(t_0)|)\Big \rangle \\&\quad +2\Big \langle u(t_0),\eta (|u(t_0)|)\nabla _{u}G(t_0,u(t_0))+u(t_0)(1-\eta (|u(t_0)|))\Big \rangle \\&\quad -2\Big \langle u(t_0),\varepsilon \, \nabla _{u}P (t_0,x(t_0),y(t_0),u(t_0))\Big \rangle \,,\\&\ge \underbrace{2|u(t_0)|\eta '(|u(t_0)|)G(t_0,u(t_0))}_{E_{1}}\\&\quad +\underbrace{2\eta (|u(t_0)|)\langle u(t_0),\nabla _{u}G(t_0,u(t_0))\rangle +2(1-\eta (|u(t_0)|))|u(t_0)|^{2} }_{E_{2}}\\&\quad -\underbrace{ |u(t_0)|^{3}\eta '(|u(t_0)|)}_{E_{3}}-\underbrace{2\varepsilon |u(t_0)||\nabla _{u}P (t_0,x(t_0),y(t_0),u(t_0))|}_{E_{4}}\,. \end{aligned}$$

From (53) and (55), we have that $E_{1}\ge 0$. Again from (55), it follows that $E_{3}\le 0$. From (52) and $|u(t_0)|>R$, we have

$$\begin{aligned} E_{2}&\ge 2\Big (\lambda \eta (|u(t_0)|)+(1-\eta (|u(t_0)|))R^{2}\Big )\ge 2\min \{\lambda ,R^{2}\}>0\,. \end{aligned}$$

Finally,

$$\begin{aligned} E_{4}\le 2|\varepsilon | (R+{{\bar{e}}})|\nabla _{u}P (t_0,x(t_0),y(t_0),u(t_0))|. \end{aligned}$$

Combining all the above facts, for $|\varepsilon |$ sufficiently small we get $f''(t_0)>0$, a contradiction.

This completes the proof. $\square$

Remark 30

The assumption (51) was introduced by Hartman [17] for the periodic problem (see also [4]). Notice that, when $L=1$, it is equivalent to asking that the constant functions $\alpha =-R$ and $\beta =R$ are a strict lower solution and a strict upper solution, respectively.

6 Examples and final remarks

As an illustrative example of application of Theorem 2, we consider the problem

$$\begin{aligned} {\left\{ \begin{array}{ll} x''= h(x) + \varepsilon \partial _x P(t,x,u), \\ u''=g(u)+\varepsilon \partial _u P(t,x,u), \\ x'(a)=0=x'(b), \qquad u'(a)=0=u'(b),\\ \end{array}\right. } \end{aligned}$$

(59)

where the functions $h,g:{\mathbb {R}}\rightarrow {\mathbb {R}}$ are continuous and $P:[0,\pi ]\times {\mathbb {R}}^2\rightarrow {\mathbb {R}}$ is continuous and has bounded continuous partial derivatives $\partial _x P(t,x,u)$ and $\partial _u P(t,x,u)$. The functions h and P are $2\pi$-periodic in x, with $\int _0^{2\pi } h(s)\, ds =0$. Concerning the function g we assume the existence of some constants $\alpha < \beta$ such that $g(\alpha )<0<g(\beta )$.

A typical example for the function h in the first equation in (59) might be $h(x)=-\sin x$, in which case we have a perturbed pendulum equation. Another choice would be the saw-tooth function $h(x)=\arcsin (\sin x)$. Concerning the second equation, possible examples for the function g are

$$\begin{aligned} \arctan u, \quad u^3, \quad \sin u, \quad \sin u^2, \quad u^5 \sin u, \quad \dots \end{aligned}$$

For the higher dimensional cases, similar examples can be constructed.

Let us now mention some possible further developments and open problems.

• 1. In assumption (A5) we require that the lower and upper solutions are strict. It would be interesting to obtain the same multiplicity result without such a strictness assumption.

• 2. The possibility of considering systems like (3) or (41) without a small parameter $\varepsilon$ has been analyzed in [18] in presence of constant lower and upper solutions. The case of non-constant lower and upper solutions remains open.

• 3. We wonder whether assumptions (A6) and (A7), and their corresponding higher dimensional versions, could be weakened.

• 4. We have treated here only the case when the lower and upper solutions are well-ordered. It would be interesting to know if the results may be extended to the non-well-ordered case.

• 5. In this paper we dealt with $C^1$-smooth lower and upper solutions. Following the ideas developed in [9], one might consider weaker regularity assumptions.

• 6. In view of the results in [11], concerning the radial solutions for an elliptic problem with Neumann boundary conditions, one could try to deal with a coupled system, where the fourth equation in (3) is replaced by

  $$\begin{aligned} (t^{n-1} v)'=t^{n-1}\big [g(t,u) - \varepsilon \partial _u P(t,x,y,u,v) \big ], \qquad t\in [0,R]. \end{aligned}$$

• 7. It would be interesting to extend the results of this paper to an infinite-dimensional setting. A version of the Poincaré–Birkhoff theorem for the periodic case in this setting has been proposed in [1]. On the other hand, the lower and upper solutions technique for second order differential equations has been extended to infinite dimensional systems in [10], also in the non-well-ordered case. We expect that the approaches in [1, 10] could be combined in order to obtain similar existence results for coupled systems as those considered in this paper.