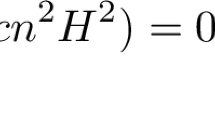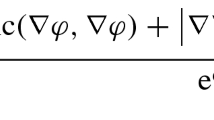Embeddedness of min–max CMC hypersurfaces in manifolds with positive Ricci curvature

Abstract

We prove that on a compact Riemannian manifold of dimension 3 or higher, with positive Ricci curvature, the Allen–Cahn min–max scheme in Bellettini and Wickramasekera (The Inhomogeneous Allen–Cahn Equation and the Existence of Prescribed-Mean-Curvature Hypersurfaces, 2020), with prescribing function taken to be a non-zero constant $\lambda$, produces an embedded hypersurface of constant mean curvature $\lambda$ ($\lambda$-CMC). More precisely, we prove that the interface arising from said min–max contains no even-multiplicity minimal hypersurface and no quasi-embedded points (both of these occurrences are in principle possible in the conclusions of Bellettini and Wickramasekera, 2020). The immediate geometric corollary is the existence (in ambient manifolds as above) of embedded, closed $\lambda$-CMC hypersurfaces (with Morse index 1) for any prescribed non-zero constant $\lambda$, with the expected singular set when the ambient dimension is 8 or higher.

FormalPara Theorem 1

For any $\lambda \in {\mathbb {R}} \setminus \{0\}$, and compact Riemannian manifold (N, g), with positive Ricci curvature and $\text {dim} \, N = n + 1\ge 3$, there exists a smooth, embedded, two-sided hypersurface M, with constant mean curvature $\lambda$ ($\lambda$-CMC), and

• 1. M is closed when $2 \le n \le 6$,

• 2. ${\overline{M}} \setminus M$ consists of finitely many points when $n = 7$,

• 3. $\text {dim}_{{\mathcal {H}}} \, ({\overline{M}} \setminus M) \le n - 7$, when $n \ge 8$.

In Theorem 1 the emphasis is on the fact that M is embedded: this appears to be a new result. The statement of Theorem 1 with embedded replaced by (the weaker notion of) quasi-embedded was on the other hand known, as detailed below (with two methods available). We recall that quasi-embedded means that the hypersurface is a smooth immersion, with any self-intersections being tangential, and with local structure around any point of tangential intersection being that of two embedded disks lying on opposite sides of each other (see [6, Definition 8]).

As it will be important for our arguments, we begin by recalling that the existence result in Theorem 1, with embedded replaced by quasi-embedded, follows from the work by the first author and Wickramasekera in [6]. In fact, [6, Theorem 1.1] proves the following more general result. Given a compact Riemannian manifold, (N, g), $\text {dim} \, N \ge 3$ (without any curvature assumptions) and a non-negative Lipschitz function $h:N\rightarrow {\mathbb {R}}$, there exists a quasi-embedded, two-sided $C^2$ hypersurface $M_{h}$ such that, for each $x \in M_{h}$, the scalar mean curvature of $M_{h}$ at x is given by h(x); the singular set $\overline{M_{h}} \setminus M_{h}$ satisfies the dimensional estimates listed in Theorem 1. The construction of $M_{h}$ is carried out in the Allen–Cahn min–max framework, and serves as a starting point for the present work. We briefly recall it here in the case $h=\lambda$ constant, with further details in Sect. 1.1.

Consider a sequence of functions $\{u_{i}\}$ in $W^{1,2}(N)$, where each $u_{i}$ is the solution of the appropriate $\varepsilon _{i}$-scaled inhomogeneous Allen–Cahn equation, with $\varepsilon _{i} \rightarrow 0$. Assuming uniform energy bound, the works of Hutchinson–Tonegawa [12] and Röger–Tonegawa [15] give, in the $\varepsilon _{i}\rightarrow 0$ limit, an integral varifold V (a “limit interface”), with generalised mean curvature $H_{V} \in L^{\infty } (\text {supp} \Vert V\Vert )$, along with a Caccioppoli set E, with $\partial ^{*} E \subset \text {supp} \, \Vert V\Vert$, such that,

$$\begin{aligned} {\left\{ \begin{array}{ll} H_{V} (x) = \lambda , \, \theta _{V} (x) = 1, &{} {\mathcal {H}}^{n} - a.e. \, x \in \partial ^{*} E, \\ H_{V} (x) = 0, \, \theta _{V} (x) \in 2 {\mathbb {Z}}_{\ge 1}, &{} {\mathcal {H}}^{n} - a.e. \, x \in \text {supp} \, \Vert V\Vert \setminus \partial ^{*} E. \end{array}\right. } \end{aligned}$$

In the presence of such a sequence $\{ u_{i} \}$, the two major roadblocks to an existence result for a $\lambda$-CMC are (i) $\partial ^{*} E$ may be empty, in which case the limit interface is actually minimal (ii) even if $\partial ^{*} E \not = \emptyset$, it may not have sufficient regularity ([6, Figure 1] illustrates how lack of regularity could prevent $\partial ^{*} E$ from being an admissible candidate). In [6] a (first) sequence $u_{i}$ is produced by means of a classical mountain pass lemma; the Morse index of $u_{i}$ is at most 1 (as a consequence of the fact that the min–max has one parameter). It is moreover shown (see [6, Remark 6.7]) that in the case of ambient manifold with positive Ricci curvature (and with $h=\lambda$ constant), occurrence (i) cannot arise, that is, $\partial ^{*} E$ is non-trivial when $u_{i}$ is the sequence obtained from the min–max. For arbitrary ambient manifolds, in the event that $u_{i}$ leads to occurrence (i), [6] implements a gradient flow that yields a (second) sequence $\{v_{i}\}$, for which $\partial ^{*} E \not = \emptyset$ and with Morse index 0. The matter is thus reduced to a regularity question for the limit interface arising from a sequence $u_{i}$ with uniformly bounded Morse index. This index control is used in a key way to obtain regularity ([6, Theorem 1.2]), whose proof relies on extensions of Y. Tonegawa’s work [18] and Tonegawa–Wickramasekera’s work [19], and crucially on the (non-variational) varifold regularity result [5, Theorem 9.1] (see also [6, Theorem 3.2]). In conclusion, [6] obtains that $V = V_{\lambda } + V_{0}$, where $\text {supp} \, \Vert V_{\lambda }\Vert = \partial E = \overline{M_{\lambda }}$ and $\text {supp} \, \Vert V_{0}\Vert = \overline{M_{0}}$; here $M_{\lambda }$ is a two-sided, quasi-embedded $\lambda$-CMC hypersurface, and $M_{0}$ an embedded minimal hypersurface, both satisfying the dimensional estimates listed in Theorem 1. Furthermore, any intersections between $M_{\lambda }$ and $M_{0}$, and self-intersections of $M_{\lambda }$, are always tangential intersections of $C^{2}$ graphs lying on one side of each other.

With this as a starting point, our first step in establishing Theorem 1 is to show that when $\text {Ric}_{g} > 0$, the one-parameter Allen–Cahn min–max just recalled does not produce any minimal components in the limit interface, i.e. $V_{0} = 0$. (As mentioned earlier, in this case [6] establishes already that $V_{\lambda } \not = 0$ for the $u_{i}$ produced by min–max.)

FormalPara Theorem 2

Let (N, g) be a compact Riemannian manifold of dimension $\ge 3$, with positive Ricci curvature, and $\lambda > 0$. The one-parameter Allen–Cahn min–max in [6], with prescribing function set to $\lambda$, produces a two-sided $\lambda$-CMC hypersurface and no minimal hypersurface.

Theorem 2 is achieved by exhibiting a suitable continuous path, admissible in the min–max construction (which employs paths that are continuous in $W^{1,2}(N)$). This path will move through functions that are each modelled on a level set of the signed distance to $M_{\lambda }$. The idea is to try to place a 1-dimensional Allen–Cahn profile along the normal direction to a given level set and thus produce a function (a point in the path). This might appear problematic due to the presence of points where the level sets are not smoothly embedded in N (which, for example, may be caused by the presence of the singular set $\overline{M_{\lambda }} \setminus M_{\lambda }$, or by the fact that $M_\lambda$ has quasi-embedded points). We handle this after observing that all “problematic points” are contained in a closed n-rectifiable set. The open complement (in N) of this n-rectifiable set is described (via a diffeomorphism) as an open subset of ${\tilde{M}} \times {\mathbb {R}}$, where ${\tilde{M}}$ is a (abstract) n-manifold whose immersion into N gives $M_\lambda$. We will refer to this open subset as the Abstract Cylinder (which is endowed with a metric pulled back from N). Each level set of the distance function becomes a subset of ${\tilde{M}} \times \{s\}$, where s is the chosen distance value. The sought path is then defined by “sliding” the 1-dimensional Allen–Cahn profiles in the ${\mathbb {R}}$-direction in the whole cylinder ${\tilde{M}} \times {\mathbb {R}}$, then restricting these functions to the Abstract Cylinder, and passing them to N. We check that this indeed produces a continuous path in $W^{1,2} (N)$. Furthermore, performing the energy calculations on the Abstract Cylinder, we see that the potentially “problematic points” do not cause any issues. The sliding argument yields a path with the (key) property that the relevant Allen–Cahn energy attains a maximum (along the path) at the function obtained in correspondence of $M_\lambda$ (signed distance equal to 0); this relies on the positivity of the Ricci curvature. This property of the path easily implies that $V_{0}= 0$ (no minimal component), for otherwise the min–max characterisation of V would be contradicted. Theorem 1 is then proven by showing that the $\lambda$-CMC hypersurface arising in Theorem 2 is, in fact, embedded. This is again done by exhibiting a suitable path (admissible in the min–max). This path is constructed by editing the previous one about its maximum, under the contradiction assumption that a non-embedded point exists in $M_\lambda$. The modification requires the identification of suitable hypersurfaces obtained by deforming $M_\lambda$ about the non-embedded point. This construction ensures that the modified path attains a maximum that is strictly smaller than the maximum obtained for the path used in the proof of Theorem 2. This contradicts the min–max characterisation. We stress that these path constructions capitalise on the a priori knowledge (from [6]) that $M_\lambda$ and $M_0$ are sufficiently regular.

We remark that Theorem 2 is somewhat interesting in its own sake: it is an open question whether (and under what assumptions) a sequence of solutions to the inhomogeneous Allen–Cahn equation with nowhere vanishing inhomogeneous term, and with a uniform bound on the Morse index, can produce minimal components. (The regularity result in [6] recalled earlier allows us to refer to the minimal and prescribed-mean-curvature components as hypersurfaces that are separately smooth, except for a possible small singular set when the ambient dimension is 8 or higher.) Theorem 2 rules out minimal components in the special instance in which the solutions come from a one-parameter min–max (in N compact with $\text {Ric}_N>0$) and the inhomogeneous term is constant.

The absence of minimal components and of non-embedded points established by Theorem 1 has, among its consequences, a Morse index estimate:

FormalPara Corollary 1

The $\lambda$-CMC hypersurface in Theorem 2 has Morse index equal to 1.

This follows directly from Mantoulidis [14]. Alternatively, the arguments of Hiesmayr [11] apply verbatim. (We refer to Sect. 9 for the definition of Morse index.)

As we recalled, [6] employs an Allen–Cahn approximation scheme to construct the $\lambda$-CMC quasi-embedded hypersurface. The statement of Theorem 1 with embedded replaced by quasi-embedded can also be obtained (without any curvature assumption on N) using the so-called Almgren–Pitts method for the min–max, see the combined works of Zhou–Zhu [22] ($2 \le n \le 6$) and Dey in [7] (for $n\ge 7$, relying on the compactness theory in [4, 5]).

Regardless of the method used for the min-max construction, and without the need of curvature assumptions, if $2 \le n \le 6$ the $\lambda$-CMC hypersurface obtained is closed and immersed (completely smooth). In White’s work [20, Theorem 35] it is proven that for each $\lambda \in {\mathbb {R}}$, there exists a generic set (in the sense of Baire category) of smooth metrics on the ambient manifold such that any closed, codimension-1 (completely smooth) immersion with constant mean curvature $\lambda$, is self-transverse. Therefore, combining the existence of quasi-embedded $\lambda$-CMC ([6] or [22]) with [20, Theorem 35], one obtains: when $2\le n \le 6$, for any $\lambda$, there exists a generic set of metrics on N, such that each admits an embedded $\lambda$-CMC hypersurface.¹

This argument relies however on the complete smoothness of the $\lambda$-CMC hypersurface, which is not available for $n\ge 7$ in the existence results. The flavour of Theorem 1 differs from the statement just given in that it allows a singular set and can handle all dimensions; moreover the class of metrics (Ricci positive metrics) is the same for all $\lambda \in {\mathbb {R}}$. We also stress that the proof of embeddedness in Theorem 1 exploits the min–max characterisation of the $\lambda$-CMC, while one can apply [20, Theorem 35] to any smooth CMC immersion, not necessarily one coming from a min–max. Theorems 1 and 2 may also hold with other assumptions on the metric on N, or other choices on the set of prescribing functions. (In these different scenarios an alternative approach to the sliding argument mentioned above could be a gradient flow, for example, along the lines of [3, Section 5.4] and [6, Section 6.9].)

1 Preliminaries

1.1 Allen–Cahn and construction of CMC immersion

We recall the min–max construction in [6], of critical points to the inhomogeneous Allen–Cahn energy,

$$\begin{aligned} {\mathcal {F}}_{\varepsilon , \lambda } (u) = \int _{N} \frac{\varepsilon }{2}|\nabla u|^2 + \frac{W(u)}{\varepsilon } - \sigma \int _{N} \lambda u, \quad \varepsilon \in (0,1), \, u \in W^{1,2} (N).\qquad \end{aligned}$$

(1)

Where W is- a smooth function on ${\mathbb {R}}$, with $W (\pm 1) = 0$ being non-degenerate minima, and $W(t) > 0$, for $t \in {\mathbb {R}} \setminus \{\pm 1\}$. Furthermore, we impose that W has only three critical points, $t = 0, \, \pm 1$, and quadratic growth outside some compact interval. For example $W(t) = (1 - t^{2})^{2} / 4$, for $t \in [-2,2]$ and has linear growth outside $[-3,3]$. The constant $\sigma$ is given by,

$$\begin{aligned} \sigma = \int _{-1}^{1} \sqrt{W(s) / 2} \, ds. \end{aligned}$$

Moreover, we take $\lambda > 0$.

Consider the first and second variations of (1) with respect to $\varphi \in C^{\infty } (N)$,

$$\begin{aligned} \delta {\mathcal {F}}_{\varepsilon , \lambda }(u)(\varphi )= & {} \int _{N} \varepsilon \nabla u \cdot \nabla \varphi + \left( \frac{W'(u)}{\varepsilon } - \sigma \lambda \right) \varphi , \end{aligned}$$

(2)

$$\begin{aligned} \delta ^{2} {\mathcal {F}}_{\varepsilon , \lambda }(u)(\varphi , \varphi )= & {} \int _{N} \varepsilon |\nabla \varphi |^2 + \frac{W''(u)}{\varepsilon } \varphi ^2. \end{aligned}$$

(3)

We say that u is a critical point of (1), if $\delta {\mathcal {F}}_{\varepsilon , \lambda } (u) (\varphi ) = 0$, for all $\varphi \in C^{\infty } (N)$, and then by standard elliptic theory we have that $u \in C^{\infty } (N)$, and strongly solves,

$$\begin{aligned} \varepsilon \Delta u = \frac{W'(u)}{\varepsilon } - \sigma \lambda . \end{aligned}$$

(4)

If $\delta ^{2} {\mathcal {F}}_{\varepsilon , \lambda } (u) (\varphi , \varphi ) \ge 0$, for all $\varphi \in C^{\infty } (N)$, then we say that u is a stable solution to (4). By Fig. 1, we see that there exists two stable constant solutions, $a_{\varepsilon } > -1$, and $b_{\varepsilon } > 1$. Furthermore, as $\varepsilon \rightarrow 0$, we have that $a_{\varepsilon } \rightarrow - 1$, and $b_{\varepsilon } \rightarrow 1$. As $\text {Ric}_{g} > 0$, [2, Proposition 7.1] shows that these are the only stable critical points of (1).

Fig. 1

Intersection points, $a_{\varepsilon }$, $b_{\varepsilon }$, and $c_{\varepsilon }$, are the solutions to $W'(t) = \varepsilon \sigma \lambda$

The existence of these isolated, stable solutions permits us to find non-trivial critical points of (2) via a min–max argument.

Proposition 1

(Existence of Min–Max Solution, [6, Proposition 5.1]) For $\varepsilon > 0$, let $\Gamma$ denote the collection of all continuous paths $\gamma :[-1,1] \rightarrow W^{1,2}(N)$, such that $\gamma (-1) = a_{\varepsilon }$, and $\gamma (1) = b_{\varepsilon }$. Then there exists an $\varepsilon _0 > 0$, such that for all $\varepsilon < \varepsilon _{0}$,

$$\begin{aligned} \inf _{\gamma \in \Gamma } \sup _{u \in \gamma ([-1,1])} {\mathcal {F}}_{\varepsilon ,\lambda } = \beta _{\varepsilon }> {\mathcal {F}}_{\varepsilon , \lambda } (a_{\varepsilon }) > {\mathcal {F}}_{\varepsilon , \lambda } (b_{\varepsilon }), \end{aligned}$$

(5)

is a critical value, i.e. there exists $u_{\varepsilon } \in W^{1,2}(N)$, critical point of ${\mathcal {F}}_{\varepsilon , \lambda }$, with ${\mathcal {F}}_{\varepsilon , \lambda } (u_{\varepsilon }) = \beta _{\varepsilon }$; moreover, $u_{\varepsilon }$ has Morse index $\le 1$.

In our Ricci positive setting, as $a_{\varepsilon }$ and $b_{\varepsilon }$ are the only stable critical points we actually have that $u_{\varepsilon }$ has Morse index equal to 1.

Now taking a sequence $\{ \varepsilon _{i} \}_{i \in {\mathbb {N}}} \subset (0, \varepsilon _{0})$, with $\varepsilon _{i} \rightarrow 0$, and associated critical points from Proposition 1, $\{ u_{i} = u_{\varepsilon _{i}} \}$, we associate the following Radon measures,

$$\begin{aligned} \mu _{i} {:}{=}(2 \sigma )^{-1} \left( \frac{\varepsilon _{i}}{2} |\nabla u_{i}|^{2} + \frac{W(u_{i})}{\varepsilon _{i}} \right) \, d \mu _{g}. \end{aligned}$$

(6)

Where $\mu _{g}$ is the volume measure of (N, g). Moreover there exists constants K, $L > 0$, such that for all i,

$$\begin{aligned} \sup _{N} |u_{i}| + \mu _{i} (N) \le K, \end{aligned}$$

(7)

and

$$\begin{aligned} \mu _{i} (N) \ge L. \end{aligned}$$

(8)

By the bounds of (7) and (8), there exists a subsequence $\{ u_{i'} \} \subset \{ u_{i} \}$, along with a $u_{0} \in BV(N)$, with $u_{0} (y) \in \{ +1, -1\}$ for all $y \in N$, and a non-zero Radon measure $\mu$, such that $u_{i'} \rightarrow u_{0}$ in $L^{1} (N)$, and $\mu _{i'} \rightharpoonup \mu$ as Radon measures. By [12, Theorem 1] and [15, Theorem 3.2], we have that $\mu$ is the weight measure of an integral n-varifold V, with the following properties:

• 1. V, is an integral n-varifold with bounded generalised mean curvature $H_{V}$, and first variation $\delta V = - H_{V} \mu _{V}$.

• 2. The set $E {:}{=}\{ u_{0} = + 1\}$ is a Caccioppoli set, with reduced boundary $\partial ^{*} E \subseteq \text {spt } \, V \subset N \setminus E \not = \emptyset$.

• 3. For ${\mathcal {H}}^{n}$-a.e. $x \in \partial ^{*}E$, $\Theta (\mu _{V}, x) = 1$, and $H_{V}(x) \cdot \nu (x) = \lambda$; where $\nu$ is the inward pointing unit normal to $\partial ^{*} E$, i.e. $\nu = \nabla u_0 / |\nabla u_0|$.

• 4. For ${\mathcal {H}}^{n}$ a.e. $x \in \text {spt} \, V \setminus \partial ^{*} E$, $\Theta (\mu _{V}, x)$ is an even integer $\ge 2$, and $H_{V} (x) = 0$.

Optimal regularity of V was then proven in [6].

• 1. $V = V_{0} + V_{\lambda }$

• 2. $V_{0}$ is a (possibly zero) stationary integral n-varifold with singular set of Hausdorff dimension at most $n - 7$.

• 3. $V_{\lambda } = |\partial ^{*} E| \not = \emptyset$, and $\partial ^{*} E$ is a quasi-embedded hypersurface with constant mean curvature $\lambda$, with respect to unit normal pointing into E. The singular set of $\partial ^{*} E$ has Hausdorff dimension at most $n - 7$.

• 4. V has a $(\lambda , 0)$-CMC structure.

By $(\lambda , 0)$-CMC structure we mean that for each point on the support of V, potentially away from a closed set of Hausdorff dimension at most $n - 7$, the local picture is one of the following,

• 1. There is a single embedded $\lambda$-CMC disk.

• 2. There are two embedded $\lambda$-CMC disks that lie on either side of each other and only touch tangentially.

• 3. There is a single embedded minimal disk

• 4. There is a single embedded $\lambda$-CMC disk and a single embedded minimal disk that only touch tangentially.

• 5. There are two embedded $\lambda$-CMC disks that lie on either side of each other, along with an embedded minimal disk, such that all three disks only touch tangentially.

For a detailed definition of a $(\lambda , 0)$-CMC structure, see [6, Definition 8]. We define the set $\text {gen-reg} \, V$, to be the set of points on $\text {supp} \, \Vert V\Vert$, which satisfy one of the local pictures of 1 to 5. For a detailed definition of $\text {gen-reg} \, V$ see [6, Definition 5].

Therefore, we have the following

Theorem 3

(Theorem 1.1 [6]) Let N be a closed Riemannian manifold of dimension $n+1 \ge 3$, with positive Ricci curvature, and let $\lambda \in (0, \infty )$ be a fixed constant. There exists a smooth, quasi-embedded hypersurface $M \subset N$, with;

• 1. ${\overline{M}} \setminus M = \emptyset$, if $2 \le n \le 6$;

• 2. ${\overline{M}} \setminus M$ is finite if $n = 7$;

• 3. $\text {dim}_{{\mathcal {H}}}({\overline{M}} \setminus M) \le n - 7$, if $n \ge 8$.

Moreover M is the image of a two sided immersion with mean curvature $H_{M} = \lambda \nu$, for a choice $\nu$ of continuous unit normal to the immersion.

We restate Theorems 1 and 2 with our new notation.

Theorem 4

Consider a closed Riemannian manifold (N, g), with positive Ricci curvature and $\text {dim} \, N = n + 1 \ge 3$. Take $\lambda \in (0, \infty )$. The limiting varifold $V = V_{\lambda } + V_{0}$ from Sect. 1.1 has the following properties

• 1. $M {:}{=}\text {gen-reg} \, V_{\lambda }$ is embedded, connected and has index 1.

• 2. $V_{0} = 0$.

This says that only case 1 can occur.

1.2 One dimensional Allen–Cahn solution

We refer to [2, Section 2.2] as a reference for this section.

We define the function ${\mathbb {H}}$ on ${\mathbb {R}}$ to denote the monotonically increasing solution to the ODE $u'' - W'(u) = 0$, with the conditions ${\mathbb {H}} (0) = 0$ and $\lim _{t \rightarrow \pm \infty } {\mathbb {H}} (t) = \pm 1$. We then define ${\mathbb {H}}_{\varepsilon } (\, \cdot \,) = {\mathbb {H}} (\varepsilon ^{-1} \, \cdot )$, which solves the ODE $\varepsilon u'' - \varepsilon ^{-1} W'(u) = 0$.

We define an approximation for ${\mathbb {H}}_{\varepsilon }$. Start by considering the following bump function

$$\begin{aligned} {\left\{ \begin{array}{ll} \chi \in C_{c}^{\infty } ({\mathbb {R}}), \\ \chi (t) = 1, &{} t \in (-1,1), \\ \chi (t) = 0, &{} t \in {\mathbb {R}} \setminus (-2,2), \\ \chi (t) = \chi (-t), &{} t \in {\mathbb {R}}, \\ \chi '(t) \le 0, &{} t \ge 0. \\ \end{array}\right. } \end{aligned}$$

For $\varepsilon \in (0, 1)$, we define the truncation of ${\mathbb {H}}_{\varepsilon }$ by

$$\begin{aligned} {\overline{{\mathbb {H}}}}_{\varepsilon } (t) {:}{=}{\left\{ \begin{array}{ll} \chi ((\varepsilon \Lambda )^{-1} t) {\mathbb {H}}_{\varepsilon } (t) + 1 - \chi ((\varepsilon \Lambda )^{-1} t), &{} t > 0, \\ \chi ((\varepsilon \Lambda )^{-1} t) {\mathbb {H}}_{\varepsilon } (t) - 1 + \chi ((\varepsilon \Lambda )^{-1} t), &{} t < 0, \end{array}\right. } \end{aligned}$$

where $\Lambda = 3 |\log \varepsilon |$. There exists a constant $\beta = \beta (W) < + \infty$, such that for all $\varepsilon \in (0,1/4)$,

$$\begin{aligned} 2 \sigma - \beta \varepsilon ^{2}< \int _{{\mathbb {R}}} \frac{\varepsilon }{2} |({\overline{{\mathbb {H}}}}_{\varepsilon })' (t)|^{2} + \frac{W({\overline{{\mathbb {H}}}}_{\varepsilon } (t))}{\varepsilon } \, dt < 2 \sigma + \beta \varepsilon ^{2}. \end{aligned}$$

2 Idea of proof

We first prove Theorem 1 for the case $\lambda > 0$. To then prove for $\lambda < 0$, we take ${\tilde{\lambda }} = - \lambda > 0$, and reverse the direction of the unit normal on the resulting ${\tilde{\lambda }}$-CMC hypersurface. From here on we take $\lambda > 0$.

For Caccioppoli sets $\Omega \subset N$, we define the following functional,

$$\begin{aligned} {\mathcal {F}}_{\lambda } (\Omega ) {:}{=}{\mathcal {H}}^{n} (\partial ^{*} \Omega ) - \lambda \mu _{g} (\Omega ). \end{aligned}$$

Recall our converging sequence of critical points $\{u_{\varepsilon _{j}}\}$, along with our limiting varifold $V = V_{\lambda } + V_{0}$, and Caccioppoli set E from Sect. 1.1. We have, as $\varepsilon _{j} \rightarrow 0$,

$$\begin{aligned} {\mathcal {F}}_{\varepsilon _{j}, \lambda } (u_{\varepsilon _{j}}) \rightarrow 2 \sigma {\mathcal {F}}_{\lambda } (E) + 2 \sigma {\mathbb {M}} (V_{0}) + \sigma \lambda \mu _{g} (N) \end{aligned}$$

Therefore, constructing minimising paths between $\emptyset$ and N for ${\mathcal {F}}_{\lambda }$, may provide insight to minimising paths from $a_{\varepsilon }$ to $b_{\varepsilon }$ for ${\mathcal {F}}_{\varepsilon , \lambda }$.

As N is compact, one obvious path that includes E, is $\{ E_{t} \}$ for $t \in [-2 \, \text {diam} (N), 2 \, \text {diam} (N)]$, where,

$$\begin{aligned} E_{t} {:}{=}\{ y :{\tilde{d}} (y) > t\}. \end{aligned}$$

Here ${\tilde{d}}$ is the signed distance function to $M {:}{=}\partial ^{*} E$, taking positive values in E, and negative values in $N \setminus E$. We also denote,

$$\begin{aligned} \Gamma _{t} {:}{=}\{ y :{\tilde{d}} (y) = t \} = \partial E_{t}. \end{aligned}$$

Assuming sufficient regularity on the sets $\Gamma _{t}$ and $E_{t}$, and the functions $t \mapsto {\mathcal {H}}^{n} (\Gamma _{t})$ and $t \mapsto \mu _{g} (E_{t})$, we have for $t > 0$,

$$\begin{aligned} \begin{aligned} {\mathcal {F}}_{\lambda } (E_{t}) - {\mathcal {F}}_{\lambda } (E)&= \int _{0}^{t} \frac{d}{ds} {\mathcal {H}}^{n} (\Gamma _{s}) \, ds - \lambda \int _{0}^{t} \frac{d}{ds} \mu _{g} (E_{s}) \, ds, \\&= \int _{0}^{t} \int _{\Gamma _{s}} \lambda - H_{\Gamma _{s}} (x) \, d {\mathcal {H}}^{n} (x) \, ds, \end{aligned} \end{aligned}$$

(9)

where $H_{\Gamma _{s}}$ is the scalar mean curvature of $\Gamma _{s}$ with respect to unit normal $\nabla {\tilde{d}}$. Recalling that $H_{\Gamma _{0}} = \lambda$, a straightforward calculation yields the following inequalities.

$$\begin{aligned} {\left\{ \begin{array}{ll} H_{\Gamma _{t}} \ge \lambda + m t, &{} t \ge 0, \\ H_{\Gamma _{t}} \le \lambda + m t, &{} t \le 0, \end{array}\right. } \end{aligned}$$

where $m = \min _{|X| = 1} \, Ric_{g} (X, X) > 0$. Therefore, by (9) for $t \ge 0$,

$$\begin{aligned} {\mathcal {F}}_{\lambda } (E_{t}) \le {\mathcal {F}}_{\lambda } (E). \end{aligned}$$

The same inequality holds for $t \le 0$. Here we see the importance of the assumption on the Ricci curvature. Therefore,

$$\begin{aligned} \gamma :t \in [-2 \, \text {diam} (N), 2 \, \text {diam} (N)] \mapsto E_{-t} \in \{ \text {Caccioppoli sets of} \, N \}, \end{aligned}$$

is a path from $\emptyset$ to N, that has maximum height ${\mathcal {F}}_{\lambda } (E)$.

We look to replicate this path in $W^{1,2} (N)$. Consider the Lipschitz function on N,

$$\begin{aligned} v_{\varepsilon }^{t} = {\overline{{\mathbb {H}}}}_{\varepsilon } ({\tilde{d}} (x) - t), \end{aligned}$$

which can be thought of as placing the truncated one dimensional Allen–Cahn solution from Sect. 1.2 along the normal profile of $\Gamma _{t}$. By the Co-Area formula, we have,

$$\begin{aligned} {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{t}) = \int _{{\mathbb {R}}} Q_{\varepsilon } (s - t) {\mathcal {H}}^{n} (\Gamma _{s}) \, ds - \sigma \lambda \int _{{\mathbb {R}}} {\overline{{\mathbb {H}}}}_{\varepsilon } (s - t) {\mathcal {H}}^{n} (\Gamma _{s}) \, ds, \end{aligned}$$

were,

$$\begin{aligned} Q_{\varepsilon } (t) = \frac{\varepsilon }{2} | \left( {\overline{{\mathbb {H}}}}_{\varepsilon } \right) ' (t) |^{2} + \frac{W\left( {\overline{{\mathbb {H}}}}_{\varepsilon } (t) \right) }{\varepsilon } \end{aligned}$$

The functions

$$\begin{aligned} t \mapsto \int _{{\mathbb {R}}} Q_{\varepsilon } (s - t) {\mathcal {H}}^{n} (\Gamma _{s}) \, ds, \hspace{0.5cm} and \hspace{0.5cm} t \mapsto \sigma \lambda \int _{{\mathbb {R}}} {\overline{{\mathbb {H}}}}_{\varepsilon } (s - t) {\mathcal {H}}^{n} (\Gamma _{s}) \, ds, \end{aligned}$$

act as smooth approximations to $t \mapsto 2 \sigma {\mathcal {H}}^{n} (\Gamma _{t})$, and $t \mapsto 2 \sigma \lambda \mu _{g} (E_{t}) - \sigma \lambda \mu _{g} (N)$, respectively.

We say that $v_{\varepsilon }^{0}$ is an Allen–Cahn approximation of M as,

$$\begin{aligned} {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{0}) \rightarrow 2 \sigma {\mathcal {H}}^{n} (M) - \sigma \lambda \mu _{g} (E) + \sigma \lambda \mu _{g} (N \setminus E) {=}{:}A_{2}, \end{aligned}$$

as $\varepsilon \rightarrow 0$, Sect. 3.6. Carrying out a calculation which replicates the previous one, we deduce that for all $\tau > 0$, there exists an $\varepsilon _{\tau } > 0$, such that for all $\varepsilon \in (0, \varepsilon _{\tau })$,

$$\begin{aligned} \max _{t \in [- 2 \, \text {diam} (N), 2 \, \text {diam} (N)]}{\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{t}) < A_{2} + \tau = A_{1} - 2 \sigma {\mathbb {M}} (V_{0}) + \tau , \end{aligned}$$

where $A_{1} {:}{=}2 \sigma {\mathcal {H}}^{n} (M) + 2 \sigma {\mathbb {M}} (V_{0}) - \sigma \mu _{g} (E) + \sigma \mu _{g} (N \setminus E)$. Connecting $v_{\varepsilon }^{2 \, \text {diam}(N)} = -1$ to $a_{\varepsilon }$, and $v_{\varepsilon }^{- 2 \, \text {diam} (N)} = + 1$ to $b_{\varepsilon }$, by constant functions, we see that we have an appropriate min–max path in $W^{1,2} (N)$.

This path proves that we cannot have a minimal piece $V_{0}$. We also get criterion for M. Indeed, as there exists a ’Wall’, [6, Lemma 5.1], that all min–max paths must climb over, we have that

$$\begin{aligned} 2 \sigma \lambda {\mathcal {H}}^{n} (M) - \sigma \lambda \mu _{g} (E) + \sigma \lambda \mu _{g} (N \setminus E) > \sigma \lambda \mu _{g} (N). \end{aligned}$$

Rearranging yields,

$$\begin{aligned} {\mathcal {H}}^{n} (M) > \lambda \mu _{g} (E). \end{aligned}$$

We note that the above path can be constructed for any suitable $\lambda$-CMC hypersurface which encloses a volume. Therefore, for any such pair (M, E), the above inequality holds, and our min–max must choose the pair that minimises the positive quantity ${\mathcal {H}}^{n} (M) - \lambda \mu _{g} (E)$. From this, we can deduce that E must be connected.

We turn our attention to proving that M is embedded. We prove by contradiction, exploiting the min–max characterisation of M. We now know that, given our sequence of critical points $\{ u_{\varepsilon _{j}} \}$, and potentially after taking a subsequence,

$$\begin{aligned} {\mathcal {F}}_{\varepsilon _{j}, \lambda } (u_{\varepsilon _{j}}) \rightarrow 2 \sigma {\mathcal {H}}^{n} (M) - \sigma \lambda \mu _{g} (E) + \sigma \lambda \mu _{g} (N \setminus E) = A_{2}, \end{aligned}$$

as $\varepsilon _{j} \rightarrow 0$. Assume that M has a non-embedded point $z_{0}$. Then for every $\varepsilon _{j} > 0$, we construct a continuous path,

$$\begin{aligned} \gamma _{\varepsilon _{j}} :[-1,1] \rightarrow W^{1,2} (N), \end{aligned}$$

where, $\gamma _{\varepsilon _{j}} (-1) = a_{\varepsilon _{j}}$, and $\gamma _{\varepsilon _{j}} (1) = b_{\varepsilon _{j}}$. This path satisfies the following, there exists a J in ${\mathbb {N}}$, and $\varsigma > 0$, independent of j, such that for all $j \ge J$,

$$\begin{aligned} \max _{t \in [-1,1]} {\mathcal {F}}_{\varepsilon _{j}, \lambda } (\gamma _{\varepsilon _{j}} (t)) < 2 \sigma {\mathcal {H}}^{n} (M) - \sigma \lambda \mu _{g} (E) + \sigma \lambda \mu _{g} (N \setminus E) - \varsigma , \end{aligned}$$

This is a contradiction of the min–max characterisation of $u_{\varepsilon _{j}}$.

We sketch the main ideas of the path in the $\varepsilon$-limit, Fig. 2.

The picture at $z_{0}$ is Fig. 3a. The limiting energy for this structure is $A_{2}$. The starting point for building this path is to construct a competitor with lower limiting energy. Then we wish to connect this competitor to $+1$ and $-1$, with energy always remaining a fixed amount below $A_{2}$.

Step 1: Construction of Competitor, (1) $\rightarrow$ (2) in Fig. 2, Sect. 5

The structure at $z_{0}$ is two smooth, embedded CMC disks, that touch tangentially at $z_{0}$ and lie either side of each other. To construct the competitor, we push these disks together, and delete portions of the disks that are pushed past each other. This reduces the area of our structure while also increasing the size of E, leading to a drop in energy.

Idea 1: Push the whole of M by some fixed distance $\rho$.

This equates to pushing M to the level $\Gamma _{- \rho }$. As seen previously, this will lead to a drop in energy. Furthermore, there is an obvious path to $+ 1$, namely we keep pushing along level sets, $\Gamma _{- r}$ for r in $[\rho , 2 \, \text {diam} (N)]$. However, there is no obvious path to $-1$. Pushing $\Gamma _{- \rho }$ in the direction of E, will increase the energy and bring us back to M, undoing the energy drop that the competitor created.

Idea 2: Push the disks together locally.

Consider open balls $B_{1} \subset \subset B_{2}$ about $z_{0}$. We smoothly bump the disks at $z_{0}$ such that inside $B_{1}$ we move the disks of distance $\rho > 0$, and outside $B_{2}$ we remain fixed. The balls $B_{1}$ and, $B_{2}$ along with $\rho$, are chosen so that the area inside $B_{1}$ gets deleted, Fig. 3b. Letting,

$$\begin{aligned} \varsigma = \frac{\sigma }{2} {\mathcal {H}}^{n} (B_{1} \cap M), \end{aligned}$$

we see that our competitor has energy lying below, $A_{2} - \varsigma$.

Step 2: Path to +1, Sect. 7

To connect to the competitor, $+ 1$ we look to copy the successful path to $+ 1$ of the competitor in Idea 1. To construct the competitor, we only edited M locally about $z_{0}$. Therefore, pushing the competitor to the level set $\Gamma _{- \rho }$ will correspond to a similar drop in energy from pushing M to $\Gamma _{- \rho }$. This is (2) $\rightarrow$ (6) in Fig. 2. See Fig. 3b and f for local pictures about $z_{0}$. From $\Gamma _{- \rho }$ we can easily connect to $+ 1$ by pushing along level sets $\Gamma _{- r}$, as previously discussed.

Step 3: Path to $-1$, Sect. 6

We look to follow a similar method as in Step 2 by connecting our competitor to a level set $\Gamma _{r_{0}}$, for $r_{0} >0$, then push this along level sets $\Gamma _{r}$ for r in $[r_{0}, 2 \, \text {diam} (N)]$ to connect it to $-1$. By pushing our competitor straight to $\Gamma _{r_{0}}$ we run the risk of pushing through M and increasing our energy back up to $A_{2}$. Therefore, we carry out our path in stages, again making use of the fact that our edit about $z_{0}$ was local.

The first stage is (2) $\rightarrow$ (3) in Fig. 2. We fix our competitor in $B_{2}$, and outside we push forward, so that outside some larger ball $B_{3}$, we line up with $\Gamma _{r_{0}}$. See Fig. 3b and c for local pictures about $z_{0}$. Again, as our edit is local about $z_{0}$, this corresponds to a similar drop in energy of pushing M to $\Gamma _{r_{0}}$, and the drop will be of order $r_{0}^{2}$. For a large enough $r_{0}$ this will give us a large enough energy drop to be able to undo the edit inside $B_{2}$, and still have our energy remain below $A_{2} - \varsigma$. This is the second stage from (3) $\rightarrow$ (4), in Fig. 2. See Fig. 3d, for local picture about non-embedded point. From here we push up inside $B_{3}$ to line up with $\Gamma _{r_{0}}$, (4) $\rightarrow$ (5) in Figs. 2, 3e. Finally, we connect to $- 1$ by sliding along level sets as previously stated.

Fig. 2

The Paths. To prove $V_{0} = 0$, we follow the path from $-1$ to (5), then the dotted line to (1), dotted line to (6), then complete the path to $+1$. The dashed line from (1) to (2) is the construction of the competitor. Then, to prove that M is embedded, we follow the path from $-1$ to $+1$ given by the solid lines. Refer to Fig. 3 for the local picture about the non-embedded point $z_{0}$ at each numbered stage on the paths

Fig. 3

Stages of the Path at the non-embedded point $z_{0}$. In each image, the dashed lines represent the original $\lambda$-CMC disks, as a reference to what we are changing at each step. Furthermore, in each image, it is the solid lines that are the boundaries between the ’$+1$’ and ’$-1$’ regions

Path at $\varepsilon$ Level

We carry out this ’pushing’, on what we refer to as our abstract cylinder, ${\tilde{M}} \times {\mathbb {R}}$. See Sect. 3.3. Here ${\tilde{M}}$ is an n-dimensional manifold and $\iota :{\tilde{M}} \rightarrow M$ is a smooth immersion. We define the following map,

$$\begin{aligned} F :{\tilde{M}} \times {\mathbb {R}}\rightarrow & {} N, \\ (x,t)\mapsto & {} \exp _{\iota (x)} (t \nu (x))), \end{aligned}$$

with $\nu$ being a smooth choice of unit normal to immersion, pointing into E. Therefore, we view points (x, t) on our cylinder ${\tilde{M}} \times {\mathbb {R}}$ as having base point $\iota (x)$ and moving length t along the geodesic with initial direction $\nu (x)$. See Fig. 4.

Recall our function $v_{\varepsilon }^{0} = {\overline{{\mathbb {H}}}}_{\varepsilon } \circ {\tilde{d}}$, then by the Co-Area formula,

$$\begin{aligned} {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{0})= & {} \int _{{\mathbb {R}}} \left( \frac{\varepsilon }{2} |({\overline{{\mathbb {H}}}}_{\varepsilon })' (t)|^{2} + \frac{W({\overline{{\mathbb {H}}}}_{\varepsilon } (t))}{\varepsilon } - \sigma \lambda {\overline{{\mathbb {H}}}}_{\varepsilon } (t) \right) \, {\mathcal {H}}^{n} (\Gamma _{t}) \, dt, \\= & {} \int _{{\mathbb {R}}} \int _{{\tilde{M}}} \left( \frac{\varepsilon }{2} |({\overline{{\mathbb {H}}}}_{\varepsilon })' (t)|^{2} + \frac{W({\overline{{\mathbb {H}}}}_{\varepsilon } (t))}{\varepsilon } - \sigma \lambda {\overline{{\mathbb {H}}}}_{\varepsilon } (t) \right) \, \theta _{t} (x) \, d {\mathcal {H}}^{n} (x) \, dt, \end{aligned}$$

where $\theta _{t} :{\tilde{M}} \rightarrow {\mathbb {R}}$, is defined by the Area Formula to be such that for a.e $t \in {\mathbb {R}}$, and any ${\mathcal {H}}^{n}$-measurable function on N,

$$\begin{aligned} \int _{\Gamma _{t}} g \, d {\mathcal {H}}^{n} = \int _{{\tilde{M}}} (g \circ F_{t}) \, \theta _{t} \, d {\mathcal {H}}^{n}, \end{aligned}$$

with $F_{t} ( \, \cdot \, ) = F ( \, \cdot \,, t)$. Then we carry out the relevant ’pushings’ by considering a continuous family of functions $\{g_{r}\}_{r \in [0,r']}\subset C({\tilde{M}})$,

$$\begin{aligned} {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{r})= & {} \int _{{\mathbb {R}}} \int _{{\tilde{M}}} \biggl ( \frac{\varepsilon }{2} |({\overline{{\mathbb {H}}}}_{\varepsilon })' (t - g_{r}(x))|^{2} + \frac{W({\overline{{\mathbb {H}}}}_{\varepsilon } (t - g_{r}(x)))}{\varepsilon } \\{} & {} \hspace{1cm} - \sigma \lambda {\overline{{\mathbb {H}}}}_{\varepsilon } (t - g_{r}(x)) \biggr ) \, \theta _{t} (x) \, d{\mathcal {H}}^{n} (x,t) \, dt. \end{aligned}$$

See Fig. 5.

Fig. 4

Local pictures about points in M

Fig. 5

How the competitor is constructed as the graph of bump functions about points $x_{0}^{1}$ and $x_{0}^{2}$ over ${\tilde{M}}$. Whatever is bumped out beyond the dotted line, on the right-hand side, is not considered in N. In other words, it is deleted

2.1 Structure of the paper

The paper is organised as follows. We start with setup:

• Section 3 is devoted to set up of objects used in the main computation.

• In Sect. 4 we carry out the main computation. The constructions that follow are carried out by plugging explicitly defined functions into this computation.

To prove Theorem 2:

• In Sect. 8.2 we build the dotted path (5) $\rightarrow$ (1) $\rightarrow$ (6) in Fig. 2. Theorem 2 then follows upon combining this with computations in Sects. 6.4 and 7.2; in these sections we build the paths (5) $\rightarrow$ $-1$, and (6) $\rightarrow$ $+1$, in Fig. 2.

To prove Theorem 1 we argue by contradiction, assuming that M has a non-embedded point $z_{0}$:

• In Sect. 5 we construct our competitor about $z_{0}$. This is the dashed path (1) $\rightarrow$ (2) in Fig. 2.

• In Sect. 6 we construct a path from the competitor to the stable constant $a_{\varepsilon }$. This is the solid path (2) $\rightarrow$ (6) $\rightarrow$ $+1$, in Fig. 2.

• In Sect. 7 we construct a path from the competitor to the stable constant $b_{\varepsilon }$. This is the solid path (2) $\rightarrow$ (3) $\rightarrow$ (4) $\rightarrow$ (5) $\rightarrow$ $-1$ in Fig. 2.

• In Sect. 8.3 we piece together this continuous path from $a_{\varepsilon }$ to $b_{\varepsilon }$, in $W^{1,2}(N)$. The energy ${\mathcal {F}}_{\varepsilon , \lambda }$, is less than $A_{2} - \varsigma$ for every point along this path, Fig. 2. This contradicts the min–max construction, proving that M is embedded.

Finally, in Sect. 9 we prove Corollary 1 (the Morse index of M is equal to 1, which also implies that M must be connected).

2.2 A note on choice of constants

The biggest subtlety in the Construction of the path in Sects. 5, 6 and 7 is the choice of constants, and the order that we choose them in. We explicitly list the order of choices here, and reference where they have been chosen.

• 1. We first choose a non-embedded point $z_{0}$

• 2. We choose $\delta = \delta (z_{0}, N, M, g, \lambda , W) > 0$, in Remarks 5, 6, 7, 8, 16.

• 3. We choose $L = L (z_{0}, N, M, g, \delta , \lambda , W) > 0$, in Remarks 12, 21.

• 4. We choose $k = k (z_{0}, N, M, g, \delta , L, \lambda , W)$, in Remark 22.

• 5. We choose $r_{0} = r_{0} (z_{0}, N, M, g, \delta , L, k, \lambda , W) > 0$, in Remarks 12, 21, 24.

• 6. We choose $\rho = \rho (z_{0}, N, M, g, \delta , L, k, r_{0}, \lambda , W) > 0$, in Remarks 9, 10, 11, 14, 18, 23.

• 7. We define $l = l (\rho )$ in (10).

• 8. We choose $\tau > 0$ in Sects. 8.2 and 8.3.

• 9. We finally choose $\varepsilon _{\tau } = \varepsilon _{\tau } (z_{0}, N, M, g, \delta , L, k, r_{0}, \rho , \tau , \lambda , W) > 0$, in Remarks 15, 19, 20 and Sects. 8.2 and 8.3.

3 Construction of objects

3.1 Signed distance function

Let $d_{{\overline{M}}} :N \rightarrow {\mathbb {R}}$ be the distance function to the closed set ${\overline{M}} \subset N$. As ${\overline{M}}$ is closed, and N is complete, Hopf–Rinow tells us that, for each z in N, the value, $d_{{\overline{M}}}(z)$, is obtained by a geodesic from z to a point on ${\overline{M}}$. Furthermore, $d_{{\overline{M}}}$ is Lipschitz, with Lipschitz constant 1.

We may choose our representative of $u_{0}$ in $L^{1} (N)$ such that the set $E = \{u_{0} = 1\}$ is an open set in N, and ${\overline{M}} = \partial E$. This allows us to define the signed distance function, ${\tilde{d}} :N \rightarrow {\mathbb {R}}$, to ${\overline{M}}$, which takes positive values in E, and negative values in $N \setminus E$,

$$\begin{aligned} {\tilde{d}}(y) = {\left\{ \begin{array}{ll} d_{{\overline{M}}} (z), &{} x \in E, \\ - d_{{\overline{M}}} (z), &{} x \not \in E. \end{array}\right. } \end{aligned}$$

This is a 1-Lipschitz function on N.

3.2 Abstract surface

M is a quasi-embedded $\lambda$-CMC hypersurface, [6, Definition 8].

Remark 1

For a point $z \in M$, there exists an n-dimensional linear subspace $T = T_{z} \subset T_{z} N$, and a unit vector $\nu _{z} \in T^{\perp }$, along with $r = r(z) >0$, $s = s(z) > 0$, and $S = S (z) >0$, such that $S < \text {inj} \, (N)$. We define the cylinder

$$\begin{aligned} C_{z, T, r, s} {:}{=}\exp _{z} \left( \{ X + t \nu _{z} :X \in B_{r}^{T_{z} N} (0) \cap T, \, t \in (-s,s) \} \right) \subset B_{S}^{N} (z), \end{aligned}$$

and, one of the following holds:

• 1. (See Fig. 4b) There exists a smooth function,

  $$\begin{aligned} f :B_{z, T, r} {:}{=}B_{r}^{T_{z} N} (0) \cap T \rightarrow (-s,s), \end{aligned}$$

  which satisfies,

  $$\begin{aligned} {\left\{ \begin{array}{ll} f(0) = 0, \\ \nabla ^{T} f (0) = 0, \\ \Delta _{T} f (0) = \lambda , \end{array}\right. } \end{aligned}$$

  and,

  $$\begin{aligned} {\overline{M}} \cap C_{z, T, r, s} = \exp _{z} ( \text {Graph} \, (f) ) = \exp _{z} ( \{ X + f(X) \nu _{z} :X \in B_{z,T,r} \} ) \end{aligned}$$

  Furthermore, we have that,

  $$\begin{aligned} E \cap C_{z, T, r, s} = \exp _{z} ( \{ X + t \nu _{z} :X \in B_{z, T, r}, \, f(X)< t < s \} ), \end{aligned}$$

  and we can define a smooth choice of unit normal to $\exp _{z} (\text {Graph} \, (f))$,

  $$\begin{aligned} \nu :\exp _{z} (\text {Graph} \, (f)) \rightarrow T (\exp _{z} (\text {Graph} \, (f)))^{\perp }, \end{aligned}$$

  such that $\nu (z) = \nu _{z}$.

• 2. (See Fig. 4a) There exists two smooth functions,

  $$\begin{aligned} f_{1}, \, f_{2} :B_{z, T, r} \rightarrow (-s,s), \end{aligned}$$

  which satisfy,

  $$\begin{aligned} {\left\{ \begin{array}{ll} f_{1} (0) = 0 = f_{2} (0), \\ f_{1} \ge f_{2}, \\ \nabla ^{T} f_{1} (0) = 0 = \nabla ^{T} f_{2} (0), \\ \Delta _{T} f_{1} (0) = \lambda = - \Delta _{T} f_{2} (0), \end{array}\right. } \end{aligned}$$

  and,

  $$\begin{aligned} {\overline{M}} \cap C_{z,T, r, s} = \bigcup _{i= 1,2} \exp _{z} (\text {Graph} \, (f_{i})) = \bigcup _{i = 1, 2} \exp _{z} (\{ X + f_{i} (X) \nu _{z} :X \in B_{z, T, r} \}). \end{aligned}$$

  Furthermore, we have that,

  $$\begin{aligned} E \cap C_{z, T, r, s}= & {} \exp _{z} (\{ X + t \nu _{z} :X \in B_{z, T, r}, \, f_{1} (X)< t< s \}) \\{} & {} \hspace{1cm} \cup \, \exp _{z} (\{ X + t \nu _{z} :X \in B_{z, T, r}, \, - s< t < f_{2} (X) \}), \end{aligned}$$

  and we can define smooth choices of unit normals,

  $$\begin{aligned} \nu _{i} :\exp _{z} (\text {Graph} \, (f_{i})) \rightarrow T (\exp _{z} (\text {Graph} \, (f)))^{\perp }, \end{aligned}$$

  such that $\nu _{1} (z) = \nu _{z}$, and $\nu _{2} (z) = - \nu _{z}$.

If Case 1 holds, then we say that z is an embedded point of M. Alternatively, if Case 2 holds, we say that z is a non-embedded point of M. In either case, the tangent space of M at z is given by, $T_{z} M {:}{=}T_{z}$.

Claim 1

([4, Remark 2.6]) The set of non-embedded points of M has ${\mathcal {H}}^{n}$-measure 0.

We define our abstract surface ${\tilde{M}}$ by

$$\begin{aligned} {\tilde{M}} = \{ (z, \nu ) :z \in M, \, \nu \in T_{z} M^{\perp }, \, \text {with} \, |\nu | = 1, \, \text {and points into} \, E \}. \end{aligned}$$

Locally ${\tilde{M}}$ is a smooth, embedded CMC disk in N, therefore, ${\tilde{M}}$ is a smooth n-dimensional manifold.

3.3 Abstract cylinder

Consider x in ${\tilde{M}}$, then $x = (z, X)$, for some z in M and X in $T_{z}M^{\perp }$. We define two, smooth projections, first from ${\tilde{M}}$ to $TM^{\perp }$,

$$\begin{aligned} \nu :(z,X) \mapsto X, \end{aligned}$$

and secondly, from ${\tilde{M}}$ to M,

$$\begin{aligned} \iota :(z,X) \mapsto z. \end{aligned}$$

From these we define the following map,

$$\begin{aligned} F :{\tilde{M}} \times {\mathbb {R}}\rightarrow & {} N, \\ (x,t)\mapsto & {} \exp _{\iota (x)} (t \nu (x)), \end{aligned}$$

which, as N is complete, is well-defined. For a fixed x in ${\tilde{M}}$, F is a unit parametrisation of a geodesic which, at time 0, passes through $\iota (x)$, with velocity $\nu (x)$. The set $\{ t :d_{{\overline{M}}}(F(x,t)) = |t| \}$, is the set of times t, at which this geodesic achieves the shortest distance from F(x, t) to ${\overline{M}}$. Consider the subset $\{t :{\tilde{d}} (F(x,t)) = t\} \subset \{ t :d_{{\overline{M}}}(F(x,t)) = |t| \}$, and its endpoints,

$$\begin{aligned} \sigma ^{+}(x)= & {} \sup \{ t :{\tilde{d}}(F(x,t)) = t \} \ge 0, \\ \sigma ^{-}(x)= & {} \inf \{ t :{\tilde{d}}(F(x,t)) = t \} \le 0. \end{aligned}$$

These are uniformly bounded functions on ${\tilde{M}}$, and in fact as the next claim shows, $\{ t :{\tilde{d}}(F(x,t)) = t \}$ is a closed and connected interval on ${\mathbb {R}}$.

Claim 2

We have that

$$\begin{aligned}{}[\sigma ^{-}(x), \sigma ^{+}(x)] = \{ t: {\tilde{d}}(F(x,t)) = t\}. \end{aligned}$$

Proof

Consider the geodesic, $\gamma : t \mapsto F(x,t)$, and define the following function,

$$\begin{aligned} f: t \mapsto {\tilde{d}}(F(x,t)). \end{aligned}$$

This is a 1-Lipschitz function with $f(0) = 0$. Indeed,

$$\begin{aligned} |f(t_{1}) - f(t_{2})| \le |d(F(x,t_{1}), F(x,t_{2}))| \le \text {Length} (\gamma _{|[t_{1}, t_{2}]}) = |t_{1} - t_{2}|. \end{aligned}$$

For $t_{0} \ge 0$, such that $f(t_{0}) \not = t_{0}$, we must have $f(t_{0}) < t_{0}$. By Lipschitz constant 1, for any $t > t_{0}$,

$$\begin{aligned} f(t)= & {} f(t) - f(t_{0}) + f(t_{0}), \\\le & {} t- t_{0} + f(t_{0}), \\< & {} t. \end{aligned}$$

Similarly, if we have $t_{0} \le 0$, such that $f(t_{0}) \not = t_{0}$, then $f(t) \not = t$, for all $t < t_{0}$.

By continuity, we have that ${\tilde{d}}(F(x, \sigma ^{+} (x))) = \sigma ^{+}(x)$, and therefore by above, for all $t \in [0, \sigma ^{+}(x)]$, we must have that ${\tilde{d}}(F(x,t)) = t$. By definition of $\sigma ^{+}(x)$, for all $t > \sigma ^{+}(x)$, ${\tilde{d}}(F(x,t)) < t$. Therefore,

$$\begin{aligned}{}[0, \sigma ^{+}(x)] = \{t \ge 0 :{\tilde{d}}(F(x,t)) = t \}. \end{aligned}$$

Similarly, $[\sigma ^{-}(x), 0] = \{ t \le 0 :{\tilde{d}}(F(x,t)) = t \}.$ $\square$

We define the abstract cylinder,

$$\begin{aligned} {\tilde{T}} = \{(x,t) :x \in {\tilde{M}}, \, t \in (\sigma ^{-}(x), \sigma ^{+}(x))\} \subset {\tilde{M}} \times {\mathbb {R}}. \end{aligned}$$

Defining the projection map from ${\tilde{M}} \times {\mathbb {R}}$ onto ${\mathbb {R}}$, $p :(x,t) \mapsto t$, then on ${\tilde{T}}$ we have that ${\tilde{d}} \circ F = p$.

We wish to work on ${\tilde{T}}$ instead of N. The following Lemma is crucial in that respect.

Lemma 1

(Geodesic Touching Lemma) For all y in $N \setminus {\overline{M}}$, there exists a geodesic from y to ${\overline{M}}$ that achieves the length of $d_{{\overline{M}}}(y)$. The end point of this geodesic on ${\overline{M}}$ must in fact be a quasi-embedded point of M, and the geodesic will hit M orthogonally.

Proof

Identical argument to [2, Lemma 3.1], except we replace the Sheeting Theorem of [21] with the Sheeting Theorem of [4]. $\square$

From this Lemma, the following result is immediate,

Proposition 2

For all y in $N \setminus ({\overline{M}} \setminus M)$, there exists an x in ${\tilde{M}}$, such that $F(x, {\tilde{d}}(y)) = y$.

Claim 3

The functions, $\sigma ^{+}, \, \sigma ^{-} :{\tilde{M}} \rightarrow {\mathbb {R}}$, are continuous.

Proof

We prove by contradiction. Suppose there exists an ${\hat{x}} \in {\tilde{M}}$ such that, $\liminf _{x \rightarrow {\hat{x}}} \sigma ^{+} (x) = \alpha < \sigma ^{+} ({\hat{x}})$. Choose $0< \delta < \sigma ^{+} ({\hat{x}}) - \alpha$, then there exists $x_{n} \rightarrow {\hat{x}}$ in ${\tilde{M}}$ such that $\sigma ^{+} (x_{n}) < \alpha + \delta$. Now consider the points,

$$\begin{aligned} z_{n} = F(x_{n}, \alpha + \delta ) \rightarrow z {:}{=}F({\hat{x}}, \alpha + \delta ). \end{aligned}$$

By Claim 2, ${\tilde{d}} (z_{n}) < \alpha + \delta$. By Proposition 2 there exists a sequence ${\tilde{x}}_{n}$, such that,

$$\begin{aligned} F({\tilde{x}}_{n}, {\tilde{d}}(z_{n})) = z_{n}. \end{aligned}$$

After potentially taking a subsequence and renumerating we have that there exists a $y \in {\overline{M}}$, such that $\iota ({\tilde{x}}_{n}) \rightarrow y$, then note $d(y, z) = {\tilde{d}} (z) = \alpha + \delta$. Therefore, by Lemma 1, $y \in M$, and as $t \mapsto F({\hat{x}}, t)$ is the unique length minimising geodesic from M to z, ${\tilde{x}}_{n} \rightarrow {\hat{x}}$ in ${\tilde{M}}$. Now we have that,

$$\begin{aligned} F(x_{n}, \alpha + \delta ) = z_{n} = F({\tilde{x}}_{n}, {\tilde{d}}(z_{n})). \end{aligned}$$

However, $(x_{n}, \alpha + \delta ) \not = ({\tilde{x}}_{n}, {\tilde{d}}(z_{n}))$, and

$$\begin{aligned} \lim _{n \rightarrow \infty } (x_{n}, \alpha + \delta ) = ({\hat{x}}, \alpha + \delta ) = \lim _{n \rightarrow \infty } ({\tilde{x}}_{n}, {\tilde{d}}(z_{n})). \end{aligned}$$

This implies that F is not a diffeomorphism about the point $({\hat{x}}, \alpha + \delta )$, and therefore by classical theory of geodesics, [16, Lemma 2.11], $t \mapsto F({\hat{x}}, t)$ is no longer length minimising to M beyond time $t = \alpha + \delta$. This contradicts $\alpha + \delta < \sigma ^{+} ({\hat{x}})$.

Now suppose that $\sigma ^{+} ({\hat{x}})< \limsup _{x \rightarrow {\hat{x}}} \sigma ^{+} (x) = \beta < + \infty$. Choose $0< \delta < \beta - \sigma ^{+} ({\hat{x}})$, and sequence $x_{n} \rightarrow {\hat{x}}$, such that,

$$\begin{aligned} \sigma ^{+} (x_{n}) > \sigma ^{+} ({\hat{x}}) + \delta . \end{aligned}$$

Define,

$$\begin{aligned} z_{n} = F(x_{n}, \sigma ^{+} ({\hat{x}}) + \delta ), \end{aligned}$$

then ${\tilde{d}}(z_{n}) = \sigma ^{+} ({\hat{x}}) + \delta$. By continuity of F,

$$\begin{aligned} z_{n} \rightarrow z {:}{=}F({\hat{x}}, \sigma ^{+} ({\hat{x}}) + \delta ). \end{aligned}$$

However, by definition of $\sigma ^{+} ({\hat{x}})$, ${\tilde{d}} (z) < \sigma ^{+} ({\hat{x}}) + \delta = {\tilde{d}} (z_{n})$. This contradicts continuity of ${\tilde{d}}$.

Similar arguments show that $\sigma ^{-}$ is also continuous. $\square$

We define the Cut Locus of M to be the following points in N,

$$\begin{aligned} \text {Cut} \, (M) = \{ F(x, \sigma ^{+} (x)) :x \in {\tilde{M}} \} \cup \{ F(x, \sigma ^{-} (x)) :x \in {\tilde{M}} \} \subset N, \end{aligned}$$

and by Proposition 2, we have that,

$$\begin{aligned} N \setminus ({\overline{M}} \setminus M) = F({\tilde{T}}) \cup \text {Cut} \, (M). \end{aligned}$$

Proposition 3

$\text {Cut} \, (M)$ is an n-rectifiable set.

To prove Proposition 3, we first classify points in $\text {Cut} (M)$,

Proposition 4

A point y in $N \setminus ({\overline{M}} \setminus M)$, lies in $\text {Cut}(M)$ if and only if at least one of the following conditions holds:

• 1. y lies in $N \setminus {\overline{M}}$, and there exists an x in ${\tilde{M}}$ such that $F(x, {\tilde{d}}(y)) = y$, and $dF_{(x, {\tilde{d}}(y))} :T_{x} {\tilde{M}} \times {\mathbb {R}} \rightarrow T_{y} N$, is non-invertible.

• 2. y lies in $N \setminus {\overline{M}}$, and there exists at least two unique geodesics from y to ${\overline{M}}$ which achieve the length $d_{{\overline{M}}}(y)$.

• 3. y is a non-embedded point of M.

Proof

Consider a point $y = F(x, 0) \in M$. If y is an embedded point of M, then case 1 of Remark 1 holds, and there exists an $S > 0$, such that ${\overline{M}} \cap B_{S}(y)$ is a smooth, embedded CMC disk. Therefore, ([13, Proposition 4.2]) there exists an r in (0, S/2), such that for all t in $(-r,r)$, ${\tilde{d}}(F(x,t)) = t$. Therefore, if $y \in M \cap \text {Cut} (M)$, then y must be a non-embedded point.

Alternatively, if y is a non-embedded point then case 2 of Remark 1 holds, and $(y, \nu )$ and $(y, - \nu )$ both lie in ${\tilde{M}}$. Moreover, for $t \in (- s, 0)$, $t < f_{2} (0)$, implying that $F((y, \nu ), t) = \exp _{y} (t \nu )$ lies in E. Therefore, ${\tilde{d}} (F((y, \nu ), t)) \ge 0$, implying that $\sigma ^{-} (y, \nu ) = 0$, and thus y is a point in $\text {Cut} (M)$.

For $y \in N \setminus {\overline{M}}$, the conclusion follows from standard theory of geodesics, see [16]. We can use this classical theory in our setting by Lemma 1. This observation is seen [2, Proposition 3.1]. $\square$

Remark 2

By point 2 of Proposition 4, $F({\tilde{T}})$ and $\text {Cut} \, (M)$ must be disjoint. Therefore, by point 1 of Proposition 4, F must be a local diffeomorphism on ${\tilde{T}}$. Moreover, by point 2, $F :{\tilde{T}} \rightarrow F({\tilde{T}})$ is a bijection.

Proof

(of Proposition 3) As $\text {Cut} (M) \cap M$ consists of non-embedded points of M, by Claim 1 we have ${\mathcal {H}}^{n} (\text {Cut} (M) \cap M) = 0$. Therefore, to prove that $\text {Cut} (M)$ is rectifiable, we just need to concern ourselves with $\text {Cut} (M) \setminus M$. This follows from the observation made in the proof of [2, Proposition 3.1], that as Lemma 1 holds, then the arguments in [13, Theorem 4.10] hold verbatim. $\square$

Remark 3

As M is smooth, we have that ${\tilde{d}}$ is smooth in $F({\tilde{T}})$, [13, Proposition 4.2].

Denoting $h = F^{*} g$, we have that $F :({\tilde{T}}, h) \rightarrow (F({\tilde{T}}), g)$, is a bijective, local isometry.

Consider the projection map,

$$\begin{aligned} p :{\tilde{M}} \times {\mathbb {R}}\rightarrow & {} {\mathbb {R}}, \\ (x,t)\mapsto & {} t. \end{aligned}$$

In ${\tilde{T}}$, we have that $p = {\tilde{d}} \circ F$, and

$$\begin{aligned} |\nabla p (x,t)|_{h} = |\nabla {\tilde{d}} (F(x,t))|_{g} = 1. \end{aligned}$$

We denote the sets,

$$\begin{aligned} {\tilde{\Gamma }}_{t} = p^{- 1} (t) \cap {\tilde{T}}, \end{aligned}$$

and,

$$\begin{aligned} \Gamma _{t} = {\tilde{d}}^{-1} (t) \subset N. \end{aligned}$$

Note,

$$\begin{aligned} F({\tilde{\Gamma }}_{t}) = {\left\{ \begin{array}{ll} \Gamma _{t} \cap F({\tilde{T}}) = \Gamma _{t} \setminus \text {Cut}(M), &{} t \not = 0, \\ \{ \text {embedded points of } M \}, &{} t = 0. \end{array}\right. } \end{aligned}$$

Denote $H_{{\tilde{\Gamma }}_{t}} (x,t)$ as the scalar mean curvature of ${\tilde{\Gamma }}_{t}$, at (x, t), with respect to unit normal $\nabla p (x,t)$, and define the following function,

$$\begin{aligned} H_{t} :{\tilde{M}}\rightarrow & {} {\mathbb {R}}, \\ x\mapsto & {} {\left\{ \begin{array}{ll} H_{{\tilde{\Gamma }}_{t}} (x,t), &{} (x,t) \in {\tilde{T}}, \\ 0, &{} (x,t) \not \in {\tilde{T}}, \end{array}\right. } \end{aligned}$$

For (x, t) in ${\tilde{T}}$, we have,

$$\begin{aligned} H_{t} (x) = - \text {tr}_{T_{(x,t)} {\tilde{\Gamma }}_{t}} h(\nabla _{\cdot } \, \nabla p (x,t), \, \cdot \,) = - \Delta _{{\tilde{\Gamma }}_{t}} p (x,t). \end{aligned}$$

However, as $\nabla p$ is a geodesic vector field

$$\begin{aligned} \nabla _{\nabla p} \nabla p = 0, \end{aligned}$$

and as $|\nabla p| = 1$,

$$\begin{aligned} h(\nabla _{X} \nabla p, \nabla p) = \frac{1}{2} X(|\nabla p|) = 0. \end{aligned}$$

Therefore, $\Delta _{{\tilde{\Gamma }}_{t}} p (x,t) = \Delta _{{\tilde{T}}} p (x,t)$, and thus for (x, t) in ${\tilde{T}}$,

$$\begin{aligned} H_{t} (x) = - \Delta p (x,t). \end{aligned}$$

Proposition 5

([10, Corollary 3.6]) For (x, t) in ${\tilde{T}}$,

$$\begin{aligned} \partial _{t} H_{t} (x) = - \nabla p (\Delta p) (x,t) \ge m, \end{aligned}$$

where $m = \inf _{|X| = 1} \text {Ric}_{g} (X,X) > 0$.

Remark 4

Consider fixed x in ${\tilde{M}}$. For $\sigma ^{-} (x) < 0$, we have $H_{0} (x) = \lambda$. If $\sigma ^{-} (x) = 0$, we still have,

$$\begin{aligned} \lim _{t \searrow 0} H_{t} (x) = \lambda . \end{aligned}$$

Thus, by Proposition 5, we have for $(x,t) \in {\tilde{T}}$,

$$\begin{aligned} {\left\{ \begin{array}{ll} H_{t} (x) \ge \lambda + m \, t, &{} t > 0, \\ H_{0} (x) = \lambda , &{} \\ H_{t} (x) \le \lambda + m \, t, &{} t < 0. \end{array}\right. } \end{aligned}$$

3.4 Area element

We define the function on ${\tilde{M}}$,

$$\begin{aligned} \theta _{t} (x) = {\left\{ \begin{array}{ll} J_{\Pi _{t}} (x), &{} (x,t) \in {\tilde{T}}, \\ 0, &{} (x,t) \not \in {\tilde{T}}, \end{array}\right. } \end{aligned}$$

where, $J_{\Pi _{t}}$ is the Jacobian of the map $\Pi _{t} :x \in {\tilde{M}} \mapsto (x,t) \in {\tilde{M}} \times {\mathbb {R}}$. By the Area Formula,

$$\begin{aligned} \int _{{\tilde{M}}} \theta _{t} \, d {\mathcal {H}}^{n} = {\mathcal {H}}^{n} ({\tilde{\Gamma }}_{t}). \end{aligned}$$

Proposition 6

([10, Theorem 3.11]) For $(x_{0}, t_{0})$ in ${\tilde{T}}$,

$$\begin{aligned} \partial _{t} \, \log (\theta _{t}) (x_{0})_{|t = t_{0}} = - H_{t_{0}}(x_{0}). \end{aligned}$$

Consider a fixed point $(x_{0}, t_{0})$ in ${\tilde{T}}$. First, consider $t_{0} \ge 0$. For all t in $(0, t_{0}]$, $(x_{0}, t)$ lies in ${\tilde{T}}$, which implies that the function $t \mapsto \theta _{t} (x_{0})$ is smooth on the interval $(0, t_{0}]$. Furthermore, $\lim _{t \rightarrow 0^{+}} \theta _{t} (x_{0}) = 1$, and applying the Fundamental Theorem of Calculus,

$$\begin{aligned} \log (\theta _{t_{0}}(x_{0})) \le - t_{0} \left( \lambda + \frac{1}{2} m t_{0} \right) . \end{aligned}$$

Therefore,

$$\begin{aligned} \theta _{t_{0}}(x_{0}) \le e^{-t_{0} \left( \lambda + \frac{1}{2} m t_{0} \right) }. \end{aligned}$$

Identical inequality holds for $t_{0} \le 0$.

The term $- t (\lambda + \frac{1}{2} mt)$ achieves a global maximum at $t = - \frac{\lambda }{m}$. Noting that for $(x_{0}, t_{0})$ not in ${\tilde{T}}$, $\theta _{t_{0}}(x_{0}) = 0$, we have that,

$$\begin{aligned} 0 \le \theta _{t_{0}}(x_{0}) \le e^{\frac{\lambda ^{2}}{2 m}}, \end{aligned}$$

for all $(x_{0}, t_{0})$ in ${\tilde{M}} \times {\mathbb {R}}$.

3.5 Construction about non-embedded point

Let $z_{0}$ in M be a non-embedded point.

Remark 5

We are in case 2 of Remark 1. We can choose $\delta = \delta (z_{0}, M, N, g)$ such that,

$$\begin{aligned} B_{2 \delta } (z_{0}) \subset C_{z_{0}, T, r, s}. \end{aligned}$$

We have three disjoint sets,

$$\begin{aligned}{} & {} E_{1} {:}{=}\exp _{z} (\{ X + t \nu :X \in B_{z_{0}, T, r}, \, f_{1} (X)< t< s \}) \cap B_{2 \delta }^{N} (z_{0}), \\{} & {} F {:}{=}\exp _{z} (\{ X + t \nu :X \in B_{z_{0}, T, r}, \, f_{2} (X) \le t \le f_{1} (X) \}) \cap B_{2 \delta }^{N} (z_{0}), \\{} & {} E_{2} {:}{=}\exp _{z} (\{ X + t \nu :X \in B_{z_{0}, T, r},\, - s<t < f_{2} (X) \}) \cap B_{2 \delta }^{N} (z_{0}). \\ \end{aligned}$$

As $\partial E_{i} \cap B_{2 \delta }^{N} (z_{0}) = \exp _{z} (\{ \text {Graph} \, (f_{i}) \}) \cap B_{2 \delta }^{N} (z_{0}) {=}{:}D_{i}$, the following signed distance functions are well-defined for $i = 1,2$,

$$\begin{aligned} {\tilde{d}}_{i} :B_{2 \delta }^{N} (z_{0})\rightarrow & {} {\mathbb {R}}, \\ y\mapsto & {} {\left\{ \begin{array}{ll} d_{D_{i}} (y), &{} y \in E_{i}, \\ - d_{D_{i}} (y), &{} y \in B_{2 \delta }^{N} (z_{0}) \setminus E_{i}. \end{array}\right. } \end{aligned}$$

For y in $B_{\delta }^{N} (z_{0}) \subset \subset B_{2 \delta }^{N} (z_{0})$,

$$\begin{aligned} {\tilde{d}} (y) = \max \{ {\tilde{d}}_{1} (y), {\tilde{d}}_{2} (y) \}. \end{aligned}$$

Furthermore, by [13, Proposition 4.2], we may choose $\delta > 0$, such that ${\tilde{d}}_{1}$ and ${\tilde{d}}_{2}$ will be smooth on $B^{N}_{2 \delta } (z_{0})$.

For $i = 1, \, 2$, we define

$$\begin{aligned} {\tilde{D}}_{i} {:}{=}\{ (z, \nu _{i} (z)) :z \in D_{i}\} \subset {\tilde{M}}, \end{aligned}$$

and points $x_{0}^{i} = (z_{0}, \nu _{i} (z_{0}))$.

Remark 6

We make a choice of $\delta = \delta (N, M, g, z_{0}) > 0$ small enough such that, for each $i = 1, \, 2$, we have open sets ${\tilde{V}}_{i} \subset {\tilde{M}} \times {\mathbb {R}}$, and maps,

$$\begin{aligned} F_{i} :{\tilde{V}}_{i} \rightarrow B_{2 \delta }^{N} (z_{0}), \end{aligned}$$

such that ${\tilde{D}}_{i} = {\tilde{V}}_{i} \cap \{t = 0\}$, and $F_{i} = F_{|{\tilde{V}}_{i}}$, is a diffeomorphism. We also insist that $\delta = \delta (N, M, g, z_{0}) > 0$, is chosen small enough such that $\text {Cut}(D_{1})$ and $\text {Cut}(D_{2})$ are empty in $B_{2 \delta } (z_{0})$. We know we can pick such a $\delta > 0$ by [13, Proposition 4.2]

By choice of $\delta > 0$ in Remark 6, and Proposition 4,

$$\begin{aligned} \text {Cut} (M) \cap B_{\delta }^{N} (z_{0}) = \{ y \in B_{\delta }^{N} (z_{0}) :{\tilde{d}}_{1} (y) = {\tilde{d}}_{2} (y) \} \subset B_{\delta }^{N} (z_{0}) \setminus E. \end{aligned}$$

Remark 7

Denote the set,

$$\begin{aligned} A = \{ y \in B_{2 \delta }^{N} (z_{0}) :{\tilde{d}}_{1} (y) = {\tilde{d}}_{2} (y) \}. \end{aligned}$$

For $i = 1, \, 2$, we consider the functions,

$$\begin{aligned} \psi _{i} :{\tilde{V}}_{i}\rightarrow & {} {\mathbb {R}}, \\ (x,t)\mapsto & {} {\tilde{d}}_{1} (F_{i} (x,t)) - {\tilde{d}}_{2}(F_{i} (x,t)). \end{aligned}$$

Therefore, $A = F_{i} (\{\psi _{i} = 0\})$. Moreover,

$$\begin{aligned} \partial _{t} \psi _{i} (x_{0}^{i}, 0) = dF_{i}^{-1} (\nabla {\tilde{d}}_{1} (z_{0})) - d F_{i}^{-1} (\nabla {\tilde{d}}_{2} (z_{0})) = 2 \partial _{t} \not = 0. \end{aligned}$$

Thus, by Implicit Function Theorem we may choose $\delta = \delta (z_{0}, N, M, g) > 0$, such that set $A = \text {Cut} \, (M) \cap B_{2 \delta }^{N} (z_{0})$ is a smooth n-submanifold in $B_{2 \delta }^{N} (z_{0})$, and $\sigma ^{-}$ is smooth on ${\tilde{D}}_{1} \cup {\tilde{D}}_{2}$.

We now look to define the push out function to construct our competitor, Fig. 5.

We wish to determine the amount we want to push out by, and the set we wish to push out on. Fix $\rho > 0$, and we set $l = l(\rho )$, to be,

$$\begin{aligned} l (\rho ) = \sup \{ t :\, for \, all \, x \, in \, B_{t}^{{\tilde{M}}}(x_{0}^{1}), \, |\sigma ^{-}(x)| < \rho \}. \end{aligned}$$

(10)

Here, $B_{t}^{{\tilde{M}}}(x)$ is the geodesic ball in ${\tilde{M}}$, about point x, of radius t. As $\sigma ^{-}$ is smooth about $x_{0}^{1}$, and $\sigma ^{-}(x_{0}^{1}) = 0$, this implies that $l(\rho ) > 0$ for all $\rho > 0$. Furthermore, $l (\rho )$ is increasing in $\rho$, implying that the limit of $l(\rho )$, as $\rho \rightarrow 0$, exists. Therefore, as $\sigma ^{-}(x) = 0$ if and only if $\iota (x)$ is a non-embedded point, and such points have ${\mathcal {H}}^{n}$-measure 0 in ${\tilde{M}}$, we have that this limit must be 0.

Remark 8

As $\sigma ^{-}$ is smooth on ${\tilde{D}}_{1}$, $\sigma ^{-} \le 0$, and $\sigma ^{-} (x_{0}^{1}) = 0$, then there exists a $C_{1} = C_{1} (N, M, g, z_{0}) < + \infty$, and a $\delta = \delta (N, M, g, z_{0})$, such that for all x in ${\tilde{D}}_{1}$,

$$\begin{aligned} \sigma ^{-} (x) \ge - C_{1} d_{{\tilde{M}}}^{2} (x, x_{0}^{1}). \end{aligned}$$

As $l(\rho ) \rightarrow 0$, as $\rho \rightarrow 0$, this implies that we can choose $\rho > 0$, Remark 9, such that

$$\begin{aligned} B_{l (\rho )}^{{\tilde{M}}} (x_{0}^{1}) \subset \subset {\tilde{D}}_{1}. \end{aligned}$$

There exists an $x'$ in ${\tilde{D}}_{1}$, such that $d_{{\tilde{M}}} (x', x_{0}^{1}) = l$, and $\sigma ^{-}(x') = - \rho$. Therefore, by Remark 8,

$$\begin{aligned} \rho \le C_{1} l^{2}. \end{aligned}$$

Remark 9

Note that we have made our first choice of $\rho = \rho (z_{0}, N, M, g, \delta )$.

We push out on disks $D_{1}$ and $D_{2}$ equally, so that they meet on the Cut Locus in $B_{\delta }^{N} (z_{0})$, which is our previously denoted set A, as seen in Fig. 5. We consider the open sets ${\tilde{W}}_{i} \subset {\tilde{D}}_{i}$, defined by,

$$\begin{aligned} {\tilde{W}}_{i} = \{ x :F_{i}(x, \sigma ^{-}(x)) \in B_{\delta }(z_{0})\}. \end{aligned}$$

Clearly $x_{0}^{i}$ lies in ${\tilde{W}}_{i}$, therefore these sets are non-empty. We can then define a diffeomorphism between ${\tilde{W}}_{1}$, and ${\tilde{W}}_{2}$.

$$\begin{aligned} \Psi :{\tilde{W}}_{1}\rightarrow & {} {\tilde{W}}_{2}, \\ x\mapsto & {} (\pi \circ F_{2}^{-1} \circ F_{1} \circ (\text {id}, \sigma ^{-})) (x), \end{aligned}$$

where we define, $\pi$ by,

$$\begin{aligned} \pi :{\tilde{M}} \times {\mathbb {R}}\rightarrow & {} {\tilde{M}}, \\ (x,t)\mapsto & {} x, \end{aligned}$$

and $(\text {id}, \sigma ^{-})$, by

$$\begin{aligned} (\text {id}, \sigma ^{-}) :{\tilde{M}}\rightarrow & {} {\tilde{M}} \times {\mathbb {R}}, \\ x\mapsto & {} (x, \sigma ^{-} (x)). \end{aligned}$$

The function $\Psi$ is smooth and has smooth inverse given by

$$\begin{aligned} \Psi ^{-1} :{\tilde{W}}_{2}\rightarrow & {} {\tilde{W}}_{1}, \\ x\mapsto & {} (\pi \circ F_{1}^{-1} \circ F_{2} \circ (\text {id}, \sigma ^{-})) (x). \end{aligned}$$

We note that, $d \Psi _{x_{0}^{1}} = Id$.

Remark 10

We choose $\rho = \rho (z_{0}, N, M, g, \delta ) > 0$, such that,

$$\begin{aligned} B_{2 l}^{{\tilde{M}}}(x_{0}^{1}) \subset \subset {\tilde{W}}_{1}. \end{aligned}$$

Consider a push out function, which lies in $C_{c}^{\infty }({\tilde{D}}_{1})$, and has the following properties,

$$\begin{aligned} f_{1} (x) = {\left\{ \begin{array}{ll} -1, &{} x \in B_{l}^{{\tilde{M}}}(x_{0}^{1}), \\ {[}-1,0], &{} x \in B_{2l}^{{\tilde{M}}} (x_{0}^{1}) \setminus B_{l}^{{\tilde{M}}} (x_{0}^{1}), \\ 0, &{} x \in {\tilde{D}}_{1} \setminus B_{2 l}^{{\tilde{M}}}(x_{0}^{1}). \end{array}\right. } \end{aligned}$$

We further impose the condition,

$$\begin{aligned} |\nabla f_{1}| \le \frac{2}{l}. \end{aligned}$$

Define $f_{2}$ in $C^{\infty }_{c}({\tilde{D}}_{2})$, by

$$\begin{aligned} f_{2} (x) = {\left\{ \begin{array}{ll} (f_{1} \circ \Psi ^{-1}) (x), &{} x \in {\tilde{W}}_{2}, \\ 0, &{} x \in {\tilde{D}}_{2} \setminus {\tilde{W}}_{2}. \end{array}\right. } \end{aligned}$$

The support of $f_{2}$ will lie in $\Psi (B_{2l}^{{\tilde{M}}} (x_{0}^{1})) \subset \subset \Psi ({\tilde{W}}_{1}) = {\tilde{W}}_{2}$. We then define the function f in $C_{c}^{\infty } ({\tilde{M}})$, by $f = f_{1} + f_{2}$.

Define the sets,

$$\begin{aligned} B_{2 l}= & {} B_{2 l}^{{\tilde{M}}} (x_{0}^{1}) \cup \Psi (B_{2 l}^{{\tilde{M}}} (x_{0}^{1})), \\ B_{l}= & {} B_{l}^{{\tilde{M}}} (x_{0}^{1}) \cup \Psi (B_{l}^{{\tilde{M}}} (x_{0}^{1})), \\ A_{l}= & {} B_{2l} \setminus B_{l}. \end{aligned}$$

We will similarly define the sets,

$$\begin{aligned} B_{t} = B_{t}^{{\tilde{M}}} (x_{0}^{1}) \cup \Psi (B_{t}^{{\tilde{M}}} (x_{0}^{1})), \end{aligned}$$

for $t > 0$, such that $B_{t}^{{\tilde{M}}} (x_{0}^{1}) \subset {\tilde{W}}_{1}$.

Remark 11

We choose $\rho = \rho (z_{0}, M, N, g, \delta , W, \lambda ) > 0$, such that

$$\begin{aligned} F_{1} \left( B_{2 l} \times (- 2 \rho , 2 \rho ) \right) \subset \subset B_{\delta }^{N}(z_{0}) \end{aligned}$$

We now look to define the function that will ’push out away from non-embedded point’. This function will define the path from (2) to (3) in Fig. 2.

Remark 12

(Choice of L and $r_{0}$) We choose $L = L(z_{0}, N, M, g, \delta ) > 0$ and $r_{0} = r_{0} (z_{0}, N, M, g, \delta ) > 0$, such that,

$$\begin{aligned} B_{L}^{{\tilde{M}}} (x_{0}^{1}) \subset \subset {\tilde{W}}_{1}, \end{aligned}$$

and,

$$\begin{aligned} F \left( B_{L} \times (- 2 r_{0}, 2 r_{0}) \right) \subset \subset B_{\delta }^{N} (z_{0}). \end{aligned}$$

For a sets ${\tilde{\Omega }}$ and $\Omega$, were $\Omega$ is open and ${\tilde{\Omega }} \subset \subset \Omega$, we define the 2-Capacity of ${\tilde{\Omega }}$ in $\Omega$ as the value,

$$\begin{aligned} \text {Cap}_{2} ({\tilde{\Omega }}, \Omega ) = \inf \left\{ \int _{\Omega } |\nabla \varphi |^{2} \, d {\mathcal {H}}^{n} :\varphi \in C_{c}^{\infty } (\Omega ), \, \varphi \ge \chi _{{\tilde{\Omega }}} \right\} . \end{aligned}$$

For $n \ge 3$, by [8, Theorem 4.15 (ix), Section 4.7.1 and Theorem 4.16, Section 4.7.2],

$$\begin{aligned} \lim _{k \rightarrow \infty } \text {Cap}_{2} (B_{\frac{L}{k}}^{{\tilde{M}}} (x_{0}^{1}), B_{L}^{{\tilde{M}}} (x_{0}^{1})) = \text {Cap}_{2} (\{x_{0}^{1}\}, B_{L}^{{\tilde{M}}} (x_{0}^{1})) = 0. \end{aligned}$$

Identical proofs show that this also holds for $n = 2$. Therefore, for all $\gamma > 0$, there exists a function $\varphi _{\gamma , k}$, such that,

$$\begin{aligned} {\left\{ \begin{array}{ll} \varphi _{\gamma , k} \in C_{c}^{\infty } (B_{L}^{{\tilde{M}}} (x_{0}^{1})), \\ \varphi _{\gamma , k} :{\tilde{M}} \rightarrow [0,1], \\ \varphi _{\gamma , k} (x) = 1, \, x \in B_{\frac{L}{k}}^{{\tilde{M}}} (x_{0}^{1}), \end{array}\right. } \end{aligned}$$

and, defining ${\tilde{\varphi }}_{\gamma , k} = \varphi _{\gamma , k} + \varphi _{\gamma , k} \circ \Psi ^{-1}$, we have

$$\begin{aligned} \int _{{\tilde{M}}} |\nabla {\tilde{\varphi }}_{\gamma , k}|^{2} \, d {\mathcal {H}}^{n} (x) < \gamma . \end{aligned}$$

We consider the function ${\tilde{f}} = 1 - {\tilde{\varphi }}_{\gamma , k}$ in $C^{\infty } ({\tilde{M}})$, and $\Vert \nabla {\tilde{f}}\Vert _{L^{2} ({\tilde{M}})}^{2} < \gamma$.

Remark 13

We will later make fixed choices for $L = L (z_{0}, M, N, g, \delta , W, \lambda )$, $r_{0} = r_{0} (z_{0}, M, N, g, \delta , W, \lambda , L)$, $\gamma = \gamma (z_{0}, N, M, g, \delta , r_{0}, L)$, and $k = k(z_{0}, N, M, g, \delta , L, \gamma )$.

Remark 14

We make a further choice of $\rho = \rho (z_{0}, N, M, g, \delta , L, r_{0}, k)$, such that,

$$\begin{aligned} B_{2l} \subset \subset B_{\frac{L}{k}}, \end{aligned}$$

We will make a further choice of $\rho$ later on, so that $\rho = \rho (z_{0}, N, M, g, \delta , L, k, r_{0})$.

3.6 Approximating function for CMC

We use the tools we have constructed to give a simple proof that function,

$$\begin{aligned} v_{\varepsilon } (y) = {\overline{{\mathbb {H}}}}_{\varepsilon } ({\tilde{d}} (y)), \end{aligned}$$

is suitable approximation of M, i.e.

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0} {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }) = 2 \sigma {\mathcal {H}}^{n} (M) - \sigma \lambda \mu _{g} (E) - \sigma \lambda \mu _{g} (N \setminus E). \end{aligned}$$

By the Co-Area formula on the function ${\tilde{d}}$,

$$\begin{aligned} {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon })= & {} \int _{N} \frac{\varepsilon }{2} |\nabla v_{\varepsilon }|^{2} + \frac{W(v_{\varepsilon })}{2} - \sigma \lambda \int _{N} v_{\varepsilon }, \\= & {} \int _{{\mathbb {R}}} \int _{\Gamma _{t}} Q_{\varepsilon } (t) \, d{\mathcal {H}}^{n} \, dt - \sigma \lambda \int _{{\mathbb {R}}} \int _{\Gamma _{t}} {\overline{{\mathbb {H}}}}_{\varepsilon } (t) \, d {\mathcal {H}}^{n} \, dt, \end{aligned}$$

where,

$$\begin{aligned} Q_{\varepsilon } (t) = \frac{\varepsilon }{2} (({\overline{{\mathbb {H}}}}_{\varepsilon })'(t))^{2} + \frac{W({\overline{{\mathbb {H}}}}_{\varepsilon } (t))}{\varepsilon }. \end{aligned}$$

Using the fact that $N \setminus F({\tilde{T}})$ is a set of 0 $\mu _{g}$-measure, and that $F :({\tilde{T}}, h) \rightarrow (F({\tilde{T}}), g)$, is a bijective local isometry, we have,

$$\begin{aligned} {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }) = \int _{{\mathbb {R}}} Q_{\varepsilon } (t) \, {\mathcal {H}}^{n} ({\tilde{\Gamma }}_{t}) \, dt - \sigma \lambda \int _{{\mathbb {R}}} {\overline{{\mathbb {H}}}}_{\varepsilon } (t) \, {\mathcal {H}}^{n} ({\tilde{\Gamma }}_{t}) \, dt. \end{aligned}$$

From analysis of ${\overline{{\mathbb {H}}}}_{\varepsilon }$, we have that, $\text {supp} \, Q_{\varepsilon } \subset [- 2 \varepsilon \Lambda , 2 \varepsilon \Lambda ]$, and

$$\begin{aligned} 2 \sigma - \beta \varepsilon ^{2} \le \int _{{\mathbb {R}}} Q_{\varepsilon } (t) \, dt \le 2 \sigma + \beta \varepsilon ^{2}. \end{aligned}$$

Furthermore,

$$\begin{aligned} {\overline{{\mathbb {H}}}}_{\varepsilon } (t) \le {\left\{ \begin{array}{ll} 1, &{} t > - 2 \varepsilon \Lambda , \\ -1, &{} t \le - 2 \varepsilon \Lambda , \end{array}\right. } \end{aligned}$$

and,

$$\begin{aligned} {\overline{{\mathbb {H}}}}_{\varepsilon } (t) \ge {\left\{ \begin{array}{ll} 1, &{} t > 2 \varepsilon \Lambda , \\ -1, &{} t \le 2 \varepsilon \Lambda . \end{array}\right. } \end{aligned}$$

Therefore,

$$\begin{aligned} {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }) \le (2 \sigma + \beta \varepsilon ^{2}) \mathop {\mathrm {ess\,sup}}\limits _{t \in [-2 \varepsilon \Lambda , 2 \varepsilon \Lambda ]} {\mathcal {H}}^{n} ({\tilde{\Gamma }}_{t}) - \sigma \lambda \int _{2 \varepsilon \Lambda }^{+ \infty } {\mathcal {H}}^{n} ({\tilde{\Gamma }}_{t}) \, dt + \sigma \lambda \int _{- \infty }^{2 \varepsilon \Lambda } {\mathcal {H}}^{n} ({\tilde{\Gamma }}_{t}) \, dt. \end{aligned}$$

Similarly,

$$\begin{aligned} {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }) \ge (2 \sigma - \beta \varepsilon ^{2}) \mathop {\mathrm {ess\,inf}}\limits _{t \in [-2 \varepsilon \Lambda , 2 \varepsilon \Lambda ]} {\mathcal {H}}^{n} ({\tilde{\Gamma }}_{t}) - \sigma \lambda \int _{- 2 \varepsilon \Lambda }^{+ \infty } {\mathcal {H}}^{n} ({\tilde{\Gamma }}_{t}) \, dt + \sigma \lambda \int _{- \infty }^{2 \varepsilon \Lambda } {\mathcal {H}}^{n} ({\tilde{\Gamma }}_{t}) \, dt. \end{aligned}$$

We have,

$$\begin{aligned} {\mathcal {H}}^{n} ({\tilde{\Gamma }}_{t}) = \int _{{\tilde{M}}} \theta _{t} (x) \, d {\mathcal {H}}^{n} (x), \end{aligned}$$

and by applying Dominated Convergence Theorem to $\theta _{t}$, we have that,

$$\begin{aligned} \lim _{t \rightarrow 0} {\mathcal {H}}^{n} ({\tilde{\Gamma }}_{t}) = \lim _{t \rightarrow 0} \int _{{\tilde{M}}} \theta _{t} (x) \, d {\mathcal {H}}^{n} (x) = {\mathcal {H}}^{n} ({\tilde{M}} \cap {\tilde{T}}) = {\mathcal {H}}^{n} ({\tilde{M}}). \end{aligned}$$

This implies that,

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0} \mathop {\mathrm {ess\,sup}}\limits _{t \in [-2 \varepsilon \Lambda , 2 \varepsilon \Lambda ]} {\mathcal {H}}^{n} ({\tilde{\Gamma }}_{t}) = {\mathcal {H}}^{n}({\tilde{M}}) = {\mathcal {H}}^{n} (M), \end{aligned}$$

and,

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0} \mathop {\mathrm {ess\,inf}}\limits _{t \in [-2 \varepsilon \Lambda , 2 \varepsilon \Lambda ]} {\mathcal {H}}^{n} ({\tilde{\Gamma }}_{t}) = {\mathcal {H}}^{n}({\tilde{M}}) = {\mathcal {H}}^{n} (M). \end{aligned}$$

The function $t \mapsto {\mathcal {H}}^{n} ({\tilde{\Gamma }}_{t})$ is measurable, implying that,

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0} \int _{\pm 2 \varepsilon \Lambda }^{+ \infty } {\mathcal {H}}^{n} ({\tilde{\Gamma }}_{t}) \, dt = \int _{0}^{+ \infty } {\mathcal {H}}^{n} ({\tilde{\Gamma }}_{t}) \, dt = {\mathcal {H}}^{n+1} (\{y \in N :{\tilde{d}} (y) > 0\}) = \mu _{g} (E), \end{aligned}$$

and,

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0} \int ^{\pm 2 \varepsilon \Lambda }_{- \infty } {\mathcal {H}}^{n} ({\tilde{\Gamma }}_{t}) \, dt = \int ^{0}_{- \infty } {\mathcal {H}}^{n} ({\tilde{\Gamma }}_{t}) \, dt = {\mathcal {H}}^{n + 1} (\{y \in N :{\tilde{d}} (y) < 0\}) = \mu _{g} (N \setminus E). \end{aligned}$$

Therefore, we have,

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0} {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }) = 2 \sigma {\mathcal {H}}^{n} (M) - \sigma \lambda \mu _{g} (E) + \sigma \lambda \mu _{g} (N \setminus E). \end{aligned}$$

4 Base computation

Consider a smooth function,

$$\begin{aligned} \eta :{\mathbb {R}} \times {\tilde{M}} \rightarrow {\mathbb {R}}. \end{aligned}$$

and define the following

$$\begin{aligned} v_{\varepsilon }^{r,\eta } :{\tilde{M}} \times {\mathbb {R}}\rightarrow & {} {\mathbb {R}}, \\ (x,t)\mapsto & {} {\overline{{\mathbb {H}}}}_{\varepsilon }(t - \eta (r,x)). \end{aligned}$$

Take (x, t) in ${\tilde{M}} \times {\mathbb {R}}$, such that $d F_{(x,t)}$ is invertible. Then the metric $h = F^{*} g$, is well defined about (x, t), and by [10, Lemma 2.11], it will have the form

$$\begin{aligned} h(x,t) = h_{{\tilde{M}} \times \{t\}} (x) + dt^{2}, \end{aligned}$$

where we define,

$$\begin{aligned} h_{{\tilde{M}} \times \{t\}} (x) {:}{=}(F^{*} g) (x,t)_{|T_{x} {\tilde{M}}}. \end{aligned}$$

Thus,

$$\begin{aligned} |\nabla v_{\varepsilon }^{r,\eta }(x,t)|^{2} = ( ({\overline{{\mathbb {H}}}}_{\varepsilon })'(t - \eta (r,x)))^{2} (1 + |\nabla _{x} \eta (r,x)| ^{2} (x,t)), \end{aligned}$$

where, $(\nabla _{x} \eta (r,x)) (x,t)$, is the gradient at (x, t), of the function $(x,t) \mapsto \eta (r,x)$, with respect to the metric h. By the co-area formula on p,

$$\begin{aligned} {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{r,\eta })= & {} \int _{{\tilde{T}}} \frac{\varepsilon }{2} |\nabla v_{\varepsilon }^{r,\eta }|^{2} + \frac{W(v_{\varepsilon }^{r,\eta })}{\varepsilon } - \sigma \lambda v_{\varepsilon }^{r,\eta } \, d \mu _{h}, \\= & {} \int _{{\mathbb {R}}} \int _{{\tilde{\Gamma }}_{t}} \frac{\varepsilon }{2} ( ({\overline{{\mathbb {H}}}}_{\varepsilon })'(t - \eta (r,x)))^{2}|\nabla _{x} \eta (r,x)|^{2}(x,t) \, d {\mathcal {H}}^{n}(x,t) \, dt \\{} & {} + \int _{{\mathbb {R}}} \int _{{\tilde{\Gamma }}_{t}} \frac{\varepsilon }{2} ( ({\overline{{\mathbb {H}}}}_{\varepsilon })'(t - \eta (r,x)))^{2} + \frac{W({\overline{{\mathbb {H}}}}_{\varepsilon }(t - \eta (r,x)))}{\varepsilon } \\{} & {} - \sigma \lambda {\overline{{\mathbb {H}}}}_{\varepsilon } (t - \eta (r,x)) \, d {\mathcal {H}}^{n} (x,t) \, dt, \\= & {} \int _{{\tilde{M}}} \int _{\sigma ^{-}(x)}^{\sigma ^{+}(x)} \frac{\varepsilon }{2} ( ({\overline{{\mathbb {H}}}}_{\varepsilon })'(t - \eta (r,x)))^{2}|\nabla _{x} \eta (r,x)|^{2}(x,t) \, \theta _{t}(x) \, dt \, d {\mathcal {H}}^{n}(x) \\{} & {} + \int _{{\tilde{M}}} \int _{\sigma ^{-}(x)}^{\sigma ^{+}(x)} \bigg (\frac{\varepsilon }{2} ( ({\overline{{\mathbb {H}}}}_{\varepsilon })'(t - \eta (r,x)))^{2} + \frac{W({\overline{{\mathbb {H}}}}_{\varepsilon }(t - \eta (r,x)))}{\varepsilon } \\{} & {} - \sigma \lambda {\overline{{\mathbb {H}}}}_{\varepsilon } (t - \eta (r,x)) \bigg ) \, \theta _{t} (x) \, dt \, d {\mathcal {H}}^{n} (x), \end{aligned}$$

In the last equality we use Fubini’s Theorem to switch the integrals.

We have,

$$\begin{aligned}{} & {} {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{r,\eta }) - {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{0,\eta }) \\{} & {} \quad = \int _{{\tilde{M}}} \int _{\sigma ^{-}(x)}^{\sigma ^{+}(x)} \frac{\varepsilon }{2} ( ({\overline{{\mathbb {H}}}}_{\varepsilon })'(t - \eta (r,x)))^{2}|\nabla _{x} \eta (r,x)|{2} (x,t) \, \theta _{t}(x) \, dt \, d {\mathcal {H}}^{n}(x) \\{} & {} \qquad - \int _{{\tilde{M}}} \int _{\sigma ^{-}(x)}^{\sigma ^{+}(x)} \frac{\varepsilon }{2} ( ({\overline{{\mathbb {H}}}}_{\varepsilon })'(t - \eta (r,x)))^{2}|\nabla _{x} \eta (0,x)|^{2} (x,t) \, \theta _{t}(x) \, dt \, d {\mathcal {H}}^{n}(x), \\{} & {} \qquad + \int _{{\tilde{M}}} \int _{\sigma ^{-}(x)}^{\sigma ^{+}(x)} (Q_{\varepsilon } (t - \eta (r,x)) - Q_{\varepsilon } (t - \eta (0,x))) \theta _{t}(x) \, dt \, d {\mathcal {H}}^{n}(x) \\{} & {} \qquad - \int _{{\tilde{M}}} \int _{\sigma ^{-}(x)}^{\sigma ^{+}(x)} \sigma \lambda ({\overline{{\mathbb {H}}}}_{\varepsilon } (t - \eta (r,x)) - {\overline{{\mathbb {H}}}}_{\varepsilon } (t - \eta (0,x))) \, \theta _{t} (x) \, dt \, d {\mathcal {H}}^{n} (x), \end{aligned}$$

We have the following two terms,

$$\begin{aligned} {I}_{\varepsilon }^{r,\eta }= & {} \int _{{\tilde{M}}} \int _{\sigma ^{-}(x)}^{\sigma ^{+}(x)} \frac{\varepsilon }{2} ( ({\overline{{\mathbb {H}}}}_{\varepsilon })'(t - \eta (r,x)))^{2}|\nabla _{x} \eta (r,x)|^{2} (x,t) \, \theta _{t}(x) \, dt \, d {\mathcal {H}}^{n}(x) \\{} & {} \quad - \int _{{\tilde{M}}} \int _{\sigma ^{-}(x)}^{\sigma ^{+}(x)} \frac{\varepsilon }{2} ( ({\overline{{\mathbb {H}}}}_{\varepsilon })'(t - \eta (0,x)))^{2}|\nabla _{x} \eta (0,x)|^{2} (x,t) \, \theta _{t}(x) \, dt \, d {\mathcal {H}}^{n}(x), \end{aligned}$$

and, by Fundamental Theorem of Calculus and Fubini’s Theorem,

$$\begin{aligned} {II}_{\varepsilon }^{r,\eta }= & {} {} \int _{{\tilde{M}}} \int _{\sigma ^{-}(x)}^{\sigma ^{+}(x)} (Q_{\varepsilon } (t - \eta (r,x)) - Q_{\varepsilon } (t - \eta (0,x))) \theta _{t}(x) \, dt \, d {\mathcal {H}}^{n}(x) \\{}{} & {} {} - \int _{{\tilde{M}}} \int _{\sigma ^{-}(x)}^{\sigma ^{+}(x)} \sigma \lambda ({\overline{{\mathbb {H}}}}_{\varepsilon } (t - \eta (r,x)) - {\overline{{\mathbb {H}}}}_{\varepsilon } (t - \eta (0,x))) \, \theta _{t} (x) \, dt \, d {\mathcal {H}}^{n} (x), \\ {}= & {} {} - \int _{0}^{r} \int _{{\tilde{M}}} \partial _{s} \eta (s,x) \int _{\sigma ^{-}(x)}^{\sigma ^{+}(x)} Q_{\varepsilon }'(t - \eta (s,x)) \, \theta _{t}(x) \, dt \, d{\mathcal {H}}^{n}(x) \, ds \\{}{} & {} {} + \int _{0}^{r} \int _{{\tilde{M}}} \partial _{s} \eta (s,x) \int _{\sigma ^{-}(x)}^{\sigma ^{+}(x)} \sigma \lambda ({\overline{{\mathbb {H}}}}_{\varepsilon })'(t - \eta (s,x)) \, \theta _{t}(x) \, dt \, d{\mathcal {H}}^{n}(x) \, ds, \\ {}= & {} {} - \int _{0}^{r} \int _{{\tilde{M}}} \partial _{s} \eta (s,x) Q_{\varepsilon }(\sigma ^{+}(x) - \eta (s,x)) \, \theta ^{+}(x) \, d{\mathcal {H}}^{n}(x) \, ds \\{}{} & {} {} + \int _{0}^{r} \int _{{\tilde{M}}} \partial _{s} \eta (s,x) Q_{\varepsilon }(\sigma ^{-}(x) - \eta (s,x)) \, \theta ^{-}(x) \, d{\mathcal {H}}^{n}(x) \, ds \\{}{} & {} {} + \int _{0}^{r} \int _{{\tilde{M}}} \partial _{s} \eta (s,x) \int _{\sigma ^{-}(x)}^{\sigma ^{+}(x)} Q_{\varepsilon }(t - \eta (s,x)) \, \partial _{t}\theta _{t}(x) \, dt \, d{\mathcal {H}}^{n}(x) \, ds \\{}{} & {} {} + \int _{0}^{r} \int _{{\tilde{M}}} \partial _{s} \eta (s,x) \int _{\sigma ^{-}(x)}^{\sigma ^{+}(x)} \sigma \lambda ({\overline{{\mathbb {H}}}}_{\varepsilon })'(t - \eta (s,x)) \, \theta _{t}(x) \, dt \, d{\mathcal {H}}^{n}(x) \, ds, \\ {}= & {} {} - \int _{0}^{r} \int _{{\tilde{M}}} \partial _{s} \eta (s,x) Q_{\varepsilon }(\sigma ^{+}(x) - \eta (s,x)) \, \theta ^{+}(x) \, d{\mathcal {H}}^{n}(x) \, ds \\{}{} & {} {} + \int _{0}^{r} \int _{{\tilde{M}}} \partial _{s} \eta (s,x) Q_{\varepsilon }(\sigma ^{-}(x) - \eta (s,x)) \, \theta ^{-}(x) \, d{\mathcal {H}}^{n}(x) \, ds \\{}{} & {} {} + \int _{0}^{r} \int _{{\tilde{M}}} \partial _{s} \eta (s,x) \int _{\sigma ^{-}(x)}^{\sigma ^{+}(x)} Q_{\varepsilon }(t - \eta (s,x)) \, (\lambda - H_{t}(x)) \, \theta _{t}(x) \, dt \, d{\mathcal {H}}^{n}(x) \, ds \\{}{} & {} {} + \lambda \int _{0}^{r} \int _{{\tilde{M}}} \Theta _{\varepsilon , \eta }^{1} (s,x) - \Theta _{\varepsilon , \eta }^{2} (s,x) \, d{\mathcal {H}}^{n}(x) \, ds, \\ \end{aligned}$$

Where,

$$\begin{aligned} \theta ^{+} (x)= & {} \lim _{t \nearrow \sigma ^{+}(x)} \theta _{t}(x), \\ \theta ^{-} (x)= & {} \lim _{t \searrow \sigma ^{-}(x)} \theta _{t}(x), \\ \Theta _{\varepsilon , \eta }^{1} (s,x)= & {} \sigma \int _{\sigma ^{-}(x)}^{\sigma ^{+}(x)} \partial _{s} \eta (s,x) ({\overline{{\mathbb {H}}}}_{\varepsilon })' (t - \eta (s,x)) \theta _{t}(x) \, dt, \\ \Theta _{\varepsilon , \eta }^{2} (s,x)= & {} \int _{\sigma ^{-}(x)}^{\sigma ^{+}(x)} \partial _{s} \eta (s,x) Q_{\varepsilon } (t - \eta (s,x)) \theta _{t} (x) \, dt. \end{aligned}$$

For the last equality of ${II}_{\varepsilon }^{r,\eta }$ we are using $\partial _{t} \theta _{t} (x) = - H_{t} (x) \theta _{t} (x)$, for t in $(\sigma ^{-}(x), \sigma ^{+} (x) )$.

5 Competitor

5.1 Calculation on ${\tilde{M}} \times {\mathbb {R}}$

Here we construct the path in Fig. 2 from (1) to (2).

Set $\eta _{1}(r,x) = r f(x)$, take r in $[0, \rho ]$, where $\rho \in (0,1)$ will be chosen later and $f :{\tilde{M}} \rightarrow {\mathbb {R}}$ as defined in Sect. 3.5.

Remark 15

(Choice in $\varepsilon _{1}$) We choose $\varepsilon _{1} = \varepsilon _{1} (\rho ) \in (0, 1/4)$, such that,

$$\begin{aligned} 2 \varepsilon _{1} \Lambda = 6 \varepsilon _{1} |\log \, \varepsilon _{1}|< < \rho . \end{aligned}$$

From here we consider $\varepsilon$ in $(0, \varepsilon _{1})$.

We have,

$$\begin{aligned} \begin{aligned} {II}_{\varepsilon }^{r,\eta _{1}} =&- \int _{0}^{r} \int _{{\tilde{M}}} f(x) Q_{\varepsilon }(\sigma ^{+}(x) - sf(x)) \, \theta ^{+}(x) \, d{\mathcal {H}}^{n}(x) \, ds \\ {}&+ \int _{0}^{r} \int _{{\tilde{M}}} f(x) Q_{\varepsilon }(\sigma ^{-}(x) - sf(x)) \, \theta ^{-}(x) \, d{\mathcal {H}}^{n}(x) \, ds \\ {}&+ \int _{0}^{r} \int _{{\tilde{M}}} f(x) \int _{\sigma ^{-}(x)}^{\sigma ^{+}(x)} Q_{\varepsilon }(t - sf(x)) \, (\lambda - H_{t}(x)) \, \theta _{t}(x) \, dt \, d{\mathcal {H}}^{n}(x) \, ds \\ {}&+ \lambda \int _{0}^{r} \int _{{\tilde{M}}} \Theta _{\varepsilon , \eta _{1}}^{1} (s,x) - \Theta _{\varepsilon , \eta _{1}}^{2} (s,x) \, d{\mathcal {H}}^{n}(x) \, ds, \end{aligned} \end{aligned}$$

(11)

Concentrate on the second term of the right hand side of (11). As the integrand is non-positive, $f = -1$ on $B_{l}$ and $\text {supp} \, Q_{\varepsilon } \subset [-2 \varepsilon \Lambda , 2 \varepsilon \Lambda ]$, we have

$$\begin{aligned}{} & {} \int _{0}^{r} \int _{{\tilde{M}}} f(x) Q_{\varepsilon }(\sigma ^{-}(x) - sf(x)) \, \theta ^{-}(x) \, d{\mathcal {H}}^{n}(x) \, ds \\{} & {} \hspace{2cm} \le - (2 \sigma - \beta \varepsilon ^{2}) \int _{B_{l} \cap \{- r + 2 \varepsilon \Lambda \le \sigma ^{-}(x) \le - 2 \varepsilon \Lambda \} } \theta ^{-} (x) \, d {\mathcal {H}}^{n}(x) \end{aligned}$$

We look for lower bounds on $\theta ^{-}$.

Remark 16

Choose $\delta = \delta (z_{0}, N, M, g) > 0$, such that,

$$\begin{aligned} \min _{y \in B_{\delta }^{N} (z_{0})} \{ \Delta {\tilde{d}}_{1} (y), \Delta {\tilde{d}}_{2} (y) \} \ge \frac{\lambda }{2}, \end{aligned}$$

and,

$$\begin{aligned} \max _{y \in B_{\delta }^{N} (z_{0})} \{ \Delta {\tilde{d}}_{1} (y), \Delta {\tilde{d}}_{2} (y) \} \le \frac{3\lambda }{2}. \end{aligned}$$

Therefore, for (x, t) in ${\tilde{T}}$, such that, F(x, t) lies in $B_{\delta }^{N} (z_{0})$, we have that,

$$\begin{aligned} \frac{\lambda }{2} \le H_{t} (x) \le \frac{3 \lambda }{2}. \end{aligned}$$

Thus by similar calculations carried out in Sect. 3.4, for all (x, t) in ${\tilde{T}}$, such that F(x, t) lies in $B_{\delta }^{N} (z_{0})$, we have,

$$\begin{aligned} \theta _{t} (x) \ge {\left\{ \begin{array}{ll} e^{- \frac{3\lambda t}{2}}, &{} t \ge 0, \\ e^{- \frac{\lambda t}{2}}, &{} t \le 0. \end{array}\right. } \end{aligned}$$

For x in $B_{l}$, we have $\sigma ^{-} (x) > - \rho$, and by choice of $\rho$ in Remark 11, we have that $F(\{x\} \times (\sigma ^{-}(x),0)) \subset B_{\delta }^{N} (z_{0})$. Thus

$$\begin{aligned} \theta ^{-} (x) = \lim _{t \searrow \sigma ^{-}(x)} \theta _{t} (x) \ge e^{- \frac{\lambda \, \sigma ^{-} (x)}{2}} \ge 1, \end{aligned}$$

for all x in $B_{l}$. Therefore,

$$\begin{aligned}{} & {} \int _{0}^{r} \int _{{\tilde{M}}} f(x) Q_{\varepsilon }(\sigma ^{-}(x) - sf(x)) \, \theta ^{-}(x) \, d{\mathcal {H}}^{n}(x) \, ds \\{} & {} \hspace{2cm} \le - 2 \sigma {\mathcal {H}}^{n} (\{ x :x \in B_{l}, \, - r + 2 \varepsilon \Lambda \le \sigma ^{-}(x) \le - 2 \varepsilon \Lambda \}) + C_{2} \varepsilon ^{2}, \end{aligned}$$

for $C_{2} = C_{2} (N, M, g, \lambda , W) < + \infty$. This is a lower bound for the area deleted in pushing the disks together.

Concentrate on First term on the right hand side of (11). By choice of $\delta > 0$ in Remark 6 and $\rho > 0$ in Remark 11 we have that for x in $\text {supp} \, (f) \subset B_{2l}$, $\sigma ^{+} (x)> 2 \rho> > 2 \varepsilon \Lambda$. Thus,

$$\begin{aligned} \int _{0}^{r} \int _{{\tilde{M}}} f(x) Q_{\varepsilon }(\sigma ^{+}(x) - sf(x)) \, \theta ^{+}(x) \, d{\mathcal {H}}^{n}(x) \, ds = 0. \end{aligned}$$

Concentrate on the third term on the right hand side of (11). Consider $s > 0$, and x in ${\tilde{M}}$, such that $s f (x) < -2 \varepsilon \Lambda$. Using the fact that $\text {supp} \, Q_{\varepsilon } \subset [-2 \varepsilon \Lambda , 2 \varepsilon \Lambda ]$, and the inequalities on $H_{t}$ in Remark 4,

$$\begin{aligned} \int _{\sigma ^{-}(x)}^{\sigma ^{+}(x)} Q_{\varepsilon }(t - sf(x)) \, (\lambda - H_{t}(x)) \, \theta _{t}(x) \, dt= & {} \int _{- 2 \varepsilon \Lambda }^{2 \varepsilon \Lambda } Q_{\varepsilon } (\xi ) (\lambda - H_{\xi + s f (x)}) \theta _{\xi + s f(x)} d \xi , \\\ge & {} 0. \end{aligned}$$

For $s f (x) \ge -2 \varepsilon \Lambda$, we have,

$$\begin{aligned} \int _{\sigma ^{-}(x)}^{\sigma ^{+}(x)} Q_{\varepsilon }(t - sf(x)) \, (\lambda - H_{t}(x)) \, \theta _{t}(x) \, dt= & {} \int _{- 2 \varepsilon \Lambda }^{2 \varepsilon \Lambda } Q_{\varepsilon } (\xi ) (\lambda - H_{\xi + s f (x)}) \theta _{\xi + s f(x)} d \xi , \\\ge & {} C_{2} \min _{t \in [-4 \varepsilon \Lambda , 2 \varepsilon \Lambda ]} (\lambda - H_{t}(x)) \theta _{t}(x), \end{aligned}$$

potentially rechoosing $C_{2} = C_{2} (M, N, g, \lambda , W)$. Therefore we have that for all r in $[0, \rho ]$,

$$\begin{aligned} {II}_{\varepsilon }^{r,\eta _{1}}\le & {} - 2 \sigma {\mathcal {H}}^{n} (\{ x :x \in B_{l}, \, - r + 2 \varepsilon \Lambda \le \sigma ^{-}(x) \le - 2 \varepsilon \Lambda \}) \\{} & {} + C_{2} \left( r \int _{B_{2 l}} q_{\varepsilon }^{1} (x) \, d {\mathcal {H}}^{n}(x) + \int _{0}^{r} \int _{{\tilde{M}}} \Theta _{\varepsilon , \eta _{1}}^{1} (s,x) - \Theta _{\varepsilon , \eta _{1}}^{2} \, d{\mathcal {H}}^{n}(x) \, ds + \varepsilon ^{2} \right) . \end{aligned}$$

where,

$$\begin{aligned} q^{1}_{\varepsilon } (x) = \max _{t \in [-4 \varepsilon \Lambda , 2 \varepsilon \Lambda ]} (H_{t} (x) - \lambda ) \theta _{t} (x) \ge 0, \end{aligned}$$

and we have potentially rechosen $C_{2} = C_{2} (M, N, g, \lambda , W)$. Therefore, for $r < 4 \varepsilon \Lambda$,

$$\begin{aligned} {II}_{\varepsilon }^{r,\eta _{1}} = C_{2} \bigg ( r \int _{B_{2 l}} q_{\varepsilon }^{1} (x) \, d {\mathcal {H}}^{n}(x) + \int _{0}^{r} \int _{{\tilde{M}}} \Theta _{\varepsilon , \eta _{1}}^{1} (s,x) - \Theta _{\varepsilon , \eta _{1}}^{2} \, d{\mathcal {H}}^{n}(x) \, ds + \varepsilon ^{2} \bigg ), \end{aligned}$$

and for $r \ge 4 \varepsilon \Lambda$,

$$\begin{aligned} {II}_{\varepsilon }^{r,\eta _{1}}\le & {} - 2 \sigma {\mathcal {H}}^{n} (\{ x :x \in B_{l}, \, -r + 2 \varepsilon \Lambda \le \sigma ^{-}(x) \le 0 \}) \\{} & {} + C_{2} \bigg ( {\mathcal {H}}^{n} ( \{ x :x \in B_{l}, -2 \varepsilon \Lambda < \sigma ^{-}(x) \le 0 \}) \\{} & {} + \int _{B_{2 l}} q_{\varepsilon }^{1} (x) \, d {\mathcal {H}}^{n}(x) + \int _{0}^{r} \int _{{\tilde{M}}} \Theta _{\varepsilon , \eta _{1}}^{1} (s,x) - \Theta _{\varepsilon , \eta _{1}}^{2} \, d{\mathcal {H}}^{n}(x) \, ds + \varepsilon ^{2} \bigg ). \end{aligned}$$

Again we are potentially rechoosing $C_{2} = C_{2} (M, N, g, \lambda , W)$.

We now turn our attention to the term,

$$\begin{aligned} {I}_{\varepsilon }^{r,\eta _{1}}= & {} \int _{{\tilde{M}}} \int _{\sigma ^{-}(x)}^{\sigma ^{+}(x)} \frac{\varepsilon }{2} ( ({\overline{{\mathbb {H}}}}_{\varepsilon })'(t - r f (x)))^{2}|r \nabla f|^{2} (x,t) \, \theta _{t}(x) \, dt \, d {\mathcal {H}}^{n}(x), \\= & {} \int _{{\tilde{M}}} \int _{- 2 \varepsilon \Lambda }^{2 \varepsilon \Lambda } \frac{\varepsilon }{2} ( ({\overline{{\mathbb {H}}}}_{\varepsilon })'(\xi ) )^{2}|r \nabla f|^{2} (x,\xi + r f (x)) \, \theta _{\xi + r f (x)}(x) \, d \xi \, d {\mathcal {H}}^{n}(x). \end{aligned}$$

Remark 17

Recall choice of $\delta = \delta (z_{0}, M, N, g)$ in Remark 6. Consider $|t| < \delta$, and x, such that $\iota (x)$ lies in $B_{\delta }^{N} (z_{0})$. Take $\{ E_{1}, \ldots , E_{n} \}$ to be an orthonormal basis for $T_{x} {\tilde{M}}$, with respect to the metric $h_{{\tilde{M}} \times \{ 0 \}}$. Then, as previously shown, we have the following metric about x on ${\tilde{M}}$,

$$\begin{aligned} (h_{{\tilde{M}} \times \{t\}})_{ij} (x) = h_{{\tilde{M}} \times \{t\}} (x) (E_{i}, E_{j}). \end{aligned}$$

For a function $\varphi$ on ${\tilde{M}}$,

$$\begin{aligned} |\nabla \varphi |^{2} (x,t) = (h_{{\tilde{M}} \times \{t\}})^{ij} (x) d \varphi (E_{i}) d \varphi (E_{j}). \end{aligned}$$

We make a further choice $\delta = \delta (z_{0}, N, M, g) > 0$, such that there exists a $C_{3} = C_{3} (z_{0}, \delta , M, N, g)$,

$$\begin{aligned} 1 \le \sup \left\{ (h_{{\tilde{M}} \times \{t\}})^{ij} (x) X_{i} X_{j} :\iota (x) \in B_{\delta }^{N} (z_{0}), \, |t| \le \delta / 2, \, \sum _{i} X_{i}^{2} = 1 \right\} \le C_{3} < \infty , \end{aligned}$$

and,

$$\begin{aligned} 0 < C_{3}^{-1} \le \inf \left\{ (h_{{\tilde{M}} \times \{t\}})^{ij} (x) X_{i} X_{j} :\iota (x) \in B_{\delta }^{N} (z_{0}), \, |t| \le \delta / 2, \, \sum _{i} X_{i}^{2} = 1 \right\} \le 1. \end{aligned}$$

By choices of $\rho$ in Remark 11, and $\varepsilon$ in Remark 15, for all x in $A_{l}$, r in $[0, \rho ]$, and $\xi$ in $[-2 \varepsilon \Lambda , 2 \varepsilon \Lambda ]$,

$$\begin{aligned} |r \nabla f|^{2} (x,\xi + r f (x)) \le C_{3} r^{2} |\nabla f|^{2}(x,0) \le 2 C_{3} \frac{r^{2}}{l^{2}}. \end{aligned}$$

Note that for x in ${\tilde{M}} \setminus A_{l}$, $|\nabla f|(x,t) = 0$, for all t. We have,

$$\begin{aligned} {I}_{\varepsilon }^{r,\eta _{1}} \le C_{3} {\mathcal {H}}^{n}(A_{l}) \frac{r^{2}}{l^{2}}, \end{aligned}$$

where we have potentially rechosen $C_{3} = C_{3} (z_{0}, N, M, g, \delta , \lambda , W) < \infty$.

For r in $[0, 4 \varepsilon \Lambda )$, we have,

$$\begin{aligned} {I}_{\varepsilon }^{r,\eta _{1}} + {II}_{\varepsilon }^{r,\eta _{1}}\le & {} C_{3} \frac{(\varepsilon \Lambda )^{2}}{l^{2}} + C_{2} \bigg ( \varepsilon \Lambda \int _{B_{2 l}} q_{\varepsilon }^{1} (x) \, d {\mathcal {H}}^{n}(x) \\{} & {} \hspace{1cm} + \int _{0}^{r} \int _{{\tilde{M}}} \Theta _{\varepsilon , \eta _{1}}^{1} (s,x) - \Theta _{\varepsilon , \eta _{1}}^{2} \, d{\mathcal {H}}^{n}(x) \, ds + \varepsilon ^{2} \bigg ). \end{aligned}$$

Again, we are potentially rechoosing $C_{3} = C_{3} (z_{0}, N, M, g, \delta , \lambda , W) < \infty$.

For r in $[4 \varepsilon \Lambda , \rho ]$ we define the following non-decreasing function,

$$\begin{aligned} P_{\varepsilon } (r) {:}{=}\frac{{\mathcal {H}}^{n} (\{ x :x \in B_{l}, \, -r + 2 \varepsilon \Lambda \le \sigma ^{-} (x) \le 0\})}{{\mathcal {H}}^{n} (A_{l})}, \end{aligned}$$

and we have,

$$\begin{aligned} {I}_{\varepsilon }^{r,\eta _{1}} + {II}_{\varepsilon }^{r,\eta _{1}}\le & {} {\mathcal {H}}^{n} (A_{l}) \left( C_{3} \frac{r^{2}}{l^{2}} - 2 \sigma P_{\varepsilon }(r) \right) \\{} & {} + C_{2} \bigg ( {\mathcal {H}}^{n} ( \{ x :x \in B_{l}, -2 \varepsilon \Lambda < \sigma ^{-}(x) \le 0 \}) + \int _{B_{2 l}} q_{\varepsilon }^{1} (x) \, d {\mathcal {H}}^{n}(x)\\{} & {} + \int _{0}^{r} \int _{{\tilde{M}}} \Theta _{\varepsilon , \eta _{1}}^{1} (s,x) - \Theta _{\varepsilon , \eta _{1}}^{2} \, d{\mathcal {H}}^{n}(x) \, ds + \varepsilon ^{2} \bigg ). \end{aligned}$$

We now define the following function on [0, 1],

$$\begin{aligned} \kappa _{\varepsilon } (s) = {\left\{ \begin{array}{ll} 0, &{} s \in [0, (4 \varepsilon \Lambda ) / \rho ), \\ C_{3} \frac{\rho ^{2}}{l^{2}} s^{2} - 2 \sigma P_{\varepsilon } (s \rho ), &{} s \in [(4 \varepsilon \Lambda ) / \rho , 1]. \end{array}\right. } \end{aligned}$$

Note that,

$$\begin{aligned} P_{\varepsilon } (\rho ) \xrightarrow {\varepsilon \rightarrow 0} \frac{{\mathcal {H}}^{n} (B_{l})}{{\mathcal {H}}^{n} (A_{l})} \xrightarrow {\rho \rightarrow 0} \frac{1}{2^{n} - 1}, \end{aligned}$$

and furthermore, recalling the bound $\rho \le C_{1} l^{2}$, $C_{1} = C_{1} (z_{0}, N, M, g, \delta ) < + \infty$, we have,

$$\begin{aligned} 0 < \frac{\rho ^{2}}{l^{2}} \le C_{1} \rho \xrightarrow {\rho \rightarrow 0} 0. \end{aligned}$$

Remark 18

Choose $\rho = \rho (z_{0}, N, M, g, \delta , \lambda , W) > 0$, such that

$$\begin{aligned} C_{3} \frac{\rho ^{2}}{l^{2}} < \frac{\sigma }{2(2^{n} - 1)}, \end{aligned}$$

and,

$$\begin{aligned} \frac{{\mathcal {H}}^{n} (B_{l})}{{\mathcal {H}}^{n}(A_{l})} > \frac{7}{8(2^{n} - 1)}. \end{aligned}$$

Remark 19

There exists an $\varepsilon _{2} = \varepsilon _{2} (z_{0}, M, N, g, \delta , W, \lambda , \rho ) > 0$, such that, $\varepsilon _{2} \le \varepsilon _{1}$, and for all $\varepsilon$ in $(0, \varepsilon _{2})$,

$$\begin{aligned} P_{\varepsilon } (\rho ) > \frac{3}{4(2^{n} - 1)}. \end{aligned}$$

From here we always choose $\varepsilon$ in $(0, \varepsilon _{2})$.

We have that,

$$\begin{aligned} \max _{s \in [0,1]} \kappa _{\varepsilon } (s) \le C_{3} \frac{\rho ^{2}}{l^{2}} < \frac{\sigma }{2(2^{n} - 1)}, \end{aligned}$$

and,

$$\begin{aligned} \kappa _{\varepsilon } (1) < - \frac{\sigma }{2^{n} - 1}. \end{aligned}$$

We have, for r in $[0, 4 \varepsilon \Lambda )$,

$$\begin{aligned} {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{r, \eta _{1}}) \le {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }) + {III}_{\varepsilon }^{1, r}, \end{aligned}$$

where,

$$\begin{aligned} {III}_{\varepsilon }^{1, r} = C_{4} \bigg ( \varepsilon \Lambda \int _{B_{2 l}} q_{\varepsilon }^{1} (x) \, d {\mathcal {H}}^{n}(x) + \int _{0}^{r} \int _{{\tilde{M}}} \Theta _{\varepsilon , \eta _{1}}^{1} (s,x) - \Theta _{\varepsilon , \eta _{1}}^{2} \, d{\mathcal {H}}^{n}(x) \, ds + (\varepsilon \Lambda )^{2} \bigg ), \end{aligned}$$

and $C_{4} = C_{4} (z_{0}, M, N, g, \delta , W, \lambda , \rho ) < +\infty$.

For r in $[4 \varepsilon \Lambda , \rho ]$,

$$\begin{aligned} {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{r, \eta _{1}}) \le {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }) + {\mathcal {H}}^{n} (A_{l}) \kappa _{\varepsilon } \left( \frac{r}{\rho } \right) + {III}_{\varepsilon }^{2, r}, \end{aligned}$$

where,

$$\begin{aligned} {III}_{\varepsilon }^{2,r}= & {} C_{2} \bigg ( {\mathcal {H}}^{n} ( \{ x :x \in B_{l}, -2 \varepsilon \Lambda < \sigma ^{-}(x) \le 0 \}) + \int _{B_{2 l}} q_{\varepsilon }^{1} (x) \, d {\mathcal {H}}^{n}(x)\\{} & {} + \int _{0}^{r} \int _{{\tilde{M}}} \Theta _{\varepsilon , \eta _{1}}^{1} (s,x) - \Theta _{\varepsilon , \eta _{1}}^{2} \, d{\mathcal {H}}^{n}(x) \, ds + \varepsilon ^{2} \bigg ). \end{aligned}$$

Furthermore,

$$\begin{aligned} {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{\rho , \eta _{1}}) \le {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }) - \frac{\sigma {\mathcal {H}}^{n} (A_{l})}{2^{n} - 1} + {III}_{\varepsilon }^{2, \rho }. \end{aligned}$$

5.2 Appropriate function on manifold

We wish to show that for every r in $[0, \rho ]$, there exists an ${\tilde{v}}_{\varepsilon }^{r,\eta _{1}}$, in $W^{1, \infty } (N) \subset W^{1,2} (N)$, such that, for every (x, t) in ${\tilde{T}}$,

$$\begin{aligned} {\tilde{v}}_{\varepsilon }^{r,\eta _{1}} (F(x,t)) = v_{\varepsilon }^{r,\eta _{1}} (x,t). \end{aligned}$$

This implies that ${\mathcal {F}}_{\varepsilon , \lambda } ({\tilde{v}}_{\varepsilon }^{r,\eta _{1}}) (N) = {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{r,\eta _{1}}) ({\tilde{T}})$. Indeed, this follows from the fact that $\mu _{g} (N \setminus F({\tilde{T}}) ) = \mu _{g} ( \text {Cut} (M) \cup ({\overline{M}} \setminus M) ) = 0$, and $F :{\tilde{T}} \rightarrow F({\tilde{T}})$ is a bijection between open sets, Remark 2,

$$\begin{aligned} {\mathcal {F}}_{\varepsilon , \lambda } ({\tilde{v}}_{\varepsilon }^{r, \eta _{1}}) (N)= & {} {\mathcal {F}}_{\varepsilon , \lambda } ({\tilde{v}}_{\varepsilon }^{r, \eta _{1}}) (N \setminus ( \text {Cut} (M) \cup ({\overline{M}} \setminus M) ) ), \\= & {} {\mathcal {F}}_{\varepsilon , \lambda } ({\tilde{v}}_{\varepsilon }^{r, \eta _{1}}) (F ({\tilde{T}})), \\= & {} {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{r, \eta _{1}}) ({\tilde{T}}). \end{aligned}$$

We have the following,

$$\begin{aligned} B_{\delta }^{N} (z_{0}) = \Upsilon _{1} \sqcup A \sqcup \Upsilon _{2}, \end{aligned}$$

where,

$$\begin{aligned} \Upsilon _{1} = \{ y \in B_{\delta }^{N} (z_{0}) :{\tilde{d}}_{1} (y) > {\tilde{d}}_{2} (y)\}, \end{aligned}$$

and,

$$\begin{aligned} \Upsilon _{2} = \{ y \in B_{\delta }^{N} (z_{0}) :{\tilde{d}}_{2} (y) > {\tilde{d}}_{1} (y)\}. \end{aligned}$$

Recall Remark 7,

$$\begin{aligned} A = \{ y \in B_{\delta }^{N} (z_{0}) :{\tilde{d}}_{1} (y) = {\tilde{d}}_{2} (y)\}, \end{aligned}$$

is a smooth n-submanifold in $B_{\delta }^{N}(z_{0})$. Recall the diffeomorphisms, for $i= 1, \, 2$, defined in Remark 6,

$$\begin{aligned} F_{i} :{\tilde{V}}_{i} \subset {\tilde{M}} \times {\mathbb {R}} \rightarrow B_{2 \delta }^{N} (z_{0}). \end{aligned}$$

We then define, ${\tilde{v}}_{\varepsilon }^{r, \eta _{1}}$,

$$\begin{aligned} {\tilde{v}}_{\varepsilon }^{r,\eta _{1}} (y) = {\left\{ \begin{array}{ll} {\overline{{\mathbb {H}}}}_{\varepsilon }({\tilde{d}}(y)), &{} y \not \in B_{\delta }^{N} (z_{0}), \\ v_{\varepsilon }^{r, \eta _{1}} (F_{1}^{-1} (y)), &{} y \in \overline{\Upsilon _{1}} \cap B_{\delta }^{N} (z_{0}), \\ v_{\varepsilon }^{r,\eta _{1}} (F_{2}^{-1} (y)), &{} y \in \overline{\Upsilon _{2}} \cap B_{\delta }^{N} (z_{0}). \end{array}\right. } \end{aligned}$$

For (x, t) in ${\tilde{T}}$, we have ${\tilde{v}}_{\varepsilon }^{r, \eta _{1}} (F(x,t)) = v_{\varepsilon }^{r, \eta _{1}} (x,t)$. Indeed, first we consider the case that F(x, t) lies in $\Upsilon _{1} \cup \Upsilon _{2}$. In $\Upsilon _{i}$, $F = F_{i}$, and we have,

$$\begin{aligned} {\tilde{v}}_{\varepsilon }^{r, \eta _{1}} (F(x,t)) = v_{\varepsilon }^{r,\eta _{1}} (F_{i}^{-1} (F(x,t))) = v_{\varepsilon }^{r, \eta _{1}} (x,t). \end{aligned}$$

As $A \subset \text {Cut} (M)$, we know that F(x, t) cannot lie on A. Last case to consider is F(x, t) lies in $N \setminus B_{\delta }^{N} (z_{0})$. By Remark 11 (x, t) must lie in ${\tilde{T}} \setminus (B_{2l} \times (-2 \rho , 2 \rho ))$. If x lies in ${\tilde{M}} \setminus B_{2 l}$, then $f (x) = 0$, and,

$$\begin{aligned} v_{\varepsilon }^{r, \eta _{1}} (x,t) = {\overline{{\mathbb {H}}}}_{\varepsilon } (t) = {\overline{{\mathbb {H}}}}_{\varepsilon }({\tilde{d}}(F(x,t))) = {\tilde{v}}_{\varepsilon }^{r, \eta _{1}} (F(x,t)). \end{aligned}$$

If x lies in $B_{2l}$, then $|t| \ge 2 \rho > r |f(x)| + 2 \varepsilon \Lambda$, and therefore,

$$\begin{aligned} v_{\varepsilon }^{r, \eta _{1}} (x,t) = {\overline{{\mathbb {H}}}}_{\varepsilon }(t - r f(x)) = {\left\{ \begin{array}{ll} 1, &{} t \ge 2 \rho > r f(x) + 2 \varepsilon \Lambda , \\ -1, &{} t \le - 2 \rho < r f (x) - 2 \varepsilon \Lambda . \end{array}\right. } \end{aligned}$$

Also, ${\tilde{d}} (F(x,t)) = t$, implies that,

$$\begin{aligned} {\tilde{v}}_{\varepsilon }^{r, \eta _{1}} (F(x,t)) = {\overline{{\mathbb {H}}}}_{\varepsilon } (t) = {\left\{ \begin{array}{ll} 1, &{} t \ge 2 \rho > 2 \varepsilon \Lambda , \\ -1, &{} t \le - 2 \rho < - 2 \varepsilon \Lambda . \end{array}\right. } \end{aligned}$$

Therefore, for all (x, t) in ${\tilde{T}}$, we have that $v_{\varepsilon }^{r,\eta _{1}} (x,t) = {\tilde{v}}_{\varepsilon }^{r, \eta _{1}} (F(x,t))$.

We now just look to show that ${\tilde{v}}_{\varepsilon }^{r, \eta _{1}}$ lies in $W^{1, \infty } (N)$. First consider y in $N \setminus F(B_{2l} \times (-2 \rho , 2 \rho ))$. There exists an x in ${\tilde{M}}$, such that, $F(x, {\tilde{d}} (y)) = y$, and $(x,{\tilde{d}} (y))$ lies in $({\tilde{M}} \times {\mathbb {R}}) \setminus (B_{2 l} \times (-2 \rho , 2 \rho ))$. By previous argument we see that,

$$\begin{aligned} {\tilde{v}}_{\varepsilon }^{r,\eta _{1}} (y) = {\overline{{\mathbb {H}}}}_{\varepsilon } ({\tilde{d}} (y)). \end{aligned}$$

and therefore, ${\tilde{v}}_{\varepsilon }^{r,\eta _{1}}$ is Lipschitz on the set $N \setminus F(B_{2 l} \times (-2 \rho , 2 \rho ))$.

As

$$\begin{aligned} F(B_{2l} \times (-2 \rho , 2 \rho )) \subset \subset B_{\delta }^{N} (z_{0}), \end{aligned}$$

showing that ${\tilde{v}}_{\varepsilon }^{r, \eta _{1}}$ is Lipschitz on $B_{\delta }^{N} (z_{0})$, implies that it is Lipschitz on N.

Consider y on A, then ${\tilde{d}}_{1} (y) = {\tilde{d}}_{2} (y)$, and by construction of f and $\Psi$,

$$\begin{aligned} f(\pi (F_{1}^{-1} (y))) = f(\pi (F_{2}^{-1} (y))). \end{aligned}$$

Therefore,

$$\begin{aligned} v_{\varepsilon }^{r,\eta _{1}} (F_{1}^{-1} (y)) = v_{\varepsilon }^{r,\eta _{1}} (F_{2}^{-1} (y)), \end{aligned}$$

and ${\tilde{v}}_{\varepsilon }^{r,\eta _{1}}$ is well defined and continuous across the smooth n-submanifold A. Thus we have that ${\tilde{v}}_{\varepsilon }^{r, \eta _{1}}$ lies in $W^{1, \infty } (B_{\delta }^{N} (z_{0}))$.

5.3 Continuity of the path

We show that the path,

$$\begin{aligned} \gamma :[0, \rho ]\rightarrow & {} W^{1,2} (N), \\ r\mapsto & {} {\tilde{v}}_{\varepsilon }^{r,\eta _{1}}, \end{aligned}$$

is continuous in $W^{1,2} (N)$.

Take r and s in $[0, \rho ]$. Recalling that $\mu _{g} (N \setminus F({\tilde{T}}) ) = \mu _{g} ( \text {Cut}(M) \cup ({\overline{M}} \setminus M) ) = 0$,

$$\begin{aligned} \Vert {\tilde{v}}_{\varepsilon }^{r, \eta _{1}} - {\tilde{v}}_{\varepsilon }^{s, \eta _{1}} \Vert _{L^{2} (N)}^{2}= & {} \int _{F({\tilde{T}})} |{\tilde{v}}_{\varepsilon }^{r, \eta _{1}} - {\tilde{v}}_{\varepsilon }^{s, \eta _{1}}|^{2}, \\= & {} \int _{{\mathbb {R}}} \int _{{\tilde{M}}} |{\overline{{\mathbb {H}}}}_{\varepsilon } (t - r f(x)) - {\overline{{\mathbb {H}}}}_{\varepsilon } (t - s f(x))|^{2} \theta _{t} (x) \, d {\mathcal {H}}^{n} (x) \, dt, \\&\xrightarrow {s \rightarrow r}&0, \end{aligned}$$

by Dominated Convergence Theorem.

Noting that, ${\tilde{v}}_{\varepsilon }^{r,\eta _{1}} = {\tilde{v}}_{\varepsilon }^{r,\eta _{1}}$ on $N \setminus B_{\delta }^{N} (z_{0})$, for all r in $[0, \rho ]$, and $\mu _{g} (B_{\delta }^{N}(z_{0}) \setminus (\Upsilon _{1} \cup \Upsilon _{2})) = \mu _{g} (A) = 0$,

$$\begin{aligned} \Vert \nabla {\tilde{v}}_{\varepsilon }^{r, \eta _{1}} - \nabla {\tilde{v}}_{\varepsilon }^{s, \eta _{1}} \Vert _{L^{2} (N)}^{2} = \int _{\Upsilon _{1} \cup \Upsilon _{2}} |\nabla {\tilde{v}}_{\varepsilon }^{r, \eta _{1}} - \nabla {\tilde{v}}_{\varepsilon }^{s, \eta _{1}}| \, d \mu _{g}. \end{aligned}$$

As $F_{i}^{-1} :(\Upsilon _{i}, g) \rightarrow (F_{i}^{-1} (\Upsilon _{i}), h)$ is an isometry, we have,

$$\begin{aligned} \Vert \nabla {\tilde{v}}_{\varepsilon }^{r, \eta _{1}} - \nabla {\tilde{v}}_{\varepsilon }^{s, \eta _{1}} \Vert _{L^{2} (N)}^{2}= & {} \int _{F_{1}^{-1} (\Upsilon _{1}) \cup F_{2}^{-1} (\Upsilon _{2})} |\nabla v_{\varepsilon }^{r,\eta _{1}} (x,t) - \nabla v_{\varepsilon }^{s,\eta _{1}} (x,t)|^{2}, \\= & {} \int _{F_{1}^{-1} (\Upsilon _{1}) \cup F_{2}^{-1} (\Upsilon _{2})} ({\overline{{\mathbb {H}}}}_{\varepsilon }' (t - r f(x)) - {\overline{{\mathbb {H}}}}_{\varepsilon }' (t - s f(x)))^{2} \\{} & {} \quad + |\nabla _{x} f(x)|^{2} (r {\overline{{\mathbb {H}}}}_{\varepsilon }' (t - r f(x)) - s {\overline{{\mathbb {H}}}}_{\varepsilon }' (t - s f(x)))^{2}, \\&\xrightarrow {s \rightarrow r}&0, \end{aligned}$$

by Dominated Convergence Theorem.

6 Path to $a_{\varepsilon }$

6.1 Fixed energy gain away from non-embedded point

We construct the path from (2) to (3) in Fig. 2.

Recall ${\tilde{f}}$ from Sect. 3.5 and set,

$$\begin{aligned} \eta _{2}(r, x) = \rho f (x) + r {\tilde{f}}(x), \end{aligned}$$

for r in $[0,r_{0}]$, where $r_{0} \in (0, \min \{1, \text {diam}(N)/2\})$, will be chosen later. Denote, $A_{L}^{k} = B_{L} \setminus B_{\frac{L}{k}}$.

Remark 20

We choose $0 < \varepsilon _{3} \le \varepsilon _{2}$, such that $2 \varepsilon _{3} \Lambda = 6 \varepsilon _{3} |\log \, \varepsilon _{3}|< < r_{0}$. From here on we consider $\varepsilon$ on $(0, \varepsilon _{3})$.

We slightly edit the Base Computation in Sect. 4. Consider $r > 2 \varepsilon \Lambda$,

$$\begin{aligned} {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{r,\eta _{2}}) - {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{r, \eta _{2}}) = {I}_{\varepsilon }^{r, \eta _{2}} + ({II}_{\varepsilon }^{r, \eta _{2}} - {II}_{\varepsilon }^{2 \varepsilon \Lambda , \eta _{2}} ) + {II}_{\varepsilon }^{2 \varepsilon \Lambda , \eta _{2}}. \end{aligned}$$

We have,

$$\begin{aligned} \begin{aligned} {II}_{\varepsilon }^{r,\eta _{2}} - {II}_{\varepsilon }^{2 \varepsilon \Lambda , \eta _{2}}&= - \int _{2 \varepsilon \Lambda }^{r} \int _{{\tilde{M}} \setminus B_{\frac{L}{k}}} {\tilde{f}} (x) Q_{\varepsilon }(\sigma ^{+}(x) - s {\tilde{f}}(x)) \, \theta ^{+}(x) \, d{\mathcal {H}}^{n}(x) \, ds \\&\quad + \int _{2 \varepsilon \Lambda }^{r} \int _{{\tilde{M}} \setminus B_{\frac{L}{k}}} {\tilde{f}}(x) Q_{\varepsilon }(\sigma ^{-}(x) - s {\tilde{f}}(x)) \, \theta ^{-}(x) \, d{\mathcal {H}}^{n}(x) \, ds \\&\quad + \int _{2 \varepsilon \Lambda }^{r} \int _{{\tilde{M}} \setminus B_{\frac{L}{k}}} {\tilde{f}}(x) \int _{\sigma ^{-}(x)}^{\sigma ^{+}(x)} Q_{\varepsilon }(t - s {\tilde{f}}(x)) \, \\ \\&\quad \times (\lambda - H_{t}(x)) \, \theta _{t}(x) \, dt \, d{\mathcal {H}}^{n}(x) \, ds \\&\quad + \lambda \int _{2 \varepsilon \Lambda }^{r} \int _{{\tilde{M}}} \Theta _{\varepsilon , \eta _{2}}^{1} (s,x) - \Theta _{\varepsilon , \eta _{2}}^{2} (s,x) \, d{\mathcal {H}}^{n}(x) \, ds. \end{aligned} \end{aligned}$$

(12)

Considering the first term on the right hand side of (12),

$$\begin{aligned} - \int _{2 \varepsilon \Lambda }^{r} \int _{{\tilde{M}} \setminus B_{\frac{L}{k}}} {\tilde{f}} (x) Q_{\varepsilon }(\sigma ^{+}(x) - s {\tilde{f}}(x)) \, \theta ^{+}(x) \, d{\mathcal {H}}^{n}(x) \, ds \le 0. \end{aligned}$$

Considering the second term on the right hand side of (12), and by applying similar arguments for when we considered the corresponding term on the right-hand side of (11) in Sect. 5.1,

$$\begin{aligned}{} & {} \int _{2 \varepsilon \Lambda }^{r} \int _{{\tilde{M}} \setminus B_{\frac{L}{k}}} {\tilde{f}}(x) Q_{\varepsilon }(\sigma ^{-}(x) - s {\tilde{f}}(x)) \, \theta ^{-}(x) \, d{\mathcal {H}}^{n}(x) \, ds \\{} & {} \quad \le C_{2} {\mathcal {H}}^{n} ( \{ x :x \in {\tilde{M}} \setminus B_{\frac{L}{k}}, \, \sigma ^{-}(x) \ge 2 \varepsilon \Lambda ({\tilde{f}}(x) - 1) \} ), \end{aligned}$$

where we are potentially rechoosing $C_{2} = C_{2} (M, N, g, W, \lambda )< + \infty$.

Considering the third term on the right hand side of (12). Applying similar arguments in $A_{L}^{k}$ from when we considered the corresponding term on the right hand side of (11) in Sect. 5.1,

$$\begin{aligned} \begin{aligned}&\int _{2 \varepsilon \Lambda }^{r} \int _{{\tilde{M}} \setminus B_{\frac{L}{k}}} {\tilde{f}}(x) \int _{\sigma ^{-}(x)}^{\sigma ^{+}(x)} Q_{\varepsilon }(t - s {\tilde{f}}(x)) \, (\lambda - H_{t}(x)) \, \theta _{t}(x) \, dt \, d{\mathcal {H}}^{n}(x) \, ds \\&\quad \le \int _{2 \varepsilon \Lambda }^{r} \int _{{\tilde{M}} \setminus B_{L}} \int _{-2 \varepsilon \Lambda }^{2 \varepsilon \Lambda } Q_{\varepsilon } (\xi ) (\lambda - H_{\xi + s} (x)) \theta _{\xi + s} (x) \, d \xi \, d {\mathcal {H}}^{n}(x) \, ds \\&\qquad + C_{2} \int _{A_{L}^{k}} q_{\varepsilon }^{2} (x) \, d {\mathcal {H}}^{n} (x), \end{aligned} \end{aligned}$$

(13)

where, $q_{\varepsilon }^{2} (x) {:}{=}\max _{t \in [-2 \varepsilon \Lambda , 4 \varepsilon \Lambda ]} ( \lambda - H_{t} (x)) \theta _{t} (x)$, and we are potentially rechoosing $C_{2} = C_{2} (M, N, g, \lambda , W) < \infty$.

Define the following measurable set,

$$\begin{aligned} \Omega _{r} = \{ x \in {\tilde{M}} :\, \sigma ^{+}(x) > 2 r \, \}. \end{aligned}$$

Remark 21

We choose $L = L (z_{0}, N, M, g, \delta ) > 0$, such that,

$$\begin{aligned} {\mathcal {H}}^{n} ({\tilde{M}} \setminus B_{L}) > \frac{3}{4} {\mathcal {H}}^{n} ({\tilde{M}}). \end{aligned}$$

Then we can find an $r_{0} = r_{0}(z_{0}, M, N, g, \delta , L) > 0$, such that, for all r in $[0, r_{0}]$,

$$\begin{aligned} {\mathcal {H}}^{n} (\{ (x, 2r) :\, x \in \Omega _{r} \setminus B_{L} \}) > \frac{1}{2} {\mathcal {H}}^{n}({\tilde{M}}). \end{aligned}$$

For all x in $\Omega _{r}$, s in $(2 \varepsilon \Lambda , r)$, and $\xi$ in $[- 2 \varepsilon \Lambda , 2 \varepsilon \Lambda ]$, $s + \xi$ lies in $(0, \sigma ^{+}(x))$. Therefore, recalling bounds on $H_{t}$ and $\theta _{t}$ from Remark 4 and Proposition 6, we have,

$$\begin{aligned} (\lambda - H_{\xi + s}(x)) \theta _{\xi + s} (x) < - m (s + \xi ) \theta _{\xi + s} \le - m (s - 2 \varepsilon \Lambda ) \theta _{2r} (x), \end{aligned}$$

Then for r in $(2 \varepsilon \Lambda , r_{0}]$, we compute an energy decrease from the first term on the right hand side of (13),

$$\begin{aligned}{} & {} \int _{2 \varepsilon \Lambda }^{r} \int _{{\tilde{M}} \setminus B_{L}} \int _{-2 \varepsilon \Lambda }^{2 \varepsilon \Lambda } Q_{\varepsilon } (\xi ) (\lambda - H_{\xi + s} (x)) \theta _{\xi + s} (x) \, d \xi \, d {\mathcal {H}}^{n}(x) \, ds \\{} & {} \quad \le - \frac{m \sigma }{2} {\mathcal {H}}^{n}({\tilde{M}}) r^{2} + C_{2} \varepsilon \Lambda , \end{aligned}$$

potentially rechoosing $C_{2} = C_{2} (N, M, g, \lambda , W) < + \infty$.

For r in $[0, 2 \varepsilon \Lambda ]$, by repeating arguments similar to those in Sect. 3.6,

$$\begin{aligned} {II}_{\varepsilon }^{r, \eta _{2}}\le & {} C_{2} \bigg ( \int _{{\tilde{M}} \setminus B_{\frac{L}{k}}} m_{\varepsilon }^{1} (x) \, d {\mathcal {H}}^{n} (x) + \varepsilon \Lambda \bigg ), \end{aligned}$$

where we are potentially rechoosing $C_{2} = C_{2} (N, M, g, W, \lambda )$, and $m_{\varepsilon }^{1} (x) = \max _{t \in [- 2 \varepsilon \Lambda , 4 \varepsilon \Lambda ]} \theta _{t} (x) - \min _{t \in [-2 \varepsilon \Lambda , 4 \varepsilon \Lambda ]} \theta _{t} (x)$.

For r in $[0, r_{0}]$, consider the term,

$$\begin{aligned} {I}_{\varepsilon }^{r, \eta _{2}} = \int _{A_{L}^{k}} \int _{- 2 \varepsilon \Lambda }^{2 \varepsilon \Lambda } \frac{\varepsilon }{2} (({\overline{{\mathbb {H}}}})' (\xi ))^{2} | r \nabla {\tilde{f}}|^{2} (x,r {\tilde{f}}(x) + \xi ) \theta _{r {\tilde{f}}(x) + \xi } (x) \, d\xi \, d {\mathcal {H}}^{n} (x). \end{aligned}$$

By choice of L and $r_{0}$ in Remark 12, and constant $C_{3} = C_{3} (z_{0}, M, N, g, \delta , \lambda , W)$ from Remark 17, we have, for all x in $A_{L}^{k}$, r in $[0, r_{0}]$, and $\xi$ in $[-2 \varepsilon \Lambda , 2 \varepsilon \Lambda ]$,

$$\begin{aligned} |\nabla {\tilde{f}}|^{2} (x,r {\tilde{f}}(x) + \xi ) \le C_{3} |\nabla {\tilde{f}}|^{2} (x, 0). \end{aligned}$$

Thus we have,

$$\begin{aligned} {I}_{\varepsilon }^{r, \eta _{2}} \le C_{3} \Vert \nabla {\tilde{f}}\Vert _{L^{2}({\tilde{M}})}^{2} r^{2}. \end{aligned}$$

Again we are potentially rechoosing $C_{3} = C_{3} (z_{0}, M, N, g, \delta , W, \lambda )$.

Remark 22

Choose $k = k (z_{0}, M, N, g, \delta , W, \lambda , L)$ such that

$$\begin{aligned} \Vert \nabla {\tilde{f}} \Vert _{L^{2}({\tilde{M}})}^{2} < C_{3}^{-1} \frac{m \sigma }{4} {\mathcal {H}}^{n} ({\tilde{M}}). \end{aligned}$$

Therefore, after potentially rechoosing $C_{3} = C_{3} (z_{0}, M, N, g, \delta , W, \lambda )$,

$$\begin{aligned} {I}_{\varepsilon }^{r,\eta _{2}} \le \frac{m \sigma }{4} {\mathcal {H}}^{n} ({\tilde{M}}) r^{2}. \end{aligned}$$

For r in $(0, 2 \varepsilon \Lambda ]$,

$$\begin{aligned} {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{r, \eta _{2}}) - {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{0, \eta _{2}}) \le {III}_{\varepsilon }^{3, r}, \end{aligned}$$

where,

$$\begin{aligned} {III}_{\varepsilon }^{3, r}= & {} C_{2} \left( \int _{{\tilde{M}} \setminus B_{\frac{L}{k}}} m_{\varepsilon } (x) \, d {\mathcal {H}}^{n} (x) + \varepsilon \Lambda \right) , \end{aligned}$$

where we are potentially rechoosing $C_{2} = C_{2} (N, M, g, W, \lambda ) < + \infty$. For r in $(2 \varepsilon \Lambda , r_{0}]$,

$$\begin{aligned} {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{r, \eta _{2}}) - {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{0, \eta _{2}}) \le - \frac{m \sigma }{4} {\mathcal {H}}^{n} ({\tilde{M}}) r^{2} + {III}_{\varepsilon }^{4,r} \end{aligned}$$

where,

$$\begin{aligned} {III}_{\varepsilon }^{4,r}= & {} C_{2} \bigg ( {\mathcal {H}}^{n} ( \{ x :x \in {\tilde{M}} \setminus B_{\frac{L}{k}}, \, \sigma ^{-}(x) \ge 2 \varepsilon \Lambda ({\tilde{f}}(x) - 1) \, \} ) \\{} & {} +\int _{A_{L}^{k}} q_{\varepsilon }^{2} (x) \, d {\mathcal {H}}^{n} (x) + \int _{2 \varepsilon \Lambda }^{r} \int _{{\tilde{M}}} \Theta _{\varepsilon , \eta _{2}}^{1} (s, x) - \Theta _{\varepsilon , \eta _{2}}^{2} \, d {\mathcal {H}}^{n} (x) \, ds \\{} & {} + \int _{{\tilde{M}} \setminus B_{\frac{L}{k}}} m_{\varepsilon } (x) \, d {\mathcal {H}}^{n} (x) + \varepsilon \Lambda \bigg ), \end{aligned}$$

again, we are potentially rechoosing $C_{2} = C_{2}(M, N, g, W, \lambda )$.

As $\eta _{2} (0, x) = \eta _{1} (\rho , x)$, we have, for r in $(0, 2 \varepsilon \Lambda ]$,

$$\begin{aligned} {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{r, \eta _{2}}) \le {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }) - \frac{\sigma {\mathcal {H}}^{n} (A_{l})}{2^{n} - 1} + {III}_{\varepsilon }^{2, \rho } + {III}_{\varepsilon }^{3, r}, \end{aligned}$$

and for r in $(2 \varepsilon \Lambda , r_{0}]$,

$$\begin{aligned} {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{r, \eta _{2}}) \le {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }) - \frac{\sigma {\mathcal {H}}^{n} (A_{l})}{2^{n} - 1} - \frac{m \sigma }{4} {\mathcal {H}}^{n} ({\tilde{M}}) r^{2} + {III}_{\varepsilon }^{2, \rho } + {III}_{\varepsilon }^{4, r}. \end{aligned}$$

We may define the appropriate function on N, for r in $[0, r_{0}]$,

$$\begin{aligned} {\tilde{v}}_{\varepsilon }^{r,\eta _{2}} (y) = {\left\{ \begin{array}{ll} {\overline{{\mathbb {H}}}}_{\varepsilon } ({\tilde{d}}(y) - r), &{} y \not \in B_{\delta }^{N} (z_{0}), \\ v_{\varepsilon }^{r,\eta _{2}} (F_{1}^{-1} (y)), &{} y \in \overline{\Upsilon _{1}} \cap B_{\delta }^{N} (z_{0}), \\ v_{\varepsilon }^{r, \eta _{2}} (F_{2}^{-1} (y)), &{} y \in \overline{\Upsilon _{2}} \cap B_{\delta }^{N} (z_{0}). \end{array}\right. } \end{aligned}$$

Following similar arguments to Sects. 5.2, and 5.3, we may show that ${\tilde{v}}_{\varepsilon }^{r, \eta _{2}}$ lies in $W^{1, \infty } (N)$, ${\mathcal {F}}_{\varepsilon , \lambda } ({\tilde{v}}_{\varepsilon }^{r, \eta _{2}}) (N) = {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{r,\eta _{2}}) ({\tilde{T}})$ and that the path ${\tilde{v}}_{\varepsilon }^{0, \eta _{2}} \rightarrow {\tilde{v}}_{\varepsilon }^{r_{0}, \eta _{2}}$ is continuous in $W^{1,2} (N)$.

6.2 Reversing construction of competitor

We construct the path from (3) to (4) in Fig. 2.

For r in $[0, \rho ]$, we set,

$$\begin{aligned} \eta _{3} (r, x) = r_{0} {\tilde{f}} (x) + (\rho - r) f(x). \end{aligned}$$

For x in $B_{2l}$,

$$\begin{aligned} \eta _{3} (r, x) = (\rho - r) f(x) = \eta _{1} (\rho - r, x), \end{aligned}$$

and for x in ${\tilde{M}} \setminus B_{2l}$,

$$\begin{aligned} \eta _{3} (r,x) = r_{0} {\tilde{f}} (x) = \eta _{3} (0, x). \end{aligned}$$

Therefore,

$$\begin{aligned} {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{r, \eta _{3}}) - {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{0, \eta _{3}}) = {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{\rho - r, \eta _{1}}) - {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{\rho , \eta _{1}}). \end{aligned}$$

As $\eta _{1} (\rho ,x) = \eta _{2} (0, x)$, and $\eta _{3}(0, x) = \eta _{2} (r_{0}, x)$, we have,

$$\begin{aligned} {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{r, \eta _{3}}) = {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{\rho - r, \eta _{1}}) + {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{r_{0}, \eta _{2}}) - {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{0, \eta _{2}}). \end{aligned}$$

Remark 23

We choose $\rho > 0$, such that,

$$\begin{aligned} \frac{\sigma {\mathcal {H}}^{n} (A_{l})}{2^{n} - 1} < \frac{m \sigma }{4} {\mathcal {H}}^{n} ({\tilde{M}}) r_{0}^{2}. \end{aligned}$$

Therefore, we have that

$$\begin{aligned} {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{r, \eta _{3}}) < {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{\rho - r, \eta _{1}}) - \frac{\sigma {\mathcal {H}}^{n} (A_{l})}{2^{n} - 1} + {III}_{\varepsilon }^{4,r_{0}}. \end{aligned}$$

Furthermore, for r in $[0, \rho - 4 \varepsilon \Lambda ]$, we have,

$$\begin{aligned} {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{r, \eta _{3}})< & {} {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }) + \frac{\sigma {\mathcal {H}}^{n} (A_{l})}{2(2^{n} - 1)} + {III}_{\varepsilon }^{2, \rho - r} - \frac{\sigma {\mathcal {H}}^{n} (A_{l})}{2^{n} - 1} + {III}_{\varepsilon }^{4,r_{0}}, \\= & {} {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }) - \frac{\sigma {\mathcal {H}}^{n} (A_{l})}{2(2^{n} - 1)} + {III}_{\varepsilon }^{2, \rho - r} + {III}_{\varepsilon }^{4,r_{0}}. \end{aligned}$$

For r in $(\rho - 4 \varepsilon \Lambda , \rho ]$, we similarly have,

$$\begin{aligned} {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{r, \eta _{3}}) < {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }) - \frac{\sigma {\mathcal {H}}^{n} (A_{l})}{2(2^{n} - 1)} + {III}_{\varepsilon }^{1, \rho - r} + {III}_{\varepsilon }^{4,r_{0}}. \end{aligned}$$

We define the appropriate function on N. For r in $[0, \rho ]$,

$$\begin{aligned} {\tilde{v}}_{\varepsilon }^{r,\eta _{3}} (y) = {\left\{ \begin{array}{ll} {\overline{{\mathbb {H}}}}_{\varepsilon } ({\tilde{d}}(y) - r_{0}), &{} y \not \in B_{\delta }^{N} (z_{0}), \\ v_{\varepsilon }^{r,\eta _{3}} (F_{1}^{-1} (y)), &{} y \in \overline{\Upsilon _{1}} \cap B_{\delta }^{N} (z_{0}), \\ v_{\varepsilon }^{r, \eta _{3}} (F_{2}^{-1} (y)), &{} y \in \overline{\Upsilon _{2}} \cap B_{\delta }^{N} (z_{0}). \end{array}\right. } \end{aligned}$$

Following similar arguments to Sects. 5.2, and 5.3, we may show that ${\tilde{v}}_{\varepsilon }^{r, \eta _{3}}$ lies in $W^{1, \infty } (N)$, ${\mathcal {F}}_{\varepsilon , \lambda } ({\tilde{v}}_{\varepsilon }^{r, \eta _{3}}) (N) = {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{r,\eta _{3}}) ({\tilde{T}})$ and that the path ${\tilde{v}}_{\varepsilon }^{0, \eta _{3}} \rightarrow {\tilde{v}}_{\varepsilon }^{\rho , \eta _{3}}$ is continuous in $W^{1,2} (N)$.

6.3 Lining up with level Set $\Gamma _{r_{0}}$

We construct path from (4) to (5) in Fig. 2

For r in $[0, r_{0}]$, consider,

$$\begin{aligned} \eta _{4} (r, x) = r_{0} {\tilde{f}} (x) + r (1 - {\tilde{f}} (x)) = (r_{0} - r) {\tilde{f}} (x) + r \ge r. \end{aligned}$$

By applying similar arguments to those in Sect. 5.1, we have

$$\begin{aligned} {II}_{\varepsilon }^{r, \eta _{4}}\le & {} C_{3} \bigg ( {\mathcal {H}}^{n} (\{ x \in B_{L} :\sigma ^{-} (x) \ge - 2 \varepsilon \Lambda \}) + \varepsilon \Lambda \\{} & {} + \int _{0}^{r} \int _{{\tilde{M}}} \Theta _{\varepsilon , \eta _{4}}^{1} (s, x) - \Theta _{\varepsilon , \eta _{4}}^{2} (s,x) \, d {\mathcal {H}}^{n} (x) \, ds \bigg ), \end{aligned}$$

where we are potentially rechoosing $C_{3} = C_{3} (z_{0}, M, N, g, \delta , W, \lambda ) < + \infty$.

We turn our attention to the term,

$$\begin{aligned} {I}_{\varepsilon }^{r,\eta _{4}}= & {} \int _{A_{L}^{k}} \int _{\sigma ^{-}(x)}^{\sigma ^{+}(x)} \frac{\varepsilon }{2} ( ({\overline{{\mathbb {H}}}}_{\varepsilon })'(t - (r_{0} - r) \\{} & {} {\tilde{f}}(x) - r))^{2} (r_{0} - r)^{2} |\nabla {\tilde{f}} |^{2} (x,t) \, \theta _{t}(x) \, dt \, d {\mathcal {H}}^{n}(x) \\{} & {} - \int _{A_{L}^{k}} \int _{\sigma ^{-}(x)}^{\sigma ^{+}(x)} \frac{\varepsilon }{2} ( ({\overline{{\mathbb {H}}}}_{\varepsilon })'(t - r_{0} {\tilde{f}}(x)))^{2} r_{0}^{2} |\nabla {\tilde{f}}|^{2} (x,t) \, \theta _{t}(x) \, dt \, d {\mathcal {H}}^{n}(x). \end{aligned}$$

For r in $[0, r_{0}]$,

$$\begin{aligned}{} & {} \int _{\sigma ^{-}(x)}^{\sigma ^{+}(x)} \frac{\varepsilon }{2} ( ({\overline{{\mathbb {H}}}}_{\varepsilon })'(t - (r_{0} - r) {\tilde{f}}(x) - r))^{2} |\nabla {\tilde{f}}|^{2} (x,t) \, \theta _{t}(x) \, dt \\{} & {} \quad \le (\sigma + \beta \varepsilon ^{2}) \max _{t \in [-2 \varepsilon \Lambda , 2 \varepsilon \Lambda ]} |\nabla {\tilde{f}}|^{2} (x, t + \eta _{4} (r,x)) \theta _{t + \eta _{4} (r,x)} (x), \\{} & {} \quad = \sigma | \nabla {\tilde{f}}|^{2} (x, \eta _{4} (r,x)) \theta _{\eta _{4} (r,x)} (x) + \beta \varepsilon ^{2} \max _{t \in [-2 \varepsilon \Lambda , 2 \varepsilon \Lambda ]} |\nabla \\{} & {} \quad {\tilde{f}}|^{2} (x, t + \eta _{4} (r,x)) \theta _{t + \eta _{4} (r,x)} (x) \\{} & {} \qquad + \sigma \Bigg ( \max _{t \in [-2 \varepsilon \Lambda , 2 \varepsilon \Lambda ]} |\nabla {\tilde{f}}|^{2} (x, t + \eta _{4} (r,x)) \\{} & {} \quad \theta _{t + \eta _{4} (r,x)} (x) - | \nabla {\tilde{f}}|^{2} (x, \eta _{4} (r,x)) \theta _{\eta _{4} (r,x)} (x) \Bigg ) \end{aligned}$$

Denote the functions,

$$\begin{aligned} q_{\varepsilon }^{3} (x, r) = \max _{t \in [-2 \varepsilon \Lambda , 2 \varepsilon \Lambda ]} |\nabla {\tilde{f}}|^{2}(x, t + \eta _{4} (r,x)) \theta _{t + \eta _{4} (r,x)} (x) - | \nabla {\tilde{f}}|^{2} (x, \eta _{4} (r,x)) \theta _{\eta _{4} (r,x)} (x), \end{aligned}$$

and,

$$\begin{aligned} p^{1}_{\varepsilon } (r) = \int _{A_{L}^{k}} q_{\varepsilon }^{3} (x, r) \, d {\mathcal {H}}^{n} (x). \end{aligned}$$

We have,

$$\begin{aligned}{} & {} \int _{A_{L}^{k}} \int _{\sigma ^{-}(x)}^{\sigma ^{+}(x)} \frac{\varepsilon }{2} ( ({\overline{{\mathbb {H}}}}_{\varepsilon })'(t - (r_{0} - r) {\tilde{f}}(x) - r))^{2} (r_{0} - r)^{2} |\nabla {\tilde{f}}|^{2} \, \theta _{t}(x) \, dt \, d {\mathcal {H}}^{n}(x) \\{} & {} \quad \le \sigma \int _{A_{L}^{k}} (r_{0} - r)^{2} |\nabla {\tilde{f}} (x)|^{2} (x, \eta _{4} (r,x)) \theta _{\eta _{4} (r,x)} (x) \, d {\mathcal {H}}^{n}(x)\\{} & {} \qquad + C_{5} (\varepsilon ^{2} + p^{1}_{\varepsilon } (r)). \end{aligned}$$

where $C_{5} = C_{5} (z_{0}, N, M, g, \delta , L, r_{0}, k, W, \lambda ) < + \infty$. Similarly we have,

$$\begin{aligned}{} & {} \int _{A_{L}^{k}} \int _{\sigma ^{-}(x)}^{\sigma ^{+}(x)} \frac{\varepsilon }{2} ( ({\overline{{\mathbb {H}}}}_{\varepsilon })'(t - r_{0} {\tilde{f}}(x)))^{2} r_{0}^{2} |\nabla {\tilde{f}}|^{2} \, \theta _{t}(x) \, dt \, d {\mathcal {H}}^{n}(x) \\{} & {} \quad \ge \sigma \int _{A_{L}^{k}} r_{0}^{2} |\nabla {\tilde{f}}|^{2} (x, \eta _{4}(0,x)) \theta _{\eta _{4} (0,x)} (x) \, d {\mathcal {H}}^{n} (x) - C_{5} (\varepsilon ^{2} + p_{\varepsilon }^{2} (0)), \end{aligned}$$

where,

$$\begin{aligned} p_{\varepsilon }^{2} (0) = \int _{A_{L}^{k}} q_{\varepsilon }^{4} (x,0) \, d {\mathcal {H}}^{n} (x), \end{aligned}$$

and

$$\begin{aligned} q_{\varepsilon }^{4} (x, r)= & {} \min _{t \in [-2 \varepsilon \Lambda , 2 \varepsilon \Lambda ]} |\nabla {\tilde{f}}|^{2} (x, t + \eta _{4} (r,x)) \\{} & {} \quad \theta _{t + \eta _{4} (r,x)} (x) - | \nabla {\tilde{f}}|^{2} (x, \eta _{4} (r,x)) \theta _{\eta _{4} (r,x)} (x) \le 0 \end{aligned}$$

Therefore we have, for r in $[0, r_{0}]$,

$$\begin{aligned} {I}_{\varepsilon }^{r, \eta _{3}}\le & {} \sigma \int _{A_{L}^{k}} (r_{0} - r)^{2} |\nabla {\tilde{f}} (x)|^{2} (x, \eta _{4}(r,x))\\{} & {} \theta _{\eta _{4}(r,x)} (x) - r_{0}^{2} |\nabla {\tilde{f}} (x)|^{2} (x, \eta _{4}(0, x)) \theta _{\eta _{4}(0,x)} (x) \, d {\mathcal {H}}^{n} (x) \\{} & {} + C_{5} ( \varepsilon ^{2} + p_{\varepsilon }^{1} (r) - p_{\varepsilon }^{2} (0) ). \end{aligned}$$

Claim 4

There exists an $r_{0} > 0$, such that for all r in $[0, r_{0}]$,

$$\begin{aligned}{} & {} \int _{A_{L}^{k}} (r_{0} - r)^{2} |\nabla {\tilde{f}} (x)|^{2} (x, \eta _{4}(r,x)) \theta _{\eta _{4}(r,x)} (x) \\{} & {} \quad - r_{0}^{2} |\nabla {\tilde{f}} (x)|^{2} (x, \eta _{4}(0, x)) \theta _{\eta _{4}(0,x)} (x) \, d {\mathcal {H}}^{n} (x) \le 0. \end{aligned}$$

Proof

For $(x,t) \in {\tilde{M}} \times {\mathbb {R}}$, denote,

$$\begin{aligned} \zeta (x,t) {:}{=}|\nabla {\tilde{f}}|^{2} (x,t) \theta _{t} (x). \end{aligned}$$

We note that $\zeta \in C^{\infty } ({\tilde{T}})$, and $\zeta (x,t) = 0$, for $(x,t) \not \in {\tilde{T}}$.

For r in $[0, r_{0}]$, denote,

$$\begin{aligned} G(r) {:}{=}\int _{A_{L}^{k}} \zeta (x, \eta _{4} (r,x)) \, d {\mathcal {H}}^{n} (x) = \int _{A_{L}^{k} \cap \{ {\tilde{f}} \not = 0\}} \zeta (x, \eta _{4} (r,x)) \, d {\mathcal {H}}^{n} (x). \end{aligned}$$

For $r \in [0,r_{0}]$, and $\nabla {\tilde{f}} (x) \not = 0$, we have that,

$$\begin{aligned} \eta _{4} (r,x) \in (\sigma ^{-}(x), \sigma ^{+} (x)), \end{aligned}$$

i.e. $(x, \eta _{4} (r, x)) \in {\tilde{T}}$. Therefore, G lies in $C^{\infty } ([0, r_{0}])$, and

$$\begin{aligned} G' (r) = \int _{ A_{L}^{k} \cap \{ {\tilde{f}} \not = 0\} } (\partial _{t} \zeta ) (x, \eta _{4} (r,x)) (1 - {\tilde{f}} (x)) \, dx. \end{aligned}$$

We may obtain a bound $|G' (r)| \le C_{6} = C_{6} (z_{0}, M, N, g, \delta , W, \lambda , L, k) < + \infty$, for $r \le R_{0} < + \infty$, $R_{0} = R_{0} (z_{0}, M, N, g, \delta , W, \lambda , L, k)$ fixed. We also have, by Remark 17, that,

$$\begin{aligned} G(0) \ge C_{3}^{-1/2} \Vert \nabla {\tilde{f}} \Vert _{L^{2}({\tilde{M}})} > 0, \end{aligned}$$

and we may choose $r_{0} > 0$, small enough such that,

$$\begin{aligned} \min _{r \in [0,r_{0}]} G(r) \ge \frac{1}{2} G(0) > 0. \end{aligned}$$

Denoting,

$$\begin{aligned} F(r) {:}{=}(r_{0} - r)^{2} G(r). \end{aligned}$$

Differentiating we obtain,

$$\begin{aligned} F'(r) = (r - r_{0}) (2 G(r) + (r - r_{0}) G' (r)). \end{aligned}$$

Thus setting, $r_{0} < G(0) / C_{6}$, we have that $F' (r) \le 0$, for all r in $[0, r_{0}]$. This completes the proof. $\square$

Remark 24

Claim 4 is a further choice of $r_{0} = r_{0} (z_{0}, M, N, g, \delta , W, \lambda , L, k) > 0$.

Therefore, there exists an $r_{0}$, such that for all r in $[0, r_{0}]$,

$$\begin{aligned} {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{r, \eta _{4}}) - {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{0, \eta _{4}})= & {} {I}_{\varepsilon }^{r, \eta _{4}} + {II}_{\varepsilon }^{r, \eta _{4}}, \\\le & {} {III}_{\varepsilon }^{5,r}, \end{aligned}$$

where

$$\begin{aligned} {III}_{\varepsilon }^{5,r}\le & {} C_{5} \bigg ( p_{\varepsilon }^{1} (r) - p_{\varepsilon }^{2} (0) + {\mathcal {H}}^{n} (\{ x \in B_{2 L} :\, \sigma ^{-} (x) \ge - 2 \varepsilon \Lambda \}) + \varepsilon \Lambda \\{} & {} + \lambda \int _{0}^{r} \int _{{\tilde{M}}} \Theta _{\varepsilon , \eta _{4}}^{1} (s,x) - \Theta _{\varepsilon , \eta _{4}}^{2} (s,x) \, d {\mathcal {H}}^{n} (x) \, ds \bigg ), \end{aligned}$$

where we are potentially rechoosing $C_{5} = C_{5}(z_{0}, M, N, g, k, L, \delta , r_{0}, W, \lambda )$.

As $\eta _{4} (0, x) = \eta _{3} (\rho , x)$, we have, for r in $[0, r_{0}]$,

$$\begin{aligned} {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{r, \eta _{4}}) \le {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }) - \frac{\sigma {\mathcal {H}}^{n} (x)}{2(2^{n} - 1)} + {III}_{\varepsilon }^{1, 0} + {III}_{\varepsilon }^{4, r_{0}} + {III}_{\varepsilon }^{5, r}. \end{aligned}$$

Consider the following function on N, for r in $[0, r_{0}]$,

$$\begin{aligned} {\tilde{v}}_{\varepsilon }^{r,\eta _{4}} (y) = {\left\{ \begin{array}{ll} {\overline{{\mathbb {H}}}}_{\varepsilon } ({\tilde{d}}(y) - r_{0}), &{} y \not \in B_{\delta }^{N} (z_{0}), \\ v_{\varepsilon }^{r,\eta _{4}} (F_{1}^{-1} (y)), &{} y \in \overline{\Upsilon _{1}} \cap B_{\delta }^{N} (z_{0}), \\ v_{\varepsilon }^{r, \eta _{4}} (F_{2}^{-1} (y)), &{} y \in \overline{\Upsilon _{2}} \cap B_{\delta }^{N} (z_{0}). \end{array}\right. } \end{aligned}$$

We can show, as in Sects. 5.2 and 5.3, that ${\tilde{v}}_{\varepsilon }^{r,\eta _{3}}$ lies in $W^{1,\infty } (N)$, ${\mathcal {F}}_{\varepsilon , \lambda } ({\tilde{v}}_{\varepsilon }^{r, \eta _{4}}) (N) = {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{r,\eta _{4}}) ({\tilde{T}})$, and that, $r \mapsto {\tilde{v}}_{\varepsilon }^{r,\eta _{4}}$ is a continuous path in $W^{1,2} (N)$.

6.4 Completing path to $a_{\varepsilon }$

We construct the path from (5) to ‘$-1$’ in Fig. 2.

Consider, for r in $[r_{0}, 2 \, \text {diam} (N)]$,

$$\begin{aligned} \eta _{5} (r, x) = r. \end{aligned}$$

By repeating similar arguments to those in Sect. 5.1, we have

$$\begin{aligned} {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{r, \eta _{5}}) - {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{r_{0}, \eta _{5}}) \le {III}_{\varepsilon }^{6,r}, \end{aligned}$$

where

$$\begin{aligned} {III}_{\varepsilon }^{6,r} = \lambda \int _{\rho }^{r} \Theta _{\varepsilon , \eta _{5}}^{1} (s,x) - \Theta _{\varepsilon , \eta _{5}}^{2} (s,x) \, d {\mathcal {H}}^{n} (x) \, ds. \end{aligned}$$

Recalling that, $\eta _{5} (r_{0}, x) = \eta _{4} (r_{0}, x)$, we have, for all r in $[r_{0}, 2 \, \text {diam} (N)]$,

$$\begin{aligned} {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{r, \eta _{5}})\le & {} {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{r_{0}, \eta _{4}}) + {III}_{\varepsilon }^{6, r}, \\< & {} {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }) - \frac{\sigma {\mathcal {H}}^{n}(A_{l})}{2(2^{n} - 1)} + {III}_{\varepsilon }^{1, 0} + {III}_{\varepsilon }^{4, r_{0}} + {III}_{\varepsilon }^{5, r_{0}} + {III}_{\varepsilon }^{6,r}. \end{aligned}$$

Define the function, ${\tilde{v}}_{\varepsilon }^{r, \eta _{5}}(y) = {\overline{{\mathbb {H}}}}_{\varepsilon } ({\tilde{d}} (y) - r)$, in N. This function lies in $W^{1, \infty } (N)$, ${\mathcal {F}}_{\varepsilon , \lambda } ({\tilde{v}}_{\varepsilon }^{r, \eta _{5}}) (N) = {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{r, \eta _{5}}) ({\tilde{T}})$, and $r \mapsto {\tilde{v}}_{\varepsilon }^{r, \eta _{5}}$ is a continuous path in $W^{1,2} (N)$.

As $|{\tilde{d}}(y)| \le \, \text {diam}(N)$, we have that,

$$\begin{aligned} {\tilde{d}} (y) - 2 \, \text {diam} (N) \le - \, \text {diam} (N) < - 2 \varepsilon \Lambda . \end{aligned}$$

Therefore,

$$\begin{aligned} {\tilde{v}}_{\varepsilon }^{2 \, \text {diam}(N), \eta _{5}} (y) = {\overline{{\mathbb {H}}}}_{\varepsilon }({\tilde{d}}(x) - 2 \, \text {diam} (N)) = - 1. \end{aligned}$$

Recall that our end point is $a_{\varepsilon } > -1$. We connect $-1$ to $a_{\varepsilon }$, by constant functions,

$$\begin{aligned} u_{\varepsilon }^{r} (y) = r \end{aligned}$$

for r in $[-1, a_{\varepsilon }]$. Then,

$$\begin{aligned} {\mathcal {F}}_{\varepsilon , \lambda } (u_{\varepsilon }^{r}) = \int _{N} \frac{W(r)}{\varepsilon } - \sigma \lambda r \, d \mu _{g} \le {\mathcal {F}}_{\varepsilon , \lambda } (u_{\varepsilon }^{-1}). \end{aligned}$$

As $u_{\varepsilon }^{- 1} = {\tilde{v}}_{\varepsilon }^{2 \, \text {diam}(N), \eta _{5}}$, we have that, for all r in $[- 1, a_{\varepsilon }]$,

$$\begin{aligned} {\mathcal {F}}_{\varepsilon , \lambda } (u_{\varepsilon }^{r}) < {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }) - \frac{\sigma {\mathcal {H}}^{n}(A_{l})}{2(2^{n} - 1)} + {III}_{\varepsilon }^{1,0} + {III}_{\varepsilon }^{4, r_{0}} + {III}_{\varepsilon }^{5, r_{0}} + {III}_{\varepsilon }^{6,2 \, \text {diam}(N)}. \end{aligned}$$

7 Path to $b_{\varepsilon }$

7.1 Lining up with level set $\Gamma _{-\rho }$

We construct the path from (2) to (6) in Fig. 2

We consider, for r in $[0, \rho ]$, and x in ${\tilde{M}}$,

$$\begin{aligned} \eta _{6} (r, x) = \rho f(x) - r (1 + f(x)). \end{aligned}$$

First consider r in $(2 \varepsilon \Lambda , \rho ]$,

$$\begin{aligned} {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{r, \eta _{6}}) - {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{0, \eta _{6}}) = {I}_{\varepsilon }^{r, \eta _{6}} + ({II}_{\varepsilon }^{r, \eta _{6}} - {II}_{\varepsilon }^{2 \varepsilon \Lambda , \eta _{6}}) + {II}_{\varepsilon }^{2 \varepsilon \Lambda , \eta _{6}} \end{aligned}$$

Similar to Sect. 6.1 we have,

$$\begin{aligned} {II}_{\varepsilon }^{r, \eta _{6}} - {II}_{\varepsilon }^{2 \varepsilon \Lambda , \eta _{6}} \le \lambda \int _{2 \varepsilon \Lambda }^{r} \int _{{\tilde{M}}} \Theta _{\varepsilon , \eta _{6}}^{1} (s,x) - \Theta _{\varepsilon , \eta _{6}}^{2} (s,x) \, d {\mathcal {H}}^{n} (x) \, ds. \end{aligned}$$

For r in $[0, 2 \varepsilon \Lambda ]$, again by similar arguments to those in Sect. 6.1

$$\begin{aligned} {II}_{\varepsilon }^{r, \eta _{6}}\le & {} C_{2} \bigg ( \int _{0}^{r} \int _{\{\rho f < - 2 \varepsilon \Lambda \}} \Theta _{\varepsilon , \eta _{6}}^{1} (s,x) - \Theta _{\varepsilon , \eta _{6}}^{2} (s,x) \, d {\mathcal {H}}^{n} (x) \, ds \\{} & {} + \int _{\{\rho f \ge - 2 \varepsilon \Lambda \}} m_{\varepsilon }^{2} (x) \, d {\mathcal {H}}^{n} (x) + \varepsilon \Lambda \bigg ), \end{aligned}$$

where,

$$\begin{aligned} m_{\varepsilon }^{2} (x) {:}{=}\max _{t \in [- 6 \varepsilon \Lambda . 2 \varepsilon \Lambda ]} \theta _{t} (x) - \min _{t \in [-6 \varepsilon \Lambda , 2 \varepsilon \Lambda ]} \theta _{t} (x), \end{aligned}$$

and we are potentially rechoosing $C_{2}(M, N, g, W, \lambda ) < \infty$.

For r in $[0,\rho ]$, we consider,

$$\begin{aligned} {I}_{\varepsilon }^{r, \eta _{6}}= & {} \int _{A_{l}} \int _{\sigma ^{-}(x)}^{\sigma ^{+}(x)} \frac{\varepsilon }{2} (({\overline{{\mathbb {H}}}}_{\varepsilon })' (t - \eta _{4} (r,x)))^{2} (\rho - r)^{2} |\nabla f|^{2} (x,t) \theta _{t}(x) \, dt \, d {\mathcal {H}}^{n}(x) \\{} & {} - \int _{A_{l}} \int _{\sigma ^{-}(x)}^{\sigma ^{+}(x)} \frac{\varepsilon }{2} (({\overline{{\mathbb {H}}}}_{\varepsilon })' (t - \eta _{4} (0,x)))^{2} \rho ^{2} |\nabla f|^{2} (x,t) \theta _{t}(x) \, dt \, d {\mathcal {H}}^{n}(x) \end{aligned}$$

Following similar arguments to Sect. 5.1, and after potentially rechoosing $C_{3} = C_{3} (z_{0}, M, N, g, \delta , W, \lambda ) < \infty$, we have that,

$$\begin{aligned} {I}_{\varepsilon }^{r, \eta _{6}} \le C_{3} {\mathcal {H}}^{n} (A_{l}) \frac{\rho ^{2}}{l^{2}}. \end{aligned}$$

Therefore, recalling our choice of $\rho > 0$ in Remark 18, we have

$$\begin{aligned} {I}_{\varepsilon }^{r, \eta _{6}} \le \frac{\sigma {\mathcal {H}}^{n} (A_{l})}{2(2^{n} - 1)}. \end{aligned}$$

Thus, for r in $[0, 2 \varepsilon \Lambda ]$,

$$\begin{aligned} {\mathcal {F}}_{\varepsilon , \lambda }(v_{\varepsilon }^{r, \eta _{6}}) - {\mathcal {F}}_{\varepsilon }(v_{\varepsilon }^{0, \eta _{6}})< & {} \frac{\sigma {\mathcal {H}}^{n} (A_{l})}{2(2^{n} - 1)} + {III}_{\varepsilon }^{7,r}, \end{aligned}$$

where,

$$\begin{aligned} {III}_{\varepsilon }^{7,r}= & {} C_{2} \bigg ( \int _{0}^{r} \int _{\{\rho f < - 2 \varepsilon \Lambda \}} \Theta _{\varepsilon , \eta _{6}}^{1} (s,x) - \Theta _{\varepsilon , \eta _{6}}^{2} (s,x) \, d {\mathcal {H}}^{n} (x) \, ds \\{} & {} + \int _{\{\rho f \ge - 2 \varepsilon \Lambda \}} m_{\varepsilon }^{2} (x) \, d {\mathcal {H}}^{n} (x) + \varepsilon \Lambda \bigg ). \end{aligned}$$

For r in $(2 \varepsilon \Lambda , \rho ]$,

$$\begin{aligned} {\mathcal {F}}_{\varepsilon , \lambda }(v_{\varepsilon }^{r, \eta _{6}}) - {\mathcal {F}}_{\varepsilon }(v_{\varepsilon }^{0, \eta _{6}})< & {} \frac{\sigma {\mathcal {H}}^{n} (A_{l})}{2(2^{n} - 1)} + {III}_{\varepsilon }^{8, r}, \end{aligned}$$

where

$$\begin{aligned} {III}_{\varepsilon }^{8,r}= & {} C_{2} \bigg ( \int _{0}^{2 \varepsilon \Lambda } \int _{\{\rho f < - 2 \varepsilon \Lambda \}} \Theta _{\varepsilon , \eta _{6}}^{1} (s,x) - \Theta _{\varepsilon , \eta _{6}}^{2} (s,x) \, d {\mathcal {H}}^{n} (x) \, ds \\{} & {} + \int _{2 \varepsilon \Lambda }^{r} \int _{{\tilde{M}}} \Theta _{\varepsilon , \eta _{6}}^{1} (s, x) - \Theta _{\varepsilon , \eta _{6}}^{2} (s, x) \, d {\mathcal {H}}^{n} (x) \\{} & {} + \int _{\{\rho f \ge - 2 \varepsilon \Lambda \}} m_{\varepsilon }^{2} (x) \, d {\mathcal {H}}^{n} (x) + \varepsilon \Lambda \bigg ). \end{aligned}$$

As $\eta _{6} (0, x) = \eta _{1} (\rho , x)$, we have, for r in $[0, 2 \varepsilon \Lambda ]$,

$$\begin{aligned} {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{r, \eta _{6}}) \le {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }) - \frac{\sigma {\mathcal {H}}^{n} (A_{l})}{2(2^{n} - 1)} + {III}_{\varepsilon }^{2, \rho } + {III}_{\varepsilon }^{7, r}, \end{aligned}$$

and for r in $(2 \varepsilon \Lambda , \rho ]$, we have,

$$\begin{aligned} {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{r, \eta _{6}}) \le {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }) - \frac{\sigma {\mathcal {H}}^{n} (A_{l})}{2(2^{n} - 1)} + {III}_{\varepsilon }^{2, \rho } + {III}_{\varepsilon }^{8, r}. \end{aligned}$$

For r in $[0, \rho ]$, we define the following function on N,

$$\begin{aligned} {\tilde{v}}_{\varepsilon }^{r,\eta _{6}} (y) = {\left\{ \begin{array}{ll} {\overline{{\mathbb {H}}}}_{\varepsilon } ({\tilde{d}}(y) + r), &{} y \not \in B_{\delta }^{N} (z_{0}), \\ v_{\varepsilon }^{r,\eta _{6}} (F_{1}^{-1} (y)), &{} y \in \overline{\Upsilon _{1}} \cap B_{\delta }^{N} (z_{0}), \\ v_{\varepsilon }^{r, \eta _{6}} (F_{2}^{-1} (y)), &{} y \in \overline{\Upsilon _{2}} \cap B_{\delta }^{N} (z_{0}). \end{array}\right. } \end{aligned}$$

We can show, as in Sects. 5.2 and 5.3 that, ${\tilde{v}}_{\varepsilon }^{r,\eta _{6}}$ lies in $W^{1,\infty } (N)$, ${\mathcal {F}}_{\varepsilon , \lambda } ({\tilde{v}}_{\varepsilon }^{r, \eta _{6}}) (N) = {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }^{r,\eta _{6}}) ({\tilde{T}})$, and the path $r \mapsto {\tilde{v}}_{\varepsilon }^{r,\eta _{6}}$ is continuous in $W^{1,2} (N)$.

7.2 Completing path to $b_{\varepsilon }$

We construct the path from (6) to ‘$+1$’ in Fig. 2. This is done in an identical way to Sect. 6.4.

For r in $[\rho , 2 \, \text {diam}(N)]$, we define the following function on N,

$$\begin{aligned} {\tilde{v}}_{\varepsilon }^{r,\eta _{7}} (y) {:}{=}{\overline{{\mathbb {H}}}}_{\varepsilon } ({\tilde{d}}(y) + r). \end{aligned}$$

Similar to arguments in Sect. 6.4 we have,

$$\begin{aligned} {\mathcal {F}}_{\varepsilon , \lambda } ({\tilde{v}}_{\varepsilon }^{r, \eta _{7}}) \le {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }) - \frac{\sigma {\mathcal {H}}^{n} (A_{l})}{2(2^{n} - 1)} + {III}_{\varepsilon }^{2, \rho } + {III}_{\varepsilon }^{8, \rho } + {III}_{\varepsilon }^{9,r}, \end{aligned}$$

where,

$$\begin{aligned} {III}_{\varepsilon }^{9,r} = \lambda \int _{\rho }^{r} \Theta _{\varepsilon , \eta _{6}}^{1} (s,x) - \Theta _{\varepsilon , \eta _{6}}^{2} (s,x) \, d {\mathcal {H}}^{n} (x) \, ds. \end{aligned}$$

Again as in Sect. 6.4, we connect ${\tilde{v}}_{\varepsilon }^{2 \, \text {diam}(N), \eta _{7}} = 1$, to $b_{\varepsilon }$, by constant functions, $u_{\varepsilon }^{r} = r$, for r in $[1, b_{\varepsilon }]$. We have that for all r in $[1, b_{\varepsilon }]$,

$$\begin{aligned} {\mathcal {F}}_{\varepsilon , \lambda } (u_{\varepsilon }^{r})\le & {} {\mathcal {F}}_{\varepsilon , \lambda } ({\tilde{v}}_{\varepsilon }^{2 \, \text {diam}(N), \eta _{7}}) \le {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }) \\{} & {} - \frac{\sigma {\mathcal {H}}^{n} (A_{l})}{2(2^{n} - 1)} + {III}_{\varepsilon }^{2, \rho } + {III}_{\varepsilon }^{8, \rho } + {III}_{\varepsilon }^{9,2 \, \text {diam} (N)}. \end{aligned}$$

Both ${\tilde{v}}_{\varepsilon }^{r, \eta _{7}}$, and $u_{\varepsilon }^{r}$ give continuous paths in $W^{1,2} (N)$ with respect to r.

8 Conclusion of the paths

8.1 Error terms

8.1.1 Theta error terms

Consider a function $\eta :{\mathbb {R}} \times {\tilde{M}} \rightarrow {\mathbb {R}}$, and the term

$$\begin{aligned} \Theta _{\varepsilon , \eta }^{1} (s, x) - \Theta _{\varepsilon , \eta }^{2} (s,x)= & {} \sigma \int _{\sigma ^{-}(x)}^{\sigma ^{+}(x)} \partial _{s} \eta (s,x) ({\overline{{\mathbb {H}}}}_{\varepsilon })' (t - \eta (s,x)) \theta _{t}(x) \, dt \\{} & {} - \int _{\sigma ^{-}(x)}^{\sigma ^{+}(x)} \partial _{s} \eta (s,x) Q_{\varepsilon } (t - \eta (s,x)) \theta _{t} (x) \, dt. \end{aligned}$$

Assuming that $\eta$ is monotone in the first variable, we have,

$$\begin{aligned} |\Theta _{\varepsilon , \eta }^{1} (s, x) - \Theta _{\varepsilon , \eta }^{2} (s,x)| \le 2 \sigma |\partial _{s} \eta (s,x)| m_{\varepsilon }(\eta (s,x), x) + C_{7} \varepsilon ^{2}, \end{aligned}$$

where,

$$\begin{aligned} m_{\varepsilon } (T, x) = \max _{t \in [T - 2 \varepsilon \Lambda , T + 2 \varepsilon \Lambda ]} \theta _{t} (x) - \min _{t \in [T - 2 \varepsilon \Lambda , T + 2 \varepsilon \Lambda ]} \theta _{t} (x). \end{aligned}$$

and $C_{7} = C_{7} (N, m, \lambda , W, |\eta |_{C^{1}}) < + \infty$.

Now we assume that $\partial _{s} \eta \ge 0$, and $|\partial _{s} \eta |_{C^{0} ({\mathbb {R}} \times {\tilde{M}})} < + \infty$. Apply Fubini’s Theorem to swap integrals,

$$\begin{aligned} \int _{0}^{r} \int _{{\tilde{M}}} \left| \Theta _{\varepsilon , \eta }^{1} (s, x) - \Theta _{\varepsilon , \eta }^{2} (s,x) \right| \, d {\mathcal {H}}^{n} (x) \, ds \le 2 \sigma \int _{{\tilde{M}}} \int _{\eta (0,x)}^{\eta (r,x)} m_{\varepsilon } (T, x) \, dT \, {\mathcal {H}}^{n} (x) + C_{7} r \varepsilon ^{2}. \end{aligned}$$

Fixing x in ${\tilde{M}}$, we see that for all T in ${\mathbb {R}} \setminus \{ \sigma ^{-}(x), \sigma ^{+}(x) \}$,

$$\begin{aligned} m_{\varepsilon } (T, x) \rightarrow 0, \, as \, \varepsilon \rightarrow 0, \end{aligned}$$

and furthermore, we have the following bounds, $0 \le m_{\varepsilon } (T, x) \le e^{\frac{\lambda ^{2}}{2m}}$. Therefore we can apply Dominated Convergence Theorem for fixed x in ${\tilde{M}}$ and r in $[0, \infty )$,

$$\begin{aligned} \int _{\eta (0,x)}^{\eta (r,x)} m_{\varepsilon } (T, x) \, dT \rightarrow 0, \, as \, \varepsilon \rightarrow 0. \end{aligned}$$

Furthermore, as $0 \le \eta (r,x) - \eta (0, x) \le |\partial _{s} \eta |_{C^{0} ({\mathbb {R}} \times {\tilde{M}})} \, r$, we have the bounds,

$$\begin{aligned} 0 \le \int _{\eta (0,x)}^{\eta (r,x)} m_{\varepsilon } (T, x) \, dT \le |\partial _{s} \eta |_{C^{0} ({\mathbb {R}} \times {\tilde{M}})} r e^{\frac{\lambda ^{2}}{2m}}. \end{aligned}$$

Therefore, again by Dominated Convergence Theorem, we have, for fixed r in $[0, \infty )$

$$\begin{aligned} \int _{{\tilde{M}}} \int _{\eta (0,x)}^{\eta (r,x)} m_{\varepsilon } (T, x) \, dT \, {\mathcal {H}}^{n} (x) \rightarrow 0, \, as \, \varepsilon \rightarrow 0. \end{aligned}$$

Define the following continuous function on $[0, +\infty )$,

$$\begin{aligned} M_{\varepsilon }^{\eta } (r) = \int _{{\tilde{M}}} \int _{\eta (0,x)}^{\eta (r,x)} m_{\varepsilon } (T, x) \, dT \, {\mathcal {H}}^{n} (x). \end{aligned}$$

We have that $M_{\varepsilon }^{\eta } (r) \rightarrow 0$, pointwise, as $\varepsilon \rightarrow 0$, and furthermore, as

$$\begin{aligned} 0 \le m_{\varepsilon _{1}} (T,x) \le m_{\varepsilon _{2}} (T,x), \end{aligned}$$

for all T in ${\mathbb {R}}$, x in ${\tilde{M}}$, and $0< \varepsilon _{1} < \varepsilon _{2}$, this implies that,

$$\begin{aligned} 0 \le M_{\varepsilon _{1}}^{\eta } (r) \le M_{\varepsilon _{2}}^{\eta }(r), \end{aligned}$$

for all r in $[0, + \infty )$. Therefore, by Dini’s Theorem, we have that,

$$\begin{aligned} M_{\varepsilon }^{\eta } \rightarrow 0, \, as \, \varepsilon \rightarrow 0, \end{aligned}$$

uniformly on compact sets of $[0, + \infty )$. Thus,

$$\begin{aligned} \int _{0}^{r} \int _{{\tilde{M}}} \left| \Theta _{\varepsilon , \eta }^{1} (s, x) - \Theta _{\varepsilon , \eta }^{2} (s,x) \right| \, d {\mathcal {H}}^{n} (x) \, ds \rightarrow 0 \end{aligned}$$

(14)

as $\varepsilon \rightarrow 0$, uniformly in r, on compact sets of $[0, + \infty )$. The same holds assuming that $\eta$ satisfies $\partial _{s} \eta \le 0$, on ${\mathbb {R}} \times {\tilde{M}}$, and $|\partial _{s} \eta |_{C^{0} ({\mathbb {R}} \times {\tilde{M}})} < + \infty$.

For $i = 1, \ldots , 7$ our $\eta _{i}$’s are monotone in the first variable and $|\partial _{s} \eta _{i}|_{C^{0} ({\mathbb {R}} \times {\tilde{M}})} < + \infty$. Therefore (14) holds for each i.

8.1.2 The other error terms

We first consider,

$$\begin{aligned} \int _{B_{2l}} q_{\varepsilon }^{1} (x) \, d {\mathcal {H}}^{n} (x), \end{aligned}$$

with,

$$\begin{aligned} q_{\varepsilon }^{1} (x) = \max _{t \in [-4 \varepsilon \Lambda , 2 \varepsilon \Lambda ]} (H_{t} (x) - \lambda ) \theta _{t} (x). \end{aligned}$$

By choice of $\varepsilon > 0$, in Remark 15, $2 \varepsilon \Lambda< < \rho$. Therefore by choice of $\rho > 0$, in Remark 11, and $\delta > 0$, from Remark 16, we have

$$\begin{aligned} 0 \le \max _{x \in B_{2 l}} q_{\varepsilon }^{1} (x) \le \frac{\lambda }{2} e^{\frac{\lambda ^{2}}{2 m}}. \end{aligned}$$

Fixing $x'$ in $B_{2 l} \setminus \{x :\sigma ^{-} (x) = 0 \}$, we see that there exists an $\varepsilon ' = \varepsilon ' (x') > 0$, such that for all $0 < \varepsilon \le \varepsilon '$,

$$\begin{aligned}{}[-4 \varepsilon \Lambda , 2 \varepsilon \Lambda ] \subset (\sigma ^{-} (x'), \sigma ^{+}(x')). \end{aligned}$$

Therefore, $(H_{t} (x') - \lambda ) \theta _{t} (x')$, is a smooth function in t on $[- 4 \varepsilon \Lambda , 2 \varepsilon \Lambda ]$, and clearly,

$$\begin{aligned} \max _{t \in [-4 \varepsilon \Lambda , 2 \varepsilon \Lambda ]} (H_{t} (x') - \lambda ) \theta _{t} (x') \rightarrow 0, \, as \, \varepsilon \rightarrow 0. \end{aligned}$$

Thus $q_{\varepsilon }^{1} \rightarrow 0$, ${\mathcal {H}}^{n}$–a.e in $B_{2l}$, and we can apply Dominated Convergence Theorem to say that

$$\begin{aligned} \int _{B_{2 l}} q_{\varepsilon }^{1} (x) \, d {\mathcal {H}}^{n} (x) \rightarrow 0, \, as \, \varepsilon \rightarrow 0. \end{aligned}$$

Identically we also have,

$$\begin{aligned} \int _{A_{L}^{k}} q_{\varepsilon }^{2} (x) \, d {\mathcal {H}}^{n} (x) \rightarrow 0, \, as \, \varepsilon \rightarrow 0, \end{aligned}$$

recalling $q_{\varepsilon }^{2} (x) = \max _{t \in [-2 \varepsilon \Lambda , 4 \varepsilon \Lambda ]} (\lambda - H_{t} (x)) \theta _{t} (x)$.

Now considering

$$\begin{aligned} q_{\varepsilon }^{3} (r,x) = \max _{t \in [-2 \varepsilon \Lambda , 2 \varepsilon \Lambda ]} \zeta (x, t + \eta _{4} (r,x)) - \zeta (x, \eta _{4} (r,x)) \end{aligned}$$

where we are recalling the function

$$\begin{aligned} \zeta (x,t) = |\nabla {\tilde{f}}|^{2} (x,t) \theta _{t} (x) \end{aligned}$$

from Claim 4. For x in $B_{2 L}$ such that ${\tilde{f}} (x) = 0$, we have that $\zeta (x,t) = 0$, for all t. Considering x in $A_{L}^{k} \cap \{ {\tilde{f}} \not = 0\}$, such that $r_{0} {\tilde{f}} (x) > 2 \varepsilon \Lambda$, then

$$\begin{aligned}{}[-2 \varepsilon \Lambda + \eta _{4} (r,x), 2 \varepsilon \Lambda + \eta _{4} (r,x)] \subset (0, 2 r_{0}) \subset (\sigma ^{-} (x), \sigma ^{+} (x)). \end{aligned}$$

Thus, for t in $[-2 \varepsilon \Lambda + \eta _{4} (r,x), 2 \varepsilon \Lambda + \eta _{4} (r,x)]$,

$$\begin{aligned} (x,t) \in {\tilde{T}} \cap ( B_{L} \times (-2 r_{0}, 2 r_{0}) ) \subset \subset {\tilde{V}}_{1} \cup {\tilde{V}}_{2}, \end{aligned}$$

where we are recalling sets ${\tilde{V}}_{1}$ and ${\tilde{V}}_{2}$ from Remark 6. Therefore, $\zeta$ is differentiable at (x, t) and

$$\begin{aligned} |\partial _{t} \zeta (x,t)| \le C(|F_{i}|_{C^{2}(B_{L} \times (-2 r_{0}, 2 r_{0}) )}, |{\tilde{f}}|_{C^{1}}, \lambda ) \le C_{6}. \end{aligned}$$

Where we are potentially rechoosing $C_{6} = C_{6} (z_{0}, M, N, g, k, L, \delta , W, \lambda )$. Therefore, for x in $A_{L}^{k}$ such that $r_{0} {\tilde{f}} (x) > 2 \varepsilon \Lambda$, we have that $0 \le q_{\varepsilon }^{3} (r,x) \le C_{6} \varepsilon \Lambda$. Furthermore, for all x in $A_{L}^{k}$,

$$\begin{aligned} |q_{\varepsilon }^{3} (r,x)| \le \max _{(x,t) \in B_{L} \times (-2 r_{0}, 2 r_{0})} \zeta (x, t) \le C_{6}. \end{aligned}$$

Again we are potentially rechoosing $C_{6} = C_{6} (z_{0}, M, N, g, k, L, \delta , W, \lambda )$.

Therefore,

$$\begin{aligned} p_{\varepsilon }^{1} (r)= & {} \int _{A_{L}^{k} \cap \{ r_{0} {\tilde{f}} > 2 \varepsilon \Lambda \}} q_{\varepsilon }^{3} (r,x) \, d {\mathcal {H}}^{n} (x) + \int _{A_{L}^{k} \cap \{0< r_{0} {\tilde{f}} \le 2 \varepsilon \Lambda \}} q_{\varepsilon }^{3} (r,x) \, d {\mathcal {H}}^{n} (x), \\\le & {} C_{6} \left( \varepsilon \Lambda + {\mathcal {H}}^{n} (\{ x \in A_{L}^{k} :0 < r_{0} {\tilde{f}} (x) \le 2 \varepsilon \Lambda \}) \right) . \end{aligned}$$

Thus

$$\begin{aligned} \max _{r \in [0, r_{0}]} p_{\varepsilon }^{1} (r) \rightarrow 0 \end{aligned}$$

as $\varepsilon \rightarrow 0$. Similarly, $p_{\varepsilon }^{2} (0) \rightarrow 0$, as $\varepsilon \rightarrow 0$.

For the remaining error terms, as ${\mathcal {H}}^{n} (\{ x \in {\tilde{M}} :\, \sigma ^{-} (x) = 0\}) = 0$, by Dominated Convergence Theorem, we have that,

$$\begin{aligned} {\mathcal {H}}^{n} (\{ x \in {\tilde{M}} :\, \sigma ^{-}(x) \ge - 2 \varepsilon \Lambda \}) \rightarrow 0, \end{aligned}$$

and

$$\begin{aligned} \int _{{\tilde{M}}} m_{\varepsilon }^{i} (x) \, d {\mathcal {H}}^{n} (x) \rightarrow 0, \end{aligned}$$

where,

$$\begin{aligned} m_{\varepsilon }^{1} (x)= & {} \max _{t \in [-2 \varepsilon \Lambda , 4 \varepsilon \Lambda ]} \theta _{t} (x) - \min _{t \in [-2 \varepsilon \Lambda , 4 \varepsilon \Lambda ]} \theta _{t} (x), \\ m_{\varepsilon }^{2} (x)= & {} \max _{t \in [-6 \varepsilon \Lambda , 2 \varepsilon \Lambda ]} \theta _{t} (x) - \min _{t \in [-6 \varepsilon \Lambda , 2 \varepsilon \Lambda ]} \theta _{t} (x). \end{aligned}$$

8.2 Path for Theorem 2

Consider the following continuous path in $W^{1,2} (N)$, for $\varepsilon > 0$,

$$\begin{aligned} \gamma _{\varepsilon } (t) = {\left\{ \begin{array}{ll} -1 - 2 \text {diam} \, (N) - t, &{} t \in [- 2 \, \text {diam} \, (N) - a_{\varepsilon } - 1, 2 \, \text {diam} \, (N)], \\ {\overline{{\mathbb {H}}}}_{\varepsilon } ({\tilde{d}} - t), &{} t \in [-2 \, \text {diam} \, (N), 2 \, \text {diam} \, (N)], \\ 1 - 2 \, \text {diam} \, (N) + t, &{} t \in [2 \, \text {diam} \, (N), 2 \, \text {diam} \, (N) + b_{\varepsilon } - 1], \end{array}\right. } \end{aligned}$$

which satisfies $\gamma _{\varepsilon } (-1 - 2 \text {diam} \, (N) - a_{\varepsilon }) = a_{\varepsilon }$, and $\gamma _{\varepsilon } (1 - 2 \, \text {diam} \, (N) + b_{\varepsilon }) = b_{\varepsilon }$.

Replacing $r_{0} = 2 \varepsilon \Lambda$, in Sect. 6.4, and $\rho = 2 \varepsilon \Lambda$, in Sect. 7.2, we see that, for all $\varepsilon$ in $(0, {\tilde{\varepsilon }})$, for some ${\tilde{\varepsilon }} = {\tilde{\varepsilon }} (N, M, g, \lambda , W) > 0$, fixed,

$$\begin{aligned} {\left\{ \begin{array}{ll} {\mathcal {F}}_{\varepsilon , \lambda } (\gamma _{\varepsilon } (t))< {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }) + {III}_{\varepsilon }^{6,2 \, \text {diam} \, (N)}, &{} t \in [- 2 \, \text {diam} \, (N) - a_{\varepsilon } - 1, 2 \, \text {diam} \, (N)], \\ {\mathcal {F}}_{\varepsilon , \lambda } (\gamma _{\varepsilon } (t))< {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }) + {III}_{\varepsilon }^{6, - t}, &{} t \in [- 2 \text {diam} \, (N), - 2 \varepsilon \Lambda ], \\ {\mathcal {F}}_{\varepsilon , \lambda } (\gamma _{\varepsilon } (t))< {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }) + {III}_{\varepsilon }^{9,t}, &{} t \in [2 \varepsilon \Lambda , 2 \text {diam} \, (N)], \\ {\mathcal {F}}_{\varepsilon , \lambda } (\gamma _{\varepsilon } (t)) < {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }) + {III}_{\varepsilon }^{9,2 \, \text {diam} \, (N)}, &{} t \in [2 \, \text {diam} \, (N), 2 \, \text {diam} \, (N) + b_{\varepsilon } - 1]. \end{array}\right. } \end{aligned}$$

Recalling from Sect. 3.6

$$\begin{aligned} {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }) \rightarrow 2 \sigma {\mathcal {H}}^{n} (M) - \sigma \lambda \mu _{g} (E) + \sigma \lambda \mu _{g} (N \setminus E), \end{aligned}$$

as $\varepsilon \rightarrow 0$, and Sect. 8.1.1,

$$\begin{aligned} \max _{t \in [2 \varepsilon \Lambda , 2 \, \text {diam} \, (N)]} \left( {III}_{\varepsilon }^{6, t} + {III}^{9, t} \right) \rightarrow 0, \end{aligned}$$

as $\varepsilon \rightarrow 0$. Therefore, for $\tau > 0$, there exists a $0 < \varepsilon _{\tau } = \varepsilon _{\tau } (N, M, g, \lambda , W) \le {\tilde{\varepsilon }}$, such that for all $\varepsilon$ in $(0, \varepsilon _{\tau })$ and t in $[- 2 \, \text {diam} \, (N) - a_{\varepsilon } - 1, 2 \, \text {diam} \, (N) + b_{\varepsilon } - 1] \setminus (-2 \varepsilon \Lambda , 2 \varepsilon \Lambda )$,

$$\begin{aligned} {\mathcal {F}}_{\varepsilon , \lambda } (\gamma _{\varepsilon } (t) ) < 2 \sigma {\mathcal {H}}^{n} (M) - \sigma \lambda \mu _{g} (E) + \sigma \lambda \mu _{g} (N \setminus E) + \tau . \end{aligned}$$

Furthermore by similar arguments to those in Sect. 3.6, and after potentially rechoosing $\varepsilon _{\tau } > 0$, we have that for all $\varepsilon$ in $(0, \varepsilon _{\tau })$

$$\begin{aligned} \max _{t \in [-2 \varepsilon \Lambda , 2 \varepsilon \Lambda ]} {\mathcal {F}}_{\varepsilon , \lambda } (\gamma _{\varepsilon } (t)) < 2 \sigma {\mathcal {H}}^{n} (M) - \sigma \lambda \mu _{g} (E) + \sigma \lambda \mu _{g} (N \setminus E) + \tau . \end{aligned}$$

Therefore this is an admissible path in $W^{1,2} (N)$, that proves that for the limiting varifold $V = V_{\lambda } + V_{0}$, we must have that $V_{0} = 0$. This completes the proof of Theorem 2.

Remark 25

Note that we can build the path $\gamma _{\varepsilon }$, for any suitable Caccioppoli set E. The suitable properties are the following:

• 1. $\partial ^{*} E \not = \emptyset$, has a quasi embedded $\lambda$-CMC structure, with respect to unit normal pointing into E.

• 2. $\partial ^{*} E$ satisfies the Geodesic Touching Lemma (Lemma 1).

From Remark 25 we can deduce that E must be a single connected component and minimises the value

$$\begin{aligned} F_{\lambda } (E) = {\mathcal {H}}^{n} (\partial ^{*} E) - \lambda \mu _{g} (E) > 0, \end{aligned}$$

among all suitable competitors.

8.3 Contradiction path for Theorem 1

Recall all the error terms from Sects. 5, 6 and 7. By Sects. 3.6 and 8.1, for $\tau > 0$, there exists an $\varepsilon _{\tau } = \varepsilon (z_{0}, M, N, g, \delta , W, \lambda , L, k, r_{0}, \rho , \tau ) \in (0, \varepsilon _{3})$, such that for all $\varepsilon$ in $(0, \varepsilon _{\tau })$, we have that

$$\begin{aligned}{} & {} {\mathcal {F}}_{\varepsilon , \lambda } (v_{\varepsilon }) + \max _{r \in [0, 4 \varepsilon \Lambda )} {III}_{\varepsilon }^{1,r} + \max _{r \in [4 \varepsilon \Lambda , \rho ]} {III}_{\varepsilon }^{2,r} + \max _{r \in [0, 2 \varepsilon \Lambda ]} {III}_{\varepsilon }^{3, r} \\{} & {} \qquad + \max _{r \in (2 \varepsilon \Lambda , r_{0}]} {III}_{\varepsilon }^{4,r} + \max _{r \in [0, r_{0}]} {III}_{\varepsilon }^{5,r} + \max _{r \in [r_{0}, 2 \, \text {diam} \, (N)]} {III}_{\varepsilon }^{6,r} \\{} & {} \qquad + \max _{r \in [0, 2 \varepsilon \Lambda ]} {III}_{\varepsilon }^{7,r} + \max _{r \in (2 \varepsilon \Lambda , \rho ]} {III}_{\varepsilon }^{8,r} + \max _{r \in [\rho , 2 \, \text {diam} \, (N)]} {III}_{\varepsilon }^{9,r} \\{} & {} \quad < 2 \sigma {\mathcal {H}}^{n} (M) - \sigma \lambda \mu _{g} (E) + \sigma \lambda \mu _{g} (N \setminus E) + \tau . \end{aligned}$$

Therefore, for any $\tau > 0$, there exists an $\varepsilon _{\tau } > 0$, such that for any $\varepsilon$ in $(0, \varepsilon _{\tau })$, we can define the continuous path,

$$\begin{aligned} \gamma _{\varepsilon } :[-1 - a_{\varepsilon }, 4 \, \text {diam}\, (N) + r_{0} + \rho + b_{\varepsilon } - 1] \rightarrow W^{1,2} (N), \end{aligned}$$

by

$$\begin{aligned}{} & {} \gamma _{\varepsilon } (t)\\{} & {} = {\left\{ \begin{array}{ll} - 1 - t, &{} t \in [-1 - a_{\varepsilon }, 0], \\ {\overline{{\mathbb {H}}}}_{\varepsilon } ({\tilde{d}} + t - 2 \, \text {diam} \, (N)), &{} [0, 2 \, \text {diam} \, (N) - r_{0}], \\ {\tilde{v}}_{\varepsilon }^{2 \, \text {diam} \, (N) - t, \eta _{4}}, &{} [2 \, \text {diam} \, (N) - r_{0}, 2 \, \text {diam} \, (N)], \\ {\tilde{v}}_{\varepsilon }^{2 \, \text {diam} \, (N) + \rho - t, \eta _{3}}, &{} [2 \, \text {diam} \, (N), 2 \, \text {diam} \, (N) + \rho ], \\ {\tilde{v}}_{\varepsilon }^{2 \, \text {diam} \, (N) + \rho +r_{0} - t, \eta _{2}}, &{} [2 \, \text {diam} \, (N) + \rho , 2 \, \text {diam} \, (N) + \rho + r_{0}], \\ {\tilde{v}}_{\varepsilon }^{t - (2 \, \text {diam} \, (N) + \rho + r_{0}),\eta _{6}}, &{} [2 \, \text {diam} \, (N) + \rho + r_{0}, 2 \, \text {diam} \, (N) + 2 \rho + r_{0}], \\ {\overline{{\mathbb {H}}}}_{\varepsilon } ({\tilde{d}} + t - (2 \, \text {diam} \, (N) + \rho + r_{0})), &{} [2 \, \text {diam} \, (N) + 2 \rho + r_{0}, 4 \, \text {diam} \, (N) + \rho + r_{0}], \\ 1 + t - (4 \, \text {diam}\, (N) + \rho + r_{0}), &{} [4 \, \text {diam}\, (N) + \rho + r_{0}, 4 \, \text {diam}\, (N) + \rho + r_{0} + b_{\varepsilon } - 1] \end{array}\right. } \end{aligned}$$

This path satisfies the following; $\gamma _{\varepsilon } (-1 - a_{\varepsilon }) = a_{\varepsilon }$, $\gamma _{\varepsilon } (4 \, \text {diam}\, (N) + r_{0} + \rho + b_{\varepsilon } - 1) = b_{\varepsilon }$, and

$$\begin{aligned} \gamma _{\varepsilon } (t) < 2 \sigma {\mathcal {H}}^{n} (M) - \sigma \lambda \mu _{g} (E) + \sigma \lambda \mu _{g} (N \setminus E) - \frac{\sigma {\mathcal {H}}^{n} (A_{l})}{2 (2^{n} - 1)} + \tau , \end{aligned}$$

for all t in $[-1 - a_{\varepsilon }, 4 \, \text {diam}\, (N) + r_{0} + \rho + b_{\varepsilon } - 1]$. This contradicts the min–max construction of M, implying that M must be embedded, and therefore completing Theorem 1.

9 Morse index

Recall the functional defined on Caccioppoli sets $\Omega \subset N$,

$$\begin{aligned} F_{\lambda } (\Omega ) = {\mathcal {H}}^{n} (\partial ^{*} \Omega ) - \lambda \mu _{g} (\Omega ). \end{aligned}$$

For a $C^{2}$ vector field X, we may take variations in direction X by considering its flow $\{ \Phi _{t} \}$. We define the first variation of $F_{\lambda }$ by,

$$\begin{aligned} \delta F_{\lambda } (\Omega ) (X) = \frac{d}{dt} F_{\lambda } (\Phi _{t} (\Omega ))_{| t = 0}, \end{aligned}$$

(15)

and the second variation by,

$$\begin{aligned} \delta ^{2} F_{\lambda } (\Omega ) (X) = \frac{d^{2}}{dt^{2}} F_{\lambda } (\Phi _{t} (\Omega ))_{| t = 0}. \end{aligned}$$

(16)

We have that $\delta F_{\lambda } (E) (X) = 0$, for all $C^{1}$ vector fields X. Note that we require M to be embedded and orientable for the following to be well defined. Consider the class of vector fields $X \in C^{2}_{c} (N \setminus ({\overline{M}} \setminus M))$, such that $X_{|M} = \varphi \nu$, where $\varphi \in C_{c}^{2} (M)$. By [1, Proposition 2.5],

$$\begin{aligned} \delta ^{2} F_{\lambda } (E) (X) = \int _{M} |\nabla ^{M} \varphi |^{2} - (|A_{M}|^{2} + \text {Ric} (\nu , \nu )) \varphi ^{2} \, d {\mathcal {H}}^{n}. \end{aligned}$$

(17)

We extend the expression on the right hand side to all functions in $W^{1,2}_{0} (M)$, and define the following quadratic form,

$$\begin{aligned} B_{M} (\varphi , \varphi ) {:}{=}\int _{M} |\nabla ^{M} \varphi |^{2} - (|A_{M}|^{2} + \text {Ric} (\nu , \nu )) \varphi ^{2} \, d {\mathcal {H}}^{n}, \hspace{1cm} \varphi \in W_{0}^{1,2} (M). \end{aligned}$$

After integrating by parts we obtain the second order elliptic operator on M,

$$\begin{aligned} L_{M} {:}{=}\Delta _{M} + |A_{M}|^{2} + \text {Ric} (\nu , \nu ). \end{aligned}$$

We restrict ourselves to a set $W \subset \subset N \setminus ({\overline{M}} \setminus M)$, to avoid our curvature term $|A_{M}|$, from potentially blowing up. A value $\kappa = \kappa (W) \in {\mathbb {R}}$ is said to be an eigenvalue of $L_{M}$ in W, if there exists an $\varphi \in W_{0}^{1,2} (W \cap M)$ such that

$$\begin{aligned} L_{M} \varphi + \kappa \varphi = 0. \end{aligned}$$

By standard elliptic theory, see [9], the spectrum of $L_{M}$ in $W \cap M$,

$$\begin{aligned} \kappa _{1} (W) \le \kappa _{2} (W) \le \cdots \rightarrow + \infty , \end{aligned}$$

is discrete and bounded from below. We then define the index of M in W by,

$$\begin{aligned} \text {ind}_{W} (M) = |\{ p :\kappa _{p} (W) < 0 \}|, \end{aligned}$$

or equivalently, it is the maximum dimension of a linear subspace of $W_{0}^{1,2} (W \cap M)$ on which $B_{M}$ is negative definite. If $\text {ind}_{W} (\text {ind} \, M) = 0$, then we say that M is stable in W and $\kappa _{p} (W) \ge 0$, for all p in ${\mathbb {N}}$, and

$$\begin{aligned} B_{M} (\varphi , \varphi ) \ge 0, \, for \, all \, \varphi \in W_{0}^{1,2} (W \cap M). \end{aligned}$$

We define,

$$\begin{aligned} \text {ind} (M) = \sup _{W \subset \subset N \setminus ({\overline{M}} \setminus M)} (\text {ind}_{W} (M)). \end{aligned}$$

As M is embedded, and our sequence of critical points $\{u_{i}\}$ from Sect. 1.1 has $\text {ind} \, u_{i} \le 1$, by [14, Theorem 1a.], we have that $\text {ind} M \le 1$.

Remark 26

As M is two-sided and embedded, and the inhomogeneous term is a constant, we may also apply the ideas and arguments of [11] verbatim to conclude that $\text {ind} M \le 1$.

Claim 5

$\text {ind} \, M = 1$.

Proof

We only need to show a lower bound, which follows from the Ricci positivity on N. We construct an appropriate function on M, using a similar argument to [2, Lemma 5.1].

We wish to prove that we can find a set $W \subset \subset N \setminus ({\overline{M}} \setminus M)$, and a function $\varphi$ in $W_{0}^{1,2} (M \cap W)$ such that,

$$\begin{aligned} B_{M} (\varphi , \varphi ) < 0. \end{aligned}$$

By the Ricci positivity of N, for any $W \subset \subset N \setminus ({\overline{M}} \setminus M)$, and $\varphi$ in $W_{0}^{1,2} (M \cap W)$, we have

$$\begin{aligned} B_{M} (\varphi , \varphi ) \le \int _{M} |\nabla ^{M} \varphi |^{2} - |A_{M}|^{2} \varphi ^{2} \, d {\mathcal {H}}^{n}. \end{aligned}$$

If ${\overline{M}} \setminus M = \emptyset$, we set $W = N$, and $\varphi = 1$,

$$\begin{aligned} B_{M} (\varphi , \varphi ) \le - \int _{M} |A_{M}|^{2} \, d {\mathcal {H}}^{n} < 0. \end{aligned}$$

For ${\overline{M}} \setminus M \not = \emptyset$, we first we note that we must have $n \ge 7$, and ${\mathcal {H}}^{n-1} ({\overline{M}} \setminus M) = 0$. Therefore, the 2-capacity of ${\overline{M}} \setminus M$ is 0, [8, Section 4.7.2, Theorem 3], implying that for all $\delta > 0$, there exists a function $f_{\delta }$ such that,

$$\begin{aligned} {\left\{ \begin{array}{ll} f_{\delta } \in C_{c}^{\infty } (N \setminus ({\overline{M}} \setminus M)), \\ f_{\delta } (y) \in [0,1], \, y \in N, \\ \int _{N} | \nabla f_{\delta }|^{2} d \mu _{g} < \delta , \\ \mu _{g} (\{ f_{\delta } = 1\}) > \mu _{g} (N) - \delta . \end{array}\right. } \end{aligned}$$

Furthermore, as $|{\overline{M}}|$ is a multiplicity 1 integral varifold with uniformly bounded generalised mean curvature, we have a monotonicity formula [17, Corollary 17.8]. The existence of such a monotonicity formula implies Euclidean volume growth about each point in ${\overline{M}}$. Therefore, there exists a constant $C_{8} = C_{8} (N, M, g)$, such that, by the construction of $f_{\delta }$ as in [8, Section 4.7.2, Theorem 3],

$$\begin{aligned} \int _{M} |\nabla ^{M} f_{\delta }|^2 \, d {\mathcal {H}}^{n} \le C_{8} \delta . \end{aligned}$$

Taking $W_{\delta } = \text {supp} \, f_{\delta } \subset \subset N \setminus ({\overline{M}} \setminus M)$, we have that $(f_{\delta })_{|M} \in W^{1,2}_{0} (M \cap W_{\delta })$, and,

$$\begin{aligned} B_{M} (f_{\delta }, f_{\delta }) \le C \delta - n^{-2} \lambda ^{2} {\mathcal {H}}^{n} (\{ f_{\delta } = 1 \} \cap M). \end{aligned}$$

We have that as we send $\delta \rightarrow 0$, ${\mathcal {H}}^{n} (\{ f_{\delta } = 1 \} \cap M) \rightarrow {\mathcal {H}}^{n} (M)$. Therefore for small enough $\delta > 0$, we have that $B_{M} (f_{\delta }, f_{\delta }) < 0$. This implies that $\text {ind} M \ge 1$. $\square$

The fact that M is connected immediately follows from this, as on each connected component we could construct a function as in Claim 5. Therefore each connected component adds atleast 1 to the index.