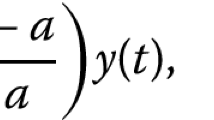1 Introduction

The Krasnoselskii theorem on fixed points in Banach spaces concerns the fixed points of operators which are the sum of two operators one is a contraction operator and the second one is completely continuous (see [21], compare also [10]). Generalizing one (or both) of the operator we can obtain generalizations of Krasnoselskii theorem. In the literature we find many generalizations of fixed point theorems related to contractions mappings (see e.g. [5, 15,16,17, 22, 23, 30,31,32, 36,37,40]). There exist also a huge number of generalizations of Schauder’s type theorem (see e.g. [11] and the references therein). In most cases, both generalizations concern the operators themselves and less the norm or topology of the space where they operate i.e. the general topological spaces were given then the generalizations of both operators were produced. These are especially seen in the case of contraction operators where the assumption of the linearity of the considered spaces is dropped (see the above mentioned papers). On extensions of contraction fixed point theorems to modular function spaces see [18,19,20]. This is not the case of generalizations of Schauder theorem. In 1950 Nakano [26] initiated the theory of modular spaces redefined and generalized by Musielak and Orlicz [25], see also [24]. The modular roughly speaking is a functional on (real) vector space which assume the value zero only at zero, is even, (in our case) is convex and not necessary triangle inequality and homogeneity conditions are satisfied. There exist a number of papers in which it has been proved fixed points theorems in modular spaces (see e.g. [18,19,20, 33] and the references therein). They concern contractive and nonexpansive maps. In all these papers except [18, 19] always so called \(\Delta _{2}\)-condition for modular functional is imposed. It implies (for convex modular) that the topology defined by modular and corresponding to it Luxemburg norm are equivalent and then some considerations are simplified. In [13] and then refined in [28] the authors proved a new version of Krasnoselskii fixed point theorems in modular spaces. However they also assumed \(\Delta _{2}\)-condition and hence in the proof they used Schauder theorem in normed space. The aim of this paper is to introduce a convex modular, but we do not define modular space and we do not assume \(\Delta _{2} \)-condition. We apply this convex modular to define topology for a given vector space and then in this topological space we consider a contraction (with respect to that modular) mapping and completely continuous mapping with respect to that topology. Then we prove for the convex sum of such mappings a Krasnoselskii type theorem. As we do not have any norm in our space in the proof of Krasnoselskii theorem we apply our own Schauder type theorem. The price we pay for lack of \(\Delta _{2}\)-condition is that we are able to prove the Krasnoselskii theorem only for convex sum of j-contraction and j-completely continuous mapping. In the last section we apply that theorem to solve the nonlinear periodic problem of Hill’s equation.

2 Definitions and notations

We present the concept of convex modular on the set X. Throughout this and next sections X denotes a vector space over \(\mathbb {R}\). We will consider X with a topology determined just by the convex modular j introduced below.

Definition 2.1

A map \(j:X\rightarrow [0,\infty ]\), is said to be a convex modular on X (see [24]) if the following three conditions hold:

  • (j1) \(j(0)=0\) \(\Leftrightarrow x=0\);

  • (j2) \(j(x)=j(-x)\), \(x\in X\);

  • (j3) j is convex i.e. \(j(\eta x+(1-\eta )y)\le \eta j(x)+(1-\eta )j(y),\) \(x,y\in X,\ \eta \in [0,1]\).

However we do not use j to define modular space, we work in X. We observe, that from (j1) and (j3) for each \(\alpha \in (0,1)\), we have

$$\begin{aligned} j(\alpha x)\le \alpha j(x)\text {, }x\in X\text {.} \end{aligned}$$

Indeed, if \(\alpha \in (0,1)\), then by (j1) and (j3) we calculate

$$\begin{aligned} j(\alpha x)=j(\alpha x+(1-\alpha )\cdot 0)\le \alpha j(x)+(1-\alpha )j(0)=\alpha j(x)\text {.} \end{aligned}$$

For each \(x\in X\) and positive \(\varepsilon >0\), define the set \(\mathcal {B} _{j}(x,\varepsilon )\) of points satisfying \(j(y-x)<\varepsilon \), i.e.

$$\begin{aligned} \mathcal {B}_{j}(x,\varepsilon )=\left\{ y:j(y-x)<\varepsilon \text { }\right\} \text {.} \end{aligned}$$

As j is convex all \(\mathcal {B}_{j}(x,\varepsilon )\) are convex and hence for \(x=0\) they are absorbing and balanced in X and closed under finite intersections. Thus these sets (\(\mathcal {B}_{j}(0,\varepsilon )\)) act as a base for the topology \((X,j(\cdot ))\) generated by j,  i.e. modular base (see [24] p. 27). Hence, it follows that \((X,j(\cdot ))\) with the modular base forms a generalization of modular spaces (see [24] p. 27) and as, in general, it does not satisfies the (\(\Delta _2)\) condition, i.e. (see [24] p. 26):

$$\begin{aligned} \text {for every } \tilde{\varepsilon }>0 \text { there is }\varepsilon >0 \text { such that } 2\mathcal {B}_{j}(0,\varepsilon ) \subset \mathcal {B}_{j}(0,\tilde{\varepsilon }) \end{aligned}$$
(2.1)

the \((X,j(\cdot ))\) is not a locally convex space (see [41] p.113). We should point out that modular base does not necessarily define a linear topology in X (see [24] p. 31). A simple example of the modular j which does not satisfies (2.1) is, for \(X=\mathbb {R}\), \(j(x)=\exp (|x|)-1+|x|,\ x\in \mathbb {R}\). However, still immediately from the definition of the convex modular, we can draw the conclusion that \(j(\cdot )\) is continuous in \((X,j(\cdot ))\) on each open set on which it is bounded. In the further part of the paper \((X,j(\cdot ))\) will denote a topological space with the topology generated by the modular j and we will write simply X instead of \((X,j(\cdot ))\).

A subsets \(T\subset X\) is bounded if

$$\begin{aligned} T\subset \mathcal {B}_{j}(0,n)\text { for some }n\in \mathbb {N}\text {.} \end{aligned}$$

We define a convergent of a sequence in X, a closet set, a compact set and a completeness of X.

Definition 2.2

\(\mathbf {(i)}\) If a sequence \(\{u_{m}\}_{m=1}^{\infty }\) in X meets the condition

$$\begin{aligned} \lim \limits _{m\rightarrow \infty }\sup \limits _{n>m}j(u_{n}-u_{m})=0\text {.} \end{aligned}$$

then we call it the j-Cauchy sequence in X.

\(\mathbf {(ii)}\) Let \(u\in X\) and let \(\{u_{m}\}_{m=1}^{\infty }\) be a sequence in X. If

$$\begin{aligned} \lim _{m\rightarrow \infty }j(u_{m}-u)=0\text {,} \end{aligned}$$

then we say that \(\{u_{m}\}_{m=1}^{\infty }\) is j-convergent to u (denote \(u_{m}\overset{j}{\rightarrow }u\) or \(\lim _{n\rightarrow \infty } ^{j}u_{n}=u\)).

\(\mathbf {(iii)}\) We say that a sequence \(\{u_{m}\}_{m=1}^{\infty }\subset X\) is j-convergent in X if \(\{u_{m}\}_{m=1}^{\infty }\) is j-convergent to u for some \(u\in X\).

\(\mathbf {(iv)}\) A subset T of space X is closed, if the limit of each j-convergent sequence of elements of T belongs to T, i.e. if for sequence \(\{u_{m}\}_{m=1}^{\infty }\subset T\) there exists \(u\in X\) such that \(\lim _{m\rightarrow \infty }j(u_{m}-u)=0\), then \(u\in T\).

\(\mathbf {(v)}\) If each j-Cauchy sequence \(\{u_{m}\}_{m=1}^{\infty }\) in X is j-convergent in X, then we say that X is j-complete space.

\(\mathbf {(vi)}\) A set \(T\subset X\) is compact in X if every sequence of elements \(\{x_k\}\subset T\) contains a subsequence, convergence to an element \(x\in T\).

In traditional fixed point theorems, the assumption of continuity and complete continuity of maps is extremely important. The introduction of modular j, allows to define a weakened form of continuity and completely continuity. Finally, we may define the j-continuous and completely j-continuous map in X.

Definition 2.3

Let \(A:X\rightarrow X\).

\((\textbf{i})\) We say that a map A is j-continuous in X, if for each sequence \(\{u_{m}\}_{m=1}^{\infty }\) in X such that \(u_{m}\overset{j}{\rightarrow }u\) we have

$$\begin{aligned} \lim _{m\rightarrow \infty }j(Au_{m}-Au)=0\text {, i.e. }Au_{m}\overset{j}{\rightarrow }Au\text {.} \end{aligned}$$

\((\textbf{ii})\) We say that a j-continuous map A is completely j -continuous in X, if the image by A of each bounded set in X is contained in a compact subset of X.

\((\textbf{iii})\) We say that a map A is j-compact in X if A(X) is contained in a compact subset of X.

Let us note the following obvious fact:

(i) If \(A:X\rightarrow X\) is j-continuous then for each sequence \(\{u_{m}\}_{m=1}^{\infty }\) in X, such that there exists limit of \(\{u_{m}\}_{m=1}^{\infty }\), we have

\(A(\lim _{m\rightarrow \infty }^{j}u_{m})=\lim _{m\rightarrow \infty }^{j}A(u_{m})\text {.}\)

3 Main results

At the beginning, we recall two fundamental theorems in the fixed point theory, i.e. Schauder’s theorem and Banach Contraction Principle. Let T be a closed, bounded, convex subset of a normed space \((Y,||\cdot ||)\) and let A, B be nonlinear operators on T.

Theorem 3.1

(Schauder Fixed Point Theory [29]) Assume that:

  • \(\mathbf {(S1)}\) \(AT\subset T\);

  • \(\mathbf {(S2)}\) A is completely continuous on T.

    Then there exists a fixed point of A, i.e. there exists \(u\in T\) such that \(Au=u\).

Theorem 3.2

(Banach Contraction Principle [4, 7]) T is not necessary bounded and convex. Assume that:

  • \(\mathbf {(B1)}\) \(BT\subset T\);

  • \(\mathbf {(B2)}\) B satisfies Lipschitz condition on T i.e. \(\left\| Bx-By\right\| \le \lambda \left\| x-y\right\| \), \(x,y\in T\), \(\lambda <1\).

    Then there exists a unique fixed point of B, i.e. there exists \(u\in T\) such that \(Bu=u\).

It is clear that we can rewrite both theorems in the language of the modular j. First we give Schauder type theorem for the space X.

Theorem 3.3

(Schauder type) Let T be a closed, bounded and convex subset of X. Assume that:

  • \(\mathbf {(Sj1)}\) \(AT\subset T\);

  • \(\mathbf {(Sj2)}\) A is completely j-continuous on T.

    Then there exists a fixed point of A, i.e. there exists \(u\in T\) such that \(Au=u\).

Proof

In spite of the fact that the proof of this theorem sounds as the proofs of most classical Schauder theorems we proceed it in details. Let \(AT\subset Y\), Y compact. Since T is a bounded, so we can assume \(Y\subset T\). Choose any \(\varepsilon >0\). Successively, pick \(\ y_{1} ,y_{2},y_{3},...\) in Y so that

$$\begin{aligned} j(y_{i}-y_{k})\ge \varepsilon \text { for }1\le i<k\le n. \end{aligned}$$
(3.1)

We keep picking new points \(y_{n}\) as long as we can. It is clear we stop with some finite n; for otherwise one could pick an infinite sequence of points \(y_{1},y_{2},y_{3},...\) that satisfied the inequalities (3.1) and this violates our assumption that Y is compact. The finite set \(y_{1},...y_{n}\) is \(\varepsilon \)-j-dense in Y in j topology i.e. for every \(y\in Y\) we have

$$\begin{aligned} j(y_{i}-y)<\varepsilon \text { for some }i=1,...,n. \end{aligned}$$

Define the convex set

$$\begin{aligned} T_{\varepsilon }=\left\{ \eta _{1}y_{1}+ \cdots +\eta _{n}y_{n}:\sum _{i=1}^{n} \eta _{i}=1,\text { }\eta _{i}\ge 0\right\} . \end{aligned}$$

Of course, \(T_{\varepsilon }\subset T\) as T is convex. Recall also that \(Y\subset T\). We construct a j-continuous function \(p_{\varepsilon }(y)\) that approximates y:

$$\begin{aligned} j(p_{\varepsilon }(y)-y)<\varepsilon \text { for all }y\in Y. \end{aligned}$$
(3.2)

To do it we define, for \(i=1,...,n,\) \(y\in Y\),

$$\begin{aligned} \varphi _{i}(y)=\left\{ \begin{array}{l} 0 \quad \quad \quad \quad \quad \quad \text { if }j(y_{i}-y)\ge \varepsilon ,\\ \varepsilon -j(y_{i}-y)\quad \text { if }j(y_{i}-y)<\varepsilon . \end{array} \right. \end{aligned}$$
(3.3)

Each of these n functions \(\varphi _{i}(y)\) is j-continuous and (3.1) guarantees \(\varphi _{i}(y)>0\) for some \(i=1,...,n.\) Next we construct the n j-continuous functions

$$\begin{aligned} \eta _{i}(y)=\varphi _{i}(y)/s(y),\text { }i=1,...,n,\text { }y\in Y\text { } \end{aligned}$$

where

$$\begin{aligned} s(y)=\varphi _{1}(y)+\cdots +\varphi _{n}(y)>0. \end{aligned}$$

Notice that \(\eta _{i}(y),\) \(i=1,...,n\) satisfy \(\sum _{i=1}^{n}\eta _{i}(y)=1,\) \(\eta _{i}(y)\ge 0\). Hence we can define j-continuous function

$$\begin{aligned} p_{\varepsilon }(y)=\eta _{1}(y)y_{1}+ \cdots +\eta _{n}(y)y_{n}. \end{aligned}$$

It is clear that \(p_{\varepsilon }:Y\rightarrow T_{\varepsilon }\), moreover by (3.3) \(\eta _{i}(y)=0\) unless \(j(y_{i}-y)<\varepsilon \). Therefore, \(p_{\varepsilon }(y)\) is a convex combination of just those points \(y_{i}\) for which \(j(y_{i}-y)<\varepsilon \) and so by (j3) we have

$$\begin{aligned} j(p_{\varepsilon }(y)-y)=j(\sum _{i=1}^{n}\eta _{i}(y)(y_{i}-y))\le \sum _{i=1}^{n}\eta _{i}(y)j(y_{i}-y)<\varepsilon . \end{aligned}$$

Thus we get (3.2). Put \(f_{\varepsilon }(x)=p_{\varepsilon }(Ax),\) \(x\in T_{\varepsilon }\), \(f_{\varepsilon }\) is j-continuous in \(T_{\varepsilon }\). The Brouwer fixed-point theorem guarantees a fixed point \(x_{\varepsilon }\) i.e. \(f_{\varepsilon }(x_{\varepsilon })=x_{\varepsilon }\). Set \(y_{\varepsilon }=Ax_{\varepsilon }\). Now let \(\varepsilon \rightarrow 0\). Take a sequence \(\{\varepsilon _{n}\}_{n=1}^{\infty }\) for which \(y_{n}\) is j-converging to a limit in \(y^{*}\in Y\) (since Y is j-compact)

$$\begin{aligned} Ax_{\varepsilon _{n}}=y_{\varepsilon _{n}}\overset{j}{\rightarrow }y^{*}\text {, as }\varepsilon _{n}\rightarrow 0. \end{aligned}$$
(3.4)

We have

$$\begin{aligned} x_{\varepsilon }=f_{\varepsilon }(x_{\varepsilon })=p_{\varepsilon } (Ax_{\varepsilon })=p_{\varepsilon }(y_{\varepsilon }),\text { }x_{\varepsilon }=y_{\varepsilon }+[p_{\varepsilon }(y_{\varepsilon })-y_{\varepsilon }]. \end{aligned}$$
(3.5)

But we have

$$\begin{aligned} j(p_{\varepsilon }(y)-y)<\varepsilon \text { for all }y\in Y \end{aligned}$$
(3.6)

so (3.4) and (3.5) imply

$$\begin{aligned} j(x_{\varepsilon _{n}}-y^{*})\rightarrow 0\text {, as }\varepsilon _{n}\rightarrow 0. \end{aligned}$$

Really, putting (3.5) in (3.6) we get the needed convergence. Since A is j-continuous (3.4) yields the fixed point: \(Ay^{*}=y^{*}\). \(\square \)

The second theorem is a generalization of Banach Contraction Principle to the space X. In literature there are several extension of Banach Contraction theorem to modular spaces see e.g. [18,19,20]. However all these extension are proved in specified modular function spaces with less or more stronger assumptions on modular. In [18, 19] modular j is also convex with additional properties and in [20] j satisfies weaken than convexity assumption but instead the \((\Delta _2)\) condition is required. It is worth to stress that lastly (see [43]) appears new generalization of the fixed points of contractions to f-quasimetric spaces endowed with f-quasimetric (it does not satisfy the symmetry condition (like (j2))) satisfying f-triangle inequality. On properties of f-quasimetric spaces see [1,2,3]. In [27] was proved that f-triangle inequality is equivalent to asymptotic triangle inequality: let M be a set consisting of at least two points and \(\rho :M\times M \rightarrow \mathbb {R}\cup \{0\}\) a function satisfying \(\rho (x,y)=0 \Leftrightarrow x=0\) then

$$\begin{aligned} \forall _{\{x_i\},\{y_i\},\{z_i\}\subset M}\ \rho (x_i,y_i)\rightarrow 0,\ \rho (y_i,z_i)\rightarrow 0\ \Rightarrow \rho (x_i,z_i)\rightarrow 0. \end{aligned}$$
(3.7)

Notice that in case of \(M=X\), X our linear space with modular j satisfying \((j1)-(j3)\), asymptotic triangle inequality (3.7) implies:

$$\begin{aligned} \forall _{\{x_i\}\subset X}\ j (x_i)\rightarrow 0,\ \Rightarrow j ((1+\alpha ) x_i)\rightarrow 0,\ \alpha >0. \end{aligned}$$
(3.8)

Really, it is enough to take in (3.7) (replacing \(\rho \) by j and our definition of convergence) \(y_i=0\) and \(z_i=-\alpha x_i\). But then (3.8) is just the condition B.2 in [25] which is equivalent to \((\Delta _2)\) from 1.32.(c) in [25]. In case of X linear for modular j condition B.2. from [25] implies (3.7). Thus if j is modular and X linear then asymptotic triangle inequality is equivalent to \((\Delta _2)\) condition. But then (with \((\Delta _2)\)) j topology in X is equivalent to norm topology with Luxemburg norm defined by j (see [24] p. 18). Therefore if our X with modular j satisfies \((\Delta _2)\) condition then Theorem 3.4 below is a particular case of the contraction theorem from [43]. But we do not assume \((\Delta _2)\) condition. However in [43] X is not linear and f-quasimetric \(\rho \) does not satisfy the symmetry condition (like (j2)) and it is not convex. We should also mention that in the case of \((q_1,q_2)\)-quasimetric spaces with \((q_1,q_2)\)-generalized triangle inequality, where the Banach fixed point theorem was proved (see [12]), \(q_1\) and \(q_2\) are \(\ge 1\). Hence, the theorem below, in some cases, is a new extension of contraction theorem to the space which is a generalization of modular space.

Theorem 3.4

(Banach type) Let T be a closed and bounded subset of j-complete space X. Assume that:

  • \(\mathbf {(Bj1)}\) \(BT\subset T\);

  • \(\mathbf {(Bj2)}\) B satisfies the j-contraction condition on T, i.e. \(j(Bx-By)\le \lambda j(x-y)\), \(x,y\in T\), \(\lambda <1\).

    Then there exists a unique fixed point of B, i.e. there exists \(u\in T\) such that \(Bu=u\).

Proof

Take any \(x_{0}\in T\) and compute \(x_{1},x_{2},...\) by \(x_{n+1}=Bx_{n}\), \(n=0,1,2,...\). The proof will be devided into five steps.

Step 1. We prove that \(\{x_{n}\}_{n\in \mathbb {N}}\) is j-Cauchy sequence. Let \(m,n\in \mathbb {N}\), \(m>n\).

From, \(\mathbf {(Bj2)}\) we calculate

$$\begin{aligned}{} & {} j(x_{n}-x_{m})=j(Bx_{n-1}-Bx_{m-1})\\{} & {} \qquad \le \lambda j(x_{n-1}-x_{m-1})=\lambda j(Bx_{n-2}-Bx_{m-2})\\{} & {} \qquad \le \lambda ^{2}j(x_{n-2}-x_{m-2})=\lambda ^{2}j(Bx_{n-3}-Bx_{m-3})\\{} & {} \qquad \le \lambda ^{3}j(x_{n-3}-x_{m-3})=...\le \lambda ^{n}j(x_{0}-x_{m-n})\text {.} \end{aligned}$$

In consequence, for each \(m>n\) we obtain

$$\begin{aligned} j(x_{n}-x_{m})\le \lambda ^{n}j(x_{0}-x_{m-n}),\ n=1,2,...\ . \end{aligned}$$

Since T is bounded, there exists \(\widehat{\varepsilon _{j}}>0\) such that \(T\subset \mathcal {B}_{j}(0,\widehat{\varepsilon }_{j})\) and therefore \(j(x_{0}-x_{m-n})<\widehat{\varepsilon _{j}}\) for each \(m,n\in \mathbb {N}\), \(m>n\). Hence for each \(m>n\) we obtain

$$\begin{aligned} j(x_{n}-x_{m})\le \lambda ^{n}\widehat{\varepsilon _{j}},\ n=1,2,...\ . \end{aligned}$$
(3.9)

Of course, since \(\lambda <1\), we have

$$\begin{aligned} \forall \varepsilon>0\ \exists n_{0}\in \mathbb {N}\ \forall \ n>n_{0} \ \{\widehat{\varepsilon _{j}}\lambda ^{n}<\varepsilon \}\text {.} \end{aligned}$$
(3.10)

Let \(\varepsilon >0\). Then, for each \(m>n>n_{0}\), by (3.9) and (3.10) we have

$$\begin{aligned} j(x_{n}-x_{m})\le \widehat{\varepsilon _{j}}\lambda ^{n}<\varepsilon \end{aligned}$$
(3.11)

and in consequence

$$\begin{aligned} \forall m>n>n_{0}\ \{j(x_{n}-x_{m})<\varepsilon \}\text {,} \end{aligned}$$

which implies that \(\{x_{n}\}_{n=1}^{\infty }\) is j-Cauchy sequence.

Step 2. There exists u in T such that \(\lim _{n\rightarrow \infty }j(x_{n}-u)=0\). Indeed, by Step 1, the sequence \(\{x_{n}\}_{n=1}^{\infty }\) is j-Cauchy. Since X is j-complete, there exists u in X such that \(\lim _{n\rightarrow \infty }j(x_{n}-u)=0\). Since T is closed, thus \(u\in T\).

Step 3. The point u is a fixed point of the map B. Indeed, since \(\{x_{n}\}_{n=1}^{\infty }\) is j-convergent, by j-continuity of B, we immediately obtain

\(B(u)=B(\lim _{n\rightarrow \infty } ^{j}x_{n})=\lim _{n\rightarrow \infty }^{j}B(x_{n} )=\lim _{n\rightarrow \infty }^{j} x_{n+1}=u\text {,}\) i.e. u is a fixed point of B.

Step 4. We show the uniqueness of a fixed point. Assume that in T there exist v and w such that \(v=Bv\) and \(w=Bw\). Then by \(\mathbf {(Bj2)}\) we have

$$\begin{aligned} j(v-w)=j(Bv-Bw)\le \lambda j(v-w)\text {.} \end{aligned}$$

Hence \((1-\lambda )j(v-w)\le 0\). Since \(\lambda <1\), thus \(j(v-w)\le 0\) and consequently \(j(v-w)=0\). Therefore, by (j1) we obtain \(v=w\). \(\square \)

Now we formulate and prove a generalization of Krasnoselskii theorem for the space X, which join the last two theorems in one. In the proof we will apply the above contraction type and Schauder type theorems for the space X.

Theorem 3.5

Assume that:

  • \(\mathbf {(T1)}\) T is a closed, bounded and convex subset of j-complete space X.

  • \(\mathbf {(T2)}\) the operator \(A:T\rightarrow T\) is completely j-continuous;

  • \(\mathbf {(T3)}\) the operator \(B:T\rightarrow T\) satisfies the j-contraction condition, i.e.

    $$\begin{aligned} j(Bx-By)\le \lambda j(x-y),\text { }x,y\in T,\text { }\lambda <1\text {;} \end{aligned}$$
    (3.12)

Then, for each fixed \(0\le \beta \le 1\) there exists a point \(u\in T\), such that \((1-\beta )Au+\beta Bu=u\).

Proof

Let \(x\in T\) and \(0\le \beta \le 1\) be arbitrary and fixed. By Theorem 3.4, we have that there exists a point \(w_x\in T\) such that

$$\begin{aligned} w_x=\beta Bw_x+(1-\beta )Ax\text {,} \end{aligned}$$
(3.13)

as if B is the contraction then by the convexity of j, the operator \(\beta B\) is a contraction too. We define an operator \(C:T\rightarrow T\) by the following formula

$$\begin{aligned} Cx=w_x\text {.} \end{aligned}$$

Hence, by (3.13), we get

$$\begin{aligned} Cx=\beta BCx+(1-\beta ) Ax\text {.} \end{aligned}$$
(3.14)

The operator C is defined on all T and as T is convex thus \(CT\subset T\). Thus the assumption (Sj1) in Schauder type theorem holds.

We show that the operator C is completely j-continuous on T. Take any sequence \(\left\{ x_{m}\right\} _{n=1}^{\infty }\subset T\). As A is completely j-continuous thus there is a subsequent of it which again denote by \(\{x_m\}\) such that \(\{Ax_m\}\) is j-convergent and so also it is j-Cauchy sequence in T. Then from (3.14),

$$\begin{aligned} Cx_{m}= & {} \beta BCx_{m}+(1-\beta )Ax_{m}\text {, }m\in \mathbb {N}\text {,} \\ Cx_{n}= & {} \beta BCx_{n}+(1-\beta )Ax_{n}\text {, }n\in \mathbb {N}\text {.} \end{aligned}$$

Consider identities

$$\begin{aligned} Cx_n-Cx_{m}=\beta BCx_n-\beta BCx_{m}+(1-\beta )Ax_n-(1-\beta )Ax_{m},\text { for all }m,n \in \mathbb {N}. \end{aligned}$$

Applying first convexity of j and next (3.12), we infer:

$$\begin{aligned} j(Cx_n-Cx_{m})&\le \beta j(BCx_n-BCx_{m})+(1-\beta )j(Ax_n-Ax_{m})\\&\le \beta \lambda j(Cx_n-Cx_{m})+(1-\beta )j(Ax_n-Ax_{m})\text {, }m,n \in \mathbb {N}\text {.} \end{aligned}$$

Therefore

$$\begin{aligned} j(Cx_n-Cx_{m})-\text { }\beta \lambda j(Cx_n-Cx_{m})\le (1-\beta )j(Ax_n-Ax_{m})\text {, }m,n \in \mathbb {N} \end{aligned}$$

and

$$\begin{aligned} j(Cx_n-Cx_{m})\leqslant \frac{1-\beta }{1-\beta \lambda }j(Ax_n-Ax_{m})\text {, } m,n \in \mathbb {N}, \end{aligned}$$
(3.15)

i.e. \(\{Cx_{m}\}\) is j-Cauchy sequence and so it is j-convergent. Hence, we infer that the image of the operator C is contained in some compact set. Thus, the assumption (Sj2) holds. Therefore, by Schauder’s type theorem, we conclude the assertion of the theorem. \(\square \)

Note that we do not assume that \(Ax+Bw\in T\) as is done in Krasnoselskii proof or that \([x=Bx+Ay,\ y\in T ] \Rightarrow x\in T\) in Burton proof (see [6]).

4 Application of Krasnoselskii theorem to a periodic problem of ODE

Now, we provide some example to illustrate the above theorem. To this effect let us consider the semilinear equation

$$\begin{aligned} x^{\prime \prime }+a(t)x=f(t,x)+g(t,x)\text {,} \end{aligned}$$
(4.1)

with \(a\in L^{1}[0,T]\) and \(f,g:[0,T]\times \mathbb {R}^{+}\rightarrow \mathbb {R}\) are Carathéodory functions.

It is noteworthy that the starting point for considerations of this type of equation is the well-known Hill differential equation: an ordinary second-order differential equation

$$\begin{aligned} x^{\prime \prime }+a(t)x=0 \end{aligned}$$

with a periodic function a(t), \(a\in L^{1}[0,T]\) with period T. The equation is named after G. Hill [14], who in studying the motion of the moon obtained the equation

$$\begin{aligned} x^{\prime \prime }(z)+(\theta _{0}+2\sum _{r=1}^{\infty }\theta _{2r}\cos 2rz)x(z)=0 \end{aligned}$$

with real numbers \(\theta _{0},\theta _{2},...\) where the series \(\sum _{r=1}^{\infty }|\theta _{2r}|\) converges and z can be complex. G. Hill gave a method for solving this equation with the use of determinants of infinite order. This was a source for the creation of the theory of such determinants, and later for the creation by E. Fredholm of the theory of integral equations (cf. Fredholm theorems).

Most important for Hill’s equations are the problems of the stability of solutions and the presence or absence of periodic solutions. The Hill’s equation is well studied (see [42]).

The same equation of Hill type was study by P.J. Torres [34]. P. J. Torres consider the general equation

$$\begin{aligned} x^{\prime \prime }+a(t)x=f(t,x)+c(t) \end{aligned}$$

with \(a,c\in L^{1}[0,T]\) and \(f:[0,T]\times \mathbb {R}^{+}\rightarrow \mathbb {R}\) a \(L^{1}\)-Carathéodory, nonnegative function, that is, f is continuous in the second variable and for every \(0<r<s\) there exists \(h_{r,s}\in L^{1}(0,T)\) such that \(|f(t,x)|\le h_{r,s}(t)\) for all \(t\in [r,s]\) and a.e. \(t\in [0,T]\). The case with f changing sign is investigated in [8]. First we consider the case from [34] as the attractive case from [8] has very similar proof to that of [34]. We do not consider the case when f contains a damping therm. The investigation of such equation require different theorem than that presented here i.e. Theorem 3.5. (compare [9]).

Following [34] we assume on the linear part of (4.1) the standing hypothesis:

(H1) The Hill’s equation \(x^{\prime \prime }+a(t)x=0\) is nonresonant and the corresponding Green’s function G(t, s) is nonnegative for every \((t,s)\in [0,T]\times [0,T].\)

Remark 4.1

The equation \(x^{\prime \prime }+a(t)x=0\) is nonresonant when its unique T -periodic solution is the trivial one. It is well known that G(t, s) is continuous and thus bounded on \([0,T]\times [0,T]\) by some constant M. Under the assumption (H1) the function \(\gamma (t)=\int _0^TG(t,s)c(s)ds\) is the unique T-periodic solution of the linear equation \(x^{\prime \prime }+a(t)x=c(t)\) (see [35]). When \(a(t) \equiv k^2\), (H1) is equivalent to \(0 < k^2 \le \mu _1\). For a nonconstant a(t), there is a \(L^p\)-criterion (see e.g. [34]) ensuring that G(t, s) is nonnegative.

On the real axis \(\mathbb {R}\) define a convex, finite function j satisfying (j1)–(j3). It is clear that j is continuous and increasing on \(\mathbb {R}^{+}\). We shall consider \(\mathbb {R}\) with the modular j. In \(\mathbb {R}\) we consider the set of continuous, T-periodic functions and denote it as \(C_{T}\) endowed with the modular \(\left\| q(\cdot )\right\| _{j}=\max _{t\in [0,T]}\) j(q(t)), \(q\in C_{T}\). It is clear and very important in the proof of the following theorem that \(\left\| \cdot \right\| _{j}\) satisfies in \(C_{T}\) the property (j1)–(j3). We make the following assumptions on f and g:

  1. 1.

    f, g are measurable in t and continuous in x,

  2. 2.

    for every \(0<r<s\) there exists \(h_{r,s}\in L^{1}(0,T)\) such that \(j(f(t,x))\le h_{r,s}(t)\) for \(t\in [r,s]\) and a.e. \(t\in [0,T]\),

  3. 3.

    there exists continuous \(0<\) \(\kappa (t)T<1,\) such that \( {\displaystyle \int _{0}^{T}} j(2G(t,s)(g(s,x_{1}(s))-g(s,x_{2}(s))))ds\le \kappa (t) {\displaystyle \int _{0}^{T}} j(x_{1}(s)-x_{2}(s))ds\) for all \(t\in [0,T]\) and \(\ x_{1},x_{2}\in C_{T}\) and \(\ x_{1}(t),x_{2}(t)\in \mathbb {R}^{+}\), \(t\in [0,T]\).

Given \(a\in L^{1}(0,T)\), we write \(a\succ 0\) if \(a\ge 0\) for a.e. \(t\in [0,T]\) and it is positive in a set of positive measure. We prove the following theorem which is a generalization of Theorem 1 form [34].

Theorem 4.1

Let us assume that there exist \(b\succ 0\) which is positive on the set of positive measure on [0, T] and \(\lambda >0\) such that

$$\begin{aligned} 0\le j(2Mf(t,x))\le const,\text { for all }x>0,\text { for a.e. }t. \end{aligned}$$
(4.2)

For \(r\succ 0\), we define

$$\begin{aligned} \gamma _{*}&=\inf _{x\ge r,t\in [0,T]}j\left( {\displaystyle \int _{0}^{T}} G(t,s)g(t,x)ds\right) ,\\ \gamma ^{*}&=\sup _{x\ge r,t\in [0,T]}j\left( {\displaystyle \int _{0}^{T}} 2G(t,s)g(t,x)ds\right) \text {.} \end{aligned}$$

If for some \(r\succ 0\) we have \(\gamma _{*}\ge r\) and \(\gamma ^{*}<+\infty \), then there exists a positive T-periodic solution of (4.1).

Proof

Let us define in \(C_{T}\) a map \(\mathcal {F}:C_{T}\rightarrow C_{T}\) as

$$\begin{aligned} \mathcal {F}[x](\cdot )= {\displaystyle \int _{0}^{T}} 2G(\cdot ,s)[f(s,x(s))+g(s,x(s))]ds=Ax(\cdot )+Bx(\cdot )\text {,} \end{aligned}$$

where \(Ax(\cdot )= {\displaystyle \int _{0}^{T}} 2G(\cdot ,s)f(s,x(s))ds\) and \(Bx(\cdot )= {\displaystyle \int _{0}^{T}} 2G(\cdot ,s)g(s,x(s))ds\). By Remark 4.1\(A,B:C_{T}\rightarrow C_{T}\).

We have to show that for some subset of \(C_{T}\) say

$$\begin{aligned} K=\left\{ x\in C_{T}:x\ge r_{*},\text { }r_{*}\le ||x||_{j}\le R\right\} , \end{aligned}$$

where \(r_{*}\) and R will be defined below, all assumptions of Theorem 3.5 are satisfied. In order to prove that K is closed it is enough to note that for \(x\in K\) \(0\le j(x(t))\le ||x||_{j}\), for all \(t\in [0,T]\). Then any sequence \(\{x_n\}\subset K\) tending to \(x\in C_T\) in the sense of \(||\cdot ||_{j}\) is such that \(\{x_n-x\}\) is obviously bounded in \(C_T\). But because j is locally Lipschitz \(\{x_n(t)-x(t)\}\) is also uniformly bounded in [0, T] in ordinary sense and equi-continuous for each \(t\in [0,T]\). Even more for each \(t\in [0,T]\) \(\{x_n(t)-x(t)\}\) is also convergent to 0. Thus by Arzelà–Ascoli theorem \(\{x_n\}\) is uniformly convergent to x and so \(x\in K\). We will check that for all \(x,y\in K\), \(\frac{1}{2}Ax+\frac{1}{2}By\in K\).

Indeed, given \(x,y\in K\), by the nonnegative sign of G, f and increasing of j for all \(t\in [0,T]\) we calculate

$$\begin{aligned} j\left( \frac{1}{2}Ax(t)+\frac{1}{2}By(t)\right) =j\left( {\displaystyle \int _{0}^{T}} G(t,s)f(s,x(s))ds+ {\displaystyle \int _{0}^{T}} G(t,s)g(s,y(s))ds\right) \\ \ge \gamma _{*}:=\text { }r_{*},\text { } \end{aligned}$$

and by convexity of j and (4.2)

$$\begin{aligned} \max _{t\in [0,T]}j\left( \frac{1}{2}Ax(t)+\frac{1}{2}By(t)\right)&\le \max _{t\in [0,T]}\frac{1}{2}j(Ax(t))+\max _{t\in [0,T]}\frac{1}{2}j(By(t))\\&\le \frac{T}{2} const+\frac{1}{2}\gamma ^{*}:=R. \end{aligned}$$

Thus, really for all \(x,y\in K\), \(\frac{1}{2}Ax+\frac{1}{2}By\in K\) with \(r_{*}\) and R just defined.

Verification of assumption (T2): Similarly as closedness of K we show that A is \(\left\| \cdot \right\| _{j}\)-completely continuous in K.

Verification of assumption (T3): Let \(x_{1},x_{2}\in K\). Then

$$\begin{aligned} \left\| Bx_{1}-Bx_{2}\right\| _{j}&=\left\| {\displaystyle \int _{0}^{T}} 2G(\cdot ,s)g(s,x_{1}(s))ds- {\displaystyle \int _{0}^{T}} 2G(\cdot ,s)g(s,x_{2}(s))ds\right\| _{j}\\&=\left\| {\displaystyle \int _{0}^{T}} 2G(\cdot ,s)(g(s,x_{1}(s))-g(s,x_{2}(s)))ds\right\| _{j}\\&\le \sup _{t\in [0,T]}\kappa (t) {\displaystyle \int _{0}^{T}} j(x_{1}(s)-x_{2}(s))ds\\&\le \sup _{t\in [0,T]}\kappa (t)T\max _{t\in [0,T]}j(x_{1} (t)-x_{2}(t))\text {.} \end{aligned}$$

In consequence B is a \(\left\| \cdot \right\| _{j}\)-contraction in \(C_{T}\).

All assumption of Theorem 3.5 hold. Using this theorem we obtain that the operator \((1/2)\mathcal {F}\) has a fixed point in K and the proof is complete. \(\square \)

Remark 4.2

Note that the above theorem is new even in the case when \(j(\cdot )=\left| \cdot \right| \), i.e. j is standard norm in \(\mathbb {R}\) (see [34]). In this case the set \(C_{T}\) with the modular j and the standard norm are in fact the same space as if x is continuous then also j(x) is continuous, i.e. j maps space of periodic continuous function on [0, T] onto itself. The advantage here to use the space \(C_{T\text { }}\) is that the operator A and B may have different properties related to j.

The next theorem is a simply extension of the former theorem to the case when f can change sign. The proof is similar to Theorem 4.1 and we omit it.

Theorem 4.2

Assume on f and g as in 1.,2.,3. before Theorem 4.1. Moreover let us assume that there exist \(b\succ 0\) which is positive on the set of positive measure on [0, T], \(\lambda >0\) and positive constants \(R>r>0\) such that

$$\begin{aligned}{} & {} f(t,x)<0\ \text {for each }0<x<r\ \text {and }t\in [0,T], \end{aligned}$$
(4.3)
$$\begin{aligned}{} & {} f(t,r)=0\ \text {uniformly in }t\in [0,T], \end{aligned}$$
(4.4)
$$\begin{aligned}{} & {} 0\le j(2Mf(t,x))\le const,\text { for all }x>r,\text { for a.e. }t\in [0,T]. \end{aligned}$$
(4.5)

Define

$$\begin{aligned} \gamma _{*}&=\inf _{x\ge r,t\in [0,T]}j\left( {\displaystyle \int _{0}^{T}}G(t,s)g(t,x)ds\right) ,\\ \gamma ^{*}&=\sup _{x\ge r,t\in [0,T]}j\left( {\displaystyle \int _{0}^{T}}2G(t,s)g(t,x)ds\right) \text {,}\\ \beta ^{*}&=\sup _{x\ge r,t\in [0,T]}j\left( {\displaystyle \int _{0}^{T}}2G(t,s)b(t)ds\right) \end{aligned}$$

and assume \(\frac{\beta ^{*}}{r^{\lambda }}+\gamma ^{*}\le R\). If \(\gamma _{*}>r\), then there exists a positive T-periodic solution of (4.1).