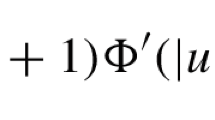Abstract
We study the system of semilinear elliptic equations
\(N\ge 4\), \(1<p<\frac{N}{N-2}\), and the matrix \((\beta _{ij})\) is symmetric and admits a block decomposition such that the entries within each block are positive or zero and all other entries are negative. We provide simple conditions on \((\beta _{ij})\), which guarantee the existence of fully nontrivial solutions, i.e., solutions all of whose components are nontrivial. We establish existence of fully nontrivial solutions to the system having a prescribed combination of positive and nonradial sign-changing components, and we give an upper bound for their energy when the system has at most two blocks. We derive the existence of solutions with positive and nonradial sign-changing components to the system of singularly perturbed elliptic equations
in the unit ball, exhibiting two different kinds of asymptotic behavior: solutions whose components decouple as \(\varepsilon \rightarrow 0\), and solutions whose components remain coupled all the way up to their limit.
Similar content being viewed by others
References
Ackermann, N., Dancer, N.: Precise exponential decay for solutions of semilinear elliptic equations and its effect on the structure of the solution set for a real analytic nonlinearity. Differ. Integr. Equ. 29(7–8), 757–774 (2016)
Bracho, J., Clapp, M., Marzantowicz, W.: Symmetry breaking solutions of nonlinear elliptic systems. Topol. Methods Nonlinear Anal. 26(1), 189–201 (2005)
Byeon, J., Sato, Y., Zhi-Qiang, W.: Pattern formation via mixed attractive and repulsive interactions for nonlinear Schrödinger systems. J. Math. Pures Appl. 106(3), 477–511 (2016)
Cerami, G., Clapp, M.: Sign changing solutions of semilinear elliptic problems in exterior domains. Calc. Var. Partial Differ. Equ. 30(3), 353–367 (2007)
Chen, Z., Chang-Shou, L., Wenming, Z.: Infinitely many sign-changing and semi-nodal solutions for a nonlinear Schrödinger system. Ann. Sc. Norm. Super Pisa Cl. Sci. 15, 859–897 (2016)
Cingolani, S., Clapp, M., Secchi, S.: Multiple solutions to a magnetic nonlinear Choquard equation. Z. Angew. Math. Phys. 63(2), 233–248 (2012)
Clapp, M., Pistoia, A.: Fully nontrivial solutions to elliptic systems with mixed couplings. Nonlinear Anal. 216, 112694 (2022)
Clapp, M., Soares, M.: Coupled and uncoupled sign-changing spikes of singularly perturbed elliptic systems. Communication in Contemporary Mathematics, to appear. arXiv:2108.00299 (2021)
Clapp, M., Srikanth, P.N.: Entire nodal solutions of a semilinear elliptic equation and their effect on concentration phenomena. J. Math. Anal. Appl. 437(1), 485–497 (2016)
Dovetta, S., Pistoia, A.: Solutions to a cubic Schrödinger system with mixed attractive and repulsive forces in a critical regime. Math. Eng. 4, 21 (2022)
Esry, B.D., Greene, C.H., Burke, J., James, P., Bohn, J.L.: Hartree-Fock theory for double condensates. Phys. Rev. Lett. 78, 3594–3597 (1997)
Lin, T.-C., Wei, J.: Spikes in two coupled nonlinear Schrödinger equations. Ann. Inst. H. Poincaré Anal. Non Linéaire 22(4), 403–439 (2005)
Lin, T.-C., Wei, J.: Ground state of \(N\) coupled nonlinear Schrödinger equations. Comm. Math. Phys. 255(3), 629–653 (2005)
Liu, J., Liu, X., Wang, Z.: Multiple mixed states of nodal solutions for nonlinear Schrödinger systems. Calc. Var. Partial Differ. Equ. 52(3–4), 586 (2015)
Sato, Y., Wang, Z.-Q.: On the multiple existence of semi-positive solutions for a nonlinear Schrödinger system. Ann. Inst. H. Poincaré C Anal. Non Linéaire 30, 1–22 (2013)
Sato, Y., Wang, Z.-Q.: On the least energy sign-changing solutions for a nonlinear elliptic system. Discrete Contin. Dyn. Syst. 35(5), 2151–2164 (2015)
Sato, Y., Wang, Z.-Q.: Least energy solutions for nonlinear Schrödinger systems with mixed attractive and repulsive couplings. Adv. Nonlinear Stud. 15(1), 1–22 (2015)
Sato, Y., Wang, Z.-Q.: Multiple positive solutions for Schrödinger systems with mixed couplings. Calc. Var. Partial Differ. Equ. 54(2), 1373–1392 (2015)
Sirakov, B.: Least energy solitary waves for a system of nonlinear Schrödinger equations in Rn. Comm. Math. Phys. 271(1), 199–221 (2007)
Soave, N.: On existence and phase separation of solitary waves for nonlinear Schrödinger systems modelling simultaneous cooperation and competition. Calc. Var. Partial Differ. Equ. 53(3–4), 689–718 (2015)
Soave, N., Tavares, H.: New existence and symmetry results for least energy positive solutions of Schrödinger systems with mixed competition and cooperation terms. J. Differ. Equ. 261(1), 505–537 (2016)
Tavares, H., You, S.: Existence of least energy positive solutions to Schrödinger systems with mixed competition and cooperation terms: The critical case. Calc. Var. Partial Differ. Equ. 59, 35 (2020)
Tavares, H., You, S., Zou, W.: Least energy positive solutions of critical Schrödinger systems with mixed competition and cooperation terms: The higher dimensional case. J. Funct. Anal. 283, 50 (2022)
Tavares, H., Terracini, S.: Sign-changing solutions of competition-diffusion elliptic systems and optimal partition problems. Ann. Inst. H. Poincaré C Anal. Non Linéaire 29, 279–300 (2012)
Wei, J., Wu, Y.: Ground states of nonlinear Schrödinger systems with mixed couplings. J. Math. Pures Appl. 141, 50–88 (2020)
Willem, M.: Minimax theorems. Progress in Nonlinear Differential Equations and their Applications 24. (Birkhäuser Boston, Boston, 1996)
Funding
M. Clapp was supported by Consejo Nacional de Ciencia y Tecnologàa (CONACYT), Mexico, through the research grant A1-S-10457. M. Soares was supported by Dirección General de Asuntos del Personal Académico de la Universidad Nacional Autónoma de México (UNAM-DGAPA), Mexico, through a postdoctoral fellowship
Author information
Authors and Affiliations
Contributions
Mónica Clapp and Mayra Soares are co-authors of this article. They share responsibility and accountability for the results.
Corresponding author
Ethics declarations
Conflict of interest
There are no relevant financial or non-financial competing interests to report.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
M. Clapp was supported by CONACYT (Mexico) through the grant A1-S-10457.
M. Soares was supported by UNAM-DGAPA (Mexico) through a postdoctoral fellowship.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Clapp, M., Soares, M. Energy estimates for seminodal solutions to an elliptic system with mixed couplings. Nonlinear Differ. Equ. Appl. 30, 11 (2023). https://doi.org/10.1007/s00030-022-00817-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00030-022-00817-9
Keywords
- Nonlinear elliptic system
- Weakly coupled
- Mixed cooperation and competition
- Positive and sign-changing components
- Singularly perturbed elliptic system