When the Fourier transform is one loop exact?

Abstract

We investigate the question: for which functions $f(x_1,\ldots ,x_n),~g(x_1,\ldots ,x_n)$ the asymptotic expansion of the integral $\int g(x_1,\ldots ,x_n) e^{\frac{f(x_1,\ldots ,x_n)+x_1y_1+\dots +x_ny_n}{\hbar }}dx_1\ldots dx_n$ consists only of the first term. We reveal a hidden projective invariance of the problem which establishes its relation with geometry of projective hypersurfaces of the form $\{(1:x_1:\ldots :x_n:f)\}$. We also construct various examples, in particular we prove that Kummer surface in ${\mathbb {P}}^3$ gives a solution to our problem.

Appendix: Explicit formulas for equations

Recall that f, g are functions in variables $\vec {x}=(x_1,x_2,\dots ,x_n)$ and we assume that the Hessian matrix $\partial ^2 f:=(\partial _i \partial _j f)_{1\le i,j \le n}$ is non-degenerate. Denote by

$$\begin{aligned} (p^{ij})_{1\le i,j\le n}:=(\partial ^2 f)^{-1} \end{aligned}$$

the inverse matrix-valued function.

Main notation: for $k\ge 1$ (all summation variables and indices are assumed to be integers),

$$\begin{aligned}{} & {} A_k:=\sum _{v\in [0,2k]} \sum _{\begin{array}{c} d_0\in [0,\infty );\\ d_1,\dots ,d_v\in [3,\infty )\\ \text{ such } \text{ that } \\ \sum _i d_i=2(k+v),\\ d_1\ge d_2\ge \dots \ge d_v \end{array}} \sum _{\begin{array}{c} a_{ij}\in [0,\infty )\\ \text{ where } {0\le i\le j\le v},\\ \text{ satisfying } \forall i:\\ d_i=\sum _{j<i} a_{ji}+\\ +2a_{ii}+\sum _{j>i}a_{ij} \end{array}} \frac{(-1)^v}{\text {Sym}_{(d_i),(a_{ij})}}\sum _{\begin{array}{c} b_{ijl},c_{ijl}\in [1,n]\\ \text{ where } \\ 1\le i\le j\le v\\ \text{ and } 1\le l\le a_{ij} \end{array}} \left( \prod _{\begin{array}{c} i,j\in [1,v]\\ l\in [1, a_{ij}] \\ \text{ such } \text{ that } \\ i\le j \end{array}}p^{b_{ijl},c_{ijl}}\right) \cdot \\{} & {} \quad \cdot \left[ \prod _{l_1\in [1, a_{00}]} (\partial _{b_{00l_1}}\partial _{c_{00l_1}})\prod _{\begin{array}{c} i\in [1,v]\\ l_2 \in [1,a_{0i}] \end{array}}\partial _{b_{0il_2}}g\right] \\{} & {} \quad \cdot \prod _{i\in [1,v]}\left[ \prod _{\begin{array}{c} j\in [0,i)\\ l_1\in [1,a_{ji}] \end{array}}\partial _{c_{jil_1}} \prod _{l_2\in [1,a_{ii}]}(\partial _{b_{iil_2}}\partial _{c_{iil_2}})\prod _{\begin{array}{c} j\in (i ,v]\\ l_3\in [1,a_{ij}] \end{array}} \partial _{b_{ijl_3}}f\right] \end{aligned}$$

Here the symmetry factor is defined by

$$\begin{aligned} \text {Sym}_{(d_i),(a_{ij})}=\prod _i m_i!\cdot \prod _{\begin{array}{c} i,j\in [0,v]\\ \text{ such } \text{ that }\\ i\le j \end{array}}{a_{ij}!}\cdot \prod _{i\in [0,v]}{2^{a_{ii}}} \end{aligned}$$

where $m_1,m_2,\dots \ge 1$ are multiplicities of the repeating terms in sequence $(d_1,d_2,\dots ,d_v)$, i.e.

$$\begin{aligned} d_1=\cdots =d_{m_1}>d_{m_1+1}=\cdots =d_{m_1+m_2}>d_{m_1+m_2+1}=\cdots \end{aligned}$$

Meaning: let us expand f at some point $\vec {x}^{(0)}$ as

$$\begin{aligned} f=f_0+f_1+f_2+f_{\ge 3} \end{aligned}$$

where $f_0=f(\vec {x}^{(0)})$ is a constant, $f_1,f_2$ are homogeneous polynomials in $\vec {x}-\vec {x}^{(0)}$ of degree 1 and 2 respectively, and $f_{\ge 3}$ is a series in $\vec {x}-\vec {x}^{(0)}$ containing terms of degrees $\ge 3$ only.

Then the formal Fourier transform, at point

$$\begin{aligned} \vec {y}^{(0)}=\partial f_{|\vec {x}^{(0)}}:=(\partial _1 f,\dots ,\partial _n f)_{|\vec {x}^{(0)}} \end{aligned}$$

is equal, after normalization, to

$$\begin{aligned}{} & {} \int g \,e^{-\frac{f-f_0-f_1}{\hbar }} d^n\vec {x}=\int g \,e^{-\frac{f_2+f_{\ge 3}}{\hbar }} d^n\vec {x}\\{} & {} \quad =\sum _{v\ge 0} \frac{(-1)^v}{v!}\hbar ^{-v}\int g f_{\ge 3}^v\,e^{-\frac{f_2}{\hbar }} d^n\vec {x}\\{} & {} \quad =(2\pi \hbar )^{n/2}\det (\partial ^2 f_{|\vec {x}^{(0)}})^{-1/2}\left( g_{|\vec {x}^{(0)}}+\sum _{k\ge 1} \hbar ^k {A_k}_{|\vec {x}^{(0)}}\right) \end{aligned}$$

In terms of (not connected) Feynman graphs, $v\ge 0$ denotes the number of vertices at which we put Taylor coefficients of $f_{\ge 3}$ (and at exactly one exceptional vertex we put Taylor coefficients of g). We label vertices by $\{0,1,\dots ,v\}=[0,v]\cap {\mathbb {Z}}$ where 0 corresponds to g, and the rest to $f_{\ge 3}$. Moreover, we assume that the ordering of vertices is chosen in such a way that $d_1\ge d_2\ge \cdots \ge d_v\ge 3$ where for all $i\in [0,v]$ number $d_i$ is the degree (valency) of vertex labeled by i. Denote by $a_{ij}\ge 0$ the number of edges connecting vertices i and j. We enumerate edges connecting i and j by $\{1,\dots , a_{ij}\}$. Then we put two space indices $b_{ijl},c_{ijl}\in [1,n]$ on two ends of the edge corresponding to $l\in [1,a_{ij}]$. The factors $\prod _i m_i!$, $\prod _{ij}a_{ij}!$ and $\prod _i 2^{a_{ii}}$ come from symmetry, the rest is the usual Wick formula.

The total number of edges e satisfies constraints:

$$\begin{aligned} e\ge {3\over 2}v, \quad k=e-v\implies e\in \{k,\dots ,3k\}\,, \end{aligned}$$

hence in the expression $A_k$ the propagator $(p^{ij})_{1\le i,j\le n}$ appears at most 3k times.

One-loop exactness is equivalent to an infinite sequence of differential equations:

$$\begin{aligned} A_1=0,~A_2=0,\dots \end{aligned}$$

(A.47)

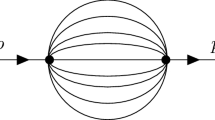
Up to symmetry, the number of distinct graphs for $A_1,A_2,A_3$ is 5, 41, 378 respectively.

For example, 5 graphs appearing in $A_1$ are the following:

and the expression $A_1$ is

$$\begin{aligned}{} & {} {1\over 2}\sum _{i,j}p^{ij}\,\partial _{ij} g-{1\over 2}\sum _{i_1 j_1 i_2 j_2}p^{i_1 j_1}p^{i_2 j_2}\,\partial _{i_1}g\, \partial _{j_1 i_2 j_2}f\\{} & {} \quad -{1\over 8}\,g\sum _{i_1 j_2 i_2 j_2}p^{i_1 j_1}p^{i_2 j_2}\,\partial _{i_1 j_1 i_2 j_2}f+{1\over 8}\,g\sum _{i_1 j_2 i_2 j_2 i_3 j_3}p^{i_1 j_1}p^{i_2 j_2}p^{i_3 j_3}\,\partial _{i_1 j_1 i_2}f \,\partial _{j_2 i_3 j_3}f\\{} & {} \quad +{1\over 12}\,g\sum _{i_1 j_1 i_2 j_2 i_3 j_3}p^{i_1 j_1}p^{i_2 j_2}p^{i_3 j_3}\,\partial _{i_1 i_2 i_3}f\,\partial _{j_1 j_2 j_3}f\,. \end{aligned}$$