Abstract
We introduce a functor from the cube to the Burnside 2-category and prove that it is equivalent to the Khovanov spectrum given by Lipshitz and Sarkar in the almost-extreme quantum grading. We provide a decomposition of this functor into simplicial complexes. This decomposition allows us to compute the homotopy type of the almost-extreme Khovanov spectra of diagrams without alternating pairs.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Khovanov homology is a powerful link invariant introduced by Mikhail Khovanov in [4] as a categorification of the Jones polynomial. More precisely, given an oriented diagram D representing a link L, he constructed a finite \(\mathbb {Z}\)-graded family of chain complexes

whose bigraded homology groups, \(Kh^{i,j}(D)\), are link invariants. The groups \(Kh^{i,j}(L)\) are known as Khovanov homology groups of L, and the indexes i and j as homological and quantum gradings, respectively.
In [7] Lipshitz and Sarkar refined this invariant to obtain, for each quantum grading j, a spectrum \(\mathcal {X}_D^j\) whose stable homotopy type is a link invariant and whose cohomology is isomorphic to the Khovanov homology of the link, i.e., \(H^{*}(\mathcal {X}_D^j)\cong Kh^{*,j}(L)\). Together with Lawson [6] they gave a neat construction of this spectrum as the realization of a 2-functor \(F^j\) from the cube category to the Burnside 2-category (see also [5, 8]).
Shortly after, another geometric realization of the (minimal) extreme Khovanov homology was given [3] in terms of an independence simplicial complex constructed from the link diagram. This construction was later shown to coincide with the one of Lipshitz and Sarkar [1] as follows: functors from the cube to the Burnside 2-category can be understood as generalizations of simplicial complexes; such a functor is a simplicial complex if it factors through the category of sets and takes values on singletons and the empty set.
On the other hand, the Khovanov spectrum of a link in its maximal extreme quantum grading is Spanier-Whitehead dual to that of its mirror image in minimal grading. This construction was exploited in [10] to make explicit computations of the Khovanov spectrum in (maximal) extreme quantum grading.
In 2018 the second author, together with Przytycki applied these techniques one step further, to the almost-extreme quantum grading. They restricted to the study of 1-adequate link diagrams, i.e., those whose 1-resolution contains no chords with both endpoints in the same circle (the extremal homology of these diagrams has been computed in [2, 9, 12]), and built a pointed semi-simplicial set whose homology is isomorphic to the almost-extreme Khovanov homology of the diagram:
Theorem
([11]) If D is a 1-adequate link diagram, then
-
(i)
The functor \(F_D^{{j_{\mathrm {almax}}}}\) gives rise to a pointed semi-simplicial set.
-
(ii)
The realization of \(F_D^{{j_{\mathrm {almax}}}}\) has the homotopy type of a wedge of spheres and possibly a copy of a (de)suspension of \(\mathbb {R}P^2\).
Their construction relates to the functor of Lawson, Lipshitz and Sarkar as follows: the category of pointed sets includes into the Burnside 2-category, and if a functor from the cube to the Burnside 2-category factors through it, then it gives rise to a pointed (augmented) semi-simpicial set.
Simplicial complexes and pointed semi-simplicial sets are simpler objects than functors to the Burnside 2-category, to which many classical tools can be applied, so these results prompt the question
Are there simpler models of the spectra of Lipshitz and Sarkar in the almost-extreme quantum grading?
Unfortunately, it turns out that \(F^{j_{\mathrm {almax}}}_D\) gives rise to a pointed semi-simplicial set if and only if D is 1-adequate. However, in this paper we overcome this problem by introducing a new functor \(M_D\), whose realization coincides with that of \(F^{j_{\mathrm {almax}}}_D\), and gives rise to an (augmented) pointed semi-simplicial set in a broader number of cases. This is achieved by constructing a natural transformation between \(M_D\) and \(F^{{j_{\mathrm {almax}}}}_D\) and proving the following result:
Theorem 1
The natural transformation is a homology isomorphism, and therefore the realizations of \(M_D\) and \(F^{{j_{\mathrm {almax}}}}_D\) are homotopy equivalent.
The functor \(M_D\) can be understood as a “change of basis” of \(F_D^{{j_{\mathrm {almax}}}}\): The relevant generators of the Khovanov chain complex in its almost-extreme degree (which is the same as the chain complex of \(F^{j_{\mathrm {almax}}}_D\)) are indexed by the circles of the state resolutions of D, whereas the generators of the chain complex associated to \(M_D\) are indexed by the edges and connected components of certain graph whose vertices are the circles of the state resolutions. A crucial property at the almost-extreme quantum grading is that the relevant involved graphs are forests, and therefore both bases have the same size (as it should be).
The functor \(M_D\) is simpler than \(F^j_D\) in the sense that it takes values in morphisms sending generators to (multiples of) generators, whereas \(F^j_D\) takes values in morphisms sending generators to sums of possibly different generators.
This simplified new basis allows us to decompose \(M_D\) in terms of independence simplicial complexes of simpler link diagrams (Proposition 7.5 and Remark 7.6). The last part of the paper is devoted to make explicit computations using this decomposition.
One of the advantages of \(M_D\) over \(F^{j_{\mathrm {almax}}}_D\) is that it gives rise to an augmented pointed semi-simplicial set if and only if the 1-resolution of the diagram contains no alternating pairs (i.e., two chords whose endpoints alternate along the same circle). Moreover, the forementioned decomposition allows us to compute the homotopy type of the realization of \(M_D\) in these cases:
Theorem 2
Let D be a diagram whose 1-resolution contains no alternating pairs.
-
(i)
The functor \(M_D\) gives rise to an augmented pointed semi-simplicial set.
-
(ii)
If D is not 1-adequate then the realization of \(M_D\) is homotopy equivalent to a wedge of spheres.
In [10] the second author conjectured (and proved for several cases) that the extreme Khovanov spectrum is always a wedge of spheres. If this conjecture were true, then the above decomposition would give an upper bound for the cone length of the spectrum \(\mathcal {X}^{j_{\mathrm {almax}}}_D\) (Remark 7.8). This bound seems to be far from optimal, as the computations of this paper and [11] produce spectra of cone length at most 2, so we rise the following question:
Are there diagrams whose almost-extreme Khovanov spectrum is not homotopy equivalent to a wedge of spheres and possibly (de)suspensions of projective planes?
The structure of the paper is as follows. In Sections 2 and 3 we recall the categorical notions that will be used along the paper. In Section 4 we develop some results on link diagrams which allow, in Section 5, to introduce the functor \(M_D\) and prove Theorem 1. In Section 6 we prove the first part of Theorem 2. In Section 7 we decompose \(M_D\) in terms of independence simplicial complexes and present three skein sequences which allow us to determine, in Section 8, the homotopy type of \(M_D\) for all links with no alternating pairs, proving the second part of Theorem 2.
2 The Burnside 2-category
A 2-category is a higher category that generalizes the notion of category, in the sense that on top of the objects and morphisms there are also 2-morphisms. More precisely, a 2-category consists of the data of
-
(1)
a collection of objects,
-
(2)
for each pair of objects X, Y, a category of morphisms \(\hom (X,Y)\),
-
(3)
for each object X, an object \(\mathrm {Id}_X\) of \(\hom (X,X)\) and
-
(4)
for each triple of objects X, Y, Z, a composition functor
$$\begin{aligned} \hom (Y,Z)\times \hom (X,Y)\rightarrow \hom (X,Z) \end{aligned}$$
which is associative and unital. The objects in \(\hom (X,Y)\) are called 1-morphisms and the morphisms in \(\hom (X,Y)\) are called 2-morphisms.
Recall that given two finite sets X, Y, a span from X to Y is a triple \((Q,s,t)\) where Q is a finite set, and \(s\) and \(t\) are a pair of functions \(X\overset{s}{\longleftarrow } Q\overset{t}{\longrightarrow } Y\).
We say that a span is free (resp. very free) if the source map s is injective (resp. bijective).
Given two spans \(X\overset{s}{\longleftarrow } Q\overset{t}{\longrightarrow } Y\) and \(X\overset{s'}{\longleftarrow } Q'\overset{t'}{\longrightarrow } Y\), a fibrewise bijection between them is a bijection \(\tau :Q\rightarrow Q'\) such that \(s'\circ \tau =s\) and \(t'\circ \tau =t\):

The composition of two fibrewise bijections of spans is the composition of bijections, and the identity morphism of a locally finite span is the identity bijection. This defines a category of spans from the set X to the set Y, which we note by \(\mathcal {B}(X,Y)\).
Definition 2.1
The Burnside 2-category, denoted by \(\mathcal {B}\), is the 2-category whose objects are finite sets, and the category of morphisms from a set X to a set Y is given by \(\mathcal {B}(X,Y)\), the category of spans from X to Y; in other words, the 1-morphisms are given by spans and 2-morphisms are fibrewise bijections.
Let \(X_1, X_2\) and \(X_3\) be three sets in \(\mathcal {B}\). Given a span \((Q_1,s_1,t_1)\) in \(\mathcal {B}(X_1,X_2)\) and a span \((Q_2,s_2,t_2)\) in \(\mathcal {B}(X_2,X_3)\), their composition is given by their fibre product \((Q_1 \times _{X_2} Q_2, s,t)\):

The composition of two fibrewise bijections \(\tau _1:Q_1 \rightarrow Q_1'\) and \(\tau _2 :Q_2 \rightarrow Q_2'\) is also given by their fibre product \(\tau _1 \times \tau _2 :Q_1 \times _{X_2} Q_2 \rightarrow Q'_1 \times _{X_2} Q'_2\) as follows

and the identity on a set X is the span \(X\overset{\mathrm {Id}}{\leftarrow } X\overset{\mathrm {Id}}{\rightarrow } X\).
Remark 2.2
Note that a span \(\mathfrak {s}= (Q,s,t)\) from X to Y is determined by the matrix whose entries are the sets \(\mathfrak {s}_{x,y} := s^{-1}(x)\cap t^{-1}(y)\), for every \(x\in X\), \(y \in Y\). Giving a fibrewise bijection \(\tau \) from a span \(\mathfrak {s}\) to a span \(\mathfrak {s}'\) is the same as giving, for each \(x\in X\) and each \(y\in Y\), a bijection \(\tau _{x,y}\) from \(\mathfrak {s}_{x,y}\) to \(\mathfrak {s}'_{x,y}\). The composition of \(\mathfrak {s}:X\rightarrow Y\) and \(\mathfrak {s}':Y\rightarrow Z\) is the span \(\mathfrak {s}''\) with \(\mathfrak {s}''_{x,z} = \bigcup _{y\in Y}\mathfrak {s}_{x,y}\times \mathfrak {s}'_{y,z}\). The span \(\mathfrak {s}\) is determined by the formal sum
for each \(x \in X\). If a coefficient \(\mathfrak {s}_{x,y}\) is not specified, we understand that \(\mathfrak {s}_{x,y} = \{x\}\) (for example, if \(\mathfrak {s}(x) = y+z\), then \(\mathfrak {s}(x) = \{x\} \cdot y + \{x\} \cdot z\)).
The category of finite sets \(\mathbf {Set}\) can be mapped into the category of pointed finite sets \(\mathbf {Set}_\bullet \) by sending X to \(X_+:=X\cup \{\mathbf {*}\}\), and a morphism \(f:X\rightarrow Y\) to the morphism \(f_+\) that coincides with f on X and sends the basepoint of \(X_+\) to the basepoint of \(Y_+\). Moreover, the category \(\mathbf {Set}_\bullet \) sits inside \(\mathcal {B}\) by sending a pointed finite set X to \(X\smallsetminus \{\mathbf {*}\}\), and a morphism \(f:X\rightarrow Y\) to the span
The inclusions \(\mathbf {Set}\, \hookrightarrow \, \mathbf {Set}_\bullet \, \hookrightarrow \, \mathcal {B}\) induce equivalences between the following 2-subcategories of \(\mathcal {B}\):
-
The essential image of \(\mathbf {Set}_\bullet \) in \(\mathcal {B}\) is the 2-subcategory of free spans.
-
The essential image of \(\mathbf {Set}\) in \(\mathcal {B}\) is the 2-subcategory of very free spans.
Fix now a commutative ring R with unit, and let \(\text {R-Mod}\) be the category of modules over R. There is a functor
sending the finite set X to the free R-module \(R\langle X\rangle \), and a span \(\mathfrak {s}:X\rightarrow Y\) to the homomorphism \(f:R\langle X\rangle \rightarrow R\langle Y\rangle \) given, for every \(x\in X\), by
Note that every pair of spans connected by a 2-morphism are sent to the same homomorphism, and therefore the functor \(\mathcal {A}\) is well-defined.
3 Cubes of pointed sets and augmented semi-simplicial pointed sets
The n-dimensional cube \(\mathbf {2^{n}}\) is the partially ordered set (poset) whose elements are n-tuples \(u=(u_1,\ldots , u_n) \in \{0,1\}^n\) endowed with the standard partial order so that \(u\geqslant v\) if \(u_i \geqslant v_i\) for all i. Following [6], we regard \(\mathbf {2^{n}}\) as the category whose objects are the elements of this poset and, for any two such elements u, v, the morphism set \({\text {Hom}}(u,v)\) has a single element \(\varphi _{u,v}\) if \(u\geqslant v\), and is empty otherwise. This category has an initial element \(\mathbf {1}=(1,1,\ldots ,1)\) and a terminal element \(\mathbf {0}= (0,0,\ldots ,0)\).
The poset map \(|\cdot |:\mathbf {2^{n}}\rightarrow \mathbb {N}\) given by \(|u|=\sum _{i} u_i\) assigns a grading to each vertex in the cube. We write \(u\succ v\) if \(u>v\) and \(|u-v|=1\), and we write \(u\succ _i v\) if, additionally, u and v differ in the ith-coordinate, i.e., if \(u_i=1\), \(v_i=0\) and \(u_j = v_j\) for \(i\ne j\).
Given \(n \in {\mathbb {Z}}\), \(n\geqslant -1\), the finite ordinal [n] is the linearly ordered set \(\{0<1<\ldots <n\}\). The augmented semi-simplicial category, \(\Delta _{\mathrm {inj*}}\), has as objects these finite ordinals, and as morphisms injective order-preserving maps between them. The inclusion \(\partial _i :[n-1]\hookrightarrow [n]\) that forgets the i-th element is called ith-face map.
Definition 3.1
Given a category \(\mathcal {C}\), let \(\mathcal {C}^\mathrm {op}\) denote its opposite category, obtained by reversing the morphisms. An n-dimensional cube of pointed (finite) sets is a functor \(F:\mathbf {2^{n}} \rightarrow \mathbf {Set}_\bullet \), while an augmented semi-simplicial pointed (finite) set is a functor \(X:\Delta _{\mathrm {inj*}}^\mathrm {op}\rightarrow \mathbf {Set}_\bullet \). As usual, we write \(X_n\) and \(\partial _i\) for X([n]) and \(X(\partial _i)\), respectively.
These two categories are related by a functor \(\lambda :\mathbf {2^{n}}\rightarrow \Delta _{\mathrm {inj*}}^\mathrm {op}\) which maps every vertex of the cube u to the ordinal \([|u|-1]\), and every morphism \(u\succ _i v\) to the opposite of the \(\left( \sum _{j<i} u_i\right) \)th-face map.
Taking left Kan extension along the functor \(\lambda :\mathbf {2^{n}}\rightarrow \Delta _{\mathrm {inj*}}^\mathrm {op}\) defines a functor
whose value on a cube of pointed sets F is defined explicitely as follows: its set of k-simplices is \(\Lambda (F)_k = \coprod _{|u|=k+1} F(u)\), for every \(u\in \mathbf {2^{n}}\), and the ith-face map \(\partial _i:\Lambda (F)_k\rightarrow \Lambda (F)_{k-1}\) is the union \(\coprod _{|u|=k+1} F(u>u[i])\), where u[i] is the vertex of the cube \(\mathbf {2^{n}}\) obtained by replacing the \((i+1)\)th one in u by a zero.
Recall from [5, Definition 4.1] that a strictly unitary lax 2-functor F from the cube \(\mathbf {2^{n}}\) to the Burnside category \(\mathcal {B}\) consists of the data:
-
(1)
a finite set \(F(v) \in {\text {Ob}}(\mathcal {B})\), for each \(v \in \{0,1\}^n\).
-
(2)
a finite span \(F(\varphi _{u,v}): F(u) \rightarrow F(v)\) in \(\mathcal {B}\), for each morphism \(\varphi _{u,v}\) in \(\mathbf {2^{n}}\).
-
(3)
a 2-isomorphism \(F_{u, v, w}\) from \(F(\varphi _{v,w})\circ F(\varphi _{u,v})\) to \(F(\varphi _{u,w})\), for each decomposition \(\varphi _{u,w} = \varphi _{v,w} \circ \varphi _{u,v}\);
satisfying that, for every \(u> v> w > z\), the following diagram commutes:

In practice, when defining a strictly unitary lax 2-functor, we use the following result, from [5, Section 4]. We keep the notation  for the morphism \(u \succ v\):
for the morphism \(u \succ v\):
Lemma 3.2
A strictly unitary lax 2-functor from the cube category \(\mathbf {2^{n}}\) to the Burnside category \(\mathcal {B}\) is uniquely determined (up to natural isomorphism) by the following data:
-
(D1)
for each vertex \(v \in \{0,1\}^n\), a finite set \(F(v) \in {\text {Ob}}(\mathcal {B})\);
-
(D2)
for each \(u\succ v\), a finite span \(F(\varphi _{u,v}): F(u) \rightarrow F(v)\) in \(\mathcal {B}\);
-
(D3)
for each two-dimensional face
 of the cube, a 2-morphism $$\begin{aligned} F_{u,v,v',w}:F(\varphi _{v,w})\times _{F(v)} F(\varphi _{u,v})\rightarrow F(\varphi _{v',w})\times _{F(v')} F(\varphi _{u,v'}), \end{aligned}$$
of the cube, a 2-morphism $$\begin{aligned} F_{u,v,v',w}:F(\varphi _{v,w})\times _{F(v)} F(\varphi _{u,v})\rightarrow F(\varphi _{v',w})\times _{F(v')} F(\varphi _{u,v'}), \end{aligned}$$
satisfying the following two conditions:
-
(C1)
for every two-dimensional face
 , \(F_{u,v',v,w}=F_{u,v,v',w}^{-1},\)
, \(F_{u,v',v,w}=F_{u,v,v',w}^{-1},\) -
(C2)
for every three-dimensional face
 , the following commutes:
, the following commutes: 
Definition 3.3
[5] A natural transformation \(\alpha :F\rightarrow G\) between two strictly unitary lax 2-functors \(F,G:\mathbf {2^{n}} \rightarrow \mathcal {B}\) is a strictly unitary lax 2-functor \(H:\mathbf {2^{n+1}}\rightarrow \mathcal {B}\) such that \(H|_{\mathbf {2^{n}}\times \{1\}} = F\) and \(H|_{\mathbf {2^{n}}\times \{0\}} = G\). For every \(u\in \mathbf {2^{n}}\), we denote by \(\alpha _u\) the morphism \(H(\varphi _{(u,1),(u,0)})\). For every \(u \succ v \in \mathbf {2^{n}}\), we denote \(\alpha _{u,v}\) the 2-morphism \(H_{(u,1),(u,0),(v,1), (v,0)}\).
We write \(\mathcal {C}^{\mathcal {D}}\) for the category whose objects are strictly unitary lax 2-functors from \(\mathcal {D}\) to \(\mathcal {C}\) and whose morphisms are natural transformations between them. When \(\mathcal {C}= \mathcal {B}\) and \(\mathcal {D}= \mathbf {2^{n}}\) the objects are called Burnside cubes.
3.1 Realizations and totalizations
Let \(\mathcal {C}\) be a model category, as the category of (pointed) topological spaces \(\mathbf {Top}\) (resp. \(\mathbf {Top}_\bullet \)), the category of spectra \(\mathbf {Sp}\), or the category \(\mathrm {Ch}(R)\) of chain complexes of R-modules, with R a commutative ring.
The totalization of a functor \(F:\mathbf {2^{n}}\rightarrow \mathcal {C}\) is the object of \(\mathcal {C}\) given by
This defines a functor
On the other hand, the relative realization of a functor \(X:\Delta _{\mathrm {inj*}}^\mathrm {op}\rightarrow \mathcal {C}\) is the object in \(\mathcal {C}\) given by
which defines a functor
A semi-simplicial object \(X:\Delta _{\mathrm {inj}}^\mathrm {op}\rightarrow \mathcal {C}\) may be seen as an augmented semi-simplicial set by defining \(X_{-1}=*\), the final object of \(\mathcal {C}\). Its relative realization is the suspension of the realization of X:
Recall now the functor \(\lambda :\mathbf {2^{n}}\rightarrow \Delta _{\mathrm {inj*}}^\mathrm {op}\) mapping every \(u\in \mathbf {2^{n}}\) to \([|u|-1]\), and every morphism \(u\succ _i v\) to the opposite of \(\left( \sum _{j<i} u_i\right) th\)-face map. Since \(\lambda \) is cofinal, \(\lambda (\mathbf {2^{n}}\smallsetminus \{0\}) = \Delta _{\mathrm {inj*}}\smallsetminus \{[-1]\}\) and \(\lambda (\mathbf {0}) = [-1]\), we have that
3.2 From Burnside cubes to chain complexes
Let R be a ring, and let \(\mathrm {Ch}(R)\) be the category of chain complexes of R-modules. There is a functor
where the first functor is \(\mathcal {A}\), defined in (2.1), and the second functor sends an R-module to the chain complex given by the R-module concentrated at degree 0.
We define the functor \(C_*(-;R)\) as the composition
where the first functor is the result of composing a 2-functor \(F:\mathbf {2^{n}} \rightarrow \mathcal {B}\) from \(\mathcal {B}^\mathbf {2^{n}}\) with K.
Its value at the Burnside cube F can also be described as the chain complex whose k-cochains are
and whose differential is
Observe that since \(\mathcal {B}\rightarrow \text {R-Mod}\) sends 2-morphisms to identities, a natural transformation between Burnside cubes induces a morphism of chain complexes.
3.3 From Burnside cubes to spectra
In [6], Lawson, Lipshitz and Sarkar gave an explicit construction of the totalization functor for cubes in the Burnside category. They associated, to each cube \(F:\mathbf {2^{n}}\rightarrow \mathcal {B}\), a spectrum \({\text {Tot}}F\), and to each map \(f :F\rightarrow G\) of Burnside cubes, a map \({\text {Tot}}f :{\text {Tot}}F\rightarrow {\text {Tot}}G\), both well-defined up to homotopy. Additionally, the homology \(H_*({\text {Tot}}F;R)\) was isomorphic to the homology of \(C_*(F;R)\), and the map induced by \({\text {Tot}}f\) on homology was the one induced by \(C_*(f;R)\).
Remark 3.4
If \(C_*(f;R)\) is a homology isomorphism then \({\text {Tot}}f\) is a homotopy equivalence of spectra.
On the other hand, in [1] the authors showed that if a cube \(F:\mathbf {2^{n}}\rightarrow \mathcal {B}\) factors through some functor \(\tilde{F}:\mathbf {2^{n}}\rightarrow \mathbf {Set}_\bullet \), then \({\text {Tot}}F = \Sigma ^\infty {\text {Tot}}\tilde{F}\), where the homotopy colimit is taken in pointed topological spaces. Therefore, by (3.2), we have:
Proposition 3.5
If a Burnside cube \(F:\mathbf {2^{n}}\rightarrow \mathcal {B}\) in the Burnside category factors through \(\mathbf {Set}_\bullet \), then the pointed semi-simplicial set \(\Lambda (\tilde{F})\) satisfies
Remark 3.6
The spectrum \({\text {Tot}}F\) is denoted |F| in [6]. The chain complex \(C_*(F;R)\) is denoted \({\text {Tot}}F\) in [5]. We reserve the notation \({\text {Tot}}\) for the totalization of a cube, \(\Vert \cdot \Vert \) for the relative realization of an augmented semi-simplicial object and \(| \cdot |\) for the realization of a semi-simplicial object.
4 Knots and graphs
4.1 States
Let D be an oriented link diagram with n ordered crossings \(\{c_1< c_2< \ldots <c_n\}\), where \(n_+\) (\(n_-\)) of them are positive (negative). A (Kauffman) state of the diagram D is an assignation of a label, 0 or 1, to each crossing in D. The order of the crossings induces a bijection between the set of states of D and the elements of \(\mathbf {2^{n}}\) by considering \(u \in \mathbf {2^{n}}\) as the state that assigns the label \(u_i\) to \(c_i\).
Smoothing a crossing \(c_i\) of D consists on replacing it by a pair of arcs and a segment connecting them; the way we smooth the crossings depends on its associated label \(u_i\), as shown in Fig. 1. The result of smoothing each crossing of D according to its label is the chord diagram D(u), a collection of disjoint circles together with some segments that we call 0- and 1-chords, depending on the value of the associated \(u_i\). We represent 1-chords as light segments, and 0-chords as dark ones.
We introduce the following notation to refer to the circles and chords of D(u):
-
Z(u) denotes the set of circles of D(u),
-
E(u) denotes the set of 0-chords of D(u),
-
\(\bar{E}(u)\) denotes the set of 1-chords of D(u),
-
\(e_i(u)\) denotes the ith chord in D(u),
-
\(\mathcal {O}_i(u)\) denotes the set of circles containing an endpoint of \(e_i(u)\) (thus \(|\mathcal {O}_i(u)|\) is either equal to 1 or 2). If \(|\mathcal {O}_i(u)|=2\) (resp. \(|\mathcal {O}_i(u)|=1\)), we say that \(e_i(u)\) is a bichord (resp. monochord).
Given a state u of D, we define its associated state graph, \(\mathcal {G}(u)\), as the labelled graph obtained by collapsing each circle of D(u) to a vertex so that each chord in D(u) becomes an edge in \(\mathcal {G}(u)\); each edge inherits a label, 0 or 1, from the associated chord. The circles and chords of D(u) are in bijection with the vertices and edges of \(\mathcal {G}(u)\). Therefore, the above notation introduced to refer to the circles and chords of D(u) will be used to refer to the vertices and edges of \(\mathcal {G}(u)\). In particular, the set of vertices of \(\mathcal {G}(u)\) is Z(u) and the set of edges labeled by 0 and 1 are E(u) and \(\bar{E}(u)\), respectively.
In this setting, write G(u) for the subgraph obtained after removing the 1-edges from \(\mathcal {G}(u)\). See Fig. 2 for such an example. We consider loops as length-1 cycles.
Recall that given \(u,v \in \mathbf {2^{n}}\), we write \(u \succ _i v\) if both vectors are equal in all but the \(i^{th}\) coordinate, where \(u_i = 1\) and \(v_i=0\). The partial order > is defined as the transitive closure of the above relation.
If \(u\succ _i v\), then D(v) is obtained from D(u) by doing surgery on D(u) along the 1-chord \(e_i(u)\) and adding a new chord \(e_i(v)\). Observe that, depending on the cardinality of \(\mathcal {O}_i(u)\), there are two possible surgeries:
-
If \(|\mathcal {O}_i(u)| = 2\), then \(|\mathcal {O}_i(v)| = 1\) and D(v) is obtained from D(u) by joining two circles into one. The graph G(v) is obtained from G(u) by identifying the two vertices in \(\mathcal {O}_i(u)\) and adding a loop (the edge \(e_i(v)\)) based on the identified vertex, as shown in Fig. 3a. We say that \(u\succ _i v\) a merging.
-
If \(|\mathcal {O}_i(u)| = 1\), then \(|\mathcal {O}_i(v)| = 2\) and D(v) is obtained from D(u) by splitting one circle into two. In this case, G(u) is obtained from G(v) by collapsing the edge \(e_i(v)\), as shown in Fig. 3b. We say that \(u\succ _i v\) is a splitting.
Remark 4.1
Given two states u and v of D so that \(u>v\), with \(|u|-|v|=k\), there exist k! possible chains
connecting them. However, the total composition of the one-by-one surgeries induced by each of the possible chains does not depend on the chosen chain.
Given a surgery \(u \succ _i v\), we compare G(u) and G(v):
Definition 4.2
Given a state \(u \in \mathbf {2^{n}}\) with \(|u| = n-k\) and a chain
connecting u to the state \(\mathbf {1}\), we define \(\Phi (u)\) as the number of loops in \(\{e_{i_{j}}(u_{j})\}_{j=1}^{k}\). In other words, \(\Phi (u)\) counts the number of mergings in the chain.
Equalities above allow us to describe G(u) in terms of \(G(\mathbf {1})\) and \(\Phi (u)\):
In particular, the above relations imply that \(\Phi (u)\) does not depend on the chosen chain connecting the states \(\mathbf {1}\) and u.
Lemma 4.3
Let \(u \in \mathbf {2^{n}}\) be a state of a link diagram D.
-
(1)
If \(\Phi (u)=0\), then G(u) is a forest, namely, it consists of a collection of \(|Z(\mathbf {1})|\) contractible components.
-
(2)
If \(\Phi (u)=1\), then the number of connected components of G(u), \(|\pi _0 G(u)|\), is either \(|Z(\mathbf {1})|\) or \(|Z(\mathbf {1})|-1\). In addition:
-
(a)
If \(|\pi _0 G(u)| = |Z(\mathbf {1})|-1\), then there is one single cycle in G(u),
-
(b)
If \(|\pi _0G(u)| = |Z(\mathbf {1})|\), then G(u) contains exactly two cycles \(\mathfrak {c}_1\) and \(\mathfrak {c}_2\) sharing a common vertex z. Moreover, in D(u) the chords corresponding to the edges of \(\mathfrak {c}_1\) adjacent to the vertex z alternate with those of \(\mathfrak {c}_2\) along the circle z. Therefore the chords corresponding to the edges of \(\mathfrak {c}_1\) and the chords corresponding to the edges of \(\mathfrak {c}_2\) lie in different regions of \(\mathbb {R}^2\smallsetminus z\).
-
(a)
Proof
The assertions concerning the homotopy type of G(u) follow from (4.2) and (4.3) after computing the Euler characteristic of G(u) as
If \(\Phi (u)=0\), then \(|\pi _0 G(u)| = |\pi _0 G(\mathbf {1})| = |Z(\mathbf {1})|\) by (4.4), and therefore G(u) contains no cycles. In the case (2a), \(|\pi _0 G(u)| = |Z(\mathbf {1})|-1\), and therefore G(u) has a single cycle, whereas in case (2b), \(|\pi _0 G(u)| = |Z(\mathbf {1})|\), and therefore there are two cycles in G(u).
We prove now that when \(\Phi (u) = 1\) and \(|\pi _0 G(u)| = |\pi _0 G(\mathbf {1})|\), the chords of \(\mathfrak {c}_1\) adjacent to the circle z alternate with those of \(\mathfrak {c}_2\) along the boundary of z.
Consider a chain as (4.1), and let \(u_{r-1}\succ _{i_r} u_{r}\) be the states right before and right after the merging is performed, respectively. Write \(\mathcal {O}_{i_r}(u_{r-1}) = \{z_1, z_2\}\) and define \(\varepsilon \) as the (possibly empty) set containing those edges \(e_{i_j}\) in the chain so that \(\mathcal {O}_{i_j}(u_{r-1}) = \{z_1,z_2\}\), for \(r < j \leqslant k\).
Since \(\Phi (u_{r-1})=0\), we have just shown that \(G(u_{r-1})\) consists on \(|Z(\mathbf {1})|\) disjoint trees. When passing from \(u_{r-1}\) to \(u_{r}\), vertices \(z_1\) and \(z_2\) are identified and the 1-edge \(e_{i_r}\) becomes a 0-loop (i.e., a length-one cycle) in \(G(u_{r})\). Figure 4a, b illustrates this process.
The case (2a) corresponds to the case when \(z_1\) and \(z_2\) belong to different connected components of \(G(u_{r-1})\). Since no more mergings are possible, no more cycles are created. Moreover, the length of the (unique) cycle \(\mathfrak {c}_1\) in G(u) is \(|\varepsilon |+1\) (see Fig. 4c).
The case (2b) corresponds to the case when \(z_1\) and \(z_2\) belong to the same connected component: the fact that there is a path connecting \(z_1\) and \(z_2\) in \(G(u_{r-1})\) implies that an additional cycle \(\mathfrak {c}_2\) is created when identifying both vertices. As illustrated in Fig. 4b, c, the condition on the alternacy of the chords holds. The planarity of D(u) completes the proof. \(\square \)
Diagrams \(D(u_{r-1})\), \(D(u_{r})\), D(u) and the associated graphs illustrating the proof of Lemma 4.3 are shown. Recall that dark (resp. light) chords corresponds to 0-chords (resp. 1-chords). In this case \(\varepsilon =\{e_\alpha , e_\gamma \}\)
4.2 Enhanced states
An enhacement of a state \(u \in \mathbf {2^{n}}\) is a map x assigning a label \(+1\) or \(-1\) to each of the circles in Z(u); we note by (u, x) the associated enhanced state. Write \(Z_+(u,x)\) and \(Z_-(u,x)\) for the subsets of elements of Z(u) labeled by \(+1\) and \(-1\), respectively. Define, for the enhanced state (u, x), the integers
which are the homological and quantum gradings for Khovanov homology, respectively [7].
Let \(x_+\) be the constant enhacement with value \(+1\) and, for a given circle \(z \in Z(u)\), let \(x_z^+\) be the enhacement assigning a positive label to every circle but z. Sometimes we will write \(u_+=(u,x_+)\).
Define
and \({j_{\mathrm {almax}}}(D) = j_{\max }(D)-2\); we refer to these numbers as extreme and almost-extreme (quantum) gradings for Khovanov homology of the diagram D. It turns out that
Proposition 4.4
Let (u, x) be an enhanced state of a diagram D with \(q(u,x) = j\). Then,
Proof
From the definition of quantum grading, it holds that
Relation (4.2) completes the proof. \(\square \)
Corollary 4.5
Let (u, x) be an enhanced state of D satisfying \(q(u,x) = {j_{\mathrm {almax}}}(D)\). Then \(\Phi (u)\leqslant 1\). Moreover,
-
(1)
if \(\Phi (u)=0\), then \(x = x_z^+\) for some \(z \in Z(u)\).
-
(2)
if \(\Phi (u)=1\), then \(x = x_+\).
Since we are interested in studying the almost-extreme Khovanov complex of a link diagram, in the next section we study the characterization of those states u so that \(\Phi (u)\) equals 0 or 1.
4.3 States with \(\Phi (u)=0,1\)
We are interested now in characterizing those states taking part in the almost-extreme Khovanov complex, i.e., given a state \(u \in \mathbf {2^{n}}\) of D, we want to determine whether there exists an enhacement x so that \(q(u,x)={j_{\mathrm {almax}}}(D)\), just by looking at \(D(\mathbf {1})\).
Definition 4.6
Given \(u\in \mathbf {2^{n}}\) a state of D and a, b, c, d chords in D(u), we say that:
-
(1)
a and b are parallel if they are bichords with their endpoints in the same circles, i.e., \(\mathcal {O}_a(u) = \mathcal {O}_b(u)=\{z,z'\}\).
-
(2)
a, b form an alternating pair if they are monochords and their endpoints alternate along the same circle, as illustrated in Fig. 5a (compare to ladybug configuration from [7]).
-
(3)
a, b, c form an alternating triple if \(\mathcal {O}_a(u) = \mathcal {O}_b(u)=\{z,z'\}\) and their endpoints alternate with the endpoints of the monochord c along z. See Fig. 5b.
-
(4)
a, b, c, d form a mixed alternating pair if the only alternating pairs among them are (a, b), (b, c) and (c, d). See Fig. 5c.
Given \(v>u\) states of D, we write \(D(v)_u\) for the chord diagram having the same circles as D(v), but only the 1-chords \(e_i(v)\) such that \(v_i \ne u_i\).
Remark 4.7
If \(w>v>u\) are states of D, then \(e_i(v) \in D(v)_u\) implies that \(e_i(w) \in D(w)_u\).
Proposition 4.8
Let u be a state of D. Then, \(\Phi (u)>0\) if and only if \(D(\mathbf {1})_u\) contains a bichord or an alternating pair, and \(\Phi (u)>1\) if and only if \(D(\mathbf {1})_u\) contains at least one of the following configurations:
-
(1)
Two non-parallel bichords.
-
(2)
An alternating pair and a bichord.
-
(3)
An alternating triple.
-
(4)
Two disjoint alternating pairs.
-
(5)
A mixed alternating pair.
The proof of the necessary condition (i.e., the implication \(\Leftarrow \)) is a case-by-case straightforward checking. We use Lemmas 4.9 and 4.10 in the proof of the sufficient condition.
Lemma 4.9
Let \(w \succ v > u\) be three states with \(\Phi (w)=\Phi (v)\). Then:
-
(1)
If \(D(v)_u\) contains a bichord, then \(D(w)_u\) contains a bichord or an alternating pair.
-
(2)
If \(D(v)_u\) contains an alternating pair, then \(D(w)_u\) contains an alternating pair.
-
(3)
If \(D(v)_u\) contains an alternating triple, then \(D(w)_u\) contains an alternating triple or a mixed alternating pair.
-
(4)
If \(D(v)_u\) contains a mixed alternating pair, then \(D(w)_u\) contains a mixed alternating pair.
-
(5)
If \(D(v)_u\) contains an alternating pair and a bichord, then \(D(w)_u\) contains an alternating pair and a bichord, or a mixed alternating pair or two disjoint alternating pairs.
Proof
Since \(\Phi (w)=\Phi (v)\), \(w \succ _i v\) is a splitting for some monochord \(e_i(w)\). The lemma follows from Remark 4.7 together with the following facts (\(i \ne j \ne k \ne l\)):
-
If \(e_j(v)\) is a bichord, then either \(e_j(w)\) is a bichord or \((e_j(w),e_i(w))\) form an alternating pair.
-
If \((e_j(v), e_k(v))\) is an alternating pair, then \((e_j(w), e_k(w))\) is an alternating pair.
-
If \((e_j(v),e_k(v),e_l(v))\) is an alternating triple, then either \((e_j(w),e_k(w),e_l(w))\) is an alternating triple, or \((e_i(w),e_j(w),e_k(w),e_l(w))\) is a mixed alternating pair.
-
If \((e_j(v),e_k(v),e_l(v),e_m(v))\) is a mixed alternating pair, then \((e_j(w),e_k(w),\) \(e_l(w),e_m(w))\) is a mixed alternating pair.
-
If \((e_j(v),e_k(v))\) is an alternating pair and \(e_l(v)\) is a bichord, then either \((e_j(w),e_k(w))\) is an alternating pair and \(e_l(w)\) is a bichord or \((e_i(w),e_j(w),\) \(e_k(w),e_l(w))\) is a mixed alternating pair, or \((e_i(w),e_l(w))\) and \((e_j(w),e_k(w))\) are disjoint alternating pairs.
\(\square \)
Lemma 4.10
Let \(w \succ v > u\) be three states with \(\Phi (w)=\Phi (v)-1\). Then:
-
(1)
If \(D(v)_u\) contains a bichord, then \(D(w)_u\) contains two non-parallel bichords.
-
(2)
If \(D(v)_u\) contains an alternating pair, then \(D(w)_u\) contains an alternating triple or an alternating pair and a bichord.
Proof
Since \(\Phi (w)=\Phi (v)-1\), \(w \succ _i v\) is a merging for some bichord \(e_i(w)\). The lemma follows from Remark 4.7 together with the following facts (\(i \ne j \ne k \ne l\)):
-
If \(e_j(v)\) is a bichord, then \(e_j(w)\) and \(e_i(w)\) are non-parallel bichords.
-
If \((e_j(v),e_k(v))\) is an alternating pair, then either \((e_j(w),e_k(w))\) is an alternating pair and \(e_i(w)\) is a bichord, or \((e_i(w),e_j(w),e_k(w))\) is an alternating triple.
\(\square \)
Proof of the sufficient condition of Proposition 4.8
Fix a chain
Consider first the case \(\Phi (u)>0\) and write m for be the minimal number such that \(u_{m-1}\succ _{i_m}u_m\) is a merging. Therefore, \(e_{i_{m}}(u_{m-1}) \in D(u_{m-1})_u\) is a bichord and applying Lemma 4.9 recursively, we deduce that \(D(\mathbf {1})_u\) contains a bichord or an alternating pair.
Consider now the case \(\Phi (u)>1\) and write \(m<p\) for the first two indices such that \(u_{m-1}\succ _{i_m}u_m\) and \(u_{p-1}\succ _{i_p}u_p\) are mergings. Therefore, \(\Phi (u_m) = \Phi (u_{p-1})\), and applying recursively Lemma 4.9 to the bichord \(e_{i_{p}}(u_{p-1}) \in D(u_{p-1})_u\) we deduce that \(D(u_m)_u\) contains a bichord or an alternating pair. Apply once Lemma 4.10 and deduce that \(D(u_{m-1})_u\) contains at least one of the following: two non-parallel bichords or an alternating triple or an alternating pair and a bichord.
Finally, applying in each case recursively Lemma 4.9 we deduce that \(D(\mathbf {1})_u\) contains at least one of the following configurations:
-
(1)
Two non-parallel bichords.
-
(2)
An alternating pair and a bichord.
-
(3)
An alternating triple.
-
(4)
Two disjoint alternating pairs.
-
(5)
A mixed alternating pair.
\(\square \)
4.4 Ladybug set
Let \(u \in \mathbf {2^{n}}\) so that \(\Phi (u)=1\). If \(|\pi _0 G(u)| = |\pi _0 G(\mathbf {1})|-1\), recall from Lemma 4.3(2a) that G(u) contains a unique cycle. We define the ladybug set of u, \(\mathcal {L}(u)\), as the singleton consisting of the connected component of G(u) containing that cycle.
Consider now the case when \(|\pi _0 G(u)| = |\pi _0 G(\mathbf {1})|\). Then, by Lemma 4.3(2b), G(u) contains two cycles \(\mathfrak {c}_1\) and \(\mathfrak {c}_2\) sharing a common vertex z. Write \(a_i,b_i\) for the edges of \(\mathfrak {c}_i\) adjacent to z, for \(i = 1,2\) (if \(\mathfrak {c}_i\) is a loop, then \(a_i=b_i\)).
The chords \(a_1,b_1,a_2,b_2\) divide the circle z into four arcs (see Fig. 6). We define the ladybug set \(\mathcal {L}(u)\) of D(u) as the set whose elements are the two arcs of z that are reached by traveling along any of the chords \(a_1,b_1,a_2,b_2\) until z, and then taking a right turn.
An example of D(u) for the case when \(\Phi (u)=1\) and \(|\pi _0 G(u)| = |\pi _0 G(\mathbf {1})|\). The cycles \(\mathfrak {c}_1\) and \(\mathfrak {c}_2\) (of length 4 and 5, respectively) divide z into four arcs. The ladybug set corresponds to the thickened arcs, i.e. \(\mathcal {L}(u) = \{P, Q\}\)
Remark 4.11
In the case when \(|\pi _0 G(u)| = |\pi _0 G(\mathbf {1})|\) and \(a_i=b_i\) for \(i=1,2\), the set \(\mathcal {L}(u)\) coincides with the right pair giving rise to the celebrated ladybug matching defined in [7].
Lemma 4.12
If \(u>v\), \(|\pi _0 G(v)|=|\pi _0 G(\mathbf {1})|\) and \(\Phi (u)=\Phi (v)=1\), then each arc in \(\mathcal {L}(u)\) intersects exactly one of the two arcs in \(\mathcal {L}(v)\) and viceversa.
Proof
Let \(\Lambda =\{e_i(u) \, | \, u_i \ne v_i\} \subset \bar{E}(u)\). Since \(\Phi (u) = \Phi (v)\), all elements in \(\Lambda \) are loops and no pair among them constitute an alternating pair.
By Lemma 4.3(2b), G(u) contains two cycles \(\mathfrak {c}_1\) and \(\mathfrak {c}_2\) sharing a common vertex \(z_u\). Write \(z_v\) for the circle in D(v) with the same property. Then \(z_v\) is obtained from \(z_u\) by performing surgery along the loops in \(\Lambda \) with their endpoints in \(z_u\).
Write \(\mathcal {L}(u) = \{P,Q\}\) and let \(\Lambda _P\) (resp. \(\Lambda _Q\)) be the subset of loops of \(\Lambda \) so that at least one of their endpoints lies in P (resp. Q). The disposition of \(\mathfrak {c}_1\) and \(\mathfrak {c}_2\) (stated in Lemma 4.3(2b)) implies that \(\Lambda _P \cap \Lambda _Q = \emptyset \). Define the following subsets of \(\mathbb {R}^2\):
The endpoints of each loop \(e_i(u) \in \Lambda _P\) (resp. \(e_i(u) \in \Lambda _Q\)) separate \(z_u\) into two arcs: write \(d_i\) for the unique arc in \(z_u\) which is disjoint from Q (resp. from P). Define the following subsets of \(\mathbb {R}^2\):
As there are no alternating pairs in \(\Lambda \), we deduce that
As a consequence, we can consider two disjoint open subsets A, B of \(\mathbb {R}^2\) such that
Each of the arcs of \(\mathcal {L}(v)\) is obtained by doing surgery on each of the arcs of \(\mathcal {L}(u)\). The surgery performed on P is supported in A, while the surgery perfomed on Q is supported in B. Since \(A \cap B = \emptyset \), it is possible to define \(P'\) (resp. \(Q'\)) as the arc of \(\mathcal {L}(v)\) obtained from P (resp. Q). Thus, P intersects \(P'\), Q intersects \(Q'\) and \(P\cap Q' = Q \cap P' = \emptyset \), as desired. \(\square \)
4.5 The bijection \(\rho _{u,v}\)
Given \(u \succ _i v\) so that \(\Phi (u) = \Phi (v) = 1\), then \(|\pi _0 G(u)|=|\pi _0 G(v)|\), and therefore it is possible to define a bijection \(\rho _{u,v}: \mathcal {L}(u) \rightarrow \mathcal {L}(v)\) in the following way:
-
(1)
If \(|\pi _0 G(v)| = |\pi _0 G(\mathbf {1})| -1\), then \(\rho _{u,v}\) maps the unique element in \(\mathcal {L}(u)\) to the unique element in \(\mathcal {L}(v)\).
-
(2)
If \(|\pi _0 G(v)| = |\pi _0 G(\mathbf {1})|\), then by Lemma 4.12 each of the two arcs in \(\mathcal {L}(u)\) intersects one of the two arcs in \(\mathcal {L}(v)\). Write \(\mathcal {L}(u) = \{P_u, Q_u\}\) and \(\mathcal {L}(v)= \{P_v, Q_v\}\), labelling the arcs so that \(P_u \cap P_v \ne \emptyset \) and \(Q_u \cap Q_v \ne \emptyset \) as subsets of \(\mathbb {R}^2\) (see Fig. 7). The bijection \(\rho _{u,v}: \mathcal {L}(u) \rightarrow \mathcal {L}(v)\) is given by sending \(P_u\) to \(P_v\) and \(Q_u\) to \(Q_v\). In particular, in those cases when none of the endpoints of the chord \(e_i(u)\) lie in \(P_u\) nor \(Q_u\), \(\rho _{u,v}\) becomes the identity.
Two examples illustrating the bijection \(\rho _{u,v}\) for the case \(u \succ _i v\), \(\Phi (u) = \Phi (v) = 1\) and \(|\pi _0 G(v)| = |\pi _0 G(\mathbf {1})|\), with the edge \(e_i(u)\) depicted in light colour. In both cases \(\rho _{u,v}: \mathcal {L}(u) \rightarrow \mathcal {L}(v)\) maps \(P_u\) to \(P_v\) and \(Q_u\) to \(Q_v\)
The following lemma follows immediately from Lemma 4.12:
Lemma 4.13
Let \(u \succ v, v' \succ w\) so that \(\Phi (u)=\Phi (w)=1\). Then the following diagram commutes

4.6 The bijection \(\mu _i(u)\)
Given \(u\succ _{i}v\) with \(\Phi (u)=0\), \(\Phi (v)=1\) (i.e., a merging), we define a function
as follows:
-
(1)
If \(|\pi _0 G(v)| = |\pi _0 G(\mathbf {1})|-1\), then \(|\mathcal {L}(v)|=1\) and we define \(\mu _i(u)\) as the unique constant function.
-
(2)
If \(|\pi _0 G(v)| = |\pi _0 G(\mathbf {1})|\), write \(\mathcal {O}_i(u)=\{z_1,z_2\}\), \(\mathcal {L}(v) = \{P,Q\}\), and assume without loss of generality that \(P \cap z_1 \ne \emptyset \) and \(Q \cap z_2\ne \emptyset \) as subsets of \(\mathbb {R}^2\). Then, we define the bijection \(\mu _i(u):\mathcal {O}_i(u) \rightarrow \mathcal {L}(v)\) by declaring \(\mu _i(u) (z_1) = P\), \(\mu _i(u) (z_2) = Q\) (see Fig. 8).
An example illustrating the bijection \(\mu _i(u)\) for the case \(u \succ _i v\), \(\Phi (u) = 0\), \(\Phi (v) = 1\) and \(|\pi _0 G(v)| = |\pi _0 G(\mathbf {1})|\). The edge \(e_i(u)\) is depicted in light colour. The bijection \(\mu _i(u) :{\mathcal {O}}_i(u) \rightarrow \mathcal {L}(v)\) sends \(z_1\) and \(z_2\) to P and Q, respectively
The next result is a consequence of Lemma 4.12.
Lemma 4.14
Let \(u\succ _i v \succ _j w\), \(u \succ _j v' \succ _i w\). Then, the following squares commute:
-
(1)
If \(\Phi (u)=\Phi (v')=0\) and \(\Phi (v)= \Phi (w)=1\), thenFootnote 1

-
(2)
If \(\Phi (u)=0\) and \(\Phi (v)=\Phi (v')=\Phi (w)=1\), then

5 Khovanov functors
In this section we review the functor given by Lipshitz and Sarkar [5, 6] and introduce a new Khovanov functor, giving a natural transformation between them which allows us to prove that the geometric realizations of both functors are homotopy equivalent at the almost-extreme quantum grading (Corollary 5.7). First, we introduce some notation.
Let u be a state of a diagram D so that \(\Phi (u)=0\). Orient G(u) by fixing, for each of its edges, one of its two possible orientations. We define, for each \(e\in E(u)\), the subgraph \(e_+ \subset G(u)\) as the connected component of \(G(u)\smallsetminus \{e\}\) towards which e is pointing. Note that \(e_+\) is well defined, since Lemma 4.3 guarantees that G(u) has no cycles.
Given any two states \(u> v\) of D, there is an inclusion of the associated graphs \(G(u) \subset G(v)\), and we define the maps
observe that the first one is an isomorphism if \(\Phi (u)=\Phi (v)\), while the second one is always injective. Additionally, if \(u\succ _i v\), there exists a Burnside morphism
mapping a circle \(z\in Z(u)\) either to itself if \(z \notin \mathcal {O}_i(u)\), or to \(\mathcal {O}_i(v)\) if \(z \in \mathcal {O}_i(u)\).
5.1 The Khovanov functor in almost-maximal grading
The key piece in the construction of the Khovanov spectra in [6] was the Khovanov functor, whose associated stable homotopy type is a link invariant. Using Lemma 3.2, we restate now this functor, adapted to the particular case of the almost-maximal quantum grading.
Given a link diagram D with n ordered crossings, consider the functorFootnote 2
defined, in a vertex \(u \in \mathbf {2^{n}}\), asFootnote 3:
On a morphism \(\varphi _{u,v}\), with \(u\succ _i v\), the span \(F_{u>v}:=F(\varphi _{u,v}):F(u)\rightarrow F(v)\) is given, for \(z \in Z(u)\) and \(u_+=(u, x_+)\), by
Finally, we specify 2-morphisms: Let \(u\succ _i v\succ _j w\) and \(u\succ _j v'\succ _i w\). We need to produce a 2-morphism \(F_{u,v,v',w}\) between the 1-morphisms \(F_{v>w} \circ F_{u>v}\) and \(F_{v'>w} \circ F_{u>v'}\).
Consider first the case when \(\Phi (u)=0\). If \(\Phi (u)=\Phi (v)=\Phi (v')=0\), \(\Phi (w)=1\), then the chords \(e_i(u)\) and \(e_j(u)\) form an alternating pair attached to some circle \(z_1\), so \(\mathcal {O}_j(v)=\mathcal {O}_i(v)\) and \(\mathcal {O}_i(v')=\mathcal {O}_j(v')\). If \(z \in Z(u)\) and \(z\ne z_1\), then \(F_{v>w}\circ F_{u>v}(z) = \emptyset \).
In the case \(z=z_1\), label the circles involved in the mergings and splittings as
Therefore,
Then, the 2-morphism \(F_{u,v,v',w}\) consists of a bijection between \(\mathcal {O}_j(v)\) and \(\mathcal {O}_i(v')\) given by the ladybug matching \(\mu _i(v')^{-1} \circ \mu _j(v): \mathcal {O}_j(v) \leftrightarrow \mathcal {L}(w) \leftrightarrow \mathcal {O}_i(v')\) (see Sect. 4.6).
If \(\Phi (u)=0\) and we are not in the previous situation, then every summand in the formal sums \((F_{v>w} \circ F_{u>v})(z)\) and \((F_{v'>w}\circ F_{u>v'})(z)\) has a singleton as coefficient, so there is a unique choice for the 2-morphism \(F_{u,v,v',w}\).
In the case when \(\Phi (u)=1\), then \(F_{v,w} \circ F_{u,v}\) and \(F_{v',w} \circ F_{u,v'}\) are empty if \(\Phi (w)>1\); otherwise, both \(F_{v,w} \circ F_{u,v}\) and \(F_{v',w} \circ F_{u,v'}\) map \(u_+\) to the formal sum \(w_+\) which has a singleton as coefficient.
Lemma 5.1
[5] F satisfies conditions (C1) and (C2) in Lemma 3.2.
The (strictly unitary lax) 2-functor F defined above is the Khovanov functor given in [6] at the almost-maximal quantum grading and, if D has \(n_-\) negative crossings, the almost-extreme (maximal) Khovanov spectrum is defined as
5.2 A new equivalent functor
We introduce now a (strictly unitary lax) 2-functor \(M :\mathbf {2^{n}} \rightarrow \mathcal {B}\), with the property that its realization coincides with the realization of F, as will be show in Corollary 5.7. As before, we start by definingFootnote 4M for the vertices of the cube, corresponding to the states of D:
On a morphism \(\varphi _{u,v}\), with \(u\succ _i v\), the span \(M_{u>v}:=M(\varphi _{u,v}):M(u)\rightarrow M(v)\) is defined either on a connected component C or an edge e of G(u) (if \(\Phi (u) = 0\)), or on the enhanced state \(u_+\) (if \(\Phi (u) = 1\)), as follows:
Remark 5.2
Observe that the expression \(\mathcal {L}(v)\cap f_{u,v}(C)\) equals either \(\mathcal {L}(v)\), in the case when \(\mathcal {O}_i(u) \cap C \ne \emptyset \), or the empty set otherwise.
Remark 5.3
Observe that the evaluation of the expression \(e_+ \cap \mathcal {O}_i(u)\) leads to either the empty set or one or two circles, as illustrated in Fig. 9. When \(e_+ \cap \mathcal {O}_i(u) = z \in Z(u)\), there are two possibilities: if \(|\pi _0 G(v)| = |\pi _0 G(\mathbf {1})|\), then \(\mu _i(u) (e_+ \cap \mathcal {O}_i(u))\) maps z to one of the two arcs in \(\mathcal {L}(v)\); however, if \(|\pi _0 G(v)| = |\pi _0 G(\mathbf {1})|-1\), then \(\mu _i(u) (e_+ \cap \mathcal {O}_i(u))\) maps z to the singleton \(\mathcal {L}(v)\).
We illustrate the three cases considered in Remark 5.3. Given D(u) and the orientation shown in G(u), \(e_+ \cap \mathcal {O}_1(u) = \emptyset \), \(e_+ \cap \mathcal {O}_2(u) = \{z_2\}\) and \(e_+ \cap \mathcal {O}_3(u) = \{z_1,z_2\}\)
Finally, given \(u\succ _i v\succ _j w\) and \(u\succ _j v'\succ _i w\), we define the 2-morphism \(M_{u,v,v',w}\) between the 1-morphisms \(M_{v>w} \circ M_{u>v}\) and \(M_{v'>w} \circ M_{u>v'}\) as follows.
Cases (a), (b) and (c) in the definition of \(M_{u,v,v',w}\). In order \(|\mathcal {L}(w)| = 2\), \(|\pi _0 G(w)|\) must be equal to \(|\pi _0 G(\mathbf {1})|\) and therefore the vertices corresponding to the two circles depicted in D(u) in cases (b) and (c) must belong to the same connected component in G(u)
First, note that \(M_{u,v,v',w}\) is trivially defined when \(\Phi (u) = \Phi (v)\) or \(|\mathcal {L}(w)|=1\), since it is a bijection between singletons. Then, we just need to specify the cases when \(\Phi (u)=0\), \(\Phi (w)=1\) and \(|\mathcal {L}(w)|=2\), depicted in Fig. 10. Moreover, the value of \(M_{v>w} \circ M_{u>v}\) and \(M_{v'>w} \circ M_{u>v'}\) on a component \(C \in \pi _0G(u)\) equals the empty set or a singleton, unless \(f_{u,w}(C)\) is the component of G(w) containing two cycles; a similar reasoning applies for edges \(e \in G(u)\), unless e (or possibly \(g_{u,v}(e)\) or \(g_{u,v'}(e)\)) points to the two circles involved in the unique merging. We define \(M_{u,v,v',w}\) in such components and edges:
- (a):
-
If \(\Phi (u)=\Phi (v)=\Phi (v')=0\), \(\Phi (w)=1\) and \(|\mathcal {L}(w)|=2\), then \(e_i(u)\) and \(e_j(u)\) form an alternating pair (see Fig. 10a) and we have
$$\begin{aligned} M_{v>w}\circ M_{u>v}(C) = \mathcal {L}(w) \cdot w_+&\overset{\mathrm {Id}}{\longleftrightarrow } M_{v'>w}\circ M_{u>v'}(C) = \mathcal {L}(w)\cdot w_+, \\ M_{v>w}\circ M_{u>v}(e) = \mathcal {L}(w) \cdot w_+&\overset{\mathrm {Id}}{\longleftrightarrow } M_{v'>w}\circ M_{u>v'}(e) = \mathcal {L}(w) \cdot w_+. \end{aligned}$$ - (b):
-
If \(\Phi (u)=\Phi (v')=0\) and \(\Phi (v)=\Phi (w)=1\) and \(|\mathcal {L}(w)|=2\), then \(e_i(u)\) is a bichord and \(e_j(u)\) a monochord (see Fig. 10b) and we have
$$\begin{aligned} M_{v>w}\circ M_{u>v}(C) = \mathcal {L}(v)\cdot w_+&\overset{\rho _{v,w}}{\longleftrightarrow } M_{v'>w}\circ M_{u>v'}(C) = \mathcal {L}(w)\cdot w_+, \\ M_{v>w}\circ M_{u>v}(e) = \mathcal {L}(v)\cdot w_+&\overset{\rho _{v,w}}{\longleftrightarrow } M_{v'>w}\circ M_{u>v'}(e) = \mathcal {L}(w)\cdot w_+. \end{aligned}$$ - (c):
-
If \(\Phi (u)=0\) and \(\Phi (v)=\Phi (v')=\Phi (w)=1\) and \(|\mathcal {L}(w)|=2\), then \(e_i(w)\) and \(e_j(w)\) are parallel bichords (see Fig. 10c) and we have:
$$\begin{aligned} M_{v>w}\circ M_{u>v}(C) = \mathcal {L}(v)\cdot w_+&\overset{\rho _{v',w}^{-1}\rho _{v,w}}{\longleftrightarrow } M_{v'>w}\circ M_{u>v'}(C) = \mathcal {L}(v')\cdot w_+, \\ M_{v>w}\circ M_{u>v}(e) = \mathcal {L}(v)\cdot w_+&\overset{\rho _{v',w}^{-1}\rho _{v,w}}{\longleftrightarrow } M_{v'>w}\circ M_{u>v'}(e) = \mathcal {L}(v')\cdot w_+. \end{aligned}$$
Lemma 5.4
The 2-functor M satisfies conditions (C1) and (C2) in Lemma 3.2 and therefore is well defined.
Proof
Condition (C1) follows from the definition of M. Consider an arbitrary three-dimensional face and denote its vertices as follows:

In order to prove condition (C2), we need to show that 2-morphisms in this cube commute. To do so, we study the bijections obtained when we move along the cube. More precisely, starting from \(M_{001>000}\circ M_{011>001}\circ M_{111>011}\) we move to \(M_{010>000}\circ M_{011>010}\circ M_{111>011}\) and continue moving along the cube following Fig. 11 until we reach again \(M_{001>000}\circ M_{011>001}\circ M_{111>011}\).
To simplify notation, write \(\rho _i\) for the morphism \(\rho _{u,v}\) if \(u\succ _i v\); then, the commutative diagram of Lemma 4.13 associated to \(u \succ _i v \succ _j w\) and \(u \succ _j v' \succ _i w\) becomes:

We just need to study the cases when \(\Phi ({111}) = 0\), \(\Phi (000)=1\) and \(|\mathcal {L}(000)|=2\) (otherwise, the coefficients involved in all compositions of 1-morphisms of the edges of the cube are singletons, and therefore the 2-morphisms commute trivially). In principle, up to permutation, there are 8 different situations attending to the value of \(\Phi \) in each vertex, depicted in Fig. 12. However, it is not hard to check that situations (a), (e) and (f) leads to inconsistency in the chord diagrams, and therefore they are not possible. We study the remaining 5 possible situations:
-
(a)
Figure 12b (i.e., \(\Phi (110) = \Phi (101) = \Phi (011) = \Phi (100) = \Phi (010) = 0 , \Phi (001) = 1\)): \(D(111)_{000}\) contains three monochords, two of them constituting an alternating pair. Coefficients involved in the three-fold compositions when moving around the cube are either singletons or the following:
$$\begin{aligned} \mathcal {L}(001)\overset{\rho _3}{\longleftrightarrow } \mathcal {L}(000) = \mathcal {L}(000) = \mathcal {L}(000) = \mathcal {L}(000) \overset{\rho _3^{-1}}{\longleftrightarrow } \mathcal {L}(001) = \mathcal {L}(001). \end{aligned}$$The composition of the 2-morphisms connecting coefficients is the identity morphism.
-
(b)
Figure 12c (i.e., \(\Phi (110) = \Phi (101) = \Phi (011) = \Phi (100) = 0 , \Phi (001) = \Phi (010) = 1\)): \(D(111)_{000}\) contains three monochords constituting two alternating pairs. Coefficients involved in the three-fold compositions when moving around the cube are either singletons or the following:
$$\begin{aligned} \mathcal {L}(001)\overset{\rho _2^{-1}\rho _3}{\longleftrightarrow } \mathcal {L}(010) = \mathcal {L}(010) \overset{\rho _2}{\longleftrightarrow } \mathcal {L}(000) = \mathcal {L}(000) \overset{\rho _3^{-1}}{\longleftrightarrow } \mathcal {L}(001) = \mathcal {L}(001). \end{aligned}$$The composition of the 2-morphisms connecting coefficients is the identity morphism.
-
(c)
Figure 12d: \(D(111)_{000}\) contains two monochords not forming an alternating pair and a bichord. Coefficients involved in the three-fold compositions when moving around the cube are either singletons or the following:
$$\begin{aligned} \mathcal {L}(011) = \mathcal {L}(011) \overset{\rho _3}{\longleftrightarrow } \mathcal {L}(010) \overset{\rho _2}{\longleftrightarrow } \mathcal {L}(000) = \mathcal {L}(000) \overset{\rho _3^{-1}}{\longleftrightarrow } \mathcal {L}(001) \overset{\rho _2^{-1}}{\longleftrightarrow } \mathcal {L}(011). \end{aligned}$$The composition of the 2-morphisms is the following square, which is a particular case of (5.4):

-
(d)
Figure 12g: \(D(111)_{000}\) contains one monochord and two parallel bichords not forming an alternating triple. Coefficients involved in the three-fold compositions when moving around the cube are either singletons or the following:
$$\begin{aligned} \mathcal {L}(011) = \mathcal {L}(011) \overset{\rho _3}{\longleftrightarrow } \mathcal {L}(010) \overset{\rho ^{-1}_{1} \rho _2}{\longleftrightarrow } \mathcal {L}(100) \overset{\rho _3^{-1}}{\longleftrightarrow } \mathcal {L}(101) = \mathcal {L}(101) \overset{\rho ^{-1}_{2} \rho _1}{\longleftrightarrow } \mathcal {L}(011). \end{aligned}$$The composition of 2-morphisms is the boundary of the union of two squares of the form (5.4) along an edge, which commutes:

-
(e)
Figure 12h: \(D(111)_{000}\) contains three parallel bichords. Coefficients involved in the three-fold compositions when moving around the cube are either singletons or the following:
$$\begin{aligned} \mathcal {L}(011) = \mathcal {L}(011) \overset{\rho _1^{-1}\rho _3}{\longleftrightarrow } \mathcal {L}(110) = \mathcal {L}(110) \overset{\rho ^{-1}_3\rho _2}{\longleftrightarrow } \mathcal {L}(101) = \mathcal {L}(101) \overset{\rho _2^{-1}\rho _1}{\longleftrightarrow } \mathcal {L}(011). \end{aligned}$$The composition of 2-morphisms is the boundary of the union of three squares of the form (5.4) along their common edges, which commutes:

\(\square \)
Situations (a), (e) and (f) are not possible when considering \(\Phi (111) = 0\), \(\Phi (000)=1\). Each 0 or 1 represent the value of \(\Phi \) in each of the vertices of the cube (5.3)
Once we have defined M, we will prove that its geometric realization is equivalent to that of the Khovanov functor F. To do so, we introduce a natural transformation \(\gamma :M\rightarrow F\) and show that the induced homomorphism \(\gamma _* :C_*(M; \mathbb {Z}) \rightarrow C_*(F; \mathbb {Z})\) is in fact an isomorphism (see Sect. 3.2).
Given a state \(u\in \mathbf {2^{n}}\), we set the natural natural transformation \(\gamma \) as follows:
Next, for each \(u\succ _i v\), we define a 2-morphism \(\gamma _{u,v}: F_{u>v} \circ \gamma _u \rightarrow \gamma _v\circ M_{u>v} \), i.e., \(\gamma _{u,v}\) makes the following diagram commute:

If \(\Phi (u) = 0\) and \(\Phi (v)=0\), \(\gamma _{u,v}\) is defined as the identity:
In the case when \(\Phi (u) = 0\) and \(\Phi (v)=1\) we define \(\gamma _{u,v}\) as \(\mu _i(u)\):
And when \(\Phi (u) = 1 = \Phi (v)\), \(\gamma _{u,v}\) is defined as the identity:
Lemma 5.5
The natural transformation \(\gamma _u\) is well defined.
Proof
We need to prove that \(\gamma _u\) satisfies conditions (C1) and (C2) in Lemma 3.2. Condition (C1) follows from definition of \(\gamma _u\). Next, we prove (C2) by showing that 2-morphisms in the following cube commutes, similar as we did in proof of Lemma 5.4:

The commutativity is clear when all coefficients are singletons, i.e., it holds unless \(\Phi (u)=0\), \(\Phi (w)=1\) and \(|\mathcal {L}(w)|=2\); thus, we have to study the three following situationsFootnote 5, corresponding again to the cases illustrated in Fig. 10:
Now, for each of the three cases above, we have to study the bijections obtained when we move along the cube: starting from \(\gamma _w \circ M_{v>w}\circ M_{u>v}\), we move to \(F_{v>w}\circ \gamma _v\circ M_{u>v}\), and continue moving along the cube following Fig. 11, until we reach again \(\gamma _w \circ M_{v>w}\circ M_{u>v}\).
We just need to consider the action of those compositions on the component \(C\in \pi _0G(u)\) such that \(f_{u,w}(C)\in \pi _0G(w)\) contains two cycles (otherwise, the value of \(F_{v>w}\circ \gamma _v\circ M_{u>v}\) is trivial, as explained in the proof of Lemma 5.4).
Consider the case (5.5), where edges \(e_i(u)\) and \(e_j(u)\) form an alternating pair (see Fig. 10(a)). Then \(F_{v>w}\circ \gamma _v\circ M_{u>v}(C)\) equals \(\mathcal {L}(w)\cdot w_+\), and we obtain the following values when moving along the cube as in Fig. 11:
We focus now in case (5.6), where \(e_j(u)\) is a loop and \(e_i(u)\) a bichord (Fig. 10(b) shows an example of this situation). In this case \(F_{v>w}\circ \gamma _v\circ M_{u>v}(C)\) equals \(\mathcal {L}(v)\cdot w_+\), and we get:
Consider the third case (5.7), where \(e_i(u)\) and \(e_j(u)\) are parallel bichords, so \(\mathcal {O}_i(u)=\mathcal {O}_j(u)\) (see Fig. 10c). Then \(F_{v>w}\circ \gamma _v\circ M_{u>v}(C) = \mathcal {L}(v)\cdot w_+\), and we obtain:
Hence, showing the commutativity of the cube reduces to proving the following equalities in the corresponding situations:
The first line holds on the nose, whereas the second and third are a consequence of the commutativity of the following squares, proved in Lemma 4.14:

\(\square \)
Proposition 5.6
\(\gamma _*:C_*(M;\mathbb {Z})\rightarrow C_*(F;\mathbb {Z})\) is an isomorphism of chain complexes.
Proof
Given a state \(u\in \mathbf {2^{n}}\) with \(\Phi (u)=0\) and a vertex \(z\in Z(u)\) in G(u), write \(C_z\) for the component of G(u) containing z and write \(E_z(u)\) for the set of edges incident to z. For each edge \(e\in E_z(u)\), set
The inverse of \(\gamma _*\) is:
\(\square \)
The above proposition together with Remark 3.4 yield to the following result:
Corollary 5.7
The spectra \({\text {Tot}}F\) and \({\text {Tot}}M\) are homotopy equivalent.
6 Pointed semi-simplicial sets
Definition 6.1
A link diagram D is 1-adequate (resp. 0-adequate) if \(\mathcal {G}(\mathbf {1})\) (resp. \(\mathcal {G}(\mathbf {0})\)) contains no loops. D is said to be adequate if it is both 0-adequate and 1-adequate. If D is either 0-adequate or 1-adequate, it is called semiadequate. A link is said to be (semi)adequate if it admits a (semi)adequate diagram.
Proposition 6.2
The functor F factors through \(\mathbf {Set}_\bullet \) if and only if the diagram D is 1-adequate. The functor M factors through \(\mathbf {Set}_\bullet \) if and only if \(D(\mathbf {1})\) contains no alternatig pairs.
Proof
From the definition of F it follows that \(F_{u>v}\) is not a function of pointed sets if and only if \(\Phi (u)=\Phi (v)=0\). This situation is avoided for all possible states \(u > v\) if and only if \(\Phi (v) > 0\) for every state \(v \ne \mathbf {1}\), or equivalently, if and only if \(\mathcal {G}(\mathbf {1})\) contains no loops.
Now, looking at the definition of M, we get that \(M_{u>v}\) is not a function of pointed sets if and only if \(\Phi (u)=0\), \(\Phi (v)=1\) and \(|\mathcal {L}(v)|=2\). This situation is avoided for all possible states \(u>v\) if and only if \(D(\mathbf {1})\) contains no alternating pairs. \(\square \)
Combining the functor \(\Lambda \) from (3.1) with the definition in (5.2) we get the following results:
Corollary 6.3
If D is 1-adequate, then \(\mathcal {X}_D^{j_{\mathrm {almax}}}\) is an iterated desuspension of the augmented semisimplicial pointed set \(\Lambda (F)\) (cf. [11]).
Corollary 6.4
If \(D(\mathbf {1})\) has no alternating pairs, then \(\mathcal {X}_D^{j_{\mathrm {almax}}}\) is an iterated desuspension of the augmented semisimplicial pointed set \(\Lambda (M)\).
7 Breaking up \(M_D\)
In this section we introduce skein sequences for \(M_D\) (Sect. 7.3). To do so, we decompose \(M_D\) into subposets of the cube \(\mathbf {2^{n}}\) (Sect. 7.2), and compare one of them with the simplicial complex \(I_D\) introduced in [3] for extreme Khovanov homology.
7.1 The simplicial complex \(I_D\)
Given a link diagram D, in [3] the authors introduce a simplicial complex whose associated cohomology complex coincides with the Khovanov homology of the link in the minimal quantum grading. We restate that construction in terms of the maximal quantum grading \(j_{\max }\).
Definition 7.1
Let D be a link diagram. Its associated Lando graph \(G_L(D)\) is constructed from \(D(\mathbf {1})\) by considering a vertex for every monochord, and an edge joining two vertices if the endpoints of the corresponding monochords alternate along the same circle. We define the independence complexFootnote 6 associated to D, \(I_D\), as the simplicial complex whose set of vertices is the same as the set of vertices of \(G_L(D)\) and \(\sigma =(e_1 e_2 \cdots e_k)\) is a simplex in \(I_D\) if and only if the vertices \(e_1, e_2, \ldots , e_k\) are independent in \(G_L(D)\), i.e., there are not edges in \(G_L(D)\) between these vertices.
Note that \(G_L(D)\) can be thought as the disjoint union of the Lando graphs arising from each of the chord diagrams in \(D(\mathbf {1})\) after removing all bichords. Moreover, if \(G_L(D) = G_L(D_1) \sqcup G_L(D_2)\), then \(I_D = I_{D_1} * I_{D_2}\), the join of both simplicial complexes.
Theorem
[3] Let L be an oriented link represented by a diagram D with p positive crossings. Then
The poset of faces of the independence complex \(I_D\) is precisely the subposet of the cube \(\mathbf {2^{n}}\) of those states u for which \(\Phi (u)=0\).
Given a set of vertices \(\{v_1,\ldots ,v_n\}\), each simplicial complex on these vertices gives rise to a downwards closed subposet of \(\mathbf {2^{n}}\) (i.e., if a state u belongs to the subposet and \(u > v\), then v belongs to the subposet too): its poset of faces. Conversely, every downwards closed subposet of \(\mathbf {2^{n}}\) is the poset of faces of some simplicial complex.
Let \(\mathbf {S}\subset \mathbf {Set}\) be the full subcategory on \(\emptyset \) and a singleton, and let \(\mathbf {S_p}\subset \mathbf {Set}_\bullet \) be the full subcategory on the basepoint and \(S^0\). Downwards closed subposets of the cube are in bijection with functors \(\mathbf {2^{n}}\rightarrow \mathbf {S}\). Subposets of the cube are in bijection with functors \(\mathbf {2^{n}}\rightarrow \mathbf {S_p}\) (see discussion in the final section of [1], for example). The realization of a subposet of the cube is the desuspension of the totalization of its associated functor \(\mathbf {2^{n}}\rightarrow \mathbf {S_p}\subset \mathbf {Set}_\bullet \). Thus, the realization of a simplicial complex X coincides with the realization of its poset of faces.
Given \(u\in \mathbf {2^{n}}\), we write \(\bar{u}\) for the state of \(\mathbf {2^{n}}\) satisfying \(\bar{u}_i \ne u_i\), for \(1\leqslant i \leqslant n\).
Definition 7.2
The categorical dual of a downwards (upwards) closed subposet \(X\subset \mathbf {2^{n}}\) is the upwards (downwards) closed subposet \(X^*\subset \mathbf {2^{n}}\rightarrow \mathbf {S_p}\) given by \(u\in X^*\) if and only if \(\bar{u}\in X\).
The complement of a downwards (upwards) closed subposet \(X\subset \mathbf {2^{n}}\) is the upwards (downwards) closed subposet \(\hat{X}\subset \mathbf {2^{n}}\) given by \(u\in \hat{X}\) if and only if \(u\notin X\).
The complement of the categorical dual of a downwards closed set X is again a downwards closed subposet of the cube whose associated simplicial complex is the Alexander dual of X. In general \(|\hat{X}|\simeq \Sigma |X|\) if X is downwards closed and \(|X^*|\) is Spanier-Whitehead dual to |X|. Observe that
-
(1)
If \(|X|\simeq |A|\vee |B|\), then \(|X^*|\simeq |A^*|\vee |B^*|\),
-
(2)
If \(|X|\simeq S^k\), then \(|X^*|\simeq S^{n-k-2}\), where n is the dimension of the cube.
Given a link diagram D, the upwards closed subposet of the cube given by those states u such that \(\Phi (u)=0\), which we denote \(X_D\), corresponds to the functor \(F^{j_{\max }}:\mathbf {2^{n}}\rightarrow \mathbf {Set}_\bullet \subset \mathcal {B}\).
Corollary 7.3
\(X_D\) is the categorical dual of the poset of faces of \(I_D\). As a consequence if \(|I_D| \simeq S^k\), then \(|X_D| \simeq S^{n-k-2}\).
7.2 Decomposing \(M_D\)
Given a state u of a diagram D, recall that we write \(D(\mathbf {1})_u\) for the chord diagram having the same circles as \(D(\mathbf {1})\) and those chords \(e_i(\mathbf {1})\) so that \(u_i \ne 1\). Given a crossing c in D, we write \(D[c=0]\) (resp. \(D[c=1]\)) for the link diagram obtained after smoothing c following a 0-label (resp. 1-label).
Definition 7.4
Given a link diagram D with n crossings, we consider the following subposets of the cube \(\mathbf {2^{n}}\):
-
\(X_D\): is the subposet of \(\mathbf {2^{n}}\) consisting of those states u so that \(\Phi (u)=0\) (as defined in previous section).
-
\(X_D^e= X_{D[e=0]}\), for any monochord \(e \in D(\mathbf {1})\).
-
\(Y_D\): is the subposet of \(\mathbf {2^{n}}\) consisting of those states u so that \(\Phi (u)=1\) and \(D(\mathbf {1})_u\) contains an alternating pair.
-
\(Z_D^b\): is the subposet of \(\mathbf {2^{n}}\) consisting of those states u so that \(\Phi (u)=1\) and \(D(\mathbf {1})_u\) contains a bichord parallel to a given bichord b of \(D(\mathbf {1})\).
Observe that each state (admitting an enhacement) in the almost-extreme complex of D belongs to one and only one of the previous subcubes \(X_D, Y_D\) or \(Z_D\) (see Corollary 4.5 and Proposition 4.8).
Proposition 7.5
The functor \(M_D\) can be realized as the following cofibre sequence
where N is the set of monochords in \(G(\mathbf {1})\) and B the set of classes of parallel bichords.
The decomposition follows because the second map is levelwise injective and the suspension of the leftmost term is precisely the quotient functor of this second map.
Remark 7.6
A Mayer-Vietoris spectral sequence allows to compute both posets \(Y_D\) and \(Z_D^b\) in terms of some posets \(X_{D'}\), where \(D'\) are partially smoothed link diagrams of D. We explain this below.
The poset \(Y_D\) can be covered with the subposets \(X_{D[e=0,f=0]}\) where \(\{e,f\}\) runs along the set of all alternating pairs in \(D(\mathbf {1})\). The k-fold intersections \(A_k\) of this covering are
where \(\{e_1,\ldots ,e_{k+1}\}\) are monochords attached to the same circle in such a way that they can be divided into two non-empty sets \(H_1\) and \(H_2\) so that all monochords in \(H_1\) alternate with all monochords in \(H_2\) and viceversa. Similarly, the poset \(Z_D^b\) can be covered with the subposets \(X_{D[b=0]}\) where b runs along the set of bichords of \(D(\mathbf {1})\), and the k-fold intersections \(B_k\) of this covering are
where \(\{b_1,\ldots ,b_k\}\) are bichords parallel to b.
Thus, the (first page of the) Mayer-Vietoris spectral sequences associated to these coverings are:
Example 7.7
Consider the torus knot T(3, q) and let \(D=D_{(3,q)}\) be its standard diagram. Since \(D(\mathbf {1})\) contains no bichords, \(Z_D^b\) is trivial. We will combine Remark 7.6 together with Corollary 7.3 to compute the realization of subposets in (7.1). More precisely, we will express \(X_D\), \(X_D^e\) and \(Y_D\) (via \(A_k\)) as the duals of independence complexes of some Lando graphs. Write \(C_{n}\) for the cycle graph of n vertices and \(L_n\) the path of length n.
-
\(G_L(D) = C_{2q}\);
-
\(G_L(D[e=0]) = L_{2q-4}\), for any monochord e in \(D(\mathbf {1})\);
-
\(G_L(D[e_1=0,e_2=0]) = C_{2q-2}\) when \(e_1\) and \(e_2\) are two consecutive monochords in \(D(\mathbf {1})\). Note that alternating pairs consist precisely in consecutive monochords;
-
\(G_L(D[e_1=0,e_2=0,e_3=0]) = L_{2q-6}\) when \(e_1,e_2,e_3\) are three consecutive monochords in \(D(\mathbf {1})\). Note that the previous condition is equivalent to require that \(e_1,e_2,e_3\) can be divided into two subsets \(H_1\) and \(H_2\) such that all monochords in each subset alternate with all monochords in the other subset.
Note that there are no n-tuples of monochords \(e_1,\ldots ,e_n\) which can be divided into two subsets \(H_1\) and \(H_2\) satisfying the condition above when \(n>3\).
Summarizing we have:
The homotopy types of the above complexes were computed in [10, Corollary 3.4 and Proposition 3.9]:
This allows to compute the almost-extreme Khovanov spectra of T(3, q) in terms of well-known independence complexes of cycles and paths, with no need to apply induction on q.
Remark 7.8
The cone-length \(c(\mathcal {X})\) of a spectrum \(\mathcal {X}\) is the least n such that there is a sequence of cofibre sequences
for \(i=0,\ldots , n-1\), such that \(\mathcal {X}_0\) is contractible, \(\mathcal {Y}_i\) is a wedge of spheres and \(\mathcal {X}_n = \mathcal {X}\). In [10] it was conjectured that \(|X_D|\) is homotopy equivalent to a wedge of spheres for any diagram D. If this were true, then Remark 7.6 would imply that the cone length of \({\text {Tot}}M_D\) is bounded above by the maximum of the following numbers:
-
(1)
the maximum number of parallel bichords plus one in \(D(\mathbf {1})\).
-
(2)
the maximum number of monochords in \(D(\mathbf {1})\) that can be partitioned into two disjoint subsets \(H_1,H_2\) such that all chords in \(H_1\) alternate with all chords in \(H_2\) and viceversa.
7.3 Skein sequences
Let a be a crossing in a link diagram D. Observe that if a is a monochord in \(D(\mathbf {1})\) we get the skein short exact sequenceFootnote 7
whereas if a is a bichord in \(D(\mathbf {1})\), then the skein short exact sequence becomes
Moreover, when a is a monochord in \(D(\mathbf {1})\) we also have the following sequence:
To verify the three above sequences note that the second map is an inclusion whose quotient is the suspension of the first spectrum.
Definition 7.9
Let D be a diagram and let a be a monochord in \(D(\mathbf {1})\). We say that a is:
-
(1)
2-free if it is not part of any alternating pair in \(D(\mathbf {1})\).
-
(2)
3-free if it is not part of any alternating triple in \(D(\mathbf {1})\).
-
(3)
free if it is 2-free and 3-free.
-
(4)
b-free if it is not part of any alternating triple involving the bichord b in \(D(\mathbf {1})\).
Lemma 7.10
Let D be a diagram and let a be a monochord in \(D(\mathbf {1})\).
-
(1)
If a is 2-free, then \(X_D,Y_D\) and all \(X_D^e\), with \(e\ne a\) a monochord, are contractible; if, additionally, \(D(\mathbf {1})\) contains another 2-free monochord, then \(X^a_D\) is contractible too.
-
(2)
If a does not form an alternating triple with a bichord b (i.e., a is b-free), then \(Z^b_D\) is contractible.
Proof
The leftmost map in skein sequence (7.4) along the crossing associated to a is identity, hence \(X_D\) is contractible. A similar reasoning works for \(X_D^e\) when \(e \ne a\).
In general, the skein sequence (7.2) does not respect the decomposition in (7.1); however, when a is 2-free, it respects the term \(Y_D\) and when a is b-free it respects \(Z_D^b\). In both cases the maps \(Y_{D[a=1]} \rightarrow Y_{D[a=0]}\) and \(Z^b_{D[a=1]} \rightarrow Z^b_{D[a=0]}\) are the identity. \(\square \)
Corollary 7.11
If \(D(\mathbf {1})\) contains at least two 2-free monochords, then
Proof
The result is direct from cofibre sequence (7.1) and Lemma 7.10(1). \(\square \)
Corollary 7.12
If D has a free monochord e, then \(M_D\simeq X_{D[e=0]}\).
Proof
Lemma 7.10 implies that the only possibly non-contractible subposet in (7.1) is \(X_D^e = X_{D[e=0]}\). \(\square \)
Lemma 7.13
Let a be a 2-free monochord in \(D(\mathbf {1})\) dividing a circle into two regions so that both of them contain at least one 2-free monochord (we say that \(D(\mathbf {1})\) contains nested monochords). Then \(M_D \simeq \Sigma M_{D[a=1]}\).
Proof
We use skein sequence (7.2) and show that \(M_{D[a=0]}\) is contractible. First, notice that the circle in the statement is split into two circles \(z_1\) and \(z_2\) when changing the 1-label of a for a 0-label, each of them attached to at least a 2-free monochord that we call c and d, respectively. Lemma 7.10(1) implies that the the only possibly non-contractible spaces when applying cofibre sequence (7.1) to \(D_{[a=0]}\) are \(Z_{D[a=0]}^{b}\).
Now, since a is 2-free in \(D(\mathbf {1})\), there is no bichord connecting \(z_1\) and \(z_2\) in \(D[a=0](\mathbf {1})\). Therefore, for any bichord b in \(D[a=0](\mathbf {1})\) at least one of the monochords c or d are b-free, so Lemma 7.10(2) implies that \(Z_{D[a=0]}^b\) is contractible for all bichords b, thus \(M_{D[a=0]}\) is contractible. \(\square \)
Definition 7.14
Two parallel bichords a and b of a chord diagram \(D(\mathbf {1})\) are equivalent if there is no monochord e so that a, b and e constitute an alternating triple.
Lemma 7.15
If D has two equivalent bichords a, b, then \(M_D \simeq \Sigma M_{D[a=1]}\).
Proof
Since a and b are equivalent, the chord b is 2-free in the chord diagram \(D[a=0](\mathbf {1})\), so Lemma 7.10(1) implies that \(X_{D[a=0]}\) is contractible. The statement follows from the skein sequence (7.3) along the chord a. \(\square \)
8 Diagrams with no alternating pairs
In this section we determine the homotopy type of \(M_D\) (thus, that of the Khovanov spectrum given by Lipshitz and Sarkar in [7] for the almost-extreme quantum grading) for diagrams D so that \(D(\mathbf {1})\) contains no alternating pairs. Observe that this determines their Khovanov homology groups at almost-extreme quantum degree.
8.1 Diagrams with no monochords
This case was studied in [11]: If D is 1-adequate (i.e., \(D(\mathbf {1})\) has no monochords), then \(M_D\) is homotopy equivalent to a wedge of spheres and possibly a suspension of the projective plane. See [11, Theorem 1.1] for the details.
8.2 Diagrams with one monochord
Proposition 8.1
Let D be a link diagram with n crossings so that \(D(\mathbf {1})\) contains a single monochord attached to a circle z, and let k be the number of circles connected to z along an alternating triple. Then,
Proof
Write e for the monochord in \(D(\mathbf {1})\). By Lemma 7.10(1), the decomposition in (7.1) becomes
The subposet \(X^e_D\) has a single element in degree \(n-1\), thus \(|X^e_D|\simeq S^{n-2}\). By Lemma 7.10(2), \(Z^b_D\) is contractible unless b forms an alternating triple with e. Therefore we may assume, up to suspension, that all bichords are attached to z and form an alternating triple with e. Moreover, using Lemma 7.15 we can assume, up to suspension, that circles are connected to z by exactly two bichords.
Therefore, for each such bichord b, the subposet \(Z^b_D\) has five elements in M-shape, with two elements in degree \(n-1\) and three in degree \(n-2\), thus \(|Z^b_D| \simeq S^{n-3}\), and the above decomposition becomes
The map to the wedge of spheres is a diagonal map. This concludes the proof. \(\square \)
8.3 Diagrams with 2-free monochords
Let D be a diagram whose associated chord diagram \(D(\mathbf {1})\) contains more than one monochord, all of them 2-free. Recall from Corollary 7.11 that in this situation \(M_D \simeq \bigvee _{[b]\in B} Z^b_D\), thus we can restrict to the independent study of each connected pair of circles when computing \(Z_D^b\).
At this point we can make some simplifications in \(D(\mathbf {1})\): Lemmas 7.13 and 7.15 allow us to remove nested monochords and equivalent bichords when computing \(M_D\) (in exchange of taking suspensions). Moreover, by Lemma 7.10(2) we can assume that \(D(\mathbf {1})\) contains no b-free monochords for any bichord b. These simplifications motivate the following definition:
Definition 8.2
A diagram D is simple if the associated chord diagram \(D(\mathbf {1})\) contains at least two monochords, all of them 2-free, and satisfies the following conditions:
-
(1)
It contains exactly two circles;
-
(2)
It contains no nested monochords;
-
(3)
There are no b-free monochords for any bichord b;
-
(4)
There are no equivalent bichords.
By definition, if D is simple then \(D(\mathbf {1})\) can be isotoped in \(S^2\) so that monochords and bichords lie in different regions (see Fig. 13). Moreover, since \(D(\mathbf {1})\) contains no nested monochords, a circle with n monochords is divided into n half-disks (each of them bounded by a monochord and an arc of the circle) and an additional region (bounded by the n monochords and n arcs of the circle) that we call polygon.
Given a monochord e in \(D(\mathbf {1})\), we write \(d_e\) for the half-disk bounded by eFootnote 8, and \(|d_e|\) for the number of bichords having one of their endpoints in \(d_e\). In simple diagrams \(|d_e|\geqslant 1\) for any monochord e.
In the proofs of Lemmas 8.3, 8.7 and 8.8 we use several results from [10, Section 3].
Lemma 8.3
Let D be a simple diagram whose associated chord diagram \(D(\mathbf {1})\) contains a monochord e so that \(|d_e|=1\). Then \(|M_D|\) is either contractible or homotopy equivalent to a sphere.
Proof
Let b be the only bichord with an endpoint in \(d_e\) and consider the skein sequence (7.3) along b:
The \(\mathbf {1}\)-resolutions corresponding to D, \(D[b=0]\) and \(D[b=0, e=0]\) illustrating the proof of Lemma 8.3 are shown in (a–c), respectively. Regions R and \(R'\) are shaded green and grey, respectively (color figure online)
The monochord e is free in \(D[b=1](\mathbf {1})\), thus by Lemma 7.10\(Z_{D[b=1]}\) is contractible, thus \(M_{D[b=1]}\) is contractible (by Corollary 7.11) and \(M_D\simeq X_{D[b=0]}\).
Now, \(D[b=0](\mathbf {1})\) has a single circle and its inner part is separated into two regions R and \(R'\) by the monochord e. See Fig. 14b. Moreover:
-
(1)
monochords in \(D(\mathbf {1})\) become internal monochords in \(D[b=0](\mathbf {1})\);
-
(2)
monochords attached to each of the circles in \(D(\mathbf {1})\) become monochords contained in each of the regions \(R, R'\) in \(D[b=0](\mathbf {1})\);
-
(3)
bichords in \(D(\mathbf {1})\) become external monochords in \(D[b=0](\mathbf {1})\) having one endpoint in R and the other one in \(R'\).
Consider now the skein sequence (7.4) along the monochord e
Condition (2) above implies that there are no alternating pairs in \(D[b=0,e=0](\mathbf {1})\) (see Fig. 14c), so the middle term in the above sequence is contractible and we have \(X_{D[b=0]}\simeq \Sigma X_{D[b=0,e=1]}\).
Assume first that b connects \(d_e\) with the region that we call polygon, then we claim that the Lando graph G of \(D[b=0,e=1]\), contains no cycles (i.e., it is a forest). In order to prove that, we proceed by contradiction. Suppose that \(C_n\) is a cycle of length n in G, with vertices \(e_1, e_2, \ldots , e_n\) numbered so that \(e_1\) is an internal chord in the region R. Conditions (1) and (2) imply that monochords \(e_{4k+1}\) and \(e_{4k+3}\) lie in R and \(R'\), respectively. Moreover, the absence of equivalent bichords in \(D(\mathbf {1})\) implies the absence of cycles of length four in G, i.e., \(n \geqslant 8\). The monochord \(e_4\) separates the external region into two subregions \(S,S'\). Since there are no cycles of length 4, \(e_2\) and \(e_6\) lie one in each of these two subregions, say \(e_2\in S\) and \(e_6\in S'\). Moreover, as the internal monochords are non-nested, all internal monochords but \(e_3\) and \(e_5\) have both endpoints in either S or \(S'\). Therefore
-
(1)
the endpoints of \(e_{1}\) lie in S (because \(e_2\) lies in S) and
-
(2)
the endpoints of \(e_{2k+1}\) lie in \(S'\) if \(k\geqslant 3\) (because \(e_{2k}\) lies in \(S'\) if \(k\geqslant 3\)).
In particular, both endpoints of \(e_{n-1}\) lie in \(S'\). This is a contradiction, since \(e_n\) is a external monochord connecting \(e_1\) and \(e_{n-1}\). Therefore G contains no cycles, and by [10, Corollary 3.7] its associated independence complex is either contractible or a sphere. Corollary 7.3 completes the proof.
Assume now that b has its endpoints in two half-discs \(d_e\) and \(d_f\), for some monochord f, and consider the skein sequence (7.4) along f. We get that \(X_{D[b=0,e=1,f=0]}\) is contractible, since all monochords in \(R'\) are 2-free. Therefore, \(X_{D[b=0,e=1]}\simeq \Sigma X_{D[b=0,e=1,f=1]}\). The latter is the same as \(X_{D'[b=0,e=1]}\), where \(D' = D[f=1]\) is a diagram where e connects \(d_e\) with the polygon, which was studied in the previous case. \(\square \)
Remark 8.4
Since simple diagrams do not contain equivalent bichords, if \(|d_e| \geqslant 4\) for some monochord e, then there exists a monochord f with \(|d_f|=1\) (\(d_f\) is connected to \(d_e\) by a bichord). In other words, if \(|d_e| > 1\) for all monochords e, then \(|d_e |\leqslant 3\) for all monochords e.
Definition 8.5
A simple diagram D so that \(2 \leqslant |d_e| \leqslant 3\) for every monochord e of \(D(\mathbf {1})\) is called super-simple.
If D is super-simple, every half-disk \(d_e\) in \(D(\mathbf {1})\) satisfies one of the three following conditions:
-
(1)
\(|d_e|=2\), and both bichords connect \(d_e\) with two contiguous half-disks in the other circle (see Fig. 15a);
-
(2)
\(|d_e|=2\), and one bichord connects \(d_e\) with a half-disk in the other circle and the other one connects \(d_e\) with the polygon in the other circle (see Fig. 15b);
-
(3)
\(|d_e|=3\), and two bichords connect \(d_e\) with two contiguous half-disks in the other circle, and the third one is placed between them and connects \(d_e\) with the polygon of the other circle (see Fig. 15c).
The next statement follows from Lemmas 8.7 and 8.8.
Proposition 8.6
Let D be a super-simple diagram. Then \(|M_D|\) is homotopy equivalent to a wedge of spheres.
Lemma 8.7
Let D be a super-simple diagram so that \(D(\mathbf {1})\) contains at least one bichord connecting a half-disk with the region called polygon. Then \(|M_D|\) is either contractible or homotopy equivalent to a sphere.
The \(\mathbf {1}\)-resolutions corresponding to D, \(D[a=0, f=1]\) and \(D[a=0, f=0]\) illustrating the proof of Lemma 8.7 are shown in (a–c), respectively. Dotted lines represent those chords that may or may not be in the diagrams
Proof
Let b be a bichord connecting a half-disk \(d_e\) in a circle \(z_1\) with the polygon of the circle \(z_2\), for some monochord e. See Fig. 16a. Since D is super-simple, there exists at least a bichord a connecting \(d_e\) with \(d_f\) for a monochord f attached to \(z_2\). We distinguish two cases, depending on whether \(z_2\) contains at least two monochords or it contains just a single monochord.
Case 1: Assume that the chord diagram \(D(\mathbf {1})\) contains more than one monochord attached to \(z_2\), and consider the skein exact sequence (7.3) along a:
We will show that \(X_{D[a=0]}\) is contractible. To do so, we apply the skein sequence (7.4) along the monochord f:
Figure 16b represents \(D[a=0, f=1](\mathbf {1})\), where b is a free monochord. Moreover, any monochord different from f attached to \(z_2\) becomes 2-free in \(D[a=0, f=0](\mathbf {1})\), as illustrated in Figure 16c. Therefore by Lemma 7.10(1) \(X_{D[a=0, f=1]}\) and \(X_{D[a=0, f=0]}\) are contractible, and so is \(X_{D[a=0]}\).
As a consequence, \(M_D \simeq \Sigma M_{D[a=1]}\). If \(|d_e| = 2\) in \(D(\mathbf {1})\), then \(|d_e|=1\) in \(D[a=1](\mathbf {1})\), and the statment holds by Lemma 8.3. If \(|d_e| = 3\) in \(D(\mathbf {1})\), then \(|d_e|=2\) in \(D[a=1](\mathbf {1})\) and it contains a bichord c connecting \(d_e\) with \(d_h\) for a monochord h (contiguous to f) attached to the circle \(z_2\). Applying the skein exact sequence (7.3) along c and repeating the same reasoning as before leads to \(M_D \simeq \Sigma ^2 M_{D[a=1,c=1]}\). Since \(|d_e|=1\) in \(D[a=1,c=1](\mathbf {1})\), Lemma 8.3 completes the proof for this case.
Case 2: Assume that there is just one monochord f attached to the circle \(z_2\) in \(D(\mathbf {1})\). Then, since D is super-simple, \(D(\mathbf {1})\) is as one of the six chord diagrams depicted in Fig. 17 (each picture leads to two possible chord diagrams, depending on whether it contains the bichord p or not). In order to compute \(M_D\) for each of these situations, we use skein sequence (7.3) together with Corollary 7.3. We also use [10, Lemma 3.2, Corollary 3.3, Corollary 3.4] to compute \(I_D\):
-
If \(D(\mathbf {1})\) is as in Fig. 17a with p: we consider the skein sequence (7.3) along the bichord c. Since the Lando graph \(G_{L}(D[c=0])\) is a path of length four, we deduce from [10, Corollary 3.4] that \(|I_{D[c=0]}|\simeq S^1\), and therefore \(|X_{D[c=0]}| \simeq S^2\). Next, we show that \(M_{D[c=1]}\) is contractible by applying the skein sequence (7.3) to \(D[c=1]\) along the bichord a (we use the fact that chord f is free in \(D_{[c=1, a=1]}(\mathbf {1})\) and use [10] to compute \(I_{D[c=1, a=0]}\)). Therefore, \(|M_D| \simeq |X_{D[c=0]}| \simeq S^2\).
-
If \(D(\mathbf {1})\) is as in Fig. 17a without p: we proceed as in the previous case, and get that both \(M_{D[c=1]}\) and \(X_{D[c=0]}\) are contractible, and so is \(M_D\).
-
If \(D(\mathbf {1})\) is as in Fig. 17b with p: we consider the skein sequence (7.3) along the bichord a. First, we compute \(|I_{D[a=0]}|\simeq S^1\), and therefore \(|X_{D[a=0]}| \simeq S^4\). Next, we show that \(M_{D[a=1]}\) is contractible by applying the skein sequence (7.3) to \(D[a=1]\) along the bichord b (we use the fact that chord e is free in \(D_{[a=1, b=1]}(\mathbf {1})\) and that \(I_{D[a=1,b=0]}\) is contractible). Therefore, \(|M_D| \simeq |X_{D[a=0]}| \simeq S^4\).
-
If \(D(\mathbf {1})\) is as in Fig. 17b without p: the procedure is analogous to the previous one, the only difference is that \(|X_{D[a=0]}| \simeq S^3\) and therefore \(|M_D| \simeq S^3\).
-
If \(D(\mathbf {1})\) is as in Fig. 17c with p: we consider the skein sequence (7.3) along the bichord a. Since \(I_{D[a=0]}\) is contractible, so is \(X_{D[a=0]}\). Next, we show that \(M_{D[a=1]}\) is also contractible by applying the skein sequence (7.3) to \(D[a=1]\) along the bichord b (we use the fact that chord e is free in \(D_{[a=1, b=1]}(\mathbf {1})\) and that \(I_{D[a=1, b=0]}\) is contractible). Therefore, \(M_D\) is contractible.
-
If \(D(\mathbf {1})\) is as in Fig. 17c without p: we proceed as in the previous case, and get that \(X_{D[a=0]}\) is contractible and \(|M_{D[a=1]}| \simeq S^3\). Therefore, \(|M_D| \simeq \Sigma |M_{D[a=1]}| \simeq S^4\).
\(\square \)
The six possible chord diagrams illustrating Case 2 of the proof of Lemma 8.7
Lemma 8.8
Let D be a super-simple diagram so that all bichords in \(D(\mathbf {1})\) connect two half-disks (i.e., there are no bichords with an endpoint in the region called polygon). Then, \(|M_D|\) is homotopy equivalent to a wedge of spheres. More precisely, if we write 2n for the number of monochords in \(D(\mathbf {1})\), then
Proof
First, notice that since all bichords in \(D(\mathbf {1})\) connect two half-disks, the number of monochords equals the number of bichords. We label the chords as follows (see Fig. 18a): we write \(e_1, \ldots , e_n\) (resp. \(f_1, \ldots , f_n)\) for the monochords attached to the circle \(z_1\) (resp. \(z_2\)), and \(a_i\) (resp. \(b_i\)) for the bichord having its endpoints in the half-disks \(d_{e_i}\) and \(d_{f_i}\) (resp. \(d_{e_{i+1}}\) and \(d_{f_i}\)), for \(1\leqslant i \leqslant n\).
Consider the skein sequence (7.3) along the bichord \(a_1\):
We study now the homotopy type of \(X_{D[a_1=0]}\). Figure 18b shows the chord diagram \(D[a_1=0](\mathbf {1})\), whose associated Lando graph \(G= G_L(D[a_1=0])\) is as depicted in Fig. 18c. Now, since vertex \(e_1\) dominatesFootnote 9\(e_2\) and vertex \(f_1\) dominates \(f_2\), it follows from [10, Lemma 3.2] that the independence complex associated to \(G_L\) is homotopy equivalent to the independence complex associated to the graph \(G-e_1-f_1\), which is a path of length \(4n-4\), \(L_{4n-4}\), whose independence complex follows from [10, Corollary 3.4]:
and by Corollary 7.3 we get:
Next, we compute the homotopy type of \(M_{D[a_1=1]}\). Consider the skein sequence (7.3) along the bichord \(b_1\):
Figure 19a, b represent the chord diagrams associated to \(D[a_1=1, b_1=1]\) and \(D[a_1=1, b_1=0]\), respectively. Notice that \(f_1\) is free and \(e_1\) is 2-free in \(D[a_1=1, b_1=1](\mathbf {1})\), hence \(M_{D[a_1=1, b_1=1]}\) is contractible by Lemma 7.10 and \(M_{D[a_1=1]} \simeq X_{D[a_1=1, b_1=0]}\). The Lando graph H associated to \(D[a_1=1, b_1=0]\) is depicted in Fig. 19c, and since vertex \(f_1\) dominates \(f_2\) and vertex \(e_2\) dominates \(e_3\), we have the following equivalence relations:
and by Corollary 7.3 we get:
Finally, we compute \(|M_D|\):
-
If \(n \equiv 0\) (mod 3), then the skein sequence (8.1) becomes:
$$\begin{aligned} S^{\frac{8n}{3}-2} \longrightarrow S^{\frac{8n}{3}-1} \longrightarrow |M_{D}|, \end{aligned}$$so \(|M_D| \simeq S^{\frac{8n}{3}-1} \vee S^{\frac{8n}{3}-1}.\)
-
If \(n \equiv 1\) (mod 3), then the skein sequence (8.1) becomes:
$$\begin{aligned} S^{\frac{8n+1}{3}-2} \longrightarrow *\longrightarrow |M_{D}|, \end{aligned}$$so \(|M_D| \simeq S^{\frac{8n+1}{3}-1}\).
-
If \(n \equiv 2\) (mod 3), then the skein sequence (8.1) becomes:
$$\begin{aligned} *\longrightarrow S^{\frac{8n+2}{3}-2} \longrightarrow |M_{D}|, \end{aligned}$$so \(|M_D| \simeq S^{\frac{8n+2}{3}-2}\).
\(\square \)
The chord diagram \(D(\mathbf {1})\) satisfying conditions in Lemma 8.8 is shown in (a). The chord diagram and the Lando graph associated to \(D[a_1=0]\) are shown in (b, c), respectively
Theorem
Let D be a diagram so that the associated chord diagram \(D(\mathbf {1})\) contains more than one monochord, all of them 2-free . Then \(|M_D|\) is homotopy equivalent to a wedge of spheres.
Proof
Since all monochords are 2-free, then \(M_D \simeq \bigvee _{[b]\in B} Z^b_D\), by Corollary 7.11, so we consider each pair of discs in \(D(\mathbf {1})\) independently. Moreover, we can remove nested monochords and equivalent bichords when computing \(M_D\) at the expense of taking suspensions (Lemmas 7.13 and 7.15). In addition, we can assume that \(D(\mathbf {1})\) contains no b-free monochords for any bichord b (otherwise, \(Z_D^b\) is contractible by Lemma 7.10(2)). Hence, we just need to prove the statement for simple diagrams. Lemma 8.3 and Proposition 8.6 complete the proof. \(\square \)
Notes
We defer the definition of \(h_{u,v}:Z(u)\longrightarrow Z(v)\) some lines until the beginning of Sect. 5.
When working with different diagrams, we write \(F_D\) to denote the functor F associated to the link diagram D.
The original functor F from [6] splits into functors \(F^j\) which associates to each state u a set \(\mathcal {E}_{u,j}\) of enhancements so that \(q(u,x) = j\), for every \(x\in \mathcal {E}_{u,j}\). When particularizing to the case when \(j=j_{almax}\), Corollary 4.5 implies that if \(\Phi (u)=0\), then the set \(\mathcal {E}_{u,j}\) can be identified with Z(u), whereas if \(\Phi (u)=1\) then \(\mathcal {E}_{u,j}=\{u_+\}\).
When working with different diagrams, we write \(M_D\) to denote the functor M associated to the link diagram D.
The case \(\Phi (u) = 0, \Phi (v) = 0, \Phi (v') = 1, \Phi (w) = 1\) is symmetric to (5.6).
The independence complex is defined in terms of a graph. Hence, given a graph G we define its associated independence complex \(I_G\) as described in Definition 7.1.
Compare to skein short exact sequences from [13].
If e is the only monochord attached to the circle, then there are two possible options for \(d_e\); in this case choose an option minimizing \(|d_e|\), without loss of generality.
Following [10], given two vertices v and w in a graph, we say that v dominates w if the adjacent vertices to w are also adjacent to v.
References
Cantero Morán, F., Silvero, M.: Extreme Khovanov spectra. Rev. Mat. Iberoam. 36(3), 661–670 (2020)
Dasbach, O.T., Lowrance, A.M.: Extremal Khovanov homology of Turaev genus one links. Fundam. Math. 250(1), 63–99 (2020)
González-Meneses, J., Manchón, P.M.G., Silvero, M.: A geometric description of the extreme Khovanov cohomology. Proc. R. Soc. Edinb. Sect. A Math. 148(3), 541–557 (2018)
Khovanov, M.: A categorification of the Jones polynomial. Duke Math. J. 101(3), 359–426 (2000)
Lawson, T., Lipshitz, R., Sarkar, S.: The Cube and the Burnside Category, Categorification in Geometry, Topology, and Physics, Contemp. Math., vol. 684, pp. 63–85. Amer. Math. Soc, Providence (2017)
Lawson, T., Lipshitz, R., Sarkar, S.: Khovanov homotopy type, Burnside category, and products. Geom. Topol. 24, 623–745 (2020)
Lipshitz, R., Sarkar, S.: A Khovanov stable homotopy type. J. Am. Math. Soc. 27(4), 983–1042 (2014)
Lipshitz, R., Sarkar, S.: Spatial refinements and Khovanov homology. Proc. Int. Congr. Math. 1, 1151–1172 (2018)
Przytycki, J.H., Sazdanović, R.: Torsion in Khovanov homology of semi-adequate links. Fundam. Math. 225(1), 277–304 (2014)
Przytycki, J.H., Silvero, M.: Homotopy type of circle graph complexes motivated by extreme Khovanov homology. J. Algebr. Comb. 48, 119–156 (2018)
Przytycki, J.H., Silvero, M.: Geometric realization of the almost-extreme Khovanov homology of semiadequate links. Geom. Dedicata 204(1), 387–401 (2020)
Sazdanovic, R., Scofield, D.: Extremal Khovanov homology and the girth of a knot. To appear in J. Knot Theory Ramif. arXiv:2003.05074v1
Viro, O.: Khovanov homology, its definitions and ramifications. Fundam. Math. 184, 317–342 (2004)
Acknowledgements
The authors thank Carles Casacuberta for his guidance and advice at early stages of this project.
Funding
Open Access funding provided thanks to the CRUE-CSIC agreement with Springer Nature.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Both authors were supported by the Spanish projects MTM2016-76453-C2, MDM-2014-0445 and FEDER. The first author was partially supported by project PID2019-108936GB-C21. The second author was partially supported by projects PID2020-117971GB-C21, US-1263032, and IJC2019-040519-I/AE.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cantero Morán, F., Silvero, M. Almost-extreme Khovanov spectra. Sel. Math. New Ser. 27, 95 (2021). https://doi.org/10.1007/s00029-021-00706-6
Accepted:
Published:
DOI: https://doi.org/10.1007/s00029-021-00706-6



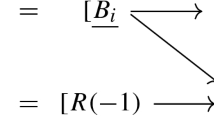
 of the cube, a 2-morphism
of the cube, a 2-morphism  ,
,  , the following commutes:
, the following commutes: 























