Abstract
Conservation laws with an x-dependent flux and Hamilton–Jacobi equations with an x-dependent Hamiltonian are considered within the same set of assumptions. Uniqueness and stability estimates are obtained only requiring sufficient smoothness of the flux/Hamiltonian. Existence is proved without any convexity assumptions under a mild coercivity hypothesis. The correspondence between the semigroups generated by these equations is fully detailed. With respect to the classical Kružkov approach to conservation laws, we relax the definition of solution and avoid any restriction on the growth of the flux. A key role is played by the construction of sufficiently many entropy stationary solutions in \({{\textbf{L}}^\infty }\) that provide global bounds in time and space.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
This paper provides a framework where Cauchy problems for x-dependent scalar conservation laws, such as

and Cauchy problems for x-dependent scalar Hamilton–Jacobi equations, such as

are globally well posed and a complete identification between the two problems is possible.
The well-posedness of both (CL) and (HJ) is here proved under the same assumptions on the function H, which is the flux of (CL) and the Hamiltonian of (HJ). These assumptions define a framework included neither in the one outlined by Kružkov in his classical work [27] devoted to (CL), nor in the usual assumptions on (HJ) found in the literature, e.g., [3, 4, 14, 25]. The identification of (CL) with (HJ) is then formalized, extending to the non-homogeneous case [26, Theorem 1.1], see also [10, Proposition 2.3]. This deep analogy also stems out from the direct identification of the constants appearing in the various stability estimates for the 2 equations, compare, for instance, (2.13) with (2.18).
A key role is played below by the handcrafted construction of a family of stationary entropy solutions to (CL), with a merely \({{\textbf{L}}^\infty }\) regularity, that provides the necessary uniform bounds on the vanishing viscosity limits, see Theorem 2.9.
The framework we propose is based on these assumptionsFootnote 1 on H:




However, in all general a priori estimates and qualitative properties, exclusively condition (C3) is used. Here, both (UC) and (WGNL) are shown to be not necessary to prove the trace at zero condition [27, Formula (2.2)], the semigroup property, the \({{\textbf{L}}_{\textbf{loc}}^{1}}\) continuity in time and the contraction property [27, Formula (3.1)] in the case of (CL).
Condition (CNH) qualifies the non-homogeneity of H and is apparently not common in the current literature on (CL) and (HJ). Our approach can be seen as somewhat related to [17, Section 5], where the space variable varies on a torus. Remarkably, X plays no quantitative role: it is required to exist, but its value is irrelevant. Thus, we expect (CNH) might possibly be relaxed.
Here, (UC) replaces the usual condition \(\sup _{(x,u) \in {\mathbb {R}}^2}\left( - \partial ^2_{xu} H (x,u)\right) < +\infty \), see (1.1), that was introduced by Kružkov back in [27, Formula (4.2)] and that has since become standard in any existence proof. Example 1.1 motivates the necessity to abandon it in the context of (CL). Moreover, this growth condition does not have, apparently, a clear counterpart among the usual assumptions on (HJ). Note, however, that several coercivity conditions appear in the context of (HJ), see, for instance, [4, § 2.4.2]. In particular, in the convex case, (UC) directly ensures \({{\textbf{L}}^\infty }\) bounds, as shown for instance in [41, Theorem 8.2.2]. Recall that also in [32, 33] some regularity assumptions on the Hamiltonian are relaxed, but not those requiring a suitable growth.
When dealing with (HJ), the convexity of H is a recurrent hypothesis, see, for instance, [3, 4, 13, 25], since it connects Hamilton–Jacobi equations to optimal control problems. On the other hand, convexity is typically not required in basic well-posedness results on scalar conservation laws, see [16, 27]. Here, differently from [3, 4, 15, 16, 41], no convexity assumption on the Hamiltonian in (HJ) is requested and, hence, characteristics are hardly of any help. Below we adopt (WGNL), which essentially asks that for a.e. x there does not exist any (non-empty) open set where \(u\mapsto H (x,u)\) is linear, but clearly allows also for infinitely many inflection points. Thus, for all x in a null set, \(u \mapsto H (x,u)\) may well be locally affine. Refer to Remark 2.22 for a stability estimate on (HJ) allowed by (WGNL).
Moreover, we neither pose any strict monotonicity assumptions on H as done, for instance, in [9] where, on the other side, H may well be only piecewise continuous in space and in time.
The classical reference for the well-posedness of general scalar balance laws is Kružkov’s paper [27]. Kružkov’s assumptions [27, § 4, p. 230] in the present notation take the form:
and the initial datum is required to satisfy \(u_o \in {{\textbf{L}}^\infty }({\mathbb {R}}; {\mathbb {R}})\). Our assumptions are not contained in Kružkov’s hypotheses. On the other hand, clearly, Kružkov result applies to general balance laws in several space dimensions.
Example 1.1
Fix positive constants \(X, V_1, V_2\) and let \(v \in {\textbf{C}}^{3} ({\mathbb {R}}; ]0, +\infty [)\) be such that \(v (x) = V_1\) for \(x < -X\) and \(v (x) = V_2\) for \(x > X\). Define \(H (x,u) \,{:=}\,v (x) \; u \; (1-u)\). Then, \(\partial _t u + \partial _x H (x,u)=0\) is the Lighthill–Whitham [29] and Richards [36] model for a flow of vehicles described by their density u along a rectilinear road with maximal speed smoothly varying from \(V_2\), for \(x>X\), to \(V_1\), for \(x < -X\).
This Hamiltonian H satisfies (C3)–(CNH)–(UC)–(WGNL) but does not satisfy the latter requirement in (1.1).
For completeness, we add that a standard truncation argument could be used to extend Kružkov result to Example 1.1, as soon as the initial datum attains values between the stationary solutions \(u (t,x) = 0\) and \(u (t,x) = 1\). Note, however, that the a priori estimates and qualitative properties in Sect. 2.1 as well as the construction of stationary solutions in Sect. 2.2 are in general preliminary to any truncation argument. Technically, it is essentially due to our adopting (UC) that we can avoid truncation arguments. Moreover, such an argument applies to (CL) but hinders our simultaneous treatment of (CL) and (HJ). Thus, we provide an existence proof alternative to that by Kružkov and explicitly state the correspondence between (CL) and (HJ) in Sects. 2.3, 2.4 and 2.5.
To our knowledge, only few results in the literature focus on the (CL) \(\leftrightarrow \) (HJ) connection. The homogeneous, x independent, stationary case is considered in the \(\textbf{BV}\) case in [26] (by means of wave front tracking), see also [8, § 6] for the case of fractional equations. An extension to \({{\textbf{L}}^\infty }\) is in the more recent [10] (where Dafermos’ [15] theory of generalized characteristics play a key role). The stationary x dependent case is considered in [6] (using semigroups generated by accretive operators). Here, we deal with the non-stationary x dependent case, relying on vanishing viscosity approximations and on the compensated compactness machinery. In this connection, note that the techniques developed in [32, 33] cannot be directly applied here, due to our need of passing to the limit also in the Hamiltonian.
Remark that in Kružkov’s paper [27], the latter condition in (1.1) is essential to obtain uniform \({{\textbf{L}}^\infty }\) and \(\textbf{BV}\) bounds on the sequence of viscous approximations in the case \(u_o \in {{\textbf{L}}^\infty }({\mathbb {R}}; {\mathbb {R}})\). In our approach, which does not rely on (1.1), the \({{\textbf{L}}^\infty }\) bound on viscous solutions depends on the fact that \(u_o \in {{\textbf{W}}^{1,\infty }}({\mathbb {R}}; {\mathbb {R}})\). We thus need to devise new additional bounds, provided by the stationary solutions to (CL), see Sect. 2.2, which are specific to the non-viscous case, and allow to pass from data in \({{\textbf{W}}^{1,\infty }}\) to data in \({{\textbf{L}}^\infty }\) at the non-viscous level.
In the literature, a recurrent tool in existence proofs for (CL) is the (parabolic) Maximum Principle, see for instance [23, Theorem B.1, Formula (B.3)] or [24, § 3.2], which provides an a priori uniform bound on vanishing viscosity approximate solutions, which is an essential step in passing to the vanishing viscosity limit. More precisely, only in the homogeneous case where \(\partial _x H \equiv 0\), the Maximum Principle ensures that
-
1.
vanishing viscosity approximate solutions have a common \({{\textbf{L}}^\infty }\) bound, and
-
2.
this bound only depends on the \({{\textbf{L}}^\infty }\) norm of the initial datum.
In the present—non-homogeneous—case, we replace (1) obtaining \({{\textbf{L}}^\infty }\) bounds on vanishing approximate solutions by means of a, here suitably adapted, Bernstein method, see [39, § 6] for a general introduction. This requires a higher regularity of the initial datum and (2) above is irremediably lost.
However, in the homogeneous case, one also takes advantage of the fact that constants are stationary solutions, ensuring 2. easily. This fact fails in the non-homogeneous case. Below, we exhibit (sort of) foliations of \({\mathbb {R}}\times [{\mathcal {U}}, +\infty [\) and \({\mathbb {R}}\times ]-\infty , -{\mathcal {U}}]\) (for a sufficiently large \({\mathcal {U}}\)) consisting of graphs of stationary solutions to (CL), each contained in a level curve of H. Then, solutions to (CL) are well known to preserve the ordering [16, Formula (6.2.8)] and 2. follows. Note that these stationary solutions need to be merely \({{\textbf{L}}^\infty }\). Therefore, in their construction, the choice of jumps deserves particular care to ensure that they turn out to be entropy admissible. In general, the solutions to (HJ) corresponding to stationary solutions to (CL) may well be non-stationary.
The differences between the construction below and the classical one by Kružkov [27] arise from the different choices of the assumptions but are not limited to that. Indeed, the two procedures differ in several key points. In [27], uniform \({{\textbf{L}}^\infty }\) “parabolic” bounds on vanishing viscosity approximate solutions to (CL) are obtained and \({{\textbf{L}}^1}\) compactness follows from Kolmogorov criterion. Here, the stationary solutions constructed as described above allow to obtain \({{\textbf{L}}^\infty }\) “hyperbolic” bounds directly on the solutions to (CL), while it is an application of the compensated compactness machinery that ensures the existence of a limit, thanks to our modified (weakened) definition of solution. Under (WGNL), also the kinetic approach in [30, 34] is likely to allow for analogous results. Moreover, in [27] the term \(-\partial _x H\) is essentially treated as a contribution to the source term. Here, we exploit the conservative form of (CL), thus respecting the analogy between (CL) and (HJ). Our weakening of Kružkov definition, motivated also by our use of compensated compactness, avoids any requirement on the trace at time \(0+\). It is of interest that this construction actually relies also on a sort of stability with respect to the flux H, where condition (WGNL) appears essential.
However, continuity in time, not proved in [27], is recovered in weak-\(*\) \({{\textbf{L}}_{\textbf{loc}}^{\infty }}({\mathbb {R}}; {\mathbb {R}})\) in Proposition 2.5 and in \({{\textbf{L}}_{\textbf{loc}}^{1}}\) in Theorem 2.6, always relying exclusively on condition (C3). Differently from [7, 42], condition (WGNL) plays here no role. Thus, in the present setting, the trace at \(0+\) condition [27, Formula (2.2)] can be omitted from the definition of solution to (CL) without any consequence.
Throughout this paper, we alternate considering (CL) and (HJ), simultaneously gathering step by step results on the two problems. When H does not depend on the space variable x, [26, Theorem 1.1] and [10, Proposition 2.3] ensure the equivalence between (CL) and (HJ). In the space homogeneous case, the correspondence between (CL) and (HJ) is exploited in [5, 31] and it is particularly effective in the characterization of the initial data evolving into a given profile at a given time, see [10, 28]. Below, we extend this equivalence to the x dependent case, while [11] is devoted to the inverse design problem in the x-dependent case. This correspondence may also suggest new properties of (CL) or (HJ), proving them in the present framework, posing the question of an intrinsic proof in more general settings, see Remark 2.22. As a matter of fact, our original goal was the detailed description of the relation between (CL) and (HJ), but such a correspondence requires the two Cauchy problems to be settled in the same framework.
In this paper, results are presented in the paragraphs in Sect. 2, while all proofs are collected in the corresponding paragraphs in Sect. 3.
Paragraph 2.1 presents the weakened definition of solution to (CL) and verifies that it still ensures uniqueness, the contraction property and continuity in time. Analogous results for (HJ) are proved independently. Proofs use neither (CNH), nor (UC) nor (WGNL) and are deferred to § 3.1.
Paragraph 2.2, where (UC) is essential, is devoted to the construction of a family of stationary entropy solutions to (CL). It has no counterpart referred to (HJ), it is intrinsic to (CL). The actual construction is in Sect. 3.2.
Paragraph 2.3 deals with the vanishing viscosity approximations to (CL) and to (HJ). The interplay between the 2 problems is exploited: all proofs, deferred to Sect. 3.3, are obtained for only one of the two equations, a quick corollary allowing to pass to the other equation.
Paragraph 2.4 ensures that vanishing viscosity solutions converge, up to subsequences, in both cases of (CL) and (HJ). The corresponding proofs in Sect. 3.4, where the (CL) case relies on the compensated compactness method.
Paragraph 2.5 collects the final results, showing the properties of the semigroups \(S^{CL}\) and \(S^{HJ}\) generated by (CL) and (HJ) and detailing how they correspond to each other. The proofs are in Sect. 3.5.
The main goal of this paper are the results in Paragraph 2.5.
2 Main results
Throughout this work, T denotes a strictly positive time or \(+\infty \).
2.1 Definitions of solution, local contraction and uniqueness
In this paragraph, we let \(u_o \in {{\textbf{L}}^\infty }({\mathbb {R}};{\mathbb {R}})\) while we require exclusively (C3) on H. No genuine nonlinearity condition is assumed, not even (WGNL), differently from [7, 42] (that have different goals and motivations).
Concerning the notion of solution to (CL), we modify that in the sense of Kružkov [27, Definition 1]. Indeed, in view of the compensated compactness technique used below, we do not require continuity in time in the sense of [27, Formula (2.2)]. On the contrary, full \({{\textbf{L}}_{\textbf{loc}}^{1}}\) continuity in time is here proved, merely on the basis of (C3).
With reference to (CL), the following quantity often recurs below, where \(x,u,k \in {\mathbb {R}}\):
Definition 2.1
A function \(u \in {{\textbf{L}}^\infty }([0,T] \times {\mathbb {R}}; {\mathbb {R}})\) is an entropy solution to (CL) if for all nonnegative test functions \(\varphi \in {\textbf{C}}_c^{1}([0,T[ \times {\mathbb {R}}; {\mathbb {R}}^+)\) and for all \(k \in {\mathbb {R}}\),
In (2.2), the integral term on the last line allows to avoid requiring the existence of the strong trace at \(0+\), as required in [27, Definition 1]. Hence, Definition 2.1 is more amenable to various limiting procedures. Nevertheless, [27, Definition 1] clearly implies Definition 2.1, while Theorem 2.6 ensures the global in time strong continuity and recovers all properties of the classical Kružkov definition, in particular the existence of the strong trace at \(0+\). Hence, Definition 2.1 and [27, Definition 1] are indeed equivalent.
Remark 2.2
Using \(k \ge {\left\| u\right\| }_{{{\textbf{L}}^\infty }([0,T]\times {\mathbb {R}}; {\mathbb {R}})}\) and \(k \le - {\left\| u\right\| }_{{{\textbf{L}}^\infty }([0,T]\times {\mathbb {R}}; {\mathbb {R}})}\) in (2.2) shows that solutions to (CL) in the sense of Definition 2.1 are also distributional solutions, in the sense that for all test function \(\varphi \in {\textbf{C}}_c^{1}([0,T[ \times {\mathbb {R}}; {\mathbb {R}})\)
We recall what we mean by entropy–entropy flux pair for (CL).
Definition 2.3
Let \(H \in {\textbf{C}}^{1} ({\mathbb {R}}^2; {\mathbb {R}})\). A pair of functions (E, F) with \(E \in \textbf{Lip}({\mathbb {R}}; {\mathbb {R}})\) and \(F \in \textbf{Lip}({\mathbb {R}}^2; {\mathbb {R}})\) is an entropy–entropy flux pair with respect to H if for all \(x \in {\mathbb {R}}\) and for a.e. \(u \in {\mathbb {R}}\)
The classical Kružkov choice in (2.4) amounts to set, for \(k \in {\mathbb {R}}\),
By (C3), we can substitute (2.4) by
where \(k \in {\mathbb {R}}\), which applies also when E is merely in \({\textbf{C}}^{0} ({\mathbb {R}}; {\mathbb {R}})\). As soon as E is Lipschitz continuous, any pair (E, F) satisfying (2.6) also satisfy Definition 2.3.
We now check that the present Definition 2.1 keeps ensuring the properties of the original Kružkov definition [27, Definition 1]. First, we deal with the choice of the admissible entropies.
Proposition 2.4
Let H satisfy (C3).
-
1.
Call u a solution to (CL) with initial datum \(u_o \in {{\textbf{L}}^\infty }({\mathbb {R}};{\mathbb {R}})\), according to Definition 2.1. Then, for any entropy–entropy flux pair (E, F) with respect to H in the sense of Definition 2.3, if E is convex and in \({\textbf{C}}^{1} ({\mathbb {R}}; {\mathbb {R}})\) then
$$\begin{aligned}{} & {} \displaystyle \int _0^T \int _{{\mathbb {R}}} \left( E\left( u (t,x)\right) \, \partial _t \varphi (t,x) + F\left( x, u (t,x)\right) \, \partial _x \varphi (t,x) \right) {\textrm{d}{x}} {\textrm{d}{t}} \nonumber \\{} & {} \quad - \int _0^T \int _{{\mathbb {R}}} \left( E'\left( u (t,x)\right) \; \partial _x H\left( x, u (t,x)\right) - \partial _x F\left( x, u (t,x)\right) \right) \varphi (t,x) {\textrm{d}{x}} {\textrm{d}{t}} \nonumber \\{} & {} \quad +\int _{{\mathbb {R}}} E\left( u_o (x)\right) \, \varphi (0,x) {\textrm{d}{x}} \ge 0 \end{aligned}$$(2.7)for any test function \(\varphi \in {\textbf{C}}_c^{1} ([0,T[ \times {\mathbb {R}}; {\mathbb {R}}_+)\).
-
2.
If \(u_o \in {{\textbf{L}}^\infty }({\mathbb {R}}; {\mathbb {R}})\), \(u \in {{\textbf{L}}^\infty }([0,T]\times {\mathbb {R}}, {\mathbb {R}})\) and (2.7) holds for any entropy–entropy flux pair (E, F) with respect to H in the sense of Definition 2.3, with E convex and in \({\textbf{C}}^{\infty }({\mathbb {R}}; {\mathbb {R}})\), then u solves (CL) in the sense of Definition 2.1.
Note that (2.7) corresponds to
in the sense of distributions.
As a first step, we prove that Definition 2.1 ensures the weak-\(*\) \({{\textbf{L}}_{\textbf{loc}}^{\infty }}({\mathbb {R}}; {\mathbb {R}})\) time continuity.
Proposition 2.5
Let H satisfy (C3). Fix the initial datum \(u_o \in {{\textbf{L}}^\infty }({\mathbb {R}}; {\mathbb {R}})\). Assume that the Cauchy Problem (CL) admits the distributional solution u in the sense of Remark 2.2. Then, for all \(a,b \in {\mathbb {R}}\) with \(a<b\), setting
we have for almost all \({\bar{t}}, t_1, t_2 \in [0,T]\)
Even without the nonlinearity condition (WGNL), we can single out a particular representative of any solution, so that we obtain the continuity in time in the (strong) \({{\textbf{L}}_{\textbf{loc}}^{1}}\) topology, the uniqueness of solutions and their stability with respect to initial data for all times. Indeed, the next theorem shows that (2.9) and (2.10) hold at every time and with the same \(K^{CL}\), provided at all times suitable representative \(u_* (t, \cdot )\) is carefully chosen.
Theorem 2.6
Let H satisfy (C3).
-
1.
Fix the initial datum \(u_o \in {{\textbf{L}}^\infty }({\mathbb {R}}; {\mathbb {R}})\). Assume that the Cauchy problem (CL) admits the solution u in the sense of Definition 2.1 on [0, T]. Then, u admits a representative, say \(u_*\), such that
-
(a)
For a.e. \(x \in {\mathbb {R}}\), \(u_* (0,x) = u_o (x)\).
-
(b)
For all \(a,b \in {\mathbb {R}}\) with \(a<b\) and for all \(t_1, t_2 \in [0,T]\)
$$\begin{aligned} {\left| \int _a^b \left( u_*(t_2,x) - u_*(t_1,x)\right) {\textrm{d}{x}} \right| } \le K^{CL} \; {\left| t_2 - t_1\right| }, \end{aligned}$$(2.11)with \(K^{CL}\) defined as in (2.8).
-
(c)
For all \(R \in {\mathbb {R}}_+\) and for all \({\bar{t}} \in [0,T]\)
$$\begin{aligned} \lim _{t \rightarrow {\bar{t}}} \int _{-R}^R {\left| u_*(t,x) - u_* ({\bar{t}},x)\right| } {\textrm{d}{x}} = 0. \end{aligned}$$(2.12)
-
(a)
-
2.
Fix the initial data \(u_o, v_o \in {{\textbf{L}}^\infty }({\mathbb {R}}; {\mathbb {R}})\). Assume that the corresponding Cauchy problems (CL) admit the solutions u, v in the sense of Definition 2.1 on [0, T]. Define
$$\begin{aligned} C&\,{:=}\,\max \left\{ {\left\| u\right\| }_{{{\textbf{L}}^\infty }([0,T] \times {\mathbb {R}}; {\mathbb {R}})} , {\left\| v\right\| }_{{{\textbf{L}}^\infty }([0,T] \times {\mathbb {R}}; {\mathbb {R}})} \right\} \,, \nonumber \\ L&\,{:=}\,\sup \left\{ {\left| \partial _u H (x,w)\right| } :x \in {\mathbb {R}}\hbox { and } {\left| w\right| } \le C \right\} \,, \end{aligned}$$(2.13)and assume \(L < +\infty \). Then, all representatives \(u_*\) and \(v_*\) satisfying Item 1 above are such that for all \(t \in [0,T]\) and for all \(R > 0\)
$$\begin{aligned} \int _{-R}^R {\left| u_* (t, x) - v_* (t, x)\right| } {\textrm{d}{x}}\le & {} \int _{-R - L t}^{R + L t} {\left| u_o (x) - v_o (x)\right| } {\textrm{d}{x}}, \end{aligned}$$(2.14)$$\begin{aligned} \int _{-R}^R [u_* (t, x) - v_* (t, x)]^+ {\textrm{d}{x}}\le & {} \int _{-R - L t}^{R + L t} [u_o (x) - v_o (x)]^+ {\textrm{d}{x}}. \end{aligned}$$(2.15)In particular,
$$\begin{aligned} {\left\| u_* (t,\cdot ) - v_* (t,\cdot )\right\| }_{{{\textbf{L}}^1} ({\mathbb {R}}; {\mathbb {R}})} \le {\left\| u_o - v_o\right\| }_{{{\textbf{L}}^1} ({\mathbb {R}}; {\mathbb {R}})}. \end{aligned}$$(2.16)
We convene that when \((u_o-v_o) \not \in {{\textbf{L}}^1} ({\mathbb {R}}; {\mathbb {R}})\) the right hand side above is \(+\infty \) and (2.16) holds. Moreover, by (2.16), if \((u_o-v_o) \in {{\textbf{L}}^1} ({\mathbb {R}}; {\mathbb {R}})\), then \(\left( u^* (t,\cdot ) -v^* (t,\cdot )\right) \in {{\textbf{L}}^1} ({\mathbb {R}}; {\mathbb {R}})\) for all t.
Remark that Definition 2.1 implies that \(C < +\infty \) in (2.14). Then, condition (CNH), if assumed, ensures that L is finite.
Turning to the Hamilton–Jacobi equation (HJ), recall the apparently entirely different framework of the standard Crandall–Lions definition of viscosity solutions.
Definition 2.7
([13, Definition 5.3]) Let \(U \in {\textbf{C}}^{0}([0,T] \times {\mathbb {R}}, {\mathbb {R}})\) satisfy \(U (0) = U_o\).
-
(i)
U is a subsolution to (HJ) when for all test functions \(\varphi \in {\textbf{C}}^{1} (]0,T[ \times {\mathbb {R}}; {\mathbb {R}})\) and for all \((t_o, x_o) \in ]0,T[ \times {\mathbb {R}}\), if \(U - \varphi \) has a point of local maximum at the point \((t_o, x_o)\), then \(\partial _{t} \varphi (t_o, x_o) + H\left( x_o,\partial _x \varphi (t_o, x_o)\right) \le 0\);
-
(ii)
U is a supersolution to (HJ) when for all test functions \(\varphi \in {\textbf{C}}^{1} (]0,T[ \times {\mathbb {R}}; {\mathbb {R}})\) and for all \((t_o, x_o) \in ]0,T[ \times {\mathbb {R}}\), if \(U - \varphi \) has a point of local minimum at the point \((t_o, x_o)\), then \(\partial _{t} \varphi (t_o, x_o) + H\left( x_o,\partial _x \varphi (t_o, x_o)\right) \ge 0\).
-
(iii)
U is a viscosity solution to (HJ) if it is both a supersolution and a subsolution.
Definition 2.7 ensures uniqueness, extending to the present framework classical results, such as those in [4, 25].
Theorem 2.8
Let H satisfy (C3).
-
1.
Fix the initial datum \(U_o \in \textbf{Lip}({\mathbb {R}}; {\mathbb {R}})\). Assume the corresponding Cauchy problem (HJ) admits the function U as solution in the sense of Definition 2.7, Lipschitz continuous in space, uniformly in time on [0, T]. Define
$$\begin{aligned} K^{HJ} \,{:=}\,\sup \left\{ {\left| H (x,p)\right| } :x \in {\mathbb {R}}, {\left| p\right| } \le {\left\| \partial _x U\right\| }_{{{\textbf{L}}^\infty }([0,T] \times {\mathbb {R}}; {\mathbb {R}})} \right\} . \end{aligned}$$(2.17)We have for all \(t_1,t_2 \in [0,T]\)
$$\begin{aligned} {\left\| U (t_2) - U (t_1)\right\| }_{{{\textbf{L}}^\infty }({\mathbb {R}};{\mathbb {R}})} \le K^{HJ} \; {\left| t_2 - t_1\right| }. \end{aligned}$$ -
2.
Fix the initial data \(U_o,V_o \in \textbf{Lip}({\mathbb {R}}; {\mathbb {R}})\). Assume the corresponding Cauchy problems (HJ) admit the functions U, respectively, V, as subsolution, respectively, supersolution, Lipschitz continuous in space, uniformly in time on [0, T]. Define
$$\begin{aligned} C&\,{:=}\,\max \left\{ {\left\| \partial _x U\right\| }_{{{\textbf{L}}^\infty }([0,T] \times {\mathbb {R}}; {\mathbb {R}})} , {\left\| \partial _x V\right\| }_{{{\textbf{L}}^\infty }([0,T] \times {\mathbb {R}}; {\mathbb {R}})}\right\} \,; \nonumber \\ L&\,{:=}\,\sup \left\{ {\left| \partial _u H (x,p)\right| } :x \in {\mathbb {R}}\,,\; {\left| p\right| } \le C \right\} \,. \end{aligned}$$(2.18)If \(L < +\infty \), then, for all \(t \in [0,T]\), for all \(R >0\)
$$\begin{aligned} \max _{{\left| x\right| } \le R} \left( U (t,x) - V (t,x)\right) \le \max _{{\left| x\right| } \le R+Lt} \left( U_o (x) - V_o (x)\right) . \end{aligned}$$(2.19)
Remark that the Lipschitz continuity assumptions in Item 2 of Theorem 2.8 precisely mean that \(C < +\infty \). Requiring also condition (CNH), then ensures that L is finite.
We underline the evident deep analogy between Theorem 2.6 referring to the conservation law (CL) and Theorem 2.8 referring to the Hamilton–Jacobi equation (HJ). The definitions (2.13) and (2.18) are essentially identical. Note moreover that the factor 2 appearing in (2.8) and not in (2.17) is a mandatory consequence of the correspondence between the two equations formalized in Sect. 2.5.
2.2 A bounding family of stationary solutions
Essential to get the necessary global in time \({{\textbf{L}}^\infty }\) bounds on the solutions to (CL) is Theorem 2.9. In the homogeneous case, a sufficient supply of stationary solutions is immediately provided by constant functions, which are clearly also entropic. Here, we need to find \({{\textbf{L}}^\infty }\) solutions that, first, are entropic and, second, are sufficiently many to ensure the necessary \({{\textbf{L}}^\infty }\) bounds, together with the order preserving property (2.15) in Theorem 2.6.
Theorem 2.9
Let H satisfy (C3)–(CNH)–(UC)–(WGNL). Then, for all \(U>0\), (CL) admits stationary entropy solutions \(u_-, u_+ \in {{\textbf{L}}^\infty }({\mathbb {R}}; {\mathbb {R}})\), i.e., solutions in the sense of Definition 2.1, that satisfy
The proof begins with a careful construction of piecewise \({\textbf{C}}^{1}\) stationary entropic solutions by means of the Implicit Function Theorem and Sard’s Lemma for a particular class of fluxes whose level sets enjoy suitable geometric properties. Then, compensated compactness allows to pass to the limit on the fluxes, essentially showing a stability of solutions with respect to the flux, thus getting back to the general case. In this connection, we recall that already in [1, 2] stationary solutions are assigned a key role in selecting solutions.
In the correspondence between (CL) and (HJ), the stationary solutions to (CL) constructed in Theorem 2.9 have as counterpart viscosity solutions to (HJ) that may well be non-stationary, see (2.28), and are Lipschitz continuous but, in general, not differentiable.
2.3 Vanishing viscosity approximations
We now proceed toward existence results both for (CL) and for (HJ), obtained through vanishing viscosity approximations, under the assumptions (C3)–(CNH)–(UC). Thus, we consider the Cauchy problems
and
As a first step, we specify what we mean by classical solutions to (2.20) and to (2.21).
Definition 2.10
Let I be an open real interval and \(\varepsilon >0\). A classical solution to (2.20) on \(]0,T[ \times I\) is a function
satisfying \(\partial _{t}u (t,x) + \partial _{x} H\left( x,u (t,x)\right) = \varepsilon \; \partial ^2_{xx} u (t,x)\) for all \((t,x) \in ]0,T[ \times I\) and \(u (0,x) = u_o (x)\) for all \(x \in {\overline{I}}\).
A classical solution to (2.21) on \(]0,T[ \times {\mathbb {R}}\) is a function
satisfying \(\partial _{t}U (t,x) + H\left( x,\partial _x U (t,x)\right) = \varepsilon \; \partial ^2_{xx} U (t,x)\) for all \((t,x) \in ]0,T[ \times I\) and \(U (0,x) = U_o (x)\) for all \(x \in {\overline{I}}\).
Note that (2.23) in Definition 2.10 requires 3 space derivatives in U, although the third derivative does not appear in (2.21).
We now prove that the Cauchy problems (2.20) and (2.21) are equivalent.
Theorem 2.11
Call I a non-empty open real interval and fix \(T > 0\). Let H satisfy (C3) and \(\varepsilon > 0\). Fix \(u_o \in {{\textbf{W}}^{1,\infty }}(I; {\mathbb {R}})\) and \(U_o \in {\textbf{C}}^{1} ({\mathbb {R}}; {\mathbb {R}})\) such that \(U_o'= u_o\). Then, the problems (2.20) and (2.21) are equivalent in the sense that:
-
(1)
Assume u is a classical solution to (2.20) on I in the sense of Definition 2.10. Then, for any \(x_o \in I\), the map \(U :[0,T] \times I \rightarrow {\mathbb {R}}\) defined by
$$\begin{aligned} \qquad \quad U (t,x) \,{:=}\,\int _{x_o}^x u (t,\xi ) {\textrm{d}{\xi }}+ \int _0^t \left( -H\left( x_o, u (\tau ,x_o)\right) + \varepsilon \, \partial _x u (\tau ,x_o) \right) {\textrm{d}{\tau }}+ U_o (x_o)\nonumber \\ \end{aligned}$$(2.24)is the solution to (2.21) on I in the sense of Definition 2.10.
-
(2)
Assume U is a classical solution to (2.21) on I in the sense of Definition 2.10. Then, the map \(u :[0,T] \times I \rightarrow {\mathbb {R}}\) defined by
$$\begin{aligned} u (t,x) \,{:=}\,\partial _x U (t,x) \end{aligned}$$is a classical solution to (2.20) on I in the sense of Definition 2.10.
We first get a priori estimates on the solutions to (2.21) and then on those to (2.20).
Theorem 2.12
Let H satisfy (C3)–(CNH)–(UC). Choose \(U_o \in {\textbf{C}}^{1} ({\mathbb {R}}; {\mathbb {R}})\) with \(U_o' \in \textbf{Lip}({\mathbb {R}}; {\mathbb {R}})\). Then, there exists a constant M such that for any \(\varepsilon >0\) sufficiently small, for any \(T \in {\mathbb {R}}_+\) and for any classical solution U to (2.21) defined on \([0,T] \times {\mathbb {R}}\) we have
Since T is arbitrary both in Theorem 2.11 and in Theorem 2.12 and moreover M in (2.25) is independent of T (and \(\varepsilon \)), both results apply also to the case \(T = +\infty \).
Corollary 2.13
Let H satisfy (C3)–(CNH)–(UC). Choose \(u_o \in {{\textbf{W}}^{1,\infty }}({\mathbb {R}}; {\mathbb {R}})\). Then, there exists a constant M such that for any \(\varepsilon >0\) sufficiently small, for any \(T \in {\mathbb {R}}_+\) and for any classical solution u to (2.20) defined on \([0,T] \times {\mathbb {R}}\) which is also bounded,
the case \(T = +\infty \) is not excluded.
Thanks to Theorem 2.11, applied with \(I={\mathbb {R}}\), the proof of Corollary 2.13 is a direct consequence of Theorem 2.12 and is hence omitted.
Theorem 2.14
Let H satisfy (C3) and (CNH). Choose an initial datum \(u_o \in {{\textbf{W}}^{1,\infty }}({\mathbb {R}}; {\mathbb {R}})\). Then, for all \(\varepsilon > 0\) sufficiently small, the Cauchy problem (2.20) admits a classical solution in the sense of Definition 2.10 on \({\mathbb {R}}\) defined for all \(t \in {\mathbb {R}}_+\).
Corollary 2.15
Let H satisfy (C3)–(CNH)–(UC). Choose \(U_o \in {\textbf{C}}^{0} ({\mathbb {R}}; {\mathbb {R}})\) with \(U'_o \in {{\textbf{W}}^{1,\infty }}({\mathbb {R}}; {\mathbb {R}})\). Then, for all \(\varepsilon > 0\) sufficiently small, the Cauchy problem (2.21) admits a classical solution in the sense of Definition 2.10 on \({\mathbb {R}}\) defined for all \(t\in {\mathbb {R}}_+\).
Thanks to Theorem 2.11, applied with \(I={\mathbb {R}}\), the proof of Corollary 2.15 is a direct consequence of Theorem 2.14 and is hence omitted.
2.4 Existence of vanishing viscosity limits
We now deal with the vanishing viscosity limit of the solutions constructed in the previous Paragraph. Differently from [27], we complete this step in the case of more regular initial data, i.e., in the case where Theorem 2.12 and Corollary 2.13 apply.
Theorem 2.16
Let H satisfy (C3)–(CNH)–(UC). Choose an initial datum \(U_o \in {\textbf{C}}^{1} ({\mathbb {R}}; {\mathbb {R}})\) with \(U'_o \in {{\textbf{W}}^{1,\infty }}({\mathbb {R}}; {\mathbb {R}})\). Let \(\varepsilon _n\) be a sequence converging to 0. Then, the sequence \(U_{\varepsilon _n}\) of the corresponding classical solutions to (2.21) on \({\mathbb {R}}\) converges uniformly on all compact subsets of \({\mathbb {R}}_+ \times {\mathbb {R}}\) to a function \(U_* \in \textbf{Lip}({\mathbb {R}}_+ \times {\mathbb {R}}; {\mathbb {R}})\) which is a viscosity solution to (HJ).
Striving to treat (CL) and (HJ) in parallel, the next statement mirrors the previous one.
Theorem 2.17
Let H satisfy assumptions (C3)–(CNH)–(UC)–(WGNL). Fix an initial datum \(u_o \in {{\textbf{W}}^{1,\infty }}({\mathbb {R}}; {\mathbb {R}})\). Then, the classical solutions \(u_\varepsilon \) to (2.20) on \({\mathbb {R}}\) converge pointwise a.e. in \({\mathbb {R}}_+ \times {\mathbb {R}}\) to a function \(u \in {{\textbf{L}}^\infty }({\mathbb {R}}_+ \times {\mathbb {R}}; {\mathbb {R}})\) which is an entropy solution to (CL).
The proof, entirely different from that of Theorem 2.16, by means of (WGNL), relies on an ad hoc adaptation of classical compensated compactness arguments, see [16, Chapter 17] or [38, Chapter 9].
2.5 The limit semigroups and their equivalence
Here, we complete all previous steps obtaining the main results, stated in terms of the existence of the semigroups generated by (CL) and (HJ), their properties and their connection.
Theorem 2.18
Let H satisfy (C3)–(CNH)–(UC)–(WGNL). For all \(T>0\) and for any initial datum \(u_o \in {{\textbf{L}}^\infty }({\mathbb {R}}; {\mathbb {R}})\), there exists a unique entropy solution in \({{\textbf{L}}^\infty }([0,T]\times {\mathbb {R}}; {\mathbb {R}})\) in the sense of Definition 2.1, to (CL) on [0, T]. Moreover, the maximal in time solution u:
- 1.:
-
is globally defined in time, corresponding to \(T=+\infty \) in Definition 2.1.
- 2.:
-
is globally bounded, in the sense that \(u \in {{\textbf{L}}^\infty }({\mathbb {R}}_+ \times {\mathbb {R}}; {\mathbb {R}})\).
There exists a unique semigroup \(S^{CL} :{\mathbb {R}}_+ \times {{\textbf{L}}^\infty }({\mathbb {R}}; {\mathbb {R}}) \rightarrow {{\textbf{L}}^\infty }({\mathbb {R}}; {\mathbb {R}})\) such that for all \(u_o\) \((t,x) \mapsto (S^{CL}_t u_o) (x)\) solves (CL) in the sense of Definition 2.1 and enjoys the properties:
- 3.a:
-
For all \(u_o \in {{\textbf{L}}^\infty }({\mathbb {R}}; {\mathbb {R}})\), the map \(t \mapsto S^{CL}_t u_o\) is Lipschitz continuous with respect to the weak-\(*\) \({{\textbf{L}}_{\textbf{loc}}^{\infty }}({\mathbb {R}}; {\mathbb {R}})\) topology in the sense that there exists a \(K>0\) such that for all \(a,b \in {\mathbb {R}}\) with \(a<b\) and for all \(t_1,t_2 \in {\mathbb {R}}_+\)
$$\begin{aligned} {\left| \int _a^b \left( (S^{CL}_{t_2} u_o) (x) - (S^{CL}_{t_1} u_o) (x)\right) {\textrm{d}{x}} \right| } \le K \; {\left| t_2-t_1\right| }. \end{aligned}$$ - 3.b:
-
For all \(u_o \in {{\textbf{L}}^\infty }({\mathbb {R}}; {\mathbb {R}})\), the map \(t \mapsto S^{CL}_t u_o\) is continuous with respect to the \({{\textbf{L}}_{\textbf{loc}}^{1}} ({\mathbb {R}}; {\mathbb {R}})\) topology, in the sense that for all \({\bar{t}} \in {\mathbb {R}}_+\) and for all \(R>0\)
$$\begin{aligned} \lim _{t \rightarrow {\bar{t}}} \int _{-R}^R {\left| (S^{CL}_t u_o) (x) - (S^{CL}_{{\bar{t}}} u_o) (x)\right| } {\textrm{d}{x}} = 0. \end{aligned}$$ - 4.:
-
For all \(u_o,v_o \in {{\textbf{L}}^\infty }({\mathbb {R}}; {\mathbb {R}})\), define L as in (2.13). Then, for all \(t \in {\mathbb {R}}_+\) and for all \(R > 0\),
$$\begin{aligned} \int _{-R}^R {\left| (S^{CL}_t u_o) (x) - (S^{CL}_t v_o) (x)\right| } {\textrm{d}{x}} \le \int _{-R - L t}^{R + L t} {\left| u_o (x) - v_o (x)\right| } {\textrm{d}{x}}. \end{aligned}$$
Thanks to (CNH), \(K^{CL}\), as defined in (2.8), can be chosen independent of a and b, resulting in the K in 3.a. Bounds L and on \({\left\| u\right\| }_{{{\textbf{L}}^\infty }({\mathbb {R}}_+\times {\mathbb {R}}; {\mathbb {R}})}\) depending on \({\left\| u_o\right\| }_{{{\textbf{L}}^\infty }({\mathbb {R}}; {\mathbb {R}})}\) are provided in the proof, see Sect. 3.5.
Theorem 2.19
Let H satisfy (C3)–(CNH)–(UC)–(WGNL). For all \(T>0\) and for any initial datum \(U_o \in \textbf{Lip}({\mathbb {R}}; {\mathbb {R}})\), there exists a unique viscosity solution \(U \in \textbf{Lip}([0,T]\times {\mathbb {R}}; {\mathbb {R}})\) in the sense of Definition 2.7, to (HJ) on [0, T]. Moreover, the maximal in time solution U
- 1.:
-
is globally defined in time, corresponding to \(T=+\infty \) in Definition 2.7.
- 2.:
-
is globally Lipschitz continuous, in the sense that \(U \in \textbf{Lip}({\mathbb {R}}_+ \times {\mathbb {R}}; {\mathbb {R}})\).
There exists a unique semigroup \(S^{HJ} :{\mathbb {R}}_+ \times \textbf{Lip}({\mathbb {R}}; {\mathbb {R}}) \rightarrow \textbf{Lip}({\mathbb {R}}; {\mathbb {R}})\) such that for all \(U_o\) \((t,x) \mapsto (S^{HJ}_t U_o) (x)\) solves (HJ) in the sense of Definition 2.7 and enjoys the properties:
- 3.:
-
For all \(U_o \in \textbf{Lip}({\mathbb {R}}; {\mathbb {R}})\), the map \(t \mapsto S^{HJ}_t U_o\) is Lipschitz continuous in the \({{\textbf{L}}^\infty }\) norm.
- 4.:
-
For all \(U_o,V_o \in \textbf{Lip}({\mathbb {R}}; {\mathbb {R}})\), define L as in (2.18). Then, for all \(t \in {\mathbb {R}}_+\) and for all \(R >0\),
$$\begin{aligned} \max _{{\left| x\right| } \le R} \left( (S^{HJ}_t U_o) (x) - (S^{HJ}_t V_o) (x)\right) \le \max _{{\left| x\right| } \le R+Lt} \left( U_o (x) - V_o (x)\right) . \end{aligned}$$
Theorem 2.20
Let H satisfy assumptions (C3)–(CNH)–(UC)–(WGNL). Let the data \(u_o \in {{\textbf{L}}^\infty }({\mathbb {R}}; {\mathbb {R}})\) and \(U_o \in \textbf{Lip}({\mathbb {R}}; {\mathbb {R}})\) be such that \(U_o' (x) = u_o (x)\) for a.e. \(x \in {\mathbb {R}}\). Then, problems (CL) and (HJ) are equivalent in the sense that for all \(t \in {\mathbb {R}}_+\) and for a.e. \(x \in {\mathbb {R}}\),
Remark 2.21
In the same setting of Theorem 2.20, formally, as a consequence of (2.27), for a fixed \(x_o \in {\mathbb {R}}\), we can write
The latter integral on the right hand side in (2.28) is meaningful only under further regularity conditions, such as in the case H is convex in u, which ensures that \(S^{CL}_t u_o \in \textbf{BV}({\mathbb {R}}; {\mathbb {R}})\).
We can rephrase the above relations with the following commutative diagrams.

Remark 2.22
The correspondence between (CL) and (HJ) is instrumental in the existence results. Qualitative properties were independently obtained. However, Theorems 2.18 and 2.19 still lack a complete identification, thus suggesting possible improvements. The correspondence above between solutions to (CL) and to (HJ) actually gives more information than what is provided by Item 4 in Theorem 2.19. Indeed, Item 4 in Theorem 2.18 implies that \(S^{HJ}_t\) is non-expansive with respect to \({{\textbf{W}}_{\textbf{loc}}^{1,1}}\), i.e.,
We do not know of a proof of this bound for (HJ) independent from (CL).
3 Analytical proofs
Throughout,  denotes the characteristic function of the set I. \({\mathcal {L}}\) stands for the Lebesgue measure in \({\mathbb {R}}\) and we call negligible a set of Lebesgue measure 0. The positive part of a real number is \([x]^+ \,{:=}\,\left( x+{\left| x\right| }\right) /2\). Throughout, we set
denotes the characteristic function of the set I. \({\mathcal {L}}\) stands for the Lebesgue measure in \({\mathbb {R}}\) and we call negligible a set of Lebesgue measure 0. The positive part of a real number is \([x]^+ \,{:=}\,\left( x+{\left| x\right| }\right) /2\). Throughout, we set
3.1 Definitions of solution, local contraction and uniqueness
Lemma 3.1
Let \(E \in {\textbf{C}}^{1} ({\mathbb {R}}; {\mathbb {R}})\) be convex. For any \(\varepsilon , r > 0\), there exist \(n \in {\mathbb {N}}\); positive weights \(w_0, w_1, \ldots , w_n \in {\mathbb {R}}\) and points \(p_0, p_1, \ldots , p_n \in {\mathbb {R}}\) such that setting for all \(u \in {\mathbb {R}}\)
we have
The expression on the right in (3.2) is relevant when \(u=p_k\). Indeed, it allows to prove that the bound on the derivatives in (3.3) holds at every u and not only at a.e. u.
Proof of Lemma 3.1
Let \(\delta \) be a modulus of uniform continuity of \(E'\) on the interval \([-r, r]\) corresponding to \(\min \{\varepsilon , \varepsilon /(2r)\}\), so that
Choose n in \({\mathbb {N}}\) such that \(n \ge 2r/\delta \). Define the points \(p_k\) and the map \(\alpha :{\mathbb {R}}\rightarrow {\mathbb {R}}\) by
Note that \(\alpha \) is non-decreasing, since \(E'\) is. Set for \(u \in [-r, r]\), \({\tilde{\eta }} (u) \,{:=}\,E (-r) + \int _{-r}^u \alpha (v) {\textrm{d}{v}}\) so that the condition on the left in (3.3) is satisfied by \({\tilde{\eta }}\), as well as the one on the right for \(u \ne p_k\). Requiring the weights \(w_0, \ldots , w_n\) to solve the \((n+1)\times (n+1)\) linear system
ensures that \({\tilde{\eta }} = \eta \) as defined in (3.2) for \(u \in [a, b]\). The matrix of the above system is
and straightforward calculations show that its determinant is \((-1)^n \, r \, 2^n\). Hence, this matrix is invertible, so that the weights \(w_0, \ldots , w_n\) are uniquely defined. Moreover, differentiating \({\tilde{\eta }}\) we get \({\tilde{\eta }}' (p_k +) - {\tilde{\eta }}' (p_k-) = 2\, w_k\). Since \({\tilde{\eta }}'\) is non-decreasing, we have that \(w_k \ge 0\). We are left to prove that the expression for \(\eta '\) in (3.2) satisfy (3.3) also at \(u = p_k\). Since \(w_k \ge 0\), by the choice (3.1) and by the construction above, we have \(E' (p_k) - \varepsilon \le \eta ' (p_k-) \le \eta ' (p_k) \le \eta ' (p_k+) \le E' (p_k) + \varepsilon \). Possibly erasing the terms vanishing because \(w_k=0\), the proof is completed. \(\square \)
Proof of Proposition 2.4
Claim 1: Proof of Item 1.
Fix a positive \(\varepsilon \) and an entropy–entropy flux pair (E, F) in the sense of Definition 2.3. Call \(\eta \) the map (3.2) constructed in Lemma 3.1 corresponding to \(\varepsilon \) and \(r \,{:=}\,{\left\| u\right\| }_{{{\textbf{L}}^\infty }({\mathbb {R}}^2; {\mathbb {R}})}\). Using (3.1), we use the following representative of \(\eta '\) and of a flux related to \(\eta \), by (2.1):
Choose a test function \(\varphi \in {\textbf{C}}_c^{1} ([0,T[ \times {\mathbb {R}}; {\mathbb {R}}_+)\) and let Y be such that \(\mathop {\textrm{spt}}\varphi \subseteq [0,T] \times [ -Y,Y]\). By the linearity in the entropy/entropy flux and by the positivity of the weights,
Estimate the last three lines separately. To bound (3.4) use (3.3) (which holds on all \({\mathbb {R}}\)):
To estimate the term (3.5), recall that from (2.6)
Using (2.4), thanks to \(H \in {\textbf{C}}^{2} ({\mathbb {R}}^2; {\mathbb {R}})\), write
so that also using (3.2) and (3.7)

Passing to (3.6), use (3.3) to compute
Adding the resulting estimates, we obtain
where \({\mathcal {O}}(1)\) depends only on \(\varphi \) and on H. The proof of Claim 1 is completed. \(\checkmark \)
Claim 2: Proof of Item 2.
Fix a regularizing kernel \(\rho \in {\textbf{C}}_c^{\infty }({\mathbb {R}}; {\mathbb {R}})\) such that \(\rho \ge 0\), \(\rho (0)=0\), \(\mathop {\textrm{spt}}\rho \subseteq [-1, 1]\), \(\rho (-x) = \rho (x)\) for all \(x \in {\mathbb {R}}\) and \(\int _{{\mathbb {R}}} \rho = 1\). For any positive \(\varepsilon \), let \(\rho _\varepsilon (x) = (1/\varepsilon ) \, \rho (x/\varepsilon )\). Fix \(k \in {\mathbb {R}}\). Let E and F be as in (2.5). Recalling (2.6), define
Clearly, \(E_\varepsilon \) is \({\textbf{C}}^{\infty }\), \(F_\varepsilon \) is \({\textbf{C}}^{1}\) and are an entropy–entropy flux pair in the sense of Definition 2.3, so that (2.4) holds. Moreover, since \(E_\varepsilon (u) = \int _{{\mathbb {R}}} {\left| u-w-k\right| } \; \rho _\varepsilon (w) {\textrm{d}{w}}\), \(\rho \ge 0\) and the map \(u \mapsto {\left| u-w-k\right| }\) is convex for \(w \in {\mathbb {R}}\), for \(\vartheta \in [0,1]\) and for \(u_1,u_2 \in {\mathbb {R}}\) we have
hence \(E_\varepsilon \) is convex.
Use (2.7) and fix any test function \(\varphi \in {\textbf{C}}_c^{1} ([0,T[ \times {\mathbb {R}}; {\mathbb {R}}_+)\):
Note that (3.8) and (3.9) ensure the uniform convergence on compact sets of \(E_\varepsilon \) to E and of \(F_\varepsilon \) to F as \(\varepsilon \rightarrow 0+\). Therefore, it is immediate to pass to the limit \(\varepsilon \rightarrow 0+\) in (3.10) and (3.12). Indeed, with the notation (2.1),
Consider now (3.11). Definition (3.9), (2.6) and (C3) ensure that \(\partial _x F_\varepsilon \) converges uniformly on compact sets to \(\partial _x F\). To deal with the term \(E'_\varepsilon \), write
so that
Since \(\rho _\varepsilon \) is even, we have that \(E'_\varepsilon \) converges pointwise everywhere to \(E'\) as \(\varepsilon \rightarrow 0+\), with \({\left| E'\right| } \le 1\). Thus, the Dominated Convergence Theorem [22, Theorem (12.24)] allows to pass to the limit also in (3.11):
Combining the obtained estimates of the limit \(\varepsilon \rightarrow 0+\) of the terms (3.10)–(3.11)–(3.12) we get (2.2), completing the proof of Claim 2 and of Proposition 2.4. \(\square \)
Proof of Proposition 2.5
We adapt the arguments in [15, Lemma 3.2]. Therein, a similar result is obtained in a different setting: a source term is present, the flux is also time dependent but convex in u. Furthermore, the definition of solution in [15] requires the existence of both traces is required at any point for all time.
Proof of (2.10). Fix \(a,b \in {\mathbb {R}}\) with \(a<b\) and \(t_1,t_2 \in {\mathbb {R}}_+\) with \(t_1 < t_2\). For \(\varepsilon \in ]0, (b-a)/2[\), choose as \(\varphi \) in (2.3) the Lipschitz continuous map \(\varphi _\varepsilon (t,x) \,{:=}\,\chi _\varepsilon (t) \; \psi _\varepsilon (x)\) where
By equality (2.3) in Remark 2.2, we obtain
Recall the Definition (2.8) of \(K^{CL}\), so that the first line above is estimated as follows:
To compute the limit as \(\varepsilon \rightarrow 0\) of the left hand side in (3.14), observe first that

An entirely similar procedure yields

Recall that \(u \in {{\textbf{L}}^\infty }([0,T] \times {\mathbb {R}}; {\mathbb {R}})\), so that \(u \in {{\textbf{L}}^1} ([0,T] \times [a,b]; {\mathbb {R}})\). By Fubini Theorem [22, Theorem 21.13], for almost all \(t \in [0,T]\), the map \(x \mapsto u (t,x)\) is in \({{\textbf{L}}^1} ([a,b]; {\mathbb {R}})\) and the map \(t \mapsto \int _a^b u (t,x) {\textrm{d}{x}}\) is in \({{\textbf{L}}^1} ([0,T]; {\mathbb {R}})\). Thus, if \(t_1\) and \(t_2\) are Lebesgue points [19, Chapter 1, § 7, Theorem 1.34] of \(t \mapsto \int _a^b u(t,x) {\textrm{d}{x}}\), we have

The latter relations, together with the limits (3.15) and (3.16), inserted in (3.14) complete the proof of (2.10).\(\checkmark \)
Proof of (2.9). Fix \(a,b \in {\mathbb {R}}\) with \(a<b\) and \({\bar{t}} \in {\mathbb {R}}_+\). For \(\varepsilon \in ]0, (b-a)/2[\), choose as \(\varphi \) in (2.3) the map \(\varphi _\varepsilon (t,x) \,{:=}\,{\bar{\chi }}_\varepsilon (t) \; \psi _\varepsilon (x)\) where
and \(\psi _\varepsilon \) is as in (3.13). Repeat a procedure analogous to the one above choosing for \({\bar{t}}\) a Lebesgue point of the map \(t \mapsto \int _a^b u (t,x) {\textrm{d}{x}}\). The use of equality (2.3) in Remark 2.2 allows to let \(u_o\) appear explicitly.
The proof of Proposition 2.5 is completed. \(\square \)
Proof of Theorem 2.6
Fix a representative u of a solution to (CL) in the sense of Definition 2.1.
Claim 1: There exists a \(u^*\) such that \(u^* = u\) a.e. and \(u^*\) satisfies (a) and (b) in Item 1.
By (2.9)–(2.10), for all \(a,b \in {\mathbb {R}}\) with \(a<b\), there exists a negligible set \({\mathcal {N}}_{a,b} \subseteq [0,T]\) such that (2.10) holds for all \(t_1,t_2 \in {\mathbb {R}}_+ {\setminus } {\mathcal {N}}_{a,b}\) and (2.9) holds for all \(\bar{t} \in {\mathbb {R}}_+ \setminus {\mathcal {N}}_{a,b}\). Define
which is also negligible by the definition of the \({{\textbf{L}}^\infty }\) norm and by Fubini Theorem [22, Theorem 21.13] (set on the left) and by the choice of \({\mathcal {N}}_{a,b}\) (union on the right). Note that for all \({\bar{t}},t_1,t_2 \in [0,T] {\setminus } {\mathcal {N}}\) and for all \(a,b \in {\mathbb {Q}}\), u satisfies (2.9) and (2.10).
Fix now \(a,b \in {\mathbb {R}}\) with \(a < b\). Choose an increasing sequence \(a_n\) and a decreasing sequence \(b_n\), both of rational numbers, such that \(\lim _{n\rightarrow +\infty } a_n = a\), \(\lim _{n\rightarrow +\infty } b_n = b\) and \(a_n < b_n\). Then, \({\left| \int _{a_n}^{b_n} \left( u({\bar{t}},x) - u_o (x)\right) {\textrm{d}{x}} \right| }\) and \({\left| \int _{a_n}^{b_n} \left( u(t_2,x) - u (t_1,x)\right) {\textrm{d}{x}} \right| }\) are uniformly bounded by the right hand sides in (2.9) and in (2.10). The Dominated Convergence Theorem [22, Theorem (12.24)] thus applies proving that u satisfies (2.9) and (2.10) for all \({\bar{t}}, t_1,t_2 \in [0,T] \setminus {\mathcal {N}}\) and also for all \(a,b \in {\mathbb {R}}\).
Hence, for any real bounded interval I,  , for a constant \(C_I\) depending on I. This bound then holds also for all piecewise constant functions and, by further approximations, we know that for all \(f \in {{\textbf{L}}^1} ({\mathbb {R}}; {\mathbb {R}})\) and for all \(\varepsilon >0\), there exists \(\delta >0\) such that if \(t_1,t_2 \in [0,T] {\setminus } {\mathcal {N}}\) and \({\left| t_2-t_1\right| } {<} \delta \), then \({\left| \int _{{\mathbb {R}}} \left( u (t_2,x) - u (t_1,x)\right) f (x) {\textrm{d}{x}}\right| } < \varepsilon \), thanks to the boundedness of \(u (t,\cdot )\) uniform in \(t \in [0,T] \setminus {\mathcal {N}}\). Hence, \(u :[0,T] {\setminus } {\mathcal {N}} \rightarrow {{\textbf{L}}^\infty }({\mathbb {R}}; {\mathbb {R}})\) is uniformly continuous with respect to the weak-\(*\) \({{\textbf{L}}_{\textbf{loc}}^{\infty }}({\mathbb {R}}; {\mathbb {R}})\) topology.
, for a constant \(C_I\) depending on I. This bound then holds also for all piecewise constant functions and, by further approximations, we know that for all \(f \in {{\textbf{L}}^1} ({\mathbb {R}}; {\mathbb {R}})\) and for all \(\varepsilon >0\), there exists \(\delta >0\) such that if \(t_1,t_2 \in [0,T] {\setminus } {\mathcal {N}}\) and \({\left| t_2-t_1\right| } {<} \delta \), then \({\left| \int _{{\mathbb {R}}} \left( u (t_2,x) - u (t_1,x)\right) f (x) {\textrm{d}{x}}\right| } < \varepsilon \), thanks to the boundedness of \(u (t,\cdot )\) uniform in \(t \in [0,T] \setminus {\mathcal {N}}\). Hence, \(u :[0,T] {\setminus } {\mathcal {N}} \rightarrow {{\textbf{L}}^\infty }({\mathbb {R}}; {\mathbb {R}})\) is uniformly continuous with respect to the weak-\(*\) \({{\textbf{L}}_{\textbf{loc}}^{\infty }}({\mathbb {R}}; {\mathbb {R}})\) topology.
Apply now Proposition A.1, which is possible since \({{\textbf{L}}^\infty }({\mathbb {R}};{\mathbb {R}})\) is weakly-\(*\) complete (as it follows, for instance, from Banach–Alaoglu Theorem [37, Theorem 3.15 and Theorem 3.18]), and obtain an extension \({\bar{u}}\) of u which is defined on all [0, T], attains values in \({{\textbf{L}}^\infty }({\mathbb {R}}; {\mathbb {R}})\) and is continuous with respect to the weak-\(*\) \({{\textbf{L}}_{\textbf{loc}}^{\infty }}({\mathbb {R}}; {\mathbb {R}})\) topology.
The bound (2.9) also ensures that \(\lim _{t \rightarrow 0+} {\bar{u}} (t) = u_o\) in the weak-\(*\) topology of \({{\textbf{L}}^\infty }({\mathbb {R}}; {\mathbb {R}})\), so that \({\bar{u}} (0) = u_o\).
Define \(u^* :[0,T] \times {\mathbb {R}}\rightarrow {\mathbb {R}}\) setting \(u^* (t,x) = u (t,x)\) for all \(t \in [0,T] {\setminus } {\mathcal {N}}\) and choose for \(u^* (t)\) a precise representative, see [19, Chapter 1, § 7, Definition 1.26], of \({\bar{u}} (t)\) for \(t \in {\mathcal {N}}\). Claim 1 is proved.\(\checkmark \)
Fix a strictly convex entropy \(E \in {\textbf{C}}^{1} ({\mathbb {R}}; {\mathbb {R}})\). Choose a corresponding entropy flux F by means of (2.4). With reference to (2.7), introduce the function \(G \in {{\textbf{L}}^\infty }({\mathbb {R}}^2; {\mathbb {R}})\)
Fubini Theorem [22, Theorem 21.13] ensures that for any \(\psi \in {\textbf{C}}_c^{1} ({\mathbb {R}}; {\mathbb {R}}_+)\), the map \(t \mapsto \int _{{\mathbb {R}}} E\left( u_* (t,x)\right) \, \psi (x) {\textrm{d}{x}}\) is in \({{\textbf{L}}^1} ([0,T]; {\mathbb {R}})\). Call \(P_\psi \) the set of its Lebesgue points [19, Chapter 1, § 7, Theorem 1.34]. Call S the countable dense subset of \({\textbf{C}}_c^{1} ({\mathbb {R}};{\mathbb {R}})\) constructed in Proposition A.2. Denote for later use
Note that \([0,T] \setminus P\) has zero Lebesgue measure, since S is countable. For all \(\psi \in {\textbf{C}}_c^{1} ({\mathbb {R}}; {\mathbb {R}})\), each \(t \in P\) is a Lebesgue point of \(t \mapsto \int _{{\mathbb {R}}} E\left( u_* (t,x)\right) \, \psi (x) {\textrm{d}{x}}\), by Proposition A.2.
Claim 2: For all \(R>0\), \(\lim _{t \rightarrow 0+,\,t \in P} \int _{-R}^R {\left| u_*(t,x) - u_o (x)\right| } {\textrm{d}{x}} = 0\).
By Item 1 in Proposition 2.4, for all \(\varphi \in {\textbf{C}}_c^{1} ([0,T[ \times {\mathbb {R}};{\mathbb {R}}_+)\)
For \(n \in {\mathbb {N}}{\setminus }\{0\}\) and \(\tau >0\), choose the test function \(\varphi _{n,\tau } \in {\textbf{C}}_c^{1} ([0,T[ \times {\mathbb {R}}; {\mathbb {R}}_+)\) defined by
Clearly,  for all \((t,x) \in {\mathbb {R}}_+ \times {\mathbb {R}}\).
for all \((t,x) \in {\mathbb {R}}_+ \times {\mathbb {R}}\).
Proceed now as in the Proof of Proposition 2.5. If \(\tau \in {\mathcal {P}}_\psi \), then
Consider the linear functional \({\mathcal {G}}_\tau \) on \({\textbf{C}}_c^{1} ({\mathbb {R}};{\mathbb {R}})\) defined by
By (3.19), for all \(\tau \in P\) as defined in (3.18), we have that \({\mathcal {G}}_\tau \psi \ge 0\) for all \(\psi \in {\textbf{C}}_c^{1} ({\mathbb {R}}; {\mathbb {R}}_+)\).
Fix a positive R. Choose a sequence \(\tau _n \in P\) with \(\tau _n {\underset{n\rightarrow +\infty }{\longrightarrow }} 0\). By [19, Chapter 1, § 9, Theorem 1.46], the sequence \(u_* (\tau _n, \cdot )\) admits a subsequence \(u_* (\tau _{n_k}, \cdot )\) and, for a.e. \(x \in {\mathbb {R}}\), a Young measure [19, Chapter 1, § 9, Definition 1.34] \(\nu _{x}\), which is a Borel probability measure on \(\left[ -{\left\| u_*\right\| }_{{{\textbf{L}}^\infty }({\mathbb {R}}_+\times {\mathbb {R}}; {\mathbb {R}})}, {\left\| u_*\right\| }_{{{\textbf{L}}^\infty }({\mathbb {R}}_+\times {\mathbb {R}}; {\mathbb {R}})} \right] \) such that for all \(\psi \in {\textbf{C}}_c^{1} ([-R,R];{\mathbb {R}}_+)\)
Since \({\mathcal {G}}_\tau \psi \ge 0\) and thanks to the Dominated Convergence Theorem [22, Theorem (12.24)], for all \(\psi \in {\textbf{C}}_c^{1} ([-R,R];{\mathbb {R}}_+)\) we have
On the other hand, by Claim 1, \(u_o (x) = \int _{{\mathbb {R}}} w {\textrm{d}{\nu _x (w)}}\) for a.e. \(x \in {\mathbb {R}}\), so that
The strict convexity of E yields the equality in Jensen [22, Exercise 30.34] hence for a.e. \(x \in {\mathbb {R}}\), \(\nu _x\) is the Dirac delta at \(u_o (x)\), ensuring the pointwise convergence, up to a subsequence, see [38, Proposition 9.1.7]. The Dominated Convergence Theorem [22, Theorem (12.24)], can be applied since for all t and for a.e. x we have \({\left| u_* (t,x)\right| } \le {\left\| u\right\| }_{{{\textbf{L}}^\infty }([0,T]\times {\mathbb {R}})}\) and implies that \(u_* (\tau _{n_k},\cdot ) {\underset{k\rightarrow +\infty }{\longrightarrow }} u_o\) in \({{\textbf{L}}^1} ([-R,R];{\mathbb {R}})\). The choice of the \(\tau _n\) is arbitrary, up to the set P, as is the choice of R. Hence, Claim 2 is proved.\(\checkmark \)
Claim 3: For all \(R>0\) and for all \(t_1 \in P\), \(\lim \limits _{t_2 \rightarrow t_1+,\,t_2 \in P} \int _{{\mathbb {R}}} {\left| u_*(t_2,x) - u_* (t_1,x)\right| } {\textrm{d}{x}} = 0\).
By Item 1 in Proposition 2.4, for all \(\varphi \in {\textbf{C}}_c^{1} ([0,T[ \times {\mathbb {R}};{\mathbb {R}}_+)\)
For \(\varepsilon > 0\) and \(t_2> t_1 > 0\), choose the test function \(\chi _\varepsilon \) as in (3.13) and define
so that  .
.
Proceed now as in the Proof of Proposition 2.5 and as in Claim 2. If \(t_1,t_2 \in P\) as defined in (3.18), then
Proceed now exactly as in the previous Claim 2 to complete the proof of Claim 3.\(\checkmark \)
Claim 4: For all \({\bar{t}} \in P\), the map \((t,x) \mapsto u_* ({\bar{t}} + t, x)\) solves \( \left\{ \begin{array}{l} \partial _{t}u + \partial _{x} H(x,u) = 0 \\ u(0,x) = u_*({\bar{t}}, x) \end{array} \right. \) in the sense of Definition 2.1for \((t,x) \in [0, T - {\bar{t}}] \times {\mathbb {R}}\).
Define for \(\varepsilon >0\)
Use \(\varphi _\varepsilon \) as a test function in (2.2) in Definition 2.1. Then,

where in the last line above we used Claim 3. Claim 4 is proved.\(\checkmark \)
Claim 5: (c) in Item 1 holds.
For any \(R>0\) define
Fix \({\bar{t}} \in [0,T[\) and choose \(t_1 \in [{\bar{t}} - 1/\ell _R, {\bar{t}}] \cap P\), \(t_2 \in [t_1, t_1 + 1/\ell _R] \cap P\). By Claim 3 and Claim 4, the maps \((t,x) \mapsto u_* (t_1+t,x)\) and \((t,x) \mapsto u_* (t_2+t,x)\) solve
also in the sense of [27, Definition 1]. By [27, Theorem 1 and Theorem 3], which we can apply thanks to (C3), for a.e. \(s \in [0, t_1 - t_2 + 1/\ell _R]\)
where we set
and recall that by Claim 3, \(\lim _{\delta \rightarrow 0+} \omega _R (\delta ) = 0\). Combine (3.21) with Claim 3 to obtain that for all \(t_2,t_3 \in [t_1, t_1+1/\ell _R] \cap P\)
The above inequality shows that the map
is uniformly continuous. Hence, it can be uniquely extended to a continuous map defined on all of \([t_1, t_1+1/\ell _R]\). Since Claim 1 ensures that \(u_*\) is continuous in the weak-\(*\) \({{\textbf{L}}_{\textbf{loc}}^{\infty }}({\mathbb {R}}; {\mathbb {R}})\) topology, this extension coincides with \(u_*\). Claim 5 follows because \({\bar{t}} \in ]t_1, t_1+1/\ell _R[\).
Claim 6: Item 2 holds.
Let \(u^*\), \(v^*\) be solutions to (CL) with data \(u_o\) and \(v_o\), satisfying (c) in Item 1, proved in Claim 5. Then, \(u^*\) and \(v^*\) are also solutions to (CL) in the sense of [27, Definition 1]. By [27, Theorem 1 and Theorem 3], which we can apply thanks to (C3), we have that if L in (2.13) is finite, for all \(R > 0\) and for almost all \(t \in [0,T]\) the following estimates hold:
Use the \({{\textbf{L}}_{\textbf{loc}}^{1}} ({\mathbb {R}}; {\mathbb {R}})\) continuity to obtain the above inequalities for all \(t \in [0,T]\), proving Claim 6 and thus completing the proof of Theorem 2.6. \(\square \)
Proof of Item 2 in Theorem 2.8
We follow the general ideas in [4, Chapter 2]. Fix \(\tau \in ]0, T[\) and \(R >0\). Define
with L as in (2.18). Let C be as in (2.18), define \({\tilde{H}} :{\mathbb {R}}\times {\mathbb {R}}\rightarrow {\mathbb {R}}\) so that
Claim 1: \({\tilde{H}} (x,p) = H (x,p)\) whenever \({\left| p\right| } \le C\), with C defined in (2.18).
For all \((x,p) \in {\mathbb {R}}\times [-C,C]\), we have \({\tilde{H}} (x,p) \le H (x,p)\). By the Mean Value Theorem, for all \(x \in {\mathbb {R}}\) and \(p_1,p_2 \in [-C,C]\), \({\left| H (x,p_1) - H (x,p_2)\right| } \le L \, {\left| p_1 - p_2\right| }\). For \(q \in [-C,C]\), \(H (x,p) \le H (x,q) + L \, {\left| q-p\right| }\) and, by the Definition (3.23) of \(\tilde{H}\), we have \(H (x,p) \le {\tilde{H}} (x,p)\), proving Claim 1.\(\checkmark \)
Claim 2: For all \(x \in {\mathbb {R}}\), the map \(p \mapsto {\tilde{H}} (x,p)\) is Lipschitz continuous with Lipschitz constant L as defined in (2.18).
Fix \(x,p_1,p_2 \in {\mathbb {R}}\). By (3.23), for all \(q \in [-C,C]\), we have
so that \({\tilde{H}} (x,p_1)- L \, {\left| p_1 - p_2\right| } \le {\tilde{H}} (x,q) + L \, {\left| p_2-q\right| }\) implying \({\tilde{H}} (x,p_1) - L \, {\left| p_1 - p_2\right| } \le {\tilde{H}} (x,p_2)\) and therefore \({\tilde{H}} (x,p_1) - {\tilde{H}} (x,p_2) \le L \, {\left| p_1 - p_2\right| }\). The analogous inequality exchanging \(p_1\) with \(p_2\) is obtained similarly, proving Claim 2.\(\checkmark \)
Claim 3: Let C, L be as in (2.18). Then, Formula (3.23) can be rewritten as
so that \({\tilde{H}}\) is continuous on \({\mathbb {R}}\times {\mathbb {R}}\).
First, by (3.23), note that for \(p \ge C\), \({\tilde{H}} (x,p) \le H (x,C) + L \, (p-C)\), while for \(q \in [-C,C]\) the other inequality follows from
which, passing to the infimum over q, also proves the third line in (3.24). The first line is analogous and the middle one follows from Claim 1, completing the proof of Claim 3.\(\checkmark \)
Claim 4: Let U, V be as in Item 2 of Theorem 2.8. Then, they are a subsolution and a supersolution of \(\partial _t w + {\tilde{H}} (x, \partial _xw) = 0\) in the sense of Definition 2.7.
Let \(\varphi \) be a \({\textbf{C}}^{1}\) test function and assume that \(U-\varphi \) admits a local maximum at \((t_o,x_o) \in ]0,T[ \times {\mathbb {R}}\). Then, for all x in a neighborhood of \(x_o\),
Passing to the limits \(x \rightarrow x_o\pm \), we get \({\left| \partial _x \varphi (t_o,x_o)\right| } \le C\) hence, by Claim 1 and using the fact that U is a subsolution of (HJ),
To complete the proof of Claim 4, repeat the same procedure with the supersolution V.\(\checkmark \)
Choose \(\chi \in {\textbf{C}}^{\infty }(]-\infty , R[; {\mathbb {R}}_+)\) satisfying
and define, for \(A>0\),
Claim 5: \(U_A\) is a strict subsolution of \(\partial _t w + {\tilde{H}} (x, \partial _xw) = 0\) on \(\Omega \) as defined in (3.22).
Let \(\varphi \in {\textbf{C}}^{1} (\Omega ;{\mathbb {R}})\), \((t_o,x_o) \in {\Omega }\) such that \(U_A - \varphi \) has a point of maximum at \((t_o, x_o)\). Then, \(\gamma \in {\textbf{C}}^{1} (\Omega ;{\mathbb {R}})\), since by the Definition (3.25) of \(\chi \), \(\gamma \) locally vanishes near \(x=0\) for \(t < \tau \). The regularity of \(\varphi \) combined with that of \((t,x) \mapsto \dfrac{A}{\tau -t} + A \, \gamma (t,x)\), together with Claim 4, ensures that
where Claim 2 was used. Recall that by (3.26)
so that
completing the proof of Claim 5.\(\checkmark \)
Claim 6: Any convergent subsequence of a maximizing sequence of \(U_A - V\) attains a limit in \(\Omega \).
For all \((t,x) \in \Omega \),
by the compactness of \({\overline{\Omega }}\) and the continuity of U, V. Introduce a maximizing sequence \((t_n, x_n) \in \Omega \), so that \(U_A (t_n,x_n) - V (t_n,x_n) {\underset{n\rightarrow +\infty }{\longrightarrow }} \sup _{\Omega } (U_A - V)\). Up to a subsequence, we have \((t_n, x_n) {\underset{n\rightarrow +\infty }{\longrightarrow }} ({\bar{t}}, {\bar{x}})\), for a suitable \(({\bar{t}}, {\bar{x}}) \in {\overline{\Omega }}\).
If \({\bar{t}} = \tau \), then (3.26) imply the bound
that would imply \(U_A (t_n,x_n) - V (t_n,x_n) {\underset{n\rightarrow +\infty }{\longrightarrow }} -\infty \), which is absurd.
If \({\left| {\bar{x}}\right| } = R + L \, (\tau - {\bar{t}})\), then, by (3.22), we have the bound
that would once again imply \(U_A (t_n,x_n) - V (t_n,x_n) {\underset{n\rightarrow +\infty }{\longrightarrow }} -\infty \), which is not acceptable, since \((t_n, x_n)\) is a maximizing sequence, completing the proof of Claim 6.\(\checkmark \)
For all \(\varepsilon >0\), \((t,x) \in \Omega \) and \((s,y) \in {\overline{\Omega }}\), define
Claim 7: For all \(\varepsilon >0\), there exist points \((t_\varepsilon ,x_\varepsilon ) \in \Omega \) and \((s_\varepsilon ,y_\varepsilon ) \in {\overline{\Omega }}\) such that \(\psi _\varepsilon (t_\varepsilon ,x_\varepsilon ,s_\varepsilon ,y_\varepsilon ) = \sup _{\Omega \times {\overline{\Omega }}} \psi _\varepsilon \).
This claim is proved by exactly the same technique used in Claim 6.\(\checkmark \)
Using Claim 7, for any \(\varepsilon > 0\) let \((t_\varepsilon , x_\varepsilon , s_\varepsilon , y_\varepsilon )\) be a point of maximum in \(\Omega \times {\overline{\Omega }}\) of \(\psi _\varepsilon \), so that \(\psi _\varepsilon (t_\varepsilon , x_\varepsilon , s_\varepsilon , y_\varepsilon ) = M_{A,\varepsilon }\).
Claim 8: \(\lim _{\varepsilon \rightarrow 0} M_{A,\varepsilon } = M_A\) and \(\lim _{\varepsilon \rightarrow 0}\frac{1}{2\varepsilon ^2} \left( (x_\varepsilon - y_\varepsilon )^2 + (t_\varepsilon -s_\varepsilon )^2\right) =0\).
Since \(U_A (t,x) -V (t,x) = \psi _\varepsilon (t,x,t,x)\) and \(U_A \le U\), we have
and therefore
Let \(\omega _V\) be a modulus of continuity of V in (t, x) on \({\overline{\Omega }}\) and compute:
proving the first limit in Claim 8. To prove the second one, refine the computations (3.28)–(3.29) above as
completing the proof of Claim 8.\(\checkmark \)
Claim 9: \(\frac{1}{\varepsilon ^2} \, {\left| x_\varepsilon -y_\varepsilon \right| } < C\).
For all y close to \(y_\varepsilon \), we have
and Claim 9 follows in the limits \(y \rightarrow y_\varepsilon \pm \).\(\checkmark \)
Claim 10: \(\max _\Omega \left( U_A - V\right) = \max _{{\left| x\right| } < R} \left( U_A (0,x) -V (0,x)\right) \).
By contradiction, assume that \(\max _\Omega \left( U_A - V\right) > \max _{{\left| x\right| } < R} \left( U_A (0,x) -V (0,x)\right) \). Using Claim 9, we can introduce a sequence \(\varepsilon _n\) converging to 0, such that \(\dfrac{1}{{\varepsilon _n}^2} \, (x_{\varepsilon _n}-y_{\varepsilon _n}) \rightarrow {\bar{p}}\) for a suitable \({\bar{p}} \in [-C,C]\) and so that \(t_{\varepsilon _n} {\underset{n\rightarrow +\infty }{\longrightarrow }} {\bar{t}}\) and \(x_{\varepsilon _n} {\underset{n\rightarrow +\infty }{\longrightarrow }} {\bar{x}}\) for a suitable \(({\bar{t}}, {\bar{x}}) \in {\overline{\Omega }}\). By Claim 8, we also have that \(s_{\varepsilon _n} {\underset{n\rightarrow +\infty }{\longrightarrow }} {\bar{t}}\) and \(y_{\varepsilon _n} {\underset{n\rightarrow +\infty }{\longrightarrow }} {\bar{x}}\). Then,
so that \(U_A (t_{\varepsilon _n}, x_{\varepsilon _n}) - V(t_{\varepsilon _n}, x_{\varepsilon _n}) {\underset{n\rightarrow +\infty }{\longrightarrow }} M_A\). Claim 6 implies that \(({\bar{t}}, {\bar{x}}) \in \Omega \). Since we are proceeding by contradiction, \({\bar{t}} >0\) and for all n sufficiently large, also \(t_{\varepsilon _n} > 0\), so that \((t_{\varepsilon _n},x_{\varepsilon _n}) \in {\Omega }\) and also \((s_{\varepsilon _n},y_{\varepsilon _n}) \in {\Omega }\).
Let now n be sufficiently large and consider the maps
The former one admits a maximum at \((t_{\varepsilon _n},x_{\varepsilon _n})\), while the latter admits a minimum at \((s_{\varepsilon _n}, y_{\varepsilon _n})\). Since \(U_A\) is a subsolution and V is a supersolution, by (3.27) in the proof of Claim 5 and Claim 4 we have
Take the difference between the last lines above, let \(n \rightarrow +\infty \) and we get the contradiction: \(A/ (\tau -{\bar{t}})^2 \le 0\), proving Claim 10.\(\checkmark \)
Conclusion.
For all \((t,x) \in \Omega \), we have \(U_A (t,x) - V (t,x) \le U (t,x) - V (t,x)\) so that
Hence, using Claim 10, for fixed \((t,x) \in \Omega \),
and in the limit \(A \rightarrow 0\) we have \(U (t,x) - V (t,x) \le \max _{{\left| x\right| } \le R + L\, T} \left( U_o (x) - V_o (x)\right) \). By the continuity of \(U-V\), the latter inequality holds for all \((t,x) \in {\overline{\Omega }}\), completing the proof of Item 2 in Theorem 2.8. \(\square \)
Proof of Item 1 in Theorem 2.8
Fix \((s,y) \in {\mathbb {R}}_+ {\times } {\mathbb {R}}\). Define \({\hat{C}} = {\left\| \partial _x U\right\| }_{{{\textbf{L}}^\infty }([0,T]{\times }{\mathbb {R}}; {\mathbb {R}})}\), recall \(K^{HJ}\) from (2.17) and set
Claim 1: For all \(x \in {\mathbb {R}}\), \(U (s,x) \le V (s,x)\) and V is a supersolution to (HJ) in the sense of Definition 2.7on \({\mathbb {R}}^2\).
The bound \(U (s,x) \le V (s,x)\) follows from (3.30) and the Lipschitz continuity of U in x.
Let \(\varphi \in {\textbf{C}}^{1} ({\mathbb {R}}^2; {\mathbb {R}})\) and fix \((t,x) \in {\mathbb {R}}^2\) such that \(V - \varphi \) has a point of minimum at (t, x). For all \(\varepsilon \in {\mathbb {R}}\), if \({\left| \varepsilon \right| }\) is sufficiently small, then
so that letting \(\varepsilon \rightarrow 0+\) we have \(\partial _t \varphi (t,x) \le K^{HJ}\), while letting \(\varepsilon \rightarrow 0-\) we have \(\partial _t \varphi (t,x) \ge K^{HJ}\). Hence, \(\partial _t \varphi (t,x) = K^{HJ}\).
Again for \({\left| \varepsilon \right| }\) is sufficiently small,
so that letting \(\varepsilon \rightarrow 0+\) we have \(\partial _x \varphi (t,x) \le {\hat{C}}\), while letting \(\varepsilon \rightarrow 0-\) we have \(\partial _x \varphi (t,x) \ge -{\hat{C}}\). Hence, \({\left| \partial _x \varphi (t,x)\right| } \le {\hat{C}}\).
The definition of \(K^{HJ}\) ensures that \(\partial _t \varphi (t,x) + H\left( x, \partial _x \varphi (t,x)\right) \ge 0\), proving Claim 1.\(\checkmark \)
Claim 2: For all \(x \in {\mathbb {R}}\), \(U (s,x) \ge W (s,x)\), W is a subsolution to (HJ) in the sense of Definition 2.7on \({\mathbb {R}}^2\).
The proof of this claim is entirely analogous to that of the previous one.\(\checkmark \)
Conclusion.
We apply Item 2 in Theorem 2.8, which was proved above, on \([s, +\infty [ \times {\mathbb {R}}\) to the couples of subsolution–supersolution (U, V) and (W, U) to get for all \((t,x) \in [s, +\infty [ \times {\mathbb {R}}\)
and by the arbitrariness of (s, y) we complete the proof of Item 1 in Theorem 2.8\(\square \)
3.2 Existence of helpful stationary solution
Here, we prove Theorem 2.9, which yields, for all \(U \in {\mathbb {R}}\), 2 stationary entropic solutions \(u_-\) and \(u_+\) to (CL) such that \({\left| u_\pm \right| } > U\). We detail the case of \(u_+\), that of \(u_-\) is similar. Further information and visualizations of the solutions constructed below, together with hints to their role as asymptotic states, can be found in [12].
Lemma 3.2
Let H satisfy (C3)–(CNH)–(UC). Fix \(U>0\). There exist \({\bar{H}} \in {\mathbb {R}}\), \(V \in {\mathbb {R}}\) and real monotone sequences \(a_n\), \(b_n\) with \(\lim _{n\rightarrow +\infty } a_n = \lim _{n\rightarrow +\infty } b_n = 0\) such that if
then:
-
1.
For all \(n \in {\mathbb {N}}\), for all \((x,u) \in {\mathbb {R}}^2\), \(H_n (x,u) = {\bar{H}}\) implies \(\nabla H_n (x,u) \ne 0\).
-
2.
For all \((x,u) \in {\mathbb {R}}^2\), \(H(x,u) = {\bar{H}}\) implies \(\nabla H (x,u) \ne 0\).
-
3.
For all \(n \in {\mathbb {N}}\), for all \((x,u) \in {\mathbb {R}}^2\), \({\left| u\right| } \le U\) implies \({\left| H_n (x,u)\right| } < {\bar{H}}\) and \({\left| H (x,u)\right| } < {\bar{H}}\).
-
4.
For all \(n \in {\mathbb {N}}\), for all \((x,u) \in {\mathbb {R}}^2\), \(u \ge V\) implies \({\left| H_n (x,u)\right| } > \bar{H}\) and \({\left| H (x,u)\right| } > {\bar{H}}\).
-
5.
For all \(n \in {\mathbb {N}}\), for all \((x,u) \in {\mathbb {R}}^2\), \(H_n (x,u) = {\bar{H}}\) and \(\partial _u H_n (x,u) = 0\) imply \(\partial ^2_{uu} H_n (x,u) {\ne } 0\).
Proof of Lemma 3.2
By (UC) we know that \({\left| H (x,u)\right| } {\underset{u \rightarrow +\infty }{\longrightarrow }} +\infty \). We assume that
the other case, namely \(\lim _{u \rightarrow +\infty } H (x,u) = -\infty \), is entirely analogous.
Introduce the map \(G :{\mathbb {R}}^2 \rightarrow {\mathbb {R}}^2\) defined by
and note that, by (C3), \(G\in {\textbf{C}}^{1}({\mathbb {R}}^2; {\mathbb {R}}^2)\).
Claim 1: There exist increasing sequences \(a_n\) and \(b_n\) converging to 0 such that for all \(n \in {\mathbb {N}}\), \((a_n,b_n)\) is a regular value for G and \(a_o > -1\), \(b_o > -1\).
This claim follows from Sard’s Lemma A.3 applied with \(f = G\), \(k = 1\), \(n_1 = n_2 = 2\). Remark that here condition (C3) is fully exploited.\(\checkmark \)
The assumption (3.31) allows to introduce
Claim 2: \({\mathcal {Y}}\) is negligible and \({\mathcal {P}}\) is countable.
The former statement directly follows from Sard’s Lemma A.3 applied first with \(f = H\) then with \(f = H_n\) and \(k = 3\), \(n_1 = 2\), \(n_2 = 1\). Fix \(n \in {\mathbb {N}}\) and define
Recall that \((a_n,b_n) \) is a regular value for G, so we have that \({\mathcal {Q}}_n\) is discrete, hence countable. As a consequence, also \(H_n ({\mathcal {Q}}_n)\) is countable.
This holds for all \(n \in {\mathbb {N}}\), hence \({\mathcal {P}} = \bigcup _{n \in {\mathbb {N}}} H_n({\mathcal {Q}}_n)\) is countable, proving Claim 2.\(\checkmark \)
Define, using (CNH),
and note that the set \(]H_1 + U + \frac{1}{2} \, U^2, +\infty [ {\setminus } ({\mathcal {Y}} \cup {\mathcal {P}})\) is not empty by Claim 2 and (3.32). Choose \({\bar{H}}\) in this set and with this choice, items 1, 2 and 5 hold by construction.
Claim 3: Item 3 holds.
Fix \(n \in {\mathbb {N}}\) and \((x,u) \in {\mathbb {R}}^2\) such that \({\left| u\right| } \le U\). Then, \({\left| H (x,u)\right| } \le H_1 < {\bar{H}}\). Moreover, thanks to Claim 1 ensuring that \({\left| a_n\right| }\le 1\) and \({\left| b_n\right| } \le 1\),
proving Claim 3.\(\checkmark \)
By (UC), we have a \(V \in {\mathbb {R}}\) such that for \((x,u) \in {\mathbb {R}}^2\) if \({\left| u\right| } \ge V\), then \({\left| H (x,u)\right| } {\ge } {\bar{H}} + 1 {>} {\bar{H}} >0\).
Claim 4: Item 4 holds.
Given this choice of V and assumption (3.32), we have that for \(u \ge V\), \(H (x,u) \ge 0\). Fix \((x,u) \in {\mathbb {R}}^2\) with \(u \ge V\). We have \(H (x,u) = {\left| H (x,u)\right| } > {\bar{H}}\) and since for all \(n \in {\mathbb {N}}\), \(a_n <0\), \(b_n <0\), we also have \(H_n (x,u) \ge H (x,u)>0\). Claim 4 is proved, as is Lemma 3.2. \(\square \)
Lemma 3.3
Let H satisfy (C3)–(CNH)–(UC) and moreover
If U, V and \({\bar{H}}\) are positive real numbers such that
Then, there exists a stationary solution \(u_+ \in {{\textbf{L}}^\infty }({\mathbb {R}}; {\mathbb {R}}^+)\), in the sense of Definition 2.1, to \(\partial _t u + \partial _x H (x,u) = 0\) that satisfies \(H\left( x, u_+ (x)\right) = {\bar{H}}\) (so that \(u_+\) attains values in ]U, V[).
Proof of Lemma 3.3
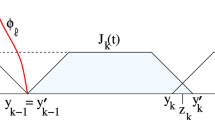
In the construction below, we refer to Fig. 1.
Left, the level set \(H (x,u) = {\bar{H}}\), with ± denoting the regions where \(H (x,u)\gtrless {\bar{H}}\). Right, the dashed line is the graph of the stationary entropic solution \(x \mapsto u_+ (x)\), which is inside this level set. The diamonds on top of the vertical lines indicate the positions of the points that, along the x axis, constitute the discrete set \({\mathcal {X}}\) defined in (3.40)
Claim 1: There exists \(u_1 >0\) such that \(H (X,u_1) = {\bar{H}}\) and \(\partial _u H (X, u_1) > 0\).
Define
Clearly, \(U \in {\mathcal {U}}\) and V is an upper bound of \({\mathcal {U}}\). Define \(u_1 \,{:=}\,\sup {\mathcal {U}}\). By (C3), \(H (X, u_1) = {\bar{H}}\) and \(\partial _u H (X, u_1) \ge 0\). By (3.38), \(\nabla H (X,u_1) \ne 0\) while (CNH) ensures that \(\partial _x H (X, u_1) = 0\). Hence, \(\partial _u H (X, u_1) > 0\), proving Claim 1.\(\checkmark \)
Call \(\pi _x :{\mathbb {R}}\times {\mathbb {R}}\rightarrow {\mathbb {R}}\) the canonical projection \(\pi _x (x,u) = x\). Introduce the set (corresponding to the diamonds in Fig. 1, right)
Claim 2: \({\mathcal {X}}\) is finite.
The set \(\left\{ (x,u) \in {\mathbb {R}}\times {\mathbb {R}}_+ :H (x,u) = {\bar{H}} \hbox { and } \partial _u H (x,u) = 0\right\} \) is closed by (C3), contained in \([-X,X]\times [U,V]\) by the choice of \({\bar{H}}\) and consists of isolated points (apply the Inverse Function Theorem to \((x,u)\rightarrow \left( H(x,u) - {\bar{H}}, \partial _u H(x,u)\right) \) and then use (3.38) and (3.39)). Hence, it is finite and so is its projection on the x axis. The proof of Claim 2 follows.\(\checkmark \)
Define \(y_* \,{:=}\,\inf {\mathcal {Y}}\) where, denoting \(\mathop {\textrm{co}}(A)\) the convex hull of A and using the notation (2.1),
Above, u piecewise \({\textbf{C}}^{1}\) on [y, X] means that that there exist finitely many pairwise disjoint open intervals \(I_\ell \) such that \([y,X] = \bigcup \overline{I_\ell }\), \(u_{|\overline{I_\ell }} \in {\textbf{C}}^{0} (\overline{I_\ell }; {\mathbb {R}})\) and \(u_{|I_\ell } \in {\textbf{C}}^{1} (I_\ell ; {\mathbb {R}})\).
Claim 3: \(y_* \in {\mathcal {Y}}\).
The Implicit Function Theorem and Claim 1 ensure that \({\mathcal {Y}}\) contains a left neighborhood of X, so that \({\mathcal {Y}} \ne \emptyset \). Moreover, \({\mathcal {Y}} \subseteq [-X,X]\), so that \(y_* = \inf {\mathcal {Y}}\) is finite.
If \({\mathcal {X}} = \emptyset \), define \({\bar{y}} \,{:=}\,X\). Otherwise, note that there exists \({\bar{y}} \in {\mathcal {Y}}\) such that \({\bar{y}} < \min ({\mathcal {X}} \cap ]y_*,X])\), since \({\mathcal {X}}\) is finite by Claim 2 and by the properties of the infimum. In both cases, there exists a map u satisfying (i), (ii), (iii) and (iv) in (3.41) defined on \([{\bar{y}},X]\). An application of the Implicit Function Theorem, since \(] y_*, {\bar{y}}] \cap {\mathcal {X}} = \emptyset \), allows to extend u down to \(y_*\) so that \(u_{| [y_*, {\bar{y}}]}\) is \({\textbf{C}}^{1}\). Hence, \(y_* \in {\mathcal {Y}}\), proving Claim 3.\(\checkmark \)
Call \(u_+\) the map corresponding to \(y_* \in {\mathcal {Y}}\) as defined in (3.41) and set \(u_* \,{:=}\,u_+ (y_*)\).
Claim 4: \(y_* = -X\)
Assume \(y_* > -X\). Then, consider first the case \(\partial _u H(y_*, u_*) \ne 0\). The Implicit Function Theorem ensures that \(u_+\) can be extended toward left in a \({\textbf{C}}^{1}\) way (so that the properties defining \({\mathcal {Y}}\) remain trivially satisfied), contradicting the above construction.
Consider now the case \(\partial _u H(y_*, u_*) = 0\). Again, the Implicit Function Theorem and the assumptions (3.38) ensure the existence of \(\varepsilon > 0\) and of a function \(\vartheta \) such that \(H(y,v) = {\bar{H}}\) with \(y \in ]y_*-\varepsilon , y_* + \varepsilon [\) and \(v \in ]u_*-\varepsilon , u_* + \varepsilon [\) is equivalent to \(y = \vartheta (v)\). Direct computations show that \(y_* = \vartheta (u_*)\), \(0 = \vartheta ' (u_*)\) and, by (3.39), \(\vartheta '' (u_*) \ne 0\). Moreover, \(y = \vartheta \left( u_+ (y)\right) \) for \(y > y_*\). Hence, \(\vartheta '' (u_*) > 0\).
There exists \(\varepsilon _* >0\) such that for all \(u \in ] u_* -\varepsilon _*, u_* + \varepsilon _*[ {\setminus } \{u_*\}\), \(\vartheta (u) > y_*\). Hence, for all \(u \in ] u_*-\varepsilon _*, u_* + \varepsilon _*[\), if \(u \ne u_*\) then \(H (y_*,u) \ne \bar{H}\).
Case 1: Suppose that \(H (y_*, u) < {\bar{H}}\) for all \(u \in ] u_*, u_* + \varepsilon _*[\).
Introduce
\({\mathcal {V}} \ne \emptyset \) since \([u_*, u_* +\varepsilon _* [ \subseteq {\mathcal {V}}\). By (3.37), \({\mathcal {V}}\) is bounded above by V and we can introduce \(v_* \,{:=}\,\sup {\mathcal {V}}\), which is finite. Note that for u near to \(v_*\)
showing that \(v_*\) is neither an isolated point of maximum nor an isolated point of minimum of \(u \mapsto H (y_*,u)\). By (3.39), it then follows that \(\partial _u H (y_*, v_*) \ne 0\) and, hence, \(\partial _u H (y_*, v_*) > 0\). Apply now the Implicit Function Theorem on the level set \(H (x,u) = {\bar{H}}\) in a neighborhood of \((y_*, v_*)\), obtaining a map \(u = \psi (x)\) defined on \(]y_* - \eta , y_* + \eta [\). Define
Clearly, \(u^\flat \) is piecewise \({\textbf{C}}^{1}\). Moreover, it satisfies (i), (ii) and (iii) because \(u_*\) and \(\psi \) (thanks to the definition of \(v_*\) as the supremum of \({\mathcal {V}}\)) satisfy them. Concerning (iv): if \(y < y_*\), simply note that \(\psi \) is \({\textbf{C}}^{1}\); for \(y > y_*\), \(u_+\) satisfies (iv) and at \(y=y_*\) we have \(u^\flat (y_*+) = u_*\), \(u^\flat (y_*-) = v_*\) and by the definition of \(v_*\), \(v_* > u_*\) and for all \(k \in ]u_*, v_* [\) by (3.42), \(H (y_*,k) \le {\bar{H}} = H (y_*,v_*)\). This implies \(y_* - \eta \in {\mathcal {Y}}\), which contradicts the choice \(y_* \,{:=}\,\inf {\mathcal {Y}}\).
Case 2: Otherwise, since \(u \mapsto H (y_*,u)\) is continuous, a connectedness argument ensures that \(H (y_*, u) > \bar{H}\) for all \(u \in ] u_*, u_* + \varepsilon _*[\).
We have \(\partial _u H (y_*, u_*) = 0\), so \(\partial ^2_{uu} H (y_*, u_*) \ge 0\) and by (3.39), \(\partial ^2_{uu} H (y_*, u_*) > 0\). Thus, for all \(u \in ]u_* - \varepsilon _*, u_* [\), \(H (y_*,u) > {\bar{H}}\). We now proceed as in the case above. Introduce
\({\mathcal {V}} \ne \emptyset \) since \(]u_*-\varepsilon _*, u_* ] \subseteq {\mathcal {V}}\). By (3.36), \({\mathcal {V}}\) is bounded below by U and we can introduce \(v_* \,{:=}\,\inf {\mathcal {V}}\), which is finite. Note that for u near to \(v_*\)
showing that \(v_*\) is neither an isolated point of maximum nor an isolated point of minimum of \(u \mapsto H (y_*,u)\). By (3.39), it then follows that \(\partial _u H (y_*, v_*) \ne 0\) and, hence, \(\partial _u H (y_*, v_*) > 0\). Apply now the Implicit Function Theorem on the level set \(H (x,u) = {\bar{H}}\) in a neighborhood of \((y_*, v_*)\), obtaining a map \(x \mapsto \psi (x)\) defined on \(]y_* - \eta , y_* + \eta [\). Define
Clearly, \(u^\flat \) is piecewise \({\textbf{C}}^{1}\). Moreover, it clearly satisfies (i), (ii) and (iii) because \(u_*\) and \(\psi \) satisfy them. Concerning (iv): for \(y < y_*\), \(\psi \) is \({\textbf{C}}^{1}\); for \(y > y_*\), \(u_+\) satisfies (iv) and at \(y=y_*\) we have \(u^\flat (y_*+) = u_*\), \(u^\flat (y_*-) = v_*\) and by the definition of \(v_*\), \(v_* < u_*\) and for all \(k \in ]u_*, v_* [\), \(H (y_*,k) > {\bar{H}} = H (y_*,v_*)\). This implies \(y_* - \eta \in {\mathcal {Y}}\), which contradicts the choice \(y_* \,{:=}\,\inf {\mathcal {Y}}\). Claim 4 is proved\(\checkmark \)
Conclusion.
First, extend \(u_+\) on \(]-\infty , -X]\) setting it to be constant and, separately, on \([X, +\infty [\) also setting it to be constant. Note that \(u_+\) is of class \({\textbf{C}}^{1}\) both on a neighborhood of \(-X\) and on a neighborhood of X, since by (CNH), \(\partial _x H (\pm X, u) = 0\) for all u and thanks to (ii) in (3.41).
Then, we verify that \(u_+\) is a Kružkov (stationary) solution in the sense Definition 2.1. (Recall the notation introduced in (2.1)). Let \(k \in {\mathbb {R}}\), \(\varphi \in {\textbf{C}}_c^{1} ([0,T[ \times {\mathbb {R}}; {\mathbb {R}}_+)\) and define:
We show that \(A + \int _0^{+\infty } \left( B (t) + C (t)\right) {\textrm{d}{t}} + D \ge 0\) considering the different terms separately.
Call \(p_1, p_2, \ldots , p_n\) (with \(p_i < p_{i+1}\)) the points of jump in \(x \mapsto u_+ (x)\), they are finitely many by the Definition (3.41) of \({\mathcal {Y}}\) and that of \(u_+\). For later use, let \(p_0 \,{:=}\,-X\) and \(p_{n+1} \,{:=}\,X\). We know that \(u_+ \in {\textbf{C}}^{1} (]p_{i}, p_{i+1}[; {\mathbb {R}}) \cap {\textbf{C}}^{0} ([p_{i}, p_{i+1}]; {\mathbb {R}})\) for \(i=0, \ldots , n\). When x is different from all \(p_1, \ldots , p_n\) and, using [27, Lemma 3], compute
since, by the definition of \(u_+\), \(H\left( x, u_+ (x)\right) \equiv {\bar{H}}\). Fix \(t \in {\mathbb {R}}_+\) and compute:
We thus obtain
and we compute the generic i-th term of the latter sum as
where we used \(H\left( x, u_+ (x)\right) = {\bar{H}}\) for all x. Clearly, if \(k \not \in \mathop {\textrm{co}}\left\{ u_+ (p_i-), u_+ (p_i+)\right\} \), the latter term vanishes. Assume \(k \in \mathop {\textrm{co}}\left\{ u_+ (p_i-), u_+ (p_i+)\right\} \). Then, property (iv) in (3.41) ensures that \(\mathop {\textrm{sgn}}\left( u_+ (p_i-) - k\right) \; \left( {\bar{H}} - H (p_i,k)\right) \ge 0\). On the other hand, being k between \(u_+ (p_i-)\) and \(u_+ (p_i+)\), \(\mathop {\textrm{sgn}}\left( u_+ (p_i+) - k\right) = - \mathop {\textrm{sgn}}\left( u_+ (p_i-) - k\right) \), so that the difference (3.44) is nonnegative and so is the test function \(\varphi \).
The proof of Lemma 3.3 is completed. \(\square \)
Lemma 3.4
Let H satisfy (C3)–(CNH)–(UC) and moreover
Let U and V be positive real numbers and \({\bar{H}}\) be negative such that
Then, there exist a stationary solution \(u_+ \in {{\textbf{L}}^\infty }({\mathbb {R}}; {\mathbb {R}}^+)\) to \(\partial _t u + \partial _x H (x,u) = 0\) in the sense of Definition 2.1 that satisfies \(H\left( x, u_+ (x)\right) = {\bar{H}}\).
When (3.35) is replaced by (3.45), the above procedure can be repeated with essentially only technical modifications. We list below the various steps, omitting the details. We stress that it is critical that the case below be treated “from left to right”, i.e., from \(-X\) to X, corresponding, with the terminology of the previous proof, to \(y_* = \sup {\mathcal {Y}}\).
Proof of Lemma 3.4
Referring to the proof of Lemma 3.3, we only describe below the necessary modifications when (3.45) substitutes (3.35).
Claim 1 is modified to: There exists a real \(u_1 >0\) such that \(H (-X,u_1) = {\bar{H}}\) and \(\partial _u H (-X, u_1) < 0\).
Introduce the set
Claim 2 is modified to: \({\mathcal {X}}\) is finite.
Define \(y_* = \sup {\mathcal {Y}}\), where, using the notation (2.1),
Claim 3 is modified to: \(y_* \in {\mathcal {Y}}\).
Claim 4 is modified to: \(y_* = X\).
Conclusion. No change is necessary. \(\square \)
Lemma 3.5
Let \(H \in {\textbf{C}}^{2} ({\mathbb {R}}^2; {\mathbb {R}})\) and (CNH) hold. Let u be a stationary solution to (CL) in the sense of Definition 2.1. Then, for any \({\textbf{C}}^{1}\) entropy–entropy flux pair (E, F), in the sense of Definition 2.3, with E convex, the entropy production distribution
is a positive measure and satisfies for all \(r \in {\mathbb {R}}_+\)
By Proposition 2.4, since u is stationary, the proof of Lemma 3.5 consists in integrating (3.50) against test functions that approximate the characteristic function of \([-r,r]\).
Proof of Theorem 2.9
Apply Lemma 3.2 to obtain \({\bar{H}}\), V and the sequence of Hamiltonians \(H_n\). Both Lemmas 3.3 and 3.4 can be applied to each \(H_n\), U, V, \(\bar{H}\) and ensure the existence of a stationary solution \(u_n\) to \(\partial _t u + \partial _x H_n (x,u) = 0\) in the sense of Definition 2.1, for each n. Moreover, \(H_n\left( x, u_n (x)\right) = {\bar{H}}\) and \(u_n\) attains values in ]U, V[.
Since: \(a_n, b_n \in [-1,1]\), both sequences vanish, (CNH) and (3.31) hold, we get
Given an entropy \(E \in {\textbf{C}}^{2} ({\mathbb {R}}; {\mathbb {R}})\), we can introduce by means of (2.6) the corresponding flux
Claim 1: For any \(R>0\) and for any convex entropy \(E \in {\textbf{C}}^{2} ({\mathbb {R}}; {\mathbb {R}})\), define \(F_n\) by (3.52). Then, \(\left\{ \partial _x \left( F_n (\cdot , u_n)\right) :n \in {\mathbb {N}}\right\} \) is relatively compact in \({{\textbf{H}}^{{-1}}} ([-R,R]; {\mathbb {R}})\).
We apply [38, Lemma 9.2.1], which we adapt here to the present (stationary) situation. By (3.51), using Proposition 2.4, straightforward computations yield:
where
The family \((u_n)\) is in \({{\textbf{L}}^\infty }([0,T]\times [-R,R]; [U,V])\), thus the family \((v_n)\) is bounded in \({{\textbf{L}}^\infty }([0,T]\times [-R,R]; {\mathbb {R}})\) by (C3) and it is also bounded in \({\mathcal {M}} ([0,T]\times [-X,X];{\mathbb {R}})\). The family \((\mu _n)\) is bounded in \({\mathcal {M}} ([0,T]\times [-X,X];{\mathbb {R}})\) by Lemma 3.5. Clearly, \(\left\{ \partial _x \left( F_n (\cdot , u_n)\right) :\varepsilon \in ]0, \varepsilon _*[ \right\} \) is bounded in \({{\textbf{W}}^{-1,\infty }} ([-R,R]; {\mathbb {R}})\). Thus, Murat Lemma [38, Lemma 9.2.1] completes the proof of Claim 1.\(\checkmark \)
By [19, Chapter 1, § 9, Theorem 1.46], the sequence \((u_n)\) admits a subsequence, which we keep denoting \((u_n)\), and, for a.e. \(x \in {\mathbb {R}}\), a Young measure [19, Chapter 1, § 9, Definition 1.34] \(\nu _{x}\), which is a Borel probability measure on [U, V] and such that
for any \(g \in {\textbf{C}}^{0} ({\mathbb {R}}; {\mathbb {R}})\) and for any \(\varphi \in {{\textbf{L}}^1} ({\mathbb {R}}; {\mathbb {R}})\). Clearly, we also obtain that for any \(\varphi \in {{\textbf{L}}^1} ([0,T] \times {\mathbb {R}}; {\mathbb {R}})\), we have
Claim 2: For any \(G \in {\textbf{C}}^{0}({\mathbb {R}}^2; {\mathbb {R}})\) such that \(G (x,u) = G (-X,u)\) for all \(x \in ]-\infty ,-X]\) and \(G (x,u) = G (X,u)\) for all \(x \in [X, +\infty [\),
Recall that \(u_n \in {{\textbf{L}}^\infty }({\mathbb {R}}; [U,V])\). In view of our later use of Fubini Theorem, we use Stone–Weierstrass Theorem [22, Corollary 7.31] so that for every \(\delta > 0\) there exist a \(\nu \in {\mathbb {N}}\) and functions \(f_1, \ldots , f_\nu \in {\textbf{C}}^{0} ([-X,X]; {\mathbb {R}})\), \(g_1, \ldots , g_\nu \in {\textbf{C}}^{0} ([U,V]; {\mathbb {R}})\) such that
Since G satisfies (CNH), for \(\ell = 1, \ldots , \nu \), introducing the functions
we can extend the latter statement (3.55) to
Recall that the support of \(\nu _x\) is included in [U, V] for a.e. x. Then,
and each term in the latter sum above converges to 0 by (3.54), since each \({\bar{f}}_\ell \, \varphi \) is in \({{\textbf{L}}^1} ([0,T]\times {\mathbb {R}}; {\mathbb {R}})\). Passing to the \(\limsup \) and using the arbitrariness of \(\delta \), Claim 2 is proved.\(\checkmark \)
Claim 3: For any \(G_n \in {\textbf{C}}^{0}({\mathbb {R}}^2; {\mathbb {R}})\) with \(G_n (x,u) = G_n (-X,u)\) for all \(x \in ]-\infty ,-X]\) and \(G_n (x,u) = G_n (X,u)\) for all \(x \in [X, +\infty [\), such that \(G_n\) converges to G uniformly on \({\mathbb {R}}\times [U,V]\),
The above assumptions ensure that G satisfies the hypotheses of Claim 2. Therefore,
where we used (3.51) and Claim 2, completing the proof of Claim 3.\(\checkmark \)
Claim 4: For any entropy \(E \in {\textbf{C}}^{2} ({\mathbb {R}}; {\mathbb {R}})\), there exists a set \(\Omega _E \subseteq {\mathbb {R}}\) such that \({\mathbb {R}}\setminus \Omega _E\) is negligible and for all \(x \in \Omega _E\)
where F is an entropy flux corresponding to E with respect to H, according to Definition 2.3.
Consider the vector fields
and assume preliminarily that E is convex. Call \(F_n\) the flux corresponding to E with respect to \(H_n\) as defined by (3.52).
Fix an arbitrary \(R>0\). In the present stationary situation, \({\nabla \cdot }V_n\) vanishes. Moreover, by Claim 1, \(\nabla \wedge W_n\) lies in a relatively compact subset of \({{\textbf{H}}^{{-1}}} ([0,T]\times [-R,R]; {\mathbb {R}})\). By the div–curl Lemma [16, Theorem 17.2.1], we have
More precisely, applying (3.56) to the sequences \(G_n (x,u) = u\, F_n (x,u) - E (u)\, H_n (x,u)\), \(G_n (x,u) = u\), \(G_n (x,u) = H_n (x,u)\), \(G_n (x,u) = F_n (x,u)\) and \(G_n (x,u) = E (x,u)\), the following limits hold in the sense of distributions over \([0,T] \times [-R,R]\), the functions being understood in \({{\textbf{L}}^2} ([0,T]\times [-R,R]; {\mathbb {R}})\), so that their products are in \({{\textbf{L}}^1} ([0,T]\times [-R,R]; {\mathbb {R}})\):
where F is an entropy flux corresponding to E with respect to H. Since R is arbitrary, equality (3.58) ensures that (3.57) is proved in the case of a convex entropy for all \((t,x) \in {\hat{\Omega }}_E\), for a set \({\hat{\Omega }}_E\) such that \(([0,T] \times {\mathbb {R}}) {\setminus } {\hat{\Omega }}_E\) is negligible.
Note that equality (3.57) is independent of time and \(([0,T]\times {\mathbb {R}}) \setminus {\hat{\Omega }}_E\) is negligible, hence we may assume that (3.57) holds for all \(x \in \Omega _E\), where \({\mathbb {R}}\setminus \Omega _E\) is negligible. Claim 4 is proved in the case of a convex entropy.
Assume now that E is not necessarily convex. Then, we can introduce two convex functions \(E_+, E_-\) of class \({\textbf{C}}^{2} ({\mathbb {R}}; {\mathbb {R}})\) such that
These functions are not uniquely defined, since adding/subtracting affine functions of w does not alter the validity of the latter requirements. Repeating the argument above, for all \(x \in \Omega _{E_+} \cap \Omega _{E_-}\), equality (3.57) holds also for the not necessarily convex entropy E, the set \({\mathbb {R}}{\setminus } (\Omega _{E_+} \cap \Omega _{E_-})\) being negligible. Claim 4 is proved.\(\checkmark \)
Call \({\mathcal {E}}\) the countable set of all polynomials with rational coefficients and define
Claim 5: The set \(\Omega \) is such that \({\mathbb {R}}{\setminus } \Omega \) is negligible and for all \(E \in {\textbf{C}}^{0} ({\mathbb {R}}; {\mathbb {R}})\) and for all \(x \in \Omega \), equality (3.57) holds, where \(F^k\) is given by (2.6), for any \(k \in {\mathbb {R}}\)..
For any \(E \in {\mathcal {E}}\) and for all \(x \in \Omega \), by Claim 4 equality (3.57) holds, \({\mathbb {R}}\setminus \Omega \) being negligible.
Let now \(E \in {\textbf{C}}^{0} ({\mathbb {R}}; {\mathbb {R}})\) be fixed. By the classical Stone–Weierstrass Theorem [22, Corollary 7.31], there exists a sequence \(E_n\) in \({\mathcal {E}}\) converging to E uniformly on [U, V]. Clearly, the sequence of fluxes \(F^k_n\) corresponding to \(E_n\) defined by (2.6) converges to the flux \(F^k\), also defined by (2.6). Since (3.57) holds in \(\Omega \) for each pair \((E_n,F^k_n)\), it also holds for \((E,F^k)\). By the arbitrariness of E, Claim 5 is proved.\(\checkmark \)
Define for all \(x \in {\mathbb {R}}\)
Claim 6: With reference to (3.59) and (3.60), for all \(x \in \Omega \),
Set for \(\xi \in \Omega \), \(E (w) \,{:=}\,{\left| w-u (\xi )\right| }\) so that by Definition 2.3\(F^{u(\xi )} (x,w) \,{:=}\,\mathop {\textrm{sgn}}\left( w-u (\xi )\right) \) \(\left( H (x,w) - H \left( x,u (\xi )\right) \right) \), see also (2.6). By Claim 5, using (2.1), we get that for all \(x \in \Omega \)
Rearranging the terms, one gets
Choose \(x = \xi \), use (2.1) to get \(\left( \int _{{\mathbb {R}}} H (\xi ,w) \, {\textrm{d}{\nu _\xi (w)}} - H\left( \xi , u (\xi )\right) \right) \int _{{\mathbb {R}}} {\left| w-u(\xi )\right| } {\textrm{d}{\nu _\xi (w)}} = 0\). Either the first factor vanishes, or \(\nu _\xi \) is Dirac delta at \(u (\xi )\). In both cases, using (3.60) and the arbitrariness of \(\xi \), Claim 6 is proved.\(\checkmark \)
Claim 7: The sequence \(u_n\) converges to u, as defined in (3.60), a.e. in \({\mathbb {R}}\).
(The content of this step is heavily inspired by [24, Section 5.4]).
From Claim 5 and from (3.61) in Claim 6, we obtain that for all \(x \in \Omega \), as defined in (3.59), and for all \(E \in {\textbf{C}}^{0} ({\mathbb {R}}; {\mathbb {R}})\)
where F is as in (2.6), for any k. For a.e. \(x \in {\mathbb {R}}\), \(\nu _x\) is a probability measure and the maps \(w \mapsto w-u (x)\), \(w \mapsto H (x,w) - H \left( x, u (x)\right) \) are sufficiently regular to ensure that the set functions
(S being any Borel set) are finite Radon measures. Hence, the two maps
are in \(\textbf{BV}({\mathbb {R}}; {\mathbb {R}})\). Since \(\mathop {\textrm{spt}}\nu _x \subseteq [U,V]\), then \(A _x (v)\) and \(B_x (v)\) vanish for \(v < U\) and attain a constant value for \(v > V\). Moreover, (3.60) implies that \(\alpha _x ({\mathbb {R}}) = 0\) while (3.61) in Claim 6 implies that \(\beta _x ({\mathbb {R}}) = 0\). Therefore, for all \(x \in {\mathbb {R}}\), both \(A_x\) and \(B_x\) are supported in [U, V]. An integration by parts, see [21, Theorem B] (in particular the remark at the bottom of [21, p. 422]), then ensures that from equality (3.62) we can deduce
and therefore
In the above equality, E can be any \({\textbf{C}}^{1}\) function, \(E'\) can be any continuous function, hence
Furthermore, we have that
Indeed, the two sides have the same distributional derivative in w by (3.64) and (3.63), while they clearly coincide when \(w = u (x)\). Inserting (3.64) in (3.65), we have
Call [a, b] the minimal (with respect to set inclusion) interval containing the support of \(\nu _x\) and assume by contradiction that \(a<b\). Note that \(A_x (w) \ne 0\) for \(w \in ]a,b[\). Indeed, by the definition of \(A_x (w)\) and since \(\nu _x\) is nonnegative, the map \(w \mapsto A_x (w)\) vanishes for \(w < a\), weakly decreases for \(w \in ]a, u (x) [\), weakly increases for \(w \in ]u (x), b [\), and then vanishes for \(w >b\). The minimality of [a, b] ensures that \(A_x\) is nonzero in both a right neighborhood of a and a left neighborhood of b. Simplifying, we thus obtain
The latter equality contradicts (WGNL) unless \(a=b\), ensuring that, for a.e. \(x \in {\mathbb {R}}\), \(\nu _x\) is a Dirac measure, which in turn implies pointwise convergence up to a subsequence by (3.54), see [38, Proposition 9.1.7]. Claim 7 is proved.\(\checkmark \)
Conclusion.
By Claim 7, up to a subsequence, we have the pointwise a.e. convergence \(u_n \rightarrow u\) as \(n \rightarrow +\infty \). The \({{\textbf{L}}^\infty }\) bound \(u_n (x) \in [U,V]\) for a.e. \(x \in {\mathbb {R}}\) allows to use the Dominated Convergence Theorem [22, Theorem (12.24)] in (2.7). By Proposition 2.4, we get that u is a weak entropy stationary solution (Definition 2.1) attaining values between U and V. This accomplishes the construction of \(u_+\), that of \(u_-\) is entirely similar. The proof of Theorem 2.9 is completed. \(\square \)
3.3 Vanishing viscosity approximations
Proof of Theorem 2.11
Let u be a classical solution to (2.20) on I. Clearly, U as defined by (2.24) satisfies (2.23), simple computations yield \(U (0,x) = U_o (x)\) and
thus U is a classical solution to (2.21) on I, proving Item (1). Verifying Item (2) is immediate, completing the proof of Theorem 2.11. \(\square \)
Lemma 3.6
Fix \(T,\varepsilon >0\). Let H satisfy (C3) and (CNH). Assume there exist bounded classical solutions \(u^-\) on \(]-\infty , -X[\) and \(u^+\) on \(]X, +\infty [\) to (2.20). Then, setting \(\Omega _X^- = (\{0\} \times ]-\infty , -X]) \cup ([0,T] \times \{-X\})\) and \(\Omega _X^+ = (\{0\} \times [X, +\infty [) \cup ([0,T] \times \{X\})\),
Proof of Lemma 3.6
We consider only the case of maxima of \(u^+\) in \([X, +\infty [\), the same procedure applies to \(u^-\) in \(]-\infty , -X[\), while straightforward sign changes apply to the case of a minimum. We follow the general lines of [23, Theorem B.1] and [24, Chapter III].
For \(\eta \in ]0,1[\), define
By the boundedness assumption on \(u^+\), it follows that \(v_\eta \) attains its global maximum at a point \((t_\eta , x_\eta ) \in [0,T] \times [X, +\infty [\). Three possible cases are in order.
Case 1: \(t_\eta = 0\) and \(x_\eta \ge X\).
For all \((t,x) \in [0,T] \times [X, +\infty [\) we have
so that
\(\checkmark \)
Case 2: \(t_\eta \in [0, T]\) and \(x_\eta = X\).
For all \((t,x) \in [0,T] \times [X, +\infty [\) we have
so that
\(\checkmark \)
Case 3: \(t_\eta \in ]0, T]\) and \(x_\eta > X\).
Then, by the choice of \((t_\eta , x_\eta )\), \(\partial _t v_\eta (t_\eta , x_\eta ) \ge 0\), \(\partial _x v_\eta (t_\eta , x_\eta ) = 0\) and \(\partial ^2_{xx}v_\eta (t_\eta ,x_\eta ) \le 0\). Equivalently, \(\partial _t u (t_\eta , x_\eta ) \ge 2\, \varepsilon \, \eta \), \(\partial _x u (t_\eta , x_h) = \eta ^3\, x_\eta \) and \(\partial ^2_{xx} u (t_\eta , x_\eta ) \le \eta ^3\). Hence, using (CNH), \(\partial _x H\left( x_\eta , u (t_\eta ,x_\eta )\right) = 0\) and
To obtain a strictly positive lower bound for the right hand side (3.70), recall that \(v_\eta (t_\eta ,x_\eta ) \ge v_\eta (X,0)\) which, together with (3.67), implies that
whence
Use now (3.71) in (3.70) and (CNH) to obtain
showing that \(\left( \partial _t u + \partial _x H (x,u) - \varepsilon \, \partial ^2_{xx} u \right) _{|t=t_\eta , x=x_\eta } > 0\) for all sufficiently small \(\eta >0\). This contradicts the choice of u, hence Case 3 is not to be considered.\(\checkmark \)
From (3.68) and (3.69), we thus obtain that for all \((t,x) \in [0,T] \times [X, +\infty [\) and \(\eta \in ]0,1[\),
Passing to the limit \(\eta \rightarrow 0\), we complete the proof of Lemma 3.6. \(\square \)
Corollary 3.7
Fix \(T,\varepsilon >0\). Let (C3) and (CNH) hold. Choose a bounded initial datum \(u_o \in {\textbf{C}}^{0} ({\mathbb {R}}; {\mathbb {R}})\). Assume there exists a bounded classical solution u to (2.20) on \({\mathbb {R}}\). Then,
Proof
Define \(u^+\), respectively, \(u^-\), the restriction of u to \([0,T] \times ]-\infty , -X[\), respectively, \([0,T] \times ]X, +\infty [\). Apply Lemma 3.6 to complete the proof. \(\square \)
Corollary 3.8
Fix \(T,\varepsilon >0\). Let H satisfy (C3) and (CNH). Choose an initial datum \(U_o \in {\textbf{C}}^{1} ({\mathbb {R}}; {\mathbb {R}})\). Assume there exists a classical solution U to (2.21) on \({\mathbb {R}}\) which is also Lipschitz continuous. Then,
Proof
By Theorem 2.11, with \(I={\mathbb {R}}\), it is sufficient to apply Corollary 3.7 to \(\partial _x U\).
\(\square \)
Proof of Theorem 2.12
Define the \(\varepsilon \) independent quantity
Claim 1: The following bound on \(\partial _tU\) holds uniformly in \(\varepsilon \):
The function \(\varphi \,{:=}\,\partial _tU\) is a classical solution to the linear parabolic Cauchy problem
The standard comparison principle, see, e.g., [18, Theorem 8, § 7.1.4], ensure for \(t \in [0, T[\) the bound \(\varphi (t,x) \in [\inf _{\xi \in {\mathbb {R}}} \varphi (0,\xi ), \sup _{\xi \in {\mathbb {R}}} \varphi (0,\xi )]\) and, equivalently,
Introduce
so that \(\psi ^{\pm } (0,x) = U_o' (x)\). Moreover, since \(\varepsilon \in ] 0, 1]\),
proving by (3.72) that \(\psi ^+\), respectively, \(\psi ^-\) is a supersolution, respectively, a subsolution to (2.21), so that the standard comparison principle for regular functions, see for instance [35, Proposition 52.6], yields \(\psi ^- \le U \le \psi ^+\). By (3.75), \(-A \le \frac{1}{t} \left( U (t,x) - U_o (x)\right) \le A\) and in the limit \(t \rightarrow 0+\) we obtain \({\left\| \partial _t U (0)\right\| }_{{{\textbf{L}}^\infty }({\mathbb {R}}; {\mathbb {R}})} \le A\) which, together with (3.74) completes the proof of Claim 1.\(\checkmark \)
Claim 2: For all \(\eta \in {\textbf{C}}^{2} ({\mathbb {R}}; {\mathbb {R}})\) with \(\eta ''>0\), define \(\omega (t,x) \,{:=}\,\eta \left( \partial _x U (t,x)\right) \). If \(\arg \max \omega \ne \emptyset \), then for any \((t^*,x^*) \in \arg \max \omega \) with \(t^* >0\),
Since U is a solution to (2.21) in the sense of Definition 2.10, we can compute:
where we used (2.21) to get to the last equality. Therefore,
Use the inequality \((a+b)^2 \ge (1-\alpha ) \, a^2 + \left( 1-\frac{1}{\alpha }\right) b^2\), that holds for \(a,b \in {\mathbb {R}}\) and \(\alpha >0\) with \(a = \partial _t U (t,x)\), \(b = H\left( x,\partial _x U (t,x)\right) \) and \(\alpha = 1/ (1-\varepsilon )\) to get, by the convexity hypothesis on \(\eta \),
Compute the above terms at \((t^*,x^*)\), where \(\partial _x \omega (t^*,x^*) = 0\), \(\partial _t \omega (t^*,x^*) \ge 0\) and \(\partial ^2_{xx}\omega (t^*,x^*) \le 0\) to obtain (3.76). Claim 2 is proved.\(\checkmark \)
Claim 3: There exists a constant B such that for all \(\varepsilon \in ]0,1/2[\) and for all \(T \in {\mathbb {R}}_+\),
By means of a function
define the maps \(\vartheta \) and \(\eta \) on all \({\mathbb {R}}\) so that
Note that \(\vartheta \) is even, hence also \(\eta \) is. We also have
Hence, \(\eta \) satisfies the assumptions of Claim 2. By Corollary 3.8, we have 2 cases.
Case 1: \(\sup _{(t,x) \in [0,T]\times {\mathbb {R}}} {\left| \partial _x U (t,x)\right| } > \sup _{x \in {\mathbb {R}}} {\left| U_o' (x)\right| }\).
Then, by Corollary 3.8 and (C3).
Hence, \(\arg \max _{[0,T]\times {\mathbb {R}}} {\left| \partial _x U\right| }\) is non-empty. If \((t^*, x^*) \in \arg \max _{[0,T]\times {\mathbb {R}}} {\left| \partial _x U\right| }\), then \(t^* >0\). Moreover, \(\eta \) is convex and even, so that \((t^*,x^*)\) is also a point of maximum of \(\omega \), as defined in Claim 2.
By Claim 1, Claim 2 and (3.78)–(3.79)–(3.80), setting \(v^* = \partial _x U (t^*,x^*)\) and, for \(\varepsilon < 1/2\),
and the latter bound above is uniform in \(\varepsilon \) and T, so that we obtained \( \left( H (x^*, v^*)\right) ^2 \le 2A^2 + \max \left\{ 1, \left( 1+r(1)\right) ^2 \right\} \le 2A^2 + \left( 1+r(1)\right) ^2\). Proceed as follows:
Claim 3 is proved in Case 1 with
Case 2: \(\sup _{(t,x) \in [0,T]\times {\mathbb {R}}} {\left| \partial _x U (t,x)\right| } = \sup _{x \in {\mathbb {R}}} {\left| U_o' (x)\right| }\).
By the Definition (3.72) of A, we have \({\left| H \left( x,U_o' (x)\right) \right| } \le A \le \sqrt{2A^2 + \left( 1+r(1)\right) ^2}\) for any \(x \in {\mathbb {R}}\). Thus, by (UC) and by the Definition (3.81) of B, we have that \({\left| U_o' (x)\right| } \le B\) for any \(x \in {\mathbb {R}}\). Hence, finally, \(\sup _{(t,x) \in [0,T]\times {\mathbb {R}}} {\left| \partial _x U (t,x)\right| } = \sup _{x \in {\mathbb {R}}} {\left| U_o' (x)\right| } \le B\), proving Claim 3 also in Case 2 and completing the proof of Theorem 2.12. \(\square \)
Recall, see, e.g., [24, § 3.2], for \(\varepsilon \in ]0,1[\) the heat kernel and its basic properties
Below, we obtain the well-posedness of the parabolic approximations (2.20) and (2.21), first in the conservation law case.
Proof of Theorem 2.14
Throughout this proof, we keep \(\varepsilon \) fixed and omit it.
Claim 1: Problem (2.20) admits a local solution in the sense of Definition 2.10.
Let T be positive and introduce the linear map \( {\mathcal {F}} :{\mathcal {V}} \rightarrow {\mathcal {V}}\) where
We now choose T so that the Banach Fixed Point Theorem can be applied. Clearly, \({\mathcal {V}}\) is closed. It is also invariant with respect to \({\mathcal {F}}\). Indeed, using (3.82) one proves the continuity of \({\mathcal {F}}v\) and the estimate
Entirely similar estimates show that \({\mathcal {F}}\) is Lipschitz continuous:
Choosing T positive and such that
an application of Banach Fixed Point Theorem ensures the existence of a map \(u \in {\mathcal {V}}\) such that \(u = {\mathcal {F}}u\), so that u solves (2.20), see, for instance, [23, Theorem B.1 and Lemma B.3] for a similar case. Claim 1 is proved.\(\checkmark \)
Below, we exploit the fact that (3.84) actually depends on \(u_o\) only through its \({{\textbf{L}}^\infty }\) norm.
Claim 2: Problem (2.20) admits a global solution.
Introduce
By Claim 1, we know that \(T_m\) is well defined and that \(T_m \ge T\) as defined in (3.84). We prove that \(T_m = +\infty \) assuming that \(T_m < +\infty \). Let C be the constant given by Corollary 2.13, which can be applied since \(u_o\) is actually required Lipschitz continuous. Fix \(\tau > 0\) so that
and note that \(T_m \ge \tau \) by Step 1. Set \(\tau _m = T_m - \tau /2\), so that \(\tau _m \in ]0, T_m[\). By the choice of \(T_m\), there exists a solution u to (2.20) in the sense of Definition 2.10 on \(]0, \tau _m[ \times {\mathbb {R}}\) and by Corollary 2.13, \({\left\| u\right\| }_{{{\textbf{L}}^\infty }([0,\tau _m] \times {\mathbb {R}}; {\mathbb {R}})} \le C\). Applying Claim 1, since \(x \mapsto u (\tau _m, x) \in {\textbf{C}}^{2}({\mathbb {R}}; {\mathbb {R}}) \cap {{\textbf{L}}^\infty }({\mathbb {R}}; {\mathbb {R}})\), we can construct a solution \(u_\tau \) in the sense of Definition 2.10 to
The concatenation
of classical solutions to (2.20) is, by construction, \({\textbf{C}}^{1}\) in time. This implies that w solves (2.20) in the sense of Definition 2.10 on \(]0, T_m + \tau /2[ \times {\mathbb {R}}\), which contradicts the definition of \(T_m\), completing the proof of Theorem 2.14. \(\square \)
3.4 Passing to the limit
Proof of Theorem 2.16
Passing to the convergence of vanishing viscosity approximations, the case of Hamilton–Jacobi equation is standard.
The existence of \(U_{\varepsilon _n}\) (for sufficiently large n) follows from Corollary 2.15. The bound (2.25) in Theorem 2.12 ensures that Ascoli–Arzelà Theorem [18, § C.7] can be applied on every compact subset of \({\mathbb {R}}_+ \times {\mathbb {R}}\). Use a diagonal argument to obtain \(U_*\) as the limit of a convergent subsequence. Clearly, \(U_*\) is Lipschitz continuous with the Lipschitz constant provided by (2.25). Proving that \(U_*\) satisfies Definition 2.7 is classical, we refer, for instance, to [4, Chapter 2] or [18, Chapter 10].
By Theorem 2.8, \(U_*\) is independent of the particular subsequence, hence the whole sequence \(U_{\varepsilon _n}\) converges to \(U_*\). \(\square \)
Proof of Theorem 2.17
Claim 1: The map \(\varepsilon \mapsto \sqrt{\varepsilon }\; \partial _x u_\varepsilon \) is bounded in \({{\textbf{L}}_{\textbf{loc}}^{2}} ({\mathbb {R}}_+ \times {\mathbb {R}}; {\mathbb {R}})\).
We now prove that for every positive T and R there is a constant \(C_{T,R}\) such that \({\left\| \sqrt{\varepsilon }\, \partial _x u_\varepsilon \right\| }_{{{\textbf{L}}^2} ([0,T]\times [-R,R];{\mathbb {R}})} \le C_{T,R}\).
For all \(\varphi \in {\textbf{C}}_c^{1} ({\mathbb {R}}; {\mathbb {R}})\) and for all \(t \in ]0,T[\), by (2.20) we have
Choose \(\varphi (t,x) = u_\varepsilon (t,x)\; \psi _R(x)^2\) where \(\psi _R \in {\textbf{C}}_c^{\infty }({\mathbb {R}}; {\mathbb {R}})\), \(\psi _R (x) = 1\) for \(x \in [-R, R]\), \(\psi _R (x) = 0\) whenever \({\left| x\right| }> R+1\) and \({\left| \psi _R' (x)\right| } \le 2\) for all \(x \in {\mathbb {R}}\). By direct computations, using also (2.20), from (3.85) we get:
so that, integrating also over t on [0, T] and using the definition of \(\psi _R\), we have
where M is as in (2.26) from Corollary 2.13. To bound the latter term, introduce the function
defined for \((t,x) \in [0,T] \times {\mathbb {R}}\). Note that by Corollary 2.13
Moreover,
hence
Multiply by \({\psi _R}^2 (x)\), integrate over \([0,T] \times {\mathbb {R}}\) and take the absolute value:
where M is as in Corollary 2.13. The two summands on the lines (3.88)–(3.89) are both independent of \(\varepsilon \). Concerning (3.90) above, integrate by parts and use (3.87) to obtain
which, again, is a quantity independent of both \(\varepsilon \) and \(u_\varepsilon \). The latter bound inserted together with (3.88) in (3.86) provides the desired \({{\textbf{L}}_{\textbf{loc}}^{2}} ({\mathbb {R}}_+ \times {\mathbb {R}}; {\mathbb {R}})\) bound. Claim 1 is proved.\(\checkmark \)
Claim 2: For any \(T,R>0\) and for any entropy \(E \in {\textbf{C}}^{2} ({\mathbb {R}}; {\mathbb {R}})\), let F be a flux satisfying (2.4). Then, the set \(\left\{ \partial _t E (u_\varepsilon ) + \partial _x \left( F (\cdot , u_\varepsilon )\right) :\varepsilon \in ]0, \varepsilon _*[\right\} \) is relatively compact in \({{\textbf{H}}^{{-1}}} ([0,T]\times [-R,R]; {\mathbb {R}})\).
This Claim essentially amounts to an application of Murat Lemma [38, Lemma 9.2.1], which we adapt here to the present situation.
Using (2.20), straightforward computations yield:
where
We now verify the following 3 assumptions to apply Murat Lemma [38, Lemma 9.2.1]:
(1): \(\left\{ \partial _t E (u_\varepsilon ) + \partial _x \left( F (\cdot , u_\varepsilon )\right) :\varepsilon \in ]0, \varepsilon _*[\right\} \) is bounded in \({{\textbf{W}}^{-1,\infty }} ([0,T]\times [-R,R]; {\mathbb {R}})\),
Indeed, by Corollary 2.13, by the regularity of E and by (2.4), the ranges of both \(\varepsilon \mapsto E (u_\varepsilon )\) and of \(\varepsilon \mapsto F\left( \cdot , u_\varepsilon \right) \) are bounded in \({{\textbf{L}}^\infty }([0,T] \times {\mathbb {R}}; {\mathbb {R}})\). Use the definition of weak derivative to complete the proof of (1).
(2): \(\left\{ v_\varepsilon :\varepsilon \in ]0, \varepsilon _*[\right\} \) bounded in the set of Radon measures \({\mathcal {M}} ([0,T]\times [-R,R]); {\mathbb {R}})\),
Indeed, Corollary 2.13 shows that the range of \(\varepsilon \mapsto {\hat{v}}_\varepsilon \) is bounded in \({{\textbf{L}}^\infty }([0,T]\times [-R,R];{\mathbb {R}})\) uniformly in \(\varepsilon \). Hence, the range of \(\varepsilon \mapsto {\hat{v}}_\varepsilon \) is bounded in \({{\textbf{L}}^1} ([0,T]\times [-R,R]; {\mathbb {R}})\), which implies the required boundedness in \({\mathcal {M}} ([0,T]\times [-R,R]); {\mathbb {R}})\). Claim 1 ensures that the range of \(\varepsilon \mapsto \varepsilon \; (\partial _x u_\varepsilon )^2\) is bounded in \({{\textbf{L}}^1} ([0,T] \times [-R,R]; {\mathbb {R}})\). This, together with the boundedness in \({{\textbf{L}}^\infty }\) ensured by Corollary 2.13, proves that the range of \(\varepsilon \mapsto \check{v}_\varepsilon \) is bounded in \({\mathcal {M}} ([0,T]\times [-R,R]; {\mathbb {R}})\).
(3): \(\left\{ w_\varepsilon :\varepsilon \in ]0, \varepsilon _*[\right\} \) relatively compact in \({{\textbf{H}}^{{-1}}} ([0,T]\times [-R,R]; {\mathbb {R}})\),
Indeed, by the \({\textbf{C}}^{2}\) regularity of E, we have \({\left| \varepsilon \; \partial _x \left( E (u_\varepsilon )\right) \right| } = \sqrt{\varepsilon }\, E' (u_\varepsilon ) \; \sqrt{\varepsilon }\, {\left| \partial _x u_\varepsilon \right| }\) which converges to 0 in \({{\textbf{L}}_{\textbf{loc}}^{2}} ([0,T]\times {\mathbb {R}}; {\mathbb {R}})\) as \(\varepsilon \rightarrow 0\) by Corollary 3.7 and by Claim 1 above. Hence, the range of \(\varepsilon \mapsto w_\varepsilon \) is relatively compact in \({{\textbf{H}}^{{-1}}} ([0,T]\times [-R,R]; {\mathbb {R}})\)
Murat Lemma [38, Lemma 9.2.1] thus applies and Claim 2 is proved.\(\checkmark \)
Introduce an arbitrary sequence \(\varepsilon _n\) converging to 0. By [19, Chapter 1, § 9, Theorem 1.46], we know there exists a Young measure [19, Chapter 1, § 9, Definition 1.34] \(\nu _{t,x}\) corresponding to a subsequence \(\varepsilon _{n_k}\), meaning that for each \((t,x) \in [0,T] \times {\mathbb {R}}\), \(\nu _{t,x}\) is a Borel probability measure on \({\mathbb {R}}\) such that for any \(g \in {\textbf{C}}^{0} ({\mathbb {R}}; {\mathbb {R}})\) and for any \(\varphi \in {{\textbf{L}}^1} ([0,T]\times {\mathbb {R}}; {\mathbb {R}})\), we have
Remark 3.9
Following a standard habit, to simplify the notation, in the sequel we write \(\varepsilon \) for \(\varepsilon _{n_k}\), \(\varepsilon \rightarrow 0\) for \(k \rightarrow +\infty \) and, correspondingly, refer to \(u_\varepsilon \) as to a sequence.
As usual, we assume that \(\varepsilon \) is sufficiently small, say \(\varepsilon \in ]0, \varepsilon _*[\) for a suitable \(\varepsilon _* >0\).
Claim 3: For any \(G \in {\textbf{C}}^{0}({\mathbb {R}}^2; {\mathbb {R}})\) such that \(G (x,u) = G (-X,u)\), for all \((x,u) \in ]-\infty ,-X] \times {\mathbb {R}}\) and \(G (x,u) = G (X,u)\) for all \((x,u) \in [X, +\infty [ \times {\mathbb {R}}\) and for any \(\varphi \in {{\textbf{L}}^1} ([0,T]\times {\mathbb {R}}; {\mathbb {R}})\),
By Corollary 2.13, the sequence \(u_\varepsilon \) attains values in \([-M,M]\), with M as in (2.26). By Stone–Weierstrass Theorem [22, Corollary 7.31] for every \(\delta > 0\) there exist an integer m and functions \(f_1, \ldots , f_m \in {\textbf{C}}^{0} ([-X,X]; {\mathbb {R}})\), \(g_1, \ldots , g_m \in {\textbf{C}}^{0} ([-M, M]; {\mathbb {R}})\) such that
By (CNH), introducing for \(\ell =1, \ldots , m\) the functions
we can extend the latter statement (3.93) to
Hence, for any \(\varphi \in {{\textbf{L}}^1} ([0,T]\times {\mathbb {R}}; {\mathbb {R}})\)
where, to get to the last inequality, we used the inclusion \(\mathop {\textrm{spt}}\nu _{t,x} \subseteq [-M,M]\). Moreover, each term in the latter sum above converges to 0 by (3.92), since each \(F_\ell \, \varphi \) is in \({{\textbf{L}}^1} ([0,T]\times {\mathbb {R}}; {\mathbb {R}})\). Then, Claim 3 is proved.\(\checkmark \)
Claim 4: For any entropy \(E \in {\textbf{C}}^{2} ({\mathbb {R}}; {\mathbb {R}})\), there exists a set \(\Omega _E \subseteq {\mathbb {R}}_+ \times {\mathbb {R}}\) such that \(({\mathbb {R}}_+ \times {\mathbb {R}}) {\setminus } \Omega _E\) is negligible and for all \((t,x) \in \Omega _E\)
where F is any entropy flux corresponding to E with respect to H, according to Definition 2.3.
(The content of this step closely follows Claim 5 in the proof of Theorem 2.9).
Consider the vector fields
where E is in \({\textbf{C}}^{2} ({\mathbb {R}}; {\mathbb {R}})\) and F is a corresponding flux defined by (2.4). By Claim 2, \({\nabla \cdot }V_\varepsilon \) and \(\nabla \wedge W_\varepsilon \) lie in sets that are relatively compact in \({{\textbf{H}}^{{-1}}} ([0,T]\times [-R,R]; {\mathbb {R}})\), for any \(R > 0\). By the div–curl Lemma [16, Theorem 17.2.1], we have
the limits in the right hand side are understood in the weak \({{\textbf{L}}^2}([0,T]\times [-R,R]; {\mathbb {R}})\) sense, while the limit in the left hand side and the equality are understood in the sense of distribution. Moreover, since both sides of (3.95) are in \({{\textbf{L}}^1}([0,T]\times [-R,R]; {\mathbb {R}})\), equality (3.95) also holds in \({{\textbf{L}}^1}([0,T]\times [-R,R]; {\mathbb {R}})\). At the same time, using (3.92) we have
Hence, we may now intend (3.94) as an equality between representatives of \({{\textbf{L}}^1} ([0,T] \times [-R,R]; {\mathbb {R}})\) functions. Call \(\Omega _E\) the set of points where (3.95) holds. By the arbitrariness of R, the complement of \(\Omega _E\) is negligible. Claim 4 is proved.\(\checkmark \)
Call now \({\mathcal {E}}\) the countable set of all polynomials with rational coefficients and define
Then, for any \(E \in {\mathcal {E}}\) and for all \((t,x) \in \Omega \), (3.94) holds and the set \(([0,T] \times {\mathbb {R}}) {\setminus } \Omega \) is negligible.
Claim 5: For all \(E \in {\textbf{C}}^{0} ({\mathbb {R}}; {\mathbb {R}})\) and for all \((t,x) \in \Omega \), equality (3.94) holds, where \(F = F^k\) is given by (2.6), for any \(k \in {\mathbb {R}}\).
For any \(E \in {\mathcal {E}}\) and for all \((t,x) \in \Omega \), (3.94) holds, the set \(([0,T] \times {\mathbb {R}}) {\setminus } \Omega \) being negligible.
Let now \(E \in {\textbf{C}}^{0} ({\mathbb {R}}; {\mathbb {R}})\) be fixed. By the classical Stone–Weierstrass Theorem [22, Corollary 7.31], there exists a sequence \(E_n\) in \({\mathcal {E}}\) converging to E uniformly on \([-M,M]\), with M as in (2.26). Clearly, the sequence of fluxes \(F^k_n\) corresponding to \(E_n\) defined by (2.6) converges uniformly to the flux \(F^k\), also defined by (2.6). Since (3.94) holds in \(\Omega \) for each pair \((E_n,F^k_n)\), repeating the same argument as in the proof of Claim 3, one proves that it also holds for \((E,F^k)\). By the arbitrariness of E, Claim 5 is proved.\(\checkmark \)
Define the limit
Claim 6: With reference to (3.96) and (3.97), for all \((t,x) \in \Omega \),
Fix \((\tau ,\xi ) \in \Omega \), set \(E (w) \,{:=}\,{\left| w-u (\tau ,\xi )\right| }\) so that by (2.6) \(F^{u(\tau ,\xi )} (x,w) \,{:=}\,\mathop {\textrm{sgn}} \left( w-u (\tau ,\xi )\right) \) \(\left( H (x,w) - H \left( x,u (\tau ,\xi )\right) \right) \). Inserting these expressions in (3.94) and using (3.97), we get that for all \((t,x) \in \Omega \)
Move the first term in the left hand side above to the right hand side to obtain
Choosing \((t,x) = (\tau ,\xi )\), there is a cancelation between the first two lines above, resulting in
Hence, either the first factor vanishes, or \(\nu _{\tau ,\xi }\) is Dirac delta at \(u (\tau ,\xi )\). In both cases, Claim 6 is proved.\(\checkmark \)
Claim 7: Up to a subsequence, the sequence \(u_\varepsilon \) converges to u, defined in (3.97), a.e. in \(\Omega \) defined in (3.96).
(This step, similarly to Claim 7 in the proof of Theorem 2.9, is inspired by [24, Section 5.4]).
Recall (3.98) from Claim 6. From (3.94) using Claim 5, we get that for \((t,x) \in \Omega \),
For a.e. \((t,x) \in [0,T] \times {\mathbb {R}}\), \(\nu _{t,x}\) is a probability measure, the maps \(w \mapsto \left( w-u (t,x)\right) F (x,w)\) and \(w \mapsto \left( H (x,w) - H \left( x, u (t,x)\right) \right) E (w)\) are sufficiently regular to ensure that the functions
(S being any Borel set) meet the requirements in the definition of finite Radon measures. Hence, the two maps
are in \(\textbf{BV}({\mathbb {R}}; {\mathbb {R}})\). Since \(\mathop {\textrm{spt}}\nu _{t,x} \subseteq [-M,M]\), then \(A _{t,x} (v)\) and \(B_{t,x} (v)\) vanish for \(v < -M\) and attain a constant value for \(v > M\). Moreover, (2.14) implies that \(\alpha _{t,x} ({\mathbb {R}}) = 0\) while (3.98) in Claim 6 implies that \(\beta _{t,x} ({\mathbb {R}}) = 0\). Therefore, for all \((t,x) \in \Omega \), both \(A_{t,x}\) and \(B_{t,x}\) are supported in \([-M,M]\). An integration by parts, see [21, Theorem B] (in particular the remark at the bottom of [21, p. 422]), then ensures that from equality (3.99) we can deduce
By means of (2.4), we then have
The above equality holds for any continuous function \(E'\), hence for all \((t,x) \in \Omega \)
A direct computation shows that \(\left( H (x,w) - H\left( x, u (t,x)\right) \right) \, A_{t,x} (w) = \left( w-u (t,x)\right) \, B_{t,x} (w)\) since the two sides have the same distributional derivative in w by (3.101) and the definitions (3.100) of \(A_{t,x}\), \(B_{t,x}\). Inserting (3.101) in the last equality, we have
Call [a, b] the minimal (with respect to set inclusion) interval containing the support of \(\nu _{t,x}\). Note that \(A_{t,x} (w) \ne 0\) for \(w \in ]a,b[\). Indeed, by the definition of \(A_{t,x} (w)\) and since \(\nu _{t,x}\) is nonnegative, the map \(w \mapsto A_{t,x} (w)\) vanishes for \(w < a\), weakly decreases for \(w \in ]a, u (t,x) [\), weakly increases for \(w \in ]u (t,x), b [\) and vanishes for \(w >b\). At the same time, the minimality of [a, b] ensures that \(A_{t,x}\) is nonzero in both a right neighborhood of a and a left neighborhood of b. Simplifying, we thus obtain
and differentiating this equality with respect to w we contradict (WGNL), unless \(a=b\), which in turn ensures that, for a.e. \((t,x) \in [0,T] \times {\mathbb {R}}\), \(\nu _{t,x}\) is a Dirac measure. We thus have the pointwise a.e. convergence, up to a subsequence, of the vanishing viscosity solutions, see [38, Proposition 9.1.7]. Claim 7 is proved.\(\checkmark \)
Claim 8: u solves (CL) in the sense of Definition 2.1.
Let (E, F) be an entropy–entropy flux pair in the sense of Definition 2.3, with E of class \({\textbf{C}}^{2}\) and convex. Using (2.20), thanks to the regularity of \(u_\varepsilon \), simple computations give
so that by the convexity of E
Fix a test function \(\varphi \in {\textbf{C}}_c^{2} ({\mathbb {R}}^2; {\mathbb {R}}_+)\), multiply both sides in (3.102) by \(\varphi \) and integrate to get
By (2.26), we have the \({{\textbf{L}}^\infty }\) boundedness of \(u_\varepsilon \) uniformly in \(\varepsilon \). Using Claim 7 and the Dominated Convergence Theorem [22, Theorem (12.24)] we obtain (2.7) for any test function \(\varphi \in {\textbf{C}}_c^{2} ({\mathbb {R}}^2; {\mathbb {R}}_+)\). A standard approximation argument allows to relax (2.7) to any test function \(\varphi \in {\textbf{C}}_c^{1} ({\mathbb {R}}^2; {\mathbb {R}}_+)\). The proof of Claim 8 follows by Item 2 in Proposition 2.4.\(\checkmark \)
Conclusion
By Claim 8, u solves (CL) in the sense of Definition 2.1 and thus its uniqueness follows from Theorem 2.6. Recall that the sequence \(\varepsilon _n\), prior to the simplification in the notation in Remark 3.9, is an arbitrary sequence converging to 0. Above, we proved that there exists a subsequence \(\varepsilon _{m_k}\) such that the corresponding subsequence \(u_{\varepsilon _{n_k}}\) converges to a limit u, independent of the choice of the initial sequence \(\varepsilon _n\). The arbitrariness of the choice of \(\varepsilon _n\) ensures that \(u_\varepsilon \), now understood as a continuous family, converges to u.
The proof of Theorem 2.17 is completed. \(\square \)
An alternative approach allowing to pass from weak to strong convergence might be adapted from [20, Items 2 and 3 in the proof of Theorem 4.1].
3.5 Properties of the limit semigroups
Proof of Theorem 2.18
Theorem 2.17 ensures the existence of a solution in the sense of Definition 2.1 globally in time, for all initial data in \({{\textbf{W}}^{1,\infty }}({\mathbb {R}}; {\mathbb {R}})\), proving 1. and 2. for such data. The uniqueness of this solution follows from estimate (2.14) in Theorem 2.6.
Define pointwise \((S^{CL}_t u_o) (x) \,{:=}\,u^* (t,x)\), where \(u^*\) is as in Theorem 2.6. We thus have the existence of a map \(S^{CL}\) defined on \({\mathbb {R}}_+ \times {{\textbf{W}}^{1,\infty }}({\mathbb {R}}; {\mathbb {R}})\) attaining values in (a precise representative in) \({{\textbf{L}}^\infty }({\mathbb {R}}; {\mathbb {R}})\), satisfying 3.a and 3.b for all \(u_o \in {{\textbf{W}}^{1,\infty }}({\mathbb {R}}; {\mathbb {R}})\) and 4. for all \(u_o,v_o \in {{\textbf{W}}^{1,\infty }}({\mathbb {R}}; {\mathbb {R}})\), thanks to Theorem 2.6.
Fix an initial datum \(u_o\) in \({{\textbf{L}}^\infty }({\mathbb {R}}; {\mathbb {R}})\). Use Theorem 2.9 to find two stationary solutions \(\check{u}\) and \({\hat{u}}\) such that for all \(x \in {\mathbb {R}}\),
Take a sequence \(u_o^n \in {{\textbf{W}}^{1,\infty }}({\mathbb {R}}; {\mathbb {R}})\) converging to \(u_o\) in \({{\textbf{L}}_{\textbf{loc}}^{1}} ({\mathbb {R}}; {\mathbb {R}})\) and such that \(u_o^n (x) \in [\check{u} (x), {\hat{u}} (x)]\) for all \(x \in {\mathbb {R}}\).
By the contraction property (2.14), for all \(t \in {\mathbb {R}}_+\), \(S^{CL}_t u_o^n\) is a Cauchy sequence in \({{\textbf{L}}_{\textbf{loc}}^{1}} ({\mathbb {R}}; {\mathbb {R}})\). Define \(S^{CL}_t u_o\) as this limit and note that (2.14) also shows that \(S^{CL}\) does not depend on the choice of the sequence \((u_o^n)\).
Nevertheless, by (2.15), for all \(t \in {\mathbb {R}}_+\), \((S^{CL}_t u_o^n) (x) \in [\check{u} (x), {\hat{u}} (x)]\) for a.e. \(x \in {\mathbb {R}}\), so that \((t,x) \mapsto (S^{CL}_t u_o) (x)\) is in \({{\textbf{L}}^\infty }({\mathbb {R}}_+ \times {\mathbb {R}}; {\mathbb {R}})\).
Moreover, \((t,x) \mapsto (S^{CL}_t u_o^n) (x)\) is a converging sequence in \({{\textbf{L}}_{\textbf{loc}}^{1}} ({\mathbb {R}}_+ \times {\mathbb {R}}; {\mathbb {R}})\). Up to the extraction of a subsequence, we have that the sequence \((t,x) \mapsto (S^{CL}_t u_o^n) (x)\) converges pointwise a.e. to \((t,x) \mapsto (S^{CL}_t u_o) (x)\). Since we have the \({{\textbf{L}}^\infty }\) bound \((S^{CL}_t u_o^n) (x) \in [\check{u} (x), {\hat{u}} (x)]\) we can pass to the limit in (2.2), apply the Dominated Convergence Theorem [22, Theorem (12.24)] and obtain that \((t,x) \mapsto (S^{CL}_t u_o) (x)\) solves (CL) in the sense of Definition 2.1.
By this construction, we immediately have that the map \(u (t,x) \,{:=}\,(S^{CL}_t u_o) (x)\) satisfies 1. and 2., while \(S^{CL}\) satisfies 3.a and 4..
Fix \(u_o \in {{\textbf{L}}^\infty }({\mathbb {R}}; {\mathbb {R}})\). Applying again Theorem 2.6, we see that the map \((t,x) \mapsto (S^{CL}_t u_o) (x)\) admits a representative that satisfies 3.b. Since \(S^{CL}\) satisfies 3.a, we can conclude that for all \(t \in {\mathbb {R}}_+\) and for a.e. \(x \in {\mathbb {R}}\) that \((S^{CL}_tu_o) (x)\) equals this representative. Hence, \(S^{CL}\) satisfies 3.b.
To complete the proof, note that \(S^{CL}\) is a semigroup, thanks to the uniqueness and \({{\textbf{L}}_{\textbf{loc}}^{1}} ({\mathbb {R}};{\mathbb {R}})\) continuity proved in Theorem 2.6 and since \(S^{CL}_t\left( {{\textbf{L}}^\infty }({\mathbb {R}}; {\mathbb {R}})\right) \subseteq {{\textbf{L}}^\infty }({\mathbb {R}}; {\mathbb {R}})\). \(\square \)
Proof of Theorem 2.19
Define for later use
Fix \(U_o \in {\mathcal {D}}\). Then, Theorem 2.16 ensures the existence of a solution U to (HJ) in the sense of Definition 2.7 globally defined in time, satisfying 1. and 2. for these data. The uniqueness of this solution follows from (2.19) in Theorem 2.8.
Define now, for all \(U_o \in {\mathcal {D}}\),
Note that Theorem 2.16 also proves 3., while 4. is a consequence of Item 2 in Theorem 2.8.
Note that \(S^{HJ}\) is not a semigroup on \({\mathcal {D}}\), since a priori \({\mathcal {D}}\) is not invariant.
Below, we use the semigroup \(S^{CL}\) as defined in Theorem 2.18.
Claim: For all \(U_o \in {\mathcal {D}}\), set \(u_o = U_o'\). Then, \((S^{CL}_t u_o) (x) = \partial _x (S^{HJ}_t U_o) (x)\) for a.e. \((t,x) \in [0,T] \times {\mathbb {R}}\).
Let \(U_o \in {\mathcal {D}}\) and set \(u_o = U_o'\), so that \(u_o \in {{\textbf{W}}^{1,\infty }}({\mathbb {R}}; {\mathbb {R}})\). For any \(\varepsilon >0\), call \(u_\varepsilon \) the classical solution to (2.20) as provided by Theorem 2.14 and \(U_\varepsilon \) that of (2.21) as provided by Corollary 2.15. By Theorem 2.11, we have \(u_\varepsilon = \partial _x U_\varepsilon \). Choose a sequence \(\varepsilon _n\) positive and vanishing to 0. Theorem 2.16 ensures that \((t,x) \mapsto U_{\varepsilon _n} (t,x)\) converges, as \(n \rightarrow +\infty \),to \((t,x) \mapsto (S^{HJ}_t U_o) (x)\) uniformly on compact sets. Similarly, Theorem 2.17 (which uses (WGNL)) ensures that \((t,x) \mapsto u_{\varepsilon _n} (t,x)\) converges pointwise a.e. to \((t,x) \mapsto (S^{CL}_t u_o) (x)\). Hence, in distributional sense, \((S^{CL}_t u_o) (x) = \partial _x (S^{HJ}_t U_o) (x)\) and therefore this equality also holds a.e. in \({\mathbb {R}}_+ \times {\mathbb {R}}\), proving the Claim.\(\checkmark \)
Fix an initial datum \(U_o\) in \(\textbf{Lip}({\mathbb {R}}; {\mathbb {R}})\). Use Theorem 2.9 to find two stationary solutions \(\check{u}\) and \({\hat{u}}\) to (HJ) such that for all \(x \in {\mathbb {R}}\),
Take a sequence \(U_o^n \in {\mathcal {D}}\) converging to \(U_o\) in \({{\textbf{L}}_{\textbf{loc}}^{\infty }}({\mathbb {R}}; {\mathbb {R}})\) and such that \((U_o^n)' (x) \in [\check{u} (x), {\hat{u}} (x)]\) for a.e. \(x \in {\mathbb {R}}\). Moreover, for a.e. \(x \in {\mathbb {R}}\),
Define \({\tilde{C}} \,{:=}\,\max \left\{ {\left\| {\hat{u}}\right\| }_{{{\textbf{L}}^\infty }({\mathbb {R}}; {\mathbb {R}})}, {\left\| \check{u}\right\| }_{{{\textbf{L}}^\infty }({\mathbb {R}}; {\mathbb {R}})}\right\} \), so that for all \(t \in {\mathbb {R}}_+\) and for all \(n \in {\mathbb {N}}\),
Similarly to (2.18), define
By Item 2 in Theorem 2.8, we have for all \(R>0\) and all \(t \in {\mathbb {R}}_+\),
hence \((t,x) {\mapsto } (S^{HJ}_t U_o^n) (x)\) is a Cauchy sequence in \({{\textbf{L}}_{\textbf{loc}}^{\infty }}({\mathbb {R}}_+ \times {\mathbb {R}}; {\mathbb {R}})\). Extend \(S^{HJ}\) to \(\textbf{Lip}({\mathbb {R}}; {\mathbb {R}})\) by \(S^{HJ}_t U_o = \lim _{n\rightarrow +\infty } S^{HJ}_t U_o^n\) and note that, by (3.104), \({\left\| \partial _x S^{HJ}_t U_o\right\| }_{{{\textbf{L}}^\infty }({\mathbb {R}}; {\mathbb {R}})} \le {\tilde{C}}\) for \(t \in {\mathbb {R}}_+\).
This extension \(S^{HJ}\) satisfies 4. by Item 2 in Theorem 2.8. Moreover, [13, Theorem 1.2] ensures that \((t,x) \mapsto (S^{HJ}_t U_o) (x)\) is a solution to (HJ) in the sense of Definition 2.7. As a consequence, 1., 2. and the existence of the maximal solution follow. Its uniqueness is guaranteed by Item 2 in Theorem 2.8. The uniform bound \({\left\| \partial _x S^{HJ}_t U_o\right\| }_{{{\textbf{L}}^\infty }({\mathbb {R}}; {\mathbb {R}})} \le {\tilde{C}}\) proves that the set \(\textbf{Lip}({\mathbb {R}}; {\mathbb {R}})\) is invariant, so that \(S^{HJ} :{\mathbb {R}}_+ \times \textbf{Lip}({\mathbb {R}}; {\mathbb {R}}) \rightarrow \textbf{Lip}({\mathbb {R}}; {\mathbb {R}})\) is a semigroup.
Since Item 1 in Theorem 2.8 implies Item 3, the proof of Theorem 2.19 is completed.
\(\square \)
Proof of Theorem 2.20
Consider first the case \(u_o \in {{\textbf{W}}^{1,\infty }}({\mathbb {R}}; {\mathbb {R}})\), so that \(U_o \in {\textbf{C}}^{1} ({\mathbb {R}}; {\mathbb {R}})\). For any \(\varepsilon >0\), call \(u_\varepsilon \) the classical solution to (2.20) as provided by Theorem 2.14 and \(U_\varepsilon \) that of (2.21) as provided by Corollary 2.15. By Theorem 2.11, we have \(u_\varepsilon = \partial _x U_\varepsilon \). Choose a sequence \(\varepsilon _n\) positive and vanishing to 0. Theorem 2.16 ensures that \((t,x) \mapsto U_{\varepsilon _n} (t,x)\) converges to \((t,x) \mapsto (S^{HJ}_t U_o) (x)\) uniformly on compact sets. Similarly, Theorem 2.17 ensures that \((t,x) \mapsto u_{\varepsilon _n} (t,x)\) converges pointwise a.e. to \((t,x) \mapsto (S^{CL}_t u_o) (x)\). Hence, in distributional sense, \((S^{CL}_t u_o) (x) = \partial _x (S^{HJ}_t U_o) (x)\) and therefore this equality also holds a.e. in \({\mathbb {R}}_+ \times {\mathbb {R}}\). This proves (2.27) in the case \(u_o \in {{\textbf{W}}^{1,\infty }}({\mathbb {R}}; {\mathbb {R}})\).
Let now \(u_o \in {{\textbf{L}}^\infty }({\mathbb {R}}; {\mathbb {R}})\). Choose a sequence \(u_o^n \in {{\textbf{W}}^{1,\infty }}({\mathbb {R}}; {\mathbb {R}})\) converging to \(u_o\) in \({{\textbf{L}}_{\textbf{loc}}^{1}} ({\mathbb {R}}; {\mathbb {R}})\). Define \(U_o^n (x) = \int _0^x u_o^n (\xi ){\textrm{d}{\xi }}\). Then, by Theorem 2.18 (which uses (WGNL)), also \((t,x) \mapsto (S^{CL}_t u_o^n) (x)\) converges to \((t,x) \mapsto (S^{CL}_t u_o) (x)\) in \({{\textbf{L}}_{\textbf{loc}}^{1}} ({\mathbb {R}}; {\mathbb {R}})\). Similarly, \((t,x) \mapsto (S^{HJ}_t U_o^n) (x)\) converges to \((t,x) \mapsto (S^{HJ}_t U_o) (x)\) by (2.19) in Theorem 2.8 uniformly on compact sets. In particular, both sequences converge in distributional sense, proving (2.27) in the general case, thanks to the uniqueness of entropy solutions to (CL) (Theorem 2.18) and of viscosity solutions to (HJ) (Theorem 2.19). \(\square \)
Data availability
Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.
Notes
In view of (CNH), in (UC) and in (WGNL) it is sufficient to consider only \(x \in [-X,X]\).
References
B. Andreianov, K. H. Karlsen, and N. H. Risebro. A theory of \(L^1\)-dissipative solvers for scalar conservation laws with discontinuous flux. Arch. Ration. Mech. Anal., 201(1):27–86, 2011.
E. Audusse and B. Perthame. Uniqueness for scalar conservation laws with discontinuous flux via adapted entropies. Proc. Roy. Soc. Edinburgh Sect. A, 135(2):253–265, 2005.
M. Bardi and I. Capuzzo-Dolcetta. Optimal control and viscosity solutions of Hamilton-Jacobi-Bellman equations. Birkhäuser Boston, MA, 1997. With appendices by M. Falcone and P. Soravia.
G. Barles. An introduction to the theory of viscosity solutions for first-order Hamilton-Jacobi equations and applications. In Hamilton-Jacobi equations: approximations, numerical analysis and applications, volume 2074 of Lect. Notes in Math., pages 49–109. Springer, Heidelberg, 2013.
A. Bressan, G. Guerra, and W. Shen. Vanishing viscosity solutions for conservation laws with regulated flux. J. Differential Equations, 266(1):312–351, 2019.
V. Caselles. Scalar conservation laws and Hamilton-Jacobi equations in one-space variable. Nonlinear Anal., 18(5):461–469, 1992.
G.-Q. Chen and M. Rascle. Initial layers and uniqueness of weak entropy solutions to hyperbolic conservation laws. Arch. Ration. Mech. Anal., 153(3):205–220, 2000.
S. Cifani and E. R. Jakobsen. Entropy solution theory for fractional degenerate convection-diffusion equations. Ann. Inst. H. Poincaré C Anal. Non Linéaire, 28(3):413–441, 2011.
G. M. Coclite and N. H. Risebro. Viscosity solutions of Hamilton-Jacobi equations with discontinuous coefficients. J. Hyperbolic Differ. Equ., 4(4):771–795, 2007.
R. M. Colombo and V. Perrollaz. Initial data identification in conservation laws and Hamilton-Jacobi equations. J. Math. Pures Appl. (9), 138:1–27, 2020.
R. M. Colombo, V. Perrollaz, and A. Sylla. Initial data identification in space dependent conservation laws and Hamilton-Jacobi equations. Preprint, 2022.
R. M. Colombo, V. Perrollaz, and A. Sylla. Peculiarities of space dependent conservation laws: Inverse design and asymptotics. arXiv:2305.08427, 2023. To appear on HYP2022 proceedings.
M. G. Crandall and P.-L. Lions. Viscosity solutions of Hamilton-Jacobi equations. Trans. Amer. Math. Soc., 277(1):1–42, 1983.
M. G. Crandall and P.-L. Lions. On existence and uniqueness of solutions of Hamilton-Jacobi equations. Nonlinear Anal., 10(4):353–370, 1986.
C. M. Dafermos. Generalized characteristics and the structure of solutions of hyperbolic conservation laws. Indiana Univ. Math. J., 26(6):1097–1119, 1977.
C. M. Dafermos. Hyperbolic conservation laws in continuum physics, volume 325 of Grundlehren der Mathematischen Wissenschaften. Springer-Verlag, Berlin, fourth edition, 2016.
L. C. Evans. Weak KAM theory and partial differential equations. In Calculus of variations and nonlinear partial differential equations, volume 1927 of Lecture Notes in Math., pages 123–154. Springer, Berlin, 2008.
L. C. Evans. Partial Differential Equations. American Math. Society, Providence, R.I., 2010.
L. C. Evans and R. F. Gariepy. Measure theory and fine properties of functions. Textbooks in Mathematics. CRC Press, Boca Raton, FL, revised edition, 2015.
G. Guerra and W. Shen. The Cauchy problem for a non strictly hyperbolic \(3\times 3\) system of conservation laws arising in polymer flooding. Commun. Math. Sci., 19(6):1491–1507, 2021.
E. Hewitt. Integration by parts for Stieltjes integrals. Amer. Math. Monthly, 67:419–423, 1960.
E. Hewitt and K. Stromberg. Real and abstract analysis. Graduate Texts in Mathematics, No. 25. Springer-Verlag, New York-Heidelberg, 1975. Third printing.
H. Holden and N. H. Risebro. Front tracking for hyperbolic conservation laws. Applied Mathematical Sciences, volume 152. Springer-Verlag, New York, 2002.
L. Hörmander. Lectures on nonlinear hyperbolic differential equations. Mathématiques & Applications (Berlin), volume 26. Springer-Verlag, Berlin, 1997.
H. Ishii. Uniqueness of unbounded viscosity solution of Hamilton-Jacobi equations. Indiana Univ. Math. J., 33(5):721–748, 1984.
K. H. Karlsen and N. H. Risebro. A note on front tracking and equivalence between viscosity solutions of Hamilton-Jacobi equations and entropy solutions of scalar conservation laws. Nonlinear Anal., 50(4, Ser. A: Theory Methods):455–469, 2002.
S. N. Kružkov. First order quasilinear equations with several independent variables. Mat. Sb. (N.S.), 81 (123):228–255, 1970.
T. Liard and E. Zuazua. Initial data identification for the one-dimensional burgers equation. IEEE Transactions on Automatic Control, 2021.
M. J. Lighthill and G. B. Whitham. On kinematic waves. II. A theory of traffic flow on long crowded roads. Proc. Roy. Soc. London. Ser. A., 229:317–345, 1955.
P.-L. Lions, B. Perthame, and E. Tadmor. A kinetic formulation of multidimensional scalar conservation laws and related equations. J. Amer. Math. Soc., 7(1):169–191, 1994.
E. Y. Panov. Uniqueness of the solution of the Cauchy problem for a first-order quasilinear equation with an admissible strictly convex entropy. Mat. Zametki, 55(5):116–129, 159, 1994.
E. Y. Panov. Erratum to: Existence and strong pre-compactness properties for entropy solutions of a first-order quasilinear equation with discontinuous flux [mr2592291]. Arch. Ration. Mech. Anal., 196(3):1077–1078, 2010.
E. Y. Panov. Existence and strong pre-compactness properties for entropy solutions of a first-order quasilinear equation with discontinuous flux. Arch. Ration. Mech. Anal., 195(2):643–673, 2010.
B. Perthame and A. E. Tzavaras. Kinetic formulation for systems of two conservation laws and elastodynamics. Arch. Ration. Mech. Anal., 155(1):1–48, 2000.
P. Quittner and P. Souplet. Superlinear parabolic problems. Birkhäuser Advanced Texts: Basler Lehrbücher. Birkhäuser Verlag, Basel, 2007. Blow-up, global existence and steady states.
P. I. Richards. Shock waves on the highway. Operations Res., 4:42–51, 1956.
W. Rudin. Functional analysis. McGraw-Hill Book Co., New York, 1973. McGraw-Hill Series in Higher Mathematics.
D. Serre. Systems of conservation laws. 2. Cambridge University Press, Cambridge, 2000. Translated from the 1996 French original by I. N. Sneddon.
J. Serrin. Gradient estimates for solutions of nonlinear elliptic and parabolic equations. Contrib. nonlin. functional Analysis, Proc. Sympos. Univ. Wisconsin, Madison 1971, 565-601 (1971)., 1971.
S. Sternberg. Lectures on differential geometry. Chelsea Publishing Co., New York, second edition, 1983. With an appendix by Sternberg and Victor W. Guillemin.
A. Sylla. Heterogeneity in scalar conservation laws: approximation and applications. Theses, Université de Tours, July 2021.
A. Vasseur. Strong traces for solutions of multidimensional scalar conservation laws. Arch. Ration. Mech. Anal., 160(3):181–193, 2001.
Acknowledgements
The authors thank Guy Barles and Cyril Imbert for useful discussions and the referees for very careful reviews. The first author was partly supported by the GNAMPA 2022 project Evolution Equations, Well Posedness, Control and Applications. This research was funded, in whole or in part, by l’Agence Nationale de la Recherche (ANR), project ANR-22-CE40-0010. For the purpose of open access, the second author has applied a CC-BY public copyright license to any Author Accepted Manuscript (AAM) version arising from this submission.
Funding
Open access funding provided by Università degli Studi di Brescia within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no conflict of interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
The next results are somewhat classical and we provide their proofs or full references for completeness.
Proposition A.1
(Extension Theorem in Locally Convex Spaces) Let X be a locally convex sequentially complete topological vector space. Fix \(f :A \rightarrow X\) with \(A \subseteq {\mathbb {R}}\). If f is uniformly continuous, then there exists a unique continuous map \({\overline{f}} :{\overline{A}} \rightarrow X\) satisfying \({\overline{f}}_{|A} = f\).
Proof
A sequence \(x_n\) in X is a Cauchy sequence if for every neighborhood U of the origin in X, there exists a \(\nu \in {\mathbb {N}}\) such that if \(n,m \in {\mathbb {N}}\) with \(m,n>\nu \), then \(x_n-x_m \in U\). Moreover, f uniformly continuous means that for every neighborhood U of the origin in X, there exists a \(\delta >0\) such that if \(t_1,t_2 \in A\) are such that \({\left| t_2-t_1\right| } < \delta \), then \(f (t_2) - f (t_1) \in U\).
Let \(t_* \in {\overline{A}} \setminus A\). Then, there exists a sequence \(t_n\) in A such that \(\lim _{n\rightarrow +\infty } t_n = t_*\). Let U be a neighborhood of the origin in X. By the uniform continuity of f, there exists an \(\varepsilon >0\) such that \(f (t'') - f (t') \in U\) whenever \({\left| t'' - t'\right| } < \varepsilon \). Thus, there exists a \(\nu \in {\mathbb {N}}\) such that if \(n,m \in {\mathbb {N}}\) with \(m,n > \nu \), then \({\left| t_m - t_n\right| }< \varepsilon \) and hence \(f (t_m) -f (t_n) \in U\), proving that \(f (t_n)\) is a Cauchy sequence converging to, say, \(x_* \in X\). Define \({\overline{f}} (t_*) = x_*\).
Any other sequence \(t'_n\) in A converging to \(t_*\) is such that the sequence defined by \(\tau _{2n} = t_n\) and \(\tau _{2n+1} = t'_n\) is a Cauchy sequence and the argument above ensures that \(\lim _{n\rightarrow +\infty } f (\tau _n) = x_*\), proving that \({\overline{f}}\) is well defined.
To prove the continuity of \({\overline{f}}\), let \(t_n\) be now a sequence in \({\overline{A}}\) converging to \(t_*\). Then, there exists a sequence \(\tau _n\) in A such that \({\left| \tau _n - t_n\right| } < 1/n\). The argument above ensures that \(\lim _{n\rightarrow +\infty } f (\tau _n) = {\overline{f}} (t_*)\), so that by the uniform continuity of f and the definition of \({\overline{f}}\) we also have \(\lim _{n\rightarrow +\infty } {\overline{f}} (t_n) = {\overline{f}} (t_*)\), ensuring the sequential continuity of \({\overline{f}}\).
Fix an open neighborhood U of 0 in X and apply [37, Theorem 1.10] with \(K = \{0\}\) and \(C = X {\setminus } U\) to obtain an open neighborhood V of 0 such that \((K+V) \cap (C+V) = \emptyset \). Since \(V = K+V\) and \(C+V\) is open, then \({\overline{V}} \cap (C+V) = \emptyset \). At the same time \(C \subseteq (C+V)\), thus \({\overline{V}} \subseteq U\). By the uniform continuity of f, there exists a positive \(\delta \) such that for all \(t_1,t_2 \in A\) with \({\left| t_2 - t_1\right| } < \delta \), we have \(\left( f (t_2) - f (t_1)\right) \in V\). The sequential closedness of \({\overline{V}}\) and the sequential continuity of \({\overline{f}}\) proved above ensures that for all \(t_1,t_2 \in {\overline{A}}\) with \({\left| t_2 - t_1\right| } < \delta \), we have \(\left( {\overline{f}} (t_2) - {\overline{f}} (t_1)\right) \in {\overline{V}} \subseteq U\), completing the proof. \(\square \)
Proposition A.2
(The set \({\textbf{C}}_c^{1}\) is separable.) There exists a countable set \(S \subset {\textbf{C}}_c^{1} ({\mathbb {R}}; {\mathbb {R}})\) with the following property: for any \(\psi \in {\textbf{C}}_c^{1} ({\mathbb {R}}; {\mathbb {R}})\) there exists a compact set \({\mathcal {K}} \subset {\mathbb {R}}\) such that for all \(\varepsilon >0\) there exists a map \(\sigma \in S\) satisfying \(\mathop {\textrm{spt}}\sigma \subseteq {\mathcal {K}}\) and \({\left\| \sigma -\psi \right\| }_{{\textbf{C}}^{1} ({\mathbb {R}}; {\mathbb {R}})} \le \varepsilon \).
Proof
For \(n \in {\mathbb {N}}{\setminus } \{0\}\), call \(\vartheta _n\) a function in \({\textbf{C}}^{\infty }({\mathbb {R}}; {\mathbb {R}})\) such that
For every polynomial p with rational coefficients, define
Clearly, \(\chi _{n,p} \in {\textbf{C}}_c^{1}({\mathbb {R}}; {\mathbb {R}})\) and the set of all such \(\chi _{n,p}\) is countable. It is also dense in \({\textbf{C}}_c^{1} ({\mathbb {R}};{\mathbb {R}})\). Indeed, choose \(\varphi \in {\textbf{C}}_c^{1} ({\mathbb {R}}; {\mathbb {R}})\) so that \(\mathop {\textrm{spt}}\varphi \subseteq [-n,n]\). By Stone–Weierstrass Theorem [22, Corollary 7.31], for every \(\varepsilon >0\) there exists a polynomial p with rational coefficients such that \(\sup _{\mathop {\textrm{spt}}\varphi } {\left| p-\varphi '\right| } < \left. \varepsilon \big / (6n+6) \right. \). Then, set \({\mathcal {K}} = [-n-1,n+1]\) and estimate
To obtain the bound in the latter line above in the case \(x \in ]n, n+1]\), use \(\int _{-\infty }^n \vartheta _n (\xi ) \, p (\xi ){\textrm{d}{\xi }}= \chi _{n.p} (n)\) and \(\varphi (n) = 0\). Hence, using (A.1), for \(x \in [n, n+1]\), we have
completing the proof. \(\square \)
Lemma A.3
(Sard’s Lemma [40, Chapter II, Theorem 3.1])
Let \(f \in {\textbf{C}}^{k} ({\mathbb {R}}^{n_1}; {\mathbb {R}}^{n_2})\). If \(k > \max \left\{ n_1 - n_2,0\right\} \), then \( {\mathcal {L}}\big (f\big (\big \{x \in {\mathbb {R}}^{n_1} :Df (x) \hbox { is not surjective}\big \}\big )\big ) = 0\).
Rights and permissions
This article is published under an open access license. Please check the 'Copyright Information' section either on this page or in the PDF for details of this license and what re-use is permitted. If your intended use exceeds what is permitted by the license or if you are unable to locate the licence and re-use information, please contact the Rights and Permissions team.
About this article
Cite this article
Colombo, R.M., Perrollaz, V. & Sylla, A. Conservation laws and Hamilton–Jacobi equations with space inhomogeneity. J. Evol. Equ. 23, 50 (2023). https://doi.org/10.1007/s00028-023-00902-1
Accepted:
Published:
DOI: https://doi.org/10.1007/s00028-023-00902-1