Rational Angles and Tilings of the Sphere by Congruent Quadrilaterals

Abstract

We apply Diophantine analysis to classify edge-to-edge tilings of the sphere by congruent almost equilateral quadrilaterals (i.e., edge combination $a^3b$). Parallel to a complete classification by Cheung, Luk, and Yan, the method implemented here is more systematic and applicable to other related tiling problems. We also provide detailed geometric data for the tilings.

1 Introduction

We study edge-to-edge tilings of the sphere by congruent polygons, such that each vertex has degree $\ge 3$. It is well known that the polygons in these tilings are triangle, quadrilateral, or pentagon. The classification of tilings of the sphere by congruent triangles, pioneered by Sommerville [19] in 1923, was completed by Ueno and Agaoka [20] in 2002. The classification of tilings of the sphere by congruent pentagons has been recently completed through a collective effort [4, 5, 9, 13, 22,23,24,25,26].

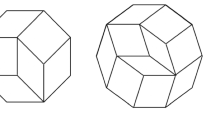
Akama and Sakano [1, 2] conducted a classification for tilings of the sphere by congruent quadrilaterals which can be subdivided into two congruent triangles. It remains to classify the tilings by congruent quadrilaterals with exactly three equal edges ($a^3b$, first picture of Fig. 1) and by congruent quadrilaterals with exactly two equal edges ($a^2bc$, second picture). Ueno and Agaoka [21], and Akama and van Cleemput [3] studied some special cases of the tilings by congruent $a^3b$ quadrilaterals. Their work is indicative of many challenges in the classification. In 2022, Cheung et al. [8] gave a complete classification for tilings of the sphere by congruent quadrilaterals as well as a modernised classification for the tilings by congruent triangles.

We call a quadrilateral with edge combination $a^3b$ almost equilateral, where a-edge and b-edge are assumed to have different lengths. The angles are indicated in the first picture of Fig. 1, likewise for the $a^2bc$ quadrilateral in the second picture. These standard configurations are implicitly assumed in this paper. We call an angle rational if its value is a rational multiple of $\pi$. Otherwise, we call the angle irrational.

Fig. 1

Quadrilaterals with edge combinations $a^3b, a^2bc$

The main purpose of this paper is to give an alternative classification for tilings of the sphere by congruent almost equilateral quadrilaterals. The key is Diophantine analysis in the following situations:

• 1. If all angles are rational, then we determine the angle values by finding all rational solutions to a trigonometric Diophantine equation which all angles must satisfy.

• 2. If some angles are irrational, then we determine all angle combinations at vertices by solving a related system of linear Diophantine equations and inequalities.

Despite the complete classification in [8], techniques in this paper have their own independent significance. Coolsaet [11] discovered the trigonometric Diophantine equation relating the angles of convex almost equilateral quadrilateral. Myerson [15] found the rational solutions to the equation. Based on their works, we made two major advancements. The first is extending the trigonometric Diophantine equation to general (not necessarily convex) almost equilateral quadrilaterals. The second is establishing a technique to determine all angle combinations at vertices using the constraint of irrational angles. This technique is based on the study in [17].

Historically, trigonometric Diophantine equations have been closely connected to many geometric situations. Conway and Jones [10] have opened doors to the exploration of many interesting geometry problems. Notable work can be seen in [14,15,16, 18].

In contrast to [8], there are two significant advantages in our approach. First, arguments in this paper are more systematic, whereas those in [8] are often sophisticated and improvised. Second, most techniques here can be computerised. In that regard, our approach is apparently more advantageous in exhaustive search and more likely to be applied to other similar problems, such as the study of non-edge-to-edge tilings of the sphere. Promising signs of such proposal can be seen in the families of non-edge-to-edge tilings by congruent triangles obtained in this paper as degenerated cases of the tilings by quadrilaterals, which supplement the discoveries by Dawson [12].

Another feature of this paper is the extrinsic geometric data of tilings, namely the formulae for the angles and edge lengths, which are intended for wider audience, such as engineers, designers, and architects. Full discussion can be seen in the version on arXiv:2204.02748.

The paper is organised as follows. Section 2 explains the main results. Section 3 explains the basic tools and the strategy. Section 4 studies the tilings where all angles are rational, and Sect. 5 studies the tilings where some angles are irrational.

2 Main Results

The main result of this paper is stated as follows.

Theorem 1

Tilings of the sphere by congruent almost equilateral quadrilaterals are earth map tiling $E_{}$ and its flip modifications, $F_1E_{},F_2E_{}$, and rearrangement $RE_{}$, and isolated earth map tilings, $S_{}1, S_{}2, S3, FS3, S5$, and special tilings, $QP_6, S4,S6$.

The tilings in the main theorem are presented in Fig. 2. The notations $E, F_{1}E, F_{2}E, RE$ in the theorem correspond to $E_{\square }^{A}1, FE_{\square }^{A}1, RE_{\square }^{A}1$ in [8], where $F_{1}E, F_{2}E$ are treated as the same flip modification in $FE_{\square }^{A}1$ under a general framework. Let f denote the number of tiles in a tiling. We also use subscripts to indicate the number of tiles. For example, the tilings E, $F_{1}E, F_{2}E$ and RE in Fig. 2 with $f=28$ are denoted as $E_{28}, F_{1}E_{28}, F_{2}E_{28}, RE_{28}$. We also remark that S1 has only two versions, $S_{12}1$ and $S_{16}1$. Each of the other Si’s has only a single fixed f. Moreover, FS3 is the flip modification of S3. We use $QP_6$ to denote the quadrilateral subdivision of the cube $P_6$.

Fig. 2

Tilings of the sphere by almost equilateral quadrilaterals: $E_{28}$, $F_{1}E_{28}$, $F_{2}E_{28}$, $RE_{28}$, $S_{12}1$, $S_{16}1$, S2, S3, FS3, $QP_6$, S4, S5, S6

We explain the structures of these tilings explicitly by their planar representations in first picture of Fig. 4, and Figs. 5, 6, 7. The angles are implicitly represented according to Fig. 3. Tiles with angles arranged in the orientation in the first picture, i.e., $\alpha \rightarrow \beta \rightarrow \gamma \rightarrow \delta$ clockwise, are marked by “ - ”. The other tiles, unmarked, have angles arranged counter-clockwise as in the second picture.

Fig. 3

Orientations of almost equilateral quadrilateral tiles

Fig. 4

Earth map tilings E by $a^3b$ tiles and by $a^2bc$ tiles

Fig. 5

Flip modifications $F_{1}E, F_{2}E$ and rearrangement RE of E

Fig. 6

Polar view of $S1, S2, S3, FS3, QP_6, S4, S5, S6$

The earth map tiling E is the first picture of Fig. 4. The vertical edges in the top row of E converge to a vertex (north pole) and those in the bottom row converge to another (south pole). The shaded tiles form a timezone. A tiling is a repetition of timezones. The second picture is the earth map tiling by congruent $a^2bc$ quadrilaterals. We may obtain E from this earth map tiling by edge reduction $c=a$ or $b=a$. The earth map tiling with exactly three timezones is the deformed cube.

For any positive integer $s < \frac{f}{2}$, let ${\mathcal {T}}_s$ be s consecutive timezones. The first picture of Fig. 5 shows the boundary of ${\mathcal {T}}_s$. If $\alpha =s\beta$, we may flip the ${\mathcal {T}}_s$ part of E with respect to $F_1$ to get a new tiling $F_{1}E$. This is the reason to call it a flip modification. In fact, we may simultaneously flip several disjoint copies of ${\mathcal {T}}_s$. Similarly, if $\gamma +\delta =s\beta$, we may simultaneously flip several disjoint copies ${\mathcal {T}}_s$ with respect to $F_2$ to get $F_{2}E$.

For $f=6q+4$ and specific combination of angle values, we may combine three copies of ${\mathcal {T}}_q$ and four more tiles as in the second picture of Fig. 5 to get a rearrangement RE of E. The third picture depicts RE when $q=4$.

Further explanations on $F_{1}E,F_{2}E,RE$ can be seen in [8, Section 2].

The isolated earth map tilings and the special tilings are in Fig. 6.

Figure 7 presents a different view of S1, S2, S3, FS3, S5. Comparing with Fig. 4, combinatorially, each of them belongs to a family of earth map tilings (with shaded timezones different from that in E). However, they can be realised as geometric tilings only for specific numbers of timezones.

There are other studies on tilings of earth map types. Two pentagonal earth map tilings (with various modifications) are constructed in [9] and a combinatorial study on pentagonal earth map tilings was given by Yan [25].

Fig. 7

Isolated earth map tilings S1, S2, S3, FS3, S5

Tables 1, 2, 3, 4 give the geometric and combinatoric data of the tilings.

Table 1 Data of isolated tilings 1

Table 2 Data of isolated tilings 2

Table 3 Data of earth map tilings 1

Table 4 Data of earth map tilings 2

3 Basic Tools

3.1 Concepts and Notations

3.1.1 Quadrilateral

A polygon is simple if the boundary is a simple closed curve. A polygon is convex if it is simple and every angle $\le \pi$. By [13, Lemma 1], at least one tile in a tiling of the sphere is simple. If all the tiles are congruent, then all tiles are simple.

For quadrilaterals in tilings, we assume that the angles and edges admit values in $(0,2\pi )$. The simple tile condition implies $a < \pi$ for both quadrilaterals in Fig. 1.

The area of the quadrilateral is the surface area $4\pi$ of the unit sphere divided by number f of tiles. Then, we get the quadrilateral angle sum

$$\begin{aligned} \alpha + \beta + \gamma + \delta = (2 + \tfrac{4}{f} )\pi . \end{aligned}$$

(1)

3.1.2 Vertex

We denote by $\alpha ^m\beta ^n\gamma ^k\delta ^l$ a vertex consisting of m copies of $\alpha$, and n copies of $\beta$, and k copies of $\gamma$, and l copies of $\delta$. For example, $\alpha \beta ^2$ is a vertex with $m=1, n=2$ and $k=l=0$. A vertex $\alpha ^m\beta ^n\gamma ^k\delta ^l$ has vertex angle sum

$$\begin{aligned} m \alpha + n \beta + k \gamma + l \delta = 2\pi . \end{aligned}$$

(2)

By (1), at least one of the non-negative integers m, n, k, l is zero.

In our practice, m, n, k, l in a vertex notation are assumed to be $>0$ unless otherwise specified. For example, $\alpha ^m\beta ^n$ does not include $\alpha ^m, \beta ^n$. Such practice is one subtle difference from [8]. To streamline the discussion, we give a shorthand argument: we simply say “by $\alpha \beta ^2$” to mean “by $\alpha \beta ^2$ being a vertex” or “by the angle sum $\alpha + 2\beta = 2\pi$ of $\alpha \beta ^2$”. We use $\alpha =\beta$ to mean $\alpha ,\beta$ having the same value. We use $\alpha \ne \beta$ to mean $\alpha , \beta$ having distinct values.

The notation $\alpha \beta ^2\cdots$ means a vertex with at least one $\alpha$ and two $\beta$’s, i.e., $m\ge 1$ and $n\ge 2$. We call the angle combination in $\cdots$ (and the sum of angles in $\cdots$) the remainder of the vertex. A b-vertex is a vertex with a b-edge (i.e., with $\gamma ,\delta$) and a ${\hat{b}}$-vertex is a vertex without b-edge (i.e., without $\gamma ,\delta$).

The critical step in classifying tilings is to find all the possible angle combinations at vertices. There are various constraints on these combinations. Examples of such constraints are the vertex angle sum and the quadrilateral angle sum. We call the combinations satisfying the constraints admissible. An anglewise vertex combination ($\text {AVC}$) is a collection of all admissible vertices in a tiling. For example, the following is $\text {AVC}$ (20) from Proposition 4.4:

$$\begin{aligned} \text {AVC}= \{ \alpha \gamma \delta , \gamma ^3\delta , \beta ^n, \alpha \beta ^n, \alpha \beta ^n\delta ^2, \beta ^n\gamma \delta , \beta ^n\gamma ^2\delta ^2 \}. \end{aligned}$$

We emphasise that m, n, k, l are generic notations reserved for the numbers of $\alpha , \beta , \gamma , \delta$. The generic n in an $\text {AVC}$ may take different values at different vertex. We remark that some vertices in an $\text {AVC}$ may not appear in a tiling. For example, the $\text {AVC}$ of the earth map tiling E below has only two vertices

$$\begin{aligned} \text {AVC}\equiv \{ \alpha \gamma \delta , \beta ^{\frac{f}{2}} \}. \end{aligned}$$

Here, we use “$\equiv$” instead of “$=$” to denote the set of all vertices which actually appear in a tiling.

An angle sum system is a linear system consisting of the quadrilateral angle sum and vertex angle sums. For example, for vertices $\alpha ^{m_1}\beta ^{n_1}\gamma ^{k_1}\delta ^{l_1}$, $\alpha ^{m_2}\beta ^{n_2}\gamma ^{k_2}\delta ^{l_2}, \alpha ^m\beta ^n\gamma ^k\delta ^l$ in a tiling, where $m_i, n_i, k_i, l_i, m, n, k, l \ge 0$ and $1 \le i \le 2$, the angles satisfy the angle sum system below

$$\begin{aligned} {\left\{ \begin{array}{ll} \alpha + \beta + \gamma + \delta = (2+\tfrac{4}{f} )\pi , \\ m_1 \alpha + n_1 \beta + k_1 \gamma + l_1 \delta = 2\pi , \\ m_2 \alpha + n_2 \beta + k_2 \gamma + l_2 \delta = 2\pi , \\ m \alpha + n \beta + k \gamma + l \delta = 2\pi . \end{array}\right. } \end{aligned}$$

If the four equations are linearly independent, then the unique solution implies that all four angles are rational. If some angle is irrational, then this angle sum system has rank $\le 3$, which we call the irrationality condition.

If $\alpha \gamma \delta$ is a vertex, we will get a different system where the irrationality condition is rank $=2$.

In fact, as seen in [8], technical and mostly ad hoc combinatorial arguments are required to derive three vertices in the majority of cases. By dividing into rational angle and irrational angle analysis albeit artificial, we can systematically determine all the vertices. Our strategy is outlined in Sect. 3.4, and implemented in Sects. 4 and 5.

The notations $\# \alpha , \# \beta$, etc., denote the total number of $\alpha$, the total number of $\beta$, etc., in a tiling. If each angle appears exactly once at the quadrilateral, then

$$\begin{aligned} f=\# \alpha = \# \beta = \# \gamma = \# \delta . \end{aligned}$$

We also, for example, denote by $\# \alpha \delta ^2$ the total number of vertex $\alpha \delta ^2$ in a tiling. For $\text {AVC}$ (16) $=\{ \alpha \delta ^2, \alpha \beta ^3, \gamma ^3\delta , \alpha ^2\beta \gamma ^2 \}$, we have

$$\begin{aligned} f&= \# \alpha = \# \alpha \delta ^2 + \# \alpha \beta ^3 + 2\# \alpha ^2\beta \gamma ^2, \\ f&= \# \beta = 3\# \alpha \beta ^3 + \# \alpha ^2\beta \gamma ^2, \\ f&= \# \gamma = 3\# \gamma ^3\delta + 2\# \alpha ^2\beta \gamma ^2, \\ f&= \# \delta =2 \# \alpha \delta ^2 + \# \gamma ^3\delta . \end{aligned}$$

3.1.3 Adjacent Angle Deduction

Angles at a vertex can be arranged in various ways. An adjacent angle deduction (AAD) is a compact notation representing the angle arrangement and the tile arrangement at a vertex. Symbolically, “ $\vert$ ” denotes an a-edge and “ ” denotes a b-edge. For example, all three pictures in Fig. 8 are AADs of $\beta ^2\gamma ^2$ for the almost equilateral quadrilateral. The AADs of in the pictures can be further represented by , and , respectively.

Fig. 8

Adjacent angle deduction (AAD)

As seen above, the AAD notations can be regarded as mini pictures. Similar to their pictorial counterparts, the notations can be rotated and reversed. For example, the AAD of the second picture can also be written as (rotation) and (reversion).

The use of AAD notation can be flexible. For example, we write $\beta ^{\alpha }\vert ^{\alpha }\beta$ (the first picture of Fig. 8) if it is our focus on $\beta ^2\gamma ^2$. We use $\beta ^{\alpha } \vert ^{\alpha } \beta \cdots$ to denote a vertex with such angle arrangement.

The AAD has reciprocity property: an AAD $\lambda ^{\theta } \vert ^{\rho } \mu$ at $\lambda \mu \cdots$ implies an AAD at $\theta ^{\lambda } \vert ^{\mu }\rho$ at $\theta \rho \cdots$ and vice versa.

We give an example of proof by AAD. Up to rotation and reversion, the possible AADs for $\alpha \vert \alpha$ are $\alpha ^{\beta } \vert ^{\beta } \alpha , \alpha ^{\beta } \vert ^{\delta } \alpha , \alpha ^{\delta } \vert ^{\delta } \alpha$. If $\beta ^2\cdots , \delta ^2\cdots$ are not vertices, then $\alpha \vert \alpha$ has unique AAD $\alpha ^{\beta } \vert ^{\delta } \alpha$. Moreover, a vertex $\alpha ^3$ has two possible AADs $\vert ^{\delta }\alpha ^{\beta }\vert ^{\delta }\alpha ^{\beta }\vert ^{\delta }\alpha ^{\beta }\vert , \vert ^{\delta }\alpha ^{\beta }\vert ^{\delta }\alpha ^{\beta }\vert ^{\beta }\alpha ^{\delta }\vert$, depicted in Fig. 9. This implies that $\beta \vert \delta \cdots$ is always a vertex.

Fig. 9

The two possible AADs of $\alpha ^3$

Some typical applications of AAD are listed below:

• If $\beta \vert \delta \cdots$ is not a vertex, then m in $\alpha ^m$ is even.

• If $\delta \vert \delta \cdots$ is not a vertex, then $\alpha ^{\delta }\vert ^{\delta }\alpha \cdots$ is also not a vertex.

• If $\beta \vert \beta \cdots , \delta \vert \delta \cdots$ are not vertices, then $\alpha \vert \alpha$ has the unique AAD $\alpha ^{\beta } \vert ^{\delta } \alpha$.

• If $\beta \vert \beta \cdots , \beta \vert \delta \cdots$ are not vertices, then $\alpha \alpha \alpha$ cannot be a vertex. In other words, there are no three consecutive $\alpha$’s at a vertex.

The application of AAD depends on the information available. It helps to conduct efficient and concise discussion in place of tens of pictures. In principle, the AAD argument can be programmed in decision algorithms.

3.2 Technique

We use “up to symmetry” to refer to the exchange $(\alpha , \gamma ) \leftrightarrow (\beta ,\delta )$ in the almost equilateral quadrilateral (Fig. 1).

3.3 Combinatorics

Let $v_i$ be the number of vertices of degree $i \ge 3$. From [8], the basic formulae about edge-to-edge tilings of the sphere by quadrilaterals are

$$\begin{aligned} f&= 6 + \sum _{h\ge 4} (h-3)v_h, \end{aligned}$$

(3)

$$\begin{aligned} v_3&= 8 + \sum _{h\ge 4} (h - 4) v_h. \end{aligned}$$

(4)

Equation (3) implies $f\ge 6$, and $f=6$ if and only if all vertices have degree 3. Equation (4) implies $v_3 \ge 8$, which further implies that degree 3 vertices always exist.

In [4, 13, 20, 22, 23], a crucial step in classification is to find all admissible vertices. This means that we need to find various constraints that angle combinations at vertices must satisfy. Here, we list some combinatorial constraints.

Lemma 3.1

(Counting Lemma, [8, Lemma 4]) In a tiling of the sphere by congruent polygons, suppose two different angles $\theta ,\varphi$ appear the same number of times in the polygon. If, at every vertex, the number of $\theta$ is no more than the number of $\varphi$, then at every vertex, the number of $\theta$ equals the number of $\varphi$.

The assumption is that every vertex is $\theta ^p\varphi ^q\cdots$ with $0 \le p \le q$ and no $\theta , \varphi$ in the remainder. The conclusion is that every vertex is $\theta ^p\varphi ^p\cdots$, with no $\theta , \varphi$ in the remainder.

Lemma 3.2

(Parity Lemma, [8, Lemma 2]) The total number of $\gamma$ and $\delta$ at any vertex is even.

Lemma 3.3

(Balance Lemma, [8, Lemma 6]) In a tiling of the sphere by congruent almost equilateral quadrilaterals, $\gamma ^2\cdots$ is a vertex if and only if $\delta ^2\cdots$ is a vertex. If $\gamma ^2\cdots , \delta ^2\cdots$ are not vertices, then every b-vertex has exactly one $\gamma$ and one $\delta$.

Lemma 3.4

[8, Lemma 9] In a tiling of the sphere by congruent quadrilaterals, if two angles $\theta _1,\theta _2$ do not appear at any degree 3 vertex, then there is a degree 4 vertex $\theta _i^3\cdots$ ($i=1$ or 2) or $\theta _i^2\theta _j\cdots$ ($i,j=1,2$), or a degree 5 vertex $\theta _1^p\theta _2^q$ ($p+q=5$).

Lemma 3.5

[8, Lemma 10] In a tiling of the sphere by congruent quadrilaterals, if $\theta ^3$ is the unique degree 3 vertex, then $f \ge 24$ and there is a degree 4 vertex without $\theta$.

Lemma 3.6

[8, Lemma 11] In a tiling of the sphere by congruent quadrilaterals, if $\theta ^2\varphi$ is the unique degree 3 vertex, then $f \ge 16$ and there is a degree 4 vertex without $\theta$.

In the last three lemmas, the technique of counting angles is involved. Whenever counting is applied, implicitly, there is a criterion for distinguishing angles which is often clear in the context.

3.4 Geometry

The geometry of the quadrilateral imposes more constraints on angle combinations at vertices.

Lemma 3.7

[8, Lemma 7] In a tiling of the sphere by congruent quadrilaterals, there is at most one angle $\ge \pi$ in the quadrilateral.

Lemma 3.8

[23, Lemma 3] In a simple almost equilateral quadrilateral, $\alpha \ge \beta$ if and only if $\gamma \ge \delta$.

Lemma 3.9

([8, Lemma 14], [3, Lemma 2.1]) In a simple almost equilateral quadrilateral

• if $\alpha , \beta , \gamma < \pi$, then $\beta + \pi > \gamma + \delta$ and $\delta + \pi > \beta + \gamma$;

• if $\alpha , \beta , \delta < \pi$, then $\alpha + \pi > \gamma + \delta$ and $\gamma + \pi > \alpha + \delta$.

Lemma 3.10

[8, Lemma 15] In a simple almost equilateral quadrilateral

• if $\gamma , \delta < \pi$, then $\alpha > \gamma$ if and only if $\beta > \delta$;

• if $\gamma < \pi$, then $\beta = \delta$ if and only if $a = b$;

• if $\delta < \pi$, then $\alpha = \gamma$ if and only if $a = b$.

In fact, the proof of [8, Lemma 15] shows that, if $\gamma <\pi$, then $\beta >\delta$ if and only if $a<b$, and $\beta =\delta$ if and only if $a=b$.

Lemma 3.11

In a simple quadrilateral, if three angles and the two edges between these angles are $<\pi$, then the other two edges are also $<\pi$.

Proof

We call a triangle standard when all edges and angles are $<\pi$. A standard triangle is simple and convex.

Fig. 10

Quadrilateral $\square PQRS$ with $\angle P, \angle Q, \angle S, PQ, PS <\pi$

Suppose $\square PQRS$ is such quadrilateral in Fig. 10 where $\angle P, \angle Q, \angle S$, $PQ, PS <\pi$. Then, PQ, PS are, respectively, contained in the left part and right part of the boundary of the lune (the intersection of two hemispheres) defined by antipodal points $P, P^{*}$, and $\angle P$. As $\angle Q, \angle S < \pi$, the rays from Q and S, which respectively coincide with QR and SR, point towards the interior of the lune. Extending the ray from Q until it meets at $Q'$ on the other side of the boundary, we get a standard triangle $\triangle PQQ'$ where $QQ' < \pi$.

If S is contained in $PQ'$ in the first picture, then $\square PQRS$ being simple and $\angle S < \pi$ imply that the ray from S will eventually intersect at R where R lies between $QQ'$. If S is outside $PQ'$, then it is contained in $Q'P^{*}$ in the second picture. Therefore, $\square PQRS$ being simple and $\angle S < \pi$ also imply that the ray from S will eventually intersect at R where R lies between $QQ'$. In either case, QR, RS are contained in the lune, and hence, $QR,RS<\pi$. $\square$

Lemma 3.12

In a simple almost equilateral quadrilateral, if $\alpha , \beta , \delta < \pi$, then $\gamma > \pi$ implies $\beta > \delta$.

Proof

By $a, \alpha , \beta , \delta < \pi$, Lemma 3.11 implies $b<\pi$. Moreover, AC, BD in Fig. 11 is contained in the lune defined by $A, A^{*}, \alpha$. Therefore, $AC,BD<\pi$ and every triangle contained in $\triangle ABD$ is a standard triangle. We also know that $\triangle ABD$ contains $\square ABCD$ and $\triangle BCD$. Let $\beta ', \delta '$ be the base angles of $\triangle BCD$ adjacent to $\beta , \delta$, respectively.

Fig. 11

$\square ABCD$ with $\alpha ,\beta , \delta < \pi$ and $\gamma >\pi$

Since $AB=AD=a$, we know that $\triangle ABD, \triangle ABC$ are isosceles triangles. Then, $\beta + \beta ' = \delta + \delta '$ and $\alpha _1 =\gamma _1$. Therefore, $\gamma > \alpha$ implies $\gamma _2>\alpha _2$. This means that $CD < AD= BC$. Then, in $\triangle BCD$, we get $\beta ' < \delta '$. Hence, $\beta > \delta$. $\square$

Lemma 3.13

In a tiling of the sphere by congruent almost equilateral quadrilaterals, we have

• $\beta = \delta$ if and only if $\gamma = \pi$;

• $\alpha = \gamma$ if and only if $\delta = \pi$.

Proof

If $\beta = \delta$, then Lemma 3.7 implies $\beta , \delta < \pi$. By $b\ne a$, Lemma 3.10 implies $\gamma \ge \pi$. Then, by Lemma 3.7, we get $\alpha <\pi$. If $\gamma > \pi$, then $\gamma > \alpha$ and Lemma 3.12 imply $\beta >\delta$, a contradiction. Hence, $\gamma = \pi$.

Fig. 12

$\triangle ABD$ with $\angle C =\gamma = \pi$

If $\gamma = \pi$, then the quadrilateral is in fact an isosceles triangle $\triangle ABD$ in Fig. 12 with edges $AB=AD=a$ and $BD=a+b$. Hence, $\beta = \delta$. $\square$

The four angles of the almost equilateral quadrilateral should be related by one single equation. To explain the equation, we need to expand our definition of polygons.

A general polygon is a closed path of piecewise geodesic arcs together with a choice of a side. A geodesic arc is a part of a great circle on the sphere. The edges of a general polygon are geodesic arcs. The vertices are where the edges meet. There are two complementary angles at each vertex. A side is fixed by a choice of one angle. Figure 13 demonstrates how a side of a general quadrilateral is fixed by the choice of angle $*$.

Fig. 13

General quadrilaterals as closed paths with chosen sides

Coolsaet [11, (2.3), Theorem 2.1] proved the following identity for convex almost equilateral quadrilateral. Cheung [6, 8] proved the identity without the convexity assumption.

Lemma 3.14

([6, Theorem 21], [8, Lemma 18]) The four angles of an almost equilateral quadrilateral satisfy

$$\begin{aligned} \sin \tfrac{1}{2}\alpha \sin \left( \delta -\tfrac{1}{2}\beta \right) =\sin \tfrac{1}{2}\beta \sin \left( \gamma -\tfrac{1}{2}\alpha \right) . \end{aligned}$$

(5)

We remark that (5) is also true if the quadrilateral is not simple. It matches the trigonometric Diophantine equation in [15, Equation (4)]. In Sect. 4, we generalise Coolsaet’s method [11, Theorem 3.2] to determine rational angles.

3.5 Preliminary Cases

There are up to four distinct angle values among $\alpha , \beta , \gamma , \delta$. If all angles have the same value, then $a=b$. Therefore, a genuine ($a\ne b$) almost equilateral quadrilateral has at least two distinct angle values.

Proposition 3.15

There is no tiling by congruent almost equilateral quadrilaterals with two distinct angle values.

It is established by [3, Theorem 3.3] that congruent convex symmetric ($\alpha =\beta$ and $\gamma =\delta$) genuine almost equilateral quadrilaterals do not admit tilings. With Lemma 3.7, this result by Akama and van Cleemput is sufficient to rule out the symmetric almost equilateral quadrilaterals.

Proof

Suppose there are two distinct angle values. Lemma 3.8 implies no three angles in the tile sharing the same value. Then, we have three possibilities: (1) $\alpha =\gamma$ and $\beta = \delta$, (2) $\alpha =\delta$ and $\beta = \gamma$, and (3) $\alpha =\beta$ and $\gamma =\delta$.

Suppose $\alpha =\gamma$ and $\beta = \delta$. Lemma 3.7 implies $\alpha , \beta , \gamma , \delta < \pi$. By $b\ne a$ and Lemma 3.13, $\alpha =\gamma$ if and only if $\delta = \pi$, contradicting $\delta < \pi$.

Suppose $\alpha =\delta$ and $\beta = \gamma$. Up to symmetry, Lemma 3.8 implies $\alpha \ge \beta = \gamma \ge \delta = \alpha$. This implies $\alpha = \beta = \gamma = \delta$, a contradiction.

Suppose $\alpha =\beta$ and $\gamma =\delta$, we know $\alpha \ne \gamma$. Lemma 3.7 implies every angles $< \pi$ so the tile is convex. The quadrilateral angle sum becomes

$$\begin{aligned} 2\alpha + 2\gamma = (2 + \tfrac{4}{f})\pi . \end{aligned}$$

By (4), we get $v_3 > 0$. Then, Parity Lemma implies that $\alpha \gamma ^2$ or $\alpha ^3$ is a vertex.

If $\alpha \gamma ^2$ is a vertex, the angle sum system implies $\alpha = \frac{4}{f}\pi$ and $\gamma = (1 - \frac{2}{f})\pi$. By convexity, Lemma 3.9 implies $\alpha + \pi > 2\gamma$, and hence, $f<8$, or $f=6$. Then, $\alpha = \gamma = \frac{2}{3}\pi$, contradicting $\alpha \ne \gamma$.

Now, $\alpha ^3$ must be a vertex. Then, $\gamma$ appears at some degree $\ge 4$ vertex. The angle sum system implies $\alpha = \frac{2}{3}\pi$ and $\gamma = (\frac{1}{3} + \frac{2}{f})\pi$. Then, we get $2\alpha + 2\gamma , \alpha + 4\gamma , 6\gamma >2\pi$, which imply that $\gamma$ only appears at $\gamma ^2\cdots = \gamma ^4$ and $\gamma = \frac{1}{2}\pi$. By $\gamma = (\frac{1}{3} + \frac{2}{f})\pi$, we get $f=12$. By $\alpha = \frac{2}{3}\pi$ and $\gamma = \frac{1}{2}\pi$, there are no other vertices, notably no $\alpha \gamma \cdots$.

The AAD at $\gamma ^4$ implies $\alpha ^2\cdots$, which is $\alpha ^3$. By $\alpha =\beta$ and $\gamma =\delta$, the two possible AADs of $\alpha ^3$ in Fig. 9 are $\vert ^{\gamma }\alpha ^{\alpha }\vert ^{\gamma }\alpha ^{\alpha }\vert ^{\gamma }\alpha ^{\alpha }\vert$ or $\vert ^{\gamma }\alpha ^{\alpha }\vert ^{\gamma }\alpha ^{\alpha }\vert ^{\alpha }\alpha ^{\gamma }\vert$. Both imply $\alpha \gamma \cdots$, a contradiction. Therefore, $\gamma ^4$ is not a vertex and there is no tiling. $\square$

Lemma 3.16

In a tiling of the sphere by congruent almost equilateral quadrilaterals with at least three distinct angle values, up to symmetry, either $\alpha \gamma \delta$ is a vertex, or one of the pairs below are vertices.

• $\alpha ^3$ and one of $\alpha \gamma ^2, \alpha \delta ^2, \beta \gamma ^2, \beta \delta ^2$;

• $\alpha ^2\beta$ and one of $\alpha \gamma ^2, \alpha \delta ^2, \beta \delta ^2$;

• $\alpha \delta ^2$ and $\beta \gamma ^2$;

• $\alpha ^3$ and one of $\gamma ^4, \delta ^4, \gamma ^3\delta , \gamma \delta ^3, \gamma ^2\delta ^2$;

• $\alpha \beta ^2$ and one of $\gamma ^4, \delta ^4, \gamma ^3\delta , \gamma \delta ^3, \gamma ^2\delta ^2$;

• $\alpha \gamma ^2$ and one of $\alpha ^4, \beta ^4, \delta ^4, \alpha ^3\beta , \alpha \beta ^3, \alpha ^2\beta ^2, \alpha ^2\delta ^2, \beta ^2\delta ^2, \alpha \beta \delta ^2$;

• $\alpha \delta ^2$ and one of $\alpha ^4, \beta ^4, \gamma ^4, \alpha ^3\beta , \alpha \beta ^3, \alpha ^2\beta ^2, \alpha ^2\gamma ^2, \beta ^2\gamma ^2, \alpha \beta \gamma ^2$.

In each of the last four items, the tiling has a unique degree 3 vertex.

If a tiling has a unique degree 3 vertex, then Lemma  3.6 (respectively Lemma 3.5) implies $f\ge 16$ (respectively $f \ge 24$).

Proof

By (4), $v_3 > 0$ means that there exists some degree 3 vertex. By Parity Lemma, the degree 3 b-vertices are $\alpha \gamma \delta , \beta \gamma \delta , \alpha \gamma ^2, \alpha \delta ^2, \beta \gamma ^2,\beta \delta ^2$, and the degree 3 ${\hat{b}}$-vertices are $\alpha ^3, \beta ^3, \alpha ^2\beta , \alpha \beta ^2$. The degree 4 vertices are

$$\begin{aligned}&\alpha ^4, \beta ^4, \gamma ^4, \delta ^4, \alpha ^3\beta , \alpha ^2\beta ^2, \alpha \beta ^3, \alpha ^2\gamma ^2, \alpha ^2\delta ^2, \alpha ^2\gamma \delta , \\&\alpha \beta \gamma ^2, \alpha \beta \delta ^2, \beta ^2\gamma ^2, \beta ^2\gamma \delta , \beta ^2\delta ^2, \gamma ^3\delta , \gamma ^2\delta ^2, \gamma \delta ^3. \end{aligned}$$

If $\alpha \gamma \delta , \beta \gamma \delta$ are both vertices, Then, $\alpha =\beta$ and Lemma 3.8 implies $\gamma = \delta$, contradicting at least three distinct angle values. Hence, only one of them can be a vertex. The pairs leading to these two equalities are dismissed.

Suppose $\alpha \gamma \delta , \beta \gamma \delta$ are not vertices.

If there are two degree 3 vertices, we then dismiss the pairs contradicting Lemma 3.8. For example, $\alpha \gamma ^2, \beta \delta ^2$ are dismissed for this reason. Meanwhile, $\alpha ^2\beta , \beta \gamma ^2$ imply $\alpha = \gamma$ whereby Lemma 3.13 implies $\delta = \pi$. Then, $\delta ^2\cdots$ is not a vertex. By Balance Lemma, $\beta \gamma ^2$ cannot be a vertex. Therefore, $\alpha ^2\beta , \beta \gamma ^2$ are also dismissed. Up to symmetry, we obtain all degree 3 pairs.

Suppose there is only one degree 3 vertex. Up to symmetry, it suffices to discuss $\alpha ^3,\alpha \beta ^2, \alpha \gamma ^2, \alpha \delta ^2$. If one of $\alpha ^3, \alpha \beta ^2$ is the only degree 3 vertex, then Lemma 3.4 and Parity Lemma imply that one of $\gamma ^4, \delta ^4, \gamma ^3\delta , \gamma \delta ^3, \gamma ^2\delta ^2$ is a vertex. If $\alpha \gamma ^2$ is the only degree 3 vertex, then Lemma 3.6 assures a degree 4 vertex without $\gamma$. Therefore, one of $\alpha ^4, \beta ^4, \delta ^4, \alpha ^3\beta , \alpha \beta ^3, \alpha ^2\beta ^2, \alpha ^2\delta ^2, \beta ^2\delta ^2, \alpha \beta \delta ^2$ is a vertex. Same for $\alpha \delta ^2$, one of $\alpha ^4, \beta ^4, \gamma ^4, \alpha ^3\beta , \alpha \beta ^3, \alpha ^2\beta ^2, \alpha ^2\gamma ^2, \beta ^2\gamma ^2$, $\alpha \beta \gamma ^2$ is a vertex. These are the remaining pairs. $\square$

We remark that, in the proof above, counting is used in Lemmas 3.4, 3.6. Because the four angles are distinguished by three distinct angle values and the b-edge, counting angles is made possible.

It will be explained in Sect. 3.4 that knowing two vertices is sufficient to determine all angle combinations at vertices. By the above lemma, we only need extra discussion for the case where $\alpha \gamma \delta$ is a vertex.

Lemma 3.17

If a tiling of the sphere by congruent almost equilateral quadrilaterals has $\alpha \gamma \delta$, then $\alpha ^2\cdots$ does not have $\gamma , \delta$.

The conclusion is that $\alpha ^2\cdots$ is a ${\hat{b}}$-vertex. Therefore, $\alpha ^2\cdots = \alpha ^m, \alpha ^{m\ge 2}\beta ^n$.

Proof

Assume the contrary. By $\alpha \gamma \delta$, Parity Lemma implies that one of $\alpha ^2\gamma ^2\cdots , \alpha ^2\delta ^2\cdots$ is a vertex. Up to symmetry of $\gamma \leftrightarrow \delta$, we may assume $\alpha ^2\gamma ^2\cdots$ is a vertex. Then, $\alpha +\gamma \le \pi$ and $\alpha \gamma \delta$ imply $\delta \ge \pi$. This implies that $\delta ^2\cdots$ is not a vertex. Then, Balance Lemma implies that $\gamma ^2\cdots$ is also not a vertex, contradicting $\alpha ^2\gamma ^2\cdots$. $\square$

Lemma 3.18

If a tiling with $f\ge 8$ has at least three distinct angle values and $\alpha \gamma \delta$ is a vertex, then $\alpha > \beta$ and $\gamma > \delta$. In particular, $\delta <\pi$. Moreover, if $\alpha ^2\cdots$ is not a vertex, then the ${\hat{b}}$-vertices are $\beta ^n, \alpha \beta ^n$ and the vertices having strictly more $\delta$ than $\gamma$ are $\alpha \delta ^2$, $\alpha \beta ^n\delta ^2$.

Proof

Assume $\delta > \gamma$. Lemma 3.8 implies $\alpha <\beta$. Then, Lemma 3.9 and $\alpha \gamma \delta$ imply $\beta +\pi > \gamma +\delta =2\pi - \alpha$, which gives $\alpha +\beta >\pi$. The angle sum system implies $\beta =\frac{4}{f}\pi$. Therefore, we have $\frac{8}{f}\pi = 2\beta> \alpha +\beta >\pi$, and hence, $f<8$, a contradiction. Lemma 3.8 implies $\alpha > \beta$ and $\delta < \gamma$. Then. Lemma 3.7 implies $\delta < \pi$.

By $\alpha \gamma \delta$, we get , , .

If $\alpha ^2\cdots$ is not a vertex, then $\beta ^{\alpha }\vert ^{\alpha }\beta \cdots$, $\beta ^{\alpha }\vert ^{\alpha }\delta \cdots$, $\delta ^{\alpha }\vert ^{\alpha }\delta \cdots$ are not vertices. By no $\beta ^{\alpha }\vert ^{\alpha }\beta \cdots$, we get $\beta ^{\alpha } \beta \cdots \beta = \beta ^{\alpha } \beta ^{\alpha }\cdots \beta ^{\alpha }$ and $\delta ^{\alpha } \beta \cdots \beta = \delta ^{\alpha }\beta ^{\alpha }\cdots \beta ^{\alpha }$. Then, implies $\alpha ^2\cdots$, a contradiction. Therefore, cannot happen. Hence, , , .

A vertex with strictly more $\delta$ than $\gamma$ contains . Since has $\alpha$, by $\alpha \gamma \delta$, we know that the vertex has no $\gamma$. Moreover, by no $\alpha ^2\cdots$, the vertex has only one . Meanwhile, $\alpha \gamma \delta$ implies that is not a vertex. Therefore, the vertex is or , which is $\alpha \beta ^n\delta ^2$. $\square$

Proposition 3.19

If $f=6$, then the tiling is uniquely given by the earth map tiling E (or the cube $P_6$) in Fig. 14 with the set of admissible vertices $\text {AVC}\equiv \{ \alpha \gamma \delta , \beta ^3 \}$.

Fig. 14

Tiling $E=P_6$

The proof is an easy exercise which can also be checked by computer.

3.6 Strategy

With groundwork in place, we assume at least three distinct angles and $f\ge 8$. Notably, by Lemma 3.8 and Proposition 3.15, we assume

$$\begin{aligned} \alpha \ne \beta , \quad \gamma \ne \delta . \end{aligned}$$

Among $\alpha , \beta , \gamma , \delta$, there are two possibilities: all angles are rational or some angle is irrational.

If all angles in a convex almost equilateral quadrilateral are rational (Sect. 4), then Coolsaet [11, Theorem 3.2] used [15, Theorem 4] to obtain all the angle relations from (5). After extending (5) to non-convex almost equilateral quadrilaterals in Lemma 3.14, we combine Coolsaet’s method with Lemma 3.16 to determine all admissible vertices.

If some angle is irrational (Sect. 5), then we apply Lemma 3.16 and the irrationality condition to determine all admissible vertices.

In both situations, the discussion is more complicated if $\alpha \gamma \delta$ is a vertex. We apply Lemmas 3.17, 3.18 to determine all admissible vertices.

4 Rational Angles

In this section, we assume that $\alpha , \beta , \gamma , \delta \in (0, 2\pi )$ are rational. Myerson’s theorem [15] has provided rational solutions to (5).

Theorem 2

[15, Theorem 4] The rational angle solutions $(x_1, x_2, x_3, x_4)$ to

$$\begin{aligned} \sin x_1 \sin x_2 = \sin x_3 \sin x_4 \end{aligned}$$

(6)

with $x_i \in [0, \frac{1}{2}\pi ]$ for $1\le i \le 4$, are given by

• I. one of the following and their permutations:

  • $x_1 = x_3 = 0$ and any rational angles $x_2, x_4$;

  • $x_1 = x_3$ and $x_2 = x_4$;

• II. $(\tfrac{1}{6}\pi , \theta , \tfrac{1}{2}\theta , \tfrac{1}{2}\pi - \tfrac{1}{2}\theta )$ for any rational angle $\theta \in [0,\frac{1}{2}\pi ]$, and its permutations;

• III. the 15 rational angle solutions listed in Table 5, and their permutations.

Table 5 Rational solutions to (6) in $[0, \frac{1}{2}\pi ]$

The permutations in the theorem are those which keep (6) invariant. They are

$$\begin{aligned}&(x_1, x_2, x_3, x_4), \; (x_1, x_2, x_4, x_3), \; (x_2, x_1, x_3, x_4),\; (x_2, x_1, x_4, x_3), \\ {}&(x_3, x_4, x_1, x_2), \; (x_4, x_3, x_1, x_2), \; (x_3, x_4, x_2, x_1),\; (x_4, x_3, x_2, x_1).\nonumber \end{aligned}$$

(7)

We remark that Type I solutions are not included in Myerson’s original theorem as they are solutions to $\{ \sin x_1 = 0, \, \sin x_3 = 0 \}$ or $\{ \sin x_1 = \sin x_3, \, \sin x_2 = \sin x_4 \}$, which may have been deemed “trivial”.

We also note that Type II solutions can be summarised by the identity

$$\begin{aligned} \sin \tfrac{1}{6}\pi \sin \theta = \sin \tfrac{1}{2}\theta \sin ( \tfrac{1}{2}\pi - \tfrac{1}{2}\theta ). \end{aligned}$$

For Type III solutions in Table 5, we remark a misprint in the previous literatures where $x_2$ of thirteenth row should be $\frac{7}{15}$ instead of $\frac{8}{15}$. With the correct value, the conclusion in [11, Theorem 3.2] is valid.

By (5), we know

$$\begin{aligned} x_1 = \tfrac{1}{2}\alpha ,\quad x_2 = \delta - \tfrac{1}{2}\beta , \quad x_3 = \tfrac{1}{2}\beta ,\quad x_4 = \gamma - \tfrac{1}{2}\alpha \end{aligned}$$

satisfy (6). If all $x_i \in [0, \frac{1}{2}\pi ]$, then we can apply Theorem 2 to determine the angles. We know $\tfrac{1}{2}\alpha ,\tfrac{1}{2}\beta \in (0, \pi )$ and the ranges of $\delta - \tfrac{1}{2}\beta , \gamma - \tfrac{1}{2}\alpha$ can be wider. To apply Theorem 2, we therefore need to “recalibrate”: for example, if $x_i \in (\frac{1}{2}\pi , \pi )$, then it should be changed to $\pi - x_i \in (0, \frac{1}{2}\pi )$. By similar modifications of switching signs and/or adding an integer multiple of $\pi$ and using $\sin (\pi - x) = \sin x$ and $\sin (-x)=-\sin x$, we may reduce all angle values to $[0, \frac{1}{2}\pi ]$ and (6) still holds.

For Type I solutions, we may bypass the calibration with the angle relations given by the subsequent Lemma 4.1. Modifying the discussion of [11, Theorem 3.2] and Type I solutions to (5), we have one of the following:

$$\begin{aligned}&\sin \left( \gamma - \tfrac{1}{2}\alpha \right) =0,\quad \sin \left( \delta - \tfrac{1}{2}\beta \right) =0; \end{aligned}$$

(8)

$$\begin{aligned}&\sin \left( \gamma - \tfrac{1}{2}\alpha \right) = \sin \tfrac{1}{2}\alpha , \quad \sin \left( \delta - \tfrac{1}{2}\beta \right) =\sin \tfrac{1}{2}\beta ; \end{aligned}$$

(9)

$$\begin{aligned}&\sin \left( \gamma - \tfrac{1}{2}\alpha \right) = \sin \left( \delta - \tfrac{1}{2}\beta \right) , \quad \sin \tfrac{1}{2}\beta = \sin \tfrac{1}{2}\alpha . \end{aligned}$$

(10)

They correspond to the following relations between the angles:

$$\begin{aligned}&{\left\{ \begin{array}{ll} 2\gamma = \alpha + 2N_1\pi , \\ 2\delta = \beta + 2N_2\pi ; \end{array}\right. } \end{aligned}$$

(11)

$$\begin{aligned}&{\left\{ \begin{array}{ll} 2\gamma =(1 + (-1)^{N_1})\alpha + 2N_1\pi , \\ 2\delta =(1 + (-1)^{N_2})\beta + 2N_2\pi ; \\ \end{array}\right. } \end{aligned}$$

(12)

$$\begin{aligned}&{\left\{ \begin{array}{ll} 2\gamma =(-1)^{N_1}(2\delta - \beta ) + \alpha + 2N_1\pi , \\ \alpha = (-1)^{N_2}\beta + 2N_2\pi . \end{array}\right. } \end{aligned}$$

(13)

After further simplification, the result is summarised below.

Lemma 4.1

In an almost equilateral quadrilateral tile with at least three distinct angles, if the angles satisfy one of (8), (9), (10), then we have one of the following:

• 1. if $\alpha , \beta , \gamma , \delta < \pi$, then $\alpha =2\gamma$ and $\beta = 2\delta$ hold;

• 2. if either one of $\alpha , \beta \ge \pi$ and all other angles $<\pi$, then one of the following is true:

  • i. $\alpha =2\gamma$ and $\beta = 2\delta$,

  • ii. $\alpha +\beta =2\pi$ and $\alpha +2\delta =\beta + 2\gamma$;

• 3. if $\gamma \ge \pi$ and all other angles $<\pi$, then one of the following is true:

  • i. $\gamma =\pi$ and $\beta = \delta$,

  • ii. $\alpha +2\pi = 2\gamma$ and $\beta = 2\delta$;

• 4. if $\delta \ge \pi$ and all other angles $<\pi$, then one of the following is true:

  • i. $\delta = \pi$ and $\alpha =\gamma$,

  • ii. $\alpha = 2\gamma$ and $\beta +2\pi = 2\delta$.

For Type II, III solutions, by Lemma 3.7, we only need to consider the calibrations in Table 6. In particular, “case $\alpha \ge \pi$” in the table means $\alpha \ge \pi$ and the other three angles $<\pi$, etc.

Table 6 Angle value calibrations

In general, there are more calibrations for angles with wider ranges. However, those ranges are not needed for tiling classification.

We generalise the scheme in [11, Theorem 3.2] in the following steps.

• Step 1. Determine angle values via

  • Type I solutions to angle relations in Lemma 4.1,

  • Type II solutions and calibrations in Table 6,

  • Type III solutions and calibrations in Table 6.

• Step 2. Dismiss angle values that fail any of the following:

  • $0< \alpha , \beta , \gamma , \delta < 2\pi$;

  • at least three distinct angle values, and at most one of them $\ge \pi$;

  • Lemmas 3.8, 3.9, 3.10, 3.12.

• Step 3. Select pairs in Lemma 3.16 that produce consistent even integer $f \ge 8$. Moreover, if one of $\alpha \beta ^2, \alpha \gamma ^2, \alpha \delta ^2$ is the unique degree 3 vertex, then we further require $f\ge 16$; and if $\alpha ^3$ is the unique degree 3 vertex, then we further require $f\ge 24$.

• Step 4. We call the selected angle values valid and use them to determine the corresponding sets of admissible vertices ($\text {AVC}$s).

For $\alpha \gamma \delta$, we need to modify the argument in Step 3 and 4 using Lemmas 3.17, 3.18, 4.3.

Finally, we construct the tilings from the $\text {AVC}$s.

Proposition 4.2

If $f\ge 8$, and all angles are rational, and $\alpha \gamma \delta , \beta \gamma \delta$ are not vertices, then the tilings are isolated earth map tilings S3, FS3 and special tilings S5, S6.

Proof

By Lemma 3.7, the discussion is divided according to: all angles are $<\pi$, or exactly one angle is $\ge \pi$. We follow the four steps above. We give an example and leave out the details of the others. The process can be swiftly executed in computer.

Case ($\alpha , \beta , \gamma , \delta <\pi$).

Type I: By the first item in Lemma 4.1, we get $\alpha =2\gamma$ and $\beta =2\delta$. Combined with the vertex angle sums of the pairs in Lemma 3.16, we find no valid angle values. The conclusion is consistent with [11, Theorem 3.2].

Type II: There are five calibrations in the first part of Table 6. Matching the first calibration $( \gamma - \frac{1}{2}\alpha , \frac{1}{2}\beta , \frac{1}{2}\alpha , \delta - \frac{1}{2}\beta )$ with a solution $(\frac{1}{6}\pi , \theta , \frac{1}{2}\pi - \frac{1}{2}\theta , \frac{1}{2}\theta )$, we obtain

$$\begin{aligned}&\tfrac{1}{6}\pi =\gamma - \tfrac{1}{2}\alpha , \quad \theta = \tfrac{1}{2}\beta , \quad \tfrac{1}{2}\pi - \tfrac{1}{2}\theta = \tfrac{1}{2}\alpha , \quad \tfrac{1}{2}\theta = \delta - \tfrac{1}{2}\beta . \end{aligned}$$

Combining the above with the quadrilateral angle sum, we solve for the angles and get

$$\begin{aligned} \alpha =(\tfrac{5}{6}-\tfrac{2}{f})\pi , \quad \beta =(\tfrac{1}{3}+\tfrac{4}{f})\pi ,\quad \gamma =(\tfrac{7}{12}-\tfrac{1}{f})\pi , \quad \delta =(\tfrac{1}{4}+\tfrac{3}{f})\pi . \end{aligned}$$

Next, we substitute the above into the angle sums of the vertices in the pairs in Lemma 3.16 and calculate the corresponding f. The vertices yield even $f\ge 8$ are $\alpha ^3 (f=12), \alpha \beta ^2 (f=12), \alpha ^2\beta (\text {any } f), \beta ^4 (f=24), \alpha \beta ^3 (f=60), \gamma ^4(f=12), \delta ^4 (f=12), \gamma ^3\delta (\text {any } f), \gamma \delta ^3(f=12), \gamma ^2\delta ^2(f=12), \beta ^2\gamma ^2(f=36), \alpha \beta \delta ^2(f=24)$. The only pairs in Lemma 3.16 with consistent f are those with unique degree 3 vertex $\alpha ^3$ or $\alpha \beta ^2$. However, both imply $f=12$, contradicting the additional requirement of $f\ge 24$ or $f\ge 16$ in Step 3. Hence, these angle values are dismissed.

We repeat the above process for the calibration $( \gamma - \frac{1}{2}\alpha , \frac{1}{2}\beta , \frac{1}{2}\alpha , \delta - \frac{1}{2}\beta )$ and all permutations (7) of the Type II solution $(\frac{1}{6}\pi , \theta , \frac{1}{2}\pi - \frac{1}{2}\theta , \frac{1}{2}\theta )$.

Then, we repeat all the above again for the other four calibrations in the first part of Table 6.

At the end, we find two solutions listed in Table 7.

Table 7 Type II and convex: vertex pairs and angle values

In $\{ \alpha \beta ^2,\gamma \delta ^3 \}$, by $f\ge 16$ we get the lower bounds, $\alpha> \tfrac{1}{3}\pi , \beta \ge \tfrac{17}{24}\pi , \gamma > \tfrac{1}{4}\pi , \delta \ge \tfrac{25}{48}\pi$. This implies $m<6$ and $n<3$ and $k<8$ and $l<4$ in (2). We substitute finitely many non-negative integers m, n, k, l within the bounds into (2) and calculate the corresponding f. We select only those with $f\ge 16$. The admissible vertices are listed below with their corresponding f values,

$$\begin{aligned}&f=20, \quad \{ \alpha \beta ^2,\gamma \delta ^3, \alpha ^2\gamma \delta \}; \\&f=24,\quad \{ \alpha \beta ^2, \alpha ^4, \gamma \delta ^3, \alpha \beta \gamma ^2, \alpha \gamma ^4 \}; \\&f=36, \quad \{ \alpha \beta ^2, \alpha ^2\delta ^2, \gamma \delta ^3, \alpha ^3\gamma ^2, \alpha \gamma ^3\delta , \gamma ^6 \}; \\&f=60,\quad \{ \alpha \beta ^2,\gamma \delta ^3, \alpha ^3\beta , \alpha ^5, \beta \gamma ^4, \alpha ^2\gamma ^4 \}; \\&f=84,\quad \{ \alpha \beta ^2,\gamma \delta ^3, \alpha ^3\gamma \delta , \gamma ^5\delta \}; \\&f=132,\quad \{ \alpha \beta ^2,\gamma \delta ^3, \alpha ^4\gamma ^2, \alpha \gamma ^6 \}. \end{aligned}$$

In $\{ \alpha \delta ^2, \alpha \beta ^3 \}$, similar calculation gives

$$\begin{aligned} f=36, \quad \{ \alpha \delta ^2, \alpha \beta ^3, \gamma ^3\delta , \alpha ^2\beta \gamma ^2, \alpha ^6 \}. \end{aligned}$$

Type III: We repeat the same process for Type II. The only difference is that the Type II solution $(\frac{1}{6}\pi , \theta , \frac{1}{2}\pi - \frac{1}{2}\theta , \frac{1}{2}\theta )$ is replaced by the Type III solutions (and their permutations) in Table 5. We find no solution.

Case ($\beta , \gamma , \delta <\pi$ and $\alpha \ge \pi$). By $\alpha \ge \pi$, we know that $\alpha ^2\cdots$ is not a vertex. It suffices to study those in the list of Lemma 3.16 without $\alpha ^2\cdots$.

Type I: By the second item in Lemma 4.1, we have $\alpha =2\gamma$ and $\beta = 2\delta$, or $\alpha +\beta =2\pi$ and $\alpha +2\delta =\beta + 2\gamma$. By the same argument in the previous case using the second part of Table 6, we find all the solutions in Table 8.

Table 8 Type I and $\alpha \ge \pi$: vertex pairs and angle values

Since the three pairs in Table 8 share the same angle values, we use these values to derive all the vertices. Therefore, we get

$$\begin{aligned} f=16, \, \text {AVC}= \{ \alpha \beta ^2, \alpha \gamma ^2, \alpha \beta \delta ^2, \beta ^4, \beta ^2\gamma ^2, \gamma ^4, \alpha \delta ^4, \beta ^3\delta ^2, \beta \gamma ^2\delta ^2, \beta ^2\delta ^4, \gamma ^2\delta ^4, \beta \delta ^6, \delta ^8 \}. \end{aligned}$$

Type II, III: By the same argument using the second part of Table 6, we find no solutions.

Case ($\alpha , \gamma , \delta <\pi$ and $\beta \ge \pi$). By the same argument, we find solutions only for Type I in Table 9.

In $\{ \alpha ^3, \beta \delta ^2 \}$, by (4) and $f=8$, we get $v_{\ge 6}=0$. Therefore, the other vertices are $\delta ^4, \alpha ^2\gamma ^2, \alpha \gamma ^4$. Therefore

$$\begin{aligned} f=8, \quad \text {AVC}= \{ \alpha ^3, \beta \delta ^2, \delta ^4, \alpha ^2\gamma ^2, \alpha \gamma ^4 \}. \end{aligned}$$

In $\{ \alpha ^2\beta , \beta \delta ^2 \}$, by the exchange $(\alpha ,\gamma ) \leftrightarrow (\beta ,\delta )$, we get the same $\text {AVC}$ derived from Table 8.

For the case $\alpha , \beta , \delta <\pi$ and $\gamma \ge \pi$ and the case $\alpha , \beta , \gamma <\pi$ and $\delta \ge \pi$, we apply the same arguments and find no solutions.

All the $\text {AVC}$s are summarised in Table 10.

Table 9 Type I and $\beta \ge \pi$: vertex pairs and angle values

Table 10 $\text {AVC}$s of rational angles without $\alpha \gamma \delta$

AVCs without tiling

In $f=8$, $\text {AVC}= \{ \alpha ^3, \beta \delta ^2, \delta ^4, \alpha ^2\gamma ^2, \alpha \gamma ^4 \}$, we have $\beta \cdots =\beta \delta ^2$. This contradicts Counting Lemma on $\beta , \delta$.

In $f=20$, $\text {AVC}= \{ \alpha \beta ^2,\gamma \delta ^3, \alpha ^2\gamma \delta \}$, applying the Counting Lemma to $\gamma ,\delta$, we know that $\gamma \delta ^3$ is not a vertex. Then, applying Lemma 3.4 to $\gamma , \delta$ in $\text {AVC}= \{ \alpha \beta ^2, \alpha ^2\gamma \delta \}$, we get a contradiction.

In $f=24$, $\text {AVC}= \{ \alpha \beta ^2, \alpha ^4, \gamma \delta ^3, \alpha \beta \gamma ^2, \alpha \gamma ^4 \}$, we have $\beta ^2\cdots = \alpha \beta ^2$ and $\gamma \delta \cdots = \gamma \delta ^3$, whereas $\alpha ^2\gamma \cdots , \alpha \delta \cdots , \beta \delta \cdots$ are not vertices. By no $\alpha \delta \cdots , \beta \delta \cdots$, the vertex $\alpha \beta \gamma ^2$ has unique AAD . The AAD of $\gamma ^{\beta }\vert ^{\beta }\alpha$ in the first picture of Fig. 15 determines tiles $T_1, T_2$. By $\beta ^2\cdots = \alpha \beta ^2$ and no $\alpha \delta \cdots$, we get $T_3$. By $\gamma \delta \cdots =\gamma \delta ^3$, we determine $T_4$ and then $T_5$. This implies $\gamma ^{\beta }\vert ^{\beta }\alpha \cdots = \alpha ^2\gamma \cdots$, a contradiction. Then, $\beta \gamma \cdots =\alpha \beta \gamma ^2$ is not a vertex. Then, the AAD $\alpha ^{\beta }\vert ^{\beta }\alpha$ in the second picture determines $T_1, T_2$. As $\beta ^2\cdots = \alpha \beta ^2$, by mirror symmetry, we also know $T_3$, which implies $\beta _3\gamma _2\cdots$, contradicting no $\beta \gamma \cdots$. Therefore, there is no $\alpha ^{\beta }\vert ^{\beta }\alpha$. Then, no $\alpha ^{\beta }\vert ^{\delta }\alpha ,\alpha ^{\beta }\vert ^{\beta }\alpha$ implies no $\alpha \alpha \alpha$. Therefore, $\alpha ^4$ is not a vertex. The AAD $\gamma ^{\beta } \vert ^{\beta } \gamma$ in the third picture implies $\alpha \delta \cdots$, a contradiction. Therefore, $\alpha \gamma ^4$ is not a vertex. The $\text {AVC}$ is reduced to $\{ \alpha \beta ^2, \gamma \delta ^3 \}$. Applying Counting Lemma to $\alpha ,\beta$, we get a contradiction.

Fig. 15

The AADs of $\alpha ^{\beta }\vert ^{\beta }\alpha$ and $\gamma ^{\beta }\vert ^{\beta }\gamma$

In $f=60$, $\text {AVC}=\{ \alpha \beta ^2,\gamma \delta ^3, \alpha ^3\beta , \alpha ^5, \beta \gamma ^4, \alpha ^2\gamma ^4 \}$, we know that $\alpha \delta \cdots$ is not a vertex. The AAD of $\gamma ^{\beta } \vert ^{\beta } \gamma \cdots$ gives the second picture of Fig. 15, contradicting no $\alpha \delta \cdots$. Then, the AAD of $\alpha ^2\gamma ^4$ is and $\beta \gamma ^4$ is not a vertex. By no $\beta \gamma \cdots , \beta \delta \cdots$, there is no $\alpha \alpha \alpha , \gamma \alpha \gamma$, and hence, $\alpha ^3\beta , \alpha ^5, \alpha ^2\gamma ^4$ are not vertices. Then, $\alpha ^2\cdots$ is not a vertex. Therefore, $\gamma \delta ^3=\delta ^{\alpha }\vert ^{\alpha }\delta \cdots$ is not a vertex, a contradiction.

Among $f=36$, $\text {AVC}=\{ \alpha \beta ^2, \alpha ^2\delta ^2, \gamma \delta ^3, \alpha ^3\gamma ^2, \alpha \gamma ^3\delta , \gamma ^6 \}$, and $f=84, \text {AVC}$ $=\{ \alpha \beta ^2,\gamma \delta ^3, \alpha ^3\gamma \delta , \gamma ^5\delta \}$, and $f=132, \text {AVC}=\{ \alpha \beta ^2,\gamma \delta ^3, \alpha ^4\gamma ^2, \alpha \gamma ^6 \}$, we have $\beta ^2\cdots =\alpha \beta ^2$ and no $\beta \gamma \cdots ,\beta \delta \cdots$. By $\beta ^2\cdots =\alpha \beta ^2$, the AAD $\alpha ^{\beta }\vert ^{\beta }\alpha$ in the third picture of Fig. 15 implies $\beta \gamma \cdots$, a contradiction. By no $\beta \delta \cdots$, we also do not have $\alpha ^{\beta }\vert ^{\delta }\alpha$. Then, by no $\alpha ^{\beta }\vert ^{\delta }\alpha$ and $\alpha ^{\beta }\vert ^{\beta }\alpha$, there is no $\alpha \alpha \alpha$. Therefore, $\alpha ^3\gamma ^2, \alpha ^3\gamma \delta , \alpha ^4\gamma ^2$ cannot be vertices. For $f=84, 132$, this means that $\alpha ^2\cdots$ is not a vertex. This implies $\gamma \delta ^3=\delta ^{\alpha }\vert ^{\alpha }\delta \cdots$ is not a vertex, a contradiction. For $f=36$, we actually have a tiling which remains to be discussed below.

AVCs with tilings

In the $\text {AVC}$ for $f=16$, there is no $\alpha ^2\cdots$. Then, there is no AAD and . This implies that $\alpha \delta ^4,\beta ^3\delta ^2, \beta ^2\delta ^4$, $\gamma ^2\delta ^4, \beta \delta ^6, \delta ^8$ are not vertices. We get

$$\begin{aligned} f=16, \quad&\text {AVC}= \{ \alpha \beta ^2, \alpha \gamma ^2, \alpha \beta \delta ^2, \beta ^4, \beta ^2\gamma ^2, \gamma ^4, \beta \gamma ^2\delta ^2 \}. \end{aligned}$$

By the proof of [8, Proposition 39], $\alpha \beta ^2, \beta \gamma ^2\delta ^2, \beta ^2\gamma ^2$ are not vertices. The $\text {AVC}$ is further reduced to

$$\begin{aligned} f=16, \quad \text {AVC}= \{ \alpha \gamma ^2, \alpha \beta \delta ^2, \beta ^4, \gamma ^4 \}. \end{aligned}$$

By no $\alpha ^2\cdots$, the vertex $\beta ^4$ has unique AAD $\vert ^{\gamma } \beta ^{\alpha }\vert ^{\gamma } \beta ^{\alpha }\vert ^{\gamma } \beta ^{\alpha }\vert ^{\gamma } \beta ^{\alpha }\vert$. Then, the AAD $\gamma ^{\beta }\vert ^{\beta }\gamma$ implies $\beta ^2\cdots = \beta ^4$, which contradicts its unique AAD. Therefore, $\gamma ^4$ is not a vertex. The $\text {AVC}$ is reduced to

$$\begin{aligned} f=16, \quad \text {AVC}= \{ \alpha \gamma ^2, \alpha \beta \delta ^2, \beta ^4 \}. \end{aligned}$$

(14)

By $\text {AVC}$ (14), we construct S3, FS3 in Fig. 16. As per the discussion in [8], the tiles are actually triangles and hence the pictures in Fig. 6.

Fig. 16

Tilings S3, FS3

In $f=36$, $\text {AVC}=\{ \alpha \beta ^2, \alpha ^2\delta ^2, \gamma \delta ^3, \alpha ^3\gamma ^2, \alpha \gamma ^3\delta , \gamma ^6 \}$, the earlier discussion already shows that $\alpha ^3\gamma ^2$ is not a vertex. The $\text {AVC}$ is reduced to

$$\begin{aligned} f=36, \quad \{ \alpha \beta ^2, \alpha ^2\delta ^2, \gamma \delta ^3, \alpha \gamma ^3\delta , \gamma ^6 \}. \end{aligned}$$

(15)

By $\text {AVC}$ (15), we construct S5 in Fig. 17.

Fig. 17

Tiling S5

In $f=36$, $\text {AVC}= \{ \alpha \delta ^2, \alpha \beta ^3, \gamma ^3\delta , \alpha ^2\beta \gamma ^2, \alpha ^6 \}$, by no $\beta \delta \cdots$ and $\delta \vert \delta \cdots$, we do not have $\alpha ^{\beta } \vert ^{\delta } \alpha , \alpha ^{\delta } \vert ^{\delta } \alpha$. Therefore, there is no $\alpha \alpha \alpha$ and $\alpha ^6$ is not a vertex. The $\text {AVC}$ is reduced to

$$\begin{aligned} f=36, \quad \{ \alpha \delta ^2, \alpha \beta ^3, \gamma ^3\delta , \alpha ^2\beta \gamma ^2 \}. \end{aligned}$$

(16)

By $\text {AVC}$ (16), we construct S6 in Fig. 18.

Fig. 18

Tiling S6

This completes the proof. $\square$

We provide the pseudocode for Propositions 4.2, 4.4. In preprocessing, we define the functions, f_Condition and Angle_Condition, for executing Step 3 in our scheme. For example, the pseudocode as written, is for the convex case. The other cases can be defined similarly.

The pseudocode for computing angles and f via Type I solutions is given in Algorithm 2 and the pseudocode for computing angles and f via Type II, III solutions is given in Algorithm 3.

In Algorithm 2, we define Vertex_Eqns by the angle relation(s) in Lemma 4.1. For example, in the convex case, we define Case_Eqns by $\alpha =2\gamma$ and $\beta =2\delta$. We define Vertex_Eqns by the vertex angle sums given by the vertices in Lemma 3.16. Then, we execute Step 2 and Step 3.

In Algorithm 3, we define Vertex_Eqns in the same way by Lemma 3.16. We define Case_Cal by the calibrations in Table 6. We define Myerson_Sol by Type II or III solutions. The quadrilateral angle sum defines Angle_Eqns. After solving $\alpha , \beta , \gamma , \delta$ (and $\theta$) in terms of f in the first procedure (Step 2), we dismiss angle values which fail the criteria in Step 2. Then, we carry out Step 3 in the second procedure.

The latest wxMaxima files (version 13.04.0) of Algorithm 2 and Algorithm 3 can be found at first author’s GitHub page https://github.com/hoien14/Rational-Angles-and-Tilings-of-the-Sphere-by-Congruent-Quadrilaterals.

Algorithm 1

Algorithm 1: Type I rational angle values

Algorithm 2

Algorithm 2: Type II, III rational angle values

We now turn our attention to tilings with $\alpha \gamma \delta$ as a vertex. To simplify the discussion, we first establish the following fact.

Lemma 4.3

If $\gamma = \pi$ and $f\ge 8$, then the set of admissible vertices is

$$\begin{aligned} \text {AVC} = \{ \alpha \gamma \delta , \alpha ^3, \alpha ^2\beta ^2, \alpha \beta ^n, \beta ^n, \beta ^n\gamma \delta \}. \end{aligned}$$

(17)

Proof

Suppose $\gamma = \pi$. Lemma 3.13 implies that the quadrilateral is in fact an isosceles triangle $\triangle ABD$ in Fig. 12 with edges $AB=AD=a$, and $BD=a+b$, and $\beta =\delta$. By Lemma 3.7, $\alpha , \beta , \delta < \pi$. Then, $\triangle ABD$ is a standard isosceles triangle. Then, by $BD>AB=AD$, $\gamma = \pi> \alpha > \beta = \delta$.

By $\gamma =\pi$ and the quadrilateral angle sum, $\alpha + 2\beta = (1 + \frac{4}{f})\pi$. By $\alpha > \beta$, we get $\alpha> ( \frac{1}{3} + \frac{4}{3f} )\pi > \beta = \delta$. Since $\gamma = \pi$, we know that $\gamma ^2\cdots$ is not a vertex. Balance Lemma implies that $\delta ^2\cdots$ is also not a vertex and every b-vertex has exactly one $\gamma$ and one $\delta$.

Assume $\alpha \gamma \delta$ is not a vertex. Then, the only b-vertex is $\gamma \cdots =\delta \cdots = \beta ^n\gamma \delta$. Counting Lemma on $\beta , \gamma$ implies $n=1$ in $\beta ^n\gamma \delta$. Then, $\gamma =\pi$ and $\beta \gamma \delta$ imply $\pi = \beta + \delta < ( \frac{2}{3} + \frac{8}{3f} )\pi$ which implies $f<8$, contradicting $f\ge 8$. Therefore, $\alpha \gamma \delta$ is a vertex. By $\gamma =\pi$, $\alpha >\delta$ and $\alpha \gamma \delta$, we get $\alpha > \frac{1}{2}\pi$. Therefore, $\alpha > \frac{1}{2}\pi$ and $\gamma =\pi$ and $\beta = \delta = \frac{4}{f}\pi$ determine all other vertices. Therefore, we obtain $\text {AVC}$ (17). $\square$

Proposition 4.4

If $f\ge 8$, and all angles are rational, and one of $\alpha \gamma \delta , \beta \gamma \delta$ is a vertex, then the tilings are earth map tiling E, its flip modifications $F_{1}E, F_{2}E$, and rearrangement RE.

Proof

Up to symmetry, we may assume $\alpha \gamma \delta$ is a vertex. By $\alpha \ne \beta$, this implies that $\beta \gamma \delta$ is not a vertex. By $f\ge 8$ and $\alpha \gamma \delta$ and the quadrilateral angle sum, we get $\beta = \frac{4}{f}\pi < \pi$. By $f\ge 8$, Lemma 3.18 implies $\delta <\pi$. Then, similar to the previous proposition, the proof is divided into three cases: every angle $<\pi$, or exactly one of $\alpha , \gamma \ge \pi$. We follow the four steps outlined before Proposition 4.2, with adjusted Step 3 and 4. The process again can be executed in computer.

Case ($\alpha , \beta , \gamma ,\delta < \pi$).

Type I: By relations $\alpha =2\gamma$ and $\beta =2\delta$ from Lemma 4.1 and $\alpha \gamma \delta$, we get

$$\begin{aligned}&f\ge 8, \quad \alpha = ( \tfrac{4}{3}-\tfrac{4}{3f} ) \pi , \quad \beta =\tfrac{4}{f}\pi ,\quad \gamma = ( \tfrac{2}{3}-\tfrac{2}{3f} ) \pi , \quad \delta =\tfrac{2}{f}\pi . \end{aligned}$$

However, $f\ge 8$ implies $\alpha >\pi$.

Type II: By matching the calibrations in first part of Table 6 and the permutations (7) of Type II solution $(\frac{1}{6}\pi , \theta , \frac{1}{2}\pi - \frac{1}{2}\theta , \frac{1}{2}\theta )$, and then by $\alpha \gamma \delta$, we get

$$\begin{aligned}&f\ge 8,\quad \alpha =\tfrac{1}{3}\pi ,\quad \beta = \tfrac{4}{f}\pi ,\quad \gamma = (\tfrac{2}{3}+\tfrac{2}{f})\pi ,\quad \delta = (1- \tfrac{2}{f})\pi ; \\&f=8,\quad \alpha = \tfrac{1}{3}\pi ,\quad \beta = \tfrac{1}{2}\pi ,\quad \gamma =\tfrac{11}{12}\pi ,\quad \delta = \tfrac{3}{4}\pi ; \\&f=12,\quad \alpha =\tfrac{4}{9}\pi ,\quad \beta = \tfrac{1}{3}\pi ,\quad \gamma = \tfrac{2}{3}\pi ,\quad \delta = \tfrac{8}{9}\pi ; \\&f=18,\quad \alpha =\tfrac{4}{9}\pi ,\quad \beta = \tfrac{2}{9}\pi ,\quad \gamma = \tfrac{11}{18}\pi ,\quad \delta = \tfrac{17}{18}\pi ; \\&f=24,\quad \alpha = \tfrac{1}{3}\pi ,\quad \beta = \tfrac{1}{6}\pi ,\quad \gamma =\tfrac{3}{4}\pi ,\quad \delta =\tfrac{11}{12}\pi . \end{aligned}$$

In the first two sets, we have $\alpha - \beta = \delta - \gamma$. In the last three sets, we have $\alpha > \beta$ and $\delta > \gamma$. All of them contradict Lemma 3.8.

Type III: We repeat the same process for with the Type II solution $(\frac{1}{6}\pi , \theta , \frac{1}{2}\pi - \frac{1}{2}\theta , \frac{1}{2}\theta )$ replaced by the Type III solutions (and their permutations) in Table 5. We get

$$\begin{aligned}&f=12,\quad \alpha =\tfrac{14}{15}\pi , \quad \beta =\tfrac{1}{3}\pi , \quad \gamma =\tfrac{23}{30}\pi , \quad \delta = \tfrac{3}{10}\pi . \end{aligned}$$

Then, we obtain the $\text {AVC}$ below

$$\begin{aligned} f=12, \quad \text {AVC}=\{ \alpha \gamma \delta , \beta \gamma \delta ^3, \beta ^6 \}. \end{aligned}$$

Applying Counting Lemma to $\gamma ,\delta$, we know that $\beta \gamma \delta ^3$ is not a vertex and

$$\begin{aligned} f = 12, \quad \text {AVC}=\{ \alpha \gamma \delta , \beta ^6 \}. \end{aligned}$$

Case ($\beta , \gamma , \delta <\pi$ and $\alpha \ge \pi$). By $\alpha \ge \pi$, we know that $\alpha ^2\cdots$ is not a vertex. By Lemma 3.18, the only vertices with strictly more $\delta$ than $\gamma$ are $\alpha \delta ^2, \alpha \beta ^n\delta ^2$. We incorporate this fact in conjunction with Balance Lemma to filter the vertices. This will be explained in Type II and III solutions.

Type I: By Lemma 4.1 and $\alpha \gamma \delta$, we get

$$\begin{aligned}&f\ge 8,\quad \alpha = ( \tfrac{4}{3}-\tfrac{4}{3f} ) \pi , \quad \beta =\tfrac{4}{f}\pi , \quad \gamma = ( \tfrac{2}{3}-\tfrac{2}{3f} ) \pi , \quad \delta =\tfrac{2}{f}\pi . \end{aligned}$$

Then, we obtain the $\text {AVC}$ as follows:

$$\begin{aligned} f \ge 8, \quad \text {AVC}= \{ \alpha \gamma \delta , \gamma ^3\delta , \beta ^n, \alpha \beta ^n, \alpha \beta ^n\delta ^2, \beta ^n\gamma ^2, \beta ^n\gamma \delta , \beta ^n\gamma ^2\delta ^2 \}. \end{aligned}$$

Type II: By the same argument, we get

$$\begin{aligned}&f=12,\quad \alpha = \tfrac{10}{9}\pi , \quad \beta = \tfrac{1}{3}\pi , \quad \gamma = \tfrac{2}{3}\pi , \quad \delta = \tfrac{2}{9}\pi ; \\&f=18,\quad \alpha = \tfrac{10}{9}\pi ,\quad \beta = \tfrac{2}{9}\pi , \quad \gamma = \tfrac{13}{18}\pi ,\quad \delta = \tfrac{1}{6}\pi . \end{aligned}$$

By angle values, we know that $\alpha \delta ^2, \alpha \beta ^n\delta ^2$ are not vertices. By Lemma 3.18 and the Balance Lemma, at every vertex, the number of $\gamma$ equals the number of $\delta$. Such vertices can only be $\beta ^6$ for the first set and $\alpha \beta ^4, \beta \gamma ^2\delta ^2, \beta ^5\gamma \delta , \beta ^{9}$ for the second. Hence, we have

$$\begin{aligned}&f=12, \quad \text {AVC}= \{ \alpha \gamma \delta , \beta ^6 \}; \\&f=18, \quad \text {AVC}= \{ \alpha \gamma \delta , \alpha \beta ^4, \beta \gamma ^2\delta ^2, \beta ^5\gamma \delta , \beta ^{9} \}. \end{aligned}$$

Type III: By the same argument, we get

$$\begin{aligned}&f=12,\quad \alpha = \tfrac{7}{5}\pi , \quad \beta = \tfrac{1}{3}\pi , \quad \gamma = \tfrac{8}{15}\pi , \quad \delta = \tfrac{1}{15}\pi ; \\&f=20,\quad \alpha = \tfrac{16}{15}\pi , \quad \beta = \tfrac{1}{5}\pi , \quad \gamma = \tfrac{23}{30}\pi , \quad \delta = \tfrac{1}{6}\pi ; \\&f=30,\quad \alpha = \tfrac{7}{5}\pi , \quad \beta = \tfrac{2}{15}\pi , \quad \gamma = \tfrac{17}{30}\pi , \quad \delta = \tfrac{1}{30}\pi . \end{aligned}$$

By the same reason in Type II, at every vertex, the number of $\gamma$ equals the number of $\delta$. Hence, we get

$$\begin{aligned} f=12, \quad \text {AVC}= \{ \alpha \gamma \delta , \beta ^6 \}. \end{aligned}$$

For the second set of angle values, we have $3\gamma +\delta >2\pi$ and the remainder of $\gamma ^2\cdots$ has value $\frac{7}{15}\pi$. No angle combinations add up to it. Then, $\gamma ^2\cdots$ is not a vertex. By Balance Lemma and Counting Lemma, every b-vertex has exactly one $\gamma$ and one $\delta$. Hence, we get

$$\begin{aligned} f=20, \quad \text {AVC}= \{ \alpha \gamma \delta , \beta ^{10} \}. \end{aligned}$$

For the third set, $\alpha \beta ^4\delta ^2$ is the only vertex with strictly more $\delta$ than $\gamma$. In the other b-vertices, the number of $\gamma$ is at least that of $\delta$. Therefore, they are $\beta ^2\gamma ^3\delta , \beta ^6\gamma ^2\delta ^2$. The only remaining vertex is $\beta ^{15}$. We obtain the third $\text {AVC}$

$$\begin{aligned} f=30, \quad \text {AVC}= \{ \alpha \gamma \delta , \beta ^2\gamma ^3\delta , \beta ^6\gamma ^2\delta ^2, \alpha \beta ^4\delta ^2, \beta ^{15} \}. \end{aligned}$$

Case ($\alpha , \beta , \delta <\pi$ and $\gamma \ge \pi$). By $\gamma \ge \pi$, we know that $\gamma ^2\cdots$ is not a vertex. Then, Balance Lemma implies no $\delta ^2\cdots$ and every b-vertex has exactly one $\gamma$ and one $\delta$.

Type I: By the same argument, we get

$$\begin{aligned}&f\ge 8,\quad \alpha = (1 - \tfrac{4}{f} ) \pi , \quad \beta =\tfrac{4}{f}\pi , \quad \gamma =\pi , \quad \delta =\tfrac{4}{f}\pi ; \\&f\ge 8,\quad \alpha = ( \tfrac{2}{3}-\tfrac{4}{3f} ) \pi ,\quad \beta =\tfrac{4}{f}\pi , \quad \gamma = ( \tfrac{4}{3}-\tfrac{2}{3f} )\pi , \quad \delta =\tfrac{2}{f}\pi . \end{aligned}$$

In the first set of angle values, by $\gamma =\pi$ and Lemma 4.3, we get $\text {AVC}$ (17).

In the second set of angle values, by $\alpha \gamma \delta$ and no $\gamma ^2\cdots , \delta ^2\cdots$, the other b-vertex can only be $\beta ^n\gamma \delta$. Meanwhile, the ${\hat{b}}$-vertices are $\alpha ^m, \beta ^n, \alpha ^m\beta ^n$. By $f\ge 8$ and $\alpha = ( \tfrac{2}{3}-\tfrac{4}{3f} ) \pi$, we have $\alpha \ge \tfrac{1}{2}\pi$. Then, $m\le 3$ in $\alpha ^m, \alpha ^m\beta ^n$. In particular, $\alpha ^m=\alpha ^3$. Therefore, we get

$$\begin{aligned} f\ge 8, \quad \text {AVC}= \{ \alpha \gamma \delta , \alpha ^3, \beta ^n, \alpha ^m\beta ^n, \beta ^n\gamma \delta \}. \end{aligned}$$

(18)

Type II: By the same argument, we get

$$\begin{aligned} f=12, \quad \alpha = \tfrac{2}{3} \pi , \quad \beta =\tfrac{1}{3}\pi , \quad \gamma =\pi , \quad \delta =\tfrac{1}{3}\pi . \end{aligned}$$

By Lemma 4.3, $\gamma =\pi$ and $f=12$, we get

$$\begin{aligned} f=12, \quad \text {AVC}= \{ \alpha \gamma \delta , \alpha ^3, \alpha ^2\beta ^2, \alpha \beta ^4, \beta ^2\gamma \delta , \beta ^6 \}. \end{aligned}$$

That is all the vertices and it is a special case of $\text {AVC}$ (17).

Type III: By the same argument, we get

$$\begin{aligned}&f=12, \quad \alpha = \tfrac{8}{15}\pi , \quad \beta = \tfrac{1}{3}\pi , \quad \gamma = \tfrac{41}{30}\pi , \quad \delta = \tfrac{1}{10}\pi ; \\&f=12, \quad \alpha = \tfrac{3}{5}\pi , \quad \beta = \tfrac{1}{3}\pi , \quad \gamma = \tfrac{17}{15}\pi , \quad \delta = \tfrac{4}{15}\pi ; \\&f=20, \quad \alpha = \tfrac{8}{15}\pi , \quad \beta = \tfrac{1}{5}\pi , \quad \gamma = \tfrac{43}{30}\pi , \quad \delta = \tfrac{1}{30}\pi . \end{aligned}$$

By no $\gamma ^2\cdots , \delta ^2\cdots$ and Parity Lemma, the first two sets of angle values give

$$\begin{aligned} f=12, \quad \text {AVC}= \{ \alpha \gamma \delta , \beta ^6 \}. \end{aligned}$$

Similarly, the third set of angle values give

$$\begin{aligned} f=20, \quad \text {AVC}= \{ \alpha \gamma \delta , \alpha ^3\beta ^2, \beta ^{10}\}. \end{aligned}$$

All of the above $\text {AVC}$s contain at least one subset which admits a tiling. It remains to explain the tilings.

AVCs with tilings

In $f=12$, $\text {AVC}=\{ \alpha \gamma \delta , \beta \gamma \delta ^3, \beta ^6 \}$, by applying Counting Lemma to $\gamma ,\delta$, we know that $\beta \gamma \delta ^3$ is not a vertex. Then, we get

$$\begin{aligned} f = 12, \quad \text {AVC}=\{ \alpha \gamma \delta , \beta ^6 \}. \end{aligned}$$

It is easy to see that the above $\text {AVC}$ is a special case of the one below

$$\begin{aligned} f\ge 8, \quad \text {AVC}=\{ \alpha \gamma \delta , \beta ^{\frac{f}{2}} \}. \end{aligned}$$

(19)

In $f=20$, $\text {AVC}= \{ \alpha \gamma \delta , \alpha ^3\beta ^2, \beta ^{10}\}$, by applying Counting Lemma to $\alpha ,\gamma$, we know that $\alpha ^3\beta ^2$ is not a vertex. The $\text {AVC}$ is reduced to

$$\begin{aligned} f=20,\quad \text {AVC}= \{ \alpha \gamma \delta , \beta ^{10} \}, \end{aligned}$$

which is also a special case of $\text {AVC}$ (19).

In $f=30$, $\text {AVC}= \{ \alpha \gamma \delta , \beta ^2\gamma ^3\delta , \beta ^6\gamma ^2\delta ^2, \alpha \beta ^4\delta ^2, \beta ^{15} \}$, we have $\alpha \beta \cdots =\alpha \beta ^4\delta ^2$ and no $\alpha ^2\cdots$. By no $\alpha ^2\cdots$, we know that $\beta ^{\alpha }\vert ^{\alpha }\beta \cdots , \beta ^{\alpha }\vert ^{\alpha }\delta \cdots$ are not vertices and $\beta \cdots \beta$ has unique AAD $\beta ^{\alpha } \vert \cdots \vert \beta ^{\alpha }$. In $\gamma ^{\beta } \vert ^{\alpha } \beta$ and $\gamma ^{\beta }\vert ^{\alpha }\delta$, we get $T_1, T_2$ in both pictures of Fig. 19. By $\alpha _1\beta _2\cdots = \alpha \beta ^4\delta ^2$ and the unique AAD of $\beta ^{\alpha } \vert \cdots \vert \beta ^{\alpha }$, we get $\beta ^{\alpha }\vert ^{\alpha }\delta \cdots$, a contradiction. Therefore, $\gamma ^{\beta } \vert ^{\alpha } \beta \cdots , \gamma ^{\beta }\vert ^{\alpha }\delta \cdots$ are not vertices. Then, is not nor . This implies that $\beta ^2\gamma ^3\delta$ is not a vertex. Applying Counting Lemma to $\gamma , \delta$, we know that $\alpha \beta ^4\delta ^2$ is not a vertex. Then, applying Counting Lemma to $\alpha ,\gamma$, we also know that $\beta ^6\gamma ^2\delta ^2$ is not a vertex. The $\text {AVC}$ is reduced to

$$\begin{aligned} f=30, \quad \text {AVC}= \{ \alpha \gamma \delta , \beta ^{15} \}, \end{aligned}$$

which is again a special case of $\text {AVC}$ (19).

Fig. 19

The AAD of $\gamma ^{\beta } \vert ^{\alpha } \beta$ and $\gamma ^{\beta }\vert ^{\alpha }\delta$

In $\text {AVC}= \{ \alpha \gamma \delta , \gamma ^3\delta , \beta ^n, \alpha \beta ^n, \alpha \beta ^n\delta ^2, \beta ^n\gamma ^2, \beta ^n\gamma \delta , \beta ^n\gamma ^2\delta ^2 \}$, we know $\alpha \gamma \cdots$ $= \alpha \gamma \delta$, and $\alpha \beta \cdots =\alpha \beta ^n, \alpha \beta ^n\delta ^2$, and $\gamma ^3\cdots = \gamma ^3\delta$, and no $\alpha \gamma ^2\cdots$. The vertices with strictly more $\gamma$ than $\delta$ are $\gamma ^3\delta , \beta ^n\gamma ^2$. The vertex with strictly more $\delta$ than $\gamma$ is $\alpha \beta ^n\delta ^2$. If $\alpha \beta ^n\delta ^2$ is a vertex, the AAD determines $T_1, T_2,T_3$ in Fig. 20. Then, $\alpha _2\gamma _1\cdots =\alpha \gamma \delta$ and we determine $T_4$. Then, $\alpha _4\beta _2\cdots = \alpha \beta ^n, \alpha \beta ^n\delta ^2$. This means that $\beta$ or $\delta$ is the angle in $T_5$ just outside $T_2$. By no $\alpha \gamma ^2\cdots$, we conclude $\gamma _2\gamma _3\cdots =\gamma ^3\cdots = \gamma ^3\delta$. This means $\# \alpha \beta ^n\delta ^2 \le \# \gamma ^3\delta$. In each vertex other than $\gamma ^3\delta , \alpha \beta ^n\delta ^2, \beta ^n\gamma ^2$, the number of $\gamma$ equals the number of $\delta$. We have $3\# \gamma ^3\delta + 2\# \beta ^n \gamma ^2 =\#\gamma =\# \delta =\# \gamma ^3\delta + 2\# \alpha \beta ^n\delta ^2$. Combining with $\# \alpha \beta ^n\delta ^2 \le \# \gamma ^3\delta$, we get $\# \beta ^n \gamma ^2 =0$, and hence, $\beta ^n\gamma ^2$ is not a vertex. The $\text {AVC}$ is reduced to

$$\begin{aligned} f\ge 8, \quad \text {AVC}= \{ \alpha \gamma \delta , \gamma ^3\delta , \beta ^n, \alpha \beta ^n, \alpha \beta ^n\delta ^2, \beta ^n\gamma \delta , \beta ^n\gamma ^2\delta ^2 \}. \end{aligned}$$

(20)

Fig. 20

The AAD of $\alpha \beta ^n\delta ^2$

We remark that $f=18$, $\text {AVC}= \{\alpha \gamma \delta , \alpha \beta ^4, \beta \gamma ^2\delta ^2, \beta ^5\gamma \delta , \beta ^{9} \}$ as a set may be viewed as a special case of $\text {AVC}$ (20). However, the angle values between the two are not compatible. Hence, they are regarded as two different sets.

If $\gamma =\pi$, then the quadrilateral degenerates into a triangle with $\text {AVC}$ (17) which is a special case of $\text {AVC}$ (18).

We summarise the $\text {AVC}$s in their most general forms below

• 1. $f\ge 8$, $\text {AVC}= \{ \alpha \gamma \delta , \beta ^{\frac{f}{2}} \}$,

• 2. $f=18$, $\text {AVC}= \{ \alpha \gamma \delta , \alpha \beta ^4, \beta \gamma ^2\delta ^2, \beta ^5\gamma \delta , \beta ^{9} \}$,

• 3. $f\ge 8$, $\text {AVC}= \{ \alpha \gamma \delta , \gamma ^3\delta , \beta ^n, \alpha \beta ^n, \alpha \beta ^n\delta ^2, \beta ^n\gamma \delta , \beta ^n\gamma ^2\delta ^2 \}$,

• 4. $f\ge 8$, $\text {AVC}= \{ \alpha \gamma \delta , \alpha ^3, \alpha ^m\beta ^n, \beta ^n, \beta ^n\gamma \delta \}$.

By the construction of tilings in [8, Propositions 35, 48], we get the earth map tiling E, its flip modifications $F_1E, F_2E$ and rearrangement RE, which will be explained below.

For the first $\text {AVC}$ in the list, for each $f\ge 8$, we get the earth map tiling E with $\text {AVC}$ (19).

In fact, consecutive $\beta$’s in [8, Figure 74] constitute consecutive timezones. Then, $\beta ^n$ as a vertex in any $\text {AVC}$ in the list means that the tiling is E. In the remaining discussion, we may focus on the tilings without $\beta ^n$.

The third $\text {AVC}$ without $\beta ^n$ is a simplified [8, $\text {AVC}$ (7.10)]. Counting Lemma implies that $\gamma ^3\delta$ is a vertex if and only if $\alpha \beta ^n\delta ^2$ is a vertex. If $\gamma ^3\delta$ is a vertex, then $\alpha \beta ^n\delta ^2$ and the angle values imply $f=6q+4$ where $q\in {\mathbb {Z}}$ and $q\ge 1$. For each such $f\ge 10$, we get the rearrangement RE with

$$\begin{aligned} RE: \text {AVC}\equiv \{ \alpha \gamma \delta , \gamma ^3\delta , \alpha \beta ^{\frac{f+2}{6}}, \alpha \beta ^{\frac{f-4}{6}}\delta ^2 \}. \end{aligned}$$

(21)

If $\gamma ^3\delta$ is not a vertex, then $\alpha \beta ^n\delta ^2$ is also not a vertex. We get [8, $\text {AVC}$ (7.9)], and for each $f\ge 8$, we get flip modifications

$$\begin{aligned}&F_{1}E: \text {AVC}\equiv \{ \alpha \gamma \delta , \alpha \beta ^n, \beta ^n\gamma \delta \}, \end{aligned}$$

(22)

$$\begin{aligned}&F_{2}E: \text {AVC}\equiv \{ \alpha \gamma \delta , \alpha \beta ^n, \beta ^n\gamma ^2\delta ^2 \}. \end{aligned}$$

(23)

The second $\text {AVC}$ without $\beta ^n$ is a special case of [8, $\text {AVC}$ (7.9)]. If $\alpha \beta ^4$ is a vertex, then we get specific flip modifications $F_{1}E, F_{2}E$ with $\text {AVC}=\{ \alpha \gamma \delta , \alpha \beta ^4, \beta ^5\gamma \delta \}$ and $\text {AVC}=\{ \alpha \gamma \delta , \alpha \beta ^4, \beta \gamma ^2\delta ^2 \}$, respectively (which are special cases of $\text {AVC}$s (22), (23), respectively).

The fourth $\text {AVC}$ without $\beta ^n$ is [8, $\text {AVC}$ (7.8)]. Counting Lemma implies that $\alpha ^3$ or $\alpha ^m\beta ^n$ is a vertex if and only if $\beta ^n\gamma \delta$ is a vertex. If $\alpha ^3$ or $\alpha ^m\beta ^n$ is a vertex, then we get

$$\begin{aligned}&F_{1}E: \text {AVC}\equiv \{ \alpha \gamma \delta , \alpha ^3, \beta ^n\gamma \delta \}, \end{aligned}$$

(24)

$$\begin{aligned}&F_{1}E: \text {AVC}\equiv \{ \alpha \gamma \delta , \alpha ^m\beta ^n, \beta ^n\gamma \delta \}. \end{aligned}$$

(25)

We list the tilings with their $\text {AVC}$s in Table 11. The construction has been explained in [8, Figures 75, 76]. $\square$

Table 11 Tilings with rational angles and vertex $\alpha \gamma \delta$

5 Irrational Angles

In this section, we assume that at least one of $\alpha , \beta ,\gamma , \delta$ is irrational, i.e., its value is not a rational multiple of $\pi$. For integers $m, n, k, l, m_i, n_i, k_i, l_i \ge 0$ where $1 \le i \le 2$, the angle sum system of vertices $\alpha ^{m_1}\beta ^{n_1}\gamma ^{k_1}\delta ^{l_1}$, $\alpha ^{m_2}\beta ^{n_2}\gamma ^{k_2}\delta ^{l_2}, \alpha ^m\beta ^n\gamma ^k\delta ^l$ has an augmented matrix

$$\begin{aligned} {[}A \vert \textbf{b}] = \left[ \begin{array}{cccc|c} 1 &{} 1 &{} 1 &{} 1 &{} 2+\tfrac{4}{f}\\ m_1 &{} n_1 &{} k_1 &{} l_1 &{} 2 \\ m_2 &{} n_2 &{} k_2 &{} l_2 &{} 2 \\ m &{} n &{} k &{} l &{} 2 \end{array}\right] . \end{aligned}$$

(26)

The above system is required to be consistent, namely rank of $[A \vert \textbf{b}] =$ rank of A. If A is invertible, then the solutions to the angle values are rational. Therefore, for some angles to be irrational, we have $\text {rank}[A \vert \textbf{b}]=\text {rank}A \le 3$, which is the irrationality condition. In practice, this means that, if we already know two vertices $\alpha ^{m_1}\beta ^{n_1}\gamma ^{k_1}\delta ^{l_1},\alpha ^{m_2}\beta ^{n_2}\gamma ^{k_2}\delta ^{l_2}$, then we get two equalities satisfied by all other vertices.

To facilitate the discussion involving (26) and determine the angle combinations, we allow some of m, n, k, l to be 0. Only after the angle combinations are determined, we require $m,n,k,l \ge 1$ in angle combinations.

Proposition 5.1

If $f\ge 8$, and some angle is irrational, and $\alpha \gamma \delta , \beta \gamma \delta$ are not vertices, then the tilings are isolated earth map tilings S1, S2, and special tilings $QP_6,S4$.

Proof

Using each pair of vertices in the list of Lemma 3.16, we set up A in (26) and determine m, n, k, l. We demonstrate how to solve the associated system of linear Diophantine equations and inequalities in two cases. The others are determined by the same procedure (implemented in computer).

Case (Degree 3 pairs). Suppose $\alpha \delta ^2, \beta \gamma ^2$ are vertices. Row operations give

$$\begin{aligned} {[}A \vert \textbf{b}] = \left[ \begin{array}{cccc|c} 1 &{} 1 &{} 1 &{} 1 &{} 2+\tfrac{4}{f}\\ 1 &{} 0 &{} 0 &{} 2 &{} 2 \\ 0 &{} 1 &{} 2 &{} 0 &{} 2 \\ m &{} n &{} k &{} l &{} 2 \end{array}\right] \rightarrow \left[ \begin{array}{cccc|c} 1 &{} 0 &{} 0 &{} 2 &{} 2 \\ 0 &{} 1 &{} 2 &{} 0 &{} 2 \\ 0 &{} 0 &{} 1 &{} 1 &{} 2(1-\tfrac{2}{f}) \\ 0 &{} 0 &{} 0 &{} \lambda &{} \mu \end{array}\right] , \end{aligned}$$

where $\lambda = 2m-2n+k-l$ and $\mu = 2(m+k-n-1)+\tfrac{4}{f}(2n-k)$.

The irrationality condition ($\text {rank}[A \vert \textbf{b}]=\text {rank}A \le 3$) implies $\lambda =\mu =0$, i.e., $2m - 2n + k - l = 0$ and $(n + 1 - m - k)f = 2(2n-k)$. As $f \ne 0$, the latter implies $2n-k\ne 0$ if and only if $n + 1 - m - k \ne 0$. In this case, we have $f=8 + \frac{2(4m - 2n + 3k-4)}{n + 1 - m - k} \ge 8$. Therefore, there are three possibilities

• (1) $2m-2n+k-l=0$, $2n-k=0$, $n+1-m-k=0$;

• (2) $2m-2n + k - l=0$, $2n-k>0$, $n+1-m-k>0$, $4m-2n+3k-4 \ge 0$;

• (3) $2m -2n + k - l=0$, $2n-k<0$, $n+1-m-k<0$, $4m-2n+3k-4 \le 0$.

The non-negative integer solutions to the first possibility are $(m,n,k,l)=(1,0,0,2), (0,1,2,0)$. The vertices are $\alpha \delta ^2, \beta \gamma ^2$.

The non-negative integer solution to the second is $(m,n,k,l)=(m,m,0,0)$. The vertex is $\alpha ^m\beta ^m$.

There is no non-negative integer solution to the third and hence no vertex.

Therefore, we get

$$\begin{aligned} \text {AVC}= \{ \alpha \delta ^2, \beta \gamma ^2, \alpha ^m\beta ^m \}. \end{aligned}$$

The arguments for the other pairs are analogous.

Case (Degree 3, 4 Pairs). In this case, one of $\alpha ^3, \alpha \beta ^2, \alpha \gamma ^2, \alpha \delta ^2$ is the unique degree 3 vertex. If $\alpha ^3$ is a vertex, then Lemma 3.5 implies $f\ge 24$. If one of $\alpha \beta ^2, \alpha \gamma ^2, \alpha \delta ^2$ is a vertex, then Lemma 3.6 implies $f\ge 16$.

Suppose $\alpha \beta ^2, \gamma ^2\delta ^2$ are vertices. We have $f\ge 16$. The irrationality condition implies $k-l=0$ and $(2- n - k)f = 4(2m - n)$. The latter and $f \ne 0$ imply $2m-n\ne 0$ if and only if $2- n - k\ne 0$. In this case, we have $f = 16 + \frac{4(2m+3n+4k-8)}{2-n-k} \ge 16$. There are three possibilities

• (1) $k-l=0$, $2m-n=0$, $2-n-k=0$;

• (2) $k-l=0$, $2m > n$, $2-n-k>0$, $2m+3n+4k-8 \ge 0$;

• (3) $k-l=0$, $2m < n$, $2-n-k<0$, $2m+3n+4k-8 \le 0$.

For each possibility, we obtain the vertices by integer linear programming for the non-negative integers m, n, k, l. Therefore, we get

$$\begin{aligned} \text {AVC}= \{ \alpha \beta ^2, \gamma ^2\delta ^2, \alpha ^{m}, \alpha ^m\beta , \alpha ^m\gamma \delta \}. \end{aligned}$$

The arguments for the other pairs are analogous.

We summarise all the $\text {AVC}$s in Table 12. The first two vertices in each $\text {AVC}$ are assumed to appear, since they come from the list of Lemma 3.16. Then, by Counting Lemma, all vertices in these $\text {AVC}$s must appear, with the exceptions of $f=24, \text {AVC}=\{ \alpha ^3, \gamma ^2\delta ^2, \beta ^4, \beta ^2\gamma \delta \}$ and $f\ge 16$, $\text {AVC}=\{ \alpha \beta ^2, \gamma ^2\delta ^2, \alpha ^m, \alpha ^m\beta , \alpha ^m\gamma \delta \}$.

Table 12 Irrational angles: $\text {AVC}$s without $\alpha \gamma \delta$

By the exchange $(\alpha , \gamma ) \leftrightarrow (\beta , \delta )$, we see that $\{ \alpha ^3, \beta \gamma ^2, \alpha \beta \delta ^2 \}$ and $\{ \alpha ^3, \beta \delta ^2, \alpha \beta \gamma ^2 \}$ become special cases of $\{ \alpha \delta ^2, \alpha \beta \gamma ^2, \beta ^n \}$ and $\{ \alpha \gamma ^2, \alpha \beta \delta ^2, \beta ^n \}$, respectively.

AVCs without tiling

We first discuss the $\text {AVC}$s from Table 12 that do not admit tilings.

As in the AAD discussion in Sect. 3.1, if $\alpha ^3$ is a vertex, then $\beta \delta \cdots$ is a vertex. Therefore, $\{ \alpha ^3, \alpha \delta ^2, \beta ^2\gamma ^2 \}, \{ \alpha ^3, \gamma ^2\delta ^2, \alpha \beta ^3 \}$, $\{ \alpha ^3, \delta ^4, \beta ^2\gamma ^2 \}$ and $\{ \alpha ^3, \gamma ^2\delta ^2, \beta ^5 \}$ do not admit no tilings.

In $\text {AVC}=\{ \alpha ^3, \alpha \gamma ^2, \beta ^2\delta ^2 \}$, all three vertices appear and the angle sum system implies $\alpha =\gamma$ and $\beta +\delta =\pi$, whereby $\delta \ne \pi$, contradicting Lemma 3.13.

In $\text {AVC}=\{ \alpha ^3, \beta \gamma ^2, \beta ^2\delta ^4 \}$, we know that $\beta ^2\delta ^4$ is a vertex, whereas $\gamma \vert \gamma \cdots$ is not a vertex. By no $\alpha \gamma \cdots$, $\gamma \vert \gamma \cdots$, we know that $\beta ^{\alpha }\vert ^{\gamma }\beta \cdots$, $\beta ^{\gamma }\vert ^{\gamma }\beta \cdots$ are not vertices. Then, $\beta \vert \beta = \beta ^{\alpha } \vert ^{\alpha } \beta$. By no $\alpha \gamma \cdots$, we know that is not a vertex. By $\beta \vert \beta = \beta ^{\alpha } \vert ^{\alpha } \beta$, the AAD of $\beta ^2\delta ^4$ is . It implies $\alpha \gamma \cdots$, a contradiction.

In $\text {AVC}=\{ \alpha ^3, \beta \delta ^2, \beta ^2\gamma ^4 \}$, the AAD of $\beta \delta ^2$ is . It implies $\alpha \gamma \cdots$, a contradiction.

In $\text {AVC}= \{ \alpha ^3, \gamma ^2\delta ^2, \beta ^4, \beta ^2\gamma \delta \}$, we know that $\alpha ^3$ is a vertex. Then, the AAD of $\alpha ^3$ implies that $\beta \delta \cdots =\beta ^2\gamma \delta$ is a vertex. By no $\alpha \beta \cdots$, the AAD of $\beta ^2\gamma \delta$ is . It implies $\alpha \gamma \cdots$, a contradiction.

In $\text {AVC}=\{ \alpha ^2\beta , \beta \delta ^2, \gamma ^k \}$, the AAD of $\beta \delta ^2$ is . This implies $\alpha \gamma \cdots$, a contradiction.

In $\text {AVC}=\{ \alpha \delta ^2, \beta ^2\gamma ^2, \alpha ^m \}$, the AAD of $\alpha \delta ^2$ is . This implies $\alpha \beta \cdots$, a contradiction.

In $\text {AVC}=\{ \alpha \delta ^2, \beta \gamma ^2, \alpha ^m\beta ^m \}$, we have $\gamma \cdots =\beta \gamma ^2$ and $\delta \cdots =\alpha \delta ^2$. Since $\alpha ^{m}\beta ^{m}$ has degree $\ge 3$, we have $m\ge 2$. This implies $\alpha , \beta <\pi$. By $\alpha \delta ^2, \beta \gamma ^2$, we have $\gamma ,\delta <\pi$. Then, the tile is convex. The vertex angle sums $\alpha + 2\delta = 2\pi = \beta + 2\gamma$ imply $\gamma - \frac{1}{2}\alpha =\delta - \frac{1}{2}\beta$. Then, (5) implies $\sin ( \gamma - \frac{1}{2}\alpha )= 0$ or $\sin \frac{1}{2}\beta = \sin \frac{1}{2}\alpha$. By convexity and $\gamma - \frac{1}{2}\alpha =\delta - \frac{1}{2}\beta$, the former gives $\delta - \tfrac{1}{2}\beta = \gamma - \tfrac{1}{2}\alpha = 0$. Then, $\alpha =2\gamma$ and $\beta =2\delta$. By $\alpha \gamma ^2$ and $\beta \delta ^2$, we get $4\pi = \alpha + 2\gamma + \beta + 2\delta = 2(\alpha +\beta )$, which implies $\alpha + \beta = 2\pi$, contradicting $\alpha ,\beta < \pi$. Hence, we get $\sin \frac{1}{2}\beta = \sin \frac{1}{2}\alpha$. By $\alpha ,\beta <\pi$, this implies $\alpha =\beta$, a contradiction.

AVCs with tilings

In $\text {AVC}=\{ \alpha \gamma ^2, \alpha \beta \delta ^2, \beta ^n \}$, as discussed in [8], the tilings are only geometrically realisable when $f=16$. In that case, the tilings are S3, FS3 and every angle is rational, a contradiction.

In $\text {AVC}=\{ \alpha ^3, \gamma ^4, \beta ^2\delta ^2 \}$, the tiling is $QP_6$, given by quadrilateral subdivision of the cube in Fig. 21.

Fig. 21

Tiling $QP_6$

In $\text {AVC}= \{ \alpha \beta ^2, \gamma ^2\delta ^2, \alpha ^m, \alpha ^m\beta , \alpha ^m\gamma \delta \}$, we have $\beta ^2\cdots = \alpha \beta ^2$ and no $\beta \gamma \cdots$, $\beta \delta \cdots$. The $\text {AVC}$ assumes that $\alpha \beta ^2$ is the unique degree 3 vertex. Then, the vertices $\alpha ^m, \alpha ^m\beta ,\alpha ^m\gamma \delta$ have degree $\ge 4$. By $\beta ^2\cdots = \alpha \beta ^2$, the third picture of Fig. 15 shows that $\alpha ^{\beta }\vert ^{\beta }\alpha \cdots$ implies $\beta \gamma \cdots$, a contradiction. Then, by no $\beta \delta \cdots , \alpha ^{\beta }\vert ^{\beta }\alpha \cdots$, the AAD of $\alpha \vert \alpha$ is $\alpha ^{\delta }\vert ^{\delta }\alpha$. This implies no $\alpha \alpha \alpha$. Therefore, we get $m=2$ in $\alpha ^m\gamma \delta$, whereas $\alpha ^m, \alpha ^m\beta$ are not vertices. The $\text {AVC}$ is reduced to

$$\begin{aligned} f=16, \quad \text {AVC}= \{ \alpha \beta ^2, \alpha ^2\gamma \delta , \gamma ^2\delta ^2 \}. \end{aligned}$$

(27)

By $\text {AVC}$ (27), we construct S4 in the first picture of Fig. 22. As $2\alpha =\gamma +\delta = \pi$, S4 is a subdivision of a non-edge-to-edge parallelogram tiling in the second picture. The right angles are $\alpha$. The non-indicated parallelogram angles are $\beta =\frac{3}{4}\pi$.

Fig. 22

Tiling S4, as a subdivision of a non-edge-to-edge tiling by parallelograms

Fig. 23

Tiling S2

In $\text {AVC}=\{ \alpha \gamma ^2, \beta ^2\delta ^2, \alpha ^m \}$, as discussed in [8], the tilings are only geometrically realisable when $f=16$ and $\alpha ^m=\alpha ^4$. We use the $\text {AVC}$ to construct S2 in the first picture of Fig. 23.

In $\text {AVC}=\{ \alpha \delta ^2, \alpha \beta \gamma ^2, \beta ^n \}$, as discussed in [8], the tilings are only geometrically realisable when $f=12,16$. We use the $\text {AVC}$ to construct $S_{12}1, S_{16}1$ in Fig. 24.

Fig. 24

Tilings $S1 = S_{12}1, S_{16}1$

This completes the proof. $\square$

Proposition 5.2

If $f\ge 8$, and some angle is irrational, and one of $\alpha \gamma \delta , \beta \gamma \delta$ is a vertex, then the tilings are earth map tiling E and its flip modifications $F_{1}E, F_{2}E$.

Proof

Up to symmetry, we may assume that $\alpha \gamma \delta$ is a vertex. By $\alpha \ne \beta$, this implies that $\beta \gamma \delta$ is not a vertex. The angle sum system gives

$$\begin{aligned} \alpha + \gamma + \delta = 2\pi , \quad \beta = \tfrac{4}{f}\pi . \end{aligned}$$

By $\alpha \gamma \delta$, at least two of $\alpha , \gamma , \delta$ are irrational. The key fact is the following: suppose $\varphi , \psi$ are irrational angles and $\varphi + \psi$ is a rational angle, then for rational numbers u, v, q, the equation $u\varphi +v\psi = q\pi$ implies $u=v$.

By $\alpha \gamma \delta$ and Lemma 3.17, we know that $\alpha ^2\cdots$ is a ${\hat{b}}$-vertex. At least two of $\alpha , \gamma , \delta$ are irrational. Therefore, we divide the discussion into the following cases.

Case ($\gamma , \delta$ are irrational, $\alpha$ is rational). By $\alpha \gamma \delta$, we know that $\gamma + \delta$ is rational. As $\gamma ,\delta$ are irrational, at each vertex, the number of $\gamma$ equals the number of $\delta$. This means that the b-vertices are $\alpha \gamma \delta , \beta ^n\gamma ^k\delta ^k, \gamma ^k\delta ^k$. The ${\hat{b}}$-vertices are $\alpha ^m, \alpha ^m\beta ^n, \beta ^n$. Therefore

$$\begin{aligned} \text {AVC}= \{ \alpha \gamma \delta , \alpha ^m, \alpha ^m\beta ^n, \beta ^n, \beta ^n\gamma ^k\delta ^k, \gamma ^k\delta ^k \}. \end{aligned}$$

(28)

Case ($\alpha , \gamma$ are irrational, $\delta$ is rational). By $\alpha \gamma \delta$, we know that $\alpha + \gamma$ is rational. As $\beta , \delta$ are rational and $\alpha , \gamma$ are irrational, at each vertex, the number of $\alpha$ equals the number of $\gamma$. Since $\alpha ^2\cdots$ can only be ${\hat{b}}$-vertex, this implies that $\alpha ^2\cdots$ is not a vertex. Then $\gamma \cdots =\alpha \gamma \cdots$ has no $\alpha , \gamma$ in the remainder. By $\alpha \gamma \delta$ and Parity Lemma, we have $\gamma \cdots =\alpha \gamma \delta$. Applying Counting Lemma to $\alpha ,\gamma$, this implies $\alpha \cdots =\alpha \gamma \delta$. Applying Counting Lemma to $\gamma ,\delta$, we get $\delta \cdots =\alpha \gamma \delta$. Then, the only other vertex is $\beta ^n$ where $n=\frac{f}{2}$. Therefore

$$\begin{aligned} \text {AVC}= \{ \alpha \gamma \delta , \beta ^{\frac{f}{2}} \}. \end{aligned}$$

(29)

Case ($\alpha , \delta$ are irrational, $\gamma$ is rational). The previous argument relies only on the parity of $\gamma , \delta$. Exchanging $\gamma \leftrightarrow \delta$ above, we get $\text {AVC}$ (29).

Case ($\alpha , \gamma , \delta$ are irrational). In this case, $\beta$ is the only rational angle. Then, $\alpha ^m, \gamma ^k, \delta ^l, \alpha ^m\beta ^n, \beta ^n\gamma ^k, \beta ^n\delta ^l$ are not vertices. Since $\alpha ^2\cdots$ can only be a ${\hat{b}}$-vertex, by no $\alpha ^m, \alpha ^m\beta ^n$, this implies that $\alpha ^2\cdots$ is not a vertex.

Suppose $\gamma >\delta$. By $\alpha \gamma \delta$ and Parity Lemma, we have $\alpha \gamma \cdots = \alpha \gamma \delta$. Then, $\alpha \cdots = \alpha \gamma \delta , \alpha \delta ^l, \alpha \beta ^n\delta ^l$. Counting Lemma on $\alpha ,\delta$ and Parity Lemma imply that $\alpha \delta ^l, \alpha \beta ^n\delta ^l$ are not vertices. Then, $\alpha \cdots = \alpha \gamma \delta$. Counting Lemma further implies that the only other vertex is $\beta ^n$. We get $\text {AVC}$ (29).

Suppose $\gamma <\delta$. We have $\alpha \delta \cdots = \alpha \gamma \delta$. Then, exchanging $\gamma \leftrightarrow \delta$ and $k \leftrightarrow l$ in the above, we get $\text {AVC}$ (29).

We summarise the AVCs below

• 1. $f\ge 8$, $\text {AVC}= \{ \alpha \gamma \delta , \beta ^{\frac{f}{2}} \}$;

• 2. $f\ge 8$, $\text {AVC}= \{ \alpha \gamma \delta , \alpha ^m, \beta ^n, \alpha ^m\beta ^n, \gamma ^k\delta ^k, \beta ^n\gamma ^k\delta ^k \}$.

By the tiling construction part of [8, Proposition 48], the earth map tilings E and their flip modifications $F_{1}E,F_{2}E$ are obtained from the above $\text {AVC}$s. We follow the same argument in [8, AVC (7.8), AVC (7.9)]. Hence, we get

$$\begin{aligned}&F_{1}E: \, \text {AVC}\equiv \{ \alpha \gamma \delta , \alpha ^m, \beta ^n\gamma \delta \}; \end{aligned}$$

(30)

$$\begin{aligned}&F_{1}E: \, \text {AVC}\equiv \{ \alpha \gamma \delta , \alpha ^m\beta ^n, \beta ^n\gamma \delta \}; \end{aligned}$$

(31)

$$\begin{aligned}&F_{2}E: \text {AVC}\equiv \{ \alpha \gamma \delta , \alpha \beta ^n, \gamma ^k\delta ^k \}; \end{aligned}$$

(32)

$$\begin{aligned}&F_{2}E: \text {AVC}\equiv \{ \alpha \gamma \delta , \alpha \beta ^n, \beta ^n\gamma ^k\delta ^k \}. \end{aligned}$$

(33)

The tilings with their $\text {AVC}$s are given in Table 13. The construction is explained in the proof of [8, Proposition 48]. $\square$

Table 13 Tilings with irrational angles and vertex $\alpha \gamma \delta$

The geometric realisation of all the tilings the previous sections can be seen in the full version on arXiv:2204.02748 or in [8]. We hereby conclude our study with the following two theorems.

Theorem 3

Tilings of the sphere by congruent almost equilateral quadrilaterals, where all angles are rational, are earth map tiling E and its flip modifications, $F_{1}E, F_{2}E$, and rearrangement RE, and isolated earth map tilings, S3, FS3, S5, and special tiling S6.

Theorem 4

Tilings of the sphere by congruent almost equilateral quadrilaterals with some irrational angles are earth map tiling E and its flip modifications, $F_{1}E, F_{2}E$, and isolated earth map tilings, S1, S2, and special tilings, $QP_6,S4$.