Abstract
A catalogue of simplicial hyperplane arrangements was first given by Grünbaum in 1971. These arrangements naturally generalize finite Coxeter arrangements and also the weak order through the poset of regions. The weak order is known to be a congruence normal lattice, and congruence normality of lattices of regions of simplicial arrangements can be determined using polyhedral cones called shards. In this article, we update Grünbaum’s catalogue by providing normals realizing all known simplicial arrangements with up to 37 lines and key invariants. Then we add structure to this catalogue by determining which arrangements always/sometimes/never lead to congruence normal lattices of regions. To this end, we use oriented matroids to recast shards as covectors to determine congruence normality of large hyperplane arrangements. We also show that lattices of regions coming from finite Weyl groupoids of any rank are always congruence normal.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The first catalogue of simplicial hyperplane arrangements of rank 3 appeared in 1971 [22]. This catalogue included three infinite families and 90 sporadic arrangements. Since then, the catalogue has changed: certain arrangements have been found to be isomorphic while some new arrangements have also been found, bringing the number of sporadic arrangements to 95 [9, 23]. The list is known to be complete for arrangements with up to 27 lines [8]. Until now, the list was scattered in various formats through several published and unpublished sources. In the present article, we provide a comprehensive list of the known rank-3 simplicial hyperplane arrangements in a usable format. Namely, we provide normal vectors realizing them along with several invariants. This is all presented in Sect. 5 and Appendices A and B. The following questions are still open: Is the list complete? Is there a finite list at all? To answer these questions, it is natural to search for structures lurking behind the list. Simplicial arrangements can be thought of as generalizations of finite Coxeter arrangements. Furthermore, they correspond to normal fans of simple zonotopes [35, Theorem 7.16]. What other combinatorial/geometric/algebraic structures regulate the list?
It turns out that finite Weyl groupoids provide an algebraic justification for around half of the sporadic arrangements. Finite Weyl groupoids are algebraic structures generalizing Weyl groups that were introduced to better understand the symmetries of Nichols algebras and related Hopf algebras [11, 24, 25]. Each Weyl groupoid originates from the data of a “Cartan graph”, leading to a so-called “root system”. In turn, these root systems generalize the usual notion of root system of a Weyl group. Notably, they form the set of normals of certain simplicial hyperplane arrangements. Finite Weyl groupoids of rank 3 have been classified and account for 53 simplicial arrangements [6].
Posets of regions form a family of combinatorial structures that encode detailed information on hyperplane arrangements and the adjacency of regions. For simplicial arrangements, the posets of regions are always lattices, no matter what the base region of the poset is [3, Theorem 3.4]. Reading showed that simpliciality can be weakened to tightness—which is a connectivity condition on facets of regions—to obtain lattices [33, Chapter 9] (see Lemma 2.6). Once again, simplicial arrangements through their lattices of regions provide generalizations, this time of the weak order of finite Coxeter groups. Unlike in the Coxeter case, a simplicial arrangement may lead to several non-isomorphic lattices of regions. Apart from being lattices, much less is known about the poset of regions of simplicial arrangements.
Lattice congruences of the weak order of Coxeter arrangements generate several objects of study. For example, the permutahedron is perhaps the most studied example of a simple zonotope that comes from the braid arrangement, or Coxeter arrangement of type A. The corresponding poset of regions is the weak order of the symmetric group and is a lattice. Moreover, Tamari and Cambrian lattices, generalized permutahedra, and associahedra are all related to lattice congruences of the weak order [26, 29, 32]. In particular, in type A and B, every lattice congruence leads to a polytope [27, 28]. To which extent do these constructions extend to general simplicial arrangements? We focus here on two important properties used to study lattice congruences and shard polytopes: congruence normality and congruence uniformity. Coxeter arrangements are congruence normal and uniform [5]. Congruence uniform lattices admit a bijection between their join-irreducible elements and the join-irreducible elements in the lattice of lattice congruences. Congruence uniform lattices are thus particularly nice lattices as they allow one to more easily study the lattice of congruences. Reading characterized congruence uniformity of posets of regions using tightness and shards (i.e. pieces of hyperplanes) [33, Corollary 9-7.22]. Reading also showed that supersolvable hyperplane arrangements have congruence uniform posets of regions for some canonical choice of base region [30]. Congruence uniform lattices admit a combinatorial construction whose geometric aspects in this context have yet to be explored in detail.
In this article, we determine congruence uniformity and normality of posets of regions of simplicial hyperplane arrangements of rank 3 and draw several conclusions. To do so, we approach posets of regions through the oriented matroids naturally associated with the normals of the hyperplane arrangements, which are presented in Appendix A. Covectors of the oriented matroid can be used to encode the “facial weak order” of simplicial hyperplane arrangements [17]. Here, we use covectors and the intersection operation as our main tools to elevate Reading’s characterization of congruence uniformity to the level of oriented matroids (see Theorem 3.18 and Corollary 3.19). Namely, we introduce shard covectors—which are covectors with some “*” entries—and show they are in bijection with shards (see Theorem 3.12).
This approach led to the following results. The posets of regions of hyperplane arrangements coming from finite Weyl groupoids are always congruence normal and congruence uniform (see Theorem 4.2). This result provides a new proof that finite Coxeter arrangements are obtainable through a finite sequence of interval doublings (i.e. congruence uniform) [5, Theorem 6]. We further classify the known rank-3 simplicial arrangements according to whether their posets of regions are always or sometimes or never congruence normal (see Table 1). The approach through covectors gives a way to determine congruence normality of posets of regions without the data of the poset or resorting to polyhedral objects (i.e. shards). Notably, this classification could not have been carried out through the computation of the posets of regions due to their large size. Hence, this framework provides an oriented matroid approach to study congruence normality and uniformity for large posets of regions. As an interesting outcome of this classification, five arrangements have exceptional behavior. Two of the five arrangements are always congruence normal: the non-crystallographic arrangement corresponding to the Coxeter group \(H_3\) and its point-line dual arrangement which has 31 hyperplanes. The three other arrangements are never congruence normal: they have yet to show any connection to other known structures. Furthermore, we provide instructive examples which give deeper insight into congruence uniformity for posets of regions. We verified that within supersolvable simplicial arrangements (by [12, Theorem 1.2] these are the arrangements in 2 of the 3 infinite families) only four are always congruence normal and all others are only sometimes congruence normal, see Theorems 4.5 and 4.6. The algorithms used to carry out the verifications and the data to construct known simplicial hyperplane arrangements are available as a Sage-package [18].
The article is structured as follows. In Sect. 2, we present the necessary background notions on lattice congruences, posets of regions, congruence normality and uniformity and the theory of shards. In Sect. 3, we recast shards and the forcing relation using covectors. In Sect. 4, we present the result of the application of the approach of Sect. 3 to the known rank-3 simplicial hyperplane arrangements. In Sect. 5, we present combinatorial and geometric invariants of the known rank-3 simplicial hyperplane arrangements with up to 37 hyperplanes. In Appendix A, we give normals to realize each of these arrangements. Finally, in Appendix B, we give a wiring diagram description for these arrangements.
2 Preliminaries
We use the following notation: \(\mathbb {N}=\{0,1,2,\ldots \}\), \(d,m\in \mathbb {N}{\setminus }\{0\}\), and \([m]:=\{1,2,\ldots ,m\}\). We use bold faced \(\mathbf {n},\mathbf {p},\mathbf {x},\) etc. to denote vectors in the real Euclidean space \(\mathbb {R}^{d}\) equipped with the usual dot product \(\mathbb {R}^d \times \mathbb {R}^d\rightarrow ~\mathbb {R}\). Let \(\mathbf {P}\) denote a finite, ordered set of vectors. The linear span of \(\mathbf {P}\) is denoted \({{\,\mathrm{span}\,}}(\mathbf {P})\), its affine hull by \({{\,\mathrm{aff}\,}}(\mathbf {P})\), and its convex hull by \({{\,\mathrm{conv}\,}}(\mathbf {P})\). To ease reading, we often abuse notation and write for instance \({{\,\mathrm{span}\,}}(\mathbf {x}_1,\mathbf {x}_2)\) instead of \({{\,\mathrm{span}\,}}(\{\mathbf {x}_1,\mathbf {x}_2\})\). The orthogonal complement of a linear subspace \(A\subseteq \mathbb {R}^d\) is denoted \(A^\top \). The relative interior of a subset \(\mathbf {P}\) of \(\mathbb {R}^d\) is denoted by \({{\,\mathrm{int}\,}}(\mathbf {P})\).
In Sect. 2.1, we review the notion of a lattice congruence. In Sect. 2.2, we define hyperplane arrangements and posets of regions. In Sects. 2.3 and 2.4, we discuss the notions of congruence normality and uniformity. Finally, in Sect. 2.5, we describe Reading’s characterization of congruence uniformity for tight hyperplane arrangements using shards. The material presented in this section is mostly based on material treated in the book chapter [33, Chapter 9].
2.1 Lattice Congruences
Let \(L=(P;\wedge ,\vee )\) be a finite lattice, where P is a poset \((P,\le )\). An element \(j \in L\) is join-irreducible if j covers a unique element \(j_\bullet \in L\). Similarly, an element \(m\in L\) is meet-irreducible if m is covered by a unique element \(m^\bullet \in L\). We denote the subposet of join-irreducible elements of a lattice L by \(L_{\vee }\) and the subposet of meet-irreducible elements by \(L_{\wedge }\). An order ideal of a poset P is a subposet \({Q \subseteq P}\) that satisfies \(x \in Q\) and \(y \le x \Rightarrow y \in Q\). The order ideals of a poset P can be ordered by containment to get the poset of order ideals denoted \(\mathcal {O}(P)\). When L is self-dual, join- and meet-irreducible elements are canonically in bijection. The dual map, therefore, allows one to refine statements involving L and its irreducible elements. Join-irreducible elements (and dually meet-irreducible elements) and posets of order ideals are very useful to understand finite distributive lattices.
Lemma 2.1
([2, Theorem 17.3]). Let L be a lattice, \(L_{\vee }\) be its subposet of join-irreducible elements, and \(\mathcal {O}(L_{\vee })\) be the poset of order ideals of \(L_{\vee }\). If L is finite and distributive, then L is isomorphic to \(\mathcal {O}(L_{\vee })\).
Recall that cosets of a normal subgroup \(N \trianglelefteq G\) determine a congruence relation and lead to a quotient group G/N, which is the image of the map sending an element to its coset. Analogously, in lattice theory, intervals play the role of cosets, and under certain conditions, they form a quotient lattice. In this case, the equivalence relation is called a lattice congruence. For a thorough discussion on congruences and quotient lattices, we refer the reader to [33, Chapter 9-5 and 9-10] and the references therein.
Definition 2.2
(Lattice congruence). An equivalence relation \(\equiv \) on the elements of a lattice L is a lattice congruence if \(x_1 \equiv x_2\) and \(y_1 \equiv y_2\) implies \(x_1 \wedge y_1 \equiv x_2 \wedge y_2\) and \(x_1 \vee y_1 \equiv x_2 \vee y_2\) for any elements \(x_1,x_2,y_1,y_2 \in L\).
Lemma 2.3
(See, e.g. [33, Proposition 9-5.2]). An equivalence relation on a lattice is a lattice congruence if and only if the following three conditions are satisfied:
-
(1)
Every equivalence class is an interval.
-
(2)
The map \(\pi _\downarrow \) sending each element to the minimal element in its equivalence class is order-preserving.
-
(3)
The map \(\pi _\uparrow \) sending each element to the maximal element in its equivalence class is order-preserving.
Given a lattice congruence, the images of \(\pi _\downarrow \) and \(\pi _\uparrow \) are sublattices, i.e. the join and meet operations are preserved on the equivalence classes, and they are referred to as quotient lattices.
Lattice congruences of a lattice can be numerous and the relations between them may be challenging to describe. In spite of that, the set of lattice congruences on a lattice L may be partially ordered by refinement. The equivalence relation with singleton classes is the smallest lattice congruence and its associated quotient lattice is the lattice itself. Furthermore, the equivalence relation with a unique class is the coarsest lattice congruence whose associated quotient lattice has exactly one element. It turns out that under this partial order by refinement, the set of lattice congruences forms a distributive lattice which is called the lattice of congruences and is denoted by \({{\,\mathrm{Con}\,}}(L)\) [19]. The lattices of congruences we consider here are finite and, therefore, complete. Consequently, given any set of relations, there is a smallest lattice congruence which contains these relations [33, Proposition 9-5.13]. This makes it possible to define two important congruences related to join- and meet-irreducible elements. Consider a join-irreducible element \(j\in L_{\vee }\), then there is a smallest lattice congruence \({{\,\mathrm{con}\,}}_\vee (j)\) such that j and \(j_\bullet \) are equivalent. Similarly, for a meet-irreducible element m, there is a smallest lattice congruence \({{\,\mathrm{con}\,}}_{\wedge }(m)\) such that m and the unique element \(m^\bullet \) that covers it are equivalent. In this case, we say that the congruence \({{\,\mathrm{con}\,}}_\vee \) contracts j, and that \({{\,\mathrm{con}\,}}_\wedge \) contracts m. As \({{\,\mathrm{Con}\,}}(L)\) is finite and distributive, we may use Lemma 2.1 to obtain that \({{\,\mathrm{Con}\,}}(L)\) is isomorphic to \(\mathcal {O}({{\,\mathrm{Con}\,}}(L)_\vee )\). That is to say that a congruence is determined by an order ideal of join-irreducible congruences, i.e., by the join-irreducibles it contracts [33, Corollary 9-5.15].
Definition 2.4
Let \({{\,\mathrm{con}\,}}_\vee : L_\vee \rightarrow {{\,\mathrm{Con}\,}}(L)\) be the map that sends a join-irreducible element \(j \in L_{\vee }\) to the smallest lattice congruence in \({{\,\mathrm{Con}\,}}(L)\) such that \(j \equiv j_\bullet \). Dually, the map \({{\,\mathrm{con}\,}}_{\wedge }\) is similarly defined for meet-irreducible elements.
The image of the map \({{\,\mathrm{con}\,}}_\vee \) is \({{\,\mathrm{Con}\,}}(L)_{\vee }\), i.e., the congruence \({{\,\mathrm{con}\,}}_\vee (j)\) is join-irreducible in \({{\,\mathrm{Con}\,}}(L)\) and for every join-irreducible congruence \(\alpha \) in \({{\,\mathrm{Con}\,}}(L)\), there exists a join-irreducible \(j\in L_\vee \) such that \({{\,\mathrm{con}\,}}_\vee (j)=\alpha \) [33, Proposition 9-5.14]. It may happen that two distinct join-irreducibles give rise to the same congruence, i.e. that \({{\,\mathrm{con}\,}}_\vee \) is not injective, leading to an equivalence relation on join-irreducible elements in \(L_\vee \). Through the map \({{\,\mathrm{con}\,}}_\vee \), these equivalence classes of join-irreducible elements in L are in bijection with join-irreducible congruences of L.
2.2 Poset of Regions of a Real Hyperplane Arrangement
A (real) hyperplane H is a codimension-1 affine subspace in \(\mathbb {R}^d\):
The vector \(\mathbf {n}\) is called the normal of H. A finite hyperplane arrangement  is a finite non-empty set of m hyperplanes. If \(a=0\) for all hyperplanes in
is a finite non-empty set of m hyperplanes. If \(a=0\) for all hyperplanes in  , then the hyperplane arrangement is called central. In this case, the hyperplanes are completely determined by their normals. We denote the hyperplanes in
, then the hyperplane arrangement is called central. In this case, the hyperplanes are completely determined by their normals. We denote the hyperplanes in  by \(H_1,\ldots ,H_m\) and often reuse their indices to refer to objects canonically related to them. The rank of
by \(H_1,\ldots ,H_m\) and often reuse their indices to refer to objects canonically related to them. The rank of  is the dimension of the linear span of the normal vectors of the hyperplanes in
is the dimension of the linear span of the normal vectors of the hyperplanes in  . The complement of the arrangement in the ambient space \((\mathbb {R}^d {\setminus }\bigcup _{i\in [m]}H_i)\) is disconnected, and the closures of the connected components are the regions of the arrangement. The set of regions of
. The complement of the arrangement in the ambient space \((\mathbb {R}^d {\setminus }\bigcup _{i\in [m]}H_i)\) is disconnected, and the closures of the connected components are the regions of the arrangement. The set of regions of  is denoted by
is denoted by  . A region is called simplicial if the normal vectors of its facet-defining hyperplanes are linearly independent. A hyperplane arrangement is simplicial if every region in its complement is simplicial. Throughout, we use the notation
. A region is called simplicial if the normal vectors of its facet-defining hyperplanes are linearly independent. A hyperplane arrangement is simplicial if every region in its complement is simplicial. Throughout, we use the notation  to denote the ith simplicial hyperplane arrangement with m hyperplanes and r regions from our catalogue of simplicial arrangements, see Appendix A. To proceed further, a base region B of
to denote the ith simplicial hyperplane arrangement with m hyperplanes and r regions from our catalogue of simplicial arrangements, see Appendix A. To proceed further, a base region B of  is chosen. For each hyperplane
is chosen. For each hyperplane  , we fix a normal vector \(\mathbf {n}_i\in \mathbb {R}^d\) such that \(\mathbf {n}_i\cdot \mathbf {x}<0\), for all \(\mathbf {x}\in B\). Given a region R of
, we fix a normal vector \(\mathbf {n}_i\in \mathbb {R}^d\) such that \(\mathbf {n}_i\cdot \mathbf {x}<0\), for all \(\mathbf {x}\in B\). Given a region R of  , the separating set \({{\,\mathrm{Sep}\,}}_B(R)\) of R is the set of hyperplanes
, the separating set \({{\,\mathrm{Sep}\,}}_B(R)\) of R is the set of hyperplanes  such that \(\mathbf {n}_i\cdot \mathbf {x}>0,\) for all \(\mathbf {x}\in R\). The separating set of a region is the set of hyperplanes that separate it from the base region B.
such that \(\mathbf {n}_i\cdot \mathbf {x}>0,\) for all \(\mathbf {x}\in R\). The separating set of a region is the set of hyperplanes that separate it from the base region B.
Definition 2.5
(Poset of regions,  ). Let
). Let  be a hyperplane arrangement with base region B. The poset of regions
be a hyperplane arrangement with base region B. The poset of regions  of
of  with base region B is the partially ordered set
with base region B is the partially ordered set  such that
such that
for all  .
.
An upper facet of a region  is a facet of R which corresponds to a cover relation of R in
is a facet of R which corresponds to a cover relation of R in  . A hyperplane arrangement is tight with respect to B when the upper facets of every region intersect pairwise along a codimension-2 face, i.e. they are neighbors in the facet-adjacency graph. When a hyperplane arrangement
. A hyperplane arrangement is tight with respect to B when the upper facets of every region intersect pairwise along a codimension-2 face, i.e. they are neighbors in the facet-adjacency graph. When a hyperplane arrangement  is tight with respect to every base region, we say that
is tight with respect to every base region, we say that  is tight. For convenience, when a hyperplane arrangement is tight, we also call the corresponding posets of regions tight. The usual definition of tightness also requires the dual statement to hold. As poset of regions are self-dual, we have restricted the statement to upper facets. The following lemma is a refinement of [3, Theorem 3.4].
is tight. For convenience, when a hyperplane arrangement is tight, we also call the corresponding posets of regions tight. The usual definition of tightness also requires the dual statement to hold. As poset of regions are self-dual, we have restricted the statement to upper facets. The following lemma is a refinement of [3, Theorem 3.4].
Lemma 2.6
Let  be a finite, central hyperplane arrangement with base region B.
be a finite, central hyperplane arrangement with base region B.
-
(1)
If
 is tight with respect to B, then
is tight with respect to B, then  is a lattice [33, Theorem 9-3.2].
is a lattice [33, Theorem 9-3.2]. -
(2)
If
 is simplicial, then
is simplicial, then  is tight [33, Proposition 9-3.3].
is tight [33, Proposition 9-3.3].
Reading developed an approach to study congruences of lattices of regions that is thoroughly described in [33, Chapter 9]. In particular, for posets of regions, tightness is equivalent to semidistributivity [33, Theorem 9-3.8] (see Sect. 2.4 for the definition of semidistributivity). Furthermore, to describe the interplay between join-irreducible elements, the combinatorial notion of “polygonality” of a lattice is used; in the case of posets of regions, this notion is equivalent to the notion of tightness [33, Theorem 9-6.10]. Using the polygonality property, it is possible to describe which join-irreducibles force other ones to be contracted. This forcing relation can then be read off from the hyperplane arrangement using pieces of hyperplanes called shards (see Definition 2.15 in Sect. 2.5). The interest in the notion of tightness lies in the fact that being tight and having acyclicity on shards characterizes congruence uniformity, see Theorem 2.19 in Sect. 2.5.
Throughout this article, we restrict our study to finite, central, and tight hyperplane arrangements, so that the posets of regions are guaranteed to be complete lattices regardless of the choice of base regions. We refer the reader to [33, Chapter 9-3, 9-6] for further details on tightness and polygonality.
2.3 Congruence Normality
Definition 2.7
(Congruence normality, [15, Section 1, p. 400]). Let L be a lattice, \(L_\vee \subseteq L\) be the subposet of join-irreducible elements of L, and \(L_\wedge \) be the subposet of meet-irreducible elements of L. The lattice L is congruence normal if
for all \(j\in L_\vee \), and \(m\in L_\wedge \). A hyperplane arrangement is called congruence normal if its lattices of regions are congruence normal for every choice of base region.
Equivalently, finite congruence normal lattices are exactly the lattices obtained from a one-element lattice by a sequence of doublings of convex sets [15, Section 3], see also [1, Theorem 3-2.39] and [21]. The following example illustrates a local condition showing how a lattice may fail to be congruence normal.
Example 2.8
Consider the lattice \(L_3\) with the Hasse diagram illustrated in Fig. 1. The element c is join-irreducible, and the smallest congruence \({{\,\mathrm{con}\,}}_\vee (c)\) such that \(b\equiv c\) is illustrated on the right-hand side.
Following Definition 2.2, setting \(b\equiv c\) forces the lattice to project onto a three-element chain. By order-reversing symmetry, the smallest congruence such that \(c\equiv d\) is the same as the smallest congruence such that \(b\equiv c\). Since c is also meet-irreducible, we get \({{\,\mathrm{con}\,}}_\wedge (c)={{\,\mathrm{con}\,}}_\vee (c)\). Since \(c\le c\), the lattice \(L_3\) is not congruence normal.
This example complements Reading’s example of forcing of polygons nicely, see, e.g. [33, Example 9-6.6] and the exercise on congruence normality of polygonal lattices [33, Exercice 9.55]. The intervals [0, d] and [b, 1] intersect on more than one cover and removing c from \(L_3\) makes it congruence normal. Unfortunately, such local obstructions may not be used on lattices of regions of a hyperplane arrangement. The corresponding Hasse diagrams are isomorphic to the 1-skeleta of the associated zonotopes, and two polygons as in the example may not intersect along more than one cover relation for convexity reasons. As we shall see in Example 2.13, there are non-congruence normal lattices of regions.
2.4 Congruence Uniformity
A lattice is join-semidistributive if for \(x,y,z \in L\),
It is meet-semidistributive if
A lattice that is both join-semidistributive and meet-semidistributive is called semidistributive.
Definition 2.9
(Congruence uniformity, [14, Definition 4.1]). Let L be a finite lattice. If the maps \({{\,\mathrm{con}\,}}_\vee \) and \({{\,\mathrm{con}\,}}_\wedge \) are injective, then L is called congruence uniform.
Congruence uniformity describes the lattice of congruences of the involved lattice through the map \({{\,\mathrm{con}\,}}_\vee \). If L is a finite congruence uniform lattice, then the map \({{\,\mathrm{con}\,}}_\vee \) gives a order-preserving bijection between \(L_\vee \) and \({{\,\mathrm{Con}\,}}(L)_\vee \). Lemma 2.1 then permits one to study the whole of \({{\,\mathrm{Con}\,}}(L)\). Congruence uniformity is a stronger condition than congruence normality in that it should be obtained from a one-element lattice by a sequence of doublings of intervals [14, Theorem 5.1].
Theorem 2.10
([15, Section 2]). A finite lattice is congruence uniform if and only if it is both congruence normal and semidistributive.
Corollary 2.11
A tight poset of regions  is congruence normal if and only if it is congruence uniform.
is congruence normal if and only if it is congruence uniform.
Proof
By Lemma 2.6, the poset of regions  of a
of a  is a finite lattice, independent of the choice of base region B. Furthermore,
is a finite lattice, independent of the choice of base region B. Furthermore,  is tight with respect to B if and only if
is tight with respect to B if and only if  is semidistributive [33, Theorem 9-3.8].
is semidistributive [33, Theorem 9-3.8].
Remark 2.12
-
(1)
Since lattices of regions are self-dual, it suffices to verify the injectivity of \({{\,\mathrm{con}\,}}_\vee \) to determine whether they are congruence uniform.
-
(2)
Semidistributivity can be described using sublattice avoidance [1, Theorem 3-1.4]. The six sublattices obstructing semidistributivity are illustrated in Figs. 1 and 2. Four out of the six non-semidistributive lattices are not congruence normal (\(L_3\), \(L_4\), \(L_5\), and \(M_3\)) and share the property that two polygons share more than 1 cover. Nevertheless, semidistributivity is neither necessary nor sufficient to obtain congruence normality: \(L_1\) and \(L_2\) are congruence normal but not semidistributive and Example 2.13 gives a poset of regions which is semidistributive but not congruence normal.
-
(3)
While considering two polygons in a polygonal lattice, and verifying congruence normality as in Example 2.8, one realizes that \(M_3\), \(L_3\), \(L_4\), and \(L_5\) should be avoided. For poset of regions, this comes as no surprise as polygonality, tightness and semidistributivity are equivalent [33, Theorem 9-3.8 and 9-6.10]. In general, one might be tempted to ask, what is the relationship between polygonal and semidistributive lattices?
Five of the six sublattices that obstruct semidistributivity, the sixth is \(L_3\) illustrated in Fig. 1
Example 2.13
([30, Figure 5] and [33, Exercise 9.69]) Figure 3 illustrates the stereographic projection of the simplicial hyperplane arrangement  in \(\mathbb {R}^3\) with 10 hyperplanes through the intersection of 5 hyperplanes which are mapped to lines. This arrangement is \(\mathcal {A}(10,1)\) in Grünbaum’s list [23, p.2-3], see Sect. 4.
in \(\mathbb {R}^3\) with 10 hyperplanes through the intersection of 5 hyperplanes which are mapped to lines. This arrangement is \(\mathcal {A}(10,1)\) in Grünbaum’s list [23, p.2-3], see Sect. 4.
The lattice of regions with respect to the base region marked by a black dot is semidistributive as the arrangement is simplicial. In Example 2.20, we use shards to demonstrate that this arrangement is not congruence normal, hence not uniform by Corollary 2.11. It is the smallest known simplicial hyperplane arrangement of rank three with that property.
Examples 2.8 and 2.13 illustrate failures to be congruence normal. Example 2.13 is particularly interesting in that it does not fail to be congruence normal because of forbidden sublattices blocking semidistributivity.
2.5 Congruence Normality of Simplicial Hyperplane Arrangements Through Shards
Reading characterized congruence uniformity of posets of regions via two conditions, the first one is tightness and the second is phrased using pieces of hyperplanes called shards. When the arrangement is central, these pieces are polyhedral cones defined through certain subarrangements.
Definition 2.14
(Rank-2 subarrangements and their basic hyperplanes, see [33, Definition 9-7.1]). Let  be a hyperplane arrangement with base region B, and let \(1\le i<j\le m\). The set
be a hyperplane arrangement with base region B, and let \(1\le i<j\le m\). The set

is called a rank-2 subarrangement of  . The two facet-defining hyperplanes of the region of
. The two facet-defining hyperplanes of the region of  that contains B are called the basic hyperplanes of
that contains B are called the basic hyperplanes of  .
.
Definition 2.15
(Shards, see [33, Definition 9-7.2]). Let  and set
and set

The intersection of the hyperplanes in \({{\,\mathrm{pre}\,}}(H_i)\) with the hyperplane \(H_i\) breaks \(H_i\) into closed regions called shards. We denote shards by capital Greek letters such as \(\Sigma ,\Theta ,\) and \(\Upsilon \). The hyperplane of  that contains a shard \(\Sigma \) is denoted by \(H_\Sigma \). We write \(\Sigma ^i\) to indicate that it is contained in \(H_i\). Hyperplanes in \({{\,\mathrm{pre}\,}}(H_i)\) are said to cut the hyperplane \(H_i\).
that contains a shard \(\Sigma \) is denoted by \(H_\Sigma \). We write \(\Sigma ^i\) to indicate that it is contained in \(H_i\). Hyperplanes in \({{\,\mathrm{pre}\,}}(H_i)\) are said to cut the hyperplane \(H_i\).
Example 2.16
(Example 2.13 continued). Figure 4 illustrates the 29 shards obtained from the base region marked with a dot.
On the one hand, due to the particular choice of projection, it is necessary to distinguish whether two unbounded straight line segments lying on a common line form 1 or 2 shards. For example, the unbounded line segments on the line labeled \(H_3\) form one shard \(\Sigma \), and \(H_4\) is basic and, therefore, is one shard itself. The unbounded line segments on the line labeled \(H_6\) form 2 distinct shards \(\Sigma '\) and \(\Sigma ''\). Similarly, the hyperplanes \(H_7\) and \(H_8\) also split like \(H_6\). On the other hand, it is possible to solve this by changing the projection to obtain only circles, though simultaneously losing symmetry.
The following directed graph records the cutting relation among hyperplanes.
Definition 2.17
(Directed graph  [31, Section 3]). Let
[31, Section 3]). Let  be the directed graph whose vertices are the hyperplanes of the arrangement
be the directed graph whose vertices are the hyperplanes of the arrangement  , and whose oriented edges are such that
, and whose oriented edges are such that
The following directed graph keeps track of the cutting relation along with the “geometric proximity” between shards.
Definition 2.18
(Shard digraph, see [31, Section 3][33, Definition 9.7.16]). Let  be the directed graph on the shards of
be the directed graph on the shards of  such that
such that

The following theorem gives a characterization of congruence uniformity in terms of the directed graph on shards.
Theorem 2.19
([33, Corollary 9-7.22]). Let  be a hyperplane arrangement with a base region B. The poset of regions
be a hyperplane arrangement with a base region B. The poset of regions  is a congruence uniform lattice if and only if
is a congruence uniform lattice if and only if  is tight with respect to B and
is tight with respect to B and  is acyclic. In this case,
is acyclic. In this case,  is isomorphic to the Hasse diagram of
is isomorphic to the Hasse diagram of  .
.
By Corollary 2.11, the theorem implies that acyclicity of the directed graph on shards  characterizes the normality and uniformity of tight posets of regions
characterizes the normality and uniformity of tight posets of regions  .
.
Example 2.20
(Example 2.16 continued). Let \(\Sigma ^6,\Theta ^{10},\Upsilon ^8\), and \(\Xi ^9\) be the shards illustrated in Fig. 5. The directed graph on shards contains the cycle \(\Sigma ^6 \rightarrow \Theta ^{10} \rightarrow \Upsilon ^8 \rightarrow \Xi ^9 \rightarrow \Sigma ^6\). Thus, for this choice of base region, the lattice of regions is not congruence normal.
A cycle in the shards of the simplicial hyperplane arrangement from Example 2.13
3 Congruence Normality Through Restricted Covectors
In this section, we recast shards as certain restricted covectors—which we call shard covectors—in the point configuration dual to the arrangement  . We then describe how to detect cycles in
. We then describe how to detect cycles in  using shard covectors. This reduces the verification of congruence normality for tight posets of regions to its simplest combinatorial expression, one that does not require the entire poset nor the usage of polyhedral objects. Furthermore, it is possible to express an obstruction to congruence normality for tight hyperplane arrangements.
using shard covectors. This reduces the verification of congruence normality for tight posets of regions to its simplest combinatorial expression, one that does not require the entire poset nor the usage of polyhedral objects. Furthermore, it is possible to express an obstruction to congruence normality for tight hyperplane arrangements.
In Sect. 3.1, we introduce restricted covectors and the intersection operation. In Sect. 3.2, we define affine point configurations and their lines. In Sect. 3.3, we interpret shards as covectors. In Sect. 3.4, we translate the forcing relation on shards into the language of covectors. Finally, in Sect. 3.5, we describe examples of obstructions to congruence normality in terms of restricted covectors.
3.1 Restricted Covectors and the Intersection Operation
For standard references on covectors and oriented matroids, we refer the reader to the books [4, 16].
Definition 3.1
(Covector and restricted covector). Let \(\mathbf {P}=\{\mathbf {p}_i\}_{i\in [m]}\) be an ordered set of vectors in \(\mathbb {R}^d\). A covector on \(\mathbf {P}\) is a vector of signs  defined as
defined as

where \(\mathbf {c}\in \mathbb {R}^d\) and \(a\in \mathbb {R}\). Given a subset \(\mathbf {U} \subseteq \mathbf {P}\) and a covector  on \(\mathbf {P}\), the restricted covector
on \(\mathbf {P}\), the restricted covector  with respect to \(\mathbf {U}\) is equal to
with respect to \(\mathbf {U}\) is equal to  on the entries \(\{j~:~\mathbf {p}_j\in \mathbf {U}\}\) and contains a “*” symbol in every other entry.
on the entries \(\{j~:~\mathbf {p}_j\in \mathbf {U}\}\) and contains a “*” symbol in every other entry.
Intuitively, a restricted covector “forgets” about certain hyperplanes while keeping them encoded. Similarly, reversing the roles of \(\mathbf {c}\) and \(\mathbf {p}_i\) above, covectors may be thought of as sign evaluations of a certain vector \(\mathbf {x}\) with respect to a set of vectors:
Definition 3.2
(Sign evaluation of a vector). Let \(\mathbf {P}=\{ \mathbf {p}_i\}_{i\in [m]}\) be an ordered set of vectors in \(\mathbb {R}^d\) and \(\mathbf {x}\in \mathbb {R}^d\). The sign evaluation of \(\mathbf {x}\) with respect to \(\mathbf {P}\) is the covector

Inspired by the composition operation on vectors (i.e. affine dependences) of oriented matroids [4, Chapter 3], we define an intersection operation on restricted covectors.
Definition 3.3
(Intersection of restricted covectors). The commutative intersection operation \(\cap \) from \({\{0,+,-,*\}\times \{0,+,-,*\}}\) to \(\{0,+,-,*\}\) is defined as

where \(\varepsilon \in \{0,+,-,*\}\). Let  be two restricted covectors, then their intersection
be two restricted covectors, then their intersection  is the vector of signs
is the vector of signs  .
.
The vector of signs  is not necessarily a covector, though it nevertheless records the information of the sign evaluation of points in an intersection. It is possible to interpret this intersection operation using subsets of the real numbers. That is, if one replaces the four symbols \(0,+,-,*\), respectively, by the sets \(\{0\},\mathbb {R}_{\ge 0},\mathbb {R}_{\le 0},\mathbb {R}\), and consider their intersections, we get exactly the same results. The associativity of this operation then follows easily.
is not necessarily a covector, though it nevertheless records the information of the sign evaluation of points in an intersection. It is possible to interpret this intersection operation using subsets of the real numbers. That is, if one replaces the four symbols \(0,+,-,*\), respectively, by the sets \(\{0\},\mathbb {R}_{\ge 0},\mathbb {R}_{\le 0},\mathbb {R}\), and consider their intersections, we get exactly the same results. The associativity of this operation then follows easily.
3.2 Affine Point Configurations and Lines
We use duality to pass from a hyperplane arrangement  in \(\mathbb {R}^d\) with a base region B to an acyclic point configuration
in \(\mathbb {R}^d\) with a base region B to an acyclic point configuration  , see [4, Section 1.2] for more detail. Indeed, the normals \(\{\mathbf {n}_i \}_{i \in [m]}\) are oriented so that the linear hyperplane orthogonal to \(\mathbf {v}_B\!\in {{\,\mathrm{int}\,}}(B)\) separates them from the base region B, i.e. \(\mathbf {v}_B\cdot \mathbf {n}_i<0\), for all \(i\in [m]\), making the set \(\{\mathbf {n}_i\}_{i\in [m]}\) acyclic.
, see [4, Section 1.2] for more detail. Indeed, the normals \(\{\mathbf {n}_i \}_{i \in [m]}\) are oriented so that the linear hyperplane orthogonal to \(\mathbf {v}_B\!\in {{\,\mathrm{int}\,}}(B)\) separates them from the base region B, i.e. \(\mathbf {v}_B\cdot \mathbf {n}_i<0\), for all \(i\in [m]\), making the set \(\{\mathbf {n}_i\}_{i\in [m]}\) acyclic.
Definition 3.4
(Affine point configuration relative to a base region). Let  be a hyperplane arrangement in \(\mathbb {R}^d\),
be a hyperplane arrangement in \(\mathbb {R}^d\),  , and \(\mathbf {v}_B\in {{\,\mathrm{int}\,}}(B)\). Let
, and \(\mathbf {v}_B\in {{\,\mathrm{int}\,}}(B)\). Let
and associate the point \(\mathbf {p}_i:=-\frac{1}{\mathbf {v}_B\cdot \mathbf {n}_i}\cdot \mathbf {n}_i \in \mathbb A_B\subset \mathbb {R}^d\) to the normal \(\mathbf {n}_i\). The ordered set of vectors \(\{\mathbf {p}_i\}_{i\in [m]}\) is the affine point configuration of  relative to the base region B and is denoted
relative to the base region B and is denoted  .
.
Choosing a different normal vector \(\mathbf {v}_B\in {{\,\mathrm{int}\,}}(B)\) yields an affine point configuration which is projectively equivalent to  . Hence, up to projective transformation, this construction does not depend on the choice of \(\mathbf {v}_B\).
. Hence, up to projective transformation, this construction does not depend on the choice of \(\mathbf {v}_B\).
Definition 3.5
(Lines of a point configuration,  ). Let \(\mathbf {P}=\{\mathbf {p}_i\}_{i\in [m]}\) be an ordered set of vectors in \(\mathbb {R}^d\) . A subset of \(\mathbf {P}\) consisting of all the points that lie on the affine hull of two distinct points of \(\mathbf {P}\) is called a line. The set of lines of \(\mathbf {P}\) is denoted by
). Let \(\mathbf {P}=\{\mathbf {p}_i\}_{i\in [m]}\) be an ordered set of vectors in \(\mathbb {R}^d\) . A subset of \(\mathbf {P}\) consisting of all the points that lie on the affine hull of two distinct points of \(\mathbf {P}\) is called a line. The set of lines of \(\mathbf {P}\) is denoted by  .
.
Lemma 3.6
Let  be a hyperplane arrangement in \(\mathbb {R}^d\) with base region B,
be a hyperplane arrangement in \(\mathbb {R}^d\) with base region B,  , and \(\mathbf {p}_i\) and \(\mathbf {p}_j\) be the two vertices of the segment \({{\,\mathrm{conv}\,}}(\ell )\).
, and \(\mathbf {p}_i\) and \(\mathbf {p}_j\) be the two vertices of the segment \({{\,\mathrm{conv}\,}}(\ell )\).
-
(i)
The lines in
 are in bijection with the rank-2 sub- arrangements of
are in bijection with the rank-2 sub- arrangements of  .
. -
(ii)
The hyperplanes \(H_i\) and \(H_j\) are the basic hyperplanes of the rank-2 subarrangement corresponding to \(\ell \).
Proof
(i) Let  , for some \(\mathcal {I}\subseteq [m]\). The subarrangement
, for some \(\mathcal {I}\subseteq [m]\). The subarrangement  is a rank-2 subarrangement if and only if
is a rank-2 subarrangement if and only if
Equivalently,
By passing to the affine point configuration in the affine space \(~\mathbb A_B\), the above statement is equivalent to  . Thus, the map sending a rank-2 subarrangement
. Thus, the map sending a rank-2 subarrangement  to the line \(\{\mathbf {p}_i~:~i \in \mathcal {I} \}\) is a bijection.
to the line \(\{\mathbf {p}_i~:~i \in \mathcal {I} \}\) is a bijection.
(ii) Let \(B|_{i,j}\) be the region of  that contains B:
that contains B:
by part (i). Let \(\mathbf {p}_k\) be the normal of a facet F of \(B|_{i,j}\) and \(\mathbf {x}\) be contained in the relative interior of F so that \(\mathbf {p}_k\cdot \mathbf {x}=0\). Since \(\mathbf {p}_i\) and \(\mathbf {p}_j\) are the vertices of \({{\,\mathrm{conv}\,}}(\ell )\), we have \(\mathbf {p}_k = \lambda _k \mathbf {p}_i +(1-\lambda _k)\mathbf {p}_j\), for some \(0 \le \lambda _k \le 1\). Then
As \(\mathbf {p}_i\!\!\cdot \mathbf {x}\le \!0\) and \(\mathbf {p}_j\!\!\cdot \mathbf {x}\le 0\), the above equality implies that \(\mathbf {p}_k\) must be \(\mathbf {p}_i\) or \(\mathbf {p}_j\).
3.3 Shards as Restricted Covectors
Let  be a tight hyperplane arrangement with respect to a base region B and
be a tight hyperplane arrangement with respect to a base region B and  be its associated affine point configuration. Every shard \(\Sigma \) of
be its associated affine point configuration. Every shard \(\Sigma \) of  has a corresponding unique join-irreducible region \(J_\Sigma \) [33, Proposition 9-7.8]. In the lattice of regions, \(J_\Sigma \) is the meet of all regions R such that
has a corresponding unique join-irreducible region \(J_\Sigma \) [33, Proposition 9-7.8]. In the lattice of regions, \(J_\Sigma \) is the meet of all regions R such that
The next lemma shows how \({{\,\mathrm{pre}\,}}(H_\Sigma )\) and \({{\,\mathrm{Sep}\,}}(J_\Sigma )\) yield a description of the shard as the intersection of half-spaces. It is originally stated for simplicial arrangements, though the same holds true for tight hyperplane arrangements.
Lemma 3.7
(see [31, Lemma 3.7]) A shard \(\Sigma \) has the following description:
To interpret shards on a hyperplane \(H_i\) as covectors, we focus on a certain subconfiguration containing \(\mathbf {p}_i\).
Definition 3.8
(Subconfiguration localized at a point). Let  . The subconfiguration
. The subconfiguration  of
of  localized at \(\mathbf {p}_i\) contains \(\mathbf {p}_i\) and the vertices of the convex hulls of lines of
localized at \(\mathbf {p}_i\) contains \(\mathbf {p}_i\) and the vertices of the convex hulls of lines of  that contain \(\mathbf {p}_i\) in their interior.
that contain \(\mathbf {p}_i\) in their interior.
Lemma 3.6 (ii) and Definition 2.17 imply the following lemma.
Lemma 3.9
The subconfiguration  satisfies
satisfies

Definition 3.10
(Shard covectors of a point). Let  . A shard covector of \(\mathbf {p}_i\) is a restricted covector
. A shard covector of \(\mathbf {p}_i\) is a restricted covector  with respect to
with respect to  such that
such that
-
\(\sigma ^i_j=*\) if and only if
 , and
, and -
the restriction of \(\sigma ^i\) to the subconfiguration
 is a covector with exactly one zero in position “i”.
is a covector with exactly one zero in position “i”.
Example 3.11
In Fig. 6, the left image illustrates the affine point configuration  for the rank-3 braid arrangement with 6 hyperplanes. The right image illustrates the subconfiguration of
for the rank-3 braid arrangement with 6 hyperplanes. The right image illustrates the subconfiguration of  localized at \(\mathbf {p}_6\),
localized at \(\mathbf {p}_6\),  .
.
There are two pairs of oppositely signed shard covectors of \(\mathbf {p}_6\):
It is possible to obtain these shard covectors by drawing a line through \(\mathbf {p}_6\) in  , and choosing a positive and a negative side. Rotating the line about \(\mathbf {p}_6\) in all possible directions, and recording the sign evaluations of the points in
, and choosing a positive and a negative side. Rotating the line about \(\mathbf {p}_6\) in all possible directions, and recording the sign evaluations of the points in  relative to the line exhausts all possibilities.
relative to the line exhausts all possibilities.
We now associate a restricted covector to each shard using the sign evaluation of vectors. Let \(\Sigma ^i\) be a shard contained in hyperplane \(H_i\), and let \(\mathbf {x}\in {{\,\mathrm{int}\,}}(\Sigma ^i)\). Using Lemmas 3.7 and 3.9, we get

Completing this sign evaluation to the configuration  , we get the restricted covector
, we get the restricted covector

This restricted covector is independent of the choice of vector \(\mathbf {x}\in {{\,\mathrm{int}\,}}(\Sigma ^i)\), thanks to Lemma 3.7, and only depends on the choice of base region B.
Theorem 3.12
Let  be a tight hyperplane arrangement with respect to a base region B. The map sending a shard \(\Sigma ^i\) to the shard covector \(\sigma ^i\) gives a bijection between the shards of
be a tight hyperplane arrangement with respect to a base region B. The map sending a shard \(\Sigma ^i\) to the shard covector \(\sigma ^i\) gives a bijection between the shards of  with base region B and the shard covectors of
with base region B and the shard covectors of  .
.
Proof
Injectivity. Suppose \(\sigma ^i = \theta ^i\) for two shards \(\Sigma ^i\) and \(\Theta ^i\), for some \(i\in [m]\). By the definition of \(\sigma ^i\) and \(\theta ^i\), the shard covectors are obtained from some points \(\mathbf {x}\in {{\,\mathrm{int}\,}}(\Sigma ^i)\) and \(\mathbf {y}\in {{\,\mathrm{int}\,}}(\Theta ^i)\) and
By Lemma 3.7, an H-description of the shard is given by the sign evaluation of any of its points in the relative interior with respect to the hyperplanes in \({{\,\mathrm{pre}\,}}(H_i)\). Because \(\Sigma ^i\) and \(\Theta ^i\) are both shards on hyperplane \(H_i\), and the sign evaluation of \(\mathbf {x}\) and \(\mathbf {y}\) agree on all normals in \({{\,\mathrm{pre}\,}}(H_i)\), \(\Sigma ^i\) and \(\Theta ^i\) must be the same.
Surjectivity. Let  be a shard covector with a unique zero at position \(i \in [m]\). Considered as a sign evaluation, there is an \(\mathbf {x}\in \mathbb {R}^d\) such that
be a shard covector with a unique zero at position \(i \in [m]\). Considered as a sign evaluation, there is an \(\mathbf {x}\in \mathbb {R}^d\) such that  . The linear hyperplane with normal \(\mathbf {x}\) separates the normal vectors in \({{\,\mathrm{pre}\,}}(H_i)\) as
. The linear hyperplane with normal \(\mathbf {x}\) separates the normal vectors in \({{\,\mathrm{pre}\,}}(H_i)\) as  dictates. Thus, \(\mathbf {x}\) is a point in the relative interior of a shard \(\Sigma ^i\) of \(H_i\) such that
dictates. Thus, \(\mathbf {x}\) is a point in the relative interior of a shard \(\Sigma ^i\) of \(H_i\) such that  .
.
By Theorem 3.12, there is a unique shard covector associated with every shard. We, therefore, use lowercase Greek letters \(\sigma ^i\) to denote the unique shard covector corresponding to a shard \(\Sigma ^i\).
Example 3.13
Consider the Coxeter arrangement \(A_2\) with three hyperplanes \(H_1, H_2, H_3\), and choose a base region B between \(H_1\) and \(H_2\) as represented in Fig. 7. Hyperplanes \(H_1\) and \(H_2\) are basic, giving shards \(\Sigma ^1\) and \(\Upsilon ^2\), and hyperplane \(H_3\) splits into two shards \(\Gamma ^3\) and \(\Theta ^3\). The affine point configuration  has three points on a line \(\mathbf {p}_1, \mathbf {p}_3, \mathbf {p}_2\), and admits exactly four shard covectors. The table shows the bijection between shards and shard covectors using the map of Theorem 3.12.
has three points on a line \(\mathbf {p}_1, \mathbf {p}_3, \mathbf {p}_2\), and admits exactly four shard covectors. The table shows the bijection between shards and shard covectors using the map of Theorem 3.12.
3.4 Forcing Relation on Covectors
In this section, we use Theorem 3.12 and interpret the shard digraph  using shard covectors of
using shard covectors of  . In Definition 2.18, the first condition to get an edge \(\Sigma ^i\rightarrow \Sigma ^j\) translates to the shard covectors of \(\mathbf {p}_j\) having a \(+\) or − at position “i”. The second condition requires one to interpret the dimension of intersection of two shards using shard covectors. To do so, we define line covectors of two hyperplanes.
. In Definition 2.18, the first condition to get an edge \(\Sigma ^i\rightarrow \Sigma ^j\) translates to the shard covectors of \(\mathbf {p}_j\) having a \(+\) or − at position “i”. The second condition requires one to interpret the dimension of intersection of two shards using shard covectors. To do so, we define line covectors of two hyperplanes.
Definition 3.14
(Line covector). Let  . A line covector of \(\ell \) is a covector
. A line covector of \(\ell \) is a covector  on
on  such that
such that

Line covectors record possible sign evaluations of non-zero points in the intersection of two hyperplanes with respect to  . They come in oppositely signed pairs which we denote by
. They come in oppositely signed pairs which we denote by  and
and  . In the case of rank-3 hyperplane arrangements, these covectors are actually cocircuits of the oriented matroid. For higher rank hyperplane arrangements, the set of 0-indices of a line covector gives a flat of rank 2 in the underlying matroid.
. In the case of rank-3 hyperplane arrangements, these covectors are actually cocircuits of the oriented matroid. For higher rank hyperplane arrangements, the set of 0-indices of a line covector gives a flat of rank 2 in the underlying matroid.
Example 3.15
(Example 3.11 continued) Let \(\ell =\{\mathbf {p}_1,\mathbf {p}_5,\mathbf {p}_6\}\). Since \(\mathbb {A}_B\) has dimension 2, the line \(\ell \) has exactly two line covectors. From Fig. 6, we deduce that the line covectors of \(\ell \) are

Lemma 3.16
Let  be an affine point configuration, \(1\le i<j\le m\), \(\ell \) be the line spanned by \(\mathbf {p}_i\) and \(\mathbf {p}_j\), and
be an affine point configuration, \(1\le i<j\le m\), \(\ell \) be the line spanned by \(\mathbf {p}_i\) and \(\mathbf {p}_j\), and  be a line covector of \(\ell \). The set
be a line covector of \(\ell \). The set  has dimension \(d-2\).
has dimension \(d-2\).
Proof
Let \(\mathbf {x}\in H_i \cap H_j\) with  . For any \(\mathbf {v}\in {{\,\mathrm{span}\,}}(\mathbf {n}_i,\mathbf {n}_j)^\perp \) and \(\varepsilon >0\), the kth entry of
. For any \(\mathbf {v}\in {{\,\mathrm{span}\,}}(\mathbf {n}_i,\mathbf {n}_j)^\perp \) and \(\varepsilon >0\), the kth entry of  is equal to
is equal to

When \(\varepsilon \) is chosen small enough, then

Thus 
Example 3.17
(Example 3.11 continued) Figure 8 shows a stereographic projection of  broken into shards. The shards \(\Theta ^{6,+}\) and \(\Sigma ^1 = H_1\) are thickened and one sees that \(H_1\) cuts \(H_6\). The shards \(\Sigma ^1\) and \(\Theta ^{6,+}\) intersect at a point so there is an oriented edge \(\Sigma ^1\rightarrow \Theta ^{6,+}\) in the shard digraph.
broken into shards. The shards \(\Theta ^{6,+}\) and \(\Sigma ^1 = H_1\) are thickened and one sees that \(H_1\) cuts \(H_6\). The shards \(\Sigma ^1\) and \(\Theta ^{6,+}\) intersect at a point so there is an oriented edge \(\Sigma ^1\rightarrow \Theta ^{6,+}\) in the shard digraph.
This fact translates to a property of the corresponding shards covectors \(\sigma ^{1}=(0,*,*,*,*,*)\) and \(\theta ^{6,+}=(+,*,-,+,-,0)\). Indeed, consider the line \(\ell =\{\mathbf {p}_1,\mathbf {p}_5,\mathbf {p}_6\}\) and the line covector  . Then
. Then  . For comparison,
. For comparison,  , and
, and  . Figure 9 illustrates the affine point configuration
. Figure 9 illustrates the affine point configuration  along with the three oriented lines describing the involved covectors.
along with the three oriented lines describing the involved covectors.
It is possible to interpret the fact that the two shards intersect at a point as follows. Apply a clockwise rotation to the line labeled \(\theta ^{6,+}\) about the point \(\mathbf {p}_6\) until it collides with the line corresponding to  . During the rotation, the line did not cross any points in
. During the rotation, the line did not cross any points in  . Similarly, applying the same with the line labeled \(\sigma ^1\) about \(\mathbf {p}_1\) does not cross any points in
. Similarly, applying the same with the line labeled \(\sigma ^1\) about \(\mathbf {p}_1\) does not cross any points in  .
.
The theorem below shows that the above equality is exactly the necessary and sufficient condition for the two involved shards to have an intersection of dimension \(d-2\).
Theorem 3.18
Let  be an affine point configuration, \(1\le i<j\le m\), and let \(\ell \) be the line spanned by \(\mathbf {p}_i\) and \(\mathbf {p}_j\). Furthermore, let \(\Sigma ^i \subseteq H_i\) and \({\Theta ^j \subseteq H_j}\) be two shards. The intersection \(\Sigma ^i \cap \Theta ^j\) has dimension \(d-2\) if and only if there exists a line covector
be an affine point configuration, \(1\le i<j\le m\), and let \(\ell \) be the line spanned by \(\mathbf {p}_i\) and \(\mathbf {p}_j\). Furthermore, let \(\Sigma ^i \subseteq H_i\) and \({\Theta ^j \subseteq H_j}\) be two shards. The intersection \(\Sigma ^i \cap \Theta ^j\) has dimension \(d-2\) if and only if there exists a line covector  such that
such that  .
.
Proof
Assume \(\dim (\Sigma ^i \cap \Theta ^j) = d-2\). Hence, there exists \(\mathbf {x}\in \Sigma ^i \cap \Theta ^j\) such that the sign evaluation  equals zero if and only if \(\mathbf {p}_k \in \ell \). Therefore,
equals zero if and only if \(\mathbf {p}_k \in \ell \). Therefore,  is a line covector of \(\ell \). If \(\mathbf {x}\) is in the boundary of \(\Sigma ^i\), then for
is a line covector of \(\ell \). If \(\mathbf {x}\) is in the boundary of \(\Sigma ^i\), then for  , either \({{\,\mathrm{sign}\,}}(\mathbf {x}\cdot \mathbf {p}_k) = {{\,\mathrm{sign}\,}}(\mathbf {z}\cdot \mathbf {p}_k)\) or \({{\,\mathrm{sign}\,}}( \mathbf {x}\cdot \mathbf {p}_k) = 0\). As
, either \({{\,\mathrm{sign}\,}}(\mathbf {x}\cdot \mathbf {p}_k) = {{\,\mathrm{sign}\,}}(\mathbf {z}\cdot \mathbf {p}_k)\) or \({{\,\mathrm{sign}\,}}( \mathbf {x}\cdot \mathbf {p}_k) = 0\). As  equals zero if and only if \(\mathbf {p}_k \in \ell \),
equals zero if and only if \(\mathbf {p}_k \in \ell \),  for all k such that
for all k such that  . Likewise,
. Likewise,  for all k such that
for all k such that  . Thus,
. Thus,

Assume now that there exists a line covector  such that
such that  . Let
. Let  . By Lemma 3.16, \(\dim (S)=d-2\). Let \(\mathbf {x}\in S\), \(\mathbf {y}\in {{\,\mathrm{int}\,}}(\Sigma ^i)\), and \(\mathbf {z}\in {{\,\mathrm{int}\,}}(\Theta ^j)\). As
. By Lemma 3.16, \(\dim (S)=d-2\). Let \(\mathbf {x}\in S\), \(\mathbf {y}\in {{\,\mathrm{int}\,}}(\Sigma ^i)\), and \(\mathbf {z}\in {{\,\mathrm{int}\,}}(\Theta ^j)\). As  , \({{\,\mathrm{sign}\,}}(\mathbf {x}\cdot \mathbf {p}_k) = {{\,\mathrm{sign}\,}}(\mathbf {y}\cdot \mathbf {p}_k)\) for all
, \({{\,\mathrm{sign}\,}}(\mathbf {x}\cdot \mathbf {p}_k) = {{\,\mathrm{sign}\,}}(\mathbf {y}\cdot \mathbf {p}_k)\) for all  . For \(\mathbf {p}_k \in \ell \), we have \(\mathbf {x}\cdot \mathbf {p}_k = 0\). For \(0 \le \lambda \le 1\), let \(\mathbf {m}_\lambda = (1-\lambda )\mathbf {y}+ \lambda \mathbf {x}\). Then
. For \(\mathbf {p}_k \in \ell \), we have \(\mathbf {x}\cdot \mathbf {p}_k = 0\). For \(0 \le \lambda \le 1\), let \(\mathbf {m}_\lambda = (1-\lambda )\mathbf {y}+ \lambda \mathbf {x}\). Then  for all k such that
for all k such that  , and \(\lambda \in [0,1)\). This shows that \(\mathbf {m}_\lambda \in \Sigma ^i\) for all \(\lambda \in [0,1)\), and thus \(\mathbf {x}\) is contained in \(\Sigma ^i\). A similar argument with \(\mathbf {z}\) shows that \(\mathbf {x}\) is in \(\Theta ^j\).
, and \(\lambda \in [0,1)\). This shows that \(\mathbf {m}_\lambda \in \Sigma ^i\) for all \(\lambda \in [0,1)\), and thus \(\mathbf {x}\) is contained in \(\Sigma ^i\). A similar argument with \(\mathbf {z}\) shows that \(\mathbf {x}\) is in \(\Theta ^j\).
Corollary 3.19
There is a directed arrow \(\Sigma ^i \rightarrow \Theta ^j\) in  if and only if \(\theta ^j_i\in \{-,+\}\) and there exists a line covector
if and only if \(\theta ^j_i\in \{-,+\}\) and there exists a line covector  such that
such that  .
.
3.5 Examples of Obstruction to Congruence Normality
Example 3.20
(Example 2.13 continued). The normal vectors \(\{\mathbf {n}_i\}_{i\in [10]}\) for this configuration can be chosen as follows. Let \(\tau = \frac{1 + \sqrt{5}}{2}\) and \( \mathbf {n}_1=(0, 1, 0), \mathbf {n}_2=(1, 0, 0), \mathbf {n}_3=(1, 1, 0), \mathbf {n}_4=(1, 1, 1), \mathbf {n}_5=(\tau +1, \tau , \tau ), \mathbf {n}_6=(\tau +1, \tau +1, 1), \mathbf {n}_7=(\tau +1, \tau +1, \tau ), \mathbf {n}_8=(2\tau ,2\tau ,\tau ), \mathbf {n}_9=(2\tau +1,2\tau ,\tau ), \mathbf {n}_{10}=(2\tau +2, 2\tau +1, \tau +1)\). Let B be the base region containing the vector \(\mathbf {v}= (-1,-1,-2)\). Figure 10 illustrates  along with four lines describing the shard covectors
along with four lines describing the shard covectors
Let \(\ell _1=\{\mathbf {p}_2,\mathbf {p}_8,\mathbf {p}_9\},\ell _2=\{\mathbf {p}_1,\mathbf {p}_6,\mathbf {p}_9\},\ell _3=\{\mathbf {p}_5,\mathbf {p}_6,\mathbf {p}_{10}\},\) and \(\ell _4=\{\mathbf {p}_1,\mathbf {p}_8,\mathbf {p}_{10}\}\) and consider the four line covectors

As \(\upsilon ^9\) has a “\(+\)” in position 8, \(H_8\) cuts \(H_9\). Furthermore, one computes that  . By Corollary 3.19, there is a directed arrow \(\Theta ^9\rightarrow \Upsilon ^9\) in
. By Corollary 3.19, there is a directed arrow \(\Theta ^9\rightarrow \Upsilon ^9\) in  . Similar computations reveal that \(\theta ^8 \rightarrow \upsilon ^9 \rightarrow \sigma ^6 \rightarrow \xi ^{10} \rightarrow \theta ^8\) is a cycle in
. Similar computations reveal that \(\theta ^8 \rightarrow \upsilon ^9 \rightarrow \sigma ^6 \rightarrow \xi ^{10} \rightarrow \theta ^8\) is a cycle in  . Thus, the poset of regions of
. Thus, the poset of regions of  with respect to the base region B is not congruence normal.
with respect to the base region B is not congruence normal.
Example 3.21
Removing the hyperplane \(H_4\) from the arrangement  and taking the base region that contains the vector \(\mathbf {v}=(-1,-1,2)\), one obtains a non-simplicial, tight (hence, semidistributive) poset of regions with 52 regions that is not congruence normal as the cycle \(\theta ^8 \rightarrow \upsilon ^9 \rightarrow \sigma ^6 \rightarrow \xi ^{10} \rightarrow \theta ^8\) still occurs in the shard digraph. Figure 11 illustrates the resulting affine point configuration. Is there a tight poset of regions which is not congruence normal with at most 8 hyperplanes?
and taking the base region that contains the vector \(\mathbf {v}=(-1,-1,2)\), one obtains a non-simplicial, tight (hence, semidistributive) poset of regions with 52 regions that is not congruence normal as the cycle \(\theta ^8 \rightarrow \upsilon ^9 \rightarrow \sigma ^6 \rightarrow \xi ^{10} \rightarrow \theta ^8\) still occurs in the shard digraph. Figure 11 illustrates the resulting affine point configuration. Is there a tight poset of regions which is not congruence normal with at most 8 hyperplanes?
Example 3.22
It is possible to have cycles in  while
while  is acyclic, settling the question raised in [30, p. 203]. Figure 12 shows the affine point configuration of arrangement
is acyclic, settling the question raised in [30, p. 203]. Figure 12 shows the affine point configuration of arrangement  with respect to the base region that contains the vector \(\approx (0.38, 2.85, -7.85)\). There is a cycle \(H_1 \rightarrow H_4 \rightarrow H_7 \rightarrow H_1\) in
with respect to the base region that contains the vector \(\approx (0.38, 2.85, -7.85)\). There is a cycle \(H_1 \rightarrow H_4 \rightarrow H_7 \rightarrow H_1\) in  . However, this cycle does not lead to any cycle among shards included in these three hyperplanes as
. However, this cycle does not lead to any cycle among shards included in these three hyperplanes as  was computed to be acyclic in this case. This can be seen geometrically as follows. Apply a rotation to the line spanned by the points 1 and 2 about the point 4 until it collides with the line spanned by the points 4 and 14. During the rotation (be it clockwise or counterclockwise) the line crossed points in
was computed to be acyclic in this case. This can be seen geometrically as follows. Apply a rotation to the line spanned by the points 1 and 2 about the point 4 until it collides with the line spanned by the points 4 and 14. During the rotation (be it clockwise or counterclockwise) the line crossed points in  . This means that a shard on hyperplane 4 intersecting with a shard on hyperplane 1 along a face of dimension \(d-2\) can not have an intersection with a shard on hyperplane 7 that has dimension \(d-2\).
. This means that a shard on hyperplane 4 intersecting with a shard on hyperplane 1 along a face of dimension \(d-2\) can not have an intersection with a shard on hyperplane 7 that has dimension \(d-2\).
4 Congruence Normality of Simplicial Hyperplane Arrangements
As the number of regions of a rank-three hyperplane arrangement grows quadratically with the number of hyperplanes, its poset of regions becomes costly to construct in practice when the number of hyperplanes gets large. Consequently, checking if a given poset of regions is obtainable through doublings of convex sets becomes impracticable. If one uses shards as geometric objects to determine congruence normality, then one needs to determine polyhedral cones contained in each hyperplane and the dimensions of intersection for pairs of shards. In contrast, the combinatorial methods developed in Sect. 3 make the determination of congruence normality for posets of regions of rank-3 hyperplane arrangements tractable and could be extended to higher dimensions given a method for determining the covectors of the oriented matroid. Additionally, the oriented matroid approach makes it possible and natural to check congruence normality for non-realizable oriented matroids.
One of the motivations for studying congruence normality is to better understand simplicial hyperplane arrangements. In rank 3, the number of simplicial hyperplane arrangements is unknown [9, 23]. So far, three infinite families and 95 sporadic arrangements have been found. It is conjectured that there are only finitely many sporadic arrangements. The largest sporadic arrangement found so far has 37 hyperplanes. In this section, we apply our reformulation of shards as shard covectors to classify which of the known simplicial hyperplane arrangements of rank 3 are congruence normal. This verification was carried out using Sage [34]. The computations took around 18 hours on 8 Intel Cores (i7-7700 @3.60 Hz). The verification for each poset of regions was computed independently, for example, the cocircuits were recomputed for each reorientation of the set of normals, but the computations of intersections on covectors were cached. The computation could be further improved by applying the reorientation on cocircuits directly to avoid recomputing them.
Our results are summarized in Table 1. We use the following notation:  denotes the ith hyperplane arrangement with m hyperplanes and r regions. The hyperplane arrangement in the ith infinite family with m hyperplanes is denoted
denotes the ith hyperplane arrangement with m hyperplanes and r regions. The hyperplane arrangement in the ith infinite family with m hyperplanes is denoted  , see Sect. 4.3. We refer to congruence normality using the acronym CN and NCN for non-congruence normality. The normals of the 119 arrangements from the known sporadic arrangements and two of the infinite families are listed in Appendix A and the corresponding wiring diagrams are listed in Appendix B. The list includes the sporadic arrangements and the arrangements from the infinite families with at most 37 hyperplanes.
, see Sect. 4.3. We refer to congruence normality using the acronym CN and NCN for non-congruence normality. The normals of the 119 arrangements from the known sporadic arrangements and two of the infinite families are listed in Appendix A and the corresponding wiring diagrams are listed in Appendix B. The list includes the sporadic arrangements and the arrangements from the infinite families with at most 37 hyperplanes.
Table 1 provides material to check the veracity of [27, Conjecture 145], which postulates the existence of certain polytopes for tight congruence normal arrangements. Section 4.1 looks at the arrangements that are always CN, Sect. 4.2 at the arrangements that are sometimes CN, and Sect. 4.4 at the arrangements that are never CN. In Sect. 4.5, we finish by discussing these results and compiling-related questions.
4.1 Always CN Simplicial Arrangements
Fifty-five of the of 119 arrangements are congruence normal, that is, for any choice of base region, the poset of regions is congruence normal, see Table 2.
Fifty-three of these arrangements come from finite Weyl groupoids of rank 3 [10]. Finite Weyl groupoids correspond to (generalized) crystallographic root systems. In the present context, affine point configurations  play the role of these root systems. A root system is crystallographic if there exists a choice of normals \(\{\mathbf {n}_i\}_{i\in [m]}\) for the hyperplanes such that for any base region, all normals are integral linear combinations of normals to the basic hyperplanes [6, Section 1]. Given a base region B, denote the set of rays of
play the role of these root systems. A root system is crystallographic if there exists a choice of normals \(\{\mathbf {n}_i\}_{i\in [m]}\) for the hyperplanes such that for any base region, all normals are integral linear combinations of normals to the basic hyperplanes [6, Section 1]. Given a base region B, denote the set of rays of  by \(\Delta \) and call the elements of
by \(\Delta \) and call the elements of  the positive roots. A positive root
the positive roots. A positive root  is constructible if
is constructible if
where  . We call
. We call  additive if every positive root in
additive if every positive root in  is constructible. If
is constructible. If  is additive, then it is possible to define the root poset
is additive, then it is possible to define the root poset  by
by
The following is a fundamental result about finite Weyl groupoids.
Theorem 4.1
([6, Corollary 5.6]. and [10, Theorem 2.10]) A simplicial arrangement  corresponds to a finite Weyl groupoid if and only if
corresponds to a finite Weyl groupoid if and only if  is additive for every choice of base region B.
is additive for every choice of base region B.
Theorem 4.1 leads directly to the following theorem, which provides a new proof that finite Coxeter arrangements are congruence normal [5, Theorem 6].
Theorem 4.2
Let  be the hyperplane arrangement of a finite Weyl groupoid \(\mathcal {W}\). For any choice of base region B, the lattice of regions
be the hyperplane arrangement of a finite Weyl groupoid \(\mathcal {W}\). For any choice of base region B, the lattice of regions  is congruence normal.
is congruence normal.
Proof
Via the contrapositive statement, having a cycle in the graph  is a necessary condition for
is a necessary condition for  not to be congruence normal. By Corollary 2.5 in [10], such a cycle between hyperplanes yields a cycle in the order defining the root poset of
not to be congruence normal. By Corollary 2.5 in [10], such a cycle between hyperplanes yields a cycle in the order defining the root poset of  . Hence, when
. Hence, when  is not congruence normal, the positive roots
is not congruence normal, the positive roots  do not lead to a root poset. Thus,
do not lead to a root poset. Thus,  cannot be additive.
cannot be additive.
Remark 4.3
There are arrangements such that  is additive, but there is no relation between \(\mathbf {p}_j\) and \(\mathbf {p}_i\) in the root poset for two positive roots \(\mathbf {p}_j\) and \(\mathbf {p}_i\) with \(H_i \in {{\,\mathrm{pre}\,}}(H_j)\). The additional assumptions that the arrangement is simplicial and
is additive, but there is no relation between \(\mathbf {p}_j\) and \(\mathbf {p}_i\) in the root poset for two positive roots \(\mathbf {p}_j\) and \(\mathbf {p}_i\) with \(H_i \in {{\,\mathrm{pre}\,}}(H_j)\). The additional assumptions that the arrangement is simplicial and  is additive with respect to every base region ensure the relation exists.
is additive with respect to every base region ensure the relation exists.
There are two additional CN arrangements that do not stem from finite Weyl groupoids. Arrangement  is the Coxeter arrangement for the Coxeter group \(H_3\) and arrangement
is the Coxeter arrangement for the Coxeter group \(H_3\) and arrangement  is its point-line dual. As discussed in [13], there is a root poset for \(H_3\) supporting the fact that its arrangement is always congruence normal. The dual arrangement
is its point-line dual. As discussed in [13], there is a root poset for \(H_3\) supporting the fact that its arrangement is always congruence normal. The dual arrangement  is also always congruence normal, as we verified directly. Is there a proof of congruence normality for
is also always congruence normal, as we verified directly. Is there a proof of congruence normality for  using duality with \(H_3\)? Example 3.22 shows that having a root poset structure on
using duality with \(H_3\)? Example 3.22 shows that having a root poset structure on  is not necessary for
is not necessary for  to be congruence normal.
to be congruence normal.
4.2 Simplicial Arrangements That Are Sometimes Congruence Normal
Sixty-one of the 119 arrangements are congruence normal for some base regions and not congruence normal for others, see Table 3. Among them is the arrangement  which appeared in Example 2.13.
which appeared in Example 2.13.
Reading proved that the poset of regions of a supersolvable hyperplane arrangements is congruence normal with respect to a canonical base region [30, Theorem 1]. In rank 3, the infinite families are exactly the irreducible supersolvable ones [12, Theorem 1.2]. However, we show below that  with \(m\ge 10\) and
with \(m\ge 10\) and  with \(m\ge 17\) always have a base region for which the associated lattice of regions is not congruence normal. For
with \(m\ge 17\) always have a base region for which the associated lattice of regions is not congruence normal. For  with \(m \le 8\) and
with \(m \le 8\) and  with \(m \le 13\), the posets of regions are always congruence normal, see Sect. 4.1.
with \(m \le 13\), the posets of regions are always congruence normal, see Sect. 4.1.
4.3 Congruence Normality for the Infinite Families
There are three infinite families of rank-3 simplicial hyperplane arrangements [22]. The first family,  with \(m \ge 3\) is the family of near-pencils in the projective plane with m hyperplanes. The second family,
with \(m \ge 3\) is the family of near-pencils in the projective plane with m hyperplanes. The second family,  , for even \(m \ge 6\) consists of the hyperplanes defined by the edges of the regular \(\frac{m}{2}\)-gon and each of its \(\frac{m}{2}\) lines of symmetry. The third family,
, for even \(m \ge 6\) consists of the hyperplanes defined by the edges of the regular \(\frac{m}{2}\)-gon and each of its \(\frac{m}{2}\) lines of symmetry. The third family,  , for \(m=4k+1\), \(k\ge 2\), is obtained from
, for \(m=4k+1\), \(k\ge 2\), is obtained from  by adding the line at infinity. Examples of these families are illustrated in Fig. 13.
by adding the line at infinity. Examples of these families are illustrated in Fig. 13.
Theorem 4.4
The near-pencil arrangements of  are congruence normal.
are congruence normal.
Proof
There is exactly one rank-2 subarrangement with at least three hyperplanes. Thus, for any choice of base region, the length of any path in the directed graph on shards is at most one, so there are no cycles.
Theorem 4.5
The second family  is sometimes congruence normal for \(m \ge 10\).
is sometimes congruence normal for \(m \ge 10\).
Proof
In rank 3, the infinite families are exactly the irreducible supersolvable ones, thus there exists a canonical choice of base region such that the poset of regions is congruence normal [12, Theorem 1.2]. On the other hand, with respect to a certain choice of base region, there is a guaranteed four cycle in the shards as demonstrated in Fig. 14. The figure shows the arrangement on two projective planes and how some of the hyperplanes intersect at infinity. To represent the central, three-dimensional hyperplane arrangement, we intersect it with the unit sphere at the origin, and use two centrally symmetric planar charts, giving the left and the right sides of the image, which are glued together in the middle by the hyperplane (a dotted line in this case) at infinity. Let the base region be bounded by \(\mathbf {e}_1\), \(\mathbf {e}_2\), and \(\mathbf {r}_2\). At point 1, the hyperplane \(\mathbf {e}_5\) is cut by \(\mathbf {r}_5\). At point 2, the hyperplane \(\mathbf {r}_6\) is cut by \(\mathbf {e}_5\). At point 3, the hyperplane \(\mathbf {e}_4\) is cut by \(\mathbf {r}_6\). At point 4, the hyperplane \(\mathbf {r}_5\) is cut by \(\mathbf {e}_4\). Thus, there is a cycle in the shard digraph. Adapting this procedure when \(m\ge 14\) similarly provides a 4-cycle for every member of  .
.
Theorem 4.6
The third family  is sometimes congruence normal for \(m \ge 17\).
is sometimes congruence normal for \(m \ge 17\).
Proof
The proof is similar to that of Theorem 4.5. For \(m \ge 17\), a four-cycle among shards still occurs, and its location relative to the base region is illustrated in Fig. 15 for \(m = 17\). The line at infinity is included in these arrangements, and one of the intersection points in the cycle occurs in a rank-2 subarrangement that includes the hyperplane at infinity. Relative to the plane graph, the cycle involves the same description as a embedded cycle for the family  .
.
4.4 Never CN Simplicial Arrangements
Three of the known simplicial arrangements of rank 3 are never congruence normal, see Table 4. That is, there is no choice of base region such that the lattice of regions is congruence normal. The first arrangement is an arrangement with 22 hyperplanes with normals related to \(\sqrt{5}\), see Fig. 16. The second arrangement has 25 hyperplanes with normals related to \(\sqrt{5}\) and is shown in Fig. 17. The third arrangement is the new sporadic arrangement found in [9]. It is the only known arrangement with 35 hyperplanes and is illustrated in Fig. 18. We are not aware of any geometric explanation for the provenance of these arrangements and why they are never congruence normal.
4.5 Observations and Consequences
We make a few remarks on the verification and its implications. The number of shards do not depend on the choice of base region: indeed, [27, Lemma 146] says that in a simplicial arrangement, the number of shards is the number of rays in the arrangement minus the dimension. So, computing the number of shards leads to the number of facets of the corresponding simple zonotope. For rank-3 simplicial arrangements, the number of shards is one less than half the number of regions. For example, the arrangements  and
and  have different numbers of hyperplanes but the same number of shards and regions.
have different numbers of hyperplanes but the same number of shards and regions.
Finally, we end with questions that arose from this investigation.
- Question 1:
-
What is the relationship between polygonal and semidistributive lattices?
- Question 2:
-
Is there a hyperplane arrangement with at most 8 hyperplanes that yields a tight poset of regions which is not congruence normal?
- Question 3:
-
Is there a proof of congruence normality for
 using duality with \(H_3\)?
using duality with \(H_3\)? - Question 4:
-
Is there a geometric explanation for the provenance of the three arrangements that are never congruence normal? Are the posets of regions all isomorphic?
- Question 5:
-
Reading used “signed subsets” to describe when an edge occurs between two shards in type A and B [31]. Can shard covectors be used in conjunction with positive roots to describe forcing on shards?
- Question 6:
-
Apart from being dual to 2-neighborly, what can be said about the combinatorial types of the regions in a tight hyperplane arrangement?
5 Invariants of Rank-3 Simplicial Hyperplane Arrangements
Table 5 gives a list of invariants for the simplicial hyperplane arrangements of rank 3 with at most 37 hyperplanes (excluding the reducible near-pencil arrangements).
The f-vector consists of the numbers of 0-, 1-, and 2-cells in the corresponding CW-complex, i.e. \(f_3\) is the number of chambers. The t-vector contains the numbers \(t_i\) of vertices which lie on exactly i lines; the r-vector contains the numbers \(r_i\) of lines on which exactly i vertices lie. The automorphism groups of the CW-complexes are listed in the column AG, the automorphism groups of the matroids are listed in the column AGM; a pair (a, b) represents the bth group of order a in the database of small groups (as included for example in the system GAP [20]). In the column EXP, we list the roots of the characteristic polynomials of the arrangements when they are all integers. The column “domain” contains the minimal field of definition for a realization of the matroid of the arrangement in characteristic zero (as computed in [7]): \(\mathbb {Z}\) stands for a crystallographic arrangement (which defines a Weyl groupoid). The other domains are
References
Kira Adaricheva and James B. Nation, Classes of semidistributive lattices, Lattice theory: special topics and applications. Vol. 2, Birkhäuser/Springer, Cham, 2016, pp. 59–101.
Garrett Birkhoff, On the combination of subalgebras, Math. Proc. Combridge Philos. Soc. 29 (1933), no. 4, 441–464.
Anders Björner, Paul H. Edelman, and Günter M. Ziegler, Hyperplane arrangements with a lattice of regions, Discrete Comput. Geom. 5 (1990), no. 3, 263–288.
Anders Björner, Michel Las Vergnas, Bernd Sturmfels, Neil White, and Günter M. Ziegler, Oriented matroids, second ed., Encyclopedia of Mathematics and its Applications, vol. 46, Cambridge University Press, Cambridge, 1999.
Nathalie Caspard, Claude Le Conte de Poly-Barbut, and Michel Morvan, Cayley lattices of finite Coxeter groups are bounded, Adv. in Appl. Math. 33 (2004), no. 1, 71–94.
Michael Cuntz, Crystallographic arrangements: Weyl groupoids and simplicial arrangements, Bull. Lond. Math. Soc. 43 (2011), no. 4, 734–744.
Michael Cuntz, Minimal fields of definition for simplicial arrangements in the real projective plane, Innov. Incidence Geom. 12 (2011), 49–60.
Michael Cuntz, Simplicial arrangements with up to 27 lines, Discrete Comput. Geom. 48 (2012), no. 3, 682–701.
Michael Cuntz, A greedy algorithm to compute arrangements of lines in the projective plane, preprint, arXiv:2006.14431 (2020), 15 pp.
Michael Cuntz and István Heckenberger, Finite Weyl groupoids of rank three, Trans. Amer. Math. Soc. 364 (2012), no. 3, 1369–1393.
Michael Cuntz and István Heckenberger, Finite Weyl groupoids, J. Reine Angew. Math. 702 (2015), 77–108.
Michael Cuntz and Paul Mücksch, Supersolvable simplicial arrangements, Adv. in Appl. Math. 107 (2019), 32–73.
Michael Cuntz and Christian Stump, On root posets for noncrystallographic root systems, Math. Comp. 84 (2015), no. 291, 485–503.
Alan Day, Characterizations of finite lattices that are bounded-homomorphic images of sublattices of free lattices, Canad. J. Math. 31 (1979), no. 1, 69–78.
Alan Day, Congruence normality: the characterization of the doubling class of convex sets, Algebra Universalis 31 (1994), no. 3, 397–406.
Jesús A. De Loera, Jörg Rambau, and Francisco Santos, Triangulations, Algorithms and Computation in Mathematics, vol. 25, Springer-Verlag, Berlin, 2010.
Aram Dermenjian, Christophe Hohlweg, Thomas McConville, and Vincent Pilaud, The facial weak order on hyperplane arrangements, arXiv:1910.03511 (2019)
Sophia Elia and Jean-Philippe Labbé, Congruence normality for hyperplane arrangements, https://github.com/sophiasage/cn_hyperarr (2020), version 0.0.1.
Nenosuke Funayama and Tadasi Nakayama, On the distributivity of a lattice of lattice-congruences, Proc. Imp. Acad. Tokyo 18 (1942), 553–554.
The GAP Group, GAP – Groups, Algorithms, and Programming, Version 4.11.0, 2020.
Winfried Geyer, The generalized doubling construction and formal concept analysis, Algebra Universalis 32 (1994), no. 3, 341–367.
Branko Grünbaum, Arrangements of hyperplanes, Proceedings of the Second Louisiana Conference on Combinatorics, Graph Theory and Computing (Louisiana State Univ., Baton Rouge, La., 1971), 1971, pp. 41–106.
Branko Grünbaum, A catalogue of simplicial arrangements in the real projective plane, Ars Math. Contemp. 2 (2009), no. 1, 1–25.
István Heckenberger, The Weyl groupoid of a Nichols algebra of diagonal type, Invent. Math. 164 (2006), no. 1, 175–188.
István Heckenberger and Volkmar Welker, Geometric combinatorics of Weyl groupoids, J. Algebraic Combin. 34 (2011), no. 1, 115–139.
Christophe Hohlweg, Carsten E. M. C. Lange, and Hugh Thomas, Permutahedra and generalized associahedra, Adv. Math. 226 (2011), no. 1, 608–640.
Arnau Padrol, Vincent Pilaud, and Julian Ritter, Shard polytopes, preprint, arXiv:2007.01008 (July 2020), 70 pp.
Vincent Pilaud and Francisco Santos, Quotientopes, Bull. Lond. Math. Soc. 51 (2019), no. 3, 406–420.
Alexander Postnikov, Permutohedra, associahedra, and beyond, Int. Math. Res. Not. (2009), no. 6, 1026–1106.
Nathan Reading, Lattice and order properties of the poset of regions in a hyperplane arrangement, Algebra Universalis 50 (2003), no. 2, 179–205.
Nathan Reading, Lattice congruences of the weak order, Order 21 (2004), no. 4, 315–344 (2005).
Nathan Reading, Cambrian lattices, Adv. Math. 205 (2006), no. 2, 313–353.
Nathan Reading, Lattice theory of the poset of regions, Lattice theory: special topics and applications. Vol. 2, Birkhäuser/Springer, Cham, 2016, pp. 399–487.
The Sage Developers, Sagemath, the Sage Mathematics Software System (Version 9.1), 2020, https://www.sagemath.org.
Günter M. Ziegler, Lectures on polytopes, GTM, vol. 152, Springer-Verlag, New York, 1995.
Acknowledgements
The authors would like to express their gratitude to Vincent Pilaud and Julian Ritter for important discussions leading to the results in this paper. Additionally, we would like to thank the two referees for their helpful comments.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Nathan Williams
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
S. Elia: With the support of the Research Training Group 2434 “Facets of Complexity”. J.-P. Labbé: With the support of the DFG Collaborative Research Center TRR 109 “Discretization in Geometry and Dynamics”.
Appendices
Appendix A: Tables of Normals
Tables 6, 7, 8, 9, 10, 11, 12, 13, and 14 give the normals for the simplicial hyperplane arrangements of rank 3 with at most 37 hyperplanes, excluding the reducible near-pencil arrangements. We use the notation  to indicate the ith hyperplane arrangement with m hyperplanes and r regions. We use the following algebraic numbers:
to indicate the ith hyperplane arrangement with m hyperplanes and r regions. We use the following algebraic numbers:
The normals for the crystallographic arrangements and their orderings are chosen in a canonical way: we chose the root system of the chamber which is lexicographically the smallest one including those with permuted coordinates. The normals for each arrangement are also ordered lexicographically. This is why we need permutations in the list of wiring diagrams in Appendix B. Although most of these simplicial arrangements are presented in Grünbaum’s catalogue [23], it requires some work to extract the normals from his pictures. One can for example obtain a realization using the matroid structure as performed in [7]. The reader interested to use the normals is invited to use the LaTeX source to extract the data. Alternatively, one may use the Sage-package CN-HyperArr [18].
Appendix B: Wiring Diagrams
In this section, we reproduce wiring diagrams that correspond to the oriented matroids defined by the irreducible simplicial arrangements of rank 3. A wiring diagram consists of a sequence of moves between wires in such a way that each pair of wires meets exactly once in some move (see, for example, [4] for details). Figure 19 shows an example: the wires in this picture correspond to the lines of the arrangement  . The moves are the intersection points. To encode the information of the moves it suffices to list for each intersection point the first and last label of the bundle of wires which meet. Thus, in this example, the moves begin with (11, 12), (3, 4), (21, 22), (12, 16), (16, 18) and so on. The tables in the appendix contain such a description for each known irreducible simplicial arrangement with up to 37 lines (Table 15). The first sequence is a bijection between these labels and the normals of Appendix A.
. The moves are the intersection points. To encode the information of the moves it suffices to list for each intersection point the first and last label of the bundle of wires which meet. Thus, in this example, the moves begin with (11, 12), (3, 4), (21, 22), (12, 16), (16, 18) and so on. The tables in the appendix contain such a description for each known irreducible simplicial arrangement with up to 37 lines (Table 15). The first sequence is a bijection between these labels and the normals of Appendix A.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cuntz, M., Elia, S. & Labbé, JP. Congruence Normality of Simplicial Hyperplane Arrangements via Oriented Matroids. Ann. Comb. 26, 1–85 (2022). https://doi.org/10.1007/s00026-021-00555-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00026-021-00555-2
Keywords
- Simplicial hyperplane arrangements
- Poset of regions
- Congruence normality and uniformity
- Covectors
- Shards


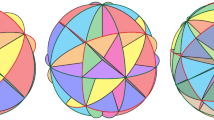


 is tight with respect to B, then
is tight with respect to B, then  is a lattice [
is a lattice [ is simplicial, then
is simplicial, then  is tight [
is tight [


 whose lattice of regions with the marked base region is not congruence normal
whose lattice of regions with the marked base region is not congruence normal
 with respect to the dotted region
with respect to the dotted region
 are in bijection with the rank-2 sub- arrangements of
are in bijection with the rank-2 sub- arrangements of  .
. , and
, and is a covector with exactly one zero in position “i”.
is a covector with exactly one zero in position “i”.
 for the rank-3 braid arrangement and the subconfiguration
for the rank-3 braid arrangement and the subconfiguration  localized at
localized at 

 shown via stereographic projection
shown via stereographic projection
 and hyperplanes describing the covectors
and hyperplanes describing the covectors  , where
, where 



 with respect to the base region containing
with respect to the base region containing 

 from
from  whose lattice of regions with the marked base region is not congruence normal
whose lattice of regions with the marked base region is not congruence normal
 from
from  whose lattice of regions with the marked base region is not congruence normal
whose lattice of regions with the marked base region is not congruence normal
 . Three points are not shown and can be obtained by continuing the line segments
. Three points are not shown and can be obtained by continuing the line segments
 . Three points are not shown and can be obtained by continuing the line segments
. Three points are not shown and can be obtained by continuing the line segments
 . Three points are not shown and can be obtained by continuing the line segments
. Three points are not shown and can be obtained by continuing the line segments using duality with
using duality with 