Simplicial Arrangements with up to 27 Lines

Abstract

We compute all isomorphism classes of simplicial arrangements in the real projective plane with up to 27 lines. It turns out that Grünbaum’s catalogue is complete up to 27 lines except for four new arrangements with 22, 23, 24, 25 lines, respectively. As a byproduct we classify simplicial arrangements of pseudolines with up to 27 lines. In particular, we disprove Grünbaum’s conjecture about unstretchable arrangements with at most 16 lines, and prove the conjecture that any simplicial arrangement with at most 14 pseudolines is stretchable.

1 Introduction

A simplicial arrangement is a finite set $\mathcal {A}=\{H_{1},\ldots,H_{n}\}$ of hyperplanes in ℝ^r such that the connected components of $\mathbb {R}^{r}\backslash\bigcup_{H\in \mathcal {A}}H$ are simplicial cones (compare [11, Definition 5.14]). For r=3, it may be visualized as a triangulation of the plane by lines (for example Fig. 1). The classification of simplicial arrangements is still an open problem. There is an impressive catalogue [7, 9] of the known simplicial arrangements in dimension three: the many sporadic cases are probably the main reason why a classification appears to be so difficult (see Conjecture 1.3).

Fig. 1

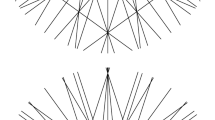
A new simplicial arrangement with 25 lines. The symbol “∞” stands for the line at infinity; removing the thicker lines gives further new simplicial arrangements with 22, 23 and 24 lines, respectively. See Sect. 5.5 for explicit coordinates

But let us assume that we have some theorem stating that a given catalogue is complete. Then it would be desirable to find a short proof. However, it is possible that a shortest proof of such a theorem is very long, so long that it would take several thousand pages to print it. In such a situation we nowadays take advantage of a computer: if the proof consists of a case-by-case analysis, i.e. we have to comb through a large tree with branches mostly leading to contradictions, then a computer is exactly the right tool to use.

In a previous work [3], together with Heckenberger we have classified the large class of crystallographic arrangements (see [5] for a definition). The method used there is an algorithm which enumerates them all. This algorithm terminates because it exploits several strong theorems. But still, a computer has to check billions of branches of the enumerating tree. We do not claim that a short proof does not exist, but any other proof would need to address the large number of sporadic arrangements arising here.

The algorithm we propose does not appear to have polynomial runtime in the number of lines of the arrangement.¹ However, since it is conjectured that the largest sporadic simplicial arrangement has 37 lines, one idea for a classification could be to determine all the simplicial arrangement with up to 37 lines, and then prove in some other way that any simplicial arrangement with more than 37 lines belongs to one of the infinite series. With this plan in mind, we are talking about algorithms with constant runtime, and thus we “only” need to make this constant small enough.

We should also note here that although we concentrate on the case of dimension three (or the projective plane), I believe that one can deduce a complete classification for all dimensions based upon a classification in dimension three. This was the case for the crystallographic arrangements mentioned above, see [2].

The most important result of our computation is:

Result 1.1

We have a complete list of all simplicial arrangements in the real projective plane with at most 27 lines.

We achieve this by enumerating wiring diagrams (or allowable sequences) and using the correspondence of Goodman and Pollack to arrangements of pseudolines. As a byproduct, we find further examples of simplicial arrangements (of pseudolines) disproving the following two conjectures:

Conjecture 1.2

([10, Conjecture 2])

Up to isomorphism, there are only 5 simplicial unstretchable arrangements of 15 or 16 pseudolines.

Conjecture 1.3

([9] or [10, Conjecture 3])

There are no simplicial arrangements of straight lines besides the three infinite families and 90 sporadic arrangements listed in [9].

We further obtain a proof for:

Conjecture 1.4

([8, Conjecture 1], [1, 6.3] or [10, 3.1])

All simplicial arrangements with at most 14 pseudolines are stretchable.

The new arrangements have 22, 23, 24 and 25 lines and are all contained in the largest one with 25 lines, see Fig. 1 for a picture and Sect. 5.5 for an explicit realization. To obtain the smaller arrangements, remove the thicker lines. Notice that the three thicker lines play the same role in the incidence, and that the ordering in which they are removed does not matter.

In view of the (to my eyes) bizarre structure of the Hasse diagram, Fig. 6 or [9, Fig. 4], and considering the great amount of computations needed for our result, it is very impressive that Grünbaum missed only four arrangements. Notice that there are a few connections missing in [9, Fig. 4]; in particular it turns out that the arrangement $\mathcal {A}(21,4)$ is not maximal but contained in the arrangement $\mathcal {A}(26,4)$. We reproduce the table [9, pp. 6–10] here (up to 27 lines) because of the new arrangements and because of a new column containing the automorphism groups of the arrangements.

This article is organized as follows: We first review some properties of wirings in general. After several preparations we then give an algorithm to enumerate simplicial wirings. Finally, we discuss stretchability and summarize the results.

2 Wiring Diagrams

We first recall some definitions (compare [1, 6.4]).

Definition 2.1

A sequence Σ=(σ ₀,…,σ _m ) of permutations in S _n is an allowable sequence if

• (1) $\sigma_{0}=\mathrm {id}_{S_{n}}=[1,\ldots,n]$,

• (2) σ _m =(1n)(2(n-1))⋯=[n,…,1],

• (3) for each i=0,…,m-1 there are a,b with 1≤a<b≤n and

  

We will encode an allowable sequence by the sequence of a’s and b’s, i.e., Σ is uniquely determined by the sequence of pairs

$$\varPsi =\bigl((a_1,b_1),(a_2,b_2),\ldots,(a_m,b_m)\bigr)$$

with

$$\sigma_{i+1}=\bigl(\sigma_i(a_{i+1})\sigma_i(b_{i+1})\bigr) \bigl(\sigma_i(a_{i+1}+1)\sigma_i(b_{i+1}-1)\bigr)\cdots\sigma_i.$$

Allowable sequences are in one-to-one correspondence to wiring diagrams (for example Fig. 2). These are a very useful representation for arrangements of pseudolines (for a proof see [6, Theorem 2.9] or [1, Theorem 6.3.3]):

Fig. 2

The unstretchable wirings with 15 lines (see Sect. 5.4 for more information)

Theorem 2.2

(Goodman and Pollack)

Every arrangement of pseudolines is isomorphic to a wiring diagram arrangement.

Remark 2.3

It is easy to give an algorithm which computes a wiring for a given arrangement of straight lines, see [6, Sect. 2] or Lemma 2.11 for more details.

Figure 2 shows examples of unstretchable wirings, i.e., the cell decompositions of ℙ² induced by the wirings are not combinatorially isomorphic to the cell decompositions induced by some arrangements of straight lines (see Sect. 4 for more details). Notice that these examples are simplicial which means that all 2-cells have exactly three vertices. We will see that there is no unstretchable simplicial wiring with less than 15 lines.

Our goal is to design an algorithm to enumerate simplicial arrangements, or more generally simplicial arrangements of pseudolines. By the above theorem, we may enumerate certain wiring diagrams instead. However, there are many different wiring diagrams which yield isomorphic arrangements. So the most important part will be to recognize symmetries to avoid computations producing no “new” wirings.

But let us first look at a naive version of such an algorithm. Let W _n denote the set of allowable sequences in S _n , equivalently the set of wiring diagrams with n rows.² During the algorithm, we will successively enlarge a sequence Ψ until it becomes an element of W _n . More precisely, we encode an allowable sequence in construction by the following data.

Definition 2.4

A wiring fragment ω consists of:

• m∈ℕ,

• σ _m =[σ _m (1),…,σ _m (n)]∈{1,…,n}ⁿ,

• Ψ=((a ₁,b ₁),(a ₂,b ₂),…,(a _m ,b _m )),

• Number of lines $\varepsilon_{m}^{i}$ going through the last junction in row i for i=1,…,n: $\varepsilon_{m}^{i}:=b_{k}-a_{k}+1$ where k is maximal with a _k ≤i≤b _k .

• For each i, the actual number $v_{m}^{i}$ of vertices of the last 2-cell between row i and i+1 (let $v_{m}^{0}$ be the number of vertices of the polygon between row n and 1),

• For each i, the actual number s _i of vertices of the first 2-cell between row i and i+1 (we define s ₀:=0),

• The maximal n≥d _m ∈ℕ such that σ _m (i)=n+1-i for all i=1,…,d _m -1,

• The minimal 1≤u _m ∈ℕ such that σ _m (i)=n+1-i for all i=u _m +1,…,n,

where σ _m and Ψ are being interpreted as the beginning of an allowable sequence and have to satisfy the corresponding axioms.

We will call ω complete if σ _m =[n,…,1]. In this case, ω “is” an allowable sequence (or a wiring), and d _m ≥u _m .

The wiring fragment is continuously updated during the algorithm. Note that we will need most variables of the wiring fragment later but mention them already in this section to avoid a second definition.

Example 2.5

Figure 3 shows a wiring fragment with the following data:

Fig. 3

A wiring fragment

Calling the following function with an initial “empty” wiring fragment ω will enumerate all wirings with n rows:

Algorithm 2.7

EnumerateWirings(ω)

Enumerates all allowable sequences in W _n

Input: A wiring fragment ω

Output: List of completions of the fragment ω to a wiring

• 1. If σ _m =[n,…,1] then return {ω}.

• 2. R←∅.

• 3. For all 1≤i<j≤n do:

• 4. If σ _m (i)<σ _m (i+1)<⋯<σ _m (j-1)<σ _m (j), then update all the data to a new fragment ω′ with Ψ′(m+1)=(i,j), and call R:=R∪EnumerateWirings(ω′).

• 5. Return R.

Of course, this algorithm will not lead very far. But let L _n be the set of isomorphism classes of arrangements with n pseudolines. We have a surjective map

$$\pi:\quad W_n \rightarrow L_n,$$

mapping a wiring to an arrangement up to isomorphisms. The most important improvements to our algorithm will be to find a smaller set $W_{n}'\subseteq W_{n}$ such that $\pi|_{W'_{n}}$ is still surjective.

Lemma 2.8

Let $W'_{n}$ be the set of allowable sequences

$$\varPsi =\bigl((a_1,b_1),(a_2,b_2),\ldots,(a_m,b_m)\bigr)$$

such that for each 1≤i<m we have

$$b_i=a_{i+1} \quad\mathit{or}\quad b_{i+1}\le a_i.$$

Then $\pi|_{W'_{n}}$ is surjective.

Proof

Observe that if Ψ(i)=(a _i ,b _i ), Ψ(i+1)=(a _i+1,b _i+1), and either a _i >b _i+1 or a _i+1>b _i , then we may interchange Ψ(i) and Ψ(i+1) without changing the image under π. Moreover, the intervals [a _i ,b _i ] and [a _i+1,b _i+1] may intersect in only one point by Definition 2.1(3). □

This gives a new version of the algorithm:

Algorithm 2.10

EnumerateWirings2(ω)

Enumerates all allowable sequences in $W'_{n}$

Input: A wiring fragment ω

Output: List of completions of the fragment ω

• 1. If σ _m =[n,…,1], then return {ω}.

• 2. R←∅.

• 3. For all i=b _m +1,…,n do:

• 4. If σ _m (b _m )<σ _m (b _m +1)<⋯<σ _m (i), then update all the data to a new fragment ω′ with Ψ′(m+1)=(b _m ,i), and call R:=R∪EnumerateWirings2(ω′).

• 5. For all 1≤i<j≤a _m do:

• 6. If σ _m (i)<σ _m (i+1)<⋯<σ _m (j-1)<σ _m (j), then update all the data to a new fragment ω′ with Ψ′(m+1)=(i,j), and call R:=R∪EnumerateWirings2(ω′).

• 7. Return R.

Further, we may reduce the symmetries by requiring a certain beginning:

Lemma 2.11

Let $W''_{n}$ be the set of allowable sequences

$$\varPsi =\bigl((a_1,b_1),(a_2,b_2),\ldots,(a_m,b_m)\bigr)$$

such that there exists an m ₀ with

$$a_1=1, \quad b_i=a_{i+1}, \quad b_{m_0}=n,$$

for i=1,…,m ₀-1. Then $\pi|_{W''_{n}}$ is surjective.

Proof

This holds by [6, Lemma 2.4]. We sketch here a construction: For a given arrangement $\mathcal {A}$, choose a line $H\in \mathcal {A}$. Modifying this line slightly we may assume that we have a line H′ on which no vertex of the arrangement lies. After the choice of a line at infinity, we rotate the line H′ and pass each vertex exactly once. By choosing a line H′ close enough to H, we ensure that the vertices on H are passed first. □

So we call EnumerateWirings2 with all possible fragments ω with m ₀ junctions as in Lemma 2.11 instead of the empty fragment. Moreover, these fragments are uniquely determined by the sequences

$$(b_1-a_1,\ldots,b_{m_0}-a_{m_0}).$$

Considering that the procedure in the proof of Lemma 2.11 depends on the choice of a line at infinity and on the orientation, we obtain:

Lemma 2.12

It suffices to start the algorithm with one representative of the orbit under the action of the dihedral group $\mathcal {D}_{m_{0}}$ on the sequence $(b_{1}-a_{1},\ldots,b_{m_{0}}-a_{m_{0}})$.

Remark 2.13

It is quite important to choose a “good” representative $\sigma\in \mathcal {D}_{m_{0}}$ for the algorithm. The following is a choice that has proved to be best to average: Let $(p_{1},\ldots,p_{m_{0}})=(b_{1}-a_{1},\ldots,b_{m_{0}}-a_{m_{0}})$. Then choose a $\sigma\in \mathcal {D}_{m_{0}}$ such that p _σ(1)=1 and $p_{\sigma(m_{0})}=1$, or choose a lexicographically greatest $(p_{\sigma(1)},\ldots,p_{\sigma(m_{0})})$, $\sigma\in \mathcal {D}_{m_{0}}$ with p _σ(1)=1 or $p_{\sigma(m_{0})}=1$.

Remark 2.14

For a vertex v, let ℓ(v) be the number of lines incident with v. Without loss of generality we may assume that the line H chosen in Lemma 2.11 contains a vertex v with maximal ℓ(v). This means that we only need to consider junctions of at most ℓ(v) lines during the algorithm.

3 Simplicial Wirings

Definition 3.1

A simplicial wiring is a wiring in which all 2-cells have exactly 3 vertices. A near pencil consists of n-1 lines having one point in common and one further line which is not incident with that point.

Simplicial wirings are much easier to enumerate than arbitrary wirings because simpliciality gives many break conditions for the algorithm. The easiest one is given by the following lemma which should be folklore:

Lemma 3.2

If a simplicial wiring has two neighboring ordinary vertices (intersection points where exactly two pseudolines meet), then it is a near pencil arrangement.

Proof

Assume that lines a and b intersect a line c at neighboring ordinary vertices. By simpliciality, the edge (a∩c,b∩c) is an edge of a triangle. This triangle can only have a∩b as third vertex because a∩c and b∩c are ordinary vertices. But then any further line necessarily meets a and b at a∩b, thus we have a near pencil arrangement. □

So since the near pencil arrangements may be ignored without loss of generality, we can stop the enumeration when two neighboring vertices are ordinary.

The following trivial relation has more applications than expected:

Lemma 3.3

If a simplicial wiring fragment is complete, i.e. σ _m =[n,…,1], then $v_{m}^{i}+s_{n-i}=3$ for all i=0,…,n.

A further important improvement is:

Lemma 3.4

If we only enumerate simplicial wirings with Algorithm 2.10, then in steps 4 and 6 it suffices to consider new pairs (k,ℓ) such that $v_{m}^{k-1}<2$ and $v_{m}^{\ell}<2$.

Proof

Otherwise $v_{m}^{i-1}$ resp. $v_{m}^{j}$ would get greater than 2 after the next move, contradicting simpliciality. □

Here are some more conditions:

Lemma 3.5

In Algorithm 2.10, arriving at junction k the enumeration will never yield a simplicial wiring if one of the following conditions is satisfied:

• (1) a _k ≥2 and σ _k (a _k )<σ _k (a _k -1) and (σ _k (a _k -1)≠n+2-a _k or σ _k (a _k )≠n+1-a _k ),

• (2) b _k <n and σ _k (b _k +1)<σ _k (b _k ) and (σ _k (b _k -1)≠n+1-b _k or σ _k (b _k +1)≠n-b _k ).

Proof

Notice first that since the last move concerned the lines in the rows a _k ,…,b _k , the actual numbers of vertices $v_{k}^{i}$ between the rows i and i+1 for a _k ≤i<b _k are all equal to 1 whereas $v_{k}^{a_{k}-1}=2=v_{k}^{b_{k}}$.

Now if σ _k (a _k )<σ _k (a _k -1), then the rows k and k-1 will not be moved anymore since otherwise $v_{k}^{a_{k}-1}>2$ which is contradicting the simpliciality. Thus in this case we know that σ _k (a _k -1)=n+2-a _k and σ _k (a _k )=n+1-a _k , hence (1). The case (2) is similar. □

Lemma 3.6

In Algorithm 2.10, arriving at junction k the enumeration will never yield a simplicial wiring if one of the following conditions is satisfied:

• (1) there is a j∈{a _k ,…,b _k } with σ _k (j)=σ _k (j+1)+1 and σ _k (j)≠n+1-j and $s_{\sigma _{k}(j+1)}=2$,

• (2) there is a j∈{a _k +1,…,b _k } with σ _k (j)=σ _k (j+1)+1 and σ _k (j-1)≠σ _k (j)+1 and $s_{\sigma_{k}(j)}=2$ and $s_{\sigma_{k}(j+1)}=2$,

• (3) there is a j∈{a _k ,…,b _k -1} with σ _k (j)=σ _k (j+1)+1 and σ _k (j+2)≠σ _k (j)-2 and $s_{\sigma_{k}(j)-2}=2$ and $s_{\sigma_{k}(j+1)}=2$.

Proof

We prove (1); (2) and (3) are similar. If j∈{a _k ,…,b _k } and σ _k (j)=σ _k (j+1)+1, then either the labels σ _k (j) and σ _k (j+1) are at their terminal position in which case σ _k (j)=n+1-j, or they are not, but then the cell that these labels will enclose at the end will have at least 2 vertices which implies $s_{\sigma_{k}(j+1)}=1$ by Lemma 3.3. □

Lemma 3.7

In Algorithm 2.10, arriving at junction k the enumeration will never yield a simplicial wiring if one of the following conditions is satisfied:

• (1) $s_{n-u_{k}}+v_{k}^{u_{k}}=3$,

• (2) d _k >1 and $s_{n-1-d_{k}}+v_{k}^{d_{k}-1}=3$.

Proof

The cells at the end of the rows (u _k ,u _k +1) and (d _k -1,d _k ) are not finished yet, future change will increase $v_{k}^{u_{k}}$ resp. $v_{k}^{d_{k}-1}$, contradicting Lemma 3.3. □

Lemma 3.8

In Algorithm 2.10, arriving at junction k the enumeration will never yield a simplicial wiring if one of the following conditions is satisfied:

• (1) σ _k (b _k )>σ(b _k +1) and b _k ≤u _k ,

• (2) d _k <a _k ≤u _k and σ _k (a _k -1)>σ(a _k ) and (v _k (n+1-a _k )≠1 or σ _k (d _k )<σ _k (a _k ) or σ _k (a _k -2)<σ _k (a _k -1) or there is a j∈{b _k +1,…,u _k } with σ _k (j)>σ _k (a _k )).

Proof

(1) If σ _k (b _k )>σ(b _k +1) and b _k ≤u _k then by Lemma 3.5(2), the rows b _k and b _k +1 will not change anymore. Thus Algorithm 2.10 would only perform moves (i,j) with i<j≤a _k from now on. This would never complete the fragment since b _k ≤u _k .

(2) If d _k <a _k ≤u _k and σ _k (a _k -1)>σ(a _k ) then the situation is slightly different because Algorithm 2.10 also jumps past a _k . But what we know is that the rows a _k -1 and a _k are finished, so all future moves will take place above or below a _k . This means that the fragment can only be completed if σ _k (j)>σ _k (a _k ) for all j>b _k and σ _k (j)<σ _k (a _k ) for all j<a _k , which explains the last part (these two conditions are equivalent). The other conditions are easy to check. □

Notice that one has to carefully choose the obstructions in the implementation because some of them do not spare enough time to compensate the time they consume. For example, the following are apparently not good enough (we therefore omit the proof):

Lemma 3.9

In Algorithm 2.10, arriving at junction k the enumeration will never yield a simplicial wiring if one of the following conditions is satisfied:

• (1) a _k =d _k +1 and σ _k (d _k +1)=n-1-d _k ,

• (2) u _k >1 and σ _k (u _k )=n+2-u _k and σ _k (u _k -1)=n+3-u _k ,

• (3) d _k ≤n-1 and σ _k (d _k )=n-d _k and σ _k (d _k +1)=n-1-d _k ,

• (4) σ _k (1)=2 and b _k +2<n and σ _k (b _k )=3 and σ _k (b _k +1)=4 and σ _k (b _k +2)=n.

We now give the algorithm for the simplicial case. It proceeds in two steps:

• Compute a list of beginnings as described in Lemma 2.11 and choose best representatives as proposed in Lemma 2.12 and Remark 2.13.

• For each representative of beginnings, create a wiring fragment ω. Call “EnumerateSimplicialWirings (ω,ℓ)” defined below, where ℓ is the maximum of the ℓ(v) for v a vertex in ω (see Remark 2.14). Notice that this step can easily be parallelized.

Algorithm 3.11

EnumerateSimplicialWirings(ω, ℓ)

Enumerates simplicial wirings starting by ω with maximal ℓ(v)=ℓ, at least one from each isomorphism class

Input: A wiring fragment ω, ℓ∈ℕ

Output: List of completions of the fragment ω

• 1. Compute the numbers d _m and u _m for ω.

• 2. If d _m =u _m , then if $v_{m}^{i}+\varepsilon_{m}^{n-i}=3$ for all i=0,…,n return {ω}, else return ∅.

• 3. Check the obstructions of Lemmas 3.5, 3.6, 3.7, 3.8 and return ∅ if one of them is satisfied.

• 4. R←∅.

• 5. If b _m ≤u _m and $v_{m}^{b_{m}-1}\le1$ then find the greatest i with σ _m (b _m )<σ _m (b _m +1)<⋯<σ _m (i) (see Lemma 3.4).

  If i-b _m <ℓ, update all the data to a new fragment ω′ with Ψ′(m+1)=(b _m ,i), and call

  $$R:=R \cup \mathbf{EnumerateSimplicialWirings}\bigl(\omega',\ell \bigr).$$

  Use s _i to ensure that Lemma 3.2 is satisfied.

• 6. If σ _m (b _m )=n-u _m or d _m ≥a _m then return R.

• 7. For all d _m ≤i<j≤a _m with j-i<ℓ do:

• 8. If σ _m (i)<σ _m (i+1)<⋯<σ _m (j-1)<σ _m (j), $v_{m}^{i-1}=1$ and $v_{m}^{j}=1$ (see Lemma 3.4), then update all the data to a new fragment ω′ with Ψ′(m+1)=(i,j), and call

  $$R:=R \cup \mathbf{EnumerateSimplicialWirings}\bigl(\omega',\ell \bigr).$$

• 9. Return R.

When the enumeration is complete, one still has to collect the wirings up to isomorphisms. We use the following observation:

Lemma 3.12

Let $\mathcal {A}$ and $\mathcal {A}'$ be simplicial arrangements of lines. Then $\mathcal {A}$ and $\mathcal {A}'$ are isomorphic if and only if the graphs given by the corresponding triangulations are isomorphic (we do not need to require a bijection between the 2-cells preserving the incidence).

Proof

It suffices to prove that for vertices v ₁, v ₂, v ₃ such that (v ₁,v ₂), (v ₂,v ₃), (v ₁,v ₃) are edges, the triple (v ₁,v ₂,v ₃) is always a 2-cell. But a pseudoline crossing (v ₁,v ₂,v ₃) would have to go through two of the three vertices which is impossible. □

In other words, we just need to test whether certain graphs are isomorphic. Such a test is implemented in most computer algebra systems that include combinatorics and is good enough to compute the isomorphism classes of the small subset of stretchable simplicial wirings (see Sect. 4 for details).

4 Stretchable Simplicial Arrangements

We now assume that we have a complete list of simplicial wirings of n lines. A very valuable necessary condition for stretchability is Pappus’ Theorem:

Theorem 4.1

(Pappus)

Let x,y,z,u,v,w∈ℝ³ with

$$\dim\langle x,y,z\rangle= 2 = \dim\langle u,v,w\rangle.$$

Then

$$\dim\bigl( \bigl(\langle x,v\rangle\cap\langle y,u\rangle\bigr) + \bigl(\langle x,w\rangle\cap\langle z,u\rangle\bigr) + \bigl(\langle z,v\rangle\cap\langle y,w\rangle\bigr) \bigr) = 2.$$

We use this theorem in the following way for a wiring ω (compare [8, Theorem 3.1]): Assume that x,y,z are distinct vertices on one line and u,v,w are distinct vertices on another line. If there are lines 〈x,v〉, 〈y,u〉, 〈x,w〉, 〈z,u〉, 〈z,v〉, 〈y,w〉 in ω, and exactly two of the intersection points

$$\langle x,v\rangle\cap\langle y,u\rangle,\qquad \langle x,w\rangle\cap\langle z,u\rangle,\qquad \langle z,v\rangle\cap\langle y,w\rangle $$

lie on a line of ω, then stretchability of ω would contradict Pappus’ Theorem.

This is an expensive test in terms of running time when implemented, because we essentially have to check the theorem for all subarrangements in question. Therefore it is not possible to include it into the above algorithm to exclude incomplete wiring fragments. However, it turns out that almost all unstretchable completed simplicial wirings of up to 27 lines do not satisfy Pappus’ Theorem. Thus it appears to be the best (known) tool to rule out wirings a posteriori: After performing the enumeration, we have a huge list of partly isomorphic simplicial wirings. It is faster to test Pappus’ Theorem on these wirings and to compute the isomorphism classes afterwards than the other way round (which explains the entries marked “?” in Fig. 4).

Fig. 4

Numbers of isomorphism classes of simplicial arrangements (without the near pencil arrangements)

For the very few remaining simplicial wirings we use [4, Algorithm 4.4]: For all our wirings, we always find five vertices p ₁,…,p ₅ in the incidence with the following properties:

• p ₁,…,p ₄ are in general position by the incidence (these may then be chosen arbitrarily in general position in ℙ² up to projectivity),

• starting with p ₁,…,p ₅ and repeatedly including lines through two points and intersections of two lines, we obtain all other vertices and lines.

Writing p ₅=(X:Y:Z) with variables X,Y,Z, the incidence constraints define an ideal I in ℝ[X,Y,Z]. For our wirings, this either yields a real realization of the wiring as arrangement of straight lines (if dimI≥0), or it proves that the wiring is unstretchable (if I=(1)).

5 Results

We now summarize the output of the computation. The running time is exponential in the number of lines: It takes only 4 seconds to find all simplicial arrangements of pseudolines with 20 lines, but for 26 lines an ordinary PC needs about two weeks. Note that this is an implementation in C and C++; the resulting data is then processed by several functions implemented in Magma. Notice also that using Lemma 2.11, it is easy to parallelize the algorithm. This way we also classify the simplicial arrangements with 27 lines in approximately one week, but to reach an enumeration of all simplicial arrangements with 28 lines one would require some new idea (or even more computational resources). But just one step further would not be a great benefit.

Figure 4 shows the numbers of simplicial arrangements of pseudolines up to isomorphisms. The entries marked “?” could, in principle, be computed easily but would require a better implementation of the function collecting the wirings up to isomorphisms or possibly just more computational resources.

5.1 Hasse Diagram

Figure 5 is a Hasse diagram of the stretchable simplicial arrangements with up to 27 lines. An edge between two arrangements means that one can remove lines from the larger one to obtain the smaller one. We have included this diagram here because it appears to be slightly different from [9, Fig. 4]. It is less well-arranged than [9, Fig. 4] because it includes the connections to the infinite series $\mathcal {A}(n,1)$ and some more edges for instance to $\mathcal {A}(7,1)$. It appears that $\mathcal {A}(21,4)$ is not maximal; it is contained in the arrangement $\mathcal {A}(26,4)$.

Fig. 5

A Hasse diagram (compare [9, Fig. 4])

5.2 Invariants

The following Table 1 is a list of the invariants of all (stretchable) simplicial arrangements with up to 27 lines except the near pencil (compare [9, pp. 6–10]). The numbers f ₀,f ₁,f ₂ are the numbers of vertices, edges and 2-cells; t _i is the number of vertices which lie on exactly i lines; r _i is the number of lines on which exactly i vertices lie.

Table 1 Invariants of simplicial arrangements with up to 27 lines

The last column shows the automorphism groups of the cell complexes given by the arrangements. The symbols A _n , B _n , G ₂, H ₃ are reflection groups of the corresponding type, $\mathcal {D}_{n}$ is the dihedral group of order 2n, $\operatorname {Alt}_{n}$ is the alternating group, and Z ₄ is the cyclic group of order 4. The automorphism groups were computed using the simplicial wiring diagrams obtained by our enumeration. It appears that for any known simplicial arrangement, a realization of its incidence is unique up to projectivity. Thus the computed automorphism groups are isomorphic to the groups of linear symmetries.

Notice that the pairs $(\mathcal {A}(17,2)$, $\mathcal {A}(17,4))$, $(\mathcal {A}(18,4)$, $\mathcal {A}(18,5))$, and $(\mathcal {A}(19,4)$, $\mathcal {A}(19,5))$ are not uniquely determined by their invariants. We distinguish $\mathcal {A}(17,2)$ and $\mathcal {A}(17,4)$ by their position in the Hasse diagram. $\mathcal {A}(19,4)$ and $\mathcal {A}(19,5))$ are not distinguishable in [9, Fig. 4]; however, they have different automorphism groups. The realization of $\mathcal {A}(19,5)$ in [9] reveals the existence of an automorphism of order 4 which does not exist for $\mathcal {A}(19,4)$. The arrangements $\mathcal {A}(18,4)$ and $\mathcal {A}(18,5)$ are not distinguishable by their invariants, they even have isomorphic automorphism groups. But since their role in both Hasse diagrams is the same, the tables in [9] and Table 1 are consistent.

5.3 Unstretchable Simplicial Arrangements That Satisfy Pappus’ Theorem

Table 2 contains the invariants for the unstretchable simplicial arrangements that satisfy Pappus’ theorem. Corresponding wirings are displayed in Fig. 6.

Fig. 6

The unstretchable simplicial wirings with 16, 17, 18, 19, 22, and 26 lines that satisfy Pappus’ theorem

Table 2 Invariants of unstretchable simplicial arrangements that satisfy Pappus’ Theorem

5.4 Unstretchable Simplicial Arrangements with 15 Lines

Figure 2 shows the wiring diagrams of the two unstretchable simplicial arrangements with 15 lines. The first one is called B ₁(15) in [10], the second one is new, we call it B ₂(15). Their invariants are in Table 3 (compare [10, Table 1]).

Table 3 Invariants of the unstretchable simplicial arrangements with 15 lines

Here, Z ₆ denotes the cyclic group of order 6.

5.5 The New Simplicial Arrangements

A realization of the new simplicial arrangement with 25 lines is the set of orthogonal complements of the following elements of ℝ³, where $\tau=\frac{\sqrt{5}+1}{2}$:

To obtain the other new arrangements, remove the following vectors (in any ordering):