Packing a Tetrahedron by Similar Tetrahedra

Abstract

Any collection of homothetic copies of some tetrahedron $T_r$, whose total volume does not exceed one quarter of the volume of $T_r$, can be packed into $T_r$ .

1 Introduction

We say that convex bodies $\ C_1, C_2, \ldots$ can be packed into a convex body C if it is possible to apply translations and rotations to the sets $C_n$ so that the resulting translated and rotated bodies are contained in C and have mutually disjoint interiors. It is known that if C is either a square [1], or a triangle (see [2] and [3]), or a disk [4], then any collection of homothetic copies of C, whose total area does not exceed half the area of C can be packed into C. The conjecture is that the same packing density is achievable for any planar convex body (see [5] and [6]). However, only the following upper bound was found [7]: any collection of homothetic copies of C, with total area not greater than a quarter of the area of C, can be packed into C.

Meir and Moser [8] proved that any collection of d-dimensional cubes, whose total volume does not exceed $2^{1-d}$ times the volume of K, can be packed into the d-dimensional cube K. In the paper [2] concerning packing of triangles, Richardson writes: “The original paper of Kranakis and Meertens [9] conjectured that Theorem 1 may be extendible to families of similar tetrahedra (in three dimensions) or even to any family of similar d-dimensional simplexes.” We confirm this conjecture in three dimensions for a tetrahedron $T_r$ of vertices (0, 0, 0), (0, 1, 0), (1, 1, 0) and (0, 0, 1). We will show that any collection of homothetic copies of $T_r$, whose total volume does not exceed one quarter of the volume of $T_r$, can be packed into $T_r$.

2 Division of $T_r$

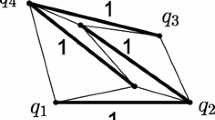
The unit cube can be divided into two congruent triangular prisms. Observe that such a prism can be partitioned into three tetrahedra congruent to $T_r$ (see Fig. 1). The unit cube can be partitioned into six tetrahedra congruent to $T_r$.

Fig. 1

Partition of a prism into three congruent tetrahedra

Denote by $\lambda T_r$ the image of $T_r$ in the homothety with ratio $\lambda$ and center (0, 0, 1). Moreover, let $\ a_1\ge a_2 \ge \ldots \$ be positive numbers, let $S_i=a_i T_r$ for $\ i=1,2,\ldots \$ and let $\ a_1^3+a_2^3+\ldots \le 1/4$. Obviously, $\ a_1+a_2 \le 1$, otherwise $\ a_1^3+a_2^3 > (1/2)^3+(1/2)^3=1/4$, which is a contradiction.

To describe the method of packing tetrahedra $S_1, S_2, \ldots$ into $T_r$, let’s introduce some notations. Denote by $k_1$ the smallest integer such that

$$\begin{aligned} a_4+a_{10}+\ldots + a_{6k_1-2}+a_{6k_1+1} > 1-a_1 \end{aligned}$$

($k_1=3$ in Fig. 3); if $a_4+a_7>1-a_1$, then $k_1=1$. Moreover, let $k_2$ be the smallest integer such that

$$\begin{aligned} a_{6k_1+4}+a_{6k_1+10}+\ldots + a_{6k_2-2}+a_{6k_2+1} > 1-a_1-a_{6k_1+1} \end{aligned}$$

($k_2= 7$ in Fig. 3). At the end of this section we will define layers and slices. According to the packing method described in Sect. 3, tetrahedra $\ S_1, \ldots , S_{6k_1}\$ will be packed into the first layer of the first slice; tetrahedra $\ S_{6k_1+1}, \ldots , S_{6k_2}\$ will be packed into the second layer of the first slice. If

$$\begin{aligned} a_1+a_{6k_1+1}+a_{6k_2+1}+\ldots +a_{6k_i+1}+a_{6k_i+2} \le 1 \end{aligned}$$

for $i\ge 2$, then denote by $k_{i+1}$ the smallest integer such that

$$\begin{aligned} a_{6k_i+4}+a_{6k_i+10}+\ldots + a_{6k_{i+1}-2}+a_{6k_{i+1}+1} > 1-a_1-a_{6k_1+1}- \ldots - a_{6k_i+1}. \end{aligned}$$

If j is the smallest integer such that

$$\begin{aligned} a_1+a_{6k_1+1}+\ldots +a_{6k_j+1}+a_{6k_j+2} > 1, \end{aligned}$$

then we take $s_1=a_{6k_j+2}$ ($j=5$ and $k_j=13$ in Fig. 3, right).

Fig. 2

Division of $T_r$

Tetrahedra will be packed into layers $L_i$ contained in slices $H_n$. In Sect. 3 we will compare the total volume of tetrahedra packed into $L_i$ with the volume of some layer $L_i^*$. Let

$$\begin{aligned} H_1 = T_r \setminus (1-a_1)T_r, \end{aligned}$$

and

$$\begin{aligned} H_1^* = (1-a_1)T_r \setminus (1-a_1-a_{s_1})T_r. \end{aligned}$$

(see Fig. 2). Moreover, let

$$\begin{aligned} L_1&= \{ (x,y,z)\in H_1 : \ 0\le x \le a_1 \}, \\ L_1^*&= \{ (x,y,z)\in H_1^* : \ 0\le x \le a_{6k_1+1} \}, \\ L_2&= \{ (x,y,z)\in H_1 : \ a_1\le x \le a_1+a_{6k_1+1} \}, \\ L_2^*&= \{ (x,y,z)\in H_1^* : \ a_{6k_1+1}\le x \le a_{6k_1+1}+a_{6k_2+1} \}, \\ L_3&= \{ (x,y,z)\in H_1 : \ a_1+a_{6k_1+1}\le x \le a_1+a_{6k_1+1}+a_{6k_2+1} \}, \\ L_3^*&= \{ (x,y,z)\in H_1^* : \ a_{6k_1+1}+a_{6k_2+1}\le x \le a_{6k_1+1}+a_{6k_2+1} +a_{6k_3+1}\}, \ \mathrm{etc.} \end{aligned}$$

Fig. 3

Bottom of $H_1$

Fig. 4

Covering $L_1^*$ with $\ S_2, S_3, \ldots , S_{s_{6k_1+1}}$

3 Packing Method

Observe that $S_1, S_2$ and $S_3$ can be packed into the part of $L_1$ with $\ y\ge 1-a_1$ (see Figs. 1, 3, 4). Moreover, $S_4, S_5, \ldots , S_{9}$ can be paced into the cube

$$\begin{aligned} \{ (x,y,z): \ 0\le x \le a_4, \ 1-a_1-a_4 \le y \le 1-a_1, \ 0\le z \le a_4 \}. \end{aligned}$$

Packing method, Part I.

Tetrahedra $S_1, S_2, \ldots , S_{6k_1}$ are packed into $L_1$ (see Figs. 3,  4, where $k_1=3$). Tetrahedra $S_{6k_i+1}, S_{6k_i+2}, \ldots , S_{6k_{i+1}}$ are packed into $L_{i+1}$, for $i=1,2, \ldots , j-1$. Moreover $S_{6k_j+1}=S_{s_1-1}$ is placed in $L_{j+1}$. Clearly, all packed tetrahedra $S_1, \ldots , S_{s_1-1}$ are contained in $H_1$.

Lemma 1

The sum of volumes of $S_2, \ldots , S_{s_1}$ is greater than the volume of $H_1^*$.

Proof

It is easy to verify that $\ c^3/2+d^3/2 \ge cd^2,$ provided that $\ 0<d\le c <1$. Consequently,

$$\begin{aligned} \frac{1}{6}a_2^3+\frac{1}{6}a_3^3+\ldots + \frac{1}{6}a_7^3 \ge 3 \cdot \frac{1}{6}a_4^3 + 3\cdot \frac{1}{6}a_7^3 \ge a_4a_7^2 \ge a_4a_{6k_1+1}^2. \end{aligned}$$

Moreover, if $a_1+a_4+a_7\le 1$, then

$$\begin{aligned} \frac{1}{6}a_8^3+\ldots + \frac{1}{6}a_{13}^3 \ge 3\cdot \frac{1}{6} a_{10}^3+3\cdot \frac{1}{6} a_{13}^3\ge a_{10}a_{6k_1+1}^2, \end{aligned}$$

etc. This means that that the total volume of tetrahedra $S_2, S_3, \ldots , S_{6k_1+1}$ is greater than the volume of $L_1^*$ (see Fig. 4). For the same reason, the total volume of tetrahedra $S_{6k_i+2}, \ldots , S_{6k_{i+1}+1}$ is greater than the volume of $L_{i+1}^*$, for $i=1,2, \ldots , j-1$. This implies that the sum of volumes of $S_2, \ldots , S_{s_1}$ is greater than the volume of $H_1^*$ (see Fig. 5 ).

Fig. 5

Covering $H_1^*$ with $L_1, L_2, \ldots , L_{k_j}$ and $S_{s_1}$

Fig. 6

$a_1+a_{6k_1+1}+\ldots +a_{6k_m+1}+a_{6k_m+2}\le 1\$ and $a_1+a_{6k_1+1}+\ldots +a_{6k_m+1}+a_{6k_m+1}> 1\$

An additional explanation is required if $\ a_1+a_{6k_1+1}+ \ldots + a_{6k_m+1}+a_{6k_m+2} \le 1$, while $\ a_1+a_{6k_1+1}+ \ldots + a_{6k_m+1}+a_{6k_m+1} > 1\$ for some integer m. We can imagine that $S_{80}$ can be packed into $L_6$ in Fig. 3 (left). In this case there is enough space to pack $\ S_{6k_m+1}, S_{6k_m+2}$ and $\ S_{6k_m+3}$ into the part of $L_{m+1}$ with $\ y \ge 1-a_{6k_m+1}$ (see Fig. 6). Clearly, at least three next tetrahedra $\ S_{6k_m+4}, S_{6k_m+5}$ and $\ S_{6k_m+6}$ can be packed into this layer. Moreover, $m<j$, i.e., $S_{6k_{m+1}+1 }$ is placed in the next layer in $H_1$. $\square$

Packing method, Part II.

Similar to Lemma 1, one can find an integer $s_2$ such that tetrahedra $S_{s_1}, \ldots , S_{s_2-1}$ can be packed into $H_2$ and that the sum of volumes of $S_{s_1+1}, \ldots S_{s_2}$ is greater than the volume of $H_2^*$, where

$$\begin{aligned} H_2 = H_1^* = (1-a_1)T_r \setminus (1-a_1-a_{s_1})T_r \end{aligned}$$

and

$$\begin{aligned} H_2^* = (1-a_1-a_{s_1})T_r \setminus (1-a_1-a_{s_1}-a_{s_2})T_r. \end{aligned}$$

Assume that $s_2, \ldots , s_k$ are defined for $k\ge 2$ and that $\ a_1+a_{s_1}+\ldots + a_{s_k} \le 1$. Then there exists an integer $s_{k+1}$ such that tetrahedra $S_{s_k}, \ldots , S_{s_{k+1}-1}$ can be packed into $H_{k+1}$ and that the sum of volumes of $S_{s_k+1}, \ldots , S_{s_{k+1}}$ is greater than the volume of $H_{k+1}^*$, where $\ H_{k+1} = H_k^* \$ and

$$\begin{aligned} H_{k+1}^*= (1-a_1- a_{s_1} - \ldots -a_{s_{k}} )T_r \setminus (1-a_1-a_{s_1}- \ldots -a_{s_{k+1}})T_r, \end{aligned}$$

provided that $\ a_1 +a_{s_1}+\ldots + a_{s_{k+1}} \le 1\$ or

$$\begin{aligned} H_{k+1}^*= (1-a_1- a_{s_1} - \ldots -a_{s_{k}} )T_r, \end{aligned}$$

provided that $\ a_1 +a_{s_1}+\ldots + a_{s_{k+1}} > 1$. In the latter case we stop the packing process; there is not enough space in $T_r$ to create a new slice of height $a_{s_{k+1}}$.

Theorem 2

Any collection of homothetic copies of $T_r$, whose total volume does not exceed 1/24, can be packed into $T_r$.

Proof

Let $S_1, S_2, \ldots$ be a collection of homothetic copies of $T_r$ with total volume not greater than 1/24. Without loss of generality we can assume that $a_1\ge a_2 \ge \ldots$, where $S_i=a_iT_r$, for $i=1,2,\ldots$ Assume that the tetrahedra cannot be packed into $T_r$ by the method described above. This implies that there is an integer l such that $a_1+a_{s_1}+\ldots +a_{s_l}>1$. The sum of volumes of $S_2, \ldots , S_{s_l}$ is greater than the sum of volumes of $H_1^*, \ldots , H_{s_l}^*$, i.e., is greater than $\frac{1}{6}(1-a_1)^3$. As a consequence, the total volume of all tetrahedra $S_1, S_2, \ldots$ is greater than

$$\begin{aligned} \frac{1}{6}a_1^3 + \frac{1}{6} (1-a_1)^3 > \frac{1}{6} \cdot \left( \frac{1}{2} \right) ^3 + \frac{1}{6} \cdot \left( \frac{1}{2} \right) ^3 = \frac{1}{24}, \end{aligned}$$

which is a contradiction. $\square$