Wallace–Simson Theorem on Four Lines Parallel to a Plane

Abstract

The impulse to study this topic came from a variant of the Wallace-Simson theorem, which deals with the locus of the point P such that the points that are symmetric to P with respect to three lines in the plane are collinear. A 3D generalization can be as follows: Given four straight lines which are parallel to a plane. Determine the locus of the point P such that points that are symmetric to P with respect to these four lines are coplanar. Surprisingly, the locus of P is a cylinder of revolution with the axis which is perpendicular to the fixed plane. Moreover, all planes given by points that are symmetric with an arbitrary point P of the locus with respect to the given four lines pass through a fixed line f. While in the planar version the fixed element is the orthocenter of the triangle given by the three lines, the role of the fixed line f with respect to the four given lines is not obvious.

1 Introduction

The well-known Wallace–Simson (W–S) theorem states: The feet of normals from an arbitrary point P in the circumcircle of a triangle to its side lines are collinear [1, 5, 7]. A variant of the W–S theorem says: For any point P in the circumcircle of a triangle, the points symmetric to P with respect to the side lines of the triangle are collinear. Moreover, all lines given by points that are symmetric to a locus point P with respect to the side lines of the given triangle pass through the orthocenter of the triangle. We will call it a symmetric variant of the W–S theorem.

There are various generalizations of the W–S theorem both planar and spatial or n-dimensional, see [6, 8,9,10,11,12,13,14].

A 3D generalization of the W–S theorem on four arbitrary straight lines which deals with the locus of the point P such that the feet of normals from P to these four lines are coplanar yields in general as the locus of P a cubic surface. It is possible to distinguish the individual positions of the lines that lead to different types of cubic surfaces (or quadrics) and their singular forms [12]. In our opinion, such a classification has not yet taken place, it is a matter of further research.

We decided to investigate the case where four given lines $k_1,k_2,k_3,k_4$ are parallel to a fixed plane. One of the reasons to present this result is that the locus of P was very unexpected to us—we got a cylinder of revolution (Theorem 1), see [2].

The main results of the paper are given in the Theorem 2 and the Theorem 3. We investigate the locus of all points P whose reflections in four mutually skew lines $k_1,k_2,k_3,k_4$ (which are parallel to a plane) are coplanar. The locus of P is again a cylinder of revolution (Theorem 2). This spatial version retains the property of the planar version—all the planes given by points that are reflected from an arbitrary locus point P in the lines $k_1,k_2,k_3,k_4$ pass through a fixed line f (Theorem 3).

The computations, especially the elimination of variables, were performed in the program CoCoA¹ [3] which is based on Gröbner bases computations [4]. Resulting figures showing the searched locus were made in MAPLE and GeoGebra.

2 W–S theorem: 4 Lines Parallel to a Plane

In this section, we deal with the 3D generalization of the W–S theorem on four straight lines that are parallel to a plane (Theorem 1). We omit the proof because a similar problem is discussed in the next section.

Theorem 1

In the Euclidean space $\mathbb {E}^3$ consider four pairwise skew straight lines $k_1,k_2,k_3,k_4$ that are parallel to a plane. Then the locus of all points P such that feet of normals from P to the given lines are coplanar is a cylinder of revolution whose axis is orthogonal to the given plane.

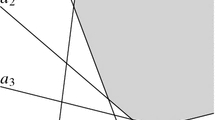
Assume that the lines $k_1,k_2,k_3,k_4$ are parallel to the xy-plane and by $z_1,z_2,z_3,z_4$ we denote their distances from the xy-plane. Let $a_1x+b_1y+c_1=0$, $a_2x+b_2y+c_2=0$, $a_3x+b_3y+c_3=0$ and $a_4x+b_4y+c_4=0$ be the equations of the orthogonal projections of $k_1,k_2,k_3,k_4$ in the xy-plane. Then the locus equation of the point $P=(p,q,r)$ is

$$\begin{aligned} K:= A(p^2 + q^2) + Bp + Cq + D=0, \end{aligned}$$

(1)

where

$A=z_2a_3a_4(a_3b_4 - a_4b_3) + z_3a_2a_4(a_4b_2 - a_2b_4) + z_4a_2a_3(a_2b_3 - a_3b_2)$,

$B=z_2(a_3c_4 + a_4c_3)(a_3b_4 - a_4b_3) + z_3(a_2c_4 + a_4c_2)(a_4b_2 - a_2b_4) + z_4(a_2c_3 + a_3c_2)(a_2b_3-a_3b_2)$,

$C=z_2(a_3a_4 + b_3b_4)(a_3c_4 - a_4c_3) + z_3(a_2a_4 + b_2b_4)(a_4c_2 - a_2c_4) + z_4(a_2a_3 + b_2b_3)(a_2c_3-a_3c_2)$,

$D=z_2c_3c_4(a_3b_4 - a_4b_3) + z_3c_2c_4(a_4b_2 - a_2b_4) + z_4c_2c_3(a_2b_3 - a_3b_2)$. $\square$

We see that the locus Eq. (1) represents a cylinder of revolution whose axis is perpendicular to the xy-plane, Fig. 1.

Fig. 1

Given four lines parallel to a plane. The locus of the point P such that the feet of normals from P to the given lines are coplanar is a cylinder of revolution

Remark 1

The coefficient A by $p^2+q^2$ in (1) depends only on the directions of the lines $k_1,k_2,k_3,k_4$ and their distances $z_1,z_2,z_3,z_4$ to the fixed xy-plane due to the absence of the terms $c_1,c_2,c_3,c_4$.

Remark 2

If all lines $k_1,k_2,k_3,k_4$ intersect a line that is perpendicular to the fixed plane (axis z in our coordinate system), then the locus of P is this line instead of the cylinder of revolution. To see this, note that in this case all coefficients $c_1,c_2,c_3$ and $c_4$ vanish. This means $B=C=D=0$ in (1).

Remark 3

Note that for any point P of the locus, the entire line passing through the point P that is perpendicular to the given plane belongs to the locus. So it is enough to examine the locus in this plane.

3 Symmetric Variant of W–S Theorem: 4 Lines Parallel to a Plane

In this section, we study the main topic of the paper—a 3D generalization of a symmetric variant of W–S theorem on four straight lines that are parallel to a plane.

The symmetric variant of the W–S theorem says that the locus of the point P such that points $K',L',M'$ which are symmetric to P with respect to the side lines of a given triangle ABC are collinear is the circumcircle of ABC. Moreover, for an arbitrary locus point P all lines given by collinear points $K',L',M'$ are concurrent at the orthocenter H of the triangle ABC, Fig. 2.

Fig. 2

Points $K',L',M'$ lie on a line which passes through the orthocenter H of ABC

The collinearity of the points $K',L',M'$ follows from the W–S theorem since a homothety centered at P with ratio 2 sends the feet K, L, M of normals from P to the sides of ABC to the collinear points $K',L',M'$.

3.1 Symmetric Variant of W–S Theorem

The following is a spatial generalization of the symmetric variant of the W–S theorem on four straight lines that are parallel to a plane.

Theorem 2

In the Euclidean space $\mathbb {E}^3$ consider four pairwise skew straight lines $k_1,k_2,k_3,k_4$ that are parallel to a plane. Then the locus of the point P such that points $X_1,X_2,X_3,X_4$ that are symmetric to P with respect to the straight lines $k_1,k_2,k_3,k_4$ are coplanar is a cylinder of revolution.

Proof

With the proper choice of a Cartesian coordinate system, we achieve that $a_1x+b_1y+c_1=0$, $a_2x+b_2y+c_2=0$, $a_3x+b_3y+c_3=0$, $a_4x+b_4y+c_4=0$ are equations of orthogonal projections of the lines $k_1,k_2,k_3,k_4$. Denote by $X_1=(x_1,y_1,z_1)$, $X_2=(x_2,y_2,z_2)$, $X_3=(x_3,y_3,z_3)$, $X_4=(x_4,y_4,z_4)$ the points that are symmetric to $P=(p,q,r)$ with respect to the lines $k_1,k_2,k_3,k_4$. Then:

$X_1$ is symmetric to P with respect to $k_1\Rightarrow$

$h_1:=a_1(p+x_1)+b_1(q+y_1)+2c_1=0, h_2:= b_1(p-x_1) - a_1(q-y_1)=0$,

$X_2$ is symmetric to P with respect to $k_2 \Rightarrow$

$h_3:=a_2(p+x_2)+b_2(q+y_2)+2c_2=0, h_4:= b_2(p-x_2) - a_2(q-y_2)=0$,

$X_3$ is symmetric to P with respect to $k_3 \Rightarrow$

$h_5:=a_3(p+x_3)+b_3(q+y_3)+2c_3=0, h_6:= b_3(p-x_3) - a_3(q-y_3)=0$,

$X_4$ is symmetric to P with respect to $k_4 \Rightarrow$

$h_7:=a_4(p+x_4)+b_4(q+y_4)+2c_4=0, h_8:= b_4(p-x_4) - a_4(q-y_4)=0$,

$X_1,X_2,X_3,X_4$ are coplanar $\Rightarrow$

$$\begin{aligned} h_9:=\left| \begin{array}{cccc} x_1, &{} y_1, &{} z_1, &{} 1\\ x_2, &{} y_2, &{} z_2, &{} 1\\ x_3, &{} y_3, &{} z_3, &{} 1\\ x_4, &{} y_4, &{} z_4, &{} 1 \end{array}\right| = 0. \end{aligned}$$

(2)

The elimination of the eight variables $x_1,y_1,\dots ,x_4,y_4$ in the ideal $J=(h_1,\dots ,h_9)$ leads to a locus equation. In fact, the computation in CoCoA does not terminate due to the complex computation.

We can introduce some simplifications that do not affect the final result. Another approach that seems more readable is the following.

By eliminating $x_1,y_1$ in $h_1=0,h_2=0$, then $x_2,y_2$ in $h_3=0,h_4=0$, etc. we get

$x_1= (- (a_1^2 - b_1^2)p - 2a_1b_1q - 2a_1c_1)/(a_1^2 + b_1^2)$,

$y_1= (- 2a_1b_1p + (a_1^2 - b_1^2)q - 2b_1c_1)/(a_1^2 + b_1^2)$,

$x_2= (- (a_2^2 - b_2^2)p - 2a_2b_2q - 2a_2c_2)/(a_2^2 + b_2^2)$,

$y_2= (- 2a_2b_2p + (a_2^2 - b_2^2)q - 2b_2c_2)/(a_2^2 + b_2^2)$,

$x_3= (- (a_3^2 - b_3^2)p - 2a_3b_3q - 2a_3c_3)/(a_3^2 + b_3^2)$,

$y_3= (- 2a_3b_3p + (a_3^2 - b_3^2)q - 2b_3c_3)/(a_3^2 + b_3^2)$,

$x_4= (- (a_4^2 - b_4^2)p - 2a_4b_4q - 2a_4c_4)/(a_4^2 + b_4^2)$,

$y_4= (- 2a_4b_4p + (a_4^2 - b_4^2)q - 2b_4c_4)/(a_4^2 + b_4^2)$.

Assume that the vectors $(a_1,b_1)$, $(a_2,b_2)$, $(a_3,b_3)$, $(a_4,b_4)$ are unit and put $a_1=c_1=0,b_1=1$ and $z_1=0$ which has no effect on the generality. We substitute $x_1,y_1,\dots ,x_4,y_4$ into the determinant (2) and after rearrangement, we get instead of (2) the relation

$$\begin{aligned} \left| \begin{array}{ccc} a_2^2p + a_2b_2q + a_2c_2, &{} a_2b_2p - a_2^2q + b_2c_2, &{} z_2/2\\ a_3^2p + a_3b_3q + a_3c_3, &{} a_3b_3p - a_3^2q + b_3c_3, &{} z_3/2\\ a_4^2p + a_4b_4q + a_4c_4, &{} a_4b_4p - a_4^2q + b_4c_4, &{} z_4/2 \end{array}\right| = 0 \end{aligned}$$

(3)

which yields (1). We obtain a cylinder of revolution, Fig. 3. $\square$

Fig. 3

The locus of all points P such that the points that are symmetric to P with respect to the given four lines are coplanar is a cylinder of revolution

3.2 Fixed Line

In this part, we will show that all planes given by the points $X_1,X_2,X_3,X_4$ pass through a fixed line for any locus point P.

Theorem 3

Let P be an arbitrary point of the locus (1). Then all planes given by the points $X_1,X_2,X_3,X_4$ that are symmetric to P with respect to the straight lines $k_1,k_2,k_3,k_4$ pass through a fixed line f.

Proof

For every point P of the locus circle (and all points on the line through P which is perpendicular to the given plane) there exists a corresponding plane given by the points $X_1,X_2,X_3,X_4$. To determine the fixed line, we proceed in the following way:

First, we find two distinct points $P_1$ and $P_2$ in the locus circle (1), whose coordinates are rational in $a_1,\dots ,a_4,b_1,\dots ,b_4,c_1,\dots ,c_4,z_1,\dots ,z_4$. In this way we avoid cases where the locus point coordinates contain radicals.

Second, we determine two planes given by points $X_1,X_2,X_3,X_4$ that correspond to the points $P_1,P_2$.

Third, we identify the intersection line f of these two selected planes.

Fourth, we verify that the line f lies in all planes corresponding to any point P in the locus circle.

Let $P_{123}$ be a plane given by the points $X_1,X_2,X_3$

$$\begin{aligned} P_{123}: \left| \begin{array}{ccc} a_2^2p + a_2b_2q + a_2c_2, &{} a_2b_2p - a_2^2q + b_2c_2, &{} z_2/2\\ a_3^2p + a_3b_3q + a_3c_3, &{} a_3b_3p - a_3^2q + b_3c_3, &{} z_3/2\\ x + p, &{} y - q, &{} z \end{array}\right| = 0, \end{aligned}$$

with $P=(p,q,0)$ obeying (1), see (3). Eliminating q in the ideal $I=(P_{123},K)$ we gain an elimination ideal generated by one polynomial (principle ideal). This gives a factored equation

$$\begin{aligned} f(p)\cdot g(x,y,z,p)=0, \end{aligned}$$

where f(p) is linear in p and does not contain x, y, z, while g(x, y, z, p) is quadratic in x, y, z, p. From $f(p)=0$ we get the first coordinate of the point $P_1=(p_1,q_1,0)$ of the locus

$$\begin{aligned} p_1=\frac{-a_2c_2z_3^2 + z_2z_3(a_2a_3 + b_2b_3)(a_3c_2 + a_2c_3) - a_3c_3z_2^2}{a_2^2z_3^2 - 2a_2a_3z_2z_3(a_2a_3 + b_2b_3) + a_3^2z_2^2}. \end{aligned}$$

The case $f(p)=0$ in $f(p)\cdot g(x,y,z,p)=0$ demonstrates the situation where the points $X_1,X_2,X_3$ are collinear and the corresponding plane is not uniquely determined. For an idea of how complex the computation is, the polynomial $f(p)\cdot g(x,y,z,p)$ in the elimination ideal has 5758 terms.

Using elimination of p in the ideal $I=(P_{123},K)$ we get the second coordinate of the point $P_1$ in the locus

$$\begin{aligned} q_1=\frac{-z_2z_3(a_2b_3 - a_3b_2)(a_2c_3 - a_3c_2)}{a_2^2z_3^2 - 2a_2a_3z_2z_3(a_2a_3 + b_2b_3) + a_3^2z_2^2}. \end{aligned}$$

Similarly, using the plane $P_{124}$ given by the points $X_1,X_2,X_4$, we eliminate p and then q in the ideal $J=(P_{124},K)$ and get the coordinates of the second point $P_2=(p_2,q_2,0)$ in the locus

$$\begin{aligned} p_2=\frac{-a_2c_2z_4^2 + z_2z_4(a_2a_4 + b_2b_4)(a_4c_2 + a_2c_4) - a_4c_4z_2^2}{a_2^2z_4^2 - 2a_2a_4z_2z_4(a_2a_4 + b_2b_4) + a_4^2z_2^2} \end{aligned}$$

and

$$\begin{aligned} q_2=\frac{-z_2z_4(a_2b_4 - a_4b_2)(a_2c_4 - a_4c_2)}{a_2^2z_4^2 - 2a_2a_4z_2z_4(a_2a_4 + b_2b_4) + a_4^2z_2^2}. \end{aligned}$$

The substitution of $p_2,q_2$ for p, q into the equation of the plane $P_{123}$ gives the equation of the plane $P_{123}(p_2,q_2)$

$$\begin{aligned} P_{123}(p_2,q_2): A_1x+B_1y+C_1z+D_1=0, \end{aligned}$$

while the substitution of $p_1,q_1$ for p, q into the equation of the plane $P_{124}$ yields the equation of the plane $P_{124}(p_1,q_1)$

$$\begin{aligned} P_{124}(p_1,q_1): A_2x+B_2y+C_2z+D_2=0, \end{aligned}$$

where $A_1,B_1,C_1,D_1$ and $A_2,B_2,C_2,D_2$ are certain polynomials containing $a_1,\dots ,a_4$, $b_1,\dots ,b_4$, $c_1,\dots ,c_4$ and $z_1,\dots ,z_4$.

Now we identify the intersection of the planes $P_{123}(p_2,q_2)$ and $P_{124}(p_1,q_1)$. The common line $f=P_{123}(p_2,q_2)\cap P_{124}(p_1,q_1)$ is

$$\begin{aligned} f: X=F+t\cdot {\varvec{{v}}}, \end{aligned}$$

where $X=(x,y,z)$, $F=(f_1,f_2,0)$, ${\varvec{{v}}}=(v_1,v_2,v_3)$, with

$f_1=(z_2a_3a_4(b_4c_3 - b_3c_4) + z_3a_2a_4(b_2c_4 - b_4c_2) + z_4a_2a_3(b_3c_2 - b_2c_3))/(z_2a_3a_4(a_3b_4 - a_4b_3) + z_3a_2a_4(a_4b_2 - a_2b_4) + z_4a_2a_3(a_2b_3 - a_3b_2))$,

$f_2=(z_2b_3b_4(a_4c_3 - a_3c_4) + z_3b_2b_4(a_2c_4 - a_4c_2) + z_4b_2b_3(a_3c_2 - a_2c_3))/(z_2a_3a_4(a_3b_4 - a_4b_3) + z_3a_2a_4(a_4b_2 - a_2b_4) + z_4a_2a_3(a_2b_3 - a_3b_2))$,

and

$v_1=4a_2a_3a_4(c_2(a_3b_4 - a_4b_3) + c_3(a_4b_2 - a_2b_4) + c_4(a_2b_3 - a_3b_2))$,

$v_2=4(a_3a_4b_2c_2(a_3b_4 - a_4b_3) + a_2a_4b_3c_3(a_4b_2 - a_2b_4) + a_2a_3b_4c_4(a_2b_3 - a_3b_2))$,

$v_3=a_3a_4z_2(a_3b_4 - a_4b_3) + a_2a_4z_3(a_4b_2 - a_2b_4) + a_2a_3z_4(a_2b_3 - a_3b_2)$.

Finally, we verify that the line f is fixed for all planes when P moves along the locus circle (1). Substitution of the coordinates of the line f for x, y and z into the equation of the plane $P_{123}$ yields

$$\begin{aligned} S=K\cdot \Big (4a_2a_3(a_3b_2 - a_2b_3)\cdot t + \frac{a_3b_3z_2 - a_2b_2z_3}{A}\Big ), \end{aligned}$$

where

$$\begin{aligned} K= A(p^2 + q^2) + Bp + Cq + D. \end{aligned}$$

However, for every point P in the locus circle (1) $K=0$ and therefore $S=0$. This implies that for every point P in the locus circle all points of the line f lie in the plane $P_{123}$.

We can conclude:

All planes given by points $X_1,X_2,X_3,X_4$ pass through the line f when P moves along the locus circle, Fig. 4. $\square$

Fig. 4

All planes given by points $X_1,X_2,X_3,X_4$ pass through a fixed straight line f when P moves along the locus circle

Remark 4

Note that if $c_1=c_2=c_3=c_4=0$, then ${\varvec{{v}}}\sim (0,0,1)$. The fixed line f is orthogonal to the xy-plane and intersects all four given lines $k_1,k_2,k_3,k_4$.

4 Conclusion

This paper deals with a 3D version of a variant of the W–S theorem, where four given lines are parallel to a plane. We examine the points P such that the points that are symmetric to P with respect to the given four lines are coplanar. The locus of P is a cylinder of revolution. This fact may be considered as another method of construction of a cylinder of revolution.

Moreover, all planes given by the points that are symmetric to P with respect to the given four lines pass through a fixed line f for every locus point P. Unlike the planar version, where the fixed element is the orthocenter of the triangle, which is given by three lines, the role of the fixed line f with respect to the four given lines is unknown. The authors will try to clarify this in the future.

The authors are still working on additional cases according to the position of the four lines.