Consecutive Colouring of Oriented Graphs

Abstract

We consider arc colourings of oriented graphs such that for each vertex the colours of all out-arcs incident with the vertex and the colours of all in-arcs incident with the vertex form intervals. We prove that the existence of such a colouring is an NP-complete problem. We give the solution of the problem for r-regular oriented graphs, transitive tournaments, oriented graphs with small maximum degree, oriented graphs with small order and some other classes of oriented graphs. We state the conjecture that for each graph there exists a consecutive colourable orientation and confirm the conjecture for complete graphs, 2-degenerate graphs, planar graphs with girth at least 8, and bipartite graphs with arboricity at most two that include all planar bipartite graphs. Additionally, we prove that the conjecture is true for all perfect consecutively colourable graphs and for all forbidden graphs for the class of perfect consecutively colourable graphs.

1 Motivation

A proper edge colouring of a graph with integers such that the colours of edges incident with each vertex form an interval is called consecutive, and the graph for which there exists a consecutive colouring is said to be consecutively colourable. The idea of this colouring first called interval colouring was introduced in 1987 by Asratian and Kamalian in [2] (available in English as [3]), and was motivated by the problem of constructing timetables without breaks for teachers and classes.

It is an NP-complete problem to decide whether a graph is consecutively colourable [15] even in a class of bipartite graphs [24]. However, some classes of graphs have been proved to admit consecutive colourings. For example, trees, regular and complete bipartite graphs [2, 16, 18], doubly convex bipartite graphs, [1, 19], grids [12], and outerplanar bipartite graphs [4, 13] are consecutively colourable. Also some classes of biregular graphs (see e.g. [9, 10, 16, 17, 20]), k-trees [8], generalized Hertz graphs [6], and generalized Sevastjanov rosettes [7] have consecutive colourings. There are many papers devoted to this topic, in particular surveys which can be found in the books [1, 22].

In this paper we consider a variant of the concept of consecutive colourability for oriented graphs. We colour the arcs of an oriented graph in such a way that for each vertex all out-arcs incident with the vertex and all in-arcs incident with the vertex obtain pairwise different colours. The model that we propose can be applied to some real problems, in particular the problem of work without breaks of electronic devices, including telephones, in the scope of handling outgoing and incoming data.

In Sect. 2, we introduce basic definitions and tools. Section 3 deals with the formulation of the main problem of the paper, i.e. the problem of the consecutive colourability of oriented graphs. We analyse its complexity and some special instances. Section 4 shows that the underlying graph of an oriented graph does not contain information needed to solve the problem. This investigation gives a background and motivates the conjecture that for each graph there is a consecutively colourable orientation. In Sect. 5, we formally pose the conjecture confirming it for some classes of oriented graphs and indicating the relationship between the conjecture and some known question. In Sect. 6, we give some concluding remarks.

2 Basic Definitions and Tools

In general, we follow the notation and terminology of [5, 11] in connection with graphs and digraphs, respectively. A graph G consists of a non-empty finite set V(G) of vertices and a finite set E(G) of pairs of distinct vertices called edges. Let G be a graph with vertex set V(G) and edge set E(G). For any $S\subseteq V(G)$ or $S\subseteq E(G)$ the symbol G[S] denotes the subgraph of G induced by S. The set of neighbours of a vertex v in G is denoted by $N_G(v)$, and $N_G[v]=N_G(v)\cup \{v\}$. By $\deg _G(v)$ we mean $|N_G(v)|$ and we call it the degree of a vertex v in a graph G. The maximum degree taken over all vertices of G is denoted by $\Delta (G)$. If there exists $r\in \mathbb {N}$ such that $\deg _G(v)=r$ for every $v\in V(G)$, then G is r-regular (or simply, regular).

A graph G is called connected if for every pair of vertices $u,v\in V(G)$ there exists a path from u to v in G. A maximal connected subgraph of G is called a connected component of G. A graph G is 2-connected if it has more than two vertices and the graph resulting by the removal any of its vertices is a connected graph. A maximal 2-connected subgraph of G is called a block of G. The equality $G=H$ means that graphs G and H are isomorphic. Let $G_1,G_2$ be graphs. By $G_1\cup G_2$ we mean a graph with vertex set $V(G_1)\cup V(G_2)$ and edge set $E(G_1)\cup E(G_2)$. A complete graph, a cycle and a path of order n are denoted by $K_n$, $C_n$ and $P_n$, respectively.

A digraph D consists of a non-empty finite set V(D) of vertices and a finite set A(D) of ordered pairs of distinct vertices called arcs. Let D be a digraph with vertex set V(D) and arc set A(D). For any $S\subseteq V(D)$ the symbol D[S] denotes the subdigraph of D induced by S. If (u, v) is an arc of D, then we say that u and v are adjacent, and that (u, v) is an out-arc of u (or that u dominates v), and that (u, v) is an in-arc of v (or that v is dominated by u). A vertex v is incident with an arc a if $a=(u,v)$ or $a=(v,u)$ for some $u\in V(D)$. The vertices which dominate a vertex v are its in-neighbours and form the set $N_D^-(v)$, the vertices which are dominated by v are its out-neighbours and form the set $N_D^+(v)$. The in-degree $\deg _D^-(v)$ and out-degree $\deg _D^+(v)$ of the vertex v are the numbers $|N_D^-(v)|$ and $|N_D^+(v)|$, respectively. The maximum in-degree and out-degree of D are denoted by $\Delta ^-(D)$ and $\Delta ^+(D)$, respectively. If there exists $r\in \mathbb {N}$ such that $\deg _D^+(v) = \deg _D^-(v)=r$ for each $v\in V(D)$, then D is r-regular (or simply, regular). We say that v is a source or a sink in a digraph D if $\deg _D^-(v)=0$ or $\deg _D^+(v)=0$, respectively. By the union of digraphs $D_1$ and $D_2$ we mean a digraph with vertex set $V(D_1)\cup V(D_2)$ and arc set $A(D_1)\cup A(D_2)$.

With any digraph D we can associate a unique graph G on the same vertex set by replacing each arc by an edge with the same ends. This graph is called the underlying graph of D and we denote it by G(D). A digraph D is said to be connected if its underlying graph G(D) is connected. By a connected component or a block of a digraph D we mean a subdigraph of D induced by vertices of a connected component or a block, respectively, of its underlying graph G(D).

One may also obtain a digraph from a graph G by replacing each edge $\{u,v\}$ by just one of two possible arcs with the same ends, i.e. by either the arc (u, v) or the arc (v, u). Such a digraph is called an orientation of G. A particular orientation of a graph is called an oriented graph. A directed path or a directed cycle is an orientation of a path or cycle in which each vertex dominates its successor in the sequence. An acyclic orientation of a graph is an orientation which does not form any directed cycle and therefore makes it into a directed acyclic graph. If an oriented graph D is acyclic, then there exists an ordering $v_1,v_2,\ldots ,v_n$ of the vertices of D (called an acyclic ordering) such that for every arc $(v_i,v_j)\in A(D)$ we have $i<j$ (see e.g. Proposition 1.4.3 in [5]). Every graph has an acyclic orientation.

In this paper we focus our attention on oriented graphs, i.e. digraphs without directed cycles of length two.

The symbols $\mathbb {Z}$ and $\mathbb {N}$ stand for the set of integers and positive integers, respectively. A proper edge colouring of a graph G is a mapping $c:E(G)\rightarrow \mathbb {Z}$ such that for every $u\in V(G)$ and all $v\in N_G(u)$ the values $c(\{u,v\})$ are pairwise different.

Let A be a finite set of integers. If $\max A-\min A-|A|+1=0$, then the set A is called an interval. A proper edge colouring of a graph such that the colours of edges incident with each vertex form an interval is called consecutive, and a graph for which there exists a consecutive colouring is said to be consecutively colourable.

Definition 1

A proper arc colouring of an oriented graph D is a mapping $c:A(D) \rightarrow \mathbb {Z}$ such that

• (i) for every $u\in V(D)$ and all $v\in N^+_D(u)$ the values c((u, v)) are pairwise different; and

• (ii) for every $u\in V(D)$ and all $v\in N^-_D(u)$ the values c((v, u)) are pairwise different.

Definition 2

A proper arc colouring of an oriented graph such that for each vertex the colours of all out-arcs incident with the vertex and the colours of all in-arcs incident with the vertex form intervals is called consecutive, and an oriented graph for which there exists a consecutive colouring is said to be consecutively colourable.

Notice that a graph (an oriented graph) is consecutively colourable if and only if each of its connected components is consecutively colourable.

3 Consecutive Colourability of Oriented Graphs Problem

We define the Consecutive Colourability of Oriented Graphs (CCOG) problem as a problem of determining whether a consecutive colouring exists for a given oriented graph. At the beginning of this section we investigate the computational complexity of this problem.

Construction 1

Let D be an oriented graph. By $G^*(D)$ we mean a graph obtained by

• (i) the replacement of each vertex $v\in V(D)$ with two vertices $v^+$, $v^-$; and

• (ii) the joining of two vertices $u^+$, $v^-$ by an edge in $G^*(D)$ if and only if there is an arc (u, v) in D.

Immediately from Construction 1, the following facts hold.

Observation 1

If D is an oriented graph, then

• (i) $G^*(D)$ is a bipartite graph with bipartition (A, B) of $V(G^*(D))$, where $A=\{v^+:\; v\in V(D)\}$ and $B=\{v^-:\; v\in V(D)\}$;

• (ii) there exists a bijection $\alpha :E(G^*(D))\rightarrow E(G(D))$ such that $\alpha (\{{u^+,v^-}\})=\{u,v\}$; and

• (iii) if a vertex v is a source (sink, respectively) in D, then $\deg _{G^*(D)}(v^-) = 0$ $(\deg _{G^*(D)}(v^+) = 0{, respectively}$).

Theorem 1

If D is an oriented graph, then D is consecutively colourable if and only if $G^*(D)$ is consecutively colourable.

Proof

Suppose that D is consecutively colourable and $c_1$ is a consecutive colouring of D. We define a consecutive colouring $c_2$ of $G^*(D)$ in the following way: $c_2(\{u^+,v^-\})=c_1((u,v))$. Similarly, if $G^*(D)$ is consecutively colourable and $c_2$ is a consecutive colouring of $G^*(D)$, then we define a consecutive colouring $c_1$ of the oriented graph D putting $c_1((u,v)) = c_2( \{ u^+ , v^- \} )$. It is very easy to see that in both cases $c_2$, $c_1$, respectively, are well defined consecutive colourings. $\square$

Corollary 1

If D is an oriented graph in which each vertex is either a sink or a source, then D is consecutively colourable if and only if its underlying graph G(D) is consecutively colourable.

Proof

If an oriented graph D satisfies the assumptions, then by Construction 1 and Observation 1(iii) there exists a subset X of the set $V(G^*(D))$ consisting of the vertices of degree zero in $G^*(D)$ such that $G^*(D)-X$ is isomorphic to G(D). Thus, $G^*(D)$ is consecutively colourable if and only if $G^*(D)-X$ is consecutively colourable, and consequently, if and only if G(D) is consecutively colourable. The application of Theorem 1 finishes the proof.$\square$

Notice that if G is a bipartite graph with bipartition (A, B) of the vertex set V(G), then we can define an oriented graph D as an orientation of G such that (u, v) is an arc of D when $u\in A$ and $v\in B$. Hence, for each bipartite graph G there exists an orientation D of G in which every vertex is either a sink or a source and the equality $G(D)=G$ holds.

Theorem 2

The problem CCOG is NP-complete.

Proof

Obviously, CCOG is in NP. We shall observe that there is a polynomial reduction from the problem of the consecutive colourability of bipartite graphs (known to be NP-complete) to CCOG. Based on an instance G, we construct an instance D for CCOG in which every vertex of D is either a source or a sink, and such that $G(D)=G$. By Corollary 1, G is consecutively colourable if and only if D is consecutively colourable. $\square$

We know that CCOG problem is NP-complete but some of the instances of this problem can be showed simply based on Theorem 1.

A decycling set of a graph is a set of edges that must be removed from this graph to destroy all its cycles. The cyclomatic number of a graph is the minimum cardinality of its decycling set. It is known that this number for a given graph G is equal to $|E(G)|-|V(G)|+k$, where k is the number of connected components of G.

Proposition 1

Let D be an oriented graph. If $k\in \mathbb {N}$ and is a cycle in $G^*(D)$, then $( v_1,v_2, \ldots , v_{2k-1}, v_{2k} )$ is a closed trail in G(D), and consequently the cyclomatic number of $G^*(D)$ does not exceed the cyclomatic number of G(D).

Proof

Consider a bijection $\alpha$ given by Observation 1(ii). Notice that if a set of edges induces a cycle in $G^*(D)$, then the set of their images by $\alpha$ induces a closed trail in G(D). Hence, if a set of edges of G(D) is a decycling set in this graph, then the set of their inverse images by $\alpha$ is a decycling set in $G^*(D)$. Indeed, if it was not a truth, then after deleting these edges from the graph $G^*(D)$, we would have at least one cycle in the subgraph of $G^*(D)$. Thus, we would have at least one closed trail in G(D), and consequently, at last one cycle in a graph G(D), which is a contradiction with the definition of the decycling set. $\square$

The next proposition is a consequence of facts that have been proved for graphs and can be found e.g. in [22] (Chapter 8 with appropriate references). In this book one can find results that all bipartite graphs with maximum degree at most three (i.e. subcubic graphs) and all bipartite graphs with a cyclomatic number at most eight are consecutively colourable. In the same survey one can also find the result that all bipartite graphs with at most fourteen vertices have consecutive colourings, and it was shown in [21] that all such graphs on fifteen vertices are consecutively colourable.

Proposition 2

Let D be an oriented graph. If at least one of the following conditions is satisfied, then D is consecutively colourable.

• (i) $\Delta ^+(D)\le 3$ and $\Delta ^-(D)\le 3$;

• (ii) the cyclomatic number of G(D) is at most 8;

• (iii) $2|V(D)|-s(D)\le 15$, where s(D) is the number of vertices in D that are either a sink or a source;

• (iv) $|V(D)|\le 7$; or

• (v) there exists $r\in \mathbb {N}$ such that D is r-regular.

Proof

Notice that each of the conditions (i)–(v) implies the statement by Theorem 1 provided that the graph $G^*(D)$ is consecutively colourable.

(i) Since $\Delta ^+(D)\le 3$ and $\Delta ^-(D)\le 3$, we have $\Delta (G^*(D))\le 3$. Thus, the graph $G^*(D)$ is consecutively colourable, because all bipartite subcubic graphs are consecutively colourable.

(ii) If the cyclomatic number of G(D) is at most 8, then by Proposition 1 the cyclomatic number of $G^*(D)$ is at most 8. Thus, the graph $G^*(D)$ is consecutively colourable, since all bipartite graphs with such cyclomatic number are consecutively colourable.

(iii) Notice that by Observation 1(iii) and Construction 1, there exists a subset X of the set $V(G^*(D))$ consisting of the vertices of degree zero in $G^*(D)$ such that $|X|=s(D)$ and $G^*(D)-X$ is a bipartite graph. Moreover, $|V(G^*(D)-X)|=2|V(D)|-s(D)\le 15$. Since all bipartite graphs with at most fifteen vertices are consecutively colourable, we obtain that $G^*(D)-X$ is consecutively colourable, and consequently, $G^*(D)$ is consecutively colourable.

(iv) It follows immediately from (iii).

(v) Since we have the same out-degrees and in-degrees in the oriented graph D, Construction 1 implies that $G^*(D)$ is a bipartite r-regular graph. It is known from König’s Theorem that the chromatic index (the minimum number of colours in a proper edge colouring) and the maximum degree of each bipartite graph are equal. Thus, there exists a proper edge colouring of $G^*(D)$ with r colours that must be consecutive. $\square$

Notice that Proposition 2 (v) concerns e.g. well known circulant oriented graphs. Moreover, from the proof of this proposition we have something more.

Observation 2

For every r-regular oriented graph there exists a consecutive colouring with r colours.

By an identification of two nonadjacent vertices $v_1$ and $v_2$ in a graph G (an oriented graph D, respectively) into a vertex w, we mean the result of the following operations on G (on D, respectively): the removal of vertices $v_1,v_2$, the addition of a new vertex w and the addition of the edges $\{w,v\}$ for all $v\in N_G(v_1)\cup N_G(v_2)$ (the arcs (w, v) for all $v\in N^+_D(v_1)\cup N^+_D(v_2)$ and (v, w) for all $v\in N^-_D(v_1)\cup N^-_D(v_2)$, respectively).

It is known that when two vertices of a graph are contained in different connected components of this graph, then the identification of these vertices in the graph preserves the consecutive colourability. For oriented graphs the analogous statement will be true if some additional conditions are satisfied.

Theorem 3

Let $D_1$, $D_2$ be disjoint oriented graphs, $v_1\in V(D_1)$, $v_2\in V(D_2)$, and let D be an oriented graph obtained by an identification of $v_1$ and $v_2$ in $D_1\cup D_2$. If both $D_1$, $D_2$ are consecutively colourable and for at least one $i\in \{1,2\}$ the vertices $v_i^+$, $v_i^-$ are contained in different connected components of $G^*(D_i)$, then D is consecutively colourable.

Proof

Without loss of generality we can assume that the vertices $v_2^+$, $v_2^-$ are contained in different connected components of $G^*(D_2)$.

Denote by $G^\prime$ and $G^{\prime \prime }$ the connected component of $G^*(D_2)$ that contains $v_2^+$ and the union of all remaining connected components of $G^*(D_2)$, respectively. Construction 1 implies that $G^*(D)$ is obtained as a result of two subsequent identifications:

• the vertices $v_1^+$ and $v_2^+$ in the union of $G^*(D_1)$ and $G^\prime$, and next

• the vertices $v_1^-$ and $v_2^-$ in the union of the result of the first identification and $G^{\prime \prime }$.

Note that graphs used in both identifications are disjoint. Since $D_1$, $D_2$ are consecutively colourable, the graphs $G^*(D_1)$, $G^*(D_2)$ are also consecutively colourable, by Theorem 1. Thus, connected components of $G^*(D_2)$ and all their possible unions are consecutively colourable. The proof follows by the preservation of the consecutive colourability of graphs with respect to the identification operation applied to disjoint graphs. $\square$

Corollary 2

If $D_1$, $D_2$ are disjoint consecutively colourable oriented graphs, $v_1\in V(D_1)$, $v_2\in V(D_2)$ and $G(D_2)$ is a forest, then the oriented graph obtained by the identification of $v_1$ and $v_2$ in $D_1\cup D_2$ is consecutively colourable.

Proof

Clearly, when $G(D_2)$ is a forest, then the vertices $v_2^+$ and $v_2^-$ are contained in different connected components of $G^*(D_2)$. Theorem 3 implies the assertion. $\square$

If G is a fixed graph, and $c:E(G)\rightarrow \mathbb {Z}$ is a proper edge colouring of G, then we denote by S(v, c) the set of colours of the edges incident with a vertex $v\in V(G)$ in the colouring c.

If D is a fixed oriented graph, and $c:A(D)\rightarrow \mathbb {Z}$ is a proper arc colouring of D, then we denote by $S^+(v,c)$ and $S^-(v,c)$ the set of colours of the out-arcs and in-arcs, respectively, incident with a vertex $v\in V(D)$ in the colouring c. If $D^{\prime }$ is a subdigraph of D, then we denote by $S^+(v,c)_{|D'}$ and $S^-(v,c)_{|D'}$ the set of colours of the out-arcs in $D^{\prime }$ and in-arcs in $D^{\prime }$, respectively, incident with a vertex $v\in V(D)$ in the colouring c.

Theorem 4

If each block of an oriented graph D is regular, then D is consecutively colourable.

Proof

Let t be the number of blocks of D. We will show that D is consecutively colourable using the induction on t. More precisely, we will show a little bit more proving that there exists a consecutive colouring c of D such that for every block $D^{\prime }$ of D and every vertex $v\in V(D)$ both sets of colours $S^+(v,c)_{|D'}$ and $S^-(v,c)_{|D'}$ are the same and are intervals.

Suppose that $t=1$. In this case D is a regular oriented graph and satisfies the assertion by Observation 2. Let us assume that D has t, $t\ge 2$, blocks. Next, let $D_1$ be a block of D whose all, except one, vertices belong to exactly one block (so-called end block) and let v be this exceptional vertex of $D_1$ belonging to more than one blocks. Let $D_2=D[(V(D)\setminus V(D_1))\cup \{v\}]$. For $i=1,2$, in $D_i$ we rename v to $v_i$. Notice that D can be obtained from two oriented graphs $D_1$ and $D_2$ by an identification of vertices $v_1\in V(D_1)$ and $v_2\in V(D_2)$ into a vertex v in $D_1\cup D_2$. By the induction hypothesis there exist a consecutive colouring $c_1$ of the oriented graph $D_1$ such that the sets of colours $S^+(v_1,c_1)$ and $S^-(v_1,c_1)$ are the same, and a consecutive colouring $c_2$ of the oriented graph $D_2$ such that the sets of colours $S^+(v_2,c_2)_{|D''}$ and $S^-(v_2,c_2)_{|D''}$ are the same for every block $D^{\prime \prime }$ of $D_2$. Now, we rename colours of the consecutive colouring $c_1$ (if it is necessary) such that the colours in $S^+(v_1,c_1)$ and $S^+(v_2,c_2)$ are pairwise different and create an interval. We finish the inductive proof taking a colouring c of D such that $c(e)=c_1(e)$ if $e\in E(D_1)$ and $c(e)=c_2(e)$ if $e\in E(D_2)$. Of course, c is the consecutive colouring of the oriented graph D. $\square$

4 Consecutive Colourability of an Oriented Graph and Its Underlying Graph

Notice that Corollary 1 leads to the conclusion that problems of the consecutive colourability of a graph and its underlying graph can be equivalent.

In this section we show that such relation is not always true. There are oriented graphs that are consecutively colourable whose underlying graphs are not consecutively colourable. There are also oriented graphs that are not consecutively colourable whose underlying graphs are consecutively colourable.

Observation 3

Every orientation of a cycle $C_n$, $n\ge 3$, is consecutively colourable.

Proof

It is enough to notice that the cyclomatic number of G(D) equals one for any orientation D of $C_n$ and apply Proposition 2(ii). $\square$

It should be mentioned here that an orientation of $K_n$ is known in the literature as a tournament, and a tournament is transitive if it is acyclic.

Theorem 5

Every transitive tournament is consecutively colourable.

Proof

Let D be a transitive tournament and let $v_1,v_2,\ldots ,v_n$ be an acyclic ordering of vertices of D. To notice that D is consecutively colourable it is enough to define a proper arc colouring c such that $c((v_i,v_j))=j-i$. Indeed,

$$\begin{aligned}&S^+(v_1,c)=\{1,\ldots ,n-1\},\;\, S^-(v_1,c)=\emptyset , \\&S^+(v_i,c)=\{1,\ldots ,n-i\},\;\, S^-(v_i,c)=\{1,\ldots ,i-1\}, \;for \;2\le i\le n-1,\\&S^+(v_n,c)=\emptyset ,\qquad \qquad \quad S^-(v_n,c)=\{1,\ldots ,n-1\}, \end{aligned}$$

which confirms that c is a consecutive colouring of D. $\square$

Recall that for every odd $n\in \mathbb {N}$, a complete graph $K_n$ and a cycle $C_n$ are not consecutively colourable [15]. However, Theorem 5 and Observation 3 immediately imply that there exist orientations of $K_n$ and $C_n$ that are consecutively colourable. Moreover, by Proposition 2(iv), if $n\le 7$, then every orientation of $K_n$ is consecutively colourable.

In the next part of this section we construct an infinite family of oriented graphs that are not consecutively colourable whose underlying graphs are consecutively colourable. Since the presentation of this family is a little bit complicated, first we show the most notable element of this family in Example 1.

To present Example 1 and its generalization, we recall the definition of the generalized Sevastjanov rosette (for details see [7]).

Definition 3

([7], Definition 3) Let $l_i,s_i\in \mathbb {N}$ for $i\in \{1,2,3\}$, and let all $s_i$ be even, $\mathbf{l}=(l_1,l_2,l_3)$ and $\mathbf{s}=(s_1,s_2,s_3)$. The graph denoted by $S_{\mathbf{l},\mathbf{s}}$ and presented in Fig. 1 is called the generalized Sevastjanov rosette.

Fig. 1

The graph $S_{\mathbf{l},\mathbf{s}}$

Note that $s_i$ is the length of the path opposite to $y_i$ that joins $y_j$ and $y_k$, where $i,j,k\in \{1,2,3\}$ and i, j, k are different indices. In what follows we consider an induced subgraph $H_i$ of the graph $G=S_{\mathbf{l},\mathbf{s}}$, where $H_i=G\left[ N_{G}[y_i]\cup \{x\}\right]$, $i\in \{1,2,3\}$.

In [14], it was shown that if $\mathbf{s}=(2,2,2)$ and $\mathbf{l}=(l,l,l)$, where $l\ge 7$, then the generalized Sevastjanov rosette $S_{\mathbf{l},\mathbf{s}}$ is not consecutively colourable.

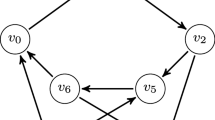
Example 1

Figures 2 and 3 show an oriented graph D and a consecutive colouring of its underlying graph G(D). Notice that D is not consecutively colourable since one of the connected components of the graph $G^*(D)$ is isomorphic to the generalized Sevastjanov rosette $S_{\mathbf{l},\mathbf{s}}$, where $\mathbf{l}=(7,7,7)$ and $\mathbf{s}=(2,2,2)$ (see Fig. 4).

Fig. 2

An oriented graph D which is not consecutively colourable

Fig. 3

The underlying graph G(D) which is consecutively colourable

Fig. 4

The graph $G^*(D)$ which is not consecutively colourable

To show the generalization of Example 1 we recall some definitions and two useful theorems [7].

Let ${\mathfrak {N}}$ denote the class of all consecutively colourable graphs. Among graphs which do not have any consecutive colouring we emphasize these ones that lack little to be consecutive colourable. Referring to this purpose the following two classes of graphs are defined and investigated in [6, 7].

$$\begin{aligned} {\mathfrak {N}}_{\le }&= \left\{ G:\hbox {each induced subgraph } H \hbox { of }G\hbox { satisfies }H\in {\mathfrak {N}}\right\} , \\ {{\mathcal {C}}}({\mathfrak {N}}_{\le })&= \left\{ G\!\notin \!{\mathfrak {N}}_{\le }:\hbox {each proper induced subgraph } H \hbox { of }G\hbox { satisfies }H\!\in \! {\mathfrak {N}}_{\le }\right\} \!. \end{aligned}$$

Graphs in ${\mathfrak {N}}_{\le }$ are called perfect consecutively colourable, and graphs in ${{\mathcal {C}}}({\mathfrak {N}}_{\le })$ are forbidden graphs for the class of perfect consecutively colourable graphs.

Notice that if G belongs to ${\mathfrak {N}}_{\le }$, then G has to be bipartite. Indeed, if it was not a truth, then an odd cycle would be an induced subgraph of G, which is impossible since every odd cycle is not consecutively colourable. Thus, G is bipartite and consecutively colourable. Moreover, it is observed in [6] that the only non-bipartite graphs in ${{\mathcal {C}}}({\mathfrak {N}}_{\le })$ are odd cycles.

Theorem 6

([7], Theorem 4) If $l_i,s_i\in \mathbb {N}$ for $i\in \{1,2,3\}$, and all $s_i$ are even, $\mathbf{l}=(l_1,l_2,l_3)$ and $\mathbf{s}=(s_1,s_2,s_3)$, then

$$\begin{aligned} S_{\mathbf{l},\mathbf{s}}\in {\mathcal {C}}({\mathfrak {N}}_{\le })\end{aligned}$$

if and only if $l_i=s_i+5$ for every $i\in \{1,2,3\}$.

Theorem 7

([7], Theorem 1) Let $l\in \mathbb {N}$, $i,j,a\in \mathbb {Z}$, $i< j$. Let G be the graph presented in Fig. 5. If $c'$ is a precolouring of G such that $c'(\{x,v_k\})=a+k$ for $1\le k\le l$, $c'(\{y,z_1\})=i$ and $c'(\{y,z_2\})=j$, then there exists a consecutive colouring c of G that is an extension of $c'$ if and only if one of the following conditions is satisfied.

• (i) $i,j\in \{a,\ldots ,a+l+1\}$ and $j-i$ is an odd integer;

• (ii) $i=a-1$ and $j\in \{a,\ldots ,a+l\}$, and $j-i$, l have different parity;

• (iii) $i\in \{a+1,\ldots ,a+l+1\}$ and $j=a+l+2$, and $j-i$, l have different parity;

• (iv) $i=a-2$ and $j=a-1$; or

• (v) $i=a+l+2$ and $j=a+l+3$.

Fig. 5

The graph G

Now, we are ready to construct an infinite family of oriented graphs that are not consecutively colourable and whose underlying graphs are consecutively colourable.

Theorem 8

Let $s_i\in \mathbb {N}$ be even and $l_i=s_i+5$ for $i\in \{1,2,3\}$, $\mathbf{s}=(s_1,s_2,s_3)$, $\mathbf{l}=(l_1,l_2,l_3)$. Let z be any of the vertices $a_{2,i}$ of $S_{\mathbf{l},\mathbf{s}}$, where i is an odd integer in the set $\{1,\ldots ,s_2-1\}$. If ${\widetilde{S}}$ is a graph obtained from $S_{\mathbf{l},\mathbf{s}}$ by the identification of vertices z and x in $S_{\mathbf{l},\mathbf{s}}$, then there exists an orientation of the graph ${\widetilde{S}}$ that is not consecutively colourable, while ${\widetilde{S}}$ is consecutively colourable.

Proof

Figure 6 shows simultaneously the orientation D of ${\widetilde{S}}$ that satisfies the statement of the theorem and a precolouring of the graph ${\widetilde{S}}$. The existence of the consecutive colouring c of ${\widetilde{S}}$ follows directly by application of Theorem 7 to the induced subgraphs $H_1,H_2,H_3$ of the graph G(D). More precisely, we apply Theorem 7(i) to the induced subgraph $H_1$ of the graph G(D) ($j=l_1+l_2+l_3+2$, $i=l_1+l_2+2$, and $j-i=l_3=s_3+5$ is odd), Theorem 7(ii) to the induced subgraph $H_2$ ($j=l_1+l_2+1$, $i=l_1$, and $j-i=l_2+1$ and $l_2$ have different parity), and Theorem 7(i) to the induced subgraph $H_3$ ($j=l_1+1$, $i=1$, and $j-i=l_1=s_1+5$ is odd). Moreover, we colour alternately, using appropriate colours, two even paths joining $y_1$ with $y_2$ and $y_2$ with $y_3$, and two odd paths joining $y_1$ with x and $y_3$ with x in the graph ${\widetilde{S}}$ (see Fig. 6).

The oriented graph D is not consecutively colourable since one of the connected components of $G^*(D)$ is isomorphic to the generalized Sevastjanov rosette $S_{(s_1+5,s_2+5,s_3+5) , (s_1,s_2,s_3) }$ which is not consecutively colourable by Theorem 6. $\square$

Fig. 6

An oriented graph D that is not consecutively colourable whose underlying graph G(D) is consecutively colourable

5 Consecutive Colouring Conjecture

Investigations given in the previous sections provoke us to state the following conjecture.

Conjecture 1

For each graph G there exists an orientation of G that is consecutively colourable.

In this section we show that Conjecture 1 holds for some classes of graphs, and we compare it with another question posed by Maria Axenovich.

A graph G is 2-degenerate if every subgraph of G has a vertex of degree at most 2. Recall that for each 2-degenerate graph G there is an ordering $v_1, \ldots ,v_n$ of vertices of G such that for every $1\le i\le n$, the vertex $v_i$ has at most two neighbours in the set $\{v_1, \ldots ,v_{i-1}\}$ [23].

We also know that there are 2-degenerate graphs that are not consecutively colourable (see e.g. [8]) but, in the forthcoming theorem, we show that Conjecture 1 holds for this class of graphs.

Theorem 9

For each 2-degenerate graph G there is an orientation of G that is consecutively colourable.

Proof

Note that the theorem holds when $|V(G)|=1$. Hence, in the next part of the proof we assume $n=|V(G)|\ge 2$. Let $v_1, \ldots ,v_n$ be an ordering of vertices of G such that for each $1\le i\le n$, the vertex $v_i$ has at most two neighbours in the set $\{v_1, \ldots ,v_{i-1}\}$, and let $G_i=G[\{v_1, \ldots ,v_i\}]$. We define an orientation of edges of G, step by step, extending the orientation of $G_{i-1}$ to the orientation of $G_{i}$ for $2\le i\le n$.

We choose freely one of at most two possible orientations of $G_2$ (either $G_2=K_2$ or $G_2=\overline{K_2}$). Next, for $3\le i\le n$, in the i-th step, we orient edges incident with $v_i$ whose second ends are in $\{v_1, \ldots ,v_{i-1}\}$. When there is at most one such edge, then we orient it arbitrarily. When there are two such edges and x, y are neighbours of $v_i$ in $\{v_1, \ldots ,v_{i-1}\}$, then we construct either two arcs $(v_i,x)$ and $(y,v_i)$ or two arcs $(v_i,y)$ and $(x,v_i)$. Denote by D the oriented graph obtained after the n-th step (D is the special orientation of G). We shall observe that $G^*(D)$ is a forest. Since each forest is consecutively colourable, the proof will be completed by Theorem 1.

Let $D_i=D[\{v_1,\ldots ,v_i\}]$. We prove that $G^*(D)$ is a forest by showing that $G^*(D_i)$ is a forest for each $2\le i\le n$. In the case $i=2$ the graph $G^*(D_i)$ has at most one edge, which obviously confirms the statement. Suppose that the statement holds for each i that is less than n, i.e. $G^*(D_i)$ is a forest for $i<n$. Note that $G^*(D_{i+1})$ is obtained from $G^*(D_i)$ by adding two new vertices $v_{i+1}^+, v_{i+1}^-$ and at most two new edges, $\{v_{i+1}^+,v_s^-\}$, $\{v_{i+1}^-,v_t^+\}$, where $v_s,v_t$ are two different vertices in $\{v_1, \ldots ,v_{i}\}$. Thus $G^*(D_{i+1})$ is a forest and next $G^*(D_j)$ is a forest for all $i+2\le j\le n$, especially for $j=n$. It completes the proof. $\square$

The next theorem leads to the reformulation of Conjecture 1 for some cases.

Proposition 3

Let G be a bipartite graph with bipartition (A, B), let D be any orientation of G, and

$$\begin{aligned} \begin{array}{c} E_1=\left\{ \{u,v\}\in E(G):(u,v)\in A(D), u\in A, v\in B\right\} , \\ E_2=\left\{ \{u,v\}\in E(G):(u,v)\in A(D), u\in B, v\in A\right\} . \end{array} \end{aligned}$$

Then D is consecutively colourable if and only if both graphs $G[E_1]$ and $G[E_2]$ are consecutively colourable.

Proof

Let $G_1=G[E_1]$, $G_2=G[E_2]$. Thus, by Construction 1, $G^*(D)=G_1\cup G_2\cup rK_1$, where $r=2|V(G)|-(|V(G_1)|+|V(G_2)|)$. Hence, D is consecutive colourable if and only if $G^*(D)$ is consecutively colourable (by Theorem 1) if and only if each component of $G^*(D)$, so also $G_1$ and $G_2$, is consecutively colourable. $\square$

In light of Proposition 3, Conjecture 1 for bipartite graphs can be rewritten in the following way.

For each bipartite graph there exists a partition of its edges into two parts so that both graphs induced by partition parts are consecutively colourable.

We do not know whether or not there exists a similar reformulation of Conjecture 1 for non-bipartite graphs. On the other hand, we realized that in 2013 Maria Axenovich (during a conference discussion) also asked about the existence of such partition for an arbitrary graph (not necessarily bipartite). We do not know the relationship between Conjecture 1 and the question posed by Maria Axenovich in the case of non-bipartite graphs. However, for bipartite graphs, we can conclude some facts.

The arboricity of a graph G is the minimum number of parts into which the set E(G) can be partitioned in such a way that a graph induced in G by each part is a forest. Since each forest is consecutively colourable and the arboricity of each planar bipartite graph is not greater than two (see e.g. [25]), we have the following two results.

Corollary 3

For each bipartite graph G whose arboricity is at most two there exists an orientation of G that is consecutively colourable.

Corollary 4

For each planar bipartite graph G there exists an orientation of G that is consecutively colourable.

As a corollary from the next theorem, we will obtain similar result for all planar graphs with girth at least 8. Recall that the girth of a graph G is the minimum length of a cycle contained in G.

Theorem 10

If the set of edges of a graph G can be partitioned into two sets $E_1,E_2$ so that the subgraph $G[E_1]$ is bipartite and consecutively colourable and $E_2$ is a matching of G, then there exists an orientation of G that is consecutively colourable.

Proof

Let $G_1=G[E_1]$. Since $G_1$ is a bipartite graph, there exists an orientation $D_1$ of $G_1$ such that every vertex is either a sink or a source in $D_1$. Now, we define an orientation of the edges in $E_2$. Let $e=\{u,v\}\in E_2$. If u and v are either both sinks or both sources in $D_1$ or at least one vertex of u and v is not a vertex of $D_1$, then we orient the edge e arbitrarily. If one vertex of u and v is a sink in $D_1$ and the other one is a source in $D_1$, then we construct an arc (u, v) when u is a sink, and an arc (v, u) otherwise. Denote by $D_2$ and D the oriented graph induced by the oriented edges from $E_2$ and E(G), respectively.

Notice that the fact that the graph $G_1$ is consecutively colourable implies that $D_1$ is consecutively colourable by Corollary 1, and consequently by Theorem 1, we have that $G^*(D_1)$ is also consecutively colourable. Moreover, Construction 1 implies that $G^*(D)=G^*(D_1)\cup G^*(D_2)$. Notice also that $G^*(D_1)$ and $G^*(D_2)$ can have isolated vertices and their edges can be incident in the graph $G^*(D)$. Let k be the number of edges of $G^*(D_2)$ each of which is not incident with any edge of $G^*(D_1)$. Clearly, $k\le |E_2|$. Observe that $G^*(D)$ is a union of k graphs $K_2$, a graph H obtained from $G^*(D_1)$ by the attachment of $|E_2|-k$ pendant edges, and some number of graphs $K_1$. Since the identification of vertices contained in different connected components of a consecutively colourable graph preserves the consecutive colourability, we have that the sequential attachment of pendant edges to a consecutively colourable graph preserves the consecutive colourability. Hence, the graph H is consecutively colourable, and consequently also $G^*(D)$ is consecutively colourable, and by Theorem 1, D is consecutively colourable. If G had isolated vertices, then its orientation that is the union of D and some number of graphs $K_1$ would be also consecutively colourable. $\square$

In [26], it was proved that edges of every planar graph G with girth at least 8 can be partitioned into two sets $E_1,E_2$ so that the graph $G[E_1]$ is a forest and $E_2$ is a matching of G. Since every forest is bipartite and consecutively colourable, Theorem 10 implies the following result.

Corollary 5

For each planar graph G with girth at least 8 there exists an orientation of G that is consecutively colourable.

Now, we come back to graphs in ${\mathfrak {N}}_{\le }$ or ${{\mathcal {C}}}({\mathfrak {N}}_{\le })$ showing that all of them confirm Conjecture 1.

Observation 4

If $G\in {\mathfrak {N}}_{\le }$, then there exists an orientation of G that is consecutively colourable.

Proof

Recall that if G belongs to ${\mathfrak {N}}_{\le }$, then G is a bipartite and consecutively colourable graph. Since for each bipartite graph G there exits an orientation D of G in which every vertex is either a sink or a source and $G(D)=G$, the proof follows by Corollary 1. $\square$

Lemma 1

Let D be an oriented graph such that G(D) is a bipartite graph with bipartition (A, B) and $G(D)\in {{\mathcal {C}}}({\mathfrak {N}}_{\le })$.

• (i) If each vertex of D is either a sink or a source, then D is not consecutively colourable.

• (ii) If D is an oriented graph obtained from an oriented graph in which each vertex is either a sink or a source by changing the orientation of every arc incident with at least one, but not all, fixed vertices from A, then D is consecutively colourable.

Proof

(i) Since $G(D)\in {{\mathcal {C}}}({\mathfrak {N}}_{\le })$, we have that G(D) is not consecutively colourable, and the result follows by Corollary 1.

To prove (ii) let $D'$ be an oriented graph in which every vertex is either a sink or a source such that D is an oriented graph obtained from $D'$ by changing the orientation of every arc incident with each vertex in $V_1$, where $V_1$ is a proper non-empty subset of A. Notice that $V(D)=V(D')=V(G(D))$. Let $E_1 = \{ e \in E(G(D) ):e \hbox { is incident with } v,\hbox {where } v \in V_1 \}$, $E_2=E(G(D))\setminus E_1$, and let $B_i=\{v\in B: v \hbox { is incident with }e,\hbox {where }e\in E_i\}$ for $i\in \{1,2\}$. Notice that $B_1$ and $B_2$ are some non-empty subsets of B. Clearly, $G(D)[E_1]$ and $G(D)[E_2]$ are subgraphs of G(D) induced by vertex sets $V_1\cup B_1$ and $(A\setminus V_1)\cup B_2$, respectively. Thus, by the definition of ${{\mathcal {C}}}({\mathfrak {N}}_{\le })$, the graphs $G(D)[E_1]$ and $G(D)[E_2]$ are consecutively colourable, and the statement follows by Proposition 3. $\square$

Theorem 11

If $G\in {{\mathcal {C}}}({\mathfrak {N}}_{\le })$, then there exists an orientation of G that is consecutively colourable.

Proof

Recall that only non-bipartite graphs in ${{\mathcal {C}}}({\mathfrak {N}}_{\le })$ are odd cycles. Observation 3 implies the required orientation in this case. In the case of bipartite graphs in ${{\mathcal {C}}}({\mathfrak {N}}_{\le })$ we can apply Lemma 1(ii). $\square$

6 Concluding Remarks

In this work, we pose the conjecture of the existence of consecutively colourable orientation of any graph. It is worth noting that this conjecture was supported by partial results. In particular, we showed its validity for all bipartite consecutively colourable graphs, perfect consecutively colourable graphs, forbidden graphs for perfect consecutively colourable graphs, 2-degenerate graphs and complete graphs. In addition, we proved the validity of the conjecture for all bipartite graphs having decomposition of the edge set into two subsets that induce forests, and for all graphs having decomposition of the edge set into two subsets such that one of them is a matching and the second one induces a consecutively colourable bipartite graph. In particular, it confirms the conjecture for all planar bipartite graphs and all planar graphs with girth at least 8.