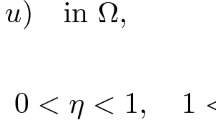Abstract
We consider a nonlinear Dirichlet problem driven by the (p, q)-Laplacian and with a reaction which is parametric and exhibits the combined effects of a singular term and of a superdiffusive one. We prove an existence and nonexistence result for positive solutions depending on the value of the parameter \(\lambda \in \overset{\circ }{{\mathbb {R}}}_+=(0,+\infty )\).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let \(\Omega \subseteq {\mathbb {R}}^N\) be a bounded domain with a \(C^2\)-boundary \(\partial \Omega \). In this paper, we study the following singular (p, q)-equation with logistic perturbation

For \(r\in (1,\infty )\) we denote the r-Laplace differential operator defined by
In problem (P\(_\lambda \)) we have the sum of two such operators with different exponents which implies that the differential operator on the left-hand side is not homogeneous. The right-hand side of (P\(_\lambda \)) has the combined effects of a singular term \(s \rightarrow \lambda s^{-\eta }\) for \(s>0\) with \(0<\eta <1\) and of a perturbation which is of logistic type, namely the function \(s \rightarrow \lambda s^{\theta -1}-f(x,s)\) for almost all (a. a.) \(x\in \Omega \). The function \(f:\Omega \times {\mathbb {R}}\rightarrow {\mathbb {R}}\) is a Carathéodory function, that is, \(x\mapsto f(x,s)\) is measurable for all \(s\in {\mathbb {R}}\) and \(s\mapsto f(x,s)\) is continuous for a. a. \(x\in \Omega \). We assume that \(f(x,\cdot )\) is \((\theta -1)\)-superlinear as \(s \rightarrow +\infty \) for a. a. \(x\in \Omega \). So, the logistic perturbation is of the superdiffusive type. We are interested in positive solutions whenever the parameter \(\lambda \) is positive.
Parametric superdiffusive logistic equations with no singular term present, were investigated by Afrouzi–Brown [1] (for semilinear Dirichlet problems), Takeuchi [23, 24] (for nonlinear Dirichlet problems driven by the p-Laplacian), Gasiński–O’Regan–Papageorgiou [3] (for nonlinear Dirichlet problems driven by a nonhomogeneous differential operator), Cardinali–Papageorgiou–Rubbioni [2], Gasiński–Papageorgiou [7] (both dealing with nonlinear problems driven by the p-Laplacian) and Papageorgiou–Rădulescu-Repovš [16] (for semilinear mixed problems). These works reveal that the superdiffusive logistic equations exhbit a kind of “bifurcation” for large values of the parameter \(\lambda >0\). More precisely, there is a critical parameter value \(\lambda _*>0\) such that the problem has at least two positive solutions for all \(\lambda >\lambda _*\), the problem has at least one positive solution for \(\lambda =\lambda _*\) and there are no positive solutions for \(\lambda \in (0,\lambda _*)\). This is in contrast to subdiffusive and equidiffusive logistic equations for which we do not have multiplicity of positive solutions, see Papageorgiou–Winkert [19].
When we introduce a singular term in the reaction, the geometry of the problem changes since \(u=0\) is no longer a local minimizer of the energy functional and so we cannot have a multiplicity result. In addition, the singular term generates an energy functional which is not \(C^1\) and so we have difficulties in using the results of critical point theory. Therefore, we need to find a way to bypass the singular term and deal with a \(C^1\)-functional to which we can apply the results of the critical point theory. Nonlinear singular problems but with a different kind of perturbation were studied recently by Papageorgiou-Winkert [20] (equations driven by the p-Laplacian) and by Papageorgiou–Rădulescu-Repovš [15] (equations driven by a nonhomogeneous differential operator).
The main result of our work here establishes the existence of a critical parameter \(\lambda _*\) such that
-
problem (P\(_\lambda \)) has at least one positive smooth solution for all \(\lambda \ge \lambda _*\);
-
problem (P\(_\lambda \)) has no positive solutions for all \(\lambda < \lambda _*\).
Finally we mention that equations driven by the sum of two differential operators of different nature (such as (p, q)-equations) arise in many mathematical models of physical processes. We refer to the survey papers of Marano–Mosconi [12] and Rădulescu [22].
2 Preliminaries and Hypotheses
In this section we present some preliminaries which are needed in the sequel and also the hypotheses on the data of problem (P\(_\lambda \)).
For every \(1 \le r< \infty \) we consider the usual Lebesgue spaces \(L^r(\Omega )\) and \(L^r(\Omega ; {\mathbb {R}}^N)\) equipped with the norm \(\Vert \cdot \Vert _r\). When \(1< r< \infty \) we denote by \(W^{1, r}(\Omega )\) and \(W^{1,r}_0(\Omega )\) the corresponding Sobolev spaces equipped with the norms \(\Vert \cdot \Vert _{1,r}\) and \(\Vert \cdot \Vert _{1,r,0}\), respectively. Because of the Poincaré inequality we can equip the space \(W^{1,r}_0(\Omega )\) with the following norm
The Banach space
is an ordered Banach space with positive cone
This cone has a nonempty interior given by
where \(n(\cdot )\) stands for the outward unit normal on \(\partial \Omega \).
Let \(r\in (1,+\infty )\) and recall that \(W^{1,r}_0(\Omega )^*=W^{-1,r'}(\Omega )\) with \(\frac{1}{r}+\frac{1}{r'}=1\). By \(\langle \cdot ,\cdot \rangle _{1,r}\) we denote the duality brackets of the pair \((W^{1,r}_0(\Omega ),W^{-1,r'}(\Omega ))\). For notational simplicity when \(r=p\), we simply write \(\langle \cdot ,\cdot \rangle \).
For \(r\in (1,+\infty )\), let \(A_r:W^{1,r}_0(\Omega )\rightarrow W^{-1,r'}(\Omega )=W^{1,r}_0(\Omega )^*\) with \(\frac{1}{r}+\frac{1}{r'}=1\) be the nonlinear map defined by
From Gasiński–Papageorgiou [5, Problem 2.192, p. 279] we have the following properties of \(A_r\).
Proposition 2.1
The map \(A_r:W^{1,r}_0(\Omega )\rightarrow W^{-1,r'}(\Omega )\) defined in (2.1) is bounded, that is, it maps bounded sets to bounded sets, continuous, strictly monotone, hence maximal monotone and it is of type \(({{\,\mathrm{S}\,}})_+\), that is,
imply \(u_n\rightarrow u\) in \(W^{1,r}_0(\Omega )\).
For \(s \in {\mathbb {R}}\), we set \(s^{\pm }=\max \{\pm s,0\}\) and for \(u \in W^{1,p}_0(\Omega )\) we define \(u^{\pm }(\cdot )=u(\cdot )^{\pm }\). It is well known that
Furthermore, given a measurable function \(g:\Omega \times {\mathbb {R}}\rightarrow {\mathbb {R}}\), we denote by \(N_g\) the corresponding Nemytskii (superposition) operator defined by
It is clear that \(x\rightarrow g(x,u(x))\) is measurable. Recall that if \(g:\Omega \times {\mathbb {R}}\rightarrow {\mathbb {R}}\) is a Carathéodory function, then g is measurable in both arguments, see, for example, Papageorgiou–Winkert [18, Proposition 2.2.31, p. 106].
If \(h_1,h_2:\Omega \rightarrow {\mathbb {R}}\) are two measurable functions, then we write \(h_1\prec h_2\) if and only if for every compact \(K\subseteq \Omega \) we have \(0<c_K\le h_2(x)-h_1(x)\) for a. a. \(x\in K\). Note that if \(h_1,h_2\in C(\Omega )\) and \(h_1(x) < h_2(x)\) for all \(x \in \Omega \), then \(h_1 \prec h_2\).
For \(u,v\in W^{1,p}_0(\Omega )\) with \(u(x)\le v(x)\) for a. a. \(x\in \Omega \) we define
Now we are ready to introduce the hypotheses on the perturbation \(f:\Omega \times {\mathbb {R}}\rightarrow {\mathbb {R}}\).
-
H:
\(f:\Omega \times {\mathbb {R}}\rightarrow {\mathbb {R}}\) is a Carathéodory function such that, for a. a. \(x\in \Omega \), \(f(x,0)=0\), \(f(x,\cdot )\) is nondecreasing and
-
(i)
$$\begin{aligned} f(x,s)\le a(x) \left( 1+s^{r-1}\right) \end{aligned}$$
for a.a. \(x\in \Omega \), for all \(s\ge 0\), with \(a\in L^{\infty }(\Omega )\) and \(\theta<r<p^*\), where \(p^*\) denotes the critical Sobolev exponent with respect to p given by
$$\begin{aligned} p^*= {\left\{ \begin{array}{ll} \frac{Np}{N-p} &{} \text {if }p<N,\\ +\infty &{} \text {if } N \le p; \end{array}\right. } \end{aligned}$$ -
(ii)
$$\begin{aligned} \lim _{s\rightarrow +\infty } \frac{f(x,s)}{s^{\theta -1}}=+\infty \quad \text {uniformly for a. a. }x\in \Omega ; \end{aligned}$$
-
(iii)
there exist \(0<{\hat{\eta }}_1 \le {\hat{\eta }}_2\) and \(\delta _0>0\) such that
$$\begin{aligned} {\hat{\eta }}_1s^{q-1} \le f(x,s) \quad \text {for a. a. }x\in \Omega \text { and for all } s\in [0,\delta _0] \end{aligned}$$and
$$\begin{aligned} \limsup _{s\rightarrow 0^+} \frac{f(x,s)}{s^{q-1}} \le {\hat{\eta }}_2\quad \text {uniformly for a. a. }x\in \Omega . \end{aligned}$$
-
(i)
Remark 2.2
With view to our problem it is clear that we are looking for positive solutions and the hypotheses above only concern the positive semiaxis \({\mathbb {R}}_+=[0,+\infty )\). Therefore, without any loss generality, we may assume that
Hypothesis H(ii) implies that \(f(x,\cdot ) \) is \((\theta -1)\)-superlinear as \(s \rightarrow +\infty \) for a. a. \(x\in \Omega \). Dropping the x-dependence for simplicity, the following functions satisfy hypotheses H
and \(\tau >q\) as well as \(\mu \ge \frac{p-1}{q-1}\).
As we already mentioned in the Introduction, the presence of the singular term leads to an energy functional which is not \(C^1\). This creates problems in the usage of variational tools. In the next section we examine an auxiliary singular problem and the solution of them will help us in order to avoid difficulties of having to do with a nonsmooth energy functional.
3 An Auxiliary Singular Problem
In this section we deal with the following parametric singular Dirichlet (p, q)-equation

For this problem we have the following existence and uniqueness result.
Proposition 3.1
If hypotheses H hold, then for every \(\lambda >0\), problem (Q\(_\lambda \)) has a unique positive solution \({\overline{u}}_\lambda \in {{\,\mathrm{int}\,}}\left( C^1_0({\overline{\Omega }})_+\right) \) and the map \(\lambda \rightarrow {\overline{u}}_\lambda \) is nondecreasing from \(\overset{\circ }{{\mathbb {R}}}_+=(0,+\infty )\) into \(C^1_0({\overline{\Omega }})\).
Proof
First we show the existence of a positive solution for problem (Q\(_\lambda \)) for every \(\lambda >0\).
To this end, let \(g \in L^{p}(\Omega )\) and \(\varepsilon >0\). We consider the following Dirichlet problem
Moreover, we consider the nonlinear operator \(V:W^{1,p}_0(\Omega )\rightarrow W^{-1,p'}(\Omega )\) defined by
Recall that \(W^{1,p}_0(\Omega ) \hookrightarrow W^{1,q}_0(\Omega )\) continuously and densely implies that \(W^{-1,q'}(\Omega )\) \(\hookrightarrow W^{-1,p'}(\Omega )\) continuously and densely as well, see Gasiński–Papageorgiou [6, Lemma 2.2.27, p. 141].
By Proposition 2.1 and the fact that \(f(x,\cdot )\) is nondecreasing, we know that \(V:W^{1,p}_0(\Omega )\rightarrow W^{-1,p'(\Omega )}\) is continuous and strictly monotone, hence, maximal monotone as well. In addition we have
which implies that \(V:W^{1,p}_0(\Omega )\rightarrow W^{-1,p'(\Omega )}\) is also coercive. Therefore, it is surjective, see Papageorgiou–Rădulescu–Repovš [14, Corollary 2.8.7, p. 135]. Note that
Hence, there exists \(v_\varepsilon \in W^{1,p}_0(\Omega )\) such that
The strict monotonicity of V implies that this solution \(v_\varepsilon \) is unique. Since \(W^{1,p}_0(\Omega )\) \(\hookrightarrow L^{p}(\Omega )\) by the Sobolev embedding theorem, we can define the solution map \(k_\varepsilon :L^{p}(\Omega )\) \(\rightarrow L^{p}(\Omega )\) by \(k_\varepsilon (g)=v_\varepsilon \). Note that
On (3.1) we take the test function \(v_\varepsilon \in W^{1,p}_0(\Omega )\) and obtain
because \(f(x,v_\varepsilon )v_\varepsilon \ge 0\). From the compactness of \(W^{1,p}_0(\Omega ) \hookrightarrow L^{p}(\Omega )\) it follows that
Suppose that \(g_n \rightarrow g\) in \(L^{p}(\Omega )\). From (3.2) we see that
Hence, by passing to a suitable subsequence if necessary, we may assume that
We have
for all \(n \in {\mathbb {N}}\). Applying \(v^n_\varepsilon -v^*_\varepsilon \in W^{1,p}_0(\Omega )\) on (3.4), passing to the limit as \(n\rightarrow \infty \) and using (3.3), we obtain
Since \(A_q\) is monotone, we derive
and due to (3.3), we get
Then, by Proposition 2.1, it follows that
So, if we pass in (3.4) to the limit as \(n\rightarrow \infty \) and use (3.5) as well as the fact that \(|g_n|\rightarrow |g|\) in \(L^{p}(\Omega )\), we obtain
Hence, \(v^*_\varepsilon =k_\varepsilon (g)\).
By the Urysohn’s criterion for the convergence of sequences we have for the initial sequence \(k_\varepsilon (g_n)\rightarrow k_\varepsilon (g)\) in \(L^{p}(\Omega )\), see Gasiński–Papageorgiou [4, p. 33]. This proves that the solution map \(k_\varepsilon \) is continuous. Therefore, we can apply the Schauder–Tychonov fixed point theorem, see Papageorgiou–Rădulescu–Repovš [14, Theorem 4.3.21, p. 298], which gives the existence of \({\hat{v}}_\varepsilon \in W^{1,p}_0(\Omega )\) such that
We have
Theorem 7.1 of Ladyzhenskaya–Ural’tseva [10, p. 286] implies that \({\hat{v}}_\varepsilon \in L^{\infty }(\Omega )\). Then, from the nonlinear regularity theory of Lieberman [11] we have that \({\hat{v}}_\varepsilon \in C^1_0({\overline{\Omega }})_+\setminus \{0\}\). Hypotheses H(i), (iii) imply that if \(\rho _\varepsilon =\Vert {\hat{v}}_\varepsilon \Vert _\infty \), then there exists \({\hat{\xi }}_{\rho _\varepsilon }>0\) such that \({\hat{\xi }}_{\rho _\varepsilon } s^{p-1}-f(x,s) \ge 0\) for a. a. \(x\in \Omega \) and for all \(s\in [0,\rho _\varepsilon ]\). Using this we obtain
Hence, we have
which implies that \({\hat{v}}_\varepsilon \in {{\,\mathrm{int}\,}}\left( C^1_0({\overline{\Omega }})_+\right) \), see Pucci–Serrin [21, pp. 111 and 120].
Therefore, we produced a solution \({\hat{v}}_\varepsilon \in {{\,\mathrm{int}\,}}\left( C^1_0({\overline{\Omega }})_+\right) \) for the following approximation of problem (Q\(_\lambda \))
In fact this solutions is unique. Indeed, if \({\tilde{v}}_\varepsilon \in W^{1,p}_0(\Omega )\) is another positive solution of (3.6), then we have
Since \(u \rightarrow A_p(u)+A_q(u)\) is strictly monotone, see Proposition 2.1, it follows that \({\hat{v}}_\varepsilon ={\tilde{v}}_\varepsilon \). This proves the uniqueness of the solution \({\hat{v}}_\varepsilon \in {{\,\mathrm{int}\,}}\left( C^1_0({\overline{\Omega }})_+\right) \) of (3.6).
claim
If \(0<\varepsilon '<\varepsilon \le 1\), then \({\hat{v}}_\varepsilon \le {\hat{v}}_{\varepsilon '}\).
We have
Now we introduce the Carathéodory function \(e_\varepsilon :\Omega \times {\mathbb {R}}\rightarrow {\mathbb {R}}\) defined by
We set \(E_\varepsilon (x,s)=\int _0^se_\varepsilon (x,t)\,dt\) and consider the \(C^1\)-functional \(\sigma _\varepsilon :W^{1,p}_0(\Omega )\rightarrow {\mathbb {R}}\) defined by
for all \(u\in W^{1,p}_0(\Omega )\). From (3.8) and since \(F\ge 0\) we see that \(\sigma _\varepsilon :W^{1,p}_0(\Omega )\rightarrow {\mathbb {R}}\) is coercive and because of the Sobolev embedding theorem it is also sequentially weakly lower semicontinuous. Therefore, by the Weierstraß-Tonelli theorem there exists \({\tilde{v}}_\varepsilon \in W^{1,p}_0(\Omega )\) such that’
This implies that \(\sigma _\varepsilon '\left( {\tilde{v}}_\varepsilon \right) =0\), that is,
for all \(h\in W^{1,p}_0(\Omega )\). Taking \(h=-{\tilde{v}}_\varepsilon ^-\in W^{1,p}_0(\Omega )\) as test function in (3.9) and applying (3.8) we obtain that \({\tilde{v}}_\varepsilon \ge 0\). Moreover, we can choose \(h=\left( {\tilde{v}}_\varepsilon -{\hat{v}}_{\varepsilon '}\right) ^+\in W^{1,p}_0(\Omega )\). Then, using once again (3.8) and also (3.7) we infer that \({\tilde{v}}_\varepsilon \le {\hat{v}}_{\varepsilon '}\). So, we have proved that
From (3.10), (3.8) and (3.9) it follows that
It is clear that \({\tilde{v}}_\varepsilon \ne 0\) and so from the first part of the proof we have \({\tilde{v}}_\varepsilon ={\hat{v}}_\varepsilon \in {{\,\mathrm{int}\,}}\left( C^1_0({\overline{\Omega }})_+\right) \). Then, due to (3.10), we obtain \({\tilde{v}}_\varepsilon \le {\tilde{v}}_{\varepsilon '}\). This proves the Claim.
Now we are ready to send \(\varepsilon \rightarrow 0^+\) in order to produce a solution for problem (Q\(_\lambda \)). So, we consider a sequence \(\varepsilon _n\rightarrow 0^+\) and set \({\hat{v}}_n={\hat{v}}_{\varepsilon _n}\) for all \(n \in {\mathbb {N}}\). We have
for all \(h \in W^{1,p}_0(\Omega )\). Testing (3.11) with \(h= {\hat{v}}_n\in W^{1,p}_0(\Omega )\) and applying the Claim gives
for all \(n\in {\mathbb {N}}\).
Let \({\hat{d}}(x)=d(x,\partial \Omega )\) for \(x \in {\overline{\Omega }}\). We know that \({\hat{d}}\in {{\,\mathrm{int}\,}}\left( C^1_0({\overline{\Omega }})_+\right) \), see Gilbarg–Trudinger [9, p. 355]. Since \({\hat{v}}_1\in {{\,\mathrm{int}\,}}\left( C^1_0({\overline{\Omega }})_+\right) \), we have
for some \(c_1,c_2,c_3,c_4>0\).
From (3.12) and (3.13) it follows that \(\{{\hat{v}}_n\}\subseteq W^{1,p}_0(\Omega )\) is bounded. Therefore we may assume that
Now we choose \(h={\hat{v}}_n-{\overline{u}}_\lambda \in W^{1,p}_0(\Omega )\) in (3.11). This yields
since \({\overline{u}_{\lambda }} \ge 0\). Then, from the convergence properties in (3.14), we conclude that
By the monotonicity of \(A_q\) we obtain
Therefore,
which by Proposition 2.1 implies that
From the Claim we know that \({\hat{v}}_1 \le {\hat{v}}_n\) for all \(n \in {\mathbb {N}}\) and so, \({\hat{v}}_1\le {\overline{u}}_\lambda \). Thus, \({\overline{u}}_\lambda \ne 0\).
For every \(h \in W^{1,p}_0(\Omega )\), since \({\hat{v}}_1\in {{\,\mathrm{int}\,}}\left( C^1_0({\overline{\Omega }})_+\right) \), by Hardy’s inequality, we have
Moreover, we have
due to (3.14). Therefore, we can apply the Dominated Convergence Theorem and obtain
We return to (3.11), pass to the limit as \(n\rightarrow \infty \) and use (3.15) as well as (3.16). We obtain
for all \(h \in W^{1,p}_0(\Omega )\). Hence, \({\overline{u}}_\lambda \) is a positive solution of (Q\(_\lambda \)) for \(\lambda >0\).
From Marino–Winkert [13] we have that
for some \(c_7>0\) and for all \(n\in {\mathbb {N}}\). Then, by hypothesis H(i) we know that
We have
for all \(n \in {\mathbb {N}}\).
Using the nonlinear regularity theory of Lieberman [11], we have that
Hence, due to (3.15), we obtain \({\hat{v}}_n\rightarrow {\overline{u}}_\lambda \) in \(C^1_0({\overline{\Omega }})\). Since \({\hat{v}}_1 \le {\overline{u}}_\lambda \), we then conclude that \({\overline{u}}_\lambda \in {{\,\mathrm{int}\,}}\left( C^1_0({\overline{\Omega }})_+\right) \).
So, we have proved that for every \(\lambda >0\), problem (Q\(_\lambda \)) has a solution \({\overline{u}}_\lambda \in {{\,\mathrm{int}\,}}\left( C^1_0({\overline{\Omega }})_+\right) \).
We need to show that this is the unique positive solution of (Q\(_\lambda \)). To this end, let \({\overline{v}}_\lambda \in W^{1,p}_0(\Omega )\) be another positive solution of (Q\(_\lambda \)). Since \(A_p\) and \(A_q\) are strictly monotone and \(f(x,\cdot )\) is nondecreasing, we have
Therefore, \({\overline{u}}_\lambda ={\overline{v}}_\lambda \).
Finally, we are going to show the monotonicity of \(\lambda \rightarrow {\overline{u}}_\lambda \). So, let \(\lambda <\mu \). We consider the Carathéodory function \(d_\mu :\Omega \times {\mathbb {R}}\rightarrow {\mathbb {R}}\) defined by
We set \(D_\mu (x,s)=\int _0^s d_\mu (x,t)\,dt\) and consider the \(C^1\)-functional \(\tau _\mu :W^{1,p}_0(\Omega )\rightarrow {\mathbb {R}}\) defined by
Since \(\tau _\mu :W^{1,p}_0(\Omega )\rightarrow {\mathbb {R}}\) is coercive, the direct method of the calculus of variations produces \({\tilde{u}}_\mu \in W^{1,p}_0(\Omega )\) such that
From (3.17) we see that
and
Hence, \({\overline{u}}_\lambda \le {\overline{u}}_\mu \). \(\square \)
4 Positive Solutions
In this section we prove the existence and nonexistence of positive solutions for problem (P\(_\lambda \)) as \(\lambda \) moves in \(\overset{\circ }{{\mathbb {R}}}_+=(0,+\infty )\).
We introduce the following two sets
Proposition 4.1
If hypotheses H hold, then \({\overline{u}}_\lambda \le u\) for all \(u \in {\mathcal {S}}_\lambda \).
Proof
Let \(u \in {\mathcal {S}}_\lambda \). We introduce the Carathéodory function \(k_\lambda :\Omega \times \overset{\circ }{{\mathbb {R}}}_+\rightarrow {\mathbb {R}}\) defined by
We consider the following Dirichlet singular (p, q)-equation
Reasoning as in the proof of Proposition 3.1, see also Papageorgiou–Rădulescu–Repovš [15, Proposition 10], we show that (4.2) has a positive solution \({\tilde{u}}_\lambda \in {{\,\mathrm{int}\,}}\left( C^1_0({\overline{\Omega }})_+\right) \). The weak formulation of (4.2) is given by
Now, we choose \(h=\left( {\tilde{u}}_\lambda -u\right) ^+\in W^{1,p}_0(\Omega )\) as test function in (4.3). Then, by applying (4.1), \(u\ge 0\) and \(u\in {\mathcal {S}}_\lambda \), we obtain
Therefore, \({\tilde{u}}_\lambda \le u\) because of the monotonicity of \(A_p\) and \(A_q\).
Then, from (4.1) and Proposition 3.1, it follows that \({\tilde{u}}_\lambda ={\overline{u}}_\lambda \in {{\,\mathrm{int}\,}}\left( C^1_0({\overline{\Omega }})_+\right) \) and so, \({\overline{u}}_\lambda \le u\) for all \(u \in {\mathcal {S}}_\lambda \). \(\square \)
Next we determine the regularity of the elements of the solution set \({\mathcal {S}}_\lambda \).
Proposition 4.2
If hypotheses H hold, then \({\mathcal {S}}_\lambda \subseteq {{\,\mathrm{int}\,}}\left( C^1_0({\overline{\Omega }})_+\right) \) for all \(\lambda >0\).
Proof
The result is trivially true if \({\mathcal {S}}_\lambda =\emptyset \). So, suppose that \({\mathcal {S}}_\lambda \ne \emptyset \) and let \(u \in {\mathcal {S}}_\lambda \). From Proposition 4.1 we know that \({\overline{u}}_\lambda \le u\) and so \(u^{-\eta } \le {\overline{u}}_\lambda ^{-\eta }\in L^{1}(\Omega )\). Recall that \({\hat{v}}_1\le {\overline{u}}_\lambda \) and \({\hat{v}}_1^{-\eta } \in L^{1}(\Omega )\), see the proof of Proposition 3.1. Therefore, using Theorem B.1 of Giacomoni–Saoudi [8], we see that \(u \in C^1_0({\overline{\Omega }})_+\setminus \{0\}\).
On account of hypotheses H(i), (ii), if \(\rho =\Vert u\Vert _\infty \), then we can find \({\hat{\xi }}_\rho >0\) such that
Using this, we have
Then, by Pucci–Serrin [21, pp. 111 and 120], we derive \(u \in {{\,\mathrm{int}\,}}\left( C^1_0({\overline{\Omega }})_+\right) \). Hence, \({\mathcal {S}}_\lambda \subseteq {{\,\mathrm{int}\,}}\left( C^1_0({\overline{\Omega }})_+\right) \). \(\square \)
Next, we are going to prove the nonemptiness of \({\mathcal {L}}\).
Proposition 4.3
If hypotheses H hold, then \({\mathcal {L}}\ne \emptyset \).
Proof
Let \({\overline{u}}_\lambda \in {{\,\mathrm{int}\,}}\left( C^1_0({\overline{\Omega }})_+\right) \) be the unique positive solution of (Q\(_\lambda \)), see Proposition 3.1. We introduce the Carathéodory function \(e_\lambda :\Omega \times {\mathbb {R}}\rightarrow {\mathbb {R}}\) defined by
We set \(E_\lambda (x,s)=\int ^s_0e_\lambda (x,t)\,dt\) and consider the functional \(\gamma _\lambda :W^{1,p}_0(\Omega )\rightarrow {\mathbb {R}}\) defined by
Since \({\overline{u}}_\lambda ^{-\eta }\in L^{1}(\Omega )\), see the proof of Proposition 3.1, we have that \(\gamma _\lambda \in C^1(W^{1,p}_0(\Omega ))\), see also Proposition 3 of Papageorgiou–Smyrlis [17].
From (4.4) and hypothesis H(ii), we infer that \(\gamma _\lambda \) is coercive. Moreover, it is also sequentially weakly lower semicontinuous. Hence, there exists a global minimizer \(u^\circ _\lambda \in W^{1,p}_0(\Omega )\) of \(\gamma _\lambda \), that is,
Let \(u \in {{\,\mathrm{int}\,}}\left( C^1_0({\overline{\Omega }})_+\right) \) and choose \(t \in (0,1)\) small so that \(tu \le {\overline{u}}_\lambda \). Recall that \({\overline{u}}_\lambda \in {{\,\mathrm{int}\,}}\left( C^1_0({\overline{\Omega }})_+\right) \) and use Proposition 4.1.22 of Papageorgiou–Rădulescu–Repovš [14, p. 274].
We have
Let \(\lambda _0 =\left\| {\overline{u}}_\lambda ^{\eta } f\left( x,{\overline{u}}_\lambda \right) \right\| _\infty \), see hypothesis H(i), and let \(\lambda >\lambda _0\). Then
So, from (4.6) we have
since \(t\in (0,1)\) and \(q<p\).
Since \(q>1\), by taking \(t\in (0,1)\) even smaller if necessary, we see that \(\gamma _\lambda (tu)<0\). Taking (4.5) into account we know that
Thus, \(u^\circ _\lambda \ne 0\).
From (4.5) we have \(\gamma _\lambda '\left( u^\circ _\lambda \right) =0\), that is,
We choose \(h=\left( {\overline{u}}_\lambda -u^\circ _\lambda \right) ^+\in W^{1,p}_0(\Omega )\) as test function in (4.7). Applying (4.4) and Proposition 3.1 gives
As before, by the monotonicity of \(A_p\) and \(A_q\) we conclude that \({\overline{u}}_\lambda \le u^\circ _\lambda \). Using this fact along with (4.4) and (4.7) we infer that
see Proposition 4.2. Therefore, \(\lambda \in {\mathcal {L}}\) and so \((\lambda _0,+\infty ) \subseteq {\mathcal {L}}\ne \emptyset \). \(\square \)
The next proposition establishes a structural property for \({\mathcal {L}}\), namely that \({\mathcal {L}}\) is an upper half-line.
Proposition 4.4
If hypotheses H hold, \(\lambda \in {\mathcal {L}}\) and \(\mu >\lambda \), then \(\mu \in {\mathcal {L}}\).
Proof
Since \(\lambda \in {\mathcal {L}}\) there exists \(u_\lambda \in {\mathcal {S}}_\lambda \subseteq {{\,\mathrm{int}\,}}\left( C^1_0({\overline{\Omega }})_+\right) \), see Proposition 4.2. From Proposition 4.1 we have \({\overline{u}}_\lambda \le u_\lambda \). Therefore,
We now introduce the Carathéodory function \(g_\mu :\Omega \times {\mathbb {R}}\rightarrow {\mathbb {R}}\) defined by
We set \(G_\mu (x,s)=\int ^s_0g_\mu (x,t)\,dt\) and consider the \(C^1\)-functional \(\varphi _\mu :W^{1,p}_0(\Omega )\rightarrow {\mathbb {R}}\) defined by
see (4.8).
From (4.8) and hypothesis H(ii) we see that \(\varphi _\mu \) is coercive and we know it is also sequentially weakly lower semicontinuous. Hence, we can find \(u_\mu \in W^{1,p}_0(\Omega )\) such that
This implies that \(\varphi _\mu '\left( u_\mu \right) =0\), that is,
We choose \(h=\left( u_\lambda -u_\mu \right) ^+\in W^{1,p}_0(\Omega )\) as test function in (4.10). Applying (4.9), \(\lambda <\mu \) and \(u_\lambda \in {\mathcal {S}}_\lambda \), we obtain
Again, from the monotonicity of \(A_p\) and \(A_q\), we deduce that \(u_\lambda \le u_\mu \). This along with (4.9) as well as (4.10) implies that \(u_\mu \in {\mathcal {S}}_\mu \subseteq {{\,\mathrm{int}\,}}\left( C^1_0({\overline{\Omega }})_+\right) \). Hence, \(\mu \in {\mathcal {L}}\). \(\square \)
So, according to Proposition 4.4, \({\mathcal {L}}\) is an upper half-line. Moreover, a byproduct of the proof of Proposition 4.4 is the following corollary.
Corollary 4.5
If hypotheses H hold, \(\lambda \in {\mathcal {L}}\), \(u_\lambda \in {\mathcal {S}}_\lambda \) and \(\mu >\lambda \), then \(\mu \in {\mathcal {L}}\) and there exists \(u_\mu \in {\mathcal {S}}_\mu \) such that \(u_\lambda \le u_\mu \).
If we strengthen a little the conditions on \(f(x,\cdot )\), we can improve the assertion of this corollary.
-
H’:
\(f:\Omega \times {\mathbb {R}}\rightarrow {\mathbb {R}}\) is a Carathéodory function such that \(f(x,0)=0\) for a. a. \(x\in \Omega \), \(f(x,\cdot )\) is nondecreasing, hypotheses H’(i), (ii), (iii) are the same as the corresponding hypotheses H(i), (ii), (iii) and
-
(iv)
for every \(\varrho >0\) there exists \({\hat{\xi }}_\varrho >0\) such that the function
$$\begin{aligned} s \rightarrow {\hat{\xi }}_\varrho s^{p-1}- f(x,s) \end{aligned}$$is nondecreasing on \([0,\varrho ]\) for a. a. \(x\in \Omega \).
-
(iv)
Remark 4.6
The examples in Sect. 2 satisfy this extra condition.
Proposition 4.7
If hypotheses H’ hold, \(\lambda \in {\mathcal {L}}\), \(u_\lambda \in {\mathcal {S}}_\lambda \) and \(\mu >\lambda \), then \(\mu \in {\mathcal {L}}\) and there exists \(u_\mu \in {\mathcal {S}}_\mu \) such that \(u_\mu -u_\lambda \in {{\,\mathrm{int}\,}}\left( C^1_0({\overline{\Omega }})_+\right) \).
Proof
From Corollary 4.5 we already know that \(\mu \in {\mathcal {L}}\) and we can find \(u_\mu \in {\mathcal {S}}_\mu \subseteq {{\,\mathrm{int}\,}}\left( C^1_0({\overline{\Omega }})_+\right) \) such that
Let \(\varrho = \Vert u_\mu \Vert _\infty \) and let \({\hat{\xi }}_\varrho >0\) be as postulated by hypothesis H’(iv). Since \(\lambda <\mu \), \(u_\lambda \in {\mathcal {S}}_\lambda \) and due to (4.11) as well as hypothesis H’(iv) we obtain
Note that since \(u_\lambda {{\,\mathrm{int}\,}}\left( C^1_0({\overline{\Omega }})_+\right) \) we have
So, from (4.12) and Proposition 7 of Papageorgiou–Rădulescu–Repovš [15], we conclude that \(u_\mu -u_\lambda \in {{\,\mathrm{int}\,}}\left( C^1_0({\overline{\Omega }})_+\right) \). \(\square \)
Let \(\lambda _*=\inf {\mathcal {L}}\).
Proposition 4.8
If hypotheses H’ hold, then \(\lambda _*>0\).
Proof
On account of hypotheses H’(ii), (iii) we can find \({\hat{\lambda }}>0\) such that
Consider \(\lambda \in (0,{\hat{\lambda }})\) and suppose that \(\lambda \in {\mathcal {L}}\). Then we can find \(u_\lambda \in {\mathcal {S}}_\lambda \subseteq {{\,\mathrm{int}\,}}\left( C^1_0({\overline{\Omega }})_+\right) \). We set \(\varrho _\lambda =\max _{{\overline{\Omega }}} u_\lambda \). Then, for \(\delta \in (0,\varrho _\lambda )\) small enough, we set \( \varrho _\lambda ^\delta =\varrho _\lambda -\delta >0\). For \({\hat{\xi }}_\lambda ={\hat{\xi }}_{\varrho _\lambda }>0\) as postulated by hypothesis H’(iv) along with (4.13), \({\hat{\lambda }}>\lambda \), \(u_\lambda \in {\mathcal {S}}_\lambda \) and \(\delta >0\) small enough, we obtain
Invoking Proposition 6 of Papageorgiou–Rădulescu–Repovš [15], we have that
a contradiction to the definition of \(\varrho _\lambda \). Therefore
\(\square \)
Next, we show that \(\lambda _*\) is admissible, that is, \(\lambda _*>0\).
Proposition 4.9
If hypotheses H’ hold, then \(\lambda _* \in {\mathcal {L}}\).
Proof
Let \(\{\lambda _n\}_{n\in {\mathbb {N}}} \subseteq {\mathcal {L}}\) be such that \(\lambda _n \searrow \lambda _*\). For every \(n \in {\mathbb {N}}\), let \(u_n \in {\mathcal {S}}_{\lambda _n}\subseteq {{\,\mathrm{int}\,}}\left( C^1_0({\overline{\Omega }})_+\right) \). From Proposition 3.1 we know that
Moreover we have
for all \(h \in W^{1,p}_0(\Omega )\) and for all \(n \in {\mathbb {N}}\).
On account of hypotheses H’(i), (ii), (iii) there exists \(c_{11}>0\) such that
for a. a. \(x\in \Omega \), for all \(s\ge 0\) and for all \(n\in {\mathbb {N}}\).
Choosing \(h =u_n \in W^{1,p}_0(\Omega )\) in (4.15) and using (4.14) and (4.16), results in
Therefore, \(\{u_n\}_{n\in {\mathbb {N}}}\subseteq W^{1,p}_0(\Omega )\) is bounded.
So, we may assume that
Taking \(h=u_n-u_*\in W^{1,p}_0(\Omega )\) as test function in (4.15), passing to the limit as \(n\rightarrow \infty \) and using (4.17) yields
see the proof of Proposition 3.1. Then, from Proposition 2.1 we conclude that
Now we can apply (4.18) along with (4.14) as well as (4.15), as in the proof of Proposition 3.1, in the limit as \(n\rightarrow \infty \), we obtain
and
for all \(h \in W^{1,p}_0(\Omega )\). Finally, we reach \(u_* \in {\mathcal {S}}_{\lambda _*}\subseteq {{\,\mathrm{int}\,}}\left( C^1_0({\overline{\Omega }})_+\right) \) and so \(\lambda _* \in {\mathcal {L}}\).
\(\square \)
So, we have \({\mathcal {L}}=[\lambda _*,+\infty )\) and we can state the following theorem for the positive solutions of problem (P\(_\lambda \)).
Theorem 4.10
If hypotheses H’ hold, then there exists \(\lambda _*>0\) such that
-
(1)
for every \(\lambda \ge \lambda _*\), problem (P\(_\lambda \)) has a positive solution \(u_\lambda \in {{\,\mathrm{int}\,}}\left( C^1_0({\overline{\Omega }})_+\right) \);
-
(2)
for every \(\lambda \in (0,\lambda _*)\), problem (P\(_\lambda \)) has no positive solutions.
Change history
02 December 2021
Open access funding note missed in the original publication. Now, it has been added in the Funding section.
References
Afrouzi, G.A., Brown, K.J.: On a diffusive logistic equation. J. Math. Anal. Appl. 225(1), 326–339 (1998)
Cardinali, T., Papageorgiou, N.S., Rubbioni, P.: Bifurcation phenomena for nonlinear superdiffusive Neumann equations of logistic type. Ann. Mat. Pura Appl. (4) 193(1), 1–21 (2014)
Gasiński, L., O’Regan, D., Papageorgiou, N.S.: A variational approach to nonlinear logistic equations. Commun. Contemp. Math. 17(3), 1450021 (2015)
Gasiński, L., Papageorgiou, N.S.: Exercises in Analysis. Part 1. Springer, Cham (2014)
Gasiński, L., Papageorgiou, N.S.: Exercises in Analysis. Part 2: Nonlinear Analysis. Springer, Cham (2016)
Gasiński, L., Papageorgiou, N.S.: Nonlinear Analysis. Chapman & Hall/CRC, Boca Raton (2006)
Gasiński, L., Papageorgiou, N.S.: Positive solutions for the Neumann \(p\)-Laplacian with superdiffusive reaction. Bull. Malays. Math. Sci. Soc. 40(4), 1711–1731 (2017)
Giacomoni, J., Saoudi, K.: \(W_0^{1, p}\) versus \(C^1\) local minimizers for a singular and critical functional. J. Math. Anal. Appl. 363(2), 697–710 (2010)
Gilbarg, D., Trudinger, N.S.: Elliptic Partial Differential Equations of Second Order, 2nd edn. Springer, Berlin (1998)
Ladyzhenskaya, O.A., Ural’tseva, N.N.: Linear and Quasilinear Elliptic Equations. Academic Press, New York (1968)
Lieberman, G.M.: The natural generalization of the natural conditions of Ladyzhenskaya and Ural’ tseva for elliptic equations. Commun. Partial Differ. Equ. 16(2–3), 311–361 (1991)
Marano, S.A., Mosconi, S.J.N.: Some recent results on the Dirichlet problem for \((p, q)\)-Laplace equations. Discrete Contin. Dyn. Syst. Ser. S 11(2), 279–291 (2018)
Marino, G., Winkert, P.: \(L^\infty \)-bounds for general singular elliptic equations with convection term. Appl. Math. Lett. 107, 106401 (2020)
Papageorgiou, N.S., Rădulescu, V.D., Repovš, D.D.: Nonlinear Analysis: Theory and Methods. Springer, Cham (2019)
Papageorgiou, N.S., Rădulescu, V.D., Repovš, D.D.: Nonlinear nonhomogeneous singular problems. Calc. Var. Partial Differ. Equ. 59(1), 9 (2020)
Papageorgiou, N.S., Rădulescu, V.D., Repovš, D.D.: Positive solutions for superdiffusive mixed problems. Appl. Math. Lett. 77, 87–93 (2018)
Papageorgiou, N.S., Smyrlis, G.: A bifurcation-type theorem for singular nonlinear elliptic equations. Methods Appl. Anal. 22(2), 147–170 (2015)
Papageorgiou, N.S., Winkert, P.: Applied Nonlinear Functional Analysis: An Introduction. De Gruyter, Berlin (2018)
Papageorgiou, N.S., Winkert, P.: On a parametric nonlinear Dirichlet problem with subdiffusive and equidiffusive reaction. Adv. Nonlinear Stud. 14(3), 565–591 (2014)
Papageorgiou, N.S., Winkert, P.: Singular \(p\)-Laplacian equations with superlinear perturbation. J. Differ. Equ. 266(2–3), 1462–1487 (2019)
Pucci, P., Serrin, J.: The Maximum Principle. Birkhäuser Verlag, Basel (2007)
Rădulescu, V.D.: Isotropic and anistropic double-phase problems: old and new. Opuscula Math. 39(2), 259–279 (2019)
Takeuchi, S.: Multiplicity result for a degenerate elliptic equation with logistic reaction. J. Differ. Equ. 173(1), 138–144 (2001)
Takeuchi, S.: Positive solutions of a degenerate elliptic equation with logistic reaction. Proc. Am. Math. Soc. 129(2), 433–441 (2001)
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Papageorgiou, N.S., Winkert, P. Existence and Nonexistence of Positive Solutions for Singular (p, q)-Equations with Superdiffusive Perturbation. Results Math 76, 169 (2021). https://doi.org/10.1007/s00025-021-01484-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00025-021-01484-5
Keywords
- (p, q)-Laplaciana
- superdiffusive perturbation
- positive solutions
- nonlinear regularity
- truncation and comparison methods