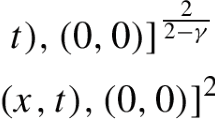Skip to main content
SpringerLink
Log in

Spectral Properties of Sturm–Liouville Problems with Strongly Singular Potentials

  • Published:
Results in Mathematics Aims and scope Submit manuscript

Abstract

This paper studies a class of singular differential equations

$$\begin{aligned} -\left( \frac{\mathrm {d}}{{\mathrm {d}}x}-\frac{k}{x^{l}}-v\right) \left( \frac{{\mathrm {d}}}{{\mathrm {d}}x}+\frac{k}{x^{l}}+v\right) y=\lambda y \text { on }J=(0,1) , \end{aligned}$$

where \(k\ge \frac{1}{2},1\le l<2\) and \(v\in L^{1}(J, {\mathbb {R}} )\) which is bounded below. Using the prüfer transformation, we get the oscillation property of the eigenfunctions. In particular, the location of eigenvalues are also described. Furthermore, we establish the continuous dependence of nth eigenvalue on the boundary condition.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Albeverio, S., Hryniv, R., Mykytyuk, Y.: Inverse spectral problems for Bessel operators. J. Differ. Equ. 241, 130–159 (2007)

    Article  MathSciNet  Google Scholar 

  2. Atkinson, F.V.: Discrete and Continuous Boundary Problems. Academic, New York (1964)

    MATH  Google Scholar 

  3. Binding, P.A., Boulton, L., Browne, P.J.: A Prüfer angle approach to singular Sturm–Liouville problems with Molčanov potentials. J. Comput. Appl. Math. 208, 226–234 (2007)

    Article  MathSciNet  Google Scholar 

  4. Binding, P.A., Browne, P.J., Karabash, I.M.: Sturm–Liouville problems for the p-Laplacian on a half-line. Proc. R. Soc. Edinb. 53, 271–291 (2010)

    Article  MathSciNet  Google Scholar 

  5. Binding, P.A., Browne, P.J., Watson, B.A.: Weighted \(p\)-Laplacian problems on a half-line. J. Differ. Equ. 260, 1372–1391 (2016)

    Article  MathSciNet  Google Scholar 

  6. Binding, P.A., Volkmer, H.: Oscillation theory for Sturm–Liouville problems with indefinite coefficients. Proc. R. Soc. Edinb. 131, 989–1002 (2001)

    Article  MathSciNet  Google Scholar 

  7. Eckhardt, J., Gesztesy, F., Nichols, R., Teschl, G.: Weyl–Titchmarsh theory for Sturm–Liouville operators with distributional potentials. Opusc. Math. 33, 467–563 (2013)

    Article  MathSciNet  Google Scholar 

  8. Guillot, J.-C., Ralston, J.V.: Inverse spectral theory for a singular Sturm–Liouville operator on [0, 1]. J. Differ. Equ. 76, 353–373 (1988)

    Article  MathSciNet  Google Scholar 

  9. Hao, X., Sun, J., Zettl, A.: Real-parameter square-integrable solutions and the spectrum of differential operators. J. Math. Anal. Appl. 376, 696–712 (2011)

    Article  MathSciNet  Google Scholar 

  10. Kong, Q., Wu, H., Zettl, A.: Dependence of the \(n\)th Sturm–Liouville eigenvalue on the problem. Math. Nachr. 188, 173–201 (1997)

    Article  MathSciNet  Google Scholar 

  11. Kong, Q., Zettl, A.: Eigenvalues of regular Sturm–Liouville problems. J. Differ. Equ. 131, 1–19 (1996)

    Article  MathSciNet  Google Scholar 

  12. Kostenko, A., Sakhnovich, A., Teschl, G.: Inverse eigenvalue problems for perturbed spherical Schrödinger operators. Inverse Probl. 26, 105013 (2010)

    Article  Google Scholar 

  13. Kostenko, A., Teschl, G.: On the singular Weyl–Titchmarsh function of perturbed spherical Schrödinger operators. J. Differ. Equ. 250, 3701–3739 (2011)

    Article  Google Scholar 

  14. Kostenko, A., Teschl, G.: Spectral asymptotics for perturbed spherical Schrödinger operators and applications to quantum scattering. Commun. Math. Phys. 322, 255–275 (2013)

    Article  Google Scholar 

  15. Serier, F.: The inverse spectral problem for radial Schrödinger operators on [0, 1]. J. Differ. Equ. 235, 101–126 (2007)

    Article  MathSciNet  Google Scholar 

  16. Weidmann, J.: Spectral Theory of Ordinary Differential Operators. Springer, Berlin (1987)

    Book  Google Scholar 

  17. Yan, J., Shi, G., Zhao, J.: Eigenvalues of Sturm–Liouville operators with distributional potentials. arXiv: 1711.07032

  18. Zettl, A.: Sturm–Liouville Theory. American Mathematical Society, Providence (2005)

    MATH  Google Scholar 

  19. Zhang, M., Sun, J., Zettl, A.: Eigenvalues of limit-point Sturm–Liouville problems. J. Math. Anal. Appl. 419, 627–642 (2014)

    Article  MathSciNet  Google Scholar 

  20. Zhornitskaya, L.A., Serov, V.S.: Inverse eigenvalue problems for a singular Sturm–Liouville operator on [0, 1]. Inverse Probl. 10, 975–987 (1994)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

This research was supported by the National Natural Science Foundation of China under Grant No. 11601372.

Author information

Authors and Affiliations

  1. School of Mathematics, Tianjin University, Tianjin, 300354, People’s Republic of China

    Yu Liu, Guoliang Shi & Jun Yan

Authors
  1. Yu Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Guoliang Shi
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jun Yan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jun Yan.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, Y., Shi, G. & Yan, J. Spectral Properties of Sturm–Liouville Problems with Strongly Singular Potentials. Results Math 74, 20 (2019). https://doi.org/10.1007/s00025-018-0941-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00025-018-0941-3

Mathematics Subject Classification

Keywords

Search

Navigation