High Resolution Model of the Vinton Salt-Dome Cap Rock by Joint Inversion of the Full Tensor Gravity Gradient Data with the Simulated Annealing Global Optimization Method

Abstract

We present a 3D high-resolution modeling methodology based on the interpretation of gravity gradient data and its joint inversion with the simulated annealing (SA) global optimization method. The geometry of the model, used as computational domain in the solution of the forward and inverse problems, is defined with an irregular ensemble of cubic prisms that recreates the interpreted shape of the target, derived from the results of applying different interpretation methods to the gravity gradient data. In our inversion approach, the linear inverse problem resulting from the domain discretization is not solved. Instead, the cost function is explored with the SA algorithm, its low misfit region is identified, and models belonging to it are selected for obtaining the mean model, which represents the most likely model among them, as well as for estimating its uncertainty. The SA inversion algorithm we applied was numerically optimized to reduce the computational burden required by the forward problem, and it was driven by optimal tuning parameters, determined by a parametric analysis. Tests on synthetic data show the efficiency of our methodology to obtain a model that approximates the synthetic target and the usefulness of the estimated uncertainty to complement the interpretation. Finally, by applying our methodology to gravity gradient data acquired over the Vinton dome located in Louisiana, USA, we obtained results that are in agreement with geological information and previous studies.

1 Introduction

Gravity gradient modeling is an important interpretation tool in geophysical exploration. It started to develop in the early 2000s, thanks to technological advances in data acquisition that made gravity gradient surveys routine for oil and mineral exploration (Zhdanov et al., 2004).

Gravity gradiometry has higher resolution than conventional gravimetry for characterizing shallow targets. Unlike conventional gravity surveys, in which only the vertical component of the gravity field, $g_z$, is measured, a gravity gradient survey measures the gradient of the gravity field in different orthogonal directions. If considering a Cartesian coordinate system, this results in the six different components of the full tensor gravity gradient (FTGG), which is more sensitive to near-surface density variations than the gravity field because its decay rate with distance is greater than that of the latter. In addition, the signal-to-noise ratio of the FTGG components is higher than the $g_z$ component because of their ability to reject common mode noise, and their horizontal components provide lateral information that cannot be provided by the $g_z$ component alone (Martinez et al., 2013).

Some methods of interpreting gravity gradient data have been developed for the purpose of improving and mapping edges and lineaments (e.g., Beiki, 2010; Salem et al., 2013), identification of anomalous three-dimensional structures (e.g., Pedersen & Rasmussen, 1990; Murphy & Brewster, 2007) and the semi-automatic interpretation of anomaly source bodies (e.g., Zhang et al., 2000; Mikhailov et al., 2007). The information obtained from them is useful for inferring some structural characteristics of the targets, such as their approximate lateral extent, depth and shape, but is insufficient to estimate their physical properties or spatial arrangement.

To achieve a better subsurface interpretation, recent inversion methods have been developed that are intended to estimate the shape and physical properties of the observed anomaly sources. Most of them have approached 3D subsurface modeling by discretizing it with regular ensembles of rectangular prisms with fixed geometry and constant but unknown density contrast, leading to the formulation of linear inverse problems. Problems formulated this way are often ill-conditioned and require the incorporation of regularization terms to stabilize the solution of the resulting system of linear equations, such as presented by Zhdanov et al. (2004) and Qin et al. (2016). Depending on the number of observed data points and the resolution of the prism ensemble employed, the problem to be solved can be challenging because of the large amount of memory required to handle the sensitivity matrices and the computational time needed to solve the system of equations. For this reason, high-performance computing strategies have been implemented to solve these large-scale inverse problems (e.g., Čuma et al., 2012; Wang et al., 2017; Hou et al., 2019).

On the other hand, only a few methods have been developed to solve the nonlinear inverse problems resulting from the discretization with prism ensembles with fixed density and unknown geometry, in which the geometry of the prisms used in the discretization is to be solved, such as those presented by Barnes and Barraud (2012) and Oliveira Jr. and Barbosa (2013).

Apart from the aforementioned methods, there are other strategies, such as global optimization methods, that have barely been applied for 3D gravity gradient inversion. These strategies are based on the exploration of the cost function in search of an optimal solution, so it is necessary to apply some constraints to reduce the non-uniqueness problem and, in case of an exhaustive exploration, also some techniques to reduce the computational cost involved.

To our knowledge, the only published method of this type was presented by Uieda and Barbosa (2012), who developed a robust gravity gradient inversion method, named the planting algorithm, to estimate density contrasts in a medium discretized by regular prisms through systematic growth around some specific prismatic elements called “seeds.” The planting algorithm includes constraints to obtain compact models, is not very sensitive to the effects of nontargeted sources and noisy data and reduces memory usage as well as computational burden. However, it only allows accretion of bodies that reduce the cost function, which could lead to stagnation at a local minimum, and no uncertainty estimate of the inverted parameters is presented.

In this work, we present a 3D high-resolution modeling approach based on the interpretation and joint inversion of gravity gradient data. We discretized the target with an irregular ensemble of identical cubic prisms, constraining its shape and location with information derived from the application of different interpretation methods, and solved the inverse problem to estimate their density contrasts with a numerically optimized SA algorithm. We retrieved a representative model and assessed its uncertainty from the low-misfit region of the cost function identified by the inversion procedure. Finally, we tested our methodology on synthetic data and on airborne gravity gradient data acquired over the Vinton dome located in southwestern Louisiana, USA, validating its potential use for interpretation purposes.

2 Methodology

2.1 Forward Gravity Gradient Modeling of a Discrete Target Constrained by Data Interpretation

The first step in our modeling approach is the construction of the discrete computational domain to solve the direct gravity gradient problem as well as to compute the sensitivity matrices needed for the inversion procedure.

We start with lateral and depth target constraints from the application of interpretation methods to the available FTGG data (Fig. 1).

Fig. 1

Illustration of target interpretation with edge enhancement and depth estimation methods applied to gravity gradient data

To define the lateral extent of the target, we apply some commonly used methods, such as the zero contours of the $T_{xx}$, $T_{yy}$ and $T_{zz}$ component data grids, tilt angle (Miller & Singh, 1994) applied to the $T_{zz}$ component ($TA\_T_{zz}$), maximum of the total horizontal gradient (THG) (Cordell, 1979) and $I_2$ invariant grid of the gravity gradient tensor (Pedersen & Rasmussen, 1990).

Given the available FTGG data, the depth to the top of the target can be estimated with the 3D Euler deconvolution (3DED) methodology (e.g., Reid et al., 1990; Zhang et al., 2000; Beiki, 2010).

Also, the target topography can be approximated with the $I_2$ invariant (Murphy & Brewster, 2007), scaling their amplitudes with the previously estimated depths (Fig. 1).

The discrete domain will be constructed with an irregular ensemble, considering that it extends from the interpreted topography to a flat base deep enough to contain the entire target (Fig. 2).

Fig. 2

a Schematic representation of the discretization of the target into an irregular ensemble of cubic prisms and the calculation of the gravity gradient at an observation point. b Each prism in the ensemble has constant density and is defined from 4 vertices. P is the point at which the gravity gradient components are calculated

Finally, it is necessary to assign density contrasts to the prisms of the computational domain to compute the forward problem. Each prism can have a different density contrast value, which can be calculated if the densities of the target and the medium in which it is immersed are known.

The gravity gradient components of the discrete target are calculated by summing the individual contributions of each of the M prisms of the ensemble at the N observation points:

$$\begin{aligned} T_{\alpha \beta }\left( k\right) = \sum _{q=1}^M{T_{\alpha \beta }(k, \rho _q)}; \; \text{ for } \; \alpha , \beta = x, y, z \; \text{ and } \; k = 1, \ldots , N \end{aligned}$$

(1)

where $T_{\alpha \beta }\left( k\right)$ represents the $T_{\alpha \beta }$ component of the gravity gradient tensor calculated at the k-th observation point because of the whole ensemble, and $T_{\alpha \beta }\left( k, \rho _q\right)$ is the contribution of the q-th prism at that point.

Now, the gravity gradient components due to each prism with constant density contrast, $\rho$, at each observation point, are calculated through the second derivatives of its gravitational potential $U\left( \vec {r}\right)$:

$$\begin{aligned} T_{\alpha \beta }\left( \vec {r}\right) = \dfrac{\partial ^2 U\left( \vec {r}\right) }{\partial \alpha \partial \beta } = \gamma \rho \int \limits _{v_0}^{} \dfrac{\partial ^2}{\partial \alpha \partial \beta } \dfrac{1}{|\vec {r}-\vec {r}_0 |} {\text{d}}v_0 \end{aligned}$$

(2)

where $\vec {r}$ and $\vec {r}_0$ are the position vectors of the observation point and the differential element of integration in the volume occupied by the prism, respectively, and $\gamma$ is the universal gravitational constant.

Solving Eq. (2) gives the numerical values of the gravity gradient components due to the discrete target. We use the numerical solutions derived by Nagy et al. (2000):

$$\begin{aligned} T_{xx}&= \gamma \rho \sum _{i=1}^{2} \sum _{j=1}^{2} \sum _{k=1}^{2} \mu _{ijk} \left[ \tan^{-1}\biggl (\dfrac{y_j z_k}{x_i r_{ijk}}\biggr )\right] \end{aligned}$$

(3)

$$\begin{aligned} T_{xy}&= -\gamma \rho \sum _{i=1}^{2} \sum _{j=1}^{2} \sum _{k=1}^{2} \mu _{ijk} \left[ {\text{ln}}\left( r_{ijk} + z_k\right) \right] \end{aligned}$$

(4)

$$\begin{aligned} T_{xz}&= -\gamma \rho \sum _{i=1}^{2} \sum _{j=1}^{2} \sum _{k=1}^{2} \mu _{ijk} \left[ {\text{ln}}\left( r_{ijk} + y_j\right) \right] \end{aligned}$$

(5)

$$\begin{aligned} T_{yy}&= \gamma \rho \sum _{i=1}^{2} \sum _{j=1}^{2} \sum _{k=1}^{2} \mu _{ijk} \left[ \tan^{-1}\biggl (\dfrac{x_i z_k}{y_j r_{ijk}}\biggr )\right] \end{aligned}$$

(6)

$$\begin{aligned} T_{yz}&= -\gamma \rho \sum _{i=1}^{2} \sum _{j=1}^{2} \sum _{k=1}^{2} \mu _{ijk} \left[ {\text{ln}}\left( r_{ijk} + x_i\right) \right] \end{aligned}$$

(7)

$$\begin{aligned} T_{zz}&= \gamma \rho \sum _{i=1}^{2} \sum _{j=1}^{2} \sum _{k=1}^{2} \mu _{ijk} \left[ \tan^{-1}\biggl (\dfrac{x_i y_j}{z_k r_{ijk}}\biggr )\right] \end{aligned}$$

(8)

where $\gamma = 6.67 \times 10^{-11} \left[ {\text {m}}^3 \,{\text {kg}}^{-1}\,\text{ s}^{-2}\right]$, $\mu _{ijk} = \mu _i \mu _j \mu _k$ ($\mu _1 = -1; \; \mu _2 = 1$) and $r_{ijk} = \sqrt{x_i^2 + y_j^2 + z_k^2}$, with $x_i = x_p - x_{0_i}$, $y_j = y_p - y_{0_j}$ and $z_k = z_p - z_{0_k}$ ($x_p$, $y_p$, $z_p$ are the coordinates of the observation point and $x_{0_i}$, $y_{0_j}$ and $z_{0_k}$ are the coordinates of the vertices that define the prism, as shown in Fig. 2).

2.2 Joint Inversion of the Gravity Gradient Data by Simulated Annealing

The gravity gradient forward problem, expressed in Eq. (1), can be rewritten as:

$$\begin{aligned} f_k = G_{kq}^f \cdot \rho _q; \; \text{ for } \; k = 1, \ldots , N \end{aligned}$$

(9)

where $G_{kq}^f$ is the sensitivity matrix of each component f of the gravity gradient tensor ($f = T_{\alpha \beta } \; \text{ for } \; \alpha , \beta = x, y, z$), and $\rho _q$ is the vector of density contrasts of the model. Each element of $G_{kq}^f$ represents the contribution of the q-th prism of the ensemble to the f-component of the gravity gradient tensor, at the k-th observation point.

The forward problem (Eq. 9) represents a linear system of equations for each gravity gradient tensor component, where each system has the same unknowns or parameters ($\rho _q$ vector), so the inverse problem consists of calculating the vector of parameters, $\rho _q$, that satisfies (Eq. 9) simultaneously for all the components of the gravity gradient tensor.

We propose to perform the gravity gradient data inversion with the SA global optimization method, which is a single-solution based-metaheuristic, inspired by the natural process of crystal formation from a mineral fluid in a high initial energy state (Kirkpatrick et al., 1983; Sen & Stoffa, 2013).

The SA method does not solve the linear system of equations (Eq. 9) to obtain a model that fits the observations. Instead, it explores, in a relatively exhaustive way, the cost function associated with the system, in search of the global optimum, requiring a large number of evaluations of the forward problem in a three nested loop algorithm (Fig. 3). The innermost loop runs through the total number of parameters (density contrasts of the M prisms of the model), distorting each of them one by one to obtain a different model at a time and accepting or rejecting them with the Metropolis criteria. The perturbation to each parameter is done by adding the product of a uniformly distributed random number in the interval $\left( -1, 1\right)$ by a real number VM, which controls the maximum perturbation amplitude: $VM \times {\text{rand}}\left( -1, 1\right)$. The intermediate loop repeats this model acceptance-rejection procedure for a NT fixed number of times at each temperature value until thermal equilibrium is reached. Finally, the outer loop executes the intermediate and inner loops by reducing the temperature in each cycle with a cooling schedule until a predefined number of iterations is reached or a tolerance error is achieved. In this work, we used the exponential cooling scheme employed by Nagihara and Hall (2001), which, according to them, guarantees convergence to the global optimum and consists of multiplying the current temperature $T_k$ by a real number ${\text{RT}} < 1.0$ to obtain the reduced temperature $T_{k+1}$: $T_{k+1} = T_k \times {\text{RT}}$.

Fig. 3

Representative flow diagram of the simulated annealing (SA) method used in the gravity gradient data inversion. Modified from Nava-Flores et al. (2016)

To reduce the computational cost required by the SA method, the forward problem (Eq. 9) is implemented as an accelerated matrix-vector product, as proposed by Ortiz-Alemán and Martin (2005). It consists of computing the forward problem for a model disturbed in the q-th parameter, by adding a previously computed problem to the product of the q-th column of the matrix $G_{kq}^f$ by the q-th parameter disturbance $\Delta \rho _q$:

$$\begin{aligned} G_{kq}^f \cdot \left( \rho _q + \Delta \rho _q\right) = G_{kq}^f \cdot \rho _q + \left[ \begin{array}{c} G_{1,q}^f \\ G_{2,q}^f \\ \vdots \\ G_{N,q}^f \end{array}\right] \cdot \Delta \rho _q \end{aligned}$$

(10)

The cost function we propose to quantify the misfit in the SA method is a weighted sum of the fitting errors of each component of the gravity gradient tensor:

$$\begin{aligned} E = \sum _f \lambda ^f \cdot L_1(f) \end{aligned}$$

(11)

where $\lambda ^f$ are the weighting factors applied to each gravity gradient tensor component f, and the fitting error is calculated with the normalized $L_1$ norm, defined as:

$$\begin{aligned} L_1\left( f\right) = \dfrac{\sum \nolimits _{k=1}^N |f_k - f_k^{\text{calc}} |}{\sum \nolimits _{k=1}^N |f_k |} \end{aligned}$$

(12)

where $f_k$ is the gravity gradient observed component and $f_k^{\text{calc}}$ is the gravity gradient calculated component.

The $\lambda ^f$ weighting factors in Eq. (11) are determined in such a way that their sum is equal to unity, and their values are inversely proportional to the maximum sensitivity of the corresponding gravity gradient component to which they are applied:

$$\begin{aligned} \sum _f \lambda ^f = 1; \; \text{ where } \; \lambda ^f = \dfrac{1}{5} \left[ 1 - \dfrac{\max\left( G^f\right) }{\sum \nolimits _f^{} \max\left( G^f\right) }\right] \end{aligned}$$

(13)

The cost function jointly evaluates the fitting of the gravity gradient tensor components assigning more weight to the less sensitive, allowing them to contribute in an equalized way to the calculated error, which is based on the $L_1$ norm, that is known to have a low sensitivity to outliers in the data.

2.3 3D Density Model Inverted and Uncertainty Estimation

The SA method is able to compute a single model with minimum fitting error, but that model is only one of a possible infinite number of models that could have the same error, given the intrinsic non-uniqueness of the gravity problem. In addition, from that single model it is not possible to assess the uncertainty of their inverted parameters. Furthermore, according to Fernández Martínez et al. (2012), the cost function may be distorted by noise in the data, which is always the case in a real scenario, creating a false global optimum whose corresponding model may not be the best for interpretation. Therefore, it is necessary to adopt a statistical approach to overcome these difficulties, assuming that the resulting model and its uncertainty will only be approximations of the optimal model.

Our approach was inspired by the work of Pallero et al. (2018), who applied the particle swarm optimization algorithm to invert gravity anomaly data and described methods to estimate the model and its uncertainty. We computed a useful model for interpretation and its uncertainty from the set of tested models during the SA inversion procedure that samples the low-misfit region of the cost function. These models are characterized by having comparable fitting errors despite being composed of different parameters, which makes them solution models of the inverse problem with virtually the same level of accuracy; therefore, a representative model extracted from the low-misfit region could be determined from them and a measure of their parameter dispersion could be used as an estimate of their uncertainty. To select them it is necessary to examine the inversion convergence curve to set a threshold value for the cost function below which all models can be considered equivalent with respect to the fitting error (Fig. 4).

Fig. 4

Convergence curve for the inversion of synthetic gravity gradient data. The convergence curve is shown as a solid line, and the constant threshold value for equivalent model selection (TRS 800) is shown as a dashed horizontal line

The resulting set of equivalent models is then averaged to obtain the mean model, which is an estimate of the most probable among them, and the uncertainty is assessed with their mean deviation:

$$\begin{aligned} Md = \dfrac{1}{w} \sum _{w=1}^M |\rho _q^w - {\bar{\rho }} | \end{aligned}$$

(14)

where $\rho _q^w$ is the w-th equivalent model and ${\bar{\rho }}$ is the mean model.

Finally, a 3D model with the estimated uncertainty values of the mean density model can be configured to analyze its spatial distribution, which can be useful to support the interpretation.

3 Tuning Parameters of the Simulated Annealing Method by Parametric Scan

The performance of the SA method depends on several parameters whose values must be entered prior to its execution. These problem-dependent tuning parameters are the initial temperature $T_0$, the cooling factor RT, the maximum disturbance amplitude VM and the number of perturbations per temperature cycle NT.

To determine optimal values for them, we propose to perform a parametric scan-based analysis by executing the inversion algorithm for different combinations of the $T_0$, RT, VM and NT parameters in two stages. In the first stage, the parametric scan is performed to identify the optimal values of $T_0$ and RT as well as to define possible suitable values for VM. It consists of several executions of the inversion algorithm with a fixed maximum number of temperature reductions and is performed only for $NT = 1$, considering that the optimal parameters identified correspond to the minimum acceptable performance, so these parameters will also lead the SA to a good performance for $NT > 1$. In the second stage, the best value of VM among the possible values identified in the first stage and the optimum value of NT are determined with another parametric scan. It consists of some executions, keeping the RT parameter fixed at 1 with a low maximum number of iterations each.

Table 1 shows the test values we proposed for the tuning parameters of the SA in the parametric scan.

Table 1 Test values for the parametric scan of the simulated annealing (SA) inversion algorithm

The results of the first parametric scan can be analyzed by clustering the model acceptance curves by temperature reduction step derived from the different executions of the inversion algorithm and displayed as a surface, as shown in Fig. 5.

Fig. 5

Model acceptance by temperature reduction step for the parametric scan of the simulated annealing (SA) method, applied to the joint inversion of synthetic gravity gradient data

The curves forming the surface of the Fig. 5 are grouped in eight blocks, corresponding to the test values for $T_0$, with six sub-blocks each, corresponding to the RT test values, and each sub-block contains six curves calculated for the different VM test values, as illustrated in Fig. 6.

Fig. 6

Perspective representation of model acceptance curves by temperature reduction step for $T_0 = 0.0001$

Inspecting the results in Figs. 5 and  6 shows the influence of the parameters $T_0$, RT and VM in the model acceptance–rejection process by the Metropolis criteria, employed in the SA algorithm throughout its executions. As the $T_0$ parameter decreases, the number of temperature reduction steps (TRS) required for the percentage of accepted models to begin a significant and sustained decline also decreases. The RT parameter acts as a regulator of the model acceptance-rejection process, causing an increase in the rejection percentage at a fewer number of temperature reductions, when it takes values close to 0.0, and maintaining the tendency to get a high acceptance percentage, when it takes values close to 1.0. Finally, the VM parameter, which limits the maximum perturbation to be applied to a model to create a new one, proportionally impacts the rejection percentage of the models with respect to the TRS, regardless of the values of $T_0$ and RT.

3.1 Selection Criteria for the $T_0$, RT and VM Parameters

At the beginning of the SA inversion algorithm, it is desirable that almost all tested models are accepted by the Metropolis criteria, which reflects a sufficiently high initial temperature to allow an adequate exploration of the solution space. It is also desirable that not many TRS pass before models begin to be rejected significantly to save computational time. Therefore, a value for $T_0$, which produces curves between $80\%$ and $100\%$ model acceptance for the first 10 TRS, for all values of the VM parameter and ${\text{RT}} \ge 0.95$ will be a good choice (Fig. 14).

The SA inversion algorithm requires a gradual cooling to perform a proper exploration of the solution space, which will allow it to escape from local optima and favor its convergence to the global optimum. By inspecting the convergence curves for the value of $T_0$ that meets the first established criterion, we will observe that they converge to the minimum at different TRS (Fig. 15). Although apparently the same error is reached in the three cases, the convergence curves generated for the smallest value of RT could reflect a premature convergence because of the relatively low value of the cooling factor, and at the other side, when RT reaches its highest value, the convergence is too slow, which would unnecessarily increase the computational cost, so an intermediate value for RT would be the best choice.

Now, since the VM parameter is an important factor influencing the convergence speed in addition to $T_0$ and RT, as shown in Fig. 15, it is important to choose the value for it that generates smooth convergence curves and at the same time does not delay convergence.

The VM and NT parameters will be chosen from the second-stage parametric scan by comparing the convergence curves for the value of the $T_0$ parameter that meets the first criterion. The curve that converges smoothly to a stable energy value in the least number of iterations will correspond to the optimal VM parameter, and that minimum number of iterations will be the optimal NT value (Fig. 16).

4 Tests on Synthetic Data

To validate our methodology, we applied it to noise-corrupted synthetic data grids of gravity gradient components (Fig. 7). The synthetic data grids consist of $101 \times 101$ regularly spaced observations each, covering an area of 25 km$^2$ (5 km $\times$ 5 km), and are contaminated by pseudo-random Gaussian noise with zero mean and standard deviation of 1.0 Eötvös. The synthetic data correspond to a model formed by an irregular ensemble of 27,959 cubic prisms of identical dimensions (25 m $\times$ 25 m $\times$ 25 m) that resembles a cap rock lying over a salt base. The model has an irregular top surface with a minimum depth of 150 m and a flat base with depth of 600 m (Fig. 8). It is formed by two units with different and constant densities, separated by a concave interface. The top unit has a density of 2750.0 kg/m$^3$, corresponding to limestone, and the bottom unit has a density of 2180.0 kg/m$^3$, corresponding to salt, according to density ranges reported by Telford et al. (1990).

Fig. 7

Synthetic noise-corrupted gravity gradient data grids. a XX component, b XY component, c XZ component, d YY component, e YZ component and f ZZ component. The synthetic data grids are produced by the model shown in Fig. 8

Fig. 8

3D visualization of the synthetic model. a Perspective view from the southeast, b perspective view with two diagonal slices and a depth slice at Z = 0.55 km, c perspective view from above of the low-density unit and d perspective view from below of the high-density unit

The background density was modeled as a sedimentary environment with varying density, according to the representative density-depth relationship for the Gulf of Mexico sediments, published by Hudec et al. (2009):

$$\begin{aligned} \rho \left( z\right) = 1400.0 + 172.0 z^{0.21} \end{aligned}$$

(15)

where $\rho$ is the sediment density in kg/m$^3$, and z is the depth in m.

Prior to applying edge enhancement and depth estimation methods, all synthetic data grids were upward continued 100 m to filter out short-wavelength noise that could strongly affect the gradient-based methods ($TA\_T_{zz}$, THG and 3DED), but the data inversion was done employing the data grids without the upward continuation (Fig. 9).

We interpreted the lateral extent of the model by inspecting the zero contours of the $T_{xx}$, $T_{yy}$ and $T_{zz}$ gravity gradient components, zero contour of the $TA\_T_{zz}$, maximum value of the THG and $I_2$ invariant grid. Although no method was able to accurately approximate the outer edge of the model, the $TA\_T_{zz}$ and $I_2$ methods yielded the best results and were the only two considered for the interpretation, by visual inspection, of the outer edge of the model shown in Fig. 10.

Fig. 9

Lateral extent of the synthetic model interpreted from edge enhancement methods. a Zero contours of the FTGG components $T_{xx}$, $T_{yy}$ (white dashed lines) and $T_{zz}$ (yellow dashed line) shown overlaying the $T_{zz}$ component map, b lateral extent of the model (white dashed line) interpreted from the $I_2$ invariant map, c maximum of the total horizontal gradient (black dashed line) shown over the THG map and d zero contour of the tilt angle applied to the $T_{zz}$ component (black dashed line) shown over the $TA\_T_{zz}$ map

Notably, the interpreted outer edge does not fully coincide with the true outer edge. The interpreted edge is slightly offset in y-direction with respect to the true edge and is also slightly wider. This is attributed to the topography of the model (Figs. 8, 12) and the shape of the invariant $I_2$ surface, which has a relatively smooth appearance over the edges of the model.

Fig. 10

a Lateral boundaries of the synthetic model inferred by the zero contours of the $T_{xx}$, $T_{yy}$ and $T_{zz}$ components as well as from the $TA\_T_{zz}$ and THG methods. b Unified interpretation of the lateral extent of the model by visual selection of the results of $TA\_T_{zz}$ and $I_2$. The true edge of the model is shown in red dashed line

To estimate the depth of the model, we applied the 3D Euler deconvolution (3DED) to the synthetic gravity gradient data using a square window of 500 m per side (equivalent to 10 grid points) with the formulation proposed by Beiki (2010), in which the solutions and the structural index (SI) are calculated. The accepted solutions were those whose depth estimation dispersion was ≤ $10.0\%$ and are shown in Fig. 11. The histogram of the calculated SI shows a peak at $SI \approx 0.5$, indicating that the model does not have an integer structural index. However, the estimated depths are in good agreement with the true depth of the model.

Fig. 11

a 3D Euler deconvolution solutions of the synthetic gravity gradient data. The interpreted outer edge of the model is shown with black line. b Histogram of the structural index calculated for the synthetic model

Now, the interpreted topography of the model, which results from scaling the amplitudes of the $I_2$ invariant grid with the depths calculated by 3DED and its lateral extent constrained by the unified interpreted outer edge, is shown in Fig. 12.

Fig. 12

Comparison of topographic surfaces of the synthetic model. a True topography of the model, b interpreted topography of the model and c depth differences between true and interpreted model topography (true minus interpreted)

The interpreted topography resembles the true topography of the model, although it presents some discrepancies in its lateral lower zone, where it reaches the maximum difference of 70 m.

We constructed the computational domain with a flat base at a maximum depth of 600 m from the interpreted topography. The geometry of this irregular ensemble correlates with that of the synthetic model, showing some minimal differences due to the inaccurate interpretation of the data. This ensemble is the constrained discrete domain, used to perform the synthetic data inversion.

Initially, a constant density value of 2750.0 kg/m$^3$ was assigned to all prisms in the discrete domain, and their density contrasts were determined with this value and the Gulf of Mexico sediment density model (Eq. 15). The search space of the inversion algorithm was limited to a minimum value given by the sediment density and to the maximum value of 2750.0 kg/m$^3$, corresponding to the cap rock (Fig. 13).

Fig. 13

3D visualization of the computational domain ensemble with initial density contrasts asigned (synthetic case). a Perspective view from the southeast, b perspective view with two diagonal slices and a depth slice at Z = 0.55 km

The parametric analysis performed to determine the optimal SA tuning parameters for synthetic data inversion yielded the acceptance curves used for the creation of Figs. 5 and 6 shown in Sect. 3. The model acceptance curves, from which the optimal value of $T_0$ was determined, are shown in Fig. 14, showing compliance with the established selection criterion: the parameter $T_0 = 0.0001$ produces acceptance curves between $80\%$ and $100\%$ for all the VM values and for ${\text{RT}} > 0.95$, for the first 10 TRS (Fig. 14).

Fig. 14

Model acceptance curves by temperature reduction step for the parametric scan applied to the simulated annealing (SA) inversion algorithm for $T_0 = 0.0001$ and ${\text{RT}} \ge 0.95$ (synthetic case). a Model acceptance curve for $T_0 = 0.0001$ and ${\text{RT}} = 0.95$, b model acceptance curve for $T_0 = 0.0001$ and ${\text{RT}} = 0. 98$ and c model acceptance curve for $T_0 = 0.0001$ and ${\text{RT}} = 0.99$

The convergence curves analyzed to determine the optimum RT value are shown in Fig. 15. For the value of ${\text{RT}} = 0.95$, the curves reach the minimum between 80 and 200 TRS, for the value of ${\text{RT}} = 0.98$, they reach it between 200 and 400 TRS, and for the value of ${\text{RT}} = 0.99$, between 400 and 700 TRS, so the value of ${\text{RT}} = 0.98$ would be the best choice to avoid premature convergence and the excessive computational cost due to a very slow temperature decrease.

Fig. 15

Convergence curves for the parametric scan applied to the simulated annealing (SA) inversion algorithm for $T_0 = 0.0001$ and ${\text{RT}} \ge 0.95$ (synthetic case). a Convergence curves for $T_0 = 0.0001$ and ${\text{RT}} = 0.95$, b convergence curves for $T_0 = 0.0001$ and ${\text{RT}} = 0.98$ and c convergence curves for $T_0 = 0.0001$ and ${\text{RT}} = 0.99$

The convergence curves used to determine the optimum values of VM and NT are shown in Fig. 16, where it is observed that for $VM \ge 25\%$ the curves converge to a stable energy value in ten iterations with a smooth behavior. Therefore, the optimum value identified for NT is 10, and the optimum value identified for VM is $25\%$.

Fig. 16

Convergence curves for the second-stage parametric scan applied to the simulated annealing (SA) inversion algorithm for $T_0 = 0.0001$ (synthetic case)

Finally, after running the inversion algorithm with the optimal parameters, we identify the low-misfit region of the cost function by inspecting the convergence curve generated by the inversion. We set the fitting error at TRS 800 as the threshold below which all models proved by the algorithm are equivalent with respect to the error because it is the value to which the convergence curve trends in the final stage of the inversion procedure, as shown in Fig. 4.

The resulting set of models that samples the low-misfit region consisted of > 20.257 million models with a maximum difference between their fitting errors of $8.39 \times 10^{-7}$. The mean model calculated from them and the uncertainty model estimated with their mean deviation (Eq. 14) are shown in Figs. 17 and 18, respectively.

Fig. 17

3D visualization of the mean density model resulting from the inversion of synthetic data. a Perspective view of the inverted mean density model, b perspective view of the cap rock-density volume, c perspective view of the salt-density volume and d perspective view of the sediment-density volume. The azimuth and elevation angles of all perspective views are $225^{\circ }$ and $45^{\circ }$, respectively

The inverted mean model presents an internal configuration of densities that is approximated to the synthetic model. From its 3D visualization, it is possible to distinguish the high density unit, corresponding to the cap rock, and low density unit, corresponding to salt. Although the inversion method does not exactly retrieve the shape of the two model density units, it was able to identify the sediment border to the south that does not correspond to the true edge of the model (Fig. 17). In addition, the inverted mean model shows a shallow zone of low density in the central part overlying the high-density volume. This zone has the appearance of a shallow layer that correlates with the area where the interpreted model topography is slightly shallower than the true topography. Also, the salt density volume of the inverted model shows two deep depressions that correlate with areas where the model topography exceeds the true topography.

Fig. 18

3D visualization of the uncertainty model resulting from the inversion of synthetic data. a Perspective view of the uncertainty model, and b perspective view of the uncertainty model with two diagonal slices and a depth slice at Z = 0.55 km. The azimuth angles of the perspective views (a) and (b) are $225^{\circ }$ and $180^{\circ }$, respectively. The elevation angle of all perspective views is $45^{\circ }$

The estimated uncertainty model shows that the zones with the highest uncertainty in the inverted mean density model, with values ranging from 200 to 212.3 kg/m$^3$, are those corresponding to the rock-salt, rock-sediment and salt-sediment interfaces. There is also a large uncertainty associated with the upper northern portion of the model, in a small area to the south and in the central deepest zone of the model.

The gravity gradient data grids created by the inverted mean density model are shown in Fig. 19. The mismatch between them and the synthetic data grids was evaluated by performing a statistical analysis of the residuals between synthetic and inverted data. The histograms of the residuals with their mean values and standard deviations are shown in Fig. 20.

Fig. 19

Gravity gradient data grids calculated for the inverted mean density model (synthetic case). a XX component, b XY component, c XZ component, d YY component, e YZ component and f ZZ component

Fig. 20

Relative frequency histograms of the residuals of the gravity gradient data calculated for the inverted mean density model (synthetic case). a XX component, b XY component, c XZ component, d YY component, e YZ component and f ZZ component

The statistical analysis of residuals shows that all the inverted data grids adequately fit the synthetic data, since their averages are close to zero and their standard deviations are close to 1.0 Eötvös, which are the values that characterize the pseudo-random Gaussian noise added to the synthetic data.

The global performance of the inversion algorithm can be resumed with the values of the Table 2.

Our joint inversion algorithm was coded in modern Fortran language (2008 standard), was compiled with the gfortran 9.4.0 compiler and was executed on a mobile workstation with 31.3 GB RAM and an Intel^® Core^TM i7-4810MQ CPU @ 2.80 GHz $\times$ 8 processor, running on a 64-bit Linux Operating System.

Table 2 Global performance of the SA algorithm applied to synthetic data inversion

Notably, forward modeling alone calculated with the numerical solutions proposed by Nagy et al. (2000), shown in Eqs. (3) to (8), takes 18.6 min (0.31 h) of computing time, while the inverse problem, consisting of 304.99 million evaluations of the forward problem, takes 9.939 h, which represents a small fraction ($1.05 \times 10^{-7}$) of the time it would require if the accelerated matrix-vector product (Ortiz-Alemán & Martin, 2005) were not implemented.

5 Application to Real Data

We applied our methodology to model the Vinton dome cap rock with the FTGG data acquired from July 3 to 6, 2008, by Bell Geospace Inc. The air gravity gradient survey was carried out with the general characteristics shown in Table 3.

Table 3 Air gravity gradient survey general characteristics

Figure 21 shows the geographical location of the area covered by the gravity gradient survey as well as the central area used for the cap rock model.

Fig. 21

Flight line location of the gravity gradient survey carried out by Bell Geospace Inc. over the Vinton dome. The central section used for the cap rock model is highlighted with dashed red lines

The data provided by Bell Geospace already included some essential processes that consisted of peak and noisy data editing, micro-leveling, terrain correction with a density of 1800 kg/m$^3$ and high-frequency noise filtering with a 150-m cut-off wavelength filter (Selman, 2010).

The area selected for modeling corresponds to the central section of the grid, where the anomaly attributed to the cap rock of the Vinton dome stands out. The area covers an area of 25 km$^2$ (5 km per side) and is located between coordinates 440.0 km and 445.0 km in the E–W direction, and 3332.0 km and 3337.0 km in the N–S direction (WGS 84/UTM zone 15 N).

Figure 22 shows the gravity gradient tensor data of the Vinton dome cap rock for the modeling selected area. The data displayed were regularly interpolated with a 50-m interval in X and Y directions (1021 data points) and upward continued to 100 m to filter out short-wavelength noise that could be associated to shallow sources that are not of interest.

Fig. 22

Gravity gradient gridded data of the Vinton dome cap rock. a XX component, b XY component, c XZ component, d YY component, e YZ component and f ZZ component

We built a model for the Vinton dome cap rock to be used as computational domain in the inversion procedure, based on information derived from the processing and interpretation of the gravity gradient data grids shown in Fig. 22. Maps of the lateral extent of the cap rock, its depth estimation with 3DED and its interpreted topography are shown in Fig. 23.

Fig. 23

a Lateral extent of the Vinton dome cap rock interpreted from edge enhancement methods. b Topography of the Vinton dome cap rock interpreted from its lateral extent interpreted, 3D Euler deconvolution and the $I_2$ invariant grid

The 3DED depth solutions are consistent with previous studies in the area (e.g., Thompson & Eichelberger, 1928; Ennen & Hall, 2011), in which the cap rock was found to have an irregular shape approximating a low pyramid with an ovoid base, flattened apex and offset to the southeast, with depths ranging from about 150 m to the southeast to 350 m to the northwest. Notably, the most representative value of the structural index, estimated from its histogram, is close to zero, corresponding to contact-type sources (Stavrev & Reid, 2007).

The geometry of the model employed as computational domain was built with an irregular ensemble of identical cubic prisms, each with constant density, constrained by the cap rock topography and a flat horizontal base at 600 m depth, deep enough to encompass the cap rock according to Thompson and Eichelberger (1928), Oliveira Jr. and Barbosa (2013) and Qin et al. (2016). The size and properties of the ensemble are shown in Table 4.

Table 4 Characteristics of the 3D computational domain of the Vinton dome cap rock

The density contrasts of the model were determined from the work of Thompson and Eichelberger (1928), who reported that the cap rock of the Vinton dome is composed of limestone, gypsum and anhydrite in succession, with average densities of 2550.0 kg/m$^3$, 2350.0 kg/m$^3$ and 2930.0 kg/m$^3$, respectively (Telford et al., 1990), and the density-depth relationship published by Hudec et al. (2009), given by Eq. (15).

The lower and upper limits of the search space of the inversion algorithm were defined by the sediment density curve (Eq. 15) as the lower limit and the density of the cap rock (2750.0 kg kg/m$^3$) as the upper limit.

We set TRS 900 as a threshold to identify the low-misfit region of the cost function for the inversion of the Vinton dome data. From the resulting set of models, we calculate the mean model, which is an estimate of the most likely model among them, and its mean deviation to estimate its uncertainty. The number of equivalent models was > 31.911 million, all with a maximum difference of $9.76 \times 10^{-07}$ between their fitting errors.

The global performance of the inversion algorithm applied to the Vinton dome data is resumed in Table 5.

Table 5 Global performance of the SA algorithm applied to the inversion of Vinton dome gravity gradient data

As we did for the synthetic case, we compared the execution time required by the forward problem with respect to the time required by the inverse problem for the Vinton dome cap rock. We found that the forward problem with the Nagy et al. (2000) solutions (Eqs. 3–8) takes 25.506 min (0.425 h) of computing time, and the inverse problem takes 13.830 h, which represents a factor of $7.8 \times 10^{-8}$ of the time that would be needed for the evaluation of the 414.59 million forward problems required by the FTGG data inversion without the accelerated matrix-vector product.

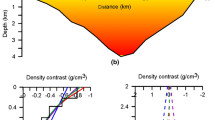
The parameter values (i.e., densities) of the resulting mean model are bimodally distributed in two well-defined sets within the limits established by the inversion algorithm, which is reflected in both the density-depth plot of the model and its histogram (Fig. 24).

Fig. 24

Density distribution of the mean model resulting from the inversion of the Vinton dome data. a Density-depth pairs of the mean model represented by dots. The lower (sediment) and upper (cap rock) limits set for the inversion algorithm are shown in solid black line and the salt density in dashed black line. b Relative frequency histogram of the mean model densities

The spatial distribution of the mean model densities was inspected by separating its parameters into three groups of prismatic bodies with densities related to the lithology expected to be found at the site: the first group, hereafter referred to as the sediment volume, was constructed by prisms with densities between 2000 and 2150 kg/m$^3$, the second group, hereafter referred to as the salt core volume, by prisms with densities between 2180 and 2200 kg/m$^3$ and the third group, hereafter referred to as the cap rock volume, by prisms with densities between 2500 and 2700 kg/m$^3$. Visualizing these groups in 3D showed that their general geometric arrangement resembles that of a salt core covered by the cap rock, with sediments present mainly on the flanks and filling shallow discontinuities, shown in Fig. 25.

Fig. 25

3D visualization of the mean density model resulting from the inversion of the Vinton dome data. a Perspective view of the mean model, b perspective view of the cap rock volume, c perspective view of the salt core volume and d perspective view of the sediment volume. The azimuth and elevation angles of all perspective views are $225^{\circ }$ and $45^{\circ }$, respectively

In addition, we configured a 3D model with the estimated uncertainty values of the mean density model to analyze its spatial distribution, which is shown in Fig. 24. We found that the highest uncertainty, given by mean deviation values ranging from 160 to 190 kg/m$^3$, corresponds to the prisms located at the contacts between the sediment, salt core and cap rock volumes. Intermediate uncertainty values, with mean deviation ranging from 55 to 150 kg/m$^3$, correspond to the internal prisms of each of the volumes and the lowest uncertainty, with mean deviation values ranging from 20 to 50 kg/m$^3$, corresponding to the sediment volume at the west and northeast edges of the model (Fig. 26).

Fig. 26

3D visualization of the uncertainty model resulting from the inversion of the Vinton dome data. a Perspective view of the uncertainty model, and b perspective view of the uncertainty model with two diagonal slices and a depth slice at Z = 0.55 km. The azimuth angles of the perspective views (a) and (b) are $225^{\circ }$ and $180^{\circ }$, respectively. The elevation angle of all perspective views is $45^{\circ }$

The cap rock volume has an elliptical shape oriented in the northeast-southwest direction that extends from a depth of 160 to 500 m. It has an irregular base that is deeper in its central section, where it reaches its maximum depth, than at the edges, where it reaches depths ranging from 250 m, at the southeast edge, to 350 m at the northwestern edge. The cap rock volume also appears to have two discontinuities with rounded cavity shape in its northwest section and a discontinuity with a detached block shape in the southeast section. In addition, it presents two shallow irregularities in its southern section that look like straight channels communicated with different orientations: one that interrupts the continuity of the volume to the south and other that communicates with it and with one of the discontinuities with rounded cavity shape. Finally, a zone of low relative density (2530–2600 kg/m$^3$) can also be distinguished in the northeast section of the cap rock volume with a linear aspect.

The discontinuities in the northeast sector of the cap rock volume, the detachment plane to the southeast and the shallow channel-shaped surface irregularity in the south, are aligned in a northeast-southwest direction, parallel to the orientation of the cap rock volume. In contrast, the shallow irregularity connecting with one of the discontinuities with rounded cavity shape to the southwest and the low density zone to the northeast are aligned in a northwest-southeast direction, shown in Fig. 27.

Fig. 27

3D visualization of the cap rock volume of the mean model resulting from the inversion of the Vinton dome data. a XY plan view with the alignment directions of the irregularities and discontinuities marked in dashed black lines (northeast-southwest direction) and dashed blue lines (northwest-southeast direction), b perspective view with azimuth angle of $225^{\circ }$ and elevation angle of $45^{\circ }$, c XZ lateral view and d YZ lateral view

The cavity-shaped discontinuities in the northwest sector of the cap rock volume have a high value of uncertainty associated with their calculated density, reaching mean deviation values between 160 and 190 kg/m$^3$, while the channel-shaped irregularities in the south and the low density zone to the northeast have intermediate values of uncertainty with mean deviations between 90 and 150 kg/m$^3$. Despite the uncertainty that these features may have, their presence cannot be discarded because their orientations are consistent with fracture patterns reported by Coker et al. (2007), related to the salt core at depths > 1000 m.

Finally, the grids of the gravity-gradient data calculated for the mean model are shown in Fig. 28. To evaluate their fitness with respect to the observed data, histograms of their residuals were calculated. They are shown in Fig. 29 with their corresponding means and standard deviations.

Fig. 28

Gravity-gradient data calculated for the mean density model resulting from the inversion of the Vinton dome data. a XX component, b XY component, c XZ component, d YY component, e YZ component and f ZZ component

Fig. 29

Relative frequency histograms of the residuals of the gravity-gradient data calculated for the mean density model resulting from the inversion of the Vinton dome data. a XX component, b XY component, c XZ component, d YY component, e YZ component and f ZZ component

The shape of the histograms of all the residuals suggests that they follow a Gaussian distribution. The mean values for the residuals of all gravity-gradient components are close to zero, ranging in absolute value from a minimum of $0.000 \; E\ddot{o}tv\ddot{o}s$ for the $T_{xy}$ and $T_{xz}$ components to a maximum of $0.272 \; E\ddot{o}tv\ddot{o}s$ for the $T_{zz}$ component, and their standard deviations vary from a minimum of $1.293 \; E\ddot{o}tv\ddot{o}s$ for the $T_{xy}$ component, to a maximum of $3.649 \; E\ddot{o}tv\ddot{o}s$ for the $T_{zz}$ component. On the other hand, the maximum point-to-point misfits in absolute value between the calculated and observed data range from a minimum of $6.578 \; E\ddot{o}tv\ddot{o}s$ for the $T_{xy}$ component to a maximum of $15.983 \; E\ddot{o}tv\ddot{o}s$ for the $T_{xx}$ component. This indicates that the gravity-gradient data grids calculated for the mean density model adequately fit the observed data grids.

6 Conclusions

We have presented a 3D high-resolution modeling methodology for gravity gradient data that consists of estimating the target geometry with an irregular ensemble of identical prisms, constraining its shape and location with information derived from the application of different interpretation methods and estimating its density distribution by joint inversion with a numerically optimized SA algorithm.

The optimized matrix-vector product included in our inversion algorithm allowed us to extensively explore the cost function associated with the inverse problem, proving to be 7–8 orders of magnitude faster than the evaluation of the forward problem with numerical solutions. Also, the parametric scan-based analysis we conducted on the SA tuning parameters allowed us to examine the relationships between them and to propose criteria to select them properly.

The identification of the low-misfit region of the cost function through the inversion convergence curve allowed us to identify the models that sample it and use them to obtain the mean model and its mean deviation as estimates of the most likely model in that region and its uncertainty, respectively, which proved to be useful in the interpretation when applyed our methodology on synthetic and real data.

By applying our methodology to the gravity gradient data of the Vinton dome, we obtained a high-resolution model with a density distribution that resembles a salt core covered by the cap rock, with sediments on the flanks and filling shallow discontinuities. The facts that the resulting model revealed volumetric units with densities and geometries associated with materials and structures reported from the study area, its general characteristics such as size and depth are compatible with previous models and the calculated data adequately fit the observed data indicate that the methodology used to built it, as well as its quality and interpretative utility, is valid and could be employed in other exploration areas with the gravity gradiometry method.