1 Introduction

Earthquakes are manifestations of dynamic ruptures that release rapidly elastic strain energy stored in the surrounding rocks (Reid, 1910). Faults are commonly modeled as infinitely thin surfaces (idealized typically as planar) sustaining only shear deformation. This classical view has been driven by far-field observations of attenuated low-pass filtered information. However, near-fault studies unambiguously show that ruptures consist of zones that can be tens to hundreds of meters wide with broken and granular (damaged) materials, and that shear deformation is accompanied locally by dynamic dilation (Fig. 1). These phenomena, although localized, strongly affect the partitioning of the stored elastic energy between dissipation and seismic radiation, changes of permeability and fluid flow, and other key aspects of earthquake physics (e.g., Aben et al., 2020; Kurzon et al., 2019; Okubo et al., 2019). Theoretical and laboratory studies of earthquake ruptures consider fracture, friction and damage processes, with most studies in the last few decades focusing on friction. In the present paper we attempt to clarify how these different processes operate in different regions of earthquake rupture zones. We focus on brittle processes and structures in low porosity crustal rocks and note that some modifications are needed for high porosity rocks and soft materials that tend to fail in a more distributed ductile fashion.

Fig. 1
figure 1

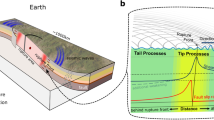
Schematic representations of rupture and fault zones for dense rocks (not to scale). a Individual dynamic rupture with a process zone at the front propagating typically at sub-Rayleigh rupture velocity (Vr), followed by intermediate and tail regions dominated by frictional sliding where some fault patches may re-rupture. The stresses are high at the front, producing fracturing in the process zone, and drop rapidly behind to a residual frictional level. The slip velocity (Vs) is several orders of magnitude below the rupture velocity and decelerates rapidly from the front to the tail. Inelastic deformation occurs in a volume that is projected on a plane in typical constitutive models. Energy dissipation involves comminution and gouge production in the rupture zone, and frictional heat occurring primarily in the tail region (e.g., Kurzon et al., 2019). The seismic radiation is a superposition of multi-scale processes that generate jointly broadband signals including high-frequency isotropic radiation, and can trigger failures ahead of the front. b Schematic map view of anastomosing network of fault segments hosting individual rupture zones as in a during single and multiple earthquakes. c A planar projection of a depth section with heterogeneous rupture/slip distribution including non-slipping patches as in slip inversions (e.g. Mai & Thingbaijam, 2014) and numerical simulations (e.g. Figure 6 of Ben-Zion & Rice, 1995). d A volumetric depth view with several rupture zones as in the field example of Fig. 3 producing a flower structure

Full size image

The rupture front has a process zone dominated by fracturing processes, where stresses beyond the elastic limit produce distributed cracking and granulation/pulverization of rocks. The amount of inelastic strain (or slip in a planar approximation) in the process zone is negligible, so friction has little relevance in the process zone. As the rupture propagates, the process zones at locations passed by the rupture front produce together a slip zone with highly cracked and granulated materials sustaining growing amounts of inelastic strain and frictional sliding. The rupture speed VR of a typical crustal earthquake is ~ 3 km/s, although some earthquakes can propagate at supershear speed (Archuleta, 1984; Rosakis, 2002) and there is also a class of slow slip events that propagate much slower (Hirose & Obara, 2005; Okal & Stewart, 1982). Since particle velocity in a continuum is proportional to stress, and the stress drops rapidly behind the rupture front, the rate of inelastic strain (or slip rate VS) also drops rapidly behind the propagating front (Fig. 1). Sections of the rupture zone close to the front with slip rates of ~ 1 m/s or more produce dynamic stress transfer that can interact significantly with the propagating front, but the interactions of sliding sections further behind diminish rapidly with increasing distance from the front. As an example, a fault section with a slip rate of 1 cm/s can hardly affect the rupture front that propagates in 1 s several km forward.

The rupture zone can be separated into several regions (Fig. 1). The rupture tip or front is dominated by fracturing processes and controls the path of the propagating rupture. Sliding sections of the rupture behind the process zone with slow slip velocities, and hence small dynamic stress transfer to the front, belong to a tail region that does not interact effectively with the rupture front. Sliding sections closer to the front with higher slip velocities, which produce sufficient dynamic stress transfer to affect appreciably the energy balance at the front, belong to an intermediate region relevant for the continuing motion of the rupture front. The extent of the intermediate region depends strongly on the geometrical properties of the rupture zone (and perhaps other features such as rock type, existence of gouge, etc.). The region ahead of the rupture front can also fail and may be referred to as a wave dominated region, where dynamic stress transfer can trigger ruptures across unbroken barriers (Das & Aki, 1977; Rice et al., 1994), lead to a subshear-to-supershear transition of the rupture velocity (e.g., Andrews, 1976; Burridge, 1973) and trigger aftershocks at large distances ahead of the rupture zone (e.g. Hill et al., 1993; Prejean et al, 2004).

Earthquake ruptures often propagate over multiple disconnected fault zones (e.g., 1992 Landers CA earthquake in California, 2010 El Mayor-Cucapah Earthquake in Baja California; 2016 Kaikoura in New Zealand), during which the rupture fronts jump to non-contiguous locations and abandon their tails. Evidently, the frictional processes at the tails are not essential for the rupture trajectories and ultimate size of earthquakes, although they contribute significantly to energy dissipation and changes to fault zone structures. We also note that seismic radiation is a superposition of contributions from different parts of the earthquake rupture. The radiation from the process zone can be dominated by dilatational components generated by fracturing and reduction of elastic moduli (e.g., Ben-Zion & Ampuero, 2009; Kurzon et al., 2021; Lyakhovsky et al., 2016), the radiation from the tail region involves primarily shear motion with variable local dilatation (e.g., Aki & Richards, 2002; Lyakhovsky & Ben-Zion, 2020), and the general breaking of multi-scale asperities in the rupture zone is expected to produce enhanced radiation at different frequency bands.

In the next section we describe observational results highlighting aspects of earthquake rupture zones and failure processes represented in Fig. 1, starting with field studies and continuing with laboratory stick–slip experiments that include fracture and friction. In Sect. 3 we briefly discuss constitutive laws for planar fracture and friction, along with nucleation of dynamic failures on a plane and in a deforming volume. In Sect. 4 we synthesize the results and suggest future studies that can significantly improve the understanding of earthquake and fault processes.

2 Observations

2.1 Field Studies

Geological and seismological studies document abundantly the ubiquitous existence in natural fault zones of hierarchical geometrical heterogeneities (Candela et al., 2012; Sagy et al., 2007; Wechsler et al., 2010; Wesnousky, 1988) and hierarchical damage zones generated by the failure events (Allam & Ben-Zion, 2012; Dor et al., 2006; Ostermeijer et al., 2020; Qiu et al., 2021; Rodriguez Padilla et al., 2022). Even major faults with very large cumulative slip have finite width, roughness, segmentation, and varying strengths that are expected to evolve with further deformation (e.g., Ben-Zion & Sammis, 2003; Manighetti et al., 2007; Scholz et al., 1993). Heterogeneous fault properties lead to strong stress heterogeneities that affect rupture dynamics (e.g., Ampuero et al., 2006; Ripperger et al., 2007; Romanet et al., 2018) and produce variable slip distributions in one or multiple simultaneously occurring rupture zones (Fig. 1c, d). The general existence of heterogeneous fault structure and pre-existing stress may lead to multiple rupture fronts nucleating simultaneously from several asperities (Campillo et al., 2001; Dublanchet et al., 2013; Lebihain et al., 2021; Mai & Beroza, 2002), complex collective slip fronts in 3D, jumps of the rupture front, and repeated acceleration and deceleration of the failure process. Source time functions of earthquakes are frequently complex, showing multiple peaks that reflect these processes. The literature on field studies of earthquake ruptures is vast. To illustrate key aspects of fracture and friction processes in earthquake rupture zones, we present three examples at different scales, starting with small-scale field results and continuing with ruptures and fault zones occupying larger crustal volumes. Some of the discussed features are also observed in laboratory experiments (Sect. 2.2).

Figure 2 shows observed damage (fracturing) and melt (friction) products in a fossilized rupture zone of a single earthquake in lower crust rocks in the Bergen arc, Norway (Petley-Ragan et al., 2019). These observations allow inferences on the space–time evolution of rupture processes, which correspond to Fig. 1a, generally not possible in large fault zones reflecting properties of many earthquake ruptures. The results show fragmented/pulverized particles surrounded by melt products within an asymmetric damage zone, and tensile cracks normal to the main fault, some of which have injection products. The field and microstructural observations were interpreted to reflect the following evolution of processes. Initial fragmentation with minimal shear occurred in the process zone around the propagating rupture tip and extended into one wall rock, followed by comminution of the fragments with increasing shear motion behind the tip. As shear heating progressed with slip accumulation further behind the tip, the cataclasites began to melt with higher melt fractions in locations with greater volume of damaged wall rock, and injection of melt products to some of the fault-normal tensile cracks (Petley-Ragan et al., 2019).

Fig. 2
figure 2

Modified from Petley-Ragan et al. (2019)

Multi-scale structural results of an earthquake rupture zone in the Bergen Arcs. a A damage zone on the northern side of the fault with pseudotachylyte (Pst), wall rock minerals showing little to no shear strain, and tensile cracks/injection veins normal to the fault. Clasts of cataclasite are entrained in the pseudotachylyte. b Backscatter electron images of cataclasite and fragmented minerals in the damage zone. Insets show grain size distribution (probability density function; PDF) of clasts and power law exponents. c Electron backscatter diffraction results for garnet in the damage zone. The orientation map (inverse pole coloring in relation to the horizontal) indicates pulverization with no shear.

Full size image

Figure 3 presents an example documenting the activation of multiple localized slip bands, within a fairly large normal fault zone in a deep south African mine, during a single earthquake rupture, corresponding to the representation in Fig. 1d. The normal fault was likely reactivated in response to mining activity, producing a comparatively large seismic event with Mw 5.1. This example shows that the rupture activated three slip bands in the fault damage zone exposed in the tunnel site shown in Fig. 3, with slip not limited to a single planar ‘principal slip zone’. The full extent of the rupture zone of that earthquake is not clear but likely includes additional volumetric components. Larger-scale activation of multiple slip and rupture zones during single earthquakes (e.g. Fig. 1b) has been observed in geological and seismological studies of many recent large events, and appears increasingly to be the norm rather than the exception. One prominent example is the 2016 M7.8 Kaikoura earthquake in New Zealand, which “ruptured at least 17 faults, only about half of which were recognized before.” (Clark et al., 2017; Nicol et al., 2018). Other examples among many others include the 2010 MW 7.2 El Mayor-Cucapah earthquake in Baja California (e.g., Fletcher et al., 2014; Wei et al., 2011), the 2012 MW 8.6 Indian Ocean event (e.g., Yue et al., 2012), the 2016 Mw 7.0 Kumamoto earthquake in Japan (e.g., Asano & Iwata, 2016; Shirahama et al., 2016), and the various large earthquakes in the Eastern California Shear Zone in the last 30 years. In addition to rupturing multiple disconnected fault segments, earthquake ruptures often produce significant distributed off-fault inelastic strain in the surrounding volume as illustrated by Fig. 4 in the context of the 1992 Mw7.3 Landers earthquake in California.

Fig. 3
figure 3

Photos of exposed normal fault zone (Dagbreek fault) cut by a mining tunnel at 1370 m depth, Welkom, South Africa that hosted a seismic event with Mw 5.1 in March, 1999. The fault zone includes four localized slip bands (Photo), three of which were activated during the event, as indicated by sheared rock bolts. This observation shows that the rupture involved at that site multiple slip bands within a pre-existing volumetric fault zone

Full size image
Fig. 4
figure 4

Modified from Fleming et al. (1998) and Milliner et al. (2015)

Rupture zone of the Landers 1992 Mw 7.3 earthquake. Left: the Landers rupture extended over 85 km over multiple segments with peak slip of about 5–6 m or larger (Gombert et al., 2018). Map view of segmented rupture trace with color code indicating orientation (Fleming et al., 1998). Right: off-fault deformation (OFD %) increases with structural complexity along the fault trace (Milliner et al., 2015). Estimates of the maximum damage zone width range from about 200–1000 m (Gombert et al., 2018; Peng et al., 2003).

Full size image

2.2 Laboratory Experiments

Laboratory fracture and friction experiments culminating in a sample-size stick–slip motion and rapid stress drop represent lab analogues for crustal earthquakes (Brace & Byerlee, 1966). Here we briefly summarize some results from a series of lab tests with different geological materials (claystone, sandstone, quartzite, granite) performed at varying loading conditions and confining pressures up to 150 MPa (Goebel et al., 2012, 2017; Guerin-Marthe et al., 2022). Depending on material and loading conditions, the samples mostly failed in episodic stick slip events accompanied by rapidly evolving bursts of acoustic emission (AE) activity (Fig. 5). Typically, AE cumulative numbers roughly follow tf−p where tf is time to failure and p is close to unity. On rough fractured faults, the AE activity spreads across the surface forming a single or a few expanding clusters (Fig. 5), while on smooth faults the AE activity is generally low or in some cases non-existent (Dresen et al., 2020; Guerin-Marthe et al., 2022). The AE clusters highlight larger asperities that persist over several stick–slip cycles. This suggests a collective failure of growing AE clusters, with jumps of the rupture front, finally leading to a system-size slip event (Goebel et al., 2012, 2017). Slip rates along the faults measured at different tests ranged from about 2 μm/s to over 160 mm/s. Often contained or system-wide slip events start with a single large acoustic emission. Here macroscopic stress drop and failure were initiated by large acoustic emissions with amplitudes significantly larger than background events (and partly clipped). The events occurred at peak stress or slightly below (Fig. 5a, A–C). The space–time sequence of large AEs A–C (Fig. 5) indicates propagation of the rupture front. AE clusters remain active for the entire duration of the slip event after the rupture front has passed, i.e., the rupture front and frictional tail were ‘detached’. AE events may also represent failures of strong brittle asperities following slow slip (Yamashita et al., 2022) or activity in an off-fault damage zone (Marty et al., 2019).

Fig. 5
figure 5

Slow stick slip event (VS = 20–40 μm/s) along a fractured surface of a quartzite sample (Stanchits et al., 2010). a Map view of acoustic emission hypocenters clustered heterogeneously across the fault surface. Recurrent clusters vary in space and time (gray ellipses). Red stars indicate a sequence of large acoustic emissions labeled A–C associated with the slip event and stress drop. Sequence A–C indicates propagating rupture front (VR = 0.05–0.8 m/s). b Cross section view showing finite width of active volume surrounding the fault (location accuracy 3 mm). c Stress drop and acoustic emission activity

Full size image

The elastic waves radiated from the rupture produce strain signals in gauges attached locally at a small distance from the fault (Guerin-Marthe et al., 2022.) indicating a passing rupture front. The offset time between signals from strain gauges often allows a rough estimate of the rupture velocity. Bulk stress drop measurements using an internal load cell represent an average that includes both rupture and slip components. In contrast, the strain gauges allow estimating local stress drops, which occur often more abruptly and over smaller slip distances (Fig. 6). The observations of separation of rupture front and slip are consistent with the representation in Fig. 1a, and in agreement with results from additional triaxial tests by Passelegue et al. (2017), rotary shear tests (Chen et al., 2021), experiments on large laboratory faults (e.g. Kammer & McLaskey, 2019; Ke et al., 2021; Ohnaka & Shen, 1999; Xu et al., 2018) and experiments on analogue materials at low normals stresses (Gvirtzman & Fineberg, 2021; Paglialunga et al., 2022; Rubino et al., 2022).

Fig. 6
figure 6

Stress drop and slip from an experiment on Mont Terri claystone at 5 MPa confining pressure (Schuster, 2022; Schuster et al., 2022). Heterogeneous stress drop of about 0.1–1 MPa from internal load cell (yellow) and strain gauges attached to the sample surface. Bulk slip rates VS were about 2.5 μm/s. Slip starts at the top of the sawcut with peak in top strain gauge SGF1 (blue). Macroscopic peak stress (yellow) and onset of stress drop coincide with peak shortening and strain drop of wall rock (black). Note that local strain/stress drops differ from the bulk sample stress drop

Full size image

Double direct shear tests were used to extensively investigate frictional rock properties of planar fault surfaces and gouge layers with evolving fabric, spatio-temporal evolution of granular slip and the transition from stable to slow and fast slip, covering a wide spectrum of slip velocities (Im et al., 2020; Marone, 1998). Frictional tests on gouges with varying mineralogical composition show relations between microstructural fabric evolution (i.e. localization) and stability of slip (Scuderi et al., 2017, 2020). A key observation is that a single fault with identical constitutive properties may host both stable slow slip and dynamic rupture events (Scuderi et al., 2017; Ye & Ghassemi, 2020). More recently, the interplay of slip modes from slow to fast was studied with high-frequency (AE) signals (Bolton et al., 2022). Complex rupture fronts were observed to arise from local slip events across a range of slip rates from aseismic failure to dynamic events (e.g. Bolton et al., 2022; McLaskey, 2019), and the combined failure of asperities of varying sizes in the sliding region were also observed to produce new rupture fronts (de Geus et al., 2019; Lebihain et al., 2021). These results converge with those of triaxial tests at high pressure with AE monitoring (Figs. 5, 6), showing superposition of local events that range from high-frequency AEs with source radii on the μm-mm scale to slip events affecting the entire sample.

3 Constitutive Models

The onset and continuing motion of the rupture front are controlled by an energy balance between the flow of strain energy to the front and dissipation in the process zone to fracturing the material ahead and around the front (Freund, 1990; Kammer et al., 2015; Svetlizky et al., 2017). As mentioned, the rupture front can jump to one or several discontiguous locations abandoning the tail. On the other hand, the sliding process in the tail and intermediate regions can spawn new local rupture fronts, thus affecting the collective rupture front. The coupled fracture-friction nature of fault failure is reflected in classical constitutive models that typically assume a planar fault relating shear stress drop to slip and accounting for slip- and rate-dependent aspects of the process for defined conditions of pressure, temperature, etc. (e.g., Dietrich, 1972; Marone, 1998; Rice & Ruina, 1983). These constitutive laws rest on linear elastic fracture mechanics (LEFM), cohesive zone slip-weakening and rate-and-state friction, as briefly described below.

Frictional slip is controlled by shear crack-like rupture fronts propagating along a fault (Aki, 1979; Rubinstein et al., 2004). Griffith’s energy balance defines a condition for the stability and onset of rupture propagation. When the stress intensity factor reaches a critical value Kc, the material fails producing rupture. For continuing rupture propagation, the energy release rate from the bulk to the rupture front, G, should reach a critical value Gc (e.g., Ben-Zion, 2003; Freund, 1990). Since the stress drops rapidly behind the rupture front (Fig. 1), slip rate is reduced with distance from the front but the slip trailing the rupture continues to accumulate for the duration of sliding at different positions.

The classical slip-weakening model (Ida, 1972; Palmer & Rice, 1973) is a shear fracture variant of the well-known Dugdale-Barenblatt cohesive zone fracture mechanics model. This describes the propagation of a planar shear band through a finite process zone of length \(L\), where the peak strength of the fault \({\tau }_{p}\) degrades over a critical slip distance \({d}_{c}\) to some residual dynamic friction \({\tau }_{r}\). The slip gradient u/L and gradual strength reduction avoid the unrealistic stress singularity at the fracture tip of LEFM. This constitutive formulation on a planar surface has been used extensively to estimate fracture energy and rupture process zone from laboratory results (Rice, 1980; Viesca & Garagash, 2015; Wong, 1982), as well as from seismological data (e.g., Abercrombie & Rice, 2005; Cocco et al., 2016). We note that using this framework for field data involves multiple assumptions, including that a planar projection of the natural process to the slip-weakening diagram (ignoring, e.g., volumetric deformation) is valid.

The slip-weakening model does not consider potential rate-dependence of shear strength and post-failure strength recovery. Field evidence and experiments show that faults and frictional contacts exhibit healing and rate-dependent effects. Dieterich (1972, 1978, 1979) proposed a rate-and-state frictional model including strength recovery of frictional contacts with time and dependency of the frictional strength on slip velocity. In particular, strength may decrease (velocity weakening) or increase (velocity strengthening) as slip rate increases, depending on pressure, temperature and other conditions. This model and subsequent formulations of rate-and-state friction (e.g. Marone, 1998) can be used to study the transition of creep to unstable slip in terms of material-dependent parameters and boundary conditions. Rotary shear experiments with slip rates of over 1 m/s examined effects of high slip velocities and accelerating and decelerating slip rates on the friction, slip process, and evolving properties of the gouge (e.g., Chen et al., 2021; Di Toro et al., 2011; Sone & Shimamoto, 2009). Laboratory measurements also show that the nominal friction coefficient depends on changes of normal stress (Linker & Dieterich, 1992; Prakash & Clifton, 1993). As discussed in the next section, multiple processes are expected to produce strong dynamic changes of normal stress during fault failure that can significantly affect the frictional energy.

Slip weakening and rate-and-state friction constitutive models predict a critical nucleation patch \({L}_{C}\) that is related to critical displacement \({d}_{c}\), stress drop \(\Delta \tau \) and elastic shear modulus \(\mu \) of the fault surroundings (Eshelby, 1957).

$${L}_{C}=C\frac{\mu }{\Delta \tau }{d}_{c},$$
(1)

where \(C\) is a constant of order 1. For a circular shear crack in elastic solid, a linear relation is predicted between displacement and crack radius (Eshelby, 1957). This implies a material-specific constant strain change and stress drop with a constant displacement-length scaling consistent generally with observations (Manighetti et al., 2007). Eshelby’s model also implies that the velocity of the rupture (crack) front \({v}_{R}\) scales with slip (particle) velocity \({v}_{S}\) (Freund & Lee, 1990; Udias et al., 2014),

$${v}_{R}=C\frac{\mu }{\Delta \tau }{v}_{S} .$$
(2)

For dynamic ruptures radiating seismic waves, a related threshold slip rate value is often assumed as \({v{^{\prime}}}_{s}\approx \frac{\Delta \tau }{\mu }{c}_{s}\) (Rice, 1993; Wynants-Morel et al., 2020) with a threshold slip velocity \({v{^{\prime}}}_{s}\) of a few mm/s.

Rupture nucleation may involve collective failure of asperities across a segmented and rough frictional fault (e.g. Campillo et al., 2001; Dahmen et al., 1998), and its propagation involves shear and volumetric deformation as the rupture accelerates and its trace follows a tortuous path generating off-fault damage (Gabriel et al., 2013; Goebel et al., 2014; Poliakov et al., 2002; Renard et al., 2019). The trailing slip motion in wake of the rupture front is governed by frictional contact forces, re-rupturing of asperities, comminution, granular flow and heat dissipation that may cause local melting and thermal pressurization.

In a rock volume not dominated by a pre-existing unhealed frictional surface, the nucleation process leading to dynamic instability is different and involves localization of distributed cracking and solid-granular transition (Ben-Zion, 2008). When the density of microcracks reaches at some location a critical level, there is dynamic instability and a phase transition of material at the rupture front from a damaged (cracked) rock to a granular phase. The subsequent shear failure is associated under sufficient compressive stress with a granular flow in the generated finite-width “slip zone”, while under low confining stress the material is fragmented (Lyakhovsky & Ben-Zion, 2014a). Following failure and stress reduction, there is a reversed transition from a granular phase to a damaged solid (Lyakhovsky & Ben-Zion, 2014b). A process of this type involving localization of brittle deformation has been documented recently before several large earthquakes (Ben-Zion & Zaliapin, 2020), and was also observed before system-size events in laboratory fracturing experiments (e.g., Goebel et al., 2012; Lockner et al., 1992; McBeck et al., 2022; Stanchits et al., 2006).

4 Discussion and Conclusions

Faults are inherently heterogeneous over all observed scales. This is seen in laboratory fracture experiments (e.g., Goebel et al., 2012, 2017; Sharon et al., 1995) and amplified in the crust by the heterogeneous geological inheritance of any natural fault zone (e.g. Ben-Zion & Sammis, 2003; Schulte-Pelkum et al., 2020). Laboratory experiments show heterogeneous slip and rupture events even on pre-existing surfaces. Earthquake rupture zones have a finite-width that can be hundreds of meters, and they sustain during shear-dominated failure also local volumetric deformation that can impact significantly the governing physics. In the present paper we attempt to clarify whether fracture, friction and volumetric damage/granulation processes are dominant in different parts of a rupture zone, or are inseparable and should be considered in all fault sections. Another issue we attempt to address is for what conditions the commonly used planar representation of faults and associated constitutive laws provide adequate (approximate) descriptions for natural earthquake ruptures.

Laboratory tests with multiple rock types indicate that Eshelby’s Eq. (1) relating slip and rupture velocities holds for slip rates ranging over about six orders of magnitude (μm/s – m/s). For all tested fault rheologies/materials (clay-rich rocks, sandstone, granite), the estimated rupture velocities are about 3–4 orders larger than the directly measured slip rates ranging between tens of μm/s up to tens of cm/s. In experiments, rupture propagation associated with slip events are inferred either indirectly from sequences of large AEs (Fig. 5), spreading of AE clusters (Wang et al., 2020), or time offset of strain signals at different positions. Strain gauges in lab experiments show a rapid strain/stress drop followed by a slow decrease (Fig. 6), consistent with an initial reduction of the stored strain energy at the rupture front and continuing reduction by the frictional sliding in the intermediate and tail regions.

The processes involved in frictional sliding are assumed to dominate the overall energy balance. Most estimates of fracture energy G based on measurements of fracture and gouge surface area suggest its contribution is < 10% and possibly < 1% of the total strain energy released in an earthquake (Chester et al., 2005; Olgaard & Brace, 1983; Rockwell et al., 2009). However, recent estimates based on fragmented materials in the damage zone of a deeply exhumed fault suggest that G is larger than typically assumed (Johnson et al., 2021). Seismological estimates of the fracture energy and stress drop may not provide reliable results since they rely on model assumptions corresponding to a far-field view and limited resolution of the source time function at the rupture front (Ben-Zion, 2019; Cocco et al., 2016). Also, seismological estimates of breakdown work (Viesca & Garagash, 2015) may include dissipation by frictional sliding, melting and possibly arrest (Ke et al., 2021). Numerical simulations of dynamic rupture on a frictional interface with off-fault plasticity show that early on the dominant energy components are the stored elastic strain and kinetic energy (radiation), but that with progressive propagation the frictional heat and off-fault dissipation become dominant (Shi et al., 2010).

While dissipation over the entire rupture zone may dominate the total energy budget, the stress concentration in the process zone and energy flux at the rupture front still control rupture propagation (Freund, 1972; Reches & Fineberg, 2022). The size of the process zone surrounding the front (Fig. 1) is expected to depend on rupture propagation distance, crack vs. pulse mode, and velocity (Andrews, 2005; Ben-Zion & Shi, 2005; Svetlizky & Fineberg, 2014). We note that dynamic changes of normal stress in the rupture zone can significantly reduce the frictional heat, as demonstrated in simulations of rupture on a bimaterial interface (Andrews & Ben-Zion, 1997). In addition to bimaterial ruptures, numerous other mechanisms are expected to produce strong changes of normal stresses in earthquake rupture zones. These include collisions of gouge particles and rough surfaces (Lomnitz-Adler, 1991; Melosh, 1979), various fluid-assisted effects (e.g., Rice, 2006; Sibson, 1973), and isotropic radiation from source volumes (and especially the process zone) sustaining reduction of elastic moduli (Ben-Zion & Ampuero, 2009; Lyakhovsky et al., 2016). It is important to study further with laboratory experiments, field data, and model simulations the effects of volumetric deformation on constitutive laws, partitioning of the stored elastic strain energy to (different forms of) dissipation and radiation during failure, and other key aspects of earthquake physics.

Ruptures of a planar interface in experiments with PMMA-type materials were shown to be quantitatively described by fracture mechanics over a range of rupture velocities (e.g. Svetlizky & Fineberg, 2014). If shear crack or pulse-like ruptures control the initiation, propagation and arrest of earthquakes, this has important consequences for the stability transition of faults, and the potential role of friction for slip stability analysis that is often used (Ben-Zion, 2001; Barras et al., 2019; Brener & Bouchbinder, 2021; Rice, 1980; Svetlitzki et al., 2019). As the elastic strain energy is stored in the entire crustal volume, frictional sliding in the rupture zone can interact with the rupture front via long-range elastic stress transfer. While this suggests “no separation of scales” in the rupture zone (Brener & Bouchbinder, 2021; Rubino et al., 2022), if the rate of stress transfer during rupture propagation to the front is sufficiently small, the interaction is minor or negligible. This allows an effective separation of scales (Fig. 1) to the rupture front, an intermediate region where the stress interaction with the front is appreciable, and a tail region that is essentially not interacting with the front (although it can still spawn minor offspring local rupture fronts). The failure of rough surfaces and gouge layers amplifying stress and strength heterogeneities can lead to intermittent rupture propagation and an interplay of rupture and sliding friction processes, which may also cause re-rupturing of frictional slip patches behind the initial rupture front (Rubino et al., 2022; Xu et al., 2018). The wave radiation during the rupture process can also trigger failures ahead of the rupture front.

Lab experiments clearly show a hierarchical complexity of the rupture process in space and time, particularly on rough surfaces. Rupture of heterogeneous faults likely involves a hierarchy of asperity and segment sizes, and numerous laboratory tests show that slow and fast rupture and slip events may coexist (Bolton et al., 2022; Dresen et al., 2020; Yamashita et al., 2021). This implies, for example, that the stability transition in a heterogeneous fault can depend on the size of the event in an opposite fashion to the nucleation of dynamic instability beyond a critical slip patch size (e.g., Dieterich, 1992; Rice, 1993). Specifically, stable large-scale (system-wide) slip and unstable small-scale (grain-scale) acoustic emissions can coexist and interact mutually (Ben-Zion, 2008; de Geus et al., 2019; Fisher, 1998). Classic estimates of the stability transition and nucleation patch size based on a smooth fault model may yield erroneous results. The fact that slow or even stable large slip events may include dynamic ruptures on the grain-asperity scale (AEs) is reminiscent of slow slip events hosting tremor. Faults may also have slow or fast slip events depending on local ratios of shear to normal stress, which may far exceed the average frictional strength (Ben-David et al., 2010; Bolton et al., 2022). Slow and fast slip events with duration times of 0.1–10 s may be contained or system-wide affecting the entire fault. Associated AE bursts shorter than 10−5 s (Figs. 5, 6) attest to loading and dynamic failure of grain-scale and larger asperities across different length scales (Dresen et al., 2020; Goebel et al., 2017; Ohnaka & Shen, 1999). As AE activity relates to roughness, preparatory fault slip on smooth faults is often dominantly aseismic and small, involving a few and generally large AEs close to failure at peak stress that initiate a macroscopic slip event (Guerin-Marthe et al., 2022).

Stick slip failure of lab faults with varying degree of heterogeneity captures important aspects of unstable failure in nature. However, several key processes are not accounted for in the related constitutive models used to interpret earthquake data. These include intermittent rupture propagation, generation of rock damage and granulation, separation of rupture front and frictional tail, strong dynamic changes of normal stresses during failure, and superposition of processes in the rupture zone radiating waves with different tensorial components and different frequency bands. Fracture mechanics, frictional constitutive laws, damage rheology, and granular mechanics describe (each) certain aspects of rupture and slip processes, but not the entire physics of earthquake rupture zones. Elements from all these frameworks are combined in a damage-breakage rheology model (Lyakhovsky & Ben-Zion, 2014a, 2014b; Lyakhovsky et al., 2016). However, the development of a more complete model for the various processes in earthquake rupture zones that is constrained and validated by detailed laboratory and field data remains a fundamental challenge. Using up-scaling methods (Kovachki et al., 2022; Matouš et al., 2017) to extrapolate results of laboratory experiments for conditions of natural faults will aid significantly the development of a more complete model for earthquake and fault phenomena.