Gravitational Potential and Attraction of a Spherical Shell: A Review

Abstract

The direct problem in gravimetry is one of the few areas of applied geophysics where complete, general and fully valid solutions are available. The common issue in the gravimetric direct problem is that there are several different solutions for even simple shaped bodies available throughout the literature. While the direct problem is single-valued, the general solutions (if possible to find analytically) are desired. The aim of the present paper is to bring clarity into the “information noise” which occurs in the literature for the case of the spherical shell/layer. We collected several different solutions and proved their equality (as special cases of the general solution). The differences between these solutions are caused by the symbolism used, but mostly by the different area of validity of each formula. The formulae are discussed and scored on several criteria. The general solutions for the gravitational potential and attraction on the rotational axis of the spherical shell are presented, as well as the solution for the biaxial ellipsoidal layer for comparison.

Appendices

Appendix A

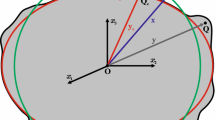
The non-symmetrical case means that the boundaries of the variable φ are set to be arbitrary, i.e. $\varphi_{1} > 0$ and $\varphi_{2} < 2\pi$, which means that the source body is the cut of the spherical ring/layer. The resultant vector g is not oriented in the direction of the polar axis but is pointed in the direction given by $\frac{{\varphi_{2} - \varphi_{1} }}{2}$, according to the symmetry of the task. While the coordinate $\varphi^{\prime}$ of the calculation point (located on the polar axis) is indeterminable directly, it has to be chosen as $\frac{{\varphi_{2} - \varphi_{1} }}{2}$ to obtain the correct orientation of the resultant g. The integrations (3) are not solvable analytically in such case, but we can, at least, calculate the $\left| {\mathbf{g}} \right|$, if the spherical segment is shifted to the position for which $\frac{{\varphi_{2} - \varphi_{1} }}{2} = 0$. Now, the size of the body is not changed, but the g consists only of the components $V_{z}$ and $V_{{\vartheta^{\prime}}}$, and so, the $\left| {\mathbf{g}} \right|$ can be obtained. The component V_z is already known (Eq. 10), so the task is reduced to the search for the expression of $V_{{\vartheta^{\prime}}}$:

$$ \begin{gathered} V_{{\vartheta^{\prime}}} \left( z \right) = G\sigma \int\limits_{\rho } {\int\limits_{\vartheta } {\int\limits_{\varphi } {\frac{{\rho^{3} z\sin^{2} \vartheta \cos \varphi }}{{A^{3/2} }}d\rho d\vartheta d\varphi } } } = \hfill \\ = \frac{2G\sigma }{{3z^{2} }}\left( {\sin \frac{{\varphi_{2} + \varphi_{1} }}{2}} \right)\left[ \begin{gathered} \left( {2z^{2} - \rho^{2} } \right)\left| {\rho - R} \right|E\left[ {\frac{\vartheta }{2},k} \right] + \frac{{\rho^{4} + \rho^{2} z^{2} - 2z^{4} }}{{\left| {\rho - R} \right|}}F\left[ {\frac{\vartheta }{2},k} \right] + \hfill \\ \frac{{\sin \vartheta \left[ { - \rho^{3} + \rho z^{2} \left( {6\cos^{2} \vartheta - 1} \right) - z\cos \vartheta \left( {\rho^{2} + 3z^{2} } \right)} \right]}}{{A^{\frac{1}{2}} }} + \hfill \\ 3z^{3} \sin^{3} \vartheta \ln \left( {\sqrt A + \rho - z\cos \vartheta } \right) \hfill \\ \end{gathered} \right]_{\rho ,\vartheta } , \hfill \\ \end{gathered} $$

(A1)

$A = \rho^{2} - 2\rho z\cos \vartheta + z^{2}$, $F\left[ {\frac{\vartheta }{2},k} \right]$ is an elliptic integral of the first kind, $E\left[ {\frac{\vartheta }{2},k} \right]$ is an elliptic integral of the second kind, $k = - \frac{4\rho z}{{\left( {\rho - z} \right)^{2} }}$. Note that, despite the fact that the “shifted” values of variable φ are substituted, the result of the integration can be rewritten with help of the original values φ₁ and φ₂.

Appendix B

Limit of Eq. (6):

$$ \mathop {\lim }\limits_{z \to 0} V\left( z \right) = \mathop {\lim }\limits_{z \to 0} \frac{\pi G\sigma }{{3z}}\left[ \begin{gathered} \left[ {2\rho^{2} - \rho z\cos \vartheta + z^{2} \left( {2 - 3\cos^{2} \vartheta } \right)} \right]\sqrt A \hfill \\ + 3z^{3} \sin^{2} \vartheta \cos \vartheta \ln \left( {\sqrt A + \rho - z\cos \vartheta } \right) \hfill \\ \end{gathered} \right]_{{\rho_{1} ,\vartheta_{1} }}^{{\rho_{2} ,\vartheta_{2} }} , $$

where $A = \rho^{2} - 2\rho z\cos \vartheta + z^{2}$.

All the terms which contain the logarithm function are zero, as well as terms with $z^{2} \left( {2 - 3\cos^{2} \vartheta } \right)\sqrt A$. The limit is then reduced to:

$$ \mathop {\lim }\limits_{z \to 0} V\left( z \right) = \frac{\pi G\sigma }{3}\mathop {\lim }\limits_{z \to 0} \frac{1}{z}\left[ {\left( {2\rho^{2} - \rho z\cos \vartheta } \right)\sqrt A } \right]_{{\rho_{1} ,\vartheta_{1} }}^{{\rho_{2} ,\vartheta_{2} }} . $$

This limit is divided into sum of two limits which are solved separately, and finally we have:

$$ \mathop {\lim }\limits_{z \to 0} V\left( z \right) = - \pi G\sigma \left[ {\rho^{2} \cos \vartheta } \right]_{{\rho_{1} ,\vartheta_{1} }}^{{\rho_{2} ,\vartheta_{2} }} . $$