Calculation of Hydroacoustic Propagation and Conversion to Seismic Phases at T-Stations

Abstract

The International Monitoring System (IMS) hydroacoustic network consists of six hydrophone stations and 5 T-stations. The IMS T-stations are high-frequency seismic stations (sample rates of 100 Hz) situated on islands or coastal stations and intended primarily to capture impulsive signals from in-water explosions. However, while there are numerous recordings of impulsive-like signals from in-water explosions at the hydrophone stations, recordings of this type of signal at the T-stations are rare. This is because the conversion of the hydroacoustic to a seismic signal as it propagates from ocean to land is inefficient, characterized both by complex geologic and topographic features and by strong attenuation. To improve the understanding of this signal conversion at T-stations, we performed numerical calculations using the spectral element code SPECFEM2D, modelling the acoustic signal as it propagates from the deep ocean through the ocean/land interface and finally, as an elastic signal, to the T-station. Environmental information from a variety of sources was gathered to construct the earth and ocean models used in the calculations. The goal of this work is to provide a set of calculated waveforms to complement the limited set of observed waveforms and to assist in the characterization of arrivals from explosion-generated hydroacoustic waves recorded at the T-stations.

1 Introduction

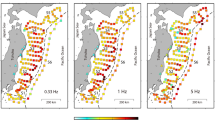
The Comprehensive Nuclear-Test-Ban Treaty calls for an International Monitoring System (IMS) for verification of compliance with the Treaty. The IMS comprises four global sensor networks: seismic, hydroacoustic, infrasound and radionuclide. The hydroacoustic network consists of 11 stations to detect, locate and characterize explosions detonated in the oceans and near the surface of the oceans (Fig. 1). Six of these are hydrophone stations, and five are T-stations, which are seismic stations positioned to be sensitive to energy from oceanic explosions that is coupled into the solid earth. The T-stations are less sensitive than the hydrophone stations, but less expensive to install and maintain, so they augment the hydrophone network to record larger events. The motivation for IMS T-station development as well as earlier efforts to understand T-phase conversion are described by Okal (2001).

Fig. 1

Locations of IMS hydroacoustic stations. The network is made of two types of stations: in-water hydrophone triad stations and island seismic (T-Phase) stations

The 5 IMS T-station locations each have two or three actual seismic stations at different locations on the island or coast, for a total of 11 seismic stations. In the following, we will refer to these 11 seismographs as T-stations. For all of these stations, we perform calculations of an incoming acoustic wave at an azimuth closest to normal incidence on the closest coastline. We also perform calculations at Ascension Island (HA10) in the direction of arrival from a series of large explosions off the coast of Florida (Fig. 2) that are used for validation of the calculations, and for Wake Island in the direction of a series of explosions off the coast of Japan. The stations, azimuths from the stations, distance to the source, ocean depth at the source and ocean depth at the grid boundary are listed in Table 1.

Fig. 2

Path from Florida Explosions to Ascension Island. The path length is approximately 7800 km

Table 1 Stations used in calculations, azimuth and distances to explosion source locations, depth of the ocean at the source and depth of the ocean at the entry to the calculation grid. ASCN and WAKE are proxy stations that have an IMS hydrophone array and a GSN seismic station

Calculations are performed using the two-dimensional spectral element code SPECFEM2D¹ (Tromp et al. 2008; Xie et al. 2016). We place a point explosion source at the distance shown in Table 1 from each station, and propagate the acoustic waves to the start of the SPECFEM2D calculation with either a modal or parabolic equation code. We calculate the incoming wavefield for source depths of 60 and 3000 m, and perform the SPECFEM2D calculations with and without anelastic attenuation. The modal and parabolic equation codes are frequency domain models, whereas SPECFEM2D is a time domain model. Therefore, time series are synthesized from the frequency domain model results using the Fourier transform, in order to enable coupling with SPECFEM2D.

There are few observations of in-water explosions at T-stations, and none to our knowledge at IMS T-stations. This is because not many large underwater explosions have been set off since the installation of the IMS stations and because of the lossy transmission from water-to-land, and the high ambient noise at the seismic stations. However, a series of explosions off the coast of Florida were recorded at the IMS hydrophone array at Ascension Island and at the Ascension Island Global Seismic Network (GSN) station, and we compare these data with our calculations. We also compare our results with the T-Phase transfer function spectra from Stevens and Hanson (2013) derived by comparing T-phases from the same earthquakes recorded at both the IMS hydrophone arrays and the IMS T-stations. These transfer function spectra were derived for all IMS T-stations and have good signal/noise characteristics over a broad frequency band (~ 2–20 Hz).

2 Development of IMS Station Calculations

Stevens et al. (2001) analyzed T-phase conversion using the Point Sur hydroacoustic station and several nearby stations along the California coast, and performed the first calculations of T-Phase conversion. Stevens et al. (2010) did similar calculations for Wake Island. In these earlier projects, we used the finite difference code TRES2D (McLaughin and Day 1994) for this purpose. For this project we are using the spectral element code SPECFEM2D (Bottero et al. 2016; Xie et al. 2016). SPECFEM2D is a higher order code that uses the Message Passing Interface (MPI)² to divide the calculation across multiple processors, so it enables much larger problems to be solved in a reasonable time. It also allows the use of unstructured mesh, which makes it easier to include complex boundaries.

The method we previously used to model the incoming acoustic signal from a distant source (Appendix in Stevens et al. 2001), could not be implemented in SPECFEM2D because SPECFEM2D calculates a scalar potential in the water and solves different equations in the water and solid regions. We found a new solution appropriate for SPECFEM2D which is given in the Appendix to this paper. It requires placing a line of pressure sources at the input location proportional to the time integral of the incoming pressure, and two lines of pressure sources to the right and left of the input location proportional to the double time integral of the incoming pressure. This reproduces the incoming pressure propagating to the right and cancels it to the left.

We use the mesh generator gmsh,³ version 4.0, to generate the mesh for all of the IMS station calculations. Gmsh generates unstructured grids based on input boundaries and points defining mesh size. The physical environmental parameters were defined using polygons. The main factors that control the calculation time are the frequency resolution required and the time step which for stability must meet the Courant condition. For the IMS station calculations, we have a minimum frequency resolution of about 50 Hz and use a time step of 1.5 × 10^–4 s. 50 Hz frequency resolution means that numerical dispersion at frequencies less than 50 Hz is small enough to be insignificant. Calculations are run for 400,000 time steps for a total duration of 60 s. The wavelength required for resolution is smaller for low velocity materials, so we need smaller cells where there are lower velocities, while the time step is controlled by the shortest travel time, so we need larger cells where there are higher velocities. Gmsh does not do this automatically, but it allows the mesh size to be specified, so the user can define smaller zones in lower velocity areas and gmsh will generate a smaller mesh size in those regions. The disadvantage of an unstructured mesh generator like gmsh is a very complicated mesh with odd-looking cells (Fig. 3). However, the mesh generated is numerically stable for finite element problems and generates accurate results.

Fig. 3

Part of the mesh generated by gmsh near the coast of Wake Island

2.1 Earth and Ocean Models

The calculations required information along each path for bathymetry, ocean sound speed and density of the ocean; and topography, sediment thickness, P-wave velocity, S-wave velocity, density and attenuation for all of the land (including sediments) within the area of the spectral element calculation. Attenuation is defined by a bulk $Q_{k}$ and shear $Q_{\mu }$. $Q_{k}$ can be set to infinite as almost all of the attenuation results from $Q_{\mu }$. Note that other references may refer to $Q_{p}$ and $Q_{s}$ corresponding to P-wave and S-wave attenuation. $Q_{s}$ and $Q_{\mu }$ are equivalent. If $Q_{k}$ is large, then $Q_{p}^{ - 1} = \left( {{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-\nulldelimiterspace} 3}} \right)\left( {{\beta \mathord{\left/ {\vphantom {\beta \alpha }} \right. \kern-\nulldelimiterspace} \alpha }} \right)^{2} Q_{\mu }^{ - 1}$ (Anderson and Hart 1978).

2.1.1 Bathymetric and Topographic Models

We conducted a search for the highest resolution and most reliable publically available global bathymetry and elevation models as of 2018. We also investigated specialized data sets that are relevant to the IMS T-stations and island seismic stations that might be used as proxies to T-stations. The elevation data for land are higher resolution than bathymetry data. For this study bathymetry has much more influence on the T-station signals.

The best publically available global elevation models for terrain above sea level is from the Shuttle Radar Topography Mission (SRTM) or products derived using that data (USGS 2009). The SRTM data was originally released at ~ 90 m resolution worldwide and ~ 30 m resolution inside the United States. In 2015, the 30 m resolution data was released for all areas covered by the mission (56 S–60 N). Updates to SRTM have been released called SRTMplus and SRTM v3.

There are various global bathymetry data grids with different horizontal resolutions. The input data to these grids significantly overlap one another. Generally, they use high resolution bathymetry soundings (either from single track echo sounders or multibeam swaths gathered from various scientific studies). This data only covers a small portion of the ocean floor. Lower resolution satellite derived bathymetry data are used to cover the vast remaining portion of the seafloor. The models differ based on which high resolution data sets are included in the bathymetry models, how bathymetry is predicted from satellite ocean level data, and how the higher resolution data are merged with the satellite derived bathymetry. Much of the ship track data that the models use overlap with one another.

We chose as our base model the Global Multi-Resolution Topography (GMRT) database (Ryan et al. 2009, version 3.5). The GMRT is updated on a regular basis incorporating new swath data approximately once per year. The GMRT’s highest resolution grid spacing is ~ 60 m. However, the effective resolution can be as great as 12 km in areas without echo sounder or multibeam data. The mixture of resolutions can cause artificial discontinuities in the data. We have attempted to avoid paths that contain major artificial discontinuities. For more minor discontinuities, we filtered the data. We extracted elevation models surrounding each of the T-stations and proxy T-stations from the GMRT database at the highest resolution (~ 60 m).

In addition to the GMRT database, we have collected two other bathymetry/elevation data models. The most recent version of SRTMplus database with a 15 arc second resolution⁴ (for a general description based on the 30 arc second grid see Becker et al., 2009), and the Generalized Bathymetric Chart of the Ocean’s (GEBCO) 2014 Grid⁵ with a 30 arc second resolution. These databases provide semi-independent alternative global bathymetry data sets for the world's oceans.

2.1.2 Crustal Structure Models

Detailed site-specific seismo-acoustic properties are not available for the crust surrounding most T-phase stations. As an alternative, we looked for global databases of crustal characteristics that may be applied to identifying appropriate properties for modelling T-phase propagation in conjunction with seismic studies of regions with similar geological features to specific T-stations. These include crustal age, sediment thickness, sediment type, sediment porosity, core samples, seismic tomography studies, and multi-channel seismic reflection studies.

Most of the T-stations are located on shield or strato-volcanic islands near mid-ocean ridges. The crustal material properties (pertinent to seismic propagation) can be viewed as perturbations to local oceanic crust. The oceanic crustal layers are categorized into three layers: Layer 1—sediments, Layers 2a, 2b, 2c—basalt formed from extruded magma or intrusive dikes, and finally Layer 3—formed from slowly cooled magma creating coarse grain gabbros. Layer 2 is ~ 2 km thick and has a high velocity gradient with depth. P-velocities range from as low as 2.5 km/s (layer 2a) up to ~ 6.2 km/s. Not all sub-layers are always present in Layer 2. Layer 3 is ~ 5 km thick and has a lower velocity gradient. The P-velocity roughly increases from ~ 6.5 to 7.2 km/s. It terminates at the Mohorovičić discontinuity.

Sediment properties affect ocean acoustic propagation by altering the reflection/transmission coefficients and varying the strength of leaky modes and interface wave conversion. Sediment velocities and attenuation factors can display a frequency dependence (Buckingham 2005), however, at the frequencies of concern in this study, we can ignore the frequency dependencies which are only significant at frequencies >> 100 Hz (Ballard and Lee 2017). Most of the T-station islands are geologically young so sediment layers are thin along the islands flanks, thus the exact properties of the sediments are less likely to strongly affect the acoustic-to-seismic transmission. The main exceptions to this generalization are HA02 and HA05 that are located along current or recent subduction boundaries leading to complex sedimentary structures such as fore-arc basins and accretionary wedges.

Sediment velocities are controlled by many factors including mineral composition, density, porosity, and grain size. Detailed sediment analysis are rarely available for the areas at T-stations so we use best estimates of P-velocity and density from global databases of sediment type and porosity. Some sediments are unable to support shear stress and can be approximated as a fluid layer.

Other material properties needed in our modeling are the intrinsic attenuation of acoustic, P, and S waves. There are a number of methods to parameterize intrinsic attenuation. In hydroacoustics, the attenuation coefficient is usually specified as the fraction of energy loss per wave cycle with units of dB/wavelength (Jensen et al. 2011). Often a modified form that is more convenient is used with units of dB/meter, which has an additional frequency dependent term that depends on the medium’s wave velocity. In seismology, the quality factor, Q, is more often used to characterize intrinsic attenuation (Lay and Wallace 1995). The quality factor can be applied to both shear and bulk modulus relaxation phenomenon. Shear wave attenuation only depends on the shear modulus relaxation, but as mentioned earlier P wave attenuation depends on both shear and bulk modulus terms. Attenuation in ocean sediments are often better quantified by the hydroacoustics community, while seismic studies often constrain one or more of the quality factor terms. We have relied on average attenuation models that best match the sediment or crustal mineralogy at each particular T-phase site.

2.1.3 Sediment Thickness

The World Data Service for Geophysics maintains a database of the total sediment thickness of the world's oceans and marginal seas (Whittaker et al. 2013),⁶ with the following description: “The new global 5-arc-min total sediment thickness grid, GlobSed, incorporates new data and several regional oceanic sediment thickness maps, which have been compiled and published for the, (1) NE Atlantic (Funck et al. 2017; Hopper et al. 2014), (2) Mediterranean (Molinari and Morelli 2011), (3) Arctic (Petrov et al. 2016), (4) Weddell Sea (Huang et al. 2014), and (5) the Ross Sea, Amundsen Sea, and Bellingshausen Sea sectors off West Antarctica (Lindeque et al. 2016; Wobbe et al. 2014). This version also includes updates in the White Sea region based on the VSEGEI map of Orlov and Fedorov (2001).”

2.1.4 Seafloor Age

Crustal velocity structure in the ocean is correlated with the age of the seafloor. The National Geophysical Data Center of the US National Oceanic and Atmospheric Administration has compiled digital models of age, age uncertainty, spreading rates and spreading symmetry of the world's ocean crust (Müller et al. 2008).⁷

2.1.5 Ocean Property Models

Ocean sound speed profiles are derived from the World Ocean Atlas 2013 version 2—WOA13v2 (Locarnini et al. 2013). The database is available with horizontal grid spacing of 1.0° and 0.25°. We are using the decadal averaged analyzed mean salinity and temperature data to estimate the vertical sound speed profile (SSP). The database include annual, seasonal, and monthly averaged values. To compute the sound speed we are using the equation proposed by Leroy et al. (2008) that uses salinity, temperature, and latitude. The resulting sound speed agree to other methods (e.g., Mackenzie 1981; Millero and Kubinski 1975) to better than 0.2 m/s. We expect the main water property that can vary throughout the year, and therefore vary the acoustic-to-seismic conversion, is the temperature gradient of the ocean’s surface layer.

2.1.6 Station Categorization

There are 5 T-stations (HA02, HA05, HA06, HA07, HA09) consisting of 11 seismometers (2 seismometers per station except HA06 which has 3 seismometers). In addition, we have selected two proxy stations which are GSN seismic stations located on mid-ocean islands co-located with IMS hydrophone stations. These are at Ascension and Wake Islands corresponding to IMS hydrophone stations HA10 and HA11.

The seafloor bottom material properties and bathymetry have the strongest influence on the acoustic-to-seismic conversion, and therefore the most obvious categorization is based on the local marine geology at each station. The marine geology for a particular T-station does not vary drastically among their constituent seismometers with the exception of HA05 (Guadeloupe). So we consider that there are 8 stations to compare and categorize: HA02, H05N, H05S, HA06, HA07, HA09, ASCN, and WAKE.

The most obvious distinction among the stations are the type of island the seismometers are located on. There are volcanic islands near mid-ocean ridges (i.e., young), islands along convergent plate boundaries, and other mid-ocean islands. The young volcanic islands include Socorro Island (HA06), Flores and Corvo Islands (HA07), Tristan da Cunha (HA09), and Ascension Island (ASCN). The convergent plate boundary islands are the Haida Gwaii Islands (HA02)—also known as Queen Charlotte Islands—and Guadeloupe Station (HA05)—La Désirade Island (H05N) and Martinique (H05S). Wake Island (WAKE) is a coral atoll in the western Pacific on > 100 Ma (mega-annum) oceanic lithosphere.

Most of the volcanic island’s geology that we consider here are roughly radially symmetric about the islands’ centers. Ascension Island has been the subject of seismic studies to determine its 3-D velocity structure (Evangelidis et al. 2004).The 3D P-velocity model at Ascension Island found a high velocity core near the center of the island, while the island flanks appear as a thickened layer 2a type oceanic crust.

The seismometers are generally located near shore (offset from the island’s center) so the 2-D paths emanating from a station are not necessary radially symmetric. We examined the seafloor slope tangential to a radial path to verify that 2-D models are sufficient, i.e., 3-D propagation modeling is not necessary for the vast majority of paths.

Details about construction of models for specific paths can be found in Hanson and Stevens (2018).

2.1.6.1 Grid Development

All grids are 70 km wide with the seismic station on the surface 60 km from the left side of the grid. The X coordinate is zero at the seismic station and so runs from − 60,000 to 10,000 m. All grids extend to a depth of approximately 9.5 km. The top surface extends above zero (sea level) to match the topography. The number of elements varies with each grid, but is approximately 1.2 million elements. We made one modification to the material properties discussed in the previous section. Some sediment layers have very low shear velocities and it would require extremely small zones to include these in the calculation to little benefit, so we set the shear velocities to zero in these zones. The sediments are attenuative and have a shear $Q_{\mu }$ associated with each layer. With the shear velocity reduced to zero, $Q_{\mu }$ no longer has meaning, so we added a finite bulk $Q_{k}$ to each layer in the calculation. We used the same values for $Q_{k}$ as the $Q_{\mu }$ in the original models. Subsequent numerical experiments showed that the $Q_{k}$ gave more attenuation than the same value $Q_{\mu }$, and that $Q_{k}$ about 10% of the P velocity would be a better value. We ran calculations for three of the structures with the $Q_{k}$ in these layers increased to that amount, and found that the effect on the modeled waveforms was insignificant because these very low velocity layers are a small part of the models.

2.1.6.2 Source Implementation

We use two codes to calculate the initialwavefield for the SECFEM2D calculation: (1) KRAKEN, a modal code and (2) RAM, a parabolic equation (PE) code.⁸ In each case, we place a point explosion source at a distance of 3000 km, with a few exceptions: (1) the path from Florida to Ascension Island starts at the location of the Florida explosions (> 7500 km); (2) we model paths in a direction normal to the coastline closest to each station, and in some cases land interferes at shorter distances than 3000 km. In those cases the explosion is placed at the closest deep water point (> 3000 m depth, see Table 1). The explosion is a simple point pressure source, and the resulting impulse response can be convolved with an explosion source model for comparison with an actual explosion. We calculate the incoming wavefield for a source depth of 60 m using both methods. We also use KRAKEN to calculate the incoming wavefield for a source depth of 3000 m. Two depths were used so we could examine differences in the converted waveforms from a shallow and deep source. 60 m is a common depth for shallow military explosions such as the Florida explosions recorded at Ascension Island discussed later. Both methods calculate a pressure field in the frequency domain. To get the time domain source needed for SPECFEM2D, we run all calculations for each path at 5901 frequencies from 1 to 60 Hz with a frequency spacing of 0.01 Hz. Results are saved at 20 m spacing from the ocean surface to the ocean bottom at a point 59 km offshore of each T-station seismometer. The spectra are then transformed to the time domain and input to the SPECFEM2D calculation using the procedure described earlier. Figure 4 shows the sound speed and density along the path from Florida to Ascension Island. Similar figures for all of the other paths are in the online supplement to this paper.

Fig. 4

Sound speed and density profiles for the path to ASCN, azimuth 304°. This is the direction to the Florida explosions. The source is at the right end; the calculated wavefield on a vertical line located 59 km from the left side of the plot is the input to the SPECFEM2D calculation. Dashed black line is the bathymetry, black blocks are bathymetry averaged over 25 km segments. Dashed red line is the velocity minimum in the sound channel. Because the actual source depth at the explosion location is too shallow for a modal solution, the source for the KRAKEN calculation was moved to the left of the continental shelf on the right side of the figure. The RAM calculation used the actual location

3 Results of IMS Station Calculations

For each earth model, we did five calculations. Our earth models include an estimate of Q for each solid layer. SPECFEM2D allows calculations with or without Q, but the calculations with Q take approximately three times as long to run, which changes the total run time for one of these calculations from about 8 h to about 24 h using 24 CPUs. We did calculations without Q for each of the source models described in the preceding paragraph, and with Q for the RAM source at 60 m depth and for the KRAKEN source at 3000 m depth. Each run generates a series of self-scaling image files of pressure, saved every 1000 time steps, and also generates a file of numbers corresponding to each point so that the images can be replotted. An example of self-scaling and replotted images are shown in Fig. 5. The automatic images show the locations of all of the points for which waveforms were saved. Waveforms are saved as horizontal and vertical velocity. Far field in-water pressure waveforms can be approximated by multiplying the horizontal velocity by the density and sound speed at the receiver point. Movies generated from the replotted images are included in the online supplement to this paper.

Fig. 5

Self-scaling image file (top) and recreated image file (bottom) at 15 s (100,000 time steps). Both files show the input source location as a vertical orange bar. The self-scaling image shows the locations of all receiver points as green dots. The replotted image shows the station location as a yellow triangle, and the location of a real or fictitious hydroacoustic station in the water (green dot). Comparison of the output at these two points is used to calculate the hydroacoustic to seismic transfer function

3.1 Waveforms and Spectrograms for in-Water Pressure and Land Seismic Stations

Waveforms were saved at the T-station location and at a point in the water to represent a hydroacoustic station for all paths. The location of the hydroacoustic station was set to 30 km from the seismic station except for Ascension Island and Wake, where the location of the hydrophone arrays on the north side of the islands was used, and H05N which was placed at 40 km because of shallow depth at 30 km. The calculated waveforms were convolved with an explosion source function at 60 m depth. The explosion yield was seven tons except for Wake at 310° for which the explosion yield was 200 kg. Seven tons was the yield of the Florida explosions, while 200 kg was the yield of the explosions off of Japan studied by Stevens et al. (2010). The source time function and spectra of the source (Arons et al. 1948) are shown in Fig. 6. Spectrograms were calculated for all waveforms. Each row in the Fig. 7 is for a different T-Station (shown in figure titles). Left column shows the pressure in the water at the location indicated by hloc in the title. Right figure shows the vertical velocity at the T-station. Spectrograms are for log pressure and log velocity. The incoming pressure field is initiated with RAM. Attenuation is included in the SPECFEM2D runs.

Fig. 6

Source time function (left) and spectra (right) for the 7 ton explosion source at 60 m and 3000 m depth

Fig. 7

Spectrograms for in-water and T-station locations for all calculations initiated with RAM at a 60 m depth, including attenuation and convolved with an explosion source (see text)

Our primary interest in this paper is on the conversion of hydroacoustic waves in the ocean to seismic waves on land, however there are also some interesting differences in the calculated hydroacoustic waveforms. Most of the waveforms have a dispersion characteristic of propagation in a sound channel—low frequencies arrive first, higher frequencies later. However there are some differences: at H06E, H06N and at H07S the high frequencies arrive coincident with the lower frequencies. All three of these are shorter paths so there is less dispersion. H07S also has a blockage in the sound channel. The hydroacoustic signal at ASCN is more spread out over a longer time, but has less of the characteristic sound channel dispersion. ASCN is a much longer path than the others, the source is at a very shallow depth, which reduces low frequencies, and there is a partial blockage along the path. The sound speed and density profiles for all paths are shown in the online supplement to this paper.

In most cases, the seismic signals at the T-stations mimic the signals at the hydroacoustic station, with the high frequencies attenuated. The attenuation is particularly strong at stations with thick, attenuative sediments such as H02 and H05. H02 and H05N also have shallow water for a considerable distance from the station, which causes early, low amplitude arrivals as the hydroacoustic wave propagates through it and generates these signals.

3.2 Phase Identification

We made an attempt to identify seismic phases (i.e. P, S, surface waves) in the calculated T-station seismograms. A search was conducted over all of the calculated waveforms for identifiable phases by filtering in specified frequency bands and then calculating the correlation between the vertical and horizontal components in waveform segments to identify linearly polarized body waves (mostly P-waves, but S-waves would also correlate), and then calculating the correlation between the vertical and the Hilbert transformed radial component to identify elliptically polarized surface waves.⁹ The correlation is defined by:

$$C=\left|Z\cdot R\right|/\sqrt{R\cdot R*Z\cdot Z}$$

where Z and R are the filtered, segmented vertical and radial (or Hilbert transformed radial) waveforms. C = 1 when Z and R are scalar multiples of each other. An example for two stations is shown in Fig. 8.

Fig. 8

Top row: ASCN; bottom: wake. Left: radial and vertical component velocity waveforms. Right: correlation between radial and vertical components (top, high correlation indicates body waves) and between the vertical component and Hilbert transformed radial component (bottom, high correlation indicates surface waves). Horizontal axis is seconds from the calculation start time. The explosion source was not included in these figures

Phase identification proved to be difficult to automate. As can be seen in the figures, some of the body waves were clearly identified, but particularly at lower frequencies the waveforms appear to be surface wave-like, but lack coherent surface wave polarization. A few clear body wave signals do stand out, however, as illustrated in Fig. 9.

Fig. 9

Ground motion from the WAKE_az310 calculation showing P-wave arrival. Left: spectrogram; right: vertical vs. radial ground motion filtered from 30 to 40 Hz in the time window 49–50 s. Coherent phase between radial and vertical shows a body wave (P-wave) arrival. The explosion source was included in this example

3.3 In-Water to T-Station Transfer Functions

Spectral amplitudes were calculated from the waveforms using power spectra derived using the multi-taper method (Matlab pmtm function). Transfer functions were calculated by taking the ratio of the smoothed spectral amplitude of the vertical velocity at the seismic station to the smoothed spectral amplitude of the in-water pressure. Smoothing (Matlab smoothdata function) helps to see the shape of the transfer functions as the raw transfer functions have fluctuations that obscure the shape (Fig. 10). Figure 11 through Fig. 15 show the spectral transfer functions derived from the SPECFEM2D calculations for all of the IMS stations discussed. The five sets of calculations are: (1) a 60 m depth source initiated with RAM without attenuation in SPECFEM2D (srctype ram.1) and (2) with attenuation (srctype ram.Q); (3) a 3000 m depth source initiated with KRAKEN without attenuation (srctype 2) and (4) with attenuation (srctype Q); and (5) a 60 m depth source initiated with KRAKEN without attenuation (srctype 1). Transfer functions for the calculations done without attenuation are remarkably flat over the whole frequency band, while the calculations done with attenuation decrease significantly with frequency. Of the five sets of calculations, srctype 1 and ram.1 are directly comparable, solving the identical problem with modal and parabolic equation methods, respectively. Most of the results are very similar, however there are some differences, particularly when parts of the path become shallow, as is the case for H07. The adiabatic approximation used in KRAKEN assumes that energy is conserved for each mode and there is no mode conversion, and it will be less accurate when changes are large enough to cause mode conversion, or when some of the modes disappear in shallow water. In these cases the RAM parabolic equation solution is better as it can handle diffraction over the shallow sections. RAM is a full-field solution and inherently includes coupling of energy between modes while KRAKEN does not couple energy between modes. RAM includes both the discrete spectrum (discrete modes) and continuous spectrum (leaky non-propagating modes) while KRAKEN only includes the discrete modes (Figs. 11, 12, 13, 14 and 15).

Fig. 10

Smoothed and unsmoothed pressure to velocity transfer function spectra in dB for station H06S. RAM 60 m source, without (left) and with (right) attenuation. Horizontal axis is frequency (Hz)

Fig. 11

Calculated T-Phase transfer functions for a 60 m depth source initiated with RAM and without attenuation in SPECFEM2D. In this and the following four figures horizontal axis is frequency (Hz); vertical axis is transfer function in dB from pressure in Pa to velocity in m/s

Fig. 12

Calculated T-Phase transfer functions for a 60 m depth source initiated with RAM and with attenuation

Fig. 13

Calculated T-Phase transfer functions for a 3000 m depth source initiated with KRAKEN and without attenuation. KRAKEN was unable to calculate H07S below 4 Hz due to the shallow water around the Azores

Fig. 14

Calculated T-Phase transfer functions for a 3000 m depth source initiated with KRAKEN and with attenuation

Fig. 15

Calculated T-Phase transfer functions for a 60 m depth source initiated with KRAKEN and without attenuation. KRAKEN was unable to calculate H07S below 4 Hz

3.4 Attenuation of Vertical and Radial Waveforms on Land

We calculated the vertical and radial velocity amplitudes within 10 km of the T-station for all of the calculations. This was done to answer two questions: (1) how much does the amplitude decay across the island or coastline and (2) is there variability between the radial and vertical components? We filter the vertical and radial components for each calculation at the 21 points on the land surface within ± 10 km of the T-station from 8 to 16 Hz, and measure the maximum amplitude of each. We separate the data into underwater and land stations. We calculate the mean amplitude normalized the amplitude at the T-station for each calculation type. This is shown in Fig. 16. The most obvious difference is the much higher attenuation when attenuation is included in SPECFEM2D. There is also a difference between the vertical and horizontal components at the underwater stations, with vertical motion reduced relative to the horizontal, presumably due to the pressure from the water above.

Fig. 16

Amplitude attenuation for each calculation type, normalized to the amplitude at the T-station (location zero). Horizontal axis is distance from the T-station in km. Left: all stations both underwater and on land. Right: on land only. Top: vertical; bottom: horizontal

4 Comparison of IMS Station Calculations with Data

Validation of the calculations is a challenge because there are no observations of T-phases from explosions recorded at IMS T-Stations. There were, however, a series of explosions off the coast of Florida that were recorded at the IMS hydroacoustic station at Ascension Island and are visible at the Ascension Island GDSN station, and we compare these results with our calculations.

The second type of validation is a comparison with the T-phase transfer function spectra from Stevens and Hanson (2013). In that project, we developed a methodology for using T-phase (earthquake data) recorded on both hydrophone and T-stations to estimate the transfer function from ocean to land, and applied it to the eleven three-component T-station seismographs. The procedure is as follows: first, signals recorded at the hydrophones are used to estimate the power spectral density functions for the in-water (hydroacoustic) T-phase arrival. Second, those spectra are compared to power spectra of the T-phase recorded at T-stations for the same earthquake. Attenuation corrections are applied for event-to-station paths for both the hydrophone and T-station paths. Ground velocity-to-pressure transfer functions are then calculated for each event/T-station pair. A secondary process rejects outliers and applies weights to combine the station pair estimates to form the best average transfer function for each T-station. These transfer function spectra were derived for all IMS T-stations and have good signal/noise characteristics over a broad frequency band (~ 2–20 Hz).

4.1 Comparison of Observed and Calculated T-Phase Transfer Functions

As discussed earlier, Stevens and Hanson (2013) calculated transfer functions by taking the ratio of velocity observed at T-stations to the pressure observed at hydroacoustic stations and applying a distance correction to each. Figure 17 shows the transfer functions for all IMS T-Stations. There was a great deal of variability in the individual transfer functions for single events, however there was enough data to give fairly stable average values. The results for all 11 T-stations are shown in Fig. 17. Figures 12 and Fig. 14 showed the transfer functions derived from the SPECFEM2D calculations with attenuation for the T-Stations. Figure 18 is a comparison of calculated and observed transfer functions for each individual station. Figure 19 shows the calculated transfer functions for the paths to ASCN and Wake.

Fig. 17

Observed mean transfer functions for all IMS T-stations from Stevens and Hanson (2013)

Fig. 18

Comparison for observed transfer functions and ± one standard deviation for each T-station together with calculated transfer functions for each source type (see text for description). In all figures horizontal axis is frequency in Hz; vertical axis is transfer function in dB from pressure in Pa to velocity in m/s

Fig. 19

Calculated T-phase transfer functions for paths to ASCN and Wake. Horizontal axis is frequency in Hz; vertical axis is transfer function in dB from pressure in Pa to velocity in m/s

Although there is considerable variability, in general the calculations with attenuation match the data quite well over the 2–20 Hz band of the observations, and the calculations extend the frequencies to 50 Hz. Attenuative stations such as H02 decrease substantially with frequency in both the observations and the data. The less attenuative island stations are relatively flat to frequency in both the calculations and the data. Station H07 has a poorly defined transfer function due to a small number of events.

4.2 Observation and Calculation of Co-located Hydroacoustic and Seismic Signals from in-Water Explosions

During June and September 2016, the US Navy conducted five approximately 7 ton TNT equivalent underwater explosions off the coast of Florida (Heyburn et al. 2016 listed in Table 2).

Table 2 Origin time, locations and magnitude of the Florida explosions

The explosions were clearly recorded at the Ascension Island hydrophone station H10N1. We looked for corresponding signals at the Ascension seismic station. As can be seen in Fig. 20, there are many signals from other sources in the data that could easily be confused with the signals we are looking for. This is particularly true of the first and fifth explosions.

Fig. 20

ASCN seismic data near the expected arrival time of the explosion signals

We obtained the H10N hydrophone data from the same time period, which places stronger constraints on the ASCN seismic data. We could find no seismic signal on ASCN and only a small hydroacoustic signal on H10N from event #3. Close examination also showed interfering arrivals with events #1 and #5. However, events #2 and #4 occurred during quieter periods and appear to show the seismic signal from the explosions. As can be seen in Fig. 21, the time difference between the hydroacoustic and seismic signals is very close, about 20 s for both events.

Fig. 21

Left: hydroacoustic signals at H10N1. Right: vertical velocity seismic signals at ASCN. All filtered from 6 to 10 Hz and normalized to pressure in Pa and velocity in m/s at 8 Hz (Fig. 22)

Fig. 22

Instrument responses for H10N1 and ASCN, normalized to response at 8 Hz. Vertical lines show the 6–10 Hz frequency band used in Fig. 22

Fig. 23

Transmission loss at 20 Hz calculated with RAM from the source location on the left to the start of the SPECFEM2D calculation on the right

Fig. 24

Snapshot of the SPECFEM2D calculation at 39.6 s. The input source location from RAM is the vertical orange line on the left. The T-station location is the yellow triangle. The green circle is the location of the hydroacoustic station used for comparison. The location used for the hydroacoustic station was chosen so that the difference in distance to the source between the hydrophone and seismic station was preserved

We calculated pressure and velocity waveforms for comparison in the following way:

• 1. The parabolic equation code RAM was used to generate the input signal. It was necessary to use RAM because the ocean depth at the source was too shallow to allow calculation with a modal code such as KRAKEN. The transmission loss calculated by RAM is shown in Fig. 23.

• 2. The spectral element code SPECFEM2D was used to propagate the input pressure through the water and on to land as described earlier in this paper, with and without anelastic attenuation. A snapshot of the calculation (with attenuation) near the time when the in-water wave disassociates into the land is shown in Fig. 24.

• 3. Calculated waveforms are saved at a number of locations in-water and on land, then convolved with an explosion source function for a 7 ton explosion at 60 m depth (Arons et al. 1948). The instrument response for the two stations is also convolved with the waveforms.

The calculated waveforms for the hydroacoustic and seismic stations are shown in Fig. 25. Both the observed and calculated seismograms were band-pass filtered from 6 to 10 Hz, where signal to noise was good in the data. Comparison with the observed waveforms in Fig. 21 (event 2 is repeated in Fig. 25) is quite good. The difference in arrival times and the relative amplitudes between the hydroacoustic and seismic signals is very consistent with the observations. The observed waveforms at the seismic station are slightly more dispersed than the calculation.

Fig. 25

Top: Calculated in-water pressure (left) and vertical velocity at the T-station (right). Bottom: observed pressure and velocity data from event 2. All filtered from 6 to 10 Hz

We calculated power spectra from each of the observed seismograms and calculated the Pressure to Velocity transfer function over the frequency band where signal to noise was reasonably good (~ 6–12 Hz). The results are shown in Fig. 26. Also shown in the figure are calculated transfer functions with and without attenuation. These transfer functions were calculated by taking the ratio of the smoothed spectral amplitude (calculated from power spectra using the multi-taper method) for each waveform. The observed transfer functions are both below the calculated transfer functions without attenuation and slightly above the calculated transfer functions with attenuation.

Fig. 26

Observed T-phase transfer functions for events 2 and 4 together with the transfer functions calculated using SPECFEM2D with and without Q. Amplitude of calculated signals are low below 5 Hz

5 Conclusions

We have performed a series of calculations of hydroacoustic phases from underwater explosions observed as seismic signals at T-stations on land. Calculations were performed with and without attenuation. The calculations used the spectral element code SPECFEM2D to model acoustic pressure in the ocean and elastic displacement velocity in the crust in the area of the T-station, coupled with a normal mode or parabolic equation model for propagation from the distant source to the SPECFEM2D domain, together with earth and ocean models based on the best available structures for paths to the T-stations. Waveforms were calculated and saved at multiple locations in the ocean and on the land surface, including at the locations of all 11 T-stations. The hydroacoustic (pressure) waves in the ocean convert to seismic (elastic) waves on land in a complicated manner generating a mix of seismic phases that consist mostly of surface waves, but with some bursts of body waves. In general, the seismic signals at the T-stations share the frequency and duration characteristics of the signals at the corresponding hydroacoustic station, with the higher frequencies attenuated. Although it was sometimes possible to identify a specific type of seismic wave (i.e. P, S, surface), the complex mix of signals made automatic signal identification difficult.

The results of the calculations were used to calculate T-phase transfer functions: the spectral ratio of the velocity on land to the pressure in the water prior to interacting with the sloping bathymetry. We find that T-phase transfer functions calculated without attenuation are remarkably flat with frequency, however transfer functions with attenuation decrease with increasing frequency and are much more consistent with observations. We compared our results with two types of observations: (1) hydroacoustic and seismic signals recorded at Ascension Island from explosions off the coast of Florida; and (2) T-phase transfer functions derived from a large set of earthquakes recorded at both the IMS T-stations and IMS hydrophone arrays. There is considerable variability in the earthquake-derived transfer functions, but there is enough data to establish well-defined mean values for most stations. The calculated transfer functions with attenuation are in good agreement with the mean values of the transfer functions derived from earthquake data. The seismic signals recorded at Ascension Island are above noise in the 6–12 Hz frequency band. The hydroacoustic and seismic signals recorded at Ascension Island are comparable in amplitude and duration to the calculated signals (with attenuation) and the measured T-phase transfer function over this frequency band is comparable to the calculated transfer function.

Appendix. Implementation of a Distant Propagating Source in SPECFEM2D

The T-phase simulations of Stevens et al. (2001), like those of the current study, each take as a starting point a propagating pressure field from an underwater explosion source, obtained from a hydroacoustic calculation. The appendix in Stevens et al. (2001) describes a method for coupling that hydroacoustic field to a fluid/solid finite difference simulation, in which case deformation is given in terms of velocity and pressure fields. SPECFEM2D instead calculates motion in the fluid domain of the model in terms of a potential $\chi$, requiring modifications to the Stevens et al. coupling scheme. We outline the hydroacoustic/SPECFEM2D coupling method here. The approximations involved parallel those of Stevens et al. (2001), which are discussed at length in the appendix to that article.

Formulation of the Coupling Problem. In Fig. 27, surface ${C}_{f}+{C}_{s}$, combined with the stress-free upper surface, encloses a volume V comprising fluid and solid elastic (or viscoelastic) sub-volumes that are inhomogeneous in both lateral and vertical directions. We formulate the general 3D problem, and specialize to 2D later when we finally describe the SPECFEM2D source implementation. Volume V is interior to the SPECFEM2D simulation volume, and contains the hydroacoustic (H) and T-Phase (T) stations of interest. A hydroacoustic field is incident on the fluid domain ${V}_{f}$ of V, from the left, and is assumed to be quiescent within and on the boundary of V at time zero (i.e., at the initiation time of the SPECFEM2D calculation). The total displacement field $u\left(x\right)$ (where $x$ is position vector $({x}_{1},{x}_{2},{x}_{3})$, and $u$ denotes vector (${u}_{1},{u}_{2},{u}_{3})$) is the sum of the incident hydroacoustic field ${u}^{inc}$ plus a scattered field ${u}^{s}$. Total displacement satisfies the homogeneous equations of motion everywhere in the interior of V,

$$\rho (x) {\ddot{u}}_{i}\left(x,t\right)-\frac{\partial }{\partial {x}_{j}}\left[{C}_{ijpq}(x)\frac{\partial {u}_{p}(x,t)}{\partial {x}_{q}}\right]=0,$$

(1)

where $\rho$ and $C$ are the density and elastic tensor (which in the fluid reduces to $\kappa {\delta }_{ij}{\delta }_{pq}$, where $\kappa$ is the bulk modulus), respectively, while ${u}^{inc}$ and ${u}^{s}$ separately satisfy (1) in the exterior and boundary of V.

Fig. 27

Diagram of the solution coupling problem. Hydroacoustic waves incident from the left are confined to a stratified fluid channel that merges into a laterally-inhomogeneous fluid domain within the volume V, where V is bounded by the free surface and a fictitious boundary ${C}_{f}+{C}_{s}$ that is interior to the SPECFEM2D solution domain. The field exterior to V consists of a field incident from the left of ${C}_{f}$, specified by a separate hydroacoustic calculation, plus the field scattered from V. Points labeled H and T indicate hydroacoustic and T-Phase stations, respectively. The fluid and solid subsets of V will be denoted ${V}_{f}$ and ${V}_{s}$, respectively

Because there are no sources interior to V, the total displacement in V satisfies the integral equation

$${u}_{n}\left(x,t\right)=-{\int }_{{C}_{f}+{C}_{s}}d{S}_{\xi } {C}_{ijpq}\left(\xi \right)\left[{u}_{p,q}(\xi ,t)*{G}_{ni}\left(x,\xi ,t\right)-{u}_{i}\left(\xi ,t\right)*\frac{\partial {G}_{np}}{\partial {\xi }_{q}}(x,\xi ,t)\right]{v}_{j},$$

(2)

(e.g., Aki and Richards, 1980), $\widehat{v}$ is the inward normal to V, $*$ denotes convolution, and $G$ is the Green’s tensor for the fluid/solid model. Henceforth, we will omit the time argument. The equation for $G$ is

$$\rho \left(x\right){\ddot{G}}_{in}\left(x,\xi \right)-\frac{\partial }{\partial {x}_{j}}\left[{C}_{ijpq}\left(x\right)\frac{\partial }{\partial {x}_{q}}{G}_{pn}\left(x,\xi \right)\right]={\delta }_{in}\delta (x-\xi ),$$

(3)

and $G$ satisfies the reciprocity relationship

$${G}_{in}\left(x,\xi \right)={G}_{ni}(\xi ,x).$$

(4)

Equation (2) breaks into the sum of integrals over ${u}^{inc}$ and ${u}^{s}$, respectively, but for $x\in V$, the integral involving the scattered field can be shown to vanish (because ${u}^{s}$ is a solution to the equations of motion in the volume exterior to V, with equivalent sources confined to the interior of V), so no approximation is involved if we replace (unknown) total displacement $u$ with the (known) incident hydroacoustic field ${u}^{inc}$. Furthermore, while ${u}^{s}$ will be of comparable magnitude to ${u}^{inc}$ on the fluid (${C}_{f}$) and solid (${C}_{s}$) parts of $\partial V$, hydroacoustic field ${u}^{inc}$ has negligible amplitude in the solid, so to a very good approximation we can represent the displacement field in V by restricting the integration in (2) to the fluid boundary ${C}_{f}$ only,

$${u}_{n}\left(x\right)\approx -{\int }_{{C}_{f}}d{S}_{\xi }{v}_{i}\kappa \left[{u}_{p,p}^{inc}\left(\xi \right)*{G}_{ni}\left(x,\xi \right)-{u}_{i}^{inc}\left(\xi \right)*\frac{\partial {G}_{np}}{\partial {\xi }_{p}}(x,\xi )\right], x\in V.$$

(5)

Fluid-Domain Source For $x$ in the fluid, we can express displacement $u$ in terms of a potential $\chi$, as

$$u\left(x\right)={\rho }^{-1}\nabla \chi (x),$$

(6)

and $\chi$ also partitions into incident and scattered fields,

$${u}^{inc}\left(x\right)={\rho }^{-1}\nabla {\chi }^{inc}(x),$$

$${u}^{s}\left(x\right)={\rho }^{-1}\nabla {\chi }^{s}(x).$$

In the fluid, (1) reduces to the homogeneous acoustic equation solved in the fluid domain of SPECFEM2D,

$$\ddot{\chi }\left(x\right)-\kappa \nabla \cdot \left[{\rho }^{-1}\nabla \chi \left(x\right)\right]\,=\,0,$$

(7)

and it follows that the pressure $- \kappa \nabla \cdot u$ is given by

$$p\left(x\right)=-\ddot{\chi }(x).$$

(8)

We introduce Green’s function $g(x,\xi )$ for (7), satisfying

$$\ddot{g}\left(x,\xi \right)-\kappa {\nabla }_{x}\cdot {\rho }^{-1}{\nabla }_{x}g\left(x,\xi \right)=\delta (x-\xi ),$$

(9)

and then the same procedure used to derive (5) leads to

$$\chi \left(x\right)={\int }_{{C}_{f}}d{S}_{\xi }{c}^{2}{v}_{i}\left[{\chi }^{inc}\left(\xi \right)*\frac{\partial g\left(x,\xi \right)}{\partial {\xi }_{i}}-\frac{\partial {\chi }^{inc}(\xi )}{\partial {\xi }_{i}}*g(x,\xi )\right],$$

(10)

where $c=\sqrt{\kappa /\rho }$. SPECFEM2D solves (7) in the fluid domain, with a source term $\phi$ on the r.h.s., and the solution for $\chi ,$ given as a surface integral in (10), can alternatively be written as a volume integral in terms of $\phi$,

$$\chi \left(x\right)={\int }_{{V}_{f}}d{V}_{\eta }g\left(x,\eta \right)*\phi (\eta ).$$

(11)

The two formulations (10) and (11) agree provided that $\phi$ is specified to be the distribution.

$$\phi \left(\eta \right)={\int }_{{C}_{f}}d{S}_{\xi }{c}^{2}\left\{{\chi }^{inc}\left(\xi \right)\left[-\widehat{v}\cdot {\nabla }_{\eta }\delta \left(\eta -\xi \right)\right]+\left[-\widehat{v}\cdot {\nabla }_{\eta }{\chi }^{inc}\left(\xi \right)\right]\delta \left(\eta -\xi \right)\right\}.$$

(12)

Applying this source term to SPECFEM2D gives the desired solution $u(x)$, for all $x\in V$.

In seismological terms, the source $\phi$ is the negative of an isotropic moment density. One way to see that is to reduce (3) to (9), which involves taking the divergence of (3) with respect to source coordinate $\xi$ and source index n. The source term in (3) then transforms to ${\nabla }_{\xi }\delta (x-\xi )$, which is the force distribution corresponding to an isotropic seismic moment, and which devolves to $- \delta (x-\xi )$ when $G(x,\xi )$ is written in terms of Green’s function for the potential.

Numerical Implementation The incident hydroacoustic solution is given as a pressure ${p}^{inc}(\xi )$, so we apply (8) to write (12) in terms of incident pressure,

$$\phi \left(\eta \right)={\int }_{{C}_{f}}d{S}_{\xi }{c}^{2}\left\{\left[\widehat{v}\cdot {\nabla }_{\eta }{p}^{\#\#inc}\left(\xi \right)\right]\delta \left(\eta -\xi \right)+{p}^{\#\#inc}\left(\xi \right)\left[\widehat{v}\cdot {\nabla }_{\eta }\delta (\eta -\xi )\right]\right\},$$

(13)

where ${p}^{\#\#}$ denotes the second time integral of the pressure. We have shown that $\phi$ is the negative of the isotropic moment density, and recognize the first term in (13) as a monopole (negative-polarity isotropic moment source) distribution on ${C}_{f}$ with density (per unit area of ${C}_{f}$) ${c}^{2}{\partial }_{v}{p}^{\#\#inc}$ (${\partial }_{v}$ indicates the derivative in direction $\widehat{v}$). The second term, then, is a dipole distribution with density ${c}^{2}{p}^{\#\#inc}$ and its axis normal to ${C}_{f}$.

SPECFEM2D calculations are 2D. In applying (13), the integration in the third dimension is already implicit in the 2D formulation, so (13) reduces to integration on a cross-sectional curve of ${C}_{f}$. We approximate the first term of (13) numerically by introducing a set of discrete monopole sources at points ${\xi }^{k}$ along the ${C}_{f}$ cross-section, with spacing $\Delta y$ and amplitude ${c}^{2}{\Delta y\partial }_{v}{p}^{\#\#inc}$ (dimensionally, moment per unit length, because we are in 2D). We represent the second term as a set of dipoles at the same spacing $\Delta y$ along the ${C}_{f}$ cross-section. We then approximate each dipole by a monopole pair centered on ${C}_{f}$ and offset by $\Delta x$ in direction $\widehat{v}$, with the exterior (to ${V}_{f}$) monopoles of each pair having amplitudes ${c}^{2}\left(\Delta y/\Delta x\right){p}^{\#\#inc}$ and the interior monopoles of each pair having amplitudes ${-c}^{2}\left(\Delta y/\Delta x\right){p}^{\#\#inc}$ (an approximation valid when the wavelength of the incident field is long compared with $\Delta x$, as is the case here). Then, the complete source approximation is

$$\phi \left(\eta \right)=M\left(\eta \right)+D(\eta ),$$

(14)

where

$$M\left(\eta \right)=\Delta y{\sum }_{k}{c}^{2}{\partial }_{v}{p}^{\#\#inc}\left({\xi }^{k}\right)\delta (\eta -{\xi }^{k}),$$

(15)

and

$$D\left(\eta \right)=\frac{\Delta y}{\Delta x}\sum_{k}{c}^{2}{p}^{\#\#inc}({\xi }^{k})\left[\delta \left(\eta -{\xi }^{k}-\Delta x\widehat{v}\right)-\delta \left(\eta -{\xi }^{k}+\Delta x\widehat{v}\right)\right].$$

(16)

In practice we have found it expedient to estimate the incident pressure gradient ${\partial }_{v}{p}^{\#\#inc}$ from the hydroacoustic displacement field. We specialize to a vertical integration surface, so that $\widehat{v}$ is horizontal. Then, to the extent that the incident field is propagating horizontally and dispersion can be neglected over the bandwidth of interest, we can use ${\partial }_{v}{p}^{\#\#inc}\approx -\rho \widehat{v}\cdot u$, which proves to be a good approximation in our application. Finally, we note that the input to the SPECFEM2D code is actually isotropic moment, equal to − $\phi$.