The Uncertainty of 2D Models Along Wide Angle Seismic Profiles

Abstract

The estimation of uncertainty for any geophysical model is important for determining how reliable the model is. It is especially important for subjective trial and error modelling techniques like forward ray-tracing modelling of wide-angle seismic data when the final result is very dependent on the interpreter’s knowledge of the area and experience. In this kind of modelling, it is common to encounter over interpretation of the seismic data without checking the uncertainty of the result, especially in the deep parts that are not constrained with other a priori knowledge. In this paper, we propose a method of estimating the uncertainty of the final models based on a one dimensional method of small error propagation generalized for 2D profiles. With a simple approximation, we estimate the uncertainty for published interpretative models of selected profiles from seismic experiments in the Central Europe. We conclude that for typical wide angle seismic profiles we can reliably interpret four layered models of the Earth’s crust based on traveltimes fitting. We also show how the number of layers influence obtained uncertainties. Estimated uncertainties for both the velocity fields and the boundaries between layers are important for future tectonic and geodynamic interpretation of those profiles.

1 Introduction

In recent decades we significantly increased the amount of seismic data gathered to study the structure of the Earth’s crust and the upper mantle in pursuit of finding the most precise description of those structures. The raytracing technique is well known and often used for modelling of wide-angle seismic data. It is the most often used in the form of seismic tomography like FAST (Zelt and Barton 1998b) realised by fast eikonal solvers, but it is still used for trial and error forward modelling using SEIS83 code (Červený and Pšenčík 1984) and Rayinvr (Zelt and Smith 1992). SEIS83 was commonly employed in interpretation of a series of 2D profiles from large experiments in Central Europe, namely: POLONAISE’97 (Guterch et al. 1999), CELEBRATION 2000 (Guterch et al. 2003) and SUDETES 2003 (Grad et al. 2003b), resulting in many detailed interpretations having an important influence on local geodynamic interpretations. In interpretation of seismic models, it is important to present the results with an estimation of the uncertainty. This problem in difficult for the results of forward modelling and most often is addressed by showing the ray coverage. More detailed analysis presents some examples of the single parameter tests, for example, by Grad et al. (2008) or Janik et al. (2002) describing the uncertainty for velocities as ±0.1 km/s and depth of interfaces as ±2 km. This approach to error is too simple, especially in cases of complicated, multi layered models. It is obvious that uncertainty for both the velocity field and the depth of interfaces will be different for each layer. A more reliable estimation is needed to exclude the possibility of the over interpretation of the field data. A quantitative estimation of the uncertainties in the final model will help create the simplest possible model that can explain the observed data, and the tectonic interpretation of the result can proceed from this point.

For inversion problems with traveltimes picked for defined phases, we have many methods to assess the resolution of models. Starting from analysing ray paths, there are ray densities as described by Kissling (1988), to widely used checkerboard tests (Zelt 1998). To assess quantitative uncertainty of inversion parameters, we can use posterior covariance matrices proposed by Tarantola (1987). For this kind of problem we suggest using those methods. However, our method is targeted for interpreters using forward modelling that tries to fit traveltimes to observed wave fields instead of precisely matched phases picked to layers. For them, and for cases where we don’t have access to original data, we propose our robust approximation.

2 Method

The method of estimation of the uncertainties for 1D layered models we employ was explained by Majdański (2013). In short, it is based on a layer-stripping modelling strategy that employs both reflected and refracted arrivals to model each layer separately. Layers are modelled in order from the shallowest to deepest. Because rays have to propagate through the shallow structures to be reflected or refracted in deeper layers, the uncertainties for deeper layers have to include the uncertainties of the layers above them. To estimate these total uncertainties, we used a simplified ray propagation in 1D layered media approach that has an analytical description and employs error propagation theory according to the Eq. (1).

$$u_{c}^{2} = \mathop \sum \limits_{i = 1}^{N} \left( {\frac{\partial f}{{\partial x_{i} }}} \right)^{2} u^{2} \left( {x_{i} } \right).$$

(1)

We used simplified ray propagation as in Fig. 1. We use a 1D model of the crust with four layers with constant velocities. In the first layer we observe the direct wave with propagation time as in Eq. 2:

$$t_{1} = \frac{s}{{V_{1} }},$$

(2)

where t is propagation time, s is offset and V is P-wave velocity, then we can calculate the velocity and its uncertainty according to Eq. 1 as:

$$V_{1} = \frac{s}{{t_{1} }},\partial V_{1}^{2} = \left( {\frac{{\partial V_{1} }}{{\partial t_{1} }}} \right)^{2} \partial t_{1}^{2} = \left( {\frac{s}{{t_{1}^{2} }}} \right)^{2} \partial t_{1}^{2} .$$

(3)

Fig. 1

Schematic representation of ray propagation in a layered model based on head waves. Diagram represents an analysis where refraction and wide-angle reflections are included; S source location, R receiver location, s offset, s _r reflection offset, V _i velocity in the ith layer, h _i thickness of the ith layer

During a synthetic test, we found that the uncertainty of position s is negligible comparing to the uncertainty in time. Propagation time for reflections in the first layer (t _r1, Fig. 1) is:

$$t_{{{\text{r}}_{1} }} = \frac{{\sqrt {4h_{1}^{2} + s_{{{\text{r}}_{1} }}^{2} } }}{{V_{1} }},$$

(4)

where s _r1 is the reflection arrival offset. Thickness of the first layer (h ₁) and its uncertainty are expressed as in Eq. 5:

$$h_{1} = \frac{1}{2}\sqrt {V_{1}^{2} t_{{{\text{r}}_{1} }}^{2} - s_{{{\text{r}}_{1} }}^{2} } , \partial h_{1}^{2} = \left( {\frac{{\partial h_{1} }}{{\partial V_{1} }}} \right)^{2} \partial V_{1}^{2} + \left( {\frac{{\partial h_{1} }}{{\partial t_{{r_{1} }} }}} \right)^{2} \partial t_{{{\text{r}}_{1} }}^{2},$$

$$\partial h_{1}^{2} = \left( {\frac{{V_{1} t_{{{\text{r}}_{1} }}^{2} }}{{2\sqrt { V_{1}^{2} t_{{{\text{r}}_{1} }}^{2} {-}s^{2} r_{1} } }}} \right)^{2} \partial V_{1}^{2} + \left( {\frac{{V^{2}_{1} t_{{{\text{r}}_{1} }} }}{{2\sqrt { V_{1}^{2} t_{{{\text{r}}_{1} }}^{2} {-}s^{2} r_{1} } }}} \right)^{2} \partial t_{{{\text{r}}_{1} }}^{2} .$$

(5)

The refraction in deeper layers is expressed as head-waves that can be modelled as refraction propagating along interfaces. The traveltime of the head wave (t ₂) is expressed as:

$$t_{2} = \frac{s}{{V_{2} }} + \frac{{2h_{1} }}{{V_{1} }}\sqrt {1 - \frac{{V_{1}^{2} }}{{V_{2}^{2} }}}.$$

(6)

If the velocities in adjacent layers are significantly different, we can simply Eq. 6 to:

$$t_{2} = \frac{{s_{2} }}{{V_{2} }} + \frac{{2h_{1} }}{{V_{1} }},$$

(7)

then we can express velocity and its uncertainty as:

$$V_{2} = \frac{{s_{2} V_{1} }}{{t_{2} V_{1} - 2h_{1} }},$$

$$\partial V_{2}^{2} = \left( {\frac{{\partial V_{2} }}{{\partial V_{1} }}} \right)^{2} \partial V_{1}^{2} + \left( {\frac{{\partial V_{2} }}{{\partial h_{1} }}} \right)^{2} \partial h_{1}^{2} + \left( {\frac{{\partial V_{2} }}{{\partial t_{2} }}} \right)^{2} \partial t_{2}^{2}.$$

(8)

The reflection in second and deeper layers (see Fig. 1) assumes vertical propagation in the upper layer, that is valid only if V ₂ ≫ V ₁. Full description is possible, but will significantly complicate underlying mathematics with no effect on the described problem. Therefore, the reflection is expressed as:

$$t_{{{\text{r}}_{2} }} = \frac{{2h_{1} }}{{V_{1} }} + \frac{{\sqrt {4h_{2}^{2} + s_{{{\text{r}}_{2} }}^{2} } }}{{V_{2} }}.$$

(9)

Then the thickness of the second layer (h ₂) and its uncertainty is expressed as:

$$h_{2} = \frac{1}{2}\sqrt {\left( {\left( {t_{{{\text{r}}_{2} }} - \frac{{4h_{1} }}{{V_{1} }}} \right)V_{2} } \right)^{2} - s_{{{\text{r}}_{2} }}^{2} },$$

$$\partial h_{2}^{2} = \left( {\frac{{\partial h_{2} }}{{\partial V_{1} }}} \right)^{2} \partial V_{1}^{2} + \left( {\frac{{\partial h_{2} }}{{\partial V_{2} }}} \right)^{2} \partial V_{2}^{2} + \left( {\frac{{\partial h_{2} }}{{\partial h_{1} }}} \right)^{2} \partial h_{1}^{2} + \left( {\frac{{\partial h_{2} }}{{\partial t_{{r_{2} }} }}} \right)^{2} \partial t_{{{\text{r}}2}}^{2}.$$

(10)

By analogy, any additional layer will result in an additional partial derivative component in the equation for the uncertainty of velocities and another one in the equation describing the uncertainty of the thickness. From synthetic tests discussed by Majdański (2013) we can see that the uncertainties of both velocities and depths of boundaries depend on offset of observed arrivals. The uncertainty of velocities decreases with larger offsets, while the uncertainty of depth of a boundary increases with larger offsets. In addition, both effects are non-linear. To assure the smallest possible uncertainties, we need good quality data that allows observation of arrivals of reflected waves for large offsets, and observation of near-offset reflections, optimally near-vertical. All estimated uncertainties depend mostly on corresponding traveltime picking precisions $\partial t$ for each observed phase. Better picking precision will significantly reduce the uncertainties.

The application of this method to 2D profiles can be realised as a series of 1D estimations along the profile, assuming a local 1D geometry. To demonstrate the proposed method application the profile S02 from SUDETES 2003 experiment (Majdanski et al. 2006) was selected. The resulting model from forward trial and error modelling was converted to a dense grid of velocities (1 × 0.1 km) that can explain main tectonic structures with only a small loss of resolution (see Majdański et al. 2009 for details). Four boundaries were sufficient to model the data from the crustal point of view, and they formed a five layer model as shown in Fig. 2a. The first layer in the original model was composed from several layers derived from geological and borehole data interpretations. All this information is included in velocities in the first layer. The uncertainty of geological and borehole based data is much smaller than the traveltime inversion result. Thus, these layers are treated as a single layer with small uncertainty. At 1 km intervals along the profile we had a column of velocities and depths of interfaces. To this column of the data, we applied our 1D estimation procedure. Partial results along the profile were combined forming the 2D plot presented in Fig. 2b. In detail, the uncertainty in each layer depends on a local velocity distribution and a local depth of boundaries, but also on the offset of observed arrivals and travel time. Offsets of observed arrivals were different for each of nine shots along this profile, thus, for this analysis, the average values were used. For the first layer offset of observed arrivals ranged from 5 to 120 km. For the calculation of the uncertainties we used a 60 km offset with corresponding propagation time of 10.2 s and based on Eq. 3 resulted in an uncertainty of ∂V ₁ = 0.029 km/s. The first boundary reflection was on average observed at 33 km with apropagation time of 7 s, and based on Eq. 5 resulted in an average uncertainty of ∂h ₁ = 0.32 km.

Fig. 2

(top) Model along profile S02 from the SUDETES 2003 experiment (Majdanski et al. 2009). The model contains five layers including the upper mantle and four interfaces. (bottom) Estimated uncertainty for velocity field is presented with colours, and for boundaries presented with error bars. In this simple model the uncertainties are rather constant for each layer with slightly larger values for the right (northern) part of the model

For the second layer, the refraction was observed to an average offset of 180 km with propagation time of 31 s resulting according to Eq. 8 in an uncertainty of ∂V ₂ = 0.025 km/s, which is lower than the one for the first layer. This is because the second layer is much thicker allowing propagation for larger distances so that the uncertainty of refraction arrivals decreases with offset. The reflection from the second layer was observed to an average offset of 110 km with propagation time of 18.8 s resulting according to Eq. 10 in a depth uncertainty ∂h ₂ = 1.6 km. Refractions in deeper layers were observed at average offsets of 210 km and reflections at offsets 180 and 100 km for layers three and four. The uncertainty values are presented in Table 1 for easier comparison. For profile S02 describing a thin 32–35 km crust, we see a structure with limited variations. Still, we recognize larger uncertainties for the Moho discontinuity in the northern part of the profile resulting from significantly higher velocities in the lower crust.

Table 1 Estimated uncertainties presented as average values of separate layers of each discussed profile

This analysis is focused on estimating how picking precision, local number of layers, their thickness and velocities will influence the uncertainties. This way we can judge if additional layers to describe some local features are justified. We are not taking into account ray densities, number of shot points or local dipping structures. Full analysis is possible (e.g., if in the form of covariance matrices, Tarantola 1987), but require detailed ray-tracing and access to all the data, traveltime picks, etc. Often forward modelling is based on fitting arrivals to observed wave field without detailed traveltimes picking. Our method will also work for known models with no access to original data, because average traveltimes and offset of arrivals for each layer can be easily calculated.

3 Application of the Method

The first profile we discuss is S01 from the SUDETES 2003 experiment. As presented by Grad et al. (2008), a 30 km thick crust with some complicated bodies in the upper crust were derived This model was rebuilt using the previously described gridding technique and is presented in Fig. 3a. The first layer is composed by several layers based on geological and borehole data. The uncertainty for velocities and depth of boundaries are negligible compared to travel time inversion. Thus, this layer is a single layer with small uncertainties. The estimated uncertainties are presented in Fig. 3b and average values are shown in Table 1. For each layer estimated averages are: (in km/s) ∂V ₁ = 0.029, ∂V ₂ = 0.032, ∂V ₃ = 0.21, ∂V ₄ = 0.45, and for boundaries: (in km) ∂h ₁ = 0.34, ∂h ₂ = 2.1, ∂h ₃ = 3.6. Compared to the single parameter estimations of Grad et al. (2008) as ±0.2 km/s for Pg, and ±2 km for Moho we see that it is not appropriate to use a single value for the whole velocity field, and that the Moho depth uncertainty should be significantly larger than for crustal layers.

Fig. 3

(top) Model along profile S01 from the SUDETES 2003 experiment (Grad 2008). The model contains four layers and three interfaces. (bottom) estimated uncertainty for velocity field presented with colours, and for boundaries presented with error bars. The estimated uncertainties varies laterally especially for the lower crust layer and the Moho boundary

The next profile we discuss is P4 from the POLONAISE’97 experiment. As presented by Grad et al. (2003a), a complicated transition structure across the Trans European Suture Zone (TESZ) from the East European Craton in the North (EEC) to Palaeozoic Platform was derived. The result was a complicated multi layers model [Fig. 8 in Grad et al. (2003a)], that is simplified in a series of the interpretation models [Fig. 17 in Grad et al. (2003a)]. Based on one of those models, profile P4 was rebuild, and it is presented in Fig. 4a and in Table 1. Complicated shallow structures in the TESZ part of the model are based on seismic reflection and borehole data with negligible uncertainties. Thus, they are described as a single layer. The crystalline crust of the model changes significantly around 300 km offset from thin 30 km crust to three layers, 50 km thick cratonic crust. The estimated uncertainties also changes significantly at that point as is presented in Fig. 4b. For the south part, we see values (in km/s): ∂V ₁ = 0.029, ∂V ₂ = 0.020, ∂V ₄ = 0.17, ∂V ₅ = 0.33 (no ∂V ₃ in this part of the model). For the north part it is (in km/s): ∂V ₁ = 0.029, ∂V ₂ = 0.022, ∂V ₃ = 0.11, ∂V ₄ = 0.24, ∂V ₅ = 0.64, which is roughly the same for shallow layers and significantly higher for the lower crust and the upper mantle. For boundaries it is (in km): south ∂h ₁ = 0.2, ∂h ₂ = 1.6, ∂h ₄ = 2.2 (no ∂h ₃ in this part), north ∂h ₁ = 0.17, ∂h ₂ = 1.2, ∂h ₃ = 2.5, ∂h ₄ = 2.7. The uncertainties depends on the number of layers, and they increase with layers. They also depend on the velocities in the overburden and are smaller for slow sediments areas. Also the crustal thickness affects our estimations, and the uncertainties, for both velocities and boundaries are larger for thicker crust.

Fig. 4

(top) Model along profile P4 from the POLONAISE’97 experiment (Grad et al. 2003a). The model contains five layers and 3–4 interfaces. (bottom) Estimated uncertainty for velocity field presented with colours, and for boundaries presented with error bars. There is significant change in uncertainties at offset 300 km corresponding to the edge of the EEC, resulting in larger uncertainties for the EEC

Profile CEL05 is similar to P4 in that it crosses the TESZ and similar tectonic units but is located to the south and crossed the Carpathian Mountains. The profile is very long being 1,400 km. The model of [Grad et al. (2006), Fig. 19] was converted using gridding technique as in Fig. 5a and in Table 1. As before, the first few kilometres in the first layer are based on geological and borehole data and have negligible uncertainty, and are, thus, described as a single layer. Again, in the crystalline part of the model we see a significant change in uncertainties (Fig. 5b) around 500 km offset. Values obtained from the estimation are (in km/s): south ∂V ₁ = 0.03, ∂V ₂ = 0.027, ∂V ₃ = 0.1, ∂V ₅ = 0.27, north ∂V ₁ = 0.03, ∂V ₂ = 0.021, ∂V ₃ = 0.19, ∂V ₄ = 0.47, ∂V ₅ = 0.63. For boundaries (in km): south ∂h ₁ = 0.33, ∂h ₂ = 1.1, ∂h ₃ = 2.2, north ∂h ₁ = 0.31, ∂h ₂ = 2.2, ∂h ₃ = 3.8, ∂h ₄ = 4.3. The Moho uncertainty is twice as large in the north as to the south. This is an effect of high velocity in the lower crust that has a large uncertainty.

Fig. 5

(top) Model along profile CEL05 from the CELEBRATION 2000 experiment (Grad et al. 2006). The model contains five layers and 3–4 interfaces. (bottom) Estimated uncertainty for the velocity field presented with colours, and for boundaries presented with error bars. As in Fig. 4, significant change in uncertainties at offset 500 km correspond to the edge of the EEC, resulting in larger uncertainties for the EEC

Next discussed profile is a combination of the TTZ and CEL03, as presented by Janik et al. (2005). It describes a complicated multi-layered structure along the TESZ. Their model contains in the crystalline crust some localised high velocity bodies and intra crust reflectors (Fig. 12 in Janik et al. 2005) and was gridded as a four layer crust model (Fig. 6a; Table 1). Again, the sediments are represented in complicated structures in the upper first few kilometres that were derived from geological and borehole data and were represented as a single layer with negligible uncertainty. The average uncertainties (Fig. 6b) are: for velocities (in km/s) ∂V ₁ = 0.03, ∂V ₂ = 0.05, ∂V ₃ = 0.17, ∂V ₄ = 0.38, ∂V ₅ = 0.64, and for boundaries (in km) ∂h ₁ = 0.5, ∂h ₂ = 1.8, ∂h ₃ = 3.4, ∂h ₄ = 3.5. For this model there are no significant differences with offset, because the sedimentary layer is observed for the whole model and no significant lateral velocity variation is observed. The uncertainties postulated by Janik et al. (2005) as ±0.1 km/s for velocities in the lower crust and ±1 km for Moho boundary should be significantly larger.

Fig. 6

(top) Model along profile CEL03 from the CELEBRATION 2000 experiment (Janik et al. 2005). The model contains five layers and four interfaces. (bottom) Estimated uncertainty for the velocity field presented with colours, and for boundaries presented with error bars. Despite the complication of this model, only small horizontal variations in uncertainty are visible. The largest uncertainties are recognized in the lower crust

The final discussed model CEL09 from CELEBRATION 2000 experiment was analysed by Hrubcová et al. (2005). It is located in the Bohemian Massif and has a triple crustal block structure. The gridded model is presented in Fig. 7 with estimated uncertainties. The uncertainties averages are: for velocities (in km/s) ∂V ₁ = 0.03, ∂V ₂ = 0.025, ∂V ₃ = 0.18, ∂V ₄ = 0.36, ∂V ₅ = 0.61, and for boundaries (in km) ∂h ₁ = 0.33, ∂h ₂ = 2.1, ∂h ₃ = 2.4, ∂h ₄ = 4.1. The middle part of the profile with only two crustal layers has much smaller uncertainties comparing to edges of the profile with separate lower crust layers.

Fig. 7

(top) Model along profile CEL09 from the CELEBRATION 2000 experiment (Hrubcová et al. 2005). The model contains five layers and 3–4 interfaces. (bottom) Estimated uncertainty for the velocity field presented with colours, and for boundaries presented with error bars. Significant variations in the uncertainties for deeper areas. Small uncertainties in the middle part are because of local two layers crust

4 Conclusions

We propose a technique for estimation of how picking precision of traveltimes affects the uncertainty of modelled layers. With this simple approximation, we can estimate the uncertainties for velocity and depth of boundaries for a given model, and show how the uncertainty will increase with each added layer. As the method is based on 1D approximation, it will be more accurate for layers not deviating much from flat ones. For strongly dipping structures, the estimates may be less accurate, but the effect of the accumulation of uncertainties by error propagation to consecutive layers will still be viable.

The estimated uncertainties for the profiles analysed for deep layers are larger than suggested by the published studies using ray-tracing modelling. For velocities in shallow layers, especially modelled using Pg arrivals observed for long distances, the estimated uncertainties are much smaller (about 0.03 km/s). The uncertainty of velocities rapidly increases with added layers, because of a cumulative effect of uncertainty for boundaries based on wide-angle data. In general, for typical picking precisions ∂t = 0.1 s, wide-angle reflections provide uncertainties >2.5 km for depth of the reflecting boundary for the 3rd and any additional layers in a model. This uncertainty will be significantly smaller for analysis based on near-vertical reflections (see Majdański 2013 for details). For interpretation of the results of ray-tracing modelling, it is important to use published tectonic interpretations and not the ray-tracing models themselves. As a general result of the analysis presented, we claim that for a typical crustal scale wide-angle seismic data (shot spacing about 30 km, receiver spacing about 3 km), with good quality data (high S/N ratio, clear long offset arrivals, picking precision about 0.1 s) crustal models containing up to 4–5 layers based on traveltime modelling can be obtained. Any number of additional layers derived on a priori geological knowledge or boreholes data with negligible uncertainty can be added without the impact on the uncertainty of deeper layers. The main limitation is time picking precision, which can vary substantially depending on depth and offset. Using a larger number of layers modelled and using a layer stripping approach will lead to unreliable models in the sense of uncertainty. More layers in models are possible if near vertical reflection data were used to model boundaries.

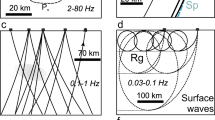
Those seeking geological interpretations would like to have models as shown in Fig. 8a, b, rather than the smooth results from tomography as presented in Fig. 8d. However, when looking at the corresponding uncertainties in Fig. 8e–g, we come to the conclusion that some trade-off between number of parameters and their uncertainties is needed. We propose that results shown in Fig. 8c with its uncertainties shown in Fig. 8g becomes a reasonable choice. We still can recognize important details, while the uncertainties are reasonably small. As always, achieving the minimum-structure model as in Occam’s razor principle should be our goal, but additional knowledge about the uncertainties is very important and should be a factor in the final interpretative result.

Fig. 8

Schematic representation of detailed models of the structure (a, b) is presented with large corresponding uncertainties (e, f). A smooth version of this model (d) is lacking details, but its uncertainty (h) is relatively small. A trade-off between complexity of the model and the uncertainty of the used parameters leads to an optimal solution (c) with the uncertainties (g)