On the Number of Eigenvalues of the Dirac Operator in a Bounded Interval

Abstract

Let $H_0$ be the free Dirac operator and $V \geqslant 0$ be a positive potential. We study the discrete spectrum of $H(\alpha )=H_0-\alpha V$ in the interval $(-1,1)$ for large values of the coupling constant $\alpha >0$. In particular, we obtain an asymptotic formula for the number of eigenvalues of $H(\alpha )$ situated in a bounded interval $[\lambda ,\mu )$ as $\alpha \rightarrow \infty$.

1 Statement of the Main Theorem

Let $H_0$ be the free Dirac operator

$$\begin{aligned} H_0=-i\sum _1^3 \gamma _j \frac{\partial }{\partial x_j}+\gamma _0, \end{aligned}$$

where $\gamma _j$ are $4\times 4$ self-adjoint matrices obeying the conditions

$$\begin{aligned} \gamma _j \gamma _k+\gamma _k \gamma _j={\left\{ \begin{array}{ll}0, \qquad \text {if}\quad j\ne k;\\ 2\, {\mathbb I}, \qquad \text {if}\quad j= k. \end{array}\right. } \end{aligned}$$

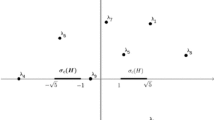
The operator $H_0$ is self-adjoint in the space $L^2({\mathbb R}^3;{\mathbb C}^4)$ consisting of functions on ${\mathbb R}^3$ that take values in ${\mathbb C}^4$. The spectrum of $H_0$ is the set $\sigma (H_0)=(-\infty ,-1]\cup [1,\infty )$.

Let $V\geqslant 0$ be a bounded potential on ${\mathbb R}^3$. Define $H(\alpha )$ to be the operator

$$\begin{aligned} H(\alpha )=H_0-\alpha V, \qquad \alpha >0. \end{aligned}$$

In the formula above, V is understood as the operator of multiplication by a matrix-valued function $V\cdot {\mathbb I}$. The case of a more general matrix-valued function will not be considered due to its little relation to Physics. Throughout the paper, we always assume that

$$\begin{aligned} V\in L^3({\mathbb R}^3)\cap L^\infty ({\mathbb R}^3). \end{aligned}$$

(1.1)

In this case, besides having a continuous spectrum that coincides with $\sigma (H_0)$, the operator $H(\alpha )$ may only have a discrete spectrum in the interval $(-1,1)$. Choose $\lambda$ and $\mu$ so that $-1<\lambda<\mu <1$. We define $N(\alpha )$ to be the number of eigenvalues of $H(\alpha )$ inside $[\lambda ,\mu )$.

Our main result is the theorem below which establishes the rate of growth of $N(\alpha )$ at infinity. The symbol $f_+$ denotes the positive part $f_+=(|f|+f)/2$ of f, which can be either a real number or a real-valued function.

Theorem 1.1

Let $\Phi$ be a continuous nonnegative function on the unit sphere in ${\mathbb R}^d$ and $1<\nu <4/3$. Let $V\geqslant 0$ be a bounded real-valued potential such that

$$\begin{aligned} V(x)=\frac{\Phi (\theta )}{|x|^\nu }\Bigl (1+o(1)\Bigr ),\qquad \text {as}\qquad |x|\rightarrow \infty , \end{aligned}$$

uniformly in $\theta =x/|x|$. Then for any $q\in (9/4,3/\nu )$ and any subinterval $[\lambda ,\mu ]\subset (-1,1)$,

$$\begin{aligned} \begin{aligned} \lim _{\alpha \rightarrow \infty }&\alpha ^{-3/\nu +q}\int _0^{\alpha } N(t)t^{-q-1}\textrm{d}t\\&\quad =\frac{\nu }{3\pi ^2(3-\nu q)}\int _{{\mathbb R}^3}\Bigl [\Bigl ((\Phi (\theta )|x|^{-\nu }+\mu )_+^2-1\Bigr )^{3/2}_+\\&\qquad -\Bigl ((\Phi (\theta )|x|^{-\nu }+\lambda )_+^2-1\Bigr )^{3/2}_+\Bigr ] \textrm{d}x. \end{aligned} \nonumber \\ \end{aligned}$$

(1.2)

Remark

If $N(\alpha ) \sim C \alpha ^{3/\nu }$ as $\alpha \rightarrow \infty$, then the right hand side of (1.2) becomes $\displaystyle \frac{\nu }{3-\nu q}\cdot C$. Thus, formula (1.2) determines the value of the constant C.

The question about the number of eigenvalues of the Dirac operator in a bounded interval is considered here for the first time. This theorem is new.

Perturbations $V\in L^3({\mathbb R}^3)$ were studied in [17] by M. Klaus and, later, in [5] by M. Birman and A. Laptev. However, the object of the study in [17] and [5] was different from $N(\alpha )$, considered in this article. The main results of [17] and [5] imply that if $V\in L^3({\mathbb R}^3)$, then the number ${\mathcal {N}}(\lambda ,\alpha )$ of eigenvalues of H(t) passing a point $\lambda \in (-1,1)$ as t increases from 0 to $\alpha$ satisfies

$$\begin{aligned} {\mathcal {N}}(\lambda ,\alpha )\sim \frac{1}{3\pi ^2} \alpha ^{3}\int _{{\mathbb R}^3} V^{3}\textrm{d}x,\qquad \text {as}\quad \alpha \rightarrow \infty . \end{aligned}$$

(1.3)

In addition, M. Klaus proved in [17] that if $V\in L^3\cap L^{3/2}$, then the asymptotic formula (1.3) holds even for $\lambda =1$. In this case, ${\mathcal {N}}(\lambda ,\alpha )$ is interpreted as the number of eigenvalues of H(t) that appear at the right edge of the gap as t increases from 0 to $\alpha$.

The crux of the problem. Observe that $N(\alpha )={\mathcal {N}}(\mu ,\alpha )-{\mathcal {N}}(\lambda ,\alpha ).$ However, since the expression on the right hand side of (1.3) does not depend on $\lambda$, this formula only implies that

$$\begin{aligned} N(\alpha )=o(\alpha ^{3}),\qquad \text {as}\quad \alpha \rightarrow \infty . \end{aligned}$$

In order to obtain an asymptotic formula for $N(\alpha )$, one would need to know the second term in the asymptotics of ${\mathcal {N}}(\lambda ,\alpha )$. The second term in (1.3) has never been obtained. This explains why the problem is challenging. Another reason why the problem is challenging is that the Dirichlet–Neumann bracketing that is often used for Schrödinger operators cannot be applied to Dirac operators. To prove Theorem 1.1, one needs to develop a new machinery rich in tools that allow us to obtain the estimate of $N(\alpha )$ stated below.

Theorem 1.2

Let $V\in L^q({\mathbb R}^3)\cap L^\infty ({\mathbb R}^3)$ with $9/4<q\leqslant 3$, and let $N(\alpha )$ be the number of eigenvalues of $H(\alpha )$ in the interval $[\lambda ,\mu )$. Then,

$$\begin{aligned} \int _0^\infty N(\alpha )\alpha ^{-q-1}\textrm{d}\alpha \leqslant C \int _{{\mathbb R}^3} V^{q}(x)\textrm{d}x \end{aligned}$$

with a constant $C>0$ depending on $\lambda$ and $\mu$ but independent of V.

Theorems 1.1 and 1.2 involve averaging of the function $N(\alpha )$. Averaging of eigenvalue counting functions also appeared in the papers [28] and [29]. However, the operators that were studied in these two papers are Schrödinger operators. These are the publications in which one discusses a periodic Schrödinger operator perturbed by a decaying potential $\alpha V$. The same model is discussed in [26, 27, 30], but the asymptotics of $N(\alpha )$ is established in [26, 27, 30] without any averaging. To obtain such strong results, the authors in these articles impose very restrictive conditions on the derivatives of V. The remaining papers [1,2,3,4, 6, 7, 10, 12,13,14,15,16, 21, 25], devoted to Schrödinger operators, do not even deal with $N(\alpha )$. Instead of that, they deal with the number ${\mathcal {N}}(\lambda ,\alpha )$ of eigenvalues passing the point $\lambda$.

Finally, we would like to mention the paper [11]. While the problems discussed in [11] are related to the discrete spectrum of a Dirac operator, they are very different from the questions studied here.

2 Compact Operators

For a compact operator T, the symbols $s_k(T)$ denote the singular values of T enumerated in the non-increasing order ($k\in {\mathbb N}$) and counted in accordance with their multiplicity. Observe that $s^2_k(T)$ are eigenvalues of $T^*T$. We set

$$\begin{aligned} n(s,T)=\#\{k: \quad s_k(T)>s\},\qquad s>0. \end{aligned}$$

For a self-adjoint compact operator T, we also set

$$\begin{aligned} n_\pm (s,T)=\#\{k: \quad \pm \lambda _k(T)>s\},\qquad s>0. \end{aligned}$$

where $\lambda _k(T)$ are eigenvalues of T. Observe that (see [8])

$$\begin{aligned} n_\pm (s_1+s_2,T_1+T_2)\leqslant n_\pm (s_1,T_1)+n_\pm (s_2,T_2), \qquad s_1,s_2>0. \end{aligned}$$

A similar inequality holds for the function n. Also,

$$\begin{aligned} n(s_1s_2,T_1T_2)\leqslant n(s_1,T_1)+n(s_2,T_2), \qquad s_1,s_2>0. \end{aligned}$$

Theorem 2.1

Let A and B be two compact operators on the same Hilbert space. Then for any $r\in {\mathbb N}$,

$$\begin{aligned} \sum _1^r s_k^p(A+B)\leqslant \sum _1^r s_k^p(A)+\sum _1^r s_k^p(B),\qquad \forall p\in (0,1], \end{aligned}$$

(2.1)

and

$$\begin{aligned} \sum _1^r s_k^p(AB)\leqslant \sum _1^r s_k^p(A) s_k^p(B),\qquad \forall p>0. \end{aligned}$$

(2.2)

The first inequality was discovered by S. Rotfeld [23]. The second estimate is called Horn’s inequality (see Section 11.6 of the book [8]).

Below we use the following notation for the positive and negative part of a self-adjoint operator T:

$$\begin{aligned} T_\pm =\frac{1}{2}(|T|\pm T). \end{aligned}$$

We also define $\textrm{sgn}(T)$ as a unitary operator having the property

$$\begin{aligned} T=\textrm{sgn}(T) |T|. \end{aligned}$$

Theorem 2.2

Let $0<p\leqslant 1$. Let $q\geqslant p$. Let A and B be two compact self-adjoint operators. Then for any $s>0$,

$$\begin{aligned}{} & {} q\int _{s}^{\infty } \Bigl (n_+(t,A)-n_+(t,B)\Bigr )t^{q -1}\textrm{d}t\nonumber \\{} & {} \qquad \leqslant \Vert B\Vert ^{q}+ \sum _{k=1}^{n_+(s,A)+1} s_k^p\Bigl (|A|^{q/p}\textrm{sgn}(A)-|B|^{q/p}\textrm{sgn}(B)\Bigr ). \end{aligned}$$

(2.3)

Moreover, if $B\leqslant A$, then

$$\begin{aligned}{} & {} q\int _{s}^{\infty } \Bigl (n_+(t,A)-n_+(t,B)\Bigr )t^{q-1}\textrm{d}t\\{} & {} \qquad \leqslant \sum _{k=1}^{n_+(s,A)+1} s_k^p\Bigl (|A|^{q/p} \textrm{sgn}(A)-|B|^{q/p}\textrm{sgn}(B)\Bigr ),\qquad \forall s>0. \end{aligned}$$

A proof of Theorem 2.2 can be found in [29].

Let $H_0$ and $V\geqslant 0$ be two self-adjoint operators acting on the same Hilbert space. Assume that V is bounded. For $\lambda \in {\mathbb R}\setminus \sigma (H_0)$, define the operator $X_\lambda$ by

$$\begin{aligned} X_\lambda =W(H_0-\lambda )^{-1}W,\qquad W=\sqrt{V}. \end{aligned}$$

(2.4)

Two points $\lambda$ and $\mu$ are said to be in the same spectral gap of $H_0$ provided $[\lambda ,\mu ]\subset {\mathbb R}\setminus \sigma (H_0)$.

Proposition 2.3

Let $0<p\leqslant 1$. Let $q\geqslant p$. Suppose the operators $X_\lambda$, $X_\mu$ are compact for the two points $\lambda <\mu$ that belong to the same spectral gap of $H_0$. Then for any $s>0$,

$$\begin{aligned}{} & {} q\int _{s}^{\infty } \Bigl (n_+(t,X_\mu )-n_+(t,X_\lambda )\Bigr )t^{q-1}\textrm{d}t\nonumber \\{} & {} \quad \leqslant \sum _{k=1}^{n_+(s,X_\mu )+1}s_k^p\Bigl (|X_\mu |^{q/p}\textrm{sgn}(X_\mu )-|X_\lambda |^{q/p}\textrm{sgn}(X_\lambda )\Bigr ). \end{aligned}$$

Proof

Here, one needs to apply Theorem 2.2 and use the fact that $X_\lambda \leqslant X_\mu$. Indeed,

$$\begin{aligned} X_\mu -X_\lambda =(\mu -\lambda )W(H_0-\lambda )^{-1}(H_0-\mu )^{-1}W \end{aligned}$$

is a nonnegative operator, because

$$\begin{aligned} (\mu -\lambda )(t-\lambda )^{-1}(t-\mu )^{-1}> 0,\qquad \text {for}\quad t\in \sigma (H_0)\subset {\mathbb R}\setminus [\lambda ,\mu ]. \end{aligned}$$

$\square$

Let ${\mathfrak {S}}_\infty$ be the class of compact operators. Note that the condition

$$\begin{aligned} W |H_0-\lambda _0|^{-1/2}\in {\mathfrak {S}}_\infty ,\qquad \text { for some}\quad \lambda _0\notin \sigma (H_0), \end{aligned}$$

(2.5)

implies that operators (2.4) are compact for all $\lambda \in {\mathbb R}\setminus \sigma (H_0).$ This is a consequence of the fact that

$$\begin{aligned} X_\lambda =W |H_0-\lambda _0|^{-1/2}\Omega \bigl (W |H_0-\lambda _0|^{-1/2}\bigr )^*, \end{aligned}$$

where $\Omega$ is a bounded operator. Moreover, (2.5) implies that, for each $\alpha >0$, the spectrum of $H(\alpha )=H_0-\alpha V$ is discrete outside of $\sigma (H_0)$ because the difference of resolvent operators $(H(\alpha )-z)^{-1}$ and $(H_0-z)^{-1}$ is compact for $\text {Im}\, z>0$.

The following proposition is called the Birman-Schwinger principle (see [3, 31]):

Proposition 2.4

Let $H_0$ and $V\geqslant 0$ be self-adjoint operators in a Hilbert space. Assume that V is a bounded operator and (2.5) holds for some $\lambda _0$. Let $\mathcal {N}(\lambda ,\alpha )$ be the number of eigenvalues of $H(t)=H_0-tV$ passing through a point $\lambda \notin \sigma (H_0)$ as t increases from 0 to $\alpha$. Then,

$$\begin{aligned} {\mathcal {N}}(\lambda ,\alpha )=n_+(s, X_\lambda ),\qquad \text {for}\quad s\alpha =1,\,\text {and}\, \, W=\sqrt{V}. \end{aligned}$$

(2.6)

The idea of the proof of (2.6) is the following. First, one shows that $\lambda \in \sigma (H(\alpha ))$, if and only if $\alpha ^{-1}\in \sigma (W(H-\lambda )^{-1}W)$. This relation holds with multiplicities taken into account. After that, one simply uses the definition of the distribution function $n_+(s,X_\lambda )$.

Corollary 2.5

Let $H_0$ and $V\geqslant 0$ be self-adjoint operators in a Hilbert space. Assume that V is a bounded operator and (2.5) holds for some $\lambda _0$. Let $N(\alpha )$ be the number of eigenvalues of the operator $H(\alpha )$ in $[\lambda ,\mu )$ contained in a gap of the spectrum $\sigma (H_0)$. Then,

$$\begin{aligned} N(\alpha )=n_+(s, X_\mu )-n_+(s, X_\lambda ),\qquad s\alpha =1. \end{aligned}$$

(2.7)

Let $p>0$. The class of compact operators T whose singular values satisfy

$$\begin{aligned} \Vert T\Vert _{{\mathfrak {S}}_p}^p:=\sum _k s^p_k(T)<\infty \end{aligned}$$

is called the Schatten class ${\mathfrak {S}}_p$.

The following statement provides a Hölder type inequality for products of compact operators that belong to different Schatten classes.

Proposition 2.6

Let $T_1\in {\mathfrak {S}}_p$ and $T_2\in {\mathfrak {S}}_q$ where $p>0$ and $q>0$. Then $T_1T_2\in {\mathfrak {S}}_r$, where $1/r=1/p+1/q$, and

$$\begin{aligned} \Vert T_1T_2\Vert _{{\mathfrak {S}}_r}\leqslant \Vert T_1\Vert _{{\mathfrak {S}}_p}\Vert T_2\Vert _{{\mathfrak {S}}_q}. \end{aligned}$$

A proof of this proposition can be found in [8].

Consider the following important example of an integral operator on $L^2({\mathbb R}^d)$:

$$\begin{aligned} \bigl (Y\,u \bigr )(x)=(2\pi )^{-d/2}\int _{{\mathbb R}^d}a(x)e^{i\xi x}b(\xi )u(\xi )\textrm{d}\xi . \end{aligned}$$

(2.8)

If F is the Fourier transform operator, [a] and [b] are operators of multiplication by the functions a and b, then

$$\begin{aligned} Y=[a]F^*[b]. \end{aligned}$$

The symbol ${\mathbb Q}$ below is used to denote the unit cube $[0,1)^d$.

Theorem 2.7

If a and b belong to $L^p({\mathbb R}^d)$ with $2\leqslant p<\infty$, then $Y\in {\mathfrak {S}}_p$ and

$$\begin{aligned} \Vert Y\Vert _{{\mathfrak {S}}_p}\leqslant C \Vert a\Vert _{L^p} \Vert b\Vert _{L^p}. \end{aligned}$$

(2.9)

If $0<p< 2$ and

$$\begin{aligned} \sum _{\nu \in {\mathbb Z}^d} \bigl ( \Vert a\Vert ^p_{ L^\infty ( {\mathbb Q}+\nu ) }+\Vert b\Vert ^p_{ L^\infty ( {\mathbb Q}+\nu ) }\bigr )<\infty , \end{aligned}$$

then $Y\in {\mathfrak {S}}_p$ and

$$\begin{aligned} \Vert Y\Vert _{{\mathfrak {S}}_p}\leqslant C \Bigl ( \sum _{\nu \in {\mathbb Z}^d} \Vert a\Vert ^p_{ L^\infty ( {\mathbb Q}+\nu ) }\Bigr )^{1/p}\Bigl ( \sum _{\nu \in {\mathbb Z}^d} \Vert b \Vert ^p_{ L^\infty ( {\mathbb Q}+\nu ) }\Bigr )^{1/p}. \end{aligned}$$

The constants in both inequalities depend only on d and p.

The proof of this theorem can be found in [7].

Let $p>0$. Besides the classes ${\mathfrak {S}}_p$, we will be dealing with the so-called weak Schatten classes $\Sigma _p$ of compact operators T obeying the condition

$$\begin{aligned} \Vert T\Vert ^p_{{\Sigma }_p}:=\sup _{s>0}s^{p} n(s,T)<\infty . \end{aligned}$$

It turns out that Y defined by (2.8) belongs to $\Sigma _p$ if $a\in L^p$ and the other factor b satisfies the condition

$$\begin{aligned} \Vert b\Vert ^p_{L^p_w}:=\sup _{s>0} \bigl ( s^p\, \textrm{measure}\{\xi \in {\mathbb R}^d:\,\, |b(\xi )|>s\} \bigr )<\infty . \end{aligned}$$

Such functions b are said to belong to the space $L^p_w({\mathbb R}^d)$. The following result is the so-called Cwikel’s inequality (see [9]).

Theorem 2.8

Let $p> 2$. Assume that $a\in L^p({\mathbb R}^d)$ and $b\in L^p_w({\mathbb R}^d)$. Then, Y defined by (2.8) belongs to the class $\Sigma _p$ and

$$\begin{aligned} \Vert Y\Vert _{{\Sigma }_p}\leqslant C \Vert a\Vert _{L^p}\Vert b\Vert _{L^p_w} \end{aligned}$$

with a constant C that depends only on d and p.

3 Preliminary Estimates

For the sake of brevity, the norms in the spaces ${\mathfrak {S}}_p$ and $L^p$ (quasinorms for $0<p<1$) will be often denoted by the symbol $\Vert \cdot \Vert _p$.

Theorem 3.1

Let p satisfy the condition $p>\frac{9}{2}$. Assume that $W\in L^p(\mathbb R^3)\cap L^\infty (\mathbb R^3)$. Let also

$$\begin{aligned}X_\lambda =W(H_0-\lambda )^{-1}W\end{aligned}$$

be the family of Birman-Schwinger operators with $H_0$ being the free Dirac operator. Then, the operator

$$\begin{aligned}T_{\lambda ,\mu }=X_\mu ^3 -X_\lambda ^3\end{aligned}$$

belongs to the Schatten class ${\mathfrak {S}}_{\frac{p}{6}}$ and

$$\begin{aligned} \Vert T_{\lambda ,\mu }\Vert _{\frac{p}{6}}\leqslant C \Vert W\Vert _p^{6}, \end{aligned}$$

(3.1)

with a constant $C>0$ that does not depend on W but might depend on $\lambda$ and $\mu$.

Proof

It is easy to see that

$$\begin{aligned} T_{\lambda ,\mu }=X_\mu ^3-X_\lambda ^3=(X_\mu -X_\lambda )X_\mu ^2+X_\lambda (X_\mu -X_\lambda )X_\mu +X_\lambda ^2(X_\mu -X_\lambda ) \end{aligned}$$

is a finite linear combination of operators of the form

$$\begin{aligned} F_{n,m}=\Bigl ( W R_\lambda W \Bigr )^{n}\Bigl (WR_\lambda R_\mu W\Bigr ) \Bigl (W R_\mu W \Bigr )^{m} \end{aligned}$$

where $R_\lambda =(H_0-\lambda )^{-1}$ and $n+m=2$. If the factors W were written before the factors $R_\lambda$ and $R_\mu$, then this term would be the operator

$$\begin{aligned} W^{6} R_\lambda ^{n+1}R_\mu ^{m+1}, \end{aligned}$$

and Theorem 2.7 would imply an estimate that is similar to (3.1). We have to show that the position of the factors does not matter that much.

For that purpose, we observe that

$$\begin{aligned} F_{2,0}= & {} \Bigl ( W R_\lambda W \Bigr )^{2}\Bigl (WR_\lambda R_\mu W\Bigr )\\= & {} \bigl (W |R_\lambda |^{2/3}\bigr )J_\lambda \bigl (|R_\lambda |^{1/3} W^{\frac{1}{2}} \bigr ) \bigl (W^{\frac{3}{2} } R_\lambda \bigr ) \Bigl (W^2R_\lambda R_\mu W\Bigr ) \end{aligned}$$

where $J_\lambda =\text {sign}(R_\lambda )$. Using inequality (2.9), we estimate the Shatten norm of the product

$$\begin{aligned} \Theta :=\bigl (W |R_\lambda |^{2/3}\bigr )J_\lambda \bigl (|R_\lambda |^{1/3} W^{\frac{1}{2}} \bigr ) \bigl (W^{\frac{3}{2} } R_\lambda \bigr ) \end{aligned}$$

Namely, we obtain that

$$\begin{aligned} \Vert \Theta \Vert _{p/3}\leqslant \Vert W |R_\lambda |^{2/3}\Vert _{p} \Vert |R_\lambda |^{1/3} W^{\frac{1}{2}}\Vert _{2p} \Vert W^{\frac{3}{2} } R_\lambda \Vert _{2p/3}. \end{aligned}$$

This leads to the estimate

$$\begin{aligned} \Vert \Theta \Vert _{p/3}\leqslant C \Vert W\Vert _p^{3} \end{aligned}$$

(3.2)

Besides (3.2) that provides an estimate of the Schatten norm of the first factor in the representation

$$\begin{aligned}F_{2,0}=\Theta \Bigl (W^2R_\lambda R_\mu W\Bigr ),\end{aligned}$$

we need an estimate for the norm of

$$\begin{aligned} B:=W^2R_\lambda R_\mu W. \end{aligned}$$

This operator can be written as

$$\begin{aligned} W^2R_\lambda R_\mu W=W^2|R_\lambda |^{4/3}J_{\lambda ,\mu } |R_\mu |^{2/3} W, \end{aligned}$$

where

$$\begin{aligned}J_{\lambda ,\mu } =|H_0-\lambda |^{4/3}R_{\lambda }R_{\mu } |H_0-\mu |^{2/3} \end{aligned}$$

is a bounded operator. Consequently,

$$\begin{aligned} \Vert B\Vert _{p/3}\leqslant \Vert J_{\lambda ,\mu }\Vert \,\Vert W^{2} |R_\lambda |^{4/3}\Vert _{\frac{p}{2}} \Vert |R_\mu |^{2/3} W \Vert _{p}. \end{aligned}$$

Therefore, by inequality (2.9),

$$\begin{aligned} \Vert B\Vert _{p/3}\leqslant C \Vert W\Vert _p^{3}. \end{aligned}$$

(3.3)

Combining the relations (3.2)–(3.3), we obtain that

$$\begin{aligned} \Vert F_{2,0}\Vert _{p/6}\leqslant C \Vert W\Vert _p^{6}. \end{aligned}$$

The estimate

$$\begin{aligned} \Vert F_{0,2}\Vert _{p/6}\leqslant C \Vert W\Vert _p^{6}. \end{aligned}$$

is obtained in the same way.

Similarly, since

$$\begin{aligned} F_{1,1}= & {} \bigl (W |R_\lambda |^{2/3}\bigr )J_\lambda \bigl (|R_\lambda |^{1/3} W^{\frac{1}{2}} \bigr ) \Bigl (W^{3/2}R_\lambda R_\mu W^{3/2}\Bigr )\\{} & {} \bigl (W^{\frac{1}{2}} |R_\mu |^{1/3}\bigr )J_\mu \bigl (|R_\mu |^{2/3} W \bigr ), \end{aligned}$$

we obtain that

$$\begin{aligned} \Vert F_{1,1}\Vert _{p/6}{} & {} \leqslant \Vert W |R_\lambda |^{2/3}\Vert _{p} \Vert |R_\lambda |^{1/3} W^{\frac{1}{2}}\Vert _{2p}\Vert |R_\mu |^{2/3}W\Vert _{p} \Vert \\{} & {} \qquad W^{\frac{1}{2}} |R_\mu |^{1/3} \Vert _{2p} \Vert W^{3/2}R_\lambda R_\mu W^{3/2}\Vert _{p/3}, \end{aligned}$$

which leads to the inequality

$$\begin{aligned} \Vert F_{1,1}\Vert _{p/6}\leqslant C \Vert W\Vert _{p}^3 \Vert W^{3/2}R_\lambda R_\mu W^{3/2}\Vert _{p/3}. \end{aligned}$$

(3.4)

Thus, we need to estimate the Schatten norm of the operator

$$\begin{aligned} B_0=W^{3/2}R_\lambda R_\mu W^{3/2}=W^{3/2}|R_\lambda |\cdot S_{\lambda ,\mu } \cdot |R_\mu | W^{3/2} \end{aligned}$$

where

$$\begin{aligned}S_{\lambda ,\mu } =|H_0-\lambda |R_{\lambda }R_{\mu } |H_0-\mu | \end{aligned}$$

is a bounded operator. Since

$$\begin{aligned} \Vert B_0\Vert _{p/3} \leqslant \Vert S_{\lambda ,\mu } \Vert \, \Vert W^{3/2} |R_\lambda | \Vert _{2p/3} \Vert |R_\mu | W^{3/2} \Vert _{2p/3}, \end{aligned}$$

we may apply inequality (2.9) to obtain that

$$\begin{aligned} \Vert B_0\Vert _{p/3}\leqslant C \Vert W\Vert _p^{3}. \end{aligned}$$

(3.5)

Finally, combining the relations (3.2)–(3.5), we conclude that

$$\begin{aligned} \Vert T_{\lambda ,\mu }\Vert _{p/6}\leqslant C \Vert W\Vert _p^{6}. \end{aligned}$$

$\square$

It follows from Proposition 2.3 that

$$\begin{aligned} p\int _0^\infty N(\alpha )\alpha ^{-p/2-1}\textrm{d}\alpha \leqslant 2\sum _k s_k^{p/6}(T_{\lambda ,\mu })=2\Vert T_{\lambda ,\mu }\Vert _{p/6}^{p/6}. \end{aligned}$$

As a consequence, applying Theorem 3.1, we obtain Theorem 1.2, saying that

$$\begin{aligned} q\int _0^\infty N(\alpha )\alpha ^{-q-1}\textrm{d}\alpha \leqslant C \Vert W\Vert _{2q}^{2q},\qquad q\in (9/4,3]. \end{aligned}$$

4 Splitting

For $\varepsilon >0$, we introduce two parts $V_1$ and $V_2$ of the potential V by setting

$$\begin{aligned} V_1(x)={\left\{ \begin{array}{ll} V(x) \qquad \text {if }\quad |x|<\varepsilon \cdot \alpha ^{1/\nu };\\ \quad 0 \qquad \quad \text {if }\quad |x|\geqslant \varepsilon \cdot \alpha ^{1/\nu }, \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} V_2=V-V_1.\end{aligned}$$

Let $N_j(t)$ be the number of eigenvalues of the operator $H_0-tV_j$ in the interval $[\lambda ,\mu )$, $j=1,2$. We want to show that

$$\begin{aligned} \int _0^{\alpha }N(t) t^{-q-1} \textrm{d}t\sim \int _0^{\alpha }N_1(t) t^{-q-1} \textrm{d}t+\int _0^{\alpha }N_2(t) t^{-q-1} \textrm{d}t,\qquad \text {as}\quad \alpha \rightarrow \infty . \end{aligned}$$

We introduce $\tilde{X}_\lambda$ by

$$\begin{aligned} \tilde{X}_\lambda =W_1(H_0-\lambda )^{-1}W_1+W_2(H_0-\lambda )^{-1}W_2, \end{aligned}$$

where $W_j=\sqrt{V}_j$ for $j=1,2$. Note that

$$\begin{aligned} n_+(t,\tilde{X}_\mu )- n_+(t,\tilde{X}_\lambda )=N_1(t)+N_2(t), \qquad \text {for}\quad 0<t\leqslant \alpha . \end{aligned}$$

As we know from (2.3), for $s=\alpha ^{-1}$,

$$\begin{aligned} \begin{aligned}&q\Bigl |\int _s^\infty \Bigl (n_+(t,X_\lambda )-n_+(t,\tilde{X}_\lambda )\Bigr )t^{q-1}\textrm{d}t\Bigr |\leqslant \Vert X_\lambda \Vert ^q+\Vert \tilde{X}_\lambda \Vert ^q+\\&\quad +\sum _{1\leqslant k\leqslant c\alpha ^3+1} s_k^{q/3}\Bigl (X_\lambda ^3-\tilde{X}_\lambda ^3\Bigr ). \end{aligned} \end{aligned}$$

(4.1)

Here, the value of the parameter q is the same as in Theorem 1.2. The constant c in the last term is the same as in the inequality $n_+(s,X_\lambda )\leqslant c s^{-3}$ (a consequence of Cwikel’s estimate). The next proposition and its corollaries show that the right hand side is of order $o(\alpha ^{3/\nu -q})$ as $\alpha \rightarrow \infty$. That allows us to replace $X_\lambda$ and $X_\mu$ by the operators $\tilde{X}_\lambda$ and $\tilde{X}_\mu$ and claim that

$$\begin{aligned} \int _0^{\alpha } N(t)t^{-q-1}\textrm{d}t= & {} \int _{\alpha ^{-1}}^\infty \Bigl (n_+(t,X_\mu )-n_+(t,X_\lambda ))\Bigr )t^{q-1}\textrm{d}t \\\sim & {} \int _{\alpha ^{-1}}^\infty \Bigl (n_+(t,\tilde{X}_\mu )-n_+(t,\tilde{X}_\lambda ))\Bigr )t^{q-1}\textrm{d}t,\qquad \text {as}\quad \alpha \rightarrow \infty . \end{aligned}$$

Proposition 4.1

Let $p>9/2$ and $\gamma \geqslant 2$. Let $W\in L^p(\mathbb R^3)\cap L^\infty (\mathbb R^3)$. Assume that the support of the function $W_2$ is contained in the set

$$\begin{aligned} \{x\in {\mathbb R}^3:\,\,\, |x|>\varepsilon \alpha ^{1/\nu }+1\}. \end{aligned}$$

Let also

$$\begin{aligned} q=\frac{3\gamma p}{6\gamma +p}. \end{aligned}$$

Then, there is an $\alpha _0>0$ such that

$$\begin{aligned} \Vert X^3_\lambda -\tilde{X}^3_\lambda \Vert _{q/3}\leqslant C \Vert W\Vert _p^{6}(\varepsilon ^{2}\alpha ^{2/\nu }+1)^{1/\gamma },\qquad \text {for}\quad \alpha >\alpha _0, \end{aligned}$$

with a constant $C>0$ independent of $\alpha$ and W.

Proof

The operator $X_\lambda ^3-\tilde{X}_\lambda ^3$ is a finite linear combination of operators of the form

$$\begin{aligned} \tilde{X}_\lambda ^{n}\Bigl (W_1R_\lambda W_2+W_2R_\lambda W_1\Bigr ) X_\lambda ^{m} \end{aligned}$$

where $R_\lambda =(H_0-\lambda )^{-1}$ and $n+m=2$.

Repeating the arguments that lead to the estimate (3.2), we obtain

$$\begin{aligned} \Vert \tilde{X}_\lambda ^{n}W^{-\frac{n}{2}}\Vert _r\leqslant C \prod _{j=1}^{n}\Vert W\Vert _p^{3/2}=C \Vert W\Vert _p^{p/r} \end{aligned}$$

(4.2)

with $r=\frac{2p}{3n}$. Similarly, we obtain that

$$\begin{aligned} \Vert W^{-\frac{m}{2}}X_\lambda ^{m}\Vert _{\tau }\leqslant C \Vert W\Vert _p^{p/\tau } \end{aligned}$$

(4.3)

with $\tau =\frac{2p}{3m}$. Negative powers of W in(4.2) and (4.3) are always multiplied by W. Therefore, the resulting products are bounded operators.

It remains to estimate norms of the operators

$$\begin{aligned} B_{1,2}:=W_1^{1+\frac{n}{2}}R_\lambda W_2^{1+\frac{m}{2}}\qquad \text {and}\qquad B_{2,1}:=W_2^{1+\frac{n}{2}}R_\lambda W_1^{1+\frac{m}{2}} \end{aligned}$$

in the classes ${\mathfrak {S}}_\varkappa$ with $\frac{1}{\varkappa }=\frac{3}{p}+\frac{1}{\gamma }$. Clearly, it is enough to estimate only the norm of $B_{1,2}$, because the adjoint of $B_{1,2}$ looks similar to $B_{2,1}$.

Let $\zeta$ be a smooth function on the real line $\mathbb R$ such that

$$\begin{aligned} \zeta (t)={\left\{ \begin{array}{ll} 1\qquad \text {for} \quad t\leqslant 0;\\ 0\qquad \text {for}\quad t\geqslant 1. \end{array}\right. } \end{aligned}$$

Define $\zeta _\alpha$ on ${\mathbb R}^3$ by

$$\begin{aligned} \zeta _\alpha (x)=\zeta (|x|-\varepsilon \alpha ^{1/\nu }). \end{aligned}$$

Then, obviously, $\zeta _\alpha W_1=W_1$ and $\zeta _\alpha W_2=0$. Using the identity

$$\begin{aligned}{}[B,A^{-1}]=A^{-1}\,[A,B]\,A^{-1}, \end{aligned}$$

we obtain that

$$\begin{aligned} W_1R_\lambda W_2=W_1 \zeta _\alpha R_\lambda W_2=W_1R_\lambda [H_0,\zeta _\alpha ]R_\lambda W_2\end{aligned}$$

The middle operator $[H_0,\zeta _\alpha ]$ is an operator of multiplication by a bounded matrix-valued function supported in the layer

$$\begin{aligned}\Omega _\alpha =\{x\in {\mathbb R}^3:\,\, \varepsilon \alpha ^{1/\nu }\leqslant |x|\leqslant \varepsilon \alpha ^{1/\nu }+1\}.\end{aligned}$$

Repeating this trick several times, we obtain by induction that

$$\begin{aligned} W_1R_\lambda W_2=j \, W_1\bigl (R_\lambda [H_0,\zeta _\alpha ]\bigr )^jR_\lambda W_2,\qquad \text {for any}\quad j\in {\mathbb N}.\end{aligned}$$

Similarly, we derive the equality

$$\begin{aligned} W_1^{1+\frac{n}{2}}R_\lambda W_2^{1+\frac{m}{2}}=j \,W_1^{1+\frac{n}{2}}\bigl (R_\lambda [H_0,\zeta _\alpha ]\bigr )^j R_\lambda W_2^{1+\frac{m}{2}},\qquad j\in {\mathbb N},\end{aligned}$$

which will be needed only in the case $j=5$. Observe now that by (2.9), the operator

$$\begin{aligned} K_\lambda :=R_\lambda [H_0,\zeta _\alpha ] R_\lambda \end{aligned}$$

belongs to the Schatten class ${\mathfrak {S}}_\gamma$ for $\gamma > 3/2$ (hence, for $\gamma \geqslant 2$) and

$$\begin{aligned} \Vert K_\lambda \Vert ^\gamma _{{\mathfrak {S}}_\gamma }\leqslant C_0\text {vol} \, \Omega _\alpha \leqslant C(\varepsilon ^2\alpha ^{2/\nu }+1),\qquad \forall \alpha >0. \end{aligned}$$

Indeed,

$$\begin{aligned} K_\lambda =R_\lambda \chi _{\Omega _\alpha }[H_0,\zeta _\alpha ] \chi _{\Omega _\alpha } R_\lambda , \end{aligned}$$

where $\chi _{\Omega _\alpha }$ is the characteristic function of the set $\Omega _\alpha$. Since the partial derivatives of $\zeta _\alpha$ are bounded by $\Vert \zeta '\Vert _{L^\infty }$, the inequality $\Vert [H_0,\zeta _\alpha ]\Vert \leqslant C$ holds for some constant C independent of $\alpha$. Therefore, we can estimate the Schatten norm of $K_\lambda$ using (2.9) as follows

$$\begin{aligned} \Vert K_\lambda \Vert _{\gamma }\leqslant C \Vert R_\lambda \chi _{\Omega _\alpha }\Vert _{2\gamma }^2\leqslant C_0\Vert \chi _{\Omega _\alpha }\Vert ^2_{2\gamma }. \end{aligned}$$

On the other hand, one can show that the norm of the operator

$$\begin{aligned} G_\lambda :=(H_0-\lambda )^2\bigl (R_\lambda [H_0,\zeta _\alpha ]\bigr )^2=(H_0-\lambda )[H_0,\zeta _\alpha ]R_\lambda [H_0,\zeta _\alpha ] \end{aligned}$$

(4.4)

is bounded uniformly in $\alpha$. Indeed, the operator $R_\lambda$ is a continuous mapping from $L^2=L^2({\mathbb R}^3;{\mathbb C}^4)$ to the Sobolev space ${\mathcal {H}}^1={\mathcal {H}}^1({\mathbb R}^3;{\mathbb C}^4)$. Moreover, since the derivatives of $\zeta _\alpha$ are bounded by the $L^\infty$-norms of the derivatives of $\zeta$, the operator of multiplication $[H_0,\zeta _\alpha ]$ can be viewed not only as an operator from $L^2$ to $L^2$ but also as a bounded operator from ${\mathcal {H}}^1$ to ${\mathcal {H}}^1$. The norms of these two different operators $[H_0,\zeta _\alpha ]$ are bounded uniformly in $\alpha$. Therefore, the mapping

$$\begin{aligned}{}[H_0,\zeta _\alpha ]R_\lambda [H_0,\zeta _\alpha ]:\,\, L^2({\mathbb R}^3)\rightarrow {\mathcal {H}}^1({\mathbb R}^3) \end{aligned}$$

is a bounded linear operator whose norm is bounded by a constant independent of $\alpha$. This implies that the norm of the operator (4.4) is bounded uniformly in $\alpha$. Now, since

$$\begin{aligned} B_{1,2}=W_1^{1+\frac{n}{2}}R_\lambda ^2 G_\lambda K_\lambda G_\lambda ^*R_\lambda ^2 W_2^{1+\frac{m}{2}}, \end{aligned}$$

we can obtain the needed estimate of the norm of $B_{1,2}$ in ${\mathfrak {S}}_\varkappa$. For that purpose, we write it as

$$\begin{aligned} B_{1,2}=W_1^{1+\frac{n}{2}}|R_\lambda |^{(n+2)/3}Q_{\lambda } |R_\lambda |^{(m+2)/3} W_2^{1+\frac{m}{2}} \end{aligned}$$

where

$$\begin{aligned}Q_{\lambda } =|H_0-\lambda |^{(n+2)/3}R^2_{\lambda }G_\lambda K_\lambda G_\lambda ^* R^2_{\lambda } |H_0-\lambda |^{(m+2)/3} \end{aligned}$$

belongs to ${\mathfrak {S}}_\gamma$ and $\Vert Q_\lambda \Vert _{{\mathfrak {S}}_\gamma }\leqslant C\Vert K_\lambda \Vert _{{\mathfrak {S}}_\gamma }$.

Obviously,

$$\begin{aligned} \Vert B_{1,2}\Vert _\varkappa \leqslant \Vert W^{1+\frac{n}{2}}|R_\lambda |^{(n+2)/3}\Vert _{\frac{2p}{(2+n)}} \Vert |R_\lambda |^{(m+2)/3} W^{1+\frac{m}{2}} \Vert _{\frac{2p}{(2+m)}}\Vert Q_\lambda \Vert _\gamma \end{aligned}$$

with $\frac{1}{\varkappa }=\frac{3}{p}+\frac{1}{\gamma }$. Therefore, by (2.9),

$$\begin{aligned} \Vert B_{1,2}\Vert _\varkappa \leqslant C \Vert W\Vert _p^{3}(\varepsilon ^{2}\alpha ^{2/\nu }+1)^{1/\gamma } \end{aligned}$$

(4.5)

Observe now that

$$\begin{aligned} \frac{1}{r}+ \frac{1}{\tau }+\frac{1}{\varkappa }=\frac{6}{p}+\frac{1}{\gamma }=\frac{3}{q}. \end{aligned}$$

(4.6)

Combining the relations (4.2)–(4.6), we obtain that

$$\begin{aligned} \Vert X^3_\lambda -\tilde{X}^3_\lambda \Vert _{q/3}\leqslant C \Vert W\Vert _p^{6}(\varepsilon ^{2}\alpha ^{2/\nu }+1)^{1/\gamma }. \end{aligned}$$

$\square$

In fact we proved more: exactly the same arguments can be used to justify the following statement.

Corollary 4.2

Let $p>9/2$, $\gamma \geqslant 2$ and

$$\begin{aligned} q=\frac{3\gamma p}{6\gamma +p}. \end{aligned}$$

Let $W\in L^p({\mathbb R}^d)\cap L^\infty ({\mathbb R}^d)$. Let the operator $T(\alpha )$ be a finite linear combination of products of three factors of the form

$$\begin{aligned} \chi ^-_{j} X_\lambda \chi _{j}^+,\qquad j=1,2,3, \end{aligned}$$

(4.7)

where $\chi ^\pm _{j}$ are characteristic functions of some subsets of ${\mathbb R}^3$ (that may depend on $\alpha$). Assume that, at least for one of the three factors (4.7) in each product, the supports of $\chi ^-_{j}$ and $\chi ^+_{j}$ are separated from each other by a spherical layer of the form

$$\begin{aligned} \{x\in {\mathbb R}^3:\,\,\, \varepsilon \alpha ^{1/\nu }+a\leqslant |x|\leqslant \varepsilon \alpha ^{1/\nu }+b\},\qquad \text {with}\quad a<b. \end{aligned}$$

(4.8)

Then, there is an $\alpha _0>0$ such that

$$\begin{aligned} \Vert T(\alpha )\Vert _{q/3}\leqslant C \Vert W\Vert _p^{6}(\varepsilon ^{2}\alpha ^{2/\nu }+1)^{1/\gamma },\qquad \text {for}\quad \alpha >\alpha _0, \end{aligned}$$

with a constant $C>0$ independent of $\alpha$ and W.

Proof

Let

$$\begin{aligned} T_0(\alpha )=\Bigl (\chi ^-_{1} X_\lambda \chi _{1}^+\Bigr )\Bigl (\chi ^-_{2} X_\lambda \chi _{2}^+\Bigr )\Bigl (\chi ^-_{3} X_\lambda \chi _{3}^+\Bigr ) \end{aligned}$$

where the supports of $\chi ^-_{j}$ and $\chi ^+_{j}$ are separated from each other by a spherical layer of the form (4.8) at least for one of the indices j.

Repeating the arguments that lead to the estimate (4.2), we obtain

$$\begin{aligned} \Vert \Bigl (\chi ^-_{1} X_\lambda \chi _{1}^+\Bigr )\Bigl (\chi ^-_{2} X_\lambda \chi _{2}^+\Bigr ) W^{-1} \Vert _{p/3}\leqslant C \Vert W\Vert _p^{3} \end{aligned}$$

(4.9)

and

$$\begin{aligned} \Vert \Bigl (\chi ^-_{1} X_\lambda \chi _{1}^+\Bigr )W^{-1/2} \Vert _{2p/3} \leqslant C \Vert W\Vert _p^{3/2} \end{aligned}$$

(4.10)

Similarly, we obtain that

$$\begin{aligned} \Vert W^{-1} \Bigl (\chi ^-_{2} X_\lambda \chi _{2}^+\Bigr )\Bigl (\chi ^-_{3} X_\lambda \chi _{3}^+\Bigr ) \Vert _{p/3}\leqslant C \Vert W\Vert _p^{3} \end{aligned}$$

(4.11)

and

$$\begin{aligned} \Vert W^{-1/2} \Bigl (\chi ^-_{3} X_\lambda \chi _{3}^+\Bigr ) \Vert _{2p/3} \leqslant C \Vert W\Vert _p^{3/2} \end{aligned}$$

(4.12)

Negative powers of W in (4.9)–(4.12) are always multiplied by W. Therefore, the resulting products are bounded operators.

It remains to estimate the Schatten norms of the operators

$$\begin{aligned} B_{j,n,m}:=\chi ^-_{j} W^{1+\frac{n}{2}}R_\lambda W^{1+\frac{m}{2}}\chi ^+_{j},\qquad n+m=2, \end{aligned}$$

in the case that the supports of $\chi ^-_{j}$ and $\chi ^+_{j}$ are separated from each other by a spherical layer of the form (4.8). The norms that are needed are the norms in the class ${\mathfrak {S}}_\varkappa$ with $\frac{1}{\varkappa }=\frac{3}{p}+\frac{1}{\gamma }$.

Let $\tilde{\zeta }$ be a smooth function on the real line $\mathbb R$ such that

$$\begin{aligned} \tilde{\zeta }(t)={\left\{ \begin{array}{ll} 1\qquad \text {for} \quad t\leqslant a;\\ 0\qquad \text {for}\quad t\geqslant b. \end{array}\right. } \end{aligned}$$

Define $\tilde{\zeta }_\alpha$ on ${\mathbb R}^3$ by

$$\begin{aligned} \tilde{\zeta }_\alpha (x)=\tilde{\zeta }(|x|-\varepsilon \alpha ^{1/\nu }). \end{aligned}$$

To be clearly defined, assume that $\tilde{\zeta }_\alpha \chi _j^-=\chi _j^-$ and $\tilde{\zeta }_\alpha \chi _j^+=0$. Then

$$\begin{aligned} \chi _j^-W^{1+\frac{n}{2}}R_\lambda W^{1+\frac{m}{2}}\chi _j^+=5\chi _j^-\,W^{1+\frac{n}{2}}\bigl (R_\lambda [H_0,\tilde{\zeta }_\alpha ]\bigr )^5 R_\lambda W^{1+\frac{m}{2}}\chi _j^+.\end{aligned}$$

Repeating the arguments that lead to the estimate (4.5) word by word, we obtain

$$\begin{aligned} \Vert B_{j,n,m}\Vert _\varkappa \leqslant C \Vert W\Vert _p^{3}(\varepsilon ^{2}\alpha ^{2/\nu }+1)^{1/\gamma } \end{aligned}$$

(4.13)

Observe now that

$$\begin{aligned} \frac{3}{p}+\frac{1}{\varkappa }=\frac{3}{q}. \end{aligned}$$

(4.14)

Combining the relations (4.9)–(4.14), we obtain that

$$\begin{aligned} \Vert T_0(\alpha )\Vert _{q/3}\leqslant C \Vert W\Vert _p^{6}(\varepsilon ^{2}\alpha ^{2/\nu }+1)^{1/\gamma }. \end{aligned}$$

$\square$

As a consequence, we immediately obtain the next result, in which $R_\lambda$ is the same as before, i.e., $R_\lambda =(H_0-\lambda )^{-1}$.

Corollary 4.3

Let $p>9/2$, $\gamma \geqslant 2$ and

$$\begin{aligned} q=\frac{3\gamma p}{6\gamma +p}. \end{aligned}$$

Let $\chi _j$ be the characteristic functions of the sets

$$\begin{aligned} \{x\in {\mathbb R}^3:\,\,\, \varepsilon \alpha ^{1/\nu }-j\leqslant |x|\leqslant \varepsilon \alpha ^{1/\nu }+j\},\qquad j=1,2,3, \end{aligned}$$

and $Y_{\lambda ,\alpha }$ be the operator defined by

$$\begin{aligned} \begin{aligned} Y_{\lambda ,\alpha }&= \chi _3\tilde{X}_\lambda \chi _2\tilde{X}_\lambda \chi _1\Bigl (W_1R_\lambda W_2+W_2R_\lambda W_1\Bigr ) \chi _1+ \chi _2\tilde{X}_\lambda \chi _1\Bigl (W_1R_\lambda W_2\\&\quad +W_2R_\lambda W_1\Bigr ) \chi _1 X_\lambda \chi _2+ \chi _1 \Bigl (W_1R_\lambda W_2+W_2R_\lambda W_1\Bigr ) \chi _1X_\lambda \chi _2X_\lambda \chi _3. \end{aligned} \end{aligned}$$

(4.15)

Then, there is an $\alpha _0>0$ such that

$$\begin{aligned} \Vert X^3_\lambda -\tilde{X}_\lambda ^3-Y_{\lambda ,\alpha }\Vert _{q/3}\leqslant C \Vert W\Vert _p^{6}(\varepsilon ^{2}\alpha ^{2/\nu }+1)^{1/\gamma },\qquad \text {for}\quad \alpha >\alpha _0, \end{aligned}$$

with a constant $C>0$ independent of $\alpha$ and W.

Proof

One only needs to realize that the operator $T(\alpha ):=X^3_\lambda -\tilde{X}_\lambda ^3-Y_{\lambda ,\alpha }$ satisfies conditions of Corollary 4.2.$\square$

On the other hand, applying Cwikel’s inequality, one can easily show that

$$\begin{aligned} \Vert Y_{\lambda ,\alpha }\Vert _{\Sigma _1}\leqslant C \int _{{\mathbb R}^3} \chi _3(x) V^3(x) \textrm{d}x\leqslant C_\varepsilon \alpha ^{2/\nu -3}\qquad \text {for}\quad \alpha >\alpha _0. \end{aligned}$$

(4.16)

Indeed, $Y_{\lambda ,\alpha }$ is a finite linear combination of products of three factors of the form $\chi _A X_\lambda \chi _B$, where $\chi _A$ and $\chi _B$ are the characteristic functions of sets contained in the support of $\chi _3$. Therefore,

$$\begin{aligned} \Vert \chi _A X_\lambda \chi _B\Vert _{\Sigma _3}\leqslant \Vert \chi _3W |R_\lambda |^{1/2}\Vert ^2_{\Sigma _6} \leqslant C \Vert \chi _3 W\Vert ^2_{L^6}=C \Bigl (\int _{{\mathbb R}^3} \chi _3(x) V^3(x) \textrm{d}x\Bigr )^{1/3}, \end{aligned}$$

which implies (4.16).

Now we rewrite (4.16) as

$$\begin{aligned} s_k\bigl (Y_{\lambda ,\alpha }\bigr )\leqslant C_\varepsilon \alpha ^{2/\nu -3} k^{-1}\qquad \text {for}\quad \alpha >\alpha _0. \end{aligned}$$

Consequently, for any positive constant $c>0$,

$$\begin{aligned} \sum _1^{[c\alpha ^3]+1}s^{q/3}_k\bigl (Y_{\lambda ,\alpha }\bigr )\leqslant C_\varepsilon \alpha ^{2/\nu -q},\qquad \text {for}\quad \alpha >\alpha _0, \end{aligned}$$

(4.17)

where $[c\alpha ^3]$ denotes the integer part of $c\alpha ^3$.

Corollary 4.4

Let $\frac{9}{4}<q<\frac{3}{\nu }$ where $\nu >1$. Assume that conditions of Theorem 1.1 are satisfied. Then,

$$\begin{aligned} \int _{\alpha ^{-1}}^\infty \Bigl (n_+(t, X_\lambda ) -n_+(t, \tilde{X}_\lambda )\Bigr )t^{q-1}\textrm{d}t=o(\alpha ^{3/\nu -q}),\qquad \text {as}\quad \alpha \rightarrow \infty . \end{aligned}$$

Proof

Choose $\gamma >\frac{q}{3-\nu q}$ and define p by

$$\begin{aligned} \frac{6}{p}=\frac{3}{q}-\frac{1}{\gamma }. \end{aligned}$$

Then, $p>6/\nu .$ Therefore, $W\in L^p({\mathbb R}^3)$. Using Rotfeld’s inequality, we obtain

$$\begin{aligned} \sum _1^{[c\alpha ^3]+1}s^{q/3}_k\bigl (X_\lambda ^3-\tilde{X}_\lambda ^3\bigr )\leqslant \sum _1^{[c\alpha ^3]+1}s^{q/3}_k\bigl (Y_{\lambda ,\alpha }\bigr )+\Vert X^3_\lambda -\tilde{X}_\lambda ^3-Y_{\lambda ,\alpha }\Vert _{q/3}^{q/3}. \nonumber \\ \end{aligned}$$

(4.18)

The inequality (4.18) estimates the last term on the right hand side of (4.1). It remains to apply Corollary 4.3 and the relation (4.17). $\square$

5 Other Consequences

The preceding discussion of the splitting principle involves a decomposition of the space ${\mathbb R}^3$ into two domains. It is easy to see that the same arguments work for all piecewise smooth domains obtained similarly by scaling by a factor of $\alpha ^{1/\nu }$. In particular, one of the domains that we have already considered can be decomposed further into smaller sets. Namely, let $Q_j$ be bounded disjoint cubes contained in the region $\{x\in {\mathbb R}^3:\,\,|x|\geqslant \varepsilon \}$, $1\leqslant j\leqslant n-1$. Let $\{\phi _{j,\alpha }\}_{j=1}^{n-1}$ be the characteristic functions of the cubes $\alpha ^{1/\nu }Q_j$. Define $\phi _{n,\alpha }$ to be the characteristic function of the complement

$$\begin{aligned} \{x\in {\mathbb R}^3:\,\,|x|\geqslant \varepsilon \alpha ^{1/\nu }\}\setminus \cup _{j=1}^{n-1} \alpha ^{1/\nu }Q_j. \end{aligned}$$

Theorem 5.1

Let $\frac{9}{4}<q<\frac{3}{\nu }$ where $\nu >1$. Assume that conditions of Theorem 1.1 are satisfied. Then

$$\begin{aligned}{} & {} \int _{\alpha ^{-1}}^\infty \Bigl (n_+\bigl (t, W_2(H_0-\lambda )^{-1}W_2\bigr ) -\sum _{j=1}^n n_+\bigl (t, \phi _{j,\alpha }W(H_0-\lambda )^{-1}W\phi _{j,\alpha }\bigr )\Bigr )t^{q-1}\textrm{d}t\\{} & {} \quad =o(\alpha ^{3/\nu -q}),\end{aligned}$$

as $\alpha \rightarrow \infty$.

To prove Theorem 5.1, it is enough to repeat the steps that were needed to prove Corollary 4.4.

Clearly, to obtain an asymptotic formula for $\int _{\alpha ^{-1}}^\infty n_+\bigl (t, W_2(H_0-\lambda )^{-1}W_2\bigr ) t^{q-1}\textrm{d}t$ one has to obtain an asymptotic formula for $\int _{\alpha ^{-1}}^\infty n_+\bigl (t, \phi _{j,\alpha }W(H_0-\lambda )^{-1}W\phi _{j,\alpha }\bigr )t^{q-1}\textrm{d}t$ for each j. The latter integral can be written as

$$\begin{aligned}{} & {} \int _{\alpha ^{-1}}^\infty n_+\bigl (t, \phi _{j,\alpha }W(H_0-\lambda )^{-1}W\phi _{j,\alpha }\bigr )t^{q-1}\textrm{d}t\\{} & {} \quad =\alpha ^{-q}\int _{1}^\infty n_+\Bigl (\frac{\tau }{\alpha }, \phi _{j,\alpha }W(H_0-\lambda )^{-1}W\phi _{j,\alpha }\Bigr )\tau ^{q-1}\textrm{d}\tau \end{aligned}$$

Observe now that, if

$$\begin{aligned} V(x)=\frac{\Phi (\theta )}{|x|^\nu },\qquad \text {for}\quad |x|>1, \end{aligned}$$

then the maximum and minimum values of $\alpha \, V$ on the cubes $\alpha ^{1/\nu } Q_j$ do not depend on $\alpha$:

$$\begin{aligned} m_j\leqslant \alpha \, V(x)\leqslant M_j,\qquad \text {for all}\quad \alpha >\varepsilon ^{-\nu }\quad \text {and all}\quad x\in \alpha ^{1/\nu }Q_j. \end{aligned}$$

The potential $\alpha V$ can be squeezed between the constant functions $m_j \phi _{j,\alpha }$ and $M_j \phi _{j,\alpha }$ on each cube $\alpha ^{1/\nu } Q_j$.

So, due to the monotonicity of the counting function $n_+$,

$$\begin{aligned}{} & {} n_+\left( \frac{\tau }{m_j},\phi _{j,\alpha }(H_0-\lambda )^{-1}\phi _{j,\alpha }\right) \leqslant n_+\left( \frac{\tau }{\alpha },\phi _{j,\alpha }W(H_0-\lambda )^{-1}W\phi _{j,\alpha }\right) \\{} & {} \quad \leqslant n_+\left( \frac{\tau }{M_j},\phi _{j,\alpha }(H_0-\lambda )^{-1}\phi _{j,\alpha }\right) , \end{aligned}$$

for any $\tau >0$.

Consequently, it remains to obtain an asymptotic formula for the quantity

$$\begin{aligned} n_+\bigl (t, \phi _{j,\alpha }(H_0-\lambda )^{-1}\phi _{j,\alpha }\bigr )\quad \text {as}\quad \alpha \rightarrow \infty \end{aligned}$$

for any fixed $t>0$. We are going to prove the following result.

Proposition 5.2

For any fixed $t>0$,

$$\begin{aligned}{} & {} n_+\bigl (t, \phi _{j,\alpha }(H_0-\lambda )^{-1}\phi _{j,\alpha }\bigr )\\{} & {} \quad \sim 3^{-1}\pi ^{-2}\alpha ^{3/\nu }\Bigl ((t^{-1}+\lambda )_+^2-1\Bigr )_+^{3/2} \textrm{vol }\, Q_j \quad \text {as}\quad \alpha \rightarrow \infty . \end{aligned}$$

Proof

Note that

$$\begin{aligned} \frac{4}{3}\pi \Bigl ((t^{-1}+\lambda )_+^2-1\Bigr )_+^{3/2}=\textrm{vol}\,\left\{ \xi \in {\mathbb R}^3:\,\,\,\,\, \bigl (\sqrt{|\xi |^2+1}-\lambda \bigr )^{-1}>t\right\} . \end{aligned}$$

Taking into account the fact that $\pm \sqrt{|\xi |^2+1}$ are eigenvalues of the symbol

$$\begin{aligned}A(\xi ):=\sum _1^3 \gamma _j \xi _j +\gamma _0\end{aligned}$$

of the operator $H_0$, we conclude that we need to prove that

$$\begin{aligned} \textrm{tr}\, \Psi \bigl (\phi _{j,\alpha }(H_0-\lambda )^{-1}\phi _{j,\alpha }\bigr )\sim \textrm{tr}\,\Bigl [\phi _{j,\alpha }\Psi \bigl ((H_0-\lambda )^{-1}\bigr )\phi _{j,\alpha }\Bigr ] \quad \text {as}\quad \alpha \rightarrow \infty , \nonumber \\ \end{aligned}$$

(5.1)

for $\Psi$ being the characteristic function of the interval $(t,\infty )$. Since such a function $\Psi$ can be squeezed between two different functions of the form

$$\begin{aligned}\Psi _\epsilon (s)= {\left\{ \begin{array}{ll} 0, \qquad \text {if}\quad s<\tau \\ (s-\tau )/\epsilon , \qquad \text {if}\quad \tau \leqslant s\leqslant \tau +\epsilon \\ 1, \qquad \text {if}\quad s>\tau +\epsilon , \end{array}\right. }\end{aligned}$$

and the quantity

$$\begin{aligned} \Bigl ((t^{-1}+\lambda )_+^2-1\Bigr )_+^{3/2} \end{aligned}$$

depends on t continuously, we only need to prove (5.1) for $\Psi$ that are continuous and vanishing near zero.

Any such function $\Psi$ can be written as

$$\begin{aligned} \Psi (s)=s^{5}\eta (s), \end{aligned}$$

where $\eta$ is a continuous function on the real line ${\mathbb R}$. Notice that, in this case,

$$\begin{aligned} \Bigl |\textrm{tr}\, \Psi \bigl (\phi _{j,\alpha }(H_0-\lambda )^{-1}\phi _{j,\alpha }\bigr )\Bigr |\leqslant \Vert \phi _{j,\alpha }(H_0-\lambda )^{-1}\phi _{j,\alpha }\Vert _{{\mathfrak {S}}_5}^5 \Vert \eta \Vert _\infty \leqslant C\alpha ^{3/\nu }\Vert \eta \Vert _\infty . \end{aligned}$$

Moreover, since $\Psi ((H_0-\lambda )^{-1})=(H_0-\lambda )^{-2}\eta (R_\lambda )(H_0-\lambda )^{-3}$,

$$\begin{aligned} \Bigl |\textrm{tr}\, \phi _{j,\alpha }\Psi \bigl ((H_0-\lambda )^{-1}\bigr )\phi _{j,\alpha }\Bigr |&\leqslant \Vert \phi _{j,\alpha }(H_0-\lambda )^{-2}\Vert _{{\mathfrak {S}}_{5/2}} \Vert (H_0-\lambda )^{-3}\phi _{j,\alpha }\Vert _{{\mathfrak {S}}_{5/3}} \Vert \eta \Vert _\infty \\&\leqslant C\alpha ^{3/\nu }\Vert \eta \Vert _\infty . \end{aligned}$$

Thus, both sides of (5.1) can be estimated by $C\alpha ^{3/\nu }\Vert \eta \Vert _\infty$. Note now that functions of a given self-adjoint operator only need to be defined on the spectrum of the operator. On the other hand, the spectrum of $(H_0-\lambda )^{-1}$ is contained in $[-L,L]$, where $L=1/(1-|\lambda |)$. Therefore, the functional $\Vert \eta \Vert _\infty$ in the last inequality is the $L^\infty$-norm of the function on the interval $[-L,L]$. Since on a finite interval, $\eta$ can be uniformly approximated by polynomials, it is enough to prove (5.1) under the assumption that $\eta$ is a polynomial. Put differently, it is enough to prove (5.1) for

$$\begin{aligned} \Psi (s)=s^{k},\qquad k\geqslant 5, \end{aligned}$$

because polynomials are finite linear combinations of power functions.

Denote $R_\lambda =(H_0-\lambda )^{-1}$, $\chi _+=\phi _{j,\alpha }$ and $\chi _-=1-\phi _{j,\alpha }.$ We are going to prove that

$$\begin{aligned} \Vert (\chi _+R_\lambda \chi _+)^k-\chi _+R_\lambda ^k\chi _+\Vert _{{\mathfrak {S}}_1}=o(\alpha ^{3/\nu }),\qquad \text { as} \quad \alpha \rightarrow \infty . \end{aligned}$$

(5.2)

For that purpose, we write $\chi _+R_\lambda ^k\chi _+$ as

$$\begin{aligned} \chi _+R_\lambda ^k\chi _+=(\chi _+R_\lambda \chi _+)^k+\sum _{j=0}^{k-1} (\chi _+R_\lambda \chi _+)^j\chi _+R_\lambda \chi _-R_\lambda ^{k-j-1}\chi _+. \end{aligned}$$

(5.3)

While the norm of the operator $\chi _+R_\lambda \chi _-$ does not tend to zero, it is still representable in the form

$$\begin{aligned}{} & {} \chi _+R_\lambda \chi _-= T_1+T_2,\qquad \text {where}\qquad \Vert T_1\Vert \rightarrow 0, \quad \text {and}\quad \Vert T_2\Vert _{{\mathfrak {S}}_{k}}=o(\alpha ^{3/(k\nu )}),\\{} & {} \text {as}\quad \alpha \rightarrow \infty . \end{aligned}$$

To see that, we define $T_2$ to be the operator

$$\begin{aligned} T_2=\Theta \chi _+R_\lambda \chi _-\Theta , \end{aligned}$$

where $\Theta$ is the operator of multiplication by the characteristic function of the layer

$$\begin{aligned} \left\{ x\in {\mathbb R}^3:\quad \textrm{dist}(x,\alpha ^{1/\nu } \partial Q_j)<\alpha ^{1/(2\nu )}\right\} . \end{aligned}$$

(5.4)

Then, the volume of the support of the function $\Theta$ does not exceed $C\alpha ^{5/(2\nu )}$ at least for large values of $\alpha$. Therefore,

$$\begin{aligned} \Vert T_2\Vert _{{\mathfrak {S}}_{k}}\leqslant C\alpha ^{5/(2k \nu )}=o(\alpha ^{3/(k\nu )}),\quad \text {as}\quad \alpha \rightarrow \infty . \end{aligned}$$

On the other hand, since the explicit expression for the integral kernel of $(H_0-\lambda )^{-1}$ shows that the latter decays exponentially fast as $|x-y|\rightarrow \infty$, we have the following estimate for the integral kernel k(x, y) of the operator $T_1$:

$$\begin{aligned} |k(x,y)|\leqslant C \bigl ((1-\Theta (x))+(1-\Theta (y))\bigr )e^{-c|x-y|}\chi _+(x)\chi _-(y). \end{aligned}$$

(5.5)

This implies that $\Vert T_1\Vert \rightarrow 0$ as $\alpha \rightarrow \infty$, because x and y for which $k(x,y)\ne 0$ are distance $\alpha ^{1/(2\nu )}$ apart from each other, while

$$\begin{aligned} \Vert T_1\Vert \leqslant \Bigl (\sup _x \int |k(x,y)|\textrm{d}y\times \sup _y \int | k(x,y)|\textrm{d}x\Bigr )^{1/2}. \end{aligned}$$

Thus, we have the following estimate

$$\begin{aligned} \begin{aligned}&\Vert (\chi _+R_\lambda \chi _+)^j\chi _+R_\lambda \chi _-R_\lambda ^{k-j-1}\chi _+\Vert _{{\mathfrak {S}}_1}\leqslant \Vert (\chi _+R_\lambda \chi _+)^jT_1R_\lambda ^{k-j-1}\chi _+\Vert _{{\mathfrak {S}}_1}\\&\quad +\Vert (\chi _+R_\lambda \chi _+)^jT_2R_\lambda ^{k-j-1}\chi _+\Vert _{{\mathfrak {S}}_1} \leqslant \Vert \chi _+R_\lambda \chi _+\Vert ^j_{{\mathfrak {S}}_{k-1}} \Vert T_1\Vert \Vert R_\lambda ^{k-j-1}\chi _+\Vert _{{\mathfrak {S}}_{(k-1)/(k-j-1)}}\\&\quad +\Vert \chi _+R_\lambda \chi _+\Vert ^j_{{\mathfrak {S}}_{k}} \Vert T_2\Vert _{{\mathfrak {S}}_{k}}\Vert R_\lambda ^{k-j-1}\chi _+\Vert _{{\mathfrak {S}}_{k/(k-j-1)}} =o(\alpha ^{3/\nu }),\qquad \text {as}\qquad \alpha \rightarrow \infty . \end{aligned} \end{aligned}$$

Combining this relation with (5.3), we obtain (5.2). $\square$

As a consequence, we obtain

Proposition 5.3

For any constant $M\geqslant 0$, we have

$$\begin{aligned} \begin{aligned} \lim _{\alpha \rightarrow \infty } \alpha ^{-3/\nu +q} \int _{\alpha ^{-1}}^\infty n_+\bigl (\alpha t, M \phi _{j,\alpha }(H_0-\lambda )^{-1}\phi _{j,\alpha }\bigr )t^{q-1}\textrm{d}t\\ =3^{-1}\pi ^{-2}\textrm{vol }\, Q_j \int _1^\infty \Bigl ((t^{-1}M+\lambda )_+^2-1\Bigr )^{3/2}_+ t^{q-1}\textrm{d}t \end{aligned} \end{aligned}$$

(5.6)

Proof

Changing the variables $\alpha t\rightarrow t$, we obtain

$$\begin{aligned} \begin{aligned} \lim _{\alpha \rightarrow \infty } \alpha ^{-3/\nu +q} \int _{\alpha ^{-1}}^\infty n_+\bigl (\alpha t, M \phi _{j,\alpha }(H_0-\lambda )^{-1}\phi _{j,\alpha }\bigr )t^{q-1}\textrm{d}t\\ =\lim _{\alpha \rightarrow \infty } \alpha ^{-3/\nu } \int _{1}^\infty n_+\bigl (t, M \phi _{j,\alpha }(H_0-\lambda )^{-1}\phi _{j,\alpha }\bigr )t^{q-1}\textrm{d}t \end{aligned} \end{aligned}$$

(5.7)

The integrand on the right hand side can be estimated according to Cwikel’s inequality:

$$\begin{aligned} n_+(t,M \phi _{j,\alpha }(H_0-\lambda )^{-1}\phi _{j,\alpha })\leqslant C t^{-3} \int _{{\mathbb R}^3} \phi _{j,\alpha }^6(x) \textrm{d}x\leqslant C \alpha ^{3/\nu }t^{-3} \textrm{vol}\, Q_j. \end{aligned}$$

Consequently, the limit on the right hand side of (5.7) can be computed by the Lebesgue dominated convergence theorem. The relation (5.6) follows now from Proposition 5.2. $\square$

To state the next result, we need to introduce the notation

$$\begin{aligned} {\mathfrak {T}}(M, \lambda )=3^{-1}\pi ^{-2}\int _1^\infty \Bigl ((t^{-1}M+\lambda )_+^2-1\Bigr )^{3/2}_+ t^{q-1}\textrm{d}t \end{aligned}$$

Theorem 5.4

Assume that

$$\begin{aligned} V(x)=\frac{\Phi (\theta )}{|x|^{\nu }},\qquad \text {for}\qquad |x|>1, \end{aligned}$$

(5.8)

where $\Phi$ is a continuous function on the unit sphere. Then

$$\begin{aligned}{} & {} \lim _{\alpha \rightarrow \infty }\alpha ^{-3/\nu +q} \int _{\alpha ^{-1}}^\infty n_+\bigl (t, W_2(H_0-\lambda )^{-1}W_2\bigr )t^{q-1}\textrm{d}t\nonumber \\{} & {} \quad =\int _{|x|>\varepsilon } {\mathfrak {T}}\bigl (\Phi (\theta )|x|^{-\nu }, \lambda \bigr ) \, \textrm{d}x. \end{aligned}$$

(5.9)

Proof

Let $m_j$ and $M_j$ be the maximum and the minimum values of V on the cube $Q_j$. Then, according to Proposition 5.3, we have

$$\begin{aligned}{} & {} 3^{-1}\pi ^{-2}\textrm{vol }\, Q_j \int _1^\infty \Bigl ((t^{-1}m_j+\lambda )_+^2-1\Bigr )^{3/2}_+ t^{q-1}\textrm{d}t\nonumber \\{} & {} \quad \leqslant \lim _{\alpha \rightarrow \infty } \alpha ^{-3/\nu +q} \int _{\alpha ^{-1}}^\infty n_+\bigl (t, \phi _{j,\alpha }W(H_0-\lambda )^{-1}W\phi _{j,\alpha }\bigr )t^{q-1}\textrm{d}t\nonumber \\{} & {} \quad \leqslant 3^{-1}\pi ^{-2}\textrm{vol }\, Q_j \int _1^\infty \Bigl ((t^{-1}M_j+\lambda )_+^2-1\Bigr )^{3/2}_+ t^{q-1}\textrm{d}t, \end{aligned}$$

(5.10)

by the monotonicity of the counting function $n_+$. Taking the sum over j on the three sides of (5.10) and using Theorem 5.1, we obtain that

$$\begin{aligned} \begin{aligned} \sum _{j=1}^n{\mathfrak {T}}(m_j, \lambda ) \textrm{vol }\, Q_j&\leqslant \lim _{\alpha \rightarrow \infty } \alpha ^{-3/\nu +q} \int _{\alpha ^{-1}}^\infty n_+\bigl (t, W_2(H_0-\lambda )^{-1}W_2\bigr )t^{q-1}\textrm{d}t\\&\leqslant \sum _{j=1}^n{\mathfrak {T}}(M_j, \lambda ) \textrm{vol }\, Q_j, \end{aligned} \end{aligned}$$

It remains to realize that the left and the right hand sides are the Riemann sums of the integral on the right hand side of (5.9). $\square$

Obviously, the condition (5.8) of the theorem can be replaced by the assumption that

$$\begin{aligned} V(x)=\frac{\Phi (\theta )}{|x|^\nu }\Bigl (1+o(1)\Bigr ),\qquad \text {as}\qquad |x|\rightarrow \infty , \end{aligned}$$

(5.11)

uniformly in $\theta =x/|x|$.

Theorem 5.5

Let $V\geqslant 0$ be a bounded real-valued potential such that (5.11) holds uniformly in $\theta$ for some continuous function $\Phi$ defined on the unit sphere. Let $9/4<q<3/\nu$ and $\nu >1$. Then,

$$\begin{aligned}{} & {} \lim _{\alpha \rightarrow \infty }\alpha ^{-3/\nu +q}\int _{\alpha ^{-1}}^\infty n_+(t,W_2(H_0-\lambda )^{-1}W_2)t^{q-1}\textrm{d}t\nonumber \\{} & {} \quad =3^{-1}\pi ^{-2}\int _1^\infty \Bigl (\int _{|x|>\varepsilon }\Bigl ((t^{-1}\Phi (\theta )|x|^{-\nu }+\lambda )_+^2-1\Bigr )^{3/2}_+ \textrm{d}x\Bigr )t^{q-1}\textrm{d}t.\nonumber \\ \end{aligned}$$

(5.12)

6 The End of the Proof

Proposition 6.1

Let $V\geqslant 0$ be a bounded real-valued potential such that (5.11) holds uniformly in $\theta$ for some continuous function $\Phi$ defined on the unit sphere. Let $9/4<q<3/\nu$ and $\nu >1$. Let also $-1<\lambda<\mu <1$. Then, It is enough to appl

$$\begin{aligned}{} & {} \limsup _{\alpha \rightarrow \infty }\alpha ^{-3/\nu +q}\int _{\alpha ^{-1}}^\infty \Bigl ( n_+(t,W_1(H_0-\mu )^{-1}W_1)\nonumber \\{} & {} \qquad - n_+(t,W_1(H_0-\lambda )^{-1}W_1)\Bigr )t^{q-1}\textrm{d}t\nonumber \\{} & {} \quad \leqslant \frac{4\pi \varepsilon ^{3-\nu q}}{3-\nu q}\Vert \Phi \Vert _{\infty }.\qquad \qquad \,\,\,\,\,\,\,\,\qquad \qquad \end{aligned}$$

(6.1)

Proof

It is enough to apply the estimate established in Theorem 1.2 with V replaced by the potential $V_1$. $\square$

Corollary 6.2

Let $V\geqslant 0$ be a bounded real-valued potential such that (5.11) holds uniformly in $\theta$ for some continuous function $\Phi$ defined on the unit sphere. Let $9/4<q<3/\nu$ and $\nu >1$. Let also $-1<\lambda<\mu <1$. Then,

$$\begin{aligned}{} & {} 3^{-1}\pi ^{-2}\int _1^\infty \Bigl (\int _{|x|>\varepsilon }\bigl (((t^{-1}\Phi (\theta )|x|^{-\nu }+\mu )_+^2-1)^{3/2}_+ \nonumber \\{} & {} \qquad -\bigl ((t^{-1}\Phi (\theta )|x|^{-\nu }+\lambda )_+^2-1\bigr )^{3/2}_+ \bigr ) \textrm{d}x\Bigr ) t^{q-1}\textrm{d}t \nonumber \\{} & {} \quad \leqslant \liminf _{\alpha \rightarrow \infty }\alpha ^{-3/\nu +q}\int _{\alpha ^{-1}}^\infty \Bigl ( n_+(t,\tilde{X}_\mu )- n_+(t,\tilde{X}_\lambda )\Bigr )t^{q-1}\textrm{d}t, \end{aligned}$$

(6.2)

while

$$\begin{aligned}{} & {} \limsup _{\alpha \rightarrow \infty }\alpha ^{-3/\nu +q}\int _{\alpha ^{-1}}^\infty \Bigl ( n_+(t,\tilde{X}_\mu )- n_+(t,\tilde{X}_\lambda )\Bigr )t^{q-1}\textrm{d}t \nonumber \\{} & {} \quad \leqslant \frac{4\pi \varepsilon ^{3-\nu q}}{3-\nu q}\Vert \Phi \Vert _{\infty }+3^{-1}\pi ^{-2}\int _1^\infty \Bigl (\int _{|x|>\varepsilon }\bigl (((t^{-1}\Phi (\theta )|x|^{-\nu }+\mu )_+^2-1)^{3/2}_+ \nonumber \\{} & {} \qquad -\bigl ((t^{-1}\Phi (\theta )|x|^{-\nu }+\lambda )_+^2-1\bigr )^{3/2}_+ \bigr ) \textrm{d}x\Bigr ) t^{q-1}\textrm{d}t. \end{aligned}$$

(6.3)

Theorem 6.3

Let $V\geqslant 0$ be a bounded real-valued potential such that (5.11) holds uniformly in $\theta$ for some continuous function $\Phi$ defined on the unit sphere. Let $9/4<q<3/\nu$ and $\nu >1$. Let also $-1<\lambda<\mu <1$. Then,

$$\begin{aligned}{} & {} \lim _{\alpha \rightarrow \infty }\alpha ^{-3/\nu +q}\int _{\alpha ^{-1}}^\infty \Bigl ( n_+(t, X_\mu )- n_+(t,X_\lambda )\Bigr )t^{q-1}\textrm{d}t\nonumber \\{} & {} \quad =3^{-1}\pi ^{-2}\int _1^\infty \Bigl (\int _{{\mathbb R}^3}\Bigl [\Bigl ((t^{-1}\Phi (\theta )|x|^{-\nu }+\mu )_+^2-1\Bigr )^{3/2}_+\nonumber \\{} & {} \qquad -\Bigl ((t^{-1}\Phi (\theta )|x|^{-\nu }+\lambda )_+^2-1\Bigr )^{3/2}_+ \Bigr ]\textrm{d}x\Bigr )t^{q-1}\textrm{d}t. \end{aligned}$$

(6.4)

Proof

According to Corollary 4.4, $\tilde{X}_\lambda$ and $\tilde{X}_\mu$ in (6.2) and (6.3) can be replaced by the operators$X_\lambda$ and $X_\mu$. After this replacement, we can pass to the limit as $\varepsilon \rightarrow 0$. $\square$

Theorem 1.1 is now a consequence of Theorem 6.3.