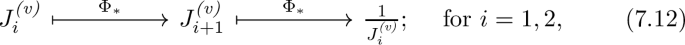Growth and Integrability of Some Birational Maps in Dimension Three

Abstract

Motivated by the study of the Kahan–Hirota–Kimura discretisation of the Euler top, we characterise the growth and integrability properties of a collection of elements in the Cremona group of a complex projective 3-space using techniques from algebraic geometry. This collection consists of maps obtained by composing the standard Cremona transformation ${{\,\textrm{c}\,}}_3\in {{\,\textrm{Bir}\,}}(\mathbb {P}^3)$ with projectivities that permute the fixed points of ${{\,\textrm{c}\,}}_3$ and the points over which ${{\,\textrm{c}\,}}_3$ performs a divisorial contraction. Specifically, we show that three behaviour are possible: (A) integrable with quadratic degree growth and two invariants, (B) periodic with two-periodic degree sequences and more than two invariants, and (C) non-integrable with submaximal degree growth and one invariant.

1 Introduction

This paper is devoted to the characterisation of the growth and integrability properties of a collection of birational transformations of the complex projective space $\mathbb {P}^3$, i.e. a subset of the so-called Cremona group, denoted by ${{\,\textrm{Bir}\,}}(\mathbb {P}^{3})$ [24, Section 7.4]. Let ${{\,\textrm{c}\,}}_M\in {{\,\textrm{Bir}\,}}(\mathbb {P}^{M})$ be the standard Cremona transformation of $\mathbb {P}^{M}$, i.e. the birational map defined as follows:

Then, this collection is obtained by composing ${{\,\textrm{c}\,}}_3$ with projectivities of finite order $g\in \mathbb {P}{{\,\textrm{Gl}\,}}(3,\mathbb {C})$ acting as permutations on a set of special points for the Cremona transformation. This set, which we will denote by $\mathscr {R}$ (see Definition 4.1), is the union of the set of fixed points and of the points over which ${{\,\textrm{c}\,}}_3$ performs a divisorial contraction. Precisely, the fixed points are the solutions of the (projective) equation ${{\,\textrm{c}\,}}_{3}([x_1:x_2:x_3:x_4])=[x_1:x_2:x_3:x_4]$, while the remaining points are the coordinate points, that is, the images of the coordinate planes of $\mathbb {P}^3$ under ${{\,\textrm{c}\,}}_3$. We call this group of projectivities the Cremona-cubes group, and we will denote it by $\mathscr {C}$ (see Definition 4.2).

The motivation to study the Cremona-cubes group comes from some recent results on the Kahan–Hirota–Kimura discretisation [55, 62] (KHK discretisation). Indeed, as it was noted in [2], the celebrated integrable discretisation of the Euler top [5, 33] produced in [55] via KHK discretisation is expressible as the composition of the standard Cremona map with two projectivities (see Lemma 2.6). We will show in Sect. 2 that, up to birational equivalence, this is the prototypical integrable birational map of the form $g\circ {{\,\textrm{c}\,}}_3$ for g in the Cremona-cubes group. In particular, in Sect. 5 we will explain why this birational map is integrable in the sense of the low growth condition.

Before to clarify what do we mean when we speak about growth properties of a birational map, we need a couple more of definitions.

It is a well-known fact that the iteration of a birational map $\Phi \in {{\,\textrm{Bir}\,}}(\mathbb {P}^{M})$ produces a (birational) discrete dynamical system defined by the recurrence:

$$\begin{aligned} \left[ x_{1}(n):\cdots :x_{M+1}(n) \right] = \Phi ^{n}\left( \left[ x_{1}(0):\cdots :x_{M+1}(0) \right] \right) , \end{aligned}$$

(1.2)

applied on some initial datum $\left[ x_{1}(0):\dots :x_{M+1}(0)\right] \in \mathbb {P}^{M}$ (see [42]). The issue is then to characterise the asymptotic behaviour of the dynamics with respect to generic initial conditions. The problem of characterising the growth of complexity of the iterates was first considered by Arnol’d in [4] for the class of diffeomorphisms. Its analogue for birational maps was first developed experimentally in a series of papers (see [22, 28, 85, 93]), which ended in the elaboration of the concept of the algebraic entropy [10]. Following Arnol’d [4] and Veselov [93], the “good” measure of the complexity of a birational map $\Phi \in {{\,\textrm{Bir}\,}}(\mathbb {P}^{M})$ is the intersection of the iterated images of a straight line with a generic hyperplane in the complex projective space. By the Bezout’s theorem in projective and multi-projective spaces (see [87, §IV.2]), this corresponds to the degree of the polynomials in the entries of $\Phi ^{n}$. Rigorously, we quote the following definition.

Definition 1.1

([10]). Given a birational map $\Phi \in {{\,\textrm{Bir}\,}}(\mathbb {P}^{M})$

$$\begin{aligned} {[}x_1:\cdots :x_{M+1}] \mapsto \left[ P_{1}(x_1,\ldots ,x_{M+1}):\cdots :P_{M+1}(x_1,\ldots ,x_{M+1}) \right] , \end{aligned}$$

(1.3)

such that its (homogeneous) polynomial entries $P_{i}\in \mathbb {C}[x_{1},\ldots ,x_{M+1}]$ are devoid of common factors, that is $\gcd (P_{1},\dots ,P_{M+1})=1$, we define its degree to be:

$$\begin{aligned} d^\Phi = \deg P_{i}, \quad \text { for any }i=1,\ldots , M+1. \end{aligned}$$

(1.4)

In the same way, for all $n\in \mathbb {N}$ we define $d_n^\Phi$ as the degree of the n-th iterate to be

$$\begin{aligned} d^\Phi _{n} = d^{\Phi ^{n}}. \end{aligned}$$

(1.5)

Remark 1.2

We make the following observations.

• (1) The degree of a birational map is invariant under conjugation by projectivities, but, in general, it is not invariant under change of coordinates (see [10, 51]).

• (2) Definition 1.1 is not the usual definition of degree in algebraic geometry. For instance, in [87, Section II.6.3] the degree of a (finite) rational map is defined to be the cardinality of a generic fibre. Nevertheless, all the rational maps in this paper will actually be birational. Hence, no ambiguity is present, and the numbers $d^{\Phi }$ and $d_{n}^{\Phi }$ are uniquely determined by the birational map $\Phi \in {{\,\textrm{Bir}\,}}(\mathbb {P}^{M})$.

• (3) It is crucial in Definition 1.1 to require that the polynomial entries have no common factors. For a given birational map $\Phi \in {{\,\textrm{Bir}\,}}(\mathbb {P}^{M})$, after some iterations common factors can appear and they must be removed. This process has geometric meaning, which we will discuss later in this section.

Having specified the notion of degree of a birational map, we give the definition of algebraic entropy which measures the growth of the complexity of a birational map.

Definition 1.3

([10]). The algebraic entropy of a birational map $\Phi \in {{\,\textrm{Bir}\,}}(\mathbb {P}^{M})$ is the following limit:

$$\begin{aligned} S_{\Phi } = \lim _{n\rightarrow \infty }\frac{1}{n}\log d_{n}^\Phi . \end{aligned}$$

(1.6)

Remark 1.4

([10, 35, 39]). The algebraic entropy has the following properties:

• by the properties of birational maps and the subadditivity of the logarithm, using Fekete’s lemma [29], the algebraic entropy always exists;

• the algebraic entropy is non-negative and bounded from above: $0\le S_\Phi \le \log d^\Phi$;

• the algebraic entropy is invariant with respect to birational conjugation. That is, given two birational maps $\Phi ,\Theta \in {{\,\textrm{Bir}\,}}(\mathbb {P}^{M})$, we have $S_{\Phi } = S_{\Theta ^{-1}\circ \Phi \circ \Theta }$;

• if $d_{n}^\Phi$ is subexponential as $n\rightarrow \infty$, e.g. polynomial, then $S_{\Phi }=0$, while, if $d_{n}^\Phi \sim a^{n}$ for some $a\in \mathbb {R}$, then $S_{\Phi } = \log a$.

Armed with the definition of algebraic entropy and the properties described in Remark 1.4, we can define the integrability according to the algebraic entropy.

Definition 1.5

([10, 50]). A birational map $\Phi \in {{\,\textrm{Bir}\,}}(\mathbb {P}^{M})$ is integrable according to the algebraic entropy if $S_{\Phi } = 0$. If $S_{\Phi }>0$, the map is said to be non-integrable or chaotic. Moreover, if $d_{n}^\Phi \sim n$ as $n\rightarrow \infty$ the map is said to be linearisable. Finally, if $d_{n}^\Phi$ is periodic, the map is said to be periodic.

Remark 1.6

Most of the known integrable maps are such that $d_{n}^{\Phi }\sim n^{2}$ as $n\rightarrow \infty$. From [11], it is known that if the orbits of the system are elliptic curves, then the degree growth is quadratic. From [23], it is known that in $\mathbb {P}^2$ the only sub-exponential behaviour are quadratic, linear, and periodic. The first is associated with the preservation of an elliptic fibration, the second with the preservation of a rational fibration, the latter with a power of the map being isotopic to the identity. In $\mathbb {P}^M$ with $M>2$, it is possible that $d_{n}^{\Phi }\sim n^{k}$ as $n\rightarrow \infty$ with $k>2$. For instance, in [3, 42, 61, 69] maps with cubic growth were presented. However, often maps with cubic growth arise from maps with quadratic growth through a procedure called inflation (see [42, 61, 95]).

Let $\Phi :X\dashrightarrow Y$ be a birational map between smooth projective varieties X, Y. Recall that the singularities, also called indeterminacies, of a birational map consist of the loci where the map is not defined. In the paper, we will denote by ${{\,\textrm{Base}\,}}\Phi$ the indeterminacy locus of the map $\Phi$.

Consider the resolution of indeterminacies of the map $\Phi$ given by the Zariski closure of the graph $Z=\overline{{{\,\textrm{graph}\,}}(\Phi )}\subset X\times Y$, i.e. the following commutative diagram

In this setting, one can define (see [16]) a notion of pullback for birational maps

$$\begin{aligned} \Phi ^*:H^2(Y,\mathbb {Z})\rightarrow H^2(X,\mathbb {Z}), \end{aligned}$$

(1.8)

defined as $\Phi ^*=\left( \pi _X|_{Z}\right) _*\circ \left( \pi _Y|_{Z}\right) ^*$, where the pullback and the pushforward on the right-hand side are the usual inverse and direct images via morphisms (see [16]).

Remark 1.7

As explained in [16], it is possible to perform the actual computation via an auxiliary smooth variety ${\widetilde{Z}}$ instead of the possibly singular closure of the graph Z. This is possible thanks to the celebrated Hironaka’s result on resolution of singularities (see [53, 54]).

The following theorem, whose proof is divided into Sects. 5, 6, and 7, summarises the results of this paper.

Theorem 1.8

Let be the set of coordinate points of $\mathbb {P}^3$. Consider a birational map of the form $\Phi =g\circ {{\,\textrm{c}\,}}_{3}\in {{\,\textrm{Bir}\,}}(\mathbb {P}^{3})$ (or $\Phi ={{\,\textrm{c}\,}}_{3}\circ g$), for some $g\in \mathscr {C}$. Then, there are three possibilities depending on the cardinality of the orbit $\langle g\rangle \cdot \mathscr {E}$ of the points in $\mathscr {E}$, under the action of g. That is:

• If , then the map is integrable in the sense of Definition 1.5, i.e. $d_n^\Phi \sim n^{2}$ as $n\rightarrow \infty$. Moreover, $\Phi$ possesses a covariant net of quadrics, and two functionally independent invariants determined by its action on $\mathscr {R}{\setminus }(\langle g\rangle \cdot \mathscr {E})$.

• If , then the map is periodic in the sense of Definition 1.5, i.e. . Moreover, $\Phi$ possesses a covariant five-dimensional linear system of quadrics, and three functionally independent invariants.

• If , then the map is non-integrable in the sense of Definition 1.5, i.e. $d_{n}^{\Phi }\sim \varphi ^{2n}$, where $\varphi$ is the golden ratio. Moreover, $\Phi$ exhibits late confinement, and it possess a covariant pencil of desmic surfaces, and one invariant.

In Theorem 1.8, by covariant linear system $\Sigma$ we mean that there exists a divisor $D\in {{\,\textrm{Div}\,}}(\mathbb {P}^3)$ such that the correspondence

is a well-defined group automorphism (see Definition 6.1). While, by invariant, we mean a meromorphic function $R:\mathbb {P}^M\dashrightarrow \mathbb {C}$ such that $R\equiv R\circ \Phi$. Finally, we say that some meromorphic functions $R_1,\ldots ,R_k$ are functionally independent if at all points of $\mathbb {P}^M$ the Jacobian matrix of the map $\mathbb {P}^M\dashrightarrow \mathbb {C}^k$, defined by $R_1,\ldots ,R_k$, has maximal rank k.

In principle, the definition of algebraic entropy in Eq. (1.6) requires one to compute all the iterates of a birational map $\Phi$ and to take the limit as $n\rightarrow \infty$. For practical purposes, this is clearly impossible. So, during the years, several heuristics methods to compute the entropy have been proposed, for instance, using the concept of generating function [70] (see also [35, 39]). On the other hand, several methods to compute the algebraic entropy exactly have been proposed. Notably, most of the approaches use the algebro-geometric structure of the projective spaces [7, 8, 23, 89, 94], with some notable exceptions [48]. In this sense, the computation of the algebraic entropy is more accessible if the singularity is confined (see [36, 94]). For instance, in this paper, we compute the algebraic entropy of integrable and non-integrable maps both confining singularities.

In the present paper, to compute the exact value of the algebraic entropy of the maps of the form $g\circ {{\,\textrm{c}\,}}_3$, for g in the Cremona-cubes group, we take the viewpoint of the construction of the space of initial values of the given map $\Phi \in {{\,\textrm{Bir}\,}}(\mathbb {P}^{M})$. This concept is the discrete analogue of Okamoto’s description [75, 76] of the continuous Painlevé equations [58], and it was conceived in [86]. To introduce this concept, we need to introduce the following definition.

Definition 1.9

([16]). A rational map $\Phi$ from a smooth projective variety X to itself is called algebraically stable if $(\Phi ^*)^n = (\Phi ^n)^*$ holds.

Remark 1.10

The concept of algebraic stability is related to the one of singularity confinement. Indeed, heuristically algebraic stability means that the singularities of the map behave in a controlled way: they either form finite or periodic patterns. Specifying to the case of interest, i.e. maps in $\mathbb {P}^{M}$, a singularity pattern will be of the following form:

$$\begin{aligned} D \xrightarrow {\Phi } \gamma _{1} \xrightarrow {\Phi } \gamma _{2}\xrightarrow {\Phi } \cdots \xrightarrow {\Phi } \gamma _{K} \xrightarrow {\Phi } D', \end{aligned}$$

(1.10)

where D, $D'$ are divisors and $\gamma _{i}$ are varieties of codimension greater than one. Finite concatenations of patterns of the form (1.10) can repeat periodically as long as the number of centres $\gamma _{i}$ stays finite (this last requirement can be false for linearisable equations [1, 49, 90]). Following [10, 94], we can compute which are the divisors contracted by the map $\Phi$ and its inverse. Precisely, calling $\Psi \in {{\,\textrm{Bir}\,}}(\mathbb {P}^{M})$ the inverse of $\Phi$ the following relations hold:

$$\begin{aligned} \Psi \circ \Phi \equiv \kappa \cdot {{\,\textrm{Id}\,}}_{\mathbb {P}^M}, \quad \Phi \circ \Psi \equiv \lambda \cdot {{\,\textrm{Id}\,}}_{\mathbb {P}^M}, \quad \kappa ,\lambda \in \mathbb {C}\left[ x_{1},\ldots ,x_{M+1} \right] . \end{aligned}$$

(1.11)

The polynomials $\kappa$ and $\lambda$ admit a possibly trivial factorisation of the form:

$$\begin{aligned} \kappa = \prod _{i=1}^{K_{\kappa }} \kappa _{i}^{d_{\kappa ,i}}, \quad \lambda = \prod _{i=1}^{K_{\lambda }} {\lambda }_{i}^{d_{\lambda ,i}}, \end{aligned}$$

(1.12)

where $\kappa _i \ne \kappa _j$ and $\lambda _i \ne \lambda _j$ for $i\ne j$. The only (prime) divisors that can be contracted to subvarieties of higher codimension by $\Phi$ are then the varieties:

$$\begin{aligned} \textrm{K}_i = \{\kappa _{i}=0\}, \quad \hbox {for }i=1,\ldots ,K_\kappa , \end{aligned}$$

(1.13)

while $\Psi$ can only contract the varieties:

$$\begin{aligned} \Lambda _j = \{\lambda _{j}=0\}\quad \hbox {for }j=1,\ldots ,K_\lambda . \end{aligned}$$

(1.14)

In Fig. 1, we present a possible blow-up blow-down sequence in $\mathbb {P}^{3}$: the surface D is mapped to a curve and then to a point, but after four steps the singularity is confined and a new surface $D'$ is found. This is a graphical representation of Eq. (1.10).

Fig. 1

A possible blow-down blow-up sequence in $\mathbb {P}^{3}$

The following result allows us to characterise algebraically stable maps from the structure of their indeterminacy locus as described in Remark 1.10.

Proposition 1.11

([6, 7, 9, 16]). Let X be a smooth projective variety, and let $\Phi \in {{\,\textrm{Bir}\,}}( X)$ be a birational map with indeterminacy locus ${{\,\textrm{Base}\,}}\Phi$. Then, the map $\Phi$ is algebraically stable if and only if it does not exist a positive integer k and a divisor E on X such that $\Phi (E \smallsetminus {{\,\textrm{Base}\,}}\Phi ) \subset {{\,\textrm{Base}\,}}( \Phi ^k)$.

Then, we define.

Definition 1.12

A space of initial values of a map $\Phi \in {{\,\textrm{Bir}\,}}(\mathbb {P}^{M})$ is the datum of a birational projective morphism $\varepsilon :B\rightarrow \mathbb {P}^{M}$ such that the variety B is smooth and the lifted (birational) maps ${\widetilde{\Phi }},{\widetilde{\Phi }}^{-1}\in {{\,\textrm{Bir}\,}}(B)$ are algebraically stable. Sometimes, we will also call space of initial values simply the variety B.

Remark 1.13

In what follows, using the canonical isomorphism ${{\,\textrm{Bir}\,}}(\mathbb {P}^3)\cong {{\,\textrm{Bir}\,}}(B)$, with abuse of notation, we will denote by $\Phi$ also the map ${\widetilde{\Phi }}$, specifying, at each instance, if we are working with the projective space or with the variety B.

Suppose now that the (prime) subvarieties $\gamma _i$, for $i=1,\ldots ,K$, of codimension greater than one encountered in the singularity pattern (1.10) of some map $\Phi$ are disjoint, i.e. $\gamma _i\cap \gamma _j=\varnothing$ for $i\not =j$ irreducible and smooth (we will just blow up reduced points). The general case is more intricate and beyond our purpose. As a consequence of Remark 1.10 and of the properties of the blowup (see [26, Proposition IV-22]), we have that

$$\begin{aligned} B = {{\,\textrm{Bl}\,}}_{\underset{i=1}{\overset{K}{\cup }}\gamma _{i}}(\mathbb {P}^{M}) \end{aligned}$$

(1.15)

is a space of initial values for $\Phi$. Denoting by $F_{i}$, for $i=1,\ldots ,K$, the exceptional divisors of $\varepsilon$, we attach to B its second cohomology group (see [38, Section 4.6.2]):

$$\begin{aligned} H^{2}(B,\mathbb {Z}) = \langle \varepsilon ^{*}H, F_{1},\dots , F_{K}\rangle _{\mathbb {Z}}. \end{aligned}$$

(1.16)

Then, the action of $(\Phi ^{-1})^{*}$ on $H^{2}(B,\mathbb {Z})$ is linear and the coefficient of the pullback of $\varepsilon ^{*}H$ via $\Phi$ agrees with the degree of $\Phi$ in the sense of Eq. (1.5). So, following [7, 89], from the algebraic stability condition we get that:

$$\begin{aligned} d_{n}^\Phi = {{\,\textrm{coeff}\,}}\left( ((\Phi ^{-1})^{*})^{n}\varepsilon ^* H, \varepsilon ^{*}H \right) = {{\,\textrm{coeff}\,}}\left( (\Phi ^{*})^{-n}\varepsilon ^* H, \varepsilon ^{*}H \right) , \end{aligned}$$

(1.17)

that is we converted the problem of finding a closed-form expression for $d_{n}^\Phi$ to a problem in linear algebra over the $\mathbb {Z}$-module $H^{2}(B,\mathbb {Z})$.

The plan of the paper is the following. In Sect. 2, we present the motivations to consider the Cremona-cubes group, taken from the recent literature on the KHK discretisation. In Sect. 3, we recall some of the needed properties of the standard Cremona transformations, and we describe their resolutions of indeterminacies in dimensions 2 and 3. We will also remark that, in dimension 3, the associated variety is singular at twelve conifold points. In Sect. 4, we introduce rigorously the Cremona-cubes group, a subgroup of $\mathbb {P}{{\,\textrm{Gl}\,}}(4,\mathbb {C})$. In Sect. 5, we prove the growth properties described in Theorem 1.8. Next, in Sect. 6, we discuss the existence of covariant linear systems of quadrics and quartics as stated in Theorem 1.8. So, in the successive Sect. 7, we construct the invariants via geometrical arguments ending the proof of Theorem 1.8. In particular, we find results matching with those of Sect. 5 because we find two invariants for integrable maps, three for periodic maps, and only one for non-integrable ones. Finally, in Sect. 8 we present some conclusion and some outlook for future works.

2 The KHK Discretisation of the Euler Top

It is a well-known fact that most of the problems in the theory of dynamical systems cannot be solved in a closed form. For instance, in [5, §5, pag. 22], V. I. Arnol’d wrote:

“Analyzing a general potential system with two degrees of freedom is beyond the capability of modern science.”

This led many scientists to develop and study methods to produce systems that could be tackled numerically [81]. In the case of ordinary differential equations, this amounts to produce discretisations, which can be solved iteratively. The problem that arises with the discretisation approach is then to preserve the known properties of the continuous systems. For instance, standard Hamiltonian systems are known to be conservative, meaning that the orbits of a Hamiltonian system cannot spiral into points (or formally, stable equilibrium points cannot be asymptotically stable). On the other hand, it is known that this property is not preserved by all numerical methods, and, for instance, a symplectic integrator cannot preserve exactly the energy and vice versa an energy-preserving integrator cannot be symplectic [96]. This considerations led to the introduction of a branch of numerical analysis called geometric integration, whose aim is to build discretisations preserving as much as possible the properties of their continuous counterparts [12, 13, 68].

In a series of unpublished lecture notes (see [62]), W. Kahan devised a method to obtain good numerical approximations in the sense outlined above: the orbits of some conservative systems did not seem to be affected by the physically and mathematically incorrect spiralling behaviour [63]. Kahan’s method was rediscovered independently by Hirota and Kimura, who used it to produce integrable discretisations of the Euler top [55] and the Lagrange top [66], followed by Suris and his collaborators who produced many more integrable examples in [77,78,79]. Before discussing our case of interest, that is the Euler top, we give a brief account of the method.

Definition 2.1

Assume we are given an M-dimensional system of first-order differential equations (also called a vector field):

$$\begin{aligned} \mathbf {\dot{x}}=\textbf{f}\left( \textbf{x} \right) , \quad \textbf{x}:\mathbb {R}^{M}\rightarrow \mathbb {R}, \quad \textbf{f}:\mathbb {R}^{M}\rightarrow \mathbb {R}^{M}. \end{aligned}$$

(2.1)

Then, its Kahan–Hirota–Kimura discretisation (KHK) is:

$$\begin{aligned} \frac{\mathbf {x'}-\textbf{x}}{h} = 2\textbf{f}\left( \frac{\mathbf {x'}+\textbf{x}}{2} \right) -\frac{\textbf{f}\left( \mathbf {x'} \right) +\textbf{f}\left( \textbf{x}\right) }{2}, \end{aligned}$$

(2.2)

where $\textbf{x} = \textbf{x}\left( n h \right)$, $\mathbf {x'}=\textbf{x}\left( (n+1)h \right)$, and $h>0$ is an infinitesimal parameter.

Remark 2.2

In this remark, we resume the most important known facts about the KHK discretisation.

• If the function $\textbf{f}$ is quadratic, then the associated map

  

  (2.3)

  where is the Jacobian of the function $\textbf{f}$, is birational (see [20, 78]). Its inverse is obtained through the substitution $h\mapsto -h$, i.e. $\varvec{\Phi }^{-1}_{h}\left( \textbf{x} \right) = \varvec{\Phi }_{-h}\left( \textbf{x} \right)$. This considerations carry over in $\mathbb {P}^M$ considering first the complexification $\mathbb {C}^M$ of $\mathbb {R}^M$ and then its compactification to $\mathbb {P}^M$ with hyperplane at infinity . We denote the corresponding map by $\Phi _{h} \in {{\,\textrm{Bir}\,}}(\mathbb {P}^{M})$ to underline the dependence on $h>0$.

• When applied to quadratic vector fields, the KHK method is the restriction of a Runge–Kutta method [81], so it is covariant with respect to affine transformations [20].

• Suppose that the vector field is Hamiltonian. That is, there exist a function $H:\mathbb {R}^{M}\rightarrow \mathbb {R}$ and a constant skew-symmetric matrix $J\in {{\,\textrm{Mat}\,}}_{M,M}\left( \mathbb {R}\right)$ such that:

  

  (2.4)

  If $\deg H = 3$, then the associated KHK discretisation admits an invariant ${\tilde{H}}_{h}$, such that $\lim _{h\rightarrow 0^{+}} {\tilde{H}}_{h}=H$ and a preserved measure which is a h-deformation of the standard Euclidean measure [19, 20].

The Euler top is the following system of three first-order quadratic equations in the variables $(x_1,x_2,x_3)\in \mathbb {R}^3$:

$$\begin{aligned} \dot{x_1} = a_1 x_2 x_3, \quad \dot{x_2} = a_2 x_1 x_3, \quad \dot{x_3} = a_3 x_1x_2. \end{aligned}$$

(2.5)

This is a well-known integrable system (see [5, §29]) whose solution was given by Euler himself in terms of elliptic functions. In fact, the Euler top belongs to a wider family of continuous integrable systems known as the Manakov systems [71, 72]. Following (2.2), the KHK discretisation of the Euler top is:

$$\begin{aligned}{} & {} \frac{x_1'-x_1}{h} = \frac{a_1}{2} (x_2'x_3+x_2x_3'), \quad \frac{x_2'-x_2}{h} = \frac{a_2}{2} (x_1'x_3+x_1x_3'), \nonumber \\{} & {} \frac{x_3'-x_3}{h} = \frac{a_3}{2} (x_1'x_2+x_1x_2'). \end{aligned}$$

(2.6)

Explicitly, from (2.3), after introducing homogeneous coordinates $[x_1:x_2:x_3:x_4]$ on $\mathbb {P}^3$ we have the following map of projective spaces:

where

$$\begin{aligned} x_1'&=- \left( { a_1} { a_2} x_3^{2}+{ a_1} { a_3} x_1^{2}-{a_2} { a_3} x_1^{2} \right) {h}^{2}x_1-4 { a_1} hx_2x_3x_4-4 x_1x_4^{2}, \end{aligned}$$

(2.8a)

$$\begin{aligned} x_2'&=- \left( { a_1} { a_2} x_3^{2}-{ a_1} { a_3} x_2^{2}+{ a_2} { a_3} x_1^{2} \right) {h}^{2}x_2-4 { a_2} hx_1x_3x_4-4 x_2x_4^{2}, \end{aligned}$$

(2.8b)

$$\begin{aligned} x_3'&= \left( { a_1} { a_2} x_3^{2}-{ a_1} { a_3} x_2^{2}-{ a_2} { a_3} x_1^{2} \right) {h}^{2} x_3 -4 { a_3} hx_1x_2x_4-4 x_3x_4^{2}, \end{aligned}$$

(2.8c)

$$\begin{aligned} x_4'&= { a_1} { a_2} { a_3} {h}^{3}x_1x_2x_3 + \left( { a_1} { a_2} x_3^{2}+{ a_1} { a_3} x_2^{2}+{ a_2} { a_3} x_1^{2}\right) {h}^{2}x_4-4 x_4^{3}. \end{aligned}$$

(2.8d)

From [55], it is known that the above system is integrable, with its Hamiltonian formulation given in [79]. Another remarkable property is the existence of a Lax pair¹ [65, 67, 88], the only known case for a KHK discretisation along with the discrete Nahm system [41]. More recently, in [2], the system (2.6) was derived using a three-dimensional analogue of the QRT construction [82, 83], that is as action of involutions on two pencils of quadrics. In the same paper [2, Prop. 7.2], the reduction of the system to a three-dimensional standard Cremona transformation composed with two projectivities is discussed (see Lemma 2.6). In the rest of this section, we will interpret this statement from a different viewpoint based on singularity confinement. Moreover, we will explain why this naturally leads to the definition of the Cremona-cubes group (see Definition 4.2).

From the heuristic point of view, if we compute the sequence of degrees of the iterations of the map in (2.7), we obtain:

$$\begin{aligned} 1, 3, 9, 19, 33, 51, 73, 99, 129, 163, 201, 243, 289\dots . \end{aligned}$$

(2.9)

The following generating function fits the values in (2.9):

$$\begin{aligned} g(s) =\frac{3s^2 + 1}{(1 - s)^3}. \end{aligned}$$

(2.10)

Applying the inverse $\mathscr {Z}$-transform (see [39]) (2.10), we get $d_n^{\Phi _h}= 2 n^2 +1$. Furthermore, by examining the sequence (2.9), we see that the deviation from the standard growth $d_n^{(s)}=3^n$ happens at the third iterate. After having explored the singularity pattern (see Fig. 2), we will see that this is not an accident, but it has a deep meaning.

Recall that $\Phi ^{-1}_h = \Phi _{-h}$ (see Remark 2.2). Then, following the idea of singularity confinement, we compute the polynomials $\kappa$ and $\lambda$ from (1.11) for (2.3):

$$\begin{aligned} \kappa = \prod _{i=1}^{4} \kappa _{i}^{2}, \quad \lambda = \prod _{i=1}^{4} \lambda _{i}^{2}, \end{aligned}$$

(2.11)

with:

$$\begin{aligned} \kappa _{1}&= \alpha _1 \alpha _2 h x_3-\alpha _1 \alpha _3 h x_2-\alpha _2 \alpha _3 h x_1-2 x_4, \end{aligned}$$

(2.12a)

$$\begin{aligned} \kappa _{2}&= \alpha _1 \alpha _2 h x_3+\alpha _1 \alpha _3 h x_2-\alpha _2 \alpha _3 h x_1+2 x_4, \end{aligned}$$

(2.12b)

$$\begin{aligned} \kappa _{3}&= \alpha _1 \alpha _2 h x_3-\alpha _1 \alpha _3 h x_2+\alpha _2 \alpha _3 h x_1+2 x_4, \end{aligned}$$

(2.12c)

$$\begin{aligned} \kappa _{4}&= \alpha _1 \alpha _2 h x_3+\alpha _1 \alpha _3 h x_2+\alpha _2 \alpha _3 h x_1-2 x_4, \end{aligned}$$

(2.12d)

and

$$\begin{aligned} \lambda _{1}&= \alpha _1 \alpha _2 h x_3 -\alpha _1 \alpha _3 h x_2 -\alpha _2 \alpha _3 h x_1+2 x_4, \end{aligned}$$

(2.13a)

$$\begin{aligned} \lambda _{2}&= \alpha _1 \alpha _2 h x_3+\alpha _1 \alpha _3 h x_2-\alpha _2 \alpha _3 h x_1-2 x_4, \end{aligned}$$

(2.13b)

$$\begin{aligned} \lambda _{3}&= \alpha _1 \alpha _2 h x_3-\alpha _1 \alpha _3 h x_2+\alpha _2 \alpha _3 h x_1-2 x_4, \end{aligned}$$

(2.13c)

$$\begin{aligned} \lambda _{4}&= \alpha _1 \alpha _2 h x_3+\alpha _1 \alpha _3 h x_2+\alpha _2 \alpha _3 h x_1+2 x_4, \end{aligned}$$

(2.13d)

for some choice of square root $\alpha _j$ of $a_{j}$, for $j=1,2,3$.

Let us consider the varieties

$$\begin{aligned} \textrm{K}_i=\left\{ \kappa _{i}=0 \right\} \hbox { and }\Lambda _{i} = \left\{ \lambda _{i}=0 \right\} . \end{aligned}$$

(2.14)

Then, for $i=1,\ldots ,4$, we have the following singularity pattern:

$$\begin{aligned} \textrm{K}_i \longrightarrow s_{i} \longrightarrow s_{i}' \dashrightarrow \Lambda _{i}, \end{aligned}$$

(2.15)

where

$$\begin{aligned} s_{1} = \left[ 2\alpha _{1}:2\alpha _{2}:-2\alpha _{3}:-\alpha _{1}\alpha _{2}\alpha _{3}h \right] ,&\quad s_{1}'= \left[ 2\alpha _{1}:2\alpha _{2}:-2\alpha _{3}:\alpha _{1}\alpha _{2}\alpha _{3}h \right] , \end{aligned}$$

(2.16a)

$$\begin{aligned} s_{2} = \left[ 2\alpha _{1}:-2\alpha _{2}:-2\alpha _{3}:\alpha _{1}\alpha _{2}\alpha _{3}h \right] ,&\quad s_{2}'= \left[ 2\alpha _{1}:-2\alpha _{2}:-2\alpha _{3}:-\alpha _{1}\alpha _{2}\alpha _{3}h \right] , \end{aligned}$$

(2.16b)

$$\begin{aligned} s_{3} = \left[ 2\alpha _{1}:-2\alpha _{2}:2\alpha _{3}:-\alpha _{1}\alpha _{2}\alpha _{3}h \right] ,&\quad s_{3}'= \left[ 2\alpha _{1}:-2\alpha _{2}:2\alpha _{3}:\alpha _{1}\alpha _{2}\alpha _{3}h \right] , \end{aligned}$$

(2.16c)

$$\begin{aligned} s_{4} = \left[ 2\alpha _{1}:2\alpha _{2}:2\alpha _{3}:\alpha _{1}\alpha _{2}\alpha _{3}h \right] ,&\quad s_{4}'= \left[ 2\alpha _{1}:2\alpha _{2}:2\alpha _{3}:-\alpha _{1}\alpha _{2}\alpha _{3}h \right] . \end{aligned}$$

(2.16d)

The singularity patterns in (2.15) are depicted in Fig. 2. This immediately explains the growth in Eq. (2.9): the deviation from the standard growth happens at the third step because after three steps the map enters the singularities. Notice that, the degree drop is exactly given by $\deg \kappa = 8$ because $\kappa$ is the common factor to be removed in the computation of the degree. A similar analysis for $\Phi _h^{-1}$ shows that on the third iterate the common factor $\lambda$, whose degree is eight, is removed.

Fig. 2

The blow-down blow-up sequence of the Euler top $\mathbb {P}^{3}$

Remark 2.3

Note that, as $h\rightarrow 0^{+}$, all the points appearing in the singularity pattern are pushed on the plane at infinity $L_{\infty } = \left\{ x_4=0 \right\}$. This has to be expected because the invariants (first integrals) of the continuous Euler top (2.5) are polynomials [5] and polynomials are singular only at infinity (see also [10, 35] for a similar discussion on the importance of singularities for polynomial maps).

The geometry of the singularity confinement is also enough to build the invariants of the system and hence to prove integrability in the naïve sense (see [42]). Indeed, by considering the net $\Sigma$ of quadrics passing through the points $s_{i}$ and $s_{i}'$, we find:

(2.17)

Then, it is easy to show that $(\Phi _{h}^{-1})^{*}(Q) = \kappa _{1} \kappa _{2} \kappa _{3} \kappa _{4} Q$, i.e. the net $\Sigma$ enjoys nice covariance properties (see Definition 6.1) with respect to the KHK discretisation of the Euler top (2.8). This easily yields two functionally independent invariants:

$$\begin{aligned} I_{1} = \frac{x_1^{2} - a_1 x_3^{2}/a_3}{ x_4^{2} - a_1a_2 x_3^{2}/4}, \quad I_{2} = \frac{x_2^{2} - a_2x_3^{2}/a_3}{ x_4^{2} - a_1a_2x_3^{2}/4}. \end{aligned}$$

(2.18)

The situation is a three-dimensional generalisation of the results in [45, 80]. Therein, it was proved how the geometric structure of the KHK discretisation of a two-dimensional system with cubic Hamiltonian determines its integrability. Moreover, a special rôle is played by the singular fibres of the associated pencil. Note that the coordinate points of $\Sigma \cong \mathbb {P}^2_{[\mu : \nu : \xi ]}$ are indeed singular members of the net.

Remark 2.4

We note that the eight points are not in general position. Indeed, in general, eight points of $\mathbb {P}^3$ generate only a pencil of quadrics. In Remark 3.2, we will explain their relation with the fixed locus of the Cremona transformation. This led us to depict them as two tetrahedra in Fig. 3. To see that they are not in general position notice, for instance, that this set of vertices contains twelve distinct co-planar quadruples. We will see in Sect. 4 how this this related to the Cremona-cubes group.

Fig. 3

The two tetrahedra in the finite chart $\left\{ x_4\ne 0 \right\} \subset \mathbb {P}^{3}$

Remark 2.5

The two invariants found in Eq. 2.18 are related to those known in the literature

$$\begin{aligned} F_{1} = \frac{x_4^2-a_1 a_3 h^2 x_2^2/4}{x_4^2-a_1a_2 h^2 x_3^2/4}, \quad F_{2} = \frac{x_4^2 - a_1a_2 h^2 x_3^2/4}{x_4^2-a_2a_3 h^2 x_1^2/4}, \end{aligned}$$

(2.19)

(see [2, 55, 79]), through the transformation

$$\begin{aligned} F_{1} = 1-\frac{a_1a_3 h^2}{4} I_{2},\quad F_{2} = \frac{1}{1-a_2a_3 h^2 I_1/4}. \end{aligned}$$

(2.20)

The following Lemma provides a motivation to study the Cremona-cubes group (see [2, Proposition 7.2.] for more details).

Lemma 2.6

The KHK discretisation of the Euler top (2.8) decomposes as $\Phi _{h} = \ell _{2}\circ {{\,\textrm{c}\,}}_{3} \circ \ell _{1}$ where $\ell _{i}:\mathbb {P}^{3}\rightarrow \mathbb {P}^{3}$ are two projectives whose representative matrices with respect to the standard homogeneous coordinate system in $\mathbb {P}{{\,\textrm{Gl}\,}}(3,\mathbb {C})$ are given by:

$$\begin{aligned} M_{\ell _{1}}&= \begin{bmatrix} \alpha _2 \alpha _3 h &{}\quad \alpha _1 \alpha _3 h &{}\quad -\alpha _1 \alpha _2 h &{}\quad -2 \\ \alpha _2 \alpha _3 h &{}\quad -\alpha _1 \alpha _3 h &{}\quad -\alpha _1 \alpha _2 h &{}\quad 2 \\ \alpha _2\alpha _3 h &{}\quad -\alpha _1 \alpha _3 h &{}\quad \alpha _1 \alpha _2 h &{}\quad -2 \\ \alpha _2 \alpha _3 h &{}\quad \alpha _1 \alpha _3 h &{}\quad \alpha _1\alpha _2 h &{}\quad 2 \end{bmatrix}, \end{aligned}$$

(2.21a)

$$\begin{aligned} M_{\ell _{2}}&= \begin{bmatrix} 2 \alpha _1 &{}\quad 2 \alpha _1 &{}\quad 2 \alpha _1 &{}\quad 2 \alpha _1 \\ 2 \alpha _2 &{}\quad -2 \alpha _2 &{}\quad -2 \alpha _2 &{}\quad 2 \alpha _2 \\ -2 \alpha _3 &{}\quad -2 \alpha _3 &{}\quad 2 \alpha _3 &{}\quad 2 \alpha _3 \\ \alpha _1 \alpha _2 \alpha _3 h &{}\quad -\alpha _1 \alpha _2 \alpha _3 h &{}\quad \alpha _1 \alpha _2 \alpha _3 h &{}\quad -\alpha _1 \alpha _2 \alpha _3 h \end{bmatrix}. \end{aligned}$$

(2.21b)

Proof

The proof consists of a direct computation. $\square$

Remark 2.7

Sometimes, when no possible confusion occurs, we will identify any linear map $\ell \in {{\,\textrm{Bir}\,}}(\mathbb {P}^{3})$ with the associated matrix $M_{\ell }\in \mathbb {P}{{\,\textrm{Gl}\,}}(3,\mathbb {C})$ and write $\ell$ in place of $M_{\ell }$.

Remark 2.8

The base loci of $\Phi _{h}$ and its inverse consist of the twelve lines on which lie the edges of two tetrahedra (see Fig. 3). Moreover, these lines are obtained as two by two intersections of the eight planes $\textrm{K}_{i}$ and $\Lambda _{i}$ introduced in (2.14):

$$\begin{aligned} L_{i,j} = \textrm{K}_{i}\cap \textrm{K}_{j}, \quad L_{i,j}' = \Lambda _{i}\cap \Lambda _{j}, \quad 1 \le i<j\le 4. \end{aligned}$$

(2.22)

That is:

$$\begin{aligned} {{\,\textrm{Base}\,}}\Phi _{h} = \bigcup _{1 \le i<j\le 4} L_{i,j}, \quad {{\,\textrm{Base}\,}}\Phi _{h}^{-1} = \bigcup _{1 \le i<j\le 4} L_{i,j}'. \end{aligned}$$

(2.23)

The importance of Lemma 2.6 is highlighted in the following simple corollary.

Corollary 2.9

The KHK discretisation of the Euler top (2.8) is projectively equivalent to the map $\Phi ^{(0)} = g_0 \circ {{\,\textrm{c}\,}}_{3}$ where

$$\begin{aligned} g_0 = \begin{bmatrix} 1&{}\quad -1&{}\quad -1&{}\quad -1 \\ -1&{}\quad 1&{}\quad -1&{}\quad -1 \\ -1&{}\quad -1&{}\quad 1&{}\quad -1 \\ -1&{}\quad -1&{}\quad -1&{}\quad 1 \end{bmatrix}. \end{aligned}$$

(2.24)

Moreover, the projectivity $g_0$ is an involution.

Proof

After noticing that $g_0=\ell _{1}\circ \ell _{2}$, the proof consists on a direct computation. $\square$

Remark 2.10

We remark that the conjugation of $\Phi _h$ by $\ell _1$ makes the discretisation parameter h disappear. This implies that the integrability properties of the system are independent from the discretisation parameter (see [46, Introduction]).

The great advantage in studying $\Phi ^{(0)}$ with respect to the original $\Phi _{h}$ is that $\Phi ^{(0)}$ is the composition of two involutions, making it strikingly similar to the QRT map construction [82, 83]. Moreover, the rows and the columns of the matrix $g_0$ are made of fixed points of the standard Cremona transformation ${{\,\textrm{c}\,}}_{3}$. This construction unveils the geometric structure underlying the KHK discretisation of the Euler top (2.8). In this paper, we consider a class of maps sharing similar behaviour (see Lemma 4.5). The most important finding is to consider birational maps decomposing as $\Phi = g \circ {{\,\textrm{c}\,}}_{3}$, where $g\in \mathbb {P}{{\,\textrm{Gl}\,}}(4,\mathbb {C})$ is a projectivity having the following properties:

• (1) up to the multiplicative action of $\mathbb {C}^*$ on the space of matrices, the entries of the matrix representing g with respect the canonical projective coordinates belong to ;

• (2) the projectivity g is represented by a matrix whose rows and columns are coordinate points or fixed points of the standard Cremona transformation ${{\,\textrm{c}\,}}_{3}$;

• (3) the order of g is finite (not necessarily an involution);

• (4) for any $k\ge 0$, $g^{k}$ verifies (1),(2) and (3).

The above requirements will be made mathematically rigorous in the next section (see Lemma 4.5 and Definition 4.2), with the definition of the Cremona-cubes group.

3 The Standard Cremona Transformation in Dimension Three

It is a classical fact known as the Noether–Castelnuovo theorem [17, 74] that the Cremona group ${{\,\textrm{Bir}\,}}(\mathbb {P}^2)$ of the projective plane is generated by $\mathbb {P}{{\,\textrm{Gl}\,}}(3,\mathbb {C})$ and the standard Cremona transformation ${{\,\textrm{c}\,}}_2$, that is the birational map defined as:

The resolution of the indeterminacy locus of the map ${{\,\textrm{c}\,}}_2$ is described in Fig. 4. The two involved $\mathbb {P}^2$’s are represented as triangles whose edges correspond to the coordinate lines, while the exagon represents a del Pezzo surface of degree six, i.e. the blow-up of $\mathbb {P}^2$ at three non-collinear points, and its edges correspond to $(-1)$-lines. The maps $\pi _1$ and $\pi _2$ are the blowups of $\mathbb {P}^2$ with centre the three coordinate points. In particular, the dotted (resp. dashed) edges correspond to exceptional lines for $\pi _1$ (resp. $\pi _2$) (see [24, Example 7.1.9] for more details).

Fig. 4

The resolution of the indeterminacies of the standard Cremona transformation in dimension 2

The situation in higher dimension happens to be much more intricate. For instance, it is no longer true that the Cremona group ${{\,\textrm{Bir}\,}}(\mathbb {P}^n)$ of the n-dimensional projective space is generated by $\mathbb {P}{{\,\textrm{Gl}\,}}(n+1,\mathbb {C})$ and the higher-dimensional analogue of standard Cremona transformation.

This section focuses on the standard Cremona transformation ${{\,\textrm{c}\,}}_3$ of $\mathbb {P}^3$. We will describe the resolution of the indeterminacies of ${{\,\textrm{c}\,}}_3$, and then, we will discuss the configuration of the fixed points of ${{\,\textrm{c}\,}}_3$.

3.1 The standard Cremona Transformation in Dimension Three

Let ${{\,\textrm{c}\,}}_3\in {{\,\textrm{Bir}\,}}(\mathbb {P}^3)$ be the standard Cremona transformation (see (1.1)). The map ${{\,\textrm{c}\,}}_3$ is well defined outside the union of the six coordinate axes of $\mathbb {P}^3$. We can solve the indeterminacy locus of the standard Cremona transformation as follows

where $B\subset ({\mathbb {P}^3})^{\times 2}$ is the closure of the graph of ${{\,\textrm{c}\,}}_3$, $B=\overline{{{\,\textrm{graph}\,}}({{{\,\textrm{c}\,}}_3})}$, and f and g are the restrictions to B of the canonical projections. Thus, B is the complete intersection defined as follows (see also [24, Example 7.2.5])

(3.3)

Let us denote by $B_{ij}$ the affine chart on B defined by

(3.4)

Then, the chart $B_{ij}$ is smooth if and only if $i=j$, otherwise $B_{ij}$ has an isolated conifold singularity. Thus, B has twelve singular points. Moreover, the exceptional divisors of g and f agree. They consist of the union of six surfaces isomorphic to $({\mathbb {P}^1})^{\times 2}$, each mapping, via g and f, onto a coordinate line of $\mathbb {P}^3$, and three projective planes which are contracted by g to coordinate points. In particular, the three coordinate points of each of the four exceptional $\mathbb {P}^2$’s are the conifold singularities of the ambient threefold B.

The variety B, which is the blowup of $\mathbb {P}^3$ along the union of the coordinate axes, can be alternatively constructed as follows (see Fig. 5):

• (1) blowup the four vertices of the standard tetrahedron of $\mathbb {P}^3$, i.e. the coordinate points of $\mathbb {P}^3$. Since we are blowing up (reduced) smooth points, the exceptional locus is the disjoint union of 4 copies of $\mathbb {P}^2$;

• (2) blowup the strict transforms of the six edges of the standard tetrahedron, i.e. the six coordinate lines of $\mathbb {P}^3$. The exceptional locus of this blowup is given by six copies of $({\mathbb {P}^1})^{\times 2}$. The four exceptional divisors of the previous step happen to be blown up at three distinct non-collinear points. As a consequence, their strict transforms are all isomorphic to a del Pezzo surface of degree six ${{\,\textrm{dP}\,}}_{6}$;

• (3) the last step consists in contracting twelve $(-1,-1)$-lines, i.e. twelve lines $L_i\cong \mathbb {P}^1$ for $i=1,\ldots ,12$ with normal bundle

  $$\begin{aligned} N_{L_i/{\widetilde{B}}}\cong {\mathscr {O}}_{\mathbb {P}^1}(-1)^{\oplus 2}\hbox { for }i=1,\ldots ,12, \end{aligned}$$

  (3.5)

  where ${\widetilde{B}}$ is the variety constructed in the previous step. To see this, notice that each line is the complete intersection of one of the del Pezzo and the strict transform of some coordinate hyperplane of $\mathbb {P}^3$.

  The lines $L_i$, for $i=1,\ldots ,12$, are the strict transforms of the coordinate lines of the exceptional divisors in step (1). Notice (see [57, Section 11.3]) that all the $L_i$’s are contracted to conifold points.

Fig. 5

The toric description of the three steps in the construction of B near a coordinate point of $\mathbb {P}^3$

Remark 3.1

When restricted to each exceptional $\mathbb {P}^2$ in step (1), the concatenation of steps (2) and (3) is a two-dimensional standard Cremona transformation.

Remark 3.2

We have:

(3.6)

where

$$\begin{aligned} \begin{aligned} p_1&=[1:-1:-1:-1], \\ p_2&=[-1:1:-1:-1], \\ p_3&=[-1:-1:1:-1], \\ p_4&=[-1:-1:-1:1], \end{aligned} \quad \begin{aligned} q_1&=[1:-1:-1:1], \\ q_{2}&=[-1:1:-1:1], \\ q_{3}&=[1:1:-1:-1], \\ q_{4}&=[1:1:1:1]. \end{aligned} \end{aligned}$$

(3.7)

These eight points correspond to two four-tuples of lines of $\mathbb {C}^4$ orthogonal with respect to the standard scalar product. In particular, these are four-tuples of points in general position. We highlight that the sets $\mathscr {P},\mathscr {Q}$ correspond to the sets via the projectivity $\ell _1^{-1}$ introduced in (2.21a). Moreover, the points in ${{\,\textrm{Fix}\,}}{{\,\textrm{c}\,}}_3$ can be interpreted as the vertices of a cube in the affine space, as depicted in Fig. 6. In this paper, by vertices of a cube we mean the base locus of a general net of quadrics of $\mathbb {P}^3$ (see [56, App. B.5.2] and [24, Section 1.5.2]). Note that we are considering only general nets in order to have a 0-dimensional² reduced base locus.

Remark 3.3

If we are interested in spaces of initial values for ${{\,\textrm{c}\,}}_3$, we do not need to work with a resolution of singularities of the variety B in Sect. 3.1, and it is enough to consider the variety

(3.8)

where

$$\begin{aligned} \begin{aligned} e_1&=[1:0:0:0], \\ e_2&=[0:1:0:0], \\ e_3&=[0:0:1:0], \\ e_4&=[0:0:0:1]. \end{aligned} \end{aligned}$$

(3.9)

Indeed, the only divisorial contractions of ${{\,\textrm{c}\,}}_3$ consist of contractions over one of the $e_i$’s and the map induced by ${{\,\textrm{c}\,}}_3$ on ${\overline{B}}$ is algebraically stable.

4 The Cremona-Cubes Group ${\mathscr {C}}$

In this section, we introduce the subgroup of $\mathbb {P}{{\,\textrm{Gl}\,}}(3,\mathbb {C})$ we are interested in. The subgroup ${\mathscr {C}}$ is defined in terms of the “special” points introduced in the previous section (see Remarks 3.2 and 3.3).

Definition 4.1

We will denote³ by $\mathscr {R}\subset \mathbb {P}^3$ the finite subset containing all the points appearing in Remarks 3.2 and 3.3, i.e.

$$\begin{aligned} \mathscr {R}=\mathscr {E}\cup \mathscr {P}\cup \mathscr {Q}. \end{aligned}$$

(4.1)

As explained in Sect. 2, we are interested in maps of the form $\Phi =g\circ {{\,\textrm{c}\,}}_3$ where $g\in \mathbb {P}{{\,\textrm{Gl}\,}}(4,\mathbb {C})$ is a projectivity of finite order that acts on the set $\mathscr {R}$.

Definition 4.2

We will call the Cremona-cubes group the subgroup $\mathscr {C}$ of $\mathbb {P}{{\,\textrm{Gl}\,}}(4,\mathbb {C})$ defined by:

(4.2)

Remark 4.3

We remark that, since $\mathscr {R}$ contains five-tuples of points in general position, we have ${{\,\textrm{Stab}\,}}_{\langle g \rangle } (\mathscr {R})=\langle {{\,\textrm{Id}\,}}_{\mathbb {P}{{\,\textrm{Gl}\,}}(4,\mathbb {C})}\rangle$, for any $g\in \mathscr {C}$ (see [31, Section 1.3]). Here, $\langle g \rangle$ denotes the cyclic subgroup of $\mathbb {P}{{\,\textrm{Gl}\,}}(4,\mathbb {C})$ generated by g, while ${{\,\textrm{Stab}\,}}_{\langle g \rangle }(\mathscr {R})$ is the following subgroup of $\langle g \rangle$:

(4.3)

This implies that all the elements $g\in \mathscr {C}$ have finite order. Indeed, suppose that there exists a $g\in \mathscr {C}$ of infinite order. In particular, for any integer $k>1$, $g^k$ is not the inverse of g. Now, since g acts on the finite set $\mathscr {R}$, there is an integer $k>1$ such that $g|_{\mathscr {R}}\equiv g^k|_{\mathscr {R}}$. This implies that $g^{1-k}$ would be a non-trivial element in ${{\,\textrm{Stab}\,}}_{\langle g \rangle } (\mathscr {R})$.

The following result tells us that, within $\mathscr {R}$, the three subsets $\mathscr {E}$, $\mathscr {P}$, and $\mathscr {Q}$ are mapped between themselves as a whole.

Lemma 4.4

The action of $\mathscr {C}$ on $\mathscr {R}$ induces an action of $\mathscr {C}$ on the set .

Proof

First notice that, if a line L of $\mathbb {P}^3$ contains at least two points of $\mathscr {R}$, then it contains either three aligned points each belonging to one of the sets $\mathscr {E},\mathscr {P}$ and $\mathscr {Q}$ or two points from the same collection $\mathscr {E},\mathscr {P}$ or $\mathscr {Q}$.

We now proceed by contradiction. Suppose, without loss of generality, that the projectivity g sends the point $e_1$ to the point $p_1$ and the point $e_2$ to the point $q_2$, i.e.

Let $L_{12}$ be the line through $p_1$ and $q_2$ and let $e_j$ be the third intersection point in $L_{12}\cap \mathscr {R}$, i.e.

(4.5)

Then, we get

$$\begin{aligned} g^{-1 }\cdot e_j \in (g^{-1}(L_{12})\smallsetminus \{e_1,e_2\})\cap \mathscr {R}. \end{aligned}$$

(4.6)

Which is a contradiction. $\square$

Now, we characterise the elements of $\mathscr {C}$ as belonging to three different classes depending on their action on the set . The following Lemma is crucial in this characterisation.

Lemma 4.5

Let $g\in \mathscr {C}\subset \mathbb {P}{{\,\textrm{Gl}\,}}(4,\mathbb {C})$ be an element of the Cremona-cubes group. Then, there is a matrix ${\widetilde{g}}\in {{\,\textrm{Gl}\,}}(4,\mathbb {C})$ representing g whose entries belong to $\{-1,0,1\}$. Moreover, g falls in one of the following cases.

• (A) Both the columns and rows of g represent the points in $\mathscr {P}$ (or in $\mathscr {Q}$).

• (B) The matrix g is a permutation matrix with signs.

• (C) The columns of g represent the points in $\mathscr {P}$, and the rows represent the points in $\mathscr {Q}$ (or viceversa).

Proof

The first part of the statement follows from the second, while the second part is a direct consequence of Lemma 4.4. Indeed, as per Lemma 4.4, g and $g^{-1}$ act on and, depending on the action on this set, we get (A), (B) or (C). $\square$

Remark 4.6

Notis that, on the contrary, even if a projectivity of finite order $g\in \mathbb {P}{{\,\textrm{Gl}\,}}(4,\mathbb {C})$ verifies (A), (B), or (C) it is not guaranteed that g belongs to $\mathscr {C}$. Indeed, in general property (4) in Sect. 2 would not be satisfied.

Remark 4.7

As a consequence of Lemma 4.5, we can divide the elements of the Cremona-cubes group according to the orbit $\langle g \rangle \cdot \mathscr {E}$ of $\mathscr {E}$ via g:

(4.7)

We have the following characterisation.

• An element $g \in \mathscr {C}$ belongs to case (A) in Lemma 4.5 if and only if $\langle g \rangle \cdot \mathscr {E}=\mathscr {E}\cup \mathscr {P}$ or $\langle g \rangle \cdot \mathscr {E}=\mathscr {E}\cup \mathscr {Q}$.

• An element $g \in \mathscr {C}$ belongs to case (B) in Lemma 4.5 if and only if $\langle g \rangle \cdot \mathscr {E}=\mathscr {E}$.

• An element $g \in \mathscr {C}$ belongs to case (C) in Lemma 4.5 if and only if $\langle g \rangle \cdot \mathscr {E}=\mathscr {E}\cup \mathscr {P}\cup \mathscr {Q}$.

We will see in Sect. 5 that the orbit $\langle g \rangle \cdot \mathscr {E}$ (4.7) plays a fundamental rôle in the confinement of singularities of the maps of the form $\Phi =g\circ {{\,\textrm{c}\,}}_{3}$ for $g\in \mathscr {C}$ (see also Theorem 1.8).

Definition 4.8

We will say that an element $g\in \mathscr {C}$ is of type (A) (resp. of type (B) or (C)) if it belongs to the case (A) (resp. (B) or (C)) in Lemma 4.5.

The following lemma investigates the relation between elements of the Cremona-cubes group of different type.

Lemma 4.9

The following properties hold for the elements in $\mathscr {C}$ (see Lemma 4.5).

• Two elements of type (A) (resp. (C)) differ by multiplication by a permutation matrix with sign having an even number of -1 (which is an element of $\mathscr {C}$ of type (B)).

• Two elements of type (B) differ by multiplication by a permutation matrix with signs, i.e. by an element of type (B). In particular, the elements of type (B) form a subgroup of $\mathscr {C}$ that we will denote by $\mathscr {C}_{{\textit{(B)}}}$.

• An element of type (A) differs by an element of type (C) by multiplication by a permutation matrix with signs having an odd number of -1 (which is an element of $\mathscr {C}$ of type (B)).

• The inverse of an element of type (A) (resp. (B) or (C)) is of the same type.

Proof

The proof of the first three points consists on a direct check, while the fourth point is a direct consequence of Remark 4.7. $\square$

Remark 4.10

Notice that the subgroup

(4.8)

has cardinality 192, and it contains four copies of the Full Octahedral Group (see [59, Section 11.4]) acting as the group of symmetries, non-necessarily preserving the orientation, of the cube with vertices $\mathscr {P}\cup \mathscr {Q}$. Precisely, chosen any coordinate $x_i$, for $i=1,\ldots ,4$, the Full Ochtahedral Group can be identified with the elements in $\mathscr {C}_{{\textit{(B)}}}$ which preserve the hyperplane . In particular, we have

$$\begin{aligned}{} & {} \mathscr {C}_{{\textit{(B)}}}\nonumber \\{} & {} \quad =\left\langle \begin{bmatrix} 1&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 1&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 1&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad -1 \end{bmatrix}, \begin{bmatrix} 1&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 1&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 1\\ 0&{}\quad 0&{}\quad 1&{}\quad 0 \end{bmatrix}, \begin{bmatrix} 1&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 1&{}\quad 0\\ 0&{}\quad 1&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 1 \end{bmatrix}, \begin{bmatrix} 0&{}\quad 1&{}\quad 0&{}\quad 0\\ 1&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 1&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 1 \end{bmatrix}\right\rangle . \nonumber \\ \end{aligned}$$

(4.9)

Notice also that the only possible orders for the elements in $\mathscr {C}_{{\textit{(B)}}}$ are 2,3,4,6. Now, as a consequence of Lemma 4.9, the Cremona-cubes group is the subgroup of $\mathbb {P}{{\,\textrm{Gl}\,}}(4,\mathbb {C})$ generated by $\mathscr {C}_{{\textit{(B)}}}$ and the projetivity $g_{0}$ of type (A) given in (2.24).

As an immediate consequence, we get the following result.

Corollary 4.11

(of Lemma 4.9). There are exactly 192 elements of each type (A), (B) and (C).

Theorem 4.12

The cardinality of $\mathscr {C}$ is

$$\begin{aligned} |\mathscr {C}|=576. \end{aligned}$$

(4.10)

Proof

The statement is a direct consequence of Corollary 4.11. Alternatively, one can directly compute the cardinality of $\mathscr {C}$ using the computer software Macaulay2 [37] with the package InvariantRing [30]. $\square$

Remark 4.13

We observe that the Cremona-cubes group $\mathscr {C}$ is isomorphic to $((A_4\times A_4)\rtimes \mathbb {Z}/2\mathbb {Z})\rtimes \mathbb {Z}/2\mathbb {Z}$, where $A_4<S_4$ is the alternating subgroup in the symmetric group of four elements, i.e. the subgroup consisting of permutations with even order. This identification is obtained using the function StructureDescription of the system for computational discrete algebra GAP [32]⁴. On the other hand, in the same way, we have that the subgroup $\mathscr {C}_{{\textit{(B)}}}<\mathscr {C}$ is isomorphic $(((\mathbb {Z}/2\mathbb {Z})^{\times 4}\rtimes \mathbb {Z}/3\mathbb {Z})\rtimes \mathbb {Z}/2\mathbb {Z})\rtimes \mathbb {Z}/2\mathbb {Z}$⁵.

4.1 The Cubes of ${{\,\textrm{c}\,}}_3$

Let us now explain the origin of the name Cremona-cubes group. The configuration of the points in $\mathscr {R}$ is known in the literature as the Reye configuration or also the $D_4$ configuration (see [21, 25]). Alternatively, one can say that the tetrahedra defined by $\mathscr {E},\mathscr {P}$ and $\mathscr {Q}$ constitute a desmic triple (see [56, App. B.5.2]). Explicitly, the elements of $\mathscr {R}$ are the points of a $(12_4\ 16_3)$ configuration, i.e. 12 points and 16 lines with the property that there are four lines through each point and three points on each line.

Let us consider the following set of hyperplanes of $\mathbb {P}^3$

(4.11)

where . Let us now focus on some affine chart , for some , with the usual affine coordinates

(4.12)

and denote by $\overline{{\mathscr {H}}}$ the following set of affine hyperplanes:

(4.13)

Fig. 6

The configuration, in the chart $\{x_1\not =0\}\subset \mathbb {P}^3$, of the points in $\mathscr {R}$

There are twelve planes in $\overline{\mathscr {H}}$. Six of them are faces of the cube with vertices $\mathscr {P}\cup \mathscr {Q}$ and the remaining six are symmetry planes of the cube containing pairs of parallel lines. Using these planes, an alternative description of the Reye configuration is given by Hilbert in terms of sextuples of co-planar points [52].

Now, a direct check shows that the Cremona-cubes group acts (with trivial stabilizer) on the set $\overline{{\mathscr {H}}}$. This observation provide a different point of view which allows one to work in an affine setting.

Another way to understand the action of $\mathscr {C}$ is to look at the three cubes $C_{\mathscr {E}\mathscr {P}}$, $C_{\mathscr {E}\mathscr {Q}}$ and $C_{\mathscr {P}\mathscr {Q}}$ which have vertices, respectively, $\mathscr {E}\cup \mathscr {P}$, $\mathscr {E}\cup \mathscr {Q}$ and $\mathscr {P}\cup \mathscr {Q}$. While the group $\mathscr {C}_{{\tiny \textit{(B)}}}$ acts by just swapping $C_{\mathscr {E}\mathscr {P}}$ and $C_{\mathscr {E}\mathscr {Q}}$ (and keeping $C_{\mathscr {P}\mathscr {Q}}$ fixed), the Cremona-cubes group $\mathscr {C}$ permutes the three cubes.

In what follows, the two net of quadrics, respectively, generated by $\mathscr {E}\cup \mathscr {P}$ and $\mathscr {E}\cup \mathscr {Q}$ will play a fundamental rôle.

Definition 4.14

We will call $\Sigma _{\mathscr {P}}$ and $\Sigma _{\mathscr {Q}}$ the nets of quadrics, respectively, generated by ${\mathscr {E}\cup \mathscr {P}}$, ${\mathscr {E}\cup \mathscr {Q}}$. Precisely, we have:

(4.14a)

(4.14b)

where

$$\begin{aligned} S_1^{(\pm )} = x_1 x_2\pm x_4 x_3, \quad S_2^{(\pm )} = x_1 x_3 \pm x_4 x_2, \quad S_3^{(\pm )} = x_1 x_4 \pm x_2 x_3. \end{aligned}$$

(4.15)

Remark 4.15

Note that the projective subspaces (planes) $\Sigma _{\mathscr {P}}, \Sigma _{\mathscr {Q}}, \subset \mathbb {P}H^0(\mathbb {P}^3,\mathscr {O}_{\mathbb {P}^3}(2))\cong \mathbb {P}^9$ do not intersect, i.e.

$$\begin{aligned} \Sigma _{\mathscr {P}} \cap \Sigma _{\mathscr {Q}}= \varnothing . \end{aligned}$$

(4.16)

In other words, there is no quadric passing through all the points in $\mathscr {R}$.

We will see in Sects. 6 and 7 that these nets are key tools in the computation of the invariants of the maps of the form $g\circ {{\,\textrm{c}\,}}_3$ for $g\in \mathscr {C}$.

Remark 4.16

In what follows, we shall consider the pencil of quartics having nodes precisely at $\mathscr {R}$ (see in Sects. 6.3 and 7.3). Its existence is a classical fact (see [56, App. B.5.2]), and it is called desmic pencil. In particular, a desmic pencil contains exactly three reducible members called desmic quartics.

5 The Spaces of Initial Values and the Algebraic Entropy

In this section, we study the confinement of the indeterminacies of the maps $\Phi \in {{\,\textrm{Bir}\,}}(\mathbb {P}^3)$ of the form $\Phi =g\circ {{\,\textrm{c}\,}}_3$, for $g\in \mathscr {C}$, via some space of initial values. We will prove in Propositions 5.3, 5.4 and 5.7 that the growth behaviour of $d_n^\Phi$ only depends on the type of $g\in \mathscr {C}$. The same result is also true for the maps of the form $\Psi ={{\,\textrm{c}\,}}_3\circ g$. Indeed, the birational transformations $\Phi = g\circ {{\,\textrm{c}\,}}_3$ and $\Psi ={{\,\textrm{c}\,}}_3\circ g$ have the same algebraic entropy because they are conjugated via $g^{-1}$ which is of the same type of g as per Lemma 4.9 (see Remark 1.4).

The results contained in this section can be seen either directly, or using the approach described in [7] for maps $\Phi$ coming from the composition of the Cremona map ${{\,\textrm{c}\,}}_M$ (1.1) with projectivities using the method of singular orbits, i.e. sequences of the form

where $1\le i,j \le 4$, $k\ge 0$, $m_1,\ldots ,m_k \in \mathbb {P}^M$. Notice that (5.1) is a special instance of (1.10). We remark that the authors in [7, Theorem A.1] gave the general expression of the matrix representing the action in cohomology induced by a map of the form $\ell \circ {{\,\textrm{c}\,}}_M$ with $\ell \in \mathbb {P}{{\,\textrm{Gl}\,}}(M+1,\mathbb {C})$, with singular orbits of prescribed form. In general, this gives an estimate of the degree growth, and for some choices of the matrix $\ell$ it allows direct computations. In this paper, we compute explicitly the sequence of degrees using induction on the action induced in cohomology over a generic plane $H\subset \mathbb {P}^{3}$ of map $\Phi = g\circ {{\,\textrm{c}\,}}_3$, $g\in \mathscr {C}$. For instance, this approach provides us formulas (5.25) leading to Eq. (5.27) in Proposition 5.7.

5.1 The Case of the Standard Cremona Transformation

We start by reviewing the case $\Phi ={{\,\textrm{c}\,}}_3$ (see. [16] for more details). Let $\overline{\varepsilon } :{\overline{B}}\rightarrow \mathbb {P}^{3}$ be the blowup of $\mathbb {P}^3$ with centre the set of coordinate points. Let us denote by $E_{i}$ the exceptional divisor over the coordinate point $e_{i}$, for $i=1,\ldots ,4$. Then, one can choose (see [38, Section 4.6.2]) the following basis of the second singular cohomology group of ${\overline{B}}$:

$$\begin{aligned} H^{2}({\overline{B}},\mathbb {Z}) = \langle \varepsilon ^*H,E_1,E_2,E_3,E_4\rangle _{\mathbb {Z}}, \end{aligned}$$

(5.2)

where H is the class of an hyperplane in $\mathbb {P}^3$ and, with abuse of notation, we have denoted by the same symbols the exceptional divisors $E_i$, for $i=1,\ldots ,4$, and their cohomology classes. Moreover, the action of the standard Cremona transformation on the second cohomology group $H^{2}({\overline{B}},\mathbb {Z})$ is expressed, in terms of the basis (5.2), by the following matrix

$$\begin{aligned} ({{\,\textrm{c}\,}}_3^{-1})^* = {{\,\textrm{c}\,}}_3^*= \begin{pmatrix} 3 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 \\ -2 &{}\quad 0 &{}\quad -1 &{}\quad -1 &{}\quad -1 \\ -2 &{}\quad -1 &{}\quad 0 &{}\quad -1 &{}\quad -1 \\ -2 &{}\quad -1 &{}\quad -1 &{}\quad 0 &{}\quad -1 \\ -2 &{}\quad -1 &{}\quad -1 &{}\quad - 1 &{}\quad 0 \end{pmatrix} \end{aligned}$$

(5.3)

see for instance [16] or [7, Eq. (3.1)] evaluated at $d=3$.

Remark 5.1

Since $\mathscr {R}\smallsetminus \mathscr {E}= {{\,\textrm{Fix}\,}}{{\,\textrm{c}\,}}_3$, also ${{\,\textrm{Bl}\,}}_{\mathscr {R}}\mathbb {P}^3$ is a space of initial values for ${{\,\textrm{c}\,}}_3$, but it is superfluous to blowup all $\mathscr {R}$.

We divide the study of the confinement of the indeterminacies accordingly to the possible types of g, namely (A), (B) or (C).

From now on, given any $g\in \mathscr {C}$, we will denote by $\varepsilon _g:B_g\rightarrow \mathbb {P}^3$ the blowup of $\mathbb {P}^3$ with center the finite set $\langle g \rangle \cdot \mathscr {E}$. Notice that, since $B_g$ is the blowup of $\mathbb {P}^3$ with centre an n-tuple of distinct reduced points, the class of its canonical divisor is:

$$\begin{aligned} -K_{B_g}=4\varepsilon _{g}^*H-2 \underset{a\in \langle g\rangle \cdot \mathscr {E}}{\sum }D_a, \end{aligned}$$

(5.4)

where $D_a$ is the exceptional divisor over the point $a\in \langle g \rangle \cdot \mathscr {E}$ (see [38, Section 1.4.2]).

Sometimes, with abuse of notation we will denote by $\Phi :B_g\dashrightarrow B_g$ the natural lift of a projective map $\Phi \in {{\,\textrm{Bir}\,}}(\mathbb {P}^3)$ to the variety $B_g$. Moreover, when no ambiguity is present, we will denote by the same symbol a divisor and its cohomology class.

Notation 5.2

In what follows, given a birational map $\Phi \in {{\,\textrm{Bir}\,}}(X)$, for X smooth projective variety, we will denote by $\Phi _{*}$ the linear operator

$$\begin{aligned} \Phi _*=(\Phi ^{-1})^*\in {{\,\textrm{Gl}\,}}(H^2(X,\mathbb {Z})). \end{aligned}$$

(5.5)

Before proceeding, we recall that, if $\varepsilon :B\rightarrow \mathbb {P}^3$ is a space of initial values for a birational map $\Phi \in {{\,\textrm{Bir}\,}}(\mathbb {P}^3)$, then the degree $d_{n}^{\Phi }$ of the n-th iterate is given by formula (1.17) (see Sect. 1).

5.2 Case (A)

Let $g\in \mathscr {C}$ be a projectivity of type (A). Without loss of generality, we can suppose that g acts on the set $\{\mathscr {E},\mathscr {P},\mathscr {Q}\}$ by swapping $\mathscr {E}$ and $\mathscr {P}$ (see Lemma 4.4). Recall that, in this case, the blowup $B_g$ of $\mathbb {P}^3$ with centre $\langle g \rangle \cdot \mathscr {E}= \mathscr {E}\cup \mathscr {P}$ is a space of initial values (see Remark 4.7). Let us fix the following basis of the second cohomology group of $B_{g}$:

$$\begin{aligned} H_{{\tiny \textit{(A)}}}^2 := H^{2}\left( B_{g},\mathbb {Z}\right) = \langle \varepsilon _{g}^*H,E_1,E_2,E_3,E_4,P_1,P_2,P_3,P_4\rangle _{\mathbb {Z}}, \end{aligned}$$

(5.6)

where, as above, H is the class of an hyperplane in $\mathbb {P}^3$, $E_i$ is the cohomology class of the exceptional divisor over the point $e_i$, for $i=1,\ldots ,4$, and $P_i$ is the cohomology class of the exceptional divisor over the point $p_i$, for $i=1,\ldots ,4$. We want to compute the action induced by $\Phi =g\circ {{\,\textrm{c}\,}}_3$ on the cohomology group $H_{{\tiny \textit{(A)}}}^2$. Equivalently, we want to compute the matrix representing $\Phi _*$ with respect to the basis (5.6).

First, notice that the action of the standard Cremona transformation on $\varepsilon _{g}^*H, E_1, \ldots , E_4$ is given by the matrix (5.3), while the elements $P_i$ are fixed by ${{{\,\textrm{c}\,}}_3}_*$ because they lie over the points $p_i$ which are fixed by ${{\,\textrm{c}\,}}_3$.

Since g sends hyperplanes to hyperplanes and it swaps the sets $\mathscr {E}$ and $\mathscr {P}$, the matrix representing $g_*$ with respect to the basis (5.6) has the following block decomposition:

where $M_1$ and $M_2$ are $4\times 4$ permutation matrices. In terms of singular orbits [7] this implies that there are four closed singular orbits of length two.

We finally obtain the action of $\Phi _{*}$ on $H_{{\tiny \textit{(A)}}}^2$ as the composition $\Phi _*=g_*\circ {{{\,\textrm{c}\,}}_3}_*$. Precisely, there exist two permutations $\sigma _1,\sigma _2$ in the symmetric group ${{\,\textrm{S}\,}}_4$ of four elements $\{1,2,3,4\}$ such that

Notice that $\sigma _1$ (resp. $\sigma _2$) corresponds to the block $M_1$ (resp. $M_2$). The same action can be recovered from the four singular orbits using [7, Eqs. (4.1,4.3)].

Then, we obtain the main result of this subsection.

Proposition 5.3

Consider the birational map $\Phi =g\circ {{\,\textrm{c}\,}}_{3} \in {{\,\textrm{Bir}\,}}(\mathbb {P}^{3})$ for $g\in \mathscr {C}$ of type (A). Then, the following formula is true for all $n\in \mathbb {N}$:

$$\begin{aligned} (\Phi _{*})^{n}(\varepsilon _{g}^{*}H ) = \left( 2n^{2}+1 \right) \varepsilon _{g}^{*}H - n\left( n-1 \right) \sum _{j=1}^{4} E_{j}- n\left( n+1 \right) \sum _{j=1}^{4} P_{j}. \end{aligned}$$

(5.9)

As a consequence, we have $d_n^\Phi =2n^2+1$, that is the map $\Phi$ is integrable according to the algebraic entropy.

Proof

First notice that the following formulas are a direct consequence of Eq. (5.8):

$$\begin{aligned} \Phi _{*}\left( \underset{j=1}{\overset{4}{\sum }} E_j\right)&=4\varepsilon _{g}^*H-3 \underset{j=1}{\overset{4}{\sum }} P_j, \end{aligned}$$

(5.10a)

$$\begin{aligned} \Phi _{*}\left( \underset{j=1}{\overset{4}{\sum }} P_j\right)&= \underset{j=1}{\overset{4}{\sum }} E_{\sigma _2(j)}= \underset{j=1}{\overset{4}{\sum }} E_{j}. \end{aligned}$$

(5.10b)

Now the proof goes by induction on $n\in \mathbb {N}$. The case $n=0$ is trivial, while the case $n=1$ follows from Eq. (5.8). We move now to the proof of the inductive step. Suppose that formula (5.9) holds true for some $n\in \mathbb {N}$, we want to prove that it is also true for $n+1$. This can be shown as follows:

$$\begin{aligned} (\Phi _{*})^{n+1}( \varepsilon _{g}^{*}H )= & {} \Phi _*\left[ \left( \Phi _*\right) ^n\left( \varepsilon _{g}^*H\right) \right] \nonumber \\= & {} \Phi _* \left[ \left( 2n^{2}+1 \right) \varepsilon _{g}^{*}H - n\left( n-1 \right) \sum _{j=1}^{4} E_{j}- n\left( n+1 \right) \sum _{j=1}^{4} P_{j}\right] \nonumber \\= & {} \left( 2n^{2}+1\right) \left( 3\varepsilon _{g}^*H-2 \underset{j=1}{\overset{4}{\sum }} P_j\right) - n\left( n-1 \right) \underset{j=5}{\overset{8}{\sum }} \left( 4\varepsilon _{g}^*H-3 \underset{j=1}{\overset{4}{\sum }} P_j\right) \nonumber \\{} & {} - n\left( n+1 \right) \underset{j=1}{\overset{4}{\sum }} E_{j} \nonumber \\= & {} \left[ 2\left( n+1 \right) ^{2}+1 \right] \varepsilon _{g}^{*}H - n\left( n+1 \right) \underset{j=1}{\overset{4}{\sum }} E_{j} - \left( n+1 \right) \left( n+2 \right) \underset{j=1}{\overset{4}{\sum }} P_{j},\nonumber \\ \end{aligned}$$

(5.11)

where the third equality is a consequence of Eq. 5.10. From Remark 1.4, since $d_{n}^{\Phi }$ is subexponential, we have $S_{\Phi }=0$, and hence, the statement follows. $\square$

5.3 Case (B)

In this case, a space of initial values is $B_g={{\,\textrm{Bl}\,}}_{\mathscr {E}}\mathbb {P}^3$ and we can chose as basis of $H^2(B_g,\mathbb {Z})$ the one given in Eq. (5.2). Recall that there is a matrix representing g which is a permutation matrix with signs. Since we will focus on the action induced on the second singular cohomology group of $B_g$ by the map $\Phi = g\circ {{\,\textrm{c}\,}}_3$, it is enough to study the action on set $\mathscr {E}$. Thus, it is enough to suppose that g is a permutation matrix in the usual sense. As a consequence, the matrix representing $g_*$ in our basis is a permutation matrix with $\varepsilon _{g}^*H$ as eigenvector, i.e.

where M is a $4\times 4$ permutation matrix. In terms of singular orbits [7], this implies that there are four closed singular orbits of length one.

After composing $g_*$ with Eq. 5.3, we obtain the action of $\Phi _{*}$ on $H_{{\tiny \textit{(B)}}}^2$:

where $\sigma$ is the element in ${{\,\textrm{S}\,}}_4$ corresponding to the matrix M. The same action can be recovered from the four singular orbits using [7, Eqs. (4.1,4.3)].

As a consequence, we have the main result of this subsection.

Proposition 5.4

Let $g\in \mathscr {C}$ be an element of type (B). Then, for the map $\Phi =g\circ {{\,\textrm{c}\,}}_3 \in {{\,\textrm{Bir}\,}}(\mathbb {P}^{3})$, the following formulas hold true for all $n\in \mathbb {N}$:

$$\begin{aligned} \left( \Phi _{*}\right) ^{n}(\varepsilon _{g}^{*}H )&= {\left\{ \begin{array}{ll} 3 \varepsilon _{g}^{*}H - 2 \underset{j=1}{\overset{4}{\sum }} E_{j} &{} \text {for }n\text { odd}, \\ \varepsilon _{g}^{*}H &{} \text {for }n\text { even}, \end{array}\right. } \end{aligned}$$

(5.14a)

$$\begin{aligned} \left( \Phi _{*}\right) ^{n}\left( E_{i}\right)&= {\left\{ \begin{array}{ll} \varepsilon _{g}^{*} H - \underset{j\ne \sigma ^{n-1}(i)}{\overset{}{\sum }} E_{\sigma ^{n}(j)} &{} \text {for }n\text { odd}, \\ E_{\sigma ^{n}(i)} &{} \text {for }n\text { even}, \end{array}\right. }&\hbox {for }i=1,\ldots ,4. \end{aligned}$$

(5.14b)

So, the map $\Phi$ is periodic (see Definition 1.5), and hence integrable, with two-periodic degrees:

$$\begin{aligned} d_{n}^\Phi = {\left\{ \begin{array}{ll} 3 &{} \text {for }n\text { odd}, \\ 1 &{} \text {for }n\text { even}. \end{array}\right. } \end{aligned}$$

(5.15)

Proof

As in the proof of Proposition 5.3, we proceed by evaluating the action of $\Phi _{*}$ on the combination $\underset{j=1}{\overset{4}{\sum }} E_j$. From (5.13), we have:

$$\begin{aligned} \Phi _{*}\left( \underset{i=1}{\overset{4}{\sum }} E_j \right) = 4 \varepsilon _{g}^{*} H - 3 \underset{j=1}{\overset{4}{\sum }} E_{j}, \end{aligned}$$

(5.16)

which, again from (5.13) implies:

$$\begin{aligned} \left( \Phi _{*}\right) ^{2}( \varepsilon _{g}^{*} H )= & {} \Phi _{*}\left( 3 \varepsilon _{g}^{*}H - 2 \underset{j=1}{\overset{4}{\sum }} E_{j}\right) \nonumber \\= & {} 3 \left( 3 \varepsilon _{g}^{*} H - 2 \underset{j=1}{\overset{4}{\sum }} E_{j}\right) -2\left[ 4 \varepsilon _{g}^{*} H - 3 \underset{j=1}{\overset{4}{\sum }} E_{j}\right] \nonumber \\= & {} \varepsilon _{g}^{*} H. \end{aligned}$$

(5.17)

As a consequence, we get formula (5.14a). On the other hand, still from (5.13) and (5.16), we have:

$$\begin{aligned} \left( \Phi _{*}\right) ^{2}\left( E_{i}\right)= & {} \Phi _{*}\left( \varepsilon _{g}^{*}H - \underset{j\ne i}{\overset{}{\sum }} E_{\sigma (j)}\right) \nonumber \\= & {} 3 \varepsilon _{g}^{*} H - 2 \underset{j=1}{\overset{4}{\sum }} E_{j} - \Phi _{*}\left( \underset{j=1}{\overset{4}{\sum }} E_{j} - E_{\sigma (i)}\right) \nonumber \\= & {} 3 \varepsilon _{g}^{*} H - 2 \underset{j=1}{\overset{4}{\sum }} E_{j} - \left[ 4 \varepsilon _{g}^{*} H - 3 \underset{j=1}{\overset{4}{\sum }} E_{j}\right] + \varepsilon _{g}^{*}H - \underset{j\ne \sigma ^{2}(i)}{\overset{}{\sum }} E_{j} \nonumber \\= & {} E_{\sigma ^{2}(j)}. \end{aligned}$$

(5.18)

Again, we obtain formula (5.14b). The periodicity of the degrees of $\Phi$ follows immediately from formulas (5.14) and (1.17). The algebraic entropy of a limited sequence is clearly zero, and this ends the proof. $\square$

An immediate corollary of Proposition 5.4 concerns the periodicity of $\Phi _*$ for $\Phi \in {{\,\textrm{Bir}\,}}(\mathbb {P}^3)$ of the form $g\circ {{\,\textrm{c}\,}}_3$, for $g\in \mathscr {C}$ of type (B).

Corollary 5.5

In the hypotheses of Proposition 5.4, we have

(5.19)

Remark 5.6

We remark that from Proposition 5.4 and Corollary 5.5 it follows that, while the degrees of the maps $\Phi =g\circ {{\,\textrm{c}\,}}_3$, with $g\in \mathscr {C}$ of type (B), are two-periodic, the map itself is not necessarily two-periodic. Indeed, from Corollary 5.5 it follows that the order of the map $\Phi$ can be 2,4, or 6. The situation here is similar to the periodic QRT maps found in [91], with the difference that, for our maps, odd orders are not possible.

5.4 Case (C)

Let $g\in \mathscr {C}$ be a projectivity of type (C). Then, a space of initial values for $\Phi =g\circ {{\,\textrm{c}\,}}_3$ is (see Remark 4.7) the variety

$$\begin{aligned} B_g={{\,\textrm{Bl}\,}}_{\mathscr {R}}\mathbb {P}^3. \end{aligned}$$

(5.20)

The cyclic subgroup of $\mathscr {C}$ generated by g acts transitively on the set $\{\mathscr {E},\mathscr {P},\mathscr {Q}\}$ (see Lemma 4.5). Without loss of generality, we can suppose that g acts as follows:

Let us fix the following basis of the second cohomology group of $B_{g}$:

$$\begin{aligned} H_{{\tiny \textit{(C)}}}^2 := H^{2}\left( B_{g},\mathbb {Z}\right) = \langle \varepsilon _{g}^*H,E_1,E_2,E_3,E_4, P_1,P_2,P_3,P_4,Q_1,Q_2,Q_3,Q_4\rangle _{\mathbb {Z}}, \end{aligned}$$

(5.22)

where H, $E_i,P_i$, for $i=1,\ldots ,4$, are as in Sect. 5.2, and $Q_{i}$, for $i=1,\ldots ,4$, is the cohomology class of the exceptional divisor contracted by $\varepsilon _{g}$ to $q_i$.

Analogously to Sect. 5.2, also in this case, the action of the standard Cremona transformation on the elements $\varepsilon _{g}^*H,E_1,E_2,E_3,E_4$ agrees with Equation (5.3) while the elements $P_i,Q_i$, for $i=1,\ldots ,4$, are fixed by ${{{\,\textrm{c}\,}}_3}_*$ because they lie over the fixed points of ${{\,\textrm{c}\,}}_3$. In terms of singular orbits [7], this implies that there are four closed singular orbits of length three.

So, as in the previous section, the linear map $g_*=(g^{-1})^*$ fixes $\varepsilon _{g}^*H$ and it permutes the remaining elements of the basis of the cohomology we have chosen. As a consequence, the matrix that represents $g_*$ with respect to the basis (5.22) has a block decomposition similar to the block decomposition given in (5.7). In particular, the cyclic subgroup of ${{\,\textrm{Gl}\,}}(H_{{\tiny \textit{(C)}}}^2,{\mathbb {Z}})$ generated by $g_*$ induces a transitive action on the set .

Finally, the action of $\Phi _{*}=g_*\circ {{{\,\textrm{c}\,}}_3}_*$ on $H_{{\tiny \textit{(C)}}}^2$ is:

where $\sigma _1,\sigma _2,\sigma _3$ are elements of ${{\,\textrm{S}\,}}_4$ corresponding to the nonzero $4\times 4$ blocks of the matrix representing $g_*$ with respect to the basis in (5.22). The same action can be recovered from the four singular orbits using [7, Eqs. (4.1,4.3)].

As a consequence of the above description, we have the main result of this subsection.

Proposition 5.7

Let $g\in \mathscr {C}$ be an element of type (C). Then, for all $n\ge 1$, the following formula holds true for the map $\Phi =g\circ {{\,\textrm{c}\,}}_{3}\in {{\,\textrm{Bir}\,}}( \mathbb {P}^{3})$:

$$\begin{aligned} (\Phi _{*})^{n}( \varepsilon _{g}^{*}H) = d_{n} \varepsilon _{g}^{*}H - f_{n}\sum _{j=1}^{4} E_{j} - b_{n}\sum _{j=1}^{4} P_{j} - c_{n}\sum _{j=1}^{4} Q_{j}, \end{aligned}$$

(5.24)

where the coefficients solve the following system of difference equations:

$$\begin{aligned} \begin{aligned} d_{n}=d_n^\Phi = 3 d_{n-1} - 4 f_{n-1}, \quad f_{n} = c_{n-1}, \\ b_{n} = 2 d_{n-1} - 3 f_{n-1}, \quad c_{n} = b_{n-1}, \end{aligned} \end{aligned}$$

(5.25)

with initial conditions:

$$\begin{aligned} d_{0}= 1, \, f_{0} = 0, \, b_{0} = 0, \, c_{0} = 0. \, \end{aligned}$$

(5.26)

This implies that the map $\Phi$ has positive algebraic entropy given by:

$$\begin{aligned} S_{{\tiny \textit{(C)}}} = 2 \log \varphi , \end{aligned}$$

(5.27)

where $\varphi$ is the golden ratio, i.e. the only positive solution of the algebraic equation $\varphi ^{2}=\varphi +1$. That is, the map $\Phi$ is non-integrable according to the algebraic entropy.

Remark 5.8

We remark that Proposition 5.7 is coherent with the upper bound on the algebraic entropy presented in [7, Theorem 4.2]. Explicitly, for maps of the form $\ell \circ {{\,\textrm{c}\,}}_M$, where $\ell \in \mathbb {P}{{\,\textrm{Gl}\,}}(M+1,\mathbb {C})$, with at least one singular orbit we have that $S_{\ell \circ {{\,\textrm{c}\,}}_M}< \log M$. Indeed, in the case of Proposition 5.7 we have $M=3$ and

$$\begin{aligned} S_{{\tiny \textit{(C)}}} = \log \left( \frac{3+\sqrt{5}}{2}\right) <\log 3. \end{aligned}$$

(5.28)

We will see in Sects. 6 and 7 that this implies a certain regularity which we do not have for “generic” maps.

Proof

As in the proof of Proposition 5.3, we start by evaluating $\Phi _*$ on the sums $\sum _{j=1}^4E_j$, $\sum _{j=1}^4P_j$ and $\sum _{j=1}^4Q_j$. Thanks to Eq. (5.23), we have:

$$\begin{aligned} \Phi _{*}\left( \underset{j=1}{\overset{4}{\sum }} E_j\right)&=4\varepsilon _{g}^*H-3 \underset{j=1}{\overset{4}{\sum }} P_j,&\end{aligned}$$

(5.29a)

$$\begin{aligned} \Phi _{*}\left( \underset{j=1}{\overset{4}{\sum }} P_j\right)&= \underset{j=1}{\overset{4}{\sum }} Q_{\sigma _2(j)}= \underset{j=1}{\overset{4}{\sum }} Q_{j},&\end{aligned}$$

(5.29b)

$$\begin{aligned} \Phi _{*}\left( \underset{j=1}{\overset{4}{\sum }} Q_j\right)&= \underset{j=1}{\overset{4}{\sum }} E_{\sigma _2(j)}= \underset{j=1}{\overset{4}{\sum }} E_{j}. \end{aligned}$$

(5.29c)

We proceed now by induction on $n\ge 1$. The case $n=1$ is a direct computation. We suppose now that Proposition 5.7 is true for some $n\ge 1$ and we prove it for $n+1$. We have:

$$\begin{aligned} \begin{aligned} (\Phi _{*})^{n+1}( \varepsilon _{g}^{*}H )&=\Phi _*\left[ \left( \Phi _*\right) ^n\left( \varepsilon _{g}^*H\right) \right] \\ {}&= \Phi _* \left[ d_{n} \varepsilon _{g}^{*}H - f_{n} \underset{j=1}{\overset{4}{\sum }} E_{j} - b_n \underset{j=1}{\overset{4}{\sum }} P_{j} - c_n \underset{j=1}{\overset{4}{\sum }} Q_{j}\right] \\ {}&=\left( 3d_n-4f_{n} \right) \varepsilon _{g}^*H-c_n \underset{j=1}{\overset{4}{\sum }} E_j-\left( 2d_{n}-3f_{n} \right) \underset{j=1}{\overset{4}{\sum }} P_j-b_n \underset{j=1}{\overset{4}{\sum }} Q_j, \end{aligned} \end{aligned}$$

(5.30)

where the third equality is a consequence of Eq. (5.29). On the other hand, we must have:

$$\begin{aligned} (\Phi _{*})^{n+1}( \varepsilon _{g}^{*}H ) = d_{n+1} \varepsilon _{g}^{*}H - f_{n+1}\sum _{j=1}^{4} E_{j} - b_{n+1}\sum _{j=1}^{4} P_{j} - c_{n+1}\sum _{j=1}^{4} Q_{j}. \end{aligned}$$

(5.31)

So, the condition is satisfied by equating with the right-hand side of (5.30) and (5.31) and invoking the linear independence of the generators of $H_2(B_g,\mathbb {Z})$. This implies that $d_n,f_n,b_n$ and $c_n$ satisfy the system (5.25) with initial conditions (5.26).

In order to compute the algebraic entropy from Definition 1.3, we need to evaluate the asymptotic behaviour of $d_{n}^{\Phi }$ in Eq. (5.25). Since the system (5.25) is linear we use the technique explained in [27, Chap. 3]. Writing the system as:

$$\begin{aligned} \begin{pmatrix} d_n \\ f_n \\ b_n \\ c_n \end{pmatrix} = M_g \begin{pmatrix} d_{n-1} \\ f_{n-1} \\ b_{n-1} \\ c_{n-1} \end{pmatrix}, \quad \hbox { where } M_g = \begin{pmatrix} 3&{}\quad -4&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 1 \\ 2&{}\quad -3&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 1&{}\quad 0 \end{pmatrix}, \end{aligned}$$

(5.32)

then the solution is:

$$\begin{aligned} \begin{pmatrix} d_n \\ f_n \\ b_n \\ c_n \end{pmatrix} = M_g^n \begin{pmatrix} d_{0} \\ f_{0} \\ b_{0} \\ c_{0} \end{pmatrix} = M_g^n \begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \end{pmatrix}. \end{aligned}$$

(5.33)

Computing $M_g^n$, e.g. using Putzer algorithm [27, Sect. 3.1.1], we obtain the following solution for all $n\in \mathbb {N}$:

(5.34)

where $\varphi$ is the golden ratio. Since $d_n=d_n^\Phi$, we have:

$$\begin{aligned} d_n^\Phi \sim \varphi ^{2n}, \quad n\rightarrow \infty , \end{aligned}$$

(5.35)

and, from (1.6), formula (5.27) follows. $\square$

6 Covariant Linear Systems

In this section, we will introduce a notion of covariant linear system with respect a fixed divisor. We will see in the next section that these objects are key tools in the computation of the invariants of the maps of the form $\Phi =g\circ {{\,\textrm{c}\,}}_3$, for $g\in \mathscr {C}$. Moreover, we will compute covariant linear systems of quadrics for g of type (A) and (B) (Propositions 6.5, 6.9 and 6.11) and covariant linear systems of quartics for g of type (C) (Proposition 6.14). As in Sect. 5, the results in this section work also for the birational maps of the form ${{\,\textrm{c}\,}}_3\circ g$ (see Remark 6.2).

In what follows, we shall need the following definition.

Definition 6.1

Let X be a smooth projective variety, and let $\Phi \in {{\,\textrm{Bir}\,}}(X)$ be a birational map. Let also $D\in {{\,\textrm{Div}\,}}(X)$ be a divisor. A linear system $\Sigma \subset |{\mathscr {L}}|$, for some line bundle ${\mathscr {L}}$, is D-covariant if, for any $E\in \Sigma$, we have $\Phi _*E\in \Sigma +D$, where

(6.1)

In this context, if $\Phi _*E=E+D$, we will say that E is D-invariant.

Remark 6.2

We remark that any result about the existence of D-covariant linear systems for maps of the form $g\circ {{\,\textrm{c}\,}}_3$, for $g\in \mathscr {C},$ also implies the existence of ${{\widetilde{D}}}$-covariant linear systems for maps of the form ${{\,\textrm{c}\,}}_3\circ g$ for some divisor ${{\widetilde{D}}}$. Indeed, g and $g^{-1}$ are of the same type as per Lemma 4.9 and the equality

$$\begin{aligned} (g\circ {{\,\textrm{c}\,}}_3)_*S=S+D \end{aligned}$$

(6.2)

implies

$$\begin{aligned} ({{\,\textrm{c}\,}}_3\circ g^{-1})_*S=S-({{\,\textrm{c}\,}}_3\circ g^{-1})_*D. \end{aligned}$$

(6.3)

Remark 6.3

Let $\Phi =g\circ {{\,\textrm{c}\,}}_3\in {{\,\textrm{Bir}\,}}(\mathbb {P}^3)$, for some $g\in \mathscr {C}$, be a birational map, and let $\Sigma$ be a D-covariant linear system for some $D\in {{\,\textrm{Div}\,}}(\mathbb {P}^3)$. Then, since $g\circ {{\,\textrm{c}\,}}_3$ only contracts the coordinate hyperplanes , for $i=1,\ldots ,4$, the divisor D has the form

$$\begin{aligned} D=\underset{i=1}{\overset{4}{\sum }}n_iH_i, \end{aligned}$$

(6.4)

for some $n_i\in \mathbb {Z}$, for $i=1,\ldots ,4$. Notice also that, if B is a space of initial values for $\Phi$, $\Sigma$ is D-covariant if and only if the linear system of the strict transform of a general member of $\Sigma$, is covariant on B, i.e. called ${\widetilde{E}}$ the strict transform of a general member $E\in \Sigma$, we have ${\Phi }_*{\widetilde{E}}\in |{\widetilde{E}}|$.

We now start a case-by-case analysis of the D-covariant linear systems of quadrics for some divisor D, i.e. projective subspaces, $\Sigma \subset |\mathscr {O}_{\mathbb {P}^3}(2)|$ with the property that, $\Phi _*\Sigma =\Sigma +D\subset |\mathscr {O}_{\mathbb {P}^3}(2+\deg (D))|$. This will be enough to compute the invariants for maps of the form $g\circ {{\,\textrm{c}\,}}_3$ for $g\in \mathscr {C}$ of type (A) and (B) as we will show in Sect. 7. For type (C), we will need to consider D-covariant linear systems of quartics.

Notation 6.4

In what follows, we will denote by $H_i$ the the divisor associated with the hyperplane . Moreover, we will denote by ${\overline{H}}$ the divisor defined as the sum of the coordinate hyperplane divisors, i.e.

$$\begin{aligned} {\overline{H}}= \underset{i=1}{\overset{4}{\sum }} H_i. \end{aligned}$$

(6.5)

Sometimes, with abuse of notation, we will denote by $H_i$ also the i-th coordinate hyperplane.

6.1 Case (A)

As in Sect. 5.2, without loss of generality, we keep the assumption that $\Phi =g\circ {{\,\textrm{c}\,}}_3$, where $g\in \mathscr {C}$ is of type (A) and that it swaps $\mathscr {E}$ and $\mathscr {P}$. Then, we have the following.

Proposition 6.5

Let $g\in \mathscr {C}$ be an element of type (A) and let $\Phi \in {{\,\textrm{Bir}\,}}(\mathbb {P}^3)$ be the projective map defined as $\Phi =g\circ {{\,\textrm{c}\,}}_3$. Then, the net of quadrics $\Sigma _{\mathscr {P}}$ in Definition 4.14 is ${\overline{H}}$-covariant. Moreover, if $\Sigma$ is a positive-dimensional D-covariant linear system of quadrics, for some $D\in {{\,\textrm{Div}\,}}(\mathbb {P}^3)$, we have $D={\overline{H}}$ and $\Sigma \subset \Sigma _{\mathscr {P}}$.

Proof

Let $S\in \Sigma _{ \mathscr {P}}$ be a general element, and let ${\widetilde{S}}$ be its strict transform via $\varepsilon _{g}$, where $\varepsilon _g$ is the same as in Sect. 5.2. We will prove that $|{\widetilde{S}}|$ is covariant, i.e. $\Phi _*{\widetilde{S}}\in |{\widetilde{S}}|$ (see Remark 6.3). We have:

$$\begin{aligned} \Phi _*{\widetilde{S}}\sim \Phi _*\left( 2\varepsilon _{g}^*H- \underset{j=1}{\overset{4}{\sum }} E_j- \underset{j=1}{\overset{4}{\sum }} P_j\right) \sim 2\varepsilon _{g}^*H- \underset{j=1}{\overset{4}{\sum }} E_j- \underset{j=1}{\overset{4}{\sum }} P_j\sim {\widetilde{S}}, \end{aligned}$$

(6.6)

where the second equality is a consequence of formulas (5.10). Therefore, the net $\Sigma _{ \mathscr {P}}$ is ${\overline{H}}$-covariant.

Now, the strict transform ${\widetilde{S}}$ of a quadric $S\in \mathbb {P}^3$ is linear equivalent to the following divisor

$$\begin{aligned} {\widetilde{S}}\sim 2\varepsilon _{g}^*H- \underset{j=1}{\overset{4}{\sum }} n_jE_j- \underset{j=1}{\overset{4}{\sum }} m_jP_j, \end{aligned}$$

(6.7)

for some non-negative integers $n_j,m_j$, for $j=1,\ldots ,4$. If we impose the covariance, we get the conditions

$$\begin{aligned} {\left\{ \begin{array}{ll} \underset{j=1}{\overset{4}{\sum }} n_j=4,\\ n_i=m_{\sigma _1(i)} &{} \hbox { for} i=1,\ldots ,4. \end{array}\right. } \end{aligned}$$

(6.8)

where $\sigma _1$ is taken from (5.8). Now, up to relabeling the coordinates, we have three possibilities, namely

$$\begin{aligned} n_1=m_1=1,\ n_2=m_2=1,\ n_3=m_3=1,\ n_4=m_4=1, \end{aligned}$$

(6.9a)

$$\begin{aligned} n_1=m_1=2,\ n_2=m_2=1,\ n_3=m_3=1,\ n_4=m_4=0, \end{aligned}$$

(6.9b)

$$\begin{aligned} n_1=m_1=2,\ n_2=m_2=2,\ n_3=m_3=0,\ n_4=m_4=0. \end{aligned}$$

(6.9c)

Notice that, the first choice works for any permutation of four elements $\sigma _1$. Moreover, the second and the third choice of coefficients cut zero-dimensional linear systems. As a consequence, the only possible D-covariant and positive-dimensional linear system is obtained for $n_i=m_{i}=1$, for $i=1,\ldots ,4$. $\square$

Remark 6.6

If g swaps $\mathscr {E}$ and $\mathscr {Q}$, the statement of Proposition 6.5 is true with $\Sigma _{\mathscr {Q}}$ instead of $\Sigma _{\mathscr {P}}$ (see Definition 4.14).

Corollary 6.7

With the same notation and hypotheses in Proposition 6.5, the anticanonical system of $B_g$ is covariant. Moreover, we have $|-K_{B_g}|=|2{\widetilde{E}}|$ where ${\widetilde{E}}$ is the strict transform of a general member of $\Sigma _{\mathscr {P}}$.

Proof

The statement follows by applying the first equivalence in (6.6) to formula (5.4). $\square$

Remark 6.8

Notice that, every pair of points $q_i,q_j$ in $\mathscr {Q}$ cuts a unique quadric $S_{ij}$ in $\Sigma _{\mathscr {P}}$. Explicitly, with the notation in Sect. 4.1, the unique quadric of $\Sigma _{\mathscr {P}}$ passing through $q_i$ and $q_j$ is reducible and it is

$$\begin{aligned} S_{ij}=H_{ij}^\bullet + H_{hk}^\bullet , \end{aligned}$$

(6.10)

where

(6.11)

The strict transform of this quadric on some space of initial values is fixed by the action of $\Phi _*=(g\circ {{\,\textrm{c}\,}}_3)_*$, i.e. $S_{ij}$ is ${\overline{H}}$-invariant if and only if is invariant under g. Therefore, the existence of ${\overline{H}}$-invariant quadrics depends on the action of g on the third tetrahedron, namely the tetrahedron with $\mathscr {Q}$ as set of vertices.

6.2 Case (B)

We have the following result.

Proposition 6.9

Let $g\in \mathscr {C}$ be an element of type (B) and let $\Phi \in {{\,\textrm{Bir}\,}}(\mathbb {P}^3)$ be the birational map defined as $\Phi =g\circ {{\,\textrm{c}\,}}_3$. Then, the 5-dimensional linear system $\Sigma _{{\tiny \textit{(B)}}}\subset |\mathscr {O}_{\mathbb {P}^3}(2)|$ consisting of the quadrics containing $\mathscr {E}$ is ${\overline{H}}$-covariant.

Proof

First notice that $\Sigma _{{\tiny \textit{(B)}}}$ is 5-dimensional because the points in $\mathscr {E}$ are in general position. Let ${\widetilde{S}}$ be the strict transform of a general quadric $S\subset \mathbb {P}^3$. As in the proof of Proposition 6.5, we will prove that $|{\widetilde{S}}|$ is covariant. We have,

$$\begin{aligned} {\widetilde{S}}\sim 2\varepsilon _{g}^*H- \underset{i=1}{\overset{4}{\sum }} n_i E_i \end{aligned}$$

(6.12)

for some $n_i\ge 0$, for $i=1,\ldots ,4$. If we now impose the covariance and we apply formulas (5.13), we find the conditions

$$\begin{aligned} {\left\{ \begin{array}{ll} \underset{i=1}{\overset{4}{\sum }} n_i=4\\ n_i=n_{\sigma (i)} &{}\hbox { for }i=1,\ldots ,4, \end{array}\right. } \end{aligned}$$

(6.13)

where $\sigma \in {{\,\textrm{S}\,}}_4$ is the element corresponding to g (see Lemma 4.5). If we impose the above conditions for any g of type (B), and hence for any $\sigma \in {{\,\textrm{S}\,}}_4$, we get

$$\begin{aligned} n_i=1\hbox { for }i=1,\ldots ,4, \end{aligned}$$

which implies the thesis. $\square$

Corollary 6.10

With the same notation and hypotheses in Proposition 6.9, the anticanonical system of $B_g$ is covariant. Moreover, we have $|-K_{B_g}|=|2{\widetilde{E}}|$ where ${\widetilde{E}}$ is the strict transform of a general member of $\Sigma _{{\tiny \textit{(B)}}}$.

The linear system $\Sigma _{{\tiny \textit{(B)}}}$ in Proposition 6.9 is ${\overline{H}}$-covariant for all the $\Phi =g\circ {{\,\textrm{c}\,}}_3$ with g of type (B), but, in some instances, there are positive dimensional linear systems, which are D-covariant for some other divisor D. However, we will show in Proposition 7.13 that $\Sigma _{{\tiny \textit{(B)}}}$ suffices for the construction of the invariants. Rigorously, we have the following.

Proposition 6.11

Let us fix the same notation and hypotheses in Proposition 6.9. We have the following possibilities.

• Suppose g fixes exactly two points of $\mathscr {E}$, say $e_1$ and $e_2$. Then, the webs $\Sigma _{1}$ and $\Sigma _{2}$ of quadrics passing through $e_3,e_4$ and having, respectively, a node at $e_1$ and $e_2$ are, respectively, $(2H_1+H_3+H_4)$-covariant and $(2H_2+H_3+H_4)$-covariant.

• Suppose g fixes $\mathscr {E}$ pointwise. Then, for any divisor of the form $D=2H_i+H_j+H_k$, where i, j and k are different, there is a web of D-covariant quadrics and, for any divisor of the form $F=2H_i+2H_j$, where $i\not =j$, there is a net of F-covariant quadrics.

Remark 6.12

Notice that the identity ${{\,\textrm{Id}\,}}\in \mathscr {C}$ belongs to case (B). Therefore, the standard Cremona transformation ${{\,\textrm{c}\,}}_3={{\,\textrm{Id}\,}}\circ {{\,\textrm{c}\,}}_3$ has the linear system $\Sigma _{{\tiny \textit{(B)}}}$ in Proposition 6.9 as a ${\overline{H}}$-covariant linear system. Moreover, the set of ${\overline{H}}$-invariant divisors for ${{{\,\textrm{c}\,}}_3}$ consists of the disjoint union, inside $\Sigma _{{\tiny \textit{(B)}}}$, of the two nets of quadrics $\Sigma _{\mathscr {P}}$ and $\Sigma _{\mathscr {Q}}$ in Definition 4.14.

6.3 Case (C)

We start this last subsection by proving that in the case (C) we do not have D-covariant linear systems of quadric anymore.

Proposition 6.13

For any divisor $D\in {{\,\textrm{Div}\,}}(\mathbb {P}^3)$, there is no D-covariant linear system of quadrics for the map $\Phi$.

Proof

The strict transform ${\widetilde{S}}$ of a quadric $S\in \mathbb {P}^3$ is linear equivalent to the following divisor

$$\begin{aligned} {\widetilde{S}}\sim 2\varepsilon _{g}^*H- \underset{j=1}{\overset{4}{\sum }} n_jE_j- \underset{j=1}{\overset{4}{\sum }} m_jP_j- \underset{j=1}{\overset{4}{\sum }} k_jQ_j \end{aligned}$$

(6.14)

for some non-negative integers $n_i,m_{i},k_{i}$ for $i=1,\ldots ,4$. If we impose the covariance, we get the conditions

$$\begin{aligned} {\left\{ \begin{array}{ll} \underset{j=1}{\overset{4}{\sum }} n_j=4\\ n_i=m_{\sigma _1(i)} &{} i=1,\ldots ,4,\\ m_{i}=k_{\sigma _2(i)} &{} i=1,\ldots ,4. \end{array}\right. } \end{aligned}$$

(6.15)

where $\sigma _1$ and $\sigma _2$ are taken from (5.23). A quadric S satisfying (6.15) must pass through all the points in $\mathscr {R}$, and a dimension count shows that a similar quadric does not exist. $\square$

Although, in this case, there are no D-covariant linear systems of quadrics, for $D\in {{\,\textrm{Div}\,}}(\mathbb {P}^3)$, there is a $2{\overline{H}}$-covariant linear system of quartics. The proof of the following proposition is similar to the proof of Proposition 6.5.

Proposition 6.14

Let $g\in \mathscr {C}$ be an element of type (C) and let $\Phi \in {{\,\textrm{Bir}\,}}(\mathbb {P}^3)$ be the projective map defined as $\Phi =g\circ {{\,\textrm{c}\,}}_3$. Then, the pencil of quartics $\Xi _{\mathscr {R}}$ nodal at all the points of $\mathscr {R}$ is $2{\overline{H}}$-invariant. Moreover, if $\Sigma$ is a positive-dimensional D-covariant linear system of quartics for some $D\in {{\,\textrm{Div}\,}}(\mathbb {P}^3)$, we have $D=2{\overline{H}}$ and $\Sigma = \Xi _{\mathscr {R}}$.

Corollary 6.15

With the same notation and hypotheses in Proposition 6.14, the anticanonical system of $B_g$ is covariant. Moreover, we have $|-K_{B_g}|=|{\widetilde{E}}|$ where ${\widetilde{E}}$ is the strict transform of a general member of $\Xi _\mathscr {R}$.

Remark 6.16

We remark that the quartic pencil

is exactly the pencil mentioned in Remark 4.16. Its base locus consists of 16 lines, namely the 16 lines of the $(12_4\ 16_3)$ configuration (see Sect. 4.1). The resolution of its indeterminacies induces the crepant resolution⁶ of each fibre (see [34]) but three, namely the desmic surfaces. Therefore, we get a one-dimensional family of surfaces

$$\begin{aligned} Y \rightarrow \mathbb {P}^1 \end{aligned}$$

(6.17)

whose generic member is a K3 surface with 16 disjoint rational curves. This is the highest possible number of disjoint rational curves on a K3 surface and it is known to be achieved by Kummer surfaces of an abelian surface of the form $A=E\times E$ for E elliptic curve (see [56, Theorem B.5.6]).

7 Construction of the Invariants

In this section, we explain how to determine the existence of invariants in the three cases listed in Lemma 4.5 and how to compute all of them. We recall that, by invariant of a map $\Phi \in {{\,\textrm{Bir}\,}}(\mathbb {P}^M)$, we mean a rational function, i.e. a degree zero element $R=P/Q\in \mathbb {C}(x_1,\ldots ,x_{M+1})$ for $P,Q\in \mathbb {C}[x_1,\ldots ,x_{M+1}]$ homogeneous, such that:

$$\begin{aligned} \Phi _*(R)(x_1,\ldots ,x_{M+1})=R(x_1,\ldots ,x_{M+1}). \end{aligned}$$

(7.1)

As for the results in Sects. 5 and 6, the results in this section hold true for the maps of the form ${{\,\textrm{c}\,}}_3\circ g$ as well. Indeed, g and $g^{-1}$ are of the same type and, after composing the equality $R\circ \Phi \equiv R$ with $\Phi ^{-1}$ we find that, if R is invariant for $g\circ {{\,\textrm{c}\,}}_3$ then, it is also invariant for ${{\,\textrm{c}\,}}_3\circ g^{-1}$.

We recall the following known fact on the construction of invariants of birational maps adapted to our setting.

Lemma 7.1

Let $\Phi \in {{\,\textrm{Bir}\,}}(\mathbb {P}^3)$ be a projective map and let $D\in {{\,\textrm{Div}\,}}(\mathbb {P}^3)$ be a divisor. Let us consider a D-covariant linear system $\Sigma \subset |\mathscr {L}|= \mathbb {P}H^0(\mathbb {P}^3,{\mathscr {L}})$, for some line bundle ${\mathscr {L}}$. Suppose that there exists a pencil $\Xi \subset \Sigma$ of D-invariant divisors. In particular, $\Xi = \mathbb {P}V_\Xi$ for some vector subspace $V_\Xi \subset H^0(\mathbb {P}^3,\mathscr {L})$. Then, one can construct invariants of the map $\Phi$ by considering the meromorphic functions of the form $f=s_1/s_2$ for any given choice of $s_1,s_2\in V_\Xi$.

For a proof of Lemma 7.1, we refer to [28] (see also [16, 40] and reference therein).

Remark 7.2

Let $\Sigma$ be a D-covariant linear system, and let $F_1,F_2\in \Sigma$ be two D-invariant elements. Then, the elements of the pencil generated by $F_1$ and $F_2$ are not necessarily D-invariant. This is a consequence of the fact that a projectivity of $\mathbb {P}^1$ is uniquely determined by its value on three points (see [31, Section 1.3]).

The results in Sect. 5 lead us to expect the following behaviour of the maps of the form $\Phi =g\circ {{\,\textrm{c}\,}}_3$:

• Case (A) the map admits two invariants,⁷

• Case (B) the map admits more than two invariants,

• Case (C) the map admits at most one invariant.

In what follows, we will prove that the actual number of invariants agrees with the expected one by showing how to construct them explicitly.

Remark 7.3

We remark that the invariants will be of degree up to twelve. This is because a $g\in \mathscr {C}$ is not guaranteed to preserve the fibres of the associated linear system, but rather they are permuted periodically. As a consequence, they will be invariants for an appropriate power of the map itself. This behaviour is linked to the notion of k-invariants introduced in [47], i.e. invariants for the k-th iterate $\Phi ^k$ of $\Phi$. In particular, it is possible to compute the invariants of $\Phi$ starting from its k-invariants (see [50, 84]). For a geometric discussion on the origin of this kind of maps in ${{\,\textrm{Bir}\,}}(\mathbb {P}^2)$, we refer to [15]. We mention that a classification and constructions of these plane maps were presented in [60, 64, 84]. We finally recall that a three-dimensional example, obtained as deflation (see [61]) of a four-dimensional map admitting an anti-invariant, was presented in [43]. The appearance of more general fibre exchanges in dimension three is, up to our knowledge, new.

7.1 Case (A)

Let $g\in \mathscr {C}$ be an element of type (A). As usual, without loss of generality (see Sect. 5.2), we can suppose that g swaps $\mathscr {E}$ and $\mathscr {P}$.

As explained in Lemma 7.1, in order to build invariants for the map $\Phi =g\circ {{\,\textrm{c}\,}}_3$, we need to find pencils of D-invariant divisors inside some D-covariant linear system. We start looking for quadrics.

As a consequence of Proposition 6.5, we have at most ${\overline{H}}$-invariant pencils quadrics in the ${\overline{H}}$-covariant net $\Sigma _{\mathscr {P}}$.

Recall that the elements in $\Sigma _{\mathscr {P}}$ are ${\overline{H}}$-invariant with respect to the map ${{\,\textrm{c}\,}}_3$ (see Remark 6.12). Therefore, since $\Phi _*= g_*\circ {{{\,\textrm{c}\,}}_3}_*$, ${\overline{H}}$-invariant divisors of $\Phi$ correspond to divisors which are invariant under g. As a consequence, the existence of ${\overline{H}}$-invariant elements in $\Sigma _{\mathscr {P}}$ is ruled by the action of g on the collection of pairs of elements in $\mathscr {Q}$ as explained in Remark 6.8.

Each pair of points , for $1\le i<j \le 4$, corresponds to one of the quadrics $S_{ij}$ in Remark 6.8. Now, the action of g on

(7.2)

is uniquely determined by the action of g on $\mathscr {Q}$.

Table 1 compares the possible cycle decompositions of the action of g on $\mathscr {Q}$, on $S_{\mathscr {Q}}$ and on $\mathscr {E}\cup \mathscr {P}$. In particular, for each possible cycle decomposition, an element g that realises it and its cycle decomposition on $\mathscr {P}\cup \mathscr {Q}$ are given. Length one cycles are omitted.

Table 1 Comparison of the possible cycle decompositions of the action of g on $\mathscr {Q}$, on $S_{\mathscr {Q}}$ and on $C_{\mathscr {E}\mathscr {P}}$

Remark 7.4

Let $s_{ij}\in \mathbb {C}[x_1,\ldots ,x_4]$ be a polynomial defining the quadric $S_{ij}\in S_\mathscr {Q}$, for $1\le i<j\le 4$. Let also $\sigma =(S_{i_1j_1}\ \cdots \ S_{i_kj_k})$, for some , be a cycle appearing in the cycle decomposition of the action of g on $S_\mathscr {Q}$.

One can try to find coefficients $\alpha _{i_sj_s} \in \mathbb {C}$, for $s\in 1,\ldots ,k$, such that the quadric

(7.3)

is ${\overline{H}}$-invariant. Notice that, in general, $S_\sigma \cap \mathscr {Q}=\varnothing$.

Moreover, if we chose appropriately a representative for $g\in \mathscr {C}\subset \mathbb {P}{{\,\textrm{Gl}\,}}(4,\mathbb {C})$, in the actual computation, we can restrict to for all $a=1,\ldots ,k$.

This observation allows one to construct a finite number (possibly zero) of ${\overline{H}}$-invariant quadrics. At most one quadric for each cycle in the cycle decomposition of the action of g on $S_\mathscr {Q}$. Now, we want to understand if they generate pointwise ${\overline{H}}$-invariant pencils, i.e. pencils whose points correspond to ${\overline{H}}$-invariant quadrics. This will help us in constructing the invariants of $\Phi$ as described in Lemma 7.1.

Proposition 7.5

Let , for $i=1,2$, be two quadrics obtained as described in Remark 7.4 and let $\Xi \subset \Sigma _{\mathscr {P}}$ be the pencil generated by $S_{\sigma _1}$ and $S_{\sigma _2}$. Then, the pencil $\Xi$ is pointwise ${\overline{H}}$-invariant if and only if the quadric

(7.4)

is ${\overline{H}}$-invariant.

Proof

We have

(7.5)

Since $S_{\sigma _1}$ and $S_{\sigma _2}$ are ${\overline{H}}$-invariant, the pencil $\Xi$ is a ${\overline{H}}$-covariant subspace of $\Sigma _{\mathscr {P}}$. Therefore, we obtain an automorphism

Now, the thesis follows from the fact that there is only one automorphism of $\mathbb {P}^1$ that fixes 3 points, city (see Remark 7.2). $\square$

Table 2 A resuming table of the invariants of the maps $\Phi =g \circ {{\,\textrm{c}\,}}_{3}$ for g chosen from Table 1

Remark 7.6

Unfortunately, Proposition 7.5 together with Remark 7.4 are not enough to compute all the invariants as predicted at the beginning of this section. Indeed, two issues can occur:

• there are less than two ${\overline{H}}$-covariant pencils of quadrics,

• there are at least two ${\overline{H}}$-covariant pencils, but the invariants produced are not functionally independent.

However, implementing the argument given in Remark 7.4 with combinatoric techniques, it is possible to construct the invariants of the maps appearing in Table 1 as a nonlinear combinations of ${\overline{H}}$-invariant quadrics. Their explicit form is presented in Table 2.

We now comment some facts about the invariants listed in Table 2.

• (i) The net $\Sigma _{\mathscr {P}}$ is pointwise ${\overline{H}}$-invariant and the quadrics are enough to construct the two expected invariants. This happens only in case (i). Moreover, from Lemma 2.6, we have that the KHK discretisation of the Euler top fits in this class.

• (ii) Although two cycle decompositions on $\mathscr {E}\cup \mathscr {P}$ are possible, the rational functions in Table 2 are invariant in both cases. The two invariants are a ratio of quadrics and of quartics, respectively. Since the ratio of quartics can be chosen as a square, it is easy to see that the function:

  $$\begin{aligned} J^{{\textit{(ii)}}} = \frac{x_1x_2+x_3x_4}{x_1x_4+x_2x_3}, \end{aligned}$$

  (7.7)

  is an anti-invariant. That is, the function (7.7) is such that:

  

• (iii) The two invariants are a ratio of quadrics and of quartics, respectively. Again, the ratio of quartics can be chosen as a square, so that the function:

  $$\begin{aligned} J^{{\textit{(iii)}}} = \frac{x_1 x_2+x_3 x_4}{(x_3-x_4)(x_1-x_2)}, \end{aligned}$$

  (7.9)

  is an anti-invariant (see Eq. (7.8)).

• (iv) The two invariants are a ratio of quartics and a ratio of sextics. We note that there is no anti-invariant, because the cycle $(S_{14}\ S_{24}\ S_{34})$ does not produce ${\overline{H}}$-invariant quadrics (see Remark 7.2). On the other hand, taking the ratios of two ${\overline{H}}$-invariants coming, respectively, from the two 3-cycles $(S_{12}\ S_{23}\ S_{13})$ and $(S_{14}\ S_{24}\ S_{34})$, we get (see Lemma 7.1) the following triple of 3-invariants given by the following ratios of quadrics:

  $$\begin{aligned} J^{{\textit{(iv)}}}_{1}= & {} \frac{(x_1+x_2) (x_3+x_4)}{(x_1-x_4)(x_2-x_3)}, \quad J^{{\textit{(iv)}}}_{2} = -\frac{(x_1+x_4) (x_2+x_3)}{(x_1-x_3)(x_2-x_4)}, \nonumber \\ J^{{\textit{(iv)}}}_{3}= & {} \frac{(x_1+x_3) (x_2+x_4)}{(x_1-x_2)(x_3-x_4)}. \end{aligned}$$

  (7.10)

  Indeed, these three functions are cyclically permuted by the map. Clearly only two of them are functionally independent.

• (v) The two invariants are both ratios of quartics. We note that there is no anti-invariant, because the cycle $(S_{13}\ S_{24})$ does not produce ${\overline{H}}$-invariant quadrics (see Remark 7.2). On the other hand, from the 4-cycle $(S_{12}\ S_{23}\ S_{34}\ S_{14})$ we get the pair of 4-invariants given by the following ratios of quadrics:

  $$\begin{aligned} J^{{\textit{(v)}}}_{1} = \frac{(x_1+x_4) (x_2+x_3)}{(x_1-x_4)(x_2-x_3)}, \quad J^{{\textit{(v)}}}_{2} = \frac{(x_1+x_2) (x_3+x_4)}{(x_1-x_2)(x_3-x_4)}. \end{aligned}$$

  (7.11)

  Indeed, $J^{{\textit{(v)}}}_{1}$ and $J^{{\textit{(v)}}}_{2}$ are such that:

  

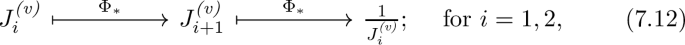
  where the indices are taken modulo 2.

Finally, we highlight that, even if there are 96 elements of type (A) swapping $\mathscr {E}$ and $\mathscr {P}$, only the invariants in Table 2 can occur. We saw this via direct check on all the 96 elements of type (A) swapping $\mathscr {E}$ and $\mathscr {P}$. Thus, for a rational function, being invariant only depends upon the action of g on $S_\mathscr {Q}$.

Remark 7.7

The results of this section suggest a relation with the KHK discretisation of another physically relevant class of systems, namely the quadratic three-dimensional Nambu systems [73, 92]. That is, the system of ODEs

(7.13)

where, for $i=1,2$, $H_{i}(\textbf{x})=\textbf{x}^{T} A_{i} \textbf{x}$ is a Nambu–Hamiltonian function. The system (7.13) is clearly integrable in the sense of Liouville, since the two Nambu–Hamiltonians are first integrals. Moreover, the system (7.13) is a generalisation of the Euler top (2.5), obtained when $A_{1}$ and $A_2$ are diagonal (see [19]). It was proven in [19] that the KHK discretisation of the system (7.13) is Liouville integrable with the two following modified Nambu–Hamiltonians:

$$\begin{aligned} {\widetilde{H}}_i(\textbf{x}) = \frac{H_i(\textbf{x})}{1+4h^2 H_3(\textbf{x})},\quad \hbox { for }i=1,2, \hbox { and } H_{3} (\textbf{x})=\textbf{x}^{T} A_1 {{\,\textrm{adj}\,}}(A_2) A_1\textbf{x}. \end{aligned}$$

(7.14)

The modified Nambu–Hamiltonians (7.14) are ratio of quadratic polynomials. Let $\Phi _{h}^{(N)},({\Phi _{h}^{(N)}})^{-1}\in {{\,\textrm{Bir}\,}}( \mathbb {P}^{3})$ be the homogeneous maps associated with the KHK discretisation of Eq. (7.13) (see Sect. 2). We conjecture that, up to conjugation by a projectivity, the map $\Phi _{h}^{(N)}$ is of type (A)-(i), i.e. it exists an analogue of Lemma 2.6 for the map $\Phi _{h}^{(N)}$. Unfortunately, in this case the computations are more intricate than in the case of the Euler top. So, we conclude this subsection by giving evidences supporting this last claim, but we leave a complete proof as a subject of further research.

We start noticing that since $\deg \Phi _{h}^{(N)}=\deg ({\Phi _{h}^{(N)}})^{-1}=3$ the degree of the polynomials $\kappa$ and $\lambda$ in (1.11) is eight. From a direct computation, we see that these polynomials are squares, i.e. $\kappa =({\tilde{\kappa }})^2$ and $\lambda =({\tilde{\lambda }})^2$. Another direct check shows that $({\tilde{\kappa }})^2$ and $({\tilde{\lambda }})^2$ admit a factorisation of the following form:

$$\begin{aligned} \kappa = \left( \kappa _{1}\kappa _{2}\kappa _{3}\kappa _{4} \right) ^{2}, \quad \lambda =\left( \lambda _{1}\lambda _{2}\lambda _{3}\lambda _{4} \right) ^{2}, \end{aligned}$$

(7.15)

where $\deg \kappa _{i}=\deg \lambda _{i}=1$, for $i=1,2,3,4$. For the sake of readability, we omit the explicit form of the polynomials $\kappa _i$ and $\lambda _i$, $i=1,2,3,4$, because they are too cumbersome.

Let us consider the net generated by the invariants ${\tilde{H}}_i$ in Eq. (7.14):

(7.16)

It is generic in the sense that its base locus consists of eight distinct points. This check can be done via Macaulay2 [37].

The matrices $A_1$ and $A_2$ are positive-definite symmetric quadratic forms. As a consequence, up to orthogonsal linear maps (see [19, Section 2.2]), we can assume $A_1={{\,\textrm{Id}\,}}$ and

$$\begin{aligned} A_2 = \begin{pmatrix} a_1 &{}\quad a_2/2 &{}\quad a_3/2 \\ a_2/2 &{}\quad a_4 &{}\quad a_5/2 \\ a_3/2 &{}\quad a_5/2 &{}\quad a_6 \end{pmatrix}, \end{aligned}$$

(7.17)

for some $a_i\in \mathbb {C}$, $i=1,\ldots ,6$. Then, the quadratic form $Q_{\mu ,\nu ,\xi }$ takes the form:

$$\begin{aligned} Q_{\mu ,\nu ,\xi }= [x_1:x_2:x_3:x_4] \mathscr {M}(\mu ,\nu ,\xi ) \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{bmatrix}, \end{aligned}$$

(7.18)

where $\mathscr {M}(\mu ,\nu ,\xi )=\mathscr {M}_{0}(\mu ,\nu ,\xi ) +\xi h^{2}\mathscr {M}_{2}(\mu ,\nu ,\xi )$ and the matrices $\mathscr {M}_{0}(\mu ,\nu ,\xi )$ and $\mathscr {M}_{2}(\mu ,\nu ,\xi )$ are given by:

$$\begin{aligned} \mathscr {M}_{0}(\mu ,\nu ,\xi )&= \begin{pmatrix} \mu +\nu a_1 &{}\quad a_2\nu /2 &{}\quad \nu a_3/2 &{}\quad 0 \\ a_2 \nu /2 &{}\quad \mu +\nu a_4 &{}\quad a_5 \nu /2 &{}\quad 0 \\ a_3 \nu /2 &{}\quad a_5 \nu /2 &{}\quad \mu +\nu a_6 &{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad \xi \end{pmatrix}, \end{aligned}$$

(7.19a)

$$\begin{aligned} \mathscr {M}_{2}(\mu ,\nu ,\xi )&= \begin{pmatrix} 4a_4 a_6 - a_5^{2} &{}\quad -2a_2 a_6+ a_3 a_5 &{}\quad a_2 a_5- 2a_3 a_4 &{}\quad 0 \\ -2a_2a_6+a_3 a_5&{}\quad 4 a_1a_6- a_3^{2}&{}\quad -2 a_1 a_5+ a_3 a_2&{}\quad 0 \\ a_2 a_5-2 a_3 a_4&{}\quad -2 a_1 a_5+ a_3 a_2 &{}\quad 4 a_1 a_4- a_2^{2} &{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0 \end{pmatrix}. \end{aligned}$$

(7.19b)

We study now the base locus of the linear system $\Sigma ^{(N)}$ (7.16). To do so, we first show that there exist six reducible members of the net $\Sigma ^{(N)}$. These members will consist of twelve distinct planes. Recall that the quadratic form associated to a symmetric matrix is factorisable if and only if its $3\times 3$ minors vanish, i.e. its rank is two. We omit the explicit computations since they are rather cumbersome, yet straightforward. However, we present the solutions and comment them.

There exist six solutions, which we divide in two families, namely:

$$\begin{aligned} {[}\mu _{i}^{(1)}:\nu _{i}^{(1)}:\xi _{i}^{(1)}]&= [\gamma _{i}:1:0], \quad i=1,2,3, \end{aligned}$$

(7.20a)

$$\begin{aligned} {[}\mu _{i}^{(2)}:\nu _{i}^{(2)}:\xi _{i}^{(2)}]&= [\pi _{2}(\delta _{i}):2\delta _{i}\pi _{1}(\delta _{i}):2\pi _{1}(\delta _{i})], \quad i=1,2,3, \end{aligned}$$

(7.20b)

where $\gamma _{i}$ are the roots of the polynomial equation:

$$\begin{aligned}&\gamma ^3+(a_1+a_4+a_6) \gamma ^2 \nonumber \\&\quad +\left( a_1 a_4+a_1 a_6+a_4 a_6- \frac{a_2^2+a_3^2+ a_5^2}{4}\right) \gamma \nonumber \\&\quad +a_1 a_4 a_6+\frac{a_2 a_3 a_5-a_1 a_5^2-a_2^2 a_6-a_3^2 a_4}{4}=0, \end{aligned}$$

(7.21)

$\delta _{i}$ are the roots of the polynomial equation:

$$\begin{aligned} \begin{aligned} \delta ^3&-4 h^2 (a_1+a_4+a_6) \delta ^2 +4 h^4 \left[ 4 (a_1 a_4+ a_1 a_6+ a_4 a_6)-a_2^2-a_3^2-a_5^2\right] \delta \\&-16 h^6 (4 a_1 a_4 a_6-a_1 a_5^2-a_2^2 a_6+a_2 a_3 a_5-a_3^2 a_4) =0, \end{aligned} \end{aligned}$$

(7.22)

and

$$\begin{aligned} \pi _{1}(\delta _{i})&= \delta _i a_5-2 h^2 (2 a_1 a_5-a_2 a_3), \end{aligned}$$

(7.23a)

$$\begin{aligned} \pi _{2}(\delta _{i})&= -(2 a_1 a_5-a_2 a_3) \delta _i^2 \nonumber \\&\quad +2 h^2 \left[ \begin{gathered} (4 a_1^2 +a_2^2 +a_3^2 +a_5^2)a_5 \\ -2 (a_1 a_2 a_3 +a_2 a_3 a_4 +a_2 a_3 a_6 + 2 a_4 a_5 a_6) \end{gathered} \right] \delta _i \nonumber \\&\quad +8 a_5 h^4 (4 a_1 a_4 a_6-a_1 a_5^2-a_2^2 a_6+a_2 a_3 a_5-a_3^2 a_4). \end{aligned}$$

(7.23b)

As a consequence, the net $\Sigma ^{(N)}$ contains exactly six reducible members. So, we end up again with a configuration of twelve planes. A direct symbolic computation to see how the eight base points are arranged on the twelve planes was not possible because of the high complexity of the involved computations.

So, to prove that up to conjugation the map $\Phi _{h}^{(N)}$ is of type (A)-(i), it remains to understand how the eight points are arranged with respect to the twelve planes.

7.2 Case (B)

In this section, we will adopt the same notation as in Sect. 7.1. Moreover, we will denote by $T_{ij}$, for $1\le i< j\le 4$, the unique quadric of $\Sigma _\mathscr {Q}$ passing through $p_i$ and $p_j$, and by $\mathscr {S}$ the set

(7.24)

To simplify the description of the invariants we use the following general result.

Lemma 7.8

Let $h\in \mathscr {C}$ be an element of type (B). Then, h commutes with ${{\,\textrm{c}\,}}_3$, i.e. $h\circ {{\,\textrm{c}\,}}_3 ={{\,\textrm{c}\,}}_3\circ h$.

Proof

The projectivity h can be represented by a permutation matrix with signs (see Lemma 4.5). Let us denote by $\sigma$ the permutation of the coordinates induced by $\sigma$. then, we have

which completes the proof. $\square$

Lemma 7.9

Let $g_1,g_2\in \mathscr {C}_{{\tiny \textit{(B)}}}\subset \mathscr {C}$ be two elements of type (B) which are conjugated in $\mathscr {C}_{{\tiny \textit{(B)}}}$, i.e. there exists $h\in \mathscr {C}_{{\tiny \textit{(B)}}}$ such that $g_2=h\circ g_1 \circ h^{-1}$. Let also $R_1\in \mathbb {C}(x_1,\ldots ,x_4)$ be an invariant of $\Phi _1=g_1\circ {{\,\textrm{c}\,}}_3$. Then, $R_2=R_1\circ h^{-1}$ is an invariant for $\Phi _2=g_2\circ {{\,\textrm{c}\,}}_3$.

Proof

The proof consists in the following chain of equalities

$$\begin{aligned} \begin{aligned} R_2\circ \Phi _2&\equiv R_1\circ h^{-1}\circ g_2\circ {{\,\textrm{c}\,}}_3\equiv R_1\circ h^{-1}\circ h\circ g_1\circ h^{-1}\circ {{\,\textrm{c}\,}}_3 \\&\equiv R_1\circ g_1\circ {{\,\textrm{c}\,}}_3\circ h^{-1}\equiv R_1\circ \Phi _1\circ h^{-1}\equiv R_2. \end{aligned} \end{aligned}$$

(7.26)

Notice that the last equality is a consequence of Lemma 7.8. $\square$

To simplify the description of the invariants in case (B) we also use the following result.

Lemma 7.10

Let $g\in \mathscr {C}_{{\tiny \textit{(B)}}}\subset \mathscr {C}$ be an element of type (B) and let $R\in \mathbb {C}(x_1,\ldots ,x_4)$ be an invariant of $\Phi =g\circ {{\,\textrm{c}\,}}_3$. Consider the birational map $\Phi ^{(k)}=g^k \circ {{\,\textrm{c}\,}}_3$. Then, the following rational function

$$\begin{aligned} {{\widetilde{R}}} = {{{\,\textrm{c}\,}}_3}_{*}(R) + R, \end{aligned}$$

(7.27)

is an invariant of $\Phi ^{(k)}$ for all $k\ge 0$. Moreover, if k is odd also R is an invariant for $\Phi ^{(k)}$. While, if k is even and ${\widetilde{R}}=0$, then $R^2$ is an invariant of $\Phi ^{(k)}$.

Proof

The proof follows from Lemma 7.8 which states that $g^k$ and ${{\,\textrm{c}\,}}_3$ commute. $\square$

Remark 7.11

Lemmas 7.8 to 7.10 hold in general on any $\mathbb {P}^M$ by considering permutation matrices with signs of size $(M+1)\times (M+1)$ and the M-dimensional standard Cremona transformation ${{\,\textrm{c}\,}}_M$.

Remark 7.12

We remark that, in the case in which the invariant ${\widetilde{R}}$ given by Lemma 7.10 vanishes, we have that R is an anti-invariant for $\Phi ^{(k)}$ when k is even. Moreover, sometimes, it can happen that ${\widetilde{R}}= R$, i.e. R is invariant, also for k even and not just for the odd case.

Finally, we observe that, given a set of m functionally independent invariants of $\Phi$, it is not guaranteed that the set of invariants constructed in Lemma 7.10 are still functionally independent.

As a consequence of Lemmas 7.9 and 7.10, if one knows the invariants of some $g\circ {{\,\textrm{c}\,}}_3$ then one can recover the invariants of all the maps of the form $h\circ {{\,\textrm{c}\,}}_3$ for $h\in \mathscr {C}_{{\tiny \textit{(B)}}}$ in the same conjugacy class of g or, for $h\in \mathscr {C}_{{\tiny \textit{(B)}}}$ of the form $g^k$ for some $k\ge 0$. A direct computation tells us that there are exactly 14 conjugacy classes in $\mathscr {C}_{{\tiny \textit{(B)}}}$. One representative for each of them is given in Table 3, while the explicit form of the invariants is shown in Table 4. To shorten the latter, we will give a set of invariants that suffices to compute all the others via Lemma 7.10. In Table 5, we will show to which conjugacy classes belong the second power of the projectivities involved in Table 3. Following Remark 7.12, the invariants in Table 4 are chosen in a way that the invariants obtained via Lemma 7.10 are functionally independent. We checked this via a case-by-case analysis performed via computer algebra.

In the next proposition, we summarise the fact that, in order to to build the invariants, we only need elements of $\Sigma _{{\tiny \textit{(B)}}}$.

Proposition 7.13

Let us consider $\Phi = g\circ {{\,\textrm{c}\,}}_3\in {{\,\textrm{Bir}\,}}(\mathbb {P}^3)$, with $g\in \mathscr {C}_{{\tiny \textit{(B)}}}$. Then, the invariants of $\Phi$ are obtained as a suitable (nonlinear) combination of the elements of $\Sigma _{{\tiny \textit{(B)}}}$.

Table 3 Representatives for the 14 conjugacy classes in $\mathscr {C}_{{\tiny \textit{(B)}}}$

Table 4 A resuming table of the invariants of the maps $\Phi =g \circ {{\,\textrm{c}\,}}_{3}$ for g chosen from Table 3 of order 2 and 3

Table 5 Relations between conjugacy classes in $\mathscr {C}_{{\tiny \textit{(B)}}}$ and invariants. The invariants are build following Lemma 7.10. Here, $R_i$ denotes the i-th invariant in Table 4 of the case in first column

Table 6 Example of the invariant of the maps of the form $\Phi =g \circ {{\,\textrm{c}\,}}_{3}$ for g of type (C)

Table 7 The first 10 values of M and k for which a construction similar to the one we carried out in this paper can be possible

7.3 Case (C)

In this case we have no ${\overline{H}}$-invariant linear system of quadrics (see Proposition 6.13) and there is only a pencil $\Xi _\mathscr {R}$ of $2{\overline{H}}$-invariant quartics (see Proposition 6.14).

Consider the following three points $S_{12,34},S_{13,24},S_{14,23}\in \Xi _\mathscr {R}$:

$$\begin{aligned} S_{12,34}&= H_{12}^++H_{12}^- + H_{34}^++H_{34}^-, \end{aligned}$$

(7.28a)

$$\begin{aligned} S_{13,24}&= H_{13}^++H_{13}^-+ H_{24}^++H_{24}^-, \end{aligned}$$

(7.28b)

$$\begin{aligned} S_{14,23}&= H_{14}^++H_{14}^-+H_{23}^++H_{23}^-, \end{aligned}$$

(7.28c)

corresponding to the desmic surfaces (see Remark 4.16). Notice that any g of type (C) acts on and this action uniquely determines the action of g on $\Xi _\mathscr {R}\cong \mathbb {P}^1$.

Remark 7.14

Let $g\in \mathscr {C}$ be an element of type (C). Then, the existence of an invariant of degree d, for $d\ge 4$ depends on the action of g on . Precisely, it depend on the number of fixed points of .

In this case we will not present tables similar to Tables 1 and 2. Instead, we will give an example for each possible fixed locus of (or equivalently the fixed locus of $g:\Xi _\mathscr {R}\rightarrow \Xi _\mathscr {R}$). These examples are listed in Table 6.

Remark 7.15

We remark that no functionally independent invariants other than the ones presented in Table 6 do exist for these maps. Indeed, if such an invariant would exist, one could use it to define a pre-symplectic structure compatible with the map (see [14]). However, from the results in [11], this would force the degree growth to be at most polynomial contradicting Proposition 5.7.

8 Conclusions

In this paper, motivated by the study of the KHK discretisation of the Euler top, we introduced a finite subgroup of $\mathbb {P}{{\,\textrm{Gl}\,}}(4,\mathbb {C})$, we called it the Cremona-cubes group and we denoted it by $\mathscr {C}$. This group is crafted in a way that it encompasses and generalises all the geometrical properties of the KHK discretisation of the Euler top. Indeed, the KHK discretisation of the Euler top is projectively equivalent to the map $\Phi ^{(0)} = g_0\circ {{\,\textrm{c}\,}}_3$, with $g_0$ as in (2.7), swapping $\mathscr {E}$ and $\mathscr {P}$. So, in order to generalise this behaviour, we considered all the projectivities acting with finite order on all the special points of the standard Cremona transformation. This yields the Cremona-cubes group (see Definition 4.2).

We studied the algebraic properties of the group $\mathscr {C}$ and we splitted it in three disjoint subsets, namely (A), (B), and (C), depending on how the projectivity $g\in \mathscr {C}$ acts on (see Remark 4.7). The birational maps of the form $\Phi =g\circ {{\,\textrm{c}\,}}_3$, for $g\in \mathscr {C}$ have different growth, covariance, and invariance properties depending on the type of g. Type (A) gives integrable maps, both in the algebraic entropy (see Proposition 5.3) and in the Liouville–Poisson sense (see Table 2). Type (B) consists of permutations with signs of the homogeneous coordinates yielding periodic maps (see Proposition 5.4). Type (C) gives non-integrable maps (see Proposition 5.7), which however do preserve an invariant of order at least four and at most twelve (see Table 6). The growth and covariance properties are discussed in a unified way for all the elements of a given type (see Propositions 6.5, 6.9, 6.11 and 6.14 for the covariance).

On the other hand, the construction of the invariants is specific to some subclasses of maps. For the maps defined from elements of type (A) we characterise completely the invariants up to their action on $\mathscr {Q}$ (resp. $\mathscr {P}$) if g swaps $\mathscr {E}$ and $\mathscr {P}$ (resp. $\mathscr {E}$ and $\mathscr {Q}$): that is, if the actions of $g,g'\in \mathscr {C}$ of type (A) agree on $\mathscr {P}$ (resp. $\mathscr {Q}$), then $g\circ {{\,\textrm{c}\,}}_{3}$ and $g'\circ {{\,\textrm{c}\,}}_{3}$ possess the same invariants (see Tables 1 and 2). It is remarkable that even though the invariants of $g\circ {{\,\textrm{c}\,}}_3$ depend only on the action of g on $\mathscr {Q}$ (resp. $\mathscr {P}$) one may not be able to recover this action starting only from the invariants (see case (ii) in Tables 1 and 2). This approach is different from the construction made in [2]. There, to a pair of quadrics, it is associated a single birational map for which the quadrics are invariant through the construction of some involution. The study of invariants of the maps of the form $g\circ {{\,\textrm{c}\,}}_{3}$ with $g\in \mathscr {C}$ of type (B) is based on the fact that these projectivities constitute a group, namely $\mathscr {C}_{{\tiny \textit{(B)}}}\subset \mathscr {C}$. We have shown that, knowing invariants of $g\circ {{\,\textrm{c}\,}}_3$, for a given $g\in \mathscr {C}_{{\tiny \textit{(B)}}}$, it is possible to recover the invariants of the maps $h\circ {{\,\textrm{c}\,}}_3$ for all $h\in \mathscr {C}_{{\tiny \textit{(B)}}}$ conjugated, in $\mathscr {C}_{{\tiny \textit{(B)}}}$ to g, or of the maps of the form $g^k\circ {{\,\textrm{c}\,}}_3$, for $k\ge 0$ (see Lemmas 7.9 and 7.10). We gave the invariants for a chosen representative in each of the ten independent conjugacy classes (see Table 4). Lastly, when $g\in \mathscr {C}$ is of type (C), we characterised completely the invariants of $g\circ {{\,\textrm{c}\,}}_3$ according to its action on the three desmic quartics belonging to the pencil introduced in Proposition 6.14. Since g acts on a set of three elements only three behaviours are possible: fixing the three surfaces and hence the whole pencil, fixing only one surface, or fixing no surface at all. We also presented the invariants in this case (see Table 6).

We remark that our construction of the invariants consists of a geometric argument which makes our work more similar to [2, 42, 82] than to other papers where invariants where successfully constructed for given maps with a given algorithm (see [18, 40, 43, 61, 77,78,79]). The main difference in this work is that we are able to characterise at once maps with all the three possible behaviours, and, even more interestingly, the number of integrable maps derived from this construction is the same as the number of periodic and non-integrable ones. This is strikingly surprising as integrable maps are deemed to be very rare.

We note that, in the construction of the Cremona-cubes group $\mathscr {C}$ it is crucial the existence of a positive integer $k\in \mathbb {N}$ such that

(8.1)

Indeed, $\dim \mathbb {P}^3+1=4$ and implying $k=2$. This translates in the fact that the vertices of the three-dimensional cube splits into the sets of vertices of two distinct three-dimensional simplices. In general, the number k corresponds to the number of distinct M-dimensional simplices in which we want to split the set of vertices of a M-dimensional cube. So, a similar construction might be possible only if there exists a positive integer $k\in \mathbb {N}$ such that

(8.2)

Explicitly, since , we want the following equality to be satisfied

$$\begin{aligned} k\cdot (M+1) = 2^M. \end{aligned}$$

(8.3)

Now, from Eq. (8.3), it directly follows that $k=2^h$ and $(M+1)=2^m$ where $h,m\in \mathbb {N}$ are positive integers such that $h+m=M$. This implies:

$$\begin{aligned} M = 2^m-1, \quad k = 2^{2^m-1-m}, \end{aligned}$$

(8.4)

so that everything is determined by the free parameter $m\in \mathbb {N}$. From Table 7, we see that the next possible case is in $\mathbb {P}^7$. This already brings the number of subsets of ${{\,\textrm{Fix}\,}}{{\,\textrm{c}\,}}_3$ formed by orthogonal sets of points of $\mathbb {P}^7$ to 16. We expect their dynamics to be quite involved. Yet, we believe that it might be possible to construct an analogue of the Cremona-cubes group with similar nice properties. Work is in progress in that direction. Incidentally, we note that the number k increases dramatically as m raises. E.g. again from Table 7, we see that, for $m=10$, k is a number with 305 digits.

We observe now that other generalisations without the need of raising the dimension are possible. Indeed, one can consider different singularity patterns contracting planes to points. This, happens easily by considering degenerations of the Nambu systems discussed in Remark 7.7: tuning the free parameters in a way that some of the $\lambda _i$’s and/or $\kappa _i$’s collapse alters the singularity structure. We are working to characterise these degenerations and their geometric properties. Moreover, in $\mathbb {P}^3$, it is possible to contract surfaces both on points and on curves. The standard Cremona transformation (1.1) only contracts planes to points (see Sect. 3.1). On the other hand the, map

contracts the coordinate planes , for $i=1,2$, to the coordinate lines and , respectively, the coordinate plane to the point [0 : 0 : 1 : 0], while the coordinate plane is mapped to itself. It is easy to see that composing $\theta$ with the projectivity $g_0$ in (2.24) yields a map $\Phi _\theta$ whose degree growth is heuristically computed to be:

$$\begin{aligned} 1, 2, 4, 7, 12, 18, 25, 34, 44, 55, 68, 82, 97, 114, 132, 151\ldots \end{aligned}$$

(8.6)

and it is fitted by the following generating function:

$$\begin{aligned} g_\theta (z) = -\frac{2z^4 + z^2 + 1}{(z - 1)^3(z^2 + z + 1)}. \end{aligned}$$

(8.7)

From (8.7), we infer that the algebraic entropy of $\Phi _\theta$ vanishes and that the degree growth is asymptotically quadratic. Nevertheless, the singularity patterns are changed: there is one singularity pattern of the form:

analogous to the one of Fig. 2, but also two of a new kind:

Work is in progress to understand the geometry of this map and its possible extensions.