Decay Estimates for the Massless Vlasov Equation on Schwarzschild Spacetimes

Abstract

We consider solutions to the massless Vlasov equation on the domain of outer communications of the Schwarschild black hole. By adapting the $r^p$-weighted energy method of Dafermos and Rodnianski, used extensively in order to study wave equations, we prove superpolynomial decay for a non-degenerate energy flux of the Vlasov field f through a well-chosen foliation. An essential step of this methodology consists in proving a non-degenerate integrated local energy decay. For this, we take in particular advantage of the redshift effect near the event horizon. The trapping at the photon sphere requires, however, to lose an $\epsilon$ of integrability in the velocity variable. Pointwise decay estimates on the velocity average of f are then obtained by functional inequalities, adapted to the study of Vlasov fields, which allow us to deal with the lack of a conservation law for the radial derivative.

Appendices

Basic Properties of the Foliation $(\Sigma _{\tau })_{\tau \in {\mathbb {R}}}$

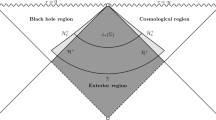
The purpose of this section is to prove Lemma 1.4. As the Regge–Wheeler coordinates degenerate at the horizon, it will be convenient to use the coordinate system $({\underline{u}}, r, \theta , \varphi ) \in {\mathbb {R}}\times {\mathbb {R}}_+^* \times ]0,\pi [ \times ]0,2 \pi [$, which covers the region ${\mathscr {B}} \cup {\mathcal {H}}^+ \cup {\mathscr {D}}$ (see Fig. 1) and which is then regular on the event horizon ${\mathcal {H}}^+$, where $r=2M$. Recall that the metric takes the following form

$$\begin{aligned} g \, = \, -\left( 1 - \frac{2M}{r} \right) \textrm{d}{\underline{u}}^2+2 \textrm{d}{\underline{u}} \textrm{d}r+r^2 \textrm{d}\mu ^{}_{{\mathbb {S}}^2} \end{aligned}$$

and that, denoting by $\partial _{{\underline{u}}}'$ and $\partial _{r}'$ the differentiation with respect to ${\underline{u}}$ and r in the coordinate system $({\underline{u}}, r, \theta , \varphi )$, we have in ${\mathscr {D}}$,

$$\begin{aligned} \partial _t \, = \, \partial _{{\underline{u}}}', \quad \partial _{{\underline{u}}} \, = \, \partial _{{\underline{u}}}'+\frac{1}{2}\left( 1 - \frac{2M}{r} \right) \partial _r', \quad \partial _u \, = \, -\frac{1}{2}\left( 1 - \frac{2M}{r} \right) \partial _r'. \end{aligned}$$

(50)

In particular, $\frac{ 1}{1-\frac{2M}{r}} \partial _u$ can be extended as a smooth vector field on ${\mathscr {B}} \cup {\mathcal {H}}^+ \cup {\mathscr {D}}$. The invariant volume element $\textrm{d}\mu ^{}_{{\mathcal {M}}}$ induced by g on ${\mathcal {M}}$ can be expressed, in the region ${\mathcal {R}}_{-\infty }^{+\infty } \subset {\mathscr {D}}$, in the following three different ways

$$\begin{aligned} \textrm{d}\mu ^{}_{{\mathcal {R}}^{+\infty }_{-\infty }} := \, \textrm{d}\mu ^{}_{{\mathcal {M}}} \Big \vert _{{\mathcal {R}}_{-\infty }^{+\infty }}= & {} \, \left( 1 -\frac{2M}{r} \right) r^2 \textrm{d}t \wedge \textrm{d}r^* \wedge \textrm{d}\mu ^{}_{{\mathbb {S}}^2} \\= & {} r^2 \textrm{d}{\underline{u}} \wedge \textrm{d}r \wedge \textrm{d}\mu ^{}_{{\mathbb {S}}^2} \, = \, \left( 1 -\frac{2M}{r} \right) \frac{r^2}{2} \textrm{d}u \wedge \textrm{d}{\underline{u}} \wedge \textrm{d}\mu ^{}_{{\mathbb {S}}^2}, \end{aligned}$$

where $\textrm{d}\mu ^{}_{{\mathbb {S}}^2}$ is the standard volume form on the unit sphere ${\mathbb {S}}^2$. As the hypersurfaces ${\mathcal {N}}_{\tau }$ are null, there is no canonical choice of normal vector $n^{}_{{\mathcal {N}}_{\tau }}$. Since

$$\begin{aligned} \textrm{d}\mu ^{}_{{\mathcal {R}}_{-\infty }^{+\infty }} \, = \, r^2g(\partial _{{\underline{u}}}, \cdot ) \wedge \textrm{d}{\underline{u}}\wedge \textrm{d}\mu ^{}_{{\mathbb {S}}^2}, \end{aligned}$$

we choose $n^{}_{{\mathcal {N}}_{\tau }}:=\partial _{{\underline{u}}}$ and the induced volume form on ${\mathcal {N}}_{\tau }$ is $\textrm{d}\mu ^{}_{{\mathcal {N}}_{\tau }}:= r^2 \textrm{d}{\underline{u}}\wedge \textrm{d}\mu ^{}_{{\mathbb {S}}^2}$. As $\tau =u-u_0$ for $r \ge R_0$ and $\Sigma _{\tau } \cap \{ r\ge R_0 \} ={\mathcal {N}}_{\tau }$, we have, for all $r \ge R_0$,

$$\begin{aligned} \begin{aligned} |\tau -u|=|u_0|, \qquad \textrm{d}\mu ^{}_{{\mathcal {R}}^{+\infty }_{-\infty }} \, = \, \gamma _0(r) \textrm{d}\tau \wedge \textrm{d}\mu ^{}_{\Sigma _{\tau }}, \quad \gamma _0(r) :=\frac{1}{2} \left( 1- \frac{2M}{r} \right) . \end{aligned} \end{aligned}$$

We have then obtained all the results of Lemma 1.4 which concern the region $r \ge R_0$ and we now focus on the domain $2\,M< r < R_0$, where $\Sigma _{\tau }$ is spacelike. We start by proving the following result.

Lemma A.1

There exists a smooth function ${\underline{U}}: [2\,M, R_0 ] \rightarrow {\mathbb {R}}$ such that, for any $\tau \ge 0$, $\Sigma _{\tau } \cap \{ r < R_0 \}$ can be parameterized, in the system of coordinates $({\underline{u}},r,\theta , \varphi )$, by

$$\begin{aligned} (r,\omega ) \in \, ]2M,R_0[ \times {\mathbb {S}}^2 \mapsto ( {\underline{U}}(r)+\tau , r, \omega ). \end{aligned}$$

Moreover, the vector field $\textbf{n}:= g^{-1} ( \textrm{d}{\underline{u}}- {\underline{U}}'(r) \textrm{d}r, \cdot )$ is normal to $\Sigma _{\tau } \cap \{ r < R_0 \}$ and timelike in the region $\{ 2\,M \le r \le R_0 \}$.

Proof

It will be convenient to work here with the coordinate system $({\underline{u}},r,\theta , \varphi )$. Since $\Sigma _{\tau } \cap \{ r< R_0 \} = \varphi _{\tau } \left( \Sigma _{0} \cap \{ r < R_0 \} \right)$, where $\varphi _{\tau }$ is the flow generated by the Killing vector field $\partial _t=\partial _{{\underline{u}}}'$, it suffices to prove the result for $\tau =0$. Then, recall that by construction, , where is a spacelike hypersurface crossing ${\mathcal {H}}^+$ to the future of the bifurcation sphere. Hence, there exists $\delta < 0$ such that . As $\widetilde{{\mathcal {S}}}$ is a smooth spherically symmetric hypersurface, for any $x \in \widetilde{{\mathcal {S}}}$, there exist an open set O containing x and a smooth function $F_O$ such that

$$\begin{aligned} \widetilde{{\mathcal {S}}} \cap O \, = \, \left\{ ({\underline{u}},r, \omega ) \in {\mathbb {R}}\times {\mathbb {R}}_+^* \times {\mathbb {S}}^2 \, / \, F_O({\underline{u}},r) \, = \, 0 \right\} . \end{aligned}$$

Since $\widetilde{{\mathcal {S}}}$ is spacelike, $\partial _t=\partial _{{\underline{u}}}' \notin T_x \widetilde{{\mathcal {S}}}$ for any x in the region $r \ge 2\,M$, so that $\partial '_{{\underline{u}}} F_O$ does not vanish on $\widetilde{{\mathcal {S}}} \cap O \cap \{ r \ge 2M \}$. According to the implicit function theorem, we obtain that for any $x \in \widetilde{{\mathcal {S}}} \cap \{ r \ge 2\,M \}$, there exist an open set $O'$ containing x and a smooth function ${\underline{U}}_{O'}$ such that

$$\begin{aligned} \widetilde{{\mathcal {S}}} \cap O' \, = \, \left\{ ({\underline{u}},r, \omega ) \in {\mathbb {R}}\times {\mathbb {R}}_+^* \times {\mathbb {S}}^2 \, / \, {\underline{u}}={\underline{U}}_{O'}(r) \right\} . \end{aligned}$$

By a connexity argument, this implies, if $\delta >0$ is chosen small enough, that there exists a smooth function ${\underline{U}}: \, ]2\,M-\delta ,+\infty [ \rightarrow {\mathbb {R}}$ such that

$$\begin{aligned} \widetilde{{\mathcal {S}}} \, = \, \left\{ ({\underline{u}},r, \omega ) \in {\mathbb {R}}\times ]2M-\delta , +\infty [ \times {\mathbb {S}}^2 \, / \, {\underline{u}}={\underline{U}}(r) \right\} . \end{aligned}$$

We then deduce that the 1-form $\textrm{d}{\underline{u}}- {\underline{U}}'(r) \textrm{d}r$ is normal to the spacelike hypersurface $\widetilde{{\mathcal {S}}}$. This implies that the $\varphi _{\tau }$-invariant vector field $\textbf{n}$ is normal to $\Sigma _{\tau } \cap \{ r^* < R_0^* \}$ and timelike on ${\mathcal {H}}^+ \cup {\mathscr {D}}$. $\square$

As we have $t={\underline{u}} -r^*$ in the region ${\mathscr {D}}$, this implies that the parameterization of $\Sigma _{\tau } \cap \{ r < R_0 \}$ in the Regge–Wheeler coordinates given in Lemma 1.4 holds. In order to prove the remaining four properties, notice first that, as $\textbf{n}$ is $\varphi _{\tau }$-invariant, $SO_3({\mathbb {R}})$-invariant and timelike on $\{ 2M \le r \le R_0 \}$, we can define the smooth function

$$\begin{aligned}{} & {} \gamma : [2M, R_0] \rightarrow {\mathbb {R}}_+^*, \quad \gamma (r) = |g(\textbf{n},\textbf{n})|^{\frac{1}{2}}, \qquad \\{} & {} \text { which satisfies}\\{} & {} \quad \exists \, C \ge 1, \; \forall \, 2M \le r \le R_0, \quad \frac{1}{C} \le \frac{1}{\gamma (r)} \le C. \end{aligned}$$

Note now that the future oriented normal vector along $\Sigma _{\tau } \cap \{ r < R_0\}$ is equal either to $\frac{\textbf{n}}{\gamma (r)}$ or to $-\frac{\textbf{n}}{\gamma (r)}$. So, as the induced volume form on $\Sigma _{\tau }$ satisfies

$$\begin{aligned}{} & {} \textrm{d}\mu ^{}_{{\mathcal {R}}^{+\infty }_{-\infty }} \, = \, -g ( n^{}_{\Sigma _{\tau }}, \cdot ) \wedge \textrm{d}\mu ^{}_{\Sigma _{\tau }}, \qquad \\{} & {} \text {we have}\\{} & {} \quad \textrm{d}\mu ^{}_{\Sigma _{\tau }} \Big \vert _{\{2M< r < R_0\}} \, = \, \gamma (r) r^2 \textrm{d}r \wedge \textrm{d}\mu ^{}_{{\mathbb {S}}^2}. \end{aligned}$$

Since $\tau = \underline{u} -\underline{U}(r)$ for $2M< r < R_0$, we have, for all $2M< r < R_0$,

$$\begin{aligned} |\tau - \underline{u}| \le \Vert \underline{U}\Vert ^{}_{L^{\infty }}, \qquad \textrm{d} \mu _{\mathcal {R}^{+\infty }_{-\infty }} \, = \, \gamma _0(r) \textrm{d} \tau \wedge \textrm{d} \mu _{\Sigma _{\tau }}, \quad \gamma _0(r) = \frac{1}{\gamma (r)}. \end{aligned}$$

Finally, in view of the properties of $\textbf{n}$, there exist smooth functions $\xi , \, \zeta :[2M,R_0] \rightarrow {\mathbb {R}}$ such that $n^{}_{\Sigma _{\tau }}= \xi (r)\partial _{{\underline{u}}}'+\zeta (r) \partial _r'$. We then deduce from (50) that there exist smooth functions $\alpha , \, \beta :[2M,R_0] \rightarrow {\mathbb {R}}$ satisfying $n^{}_{\Sigma _{\tau }}= \alpha (r)\partial _{{\underline{u}}}+\frac{\beta (r)}{1-\frac{2\,M}{r}} \partial _u$. As $n^{}_{\Sigma _{\tau }}$ is unitary and timelike, we have using (4) that $\alpha (r) \beta (r)=1$ for all $2\,M< r < R_0$. By continuity, the relation holds for all $r \in [2\,M,R_0]$ and this implies, since $n^{}_{\Sigma _{\tau }}$ is future oriented, that $\beta$ and $\alpha =1/\beta$ are both strictly positives on $[2M,R_0]$. This concludes the proof of Lemma 1.4.

Controlling all the Components of the Energy–Momentum Tensor

We prove here a general result which motivates the introduction of the redshift vector field $\textrm{N}$. More precisely, we prove that if T and ${\widetilde{T}}$ are strictly timelike vector fields, then, on any compact set, ${\mathbb {T}}[f](T,{\widetilde{T}})$ controls uniformly all the components of the energy–momentum tensor ${\mathbb {T}}[f]$ of the Vlasov field f.

Let $({\mathcal {M}},g)$ be a smooth time-oriented and oriented four-dimensional Lorentzian manifold and consider the bundle of future light cones

$$\begin{aligned}{} & {} {\mathcal {P}} \,:= \, \bigcup _{x \in {\mathcal {M}}} {\mathcal {P}}_x, \\{} & {} {\mathcal {P}}_x\,:= \, \{ (x,v) \, / \, v \in T^{\star }_x {\mathcal {M}},\quad g^{-1}_x(v,v)=0, \, \text {{ v} future oriented} \}. \end{aligned}$$

Given a coordinate system $(U,x^0,x^1,x^2, x^3)$ on ${\mathcal {M}}$, for any $y \in U \subset {\mathcal {M}}$, we can decompose any $v \in T^{\star }_y {\mathcal {M}}$ as $v= v_{\alpha } \textrm{d}{x^{\alpha }}\vert _{ y}$. Consequently, $(x^{\alpha },v_{\alpha })$ is a coordinate system on $T^{\star } {\mathcal {M}}$, called conjugates to $(x^0,x^1,x^2, x^3)$. The metric g induces the invariant volume element $\textrm{d}\mu ^{}_{T^{\star }_x {\mathcal {M}}}= |\det g^{-1}_x|^{\frac{1}{2}} \textrm{d}v_0 \wedge \textrm{d}v_1 \wedge \textrm{d}v_2 \wedge \textrm{d}v_3$ on $T^{\star }_x {\mathcal {M}}$. It induces a volume form on ${\mathcal {P}}_x$, satisfying $\textrm{d}\mu ^{}_{{\mathcal {P}}_x} = \textrm{d}q \wedge \textrm{d}\mu ^{}_{T^{\star }_x {\mathcal {M}}}$ with $q(v):= \frac{1}{2}g^{-1}_x(v,v)$. We can then define the energy–momentum tensor of any sufficiently regular function $f: {\mathcal {P}} \rightarrow {\mathbb {R}}$ by

$$\begin{aligned}{} & {} {\mathbb {T}}[f]_{\alpha \beta } := \int _{{\mathcal {P}}} f \, v_{\alpha } v_{\beta } \textrm{d}\mu ^{}_{{\mathcal {P}}}, \end{aligned}$$

(51)

where

$$\begin{aligned} \int _{{\mathcal {P}}} f \, v_{\alpha } v_{\beta } \textrm{d}\mu ^{}_{{\mathcal {P}}}:= x \mapsto \int _{{\mathcal {P}}_x} f v_{\alpha } v_{\beta } \textrm{d}\mu ^{}_{{\mathcal {P}}_x}. \end{aligned}$$

If $x^0$ is a temporal function, then $(x^0,x^1,x^2, x^3,v_1,v_2,v_3)$ are smooth coordinates on ${\mathcal {P}}$ since we have

$$\begin{aligned} v_0= & {} -\frac{1}{g^{00}} \left( g^{0j}v_j- \sqrt{ (g^{0j}v_j)^2-g^{00}g^{ij} v_iv_j }\right) , \\ \quad \textrm{d}\mu ^{}_{{\mathcal {P}}_x}= & {} \frac{ |\det g^{-1}_x|^{\frac{1}{2}}}{ v_{\alpha } g^{\alpha 0}} \textrm{d}v_1 \wedge \textrm{d}v_2 \wedge \textrm{d}v_3. \end{aligned}$$

Lemma B.1

Consider a smooth nonnegative function $f: {\mathcal {P}} \rightarrow {\mathbb {R}}_+$ and a compact subset ${\mathcal {K}} \subset {\mathcal {M}}$. Let $X, \,{\widetilde{X}}, \, T, \, {\widetilde{T}}$ be four smooth vector fields such that T and ${\widetilde{T}}$ are strictly timelike and future oriented on ${\mathcal {K}}$. Then, there exists $D >0$ such that

$$\begin{aligned} \forall \, x \in {\mathcal {K}}, \; \forall \, v \in {\mathcal {P}}_x, \qquad |v(X)| \, \le \, - D \, v(T). \end{aligned}$$

Moreover, there exists $C>0$ such that $|{\mathbb {T}}|f](X,{\widetilde{X}})| \le C \cdot {\mathbb {T}}[f](T,{\widetilde{T}})$ holds uniformly on ${\mathcal {K}}$.

Proof

We start by the first estimate. Let $x \in {\mathcal {K}}$ and consider a coordinate system $(x^0,\dots x^3)$, defined on an open set $U_x$ containing x, such that $x^0$ is a smooth temporal function. Let further $O_x$ be an open set such that $x \in O_x$ and $\overline{O_x} \subset U_x$. If the result holds on $O_x \cap {\mathcal {K}}$ for any $x \in {\mathcal {K}}$, then it holds on the compact ${\mathcal {K}}$ since it can be covered by a finite number of such open sets $O_x$. Consequently, it suffices to prove the result on $O_x \cap {\mathcal {K}}$. Introduce now the compact set

$$\begin{aligned} {\mathcal {Q}} \,:= \, \{ (y,v) \, / \, y \in \overline{O_x} \cap {\mathcal {K}}, \quad v \in {\mathcal {P}}_y, \quad |v|^2:= |v_1|^2+|v_2|^2+|v_3|^2=1 \}. \end{aligned}$$

Note that $v(T) <0$ on ${\mathcal {K}}$ for any $v \in {\mathcal {P}}$. Indeed, v is causal, T is strictly timelike on ${\mathcal {K}}$ and they are both future oriented. Consequently, we have $S:=\sup _{{\mathcal {Q}}} |v(X)| < +\infty$, $I:=\inf _{{\mathcal {Q}}} -v(T) >0$ and the first inequality of the lemma holds on $O_x \cap {\mathcal {K}}$, with $D = \frac{S}{I}$. Together with the definition (51) of ${\mathbb {T}}[f]$, this directly implies the second estimate. $\square$