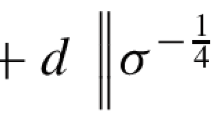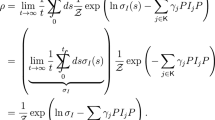Concentration Inequalities for Output Statistics of Quantum Markov Processes

Abstract

We derive new concentration bounds for time averages of measurement outcomes in quantum Markov processes. This generalizes well-known bounds for classical Markov chains, which provide constraints on finite-time fluctuations of time-additive quantities around their averages. We employ spectral, perturbation and martingale techniques, together with non-commutative $L_2$ theory, to derive: (i) a Bernstein-type concentration bound for time averages of the measurement outcomes of a quantum Markov chain, (ii) a Hoeffding-type concentration bound for the same process, (iii) a generalization of the Bernstein-type concentration bound for counting processes of continuous-time quantum Markov processes, (iv) new concentration bounds for empirical fluxes of classical Markov chains which broaden the range of applicability of the corresponding classical bounds beyond empirical averages. We also suggest potential application of our results to parameter estimation and consider extensions to reducible quantum channels, multi-time statistics and time-dependent measurements, and comment on the connection to so-called thermodynamic uncertainty relations.

1 Introduction

Quantum Markov chains describe the evolution of a quantum system, which interacts successively with a sequence of identically prepared ancillary systems (input probes) modelling a memoryless environment [1, 26, 53]. Such dynamics can be seen as discrete-time versions of continuous-time open system evolutions as encountered in quantum optics [9, 21, 25, 30, 33, 36, 64] and formalize the input–output theory of quantum filtering and control [15, 23, 44, 61, 69]. The two settings are in fact closely connected and can be related explicitly by time discretizing techniques [5, 13, 60].

After the interaction, the probes (output) are in a finitely correlated state [35], which carries information about the dynamics; such information can be extracted by performing successive measurements on the outgoing probes. The stochastic process given by the sequence of measurement outcomes has received significant attention in recent years. The ergodic properties of this process have been studied in [4, 27, 28, 54, 68], while those of the corresponding conditional system state (filter) have been analysed in [2, 17, 20, 55]. The large deviation theory of additive functionals of the measurement process was established in [49] and extended in [58]. Motivated by the interest in understanding the irreversible essence of repeated quantum measurements from a statistical mechanics perspective, the papers [16, 19] have investigated large-time asymptotics of the entropy production. In the context of open quantum walks [6], the asymptotics of the process obtained measuring the position of the walker on the graph have been studied [4, 10, 27, 28, 66]. Another class of problems relates to fluctuations of measurement outcomes, which can be used to uncover dynamical phase transitions of the quantum evolution, see for example [38, 50, 68]. In the one-atom maser, non-demolition measurements of outgoing atoms have been used for reconstructing the initial photon distribution of a resonant electromagnetic cavity [46]. Further theoretical studies on the asymptotics of non-demolition measurements have been carried out in [7, 11, 12].

In contrast to the recent progress in understanding the asymptotics of the outcome process, much less is known on the finite-time properties. Notable recent results in this direction are the deviation bounds and concentration inequalities for quantum counting processes and homodyne measurements obtained in [18] (hence regarding continuous-time models). The main aim of the present work is to provide new classes of concentration inequalities for additive functionals of the finite-time measurement process, which complement the results of [18] and offer more explicit bounds. We denote by $X_1,\dots ,X_n$ the outcomes of the measurements on the first n output probes, and we consider a generic function $f:I \rightarrow {\mathbb {R}}$ defined on the set I of all possible outcomes (we will mainly consider the situation in which we perform the same measurement on every probe, treating the general case in Sect. 5.3); under certain ergodicity conditions on the dynamics, the empirical average process $\frac{1}{n}\sum _{k=1}^{n} f(X_k)$ converges almost surely to its stationary value $\pi (f)$, and we aim at finding an upper bound for the probability that $\frac{1}{n}\sum _{k=1}^{n} f(X_k)$ deviates from $\pi (f)$ more than $\gamma$ for some fixed $n \in {\mathbb {N}}$ and $\gamma >0$.

To get the general flavour of the results, we briefly discuss here the case of independent random variables for which there is a well-established theory even for more general functions than the time average [22]; two well-known bounds in this case are given by Bernstein’s and Hoeffding’s inequalities. Assuming for simplicity that $(X_k)_{k=1}^{n}$ are independent and identically distributed centred random variables, and that ${\mathbb {E}}[X^2_1]\le b^2$ and $|X_1| \le c$ almost surely, Bernstein’s inequality reads as follows (see [22, Theorem 2.10]):

$$\begin{aligned}{\mathbb {P}}\left( \frac{1}{n} \sum _{k=1}^n X_k \ge \gamma \right) \le \exp \left( -n \frac{\gamma ^2 b^2}{c^2} h \left( \frac{2\gamma c}{b^2} \right) \right) , \end{aligned}$$

where $h(x)=(\sqrt{1+x}+x/2+1)^{-1}$; the bound depends on the random variables through their variance and their magnitude in absolute value. On the other hand, Hoeffding’s inequality only depends on the extension of the range of $X_1$: if we have that $a \le X_1 \le b$ almost surely, one can show ([22, Theorem 2.8]) that

$$\begin{aligned} {\mathbb {P}}\left( \frac{1}{n} \sum _{k=1}^n X_k \ge \gamma \right) \le \exp \left( -n \frac{2 \gamma ^2}{(b-a)^2} \right) . \end{aligned}$$

Much work has been done for extending these results to irreducible Markov chains. New Bernstein- and Hoeffding-type inequalities were recently obtained in order to tackle problems coming from statistics and machine learning [34, 51], while Lezaud [56] and Glynn et al. [42] derived bounds that have an intuitive interpretation and depend on relatively simple dynamical properties. More specifically, the latter bounds involve the range and stationary variance of the function f, and the spectral gap of the (multiplicative symmetrization of the) transition matrix P of the Markov chain (Bernstein case) or the norm of the pseudo-resolvent $(\textrm{Id}-P)^{-1}$ (Hoeffding case).

In this paper, we find analogous bounds for the class of stochastic processes given by repeated measurements on the output probes of a quantum Markov process. On a technical level, we exploit perturbation theory and spectral methods used in [27, 28, 68] for proving the law of large numbers, central limit theorem and large deviation principle for the output process. We also use a generalization of Poisson’s equation to decompose the empirical average into a martingale with bounded increments and a negligible reminder as in [4]. Using these tools, we obtain quantum bounds which share the useful properties of the classical results in [56] and [42].

Our main results are:

• A Bernstein-type concentration bound for time averages of the measurement outcomes of a quantum Markov process, Theorem 3.

• A Hoeffding-type concentration for the same process, Theorem 4.

• A generalization of the Bernstein-type concentration bound for counting processes of continuous-time quantum Markov processes, Theorem 6.

• By specializing to classical Markov chains, we obtain a new concentration bound for empirical fluxes, thus extending the range of applicability of the corresponding classical bounds beyond empirical averages, Proposition 7 and Proposition 8.

The paper is organized as follows: In Sect. 2, we introduce in more detail the mathematical model and we recall the objects and results that will be used to prove the main theorems. Section 3 is devoted to prove the main results of the paper: a Bernstein-type and a Hoeffding-type inequalities for the output process of quantum Markov chains. In Sect. 4, we show how perturbation theory and spectral techniques can be used to derive concentration inequalities for the case of quantum counting processes too. This result integrates the bounds obtained in [18], providing a simple bound also for the case of counting processes and non-self-adjoint generators. Moreover, it bypasses the problem of establishing functional inequalities and estimating the constants appearing in the inequalities. In Sect. 5, we present extensions and applications of the previous results. Finally, in Sect. 6 we provide our conclusions and outlook.

2 Notation and Preliminaries

2.1 Quantum Channels and Irreducibility

We consider a finite-dimensional Hilbert space ${\mathbb {C}}^d$, and we denote by $M_d({\mathbb {C}})$ the set of $d\times d$ matrices with complex entries. When considering the evolution of a quantum system described by ${\mathbb {C}}^d$ in the Schrödinger picture, one endows $M_d({\mathbb {C}})$ with the trace norm, i.e.

$$\begin{aligned}\Vert x\Vert _1:= \textrm{tr}(|x|), \quad \forall x \in M_d({\mathbb {C}}), \end{aligned}$$

where we recall that |x| is the unique positive semidefinite square root of $x^*x$ in the sense of functional calculus. A state is any positive semidefinite $x \in M_d({\mathbb {C}})$ with unit trace. In the Heisenberg picture, $M_d({\mathbb {C}})$ is considered together with the uniform norm, that is

$$\begin{aligned}\Vert x\Vert :=\sup _{u \in {\mathbb {C}}^d, \Vert u\Vert =1}\Vert xu\Vert , \quad \forall x \in M_d({\mathbb {C}}). \end{aligned}$$

An observable is any self-adjoint element $x \in M_d({\mathbb {C}})$. We recall that the dual of $M_d({\mathbb {C}})$ considered with the uniform norm can be identified with $M_d({\mathbb {C}})$ with the trace norm via the following isometry:

$$\begin{aligned}(M_d({\mathbb {C}}),\Vert \cdot \Vert _1) \ni x \mapsto \textrm{tr}(\cdot x) \in (M_d({\mathbb {C}}),\Vert \cdot \Vert )^*. \end{aligned}$$

We consider a completely positive unital linear map (that is, a quantum channel in the Heisenberg picture) $\Phi : M_d({\mathbb {C}})\rightarrow M_d({\mathbb {C}})$ and we denote by $\Phi ^*$ the dual of $\Phi$, which is the completely positive and trace preserving (that is, stochastic) map uniquely defined by the relation:

$$\begin{aligned}\textrm{tr}(x\Phi (y))=\textrm{tr}(\Phi ^*(x)y), \quad \forall x,y \in M_d({\mathbb {C}}). \end{aligned}$$

We recall that every completely positive map $\eta$ admits a Kraus representation $\eta (x)=\sum _{j}W_j^*xW_j$, where $\{W_j\} \subseteq M_d({\mathbb {C}})$ is a finite collection of operators (called Kraus operators), and $\eta$ is a quantum channel if and only if $\sum _{j}W^*_jW_j=\textbf{1}$. Unless stated otherwise, throughout this paper we will make the following assumption.

Hypothesis (H): $\Phi$ is such that its dual admits a unique faithful invariant state $\sigma$, that is $\Phi ^*(\sigma )=\sigma$ and $\sigma >0$.

We recall that hypothesis (H) is satisfied if and only if the following equivalent statements hold:

• 1. 1 is an algebraically simple eigenvalue of $\Phi$ with positive eigenvector,

• 2. let $\{V_i\}_{i \in I}$ be a choice of Kraus operators for $\Phi$, then for every $v \in {\mathbb {C}}^d$, $v \ne 0$

  $$\begin{aligned}\textrm{span}\{V_{i_n} \cdots V_{i_1}v: n \in {\mathbb {N}}, i_1,\dots i_n \in I\}={\mathbb {C}}^d. \end{aligned}$$

In this case, the map $\Phi$ is said to be irreducible. The equivalence is a special instance of Perron–Frobenius theory for completely positive (not necessarily unital) maps and that we report in the following proposition (for more details, see [70, Chapter 6] and [28, Section 3]).

Proposition 1

Let $\eta$ be a completely positive map acting on $M_d({\mathbb {C}})$ for some finite-dimensional Hilbert space ${\mathbb {C}}^d$; then, its spectral radius $r(\eta ):=\sup \{|z|:z \in \textrm{Sp}(\eta )\}$ is an eigenvalue of $\eta$ with positive semidefinite corresponding eigenvector $x \ge 0$. Moreover, the following are equivalent:

• 1. $r(\eta )$ is algebraically simple and $x>0$,

• 2. let $\{W_j\}_{j \in J}$ be a choice of Kraus operators for $\eta$, then for every $v \in {\mathbb {C}}^d$, $v \ne 0$

  $$\begin{aligned}\textrm{span}\{W_{j_n} \cdots W_{j_1}v: n \in {\mathbb {N}}, j_1,\dots j_n \in J\}={\mathbb {C}}^d. \end{aligned}$$

A stronger assumption, which will not be required for our results, but provides a clearer picture of the dynamical aspects, is primitivity. The channel $\Phi$ is called primitive if it satisfies hypothesis (H), and in addition, it is aperiodic, i.e. its peripheral spectrum (the set of eigenvalues with absolute value 1) contains only the eigenvalue 1.

2.2 KMS-Inner Product

There are several ways of equipping $M_d({\mathbb {C}})$ with a Hilbert space structure, see for instance [3, 62] for connections with quantum statistics. In the derivation of our results, we will make use of the Kubo–Martin–Schwinger (KMS) inner product associated with a positive definite state $\sigma$, which is defined as follows:

$$\begin{aligned} \langle x,y \rangle :=\textrm{tr}((\sigma ^{\frac{1}{4}} x \sigma ^{\frac{1}{4}})^* (\sigma ^{\frac{1}{4}}y\sigma ^{\frac{1}{4}}))=\textrm{tr}(\sigma ^{\frac{1}{2}}x^* \sigma ^{\frac{1}{2}}y), \quad x,y \in M_d({\mathbb {C}}). \end{aligned}$$

(1)

As usual, we write $\Vert x\Vert _2$ for $\langle x,x \rangle ^{1/2}$. Given any map $\eta$ acting on $M_d({\mathbb {C}})$, we denote $\textrm{TR}(\eta )$ the trace of $\eta$, that is the unique linear functional on linear maps acting on $M_d({\mathbb {C}})$ which is cyclic and such that $\textrm{TR}(\textrm{Id})=\dim (M_d({\mathbb {C}}))=d^2$; we recall that, given any orthonormal basis $\{x_j\}_{j=1}^{d^2}$ of $M_d({\mathbb {C}})$ with respect to the KMS product, the usual formula for computing the trace as the sum of diagonal elements holds true:

$$\begin{aligned}\textrm{TR}(\eta )=\sum _{j=1}^{d^2} \langle x_j,\eta (x_j) \rangle . \end{aligned}$$

We will use the notation $\eta ^\dagger$ for referring to the adjoint with respect to the KMS product of the linear map $\eta$ acting on $M_d({\mathbb {C}})$; it is easy to see that $\eta ^\dagger = \Gamma _\sigma ^{-\frac{1}{2}} \circ \eta ^* \circ \Gamma _\sigma ^{\frac{1}{2}}$, where $\Gamma ^\alpha _\sigma$ is the completely positive map defined as $x\mapsto \sigma ^\alpha x \sigma ^\alpha$, for $\alpha \in {\mathbb {R}}$. If $\eta$ is completely positive, so does $\eta ^\dagger$ and this is what motivates our choice of inner product, since the KMS product is the only one with this property. Moreover, a Kraus decomposition of $\eta$ induces a Kraus decomposition of $\eta ^\dagger$: if $\eta (x)=\sum _{j}W_j^*xW_j$ it is easy to see that

$$\begin{aligned} \eta ^\dagger (x)=\sum _{j}\left\{ \sigma ^{\frac{1}{2}}W^*_j\sigma ^{-\frac{1}{2}} \right\} ^*x \left\{ \sigma ^{\frac{1}{2}}W^*_j\sigma ^{-\frac{1}{2}}\right\} . \end{aligned}$$

Let $\Phi$ be a quantum channel and assume that $\sigma$ is an invariant state for $\Phi$; then, $\Phi ^\dagger$ is again a quantum channel with invariant state $\sigma$:

$$\begin{aligned} \Phi ^\dagger (\textbf{1})=\sigma ^{-\frac{1}{2}} \Phi ^*(\sigma ^{\frac{1}{2}}\textbf{1}\sigma ^{\frac{1}{2}}) \sigma ^{-\frac{1}{2}}=\textbf{1}, \quad \Phi ^{\dagger *}(\sigma )=\sigma ^{\frac{1}{2}} \Phi (\sigma ^{-\frac{1}{2}} \sigma \sigma ^{-\frac{1}{2}})\sigma ^{\frac{1}{2}}=\sigma . \end{aligned}$$

The compatibility of KMS-inner product with the convex cone of positive semidefinite matrices allows to decompose every self-adjoint matrix into the difference of two orthogonal positive semidefinite matrices (see [29, Theorem 3.9]): given $x \in M_d({\mathbb {C}})$, $x=x^*$ we can write

$$\begin{aligned} x=\underbrace{\sigma ^{-\frac{1}{4}}(\sigma ^{\frac{1}{4}}x\sigma ^{\frac{1}{4}})_+ \sigma ^{-\frac{1}{4}}}_{:=x_{\sigma ,+}}-\underbrace{\sigma ^{-\frac{1}{4}}(\sigma ^{\frac{1}{4}}x\sigma ^{\frac{1}{4}})_- \sigma ^{-\frac{1}{4}}}_{:=x_{\sigma ,-}}, \end{aligned}$$

where $(y)_+$ ($(y)_-$) denotes the positive (negative) part of a self-adjoint operator $y \in M_d({\mathbb {C}})$ in the sense of functional calculus. It is easy to see that $x_{\sigma ,\pm } \ge 0$ and that they are orthogonal with respect to the KMS-product. A simple consequence is the following useful fact, which will be used in the proof of our main theorem. With a slight abuse of notation, given a map $\eta$ acting on $M_d({\mathbb {C}})$, we denote by $\Vert \eta \Vert _2$ the operator norm of $\eta$ induced considering $M_d({\mathbb {C}})$ endowed with the norm $\Vert \cdot \Vert _2$.

Lemma 2

Let $\eta _1$ and $\eta _2$ two positive maps defined on $M_d({\mathbb {C}})$; then,

$$\begin{aligned}\Vert \eta _1-\eta _2\Vert _2 \le \Vert \eta _1+\eta _2\Vert _2. \end{aligned}$$

Proof

Every $x \in M_d({\mathbb {C}})$ can be decomposed into the sum of two self-adjoint operators: its real part $\Re {(x)}:=(x+x^*)/2$ and its imaginary part $\Im {(x)}=(x-x^*)/(2i)$ and the KMS-norm is compatible with this decomposition, in the sense that

$$\begin{aligned}\Vert x\Vert _2^2=\Vert \Re {(x)}\Vert _2^2+ \Vert \Im {(x)}\Vert _2^2. \end{aligned}$$

Since $\eta _1$ and $\eta _2$ are positive, $\eta _1-\eta _2$ and $\eta _1+\eta _2$ are real, meaning that they preserve the real subspace of self-adjoint operators. These two facts imply that $\eta _1-\eta _2$ and $\eta _1+\eta _2$ attain their norms on the set of self-adjoint operators of norm one. Let us consider $x \in M_d({\mathbb {C}})$, $x=x^*$ such that $\Vert x\Vert _2=1$ and $\Vert (\eta _1-\eta _2)(x)\Vert _2=\Vert \eta _1-\eta _2\Vert _2$; if we define $|x|_\sigma :=x_{\sigma ,+}+x_{\sigma ,-}$, we have that $\Vert |x|\Vert _2=1$ and

$$\begin{aligned} \begin{aligned} \Vert \eta _1-\eta _2\Vert _2^2&=\Vert \eta _1-\eta _2(x)\Vert _2^2=\Vert (\eta _1(x_{\sigma ,+})\\&\quad +\eta _2(x_{\sigma ,-}))-(\eta _1(x_{\sigma ,-})+\eta _2(x_{\sigma ,+}))\Vert _2^2\\&= \Vert \eta _1(x_{\sigma ,+})+\eta _2(x_{\sigma ,-})\Vert _2^2+\Vert \eta _1(x_{\sigma ,-})+\eta _2(x_{\sigma ,+})\Vert _2^2\\&\quad -2 \underbrace{\langle \eta _1(x_{\sigma ,+})+\eta _2(x_{\sigma ,-}),\eta _1(x_{\sigma ,-})+\eta _2(x_{\sigma ,+}) \rangle }_{\ge 0} \\&\le \Vert \eta _1(x_{\sigma ,+})+\eta _2(x_{\sigma ,-})\Vert _2^2+\Vert \eta _1(x_{\sigma ,-})+\eta _2(x_{\sigma ,+})\Vert _2^2+2\langle \eta _1(x_{\sigma ,+})\\&\quad +\eta _2(x_{\sigma ,-}),\eta _1(x_{\sigma ,-})+\eta _2(x_{\sigma ,+}) \rangle \\&=\Vert \eta _1+\eta _2(|x|_\sigma )\Vert _2^2 \le \Vert \eta _1+\eta _2\Vert _2^2. \end{aligned} \end{aligned}$$

$\square$

2.3 Output Process of Quantum Markov Chains

In the input–output formalism [36], a quantum Markov chain is described as a quantum system interacting sequentially with a chain of identically prepared ancillary systems (the input). After the interaction, the ancillary systems form the output process and can be measured to produce a stochastic detection record called quantum trajectory. More formally, let us denote by $\mathfrak {h}={\mathbb {C}}^d$ the system Hilbert space and by $\mathfrak {h}_a$ the ancilla space, and assume that the latter is prepared in the initial state $|\chi \rangle \in \mathfrak {h}_a$; the interaction between the system and a single ancilla is described by a unitary operator $U: \mathfrak {h}\otimes \mathfrak {h}_a \rightarrow \mathfrak {h}\otimes \mathfrak {h}_a$. The reduced evolution of the state of the system after one interaction with the ancillas is described by the following quantum channel called the transition operator

$$\begin{aligned} \Phi ^*: \rho \mapsto \textrm{tr}_{\mathfrak {h}_a}(U \rho \otimes |\chi \rangle \langle \chi | U^*). \end{aligned}$$

Any orthonormal basis $\{|i\rangle \}_{i \in I}$ for $\mathfrak {h}_a$, induces a Kraus decomposition for $\Phi ^*$:

$$\begin{aligned} \Phi ^*(x)=\sum _{i \in I} V_i x V_i^*, \quad V_i:= \langle i| U |\chi \rangle , \qquad x \in M_d({\mathbb {C}}). \end{aligned}$$

If the system is initially prepared in the state $\rho$, after n times steps its state is given by $\Phi ^{*n}(\rho )$. In general, hypothesis (H) does not guarantee convergence to the stationary state, i.e. $\lim _{n\rightarrow \infty } \Phi ^*(\rho ) = \sigma$. However, if $\Phi$ primitive (i.e. it satisfies hypothesis (H) and is aperiodic), then any initial state converges to the stationary state.

Suppose now that, after every interaction between the system and the chain of ancillas, we perform a measurement corresponding to the basis $\{|i\rangle \}_{i \in I}$. The sequence of the outcomes of the measurements $(X_n)_{n \in {\mathbb {N}}}$ is a classical I-valued stochastic process whose law is uniquely determined by the following collection of finite-dimensional distributions: for every $n \in {\mathbb {N}}$, $i_1,\dots , i_n \in I$

$$\begin{aligned} {\mathbb {P}}_\rho (X_1=i_1,\dots , X_n=i_n)=\textrm{tr}(V_{i_n} \cdots V_{i_1} \rho V_{i_1}^* \cdots V_{i_n}^*). \end{aligned}$$

(2)

Note that if the system starts in the invariant state $\sigma$, the law of the outcome process is stationary: for every $n,k \in {\mathbb {N}}$, $i_1,\dots , i_k \in I$

$$\begin{aligned}\begin{aligned}&{\mathbb {P}}_\sigma (X_{n}=i_1,\dots ,X_{n+k-1}=i_k)=\textrm{tr}(V_{i_k} \dots V_{i_1} \Phi ^{*(n-1)}(\sigma )V_{i_1}^* \cdots V_{I_k}^*)\\&=\textrm{tr}(V_{i_k} \dots V_{i_1} \sigma V_{i_1}^* \cdots V_{I_k}^*)={\mathbb {P}}_\sigma (X_1=i_1,\dots , X_{k}=i_k). \end{aligned} \end{aligned}$$

We denote by $\pi$ the law of a single measurement under the stationary measure ${\mathbb {P}}_\sigma$, i.e. $\pi (i)=\textrm{tr}(\sigma V_i^*V_i)$ for every $i \in I$.

From (2), it follows that the joint distribution of two measurements at different times $m>n \in {\mathbb {N}}$ is given by

$$\begin{aligned} {\mathbb {P}}_\rho (X_n=i,X_m=j)=\textrm{tr}(V_i^*\Phi ^{*n-1}(\rho )V_i \Phi ^{m-n-1}(V_j^*V_j)). \end{aligned}$$

(3)

If $\Phi$ is primitive, then $\Phi ^{k}(V_j^*V_j)$ converges to $\pi (j)\textbf{1}$ for large k so the correlations between $X_n$ and $X_m$ decay exponentially with $m-n$. In fact, it has been shown that hypothesis (H) suffices to establish several ergodic results [4, 28, 68]: given any function $f: I \rightarrow {\mathbb {R}}$, the process $(f(X_n))_{n \in {\mathbb {N}}}$ satisfies a strong law of large numbers, a central limit theorem and a large deviation principle. In particular,

$$\begin{aligned} \lim _{n \rightarrow +\infty } \frac{1}{n} \sum _{k=1}^{n} f(X_k)=\pi (f)\quad {\mathbb {P}}_\rho \text {-a.s.} \end{aligned}$$

(4)

where $\pi (f)=\sum _{i \in I} f(i) \pi (i)$. For the reader interested in what happens removing assumption (H), we refer to [27, 41]; we will come back to this in Sect. 5.2.

Despite the fact that the asymptotic behaviour of the process $(f(X_n))_{n \in {\mathbb {N}}}$ is rather well understood, less is known about its finite time properties, with the notable exception of the recent concentration results for continuous-time Markov dynamics [18]. The main goal of the present work is to derive alternative concentration bounds, i.e. upper bounds on the probability that $\frac{1}{n} \sum _{k=1}^{n} f(X_k)$ deviates from the limit value more than $\gamma >0$

$$\begin{aligned} {\mathbb {P}}_\rho \left( \frac{1}{n} \sum _{k=1}^{n} f(X_k)\ge \pi (f)+\gamma \right) . \end{aligned}$$

(5)

Note that by replacing f with $-f$ one obtains an upper bound for the probability of left deviations from the limit value and using the union bound, one can easily control deviations on both sides.

3 Quantum Markov Chains

3.1 Bernstein-Type Inequality

In this section, we prove a Bernstein-type inequality which provides a sub-Gaussian bound for small deviations and a subexponential one for bigger deviations. The inequality involves the spectral gap of the multiplicative symmetrization of the transition operator $\Phi$, and the stationary variance and range of the function f. The strategy of the proof is inspired by the classical result [56, Theorem 3.3] and relies on perturbation theory and spectral analysis, which is also the approach used in [28, 68] for proving the law of large numbers and the large deviation principle for the process $(f(X_k))_{k \in {\mathbb {N}}}$.

Theorem 3

Assume that $\Psi :=\Phi ^\dagger \Phi$ is irreducible, and let $f:I \rightarrow {\mathbb {R}}$ such that $\pi (f)=0$, $\pi (f^2)=b^2$ and $\Vert f \Vert _\infty :=\max _{i \in I} |f(i)|=c$ for some $b,c>0$. Then for every $\gamma > 0$, $n \ge 1$

$$\begin{aligned} {\mathbb {P}}_\rho \left( \frac{1}{n} \sum _{k=1}^{n} f(X_k)\ge \gamma \right) \le N_\rho \exp \left( -n \frac{\gamma ^2 \varepsilon }{6b^2}h\left( \frac{10c \gamma }{3b^2}\right) \right) , \end{aligned}$$

(6)

where $\varepsilon$ is the spectral gap of $\Psi$, $N_\rho :=\Vert \sigma ^{-\frac{1}{2}}\rho \sigma ^{-\frac{1}{2}}\Vert _2$ and $h(x)=(\sqrt{1+x}+x/2+1)^{-1}$.

We remark that a sufficient (but not necessary) condition for $\Psi$ to be irreducible is that $\Phi$ is positivity improving, i.e. that $\Phi (x)>0$ for every $x \ge 0$.

In order to highlight the underlying idea, we postponed to Section A in Appendix the more technical steps of the following proof.

Proof

We split the proof in 3 steps. The strategy is to use Markov inequality to bound the deviation probabilities in terms of the moment-generating function (Chernoff bound), which is then bounded using perturbation theory and spectral properties.

1. Upper Bound for the Moment-Generating Function (Laplace Transform)

An easy computation shows that the Laplace transform of $n{\bar{f}}_n:= \sum _{k=1}^{n} f(X_k)$ can be expressed in terms of the deformed transition operator $\Phi _u(x)=\sum _{i \in I} e^{u f(i)}V_i^* x V_i$, $u>0$:

$$\begin{aligned} {\mathbb {E}}_\rho [e^{n u{\bar{f}}_n}]&=\textrm{tr}(\rho \Phi _u^n(\textbf{1}))=\textrm{tr}\left( \sigma ^{\frac{1}{2}}(\sigma ^{-\frac{1}{2}}\rho \sigma ^{-\frac{1}{2}})\sigma ^{\frac{1}{2}} \Phi _u^n(\textbf{1})\right) =\langle \sigma ^{-\frac{1}{2}}\rho \sigma ^{-\frac{1}{2}}, \Phi _u^n(\textbf{1}) \rangle \nonumber \\&\le \Vert \sigma ^{-\frac{1}{2}}\rho \sigma ^{-\frac{1}{2}}\Vert _2 \cdot \Vert \textbf{1}\Vert _2 \cdot \Vert \Phi _u^n\Vert _2 = \Vert \sigma ^{-\frac{1}{2}}\rho \sigma ^{-\frac{1}{2}}\Vert _2 \cdot \Vert \Phi _u^n\Vert _2. \end{aligned}$$

(7)

By $\Vert \Phi _u^n\Vert _2$, we mean the operator norm of $\Phi _u^n$ induced by $M_d({\mathbb {C}})$ endowed with the KMS-norm. The rest of the proof aims to upper bound $\Vert \Phi _u^n\Vert _2$; a first remark is that

$$\begin{aligned}\Vert \Phi _u^n\Vert _2\le \Vert \Phi _u\Vert ^n_2=\Vert \Psi _u\Vert ^{\frac{n}{2}}_2=r(u)^{\frac{n}{2}}, \end{aligned}$$

where $\Psi _u:=\Phi ^\dagger _u \Phi _u$ and r(u) is the spectral radius of $\Psi _u$. Notice that for every $u \in {\mathbb {R}}$, $\Phi _u(x)=\sum _{i \in I} (e^{\frac{u f(i)}{2}}V_i)^* x (e^{\frac{u f(i)}{2}}V_i)$ is completely positive, therefore $\Phi ^\dagger _u$ and $\Psi _u$ are completely positive too; Proposition 1 ensures that r(u) is an eigenvalue of $\Psi _u$. Moreover, we can write

$$\begin{aligned} \Psi _u(x)=\Phi ^\dagger _u \Phi _u(x)=\sum _{i,j \in I} \left\{ e^{\frac{u(f(i)+f(j))}{2}}K_{i,j}\right\} ^* x \left\{ e^{\frac{u(f(i)+f(j))}{2}} K_{i,j}\right\} , \end{aligned}$$

(8)

where $K_{i,j}=V_i \sigma ^{\frac{1}{2}}V^*_j\sigma ^{-\frac{1}{2}}$ are the Kraus operators of $\Psi$. Since $\Psi$ is irreducible by assumption, its Kraus operators satisfy condition 2 in Proposition 1. Since the Kraus operators of $\Psi _u$ are multiples of $K_{i,j}$, they also satisfy condition 2, and therefore, r(u) is an algebraically simple eigenvalue of $\Psi _u$ for every $u \in {\mathbb {R}}$.

2. Perturbation Theory

Direct computations show that $\Psi _u$ is an analytic perturbation of $\Psi =\Psi _0$: first notice that

$$\begin{aligned} \Phi _u(x)=\sum _{k=0}^{+\infty } \frac{u^k}{k!}\underbrace{\sum _{i \in I}f(i)^k V_i^* x V_i }_{=:\Phi ^{(k)}} \end{aligned}$$

(9)

and that $\Phi ^{(0)}=\Phi$. Therefore, we can write

$$\begin{aligned} \Psi _u= & {} \Phi _u^\dagger \Phi _u=\left( \sum _{k=0}^{+\infty } \frac{u^k}{k!}\Phi ^{(k)\dagger }\right) \left( \sum _{k=0}^{+\infty } \frac{u^k}{k!}\Phi ^{(k)}\right) \nonumber \\= & {} \sum _{k=0}^{+\infty } \frac{u^k}{k!} \underbrace{\sum _{l=0}^k \left( {\begin{array}{c}k\\ l\end{array}}\right) \Phi ^{(l)\dagger } \Phi ^{(k-l)}}_{=:\Psi ^{(k)}} \end{aligned}$$

(10)

and it is easy to see that $\Psi ^{(0)}=\Psi$. The norms of $\Psi ^{(k)}$’s are upper bounded by a geometric sequence (point 2 in Lemma 10):

$$\begin{aligned}\Vert \Psi ^{(k)} \Vert _2 \le 2c (2c)^{k-1} \hbox { for}\ k \ge 1. \end{aligned}$$

Therefore, perturbation theory ([52, Section II.2.2]) tells us that for $|u| < \varepsilon /(2c(2+\varepsilon ))$ (where $\varepsilon$ is the spectral gap of $\Psi$) we can expand r(u) around 0:

$$\begin{aligned}r(u)=1+\sum _{k=1}^{+\infty }r^{(k)}u^k.\end{aligned}$$

Using the explicit expression of the $r^{(k)}$’s one can show (see Lemma 11), the following upper bound on r(u):

$$\begin{aligned} r(u) \le \textrm{exp} \left( u^2\frac{6b^2}{\varepsilon } \left( 1-\frac{10cu}{\varepsilon } \right) ^{-1}\right) , \quad 0 \le u < \varepsilon /(10c). \end{aligned}$$

3. Chernoff Bound and Fenchel–Legendre Transform

Now that we have an upper bound for the Laplace transform, we apply the usual machinery of the Chernoff bound: using Markov inequality we obtain that for every $0 \le u < \varepsilon /(10c)$

$$\begin{aligned}\begin{aligned} {\mathbb {P}}_\rho ({\bar{f}}_n\ge \gamma )&={\mathbb {P}}_\rho (e^{n u{\bar{f}}_n}\ge e^{n u\gamma }) \le e^{-nu\gamma } {\mathbb {E}}_\rho [e^{nu{\bar{f}}}]\\&\le N_\rho \exp \left( -n\left( \gamma u-u^2\frac{3b^2}{\varepsilon } \left( 1-\frac{10cu}{\varepsilon } \right) ^{-1} \right) \right) .\\ \end{aligned} \end{aligned}$$

Taking the infimum of the rhs over admissible values of u, we obtain

$$\begin{aligned}{\mathbb {P}}_\rho \left( \frac{1}{n} \sum _{k=1}^{n} f(X_k) \ge \gamma \right) \le N_\rho \exp \left( -n \frac{\gamma ^2 \varepsilon }{6b^2}h\left( \frac{10c \gamma }{3b^2}\right) \right) \end{aligned}$$

for $h(x)=(\sqrt{1+x}+x/2+1)^{-1}$. $\square$

3.1.1 Comparison to the Classical Concentration Bound

For easier comparison between the bound in Theorem 3 and the classical Markov chains results in [56], we report the latter below. Let $X_n$ an irreducible Markov chain on the (finite) state space E with transition matrix P, initial law $\nu$ and invariant measure $\pi$ and let $f:E \rightarrow {\mathbb {R}}$ be a bounded function with $\pi (f)=0$, $\pi (f^2)=b^2$ and $\Vert f\Vert _\infty =c$. Then

• 1. if P is self-adjoint

  $$\begin{aligned}{\mathbb {P}}_\nu \left( \frac{1}{n}\sum _{k=1}^{n}f(X_k)\ge \gamma \right) \le \left\| \frac{d\nu }{d\pi }\right\| _2 e^{c \varepsilon /5} \exp \left( -n \frac{\gamma ^2 \varepsilon }{2b^2}h\left( \frac{5c \gamma }{b^2}\right) \right) , \end{aligned}$$

  where $\varepsilon$ is the spectral gap of P,

• 2. if $P^\dagger P$ is irreducible

  $$\begin{aligned} {\mathbb {P}}_\nu \left( \frac{1}{n}\sum _{k=1}^{n}f(X_k)\ge \gamma \right) \le \left\| \frac{d\nu }{d\pi }\right\| _2 \exp \left( -n \frac{\gamma ^2 \varepsilon }{4b^2}h\left( \frac{5c \gamma }{b^2}\right) \right) , \end{aligned}$$

  (11)

  where $\varepsilon$ is the spectral gap of $P^\dagger P$.

$P^\dagger$ is the adjoint of P with respect to the inner product induced by $\pi$. The difference in the constants appearing in the bound in equation (6) and in the classical one (equation (11)) comes from the worse upper bound one can get for $r^{(2)}$ (equation (29)) in this more general setting.

In order to obtain the result for P self-adjoint, a crucial observation is that, in this case, $P_u:=PE_u$ (where $E_u=(\delta _{xy}e^{uf(x)})_{x,y \in E}$), is similar to a self-adjoint matrix: indeed, $PE_u=E_u^{-1/2}(E_u^{1/2}P E_u^{-1/2}) E_u^{-1/2}$. However, this is not the case for $\Phi _u$, as the following elementary example shows. Let us consider a three-dimensional quantum system, an orthonormal basis $\{|k\rangle \}_{k=0}^2$ and the quantum channel $\Phi$ with the following Kraus operators:

$$\begin{aligned}V_{k,k+1}=\frac{1}{2} |k+1\rangle \langle k|, \quad V_{k,k-1}= \frac{1}{2} |k-1\rangle \langle k|, \quad \text { for } k=0,1,2, \end{aligned}$$

where $k+1$ and $k-1$ are understood as modulo 3. In this case, the index set of Kraus operators is $I=\{(k,k+1),(k,k-1): k=0,1,2\}$. $\Phi$ is self-adjoint, but if we pick the function $f(k,k+1)=a$ and $f(k,k-1)=b$ for some real numbers $a \ne b$, then corresponding perturbation $\Phi _u$ has complex eigenvalues for every $u >0$, hence it cannot be similar to a self-adjoint map. A way of better understanding the difference between the classical and the quantum setting highlighted by the example is to notice that $\Phi$ is a quantum dilation of the symmetric random walk on a three vertex ring: indeed, $\Phi$ preserves the algebra

$$\begin{aligned}\Delta :=\left\{ x \in M_d({\mathbb {C}}): x=\sum _{k=0}^2 x(k) |k\rangle \langle k| \right\} ,\end{aligned}$$

which is isomorphic to the algebra of functions on three points

$$\begin{aligned}\ell ^\infty (E):=\{g:E \rightarrow {\mathbb {C}}\}, \quad E=\{0,1,2\},\end{aligned}$$

and its restriction to it is given by the transition matrix corresponding to the symmetric random walk on three vertices, i.e. $P=(p_{lk})$ where $p_{lk}=\frac{1}{2} (\delta _{k,l+1} + \delta _{k,l-1})$; f is a function of the jumps of the random walk and not of its states and the restriction of $\Phi _u$ to the diagonal algebra $\Delta$ is given by a perturbation of P of the form $P_u=(p_{lk}e^{u f(l,k)})$, which belongs to a more general class of perturbations of P than the one considered in [56]. In Sect. 5.1, we will show how this fact allows to prove new concentration inequalities for fluxes of classical Markov chains.

3.2 Hoeffding-Type Inequality

In this section, we prove a second quantum concentration bound inspired by classical result [42], which relies on the application of a fundamental inequality for centred bounded random variables (Hoeffding’s inequality) and the fact that $\frac{1}{n}\sum _{i=0}^{n-1}f(X_i)$ can be decomposed into a martingale with bounded increments and a bounded reminder. The same martingale decomposition was also used in [4] for proving the law of large number and the central limit theorem for $(f(X_k))_{k \in {\mathbb {N}}}$. The following inequality does not involve any measure of the variance of the function f at stationarity and, instead of the spectral gap of the multiplicative symmetrization of the quantum channel, it depends on the norm of the pseudo-resolvent $(\textrm{Id}-\Phi )^{-1}$. We remark that, contrary to Theorem 3, in this case there are no further assumptions on $\Phi$.

Theorem 4

For every $f:I \rightarrow {\mathbb {R}}$ such that $\pi (f)=0$ and $\Vert f\Vert _\infty =c$ for some $c >0$, then for every $\gamma > 0$

$$\begin{aligned} {\mathbb {P}}_\rho \left( \frac{1}{n} \sum _{k=1}^{n} f(X_k)\ge \gamma \right) \le \exp \left( - \frac{(n \gamma -2G)^2}{2(n-1)G^2}\right) \text { for } n \gamma \ge 2G, \end{aligned}$$

(12)

where $G=(1+\Vert (\textrm{Id}-\Phi )^{-1}_{|\mathcal {F}}\Vert _\infty )c$ and $\mathcal {F}:=\{x \in M_d({\mathbb {C}}): \textrm{tr}(\sigma x)=0\}$.

With a slight abuse of notation, we write $\Vert (\textrm{Id}-\Phi )^{-1}_{|\mathcal {F}}\Vert _\infty$ for denoting the operator norm of $(\textrm{Id}-\Phi )^{-1}_{|\mathcal {F}}$ induced by considering the uniform norm on ${{\mathcal {F}}}$. Notice that for $n=1$, the constraint on $\gamma$ implies that $\gamma \ge 2c=2\Vert f\Vert _\infty$ and consequently ${\mathbb {P}}_\rho ( f(X_1)\ge \gamma ) =0$.

Before presenting the proof of Theorem 4, we need the following technical lemma.

Lemma 5

Let us define $\textbf{F}=\sum _{i \in I} f(i) V_i^*V_i$. The equation

$$\begin{aligned} (\textrm{Id} -\Phi )(A)=\textbf{F} \end{aligned}$$

(13)

admits a solution and all the solutions differ for a multiple of the identity. We denote by $A_f$ the unique solution such that $\textrm{tr}(\sigma A_f)=0$; we have that $\Vert A_f\Vert \le c \Vert (\textrm{Id}-\Phi )^{-1}_{|\mathcal {F}}\Vert _\infty$ where $\mathcal {F}:=\{x \in M_d({\mathbb {C}}): \textrm{tr}(\sigma x)=0\}$.

Proof

The proof that $\textrm{Id}-\Phi$ is a bijection onto ${{\mathcal {F}}}$ (which implies the existence and uniqueness of $A_f$ since $\textbf{F} \in {{\mathcal {F}}}$) is the same as in [4, Lemma 5.1]. From $A_f = (\textrm{Id}-\Phi )^{-1}(\textbf{F})$, we get that $\Vert A_f\Vert \le \Vert (\textrm{Id}-\Phi )^{-1}_{|\mathcal {F}}\Vert _\infty \Vert \textbf{F}\Vert$. To conclude, we only need to show that $\Vert \textbf{F} \Vert \le c$: notice that $\textbf{F}$ can be written as the difference of two positive semidefinite matrices as

$$\begin{aligned}{} \textbf{F}=\sum _{\begin{array}{c} i \in I \\ f(i)\ge 0 \end{array}} f(i) V_i^* V_i - \sum _{\begin{array}{c} i \in I \\ f(i)< 0 \end{array}} |f(i)| V_i^* V_i,\end{aligned}$$

hence by [71, Corollary 3.17] we have that $\Vert \textbf{F}\Vert \le \Vert \sum _{ i \in I} |f(i)| V_i^*V_i\Vert \le c$.

$\square$

Proof

For clarity, we split the proof in three steps.

1. Poisson Equation

We start by discussing the quantum trajectories Markov process and its associated Poisson equation, which is a key tool in the proof. The pair $(X_n, \rho _n)$ consisting of the n-th measurement outcome $X_n\in I$ and the conditional system state $\rho _n$ is a Markov chain with

$$\begin{aligned}{\mathbb {P}}_\rho \left( X_{n+1}=i, \rho _{n+1}=\left. \frac{V_i \omega V_i^*}{\textrm{tr}(V_i \omega V_i^*)} \right| X_n=j, \rho _n =\omega \right) = \textrm{tr}(V_i \omega V_i^*). \end{aligned}$$

and initial condition

$$\begin{aligned} X_1 =i \quad \textrm{and} \quad \rho _1 = \frac{V_i \rho V_i^*}{\textrm{tr}(V_i \rho V_i^*)} \text { with probability } \textrm{tr}(V_i \rho V_i^*). \end{aligned}$$

Its transition operator P is given by

$$\begin{aligned} Pg(i,\omega ):=\sum _{j \in I} g\left( j, \frac{V_j \omega V_j^*}{\textrm{tr}(V_j \omega V_j^*)} \right) \textrm{tr}(V_j \omega V_j^*). \end{aligned}$$

The associated Poisson equation is

$$\begin{aligned} F(i,\omega )=g(i,\omega )-Pg(i,\omega ) \end{aligned}$$

(14)

where $F(i,\omega )$ is a given function, and one is interested in finding $g(i,\omega )$. We will provide an heuristic explanation on how to find a solution of the Poisson equation. Whenever it is well defined, a natural candidate for g is the function $g(i,\omega )=\sum _{n \ge 1} {\mathbb {E}}[F(X_n,\rho _n)|X_1=i,\rho _1=\omega ]=\sum _{n \ge 0}P^{n}(F)(i,\omega )$; indeed

$$\begin{aligned}g(i,\omega )-Pg(i,\omega )=\sum _{n \ge 0} P^n F(i,\omega )-\sum _{n \ge 1} P^n F(i,\omega )=F(i,\omega ). \end{aligned}$$

We now consider a function F, which does not depend on the second argument $F(i,\omega ) =f (i)$. Using the explicit expression of P, we can write

$$\begin{aligned}g(i,\omega )=f(i)+\textrm{tr}\left( \sum _{n \ge 0} \Phi ^n(\textbf{F}) \omega \right) = f(i)+\textrm{tr}( (\textrm{Id} -\Phi )^{-1}(\textbf{F}) \omega ) \end{aligned}$$

where $\textbf{F}=\sum _{i \in I} f(i) V_i^*V_i$. Lemma 5 shows that $A_f:=(\textrm{Id}-\Phi )^{-1}(\textbf{F})$ is well defined and it is an easy computation to verify that

$$\begin{aligned} f(i)=g(i, \omega )-Pg(i,\omega ), \quad g(i, \omega ):=f(i)+ \textrm{tr}(A_f \omega ). \end{aligned}$$

Moreover, $\Vert g\Vert _\infty \le c(1+\Vert (\textrm{Id}-\Phi )^{-1}_{|\mathcal {F}}\Vert _\infty )$.

2. Hoeffding’s Inequality

Following the proof of [4, Theorem 5.2], we can use the previous step to write $\sum _{k=1}^n f(X_k)$ as a martingale with bounded increments and a bounded reminder:

$$\begin{aligned}\begin{aligned} \sum _{k=1}^n f(X_k)&=\sum _{k=1}^n g(X_k,\rho _k)-{\mathbb {E}}_\rho [g(X_{k+1}, \rho _{k+1})|X_k,\rho _k]\\&=\sum _{k=2}^{n} \underbrace{g(X_k,\rho _k)-{\mathbb {E}}_\rho [g(X_{k}, \rho _{k})|X_{k-1},\rho _{k-1}]}_{D_k}\\&\quad +g(X_1, \rho _1)-{\mathbb {E}}_\rho [g(X_{n+1}, \rho _{n+1})|X_n,\rho _n].\\ \end{aligned} \end{aligned}$$

We can easily bound from above the Laplace transform of $\sum _{k=1}^n f(X_k)$ in the following way: for every $u>0$

$$\begin{aligned}\begin{aligned} {\mathbb {E}}_\rho \left[ e^{u\sum _{k=1}^n f(X_k)} \right]&\le e^{2\Vert g\Vert _\infty u} {\mathbb {E}}_\rho \left[ e^{u\sum _{k=2}^{n-1} D_k} {\mathbb {E}}_\rho \left[ e^{u D_n}|X_{n-1}, \rho _{n-1},\dots , X_1,\rho _1 \right] \right] \\&\le e^{2\Vert g\Vert _\infty u} e^{\Vert g\Vert _\infty ^2 u^2/2} {\mathbb {E}}_\rho \left[ e^{u\sum _{k=2}^{n-1} D_k}\right] \end{aligned} \end{aligned}$$

where in the last equation we used Hoeffding’s Lemma [22, Lemma 2.2]. By induction, we get

$$\begin{aligned}{\mathbb {E}}_\rho \left[ e^{u\sum _{k=1}^n f(X_k)} \right] \le exp(2\Vert g\Vert _\infty u+(n-1)\Vert g\Vert _\infty ^2 u^2/2). \end{aligned}$$

3. Fenchel–Legendre Transform

As in point 4. of the proof of Theorem 3, the final statement follows using Markov inequality and optimizing (remembering that $u>0$). $\square$

4 Quantum Counting Processes

In this section, we consider continuous-time concentration bounds for counting measurements in the output of a quantum Markov process. In this context, alternative concentration bounds have been recently obtained in [18]. In that paper, the authors first prove a bound for general quantum measurement processes which is sharp, but depends on quantities which may be hard to calculate in practical situations (Theorem 6); then, using functional inequalities, they are also able to derive further concentration bounds involving easily computable quantities, but only in the diffusive case for symmetric generators (Theorems 8 and 9 and Corollary 2). Theorem 6 aims at providing easily computable bounds for counting processes too. In this section, we show that the same perturbative analysis as in the proof of Theorem 3 can be used to take a first step towards filling this gap. More precisely, we consider a continuous-time quantum Markov process with GKLS generator [36] given by

$$\begin{aligned} {{\mathcal {L}}}(x)+i[H,x]=\sum _{i \in I} L^*_i x L_i -\frac{1}{2}\{L^*_iL_i,x\}, \quad x \in M_d({\mathbb {C}})\end{aligned}$$

(15)

where $[x,y]:=xy-yx$, $\{x,y\}:=xy+yx$, $H \in M_d({\mathbb {C}})$ is self-adjoint and $\{L_i\}_{i \in I}$ is a finite collection of operators in $M_d({\mathbb {C}})$. It is well known that the family of maps $\Phi _t:=e^{t {{\mathcal {L}}}}$ for $t\ge 0$ is a uniformly continuous semigroup of quantum channels. Analogously to the discrete time case, we need to make an irreducibility assumption.

$$\begin{aligned} \text {There exists a unique faithful state } \sigma \text { such that } {{\mathcal {L}}}^*(\sigma )=0. \end{aligned}$$

(H′)

Hypothesis (H$^\prime$) means that $(\Phi _t)_{t \ge 0}$ is irreducible. There are many ways of defining quantum counting processes: we will follow the formulation of Davis and Srinivas [32, 67] and we refer to [18] and references therein for their definition through quantum stochastic calculus and quantum filtering or how to characterize them using stochastic Schrödinger equations. Before doing that, it is convenient to introduce some notation: we define the completely positive map ${{\mathcal {J}}}_i(x)=L_i^*x L_i$ and the semigroup of completely positive maps $e^{t {{\mathcal {L}}}_0}(x)=e^{t G^*} x e^{t G}$, where $G:= i H-\frac{1}{2} \sum _{i \in I} L_i^*L_i$. As the process that we studied in previous sections, also the one we are about to define can be used to model the stochastic process coming from indirect measurements performed on a certain quantum system. We assume that the system is coupled to |I| detectors: when the i-th detector clicks, the state of the system evolves according to the map $\rho \mapsto {{\mathcal {J}}}^*_i(\rho )/\textrm{tr}({{\mathcal {J}}}^*_i(\rho ))$, while in between detections the evolution is dictated by $e^{t {{\mathcal {L}}}^*_0}(\rho )$. At time t the instantaneous intensity corresponding to the i-th detector is given by $\textrm{tr}({{\mathcal {J}}}_i^*(\rho _{t-}))$, where $\rho _t$ is the stochastic process describing the evolution of the state of the system. More formally, we can use Dyson’s expansion of the semigroup $\Phi _t$ in order to define a proper probability measure on $\Omega _t=\{(t_1,i_1,\dots ,t_k,i_k): k \in {\mathbb {N}}, 0 \le t_1 \le \dots \le t_k \le t, i_1,\dots , i_k \in I\}$:

$$\begin{aligned}\begin{aligned} \Phi ^*_t(\rho )=e^{t{{\mathcal {L}}}^*_0}(\rho )+\sum _{k=1}^{+\infty } \sum _{i_1,\dots , i_k \in I} \int _0^t \cdots \int _0^{t_2} e^{(t-t_k){{\mathcal {L}}}^*_0}{{\mathcal {J}}}^*_{i_k} \cdots {{\mathcal {J}}}^*_{i_k} e^{t_1{{\mathcal {L}}}^*_0}(\rho ) dt_1 \cdots dt_k. \end{aligned} \end{aligned}$$

Notice that

$$\begin{aligned}\Omega _t=\{\emptyset \} \cup \bigcup _{k=1}^{+\infty } I^k \times \{(t_1,\dots ,t_k)\in [0,t]^k: t_1 \le \dots \le t_k\}, \end{aligned}$$

so there is a natural way of endowing it with the $\sigma$-field induced by considering the $\sigma$-field of all the subsets on $\{\emptyset \}$ and I, and the Lebesgue $\sigma$-field on $\{(t_1,\dots ,t_k)\in [0,t]^k: t_1 \le \dots \le t_k\}$. We denote by $d\mu$ the unique measure such that $\mu (\{\emptyset \})=1$ and $\mu (\{(i_1,\dots , i_k)\times B)$ is the Lebesgue measure of B for every $(i_1,\dots , i_k) \in I^k$, $B \subseteq \{(t_1,\dots ,t_k)\in [0,t]^k: t_1 \le \dots \le t_k\}$. Notice that the following normalization condition holds true

$$\begin{aligned}\begin{aligned} 1&=\textrm{tr}(\Phi _t(\rho ))\\&=\textrm{tr}(e^{t{{\mathcal {L}}}^*_0}(\rho ))+\sum _{k=1}^{+\infty } \int _0^t \cdots \int _0^{t_2} \textrm{tr}(e^{(t-t_k){{\mathcal {L}}}^*_0}{{\mathcal {J}}}^*_{i_k} \cdots {{\mathcal {J}}}^*_{i_k} e^{t_1{{\mathcal {L}}}^*_0}(\rho )) dt_1 \cdots dt_k,\\ \end{aligned} \end{aligned}$$

and that the expression below safely defines a probability density on $\Omega _t$:

$$\begin{aligned} \frac{d {\mathbb {P}}_\rho }{d \mu }(\emptyset )=\textrm{tr}(e^{t{{\mathcal {L}}}^*_0}(\rho )), \frac{d {\mathbb {P}}_\rho }{d \mu }(t_1,i_1,\dots ,t_k,i_k)=\textrm{tr}(e^{(t-t_k){{\mathcal {L}}}^*_0}{{\mathcal {J}}}^*_{i_k} \cdots {{\mathcal {J}}}^*_{i_k} e^{t_1{{\mathcal {L}}}^*_0}(\rho )).\nonumber \\ \end{aligned}$$

(16)

We will derive a deviation bound for the random variable $N_i(t)$ that counts the number of clicks of the i-th detector until time t, i.e.

$$\begin{aligned}N_i(t)(\emptyset )=0, \quad N_i(t)(t_1,i_1,\dots ,t_k,i_k)=\sum _{l=1}^k \delta _{i,i_l}. \end{aligned}$$

We recall that the real part of an operator $\eta :M_d({\mathbb {C}})\rightarrow M_d({\mathbb {C}})$ is defined as $\Re (\eta ):=(\eta +\eta ^\dagger )/2$.

Theorem 6

Consider an arbitrary, but fixed index $i\in I$ and define ${{\mathcal {A}}}:=\Re ({{\mathcal {L}}})$ and ${{\mathcal {B}}}=\Re ({{\mathcal {J}}}_i)$. Assuming that ${{\mathcal {A}}}$ generates an irreducible quantum Markov semigroup, then for any $t \ge 0$, $\gamma >0$ the following inequality holds true:

$$\begin{aligned} {\mathbb {P}}_\rho \left( \frac{N_i(t)}{t}-m_i \ge \gamma \right) \le N_\rho \exp \left( -t \left( \frac{\gamma ^2}{2 \left( m+\frac{2 b^2}{\varepsilon }+ \left( \frac{5\alpha }{\varepsilon } \vee \frac{5}{2}\right) \gamma \right) } \right) \right) \nonumber \\ \end{aligned}$$

(17)

where $m:=\textrm{tr}(L_i^*L_i \sigma )$ is the intensity of $N_i$ at stationarity, $N_\rho :=\Vert \sigma ^{-\frac{1}{2}}\rho \sigma ^{-\frac{1}{2}}\Vert _2$, $\alpha := \Vert {{\mathcal {B}}}\Vert _2$, $b:=\Vert {{\mathcal {B}}}(\textbf{1})\Vert _2$ and $\varepsilon$ is the spectral gap of ${{\mathcal {A}}}$.

Once again, with a slight abuse of notation, we denote by $\Vert {{\mathcal {B}}}\Vert _2$ the operator norm of ${{\mathcal {B}}}$ induced by considering $M_d({\mathbb {C}})$ with the KMS-norm. We point out that the spectral gap of ${{\mathcal {A}}}$ appears also in the (finite time) upper bound on auto-correlation functions, which has recently been derived in [57]. We remark that a sufficient condition for ${{\mathcal {A}}}$ to generate an irreducible quantum Markov semigroup is that $[H,\sigma ]=0$. Indeed, both ${{\mathcal {L}}}$ and ${{\mathcal {L}}}^\dagger$ generate irreducible quantum Markov semigroups with faithful invariant state $\sigma$; hence, $\sigma$ is a faithful invariant state for ${{\mathcal {A}}}$ too. Moreover, we can easily compute the GKLS form of ${{\mathcal {L}}}^\dagger$ induced by the one of ${{\mathcal {L}}}$ in Eq. (15), which reads

$$\begin{aligned}{{\mathcal {L}}}^\dagger (x)=i[\sigma ^{-\frac{1}{2}} H \sigma ^{\frac{1}{2}},x]+\sum _{i \in I} L_i^{\prime *} x L^\prime _i -\frac{1}{2}\{L^{\prime *}_iL^\prime _i,x\}, \quad x \in M_d({\mathbb {C}}), \end{aligned}$$

where we omit the exact expression of $L_i^\prime$’s. Since we assumed that $[H,\sigma ]=0$, $\sigma ^{-\frac{1}{2}} H \sigma ^{\frac{1}{2}}=H$. Putting together the GKLS forms of ${{\mathcal {L}}}$ and ${{\mathcal {L}}}^\dagger$, we can express ${{\mathcal {A}}}=({{\mathcal {L}}}+{{\mathcal {L}}}^\dagger )/2$ as

$$\begin{aligned}\begin{aligned} i[H,x]&+\frac{1}{2} \left( \sum _{i \in I} L^{\prime *}_i x L^\prime _i -\frac{1}{2}\{L^{\prime *}_iL^\prime _i,x\} \right. \\&+\left. \sum _{i \in I} L_i^* x L_i -\frac{1}{2}\{L_i^*L_i,x\} \right) , \quad x \in M_d({\mathbb {C}}).\\ \end{aligned} \end{aligned}$$

The irreducibility of a quantum Markov semigroup with faithful invariant state is equivalent to the fact that the commutant of the Hamiltonian, the noise operators and their adjoints are equal to ${\mathbb {C}} \textbf{1}$ ([70, Theorem 7.2]); hence, we can conclude that ${{\mathcal {A}}}$ generates an irreducible quantum Markov semigroup: indeed, we have that

$$\begin{aligned}\{H,L_i,L_i^*, L_i^\prime , L_i^{\prime *}\}^\prime = \{H,L_i,L_i^*\}^\prime \cap \{H,L_i^\prime , L_i^{\prime *}\}^\prime ={\mathbb {C}}\textbf{1}. \end{aligned}$$

Proof

Using the explicit expression of the density of ${\mathbb {P}}_\rho$ given in Eq. (16), one can show that the Laplace transform of $N_i(t)$ can be expressed in terms of a smooth perturbation of the Lindblad generator:

$$\begin{aligned}{\mathbb {E}}_\rho [e^{u N_i(t)}]=\textrm{tr}(\rho e^{t{{\mathcal {L}}}_u}(\textbf{1})) \end{aligned}$$

where ${{\mathcal {L}}}_u(\cdot )={{\mathcal {L}}}(\cdot )+(e^u-1){{\mathcal {J}}}_i(\cdot )$; we refer to Appendix A in [18] for a proof using quantum stochastic calculus. Using Lumer–Phillips theorem, we get to

$$\begin{aligned}{\mathbb {E}}_\rho [e^{uN_i(t)}] \le N_\rho e^{t r(u)} \le N_\rho e^{t |r(u)|}, \end{aligned}$$

where r(u) is the largest eigenvalue of ${{\mathcal {A}}}_u:=\Re ({{\mathcal {L}}}_u)$. Notice that ${{\mathcal {A}}}_u$ is a smooth perturbation of ${{\mathcal {A}}}:=\Re ({{\mathcal {L}}})$:

$$\begin{aligned}{{\mathcal {A}}}_u= {{\mathcal {A}}}+\sum _{k\ge 1} \frac{u^k}{k!} {{\mathcal {B}}} \end{aligned}$$

and ${{\mathcal {B}}}=\Re ({{\mathcal {J}}}_i)$. From perturbation theory, we get that if ${{\mathcal {A}}}$ is the generator of an irreducible quantum Markov semigroup with spectral gap equal to $\varepsilon$ and if we call $\alpha := \Vert {{\mathcal {B}}}\Vert _2$, we can expand $r(u)=\sum _{k \ge 1}r^{(k)} u^k$ around $u=0$ for $u <(2\alpha \varepsilon ^{-1}+1)^{-1}$ and the coefficients $r^{(k)}$’s are provided by the following expression:

$$\begin{aligned}r^{(k)}=\sum _{p=1}^k \frac{(-1)^p}{p} \sum _{\begin{array}{c} \nu _1+\dots +\nu _p=k,\, \nu _i\ge 1\\ \mu _1+\dots +\mu _p=p-1, \, \mu _j\ge 0 \end{array}} \frac{1}{\nu _1! \cdots \nu _p!}\textrm{TR}({{\mathcal {B}}} S^{(\mu _1)}\cdots {{\mathcal {B}}}S^{(\mu _p)}), \end{aligned}$$

$S^{(0)}=-|\textbf{1}\rangle \langle \textbf{1}|$ and for $\mu \ge 1$, $S^{(\mu )}$ is the $\mu$-th power of

$$\begin{aligned}S^{(1)}=({{\mathcal {A}}}+|\textbf{1}\rangle \langle \textbf{1}|)^{-1}-|\textbf{1}\rangle \langle \textbf{1}|.\end{aligned}$$

Notice that $\Vert S^{(\mu )}\Vert _2=\varepsilon ^{-\mu }$ for $\mu \ge 1$. This time we get that

$$\begin{aligned}r^{(1)}=\langle \textbf{1}, {{\mathcal {B}}}(\textbf{1}) \rangle =\textrm{tr}(\sigma L_i^*L_i):=m,\end{aligned}$$

which is the intensity of $N_i$ in the stationary regime. For the other terms, we need to introduce the notation $b:=\Vert {{\mathcal {B}}}(\textbf{1})\Vert _2$; then we get that

$$\begin{aligned}|r^{(2)}|\le \frac{m}{2}+ |\langle {{\mathcal {B}}}(\textbf{1}), S^{(1)} {{\mathcal {B}}}(\textbf{1}) \rangle \le \frac{m}{2}+ \frac{b^2}{\varepsilon } \end{aligned}$$

and, for $k \ge 3$,

$$\begin{aligned}|r^{(k)}|\le {\left\{ \begin{array}{ll}\frac{m}{k!}+ \frac{b^2}{5 \alpha }\left( \frac{5\alpha }{\varepsilon } \right) ^{k-1} &{} \text { if } 2\alpha /\varepsilon \ge 1 \\ \frac{m}{k!}+ \frac{2b^2}{ 5 \varepsilon } \left( \frac{5}{2} \right) ^{k-1}&{} \text { o.w.}\\ \end{array}\right. }, \end{aligned}$$

where we used that $\nu _1! \cdots \nu _p! \ge 2^{k-p}$ and for $p \ge 2$

$$\begin{aligned}\left| \frac{\textrm{TR}({{\mathcal {B}}} S^{(\mu _1)}\cdots {{\mathcal {B}}}S^{(\mu _p)})}{\nu _1! \cdots \nu _p!} \right| \le \frac{b^2}{\alpha } \left( \frac{2 \alpha }{\epsilon } \right) ^{p-1}\frac{1}{2^{k-1}} \le {\left\{ \begin{array}{ll} \frac{b^2}{\alpha } \left( \frac{ \alpha }{\epsilon } \right) ^{k-1} &{} \text { if } \frac{2 \alpha }{\epsilon } \ge 1 \\ \frac{b^2}{\alpha } \left( \frac{2 \alpha }{\epsilon } \right) \frac{1}{2^{k-1}} &{} \text { o.w. } \end{array}\right. } \end{aligned}$$

Wrapping up everything, we obtain that

$$\begin{aligned} |r(u)| \le m(e^{u}-1) + \frac{b^2}{\varepsilon }u^2 \left( 1-\left( \frac{5\alpha }{\varepsilon } \vee \frac{5}{2}\right) u\right) ^{-1}. \end{aligned}$$

(18)

Hence, one gets that for every $u>0$

$$\begin{aligned} \begin{aligned} {\mathbb {P}}_\rho \left( \frac{N_t}{t}-m \ge \gamma \right) \le N_\rho \exp \left( -t \left( \gamma u- m(e^u-u-1)-\frac{b^2}{\varepsilon }u^2 \left( 1-\left( \frac{5\alpha }{\varepsilon } \vee \frac{5}{2}\right) u \right) ^{-1} \right) \right) \end{aligned}\nonumber \\ \end{aligned}$$

(19)

Notice that the term $e^{tm(e^u-1)}$ in the r.h.s. of Eq. (19) is exactly the Laplace transform of a Poisson process with intensity m. The extra terms come from the correlations between the process $N_t$ at different times and the convergence towards the stationary regime. The statement follows from the same computations as in [51, Lemma 9]. $\square$

Below we provide some simple bounds for some of the quantities appearing in inequality (17).

• Using triangular inequality, we get

  $$\begin{aligned}b:=\Vert {{\mathcal {B}}}(\textbf{1})\Vert _2\le \frac{\Vert L_i^*L_i\Vert _2+\Vert (\sigma ^{\frac{1}{2}} L^*_i\sigma ^{-\frac{1}{2}})^*(\sigma ^{\frac{1}{2}} L^*_i\sigma ^{-\frac{1}{2}})\Vert _2}{2}.\end{aligned}$$

  Then, we can apply Cauchy–Schwarz inequality:

  $$\begin{aligned}\Vert L_i^*L_i\Vert _2=\textrm{tr}(\sigma ^{\frac{1}{2}}L_i^*L_i \sigma ^{\frac{1}{2}}L_i^*L_i)^{\frac{1}{2}} \le \textrm{tr}(\sigma (L_i^*L_i)^2)^{\frac{1}{2}} \le \Vert L^*_i L_i\Vert ^{\frac{1}{2}} m^{\frac{1}{2}} \end{aligned}$$

  and

  $$\begin{aligned}\Vert (\sigma ^{\frac{1}{2}} L^*_i\sigma ^{-\frac{1}{2}})^*(\sigma ^{\frac{1}{2}} L^*_i\sigma ^{-\frac{1}{2}})\Vert _2\le \Vert (\sigma ^{\frac{1}{2}} L^*_i\sigma ^{-\frac{1}{2}})^*(\sigma ^{\frac{1}{2}} L^*_i\sigma ^{-\frac{1}{2}})^*\Vert ^{\frac{1}{2}} m^{\frac{1}{2}}. \end{aligned}$$

• Notice that

  $$\begin{aligned}\alpha :=\Vert {{\mathcal {B}}}\Vert _2\le \Vert L_i^* \cdot L_i\Vert _2=\Vert (\sigma ^{\frac{1}{2}} L^*_i\sigma ^{-\frac{1}{2}})^*\cdot (\sigma ^{\frac{1}{2}} L^*_i\sigma ^{-\frac{1}{2}})\Vert _2.\end{aligned}$$

  Let us denote by $\textrm{Sp}(\sigma )$ the spectrum of $\sigma$; since

  $$\begin{aligned}\begin{aligned}&L_i \sigma L^*_i \le L_i L_i^* \le \frac{\Vert L_i L_i^*\Vert }{\min (\textrm{Sp}(\sigma ))} \sigma , \\&(\sigma ^{\frac{1}{2}} L^*_i\sigma ^{-\frac{1}{2}}) \sigma (\sigma ^{\frac{1}{2}} L^*_i\sigma ^{-\frac{1}{2}})^* \le \frac{\Vert (\sigma ^{\frac{1}{2}}L^*_i\sigma ^{-\frac{1}{2}}) (\sigma ^{\frac{1}{2}} L^*_i\sigma ^{-\frac{1}{2}})^*\Vert \sigma }{\min (\textrm{Sp}(\sigma ))}, \end{aligned} \end{aligned}$$

  Lemma 1.3 in [59] implies that

  $$\begin{aligned}\Vert {{\mathcal {B}}}\Vert _2 \le \min \{\Vert L_i L_i^*\Vert ,\Vert (\sigma ^{\frac{1}{2}}L^*_i\sigma ^{-\frac{1}{2}}) (\sigma ^{\frac{1}{2}} L^*_i\sigma ^{-\frac{1}{2}})^*\Vert \}/\min (\textrm{Sp}(\sigma )).\end{aligned}$$

We remark that the proof of Theorem 6 works also for the more general case of the counting processes $Y_j$ defined in [18], which correspond to a change of basis before detection.

5 Extensions and Applications

5.1 Concentration Bounds for Fluxes of Classical Markov Chains

Let us consider a classical Markov chain $(X_{n})_{n\ge 1}$ with finite state space E and transition matrix $P=(p_{xy})_{x,y \in E}$ which is irreducible and admits a unique invariant measure $(\sigma _x)_{x \in E}$. Instead of looking at functions of the state of the Markov chain, one may be interested in having concentration bounds for empirical fluxes, i.e. empirical means of functions of the jumps $f:E^2 \rightarrow {\mathbb {R}}$ (for instance for estimating jump probabilities). Having a wide range of concentration bounds for the empirical mean of functions of the state of a Markov chain, a first natural attempt is considering fluxes as functions of the state of the doubled up Markov chain $({\tilde{X}}_n)_{n \ge 1}$, which is the Markov chain with state space ${\tilde{E}}:=\{(x,y) \in E^2:p_{xy}>0\}$ and with transition matrix given by ${\tilde{P}}=({\tilde{p}}_{(x,y)(z,w)})$, with ${\tilde{p}}_{(x,y)(z,w)}=\delta _{y,z}p_{yw}$; if P is irreducible, then so is ${\tilde{P}}$ and its unique invariant distribution is the measure $(\sigma _x p_{xy})_{x,y}$. However, in general the matrix ${\tilde{P}}$ behaves in a less nice way than P: for instance, Theorems 1.1 and 3.3 in [56] can never be applied to the doubled up Markov chain for non-trivial models, since both ${\tilde{P}}$ being self-adjoint or ${\tilde{P}}^\dagger {\tilde{P}}$ being irreducible imply that E is a singleton (the adjoint of ${\tilde{P}}$ is taken with respect to the inner product induced by the unique invariant measure for the doubled-up Markov chain). Remarkably, we can carry out the proofs of Theorems 3 and 4 in this classical setting and they provide concentration inequalities for empirical fluxes involving the matrix P instead of ${\tilde{P}}$: this reflects the fact that P already contains all the information about jumps. Let $\nu$ be any initial probability measure on E; for the Bernstein bound, it is enough to notice that for every $u>0$

$$\begin{aligned}{\mathbb {E}}_\nu [e^{u \sum _{k=1}^{n} f(X_k,X_{k+1})}]=\nu \cdot P_u^{n} \cdot \textbf{1} \end{aligned}$$

where $(P_u)_{xy}=p_{xy}e^{uf(x,y)}$ and $\textbf{1}$ is the constant function on E equal to 1. The proof of Theorem 3 can be carried out replacing $M_d({\mathbb {C}})$ with $\ell ^\infty (E):=\{f:E \rightarrow {\mathbb {C}}\}$ and $\Phi$ with P; in this particular setting, $\ell ^\infty (E)$ can be turned into a Hilbert space with respect to the inner product

$$\begin{aligned}\langle h, g \rangle =\sum _{x \in E}\sigma _x {\overline{h}}(x)g(x), \quad h,g \in \ell ^\infty (E) \end{aligned}$$

The Bernstein-type inequality for fluxes reads as follows. We recall that ${\tilde{E}}:=\{(x,y) \in E^2:p_{xy}>0\}$, $\pi (x,y)=\sigma _xp_{xy}$.

Proposition 7

If $Q:=P^\dagger P$ is irreducible, then for every $f:{\tilde{E}} \rightarrow {\mathbb {R}}$ such that $\pi (f)=0$, $\pi (f^2)=b^2$ and $\Vert f \Vert _\infty =c$ for some $b,c>0$ and for every $\gamma > 0$, $n \ge 1$

$$\begin{aligned} {\mathbb {P}}_\nu \left( \frac{1}{n} \sum _{k=1}^{n} f(X_k,X_{k+1})\ge \gamma \right) \le N_\nu \exp \left( -n \frac{\gamma ^2 \varepsilon }{6b^2}h\left( \frac{10c \gamma }{3b^2}\right) \right) \end{aligned}$$

(20)

where $\varepsilon$ is the spectral gap of Q, $N_\nu :=\Vert \frac{d\nu }{d\sigma }\Vert _2$ and $h(x)=(\sqrt{1+x}+x/2+1)^{-1}$.

Regarding the Hoeffding-type inequality, one just needs to notice that, calling $a_f \in \ell ^\infty (E)$ the unique centred solution of

$$\begin{aligned}(\textrm{Id}-P)(h)(x)=\sum _{y \in E}p_{xy}f(x,y), \quad h \in \ell ^\infty (E), \end{aligned}$$

for every $k \ge 1$, we can write $f(X_k,X_{k+1})=g(X_k,X_{k+1})-{\mathbb {E}}_\nu [g(X_k,X_{k+1})|X_{k-1},X_k]$, where $g(x,y)=f(x,y)+a_f(y)$ (once again we assume that $\pi (f)=0$). Repeating the same steps as in the proof of Theorem 4, we can obtain the following.

Proposition 8

For every $f:{\tilde{E}} \rightarrow {\mathbb {R}}$ such that $\pi (f)=0$ and $\Vert f\Vert _\infty =c$ for some $c >0$, then for every $\gamma > 0$

$$\begin{aligned} {\mathbb {P}}_\nu \left( \frac{1}{n} \sum _{k=1}^{n} f(X_k,X_{k+1})\ge \gamma \right) \le \exp \left( - \frac{(n \gamma -2G)^2}{2(n-1)G^2}\right) \text { for } n \gamma \ge 2G, \end{aligned}$$

(21)

where $G=(1+\Vert (\textrm{Id}-P)^{-1}_{|\mathcal {F}}\Vert _\infty )c$ and $\mathcal {F}:=\{h \in \ell ^\infty (E): \sigma (h)=0\}$.

In the same spirit, one can obtain new bounds for empirical fluxes of continuous-time Markov chains too; we aim at studying some applications of such bounds in a future work.

5.2 Reducible Quantum Channels

The study of some physically relevant models requires hypothesis (H) to be dropped: for instance, in the case of non-demolition measurements [11, 12], where the interaction between the system and the ancillas is such that it preserves some non-degenerate observable $A=\sum _{j=1}^d \alpha _j |\alpha _j\rangle \langle \alpha _j| \in M_d({\mathbb {C}})$; hence, it is of the form

$$\begin{aligned}U=\sum _{j=1}^d |\alpha _j\rangle \langle \alpha _j| \otimes U_j \in M_{d \times \dim (\mathfrak {h}_a)}({\mathbb {C}}) \end{aligned}$$

for some collection of unitary operators $(U_j)$ acting on the ancillary system (which is described by the Hilbert space $\mathfrak {h}_a$). In this case, Kraus operators of $\Phi ^*(\rho )=\textrm{tr}_{\mathfrak {h}_a}(U \rho \otimes |\chi \rangle \langle \chi | U^*)$ induced by the measurement on the ancilla corresponding to the orthonormal basis $\{|i\rangle \}_{i \in I}$ are given by

$$\begin{aligned}V_i=\sum _{j=1}^d \langle i| U_j| \chi \rangle |\alpha _j\rangle \langle \alpha _j|, \quad i \in I. \end{aligned}$$

It is easy to see that $\Phi$ is positive recurrent, but it is not irreducible anymore: any $|\alpha _j\rangle \langle \alpha _j|$ is an invariant state for $\Phi$. If we do not assume that $\Phi$ is irreducible, the first issue we need to take into account is that in general $\frac{1}{n}\sum _{k=1}^{n}f(X_k)$ does converge to a non-trivial random variable: for instance, in the case of non-demolition measurements, one can show that there exists a random variable $\Gamma$ taking values in $\{1,\dots , d\}$ such that

$$\begin{aligned}\lim _{n \rightarrow +\infty }\frac{1}{n}\sum _{k=1}^{n}f(X_k)=m_\Gamma \quad {\mathbb {P}}_\rho \text {-a.s.,} \end{aligned}$$

where $m_j=\sum _{i \in I} f(i) |\langle i|U_j |\chi \rangle |^2$. What one can do, then, is to upper bound the probability that $\frac{1}{n}\sum _{k=1}^{n}f(X_k)$ deviates from $m_\Gamma$. Leaving aside non-demolition measurements, we will present the result in the case of general quantum Markov chains assuming only the existence of a faithful invariant state for $\Phi ^*$. It is well known [14] that we can always find a (non-unique) decomposition

$$\begin{aligned} {\mathbb {C}}^d= \bigoplus _{j \in J}\mathfrak {h}_j \end{aligned}$$

(22)

such that

• 1. $\mathfrak {h}_j \perp \mathfrak {h}_{j^\prime }$ if $j \ne j^\prime$ (orthogonality),

• 2. if $\textrm{supp}(\rho )\subseteq \mathfrak {h}_j$, then $\textrm{supp}(\Phi ^*(\rho ))\subseteq \mathfrak {h}_j$ (invariance),

• 3. $\Phi ^*$ restricted to $p_{\mathfrak {h}_j}M_d({\mathbb {C}})p_{\mathfrak {h}_j}$ is irreducible with unique invariant state $\sigma _j$ (minimality),

where we used the notation $p_{\mathfrak {h}_j}$ to denote the orthogonal projection onto $\mathfrak {h}_j$; one can show that 2. is equivalent to

$$\begin{aligned}2^\prime . \qquad [V_i,p_{\mathfrak {h}_j}]=0 \quad \forall i \in I, j \in J. \end{aligned}$$

If the system initially starts in a state $\rho$ supported on only one of the $\mathfrak {h}_j$’s, it is easy to see that 2. and 3. imply that we are back to the case of an irreducible quantum channel. Otherwise, the decomposition in Eq. (22) allows to express ${\mathbb {P}}_\rho$ as a convex mixture of probability measures corresponding to irreducible quantum channels:

$$\begin{aligned} \begin{aligned}&{\mathbb {P}}_\rho (i_1,\dots ,i_n)=\textrm{tr}(V_{i_n} \cdots V_{i_1} \rho V_{i_1}^* \cdots V_{i_n}^*)\\&\quad =\sum _{j \in J}\underbrace{\textrm{tr}(p_{\mathfrak {h}_j} \rho )}_{=:\lambda _j(\rho )} \textrm{tr}\left( p_{\mathfrak {h}_j}V_{i_n}p_{\mathfrak {h}_j} \cdots p_{\mathfrak {h}_j}V_{i_1}p_{\mathfrak {h}_j} \underbrace{\frac{p_{\mathfrak {h}_j}\rho p_{\mathfrak {h}_j}}{\textrm{tr}(p_{\mathfrak {h}_j} \rho )}}_{=:\rho _j} (p_{\mathfrak {h}_j}V_{i_1} p_{\mathfrak {h}_j})^*\cdots (p_{\mathfrak {h}_j}V_{i_n}p_{\mathfrak {h}_j})^* \right) \\&\quad =\sum _{j \in J} \lambda _j(\rho ) {\mathbb {P}}_{\rho _j}(i_1,\dots , i_n). \end{aligned} \end{aligned}$$

The last result that we need to recall ([41, Theorem 3.5.2]) is that, given any $f:I \rightarrow {\mathbb {R}}$, there exists a random variable $\Gamma$ taking values in J such that

$$\begin{aligned}\lim _{n \rightarrow +\infty }\frac{1}{n}\sum _{k=1}^{n}f(X_k)=\pi _\Gamma (f) \quad {\mathbb {P}}_\rho \text {-a.s.,} \end{aligned}$$

where $\pi _j(f)=\sum _{i \in I} f(i) \pi _j(i)$ and $\pi _j(i)=\textrm{tr}(\sigma _j V_i^*V_i)$. As we already mentioned, under ${\mathbb {P}}_{\rho _j}$

$$\begin{aligned}\lim _{n \rightarrow +\infty }\frac{1}{n}\sum _{k=0}^{n-1}f(X_k)=\pi _j(f) \text { a.s.,} \end{aligned}$$

which means that $\textrm{supp}({\mathbb {P}}_{\rho _j}) \subseteq \{\pi _\Gamma (f)=\pi _j(f)\}$. We have now all the ingredients required to apply previous results in this more general instance: let $\gamma >0$, $n \ge 1$, then

$$\begin{aligned}{\mathbb {P}}_\rho \left( \left| \frac{1}{n}\sum _{k=1}^{n}f(X_k)-\pi _\Gamma (f) \right| \ge \gamma \right) = \sum _{j \in J}\lambda _j(\rho ){\mathbb {P}}_{\rho _j}\left( \left| \frac{1}{n}\sum _{k=1}^{n}f(X_k)-\pi _j(f) \right| \ge \gamma \right) \end{aligned}$$

and we can apply either Theorem 3 or Theorem 4 for upper bounding every ${\mathbb {P}}_{\rho _j}\left( \left| \frac{1}{n}\sum _{k=1}^{n}f(X_k)-\pi _j(f) \right| >\gamma \right)$. We remark that for applying Theorem 3, $\Phi ^\dagger _{|p_{\mathfrak {h}_j}M_d({\mathbb {C}})p_{\mathfrak {h}_j}} \Phi _{|p_{\mathfrak {h}_j}M_d({\mathbb {C}})p_{\mathfrak {h}_j}}$ needs to be irreducible (the adjoint is taken with respect to the KMS-inner product induced by $\sigma _j$), while Theorem 4 requires that $n\gamma >2(1+\Vert (\textrm{Id}-\Phi _{|p_{\mathfrak {h}_j}M_d({\mathbb {C}})p_{\mathfrak {h}_j}})_{{{\mathcal {F}}}_j}^{-1}\Vert _\infty )$ for ${{\mathcal {F}}}_j:=\{x \in p_{\mathfrak {h}_j}M_d({\mathbb {C}})p_{\mathfrak {h}_j}: \textrm{tr}(\sigma _j x)=0\}$ (by $\Phi _{|p_{\mathfrak {h}_j}M_d({\mathbb {C}})p_{\mathfrak {h}_j}}$ we mean $(\Phi ^*_{|p_{\mathfrak {h}_j}M_d({\mathbb {C}})p_{\mathfrak {h}_j}})^*$).

5.3 Time-Dependent and Imperfect Measurements

Both inequalities in Theorems 3 and 4 can be easily generalized to the setting where we allow the measurement to change along time and the evolution of the system state after the measurement is taken to be more general (including imperfect measurements). Let us consider $\Phi$ an irreducible quantum channel with unique faithful invariant state $\sigma$ and suppose that for any time $n \in {\mathbb {N}}$ we consider a (possibly) different unravelling of $\Phi$, i.e. a collection of completely positive, sub-unital maps $\{\Phi _{i,n}\}_{i \in I_n}$ such that $|I_n|<+\infty$ and $\Phi =\sum _{i \in I_n} \Phi _{i,n}$; at any time we pick a function $f_n:I_n \rightarrow {\mathbb {R}}$. In the time inhomogeneous case, even if the system starts from the unique invariant state $\sigma$, the law of the process changes at any time: under ${\mathbb {P}}_\sigma$, $X_k$ is distributed according to the probability measure $\pi _k$ defined as follows:

$$\begin{aligned}\pi _k(i)=\textrm{tr}(\Phi _{i,k}^*(\sigma )), \quad i \in I_k. \end{aligned}$$

We denote by $\pi _k(f_k)$ the expected value of $f_k$ under $\pi _k$, i.e. $\pi _k(f_k)=\sum _{i \in I_k} f_k(i) \pi _k(i)$.

The proofs of Theorems 3 and 4 can be carried out in this more general setting with minimal modifications:

• Bernstein-Type Inequality:

  $$\begin{aligned} {\mathbb {P}}_\rho \left( \frac{1}{n} \sum _{k=1}^{n}\left( f_k(X_k)- \pi _k(f) \right) \ge \gamma \right) \le N_\rho \exp \left( - n\frac{\gamma ^2 \varepsilon }{6b_n^2}h\left( \frac{10 c_n \gamma }{3b_n^2}\right) \right) \end{aligned}$$

  (23)

  where $N_\rho =\Vert \sigma ^{-\frac{1}{2}}\rho \sigma ^{-\frac{1}{2}}\Vert _2$, $\pi _k(f_k):=\sum _{i \in I_k} f_k(i) \textrm{tr}(\Phi _{i,k}^*(\sigma ))$, $c_n:=\max _{k=1,\dots ,n}\Vert f_k-\pi _k(f_k)\Vert _\infty$ and $b_n^2:=\frac{1}{n} \sum _{k=1}^{n}\pi _k((f_k-\pi _k(f_k))^2)$. Explicit computations show that, in this case, the Laplace transform has the following form:

  $$\begin{aligned}{} & {} {\mathbb {E}}_\rho [e^{u \sum _{k=1}^{n}(f_k(X_k)-\pi _k(f_k))}]\\{} & {} \quad =\textrm{tr}(\rho \Phi _{u,1} \cdots \Phi _{u,n}(\textbf{1}))\\{} & {} \quad \le \Vert \sigma ^{-\frac{1}{2}}\rho \sigma ^{-\frac{1}{2}}\Vert _2 \cdot \prod _{k=1}^{n}\Vert \Phi _{u,k}\Vert _2,\end{aligned}$$

  where $\Phi _{u,k}(x)=\sum _{i \in I_k} e^{u (f_k(i)-\pi _k(i))} \Phi _{i,k}(x)$. One can use the same techniques as in the proof of Theorem 3 to upper bound every single $\Vert \Phi _{u,k}\Vert _2$ getting to the expression below:

  $$\begin{aligned}\begin{aligned} {\mathbb {E}}_\rho [e^{u \sum _{k=1}^{n}(f_k(X_k)-\pi _k(f_k))}]&\le N_\rho e^{ \frac{3u^2}{\varepsilon } \sum _{k=1}^{n} \pi _k((f_k-\pi _k(f_k))^2) \left( 1-\frac{10 \Vert f_k-\pi _k(f_k)\Vert _\infty u}{\varepsilon } \right) ^{-1}} \\&\le N_\rho e^{-n\left( -\frac{3u^2}{\varepsilon } \frac{1}{n}\sum _{k=1}^{n} \pi _k((f_k-\pi _k(f_k))^2)\left( 1-\frac{10c_n u}{\varepsilon } \right) ^{-1} \right) }. \\ \end{aligned}\end{aligned}$$

  Applying Chernoff bound and optimizing on $u>0$, one obtains Eq. (23).

• Hoeffding-Type Inequality

  $$\begin{aligned}{} & {} {\mathbb {P}}_\rho \left( \frac{1}{n} \sum _{k=1}^{n}\left( f_k(X_k)- \pi _k(f) \right) \ge \gamma \right) \nonumber \\{} & {} \quad \le \exp \left( - \frac{(n \gamma -G_n)^2}{(n-1) G_n^2}\right) \text { for } n \gamma \ge G_n, \end{aligned}$$

  (24)

  where $G_n=(1+\sum _{j=0}^{n-2}\Vert \Phi _{|\mathcal {F}}^j\Vert _\infty )c_n$ ($\sum _{j=0}^{-1}$ must be interpreted as 0), $\mathcal {F}:=\{x \in M_d({\mathbb {C}}): \textrm{tr}(\sigma x)=0\}$ and $c_n$ is the same as above. Let us define

  $$\begin{aligned}Z_k^{(n)}=\sum _{j=k}^{n} {\mathbb {E}}_\rho [f(X_j)|X_1, \rho _1,\dots , X_k, \rho _k]. \end{aligned}$$

  Notice that for $k=1,\dots , n-1$, $Z_k^{(n)}=f_k(X_k)+{\mathbb {E}}_\rho [Z_{k+1}^{(n)}pg{ }|X_1,\rho _1,\dots , X_k,\rho _k]$, hence we can write

  $$\begin{aligned} \sum _{k=1}^{n} f_k(X_k)=\sum _{k=2}^{n}\underbrace{Z_k^{(n)}-{\mathbb {E}}_\rho [Z_{k}^{(n)}|X_1,\rho _1,\dots , X_{k-1},\rho _{k-1}]}_{D_k}+Z_1^{(n)}. \end{aligned}$$

  By Markov property, we have that $Z_k^{(n)}=g_k^{(n)}(X_k,\rho _k)$ and using the explicit expression of the transition operator of $(X_n,\rho _n)$, one gets that $g_k^{(n)}$ has the following form:

  $$\begin{aligned} g_k^{(n)}(i,\omega )= & {} f_k(i)+\sum _{j=0}^{n-k-1} \textrm{tr}(\omega \Phi ^j(\textbf{F}_{k+j+1})), \\ \textbf{F}_{k+j+1}= & {} \sum _{i \in I_{k+j+1}}f_{k+j+1}(i)\Phi _{i,k+j+1}(\textbf{1}). \end{aligned}$$

  Equation (24) follows from the same reasoning as in the proof of Theorem 4 once we observe that

  $$\begin{aligned}\Vert g_k^{(n)}\Vert _\infty \le \left( 1+\sum _{j=0}^{n-k-1}\Vert \Phi _{|\mathcal {F}}^j\Vert _\infty \right) c_n \le \left( 1+\sum _{j=0}^{n-2}\Vert \Phi _{|\mathcal {F}}^j\Vert _\infty \right) c_n. \end{aligned}$$

It would be interesting to generalize these results to the case where measurements are chosen adaptively, i.e. they may depend on the outcomes of the previous measurements; this would find applications for instance in the task of estimating unknown parameters of the unitary interaction U between the system and the ancillas (see Sect. 5.5), since an adaptive measurement strategy has been recently shown to be able to asymptotically extract from the output ancillas the maximum amount of information about the unknown parameter [43].

5.4 Multi-time Statistics

In some cases, one is interested in functions of the output measurements at different times: for instance, as in the case of classical Markov chains treated in Sect. 5.1, the task could be estimating the rate of jump at stationarity from a certain state to another. Previous techniques still provide bounds for this kind of situations: given $m\ge 2$ and $f:I^m \rightarrow {\mathbb {R}}$, the natural stochastic process to consider is the one given by $({\underline{X}}_n,\rho _n)$ where ${\underline{X}}_n:=(X_k,\dots ,X_{k+m-1})$ and $\rho _n$ is the conditional system state. It is easy to see that it is a Markov process with the following transition probabilities: for every $i_1,\dots , i_m \in I$

$$\begin{aligned} \begin{aligned}&{\mathbb {P}}_\rho \left( {\underline{X}}_1=(i_1,\dots ,i_m),\rho _1=\frac{V_{i_m}\cdots V_{i_1}\rho V_{i_1}^*\cdots V_{i_m}^*}{\textrm{tr}(V_{i_m}\cdots V_{i_1}\rho V_{i_1}^*\cdots V_{i_m}^*)} \right) \\&\quad =\textrm{tr}(V_{i_m}\cdots V_{i_1}\rho V_{i_1}^*\cdots V_{i_m}^*) \end{aligned} \end{aligned}$$

and for every $n\ge 1$, $j \in I$

$$\begin{aligned} \begin{aligned}&{\mathbb {P}}_\rho \left( {\underline{X}}_{n+1}=(i_2,\dots ,i_m,j),\rho _{n+1}=\left. \frac{V_{j}\omega V_{j}^*}{\textrm{tr}(V_{j}\omega V_{j}^*)} \right| {\underline{X}}_n=(i_1,\dots , i_m), \rho _n=\omega \right) \\&\quad =\textrm{tr}(V_{j}\omega V_{j}^*).\\ \end{aligned} \end{aligned}$$

All the other possibilities occur with zero probability.

The transition operator corresponding to this enlarged process is the following:

$$\begin{aligned}P(g)(i_1,\dots ,i_m,\omega )=\sum _{j \in I}g\left( i_2,\dots ,i_m,j,\frac{V_j\omega V^*_j}{\textrm{tr}(V_j\omega V^*_j)} \right) \textrm{tr}(V_j \omega V_j^*) \end{aligned}$$

where $i_1,\dots ,i_m \in I$, $\omega$ is a state on $\mathfrak {h}$ and g is a bounded measurable function. With the same heuristic reasoning used for one-time statistics, we can provide a solution for the Poisson equation in this case too. Let us define the following function:

$$\begin{aligned}g({\underline{i}}, \omega )=f({\underline{i}})+\textrm{tr}(\omega (B^{(m)}({\underline{i}})+A^{(m)}_f)) \end{aligned}$$

where ${\underline{i}}=(i_1,\dots ,i_m) \in I^m$, $\omega$ is a state on $\mathfrak {h}$,

$$\begin{aligned}B^{(m)}({\underline{i}})=\sum _{k=1}^{m-1} \underbrace{\sum _{j_1,\dots ,j_k \in I} f(i_{k+1},\dots , i_{m},j_1,\dots ,j_k)V_{j_k}^*\cdots V_{j_1}^*V_{j_1}V_{j_k}}_{=:F_k^{(m)}} \end{aligned}$$

and $A_f^{(m)}$ is the unique solution of

$$\begin{aligned}(\textrm{Id}-\Phi )(A_f^{(m)})=F_m^{(m)}, \quad F_m^{(m)}:=\sum _{j_1,\dots ,j_m \in I} f(j_1,\dots ,j_m)V_{j_m}^*\cdots V_{j_1}^*V_{j_1}V_{j_m} \end{aligned}$$

such that $A_f^{(m)} \in {{\mathcal {F}}}=\{x \in M_d({\mathbb {C}}): \textrm{tr}(\sigma x)=0\}$. Notice that $A_f^{(m)}$ exists if

$$\begin{aligned}\textrm{tr}(\sigma F_m^{(m)})=\sum _{j_1,\dots ,j_m \in I} f(j_1,\dots ,j_m)\textrm{tr}(\sigma V_{j_m}^*\cdots V_{j_1}^*V_{j_1}V_{j_m})=0, \end{aligned}$$

which means that the function f is centred with respect to the probability measure $\pi ^{(m)}(j_1,\dots , j_m)=\textrm{tr}(\sigma V_{j_m}^*\cdots V_{j_1}^*V_{j_1}V_{j_m})$ (which is the law of m consecutive measurements in the stationary regime). Reasoning as for $m=1$, we get the following inequality.

Proposition 9

For every $m\ge 1$, $f:I^m \rightarrow {\mathbb {R}}$ such that

$$\begin{aligned}\pi ^{(m)}(f)=\sum _{j_1,\dots , j_m \in I} f(j_1,\dots , j_m) \textrm{tr}(\sigma V_{j_1}^* \cdots V_{j_m}^* V_{j_m} \cdots V_{j_1})=0\end{aligned}$$

and $\Vert f\Vert _\infty =c$ for some $c >0$, then for every $\gamma > 0$

$$\begin{aligned} {\mathbb {P}}_\rho \left( \frac{1}{n} \sum _{k=1}^{n} f({\underline{X}}_k)\ge \gamma \right) \le \exp \left( - \frac{(n \gamma -2G)^2}{2 (n-1) G^2}\right) \text { for } n \gamma \ge 2G, \end{aligned}$$

(25)

where $G=(m+\Vert (\textrm{Id}-\Phi )^{-1}_{|\mathcal {F}}\Vert _\infty )c$ and $\mathcal {F}:=\{x \in M_d({\mathbb {C}}): \textrm{tr}(\sigma x)=0\}$.

In order to apply the techniques employed to derive the Bernstein-type bound to the multi-time statistics case, one needs to consider the extended quantum channel corresponding to the stochastic process of m consecutive measurement outcomes (see [68]) and the result can be proved under the assumption that the multiplicative symmetrization of such channel is irreducible; however, the discussion in Sect. 5.1 about the doubled-up process corresponding to a classical Markov chain shows that this may never be the case.

5.5 Parameter Estimation

Concentration inequalities in Theorems 3 and 4 can be used in order to find confidence intervals for dynamical parameters (and possibly perform hypothesis testing): suppose that the unitary interaction U between the system and the ancillas depends on an unknown parameter $\theta \in \Theta \subseteq {\mathbb {R}}$, which we want to estimate via indirect measurements. Kraus operators $V_i(\theta )$ and the steady state $\sigma (\theta )$ depend on the parameter too and so does the asymptotic mean:

$$\begin{aligned}\pi (f)(\theta )=\sum _{i \in I} f(i) \textrm{tr}(\sigma (\theta )V_i(\theta )^*V_i(\theta )).\end{aligned}$$

For the sake of clarity, we are now going to treat the simplest case in which ${\overline{f}}_n:=\frac{1}{n}\sum _{k=1}^{n}f(X_k)$ is a consistent estimator for $\theta$, i.e. when $\pi (f)(\theta )=\theta$; however, one can easily generalize the same reasoning to more general instances. Theorems 3 and 4 can be used to estimate the probability that $\theta$ lays in an interval centred at ${\overline{f}}_n$: indeed, for every $\gamma >0$

$$\begin{aligned}\begin{aligned}&{\mathbb {P}}_{\rho ,\theta } \left( \theta \in \left( f_n - \gamma , f_n+ \gamma \right) \right) ={\mathbb {P}}_{\rho ,\theta } \left( \left| f_n-\theta \right| < \gamma \right) =1-{\mathbb {P}}_{\rho ,\theta } \left( \left| f_n-\theta \right| \ge \gamma \right) \\&\quad \ge 1-2N_\rho \exp \left( -\max \left\{ n\frac{ \gamma ^2 \varepsilon (\theta )}{8b^2(\theta )}h \left( \frac{5c \gamma }{b^2(\theta )}\right) , \frac{(n \gamma -2G(\theta ))^2}{2(n-1)G(\theta )^2} 1_{\{n\gamma >2G(\theta )\}}\right\} \right) . \end{aligned} \end{aligned}$$

Since the real value of the parameter $\theta$ is unknown, one is usually interested in lower bounding ${\mathbb {P}}_{\rho ,\theta } \left( \theta \in \left( f_n - \gamma , f_n+ \gamma \right) \right)$ uniformly for $\theta \in \Theta$ or its average with respect to a certain prior measure $\mu$ on $\Theta$, i.e. $\int _{\Theta }{\mathbb {P}}_{\rho ,\theta } \left( \theta \in \left( f_n - \gamma , f_n+ \gamma \right) \right) d\mu (\theta )$; in order to obtain meaningful lower bounds, in the first case one needs either $1/\varepsilon (\theta )$ or $G(\theta )$ to be uniformly bounded, while in the second case it is enough that the set where $1/\varepsilon (\theta )$ or $G(\theta )$ grows unboundedly is given a small probability by the prior $\mu$. We remark that $1/\varepsilon (\theta )$ and $G(\theta )$ approaching $+\infty$ is a phenomenon related to $\Phi _\theta (\cdot ):= \sum _{i \in I} V_i^*(\theta ) \cdot V_i(\theta )$ losing ergodicity and approaching a phase transition.

6 Conclusions and Outlook

We derived a generalization of Bernstein’s and Hoeffding’s concentration bounds for the time average of measurement outcomes of discrete-time quantum Markov chains.

Our results hold under quite general and easily verifiable assumptions and depend on simple and intuitive quantities related to the quantum Markov chain. We were also able to apply the same techniques employed for showing the Bernstein-type inequality to provide a concentration bound for the counting process of a continuous-time quantum Markov process; this result complements deviation bounds obtained using different techniques in [18]. While our strategy was inspired by works on concentration bounds for the empirical mean for classical Markov chains [34, 42, 51, 56], when restricted to the classical setting, our results provide extensions to empirical fluxes of the corresponding classical bounds.

Our work here finds a natural application in the study of finite-time fluctuations of dynamical quantities in physical systems, something of core interest in both classical and quantum statistical mechanics. Our work provides the tools to deal with problems which are tackled using concentration bounds in statistical models which involve the more general class of stochastic processes that can be seen as output processes of quantum Markov chains (which include important examples, e.g. independent random variables, Markov chains, hidden Markov models).

Our results should be useful in several areas. One is the estimation of dynamical parameters in quantum Markov evolutions, where a natural extension of our results would be to the case where measurements are chosen adaptively in time [43], and to more general additive functionals of the measurement trajectory. A second area of interest is in the connection to so-called thermodynamic uncertainty relations (TURs), which are general lower bounds on the size of fluctuations in trajectory observables such as time-integrated currents or dynamical activities. TURs were postulated initially for classical continuous-time Markov chains [8] (and proven via large deviation methods [40]) and later generalized in various directions, including finite time [63], discrete Markov dynamics [65], first-passage times [37, 39], and quantum Markov processes Refs. [24, 31, 45, 48]. The concentration bounds like the ones we consider here bound the size of fluctuation from above and are therefore complementary to TURs. It will be interesting to see how to use the concentration bounds for fluxes obtained here to formulate “inverse TURs” that upper-bound dynamical fluctuations in terms of general quantities of interest like entropy production and dynamical activity, as happens with standard TURs.

Appendix A: Technical Lemmas for Proving Theorem 3

We recall that $b^2=\pi (f^2)$ and $c=\Vert f\Vert _\infty$; the definitions of $\Psi ^{(m)}$ and $\Phi ^{(m)}$ can be found in Eqs. (9) and (10).

Lemma 10

Let k and m be two natural numbers; the following bounds hold true:

• 1. $\Vert \Phi ^{(m)\dagger } \Phi ^{(k)}\Vert _2 \le c^{m+k}$,

• 2. $\Vert \Psi ^{(m)}\Vert _2 \le {(2c)}^m$,

• 3. $\Vert \Phi ^{(m)\dagger }\Phi ^{(k)}(\textbf{1})\Vert _2 \le c^{m+k-1}b$ for $m+k \ge 1$,

• 4. $\Vert \Psi ^{(m)} (\textbf{1}) \Vert _2 \le 2{(2 c)}^{m-1}b$ for $m \ge 1$,

• 5. $|\langle \textbf{1}, \Psi ^{(m)} (\textbf{1})\rangle | \le 4{(2c)}^{m-2}b^2$ for $m \ge 2$.

Proof

1. Lemma 1.3 in [59] ensures that if we consider a completely positive map $\eta :M_d({\mathbb {C}})\rightarrow M_d({\mathbb {C}})$ such that $\eta ^*(\sigma )\le \sigma$, then $\Vert \eta \Vert _2 \le 1$. If we apply it to $\Phi$ and $\Phi ^\dagger$, we get $\Vert \Phi ^\dagger \Phi \Vert _2 \le 1$, which proves equation in point 1. in the case $k=m=0$. If $k+m\ge 1$, notice that we can write

$$\begin{aligned}\begin{aligned} \frac{\Phi ^{(m)\dagger } \Phi ^{(k)}(x)}{c^{m+k}}&=\underbrace{\sum _{\begin{array}{c} j,i \in I:\\ f(j)^m f(i)^k\ge 0 \end{array}}\frac{f(j)^m f(i)^k}{c^{m+k}} K_{i,j}^* x K_{i,j}}_{\eta _+(x)}\\&-\underbrace{\sum _{\begin{array}{c} j,i \in I:\\ f(j)^m f(i)^k< 0 \end{array}}-\frac{f(j)^m f(i)^k}{c^{m+k}} K_{i,j}^*x K_{i,j}}_{\eta _-(x)}.\\ \end{aligned} \end{aligned}$$

$\eta _{\pm }$ are completely positive and, since $\Vert f\Vert _\infty = c$, they also satisfy $(\eta _++\eta _-)^*(\sigma ) \le \Phi ^{*} \Phi ^{ \dagger *} (\sigma ) = \sigma$, hence $\Vert \eta _++\eta _- \Vert _2 \le 1$ and we get the thesis using Lemma 2.

2. By the explicit form of $\Psi ^{(m)}$ and point 1., we get

$$\begin{aligned}\Vert \Psi ^{(m)}\Vert _2 \le \sum _{l=0}^m \left( {\begin{array}{c}m\\ l\end{array}}\right) \Vert \Phi ^{(m)\dagger } \Phi ^{(m-l)}\Vert _2 \le \left( \sum _{l=0}^m \left( {\begin{array}{c}m\\ l\end{array}}\right) \right) c^{m}={(2c)}^m. \end{aligned}$$

3. Let us introduce the following self-adjoint operator

$$\begin{aligned} F^{(m,k)}:=\Phi ^{(m)\dagger } \Phi ^{(k)}(\textbf{1})=\sum _{i,j \in I}f(i)^k f(j)^m K_{i,j}^*K_{i,j}, \end{aligned}$$

where we recall that $K_{i,j}=V_i \{\sigma ^{\frac{1}{2}}V^*_j\sigma ^{-\frac{1}{2}} \}$ are the Kraus operators of $\Psi$; notice that $F^{(m,k)}$ is a convex combination with operator weights $K_{i,j}^* K_{i,j}$ of the matrices $f(i)^k f(j)^m \textbf{1}$. We get that

$$\begin{aligned}\begin{aligned} \Vert \Phi ^{(m)\dagger } \Phi ^{(k)}( \textbf{1}) \Vert _2&=\textrm{tr}(\sigma ^{\frac{1}{2}}F^{(m,k)}\sigma ^{\frac{1}{2}}F^{(m,k)})^{\frac{1}{2}}\le \textrm{tr}\left( \sigma \left( F^{(m,k)}\right) ^2 \right) ^{\frac{1}{2}} \\&\le \left( \sum _{i,j \in I} f(i)^{2k}f(j)^{2m}\textrm{tr}(\sigma K_{i,j}^*K_{i,j}) \right) ^{\frac{1}{2}},\\ \end{aligned} \end{aligned}$$

where we used Cauchy–Schwarz inequality for the trace and operator Jensen’s inequality (see for instance [47, Theorem 2.1]), since $t^2$ is operator convex on the whole real line. Notice that the last term of the previous equation can be expressed as ${\tilde{\pi }}(f(i)^{2k}f(j)^{2m})^{\frac{1}{2}}$, where ${\tilde{\pi }}$ is the probability measure on $I^2$ defined as ${\tilde{\pi }}(i,j)=\textrm{tr}(\sigma K_{i,j}^*K_{i,j})$; an easy computation shows that ${\tilde{\pi }}$ has marginals equal to $\pi$. If $k=0$ (and analogously if $m=0$), we get that

$$\begin{aligned}{\tilde{\pi }}(f(i)^{2k}f(j)^{2m})^{\frac{1}{2}}=\pi (f^{2m})^{\frac{1}{2}} \le c^{m-1}b, \end{aligned}$$

otherwise, if both m and k are bigger or equal than 1, we can still get the same bound:

$$\begin{aligned}{\tilde{\pi }}(f(i)^{2m}f(j)^{2k})^{\frac{1}{2}} \le \pi (f^{2m})^{\frac{1}{2}}c^{k} \le c^{m+k-1}b. \end{aligned}$$

4. Because of point 3., we obtain

$$\begin{aligned} \Vert \Psi ^{(m)} (\textbf{1}) \Vert _2 \le \sum _{l=0}^m \left( {\begin{array}{c}m\\ l\end{array}}\right) \Vert \Phi ^{(l)\dagger } \Phi ^{(m-l)} (\textbf{1})\Vert _2 \le 2 {(2c)}^{m-1}b. \end{aligned}$$

5. From the estimate in point 3., and the explicit expression of $\Psi ^{(m)}$ we have that:

$$\begin{aligned} \begin{aligned} |\langle \textbf{1}, \Psi ^{(m)}(\textbf{1}) \rangle |&\le \sum _{l=0}^m \left( {\begin{array}{c}l\\ m\end{array}}\right) |\langle \Phi ^{(l)}(\textbf{1}),\Phi ^{(m-l)}(\textbf{1}) \rangle | \\&\le \sum _{l=0}^m \left( {\begin{array}{c}l\\ m\end{array}}\right) \Vert \Phi ^{(l)}(\textbf{1})\Vert _2 \Vert \Phi ^{(m-l)}(\textbf{1}) \Vert _2 \le 4 {(2c)}^{m-2}b^2. \end{aligned} \end{aligned}$$

In case $l=0$ or $l=m$, we do not make use of estimate in point 3., but the upper bound follows from the observation that $\langle \textbf{1},\Phi ^{(m)}(\textbf{1}) \rangle =\langle \Phi ^{(m)}(\textbf{1}),\textbf{1} \rangle =\pi (f^m)$.

$\square$

We recall that r(u) is the spectral radius of $\Psi _u$ (see Eq. (8)) and that $\varepsilon$ is the spectral gap of $\Psi :=\Phi ^\dagger \Phi$.

Lemma 11

For every $0 \le u < \varepsilon /(10c)$, the following bound holds true:

$$\begin{aligned} r(u) \le \textrm{exp}\left( u^2\frac{6b^2}{\varepsilon } \left( 1-\frac{10cu}{\varepsilon } \right) ^{-1}\right) . \end{aligned}$$

Proof

For $0 \le u \le \varepsilon /(2c(2+\varepsilon ))$, we can write

$$\begin{aligned}r(u)=1+\sum _{u \ge 1} r^{(k)}u^k \end{aligned}$$

and

$$\begin{aligned}r^{(k)}=\sum _{p=1}^k \frac{(-1)^p}{p} \sum _{\begin{array}{c} \nu _1+\dots +\nu _p=k,\, \nu _i\ge 1\\ \mu _1+\dots +\mu _p=p-1, \, \mu _j\ge 0 \end{array}} \frac{1}{\nu _1! \cdots \nu _p!}\textrm{TR}(\Psi ^{(\nu _1)} S^{(\mu _1)}\cdots \Psi ^{(\nu _p)}S^{(\mu _p)}), \end{aligned}$$

where $S^{(0)}=-|\textbf{1}\rangle \langle \textbf{1}|$ and for $\mu \ge 1$, $S^{(\mu )}$ is the $\mu$-th power of

$$\begin{aligned}S^{(1)}=(\Psi -\textrm{Id}+|\textbf{1}\rangle \langle \textbf{1}|)^{-1}-|\textbf{1}\rangle \langle \textbf{1}|.\end{aligned}$$

Notice that $\Vert S^{(\mu )}\Vert _2=\varepsilon ^{-\mu }$ for $\mu \ge 1$. More details can be found in [56, Section 2].

In order to obtain an upper bound for r(u), we derive upper bounds for $|r^{(k)}|$ for every k. The coefficient $r^{(1)}$ can be easily shown to be equal to zero due to the fact that f is centred:

$$\begin{aligned}|\textrm{TR}(\Psi ^{(1)} S^{(0)})|\le 2|\langle \textbf{1},\Phi ^{(1)} (\textbf{1}) \rangle |=2\pi (f)=0. \end{aligned}$$

For bigger values of k, we will make extensive use of the estimates in Lemma 10. Fix $k\ge 2$. Since $\mu _1+\dots +\mu _p=p-1$, there must be a certain $j \in \{1,\dots ,p\}$ such that $\mu _j=0$; by the cyclicity of the trace, without loss of generality we can assume that $\mu _p=0$. Using the estimates in Lemma 10 we get that for $p=1$

$$\begin{aligned}|\textrm{TR}(\Psi ^{(k)} S^{(0)})|= |\langle \textbf{1},\Psi ^{(k)} (\textbf{1}) \rangle |\le 4{(2c)}^{k-2} b^2. \end{aligned}$$

Hence,

$$\begin{aligned} \frac{|\textrm{TR}(\Psi ^{(k)} S^{(0)})|}{k!}\le 2 {(2c)}^{k-2}b^2 \le \frac{b^2}{c}\left( \frac{2c}{\varepsilon } \right) ^{k-1}. \end{aligned}$$

(26)

If $p\ge 2$, then

$$\begin{aligned}\begin{aligned}&|\textrm{TR}(\Psi ^{(\nu _1)} S^{(\mu _1)}\cdots \Psi ^{(\nu _p)}S^{(\mu _p)})|=|\langle \textbf{1},\Psi ^{(\nu _1)} S^{(\mu _1)}\cdots \Psi ^{(\nu _p)} (\textbf{1}) \rangle | \\&\quad \le \varepsilon ^{1-p} {(2c)}^{k-\nu _1-\nu _p} \Vert \Psi ^{(\nu _1)}(\textbf{1})\Vert _2\Vert \Psi ^{(\nu _p)}(\textbf{1})\Vert _2 \\&\quad \le \varepsilon ^{1-p} {(2c)}^{k-\nu _1-\nu _p} 2^2{(2c})^{\nu _1+\nu _p-2}b^2 \\&\quad \le \varepsilon ^{1-p} 2^{k} c^{k-2}b^2. \end{aligned} \end{aligned}$$

Hence,

$$\begin{aligned} \frac{|\textrm{TR}(\Psi ^{(\nu _1)} S^{(\mu _1)}\cdots \Psi ^{(\nu _p)}S^{(\mu _p)})|}{\nu _1!\cdots \nu _p!} \le \frac{2b^2}{c}\left( \frac{2c}{\varepsilon } \right) ^{k-1}. \end{aligned}$$

(27)

For $k \ge 3$, the following upper bound holds true (we refer to [56] for more details):

$$\begin{aligned}\sum _{p=1}^k \frac{1}{p} \sum _{\begin{array}{c} \nu _1+\dots +\nu _p=k,\, \nu _i\ge 1\\ \mu _1+\dots +\mu _p=p-1, \, \mu _j\ge 0 \end{array}} \le 5^{k-2}. \end{aligned}$$

We conclude that for $k \ge 3$

$$\begin{aligned} |r^{(k)}| \le \frac{2b^2}{5c}\left( \frac{10c}{\varepsilon } \right) ^{k-1}. \end{aligned}$$

(28)

For $k=2$, we upper bound $|r^{(2)}|$ in the following way: indeed, thank to Eqs. (26) and (27), we obtain

$$\begin{aligned} |r^{(2)}|=\left| \frac{\textrm{TR}(\Psi ^{(2)} S^{(0)})}{2}-\langle \Psi ^{(1)}(\textbf{1}), S^{(1)}\Psi ^{(1)}(\textbf{1})\rangle \right| \le 2b^2+\frac{4b^2}{\varepsilon } \le \frac{6 b^2}{\varepsilon }. \end{aligned}$$

(29)

Putting everything together we get that for $0 \le u < \varepsilon /(10c)$

$$\begin{aligned}\begin{aligned} r(u)&\le 1+ \sum _{k\ge 1} |r^{(k)}|u^k \le 1+ u^2\frac{6b^2}{\varepsilon }\sum _{k\ge 0} \left( \frac{10cu}{\varepsilon } \right) ^{k}\\&\le 1+ u^2\frac{6b^2}{\varepsilon } \left( 1-\frac{10cu}{\varepsilon } \right) ^{-1} \le e^{u^2\frac{6b^2}{\varepsilon } \left( 1-\frac{10cu}{\varepsilon } \right) ^{-1}}.\\ \end{aligned} \end{aligned}$$

$\square$