Abstract
We propose a model for three-dimensional solids on a mesoscopic scale with a statistical mechanical description of dislocation lines in thermal equilibrium. The model has a linearized rotational symmetry, which is broken by boundary conditions. We show that this symmetry is spontaneously broken in the thermodynamic limit at small positive temperatures.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Motivation and Background
The perhaps most fundamental mathematical problem of solid-state physics is that of crystallization, which in a classical version could be formulated as follows. Let \(v: \mathbb {R}_{>0}\rightarrow \mathbb {R}\) be a two-body potential of Lennard–Jones type and consider the N-particle energy
The Grand Canonical Gibbs measure at inverse temperature \(\beta >0\) and fugacity \(z>0\) in finite volume \(\Omega \subset \mathbb {R}^3\) is the point process on \(\Omega \) given by
for measurable \(B \subseteq \bigcup _{N\in \mathbb {N}_0}\Omega ^N\) modulo permutations of particles with the appropriate normalizing constant \(Z_{\Omega ,\beta ,z}\). The crystallization problem is to prove that at low temperature and high density, i.e., large but finite inverse temperature \(\beta \) and fugacity z, there exist corresponding infinite volume Gibbs measures that are non-trivially periodic with the symmetry of a crystal lattice. This problem remains far out of reach. Unfortunately, even the zero temperature case, i.e., studying the limiting minimizers of the finite volume energy, is open and appears to be very difficult. For the zero temperature case in two dimensions, see Theil [21] and references therein; for important progress on the problem in three dimensions, see Flatley and Theil [9] and references therein. Detailed understanding of the zero temperature case is a prerequisite for understanding the low temperature regime, but in addition, any description at finite temperature must explain spontaneous breaking of the rotational symmetry and take into account the possibility of crystal dislocations. This significantly complicates the problem because proving spontaneous breaking of continuous symmetries is already notoriously difficult in models where the ground states are obvious, such as in the O(3) spin model, for which the only robust method is the very difficult work of Balaban, see [3] and references therein.
With a realistic microscopic model out of reach, we start from a mesoscopic rather than microscopic perspective to understand the effect of the dislocations. We expect the latter to be a fundamental aspect also of the original problem. Our model does not account for the full rotational symmetry, but is only invariant under linearized rotations. More precisely, our model for deformed solids in three dimensions consists of a gas of closed vector-valued defect lines which describe crystal dislocations on a mesoscopic scale. For this model, we show that the breaking of the linearized rotational symmetry persists in the thermodynamic limit.
Our model is strongly motivated by the one introduced and studied by Kosterlitz and Thouless [17], and refined by Nelson and Halperin [19], and Young [23]. The Kosterlitz–Thouless model has an energy that consists of an elastic contribution and a contribution due to crystal dislocations. These two contributions are assumed independent. This KTHNY theory explains crystallization and the melting transition in two dimensions, as a transition mediated by vector-valued dislocations effectively interacting through a Coulomb interaction. For a textbook treatment of this phenomenology, see Chaikin and Lubensky [6]. The Kosterlitz–Thouless model for two-dimensional melting is closely related to the two-dimensional rotator model, studied by Kosterlitz and Thouless in the same paper as the melting problem, following previous insight by Berezinskiĭ [4]. For their model of a two-dimensional solid, the assumption that the energy consists of elastic and dislocation contributions, which can be assumed to be essentially independent, is not derived from a realistic microscopic model. On the other hand, the rotator model admits an exact description in terms of spin waves (corresponding to the elastic energy) and vortices described by a scalar Coulomb gas. In this description, the spin wave and vortex contributions are not far from independent, and, in fact, in the Villain version of the rotator model [22], they become exactly independent. Based on a formal renormalization group analysis, Kosterlitz and Thouless proposed a novel phase transition mediated by unbinding of the topological defects, the Berezinskiĭ–Kosterlitz–Thouless transition. In the two-dimensional rotator model, the existence of this transition was proved by Fröhlich and Spencer [12]. For recent results on the two-dimensional Coulomb gas, see Falco [8]. In higher dimensions, the description of the rotator model in terms of spin waves and vortex defects remains valid, except that the vortex defects, which are point defects in two dimensions, now become closed vortex lines [13] as in our solid model. Using this description and the methods they had introduced for the two-dimensional case, Fröhlich and Spencer [12, 13] proved long-range order for the rotator model at low temperature in dimensions \(d\geqslant 3\), without relying on reflection positivity. The latter is a very special feature used in [11] to establish long-range order for the O(n) model exactly with nearest neighbor interaction on \(\mathbb {Z}^d\), \(d\geqslant 3\). In general, proving spontaneous symmetry breaking of continuous symmetries remains a difficult problem. However, aside from the most general approach of Balaban and reflection positivity, for abelian spin models, several other techniques exist [13, 16].
As discussed above, our model, defined precisely in (1.25), is closely related to the Kosterlitz–Thouless model, see for example [6, (9.5.1)]. Our analysis is based on the Fröhlich–Spencer approach for the rotator model [12, 13].
In a parallel study of Giuliani and Theil [14] following Ariza and Ortiz [1], a model very similar to ours is examined, but with a microscopic interpretation, describing locations of individual atoms. In particular, it also has a linearized rotational symmetry.
In [15, 18] (see also [2]), some of us studied other simplified models for crystallization. These models have full rotational symmetry, but do not permit dislocations. In [18] defects were excluded, while in the model in [15] isolated missing single atoms were allowed.
1.2 A Linear Model for Dislocation Lines on a Mesoscopic Scale
1.2.1 Linearized Elastic Deformation Energy
An elastically deformed solid in continuum approximation can be described by a deformation map \(f:\mathbb {R}^3\rightarrow \mathbb {R}^3\) with the interpretation that for any point x in the undeformed solid f(x) is the location of x after deformation. The Jacobi matrix \(\nabla f:\mathbb {R}^3\rightarrow \mathbb {R}^{3\times 3}\) describes the deformation map locally in linear approximation. Only orientation preserving maps, \(\det \nabla f>0\), make sense physically. The elastic deformation energy \(E_{\mathrm {el}}(f)\) is modeled to be an integral over a smooth elastic energy density \(\rho _{\mathrm {el}}:\mathbb {R}^{3\times 3}\rightarrow \mathbb {R}\) (respectively \({{\tilde{\rho }}}_{\mathrm {el}}:\mathbb {R}^{3\times 3}\rightarrow \mathbb {R}\)):
where the second representation holds under the assumption of rotation invariance; see Appendix A.1.1. From now on, we consider only small perturbations \(f=\mathrm {i}\mathrm {d}+\varepsilon u:\mathbb {R}^3\rightarrow \mathbb {R}^3\) of the identity map as deformation maps. The parameter \(\varepsilon \) corresponds to the ratio between the microscopic and the mesoscopic scale. We Taylor-expand \({\tilde{\rho }}_{\mathrm {el}}\) around the identity matrix \(\text {Id}\) using that \({\tilde{\rho }}_{\mathrm {el}}\) is smooth near \(\text {Id}\), obtaining
with a positive definite quadratic form F on symmetric matrices. Under the assumption of isotropy (see Appendix A.1), writing \(|{\cdot }|\) for the Euclidean norm, the general form for F is
In elasticity theory, the constants \(\lambda \) and \(\mu \) are the so-called Lamé coefficients. Even for cubic monocrystals, the isotropy assumption is restrictive for realistic models. While it is not important for our analysis, we nonetheless assume isotropy to keep the notation somewhat simpler. We refer to [6, Chapters 6.4.2 and 6.4.3] for a discussion on the number of elastic constants necessary in order to describe various crystal systems. Summarizing, we have the following model for the linearized elastic deformation energy:
for measurable \(w:\mathbb {R}^3\rightarrow \mathbb {R}^{3\times 3}\) and for F as in (1.5).
1.2.2 Burgers Vector Densities
The following model is intended to describe dislocation lines on a mesoscopic scale as they appear in solids at positive temperature. We describe the solid by a smooth map \(w:\mathbb {R}^3\rightarrow \mathbb {R}^{3\times 3}\) replacing the map \(\nabla u:\mathbb {R}^3\rightarrow \mathbb {R}^{3\times 3}\) from Sect. 1.2.1. If dislocation lines are absent, the model described now boils down to the setup of Sect. 1.2.1 with \(w=\nabla u\) being a gradient field. The field
is intended to describe the Burgers vector density. It vanishes if and only if \(w=\nabla u\) is a gradient field. One can interpret \(b_{ijk}\) as the k-th component of the resulting vector per area if one goes through the image in the deformed solid of a rectangle which is parallel to the i-th and j-th coordinate axis. The antisymmetry \(b_{ijk}=-b_{jik}\) can be interpreted as the change of sign if the orientation of the rectangle is changed. Any smooth field \(b:\mathbb {R}^3\rightarrow \mathbb {R}^{3\times 3\times 3}\) which is antisymmetric in its first two indices is of the form \(b=d_1w\) with some \(w:\mathbb {R}^3\rightarrow \mathbb {R}^{3\times 3}\) if and only if
where
denotes the exterior derivative with respect to the first two indices. Being antisymmetric in its first two indices, it is convenient to write the Burgers vector density b in the form
where \(\tilde{b}:\mathbb {R}^3\rightarrow \mathbb {R}^{3\times 3}\) and \(\varepsilon _{ijk}=\det (e_i,e_j,e_k)\) with the standard unit vectors \(e_i\in \mathbb {R}^3\), \(i\in [3]:=\{1,2,3\}\). The integrability condition (1.9) can be written in the form
In view of this equation, one may visualize \(\tilde{b}\) to be a sourceless vector-valued current.
1.2.3 Model Assumptions
In linear approximation, the leading order total energy of a deformed solid described by \(w:\mathbb {R}^3\rightarrow \mathbb {R}^{3\times 3}\) is modeled to consist of an “elastic” part and a local “dislocation” part:
where \(H_{\mathrm {el}}(w)\) was introduced in (1.7). The field w consists of an exact contribution (modeling purely elastic fluctuations) and a co-exact contribution representing the elastic part of the energy induced by dislocations. Both these contributions are contained in \(H_{\mathrm {el}}(w)\), while \(\mathcal H_{\mathrm {disl}}(d_1w)\) is intended to model only the local energy of dislocations. The dislocation part \(\mathcal H_{\mathrm {disl}}(b)\in [0,\infty ]\) is defined for measurable \(b:\mathbb {R}^3\rightarrow \mathbb {R}^{3\times 3\times 3}\) being antisymmetric in its first two indices.
We describe now a formally coarse-grained model for dislocation lines: Dislocation lines are only allowed in the set \(\Lambda \) of undirected edges of a mesoscopic lattice in \(\mathbb R^3\). Let \(V_\Lambda \) denote its vertex set. As a lattice, the graph \((V_\Lambda ,\Lambda )\) is of bounded degree. To model boundary conditions, we only allow dislocation lines on a finite subgraph \(G=(V,E)\) of \((V_\Lambda ,\Lambda )\), ultimately taking the thermodynamic limit \(E\uparrow \Lambda \). We write \(E\Subset \Lambda \) if E is a finite subset of \(\Lambda \). We denote the edge between adjacent vertices \(x,y\in V_\Lambda \) by \(\{x,y\}\). The graph \((V_\Lambda ,\Lambda )\) is not intended to describe the atomic structure of the solid, as it lives on a mesoscopic scale. Rather, it is just a tool to introduce a coarse-grained structure which eventually makes the model discrete.
To every edge \(e=\{x,y\}\), we associate a counting direction, which has no physical meaning but serves only for bookkeeping purposes. The Burgers vectors on the finite subgraph \(G=(V,E)\) are encoded by a family \(I=(I_e)_{e\in E}\in (\mathbb {R}^3)^E\) of vector-valued currents flowing through the edges in counting direction. A vector \(I_e\) means the Burgers vector associated with a closed curve surrounding the dislocation line segment [x, y] in positive orientation with respect to the counting direction. The family of currents I should fulfill Kirchhoff’s node law
where \(s\in \{1,-1,0\}^{V_\Lambda \times \Lambda }\) is the signed incidence matrix of the graph \((V_\Lambda ,\Lambda )\), defined by its entries
The distribution of the current in space encoded by I is supported on the union of the line segments [x, y], with \(\{x,y\}\in E\). Thus, it is a rather singular object having no density with respect to the Lebesgue measure on \(\mathbb {R}^3\). We describe it as follows by a matrix-valued measure \(J(I):{\text {Borel}}(\mathbb {R}^3)\rightarrow \mathbb {R}^{3\times 3}\) on \(\mathbb {R}^3\), supported on the union of all edges: For \(e=\{x,y\}\in \Lambda \), let \(\lambda _e:{\text {Borel}}(\mathbb {R}^3)\rightarrow \mathbb {R}_{\ge 0}\) denote the 1-dimensional Lebesgue measure on the line segment [x, y]; it is normalized by \(\lambda _{e}(\mathbb {R}^3)=|x-y|\). Furthermore, let \(n_e\in \mathbb {R}^3\) denote the unit vector pointing in the counting direction of the edge e. The matrix-valued measure J(I) is then defined by
Thus, the index k encodes a component of the Burgers vector and the index j a component of the direction of the dislocation line.
Heuristically, the current distribution J(I) is intended to describe a coarse-grained picture of a much more complex microscopic dislocation configuration: On an elementary cell of the mesoscopic lattice this microscopic configuration is replaced by a vector-valued current on a single dislocation line segment, encoding the effective Burgers vector. Because the outcome J of this heuristic coarse-graining procedure is such a singular object supported on line segments, its elastic energy close to the dislocation lines would be ill-defined. Hence, the coarse-graining must be accompanied by a smoothing operation.
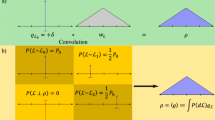
More precisely, the Burgers vector density \(\tilde{b}(I)\) associated with I is modeled by the convolution of J(I) with a form function \(\varphi \):
Here, the form function \(\varphi :\mathbb {R}^3\rightarrow \mathbb {R}_{\ge 0}\) is chosen to be smooth, compactly supported, with total mass \(\Vert \varphi \Vert _1=1\), and \(\varphi (0)>0\).
Altogether, this yields the Burgers vector density as a function of I:
For a graphical illustration of I and b(I) see Fig. 1.
It is shown in Appendix A.2 that the Kirchhoff node law (1.14) implies that \(\tilde{b}(I)\) is sourceless, i.e., Eq. (1.12) holds for it, or equivalently, that the integrability condition \(d_2b=0\) is valid.
We now impose an additional discreteness condition on I, which encodes the restriction that Burgers vectors should take values in a microscopic lattice reflecting the atomic structure of the solid. Let \(\Gamma \subset \mathbb {R}^3\) be a lattice, interpreted as the microscopic lattice (scaled to length scale 1). We set
Note that the current I is indexed by the edges in the mesoscopic graph (V, E) but takes values in the microscopic lattice \(\Gamma \). One should not confuse the mesoscopic graph (V, E) nor the mesoscopic lattice \(\Lambda \) with the microscopic lattice \(\Gamma \); they have nothing to do with each other. A motivation for the introduction of two different lattices \(\Gamma \) and \(V_\Lambda \) on two different length scales is described in the discussion of the model at the end of this section.
From now on, we abbreviate \(H_{\mathrm {disl}}(I):=\mathcal H_{\mathrm {disl}}(b(I))\) and \({{\,\mathrm{supp}\,}}I:=\{e\in E:I_e\ne 0\}\). We require the following general assumptions:
Assumption 1.1
-
Symmetry:\(H_{\mathrm {disl}}(I)=H_{\mathrm {disl}}(-I)\) for all \(I\in \mathcal I\).
-
Locality: For \(I=I_1+I_2\) with \(I_1,I_2\in \mathcal I\) such that no edge in \({{\,\mathrm{supp}\,}}I_1\) has a common vertex with another edge in \({{\,\mathrm{supp}\,}}I_2\) we have \(H_{\mathrm {disl}}(I)=H_{\mathrm {disl}}(I_1)+H_{\mathrm {disl}}(I_2)\). Moreover, \(H_{\mathrm {disl}}(0)=0\).
-
Lower bound: For some constant \(c>0\) and all \(I\in \mathcal I\),
$$\begin{aligned} H_{\mathrm {disl}}(I)\ge c\Vert I\Vert _1 := c \sum _{e\in E} |I_e|. \end{aligned}$$(1.20)
Condition (1.20) reflects the local energetic costs of dislocations in addition to the elastic energy costs reflected by \(H_{\mathrm{el}}(w)\).
One obtains typical examples for \(H_{\mathrm {disl}}(I)\) by requiring a number of assumptions on the form function \(\varphi \) and \(\mathcal H_{\mathrm {disl}}(b)\): First, for all \(\{u,v\},\{x,y\}\in \Lambda \) with \(\{u,v\}\cap \{x,y\}=\emptyset \), we assume \(([u,v]+{{\,\mathrm{supp}\,}}\varphi )\cap ([x,y]+{{\,\mathrm{supp}\,}}\varphi )=\emptyset \). Furthermore,
Roughly speaking, the last condition means that different edges \(e\in \Lambda \) do not overlap too much after broadening with \({{\,\mathrm{supp}\,}}\varphi \). Finally, for all b,
for some constant \({c_{1}}>0\), and for \(b=b_1+b_2\) with \({{\,\mathrm{supp}\,}}b_1\cap {{\,\mathrm{supp}\,}}b_2=\emptyset \), it is true that \(\mathcal H_{\mathrm {disl}}(b)=\mathcal H_{\mathrm {disl}}(b_1)+\mathcal H_{\mathrm {disl}}(b_2)\). One particular example is obtained by taking equality in (1.22).
1.3 Model and Main Result
One summand in the Hamiltonian of our model is defined by
for all \(I\in (\mathbb {R}^3)^E\) satisfying (1.14). The condition that w is compactly supported reflects the boundary condition, in the sense that close to infinity the solid must not be moved away from its reference location. The symmetry with respect to linearized global rotations is reflected by the fact \(H_\mathrm{el}(w)=H_{\mathrm{el}}(w+w_{\mathrm{{const}}})\) for every constant antisymmetric matrix \(w_{\mathrm{{const}}}\in \mathbb {R}^{3\times 3}\). Only the boundary condition, i.e., only the restriction that w should have compact support, breaks this global symmetry. This paper is about the question whether this symmetry breaking persists in the thermodynamic limit \(E\uparrow \Lambda \).
Because \(H_{\mathrm{el}}\) is positive semidefinite, \(H^*_{\mathrm{el}}\) is positive semidefinite as well, cf. (2.36). This gives us the following linearized model for the dislocation lines at inverse temperature \(\beta <\infty \):
where \(\delta _I\) denotes the Dirac measure in \(I\in \mathcal {I }\) and we use the convention \(\mathrm {e}^{-\infty }=0\) throughout the paper. Whenever the E-dependence is kept fixed, we use the abbreviations \(Z_\beta =Z_{\beta ,E}\) and \(P_\beta =P_{\beta ,E}\).
The following preliminary result shows that any sequence of smooth configurations satisfying the boundary conditions (i.e., being compactly supported) with prescribed Burgers vectors has a limit \(w^*\) in \(L^2\) provided that the energy is approaching the infimum of all energies within the class. We show later that this limit is a unique minimizer of \(H_{\mathrm{el}}\) in a suitable Sobolev space. An explicit description of \(w^*\) is provided in Lemma 2.2.
Proposition 1.2
(Compactly supported approximations of the minimizer). For any \(I\in \mathcal I\), there is a bounded smooth function \(w^*(\cdot ,I)\in L^2(\mathbb {R}^3,\mathbb {R}^{3\times 3})\) such that for any sequence \((w^n)_{n\in \mathbb {N}}\) in \(C^\infty _c(\mathbb {R}^3,\mathbb {R}^{3\times 3})\) with \(d_1w^n=b(I)\) for all \(n\in \mathbb {N}\) and \(\lim _{n\rightarrow \infty }H_{\mathrm{el}}(w^n)=H^*_{\mathrm{el}}(I)\) we have \(\lim _{n\rightarrow \infty }\Vert w^n-w^*(\cdot ,I)\Vert _2=0\).
In the whole paper, constants are denoted by \(c_1,c_2,\), etc. They may depend on the fixed model ingredients: the microscopic lattice \(\Gamma \), the mesoscopic lattice \(\Lambda \), the constant c from formula (1.20), and the form function \(\varphi \). All constants keep their meaning throughout the paper. Similarly, the expression “\(\beta \) large enough” means “\(\beta >\beta _0\) with some constant \(\beta _0\) depending also only on \(\Gamma \), \(\Lambda \), c, and \(\varphi \).”
The following theorem shows that the breaking of linearized rotational symmetry \(w\leadsto w+w_{\mathrm{{const}}}\) induced by the boundary conditions persists in the thermodynamic limit \(E\uparrow \Lambda \), provided that \(\beta \) is large enough.
Theorem 1.3
(Spontaneous breaking of linearized rotational symmetry).
There is a constant \({c_{2}}>0\) such that for all \(\beta \) large enough and for all \(t\in \mathbb {R}\),
and consequently
We remark that the symmetry \(I\leftrightarrow -I\) implies that \(w^*(x,I)\) is a centered random matrix. Since \(w^*(x,I)\) encodes in particular the orientation of the crystal at location x, this result may be interpreted as the presence of long-range orientational order in the thermodynamic limit.
Discussion of the model If we compare our model to the rotator model, purely elastic deformations correspond to “spin wave” contributions, while deformations induced by the Burgers vectors correspond to “vortex” contributions. In our model, the purely elastic deformations are orthogonal to the deformations induced by the Burgers vectors in a suitable inner product \(\left\langle {{\cdot }} \, \, ,\, {{\cdot }}\right\rangle _F\); this is made precise in Eq. (2.40). Therefore, we do not model the purely elastic part stochastically. It would not be relevant for our purposes, because in a linearized model, it is expected to be independent of the Burgers vectors anyway.
The mixed continuum/lattice structure of the model has the following motivation: A realistic microscopic description of a crystal at positive temperature would be very complicated, including, e.g., vacancies and interstitial atoms. This makes a global indexing of all atoms by a lattice intrinsically hard. On a mesoscopic scale, we expect that these difficulties can be neglected when the elastic parameters of the model are renormalized. Our model should be understood as a two-scale description of the crystal in which the microscopic Burgers vectors are represented on a scale such that their discreteness is still visible, but the physical space is smoothed out; recall that the factor \(\varepsilon \) used in approximation (1.4) encodes the ratio between the two scales. Hence, we use continuous derivatives in physical space, but discrete calculus for the Burgers vectors. The mesoscopic lattice \(V_\Lambda \) serves only as a convenient spatial regularization. Unlike the microscopic lattice \(\Gamma \), it has no intrinsic physical meaning.
Organization of the paper. In Sect. 2, we identify the minimal energy configuration \(w^*\) in the sense of Proposition 1.2 in the appropriate Sobolev space. Section 3 deals with the statistical mechanics of Burgers vector configurations by means of a Sine–Gordon transformation and a cluster expansion in the spirit of the Fröhlich-Spencer treatment of the Villain model [12, 13]. Section 4 provides the bounds for the observable, which manifests the spontaneous breaking of linearized rotational symmetry. It uses variants of a dipole expansion, which we provide in the Appendix.
2 Minimizing the Elastic Energy
In this section, we collect various properties of \(H_{\mathrm{el}}^*(I)\) defined in (1.23). In particular, we prove Proposition 1.2.
2.1 Sobolev Spaces
Let \({\mathbb V} \) be a finite-dimensional \(\mathbb {C}\)-vector space with a norm \(|\cdot |\) coming from a scalar product \(\left\langle {\cdot } \, \, ,\, {\cdot }\right\rangle _{{\mathbb V} }\). For integrable \(f:\mathbb {R}^3\rightarrow {\mathbb V} \), let
denote its Fourier transform, normalized such that the transformation becomes unitary. For any \(\alpha \in \mathbb {R}\) and \(f\in C^\infty _c(\mathbb {R}^3,{\mathbb V} )\), we define
We set
Then, \(\Vert f\Vert ^\vee _\alpha \) is a norm on the \(\mathbb {C}\)-vector space \(C_\alpha ({\mathbb V} )\). For \(\alpha >-3/2\), we know that \(C_\alpha ({\mathbb V} )=C^\infty _c(\mathbb {R}^3,{\mathbb V} )\) because \(|k|^{2\alpha }\) is integrable near 0 and \(\hat{f}\) decays fast at infinity. Let \((L^{2\vee }_\alpha ({\mathbb V} ),\Vert {\cdot }\Vert ^\vee _\alpha )\) denote the completion of \((C_\alpha ({\mathbb V} ),\Vert {\cdot }\Vert ^\vee _\alpha )\) and \(L^2_\alpha ({\mathbb V} ):= \big \{g:\mathbb {R}^3\rightarrow {\mathbb V} \text { measurable mod changes on null sets}: \Vert g\Vert _{2,\alpha }<\infty \big \}\). The Fourier transform \(f\mapsto \hat{f}\) gives rise to a natural isometric isomorphism \(L^{2\vee }_\alpha ({\mathbb V} )\rightarrow L^2_\alpha ({\mathbb V} )\). For any \(\alpha \in \mathbb {R}\), the sesquilinear form
extends to a continuous sesquilinear form
Partial derivatives \(\partial _j:C^\infty _c(\mathbb {R}^3,{\mathbb V} )\rightarrow C^\infty _c(\mathbb {R}^3,{\mathbb V} )\) (acting component-wise) extend to bounded operators \(\partial _j:L^{2\vee }_{\alpha +1}({\mathbb V} )\rightarrow L^{2\vee }_\alpha ({\mathbb V} )\). Consequently, the (component-wise) Laplace operator \(\Delta =\sum _{j\in [3]}\partial _j^2\) extends to an isometric isomorphism \(\Delta :L^{2\vee }_{\alpha +2}({\mathbb V} )\rightarrow L^{2\vee }_\alpha ({\mathbb V} )\).
We will mainly have \({\mathbb V} ={\mathbb V} _j\) for \(j\in \mathbb {N}_0\), where
endowed with the norm
Functions with values in \({\mathbb V} _j\) are just \(\mathbb {C}^3\)-valued j-forms. Note that the last index k has a special role since there is no antisymmetry condition for it. The real part of the space \({\mathbb V} _0=\mathbb {C}^3\) may be interpreted as a vector space containing Burgers vectors. For any \(\alpha \in \mathbb {R}\) and \(j\in \mathbb {N}_0\), we introduce the exterior derivative \(d_j:L^{2\vee }_{\alpha +1}({\mathbb V} _j)\rightarrow L^{2\vee }_\alpha ({\mathbb V} _{j+1})\) and co-derivative \(d_j^*:L^{2\vee }_{\alpha +1}({\mathbb V} _{j+1})\rightarrow L^{2\vee }_\alpha ({\mathbb V} _j)\),
They are adjoint to each other in the sense that for any \(\alpha \in \mathbb {R}\),
Since in the following we are mostly interested in the cases \(j=0,1,2\), we spell out the definition of \(d_j\) explicitly:
The Laplace operator \(\Delta :L^{2\vee }_{\alpha +2}({\mathbb V} _j)\rightarrow L^{2\vee }_\alpha ({\mathbb V} _j)\) then fulfills
here, \(d_{-1}\) and \(d_{-1}^*\) should be interpreted as 0. Equation (2.14) is only important for \(j=0,1,2,3\) because \({\mathbb V} _j=\{0\}\) holds for \(j\ge 4\) in three dimensions. To see (2.14), we calculate
and
2.2 Elastic Hamiltonian
Given \(I\in \mathcal I\) and \(b=b(I)\), we calculate now \(H^*_{\mathrm{el}}(I)\). To begin with, we observe that \(H_{\mathrm{el}}\), introduced in (1.7), is a quadratic form, and therefore, it can be written as
with a sesquilinear form \(\left\langle {{\cdot }} \, \, ,\, {{\cdot }}\right\rangle _F\) depending on F defined in (1.5). More precisely, using \(\left\langle {A} \, \, ,\, {B}\right\rangle ={{\,\mathrm{Tr}\,}}(AB^t)\) for the Euclidean scalar product for matrices A, B, we introduce \(\left\langle {{\cdot }} \, \, ,\, {{\cdot }}\right\rangle _F:L^2(\mathbb {R}^3,\mathbb {C}^{3\times 3})\times L^2(\mathbb {R}^3,\mathbb {C}^{3\times 3})\rightarrow \mathbb {C}\) through
Because of the stability condition (1.5), the inner product \(\left\langle {{\cdot }} \, \, ,\, {{\cdot }}\right\rangle _F\) is positive semidefinite. For any \(\alpha \in \mathbb {R}\), we consider the restriction of \(\left\langle {{\cdot }} \, \, ,\, {{\cdot }}\right\rangle _F\) to \(C_{-\alpha }({\mathbb V} _1)\times C_{\alpha }({\mathbb V} _1)\), and then extend it to a sesquilinear form \(\left\langle {{\cdot }} \, \, ,\, {{\cdot }}\right\rangle _F:L^{2\vee }_{-\alpha }({\mathbb V} _1)\times L^{2\vee }_\alpha ({\mathbb V} _1)\rightarrow \mathbb {C}\) being continuous w.r.t. \(\Vert {\cdot }\Vert _{-\alpha }^\vee \) and \(\Vert {\cdot }\Vert _\alpha ^\vee \).
In (1.23), we may take the infimum over \(w^b+\ker (d_1) \) with a suitable \(w^b\in L^{2\vee }_{0}({\mathbb V} _1) = L^2(\mathbb {R}^3,\mathbb {C}^{3\times 3})\) satisfying \(d_1w^b=b(I)\). We claim that a convenient choice is
To see this, we observe that \(\Delta ^{-1}\) commutes with \(d_1\) and \(d_1^*\) because \(\Delta ^{-1}\) corresponds to multiplication with the scalar \(|k|^{-2}\) in Fourier space, and \(d_1,d_1^*\) correspond to (multi-component) multiplication operators in Fourier space, as well. Therefore, since \(b=b(I)\in {\text {ker}}(d_2:L^{2\vee }_{-1}({\mathbb V} _2)\rightarrow L^{2\vee }_{-2}({\mathbb V} _3))\), we obtain
Using that \({\text {ker}}(d_1:C_0({\mathbb V} _1)\rightarrow C_{-1}({\mathbb V} _2))\) is dense in \({\text {ker}}(d_1:L^{2\vee }_0({\mathbb V} _1)\rightarrow L^{2\vee }_{-1}({\mathbb V} _2)) = {\text {range}}(d_0:L^{2\vee }_1({\mathbb V} _0)\rightarrow L^{2\vee }_{0}({\mathbb V} _1))\), we obtain
2.3 Minimizer
Differential operators In order to analyze the \(d_0\psi \)-dependence in (2.21), we derive an adjoint \(\nabla ^F\) for \(d_0\) with respect to \(\left\langle {{\cdot }} \, \, ,\, {{\cdot }}\right\rangle _F\) and \(\left\langle {{\cdot }} \, \, ,\, {{\cdot }}\right\rangle \). Let \(\nabla ^F:L^{2\vee }_{-\alpha +1}({\mathbb V} _1)\rightarrow L^{2\vee }_{-\alpha }({\mathbb V} _0)\),
Indeed, it satisfies the following adjointness relation for any \(g\in L^{2\vee }_{-\alpha }({\mathbb V} _1)\) and \(f\in L^{2\vee }_{\alpha +1}({\mathbb V} _0)\) (using that \(-\partial _j\) is adjoint to \(\partial _j\) w.r.t. \(\left\langle {{\cdot }} \, \, ,\, {{\cdot }}\right\rangle \)):
The identity \(\left\langle {d_0\psi } \, \, ,\, {d_0 \psi }\right\rangle _F=\left\langle {\nabla ^Fd_0\psi } \, \, ,\, {\psi }\right\rangle \) motivates us to introduce the following differential operator for any \(\alpha \in \mathbb {R}\):
At this moment, we are most interested in the case \(\alpha =-1\); the case of general values for \(\alpha \) is needed for regularity considerations in the proof of Proposition 1.2 later on.
Lemma 2.1
(Properties of D). For any \(\alpha \in \mathbb {R}\), the map \(D:L^{2\vee }_{\alpha +2}({\mathbb V} _0)\rightarrow L^{2\vee }_\alpha ({\mathbb V} _0)\) is invertible with the inverse \(D^{-1}:L^{2\vee }_\alpha ({\mathbb V} _0)\rightarrow L^{2\vee }_{\alpha +2}({\mathbb V} _0)\),
In coordinate notation,
The map D is symmetric for \(\alpha =-1\), i.e., \(\left\langle {{\tilde{\psi }}} \, \, ,\, {D\psi }\right\rangle =\left\langle {D{\tilde{\psi }}} \, \, ,\, {\psi }\right\rangle \) for \(\psi ,{\tilde{\psi }}\in L^{2\vee }_1({\mathbb V} _0)\), and bounded from above and from below as follows:
Proof
Using \({\text {div}}{\text {grad}}=\Delta \) and abbreviating
we calculate
and similarly \(DD^{-1}={\text {id}}\).
By the adjointness property (2.23), the symmetry of D is obvious by its definition: \(2\left\langle {D\psi '} \, \, ,\, {\psi }\right\rangle =\left\langle {\nabla ^Fd_0\psi '} \, \, ,\, {\psi }\right\rangle =\left\langle {d_0\psi '} \, \, ,\, {d_0 \psi }\right\rangle _F\) for \(\psi ,\psi '\in L^{2\vee }_1({\mathbb V} _0)\). Furthermore, one has
We claim that
This is best seen using a Fourier transform and the Cauchy–Schwarz inequality in \(\mathbb {C}^3\):
where \(k\cdot \widehat{\psi }(k)\) denotes the Euclidean scalar product in \(\mathbb {C}^3\). Using fact (2.32) and the stability condition for \(\mu \) and \(\lambda \) given in (1.5), which implies \(\mu +\lambda >0\), we obtain also claim (2.28). \(\square \)
Definition of the minimizer. In the next lemma, it is shown that the minimizer of the elastic energy has the following form:
with \(w^b\) defined in (2.19),
Lemma 2.2
(Minimizer of the elastic energy). The infimum in (2.21) is a minimum:
It is unique in the following sense: For all \(w\in L^{2\vee }_0({\mathbb V} _1)\) with \(d_1w=b(I)\) and \(\left\langle {w} \, \, ,\, {w}\right\rangle _F=\left\langle {w^*} \, \, ,\, {w^*}\right\rangle _F\), we have \(w=w^*\). The summands of the minimizer \(w^*\) given in (2.34) have the following components:
Proof
The calculation \(\nabla ^F(w^b+d_0\psi ^*)= \nabla ^F(w^b-\frac{1}{2}d_0D^{-1}\nabla ^F w^b) = \nabla ^Fw^b-DD^{-1}\nabla ^F w^b=0 \) shows that the function \(\psi ^*\) solves the system of equations
or equivalently, using (2.23) and (2.34),
By the above, the following calculation shows that \(w^*\) is a minimizer in (2.21) as claimed: For all \(f\in L^{2\vee }_1({\mathbb V} _0)\):
Furthermore, using (2.28) we obtain:
In particular, \(d_0f\ne 0\) implies \(\left\langle {d_0f} \, \, ,\, {d_0 f}\right\rangle _F>0\), which yields the claimed uniqueness of the minimizer. Let \(i,j\in [3]\). Identity (2.37) follows from definition (2.19) of \(w^b\). Using it, we express \(v^b \in L^{2\vee }_{-1}({\mathbb V} _0)\) as follows:
Because of the antisymmetry \(\partial _k\partial _l(\Delta ^{-1}b)_{lkj} =-\partial _l\partial _k(\Delta ^{-1}b)_{klj}\), one term dropped out in the last step. It follows that
Using \(\sum _{l,m}\partial _m\partial _lb_{lmk}=0\) from the antisymmetry \(b_{lmk}=-b_{mlk}\), this equals
This shows that \(d_0\psi ^*\) has the form given in (2.38). \(\square \)
Regularity of the minimizer.
Proof of Proposition 1.2
We set \(L_{>\alpha }^{2\vee }({\mathbb V} ):=\bigcap _{\alpha ':\alpha '>\alpha }L_{\alpha '}^{2\vee }({\mathbb V} )\). From \(b(I)\in C^\infty _c(\mathbb {R}^3,{\mathbb V} _2)=\bigcap _{\alpha >-3/2}C_\alpha ({\mathbb V} _2)\)\(\subseteq L_{>-3/2}^{2\vee }({\mathbb V} _2)\) it follows from (2.19) that \(w^b\in L_{>-1/2}^{2\vee }({\mathbb V} _1)\). Hence, by (2.35), \(v^b\in L_{>-3/2}^{2\vee }({\mathbb V} _0)\), and then \(\psi ^*=D^{-1}v^b\in L_{>1/2}^{2\vee }({\mathbb V} _0)\). We conclude \(w^*=w^b+d_0\psi ^*\in L_{>-1/2}^{2\vee }({\mathbb V} _1)\). By Sobolev’s embedding theorem, \(w^*\) is a bounded smooth function with all derivatives being bounded. In particular, pointwise evaluation \(w^*(x)\) of \(w^*\) makes sense for every \(x\in \mathbb {R}^3\).
For the remaining claim, take a sequence \(f^n\in L_1^{2\vee }({\mathbb V} _0)\), \(n\in \mathbb {N}\), with \(H_{\mathrm{{el}}}(w^*+d_0f^n)\rightarrow H_{\mathrm{{el}}}(w^*)=H_{\mathrm{{el}}}^*(I)\) as \(n\rightarrow \infty \). Using \({\text {ker}}(d_1:L^{2\vee }_0({\mathbb V} _1)\rightarrow L^{2\vee }_{-1}({\mathbb V} _2)) = {\text {range}}(d_0:L^{2\vee }_1({\mathbb V} _0)\rightarrow L^{2\vee }_{0}({\mathbb V} _1))\), it suffices to show that \(\Vert d_0f^n\Vert _2\) converges to 0 as \(n\rightarrow \infty \). In view of system (2.40) of equations, we know
Using comparison (2.28) between D and \(-\Delta \), we conclude
\(\square \)
We remark that the facts \(d_2b(I)=0\) and \(b(I)\in C^\infty _c(\mathbb {R}^3,{\mathbb V} _2)\) imply \(\int _{\mathbb {R}^3}b(I)(x)\,\mathrm{d}x=0\) and hence \(b(I)\in C_\alpha ({\mathbb V} _2)\) for all \(\alpha >-5/2\), not only for all \(\alpha >-3/2\). As a consequence, \(w^*\in L_{>-3/2}^{2\vee }({\mathbb V} _1)\).
3 Cluster Expansion
We now develop a cluster expansion (polymer expansion) of the measures \(P_{\beta ,E}\) defined in (1.25), using the strategy of Fröhlich and Spencer [13]. In the following, \(E\Subset \Lambda \) is a given finite set of edges in the mesoscopic lattice. We take the thermodynamic limit \(E\uparrow \Lambda \) only in the end.
3.1 Sine–Gordon Transformation
The elastic energy \(H^*_{\mathrm{el}}(I)\) defined in (1.23) is a quadratic form. If \(I=I_1+\cdots +I_n\) is the decomposition of I into its connected components, the mixed terms in \(H^*_{\mathrm{el}}(I)\) induce non-local interactions between different \(I_i\) and \(I_j\). The Sine–Gordon transformation introduced now is a tool to avoid these non-localities.
Because the quadratic form \(H^*_{\mathrm{el}}\) is positive semidefinite, the function \(\exp \{-\beta H^*_{\mathrm{el}}\}\) is the Fourier transform of a centered Gaussian random vector \(\phi =(\phi _e)_{e\in E}\) on some auxiliary probability space with corresponding expectation operator denoted by \({\mathbb E} \):
For any observable of the form \(\mathcal I\ni I\mapsto \left\langle {\sigma } \, \, ,\, {I}\right\rangle \) with \(\sigma \in \mathbb {R}^E\), we define
In order to exchange expectation and summation, we used that \(\mathrm {e}^{-\beta H_{\mathrm{disl}}(I)}\) is summable over the set \(\mathcal I\) by (1.20). Note that \(Z_\beta =Z_\beta (0)\) implies
3.2 Preliminaries on Cluster Expansions
In this section, we collect some background on cluster expansions (polymer expansions). For recent treatments of cluster expansions, see in particular Poghosyan and Ueltschi [20] or Bovier and Zahradník [5] and references. To make our presentation most accessible, we use the textbook version given in [10].
Let \(\mathcal B\) denote the set of all non-empty connected subsets of E. We call \(X,Y\in \mathcal B\) compatible, \(X\not \sim Y\), if no edge in X has a common vertex with an edge in Y. Otherwise X, Y are called incompatible, \(X\sim Y\). In particular, \(X\sim X\). Recall \({{\,\mathrm{supp}\,}}I=\{e\in E:I_e\ne 0\}\) for \(I\in \mathcal I\), where \(\mathcal I\) is defined in (1.19). Let
The incompatibility relation \(\sim \) on \(\mathcal B\) is inherited to an incompatibility relation, also denoted by \(\sim \), on \(\mathcal J\) via
Every subset of E can be uniquely decomposed in a set of pairwise compatible connected components, which is a subset of \(\mathcal B\). For \(n\in \mathbb {N}\), let
Consider \(I\in \mathcal I\) and the connected components \(X_1,\ldots ,X_n\) (\(n\in \mathbb {N}_0\)) of \({{\,\mathrm{supp}\,}}I\). We set \(I_j:=I1_{X_j}\in \mathcal J\). Here, it is crucial that Kirchhoff rule (1.14) holds for I if and only if it holds for all \(I_j\). Then, using the locality of \(H_{\mathrm{disl}}\) given in Assumption 1.1, we obtain
For \(I\in \mathcal I\) and some \(\beta >0\), we abbreviate
The function K fulfills the following important factorization property: For \(I\in \mathcal I\) with connected components \(I_1,\ldots ,I_n\) as above, one has
This fact relies on the dimension being at least 3. In \(d=2\), the Burgers vector density would not be locally neutral, resulting in a significant complication of the argument (as in [12] compared to [13]). In view of definition (3.2) of \(\mathcal Z_{\beta ,\phi }\), equation (3.10) yields
The summand 1 comes from the contribution of \(I=0\), using \(H_\mathrm{disl}(0)=0\). Recall that by (1.20) \(|K(I,\phi )|=\mathrm {e}^{-\beta H_{\mathrm{disl}}(I)}\le \mathrm {e}^{-\beta c\Vert I\Vert _1}\) is summable over \(I\in \mathcal I\), which shows that all expressions in (3.11) are absolutely summable. To control \(\mathcal Z_{\beta ,\phi }\), we use a cluster expansion. Next we cite the relevant theorems.
Let \(\mathcal G_n\) denote the set of all connected subgraphs \(G_n=([n],E_n)\) of the complete graph with vertex set \([n]=\{1,\ldots ,n\}\). Let \(\mathcal E_n=\{E_n:G_n=([n],E_n)\in \mathcal G_n\}\) denote the set of all corresponding edge sets. Consider the Ursell functions
Let \({\tilde{\mathcal J}}\) be any finite set endowed with a reflexive and symmetric incompatibility relation \(\sim \). We define \({\tilde{\mathcal J}}_{\not \sim }^n\) by (3.7) with \(\mathcal J\) replaced by \({\tilde{\mathcal J}}\).
Fact 3.1
(Formal cluster expansion, [10, Proposition 5.3]). For every \(I\in {\tilde{\mathcal J}}\), let K(I) be a variable. Consider the polynomial in these variables
As a formal power series
Moreover, if the right-hand side in (3.14) is absolutely summable, then equation (3.14) holds also in the classical sense as follows: \(\exp ({\text {rhs}} (3.14))=\mathrm{Z}\).
A criterion for convergence of the cluster expansion is cited in the following fact:
Fact 3.2
(Convergence of cluster expansions, [10, Theorem 5.4]). Assume that there are “sizes” \((a(I))_{I\in {\tilde{\mathcal J}}}\)\(\in \mathbb {R}_{\ge 0}^{{\tilde{\mathcal J}}}\) and “weights” \((K(I))_{I\in {\tilde{\mathcal J}}}\in \mathbb {C}^{{\tilde{\mathcal J}}}\) such that for all \(I\in {\tilde{\mathcal J}}\), the following bound holds:
Then, we have for all \(J\in {\tilde{\mathcal J}}\):
Moreover, in this case, series (3.14) is absolutely convergent.
3.3 Partial Partition Sums
We take a sequence \((\mathcal J_m)_{m\in \mathbb {N}}\) of finite subsets \(\mathcal J_m\subseteq \mathcal J\) with \(\mathcal J_m\uparrow \mathcal J\) and set \(\mathcal J_\infty :=\mathcal J\), with \(\mathcal J\) being defined in (3.5). For \(m\in \mathbb {N}\cup \{\infty \}\) and \(I\in \mathcal I\), let
whenever this double series is absolutely convergent. Note that \(z_m(\beta ,I)=z_m(\beta ,-I)\) because \(H_{\mathrm{disl}}(I)=H_\mathrm{disl}(-I)\) by Assumption 1.1. We abbreviate also \(z(\beta ,I):=z_\infty (\beta ,I)\). Uniformly in m, the summands in series (3.17) are dominated by the corresponding ones in \(z^+(\beta ,I):=z^+_\infty (\beta ,I)\), where
By monotone convergence for series,
For \(I\in \mathcal I\), we define its size
Here, \({{\,\mathrm{diam}\,}}\) denotes the diameter in the graph distance in the mesoscopic lattice \(G=(V,E)\). The size has the following properties. For \(I_1,I_2\in \mathcal I\) with \(I_1\sim I_2\), one has
Recall that I takes values in the microscopic lattice \(\Gamma \). We set
and observe for all \(I\in \mathcal I\):
If in addition \({{\,\mathrm{supp}\,}}I\) is connected, we have \({{\,\mathrm{diam}\,}}{{\,\mathrm{supp}\,}}I\le |{{\,\mathrm{supp}\,}}I|\) and hence
with the constant \(c_{3}:=1+\eta ^{-1}\). Using the constant c from (1.20), let \(c_{4}=c_{4}(c,\eta ):=c/(2c_{3})\). Then, for \(I\in \mathcal I\), it follows
We choose now a constant \(c_{5}=c_{5}(c,\eta )\) with \(0<c_{5}<c_{4}\) and set \(c_{6}=c_{6}(c,\eta ):=c_{4}-c_{5}>0\). Fact 3.2 is applied twice, later with the weight \(K(I,\phi )\) introduced in (3.9), but first with the weight
and the size function \(a:\mathcal J\rightarrow \mathbb {R}_{>0}\),
The following lemma serves to verify hypothesis (3.15) of the cluster expansion.
Lemma 3.3
(Peierls argument). There is \(c_{7}>0\) such that for all \(\beta \) large enough,
Furthermore, one has
and hypothesis (3.15) holds for \({\tilde{\mathcal J}}=\mathcal J_m\) for all \(m\in \mathbb {N}\) and all \(\beta \) large enough.
Proof
Claim (3.28) is verified as follows: Take \(o\in E\Subset \Lambda \). We estimate
Dropping the condition that J should fulfill the Kirchhoff rules, we obtain the following bound for any given \(X\in \mathcal B\):
with the abbreviation
Because \(\Gamma \) is a three-dimensional lattice, for any \(k\in \mathbb {N}\) there are at most \(c_{9}k^2\) lattice points within distance \([\eta k,\eta {(k+1)})\) from 0, where \(c_{9}>0\) is a constant only depending on \(\Gamma \). Thus,
for all large \(\beta \) and a positive constant \(c_{10}=c_{10}(\eta ,c_{6},c_{9})\). Substituting (3.31) and (3.33) into (3.30), we obtain
The last sum is estimated with the following Peierls argument: Let \(M<\infty \) be the maximal vertex degree in the mesoscopic lattice with edge set \(\Lambda \). Let \(n\in \mathbb {N}\). For every set \(X\in \mathcal B\) with \(o\in X\) and \(|X|=n\), there is a closed path of length 2n steps that starts in o and visits every edge in X. There are at most \(M^{2n}\) choices of closed paths of length 2n starting in o, and therefore at most \(M^{2n}\) choices of X. We conclude for all large \(\beta \):
with \(c_{7}>0\) only depending on \(c_{10}\) and M. This proves claim (3.28).
Next, we prove claim (3.29). We observe that (3.23) and (3.24) imply \(\eta |{{\,\mathrm{supp}\,}}J|\le \Vert J\Vert _1\le {{\,\mathrm{size}\,}}J\). Using this, \(c_{4}-c_{5}=c_{6}\), and (3.28), claim (3.29) follows from the estimate
Note that we have dropped the index m in the last two sums.
To verify (3.15) for \({\tilde{\mathcal J}}=\mathcal J_m\), we define the closure of any edge set \(F\subseteq E\) by
Let \(m\in \mathbb {N}\) and \(I\in \mathcal J_m\). Summing (3.36) over \(o\in \overline{{{\,\mathrm{supp}\,}}I}\), we conclude
for all large \(\beta \), uniformly in \(I\in \mathcal J_m\). Here, we have used that \(\mathrm {e}^{-\beta c_{7}}M\le \beta c_{5}\eta \) for large \(\beta \). \(\square \)
Lemma 3.4
(Exponential decay of partial partition sums). For all sufficiently large \(\beta >0\) and \(m\in \mathbb {N}\cup \{\infty \}\), the following holds with the constants \(c_{4}=c/(2c_{3})\) and \(c_{7}\) as in Lemma 3.3:
In particular, in this case, \(z_m(\beta ,I)\) is well defined for all \(I\in \mathcal I\) and fulfills the same bound
Proof
Using (3.19) and monotone convergence for series, it suffices to consider only finite \(m\in \mathbb {N}\) to prove (3.39). Let \(\beta >0\), \(I\in \mathcal I{\setminus }\{0\}\), and \(m\in \mathbb {N}\). Inserting (3.25) into definition (3.18) of \(z_m^+\) yields
For \((I_1,\ldots ,I_n)\in \mathcal J^n_m\) with \(U(I_1,\ldots ,I_n)\ne 0\) and \(I=I_1+\cdots +I_n\) as in the above summation, we have
from (3.21), and hence, taking again the constant \(c_{4}=c/(2c_{3})\)
We choose a reference edge \(o\in {{\,\mathrm{supp}\,}}I\). Substituting (3.43) and (3.26) in (3.41) yields
The inner sum on the right-hand side can be extended to run over all n-tuples \((I_1,\ldots ,I_n)\) in \(\mathcal J_m^n\) with \(o\in {{\,\mathrm{supp}\,}}I_1\cup \ldots \cup {{\,\mathrm{supp}\,}}I_n\), since by definition, for any I which cannot be written as a sum of such \(I_1,\ldots , I_n\), for some \(n\in \mathbb {N}\), \(z^+_m(\beta ,I)=0\) or \(o\notin {{\,\mathrm{supp}\,}}I\). It follows
As we observed above, it suffices to consider only finite m in claim (3.39). It remains to show that for \(\beta \) large enough it is true that
Note that this condition does not involve I. Because \(|U(I_1,\ldots ,I_n)|\) is invariant under permutation of its arguments, we can bound \(C_{m,o,\beta }\) by
for the summand indexed by \(n=1\) we have used \(U(I_1)=1\).
By Lemma 3.3, we may apply Fact 3.2, yielding
Combining (3.47), (3.48), and (3.29) from Lemma 3.3 gives
yielding claim (3.46). Since \(|z_m(\beta ,I)|\le z_m^+(\beta ,I)\), claim (3.40) is an immediate consequence of (3.39). \(\square \)
3.4 Gaussian Lower Bound for Fourier Transforms
Next, we apply a cluster expansion with \(K(I,\phi )\) defined in (3.9) to obtain a representation of \(\mathcal Z_{\beta ,\phi }\) and finally a bound for the Fourier transform of the observable.
Lemma 3.5
(Partition sums in the presence of \(\phi \)). For all \(\beta \) large enough, the following identity holds for any \(\phi \in \mathbb {R}^E\):
Proof
Recall definitions (3.17) and (3.18) of \(z_m\) and \(z_m^+\). Take any \(\phi \in \mathbb {R}^E\). Rearranging a multiple series with positive summands and using (3.39) for \(\beta \) large enough, we obtain
Using this as a dominating series and the fact \(|K(I,\phi )|=\mathrm {e}^{-\beta H_{\mathrm{disl}}(I)}\), the following rearrangement of the series is valid for all \(m\in \mathbb {N}\):
By (3.25),
According to Lemma 3.3 and Facts 3.1 and 3.2, one has for all \(m\in \mathbb {N}\):
From monotone convergence, we know
the finiteness follows as in the argument described below (3.11). Consequently, applying dominated convergence in (3.54) and using \(\mathcal J_m\uparrow \mathcal J\) and (3.11) yields
On the other hand, from (3.51) and dominated convergence for series,
Taking the limit \(m\rightarrow \infty \) in equation (3.52) yields the first equality in claim (3.50).
The second equality of claim (3.50) follows from the following symmetry consideration. One has \(I\in \mathcal I\) if and only if \(-I\in \mathcal I\) and \(z(\beta ,I)=z(\beta ,-I)\) by definition, and hence
The last series converges absolutely, and its absolute value is bounded by \(\sum _{I\in \mathcal I}z^+(\beta ,I)<\infty \). \(\square \)
Lemma 3.6
(Gaussian lower bound for Fourier transforms). For all \(\beta \) large enough, the following holds for any \(\sigma \in \mathbb {R}^E\):
Proof
By (3.4), (3.3), and Lemma 3.5, we have
Using
and the bound
we obtain
We take the average over an auxiliary sign \(\Sigma \) taking values \(\pm 1\). We substitute \(\phi \) by \(\Sigma \phi \) in (3.64). Then, using the facts \(\cos \left\langle {\Sigma \phi } \, \, ,\, {I}\right\rangle =\cos \left\langle {\phi } \, \, ,\, {I}\right\rangle \) and \(\sin \left\langle {\Sigma \phi } \, \, ,\, {I}\right\rangle =\Sigma \sin \left\langle {\phi } \, \, ,\, {I}\right\rangle \), it follows
Note that \(\sum _{I\in \mathcal I}z(\beta ,I)\sin \left\langle {\phi } \, \, ,\, {I}\right\rangle \sin \left\langle {\sigma } \, \, ,\, {I}\right\rangle \) converges absolutely for \(\beta \) large enough by Lemma 3.5. Since \(\frac{1}{2}(\mathrm {e}^x+\mathrm {e}^{-x})\ge 1\) for all \(x\in \mathbb {R}\), we obtain
Using that \(\phi \) is centered Gaussian and \(\mathcal Z_{\beta ,\phi }\) is bounded and positive, we conclude
In view of (3.60) and \({\mathbb E} [\mathcal Z_{\beta ,\phi }]>0\), this proves the claim. \(\square \)
4 Proof of the Main Result
4.1 Bounding the Observable
For \(I\in \mathcal I\) and \(b=b(I)\) as in (1.18), we take the minimizer \(w^*:\mathbb {R}^3\rightarrow \mathbb {R}^{3\times 3}\) defined in (2.34) and set \(w^*(x,I):=w^*(x)\). For arbitrary \(x,y\in \mathbb {R}^3\), we choose \(\sigma (x,y)=(\sigma _{ij}(x,y))_{i,j\in [3]}\in (\mathbb {R}^E)^{[3]\times [3]}\) satisfying the equation
for all \(I\in \mathcal I\). Such a choice is possible because \(w^*(x,I)\) is a linear function of I.
Lemma 4.1
(Bounding the observable). There are a function \(W:\Lambda \times \mathbb {R}^3\times \bigcup _{E\Subset \Lambda } (\mathcal I(E){\setminus }\{0\})\rightarrow \mathbb {R}_{\ge 0}\) with
and \(\beta _1>0\) such that for all \(E\Subset \Lambda \), \(I\in \mathcal I(E){\setminus }\{0\}\), \(o\in {{\,\mathrm{supp}\,}}I\), \(x\in \mathbb {R}^3\), \(\beta \ge \beta _1\) and \(i,j\in [3]\) we have
Proof
Take \(E\Subset \Lambda \), \(I\in \mathcal I(E){\setminus }\{0\}\), \(o\in {{\,\mathrm{supp}\,}}I\), \(x\in \mathbb {R}^3\), and \(i,j\in [3]\). We choose a vertex \(v(o)\in o\). We set
Since \({{\,\mathrm{size}\,}}I\) is bounded away from 0, there is a constant \(c_{12}>0\) such that \(R(I,o)\le c_{12}{{\,\mathrm{size}\,}}I\). By definition (1.18) of b(I), one has the bound \(\Vert b_{lij}(I)\Vert _1\le c_{13}\Vert I\Vert _1\le c_{13}{{\,\mathrm{size}\,}}I\) for all its components, with some constant \(c_{13}>0\). Hence, we obtain
Because b is compactly supported and divergence-free in the sense of equation (1.12),
by the fundamental theorem of calculus. Recall the representation \(w^*=w^b+d_0\psi ^*\) with \(w^b\), \(d_0\psi ^*\) as in (2.37) and (2.38). We now establish bound (4.3) in two steps, first for x far from o, then close to o. A key estimate is provided by bounds on integral kernels proven in Appendix A.3.
Case 1: First we consider the case \(|v(o)-x|\ge 2R(I,o)\). It follows from (2.37) and the second inequality in (A.15) from Lemma A.1 (see Appendix A.3) in the case that \(v(o)=0\) is the origin that
with the constant \(c_{14}=72c_{12}c_{13}/\pi \).
The stability condition (1.5) implies \(|\lambda |/|2\mu +\lambda |\le 1\). In the same way as in (4.8), (2.38) and the second inequality in (A.37) from Lemma A.3 (see again Appendix A.3) in the case that \(v(o)=0\) is the origin give
with the constant \(c_{15}=1944c_{12}c_{13}/\pi \). It follows still in the case \(v(o)=0\)
The next step involves translation invariance: Shifting both x and I by a mesoscopic lattice vector \(v\in V_\Lambda \) does not change \(w^*_{ij}(x,I)\) because \((x,I)\mapsto b(I)(x)\) has the same translation invariance. Because inequality (4.10) is written in a translation-invariant form, it holds also if we drop the assumption \(v(o)=0\). This yields
for all \(\beta \ge \beta _1\) for sufficiently large \(\beta _1\), neither depending on o, x, nor I.
Case 2: Next we consider the case \(|v(o)-x|<2R(I,o)\). We recall the definition of \(J_{jk}(I)\) from (1.16). We now use the symbol \(\Vert {\cdot }\Vert _1\) in two different ways. On the one hand, \(\Vert I\Vert _1=\sum _{e\in E}|I_e|\) for I. On the other hand, \(\Vert J_{jk}(I)\Vert _1\) denotes the total unsigned mass of the signed measure \(J_{jk}(I)\) given by the following definition: For any signed measure \(\tilde{J}\) on \(\mathbb {R}^3\) with Hahn decomposition \(\tilde{J}=\tilde{J}_+-\tilde{J}_-\), we define \(\Vert \tilde{J}\Vert _1:=\tilde{J}_+(\mathbb {R}^3)+\tilde{J}_-(\mathbb {R}^3)\). With this interpretation, we have
Combining this with (A.50) and (A.51) from Lemma A.4 in Appendix A.3.3 yields the bound
for all \(x\in \mathbb {R}^3\) and all \(I\in \mathcal I{\setminus }\{0\}\) with a constant \(c_{16}>0\). Note that
with a constant \(c_{17}>0\) depending on the lattice spacing in \(\Lambda \). Squaring (4.13), we obtain
again for all \(\beta \ge \beta _1\) for sufficiently large \(\beta _1\), neither depending on o, x, nor I.
Combining the two cases, claim (4.3) holds for
To bound \(\sum _{o:|v(o)-x|\ge 2R(I,o)}|v(o)-x|^{-6}\), observe that R(I, o) is bounded away from 0 uniformly in I and o, and that \(|v(o)-x|^{-6}\) is summable away from x in three dimensions. We use (4.14) to bound \(\sum _{o:|v(o)-x|<2R(I,o)}({{\,\mathrm{size}\,}}I)^{-3}\). We conclude
uniformly in x, \(E\Subset \Lambda \), and \(I\in \mathcal I(E)\), with a constant \(c_{11}\) depending on \(\Lambda \).
\(\square \)
4.2 Identifying Long-Range Order
We finally prove now our main result.
Proof of Theorem 1.3
Applying Lemma 3.6 yields for \(t\in \mathbb {R}\), \(E\Subset \Lambda \), \(x,y\in \mathbb {R}^3\), and \(i,j\in [3]\)
We may drop the summand indexed by \(I=0\) because \(\left\langle {\sigma _{ij}(x,y)} \, \, ,\, {0}\right\rangle =0\). Inserting (4.3) and employing Lemma 3.4 in the last line in (4.19), we obtain for sufficiently large \(\beta \) that
with a constant \({c_{2}}={c_{2}}(c_{11},c_{7})>0\), where \(c_{11}\) was defined in (4.2). Mind that \({c_{2}}\) does not depend on \(x,y,i,j,E,\beta \). This proves the first claim.
By Theorem 3.3.9 in [7], for \(\beta \) large enough, the variance of \(\left\langle {\sigma _{ij}(x,y)} \, \, ,\, {I}\right\rangle \) exists and fulfills
where the last inequality is a consequence of the lower bound (1.26). \(\square \)
We remark that the two reflection symmetries \(H_{\mathrm{el}}(-w)=H_\mathrm{el}(w)\) and \(H_{\mathrm{disl}}(-I)=H_{\mathrm{disl}}(I)\) imply that \(w^*(x,-I)=-w^*(x,I)\) and \(w^*(x,I)\) are equal in distribution with respect to \(P_{\beta ,E}\), jointly in \(x\in \mathbb {R}^3\). In particular, the first inequality in (4.20) is actually an equality.
References
Ariza, M.P., Ortiz, M.: Discrete crystal elasticity and discrete dislocations in crystals. Arch. Ration. Mech. Anal. 178(2), 149–226 (2005)
Aumann, S.: Spontaneous breaking of rotational symmetry with arbitrary defects and a rigidity estimate. J. Stat. Phys. 160(1), 168–208 (2015)
Balaban, T., O’Carroll, M.: Low temperature properties for correlation functions in classical \(N\)-vector spin models. Commun. Math. Phys. 199(3), 493–520 (1999)
Berezinskiĭ, V.L.: Destruction of long-range order in one-dimensional and two-dimensional systems having a continuous symmetry group. I. Classical systems. Ž. Èksper. Teoret. Fiz. 59, 907–920 (1970)
Bovier, A., Zahradník, M.: A simple inductive approach to the problem of convergence of cluster expansions of polymer models. J. Statist. Phys. 100(3–4), 765–778 (2000)
Chaikin, P.M., Lubensky, T.C.: Principles of Condensed Matter Physics. Cambridge University Press, Cambridge (1995)
Durrett, R.: Probability: Theory and Examples, volume 31 of Cambridge Series in Statistical and Probabilistic Mathematics, 4th edn. Cambridge University Press, Cambridge (2010)
Falco, P.: Kosterlitz–Thouless transition line for the two dimensional Coulomb gas. Commun. Math. Phys. 312(2), 559–609 (2012)
Flatley, L.C., Theil, F.: Face-centered cubic crystallization of atomistic configurations. Arch. Ration. Mech. Anal. 218(1), 363–416 (2015)
Friedli, S., Velenik, Y.: Statistical Mechanics of Lattice Systems. A Concrete Mathematical Introduction. Cambridge University Press, Cambridge (2018)
Fröhlich, J., Simon, B., Spencer, T.: Infrared bounds, phase transitions and continuous symmetry breaking. Commun. Math. Phys. 50(1), 79–95 (1976)
Fröhlich, J., Spencer, T.: The Kosterlitz–Thouless transition in two-dimensional abelian spin systems and the Coulomb gas. Commun. Math. Phys. 81(4), 527–602 (1981)
Fröhlich, J., Spencer, T.: Massless phases and symmetry restoration in abelian gauge theories and spin systems. Commun. Math. Phys. 83(3), 411–454 (1982)
Guiliani, A., Theil, F.: In preparation
Heydenreich, M., Merkl, F., Rolles, S.W.W.: Spontaneous breaking of rotational symmetry in the presence of defects. Electron. J. Probab. 19(111), 1–17 (2014)
Kennedy, T., King, C.: Spontaneous symmetry breakdown in the abelian Higgs model. Commun. Math. Phys. 104(2), 327–347 (1986)
Kosterlitz, J.M., Thouless, D.J.: Ordering, metastability and phase transitions in two-dimensional systems. J. Phys. C: Solid State Phys. 6(7), 1181–1203 (1973)
Merkl, F., Rolles, S.W.W.: Spontaneous breaking of continuous rotational symmetry in two dimensions. Electron. J. Probab. 14(57), 1705–1726 (2009)
Nelson, D.R., Halperin, B.I.: Dislocation-mediated melting in two dimensions. Phys. Rev. B 19, 2457–2484 (1979)
Poghosyan, S., Ueltschi, D.: Abstract cluster expansion with applications to statistical mechanical systems. J. Math. Phys. 50(5), 053509 (2009)
Theil, F.: A proof of crystallization in two dimensions. Commun. Math. Phys. 262(1), 209–236 (2006)
Villain, J.: Theory of one- and two-dimensional magnets with an easy magnetization plane. II. The planar, classical, two-dimensional magnet. J. de Physique 36(6), 581–590 (1975)
Young, A.P.: Melting and the vector Coulomb gas in two dimensions. Phys. Rev. B 19, 1855–1866 (1979)
Acknowledgements
The authors would like to thank an anonymous referee for constructive comments helping us to improve the paper. Visits of RB to Munich were supported by LMU’s Center for Advanced Studies.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Vieri Mastropietro.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A. Appendix
Appendix A. Appendix
1.1 Elasticity Theory
1.1.1 Description of an Elastically Deformed Solid in Continuum Approximation
From Sect. 1.2.1, we recall that the elastic deformation energy \(E_{\mathrm {el}}(f)\) is modeled to be an integral over a smooth elastic energy density \(\rho _{\mathrm {el}}:\mathbb {R}^{3\times 3}\rightarrow \mathbb {R}\):
We assume furthermore:
-
\(\rho _{\mathrm {el}}\) takes its minimum value 0 at the identity matrix \(\text {Id}\). This means that the non-deformed solid has minimal energy.
-
The elastic energy density is insensitive to rotations of the solid:
$$\begin{aligned} \rho _{\mathrm {el}}(RM)=\rho _{\mathrm {el}}(M), \quad (R\in {\text {SO}}(3), M\in {\text {GL}}_+(3)), \end{aligned}$$(rot inv)where \({\text {GL}}_+(3)=\{M\in \mathbb {R}^{3\times 3}:\det M>0\}\). In other words, deforming the solid and then rotating it costs the same elastic energy as only deforming it with the same deformation.
Note that reflections \(R\in {\text {O}}(3){\setminus }{\text {SO}}(3)\) or singular or orientation reversing linearized deformations \(M\in \mathbb {R}^{3\times 3}\) with \(\det M\le 0\) do not make sense physically in this context.
For \(M,N\in {\text {GL}}_+(3)\), it is equivalent that \(M^tM=N^tN\) and that there exists \(R\in {\text {SO}}(3)\) such that \(N=RM\). As a consequence, \(\rho _{\mathrm {el}}(M)\) is a function of \(M^tM\). We set \({\tilde{\rho }}_{\mathrm {el}}(M^tM):=\rho _{\mathrm {el}}(M)\).
Note that assumption (rot inv) of rotational invariance does not imply isotropy of the solid, which is defined by
Thus, anisotropy means that first rotating the solid and then deforming it with a given deformation might cost a different elastic energy than deforming it with the same deformation without rotating it first. Although the isotropy assumption is an oversimplification for any real monocrystal, we assume it to keep the presentation simple.
1.1.2 Linearization
We now consider only small perturbations \(f=\mathrm {i}\mathrm {d}+\varepsilon u:\mathbb {R}^3\rightarrow \mathbb {R}^3\) of the identity map as deformation maps. For \(\nabla f=\text {Id}+\varepsilon \nabla u\), we obtain
Substituting this into (1.4) gives
If \(\mathbb {R}\ni \varepsilon \mapsto R_\varepsilon \in {\text {SO}}(3)\) is a path of rotations with \(R_0=\text {Id}\), then \(\frac{d}{d\varepsilon }R_\varepsilon |_{\varepsilon =0}\) is antisymmetric. Hence, the Taylor-approximated energy density \(\varepsilon ^2 F(\nabla u+ (\nabla u)^t)\) is not influenced by linearized rotations.
If assumption (isotropy) holds, then
holds for all positive definite matrices \(A=A^t\) and \(R\in {\text {SO}}(3)\). Taylor-expanded this means
for all symmetric matrices \(U=U^t\) and \(R\in {\text {SO}}(3)\). Thus, F(U) depends only on the list a, b, c of eigenvalues of U (with multiplicities). For diagonal matrices \(U={{\,\mathrm{diag}\,}}(a,b,c)\), the only quadratic forms which are symmetric in a, b, c are linear combinations of \(({{\,\mathrm{Tr}\,}}U)^2=(a+b+c)^2\) and \(|U|^2=a^2+b^2+c^2\). Thus, under an isotropy assumption, we have
with real constants \(\lambda \) and \(\mu \) and \(e^t=(1,1,1)\). The matrix \(\mu \text {Id}+\frac{\lambda }{2}ee^t\) has the double eigenvalue \(\mu \) with eigenspace \(e^\perp \) and a single eigenvalue \(\mu +3\lambda /2\) with eigenspace \(\mathbb {R}e\). Hence, the quadratic form F is positive definite if and only if \(\mu \) and \(\lambda \) satisfy the conditions given in (1.5). Summarizing, we have the model for the linearized elastic deformation energy given in (1.6)–(1.7).
1.2 From Kirchhoff’s Node Rule to Continuum Sourceless Currents
We show that Kirchhoff’s node rule for the discrete current I implies absence of sources for its smoothed variant \(\tilde{b}(I)\). For \(e\in E\) from \(x\in V\) to \(y\in V\) in its counting direction, we write \(x=v_-(e)\) and \(y=v_+(e)\). We rewrite (1.17) as
As a consequence of Kirchhoff’s rule (1.14), \(\tilde{b}(I)\) is indeed divergence-free:
1.3 Integral Kernels
1.3.1 Bounds for the Dipole Expansion
In this Appendix, we derive a simplified version of the dipole expansion for the Coulomb potential, which we need as ingredient to identify long-distance bounds for the observable \(w^*\) in the proof of Lemma 4.1.
Let \(\rho \in C^\infty _c(\mathbb {R}^3,\mathbb {R})\). We define its total charge
We take a radius \(R>0\) such that
and the first unsigned moment
The inverse Laplacian \(-\Delta ^{-1}\) is described by convolution with the Coulomb potential
Lemma A.1
(Simplified dipole expansion). For all \(x\in \mathbb {R}^3\) with \(|x|\ge 2R\) and \(i\in [3]\), we know that
with the error bounds
Proof
Let \(x\in \mathbb {R}^3\) with \(|x|\ge 2R\) and \(y\in {\text {supp}}\rho \). Then for all \(t\in [0,1]\), we have
We apply
to
In this proof, \(\partial _i=\partial /\partial x_i\) always refers to the variable \(x_i\). Using \(\partial _i|x|^\alpha =\alpha x_i|x|^{\alpha -2}\), we calculate:
Consequently, we can bound the integrand in (A.17) and its \(\partial _i\) derivative as follows:
We obtain
and hence claim (A.13) holds with the error term
It is bounded as follows:
This shows the first claimed bound in (A.15).
Substituting (A.22) in the \(\partial _i\) derivative of equation (A.23), i.e., in
the second claimed bound in (A.15) follows, too. \(\square \)
1.3.2 Properties of \(\partial _i\partial _j\Delta ^{-2}\)
Next, we describe \(\partial _i\partial _j\Delta ^{-2}\) explicitly by an integral kernel. We derive it from its Fourier transform, cf. (2.1).
Lemma A.2
(Integral kernel of \(\partial _i\partial _j\Delta ^{-2}\)). For any Schwartz functions \(f,g:\mathbb {R}^3\rightarrow \mathbb {C}\), we have
Proof
Using
for \(k\in \mathbb {R}^3{\setminus }\{0\}\), we rewrite the left hand side in claim (A.27) as follows:
(by Plancherel). Here, the application of Fubini’s theorem is justified because of
since \(1/|k|^2\) is integrable near 0 in 3 dimensions. We transform \(t=\frac{1}{z}\), \(z^{-\frac{1}{2}}\,\mathrm{d}z=-t^{-\frac{3}{2}}\,\mathrm{d}t\) and use
to obtain
The application of Fubini’s theorem in the last step is justified below. Now, substituting \(s=\frac{t}{2}|x|^2\), \(t=\frac{2s}{|x|^2}\), \(\sqrt{t}\,\mathrm{d}t=2\sqrt{2}\sqrt{s}\frac{ds}{|x|^3}\), \(t^{-\frac{1}{2}}\,\mathrm{d}t=\frac{\sqrt{2}}{|x|}s^{-\frac{1}{2}}\,ds\) and using \(\Gamma (\frac{1}{2})=\sqrt{\pi }\), \(\Gamma (\frac{3}{2})=\frac{\sqrt{\pi }}{2}\), we calculate
and similarly
which is integrable near 0. Together with the fast decay of f and g, this bound justifies the application of Fubini’s theorem in the last step of (A.32). Substitution of calculation (A.33) in (A.32) proves claim (A.27). \(\square \)
Next, we derive a variant of the simplified dipole expansion presented in Sect. A.3.1 (using the notation from there), but now for the operator \(\partial _i\partial _j\Delta ^{-2}\) rather than \(\Delta ^{-1}\). This is used in the proof of Lemma 4.1.
Lemma A.3
(Long-range asymptotics of \(\partial _i\partial _j\Delta ^{-2}\)). For all \(x\in \mathbb {R}^3\) with \(|x|\ge 2R\) and \(i,j,k\in [3]\), we have
with the error bounds
Proof
Recall that for \(x\in \mathbb {R}^3\) with \(|x|\ge 2R\), \(y\in {\text {supp}}\rho \), and all \(t\in [0,1]\), we have \(|x-ty|\ge |x|/2\ge R\). We apply (A.17) to
We calculate:
Using the Cauchy–Schwarz inequality, it follows
We obtain
and hence claim (A.35) with an error term \(r_1'\) bounded by
This shows the first claimed bound in (A.37).
For the partial derivatives \(\partial _k\) with respect to \(x_k\), we obtain:
Consequently,
This proves the second bound in (A.37). \(\square \)
1.3.3 Integral Kernels Close to the Diagonal
Recall that \(\Vert \tilde{J}\Vert _1\) denotes the total unsigned mass of a signed measure \(\tilde{J}\).
Lemma A.4
(Uniform bounds). For the form function \(\varphi \) introduced in Sect. 1.2.3, one has
Additionally, for any signed measure J with \(\Vert J\Vert _1<\infty \) and for all \(l,i,j\in [3]\), one has
Proof
The operators \(\partial _l\Delta ^{-1}\) and \(\partial _l\partial _i\partial _j\Delta ^{-2}\) have the integral kernels \(k_1(x-y)\) and \(k_2(x-y)\), respectively, where
cf. (A.27), (A.38), and (A.40). Since both kernels are bounded by \(O(|z|^{-2})\), they are locally integrable and decay at infinity. Because \(\varphi \) is compactly supported and bounded, claims (A.48) and (A.49) follow. The remaining claims follow from \(\Vert k*J\Vert _\infty \le \Vert k\Vert _\infty \Vert J\Vert _1\) with \(k=k_1\) and \(k=k_2\), respectively. \(\square \)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Bauerschmidt, R., Conache, D., Heydenreich, M. et al. Dislocation Lines in Three-Dimensional Solids at Low Temperature. Ann. Henri Poincaré 20, 3019–3057 (2019). https://doi.org/10.1007/s00023-019-00829-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00023-019-00829-9