Generalization of Simson–Wallace theorem: planar and spatial formulation

Abstract

The paper studies a problem that represents a natural spatial generalization of the well-known Simson–Wallace theorem: Let four skew lines parallel to a fixed plane be given. Determine the locus of the point P in space so that the reflections of P in the given lines are coplanar. The result was very surprising for us — we get a cylinder of revolution. By orthogonal projection onto the given plane, the problem is reformulated as a planar one and subsequently solved synthetically. This solution turns out to have many properties in common with the classical Simson–Wallace theorem.

1 Introduction

The classical Simson–Wallace theorem, discovered in 1799 by William Wallace [2], can be formulated as follows:

Simson–Wallace Theorem Let a triangle ABC be given. Consider reflections $P_a,P_b,P_c$ of a point P in lines a, b, c of the triangle. Then the points $P_a,P_b,P_c$ are collinear iff P lies on the circumcircle of the triangle. Moreover, the line given by $P_a,P_b,P_c$ always passes through the orthocenter of the triangle.

This theorem can be made a bit more complicated: Consider three skew lines a, b, c in 3-dimensional Euclidean space, which we will call space for short, that are parallel to a given plane. What is the locus of the point P such that the reflections $P_a,P_b$ and $P_c$ of the point P in the lines are collinear?

As will be shown later in the paper, the general solution to this problem is not interesting enough— the locus is a straight line perpendicular to the given plane. However, this problem can be modified further. This brings us to our problem:

Problem 1, formulation 1 Let four lines (skew lines in general) a, b, c, d in space, parallel to a fixed plane, be given. What is the locus of the point P such that reflections $P_a,P_b,P_c$ and $P_d$ of the point P in the given lines are coplanar?

Originally, the authors solved this problem by analytical methods [1]. For now, we reveal that the locus is a cylinder of revolution with the axis perpendicular to the fixed plane, Fig. 1.

Fig. 1

The locus of P is a cylinder of revolution

In the following we solve the problem synthetically (Theorem 3.2).

Furthermore, we will show that if we restrict the locus of the point P to the fixed plane (or any plane parallel to it) then all planes determined by the points $P_a,P_b,P_c,P_d$ contain a fixed line about which they rotate.

More precisely, we will prove the following: The intersection of the plane determined by $P_a,P_b,P_c,P_d$ and the fixed plane contains a fixed point for all points P of the locus confined to the fixed plane (Theorem 3.4).

In addition we will show how the locus of the point P belonging to the fixed plane (i.e. a certain circle) can be constructed by Euclidean means (Problem 2).

Finally, we will state a planar generalization of Simson–Wallace theorem (Theorem 4.1).

2 Equivalent planar formulation of the problem

First, let us notice that the points $P_a,P_b,P_c$ and $P_d$ are coplanar iff the feet of perpendiculars dropped from P to the lines a, b, c, d are coplanar. This means that if some point P of the space satisfies the condition, the whole line perpendicular to the fixed plane and passing through P also satisfies it, since the feet of normals for all points of the line are identical. Therefore, to solve the problem, it is sufficient to search for the locus of the point P that lies in any plane parallel to a fixed plane.

Suppose that this fixed plane has zero height. Let the lines a, b, c, d have heights $h_a,h_b,h_c,h_d$ respectively. The images $P_a,P_b,P_c$ and $P_d$ have heights $2h_a, 2h_b,2h_c,2h_d.$ Let us consider the line $P_a P_b$ and mark on it the point $X_{ab}$ which has zero height, in other words, which lies in the fixed plane. If there is no such point, let us define it to be improper point of the line. Analogically, let us denote the points by $X_{bc}$ and $X_{cd}.$ Clearly, if the points $P_a,P_b,P_c,P_d$ are coplanar, the points $X_{ab},X_{bc}$ and $X_{cd}$ are collinear (and all other points $X_{ac},X_{ad},X_{bd}$ defined similarly).

The converse implication also holds: If these three points are collinear the four images of P are coplanar, (we leave the justification to the reader). Moreover, for the point $X_{ab}$ the relation

$$\begin{aligned} \frac{|P_a X_{ab}|}{|P_b X_{ab}|}=\frac{h_a}{h_b} \end{aligned}$$

(2.1)

holds. (If $h_b=0$ then $X_{ab}=P_b,$ if further $h_a=0$ then the set $\{X_{ab},X_{bc},X_{cd}\}$ can be replaced by $\{X_{bc}=P_b,X_{cd},X_{ac}=P_a\}$ and procedure will be the same. Finally, if three heights will be zero but not the fourth one, the problem is possible reduce to the Simson–Wallace Theorem).

Therefore, if the points $P_a$ and $P_b$ are constructed, one can easily construct the point $X_{ab}$ — for example, as the image of $P_a$ in a homothety with centre $P_b$ and ratio $h_b/(h_a+h_b).$ This reasoning is easily extended to negative heights if considering oriented lengths in the Eq. (2.1). Analogically, we arrive at equations

$$\begin{aligned} \frac{|P_b X_{bc}|}{|P_c X_{bc}|}=\frac{h_b}{h_c},\quad \frac{|P_c X_{cd}|}{|P_d X_{cd}|}=\frac{h_c}{h_d}\ . \end{aligned}$$

On the basis of these facts the whole problem is reformulated into a planar one. Consider the orthogonal projections of the lines a, b, c, d into the fixed plane and denote them by $a',b',c'$ and $d'$. Further denote the projections of the points $P_a, P_b, P_c$ and $P_d$ by $P_a', P_b', P_c'$ and $P_d'.$ Then for the points $X_{ab}, X_{bc}, X_{cd}$ relations

$$\begin{aligned} \frac{|P_a' X_{ab}|}{|P_b' X_{ab}|}=\frac{h_a}{h_b}, \quad \frac{|P_b' X_{bc}|}{|P_c' X_{bc}|}=\frac{h_b}{h_c}, \quad \frac{|P_c' X_{cd}|}{|P_d' X_{cd}|}=\frac{h_c}{h_d} \end{aligned}$$

hold.

It is easy to see that the points $P_a', P_b', P_c'$ and $P_d'$ are symmetrical images of P with respect to the lines $a', b', c', d'.$ The points $P_a,P_b,P_c$ and $P_d$ are coplanar iff the points $X_{ab},X_{bc},X_{cd}$ are collinear. Thus we have achieved a planar formulation of the problem:

Problem 1, formulation 2: Let four lines a, b, c, d in a plane be given. Consider a point P in the plane and its reflections $P_a,P_b,P_c,P_d$ in the lines a, b, c, d. Let the point $X_{ab}$ be on the line $P_aP_b$ such that

$$\begin{aligned} \frac{|P_a X_{ab}|}{|P_b X_{ab}|}=\frac{h_a}{h_b}=k_{ab}, \end{aligned}$$

where $k_{ab}$ is a given real constant and |AB| is the oriented distance. Analogically let us define the points $X_{bc}$ and $X_{cd}$

$$\begin{aligned} \frac{|P_a X_{ab}|}{|P_b X_{ab}|}=k_{ab},\quad \frac{|P_b X_{bc}|}{|P_c X_{bc}|}=k_{bc}, \quad \frac{|P_c X_{cd}|}{|P_d X_{cd}|}=k_{cd}\ . \end{aligned}$$

(2.2)

What is the locus of the point P in the plane if the points $X_{ab},X_{bc}$ and $X_{cd}$ are collinear?

3 Solution of the planar formulation of Problem 1

First we prove the following

Lemma 3.1

A point $X_{ab}$ ($X_{bc}, X_{cd}),$ defined by Eq. (2.2), depends on an arbitrary point P as follows:

$$\begin{aligned} R_{ab}\circ H_{ab}(P)=X_{ab}, \end{aligned}$$

(3.1)

where $H_{ab}$ is a homothety and $R_{ab}$ is a reflection in a line, Fig. 2.

Proof

The following considerations are related to Fig. 2.

Fig. 2

Point $X_{ab}$ depends on the point P by composition of a homothety centered at B and reflection in a (red) line BZ

Let $a=AB$ and $b=BC.$ Then the triangle $P_a BP_b$ has the same shape regardless of the position of the point P: it is isosceles and $\angle P_aBP_b=\angle 2ABC$, since if we reflect the point $P_b$ in the line b and then its image in a, we get $P_a.$

However composition of two reflections is a rotation about the angle which is two times the angle formed by the lines a and b. At the same time the position of the point $X_{ab}$ on the line $P_aP_b$ is uniquely determined by the constant $k_{ab}.$ This means that the relative position of the point $X_{ab}$ is fixed with respect to the segment $P_aP_b$ and therefore the angle $\alpha =\angle P_bBX_{ab}$ is constant. Thus the angle $\beta$ between the angle bisector BZ of the angle $PBX_{ab}$ and the line b is constant

$$\begin{aligned} \beta =\angle CBZ=\frac{\angle PBX_{ab}}{2}+\frac{\angle PBP_b}{2}=\frac{\angle P_bBX_{ab}}{2}=\frac{\alpha }{2}, \end{aligned}$$

Fig. 2.

(In order to prove it for all possible positions of the point P, oriented angles have to be used). Therefore the angle bisector BZ is a fixed line regardless of the position of P. If the ratio of the lengths

$$\begin{aligned} \frac{|BX_{ab}|}{|PB|}=k \end{aligned}$$

(3.2)

is a constant, we are done since $H_{ab}$ is a homothety with the centre B and ratio k, $R_{ab}$ is a reflection with respect to the angle bisector of $\angle PBX_{ab}.$ The proof that the right-hand side of (3.2) is a constant follows directly from the fact that the triangle $BP_bX_{ab}$ always has the same shape

$$\begin{aligned} k=\frac{|X_{ab}B|}{|PB|}=\frac{|X_{ab}B|}{|P_bB|}=\textrm{constant}\ . \end{aligned}$$

$\square$

Now consider the lines $c=CD$ and $d=DA$ and construct points $X_{bc}$ and $X_{cd}.$ These points depend on the point P according to Lemma 3.1 as follows

$$\begin{aligned} R_{bc}\circ H_{bc}(P)=X_{bc},\quad R_{cd}\circ H_{cd}(P)=X_{cd}, \end{aligned}$$

(3.3)

where $R_{bc},R_{cd}$ and $H_{bc},H_{cd}$ denote reflections and homotheties respectively.

Relations (3.1) and (3.3) imply relations between $X_{ab},X_{bc}$ and $X_{cd}$

$$\begin{aligned} X_{ab}= & {} R_{ab}\circ H_{ab}(P)=R_{ab}\circ H_{ab}(H_{bc}^{-1}\circ R_{bc}^{-1}(X_{bc})), \\ X_{cd}= & {} R_{cd}\circ H_{cd}(P)=R_{cd}\circ H_{cd}(H_{bc}^{-1}\circ R_{bc}^{-1}(X_{bc})), \end{aligned}$$

where $H^{-1}$ and $R^{-1}$ are inverse homothety and reflection respectively.

However

$$\begin{aligned} X_{ab}=R_{ab}\circ H_{ab}(H_{bc}^{-1}\circ R_{bc}^{-1}(X_{bc}))=O_{S_1}\circ H_{S_1}(X_{bc}), \end{aligned}$$

(3.4)

where $O_{S_1}$ is a rotation and $H_{S_1}$ is a homothety. The common centre of the rotation and the homothety is a point $S_1$ [3]. Similarly,

$$\begin{aligned} X_{cd}=R_{cd}\circ H_{cd}(H_{bc}^{-1}\circ R_{bc}^{-1}(X_{bc}))=O_{S_2}\circ H_{S_2}(X_{bc}), \end{aligned}$$

(3.5)

where $O_{S_2}$ and $H_{S_2}$ is a rotation and a homothety with the common centre $S_2.$ Now we are able to prove

Theorem 3.2

The points $X_{ab},X_{bc}$ and $X_{cd}$ are collinear iff the point P lies on a certain circle. (In special cases, it can also be a point, a line or the whole plane. However, a point and a line can be considered as a special form of a circle.)

First we prove the Lemma 3.3, the trivial consequence of which will be the proof of Theorem 3.2.

Lemma 3.3

If the points $X_{ab},X_{bc}$ and $X_{cd}$ are collinear then the locus of points $X_{bc}$ is a certain circle k.

Proof

All of the following considerations are related to Fig. 3. Relation (3.4) implies that the triangle $X_{bc} S_1 X_{ab}$ has the same shape for all positions of $X_{bc}.$ Similarly, from relation (3.5) we conclude that the triangle $X_{bc} S_2 X_{cd}$ has the same shape as well. However, this means that the angles $X_{ab} X_{bc} S_1$ and $S_2 X_{bc} X_{cd}$ are constant for any position of the point $X_{bc}$ and hence for any position of the point P. If the points $X_{ab}, X_{bc}$ and $X_{cd}$ are collinear the following relation between the oriented angles holds

$$\begin{aligned} 0=\angle X_{ab} X_{bc} X_{cd}=\angle X_{ab}X_{bc}S_1+\angle S_1X_{bc}S_2 + \angle S_2X_{bc}X_{cd}. \end{aligned}$$

Written differently

$$\begin{aligned} \angle S_1 X_{bc} S_2=-\angle X_{ab} X_{bc} S_1 - \angle S_2 X_{bc} X_{cd}=\textrm{constant}. \end{aligned}$$

Thus, the point $X_{bc}$ lies on the circle (in a special case on the line) k passing through the points $S_1,S_2.$ It is clear that for every point $X_{bc}$ of the circle k three points $X_{ab}, X_{bc}$ and $X_{cd}$ are collinear. $\square$

Now the proof of the Theorem 3.2 follows.

Fig. 3

The locus points $X_{bc}$ have to be a circle k passing through the points $S_1,S_2$

Proof

According to Lemma 3.3 the point $X_{bc}$ lies on the circle k and the points P and $X_{bc}$ are linked by relation (3.3). Thus

$$\begin{aligned} c=H_{bc}^{-1}\circ R_{bc}^{-1}(k) \end{aligned}$$

and the locus of P is a circle c. $\square$

Theorem 3.4

The line given by points $X_{ab}, X_{bc}, X_{cd}$ has a fixed point F when P moves along the locus circle. (Here we suppose that the locus is a circle and not a line).

Proof

Denote by F the second intersection of the line given by points $X_{ab}, X_{bc},$ $X_{cd}$ with the circle k,  then

$$\begin{aligned} \angle FX_{bc}S_1=\angle X_{ab}X_{bc}S_1, \end{aligned}$$

Fig. 3. However, the angle $X_{ab}X_{bc}S_1$ is constant, so the point F is fixed, common to all lines given by $X_{ab}, X_{bc}, X_{cd}$. $\square$

At the end of this paper we show how to construct the locus circle c.

Problem 2 Construct the circle c that is a solution of the plane formulation of the Problem 1.

Construct three points P for which the points $X_{ab},X_{bc}$ and $X_{cd}$ are collinear. It is obvious that if the points $P_a,P_b,P_c,P_d$ are collinear then the three points $X_{ab},X_{bc},X_{cd}$ are collinear as well. The point P for which the four points are collinear is the so-called Miquel point M of a quadrilateral formed by the lines a, b, c, d. If E is the intersection of the lines a and c, then the second intersection of the circles (BCE) and (ADE) is the Miquel point [2]. Thus we have the first point we are looking for, $P=M.$

Three points are also in a line if two of them coincide. We look for points P such that $X_{bc}=X_{ab}$ and $X_{bc}=X_{cd}.$

If $X_{bc}=X_{ab}$ then the points $P_a,P_b,P_c$ are collinear. In other words the points $P_a,P_b,P_c$ lie on a Simson line of a certain point P. (Here we mean by “Simson line” a line determined by collinear reflections of the point P with respect to the lines a, b, c of a triangle. However, the most common meaning of the Simson line is a line which is determined by feet of perpendiculars dropped from P to the lines of a triangle). It is well known that the point P must lie on the circumcircle of the triangle formed by the lines a, b, c.

Auxiliary construction related to Problem 2

Let a triangle BCE be given by the lines $CE=a,BC=b$ and $CE=c.$ Consider an arbitrary point P of the plane, its reflections $P_a,P_b$ and $P_c$ in the lines a, b, c and the points $X_{ab}$ and $X_{bc}$ defined by relations (2.2). The construction of a point $P_1$ of the plane for which $X_{ab}=X_{bc}$ is as follows.

Fig. 4

Construction of the point $P_1$ for which $X_{ab}=X_{bc}$

Construction

Considerations are related to Fig. 4. Consider the Simson line of a point P moving on the circle (BCE). As we know, this line always passes through the orthocenter $H_{bce}$ of the triangle BCE. Furthermore, the angle $P_bX_{ab}B$ is constant (see Lemma 3.1). This means that the oriented angle $H_{bce}X_{ab}B$ is constant. Thus, if we construct a single point $X_{ab}$ on any Simson line, then the circle $l_1$ circumscribed about the triangle $H_{bce}X_{ab}B$ is the locus of all points $X_{ab}$ corresponding to all Simson lines of points P.

Fig. 5

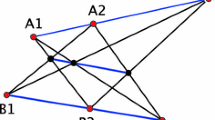
Example of the solution. The searched locus is the circle $(P_1 P_2 M).$ For the constants (2.2) values $k_{ab}=k_{bc}=k_{cd}=1/3$ were chosen

Repeating the same argument for the point $X_{bc}$ we arrive at the constant oriented angle $H_{bce}X_{bc}C.$ Therefore the circle $l_2$ passing through the points $H_{bce},C$ and the point $X_{bc}$ belonging to any Simson line of P, is the locus of all points $X_{bc}$ corresponding to all Simson lines. If $X_{ab}=X_{bc}$ holds, this point must be the second intersection $S_1$ of the circles, $S_1=l_1\cap l_2\ne H_{bce}.$

After the construction of the point $S_1$ we obtain the Simson line of the point $P_1$ we are looking for. It is a line $S_1H_{bce}.$ Now it is easy to construct the point $P_1$ — it is the intersection of the reflections of the line $S_1H_{bce}$ in any two sides of the triangle BCE.

One observation The Auxiliary Construction established a solution of the spatial problem: Let three skew lines a, b, c parallel to a fixed plane be given. Determine a point P belonging to the fixed plane whose reflections $P_a,P_b,P_c$ in the lines a, b, c are collinear. The solution of the problem mentioned in the introduction is a line perpendicular to the fixed plane and passing through the point $P_1.$ $\Box$

Let us return to the solution of the Problem 2. Applying the Auxiliary Construction to the triangle BCE we find the point $P_1$ for which $X_{ab}=X_{bc}.$ Applying the construction to the triangle CDG, where G is the intersection of the lines b, d, we find the point $P_2$ for which $X_{bc}=X_{cd}.$ The circle passing through the points $M,P_1$ and $P_2$ is the searched locus.

In Fig. 5 the circle $(P_1 P_2 M)$ is depicted. The three collinear points are shown in green for $P=M$ and in red for an arbitrary point P of the circle $(P_1 P_2 M).$ The line given by the points $X_{ab}, X_{bc}, X_{cd}$ passes

through a fixed point, which can be constructed as the second intersection of the Simson line of the point M and the circle $(S_1 X_{bc} S_2).$

4 Conclusion

We presented a generalization of the Simson–Wallace theorem which has a spatial and planar formulation. It has many features in common with the original theorem, namely, that the solution is a circle (in the spatial formulation a cylinder of revolution) and that the line of collinear points has a fixed point. (In the spatial formulation, the fixed point belongs to the intersection of a plane $P_a P_b P_c P_d$ and the fixed plane. It is not difficult to show that the plane $P_a P_b P_c P_d$ has a fixed line iff the points P are confined on any plane parallel to the fixed plane.)

There is a slightly more general formulation of the Simson–Wallace theorem that is closely related to the planar formulation of the presented problem:

Theorem 4.1

Let three arbitrary homotheties $H_1,H_2,H_3$ and three lines $R_1,R_2$ and $R_3$ be given. Consider points $X_1,X_2$ and $X_3$ defined by relations

$$\begin{aligned} X_1=H_1\circ R_1(P),\quad X_2=H_2\circ R_2(P),\quad X_3=H_3\circ R_3(P), \end{aligned}$$

where $H_1(P)$ is the image of a point P in the homothety $H_1$ and $R_1(P)$ is a reflection of P in the line $R_1$ (similarly for the other indices). Then the points $X_1,X_2, X_3$ are collinear iff the point P belongs to a circle (in special cases to a line).

This theorem may be proved by almost the same considerations that were used in this article.

The authors are looking for further generalizations, both in plane and in space.