1 Introduction

We consider an infinite polygon \((x_j)_{j \in \mathbb {Z}}\) given by its vertices \(x_j \in \mathbb {R}^n\) in an n-dimensional real vector space \(\mathbb {R}^n\) resp. an n-dimensional affine space \(\mathbb {A}^n\) modelled after \(\mathbb {R}^n.\) For a parameter \(\alpha \in (0,1)\) we introduce the polygon \(M_{\alpha }(x)\) whose vertices are given by

$$\begin{aligned} \left( M_{\alpha }(x)\right) _j:=(1-\alpha ) x_j+\alpha x_{j+1}. \end{aligned}$$

For \(\alpha =1/2\) this defines the midpoints polygon \(M(x)=M_{1/2}(x).\) On the space \(\mathcal {P}=\mathcal {P}(\mathbb {R}^n)\) of polygons in \(\mathbb {R}^n\) this defines a discrete curve shortening process \(M_{\alpha }: \mathcal {P}\longrightarrow \mathcal {P},\) already considered by Darboux [4] in the case of a closed resp. periodic polygon. For a discussion of this elementary geometric construction see Berlekamp et al. [1].

Fig. 1
figure 1

The parabola \(c(t)=(t^2/2 , t)\) as soliton of the midpoints map M

Full size image

The mapping \(M_{\alpha }\) is invariant under the canonical action of the affine group. The affine group \(\mathrm{Aff}(n)\) in dimension n is the set of affine maps \((A,b): \mathbb {R}^n \longrightarrow \mathbb {R}^n, x \longmapsto Ax +b.\) Here \(A \in \text {Gl}(n)\) is an invertible matrix and \(b \in \mathbb {R}^n\) a vector. The translations \(x \longmapsto x+b\) determined by a vector b form a subgroup isomorphic to \(\mathbb {R}^n.\) Let \(\alpha \in (0,1).\) We call a polygon \(x_j\) a soliton for the process \(M_{\alpha }\) (or affinely invariant under \(M_{\alpha }\)) if there is an affine map \((A,b)\in \mathrm{Aff}(n)\) such that

$$\begin{aligned} \left( M_{\alpha }(x)\right) _j=A x_j +b \end{aligned}$$
(1)

for all \(j \in \mathbb {Z}.\) In Theorem 1 we describe these solitons explicitly and discuss under which assumptions they lie on the orbit of a one-parameter subgroup of the affine group acting canonically on \(\mathbb {R}^n.\) We call a smooth curve \(c:\mathbb {R}\longrightarrow \mathbb {R}^n\) a soliton of the mapping \(M_{\alpha }\) resp. invariant under the mapping \(M_{\alpha }\) if there is for some \(\epsilon >0\) a smooth mapping \(s \in (-\epsilon ,\epsilon )\longmapsto (A(s),b(s))\in \mathrm{Aff}(n)\) such that for all \(s\in (-\epsilon ,\epsilon )\) and \(t \in \mathbb {R}\!:\)

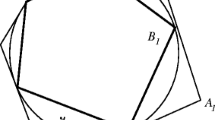
$$\begin{aligned} \tilde{c}_s(t):=(1-\alpha )c(t)+\alpha c(t+s)= A(s)c(t)+b(s). \end{aligned}$$
(2)

Then for some \(t_0 \in \mathbb {R}\) and \(s \in (-\epsilon ,\epsilon )\) the polygon \(x_j=c(js+t_0), j\in \mathbb {Z}\) is a soliton of \(M_{\alpha }.\) The parabola is an example of a soliton of \(M=M_{1/2},\) cf. Fig. 1 and Example 1, Case (e). We show in Theorem 2 that the smooth curves invariant under \(M_{\alpha }\) coincide with the orbits of a one-parameter subgroup of the affine group \(\mathrm{Aff}(n)\) acting canonically on \(\mathbb {R}^n.\) For \(n=2\) we give a characterization of these curves in terms of the general-affine curvature in Sect. 5.

The authors discussed solitons, i.e. curves affinely invariant under the curve shortening process \(T: \mathcal {P}(\mathbb {R}^n)\longrightarrow \mathcal {P}(\mathbb {R}^n)\) with

$$\begin{aligned} \left( T(x)\right) _j= \frac{1}{4}\left\{ x_{j-1}+2x_j+x_{j+1}\right\} \end{aligned}$$
(3)

in [9]. The solitons of \(M=M_{1/2}\) form a subclass of the solitons of T,  since \(\left( T(x)\right) _j= \left( M^2(x)\right) _{j-1}.\) Instead of the discrete evolution of polygons one can also investigate the evolution of polygons under a linear flow, cf. Viera and Garcia [11] and [9, Sec. 4] or a non-linear flow, cf. Glickenstein and Liang [5].

2 The affine group and systems of linear differential equations of first order

The affine group \(\mathrm{Aff}(n)\) is a semidirect product of the general linear group \(\text {Gl}(n)\) and the group \(\mathbb {R}^n\) of translations. There is a linear representation

$$\begin{aligned} (A,b) \in \mathrm{Aff}(n) \longrightarrow \left( \begin{array}{c|c} A &{} b\\ \hline 0 &{}1 \end{array} \right) \in \text {Gl}(n+1), \end{aligned}$$

of the affine group in the general linear group \(\text {Gl}(n+1),\) cf. [8, Sec. 5.1]. We use the following identification

$$\begin{aligned} \left( \begin{array}{c|c} A &{} b\\ \hline 0 &{}1 \end{array} \right) \left( \begin{array}{c} x\\ \hline 1 \end{array} \right) = \left( \begin{array}{c} A x+b\\ \hline 1 \end{array} \right) . \end{aligned}$$
(4)

Hence we can identify the image of a vector \(x \in \mathbb {R}^n\) under the affine map \(x \longmapsto Ax+b\) with the image \(\left( \begin{array}{c}Ax +b\\ \hline 1 \end{array}\right) \) of the extended vector \(\left( \begin{array}{c}x\\ \hline 1\end{array}\right) \). Using this identification we can write down the solution of an inhomogeneous system of linear differential equations with constant coefficients using the power series \(F_B(t)\) which we introduce now:

Proposition 1

For a real (n, n)-matrix \(B \in M_{\mathbb {R}}(n)\) we denote by \(F_B(t)\in M_{\mathbb {R}}(n)\) the following power series:

$$\begin{aligned} F_B(t)=\sum _{k=1}^{\infty } \frac{t^k}{k!}B^{k-1}. \end{aligned}$$
(5)
  1. (a)

    We obtain for its derivative:

    $$\begin{aligned} \frac{d}{dt} F_B(t)=\exp (Bt)=BF_B(t)+\mathbb {1}. \end{aligned}$$
    (6)

    The function \(F_B(t)\) satisfies the following functional equation:

    $$\begin{aligned} F_B(t+s)=F_B(s)+\exp (Bs)F_B(t), \end{aligned}$$
    (7)

    resp. for \(j \in \mathbb {Z}, j\ge 1:\)

    $$\begin{aligned} F_B(j)= & {} \left\{ \mathbb {1}+\exp (B)+\exp (2B)+\cdots + \exp ((j-1)B)\right\} F_B(1)\\= & {} \left( \exp (B)-\mathbb {1}\right) ^{-1}\left( \exp (jB)-\mathbb {1}\right) F_B(1). \end{aligned}$$
  2. (b)

    The solution c(t) of the inhomogeneous system of linear differential equations

    $$\begin{aligned} \dot{c}(t)=B c(t)+d \end{aligned}$$
    (8)

    with constant coefficients (i.e. \(B\in M_{\mathbb {R}}(n,n),d\in \mathbb {R}^n\)) and with initial condition \(v=c(0)\) is given by:

    $$\begin{aligned} c(t)=v+F_B(t)\left( Bv+d\right) =\exp (Bt)(v)+F_B(t)(d). \end{aligned}$$
    (9)

Proof

(a) Equation (6) follows immediately from Eq. (5). Then we compute

$$\begin{aligned} \frac{d}{dt} \left( F_B(t+s)- \exp (Bs)F_B(t)\right) =\exp (B(t+s))-\exp (Bs)\exp (Bt)=0. \end{aligned}$$

Since \(F_B(0)=0\) Eq. (7) follows. And this implies Eq. (8).

(b) We can write the solution of the differential equation (8)

$$\begin{aligned} \frac{d}{dt} \left( \begin{array}{c} c(t)\\ \hline 1 \end{array} \right) = \left( \begin{array}{c|c} B&{}d\\ \hline 0&{}0 \end{array} \right) \left( \begin{array}{c} c(t)\\ \hline 1 \end{array} \right) \end{aligned}$$

as follows:

$$\begin{aligned} \left( \begin{array}{c} c(t)\\ \hline 1 \end{array} \right)= & {} \exp \left( \left( \begin{array}{c|c} B&{} d\\ \hline 0&{}0 \end{array} \right) t \right) \left( \begin{array}{c} v \\ \hline 1 \end{array} \right) \\ \nonumber= & {} \left( \begin{array}{c|c} \exp (Bt)&{} F_B(t)(d)\\ \hline 0&{}1 \end{array} \right) \left( \begin{array}{c} v \\ \hline 1 \end{array} \right) = \left( \begin{array}{c} \exp (Bt)(v)+F_B(t)(d) \\ \hline 1 \end{array} \right) \end{aligned}$$
(10)

which is Eq. (9). One could also differentiate Eq. (9) and use Eq. (6)\(\square \)

Remark 1

Equation (2) shows that c(t) is the orbit

$$\begin{aligned} t \in \mathbb {R}\longmapsto c(t)=\exp \left( \left( \begin{array}{c|c} B&{} d\\ \hline 0&{}0 \end{array} \right) t \right) \left( \begin{array}{c} v \\ \hline 1 \end{array} \right) \in \mathbb {R}^n. \end{aligned}$$

of the one-parameter subgroup

$$\begin{aligned} t \in \mathbb {R}\longmapsto \exp \left( \left( \begin{array}{c|c} B&{} d\\ \hline 0&{}0 \end{array} \right) t \right) \in \mathrm{Aff}(n)\end{aligned}$$

of the affine group \(\mathrm{Aff}(n)\) acting canonically on \(\mathbb {R}^n.\)

3 Polygons invariant under \(M_{\alpha }\)

Theorem 1

Let \((A,b): x \in \mathbb {R}^n \longmapsto Ax + b\in \mathbb {R}^n\) be an affine map and \(v \in \mathbb {R}^n.\) Assume that for \(\alpha \in (0,1)\) the value \(1-\alpha \) is not an eigenvalue of A,  i.e. the matrix \(A_{\alpha }:= \alpha ^{-1}\left( A+(\alpha -1)\mathbb {1}\right) \) is invertible. Then the following statements hold:

(a) There is a unique polygon \(x \in \mathcal {P}(\mathbb {R}^n)\) with \(x_0=v\) which is a soliton for \(M_{\alpha }\) resp. affinely invariant under the mapping \(M_{\alpha }\) with respect to the affine map (A, b),  cf. Eq. (1). If \(b_{\alpha }=\alpha ^{-1}b,\) then for \(j>0:\)

$$\begin{aligned} x_j= & {} A_{\alpha }^j(v)+ A_{\alpha }^{j-1}\left( b_{\alpha }\right) +\cdots + A_{\alpha }\left( b_{\alpha }\right) + b_{\alpha }\nonumber \\= & {} v+\left( A_{\alpha }^j-\mathbb {1}\right) \left( v + \left( A_{\alpha }-\mathbb {1}\right) ^{-1} \left( b_{\alpha }\right) \right) . \end{aligned}$$
(11)

and for \(j<0:\)

$$\begin{aligned} x_j= & {} A_{\alpha }^j(v)- A_{\alpha }^{j}\left( b_{\alpha }\right) +\cdots + A_{\alpha }^{-1}\left( b_{\alpha }\right) \nonumber \\= & {} v+\left( A_{\alpha }^j-\mathbb {1}\right) \left( v - \left( A_{\alpha }^{-1}-\mathbb {1}\right) ^{-1} \left( A_{\alpha }^{-1} (b_{\alpha } \right) \right) . \end{aligned}$$
(12)

(b) If \(A_{\alpha }=\exp \left( B_{\alpha }\right) \) for a (n, n)-matrix \(B_{\alpha }\) and if \(b_{\alpha }=F_{B_{\alpha }}(1)\left( d_{\alpha }\right) \) for a vector \(d_{\alpha }\in \mathbb {R}^n\) then the polygon \(x_j\) lies on the smooth curve

$$\begin{aligned} c(t)=v+ F_{B_{\alpha }}(t)\left( B_{\alpha }v+d_{\alpha }\right) \end{aligned}$$

i.e. \(x_j=c(j)\) for all \(j \in \mathbb {Z}.\)

Proof

(a) By Eq. (1) we have

$$\begin{aligned} (1-\alpha ) x_j +\alpha x_{j+1}=A x_j+b \end{aligned}$$

for all \(j \in \mathbb {Z}.\) Hence the polygon is given by \(x_0=v\) and the recursion formulae

$$\begin{aligned} x_{j+1}=A_{\alpha }(x_j)+b_{\alpha }\,;\, x_{j}=A_{\alpha }^{-1} \left( x_{j+1}-b_{\alpha }\right) . \end{aligned}$$

for all \(j \in \mathbb {Z}.\) Then Eqs. (11) and (12) follow.

(b) For \(A_{\alpha }=\exp B_{\alpha }; b_{\alpha }=F_{B_{\alpha }}(d_{\alpha })\) we obtain from Eq. (6) for all \(j \in \mathbb {Z}:\) \(A_{\alpha }-\mathbb {1}=B_{\alpha }F_{B_{\alpha }}(1)\) and \(A_{\alpha }^j-\mathbb {1}=B_{\alpha }F_{B_{\alpha }}(j).\) Hence for \(j>0:\)

$$\begin{aligned} x_j= & {} v+ \left( A_{\alpha }^j-\mathbb {1}\right) \left( v+ \left( A_{\alpha }-\mathbb {1}\right) ^{-1} b_{\alpha } \right) \\= & {} v+B_{\alpha } F_{B_{\alpha }}(j) \left( v+\left( B_{\alpha } F_{B_{\alpha }}(1) \right) ^{-1} (b_{\alpha }) \right) \\= & {} v+F_{B_{\alpha }}(j) \left( B_{\alpha } v+d_{\alpha } \right) =c(j). \end{aligned}$$

The functional Eq. (7) for \(F_B(t)\) implies \(0=F_B(0)=F_B(-1+1)=F_B(-1)+\exp (-B)F_B(1),\) hence

$$\begin{aligned} F_B(-1)=-\exp (-B)F_B(1)\,;\, F_B(-1)^{-1}=-\exp (B)F_B(1)^{-1}. \end{aligned}$$

Note that the matrices \(B, F_B(t), F_B(t)^{-1}\) commute. With this identity we obtain for \(j<0:\)

$$\begin{aligned} x_j= & {} v+ \left( A_{\alpha }^j-\mathbb {1}\right) \left( v- \left( A_{\alpha }^{-1}-\mathbb {1}\right) ^{-1} \left( A_{\alpha }^{-1} b_{\alpha } \right) \right) \\= & {} v+B_{\alpha } F_{B_{\alpha }}(j) \left( v-\left( B_{\alpha } F_{B_{\alpha }}(-1) \right) ^{-1} \exp (-B_{\alpha })(b_{\alpha }) \right) \\= & {} v+B_{\alpha } F_{B_{\alpha }}(j) \left( v- F_{B_{\alpha }}(-1)^{-1} B_{\alpha }^{-1} \exp (-B_{\alpha }) F_{B_{\alpha }}(1)(d_{\alpha }) \right) \\= & {} v+F_{B_{\alpha }}(j) \left( B_{\alpha } v+d_{\alpha } \right) =c(j). \end{aligned}$$

\(\square \)

Remark 2

(a) Using the identification Eq. (4) we can write

$$\begin{aligned} \left( \begin{array}{c} x_{j+1} \\ \hline 1 \end{array} \right) = \left( \begin{array}{c|c} A_{\alpha }&{} b_{\alpha }\\ \hline 0&{}1 \end{array} \right) \left( \begin{array}{c} x_j\\ \hline 1 \end{array} \right) ; \left( \begin{array}{c} x_{j} \\ \hline 1 \end{array} \right) = \left( \begin{array}{c|c} A_{\alpha }&{} b_{\alpha }\\ \hline 0&{}1 \end{array} \right) ^j \left( \begin{array}{c} v\\ \hline 1 \end{array} \right) \end{aligned}$$
(13)

for all \(j\in \mathbb {Z}.\)

(b) If \(A_{\alpha }=\exp \left( B_{\alpha }\right) \) for a (n, n)-matrix \(B_{\alpha }\) and if \(b_{\alpha }=F_{B_{\alpha }}(1)\left( d_{\alpha }\right) \) for a vector \(d_{\alpha }\in \mathbb {R}^n\) then we obtain from Eq. (10):

$$\begin{aligned} \left( \begin{array}{c} c(t)\\ \hline 1 \end{array} \right)= & {} \exp \left( \left( \begin{array}{c|c} B_{\alpha }&{} d_{\alpha }\\ \hline 0&{}0 \end{array} \right) t \right) \left( \begin{array}{c} v \\ \hline 1 \end{array} \right) = \left( \begin{array}{c|c} \exp (B_{\alpha }t)&{} F_{B_{\alpha }}(t)(d_{\alpha })\\ \hline 0&{}1 \end{array} \right) \left( \begin{array}{c} v \\ \hline 1 \end{array} \right) \\= & {} \left( \begin{array}{c} \exp (B_{\alpha }t)(v)+ F_{B_{\alpha }}(t)(d_{\alpha }) \\ \hline 1 \end{array} \right) =\left( \begin{array}{c} v+F_{B_{\alpha }}(t) \left( B_{\alpha }v+d_{\alpha }\right) \\ \hline 1 \end{array} \right) \end{aligned}$$

Hence \(t \in \mathbb {R}\longmapsto c(t)\in \mathbb {R}^n\) is the orbit of a one-parameter subgroup of the affine group applied to the vector v.

4 Smooth curves invariant under \(M_{\alpha }\)

For a smooth curve \(c: \mathbb {R}\longrightarrow \mathbb {R}^n\) and a parameter \(\alpha \in (0,1)\) we define the one-parameter family \(\tilde{c}_s:\mathbb {R}\longrightarrow \mathbb {R}^n, s \in \mathbb {R}\) by Eq. (2). And we call a smooth curve \(c: \mathbb {R}\longrightarrow \mathbb {R}^n\) a soliton of the mapping \(M_{\alpha }\) (resp. affinely invariant under \(M_{\alpha }\)) if there is \(\epsilon >0\) and a smooth map \( \in (-\epsilon ,\epsilon ) \longrightarrow (A,b) \in \mathrm{Aff}(n)\) such that

$$\begin{aligned} \tilde{c}_s(t)= (1-\alpha )c(t)+\alpha c(t+s)= A(s)(c(t))+b(s). \end{aligned}$$
(14)

Then we obtain as an analogue of [9, Thm.1]:

Theorem 2

Let \(c:\mathbb {R}\longrightarrow \mathbb {R}^n\) be a soliton of the mapping \(M_{\alpha }\) satisfying Eq. (14). Assume in addition that for some \(t_0 \in \mathbb {R}\) the vectors \(\dot{c}(t_0),\ddot{c}(t_0), \ldots ,c^{(n)}(t_0)\) are linearly independent.

Then the curve c is the unique solution of the differential equation

$$\begin{aligned} \dot{c}(t)=Bc(t)+d \end{aligned}$$

for \(B=\alpha ^{-1}A'(0), d=\alpha ^{-1}b'(0)\) with initial condition \(v=c(0).\)

And \(A(s)=(1-\alpha )\mathbb {1}+ \alpha \exp (Bs), b(s)=\alpha F_B(s)(d).\)

Hence the curve c(t) is the orbit of a one-parameter subgroup

$$\begin{aligned} t \in \mathbb {R}\longmapsto B(t):=\exp \left( \left( \begin{array}{c|c} B&{} d\\ \hline 0&{}0 \end{array} \right) t \right) =\left( \exp (Bt), F_B(t)(d)\right) \in \mathrm{Aff}(n)\end{aligned}$$

of the affine group, i.e.

$$\begin{aligned} c(t)=B(t)\left( \begin{array}{c} v \\ \hline 1 \end{array}\right) =v+F_B(t)\left( Bv+d\right) \,, \end{aligned}$$

cf. Remark 1.

Remark 3

For an affine map \((A,b)\in \text {Gl}(n),b\in \mathbb {R}^n\) the linear isomorphism A is called the linear part. For \(n=2\) we discuss the possible normal forms of \(A \in \text {Gl}(2)\) resp. the normal forms of the one-parameter subgroup \(\exp (tB)\) and of the one-parameter family \(A(s)= (1-\alpha )+\mathbb {1}+\exp (Bs)\) introduced in Theorem 2. This will be used in Sect. 5.

  1. 1.

    \(A=\begin{pmatrix} \lambda &{}\quad 0\\ 0&{}\quad \mu \end{pmatrix}\) for \(\lambda ,\mu \in \mathbb {R}-\{0\},\) i.e. A is diagonalizable (over \(\mathbb {R}\)), then A is called scaling, for \(\lambda =\mu \) it is called homothety. For an endomorphism B which is diagonalizable over \(\mathbb {R}\) the one-parameter subgroup \(B(t)=\exp (Bt)\) as well as the one-parameter family \(A(s)=(1-\alpha )\mathbb {1}+\alpha \exp (Bs)\) consists of scalings.

  2. 2.

    \(A=\begin{pmatrix} a&{}\quad -b\\ b&{}\quad a \end{pmatrix}\) for \(a,b\in \mathbb {R}, b\not =0,\) i.e. A has no real eigenvalues. Then A is called a similarity, i.e. a composition of a rotation and a homothety. For an endomorphism B with no real eigenvalues the one-parameter subgroup \(B(t)=\exp (Bt), t\not =0\) as well as the one-parameter family \(A(s)=(1-\alpha )\mathbb {1}+\alpha \exp (Bs), s\not =0\) consist of affine mappings without real eigenvalues, i.e. compositions of non-trivial rotations and homotheties.

  3. 3.

    \(A=\begin{pmatrix} 1&{}\quad 1\\ 0 &{}\quad 1 \end{pmatrix}\) is called shear transformation. Hence the matrix A has only one eigenvalue 1 and is not diagonalizable. If B is of the form \(B=\begin{pmatrix} 0&{}\quad 1\\ 0&{}\quad 0 \end{pmatrix},\) i.e. B is nilpotent, then the one-parameter subgroup \(B(t)=\exp (Bt), t\not =0\) as well as the one-parameter family \(A(s)=(1-\alpha )\mathbb {1}+\alpha \exp (Bs), s\not =0\) consist of shear transformations.

  4. 4.

    \(A=\begin{pmatrix} \lambda &{}\quad 1 \\ 0 &{}\quad \lambda \end{pmatrix}\) with \(\lambda \in \mathbb {R}-\{0,1\}.\) Then A is invertible with only one eigenvalue \(\lambda \not =1\) and not diagonalizable. This linear map is a composition of a homothety and a shear transformation. The one-parameter subgroup \(B(t)=\exp (Bt), t\not =0\) as well as the one-parameter family \(A(s)=(1-\alpha )\mathbb {1}+\alpha \exp (Bs), s\not =0\) consist of linear mappings with only one eigenvalue different from 1 which are not diagonalizable. Hence they are compositions of non-trivial homotheties and shear transformations, too.

We use the following convention: For a one-parameter family \(s \mapsto c_s\) of curves or a one-parameter family \(s \mapsto A(s), s \mapsto b(s)\) of affine maps we denote the differentiation with respect to the parameter s by \('.\) On the other hand we use for the differentiation with respect to the curve parameter t of the curves \(t \mapsto c(t), t \mapsto c_s(t)\) the notation \(\dot{c}, \dot{c_s}.\)

Proof

The proof is similar to the Proof of Theorem [9, Thm.1]: Let

$$\begin{aligned} c_{s}(t)=A(s)c(t)+b(s)= (1-\alpha ) c(t)+\alpha c(t+s). \end{aligned}$$
(15)

For \(s=0\) we obtain \( c(t)=c_{0}(t)=A(0)c(t)+b(0) \) for all \(t \in \mathbb {R},\) resp. \( \left( A(0)-\mathbb {1}\right) (c(t))=-b(0) \) for all t. We conclude that

$$\begin{aligned} \left( A(0)-\mathbb {1}\right) \left( c^{(k)}(t)\right) =0 \end{aligned}$$
(16)

for all \(k\ge 1.\) Since for some \(t_0\) the vectors \(\dot{c}(t_0),\ddot{c}(t_0),\ldots ,c^{(n)}(t_0)\) are linearly independent by assumption we conclude from Eq. (16): \(A(0)=\mathbb {1},b(0)=0.\) Eq. (15) implies for \(k\ge 1:\)

$$\begin{aligned} A(s)c^{(k)} (t)= (1-\alpha ) c^{(k)}(t)+\alpha c^{(k)}(t+s) \end{aligned}$$

and hence

$$\begin{aligned} A'(s)c^{(k)}(t)=\alpha c^{(k+1)}(t+s). \end{aligned}$$

We conclude from Eq. (15):

$$\begin{aligned} \frac{\partial c_{s}(t)}{\partial s}= & {} A'(s)c(t)+b'(s)\\= & {} \frac{\partial c_{s}(t)}{\partial t}- (1-\alpha ) \, \dot{c}(t)= \left( A(s)-(1-\alpha )\mathbb {1}\right) \dot{c}(t). \end{aligned}$$

Since \(A(0)=\mathbb {1}\) the endomorphisms \(A(s)+(\alpha -1)\mathbb {1}\) are isomorphisms for all \(s \in (0,\epsilon )\) for a sufficiently small \(\epsilon >0.\) Hence we obtain for \(s \in (0,\epsilon ):\)

$$\begin{aligned} \dot{c}(t)= \left( A(s)+(\alpha -1)\mathbb {1}\right) ^{-1}A'(s)c(t) + \left( A(s)+(\alpha -1)\mathbb {1}\right) ^{-1}b'(s). \end{aligned}$$
(17)

Differentiating with respect to s : 

$$\begin{aligned} \left( \left( A(s)+(\alpha -1)\mathbb {1}\right) ^{-1} A'(s)\right) '\left( c(t)\right) + \left( \left( A(s)+(\alpha -1)\mathbb {1}\right) ^{-1} b'(s)\right) ' =0 \end{aligned}$$

and differentiating with respect to t : 

$$\begin{aligned} \left( \left( A(s)+(\alpha -1)\mathbb {1}\right) ^{-1} A'(s)\right) 'c^{(k)}(t)=0; \quad k=1,2,\ldots ,n. \end{aligned}$$

By assumption the vectors \(\dot{c}(t_0),\ddot{c}(t_0),\ldots ,c^{(n)}(t_0)\) are linearly independent. Therefore we obtain \(\left( \left( A(s)+(\alpha -1)\mathbb {1}\right) ^{-1} A'(s)\right) '=0.\) Let \(B=\alpha ^{-1}A'(0) , d=\alpha ^{-1} b'(0).\) Then we conclude

$$\begin{aligned} A'(s)= \left( A(s)+(\alpha -1)\mathbb {1}\right) B;\quad b'(s)= \left( A(s)+(\alpha -1)\mathbb {1}\right) (d), \end{aligned}$$
(18)

We obtain from Eq. (17):

$$\begin{aligned} \dot{c}(t)=B c(t)+d. \end{aligned}$$

Equation (18) with \(A(0)=\mathbb {1}\) implies \(A(s)=(1-\alpha )\mathbb {1}+\alpha \exp (Bs).\) And we obtain \(b'(s)=\alpha \exp (Bs)(d)=\alpha F_B'(s)(d).\) Hence \(b(s)=\alpha F_B(s)(d)\) since \(b(0)=0.\) \(\square \)

As a consequence we obtain the following

Theorem 3

For a (n, n)-matrix B and a vector d any solution of the inhomogeneous linear differential equation \(\dot{c}(t)=B c(t)+d\) with constant coefficients is a soliton of the mapping \(M_{\alpha }.\) These solitons are orbits of a one-parameter subgroup of the affine group, i.e. they are of the form given in Eq. (9).

Proof

Any solution of the equation \(\dot{c}(t)=B c(t)+d\) has the form

$$\begin{aligned} c(t)=v+F_B(t)(Bv+d) \end{aligned}$$

with \(v=c(0),\) cf. Proposition 1. Then with \(A(s)=(1-\alpha )\mathbb {1}+\alpha \exp (Bs)\) and \(b(s)=\alpha F_B(s)(d)\) we conclude from Eqs. (6) and (7):

$$\begin{aligned} \tilde{c}_s(t)= & {} (1-\alpha )c(t)+\alpha c(t+s)\\= & {} v+(1-\alpha )F_B(t)(Bv+d) +\alpha F_B(t+s)(Bv+d)\\= & {} v+(1-\alpha )(c(t)-v)+ \alpha \left( F_B(s)+ \exp (Bs) F_B(t)\right) (Bv+d)\\= & {} (1-\alpha ) c(t)+\alpha \exp (Bs)(v)+ \alpha F_B(s)(d) + \alpha \exp (Bs)(c(t)-v)\\= & {} \left( \left( 1-\alpha \right) \mathbb {1}+\alpha \exp (Bs)\right) (c(t)) +\alpha F_B(s)(d) \\= & {} A(s)c(t)+b(s). \end{aligned}$$

Hence c is a soliton of the mapping \(M_{\alpha },\) cf. Eq. (14).\(\square \)

Remark 4

In [9] the authors consider the curve shortening process \(T: \mathcal {P}(\mathbb {R}^n)\longrightarrow \mathcal {P}(\mathbb {R}^n), T(x)_j=M^2(x)_{j-1}\) satisfying Eq. (3). Hence the midpoints mapping M is applied twice followed by an index shift. The smooth curves \(c=c(t)\) invariant under this process can be characterized as solutions of a inhomogeneous linear system of second order differential equations

$$\begin{aligned} \ddot{c}(t)=Bc(t)+d \end{aligned}$$

for a (n, n)-matrix B and a vector d,  cf. [9, Thm. 2]. These solutions can be reduced to a system of first order differential equations, cf. [9, Rem. 1]. Explicit formulas for these solutions can be written down in terms of power series in t whose coefficients are expressed in terms of powers of B. If \(B=B_1^2, d=B_1(d_1)\) for a (n, n)-matrix \(B_1\) and a vector \(d_1\in \mathbb {R}^n,\) then the orbits of one-parameter subgroups of the affine group \(\mathrm{Aff}(\mathbb {R}^n)\) acting on \(\mathbb {R}^n\) satisfying

$$\begin{aligned} \dot{c}(t)=B_1c(t)+d_1 \end{aligned}$$

are particular solutions. In the next section we will see that for \(n=2\) the solitons of the midpoints mapping have constant affine curvature. On the other hand not all solitons of the process T have constant affine curvature, cf. [9, Sec. 5].

5 Curves with constant affine curvature

The orbits of one-parameter subgroups of the affine group \(\mathrm{Aff}(2)\) acting on \(\mathbb {R}^2\) can also be characterized as curves of constant general-affine curvature parametrized proportional to general-affine arc length unless they are parametrizations of a parabola, an ellipse or a hyperbola. This will be discussed in this section. The one-parameter subgroups are determined by an endomorphism B and a vector d. We describe in Proposition 2 how the general-affine curvature can be expressed in terms of the matrix B.

For certain subgroups of the affine group \(\mathrm{Aff}(2)\) one can introduce a corresponding curvature and arc length. One should be aware that sometimes in the literature the curvature related to the equi-affine subgroup \(S\mathrm{Aff}(2)\) generated by the special linear group \(\mathrm{SL}(2)\) of linear maps of determinant one and the translations is also called affine curvature. We distinguish in the following between the equi-affine curvature \(k_{ea}\) and the general-affine curvature \(k_{ga}\) as well as between the equi-affine length parameter \(s_{ea}\) and the general-affine length parameter \(s_{ga}.\)

We recall the definition of the equi-affine and general-affine curvature of a smooth plane curve \(c:I \longrightarrow \mathbb {R}^2\) with \(\det (\dot{c}(t) \, \ddot{c}(t))= |\dot{c}(t) \, \ddot{c}(t)|\not =0\) for all \(t\in I.\)

By eventually changing the orientation of the curve we can assume \(|\dot{c}(t) \, \ddot{c}(t)|>0\) for all \(t\in I.\) A reference is the book by P. and A.Schirokow [10, §10] or the recent article by Kobayashi and Sasaki [7]. Then \(s_{ea}(t):= \int \left| \dot{c}(t) \ddot{c}(t)\right| ^{1/3}\,dt\) is called equi-affine arc length. We denote by \(t=t(s_{ea})\) the inverse function, then \(\tilde{c}(s_{ea})=c(t(s_{ea}))\) is the parametrization by equi-affine arc length. Then \(\tilde{c}'''(s_{ea}), \tilde{c}'(s_{ea})\) are linearly dependent and the equi-affine curvature \(k_{ea}(s_{ea})\) is defined by

$$\begin{aligned} \tilde{c}'''(s_{ea})=-k_{ea}(s_{ea})\, \tilde{c}'(s_{ea}) \end{aligned}$$

resp.

$$\begin{aligned} k_{ea}(s_{ea})=\left| \tilde{c}''(s_{ea})\tilde{c}'''(s_{ea})\right| . \end{aligned}$$

Assume that \(c=c(s_{ea}), s_{ea}\in I\) is a smooth curve parametrized by equi-affine arc length for which the sign \( \epsilon =\mathrm {sign}( k_{ea}(s_{ea}))\in \{0, \pm 1\}\) of the equi-affine curvature is constant. If \(\epsilon =0\) then the curve is up to an affine transformation a parabola \((t,t^2).\) Now assume \(\epsilon \not =0\) and let \(\mathrm{K}_{ea}=|k_{ea}|=\epsilon k_{ea}.\) Then the general-affine arc length \(s_{ga}=s_{ga}(s_{ea})\) is defined by

$$\begin{aligned} s_{ga}=\int \sqrt{\mathrm{K}_{ea}(s_{ea})}\,ds_{ea}. \end{aligned}$$
(19)

We call a curve \(c=c(t)\) parametrized proportional to general-affine arc length if \(t=\lambda _1s_{ga}+\lambda _2\) for \(\lambda _1,\lambda _2 \in \mathbb {R}\) with \(\lambda _1\not =0.\) The general-affine curvature \(k_{ga}=k_{ga}(s_{ea})\) is defined by

$$\begin{aligned} k_{ga}(s_{ea})=\mathrm {K}_{ea}'(s_{ea}) \mathrm {K}_{ea}(s_{ea})^{-3/2} = -2 \left( \mathrm {K}_{ea}^{-1/2} (s_{ea}) \right) '. \end{aligned}$$
(20)

If the general-affine curvature \(k_{ga}\) (up to sign) and the sign \(\epsilon \) is given with respect to the equi-affine arc length parametrization, then the equi-affine curvature \(k_{ea}=k_{ea}(s_{ea})\) is determined up to a constant by Eq. (20). Hence the curve is determined up to an affine transformation. The invariant \(k_{ga}\) already occurs in Blaschke’s book  [2, §10, p.24]. Curves of constant general-affine curvature are orbits of a one-parameter subgroup of the affine group. These curves already were discussed by Klein and Lie [6] under the name W-curves.

Proposition 2

For a non-zero matrix \(B \in M_{\mathbb {R}}(2,2)\) and vectors \(d, v\in \mathbb {R}^2\) where \(Bv+d\) is not an eigenvector of B let \(c:\mathbb {R}\longrightarrow \mathbb {R}^2\) be the solution of the differential equation \(c'(t)=B c(t)+d; c(0)=v,\) i.e. \(c(t)=v+F_B(t)(Bv+d)=\exp (tB)(v)+F_B(t)(d).\) We assume that \(\beta =\left| c'(0)c''(0)\right| ^{1/3}= \left| Bv+d B(Bv+d)\right| ^{1/3} >0.\) Define

$$\begin{aligned} k=k(B)=-2+9\det (B)/\mathrm{tr}^2(B); \quad K=K(B)=|k(B)|^{-1/2}. \end{aligned}$$
(21)

(a) If \(\mathrm{tr}(B)=0\) then the curve is parametrized proportional to equi-affine arc length and the equi-affine curvature is constant \(k_{ea}=\det (B)/\beta ^2\) and \( \epsilon =\mathrm{sign}(\det (B)),\) the curve is a parabola, if \(\epsilon =0,\) an ellipse, if \(\epsilon >0,\) or a hyperbola, if \(\epsilon <0,\) cf. Remark 5.

(b) If \(\mathrm{tr}(B)\not =0\) then we can choose a parametrization by equi-affine arc length \(s_{ea}\) such that the equi-affine curvature \(k_{ea}\) is given by:

$$\begin{aligned} k_{ea}(s_{ea})= k(B){s_{ea}}^{-2}. \end{aligned}$$
(22)

If \(k(B)=0\) the curve has vanishing equi-affine curvature and is a parametrization of a parabola, cf. the Remark 5. If \(k(B)\not =0\) then the general-affine curvature is defined and constant:

$$\begin{aligned} k_{ga}(s_{ea})=-2 K(B). \end{aligned}$$
(23)

Up to an additive constant the general-affine arc length parameter \(s_{ga}\) is given by:

$$\begin{aligned} s_{ga}=\frac{\mathrm{tr}B}{3 K(B)}\,t. \end{aligned}$$

Hence the curve c(t) is parametrized proportional to general-affine arc length.

Remark 5

It is well-known that the curves of constant equi-affine curvature are parabola, hyperbola or ellipses, cf.[2, §7]. For \(k_{ea}=0\) we obtain a parabola: \(c(t)=c(0)+c'(0)s_{ea}+c''(0)s_{ea}^2/2,\) for \(k_{ea}>0\) the ellipse \(c(s_{ea})=\left( a \cos (\sqrt{k_{ea}}s_{ea}), b \sin (\sqrt{k_{ea}}s_{ea})\right) \) with \(k_{ea}=(ab)^{-2/3}\) and for \(k_{ea}<0\) the hyperbola \(c(s_{ea})=\left( a \cosh (\sqrt{-k_{ea}}s_{ea}), b \sinh (\sqrt{-k_{ea}}s_{ea})\right) \) with \(k_{ea}=-(ab)^{-2/3}.\) Here \(a,b>0.\)

Proof

Following Proposition 1 we obtain as solution of the differential equation: \(c(t)=v+F_B(t)(Bv+d),\) hence for the derivatives: \(c^{(k)}(t)=B^{k-1} \exp (tB)(Bv+d).\) Then :

$$\begin{aligned} \left| \dot{c}(t) \, \ddot{c}(t)\right|= & {} \left| \exp (Bt)\right| \left| bv+d B(Bv+d)\right| \\= & {} \exp \left( \mathrm{tr}(B)t\right) \left| Bv+d B(Bv+d)\right| . \end{aligned}$$

Let \(\beta = \left( \left| Bv+d B(Bv+d) \right| \right) ^{1/3}\) and \(\tau =\mathrm{tr}(B).\) Then

$$\begin{aligned} |\dot{c}(t) \, \ddot{c}(t)|=\beta ^3\exp (\tau t). \end{aligned}$$

(a) If \(\tau =0\) then \(s_{ea}=t\beta ,\) i.e. the curve is parametrized proportional to equi-affine arc length and

$$\begin{aligned} \tilde{c}(s_{ea})=c(t(s_{ea}))=c(s_{ea}/\beta )= v+F_B(s_{ea}/\beta )(Bv+d). \end{aligned}$$

Then

$$\begin{aligned} \tilde{c}'(s_{ea})= & {} \beta ^{-1}\exp (Bs_{ea}/\beta )(Bv+d)\\ \tilde{c}'''(s_{ea})= & {} \beta ^{-3}B^2\exp (Bs_{ea}/\beta )(Bv+d) =-\det (B)\beta ^{-2}\tilde{c}'(s_{ea}). \end{aligned}$$

Here we use that by Cayley–Hamilton \(B^2-\tau B=B^2=-\det (B) \cdot \mathbb {1}.\) Hence we obtain \(k_{ea}(s_{ea})=\det (B)/\beta ^2\) and \(\epsilon = \mathrm{sign}(\det (B)).\) Then the claim follows from Remark 5.

(b) Assume \(\tau \not =0.\) Then the equi-affine arc length \(s_{ea}=s_{ea}(t)\) is given by

$$\begin{aligned} s_{ea}(t)=\beta \int \exp (\tau t/3)\,dt= \frac{3\beta }{\tau }\exp (\tau t/3). \end{aligned}$$
(24)

Hence the equi-affine arc length parametrization of c is given by

$$\begin{aligned} \tilde{c}(s_{ea})=v +F_B\left( \frac{3}{\tau } \ln \left( \frac{\tau }{3\beta }s_{ea}\right) \right) (Bv+d). \end{aligned}$$

Then we can express the derivatives:

$$\begin{aligned} \tilde{c}'(s_{ea})= & {} \frac{3}{\tau }\, \frac{1}{s_{ea}}\exp \left( \frac{3}{\tau } B\ln \left( \frac{\tau }{3\beta }s_{ea}\right) \right) (Bv+d)\\ \tilde{c}''(s_{ea})= & {} \left( \frac{3}{\tau }B-\mathbb {1}\right) \frac{1}{s_{ea}}\tilde{c}'(s_{ea})\\ \tilde{c}'''(s_{ea})= & {} \left( \frac{3}{\tau }B-\mathbb {1}\right) \left( \frac{3}{\tau }B-2\mathbb {1}\right) \frac{1}{s_{ea}^2}\tilde{c}'(s_{ea})\\= & {} -\left( \frac{9\det (B)}{\tau ^2}-2 \right) \frac{1}{s_{ea}^2}\tilde{c}'(s_{ea}). \end{aligned}$$

Here we used that by Cayley–Hamilton \(B^2-\tau B=-\det B\cdot \mathbb {1}.\) Hence we obtain for the equi-affine curvature

$$\begin{aligned} k_{ea}(s_{ea})=\frac{k(B)}{s_{ea}^2}. \end{aligned}$$
(25)

Then \(\epsilon =\mathrm{sign}\, k(B)\) and for \(k(B)\not =0\) we obtain from Eqs. (20) and (25):

$$\begin{aligned} k_{ga}(s_{ea})=- \frac{2 }{K(B)}. \end{aligned}$$

And for the general-affine arc length we obtain

$$\begin{aligned} s_{ga}= \ln (|s_{ea}|)/K(B) \,, \end{aligned}$$

resp. up to an additive constant:

$$\begin{aligned} s_{ga}= \frac{\tau t}{3 K(B)} \end{aligned}$$

using Eq. (24).

The parametrization by general-affine arc length is given by

$$\begin{aligned} c^*(s_{ga})=v+ F_B\left( 3 K(B) s_{ga}/\tau \right) (Bv+d). \end{aligned}$$

\(\square \)

Example 1

Depending on the real Jordan normal forms of the endomorphism B we investigate the solitons c(t),  their special and general affine curvature. The normal forms of the corresponding one-parameter subgroup \(B(t)=\exp (Bt)\) as well of the one-parameter family \(A(s)=(1-\alpha )\mathbb {1}+\exp (Bs)\) follow from Remark 3. Since \(c(\mu t)=\exp (\mu B t)\) the multiplication of B with a non-zero real \(\mu \) corresponds to a linear reparametrization of the curve. If B has a non-zero real eigenvalue we can assume without loss of generality that it is 1 and in the case of a non-real eigenvalue we can assume that it has modulus 1.

  1. (a)

    Let \(B= \left( \begin{array}{cc} 1 &{} 0\\ 0 &{} \lambda \end{array} \right) , d=(0,0), c(0)=(1,1)\) and \(\lambda \not =0,1.\) Then \(\beta =(\lambda (1-\lambda ))^{1/3}\not =0, \mathrm{tr}B=1+\lambda \) and \(c(t)=\left( \exp ( t), \exp (\lambda t)\right) .\) Up to parametrization we have \(c(u)=\left( u, u^{\lambda }\right) .\)

    If \(\lambda =-1\) then c is a parametrization of a hyperbola, \(\mathrm{tr}B=0\) and \(k_{ea}=- 2^{-2/3},\) cf. Remark 5.

    If \(\lambda \not =-1\) we obtain for the equi-affine curvature with respect to a equi-affine parametrization \(s_{ea}\) from Eq. (22):

    $$\begin{aligned} k_{ea}(s_{ea})=\left( 9\frac{\det B}{\mathrm{tr}^2B}-2\right) \frac{1}{s_{ea}^2}= -\frac{(\lambda -2)( 2\lambda -1)}{ (\lambda +1)^2}\frac{1}{s_{ea}^2}. \end{aligned}$$

    For \(\lambda =1/2,2\) we obtain a parametrization of a parabola with vanishing equi-affine curvature, cf. Remark 5. Now we assume \(\lambda \not =1/2,2.\) Hence \(\epsilon =1\) if and only if \(1/2<\lambda <2.\) The affine curvature \(k_{ga}\) is constant:

    $$\begin{aligned} k_{ga}=- 2\,\frac{ |\lambda +1|}{ \sqrt{|(\lambda -2)(2\lambda -1)|} }\,, \end{aligned}$$

    cf. [7, Ex.2.14]. We have \(\epsilon =1\) if and only if \(1/2<\lambda <2,\) then \(k_{ga}\in (-\infty ,-4).\) And \(\epsilon =-1\) if and only if \(\lambda <1/2, \lambda \not =0\) or \(\lambda >2,\) then \(k_{ga}\in (-\infty ,-\sqrt{2})\cup (-\sqrt{2},0).\)

    Hence in this case the corresponding one-parameter subgroup

    $$\begin{aligned} B(t)= \begin{pmatrix} \exp (t)&{}\quad 0\\ 0&{}\quad \exp (\lambda t) \end{pmatrix} \end{aligned}$$

    as well as the one-parameter family

    $$\begin{aligned} A(s)=\begin{pmatrix} 1-\alpha +\alpha \exp (s)&{}\quad 0\\ 0&{}\quad 1-\alpha + \alpha \exp (\lambda s) \end{pmatrix} \end{aligned}$$

    consist of scalings.

  2. (b)

    \(B= \left( \begin{array}{cc} 0 &{} 0\\ 0 &{} 1 \end{array} \right) \) and \(d=(1,0).\) Then the solution of the Equation \(\dot{c}(t)=B c(t)+d\) with \(c(0)=(0,1)\) is of the form \(c(t)=(t,\exp (t)).\) Then we obtain \(\epsilon =-1\) and \(k_{ga}=-\sqrt{2}.\) The corresponding one-parameter subgroup B(t) as well as the one-parameter family A(s) consist of scalings, the affine transformation (A(s), b(s) is given by \((A(s),b(s))= \left( \begin{pmatrix} 1&{}0\\ 0&{}1-\alpha +\alpha \exp (s) \end{pmatrix}, \alpha \begin{pmatrix} s\\ 0 \end{pmatrix} \right) ,\) i.e. a composition of scalings and translations.

  3. (c)

    If \(B= \left( \begin{array}{cc} 1 &{} 1\\ 0 &{} 1 \end{array}\right) , d=(0,0), c(0)=(1,1)\) then \(c(t)=\left( (t+1)\exp ( t), \exp ( t)\right) \) i.e. up to an affine transformation and a reparametrization the curve is of the form \(c(u)=(u, u\ln (u)).\) Then \(\epsilon =1\) and \(k_{ga}=-4.\) The corresponding one-parameter subgroup B(t) as well as the one-parameter family A(s) consist of compositions of a homothety and a shear transformations;

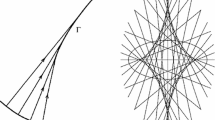
    $$\begin{aligned} B(t)=\exp (t) \cdot \begin{pmatrix} 1&{}\quad t\\ 0&{}\quad 1 \end{pmatrix}\,;\, A(s)= \begin{pmatrix} 1-\alpha +\alpha \exp (s)&{}\quad \alpha s \exp (s)\\ 0&{}\quad 1-\alpha +\alpha \exp (s) \end{pmatrix}, \end{aligned}$$

    cf. Fig. 2.

  4. (d)

    If \(B= \left( \begin{array}{rr} a &{} -b\\ b &{} a \end{array} \right) \) with \(b\not =0, a^2+b^2=1, d=0, c(0)=(1,0)\) then \(c(t)=\exp (at)\left( \cos (b t), \sin (b t)\right) \). For \(a=0,\) this is a circle with \(k_{ea}=1.\) Now we assume \(a\not =0:\) Then \(\epsilon =\mathrm{sign}(9 \det (B)-2 \mathrm{tr}^2(B))= \mathrm{sign}(a^2+9b^2)=1\) and we obtain for the general-affine curvature \(k_{ga}=-4 |a| /\sqrt{a^2+9b^2}=-4|a|/\sqrt{9-8a^2}\,,\) i.e. \(k_{ga}\in (-4,0).\) The corresponding one-parameter subgroup B(t) as well as the one-parameter family A(s) consist of similarities.

  5. (e)

    If \(B= \left( \begin{array}{cc} 0 &{} 1\\ 0 &{} 0 \end{array} \right) \) one can choose \(c(0)=(0,0),d=(0,1)\) and obtain \(c(t)=(t^2/2,t),\) i.e. a parabola. In this case the one parameter subgroup \(B(t)=\exp (tB)\) consists of shear transformations. The one-parameter family \((A(s),b(s))= \left( \begin{pmatrix} 1&{}\alpha s\\ 0&{}1 \end{pmatrix}, \alpha \begin{pmatrix} s^2/2\\ s \end{pmatrix} \right) \) consists of a composition of a shear transformation and a translation, cf. Fig. 1. For the affine curve shortening flow the parabola is a translational soliton. Therefore it is also called the affine analogue of the grim reaper, cf. [3, p. 192]. For the curve shortening process T defined by Eq. (3) the parabola is also a translational soliton, cf. [9, Sec. 5, Case (5)].

Fig. 2
figure 2

The soliton \(c(t)=( (t+1)\exp (t), \exp (t))\) with the family \(c_s(t)=A(s)c(t)\)

Full size image

Note that the parabola occurs twice, in Case (a) it occurs with the parametrization \(c(t)=(\exp (t),\exp (2t)),\) in Case (e) it occurs with a parametrization proportional to equi-affine arc length. Summarizing we obtain from Theorems 2 and 3 together with Proposition 2 resp. Example 1 the following

Theorem 4

Let \(c:\mathbb {R}\longrightarrow \mathbb {R}^2\) be a smooth curve for which \(\dot{c}(0),\ddot{c}(0)\) are linearly independent. Then c is a soliton of the mappings \(M_{\alpha },\alpha \in (0,1),\) in particular of the midpoints mapping \(M=M_{1/2},\) if it is a curve of constant equi-affine curvature parametrized proportional to equi-affine arc length, or a parabola with the parametrization \(c(t)=(\exp (t),\exp (2t))\) up to an affine transformation, or if it is a curve of constant general-affine curvature parametrized proportional to general-affine arc length.