1 Introduction

This note considers the evolution of a passive scalar f in a domain \(\Omega \subset \mathbb {R}^d\), \(d=2,3\), that is advected by an external velocity field \({\varvec{v}}:\Omega \rightarrow \mathbb {R}^d\) and is undergoing molecular diffusion. Our interest is to study quantitatively how the combined effect of diffusion and advection leads to faster time-scales of homogenization for f compared to the case when only diffusion is present. The passive scalar satisfies the advection–diffusion equation

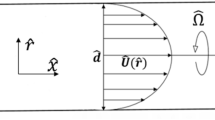
$$\begin{aligned} {\left\{ \begin{array}{ll}\partial _{t}f+{\varvec{v}}\cdot \nabla f=\nu \Delta f, \qquad {\varvec{x}}\in \Omega , \, t>0,\\ f|_{t=0}=f^{in}, \qquad \partial _{{\varvec{n}}} f|_{\partial \Omega }=0. \end{array}\right. } \end{aligned}$$
(1.1)

where \(\nu >0\) is the diffusion coefficient and \({\varvec{n}}\) is the outward unit normal to \({\partial }\Omega \). We are interested in the regime where \(\nu \ll 1 \), in which dissipative effects are observed on large time-scales of order \(O(\nu ^{-1})\). Since the average over the domain is conserved, we always assume that . The domain \(\Omega \) will either be a disc of radius \(R>0\), denoted by D, or the infinite pipe \(D\times \mathbb {R}\), and the velocity field is respectively

$$\begin{aligned} {\varvec{v}}= rv(r) \hat{{{\textsf{e}}}}_{\theta }, \quad \text {in } D,\qquad {\varvec{v}}= v(r)\hat{{{\textsf{e}}}}_{z}\quad \text {in } D\times \mathbb {R}. \end{aligned}$$
(1.2)

Here \(\hat{{{\textsf{e}}}}_{\theta }\) and \(\hat{{{\textsf{e}}}}_{z}\) are the unit vectors in the angular direction in D and in the vertical direction in \(D\times \mathbb {R}\), respectively. This situation and similar have been recently studied in [6,7,8], in analogy with the case of passive scalars advected by shear flows [1, 3].

The purpose of this short note is twofold: on the one hand, we identify precise conditions on the velocity field in the pipe setting that guarantee the enhanced dissipation [5] and Taylor dispersion [2, 10, 11] mechanisms. On the other hand, we derive a dissipation enhancement result in the disc for a general class of radial velocity fields. In particular, we will assume the following for the profile v(r) of the velocity field in (1.2).

Assumption 1.1

The first m derivatives of \(v:[0,R]\rightarrow \mathbb {R}\) do not vanish simultaneously; that is,

$$\begin{aligned} \sum _{n=1}^m|{v^{(n)}(r)}|\ne 0 \end{aligned}$$

for every \(0\le r\le R\).

We now state our main results, considering differently the pipe and the disc cases.

1.1 Pipe Parallel Flows

When \(\Omega =D\times \mathbb {R}\), the Eq. (1.1) can be written in cylindrical coordinates as

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \partial _{t}f+v(r)\partial _{z}f = \nu \left( \frac{1}{r}\partial _{r}(r\partial _{r}) + \frac{1}{r}\partial _{\theta }^2 + \partial _{z}^2 \right) f,&{}(r,\theta ,z)\in [0,R]\times \mathbb {T}\times \mathbb {R}, \\ f\vert _{t=0}=f^{in}, \qquad \partial _{{\varvec{n}}} f|_{\partial \Omega }=0. \end{array}\right. } \end{aligned}$$
(1.3)

Taking the partial Fourier transform along the axial coordinate z on both sides of the equation, we see then that for each \(k\in \mathbb {R}\) the Fourier component

$$\begin{aligned} \hat{f}_k(t,r,\theta )=\int _\mathbb {R}f(t,r,\theta ,z)\textrm{e}^{-ikz}\,{}\textrm{d}z \end{aligned}$$

satisfies the equation

$$\begin{aligned} \partial _{t}\hat{f}_k+ikv(r)\hat{f}_k = \nu \big ( \Delta _{r,\theta }- k^2 \big ) \hat{f}_k, \end{aligned}$$
(1.4)

where we denote

$$\begin{aligned} \Delta _{r,\theta }:=\frac{1}{r}\partial _{r}(r\partial _{r}) + \frac{1}{r^2}\partial _{\theta }^2. \end{aligned}$$
(1.5)

In particular, each Fourier mode \(\hat{f}_k\) evolves independently from all the others, so in the following, it suffices to consider the Eq. (1.4) for a fixed parameter k. A further reduction can be made by considering the function

$$\begin{aligned} g_k=\textrm{e}^{\nu k^2t}\hat{f}_k \end{aligned}$$

that satisfies

$$\begin{aligned} \partial _{t}g_k+ikv(r)g_k=\nu \Delta _{r,\theta }g_k. \end{aligned}$$
(1.6)

Notice that \(g_k\) already incorporates the diffusion along the channel. Our first main result is the following.

Theorem 1

Let \(v:[0,R]\rightarrow \mathbb {R}\) satisfy Assumption 1.1 and let \(k\ne 0\). Then, there exist constants \(c_1,C_1>0\), independent of \(\nu ,k\), such that for all initial data \(g_k^{in}\in L^2(D)\) the solution to (1.6) satisfies

$$\begin{aligned} \Vert {g_k(t)} \Vert _{L^2(D)}\le C_1 \text {e}^{-c_1{\Lambda _{\nu ,k}}t} \Vert {g^{in}_k} \Vert _{L^2(D)} \quad \text{ where }\quad \Lambda _{\nu ,k}= {\left\{ \begin{array}{ll} \nu ^{\frac{m}{m+2}}|{k}|^{\frac{2}{m+2}},&{}{} \text{ if }\ 0<\nu \le |{k}|,\\ \frac{k^2}{\nu },&{}{} \text{ if }\ 0<|{k}|\le {\nu }, \end{array}\right. } \end{aligned}$$
(1.7)

for every \(t\ge 0\). For the solution to (1.4) with initial data \(g_k^{in}=\hat{f}^{in}_k\), we have the estimate

$$\begin{aligned} \Vert \hat{f}_k(t)\Vert _{L^{2}(D)}\le C_1 \textrm{e}^{-(\nu k^2+c_1{\Lambda _{\nu ,k}})t}\Vert \hat{f}_k^{in}\Vert _{L^{2}(D)}, \end{aligned}$$

for every \(t\ge 0\).

The bounds in the theorem above are analogous to the ones obtained in [7] for multi-dimensional shear flows. In fact, they also proved the same result as in Theorem 1 for the velocity field \(v(r)=1-r^m\) in the disc of radius 1. However, a general condition analogous to that required in Assumption 1.1 was not identified. The proof of Theorem 1, given in Sect. 2, is inspired by the arguments in [7]. In particular, we obtain (1.7) as a consequence of a pseudospectral lower bound and the application of a result of Wei [12]*Theorem 1.3, see also Theorem 3 below.

Having at hand the k by k estimate (1.7), we are also able to quantify precisely the time-decay for the solution to the original problem (1.3).

Theorem 2

Let \(f^{in}\in L^1_zL^2_{r,\theta }\), and let \(v:[0,R]\rightarrow \mathbb {R}\) satisfy Assumption 1.1. Then, there exist constants \(c_2,C_2>0\), independent of \(\nu \), such that the solution to (1.3) satisfies

$$\begin{aligned} \Vert {f(t)} \Vert _{L^{\infty }_zL^{2}_{r,\theta }} \le C_2 \left( \sqrt{\frac{\nu }{t}} + \frac{\textrm{e}^{- c_2\nu t}}{(\nu ^{\frac{m}{m+2}} t)^{\frac{m+2}{2}}} \right) \Vert {f^{in}} \Vert _{L^{1}_zL^{2}_{r,\theta }}. \end{aligned}$$
(1.8)

for every \(t\ge 0\).

With (1.8) we have a precise quantification of the Taylor dispersion mechanism for the problem at hand, see also [4] where these types of bounds were obtained in another context. The factor \(\sqrt{\nu /t}\) is analogous to the standard heat equation with diffusivity coefficient \(\nu ^{-1}\) and it is related to low frequencies. On the other hand, the presence of the advection allows us to prove the algebraic decay on a time-scale \(O(\nu ^{-\frac{m}{m+2}})\), which is related to the enhanced dissipation mechanism.

The choice of the norms on which to quantify the decay is rather natural from the available k by k bounds. From a physical point of view, the flow is stretching the concentration towards spatial infinity in the z-direction. Combining this with enough integrability in z, the stretching generated by the flow makes the concentration intersect smaller sets in the discs orthogonal to z, so that a decay can be effectively quantified even if the diffusion is still not efficient on the time-scale under consideration.

1.2 Circular Flows in a Disc

When we consider the Eq. (1.1) with \(\Omega =D\) and \({\varvec{v}}=rv(r)\hat{{{\textsf{e}}}}_\theta \), the problem we have at hand is

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _{t}f+v(r)\partial _{\theta }f=\nu \Delta _{r,\theta }f, \qquad (r,\theta )\in [0,R]\times \mathbb {T},\\ f\vert _{t=0}=f^{in}, \qquad \partial _{{\varvec{n}}}f|_{\partial \Omega }=0, \end{array}\right. } \end{aligned}$$
(1.9)

where we recall that \(\Delta _{r,\theta }\) is defined in (1.5). If we now take a partial Fourier transform in the angular direction, namely

$$\begin{aligned} \hat{f}_{\ell }=\frac{1}{2\pi }\int _\mathbb {T}f(t,r,\theta )\textrm{e}^{-i\ell \theta }\,{}\textrm{d}\theta \end{aligned}$$

the Fourier coefficients \(\hat{f}_\ell \) of a solution f to Eq. (1.9) satisfy

$$\begin{aligned} \partial _{t}\hat{f}_\ell +i\ell v(r)\hat{f}_\ell =\nu \left( \frac{1}{r}\partial _r(r\partial r)-\frac{\ell ^2}{r^2}\right) \hat{f}_\ell \end{aligned}$$
(1.10)

for each \(\ell \in \mathbb {Z}\). The analogy with (1.6) is the following: if we take the angular Fourier transform in (1.6), we get

$$\begin{aligned} \partial _{t}\hat{g}_{k,\ell } + ik v(r)\hat{g}_{k,\ell } = \nu \left( \frac{1}{r}\partial _{r}(r\partial _{r}) -\frac{\ell ^2}{r^2}\right) \hat{g}_{k,\ell }. \end{aligned}$$
(1.11)

Hence, (1.10) is the Eq. (1.11) for the choice of parameters \(\ell =k\). We can therefore recover the bounds on \(\hat{f}_\ell \) from the ones we have for \(g_{\ell ,\ell }\) in Theorem 1. Observing that \(|\ell |\ge 1>\nu \), we obtain the following.

Corollary 1.2

Let \(v:[0,R]\rightarrow \mathbb {R}\) satisfy Assumption 1.1 and \(\ell \ne 0\). Then, there exist constants \(c_3,C_3>0\), independent of \(\nu ,\ell \), such that for all initial data \(\hat{f}_{\ell }^{in}\in L^2(0,R)\) the solution to (1.10) satisfy

$$\begin{aligned} \Vert \hat{f}_\ell (t)\Vert _{L^{2}(0,R)}\le C_3 \textrm{e}^{-c_3\nu ^{\frac{m}{m+2}}|{\ell }|^{\frac{2}{m+2}}t}\Vert \hat{f}^{in}_\ell \Vert _{L^{2}(0,R)}, \end{aligned}$$

for every \(t\ge 0\).

The bound in the physical space for f now it directly follows by Parseval’s identity. Namely, if

$$\begin{aligned} \int _{\mathbb {T}} f^{in}(r,\theta ) \,{}\textrm{d}\theta =0, \end{aligned}$$

we obtain that

$$\begin{aligned} \Vert f(t)\Vert _{L^{2}(D)}\le C_4 \textrm{e}^{-c_3\nu ^{\frac{m}{m+2}}t} \Vert {f^{in}}\Vert _{L^{2}(D)}, \end{aligned}$$

for a suitable constant \(C_4>0\). Therefore we capture the enhanced dissipation mechanism, telling us that the solution is decaying on a time-scale \(O(\nu ^{-\frac{m}{m+2}})\), which is always faster than \(O(\nu ^{-1})\). When the angular average, corresponding to \(\hat{f}_0\), is not zero, we would obtain that f is converging towards its angular average on the fast time-scale. Notice that \(\hat{f}_0\) is not conserved but it satisfies a standard 1d heat equation, therefore we cannot expect to have decay on a faster time-scale for it.

2 Semigroup Decay via Resolvent Estimates

The main tool we will employ in the proof of Theorem 1 is a quantitative version of the Gearhart–Prüss obtained by Wei in [12, Theorem 1.3] (see also [9]), which we reproduce below for the reader’s convenience.

Theorem 3

Let X be a Hilbert space and \(H:{\mathcal {D}}(H)\rightarrow X\) be an m-accretive operator on X. Then

$$\begin{aligned} \Vert {\textrm{e}^{-tH}} \Vert _{X\rightarrow X}\le \textrm{e}^{-t\Psi (H)+\pi /2} \end{aligned}$$
(2.1)

in which the quantity \(\Psi (H)\) is the pseudospectral abscissa of H, defined as

$$\begin{aligned} \Psi (H)=\inf \{\Vert {(H-z)f} \Vert _X\mid z\in i\mathbb {R}, f\in {\mathcal {D}}(H), \Vert {f} \Vert _X=1\}. \end{aligned}$$

We rewrite the Eq. (1.6) as

$$\begin{aligned} \partial _{t}g_k+Hg_k=0, \end{aligned}$$

where the operator \(H:{\mathcal {D}}(H)\rightarrow L^{2}(D)\) is defined as

$$\begin{aligned} H=-\nu \Delta _{r,\theta }+ikv(r), \qquad {\mathcal {D}}(H)= H^2(D) \end{aligned}$$
(2.2)

which is indeed m-accretive [8]. Thus, by the Lumer-Phillips theorem, the unique mild solution to Eq. (1.6) is given by a strongly continuous semigroup in \(L^{2}(D)\), namely, for the initial datum \(g_k^{in}\in L^{2}(D)\),

$$\begin{aligned} g_k(t)=\textrm{e}^{-tH}g_k^{in} \end{aligned}$$

solves Eq. (1.6). Moreover, by Theorem 3, the operator \(\textrm{e}^{-tH}\) satisfies the estimate (2.1). Hence, the proof of Theorem 1 is reduced in proving a pseudospectral bound for the operator H defined in (2.2).

2.1 Pseudospectral Bounds

Being k a fixed parameter from now on, let us write

$$\begin{aligned} H_\lambda =H-ik\lambda =-\nu \Delta _{r,\theta }+ik(v(r)-\lambda ). \end{aligned}$$
(2.3)

To prove Theorem 1, it suffices to show that

$$\begin{aligned} \Vert {H_\lambda g} \Vert _{L^{2}(D)}\ge c_1\Lambda _{\nu ,k}\Vert {g} \Vert _{L^{2}(D)}, \end{aligned}$$
(2.4)

for every \(g\in {\mathcal {D}}(H)\), where the constant \(c_1\) needs to be chosen uniformly in \(\lambda \in \mathbb {R}\).

In the computations that follow, we frequently omit the subscripts on the notation for norms and inner products in \(L^2(D)\), where no ambiguity can occur as to the relevant function space.

The strategy for proving (2.4) is as follows: we choose, for each \(\lambda \in \mathbb {R}\), a neighbourhood \(\mathcal {E}_\lambda \subseteq [0,R]\) of the level set \(E_\lambda =v^{-1}(\lambda )\), and split the domain of integration

$$\begin{aligned} \Vert {g} \Vert ^2= \int _{|{x}|\in [0,R]\setminus \mathcal {E}_\lambda }|{g}|^2\,{}\textrm{d}x + \int _{|{x}|\in \mathcal {E}_\lambda }|{g}|^2\,{}\textrm{d}x. \end{aligned}$$
(2.5)

in order to get upper bounds for each of the two integrals on the right-hand side. The motivation behind this is that, away from the annulus \(\{x\in D:|{x}|\in \mathcal {E}_\lambda \}\), the convection term \(v-\lambda \) in (2.3) is bounded away from zero, which allows us to recover a bound on the \(L^2\) norm in terms of \(H_{\lambda }\) thanks to the invertibility of \(v-\lambda \). On the other hand, in the integral over the region where \(|{x}|\in \mathcal {E}_\lambda \), we exploit some Poincaré-type inequality where we can gain smallness parameters from the measure of the set \(\mathcal {E}_\lambda \). That the latter set is indeed small is consequence of Assumption  1.1. We thus choose the sets \(\mathcal {E}_\lambda \) as follows.

Definition 2.1

Let \(m\in \mathbb {N}\) be the one in Assumption 1.1. Define

  • \(E_{\lambda ,\delta }\) to be the preimage under v of the interval \((\lambda -\delta ^m,\lambda +\delta ^m)\), that is, \(E_{\lambda ,\delta }=\{r\in [0,R]\mid |{v(r)-\lambda }|<\delta ^m\}\).

  • \(\mathcal {E}_{\lambda ,\delta }\) to be the neighbourhood of the set \(E_{\lambda ,\delta }\) with thickness \(\delta \), that is, \(\mathcal {E}_{\lambda ,\delta }=\{r\in [0,R]\mid \textrm{dist}(x, E_{\lambda ,\delta })<\delta \}\).

We collect in the next two propositions the bounds we have for the two integrals on the right-hand side of (2.5). Away from the level sets we have the following result.

Proposition 2.2

Let \(\mathcal {E}_{\lambda ,\delta }\) be the set defined in Definition 2.1. Then, for any \(g\in {\mathcal {D}}(H)\) the following holds true

$$\begin{aligned} \int _{|x|\in [0,R]\setminus \mathcal {E}_{\lambda ,\delta }}|g|^2 \,{}\textrm{d}x\le \frac{1}{4} \Vert g\Vert ^2+\left( \frac{1}{|k|\delta ^m}+\frac{\nu }{|k|^2\delta ^{2m+2}}\right) \Vert H_\lambda g\Vert \Vert g\Vert . \end{aligned}$$
(2.6)

Near the level sets, we can prove the result below.

Proposition 2.3

Let \(\mathcal {E}_{\lambda ,\delta }\) be the set defined in Definition 2.1. Then there exists a constant \(\tilde{C}>0\) such that, for any \(g\in {\mathcal {D}}(H)\), the following holds true

$$\begin{aligned} \int _{|x|\in \mathcal {E}_{\lambda ,\delta }}|g|^2 \,{}\textrm{d}x\le \frac{1}{2} \Vert g\Vert ^2+\frac{\tilde{C}\delta ^2}{\nu }\Vert H_\lambda g\Vert \Vert g\Vert . \end{aligned}$$
(2.7)

We postpone the proof of Propositions 2.2–2.3 to the end of this section. With the bounds (2.6) and (2.7) at hand, we are ready to present the proof of Theorem 1.

Proof of Theorem 1

Summing together (2.6) and (2.7) and rearranging, we have for all \(\lambda \in \mathbb {R}\) and \(\delta >0\) that

$$\begin{aligned} \Vert {g} \Vert ^2 \le 4 \left( \frac{1}{|{k}|\delta ^m} + \frac{\nu }{|{k}|^2\delta ^{2m+2}} + \frac{\tilde{C}\delta ^2}{\nu } \right) \Vert {H_\lambda g} \Vert \Vert {g} \Vert . \end{aligned}$$

We now make a choice of \(\delta \) depending on the parameters \(\nu \) and k:

  • If \(0<\nu \le |{k}|\), then the sharpest bound we can recover is by choosing \(\delta =\delta _0\nu ^{\frac{1}{m+2}}|{k}|^{-\frac{1}{m+2}}\), resulting in \(\Vert {g} \Vert ^2\le c_1\nu ^{-\frac{m}{m+2}}|{k}|^{-\frac{2}{m+2}} \Vert {H_\lambda g} \Vert \Vert {g} \Vert \) with the constant \(c_1=4(\delta _0^{-m}+\delta _0^{-(2m+2)} +\tilde{C}\delta _0^2 )\) where \(\delta _0\) is the one given in Lemma 2.5.

  • If instead \(0<|{k}|\le \nu \), observing that

    $$\begin{aligned} \frac{1}{|{k}|\delta ^m} + \frac{\nu }{|{k}|^2\delta ^{2m+2}} + \frac{\tilde{C}\delta ^2}{\nu } = \frac{\nu }{k^2}\Bigg ( \frac{|{k}|}{\nu }\frac{1}{\delta ^m} + \frac{1}{\delta ^{2m+2}} + \frac{k^2}{\nu ^2}\tilde{C}\delta ^2 \Bigg ). \end{aligned}$$

    Since \(|k|/\nu \le 1\), we choose \(\delta =\delta _0\), and find that \(\Vert {g} \Vert ^2\le c_1\frac{\nu }{k^2}\Vert {H_\lambda g} \Vert \Vert {g} \Vert \), with the same constant \(c_1\) as in the previous case.

Altogether we recover inequality (2.4), thanks to which we can apply Theorem 3 and conclude the proof of Theorem 1. \(\square \)

It thus remains to show the proofs of Proposition 2.2-2.3, which we present in the next two sections.

2.2 Bounds Away from Level Sets

In this section, we aim at proving Proposition 2.2. To this end, we follow the strategy in [7], and we introduce the function

$$\begin{aligned} \chi (r)=\varphi (\textrm{sign}(v(r)-\lambda )\textrm{dist}(r,E_{\lambda ,\delta })/\delta ), \end{aligned}$$

in which

$$\begin{aligned} \varphi (s)={\left\{ \begin{array}{ll} s,&{}\text {if} |{s}|\le 1,\\ \textrm{sign}(s),\quad &{}\text {otherwise.} \end{array}\right. } \end{aligned}$$

We are now ready to prove Proposition 2.2.

Proof of Proposition 2.2

By the definition of \(\chi \), we know that \(\chi (v-\lambda )\ge 0\). Moreover, in the set \(\mathcal {E}_{\lambda ,\delta }\) we have \(|v-\lambda |\ge \delta ^m\). Therefore

$$\begin{aligned} \int _{|{x}|\in [0,R]\setminus {\mathcal {E}_{\lambda ,\delta }}}|{g}|^2\,{}\textrm{d}x \le \int _\mathbb {T}\int _0^R\frac{(v(r)-\lambda )\chi (r)}{\delta ^m}|{g(r,\theta )}|^2 r\,{}\textrm{d}r\,{}\textrm{d}\theta = \frac{1}{\delta ^m} \langle (v-\lambda )\chi g,g\rangle _{}. \end{aligned}$$
(2.8)

To estimate the term \(\langle (v-\lambda )\chi g,g\rangle _{}\), observe that

$$\begin{aligned} \begin{aligned} \Vert {H_\lambda g} \Vert \Vert {g} \Vert&\ge \textrm{Im}{\langle H_\lambda g,\chi g\rangle _{}}\\&= \nu \textrm{Im}{\langle \Delta _{r,\theta }g,\chi g\rangle _{}} + \textrm{Im}{\langle ik(v-\lambda )g,\chi g\rangle _{}}\\&= -\nu \textrm{Im}{\langle \partial _rg,(\partial _r\chi )g\rangle _{}}+ k\langle (v-\lambda )g,\chi g\rangle _{}, \end{aligned} \end{aligned}$$
(2.9)

in which we recognise the relevant term on the final line. Noting that \(|{\partial _{r}\chi }|<\delta ^{-1}\), it then follows from (2.9) and the triangle inequality that

$$\begin{aligned} \langle (v-\lambda )\chi g,g\rangle _{} \le \frac{1}{|{k}|}\left( \Vert {H_\lambda g} \Vert \Vert {g} \Vert +\frac{\nu }{\delta } \Vert {\nabla g} \Vert \Vert {g} \Vert \right) . \end{aligned}$$
(2.10)

Observe also that

$$\begin{aligned} \nu \Vert {\nabla g} \Vert ^2=\textrm{Re}\langle H_\lambda g,g\rangle _{}\le \Vert {H_\lambda g} \Vert \Vert {g} \Vert . \end{aligned}$$
(2.11)

Thus, combining (2.8) with (2.10) and (2.11), we have

$$\begin{aligned} \begin{aligned} \int _{|{x}|\in [0,R]\setminus {\mathcal {E}_{\lambda ,\delta }}} |{g}|^2 \,{}\textrm{d}x&\le \frac{1}{\delta ^m} \langle (v-\lambda )\chi g,g\rangle _{}\\&\le \frac{1}{|{k}|\delta ^m} \left( \Vert {H_\lambda g} \Vert \Vert {g} \Vert +\frac{\nu }{\delta } \Vert {\nabla g} \Vert \Vert {g} \Vert \right) \\&\le \frac{1}{|{k}|\delta ^m} \left( \Vert {H_\lambda g} \Vert \Vert {g} \Vert +\frac{\nu ^\frac{1}{2}}{\delta } \Vert {H_\lambda g} \Vert ^\frac{1}{2}\Vert {g} \Vert ^{\frac{3}{2}} \right) \\&\le \left( \frac{1}{|{k}|\delta ^m} + \frac{\nu }{|{k}|^2\delta ^{2m+2}} \right) \Vert {H_\lambda g} \Vert \Vert {g} \Vert + \frac{1}{4} \Vert {g} \Vert ^2, \end{aligned} \end{aligned}$$

where we also applied the Young’s inequality on the product \(\nu ^\frac{1}{2}\delta ^{-(m+1)} \Vert {H_\lambda g} \Vert ^\frac{1}{2}\Vert {g} \Vert ^\frac{1}{2}\) on the penultimate line. \(\square \)

2.3 Bounds Near Level Sets

To prove Proposition 2.3, we use two results from [7]. The first of these is a Poincaré-type bound which appears in [7, Lemma B.1]:

Lemma 2.4

For all \(g\in H^1(D)\) and all \(R\ge R_2\ge R_1\ge 0\), we have

$$\begin{aligned} \int _{R_1\le |{x}|\le R_2}|g|^2\,{}\textrm{d}x \le 2(R_2-R_1)\Vert {g} \Vert \Vert {\nabla g} \Vert . \end{aligned}$$

The second result is that \(\mathcal {E}_{\lambda ,\delta }(v)\) is covered by a finite union of intervals whose total length is in \(O(\delta )\) as \(\delta \longrightarrow 0\).

Lemma 2.5

Let \(v\in C^{m}([0,R])\) satisfy Assumption ’1.1. Then there exist constants \(C_0,\delta _0>0\) and, for each \(\lambda \in \mathbb {R}\) and \(\delta >0\), a choice of a finite family \(\mathcal {V}^m_{\lambda ,\delta }\) of intervals such that

$$\begin{aligned} \mathcal {E}_{\lambda ,\delta }(v)\subseteq \bigcup \mathcal {V}^m_{\lambda ,\delta }\subseteq [0,R]\end{aligned}$$

and such that for all \(\lambda \in \mathbb {R}\) and \(0<\delta \le \delta _0\) we have that

$$\begin{aligned} \sum _{V\in \mathcal {V}^m_{\lambda ,\delta }}|{V}|<C_0\delta . \end{aligned}$$
(2.12)

Proof

This Lemma can be extracted from the proof of [7, Lemma 2.6], where such coverings by intervals are constructed in order to bound the measure \(|{\mathcal {E}_{\lambda ,\delta }}|\) of the level set neighbourhoods.

Observe first that it suffices to prove this result with \(E_{\lambda ,\delta }\) in place of \(\mathcal {E}_{\lambda ,\delta }\), since one may enlarge by \(\delta \) each interval in a covering of \(E_{\lambda ,\delta }\) to produce one for \(\mathcal {E}_{\lambda ,\delta }\) that still satisfies (2.12) but with a worse constant \(C_0\). Moreover, since \(E_{\lambda ,\delta }\) is empty for \(\lambda \) outside of a compact neighbourhood of \(v([0,R])\subseteq \mathbb {R}\), it suffices to be able to choose \(C_0\) locally constant near each \(\lambda _0\) in this neighbourhood.

Fix now \(\lambda _0\in \mathbb {R}\). The idea is to use the fact that \(E_{\lambda ,\delta }\) is a union of level sets \(E_\lambda \) with \(\lambda \) close to \(\lambda _0\):

$$\begin{aligned} E_{\lambda ,\delta }=\bigcup _{|{\lambda -\lambda _0}|<\delta ^m}E_\lambda \end{aligned}$$

and by the continuity of the function v, we expect the level set \(E_\lambda \) not too change to much when \(\lambda \) is perturbed away from \(\lambda _0\). Indeed, using Assumption 1.1, \(E_{\lambda _0}=v^{-1}(\lambda _0)\) consists of finitely many elements \(r_1,\dots ,r_{N_{\lambda _0}}\). Near each \(r_i\), the function v is approximated by its Taylor series

$$\begin{aligned} v(r)\approx \lambda +a_i(r-r_i)^{n_i} \quad \text {where}\quad a_i=\frac{v^{(n_1)}(r_i)}{n_i!}, \end{aligned}$$

in which \(n_i\in \mathbb {N}\) is the order of the lowest-order derivative of v which does not vanish at \(r_i\); again by Assumption 1.1 we have that \(1\le n_i\le m\). For small \(\delta >0\), the function v then approximately maps the interval \(\mathcal {B}_{\delta }(r_i)\subseteq [0,R]\) to the interval \(\mathcal {B}_{a_i\delta ^{n_i}}(\lambda )\subseteq \mathbb {R}\). Conversely, one is able to choose \(R_0>0\) such that

$$\begin{aligned} v^{-1}(\mathcal {B}_{\delta ^{m}}(\lambda ))\subseteq \bigcup _{r_i\in E_\lambda }\mathcal {B}_{R_0\delta }(r_i) \end{aligned}$$
(2.13)

for all sufficiently small \(\delta >0\). Once again we refer to the reference [7] for the details of this computation.

Choose now \(V_i=\mathcal {B}_{R_0\delta }(r_i)\) for \(i=1,\dots ,N_{\lambda _0}\). Then (2.13) is precisely the statement that the collection \(\{V_i\}_{i=1}^{N_{\lambda _0}}\) covers \(E_{\lambda ,\delta }\) for all \(\lambda \) in a small neighbourhood around near \(\lambda _0\). Finally, choosing \(C_0=2N_{\lambda _0}R_0\), we find that (2.12) is satisfied: \(\sum _{i=1}^{N_{\lambda _0}}|{V_i}|=2N_{\lambda _0}R_0\delta =C_0\delta \). \(\square \)

With the covering by intervals \(\mathcal {V}^m_{\lambda ,\delta }\) just obtained in Lemma 2.5, we are to prove Proposition 2.3.

Proof of Proposition 2.3

First, we observe that for any \(V\in \mathcal {V}^m_{\lambda ,\delta }\), thanks to Lemma 2.4 we have

$$\begin{aligned} \int _{|{x}|\in V}|{g}|^2\,{}\textrm{d}x\le 2|{V}|\Vert {g} \Vert \Vert {\nabla g} \Vert . \end{aligned}$$

Therefore,

$$\begin{aligned} \begin{aligned} \int _{|{x}|\in \mathcal {E}} |{g}|^2 \,{}\textrm{d}x&\le \sum _{V\in \mathcal {V}^m_{\lambda ,\delta }} \int _{|{x}|\in V}|{g}|^2\,{}\textrm{d}x \le \Vert {g} \Vert \Vert {\nabla g} \Vert \sum _{V\in \mathcal {V}^m_{\lambda ,\delta }} 2|{V}| \\&\le 2C_0\delta \Vert {g} \Vert \Vert {\nabla g} \Vert \le \frac{1}{2}\Vert {g} \Vert ^2 + 2{C_0}^2\delta ^2 \Vert {\nabla g} \Vert ^2, \end{aligned} \end{aligned}$$

where we have used Lemma 2.5, followed by Young’s inequality on the final line. Combining this with (2.11) we find that

$$\begin{aligned} \int _{|{x}|\in \mathcal {E}} |{g}|^2 \,{}\textrm{d}x \le \frac{1}{2}\Vert {g} \Vert ^2+ \frac{2C_0^2\delta ^2}{\nu }\Vert {H_\lambda g} \Vert \Vert {g} \Vert . \end{aligned}$$

3 Estimates in Physical Space

In this Section we prove Theorem 2, which gives a decay estimate on the \(L^{\infty }_zL^{2}_{r,\theta }\) norm of a solution to (1.3) when the initial datum belongs to \(L^{1}_zL^{2}_{r,\theta }\).

Proof of Theorem 2

Using that the Fourier transform is a continuous map between \(L^{1}\) and \(L^{\infty }\) together with Hölder’s inequality, thanks to Theorem 1 we have that

$$\begin{aligned} \begin{aligned} \Vert {f(t)} \Vert _{L^{\infty }_zL^{2}_{r,\theta }}&\lesssim \Vert \hat{f}(t)\Vert _{L^1_kL^2_{r,\theta }} \lesssim \int _\mathbb {R}\textrm{e}^{-c_1\Lambda _{\nu ,k}t}\Vert \hat{f}^{in}_k\Vert _{L^2_{r,\theta }}\,{}\textrm{d}k\\&\lesssim \Vert \hat{f}^{in}\Vert _{L^\infty _kL^2_{r,\theta }}\int _\mathbb {R}\textrm{e}^{-c_1\Lambda _{\nu ,k}t}\,{}\textrm{d}k\\&\lesssim \Vert {f^{in}} \Vert _{L^{1}_zL^{2}_{r,\theta }}\int _\mathbb {R}\textrm{e}^{-c_1\Lambda _{\nu ,k}t}\,{}\textrm{d}k. \end{aligned} \end{aligned}$$

Then, we control the integral above by splitting the domain of integration in two regions, namely \(|{k}|\le \nu \) and \(|k|>\nu \) which is where the definition of \(\Lambda _{\nu ,k}\) changes. In particular, we have

$$\begin{aligned} \int _\mathbb {R}\textrm{e}^{-c_1\Lambda _{\nu ,k}t}\,{}\textrm{d}k&=\int _{|{k}|\le \nu } \textrm{e}^{-c_1\nu ^{-1}k^2 t}\,{}\textrm{d}k+\int _{|{k}|>\nu } \textrm{e}^{-c_1\nu ^{\frac{m}{m+2}}|{k}|^{\frac{2}{m+2}} t}\,{}\textrm{d}k:=\mathcal {I}_{\le \nu }+\mathcal {I}_{>\nu }. \end{aligned}$$

For the low-frequency region, a change of variables shows that

$$\begin{aligned} \mathcal {I}_{\le \nu }= & {} \sqrt{\frac{\nu }{c_1 t}} \int _{|{\eta }|\le \sqrt{c_1\nu t}}\textrm{e}^{-\eta ^2}\,{}\textrm{d}\eta \nonumber \\{} & {} \lesssim \sqrt{\frac{\nu }{ t}}. \end{aligned}$$
(3.1)

For the second integral, since \(\nu ^{\frac{m}{m+2}}|{\nu }|^{\frac{2}{m+2}}=\nu \), we estimate as follows:

$$\begin{aligned} \begin{aligned} \mathcal {I}_{> \nu }&\le \textrm{e}^{-\frac{1}{2}c_1\nu t} \int _{|{k}|>\nu } \textrm{e}^{-\frac{1}{2}c_1\nu ^{\frac{m}{m+2}}|{k}|^{\frac{2}{m+2}}t}\,{}\textrm{d}k\\&= \textrm{e}^{-\frac{1}{2}c_1\nu t} \nu ^{-\frac{m}{2}} \left( \frac{1}{2} c_1 t\right) ^{-\frac{m+2}{2}} \int _{|{\eta }|>(\frac{1}{2}c_1\nu t)^{\frac{m+2}{2}}} \textrm{e}^{-\eta ^{\frac{2}{m+2}}}\,{}\textrm{d}\eta \\&\lesssim \frac{\textrm{e}^{-\frac{1}{2}c_1\nu t}}{(\nu ^{\frac{m}{m+2}} t)^{\frac{m+2}{2}}}, \end{aligned} \end{aligned}$$

which combined with (3.1) proves the desired result.