On the Bingham Flow in a Thin Y-Like Shaped Structure

Abstract

We consider the steady Bingham flow in a two-dimensional thin Y-like shaped structure, with no-slip boundary conditions and under the action of given external forces. After passage to the limit with respect to a small parameter related to the thickness of the domain, we obtain three uncoupled problems. Each of these problems describes an anisotropic flow, corresponding to a lower-dimensional “Bingham-like” constitutive law. These results are in accordance with the engineering models.

1 Introduction

We consider a steady Bingham flow in a two-dimensional thin Y-like shaped structure, with no-slip boundary conditions and under the action of given external forces.

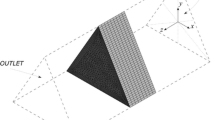
We take the following multi-structure $\Omega _n$ (see Fig. 1), where $h_n$ is a small positive parameter representing the order of the thickness of each branch, $\alpha \in \left[ 0,\frac{\pi }{2}\left[ \text {and }\beta \in \right] -\frac{\pi }{2},0\right]$ are two angles describing the deviation of the two oblique branches from the vertical direction, and $\frac{L^r}{\cos \alpha }$, $\frac{L^l}{\cos \beta }$, and $L^b$ are the main lengths of the three branches (from now on, the exponents r, l and b stand for right, left and below, respectively).

The Bingham fluid is a particular non-newtonian fluid, used as a model for viscoplastic materials as the volcanic lava, the mud for the oil extraction, some paints, etc. (for instance, see [6, 16, 17]). Its constitutive law is non linear and is characterized by the presence of a given threshold (see (2.3)). The fluid moves like a rigid body as long as a certain function of the stress tensor is below the threshold and obeys a non linear constitutive law beyond the threshold. In this perspective, also the blood can be modelized as a Bingham fluid in the first approximation, since it has a yield stress as the Bingham fluid, but at high shear stress it behaves as a pseudoplastic fluid. Thus, the Bingham fluid in our geometry can also modelize the microcirculation in blood vessels.

Fig. 1

The thin domain $\Omega _n$

According to [19], the steady flow of a Bingham fluid in $\Omega _n$, with no-slip boundary conditions, corresponds to the following variational inequality,

$$\begin{aligned} \left\{ \begin{array}{ll} \left( \text {u}_n,\text {p}_n\right) \in \left( H_0^1(\Omega _n)\right) ^2\times \left( L^2(\Omega _n)/\mathbf {\mathbb {R}}\right) , \quad \hbox {div} (\text {u}_n)=0\hbox { in }\Omega _n,\\ \displaystyle {\int _{\Omega _n} \left( h_n^2\mu D\text {u}_n D\left( \text {v}-\text {u}_n\right) + h_ng\vert D\text {v}\vert -h_ng\vert D\text {u}_n\vert \right) dX_1dx_2}\\ \displaystyle {\ge \int _{\Omega _n} \left( \text {f}_n \left( \text {v}-\text {u}_n\right) +\text {p}_n div \left( \text {v}-\text {u}_n \right) \right) dX_1dx_2 \quad \forall \text {v}\in \left( H_0^1(\Omega _n)\right) ^2,} \end{array} \right. \end{aligned}$$

(1.1)

where, $h_n^2 \mu$ and $h_n g$, with $\mu$ and g two positive constants, are the viscosity and the yield stress, respectively, $f_n$ is the given external force, and the unknown $(\text {u}_n ,\text {p}_n )$ represents the velocity and the pressure of the fluid.

Our aim is to study the asymptotic behavior of problem (1.1) as $h_n$ tends to zero. Indeed, the very small size of $h_n$ could not allow us to solve numerically this problem, since the construction of appropriate meshes could not be possible. Consequently, an asymptotic analysis of this problem is needed.

By the dimensional reduction method introduced in [15], we first rescale the problem (1.1) in a fixed domain, independent on $h_n$, by using the three different transformations given in (3.2) and we get problem (3.8). Then, assuming suitable convergence conditions on the external forces (see (3.9)), after passage to the limit we obtain three uncoupled problems (see Theorem 4.1). Each of these problems describes an anisotropic flow, corresponding to a lower-dimensional ”Bingham-like” constitutive law (see (8.3)). These results are in accordance with the engineering models. Indeed, for the one-dimensional ”Bingham-like” constitutive law used in engineering, one may refer, for instance, to [29]. In [29], first the authors give the one-dimensional ”Bingham-like” constitutive law (8.3), employed in order to modelize the Bingham flow in a two-dimensional domain with small thickness. Then, in a two-dimensional domain with small thickness they consider a Bingham flow with a two-viscosities constitutive law. Under some constraints on the viscosities, they perform a perturbation analysis of the two-dimensional model and thus they formally derive the previous given one-dimensional ”Bingham-like” constitutive law (8.3). In our case, starting by a two-dimensional Bingham flow stated in a thin domain of thickness $h_n$, considering a viscosity of the fluid of order $h_n^2$ and a yield stress of order $h_n$, we rigorously derive the one-dimensional ”Bingham-like” constitutive law (8.3), performing a full asymptotic analysis, by passing to the limit as $h_n$ tends to zero in the variational formulation (1.1) of the problem under consideration.

Let us point out that rescaling the problem from a thin oblique branch to a fixed one involves differential operators that are quite sophisticated and more difficult to handle than those obtained in [10,11,12]. This leads to further difficulties on a priori estimates for the velocity, but especially for the pressure. Indeed, unlike in [10,11,12], a priori estimates on the velocity imply that the two components $(u_1,u_2)$ of the limit velocity on each oblique branch are both non-zero and linked by a constraint of the type $u_1=c u_2$, where the real constant c only depends on the angle (see (5.8)). The latter property will guide the choice of suitable test functions for obtaining a priori estimates on the pressure, that will be only local, in the sense that they depend on the branch. This requires working with three different pressures. Consequently, for passing to the limit in each branch, we first get a local reformulation of our problem. Eventually, test functions satisfying the constraint $u_1=c u_2$ will be used for passing to the limit and for deducing the variational inequality satisfied by $u_2$ in each branch. As far as the limit force is concerned, only its projection on the axis of each branch is involved in the limit inequalities (see the first term in the right-hand side of (4.8), (4.9), (4.10), and Remark 4.2). The limit velocity in the vertical branch is classical by now. Indeed, as already observed in [10,11,12], the component in the transverse direction, i.e. $u_1$, is zero, while $u_2$ is the solution to problem (4.10). One of the novelties of this paper appears in the limit velocities in the two oblique branches. On each oblique branch, the velocity has two non-zero components and its direction coincides with the axis of the branch (see Remark 4.2).

Let us remark that the case corresponding to $\alpha = \frac{\pi }{2}$ and/or $\beta = - \frac{\pi }{2}$ is not included in our study, since in this particular case the initial domain $\Omega _n$ degenerates, at least one of the branches becoming a horizontal line. We refer [10] for the study of this problem in a T-structure, which is not a particular case of the present work.

Note that problem (1.1) becomes the system modeling the Stokes flow in a thin multi-structure when $g=0$. For such problems we refer to [7, 31]. For Navier-Stokes flow in a thin tube or thin layer we refer to [13, 30, 36], while for multi-structures we refer to [23, 32, 33].

As far as the study of Bingham flow in domains depending on small geometrical parameters is concerned, we recall that the first results for the Bingham flow in periodic domains are obtained in [28]. The justification of the convergence for these results is due to [8, 9]. In the recent paper [5], the authors present a model of Bingham flow in a thin periodic domain which contains an array of obstacles modelized as vertical cylinders. Up to our knowledge, the first convergence result on Bingham flow in thin periodic domains is due to [1], followed by [2]. We refer to [18] for Bingham flows in periodic domains of infinite length. We refer to [14] for Bingham flows in a thin domain with periodically oscillating boundary. For other models of non-newtonian fluid in thin multi-structures we refer to [34, 35].

For other problems in thin multi-structures we refer to [3, 4, 20,21,22, 24,25,26,27].

The paper is organized as follows. In Sect. 2 we introduce the domain $\Omega _n$, the physical properties of the Bingham fluid, and the variational inequality which modelizes the flow. In Section 3 the problem is rescaled on a fixed domain. Section 4 contains the main result of the paper, the convergence theorem. A priori estimates and convergence results for the velocity and the pressure are obtained in Sect. 5 and in Sect. 6, respectively. These last results will allow us to prove the convergence theorem in Sect. 7. The paper ends with some conclusions, in Sect. 8.

2 The Setting of the Problem

In what follows, a generic element of $\mathbb {R}^{2}$ is denoted by $(X_1,x_2)$ or $(x_1x_2)$.

Let $\alpha \in [0,\frac{\pi }{2}[$ and $\beta \in ]-\frac{\pi }{2},0]$, $L^r,L^l,L^b\in ]0,+\infty [$, for every $n \in \mathbb {N}$ let $h_n\in ]0,1[$ be a small parameter, and let $\Omega _n$ be the thin two-dimensional Y-like shaped domain defined by

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \Omega _n=\Omega ^r_n\cup \Omega ^l_n\cup \Omega ^b_n,\\ \displaystyle \Omega ^r_n=\left\{ (X_1,x_2)\in \mathbb {R}^2: \,\,0<x_2<L^r,\quad x_2\tan \alpha<X_1< x_2\tan \alpha +\frac{h_n}{2}\right\} ,\\ \displaystyle \Omega ^l_n=\left\{ (X_1,x_2)\in \mathbb {R}^2: \,\,0<x_2<L^l,\quad x_2\tan \beta -\frac{h_n}{2}<X_1< x_2\tan \beta \right\} ,\\ \displaystyle \Omega ^b_n=\left]-\frac{h_n}{2},\frac{h_n}{2}\right[\times ]-L^b,0] .\end{array}\right. \end{aligned}$$

(2.1)

In $\Omega _n$ we consider the non linear flow of a Bingham fluid. If $\text {u}_n=\left( \text {u}_{n1},\text {u}_{n2}\right)$ and $\text {p}_n$ denote its velocity and pressure, respectively, the corresponding stress tensor is defined by

$$\begin{aligned} \sigma _{ij}(\text {u}_n, \text {p}_n)= -\text {p}_n \delta _{ij}+ g h_n \frac{e_{ij}(\text {u}_n)}{\sqrt{e_{II}(\text {u}_n)}}+2 \mu h_n^2e_{ij}(\text {u}_n), \end{aligned}$$

(2.2)

where $\delta _{ij}$ is the Kronecker symbol, g is a strictly positive constant related to the yield stress of the fluid, $\mu$ is a strictly positive constant related to the viscosity of the fluid,

$$\begin{aligned} e(\text {u}_n) = \displaystyle \frac{1}{2} \left[ D(\text {u}_n) + D^T(\text {u}_n)\right] ,\quad e_{II}(\text {u}_{n}) =\dfrac{1}{2} {\displaystyle \sum \limits _{i,j=1}^{2}} e_{ij}(\text {u}_{n})e_{ij}(\text {u}_{n}), \end{aligned}$$

with $D(\text {u}_n) = \begin{pmatrix} \frac{\partial \text {u}_{n1}}{\partial X_1} &{} \frac{\partial \text {u}_{n1}}{\partial x_2}\\ \frac{\partial \text {u}_{n2}}{\partial X_1} &{} \frac{\partial \text {u}_{n2}}{\partial x_2} \end{pmatrix}$ and $D^T(\text {u}_n)$ the transposed of $D(\text {u}_n)$. Moreover, we set

$$\begin{aligned} \sigma _{ij}^{e}(\text {u}_n) =g h_n\frac{e_{ij}(\text {u}_n)}{\sqrt{e_{II}(\text {u}_n)}}+2\mu h_n^2 e_{ij}(\text {u}_n), \,\,\forall i,j\in \{1,2\};\quad \sigma _{II}(\text {u}_n) =\dfrac{1}{2} {\displaystyle \sum \limits _{i,j=1}^{2}} {\sigma }_{ij}^{e}(\text {u}_n){\sigma }_{ij}^{e}(\text {u}_n). \end{aligned}$$

We remark that (2.2), i.e., the constitutive law of the Bingham fluid, is valid only if $e_{II}(\text {u}_{n})\ne 0$. In [19] it is shown that this constitutive law is equivalent to the following one

$$\begin{aligned} \left\{ [Arrayl]\begin{array}{rcl} \sqrt{\sigma _{II}(\text {u}_n)}\le g h_n &{} \Leftrightarrow &{} e_{ij}(\text {u}_{n})=0,\\ \sqrt{\sigma _{II}(\text {u}_n)}> g h_n &{} \Leftrightarrow &{} e_{ij}(\text {u}_{n})=\dfrac{1}{2\mu h_n^2}\left( 1-\dfrac{g h_n }{\sqrt{\sigma _{II}(\text {u}_n)}}\right) {\sigma }_{ij}^{e}(\text {u}_n). \end{array} \right. \end{aligned}$$

(2.3)

We point out that this is a threshold law: as long as the shear stress $\displaystyle \sqrt{\sigma _{II}(\text {u}_n)}$ is below $g h_n$, the fluid behaves as a rigid solid. When the value of the shear stress $\displaystyle \sqrt{\sigma _{II}(\text {u}_n)}$ exceeds $g h_n$, then the fluid flows obeying a non linear law.

We also suppose that the fluid is incompressible, that is

$$\begin{aligned} {\text {div}}\text {u}_{n}= \frac{\partial \text {u}_{n1}}{\partial X_1} +\frac{\partial \text {u}_{n2}}{\partial x_2}= 0\,\,\,\,\text {in}\,\,\Omega _{n}. \end{aligned}$$

(2.4)

Moreover, we apply to the fluid a given external force $\text {f}_n=\left( \text {f}_{n1},\text {f}_{n2}\right)$ belonging to $\left( L^2 \left( \Omega _n\right) \right) ^2$, and then we have the following relations

$$\begin{aligned} \frac{\partial \sigma _{i1}}{\partial X_1} + \frac{\partial \sigma _{i2}}{\partial x_2}= \text {f}_{ni}\,\,\,\,\text {in}\,\,\Omega _{n},\quad i=1,2. \end{aligned}$$

(2.5)

Furthermore, we assume the no-slip condition to the boundary of the domain, which reads

$$\begin{aligned} \text {u}_n=0 \,\,\,\, \text {on} \,\, \partial \Omega _n. \end{aligned}$$

(2.6)

In [19] it is shown that the velocity $\text {u}_{n}$ satisfying (2.2), (2.4), (2.5) and (2.6) solves the following variational inequality

$$\begin{aligned} \left\{ \begin{array}{ll} \text {u}_n \in \left( H_0^1(\Omega _n)\right) ^2,\quad \hbox {div} (\text {u}_n)=0\hbox { in }\Omega _n,\\ \displaystyle {\int _{\Omega _n} \left( h_n^2\mu D\text {u}_n D\left( \text {v}-\text {u}_n\right) +h_ng\vert D\text {v}\vert -h_ng\vert D\text {u}_n\vert \right) dX_1dx_2}\\ \displaystyle {\ge \int _{\Omega _n} \text {f}_n \left( \text {v}-\text {u}_n\right) dX_1dx_2}\quad \forall \text {v}\in \left( H_0^1(\Omega _n)\right) ^2: \hbox {div} (\text {v}) =0\hbox { in }\Omega _n. \end{array} \right. \end{aligned}$$

(2.7)

For each n, this inequality admits a unique solution $\text {u}_n$. According to [19], problem (2.7) is equivalent to the following one

$$\begin{aligned} \left\{ \begin{array}{ll} \left( \text {u}_n,\text {p}_n\right) \in \left( H_0^1(\Omega _n)\right) ^2\times \left( L^2(\Omega _n)/\mathbf {\mathbb {R}}\right) , \quad \hbox {div} (\text {u}_n)=0\hbox { in }\Omega _n,\\ \displaystyle {\int _{\Omega _n} \left( h_n^2\mu D\text {u}_n D\left( \text {v}-\text {u}_n\right) + h_ng\vert D\text {v}\vert -h_ng\vert D\text {u}_n\vert \right) dX_1dx_2} \\ \displaystyle {\ge \int _{\Omega _n} \left( \text {f}_n \left( \text {v}-\text {u}_n\right) +\text {p}_n div \left( \text {v}-\text {u}_n \right) \right) dX_1dx_2 \quad \forall \text {v}\in \left( H_0^1(\Omega _n)\right) ^2.} \end{array} \right. \end{aligned}$$

(2.8)

which admits a solution $( \text {u}_n, \text {p}_n )$, such that $\text {u}_n$ is unique, but $\text {p}_n$ is not unique.

The aim of this paper is to study the asymptotic behavior, as n diverges, of problem (2.8), under suitable assumption on the given data $\left\{ \text {f}_n\right\} _{n \in \mathbb {N}}$ and on the assumption

$$\begin{aligned} \lim _{n } h_n= 0. \end{aligned}$$

(2.9)

We note that the pressure $\text {p}_n$ is not unique. If $\text {p}_n$ is a solution of (2.8), then $\text {p}_n +c$ is also a solution of (2.8), for every $c \in {\mathbb {R}}.$ In particular, the constant c can be choosen such that the average of $\text {p}_n +c$ is zero on a subset of $\Omega _n$.

3 The Rescaled Problem

Set now

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \Omega =\Omega ^r\cup \Omega ^l\cup \Omega ^b,\\ \displaystyle \Omega ^r=\left\{ (x_1,x_2)\in \mathbb {R}^2: \,\,0<x_2<L^r,\quad x_2\tan \alpha<x_1< x_2\tan \alpha +\frac{1}{2}\right\} ,\\ \displaystyle \Omega ^l=\left\{ (x_1,x_2)\in \mathbb {R}^2: \,\,0<x_2<L^l,\quad x_2\tan \beta -\frac{1}{2}<x_1< x_2\tan \beta \right\} ,\\ \displaystyle \Omega ^b=]-\frac{1}{2},\frac{1}{2}[\times ]-L^b,0] .\end{array}\right. \end{aligned}$$

(3.1)

In order to pass to the limit in (2.8), the first step consists in rewriting problems (2.7) and (2.8) on the domain $\Omega$ (which is independent of n). This is done as usual, by a domain dilatation technique (see [15]), through the three different maps

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle x=(x_{1},x_{2})\in \Omega ^{r} \longrightarrow (h_{n}(x_{1}-x_2\tan \alpha )+x_2\tan \alpha , x_{2})\in \Omega _{n}^{r},\\ \displaystyle x=(x_{1},x_{2})\in \Omega ^{l} \longrightarrow (h_{n}(x_{1}-x_2\tan \beta )+x_2\tan \beta , x_{2})\in \Omega _{n}^{l},\\ \displaystyle x=(x_{1},x_{2})\in \Omega ^{b} \longrightarrow (h_{n}x_{1}, x_{2})\in \Omega _{n}^{b}. \end{array}\right. \end{aligned}$$

(3.2)

More precisely, for every $n \in \mathbb {N}$ we set

$$\begin{aligned}&\left\{ \begin{array}{ll}\displaystyle {D_{n}^{r}: v\in \left( H^{1}(\Omega ^{r})\right) ^2\longrightarrow \left( \frac{1}{h_{n}}\partial _{x_1}v,\partial _{x_2}v-\frac{1-h_n}{h_n}\tan \alpha \partial _{x_1}v\right) \in (L^{2}(\Omega ^{r}))^{2} \times (L^{2}(\Omega ^{r}))^{2} ,}\\ \displaystyle {D_{n}^{l}: v\in \left( H^{1}(\Omega ^{l})\right) ^2\longrightarrow \left( \frac{1}{h_{n}}\partial _{x_1}v,\partial _{x_2}v-\frac{1-h_n}{h_n}\tan \beta \partial _{x_1}v\right) \in (L^{2}(\Omega ^{l}))^{2} \times (L^{2}(\Omega ^{l}))^{2} ,}\\ \displaystyle {D_{n}^{b}: v\in \left( H^{1}(\Omega ^{b})\right) ^2\longrightarrow \left( \frac{1}{h_{n}}\partial _{x_1}v,\partial _{x_2}v\right) \in (L^{2}(\Omega ^{b}))^{2} \times (L^{2}(\Omega ^{b}))^{2} ,}\\ \displaystyle {div_{n}^{r}:v=\left( v_{1}, v_{2} \right) \in \left( H^{1}(\Omega ^{r})\right) ^2\longrightarrow \frac{1}{h_{n}}\partial _{x_1}v_1+ \partial _{x_2}v_2-\frac{1-h_n}{h_n}\tan \alpha \partial _{x_1}v_2\in L^{2}(\Omega ^{r}),}\\ \displaystyle {div_{n}^{l}:v=\left( v_{1}, v_{2} \right) \in \left( H^{1}(\Omega ^{l})\right) ^2\longrightarrow \frac{1}{h_{n}}\partial _{x_1}v_1+ \partial _{x_2}v_2-\frac{1-h_n}{h_n}\tan \beta \partial _{x_1}v_2\in L^{2}(\Omega ^{l}),}\\ \displaystyle {div_{n}^{b}:v=\left( v_{1}, v_{2} \right) \in \left( H^{1}(\Omega ^{b})\right) ^2\longrightarrow \frac{1}{h_{n}}\partial _{x_1}v_1+ \partial _{x_2}v_2\in L^{2}(\Omega ^{b}),} \end{array}\right. \end{aligned}$$

(3.3)

$$\begin{aligned}&\left\{ \begin{array}{l} f_{n}^{r}: x=(x_{1}, x_{2})\in \Omega ^{r}\longrightarrow \text {f}_{n}(h_{n}(x_{1}-x_2\tan \alpha )+x_2\tan \alpha , x_{2}),\\ f_{n}^{l}: x=(x_{1}, x_{2})\in \Omega ^{l}\longrightarrow \text {f}_{n}(h_{n}(x_{1}-x_2\tan \beta )+x_2\tan \beta , x_{2}),\\ f_{n}^{b}: x=(x_{1}, x_{2})\in \Omega ^{b}\longrightarrow \text { f}_{n}(h_{n}x_{1}, x_{2}),\end{array}\right. \end{aligned}$$

(3.4)

and

$$\begin{aligned} \begin{array}{ll} \widetilde{{{\mathcal {V}}}}_n=\Big \{ v\in \left( H_0^1(\Omega )\right) ^2\,:\, div^r_n(v)=0\hbox { in }\Omega ^r, \,\, div^l_n(v)=0\hbox { in }\Omega ^l, \,\, div^b_n(v)=0\hbox { in }\Omega ^b\Big \}. \end{array}\end{aligned}$$

(3.5)

If $\text {u}_n$ solves (2.7) (or equivalently $\left( \text {u}_n,\text {p}_n\right)$ solves problem (2.8)), then $u_n$ (or equivalently $\left( u_n,p_n\right)$) defined by

$$\begin{aligned} \left\{ \begin{array}{ll} u_n(x_1,x_2)=\left\{ \begin{array}{ll} \text {u}_{n}(h_{n}(x_{1}-x_2\tan \alpha )+x_2\tan \alpha , x_{2}),\hbox { in }\Omega ^r, \\ \text {u}_{n}(h_{n}(x_{1}-x_2\tan \beta )+x_2\tan \beta , x_{2}),\hbox { in }\Omega ^l, \\ \text {u}_n(h_n x_1, x_2)\hbox { in }\Omega ^b,\end{array}\right. \\ p_n(x_1,x_2)=\left\{ \begin{array}{ll} \text {p}_{n}(h_{n}(x_{1}-x_2\tan \alpha )+x_2\tan \alpha , x_{2}),\hbox { in }\Omega ^r, \\ \text {p}_{n}(h_{n}(x_{1}-x_2\tan \beta )+x_2\tan \beta , x_{2}),\hbox { in }\Omega ^l, \\ \text {p}_n(h_n x_1, x_2)\hbox { in }\Omega ^b,\end{array}\right. \end{array}\right. \end{aligned}$$

(3.6)

solves

$$\begin{aligned} \left\{ \begin{array}{ll} u_n\in \widetilde{{{\mathcal {V}}}}_n ,\\ \displaystyle {\int _{\Omega ^r} \left( h_n^2 \mu D^r_n u_n D^r_n\left( v-u_n\right) +h_n g\vert D^r_n v\vert -h_n g\vert D^r_n u_n\vert \right) dx_1dx_2}+\\ \displaystyle {+\int _{\Omega ^l} \left( h_n^2 \mu D^l_n u_n D^l_n\left( v-u_n\right) +h_n g\vert D^l_n v\vert -h_n g\vert D^l_n u_n\vert \right) dx_1dx_2}+\\ \displaystyle {+\int _{\Omega ^b} \left( h_n^2 \mu D^b_n u_n D^b_n\left( v-u_n\right) +h_n g\vert D^b_n v\vert -h_n g\vert D^b_n u_n\vert \right) dx_1dx_2}\\ \displaystyle {\ge \int _{\Omega ^r} f^r_n \left( v-u_n\right) dx_1dx_2+\int _{\Omega ^l} f^l_n \left( v-u_n\right) dx_1dx_2+\int _{\Omega ^b} f^b_n \left( v-u_n\right) dx_1dx_2}\,\,\,\forall v\in \widetilde{ {{\mathcal {V}}}}_n , \end{array} \right. \end{aligned}$$

(3.7)

or equivalently

$$\begin{aligned} \left\{ \begin{array}{ll} u_n\in \widetilde{{{\mathcal {V}}}}_n , \quad p_n\in L^2(\Omega )/\mathbf {\mathbb {R}},\\ \displaystyle {\int _{\Omega ^r} \left( h_n^2 \mu D^r_n u_n D^r_n\left( v-u_n\right) +h_n g\vert D^r_n v\vert -h_n g\vert D^r_n u_n\vert \right) dx_1dx_2}+\\ \displaystyle {+\int _{\Omega ^l} \left( h_n^2 \mu D^l_n u_n D^l_n\left( v-u_n\right) +h_n g\vert D^l_n v\vert -h_n g\vert D^l_n u_n\vert \right) dx_1dx_2}+\\ \displaystyle {+\int _{\Omega ^b} \left( h_n^2 \mu D^b_n u_n D^b_n\left( v-u_n\right) +h_n g\vert D^b_n v\vert -h_n g\vert D^b_n u_n\vert \right) dx_1dx_2}\\ \displaystyle {\ge \int _{\Omega ^r} \left( f^r_n \left( v-u_n\right) +p_n div^r_n \left( v-u_n\right) \right) dx_1dx_2}\\ \displaystyle {+ \int _{\Omega ^l} \left( f^l_n \left( v-u_n\right) +p_n div^l_n \left( v-u_n\right) \right) dx_1dx_2}\\ \displaystyle {+\int _{\Omega ^b} \left( f^b_n \left( v^b-u_n\right) +p_n div^b_n \left( v-u_n\right) \right) dx_1dx_2}\quad \forall v\in \left( H_0^1(\Omega )\right) ^2 , \end{array} \right. \end{aligned}$$

(3.8)

Conversely, if $u_n$ solves (3.7) (or equivalently $\left( u_n,p_n\right)$ solves (3.8)), then $\text {u}_n$ (or equivalently $\left( \text {u}_n,\text {p}_n\right)$) defined by

$$\begin{aligned}\left\{ \begin{array}{ll} \text {u}_n(x_1,x_2)=\left\{ \begin{array}{ll} u_{n}\left( \dfrac{X_1-x_2\tan \alpha }{h_n}+x_2\tan \alpha , x_{2}\right) \hbox { in }\Omega ^r_n, \\ u_{n}\left( \dfrac{X_1-x_2\tan \beta }{h_n}+x_2\tan \beta , x_{2}\right) \hbox { in }\Omega ^l_n, \\ u_n\left( \dfrac{ X_1}{h_n}, x_2\right) \hbox { in }\Omega ^b_n,\end{array}\right. \\ \text {p}_n(x_1,x_2)=\left\{ \begin{array}{ll} p_{n}\left( \dfrac{X_1-x_2\tan \alpha }{h_n}+x_2\tan \alpha , x_{2}\right) \hbox { in }\Omega ^r_n, \\ p_{n}\left( \dfrac{X_1-x_2\tan \beta }{h_n}+x_2\tan \beta , x_{2}\right) \hbox { in }\Omega ^l_n, \\ p_n\left( \dfrac{ X_1}{h_n}, x_2\right) \hbox { in }\Omega ^b_n,\end{array}\right. \end{array}\right. \end{aligned}$$

solves (2.7) (or equivalently (2.8)). Therefore, the goal of this paper becomes to study the asymptotic behavior, as n diverges, of problem (3.8). To this aim, we assume

$$\begin{aligned} \left\{ \begin{array}{ll}f^r_n\rightarrow f^r=\left( f^r_1,f^r_2\right) \hbox { strongly in } \left( L^2\left( \Omega ^r\right) \right) ^2,\\ f^l_n\rightarrow f^l=\left( f^l_1,f^l_2\right) \hbox { strongly in } \left( L^2\left( \Omega ^l\right) \right) ^2,\\ f^b_n\rightarrow f^b=\left( f^b_1,f^b_2\right) \hbox { strongly in } \left( L^2\left( \Omega ^b\right) \right) ^2.\end{array}\right. \end{aligned}$$

(3.9)

4 The Main Results

In order to give the main result of our paper, according to [11] we introduce the applications

$$\begin{aligned} T^r: L^2(\Omega ^r)\rightarrow L^2(]0,L^r[),\quad T^l: L^2(\Omega ^l)\rightarrow L^2(]0,L^l[) ,\quad T^b: L^2(\Omega ^b)\rightarrow L^2(]-L^b,0[), \end{aligned}$$

defined by

$$\begin{aligned} \left\{ \begin{array}{ll}T^r(w):x_2\in ]0,L^r[\rightarrow {\displaystyle \int _{x_2\tan \alpha }^{x_2\tan \alpha +\frac{1}{2}} w(x_1,x_2)dx_1} ,\quad \forall w\in L^2(\Omega ^r),\\ T^l(w):x_2\in ]0,L^l[\rightarrow {\displaystyle \int _{x_2\tan \beta -\frac{1}{2}}^{x_2\tan \beta } w(x_1,x_2)dx_1}, \quad \forall w\in L^2(\Omega ^l),\\ T^b(w):x_1\in ]-L^b,0[\rightarrow {\displaystyle \int _{-\frac{1}{2}}^{\frac{1}{2}} w(x_1,x_2)dx_1}, \quad \forall w\in L^2(\Omega ^b),\end{array}\right. \end{aligned}$$

(4.1)

respectively, and we set

$$\begin{aligned}&\begin{array}{ll} W^r=\Big \{ &{}w\in L^2(\Omega ^r)\,\,:\,\, T^r(w)\in H_0^1(]0,L^r[),\quad \partial _{x_1}w\in L^2(\Omega ^r) , \\ &{}w=0 \hbox { on }\left\{ (x_1,x_2)\in \mathbb {R}^2: \,\,0<x_2<L^r,\quad x_1= x_2\tan \alpha \, \vee \, x_1= x_2\tan \alpha +\frac{1}{2}\right\} \Big \}, \end{array}\nonumber \\&\begin{array}{ll} W^l=\Big \{ &{}w\in L^2(\Omega ^l)\,\,:\,\,T^l(w)\in H_0^1(]0,L^l[),\quad \partial _{x_1}w\in L^2(\Omega ^l) , \\ &{}w=0 \hbox { on }\left\{ (x_1,x_2)\in \mathbb {R}^2: \,\,0<x_2<L^l,\quad x_1= x_2\tan \beta \, \vee \, x_1= x_2\tan \beta -\frac{1}{2}\right\} \Big \}, \end{array}\nonumber \\&\begin{array}{ll} W^b=\left\{ w\in L^2(\Omega ^b):T^b(w)\in H_0^1(]-L^b,0[),\, \partial _{x_1}w\in L^2(\Omega ^b) , \, w=0 \hbox { on }\left\{ -\frac{1}{2},\frac{1}{2}\right\} \times ]-L^b,0[ \right\} , \end{array}\nonumber \\&\left\{ \begin{array}{ll} W^r_0=\left\{ w\in W^r(\Omega ^r)\,\,:\,\, T^r(w)=0 \hbox { in } ]0,L^r[\right\} ,\\ W^l_0=\left\{ w\in W^l(\Omega ^l)\,\,:\,\, T^l(w)=0 \hbox { in } ]0,L^l[\right\} ,\\ W^b_0=\left\{ w\in W^b(\Omega ^b)\,\,:\,\,T^b(w)=0 \hbox { in } ]-L^b,0[\right\} . \end{array}\right. \end{aligned}$$

(4.2)

Theorem 4.1

Assume that (2.9) and (3.9) hold true. For every $n\in \mathbb {N}$ let $\left( u_n,p_n\right)$, $\left( u_n,q_n\right)$, and $\left( u_n,s_n\right)$ be three solutions to (3.8) such that

$$\begin{aligned} \int _{\Omega ^r}p_ndx_1dx_2=0,\quad \int _{\Omega ^l}q_ndx_1dx_2=0,\quad \int _{\Omega ^b}s_ndx_1dx_2=0 \quad \forall n\in \mathbb {N}, \end{aligned}$$

and set

$$\begin{aligned} u^r_n={u_n}_{|_{\Omega ^r}}, \quad u^l_n={u_n}_{|_{\Omega ^l}}, \quad u^b_n={u_n}_{|_{\Omega ^b}}. \end{aligned}$$

Let $W^r_0(\Omega ^r)$, $W^l_0(\Omega ^l)$, and $W^b_0(\Omega ^b)$ be defined in (4.2). Then, there exist $u^r$ in $W^r_0(\Omega ^r)$, $u^l$ in $W^l_0(\Omega ^l)$, and $u^b$ in $W^b_0(\Omega ^b)$ such that

$$\begin{aligned}&\left\{ \begin{array}{ll}u^r_n \rightharpoonup ( u^r\tan \alpha ,u^r) \hbox { weakly in }\left( L^2(\Omega ^r)\right) ^2,\\ \partial _{x_1}u^r_n \rightharpoonup (\partial _{x_1}u^r \tan \alpha ,\partial _{x_1}u^r) \hbox { weakly in }\left( L^2(\Omega ^r)\right) ^2,\\ h_nu^r_n \rightharpoonup 0 \hbox { weakly in }\left( H^1(\Omega ^r)\right) ^2,\end{array}\right. \end{aligned}$$

(4.3)

$$\begin{aligned}&\left\{ \begin{array}{ll}u^l_n \rightharpoonup ( u^l\tan \beta ,u^l) \hbox { weakly in }\left( L^2(\Omega ^l)\right) ^2,\\ \partial _{x_1}u^l_n \rightharpoonup (\partial _{x_1}u^l \tan \beta ,\partial _{x_1}u^l) \hbox { weakly in }\left( L^2(\Omega ^l)\right) ^2,\\ h_nu^l_n \rightharpoonup 0 \hbox { weakly in }\left( H^1(\Omega ^l)\right) ^2,\end{array}\right. \end{aligned}$$

(4.4)

$$\begin{aligned}&\left\{ \begin{array}{ll}u^b_n \rightharpoonup ( 0,u^b) \hbox { weakly in }\left( L^2(\Omega ^b)\right) ^2,\\ \partial _{x_1}u^b_n \rightharpoonup (0,\partial _{x_1}u^b) \hbox { weakly in }\left( L^2(\Omega ^b)\right) ^2,\\ h_nu^b_n \rightharpoonup 0 \hbox { weakly in }\left( H^1(\Omega ^b)\right) ^2,\end{array}\right. \end{aligned}$$

(4.5)

as n diverges. Moreover, there exist an increasing sequence of positive numbers, still denoted by $\{n\}$, and (in possible dependence on the subsequence) three functions independent of $x_1$: p in $L^2(\Omega ^r)$, q in $L^2(\Omega ^l)$, and s in $L^2(\Omega ^b)$ such that

$$\begin{aligned}&\int _{\Omega ^r}pdx_1dx_2=0, \quad \int _{\Omega ^l}qdx_1dx_2=0, \hbox {and } \int _{\Omega ^b}sdx_1dx_2=0, \end{aligned}$$

(4.6)

$$\begin{aligned}&{p_n}_{|_{\Omega ^r}} \rightharpoonup p \hbox { weakly in }L^2(\Omega ^r),\, {q_n}_{|_{\Omega ^l}} \rightharpoonup q \hbox { weakly in }L^2(\Omega ^l),\, {s_n}_{|_{\Omega ^b}} \rightharpoonup s \hbox { weakly in }L^2(\Omega ^b), \end{aligned}$$

(4.7)

as n diverges. Furthermore, $(u^r,p)$, $(u^l,q)$, and $(u^b,s)$ solve

$$\begin{aligned}&\left\{ \begin{array}{ll} u^r\in W^r_0(\Omega ^r),\quad p\in L^2(\Omega ^r),\\ \displaystyle {\int _{\Omega ^r}\left( \mu \left( 1+\tan ^2\alpha \right) ^2\partial _{x_1}u^r\partial _{x_1}\left( w-u^r\right) +g \left( 1+\tan ^2\alpha \right) \left( \vert \partial _{x_1}w\vert -\vert \partial _{x_1}u^r\vert \right) \right) dx_1dx_2}\\ \displaystyle { \ge \int _{\Omega ^r} \left( f^r_1\tan \alpha +f^r_2\right) \left( w-u^r\right) dx_1dx_2+ \int _0^{L^r}p \frac{d \left( T^r(w-u^r)\right) }{dx_2}dx_2\,\, \forall w\in W^r(\Omega ^r),} \end{array} \right. \end{aligned}$$

(4.8)

$$\begin{aligned}&\left\{ \begin{array}{ll} u^l\in W^l_0(\Omega ^l),\quad q \in L^2(\Omega ^l),\\ \displaystyle {\int _{\Omega ^l} \left( \mu \left( 1+\tan ^2\beta \right) ^2\partial _{x_1}u^l\partial _{x_1}\left( w-u^l\right) +g \left( 1+\tan ^2\beta \right) \left( \vert \partial _{x_1}w\vert -\vert \partial _{x_1}u^l\vert \right) \right) dx_1dx_2}\\ \displaystyle { \ge \int _{\Omega ^l} \left( f^l_1\tan \beta +f^l_2\right) \left( w-u^l\right) dx_1dx_2+ \int _0^{L^l}q \frac{d\left( T^l(w-u^l)\right) }{dx_2}dx_2\quad \forall w\in W^l(\Omega ^l), } \end{array} \right. \end{aligned}$$

(4.9)

$$\begin{aligned}&\left\{ \begin{array}{ll} u^b\in W^b_0(\Omega ^b),\quad s \in L^2(\Omega ^b),\\ \displaystyle {\int _{\Omega ^b} \left( \mu \partial _{x_1}u^b \partial _{x_1}\left( w-u^b\right) +g\left( \vert \partial _{x_1} w\vert - \vert \partial _{x_1} u^b\vert \right) \right) dx_1dx_2} \\ \displaystyle {\ge \int _{\Omega ^b} f^b_2 \left( w-u^b\right) dx_1dx_2+\int _{-L^b}^0 s\frac{d\left( T^b(w-u^b)\right) }{dx_2}dx_2}\quad \forall w\in W^b(\Omega ^b), \end{array} \right. \end{aligned}$$

(4.10)

respectively, where $(f^r_1,f^r_2)$, $(f^l_1,f^l_2)$, and $f^b_2$ are given by (3.9). Furthermore, $u^r$, $u^l$, and $u^b$ are unique.

Remark 4.2

The limit velocity in the right branch is $u^r (\hbox {tan}\,\alpha , 1)$ (see (4.3)). We note that $\alpha$ describes the deviation of the right branch from the $x_2$-axis, then the direction $(\hbox {tan}\,\alpha , 1)$ of the limit velocity is exactly along the axis of the right branch. Moreover, as far as the limit force $(f^r_1,f^r_2)$ is concerned, only its projection on the axis of the right branch is involved in problem (4.8). Indeed,

$$\begin{aligned} f^r_1\tan \alpha +f^r_2=\pm \left\| \hbox {P}_{|_{(\tan \alpha ,1)}}(f^r_1,f^r_2)\right\| \sqrt{1+\tan ^2\alpha }, \end{aligned}$$

where $\hbox {P}_{|_{(\tan \alpha ,1)}}$ denotes the projection operator on the axis $x=y\tan \alpha .$

If $\alpha =0$, then the domain $\Omega ^r$ is a vertical rectangle, $\tan \alpha =0$, and the first limit in (4.3) is $(0, u^r)$. This is in accordance with the results obtained in [10,11,12].

A similar remark holds true for problem (4.9) stated in the left branch, and for problem (4.10) stated in the vertical branch (which corresponds to the previous cases with $\alpha =0$).

5 A Priori Estimates and Convergence Result for the Velocity

In order to use compactness results for passing to the limit in the terms involving the velocity, we first derive a priori estimates for this function.

Proposition 5.1

Assume (2.9) and (3.9) hold true. For every $n\in \mathbb {N}$ let $u_n$ be the solution to (3.7). Then there exists a positive constant c independent on n such that

$$\begin{aligned}&h_n \left\| D^r_nu_n\right\| _{\left( L^2(\Omega ^r)\right) ^4}\le c,\quad h_n\left\| D^l_nu_n\right\| _{\left( L^2(\Omega ^l)\right) ^4}\le c, \quad h_n\left\| D^b_nu_n\right\| _{\left( L^2(\Omega ^b)\right) ^4}\le c\quad \forall n \in \mathbb {N},\end{aligned}$$

(5.1)

$$\begin{aligned}&\left\| u_n\right\| _{\left( L^2(\Omega )\right) ^2}\le c\quad \forall n \in \mathbb {N}. \end{aligned}$$

(5.2)

Proof

Choosing $v=0$ and $v=2u_n$ as test functions in (3.7), and comparing the variational inequalities which are obtained give that

$$\begin{aligned} \begin{array}{ll} \displaystyle {\int _{\Omega ^r} \left( h_n^2\mu \left| D^r_n u_n\right| ^2+h_ng\vert D^r_n u_n\vert \right) dx_1dx_2+\int _{\Omega ^l} \left( h_n^2\mu \left| D^l_n u_n\right| ^2+h_ng\vert D^l_n u_n\vert \right) dx_1dx_2}\\ \displaystyle {+\int _{\Omega ^b} \left( h_n^2 \mu \left| D^b_n u_n \right| ^2+h_n g\vert D^b_n u_n\vert \right) dx_1dx_2}\\ \displaystyle {= \int _{\Omega ^r} f^r_n u_n dx_1dx_2+\int _{\Omega ^l} f^l_n u_n dx_1dx_2+\int _{\Omega ^b} f^b_n u_n dx_1dx_2} \quad \forall n\in \mathbb {N}.\end{array} \end{aligned}$$

(5.3)

On the other hand, the homogeneous boundary conditions of $u_n$ provide

$$\begin{aligned} \left\{ \begin{array}{ll} \left\| u_n\right\| _{\left( L^2(\Omega ^r)\right) ^2}\le \left\| \partial _{x_1}u_n\right\| _{\left( L^2(\Omega ^r)\right) ^2} \le \left\| h_n D^r_nu_n\right\| _{\left( L^2(\Omega ^r)\right) ^4} ,\\ \left\| u_n\right\| _{\left( L^2(\Omega ^l)\right) ^2}\le \left\| \partial _{x_1}u_n\right\| _{\left( L^2(\Omega ^l)\right) ^2} \le \left\| h_n D^l_nu_n\right\| _{\left( L^2(\Omega ^l)\right) ^4} ,\\ \left\| u_n\right\| _{\left( L^2(\Omega ^b)\right) ^2}\le \left\| \partial _{x_1}u_n\right\| _{\left( L^2(\Omega ^b)\right) ^2} \le \left\| h_n D^b_nu_n\right\| _{\left( L^2(\Omega ^b)\right) ^4} ,\end{array} \right. \quad \forall n\in \mathbb {N}.\end{aligned}$$

(5.4)

Applying the Hölder inequality to the right-hand side of (5.3) and using (5.4) imply

$$\begin{aligned} \begin{array}{ll} \displaystyle {\mu \int _{\Omega ^r}\left| h_n D^r_n u_n\right| ^2dx_1dx_2+\mu \int _{\Omega ^l}\left| h_n D^l_n u_n\right| ^2dx_1dx_2+ \mu \int _{\Omega ^b}\left| h_n D^b_n u_n \right| ^2dx_1dx_2}\\ \displaystyle {\le \left\| f^r_n\right\| _{\left( L^2(\Omega ^r)\right) ^2} \left\| h_n D^r_nu_n\right\| _{\left( L^2(\Omega ^r)\right) ^4}+\left\| f^l_n\right\| _{\left( L^2(\Omega ^l)\right) ^2} \left\| h_n D^l_nu_n\right\| _{\left( L^2(\Omega ^l)\right) ^4}} \\ \displaystyle {+\left\| f^b_n\right\| _{\left( L^2(\Omega ^b)\right) ^2} \left\| h_n D^b_nu_n\right\| _{\left( L^2(\Omega ^b)\right) ^4}} \quad \forall n\in \mathbb {N}. \end{array}\end{aligned}$$

(5.5)

Eventually, (5.1) follows from (5.5), (3.9), and the following inequality

$$\begin{aligned} (\gamma +\delta +\eta )^2\le 3(\gamma ^2+\delta ^2+\eta ^2)\quad \forall \gamma ,\delta ,\eta \in [0,+\infty [; \end{aligned}$$

while (5.2) follows from (5.4) and (5.1). $\square$

Proposition  5.1 implies the following result.

Proposition 5.2

Let $T^r$, $T^l$ and $T^b$ be defined in (4.1). Assume (2.9) and (3.9) hold true. For every $n\in \mathbb {N}$ let $u_n=\left( {u_{n}}_1,{u_{n}}_2\right)$ be the solution to (3.7). Then there exist a subsequence of $\mathbb {N}$, still denoted by $\{n\}$, and $u=(u_1,u_2)$ in $\left( L^2(\Omega )\right) ^2$ with $\partial _{x_1}u$ in $\left( L^2(\Omega )\right) ^2$ such that

$$\begin{aligned}&\left\{ \begin{array}{ll}u_n \rightharpoonup u \hbox { weakly in }\left( L^2(\Omega )\right) ^2,\quad \partial _{x_1}u_n \rightharpoonup \partial _{x_1}u \hbox { weakly in }\left( L^2(\Omega )\right) ^2,\\ h_nu_n \rightharpoonup 0 \hbox { weakly in }\left( H^1(\Omega )\right) ^2,\end{array}\right. \end{aligned}$$

(5.6)

$$\begin{aligned}&\begin{array}{ll} u=0 \hbox { on }\left\{ (x_1,x_2)\in \mathbb {R}^2: \,\,0<x_2<L^r,\quad x_1= x_2\tan \alpha \,\, \vee \,\, x_1= x_2\tan \alpha +\frac{1}{2}\right\} \\ \cup \left\{ (x_1,x_2)\in \mathbb {R}^2: \,\,0<x_2<L^l,\quad x_1= x_2\tan \beta \,\, \vee \,\, x_1= x_2\tan \beta -\frac{1}{2}\right\} \\ \cup \left( \left\{ \pm \frac{1}{2}\right\} \times ]-L^b,0[\right) ,\end{array} \end{aligned}$$

(5.7)

$$\begin{aligned}&u_1=\tan \alpha \, u_2\hbox { a.e. in }\Omega ^r,\quad u_1=\tan \beta \, u_2\hbox { a.e. in }\Omega ^l,\quad u_1=0\hbox { a.e. in }\Omega ^b,\end{aligned}$$

(5.8)

$$\begin{aligned}&T^r(u_2)=0\hbox { a.e. in }]0,L^r[, \,\, T^l(u_2)=0\hbox { a.e. in }]0,L^l[,\,\, T^b(u_2)=0\hbox { a.e. in }]-L^b,0[.\end{aligned}$$

(5.9)

Proof

Statements in (5.6) and in (5.7) follow from Proposition 5.1.

The first equality in (5.8) is obtained by passing to the limit in

$$\begin{aligned} \partial _{x_1}{u_{n}}_1+h_n \partial _{x_2}{u_{n}}_2-(1-h_n)\tan \alpha \, \partial _{x_1}{u_{n}}_2= h_n div^r_n(u_n)=0 \hbox { in } \Omega ^r, \quad \forall n\in \mathbb {N}, \end{aligned}$$

and taking into account the last two convergences in (5.6), and (5.7). Similarly, one can prove the last two equalities in (5.8).

As far as the proof of (5.9) is concerned, equality $div^r_n(u_n)=0$ in $\Omega ^r$ provides

$$\begin{aligned} \begin{array}{ll} \displaystyle {\int _{\Omega ^r} \left( \frac{1}{h_n}\partial _{x_1}{u_{n}}_1+\partial _{x_2}{u_{n}}_2-\frac{1-h_n}{h_n}\tan \alpha \,\partial _{x_1}{u_{n}}_2\right) \varphi (x_2)dx_1dx_2=0} \\ \forall \varphi \in C_0^\infty (]0,1[), \quad \forall n\in \mathbb {N}.\end{array}\end{aligned}$$

(5.10)

On the other side, the boundary conditions of $u_n$ give

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle {\int _{\Omega ^r}\partial _{x_1}{u_{n}}_1\varphi (x_2)dx_1dx_2=\int _{\partial \Omega ^r}{u_{n}}_1\varphi (x_2)\nu _1dx_1dx_2=0,} \\ \displaystyle {\int _{\Omega ^r}\partial _{x_1}{u_{n}}_2\varphi (x_2)dx_1dx_2=\int _{\partial \Omega ^r}{u_{n}}_2\varphi (x_2)\nu _1dx_1dx_2=0,} \end{array}\forall \varphi \in C_0^\infty (]0,1[), \,\,\forall n\in \mathbb {N},\right. \end{aligned}$$

(5.11)

where $\nu _1$ is the first component of the exterior unit normal on $\partial \Omega ^r$. Taking into account again the boundary conditions of $u_n$ and combining (5.10) with (5.11) provide

$$\begin{aligned}\begin{array}{ll} \displaystyle {\int _0^{L^r}\partial _{x_2}\left( T^r\left( {u_{n}}_2\right) \right) \varphi (x_2)dx_2= \int _0^{L^r}\partial _{x_2}\left( \int _{x_2\tan \alpha }^{x_2\tan \alpha +\frac{1}{2}} {u_{n}}_2(x_1,x_2)dx_1\right) \varphi (x_2)dx_2 }\\ \displaystyle {= \int _0^{L^r} \left[ \tan \alpha {u_{n}}_2\left( x_2\tan \alpha +\frac{1}{2},x_2\right) - \tan \alpha {u_{n}}_2\left( x_2\tan \alpha ,x_2\right) \right] \varphi (x_2)dx_2} \\ \displaystyle { +\int _0^{L^r}\left[ \int _{x_2\tan \alpha }^{x_2\tan \alpha +\frac{1}{2}} \partial _{x_2}{u_{n}}_2(x_1,x_2)dx_1\right] \varphi (x_2)dx_2}\\ \displaystyle {= \int _{\Omega ^r}\partial _{x_2}{u_{n}}_2\varphi (x_2)dx_1dx_2=0\quad \forall \varphi \in C_0^\infty (]0,L^r[), \quad \forall n\in \mathbb {N},}\end{array}\end{aligned}$$

which implies

$$\begin{aligned} T^r\left( {u_{n}}_2\right) =0\hbox { a.e. in }]0,L^r[, \quad \forall n\in \mathbb {N},\end{aligned}$$

(5.12)

since $T^r\left( {u_{n}}_2\right) (1)=0$. Eventually, combining the first convergence in (5.6) with (5.12) provides the first equality in (5.9), since $T^r$ is weakly continuous, being strongly continuous. Similarly, one can prove the last two equalities in (5.9). $\square$

6 A Priori Estimates and Convergence Result for the Pressure

In what follows, we set

$$\begin{aligned} \begin{array}{ll} W_{reg}=\Big \{w=(w_1,w_2)\in \left( L^2(\Omega )\right) ^2: {w_2}_{|_{\Omega ^r}}\in H^1_0(\Omega ^r), \quad {w_2}_{|_{\Omega ^l}}\in H^1_0(\Omega ^l),\\ {w_2}_{|_{\Omega ^b}}\in H^1_0(\Omega ^b), \quad w_1=\tan \alpha w_2 \hbox { in }\Omega ^r,\quad w_1=\tan \beta w_2 \hbox { in }\Omega ^l,\quad w_1=0\hbox { in }\Omega ^b \Big \}.\end{array} \end{aligned}$$

(6.1)

Proposition 6.1

Assume that (2.9) and (3.9) hold true. For every $n\in \mathbb {N}$ let $\left( u_n,p_n\right)$ be a solution to (3.8). Then there exists a positive constant c independent on n such that

$$\begin{aligned}&\left\| \partial _{x_1}p_n\right\| _{H^{-1}(\Omega )}\le h_n c, \end{aligned}$$

(6.2)

$$\begin{aligned}&\left\| \partial _{\nu _\alpha }p_n\right\| _{H^{-1}(\Omega ^r)}\le c,\quad \left\| \partial _{\nu _{\beta }}p_n\right\| _{H^{-1}(\Omega ^l)}\le c, \quad \left\| \partial _{x_2}p_n\right\| _{H^{-1}(\Omega ^b)}\le c, \end{aligned}$$

(6.3)

for every $n \in \mathbb {N}$, where

$$\begin{aligned} \nu _\alpha =\left( \frac{\tan \alpha }{\sqrt{\tan ^2\alpha +1}}, \frac{1}{\sqrt{\tan ^2\alpha +1}}\right) ,\quad \nu _{\beta }=\left( \frac{\tan \beta }{\sqrt{\tan ^2\beta +1}}, \frac{1}{\sqrt{\tan ^2\beta +1}}\right) . \end{aligned}$$

(6.4)

Moreover,

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle {\left\| p_n\right\| _{L^2(\Omega _r)}\le c\left( 1+\left| \int _{\Omega _r} p_ndx_1dx_2\right| \right) ,}\quad \displaystyle { \left\| p_n\right\| _{L^2(\Omega _l)}\le c\left( 1+\left| \int _{\Omega _l} p_ndx_1dx_2\right| \right) ,}\\ \displaystyle { \left\| p_n\right\| _{L^2(\Omega _b)}\le c\left( 1+\left| \int _{\Omega _b} p_ndx_1dx_2\right| \right) ,\quad \forall n \in \mathbb {N}.} \end{array}\right. \end{aligned}$$

(6.5)

Proof

Choosing $v=w+u_n$ as test functions in (3.8), with w in $(H^1_0(\Omega ))^2$, gives

$$\begin{aligned} \begin{array}{ll} \displaystyle {\int _{\Omega ^r} \left( h_n^2\mu D^r_n u_n D^r_nw+h_ng\vert D^r_n( w+u_n)\vert -h_ng\vert D^r_n u_n\vert \right) dx_1dx_2}\\ \displaystyle {+\int _{\Omega ^l} \left( h_n^2\mu D^l_n u_n D^l_nw+h_ng\vert D^l_n( w+u_n)\vert -h_ng\vert D^l_n u_n\vert \right) dx_1dx_2}\\ \displaystyle {+\int _{\Omega ^b} \left( h_n^2\mu D^b_n u_n D^b_nw+h_ng\vert D^b_n( w+u_n)\vert -h_ng\vert D^b_n u_n\vert \right) dx_1dx_2}\\ \displaystyle {\ge \int _{\Omega ^r} \left( f^r_n w+p_n div^r_n w\right) dx_1dx_2+ \int _{\Omega ^l} \left( f^l_n w+p_n div^l_n w\right) dx_1dx_2}\\ \displaystyle {+ \int _{\Omega ^b} \left( f^b_n w+p_n div^b_n w\right) dx_1dx_2}\quad \forall w\in (H^1_0(\Omega ))^2, \quad \forall n \in \mathbb {N} . \end{array} \end{aligned}$$

(6.6)

Applying the Hölder inequality in (6.6) provides

$$\begin{aligned} \begin{array}{ll} \displaystyle {\int _{\Omega ^r} p_n div^r_n w dx_1dx_2+\int _{\Omega ^l} p_n div^l_n w dx_1dx_2+\int _{\Omega ^b} p_n div^b_n w dx_1dx_2}\\ \le h_n^2\mu \left\| D^r_n u_n \right\| _{\left( L^2\left( \Omega ^r\right) \right) ^4} \left\| D^r_nw \right\| _{\left( L^2\left( \Omega ^r\right) \right) ^4} +h_ng \left\| D^r_n w \right\| _{\left( L^1\left( \Omega ^r\right) \right) ^4}+ \left\| f^r_n \right\| _{\left( L^2\left( \Omega ^r\right) \right) ^2} \left\| w \right\| _{\left( L^2\left( \Omega ^r\right) \right) ^2}\\ +h_n^2\mu \left\| D^l_n u_n \right\| _{\left( L^2\left( \Omega ^l\right) \right) ^4}\left\| D^l_nw \right\| _{\left( L^2\left( \Omega ^l\right) \right) ^4}+h_ng \left\| D^l_n w \right\| _{\left( L^1\left( \Omega ^l\right) \right) ^4}+\left\| f^l_n \right\| _{\left( L^2\left( \Omega ^l\right) \right) ^2} \left\| w \right\| _{\left( L^2\left( \Omega ^l\right) \right) ^2} \\ +h_n^2\mu \left\| D^b_n u_n \right\| _{\left( L^2\left( \Omega ^b\right) \right) ^4}\left\| D^b_nw \right\| _{\left( L^2\left( \Omega ^b\right) \right) ^4} +h_ng \left\| D^b_n w \right\| _{\left( L^1\left( \Omega ^b\right) \right) ^4}+ \left\| f^b_n \right\| _{\left( L^2\left( \Omega ^b\right) \right) ^2} \left\| w \right\| _{\left( L^2\left( \Omega ^b\right) \right) ^2} \\ \forall w\in (H^1_0(\Omega ))^2, \quad \forall n \in \mathbb {N} . \end{array} \end{aligned}$$

Consequently, using (3.9), (5.1), the Hölder inequality, and the Poincaré inequality ensure the existence of a positive constant c such that

$$\begin{aligned} \begin{array}{ll} \displaystyle {\left| \int _{\Omega ^r} p_n div^r_n w dx_1dx_2+\int _{\Omega ^l} p_n div^l_n w dx_1dx_2+\int _{\Omega ^b} p_n div^b_n w dx_1dx_2\right| \le ch_n }\\ \displaystyle {\left( \left\| D^r_nw\right\| _{\left( L^2\left( \Omega ^r\right) \right) ^4}+\left\| D^l_nw \right\| _{\left( L^2\left( \Omega ^l\right) \right) ^4} +\left\| D^b_nw \right\| _{\left( L^2\left( \Omega ^b\right) \right) ^4}\right) }\,\, \forall w\in (H^1_0(\Omega ))^2, \,\, \forall n \in \mathbb {N} .\end{array} \end{aligned}$$

(6.7)

Now, in (6.7) choosing $w=(w_1,w_2)\in (H^1_0(\Omega ))^2$ with $w_2=0$ in $\Omega$ gets

$$\begin{aligned} \displaystyle {\left| \int _{\Omega } p_n \partial _{x_1}w_1 dx_1dx_2\right| \le ch_n \left\| Dw_1 \right\| _{\left( L^2\left( \Omega \right) \right) ^2} \quad \forall w_1\in H_0^1(\Omega ), \quad \forall n \in \mathbb {N},} \end{aligned}$$

with a positive constant c independent of $w_1\in H_0^1(\Omega )$ and of $n \in \mathbb {N}$, which implies (6.2).

Now, in (6.7) choosing $w=(w_1,w_2)$ in $W_{reg}$ defined in (6.1) gets

$$\begin{aligned} \begin{array}{ll} \displaystyle {\left| \int _{\Omega ^r} p_n \left( \partial _{x_2}w_2+\tan \alpha \partial _{x_1}w_2 \right) dx_1dx_2+\int _{\Omega ^l} p_n \left( \partial _{x_2}w_2+\tan \beta \partial _{x_1}w_2 \right) dx_1dx_2+\int _{\Omega ^b} p_n \partial _{x_2 } w_2 dx_1dx_2\right| }\\ \displaystyle {\le c \left\| Dw_2\right\| _{\left( L^2\left( \Omega \right) \right) ^2}}\quad \forall w_2\in L^2(\Omega ) : {w_2}_{|_{\Omega ^r}}\in H^1_0(\Omega ^r), \,\, {w_2}_{|_{\Omega ^l}}\in H^1_0(\Omega ^l), \,\, {w_2}_{|_{\Omega ^b}}\in H^1_0(\Omega ^b), \,\, \forall n \in \mathbb {N} ,\end{array} \end{aligned}$$

with a positive constant c independent of $w_2$ and of n. Consequently, there exists a positive constant c such that

$$\begin{aligned}\left\{ \begin{array}{ll} \displaystyle {\left| \int _{\Omega ^r} p_n \partial _{\nu _\alpha }w_2 dx_1dx_2\right| \le c \left\| Dw_2\right\| _{\left( L^2\left( \Omega ^r\right) \right) ^2} \quad \forall w_2\in H^1_0(\Omega ^r),} \\ \displaystyle {\left| \int _{\Omega ^l} p_n \partial _{\nu _{\beta }}w_2 dx_1dx_2\right| \le c \left\| Dw_2\right\| _{\left( L^2\left( \Omega ^l\right) \right) ^2} \quad \forall w_2\in H^1_0(\Omega ^l),}\\ \displaystyle {\left| \int _{\Omega ^b} p_n \partial _{x_2 } w_2 dx_1dx_2\right| \le c \left\| Dw_2\right\| _{\left( L^2\left( \Omega ^b\right) \right) ^2} \quad \forall w_2\in H^1_0(\Omega ^b),} \end{array}\right. \quad \forall n \in \mathbb {N} , \end{aligned}$$

where $\nu _\alpha$ and $\nu _\beta$ are defined in (6.4), which implies the estimates in (6.3).

Let us just prove the first estimate in (6.5). The proof of the other ones is similar.

Thanks to (6.2), one has

$$\begin{aligned} \left\| \partial _{x_1}p_n\right\| _{H^{-1}(\Omega _r)}\le \left\| \partial _{x_1}p_n\right\| _{H^{-1}(\Omega )}\le h_n c\quad \forall n \in \mathbb {N}, \end{aligned}$$

(6.8)

with a constant c independent of $n\in \mathbb {N}$. Then, from (6.3), (6.8), and the relation

$$\begin{aligned} \partial _{x_2}w=\sqrt{\tan ^2\alpha +1}\partial _{\nu _\alpha }w- \tan \alpha \partial _{x_1}w\quad \forall w\in H_0^1(\Omega _r), \end{aligned}$$

it follows that

$$\begin{aligned}\begin{array}{ll} \displaystyle {\left| \int _{\Omega ^r} p_n \partial _{x_2}wdx_1dx_2\right| \le \sqrt{\tan ^2\alpha +1}\left| \int _{\Omega ^r} p_n \partial _{\nu _\alpha }wdx_1dx_2\right| + \tan \alpha \left| \int _{\Omega ^r} p_n \partial _{x_1}w dx_1dx_2\right| }\\ \displaystyle {\le c\left( \sqrt{\tan ^2\alpha +1}+h_n\tan \alpha \right) \Vert Dw\Vert _{H_0^1(\Omega _r)}\quad \forall w\in H_0^1(\Omega _r), \quad \forall n \in \mathbb {N} , }\end{array} \end{aligned}$$

which implies that

$$\begin{aligned} \left\| \partial _{x_2}p_n\right\| _{H^{-1}(\Omega _r)}\le c\quad \forall n \in \mathbb {N},\ \end{aligned}$$

(6.9)

with a positive constant c independent of $n\in {\mathbb {N}}$.

Eventually, the first estimate in (6.5) follows from Lemma 6.1 in [37], (6.8) and (6.9). $\square$

Proposition 5.2 and Proposition 6.1 imply the following result.

Corollary 6.2

Assume that (2.9) and (3.9) hold true. For every $n\in \mathbb {N}$ let $\left( u_n,p_n\right)$, $\left( u_n,q_n\right)$, and $\left( u_n,s_n\right)$ be three solutions to (3.8) such that

$$\begin{aligned} \int _{\Omega ^r}p_ndx_1dx_2=0,\quad \int _{\Omega ^l}q_ndx_1dx_2=0,\quad \int _{\Omega ^b}s_ndx_1dx_2=0 \quad \forall n\in \mathbb {N}. \end{aligned}$$

Then there exist an increasing sequence of positive numbers, still denoted by $\{n\}$, and (in possible dependence on the subsequence) three functions independent of $x_1$: p in $L^2(\Omega ^r)$, q in $L^2(\Omega ^l)$, and s in $L^2(\Omega ^b)$ such that

$$\begin{aligned}&\int _{\Omega ^r}pdx_1dx_2=0, \quad \int _{\Omega ^l}qdx_1dx_2=0, \quad \int _{\Omega ^b}sdx_1dx_2=0,\\&\quad \begin{array}{lll}{p_n}_{|_{\Omega ^r}} \rightharpoonup p \hbox { weakly in }L^2(\Omega ^r),\,\, {q_n}_{|_{\Omega ^l}} \rightharpoonup q \hbox { weakly in }L^2(\Omega ^l),\,\, {s_n}_{|_{\Omega ^b}} \rightharpoonup s \hbox { weakly in }L^2(\Omega ^b).\end{array} \end{aligned}$$

7 Proof of Theorem 4.1

Proof

By virtue of Proposition 5.2 and Corollary 6.2, there exists an increasing sequence of positive numbers, still denoted by $\{n\}$, and (in possible dependence on the subsequence) there exist $u^r$ in $W^r_0(\Omega ^r)$, $u^l$ in $W^l_0(\Omega ^l)$, $u^b$ in $W^b_0(\Omega ^b)$, p in $L^2(\Omega ^r)$, q in $L^2(\Omega ^l)$, and s in $L^2(\Omega ^b)$, with p, q, and s independent of $x_1$, such that (4.3)-(4.7) hold true. In what follows, n take values in this increasing sequence of positive numbers. It remains to prove that $(u^r, p)$, $(u^l, q)$, and $(u^b, s)$ solve (4.8), (4.9), and (4.10), respectively. The uniqueness of $u^r$, $u^l$, and $u^b$ can be proved as in [12]. It implies that limits in (4.3)-(4.5) hold true for the whole sequence.

In (3.7) choosing $v=0$ first, then $v=2u_n$, and comparing provide

$$\begin{aligned} \begin{array}{ll}\displaystyle {\int _{\Omega ^r}\left( h_n^2\mu \vert D^r_nu_n\vert ^2+h_ng\vert D^r_nu_n\vert \right) dx_1dx_2+\int _{\Omega ^l}\left( h_n^2\mu \vert D^l_nu_n\vert ^2+h_ng\vert D^l_nu_n\vert \right) dx_1dx_2}\\ \displaystyle {+ \int _{\Omega ^b}\left( h_n^2\mu \vert D^b_nu_n\vert ^2+h_ng\vert D^b_nu_n\vert \right) dx_1dx_2 }\\ \displaystyle {=\int _{\Omega ^r}f^r_nu_ndx_1dx_2+\int _{\Omega ^l}f^l_nu_ndx_1dx_2+\int _{\Omega ^b}f^b_nu_ndx_1dx_2\quad \forall n\in \mathbb {N}.} \end{array} \end{aligned}$$

(7.1)

Combining (3.8) and (7.1), and recalling that

$$\begin{aligned} div^r_n(u_n)=0\hbox { in }\Omega ^r,\quad div^l_n(u_n)=0\hbox { in }\Omega ^l,\quad div^b_n(u_n)=0\hbox { in }\Omega ^b, \end{aligned}$$

give

$$\begin{aligned} \begin{array}{ll}\displaystyle {\int _{\Omega ^r} \left( h_n^2\mu D^r_nu_n D^r_nv +h_ng\vert D^r_nv\vert \right) dx_1dx_2+ \int _{\Omega ^l} \left( h_n^2\mu D^l_nu_n D^l_nv +h_ng\vert D^l_nv\vert \right) dx_1dx_2}\\ \displaystyle {+ \int _{\Omega ^b} \left( h_n^2\mu D^b_nu_n D^b_nv +h_ng\vert D^b_nv\vert \right) dx_1dx_2\ge \int _{\Omega ^r}\left( f^r_nv+ p_ndiv^r_n v\right) dx_1dx_2}\\ \displaystyle {+\int _{\Omega ^l}\left( f^l_nv+ p_ndiv^l_n v\right) dx_1dx_2+\int _{\Omega ^b}\left( f^b_nv+ p_ndiv^b_n v\right) dx_1dx_2\quad \forall v\in \left( H_0^1(\Omega )\right) ^2. } \end{array} \end{aligned}$$

(7.2)

Choosing

$$\begin{aligned} v=(\tan \alpha w,w)\hbox { in }\Omega ^r,\quad v=0\hbox { in }\Omega ^l,\quad v=0\hbox { in }\Omega ^b, \end{aligned}$$

with w in $H_0^1(\Omega ^r)$, as test function in (7.2) gets

$$\begin{aligned} \begin{array}{ll} \displaystyle {\int _{\Omega ^r} \left( h_n^2\mu D^r_nu_n D^r_n(\tan \alpha w,w) +h_ng\vert D^r_n(\tan \alpha w,w)\vert \right) dx_1dx_2}\\ \displaystyle {\ge \int _{\Omega ^r}\left( \left( f^r_{n1}\tan \alpha +f^r_{n2}\right) w+ \sqrt{\tan ^2\alpha +1} \, p_n\partial _{\nu _{\alpha }}w\right) dx_1dx_2\quad \forall w\in H_0^1(\Omega ^r).} \end{array} \end{aligned}$$

(7.3)

Then passing to the limit, as n diverges, in (7.3) and using (3.9), (4.3)-(4.7) lead to

$$\begin{aligned} \begin{array}{ll} \displaystyle {\int _{\Omega ^r} \left( \mu \left( 1+\tan ^2\alpha \right) ^2\partial _{x_1}u^r\partial _{x_1}w+g \left( 1+\tan ^2\alpha \right) \vert \partial _{x_1}w\vert \right) dx_1dx_2} \\ \displaystyle {\ge \int _{\Omega ^r} \left( f^r_1\tan \alpha +f^r_2\right) wdx_1dx_2+\sqrt{\tan ^2\alpha +1} \int _{\Omega ^r} p\partial _{\nu _{\alpha }}w dx_1dx_2\quad \forall w\in H_0^1(\Omega ^r).} \end{array} \end{aligned}$$

(7.4)

About the last integral in (7.4), since p is independent of $x_1$ and $T^r(u^r)=0$, one has

$$\begin{aligned} \begin{array}{ll} \displaystyle { \sqrt{\tan ^2\alpha +1} \int _{\Omega ^r}p\partial _{\nu _{\alpha }}w dx_1dx_2}\\ \displaystyle {=\int _0^{L^r}p\left( \tan \alpha \int _{x_2\tan \alpha }^{x_2\tan \alpha +\frac{1}{2}} \partial _{x_1}wdx_1+\int _{x_2\tan \alpha }^{x_2\tan \alpha +\frac{1}{2}} \partial _{x_2}wdx_1\right) dx_2=}\\ \displaystyle {\int _0^{L^r}p\left( \int _{x_2\tan \alpha }^{x_2\tan \alpha +\frac{1}{2}} \partial _{x_2}wdx_1\right) dx_2 =\int _0^{L^r}p\partial _{x_2}\left( \int _{x_2\tan \alpha }^{x_2\tan \alpha +\frac{1}{2}} w dx_1\right) dx_2 }\\ \displaystyle {- \int _0^{L^r} p\left[ \tan \alpha w\left( x_2\tan \alpha +\frac{1}{2},x_2\right) - \tan \alpha w\left( x_2\tan \alpha ,x_2\right) \right] dx_2} \\ \displaystyle {= \int _0^{L^r}p\frac{d}{dx_2}\left( T^r(w)\right) dx_2= \int _0^{L^r}p \frac{d}{dx_2}\left( T^r(w-u^r)\right) dx_2 \quad \forall w\in H^1_0(\Omega ^r).} \end{array} \end{aligned}$$

(7.5)

Combining (7.4) and (7.5) gives

$$\begin{aligned} \begin{array}{ll} \displaystyle {\int _{\Omega ^r} \left( \mu \left( 1+\tan ^2\alpha \right) ^2\partial _{x_1}u^r\partial _{x_1}w+g \left( 1+\tan ^2\alpha \right) \vert \partial _{x_1}w\vert \right) dx_1dx_2}\\ \displaystyle {\ge \int _{\Omega ^r} \left( f^r_1\tan \alpha +f^r_2\right) w dx_1dx_2+ \int _0^{L^r}p \frac{d}{dx_2}\left( T^r(w-u^r)\right) dx_2\quad \forall w\in H_0^1(\Omega ^r).} \end{array} \end{aligned}$$

(7.6)

A density argument (see [12]) ensures that (7.6) holds true with w in $W^r$, i.e.

$$\begin{aligned} \begin{array}{ll} \displaystyle {\int _{\Omega ^r} \left( \mu \left( 1+\tan ^2\alpha \right) ^2\partial _{x_1}u^r\partial _{x_1}w+g \left( 1+\tan ^2\alpha \right) \vert \partial _{x_1}w\vert \right) dx_1dx_2}\\ \displaystyle {\ge \int _{\Omega ^r} \left( f^r_1\tan \alpha +f^r_2\right) w dx_1dx_2+ \int _0^{L^r}p \frac{d}{dx_2}\left( T^r(w-u^r)\right) dx_2\quad \forall w\in W^r.} \end{array} \end{aligned}$$

(7.7)

In particular, choosing $w=u^r\in W^r_0\subset W^r$ in (7.7) gives

$$\begin{aligned} \begin{aligned} \begin{array}{ll} \displaystyle {\int _{\Omega ^r} \left( \mu \left( 1+\tan ^2\alpha \right) ^2\vert \partial _{x_1}u^r\vert ^2+g \left( 1+\tan ^2\alpha \right) \vert \partial _{x_1}u^r\vert \right) dx_1dx_2}\ \\ \displaystyle {\ge \int _{\Omega ^r} \left( f^r_1\tan \alpha +f^r_2\right) u^r dx_1dx_2.} \end{array} \end{aligned}\end{aligned}$$

(7.8)

Arguing as above, but replacing $p_n$ with $q_n$ in (3.8), gives variational inequality (7.2) with $p_n$ replaced by $q_n$. Then, choosing $v=0$ in $\Omega ^r$, $v=(\tan \beta w,w)$ in $\Omega ^l$, $v=0$ in $\Omega ^b$, with w in $H_0^1(\Omega ^l)$, as test function in this new variational inequality, and then passing to the limit in it, as $n\rightarrow +\infty$, the same arguments used above lead to

$$\begin{aligned} \begin{array}{ll} \displaystyle {\int _{\Omega ^l} \left( \mu \left( 1+\tan ^2\beta \right) ^2\partial _{x_1}u^l\partial _{x_1}w+g \left( 1+\tan ^2\beta \right) \vert \partial _{x_1}w\vert \right) dx_1dx_2} \\ \displaystyle {\ge \int _{\Omega ^r} \left( f^l_1\tan \beta +f^l_2\right) w dx_1dx_2+ \int _0^{L^l}q \frac{d}{dx_2}\left( T^l(w-u^l)\right) dx_2\quad \forall w\in W^l.} \end{array} \end{aligned}$$

(7.9)

In particular, choosing $w=u^l\in W^l_0\subset W^l$ in (7.9) gives

$$\begin{aligned} \begin{array}{ll} \displaystyle {\int _{\Omega ^l} \left( \mu \left( 1+\tan ^2\beta \right) ^2\vert \partial _{x_1}u^l\vert ^2+g \left( 1+\tan ^2\beta \right) \vert \partial _{x_1}u^l\vert \right) dx_1dx_2} \\ \displaystyle {\ge \int _{\Omega ^l} \left( f^l_1\tan \beta +f^l_2\right) u^l dx_1dx_2.} \end{array} \end{aligned}$$

(7.10)

Similarly, one can obtain (7.2) with $p_n$ replaced by $s_n$. Then, choosing $v=0$ in $\Omega ^r$, $v=0$ in $\Omega ^l$, $v=(0,w)$ in $\Omega ^b$, with w in $H_0^1(\Omega ^b)$, as test function in this new variational inequality, and then passing to the limit in it, as $n\rightarrow +\infty$, the same arguments used above lead to

$$\begin{aligned} \begin{array}{ll} \displaystyle {\int _{\Omega ^b} \left( \mu \partial _{x_1}u^b\partial _{x_1}w+g\vert \partial _{x_1}w\vert \right) dx_1dx_2} \\ \displaystyle {\ge \int _{\Omega ^b} f^b_2 w dx_1dx_2+ \int _{-L^b}^0s\frac{d}{dx_2}\left( T^b(w-u^b)\right) dx_2\quad \forall w\in W^b.} \end{array} \end{aligned}$$

(7.11)

In particular, choosing $w=u^b \in W^b_0\subset W^b$ in (7.11) gives

$$\begin{aligned} \begin{array}{ll} \displaystyle {\int _{\Omega ^b} \left( \mu \vert \partial _{x_1}u^b\vert ^2+g\vert \partial _{x_1}u^b\vert \right) dx_1dx_2\ge \int _{\Omega ^b} f^b_2 u^b dx_1dx_2.} \end{array} \end{aligned}$$

(7.12)

Now, adding (7.8), (7.10), and (7.12) provides

$$\begin{aligned} \begin{array}{ll} \displaystyle {\int _{\Omega ^r} \left( \mu \left( 1+\tan ^2\alpha \right) ^2\vert \partial _{x_1}u^r\vert ^2+g \left( 1+\tan ^2\alpha \right) \vert \partial _{x_1}u^r\vert \right) dx_1dx_2}\\ \displaystyle {+\int _{\Omega ^l} \left( \mu \left( 1+\tan ^2\beta \right) ^2\vert \partial _{x_1}u^l\vert ^2+g \left( 1+\tan ^2\beta \right) \vert \partial _{x_1}u^l\vert \right) dx_1dx_2}\\ \displaystyle {+ \int _{\Omega ^b} \left( \mu \vert \partial _{x_1}u^b\vert ^2+g\vert \partial _{x_1}u^b\vert \right) dx_1dx_2} \\ \displaystyle {\ge \int _{\Omega ^r} \left( f^r_1\tan \alpha +f^r_2\right) u^r dx_1dx_2+\int _{\Omega ^l} \left( f^l_1\tan \beta +f^l_2\right) u^l dx_1dx_2+\int _{\Omega ^b} f^b_2 u^b dx_1dx_2.} \end{array} \end{aligned}$$

(7.13)

On the other hand, passing to the limit in (7.1) and using (3.9), (4.3), (4.4), (4.5), and a l.s.c. argument provide

$$\begin{aligned} \begin{array}{ll} \displaystyle {\int _{\Omega ^r} \left( \mu \left( 1+\tan ^2\alpha \right) ^2\vert \partial _{x_1}u^r\vert ^2+g \left( 1+\tan ^2\alpha \right) \vert \partial _{x_1}u^r\vert \right) dx_1dx_2}\\ \displaystyle {+\int _{\Omega ^l} \left( \mu \left( 1+\tan ^2\beta \right) ^2\vert \partial _{x_1}u^l\vert ^2+g \left( 1+\tan ^2\beta \right) \vert \partial _{x_1}u^l\vert \right) dx_1dx_2}\\ \displaystyle {+ \int _{\Omega ^b} \left( \mu \vert \partial _{x_1}u^b\vert ^2+g\vert \partial _{x_1}u^b\vert \right) dx_1dx_2} \\ \displaystyle {\le \int _{\Omega ^r} \left( f^r_1\tan \alpha +f^r_2\right) u^r dx_1dx_2+\int _{\Omega ^l} \left( f^l_1\tan \beta +f^l_2\right) u^l dx_1dx_2+\int _{\Omega ^b} f^b_2 u^b dx_1dx_2.} \end{array} \end{aligned}$$

(7.14)

Combining (7.13) and (7.14) implies

$$\begin{aligned} \begin{array}{ll} \displaystyle {\int _{\Omega ^r} \left( \mu \left( 1+\tan ^2\alpha \right) ^2\vert \partial _{x_1}u^r\vert ^2+g \left( 1+\tan ^2\alpha \right) \vert \partial _{x_1}u^r\vert \right) dx_1dx_2}\\ \displaystyle {+\int _{\Omega ^l} \left( \mu \left( 1+\tan ^2\beta \right) ^2\vert \partial _{x_1}u^l\vert ^2+g \left( 1+\tan ^2\beta \right) \vert \partial _{x_1}u^l\vert \right) dx_1dx_2}\\ \displaystyle {+ \int _{\Omega ^b} \left( \mu \vert \partial _{x_1}u^b\vert ^2+g\vert \partial _{x_1}u^b\vert \right) dx_1dx_2} \\ \displaystyle {=\int _{\Omega ^r} \left( f^r_1\tan \alpha +f^r_2\right) u^r dx_1dx_2+\int _{\Omega ^l} \left( f^l_1\tan \beta +f^l_2\right) u^l dx_1dx_2+\int _{\Omega ^b} f^b_2 u^b dx_1dx_2.} \end{array} \end{aligned}$$

(7.15)

Now comparing (7.8), (7.10), (7.12), and (7.15) leads to

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle {\int _{\Omega ^r} \left( \mu \left( 1+\tan ^2\alpha \right) ^2\vert \partial _{x_1}u^r\vert ^2+g \left( 1+\tan ^2\alpha \right) \vert \partial _{x_1}u^r\vert \right) dx_1dx_2} \\ \displaystyle {=\int _{\Omega ^r} \left( f^r_1\tan \alpha +f^r_2\right) u^r dx_1dx_2,}\\ \displaystyle {\int _{\Omega ^l} \left( \mu \left( 1+\tan ^2\beta \right) ^2\vert \partial _{x_1}u^l\vert ^2+g \left( 1+\tan ^2\beta \right) \vert \partial _{x_1}u^l\vert \right) dx_1dx_2} \\ \displaystyle {=\int _{\Omega ^l} \left( f^l_1\tan \beta +f^l_2\right) u^l dx_1dx_2,}\\ \displaystyle {\int _{\Omega ^b} \left( \mu \vert \partial _{x_1}u^b\vert ^2+g\vert \partial _{x_1}u^b\vert \right) dx_1dx_2=\int _{\Omega ^b} f^b_2 u^b dx_1dx_2.} \end{array}\right. \end{aligned}$$

(7.16)

Eventually, (7.7), (7.9), (7.11), and (7.16) ensure that $(u^r, p)$, $(u^l, q)$, and $(u^b, s)$ solve (4.8), (4.9), and (4.10), respectively. $\square$

8 A Lower-Dimensional “Bingham-like” Law

We analyze limit problem (4.8), stated in the right branch of the domain. By taking as test function $\displaystyle \frac{w}{1+ \tan ^2\alpha }$ and denoting $\displaystyle {\widetilde{u}}^r= (1+ \tan ^2\alpha )u^r,\, {\widetilde{p}} = \frac{p}{1+ \tan ^2\alpha }$, problem (4.8) becomes

$$\begin{aligned} \left\{ \begin{array}{ll} {\widetilde{u}}^r \in W^r_0(\Omega ^r),\quad {\widetilde{p}}\in L^2(\Omega ^r),\\ \displaystyle {\int _{\Omega ^r} \mu \partial _{x_1} {\widetilde{u}}^r\partial _{x_1}\left( w-{\widetilde{u}}^r\right) +g \left( \vert \partial _{x_1}w\vert -\vert \partial _{x_1}{\widetilde{u}}^r\vert \right) dx_1dx_2}\\ \displaystyle { \ge \int _{\Omega ^r} \frac{\left( f^r_1\tan \alpha +f^r_2\right) }{ 1+\tan ^2\alpha } \left( w-{\widetilde{u}}^r\right) dx_1dx_2+ \int _0^{L^r}{\widetilde{p}} \frac{d\left( T^r(w-{\widetilde{u}}^r)\right) }{dx_2}dx_2}\,\,\,\forall w\in W^r(\Omega ^r). \end{array} \right. \end{aligned}$$

(8.1)

According to Sect. 5 in [12], the following differential equation in $\Omega ^r$ is derived from problem (8.1)

$$\begin{aligned} -\partial _{x_1}\left[ \mu \partial _{x_1} {\widetilde{u}}\,^r(x_1,x_2) + g \,\hbox {sgn}\left( \partial _{x_1} {\widetilde{u}}\,^r (x_1,x_2) \right) \right] = \frac{f_1^r(x_1,x_2)\tan \alpha + f^r_2(x_1,x_2) }{ 1+\tan ^2\alpha } - {\widetilde{p}}\,^{\prime }(x_2), \end{aligned}$$

which is valid if $\displaystyle \partial _{x_1} {\widetilde{u}}^r \ne 0$ and where $\hbox {sgn}$ states for the signum function.

As in [11, 12], we define, up to an additive function of $x_2$, the limiting stress tensor

$$\begin{aligned} \sigma _{21}=- {\widetilde{p}}\,^{\prime } (x_2)+ {\widetilde{\sigma }}_{21}, \hbox { with } \displaystyle \widetilde{\sigma }_{21}=\mu \partial _{x_1}{\widetilde{u}}^r+ g \,\hbox {sgn}\left( \partial _{x_1} {\widetilde{u}}^r \right) . \end{aligned}$$

(8.2)

This is exactly the following lower-dimensional “Bingham-like” law describing the limit strain tensor, corresponding to the model used in the engineering literature for the Bingham flow in thin domains (for instance, see [29])

$$\begin{aligned} \vert \widetilde{\sigma }_{21} \vert \le g \Leftrightarrow \mu \partial _{x_1}{\widetilde{u}}^r= 0 ,\quad \quad \vert \widetilde{\sigma }_{21} \vert > g \Leftrightarrow \mu \partial _{x_1}{\widetilde{u}}^r = \widetilde{\sigma }_{21} -g \, \hbox {sgn}\left( \partial _{x_1}{\widetilde{u}}^r \right) , \end{aligned}$$

(8.3)

where $\widetilde{\sigma }_{21}$ represents the constraint. Indeed, we notice that, if $\partial _{x_1}{\widetilde{u}}^r \ne 0$, then relation (8.2) implies $\vert \widetilde{\sigma }_{21}\vert > g$. Consequently, if $\vert \widetilde{\sigma }_{21} \vert \le g$, we have $\partial _{x_1}{\widetilde{u}}^r= 0$.

We note that the constitutive law (8.3) is the limit of the initial constitutive law (2.3).

Analogous results hold true for the limit problem (4.9), stated in the left branch, as far as for the limit problem (4.10), stated in the vertical branch: in each case one can exhibit a lower-dimensional “Bingham-like” law.