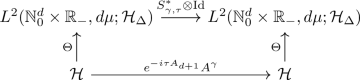The Drury–Arveson Space on the Siegel Upper Half-space and a von Neumann Type Inequality

Abstract

In this work we study what we call Siegel–dissipative vector of commuting operators $(A_1,\ldots , A_{d+1})$ on a Hilbert space ${{\mathcal {H}}}$ and we obtain a von Neumann type inequality which involves the Drury–Arveson space DA on the Siegel upper half-space ${{\mathcal {U}}}$. The operator $A_{d+1}$ is allowed to be unbounded and it is the infinitesimal generator of a contraction semigroup $\{e^{-i\tau A_{d+1}}\}_{\tau <0}$. We then study the operator $e^{-i\tau A_{d+1}}A^{\alpha }$ where $A^{\alpha }=A_1^{\alpha _1}\cdots A^{\alpha _d}_d$ for $\alpha \in {\mathbb N}_0^d$ and prove that can be studied by means of model operators on a weighted $L^2$ space. To prove our results we obtain a Paley–Wiener type theorem for DA and we investigate some multiplier operators on DA as well.

1 Introduction

The Drury–Arveson space $DA({\mathbb B}^{d+1})$ on the unit ball of ${\mathbb C}^{d+1}$ is a renowned Hilbert space of holomorphic functions endowed with the inner product

$$\begin{aligned} \langle \sum _{\alpha \in {\mathbb N}_0^{d+1}}b_\alpha z^\alpha ,\sum _{\alpha \in {\mathbb N}_0^{d+1}}c_\alpha z^\alpha \rangle _{DA({\mathbb B}^{d+1})} :=\sum _{\alpha \in {\mathbb N}_0^{d+1}}b_\alpha \overline{c_\alpha }\frac{\alpha !}{|\alpha |!}. \end{aligned}$$

We refer the reader to [4, Theorem 6.1] for an exact integral representation of such inner product. The space $DA({\mathbb B}^{d+1})$ is a reproducing kernel Hilbert space with kernel $K(z,w)=(1-z\cdot {\overline{w}})^{-1}$ and may be considered the natural multi-dimensional version of the Hardy space on the unit disc $H^2({\mathbb D})$; one of the main reasons being that $DA({\mathbb B}^{d+1})$ plays the same role as $H^2({\mathbb D})$ in a multi-dimensional version of the famous von Neumann Inequality.

Theorem 1.1

(Drury [9]) Let ${{\mathcal {H}}}$ be a Hilbert space and consider the $(d+1)$-tuple $T=(T_1,\ldots , T_{d+1})$ of linear operators on ${{\mathcal {H}}}$ satisfying

• (i) $T_jT_k-T_kT_j=0$ for all $j,k=1,\ldots ,d+1$;

• (ii) $\sum _{j=1}^{d+1}\Vert T_j v\Vert _{{{\mathcal {H}}}}^2\le \Vert v\Vert ^2_{{{\mathcal {H}}}}$ for all $v\in {{\mathcal {H}}}$.

Let $p(z)=p(z_1,\ldots ,z_{d+1})$ be a complex polynomial. Then,

$$\begin{aligned} \Vert p(T)\Vert _{_{{{\mathcal {B}}}({{\mathcal {H}}})}}\le \Vert p\Vert _{{{\mathcal {M}}}(DA({\mathbb B}^{d+1}))} \end{aligned}$$

where $\Vert \cdot \Vert _{{{\mathcal {B}}}({{\mathcal {H}}})}$ and $\Vert \cdot \Vert _{{{\mathcal {M}}}(DA({\mathbb B}^{d+1}))}$ denote the norm of bounded linear operators on ${{\mathcal {H}}}$ and the multiplier operator norm on the Drury–Arveson space on the unit ball respectively.

In the case $d=0$ Drury’s result reduces to the classical von Neumann Inequality ( [22]) and the multiplier operator norm on $H^2({\mathbb D})$ takes the place of $\Vert \cdot \Vert _{{{\mathcal {M}}}(DA(\mathbb B^{d+1}))}$. Namely, given a Hilbert space ${{\mathcal {H}}}$ and $T:{{\mathcal {H}}}\rightarrow {{\mathcal {H}}}$ a contraction, i.e., $\Vert T\Vert _{{{\mathcal {B}}}({{\mathcal {H}}})}\le 1$, the von Neumann Inequality states that, for any polynomial p(z),

$$\begin{aligned} \Vert p(T)\Vert _{{{\mathcal {B}}}({{\mathcal {H}}})}\le \Vert p\Vert _{{{\mathcal {M}}}(H^2({\mathbb D}))}=\Vert p\Vert _{\infty }. \end{aligned}$$

It is possible to prove an analogous result modeled on the upper-half plane, which is the unbounded biholomorphic realization of the unit disk ${\mathbb D}$ via the Cayley transform. Let A be any bounded dissipative operator on a Hilbert space ${{\mathcal {H}}}$, that is, such that $\frac{1}{i} (A-A^*)\ge 0$, then

$$\begin{aligned} \Vert f(A)\Vert _{{{\mathcal {B}}}({{\mathcal {H}}})}\le \sup _{{\text {Im}}z>0}|f(z)| \end{aligned}$$

for any rational function f which is bounded on the upper half-plane, see [23].

The main goal of this paper is to prove a version of Theorem 1.1 on an unbounded biholomorphic realization of the unit ball ${\mathbb B}^{d+1}$ in ${\mathbb C}^{d+1}$, that is, the Siegel upper-half space ${{\mathcal {U}}}$,

$$\begin{aligned} {{\mathcal {U}}}=\left\{ (\zeta ,\zeta _{d+1}):{\mathbb C}^{d+1}: {\text {Im}}\zeta _{d+1}> \textstyle {\frac{1}{4}}|\zeta |^2\right\} . \end{aligned}$$

(1.1)

The biholomorphism between the ball and the Siegel half-space is given by the multi-dimensional Cayley transform ${{\mathcal {C}}}:\mathbb B^{d+1}\rightarrow {{\mathcal {U}}}$,

$$\begin{aligned} {\mathcal {C}}(\omega ,\omega _{d+1})=\bigg (\frac{2\omega }{1-\omega _{d+1}},i\frac{1+\omega _{d+1}}{1-\omega _{d+1}}\bigg ). \end{aligned}$$

(1.2)

The Drury–Arveson space on ${{\mathcal {U}}}$, that we shall simply denote by DA, was studied in [6] and [4], where an integral expression for the norm was also obtained. Let $\rho (\zeta ,\zeta _{d+1})={\text {Im}}\zeta _{d+1}-\frac{1}{4}|\zeta |^2$ and let n be an integer such that $n>d/2$. Then, we define the space $DA_{(n)}$ as

$$\begin{aligned}&DA_{(n)}=\Big \{ F\in {\text {Hol}}({{\mathcal {U}}}) : \mathrm{(i)} \displaystyle { \lim _{|\zeta |\le R,\, {\text {Im}}\zeta _{d+1}\rightarrow +\infty } F(\zeta ,\zeta _{d+1}) =0} \,;\nonumber \\&\mathrm{(ii)} \displaystyle {\int _{{\mathcal {U}}}|\rho ^n(\zeta ,\zeta _{d+1}) \partial _{\zeta _{d+1}}^n F(\zeta ,\zeta _{d+1})|^2 \, \rho ^{-d-1}(\zeta ,\zeta _{d+1}) d\zeta d\zeta _{d+1} <+\infty }\, \Big \}\,. \end{aligned}$$

(1.3)

The space $DA_{(n)}$ does not actually depend on n, so that we simply write DA in place of $DA_{(n)}$. We refer the reader to Sect. 3 for this and other properties of the space DA.

We now describe the operator-theorical condition we shall work with.

Definition 1.2

Let ${{\mathcal {H}}}$ be a Hilbert space and let $(A_1,\ldots , A_{d+1})$ be a vector of operators on ${{\mathcal {H}}}$ and let $r(iA_{d+1})$ be the resolvent set of $iA_{d+1}$. We say that $(A_1,\ldots ,A_{d+1})$ is a Siegel–dissipative vector of commuting operators if:

• (i) the operators $A_1,\dots A_d$ are bounded and $(0,+\infty ) \subseteq r (i A_{d+1})$;

• (ii) the operators $A_1, \dots A_d$ commute with each other and they strongly commute with $A_{d+1}$;

• (iii) the following condition holds:¹

  $$\begin{aligned} {\text {Im}}\langle A_{d+1}v , v \rangle _{{{\mathcal {H}}}}\ge \frac{1}{4}\sum _{i=1}^d \Vert {A_i v}\Vert ^2_{{{\mathcal {H}}}}, \,\,\, \forall v \in {\text {Dom}}(A_{d+1}). \end{aligned}$$

  (1.4)

Given two operators U and T on ${{\mathcal {H}}}$, U densely defined and closed, T bounded, we say that U and T strongly commute if UT is an extension of TU. In other words $T({{\mathcal {H}}}) \subseteq {\text {Dom}}(U)$ and $TUv=UTv$ for all $v \in {\text {Dom}}(U)$.

We point out that from the conditions above and the Lumer–Philips Theorem (Theorem 2.5) it follows that $iA_{d+1}$ is the infinitesimal generator of a (unique) semigroup of contractions $\{e^{-i\tau A_{d+1}}\!\}_{\tau \le 0}$ that commutes with all the $A_j$’s, see Lemma 5.1. Our von Neumann type inequality reads as follows.

Theorem 1.3

Let ${{\mathcal {H}}}$ be a Hilbert space and let $(A_1,\ldots ,A_{d+1})$ be a Siegel–dissipative vector of commuting operators. For any $\tau _j<0$, $j=1,\dots ,d$, set $M_j = e^{-i\tau _j A_{d+1}}A_j$ and $m_j(\zeta ,\zeta _{d+1}) = e^{-i\tau _j \zeta _{d+1}}\zeta _j$. Let p denote any polynomial in d variables. Then we have that $m_j\in {{\mathcal {M}}}(DA)$ for $j=1,\dots ,d$, and

$$\begin{aligned} \Vert p\big ( M_1,\dots , M_d)\Vert _{{{\mathcal {B}}}({{\mathcal {H}}})}\le \Vert p\big ( m_1,\dots , m_d) \Vert _{{{\mathcal {M}}}(DA)} , \end{aligned}$$

(1.5)

where ${{\mathcal {M}}}(DA)$ is the space of pointwise multipliers on the Drury–Arveson space DA.

A few remarks are now in order. The space DA is a reproducing kernel Hilbert space, and, with respect to the $DA_{(n)}$-norm, its reproducing kernel is

$$\begin{aligned} K_{DA}((\omega ,\omega _{d+1}),(\zeta ,\zeta _{d+1)}) = \gamma _{d,n} \Big ( \frac{\omega _{d+1}-\overline{\zeta }_{d+1}}{2i} - \textstyle {\frac{1}{4}} \omega \cdot \overline{\zeta } \Big )^{-1} \,, \end{aligned}$$

where $\gamma _{d,n}= \frac{4^n}{(4\pi )^{d+1}\Gamma (2n-d)}$. Hence, notice that the condition (1.4) is modelled after the reproducing kernel of DA. In general, it is a well established phenomenon that von Neumann type inequalities hold as long as one can suitably interpret the condition $K^{-1}(A,A)\ge 0$, where K is the reproducing kernel of a space of holomorphic functions in some domain in ${\mathbb C}^d$. A precise formulation of this result is stated and proved in [2]. There the authors use the Dunford-Riesz functional calculus to define $K^{-1}(A, A)$. This is possible since they are working with bounded operators with some additional assumptions on their spectrum. Furthermore, they assume that the multiplication by any coordinate function is a continuous (bounded) operation. Our setting differs in these two latter aspects. The last operator $A_{d+1}$ is allowed to be unbounded and also the multiplication by any coordinate is an unbounded operation in DA.

We also mention that, in the case when all the operators are bounded, a proof of the von Neumann type inequality (1.5) could probably be obtained by means of the Cayley transform, the classical inequality of Drury on the unit ball and some classical results in operator theory as it was pointed out to us by M. Hartz in a private communication. Nevertheless, in the footsteps of Drury’s proof, we prefer to use a direct approach, without relying on the known results on the unit ball, for two main reasons. First, we have greater generality by allowing one operator to be unbounded. Second, and more importantly, we develop some machinery we believe it is interesting in its own right and has the potential to be used in the context of the theory of shift-invariant subspaces of DA, as in the spirit of Buerling–Lax’s Theorem [12], in the Siegel half-space setting.

In order to follow such a plan, we further investigate some operator-theorical properties of DA. On the space ${\mathbb N}_0^d\times {\mathbb R}_-$ we consider the measure

$$\begin{aligned} d\mu (\alpha ,\lambda ) =\alpha !\left( \frac{2}{|\lambda |}\right) ^{|\alpha |}|\lambda |^{2d}\, d\alpha \, d\lambda \end{aligned}$$

(1.6)

with $d\lambda$ denoting the Lebesgue measure on ${\mathbb R}_{-}$ and $d\alpha$ the counting measure on ${\mathbb N}_0^{d}$.

Theorem 1.4

The map ${{\mathscr {S}}}:\, L^2({\mathbb N}_0^d\times {\mathbb R}_-,\,d\mu )\rightarrow DA$ defined as

$$\begin{aligned} ({{\mathscr {S}}}\varphi ) (\zeta ,\zeta _{n+1}) = \frac{1}{(2\pi )^{d+1}} \int _{{\mathbb N}_0^d\times {\mathbb R}_-} \zeta ^\alpha e^{-i\lambda \zeta _{d+1}} \overline{\varphi (\alpha ,\lambda )}\,|\lambda |^d\, d\alpha d\lambda \end{aligned}$$

is a conjugate linear surjective isometry. The inverse map ${{\mathscr {S}}}^{-1}$ is explicitly given in (3.1).

If for some $\varepsilon >0$ the $(d+1)$-tuple $(A_1,\dots ,A_d,A_{d+1}-i\varepsilon {{\,\mathrm{Id}\,}})$ is Siegel-dissipative, we say that $(A_1,\ldots ,A_{d+1})$ is strongly Siegel–dissipative. In this case, for $v,v'\in {\text {Dom}}(A_{d+1})$ consider the inner product

$$\begin{aligned} \langle v,v'\rangle _{\Delta }:=\frac{1}{2i}\big (\langle A_{d+1}v,v'\rangle _{{{\mathcal {H}}}}-\langle v,A_{d+1}v'\rangle _{{{\mathcal {H}}}}\big )-\frac{1}{4}\sum _{i=1}^{d}\langle v,v'\rangle _{{{\mathcal {H}}}} \end{aligned}$$

so that

$$\begin{aligned} \Vert v \Vert ^2 _{\Delta } ={\text {Im}}\langle A_{d+1}v , v \rangle _{{{\mathcal {H}}}}-\frac{1}{4} \sum _{i=1}^d \Vert A_i v \Vert ^2_{{{\mathcal {H}}}} \ge \varepsilon \Vert v \Vert ^2_{{{\mathcal {H}}}}, \,\,\, \forall v \in {\text {Dom}}(A_{d+1}), \end{aligned}$$

which is a stronger condition than (1.4). If ${{\mathcal {H}}}_\Delta =({\text {Dom}}{A_{d+1}},\Vert \cdot \Vert _{\Delta })$ we define

$$\begin{aligned} \begin{aligned} {{\mathcal {L}}}^2&(\Delta ):=L^2({\mathbb N}_0^d\times {\mathbb R}_{-},d\mu ;{{\mathcal {H}}}_\Delta )\\&=\Big \{ g :{\mathbb N}_0^d\times {\mathbb R}_{-} \rightarrow {\text {Dom}}A_{d+1}: \sum _{\alpha \in {\mathbb N}_0^d}\int _{-\infty }^0 \Vert g (\alpha ,\lambda )\Vert ^2_\Delta \ d\mu (\alpha ,\lambda )<+\infty \Big \}. \end{aligned} \end{aligned}$$

With our assumptions it follows that ${{\mathcal {L}}}^2(\Delta )$ is a pre-Hilbert space. Before stating our result on $d+1$-tuples of operators we also need to study some weighted shift operators on $L^2({\mathbb N}_0^d\times {\mathbb R}_-,\, d\mu )$, which correspond to some multiplier operators on DA (see Sect. 4). If $\alpha ,\gamma \in {\mathbb N}_0^d$ we write $\alpha \ge \gamma$ meaning that $\alpha _i\ge \gamma _i$ for all $i=1,\ldots ,d$. Then, we prove the following.

Theorem 1.5

Let $\gamma \in {\mathbb N}_0^d$ and $\tau <0$. Then, the operator

$$\begin{aligned} (S_{\gamma ,\tau } \varphi )(\alpha ,\lambda ) = {\left\{ \begin{array}{ll} \frac{|\lambda -\tau |^d}{|\lambda |^d}\varphi (\alpha - \gamma , \lambda - \tau ) &{} \text {if} \quad \lambda <\tau \wedge \alpha \ge \gamma ;\\ \\ 0 &{} \text {otherwise,} \end{array}\right. } \end{aligned}$$

extends to a bounded linear operator on $L^2({\mathbb N}_0^d\times {\mathbb R}_-, d\mu )$ unitarily equivalent to the multiplier operator on DA with multiplier $\zeta ^\gamma e^{-i\tau \zeta _{d+1}}$. Furthermore, its adjoint is given by the formula

$$\begin{aligned} (S_{\gamma ,\tau }^*\varphi )(\alpha , \lambda ) = \frac{|\lambda +\tau |^{d-|\alpha |-|\gamma |}}{|\lambda |^{d-|\alpha |}} \frac{(\alpha +\gamma )!}{\alpha ! } 2^{|\gamma |} \varphi (\alpha +\gamma , \lambda + \tau ). \end{aligned}$$

We remark that, if we call the multipliers $m_j$, $j=1,\dots ,d$, that appear in Theorem 1.3 the shift operators on DA, then the operators $S_{\gamma ,\tau }$ correspond to the operators ${{\mathscr {S}}}^{-1} m_j {{\mathscr {S}}}$. Finally, we have the following result.

Theorem 1.6

Let $(A_1,\ldots ,A_{d+1})$ be a strongly Siegel–dissipative vector of commuting operators and set $A^{\alpha }= A_1^{\alpha _1}\cdots A^{\alpha _d}_d$ for any multi-index $\alpha \in {\mathbb N}_0^d$. Then:

• (i) the map $\Theta :{{\mathcal {H}}}\rightarrow L^2(\mathbb {N}_0^d\times {\mathbb R}_{-},d\mu ; {{\mathcal {H}}}_\Delta )$ defined as

  $$\begin{aligned} (\Theta v)(\alpha ,\lambda )=\frac{|\lambda |^{|\alpha |-d}}{\alpha ! 2^{|\alpha |-\frac{1}{2}}}e^{-i\lambda A_{d+1}}A^\alpha v \end{aligned}$$

  is an isometric embedding, i.e.,

  $$\begin{aligned} \Vert \Theta v\Vert _{{{\mathcal {L}}}^2(\Delta )}=\Vert v\Vert _{{{\mathcal {H}}}}, \,\,\, \forall v \in {{\mathcal {H}}}. \end{aligned}$$

• (ii) the diagram

  

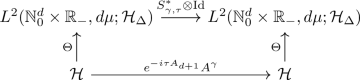  (1.7)

  commutes.

We conclude this introduction pointing out that the Drury–Arveson space $DA({\mathbb B}^{d+1})$ on the unit ball of ${\mathbb C}^{d+1}$ has drawn considerable interest since its first appearance in the works of Drury and of Arveson [7, 9]. We mention [3, 5, 6, 10, 16] and references therein. The Drury–Arveson space on ${{\mathcal {U}}}$ was studied in [6] and [4]; see also [8] for the case of more general Siegel type domains.

The paper is organized as follows. In Sect. 2 we recall some preliminary facts, in Sect. 3 we study the space DA and we prove Theorem 1.4. In Sect. 4 we study some multiplier operators on DA and we prove Theorem 1.5. We conclude proving Theorem 1.6 and Theorem 1.3 in Sect. 5.

2 Preliminary Facts

In this section we first recall some basic facts on the Siegel half-space, the Heisenberg group and the group Fourier transform. Then we also recall some simple properties of semigroups of operators on a Hilbert space.

2.1 The Siegel Upper Half-space and the Heisenberg Group

The Siegel upper half-space is defined in (1.1) and it is biholomorphically equivalent to the unit ball ${\mathbb B}^{d+1}$ via the Cayley transfom (1.2). Standard references for the facts that follow are e.g. [11, 17, 20]. We introduce new coordinates on ${{\mathcal {U}}}$ setting $\Psi (\zeta ,\zeta _{d+1})=(z,t,h)$ where

$$\begin{aligned} {\left\{ \begin{array}{ll} z=\zeta \\ t= {\text {Re}}\zeta _{d+1}\\ h ={\text {Im}}\zeta _{d+1} -\frac{1}{4}|\zeta |^2 \,. \end{array}\right. } \end{aligned}$$

Then, if ${{\mathbf {U}}}={\mathbb C}^d\times {\mathbb R}\times (0,+\infty )$, $\Psi : \overline{{{\mathcal {U}}}}\rightarrow \overline{{{\mathbf {U}}}}$ is a $C^\infty$-diffeomorphism and $\Psi ^{-1}$ is given by

$$\begin{aligned} \Psi ^{-1} (z,t,h) = \bigl (z,t+i\textstyle {\frac{1}{4}}|z|^2+ih\bigr ) =: (\zeta ,\zeta _{d+1}) \,. \end{aligned}$$

Notice that $h=\varrho (\zeta ,\zeta _{d+1})$ and $\Psi (\zeta , t+\frac{i}{4}|\zeta |^2)=(z,t,0)$. In this case we write [z, t] in place of (z, t, 0) and we also use the abuse of notation $[z,t]\in \partial {{\mathcal {U}}}$. We now let the points in $\partial {{\mathcal {U}}}$ act on $\overline{{{\mathcal {U}}}}$ as biholomorphic maps in the following way. For $[z,t]\in \partial {{\mathcal {U}}}$ set

$$\begin{aligned} \Phi _{[z,t]} (\omega ,\omega _{d+1}) = \bigl (\omega +z, \omega _{d+1} +t +i\textstyle {\frac{1}{4}}|z|^2+ \frac{i}{2} \omega \cdot {\bar{z}} \bigr ) \,, \end{aligned}$$

(2.1)

where $\omega \cdot {\bar{z}}=\sum _{j=1}^d\omega _j{\bar{z}}_j$ denotes the inner product in ${\mathbb C}^d$. Notice that

$$\begin{aligned} \varrho \Bigl ( \Phi _{[z,t]} (\omega ,\omega _{d+1})\Bigr )&= \varrho (\omega ,\omega _{d+1})\,, \end{aligned}$$

that is, the maps $\Phi _{[z,t]}$ preserve the defining function $\varrho$. In particular, for $(\omega ,\omega _{d+1})\in \partial {{\mathcal {U}}}$ and $[w,s]=\Psi (\omega ,\omega _{d+1})$, by (2.1) we have

$$\begin{aligned} \Phi _{[z,t]} \big ( (\omega ,\omega _{d+1})\big )&= \Phi _{[z,t]} \Big ( \Psi ^{-1} (w,s,0)\Big ) = \Phi _{[z,t]} \bigl (w,s+i\textstyle {\frac{1}{4}}|w|^2\bigr ) \nonumber \\&=\bigl (w+z,s+\textstyle {\frac{i}{4}}|w|^2+t+ \textstyle {\frac{i}{4}}|z|^2 +\textstyle {\frac{i}{2}} w\cdot \bar{z}\bigr ) \nonumber \\&=\bigl [ w+z,s+t -\textstyle {\frac{1}{2}}{\text {Im}}(w \cdot \bar{z})\bigr ] \nonumber \\&=: [w,s][z,t] \, . \end{aligned}$$

Hence, it is possible to introduce a group structure on $\partial {{\mathcal {U}}}$ itself.

Definition 2.1

The Heisenberg group ${\mathbb H}_d$ is the set ${\mathbb C}^d\times {\mathbb R}$ endowed with product

$$\begin{aligned}{}[w,s][z,t] = \big [ w+z, s+t -\textstyle {\frac{1}{2}} {\text {Im}}(w\cdot {\bar{z}})\big ] \,. \end{aligned}$$

The right and left Haar measures on the Heisenberg group coincide with the Lebesgue measure on ${\mathbb C}^d\times {\mathbb R}$. In particular, the Lebesgue measure is both left and right translation invariant.

We now recall the basic facts for the Fourier transform on the Heisenberg group. For $\lambda \in {\mathbb R}{\setminus }\{0\}$ define the Fock space

$$\begin{aligned} {{\mathcal {F}}}^\lambda =\bigg \{ F \in {\text {Hol}}({\mathbb C}^d):\ \bigg ( \frac{|\lambda |}{2\pi } \bigg )^d \int _{{\mathbb C}^d} |F(z)|^2\, e^{-\frac{\lambda }{2} |z|^2}dz <+\infty \bigg \} \end{aligned}$$

when $\lambda >0$, and ${{\mathcal {F}}}^\lambda = {{\mathcal {F}}}^{|\lambda |}$ when $\lambda <0$. The Fock space is a reproducing kernel Hilbert space with reproducing kernel $e^{\frac{|\lambda |}{2}z\cdot \overline{w}}$. A complete orthonormal basis of ${{\mathcal {F}}}^\lambda$ is given by the normalized monomials $\{z^\alpha /\Vert z^\alpha \Vert _{{{\mathcal {F}}}^\lambda }\}_{\alpha \in {\mathbb N}_0^d}$, where

$$\begin{aligned} \Vert z^\alpha \Vert _{{{\mathcal {F}}}^\lambda }^2 = \alpha ! \bigg (\frac{2}{|\lambda |}\bigg )^{|\alpha |} \,. \end{aligned}$$

For $[z,t]\in {\mathbb H}_d$, the Bargmann representation $\sigma _\lambda [z,t]$ is the operator acting on ${{\mathcal {F}}}^\lambda$ given by,

$$\begin{aligned} \sigma _\lambda [z,t] F (w) = e^{i\lambda t-\frac{\lambda }{2} w\cdot \overline{z} -\frac{\lambda }{4} |z|^2} F(w+z) \end{aligned}$$

if $\lambda >0$, and, if $\lambda <0$, as $\sigma _\lambda [z,t] = \sigma _{-\lambda } [\overline{z},-t]$, that is,

$$\begin{aligned} \sigma _\lambda [z,t] F (w) = e^{i\lambda t+\frac{\lambda }{2} w\cdot z +\frac{\lambda }{4} |z|^2} F(w+{\bar{z}}) \,. \end{aligned}$$

If $f\in L^1({\mathbb H}_d)$, for $\lambda \in {\mathbb R}\setminus \{0\}$, $\sigma _\lambda (f)$ is the operator acting on ${{\mathcal {F}}}^\lambda$ as

$$\begin{aligned} \sigma _\lambda (f) F (w) = \int _{{\mathbb H}_d} f[z,t] \sigma _\lambda [z,t]F (w)\, dzdt\,. \end{aligned}$$

If $f\in L^2({\mathbb H}_d)$, we have Plancherel’s formula

$$\begin{aligned} \Vert f\Vert _{L^2({\mathbb H}_d)}^2 = \frac{1}{(2\pi )^{d+1} } \int _{{\mathbb R}} \Vert \sigma _\lambda (f)\Vert _{{\text {HS}}}^2 |\lambda |^d\, d\lambda \,, \end{aligned}$$

where $\Vert \sigma _\lambda (f)\Vert ^2_{{\text {HS}}}=\sum _{\alpha }\Vert \sigma _{\lambda }(f)e_\alpha \Vert ^2_{{{\mathcal {F}}}^\lambda }$ is the Hilbert–Schmidt norm of $\sigma _\lambda (f)$ and $e_\alpha =z^\alpha /\Vert z^\alpha \Vert _{{{\mathcal {F}}}^\lambda }$. If $f\in L^1\cap L^2({\mathbb H}_d)$ the following inversion formula holds:

$$\begin{aligned} f[z,t] = \frac{1}{(2\pi )^{d+1}} \int _{{\mathbb R}} {\text {tr}}\big ( \sigma _\lambda (f)\sigma _\lambda [z,t]^*\big ) |\lambda |^d\, d\lambda . \end{aligned}$$

2.2 The Drury–Arveson Space on $\mathcal {U}$

In [4] a family of holomorphic function spaces on ${{\mathcal {U}}}$ depending on a real parameter $\nu$ was studied and characterized by means of the group Fourier transform on ${\mathbb H}_d$. This family of spaces includes weighted Bergman spaces, the Hardy space, weighted Dirichlet spaces and the Dirichlet space. In particular, the Drury–Arveson space DA was identified as a particular weighted Dirichlet space. Here we recall the results in [4] we need in the rest of the paper.

Definition 2.2

We define the space ${{\mathcal {L}}}^2_{DA}$ as the space of functions $\tau$ on ${\mathbb R}\setminus \{0\}$ such that:

$$\begin{aligned} \begin{aligned} {\mathrm {(i)}}&~\tau (\lambda ):{{\mathcal {F}}}^\lambda \rightarrow {{\mathcal {F}}}^\lambda \,is\,a\, \text {Hilbert{--}Schmidt}\,\text {operator}\,\text {for}\, \text {every}\,\lambda ;\\ {\mathrm {(ii)}}&~\tau (\lambda )=0 \, in \, \lambda >0;\\ {\mathrm {(iii)}}&~{\text{ ran }}( \tau (\lambda )) \subseteq {\text{ span }}\{1\};\\ {\mathrm {(iv)}}&~\displaystyle { \Vert \tau \Vert _{{{\mathcal {L}}}^2_{DA}}^2: = \frac{1}{(2\pi )^{d+1}} \int _{-\infty }^0 \Vert \tau (\lambda )\Vert _{{\text{ HS }}}^2 \, |\lambda |^{2d} d\lambda <+\infty }. \end{aligned} \end{aligned}$$

The following result holds true.

Theorem 2.3

([4]) Let $n>\frac{d}{2}$. Let $f\in DA_{(n)}$ defined as in (1.3). Then, there exists $\tau \in {{\mathcal {L}}}^2_{DA}$ such that, for $(\zeta ,\zeta _{d+1})\in {{\mathcal {U}}}$,

$$\begin{aligned} f(\zeta ,\zeta _{d+1}) = (f\circ \Psi ^{-1})(z,t,h) = \frac{1}{(2\pi )^{d+1}} \int _{-\infty }^0 e^{h\lambda } {\text {tr}}\big ( \tau (\lambda )\sigma _\lambda [z,t]^*\big ) \, |\lambda |^d d\lambda \,, \end{aligned}$$

(2.2)

and

$$\begin{aligned} \Vert f\Vert _{DA_{(n)}}^2 = \frac{\Gamma (2n-d)}{2^{2n-d}} \Vert \tau \Vert _{{{\mathcal {L}}}^2_{DA}}^2 \,. \end{aligned}$$

(2.3)

Conversely, given $\tau \in {{\mathcal {L}}}^2_{DA}$, let f be defined as in (2.2). Then $f\in DA_{(n)}$ and (2.3) holds. Therefore, for each $n>\frac{d}{2}$, the spaces $DA_{(n)}$ all coincide and their norms satisfy (2.3).

Hence, we simply write DA in place of $DA_{(n)}$.

2.3 Semigroups of Operators

A semigroup of operators on a Hilbert space ${{\mathcal {H}}}$ is a one parameter family of bounded linear operators $\{T_t\}_{t\ge 0}$ on ${{\mathcal {H}}}$ such that:

• (i) $T_0 = {{\,\mathrm{Id}\,}}$;

• (ii) $T_{t+s}=T_t T_s, \,\,\, \forall s ,t > 0.$

If in addition $T_t$ converges to the identity operator ${{\,\mathrm{Id}\,}}$ in the strong operator topology as $t \searrow 0$, the semigroup is called strongly continuous or $C_0$. From now on we will focus exclusively on $C_0$ semigroups. The infinitesimal generator G of a $C_0$ semigroup $\{T_t\}_{t\ge 0}$ is a linear operator defined on the subspace ${\text {Dom}}(G)$ of $v\in {{\mathcal {H}}}$ such that the limit

$$\begin{aligned} \lim _{t\searrow 0 } \frac{T_t v - v}{t}=: G v \end{aligned}$$

exists in the norm topology. It can be shown that G on its domain ${\text {Dom}}(G)$ is a linear densely defined closed operator [13, Section 34, Theorem 4]. In particular, we will be interested in the characterization of infinitesimal generators for contraction semigroups, i.e., semigroups $\{T_t\}_{t\ge 0}$ such that each $T_t$ is a contraction, which is provided by the Lumer-Philips Theorem.

Definition 2.4

A densely define operator G on a Hilbert space ${{\mathcal {H}}}$ is called dissipative if

$$\begin{aligned} {\text {Re}}\, \langle Gv , v \rangle _{{{\mathcal {H}}}} \le 0, \,\,\, \forall v \in {\text {Dom}}(G). \end{aligned}$$

It is called maximal dissipative, if it is dissipative and its resolvent set r(G) includes ${\mathbb R}_+=(0,+\infty )$.

For the following renowned theorem we refer the reader, for instance, to [13, p. 432].

Theorem 2.5

(Lumer-Philips) A densely defined operator G is the infinitesimal generator of a (unique) semigroup of contractions if and only if it is maximal dissipative.

The following is a very well-known lemma that we shall need in what follows.

Lemma 2.6

Let $\{T_t\}_{t\ge 0}$ be a semigroup of bounded operators on a Hilbert space ${{\mathcal {H}}}$. Suppose that:

• (i) there exists $\delta > 0$ such that $\sup _{0<t<\delta } \Vert T_t\Vert _{{{\mathcal {B}}}({{\mathcal {H}}})} < +\infty$;

• (ii) for some dense subset ${{\mathcal {D}}}\subseteq {{\mathcal {H}}}$, $T_t f \rightarrow f$ for all $f \in {{\mathcal {D}}}$ as $t \searrow 0~t$

Then, $\{T_t\}_{t\ge 0}$ is a strongly continuous semigroup.

We remark that we will work with semigroups that appear to have a negative parameter $\tau$; this is to stay consistent with [4]. When we use this notation we simply mean that the semigroup has the positive parameter $t=-\tau$.

3 Proof of Theorem 1.4

The proof of Theorem 1.4 follows at once from the next two lemmas. Recall that the measure $\mu$ on ${\mathbb N}_0^d\times {\mathbb R}_-$ is defined in (1.6). Now define

$$\begin{aligned} \varphi (\alpha ,\lambda )=\Vert z^\alpha \Vert ^{-1}_{{{\mathcal {F}}}^\lambda }\langle e_0, \sigma _{\lambda }(f_0)(e_\alpha )\rangle _{{{\mathcal {F}}}^{\lambda }}. \end{aligned}$$

Lemma 3.1

The map $\Phi : DA\cap H^2\rightarrow L^2({\mathbb N}_0^d\times {\mathbb R}_-, d\mu )$ defined as

$$\begin{aligned} \Phi (f) (\alpha ,\lambda )= \varphi (\alpha ,\lambda ), \end{aligned}$$

(3.1)

extends to a conjugate linear isometry $\Phi : DA\rightarrow L^2({\mathbb N}_0^d\times {\mathbb R}_-, d\mu )$. Its inverse is the map ${{\mathscr {S}}}$ of Theorem 1.4.

Proof

First we assume that $f\in DA\cap H^2$ where $H^2$ denotes the Hardy space on ${{\mathcal {U}}}$. This intersection is dense in DA ([4, Lemma 4.2]) and every $f\in H^2$ admits a boundary value function $f_0\in L^2(\partial {{\mathcal {U}}})$. Moreover, for such function f the function $\tau \in {{\mathcal {L}}}^2_{DA}$ in formula (2.2) actually coincides with the Fourier transform of its boundary value function, that is, $\tau (\lambda )=\sigma _{\lambda }(f_0)$ (see [4, 14]).

Let $\{e_\alpha \}_\alpha$ be the orthonormal basis of normalized monomials of the Fock space ${{\mathcal {F}}}^{\lambda }$ and let $F=\sum _{\alpha }F_\alpha e_\alpha$ be a function in ${{\mathcal {F}}}^{\lambda }$. Then, for every function $f\in DA\cap H^2$, we have

$$\begin{aligned} \sigma _\lambda (f_0)(F)&=\sum _{\alpha \in {\mathbb N}^d_0}F_\alpha \sigma _{\lambda }(f_0)(e_\alpha )=\sum _{\alpha \in {\mathbb N}^d_0}F_\alpha \langle \sigma _{\lambda }(f_0)(e_\alpha ), e_0\rangle _{{{\mathcal {F}}}^\lambda }e_0 \end{aligned}$$

thanks to property (iii) in Definition 2.2. Thus,

$$\begin{aligned} \sigma _{\lambda }(f_0)(F)=\langle F, \Phi _\lambda \rangle _{{{\mathcal {F}}}^\lambda }e_0 \end{aligned}$$

where

$$\begin{aligned} \Phi _\lambda&=\sum _{\alpha \in {\mathbb N}^d_0}\overline{\langle \sigma _{\lambda }(f_0)(e_\alpha ), e_0\rangle _{{{\mathcal {F}}}^\lambda }}e_\alpha \\&=\sum _{\alpha \in {\mathbb N}^d_0}\langle e_0, \sigma _{\lambda }(f_0)(e_\alpha )\rangle _{{{\mathcal {F}}}^{\lambda }}e_\alpha \\&=\sum _{\alpha \in {\mathbb N}^d_0} \Vert z^\alpha \Vert ^{-1}_{{{\mathcal {F}}}^\lambda }\langle e_0, \sigma _{\lambda }(f_0)(e_\alpha )\rangle _{{{\mathcal {F}}}^{\lambda }} z^\alpha . \end{aligned}$$

In particular, we deduce that $\Vert z^\alpha \Vert _{{{\mathcal {F}}}^{\lambda }}\varphi (\alpha ,\lambda )=\langle \Phi _\lambda ,e_\alpha \rangle _{{{\mathcal {F}}}^\lambda }$. Now,

$$\begin{aligned} \Vert \sigma _{\lambda }(f_0)\Vert ^2_{{\text {HS}}}&=\sum _{\alpha \in \mathbb {N}_0^d}\Vert \sigma _{\lambda }(f_0)e_\alpha \Vert _{{{\mathcal {F}}}^{\lambda }}^2\\&=\sum _{\alpha \in \mathbb {N}_0^d}|\langle e_\alpha , \Phi _\lambda \rangle _{{{\mathcal {F}}}^{\lambda }}|^2\Vert e_0\Vert _{{{\mathcal {F}}}^{\lambda }}^2\\&=\sum _{\alpha \in \mathbb {N}_0^d}|\langle e_\alpha , \Phi _\lambda \rangle _{{{\mathcal {F}}}^{\lambda }}|^2, \end{aligned}$$

since $\{e_\alpha \}_\alpha$ is an orthonormal basis in ${\mathcal {F}}^\lambda$. However,

$$\begin{aligned} |\langle e_\alpha , \Phi _\lambda \rangle _{{{\mathcal {F}}}^{\lambda }}|=\Vert z^\alpha \Vert _{{{\mathcal {F}}}^{\lambda }}|\varphi (\alpha ,\lambda )|, \end{aligned}$$

so that

$$\begin{aligned} \Vert \tau (\lambda )\Vert ^2_{{\text {HS}}}=\sum _{\alpha \in \mathbb {N}_0^d}\alpha ! (2/|\lambda |)^{|\alpha |}|\varphi (\alpha ,\lambda )|^2. \end{aligned}$$

In conclusion,

$$\begin{aligned} \begin{aligned} \Vert f\Vert _{DA}^2&= c_d \int _{-\infty }^0\sum _{\alpha \in \mathbb {N}_0^d}\alpha ! (2/|\lambda |)^{|\alpha |}|\varphi (\alpha ,\lambda )|^2 |\lambda |^{2d}\, d\lambda \\&=c_d\int _{\mathbb {N}_0^d\times \mathbb R_{-}}|\varphi (\alpha ,\lambda )|^2\, d\mu (\alpha ,\lambda ). \end{aligned} \end{aligned}$$

(3.2)

$\square$

Lemma 3.2

Let $f\in DA$. Then, with the notation above and setting $\zeta =(\zeta _1,\ldots ,\zeta _d)$, we have

$$\begin{aligned} f(\zeta ,\zeta _{d+1})= \frac{1}{(2\pi )^{d+1}} \int _{{\mathbb N}_0^d\times {\mathbb R}_{-}} \zeta ^\alpha e^{-i\lambda \zeta _{d+1}} \overline{\varphi (\alpha ,\lambda )}\,|\lambda |^d\, d\alpha d\lambda . \end{aligned}$$

(3.3)

Proof

If $(\zeta ,\zeta _{d+1})=\Psi ^{-1}(z,t,h)$ we know from Theorem 2.3 that there exists $\tau \in {{\mathcal {L}}}^2_{DA}$ such that

$$\begin{aligned} (f\circ \Psi ^{-1})(z,t,h)= \frac{1}{(2\pi )^{d+1}} \int _{-\infty }^0 e^{h\lambda } {\text {tr}}\big ( \tau (\lambda )\sigma _\lambda [z,t]^*\big ) \, |\lambda |^d d\lambda \,. \end{aligned}$$

Using the fact that $\tau (\lambda )$ is a rank one operator such that ${{\,\mathrm{rank}\,}}\{\tau (\lambda )\}\subseteq {{\,\mathrm{span}\,}}\{e_0\}$ for every $\lambda$ we get

$$\begin{aligned} {\text {tr}}(\tau (\lambda )\sigma _\lambda [z,t]^*)&= {\text {tr}}(\sigma _\lambda [z,t]^*\tau (\lambda ))\\&= \sum _{\alpha \in \mathbb {N}_0^d}\langle \tau (\lambda )e_\alpha , \sigma _\lambda [z,t]e_\alpha \rangle \\&=\sum _{\alpha \in \mathbb {N}_0^d}\langle \tau (\lambda )e_\alpha , P_0\sigma _\lambda [z,t]e_\alpha \rangle \end{aligned}$$

where $P_0$ denotes the orthogonal projection onto the subspace generated by $e_0$. Moreover, it holds (see also (26) in [4])

$$\begin{aligned} P_0 \sigma _\lambda [z,t] e_\alpha =\bigg ( \frac{1}{\sqrt{\alpha !}} \bigg (\frac{|\lambda |}{2}\bigg )^{|\alpha |/2} \bigg ( \frac{|\lambda |}{2\pi } \bigg )^d e^{i\lambda t+ \frac{\lambda }{4} |z|^2} {\bar{z}}^\alpha \bigg ) e_0. \end{aligned}$$

Thus,

$$\begin{aligned} {\text {tr}}(\tau (\lambda )\sigma _\lambda [z,t]^*)&=\sum _{\alpha \in \mathbb {N}_0^d}\langle \tau (\lambda )e_\alpha , P_0\sigma _\lambda [z,t]e_\alpha \rangle \\&= \sum _{\alpha \in \mathbb {N}_0^d} \langle e_\alpha , \Phi _\lambda \rangle \langle e_0 , P_0\sigma _\lambda [z,t]e_\alpha \rangle \\&= \sum _{\alpha \in \mathbb {N}_0^d} \langle e_\alpha , \Phi _\lambda \rangle \overline{\langle P_0\sigma _\lambda [z,t]e_\alpha , e_0 \rangle }\\&= \sum _{\alpha \in \mathbb {N}_0^d} \frac{1}{\sqrt{\alpha !}} \Big ( \frac{|\lambda |}{2} \Big )^{|\alpha |/2}e^{-i\lambda t+\frac{\lambda }{4}|z|^2}z^\alpha \langle e_\alpha , \Phi _\lambda \rangle \\&= \sum _{\alpha \in \mathbb {N}_0^d} \frac{1}{\sqrt{\alpha !}} \Big ( \frac{|\lambda |}{2} \Big )^{|\alpha |/2} \Vert z^\alpha \Vert \overline{\varphi (\alpha ,\lambda )} e^{-i\lambda t+\frac{\lambda }{4}|z|^2}z^\alpha .\\&=\sum _{\alpha \in {\mathbb N}_0^d}\overline{\varphi (\alpha ,\lambda )} e^{-i\lambda t+\frac{\lambda }{4}|z|^2}z^\alpha , \end{aligned}$$

where the series converges absolutely since $\phi \in L^2(\mathbb N^d_0\times \mathbb R_-,d\mu )$. Hence by (2.2),

$$\begin{aligned} f(\zeta , \zeta _{d+1})&= (f\circ \Psi ^{-1})(z,t,h)\\&=\frac{1}{(2\pi )^{d+1}} \int _{-\infty }^0 e^{h\lambda } \sum _{\alpha \in \mathbb {N}_0^d} \overline{\varphi (\alpha ,\lambda )} e^{-i\lambda t+\frac{\lambda }{4}|z|^2}z^\alpha \, |\lambda |^d d\lambda \,\\&= \frac{1}{(2\pi )^{d+1}} \int _{{\mathbb N}_0^d\times {\mathbb R}_{-}} z^\alpha e^{-i\lambda (t-i(\frac{|z|^2}{4}+h))} \overline{\varphi (\alpha ,\lambda )}\,|\lambda |^d\, d\alpha d\lambda \\&= \frac{1}{(2\pi )^{d+1}} \int _{{\mathbb N}_0^d\times {\mathbb R}_{-}} \zeta ^\alpha e^{-i\lambda \zeta _{d+1}} \overline{\varphi (\alpha ,\lambda )}\,|\lambda |^d\, d\alpha d\lambda \end{aligned}$$

as we wished to show. $\square$

4 Pointwise Multipliers on the Drury–Arveson Space

In this section we explicitly study some multiplier operators on DA and we prove Theorem 1.5. Recall that given a function m the associated multiplier operator is the operator $f\mapsto mf$. The problem of characterizing the multiplier algebra of a given reproducing kernel Hilbert function space is a classical problem. In the case of the Drury–Arveson space on the unit ball $DA(\mathbb B^{d+1})$ this problem turned out to be very challenging; a first important result is due to J. Ortega and J. Fäbrega [15]. Their result reads as follows. Let $n\in {\mathbb N}_0$ be such that $2n>d$ and for f in ${\text {Hol}}(\mathbb B^{d+1})$ define the measure

$$\begin{aligned} d\nu _{f}(w)=|{\mathcal {R}}^n f(w)|^2(1-|w|^2)^{2n-d-1}\, d\nu (w), \end{aligned}$$

where ${\mathcal {R}}$ is the radial derivative, $d\nu$ is the normalized Lebesgue measure on $\mathbb B^{d+1}$ and $w\in \mathbb B^{d+1}$. Then, f is a $DA(\mathbb B^{d+1})$-multiplier if and only if $f\in H^\infty (\mathbb B^{d+1})$ and $d\nu _f$ is a Carleson measure for $DA(\mathbb B^{d+1})$. A few years later N. Arcozzi, R. Rochberg and E. Sawyer in [5] completely characterized the Carleson measures of $DA(\mathbb B^{d+1})$; see also [18, 19, 21]. Hence, the multiplier algebra of the Drury–Arveson space on the unit ball is completely characterized. Nonetheless, there is still interest in finding an easier characterization and we refer the reader, for instance, to [10].

From [5, 15] we can also deduce an indirect characterization of the multiplier algebra for DA on the Siegel half-space. Indeed, let ${\mathcal {C}}$ be the multi-dimensional Cayley transform defined in (1.2). Then, up to an irrelevant multiplicative constant,

$$\begin{aligned} K^{{\mathcal {U}}}_{DA}\big ({\mathcal {C}}(z,z_{d+1}),&{\mathcal {C}}(w,w_{d+1})\big )\\&=(1-z_{d+1})K^{\mathbb B^{d+1}}_{DA}\big ((z,z_{d+1}),(w,w_{d+1})\big )(1-\overline{w_{d+1}}) \end{aligned}$$

where $K^{{\mathcal {U}}}_{DA}$ and $K^{\mathbb B^{d+1}}_{DA}$ denote the reproducing kernel of DA and $DA(\mathbb B^{d+1})$ respectively, and $(z,z_{d+1}),(w,w_{d+1})\in {\mathbb B}^{d+1}$. From the abstract theory of reproducing kernel Hilbert spaces (see, for instance, [1, Chapter 2.6]) we deduce that

$$\begin{aligned} f\mapsto (1-z_{d+1})^{-1}(f\circ {\mathcal {C}}) \end{aligned}$$

is a surjective isometry from DA onto $DA({\mathbb B}^{d+1})$ and that m is a multiplier for DA if and only if $(m\circ {\mathcal {C}})$ is a multiplier for $DA({\mathbb B}^{d+1})$.

For our goal we need to study the multiplier operators associated to the functions $\zeta ^\gamma =\zeta _1^{\gamma _1}\cdots \zeta _{d}^{\gamma _d}$, $e^{-i\tau \zeta _{d+1}}$ for $\tau <0$ and $\zeta ^\gamma e^{-i\tau \zeta _{d+1}}$. However, we do not rely on the multiplier characterization on the unit ball since it is easier to study them directly. The proof of the following lemma is standard and we omit it.

Lemma 4.1

The set

$$\begin{aligned} {{\mathcal {D}}}=\big \{f\in L^2({\mathbb N}_0^d\times {\mathbb R}_{-}, d\mu ): {{\,\mathrm{supp}\,}}{f}\text { is compact and }f(\alpha ,\cdot )\in C_c^{\infty }\, \forall \alpha \in {\mathbb N}_0^d\big \}. \end{aligned}$$

is dense in $L^2({\mathbb N}_0^d\times {\mathbb R}_{-}, d\mu )$.

We now study the multiplier operator associated to the monomial $\zeta ^\gamma , \gamma \in {\mathbb N}_0^d$. Although this operator is unbounded on DA, as it is easily seen, it is closed and densely defined.

Lemma 4.2

Let $\gamma \in {\mathbb N}_0^d$. Then, the multiplier operator $m_\gamma$ associated to the function $\zeta ^\gamma =\zeta _1^{\gamma _1}\cdots \zeta _d^{\gamma _d}$ is a closed densely defined operator on DA.

Proof

Let us consider ${{\mathcal {D}}}_\gamma =\{f\in DA: \zeta ^\gamma f\in DA\}$ as domain of our multiplier operator. Let $\{f_n\}_n\subseteq {{\mathcal {D}}}_\gamma$ be a sequence such that $f_n\rightarrow f$ in DA and $\zeta ^\gamma f_n\rightarrow g\in DA$. Since DA is a reproducing kernel Hilbert space we also have that $f_n\rightarrow f$ and $\zeta ^\gamma f_n\rightarrow g$ uniformly on compact sets. Hence, $\zeta ^\gamma f_n\rightarrow \zeta ^\gamma f$ uniformly on compact sets as well and $\zeta ^\gamma f=g$. In particular both f and $\zeta ^\gamma f$ are in DA so that f belongs to the domain ${{\mathcal {D}}}_\gamma$. Thus, our operator is closed.

To prove that ${{\mathcal {D}}}_\gamma$ is dense we exploit the previous Lemma 4.1. Let $\varphi \in {{\mathcal {D}}}$ and define $f \in DA$ by (3.3). Then,

$$\begin{aligned} \zeta ^\gamma f(\zeta ,\zeta _{d+1})&= \frac{1}{(2\pi i)^{d+1}}\int _{{\mathbb N}_0^d\times {\mathbb R}_-} \zeta ^{\alpha +\gamma } e^{-i\lambda \zeta _{d+1}} \overline{\varphi (\alpha ,\lambda )} \,|\lambda |^d\, d\alpha d\lambda \\&= \frac{1}{(2\pi )^{d+1}}\int _{{{\,\mathrm{supp}\,}}\varphi }\zeta ^{\alpha } e^{-i \lambda \zeta _{d+1}} \overline{\varphi (\alpha -\gamma ,\lambda )} \,|\lambda |^d \chi _{\{\alpha \ge \gamma \}}(\alpha )\, d\alpha d\lambda \end{aligned}$$

where $\chi _{\{\alpha \ge \gamma \}}(\alpha )$ is the characteristic function of the set $\{\alpha \in {\mathbb N}_0^d: \alpha _i \ge \gamma _i, i=1,\ldots ,d \}$. Recall that ${{\,\mathrm{supp}\,}}\varphi$ is a compact subset of ${\mathbb N}_0^d\times {\mathbb R}_-$ and assume that $(\alpha ,\lambda )\in {{\,\mathrm{supp}\,}}\varphi$ implies $|\alpha |<N$ for some positive integer N and $\lambda \in I$ where I is a compact subset of ${\mathbb R}_-$. From (3.2) we have

$$\begin{aligned} \Vert \zeta ^\gamma f\Vert ^2_{DA}&= c_d \int _I\sum _{|\alpha -\gamma |<N}|\varphi (\alpha -\gamma ,\lambda )|^2\, \alpha ! \big (\frac{2}{|\lambda |}\big )^{|\alpha |}|\lambda |^{2d} \chi _{\{\alpha \ge \gamma \}}(\alpha )\, d\alpha d\lambda \\&= c_d\int _I\sum _{|\alpha |<N} |\varphi (\alpha ,\lambda )|^2 \frac{(\alpha +\gamma )!}{\alpha !}\Big (\frac{2}{|\lambda |}\Big )^{|\gamma |}\, d\mu (\alpha ,\lambda )\\&\le c_d(\varphi )\int _I\sum _{|\alpha |<N} |\varphi (\alpha ,\lambda )|^2 \, d\mu (\alpha ,\lambda )\\&= c_d(\varphi )\Vert f\Vert _{DA}^2 \end{aligned}$$

where $c_d(\varphi )$ is a constant depending on the compact support of $\varphi$ (and on the dimension d). The density of ${{\mathcal {D}}}_\gamma$ in DA now follows from the density of ${{\mathcal {D}}}$ in $L^2({\mathbb N}_0^d\times {\mathbb R}_-,\ d\mu )$ and Theorem 1.4. $\square$

We now investigate the other multiplier operators we are interested in and see that they are actually bounded on the Drury–Arveson space.

Lemma 4.3

The pointiwise multiplier operators associated to the functions $\{ e^{-i\tau \zeta _{d+1}} \}_{\tau <0}$ form a strongly continuous semigroup of contractions on DA with corresponding infinitesimal generator the multiplier operator corresponding to the function $i \zeta _{d+1}$.

Proof

From the inversion formula (3.3) we have

$$\begin{aligned} e^{-i\tau \zeta _{d+1}}f(\zeta ,\zeta _{d+1})&= \frac{1}{(2\pi i)^{d+1}}\int _{{\mathbb N}_0^d\times {\mathbb R}_-} \zeta ^\alpha e^{-i (\lambda +\tau )\zeta _{d+1}} \overline{\varphi (\alpha ,\lambda )}\,|\lambda |^d\, d\alpha d\lambda \\&=\frac{1}{(2\pi i)^{d+1}}\int _{{\mathbb N}_0^d\times {\mathbb R}_-} \zeta ^\alpha e^{-i \lambda \zeta _{d+1}} \overline{\varphi (\alpha ,\lambda -\tau )}\big |\frac{\lambda - \tau }{\lambda }\big |^d\chi _{(-\infty ,\tau )}(\lambda )\,|\lambda |^d\, d\alpha d\lambda \end{aligned}$$

where $\chi _{(-\infty ,\tau )}$ is the characteristic function of the interval $(-\infty ,\tau )$. Thus, by (3.2) we get

$$\begin{aligned} \Vert e^{-i\tau \zeta _{d+1}}f\Vert _{DA}^2&=\int _{{\mathbb N}_0^d\times {\mathbb R}_-}|\varphi (\alpha ,\lambda -\tau )|^2 \big |\frac{\lambda -\tau }{\lambda }\big |^{2d}\chi _{(-\infty ,\tau )}(\lambda )\, d\mu (\alpha ,\lambda )\\&=\int _{{\mathbb N}_0^d\times {\mathbb R}_-} |\varphi (\alpha ,\lambda )|^2\big |\frac{\lambda }{\lambda +\tau }\big |^{|\alpha |}\, d\mu (\alpha ,\lambda )\\&\le \int _{{\mathbb N}_0^d\times {\mathbb R}_-} |\varphi (\alpha ,\lambda )|^2\, d\mu (\alpha ,\lambda )\\&=\Vert f\Vert _{DA}^2. \end{aligned}$$

Hence, we conclude that $e^{-i\tau \zeta _{d+1}}$ is a contractive multiplier. The semigroup property is automatically satisfied. Since $e^{-i\tau \zeta _{d+1}}f$ converges in norm to f for all $f\in {{\mathcal {D}}}$ and the semigroup has uniformly bounded seminorm, it is strongly continuous by Lemma 2.6. Then, by definition, the infinitesimal generator is given by

$$\begin{aligned} \lim _{\tau \rightarrow 0^-}\frac{(e^{-i\tau \zeta _{d+1}}-1)f}{-\tau }=i\zeta _{d+1}f \end{aligned}$$

and the proof is concluded. $\square$

Lemma 4.4

Let $(\gamma ,\tau )\in {\mathbb N}_0^d\times {\mathbb R}_-, \tau < 0$. Then, the multiplier operator associated to the muliplier $\zeta ^{\gamma } e^{-i\tau \zeta _{d+1}}$ extends to a bounded operator on DA.

Proof

Let ${{\mathcal {D}}}$ be as in Lemma 4.1 and let $f\in {{\mathcal {D}}}$. We have

$$\begin{aligned}&\zeta ^\gamma e^{-i\tau \zeta _{d+1}} f(\zeta ,\zeta _{d+1}) =\frac{1}{(2\pi i)^{d+1}}\int _{{\mathbb N}_0^d\times {\mathbb R}_-} \zeta ^{\alpha +\gamma } e^{-i (\lambda +\tau )\zeta _{d+1}} \overline{\varphi (\alpha ,\lambda )}\,|\lambda |^d\, d\alpha d\lambda \\&\quad =\frac{1}{(2\pi i)^{d+1}}\int _{{\mathbb N}_0^d\times {\mathbb R}_-} \!\!\!\!\!\!\!\!\zeta ^{\alpha } e^{-i \lambda \zeta _{d+1}} \overline{\varphi (\alpha -\gamma ,\lambda -\tau )}\,|\lambda -\tau |^d \chi _{(-\infty ,\tau )}(\lambda )\chi _{\{\alpha \ge \gamma \}}(\alpha )\, d\alpha d\lambda \\&\quad =\frac{1}{{(2\pi i)^{d+1}}}\int _{{\mathbb N}_0^d\times {\mathbb R}_-} \!\!\!\!\!\!\!\!\zeta ^{\alpha } e^{-i \lambda \zeta _{d+1}} \overline{\varphi (\alpha -\gamma ,\lambda -\tau )}\,\big |\frac{\lambda -\tau }{\lambda }\big |^d\chi _{(-\infty ,\tau )}(\lambda )\chi _{\{\alpha \ge \gamma \}}(\alpha ) |\lambda |^d d\alpha d\lambda \end{aligned}$$

where $\chi _{\{\alpha \ge \gamma \}}(\alpha )$ is the characteristic function of the set $\{\alpha \in {\mathbb N}_0^d: \alpha _i\ge \gamma _i, i=1,\ldots ,d\}$. Hence, setting $m_{\gamma ,\tau }(\zeta ,\zeta _{d+1})=\zeta ^\gamma e^{-i\tau \zeta _{d+1} }$,

$$\begin{aligned} \begin{aligned} \Vert m_{\gamma ,\tau }&f\Vert _{DA}^2\\&=\int _{{\mathbb N}_0^d\times {\mathbb R}_-}|\varphi (\alpha -\gamma ,\lambda -\tau )|^2\,\big |1-\frac{\tau }{\lambda }\big |^{2d}\chi _{(-\infty ,\tau )}(\lambda )\chi _{\{\alpha \ge \gamma \}}(\alpha )\, d\mu (\alpha ,\lambda )\\&=\int _{{\mathbb N}_0^d\times {\mathbb R}_-}|\varphi (\alpha ,\lambda )|^2 2^{|\gamma |}\frac{|\lambda |^{|\alpha |}}{|\lambda +\tau |^{|\alpha +\gamma |}}\frac{(\alpha +\gamma )!}{\alpha !}\, d\mu (\alpha ,\lambda ). \end{aligned} \end{aligned}$$

Therefore,

$$\begin{aligned} \Vert m_{\gamma ,\tau } \Vert _{{{\mathcal {M}}}(DA)}^2 \le \sup _{\alpha \in {\mathbb N}_0^d, \lambda < 0 } 2^{|\gamma |}\frac{|\lambda |^{|\alpha |}}{|\lambda +\tau |^{|\alpha +\gamma |}}\frac{(\alpha +\gamma )!}{\alpha !}. \end{aligned}$$

In order to calculate this supremum we first maximize over $\lambda$. For symmetry we can consider $\lambda >0$ and $\tau >0$. We find that when $|\alpha |\ne 0$ the maximum is achieved for $\lambda = \frac{|\alpha |}{|\gamma |}\tau ,$ whereas for $\alpha = 0$ the expression is decreasing in $\lambda$ and therefore the maximum is achieved at $\lambda = 0$.

Substituting the value for $\lambda$ in the expression above we find

$$\begin{aligned} 2^{|\gamma |}&\frac{|\alpha |^{|\alpha |}\tau ^{|\alpha |}}{|\gamma |^{|\alpha |}} \frac{1}{\tau ^{|\alpha +\gamma |}\big (\frac{|\alpha |}{|\gamma |}+1\big )^{|\alpha +\gamma |}}\frac{(\alpha +\gamma )!}{\alpha !} =\\&=\big ( \frac{2}{\tau }\big )^{|\gamma |} \Big ( 1 + \frac{|\gamma |}{|\alpha |} \Big )^{-|\alpha |} \frac{(\alpha + \gamma ) !}{\alpha ! } \Big ( \frac{|\alpha |}{|\gamma |} +1 \Big )^{-|\gamma |} . \end{aligned}$$

Note that the first factor is constant, the second is decreasing in $|\alpha |$ and tends to $e^{-|\gamma |}$ as $|\alpha | \rightarrow + \infty .$ For the last term notice that

$$\begin{aligned} \frac{(\alpha + \gamma )! }{\alpha !} \Big ( \frac{|\alpha |}{|\gamma |} + 1\Big )^{-|\gamma |}&= \prod _{i=1}^d \frac{(\alpha _i + \gamma _i)!}{\alpha _i ! \Big ( \frac{|\alpha |}{|\gamma |}+1 \Big )^{\gamma _i} } \\&\le \prod _{i=1}^d \frac{(|\alpha | + \gamma _i)!}{|\alpha | ! \Big ( \frac{|\alpha |}{|\gamma |}+1 \Big )^{\gamma _i} } \\&\le \gamma ! \prod _{i=1}^d \Big ( \frac{|\alpha | + 1}{\frac{|\alpha |}{|\gamma |}+1} \Big )^{\gamma _i} \\&\le \gamma ! |\gamma |^{|\gamma |}. \end{aligned}$$

This proves that the multiplier operator associated to $m_{\gamma ,\alpha }$ is bounded with norm less than

$$\begin{aligned} \max \Big \{ \gamma ! \big ( \frac{2}{\tau }\big )^{|\gamma |}, \gamma ! \big ( \frac{2}{\tau }\big )^{|\gamma |} \frac{|\gamma |!}{\sqrt{2\pi |\gamma |}} \Big \}, \end{aligned}$$

where we used Stirling’s asymptotic. $\square$

We now prove Theorem 1.5

Proof

The proof of the unitary equivalence of the two operators follows essentially from the computation in Lemma 4.4. For the computation of the adjoint operator, if $\langle \cdot ,\cdot \rangle$ denotes the inner product in $L^2({\mathbb N}_0^d\times {\mathbb R}_-, d\mu )$, we have

$$\begin{aligned} \langle S^*_{\gamma ,\tau }\varphi ,\psi \rangle&= \langle \varphi , S_{\gamma ,\tau }\psi \rangle \\&=\int _{\{\alpha \ge \gamma \}}\int _{\{\lambda <\tau \}}\varphi (\alpha ,\lambda ) \frac{|\lambda -\tau |^d}{|\lambda |^d}\overline{\psi (\alpha - \gamma , \lambda - \tau )}\, d\mu (\alpha ,\lambda )\\&=\int _{{\mathbb N}_0^d\times {\mathbb R}_-} \frac{|\lambda +\tau |^{d-|\alpha |-|\gamma |}}{|\lambda |^{d-|\alpha |}} \frac{(\alpha +\gamma )!}{\alpha ! } 2^{|\gamma |} \varphi (\alpha +\gamma , \lambda + \tau ) \overline{\psi (\alpha ,\lambda )}\, d\mu (\alpha ,\lambda ) \end{aligned}$$

and the conclusion follows. $\square$

5 The von Neumann Type Inequality

In this section we prove our main results Theorem 1.6 and Theorem 1.3. We first prove a couple of lemmas.

Lemma 5.1

Let T be a bounded operator on a Hilbert space ${{\mathcal {H}}}$ and let U be a densely defined closed operator. Assume that U is the infinitesimal generator of a (unique) $C_0$ semigroup $\{e^{\tau U}\}_{\tau >0}$ and assume that T and U strongly commute. Then, T and $e^{\tau U}$ commute for all $\tau >0$.

Proof

Consider some $\lambda _0 \in r(T)$, the resolvent set of the operator T. Then an algebraic computation shows that the bounded operators

$$\begin{aligned} Z_\tau : = (T-\lambda _0 {{\,\mathrm{Id}\,}})^{-1} e^{\tau U} (T-\lambda _0 {{\,\mathrm{Id}\,}}) \end{aligned}$$

form a $C_0$-semigroup. For $v\in {\text {Dom}}(U)$, since T and U strongly commute, $Th-\lambda _0 v \in {\text {Dom}}(U)$ and

$$\begin{aligned} \lim _{\tau \searrow 0} \frac{Z_\tau v - v}{\tau }&= (T-\lambda _0{{\,\mathrm{Id}\,}})^{-1} \lim _{\tau \searrow 0} \frac{e^{ \tau U} (T-\lambda _0 {{\,\mathrm{Id}\,}})v- (T-\lambda _0 {{\,\mathrm{Id}\,}})v}{\tau } \\&= (T-\lambda _0{{\,\mathrm{Id}\,}})^{-1} U (Tv-\lambda _0v) = Uv. \end{aligned}$$

By the uniqueness of the infinitesimal generator we conclude that $Z_\tau = e^{\tau U}$. In other words,

$$\begin{aligned} e^{\tau U} T = T e^{\tau U} \end{aligned}$$

for all $\tau >0$, as we wished to show. $\square$

Proof of Theorem 1.6

Set $A=(A_1\cdots A_d)$, let $v\in {{\mathcal {H}}}$ and notice that, since for $1\le i \le d$ the operators $A_i$ strongly commute with $A_{d+1}$, by [13, Section 34, Theorem 4(i)] we can infer that $e^{-i\tau A_{d+1}} A^\alpha v \in {\text {Dom}}A_{d+1}$. Therefore, the map $\Theta$ is well-defined. Furthermore,

$$\begin{aligned} \Vert \Theta v\Vert ^2_{{{\mathcal {L}}}^2(\Delta )}&=\int _{{\mathbb N}_0^d\times {\mathbb R}_{-}}\Vert \Theta v(\alpha ,\lambda )\Vert ^2_\Delta d\mu (\alpha ,\lambda )\\&=\int _{{\mathbb N}_0^d\times {\mathbb R}_{-}}\Vert e^{-i\lambda A_{d+1}} A^\alpha v\Vert _\Delta ^2 \frac{|\lambda |^{|\alpha |}}{2^{|\alpha |-1}\alpha !}\, d\alpha d\lambda \\&=\int _{{\mathbb N}_0^d\times {\mathbb R}_{-}}{\text {Im}}\langle A_{d+1} e^{-i\lambda A_{d+1}} A^\alpha v, e^{-i\lambda A_{d+1}}A^\alpha v \rangle _{{\mathcal {H}}}\, \frac{|\lambda |^{|\alpha |}}{2^{|\alpha |-1}\alpha !}\,d\alpha d\lambda \\\&\quad -\int _{{\mathbb N}_0^d\times {\mathbb R}_{-}} \sum _{i=1}^d \langle A^{\alpha +e_i} e^{-i\lambda A_{d+1}}v, A^{\alpha +e_i}e^{-i\lambda A_{d+1}}v \rangle _{{{\mathcal {H}}}}\, \frac{|\lambda |^{|\alpha |}}{2^{|\alpha |+1}\alpha !}\,d\alpha d\lambda . \end{aligned}$$

Now we observe that for $v\in {\text {Dom}}A_{d+1}$ we have

$$\begin{aligned} \partial _\lambda \Vert e^{-i\lambda A_{d+1}}v\Vert ^2_{{{\mathcal {H}}}}&=\langle -iA_{d+1}e^{-i\lambda A_{d+1}}v, e^{-i\lambda A_{d+1}}v\rangle _{{{\mathcal {H}}}}\\&\qquad +\langle e^{-i\lambda A_{d+1} }v,-i A_{d+1}e^{-i\lambda A_{d+1}}v\rangle _{{{\mathcal {H}}}}\\&= 2{\text {Im}}\langle A_{d+1} e^{-i\lambda A_{d+1}} v, e^{-i\lambda A_{d+1}}v \rangle _{{\mathcal {H}}}. \end{aligned}$$

From the fact that $(A_1, \dots , A_{d+1})$ is strongly Siegel–dissipative we deduce that $iA_{d+1}+\varepsilon {{\,\mathrm{Id}\,}}$ is maximal dissipative. In this case the Lumer–Philips Theorem guarantees that $iA_{d+1}+\varepsilon {{\,\mathrm{Id}\,}}$ generates a contraction semigroup; in other words, for any $v\in {{\mathcal {H}}}, \tau < 0$,

$$\begin{aligned} e^{-\tau \varepsilon } \Vert e^{-i\tau A_{d+1}} v \Vert _{{{\mathcal {H}}}} \le \Vert v\Vert _{{{\mathcal {H}}}} . \end{aligned}$$

Therefore, $\Vert e^{-i\tau A_{d+1}} v \Vert _{{{\mathcal {H}}}}$ decays exponentially and we can integrate by parts as follows,

$$\begin{aligned} \Vert \Theta v\Vert ^2_{{{\mathcal {L}}}^2(\Delta )}&=\sum _{\alpha \in {\mathbb N}_0^d}\int _{-\infty }^0 \partial _\lambda \Vert e^{-i\lambda A_{d+1}} A^\alpha v\Vert ^2_{{{\mathcal {H}}}}\, \frac{|\lambda |^{|\alpha |}}{2^{|\alpha |}\alpha !}\, d\lambda \\&\qquad - \sum _{\alpha \in {\mathbb N}_0^d}\int _{-\infty }^0 \sum _{i=1}^d \Vert A^{\alpha +e_i}e^{-i\lambda A_{d+1}}v\Vert ^2_{{{\mathcal {H}}}}\, \frac{|\lambda |^{|\alpha |}}{2^{|\alpha |+1}\alpha !}d\lambda \\&=\Vert v\Vert ^2_{{{\mathcal {H}}}}+\sum _{\alpha \in {\mathbb N}_0^d \setminus \{ 0 \}}\int _{-\infty }^0\partial _\lambda \Vert e^{-i\lambda A_{d+1}} 2^{-\frac{|\alpha |}{2}}A^\alpha v\Vert ^2_{{{\mathcal {H}}}}\, \frac{|\lambda |^{|\alpha |}}{\alpha !}d\lambda \\&\qquad - \sum _{i=1}^d \sum _{\alpha \in {\mathbb N}_0^d }\int _{-\infty }^0 \Vert e^{-i\lambda A_{d+1}} 2^{-\frac{|\alpha |+1}{2}}A^{\alpha + e_i }v\Vert ^2_{{{\mathcal {H}}}}\, \frac{|\lambda |^{|\alpha |}}{\alpha !}d\lambda \\&=\Vert v\Vert ^2_{{{\mathcal {H}}}}+\sum _{\alpha \in {\mathbb N}_0^d \setminus \{ 0 \}}\int _{-\infty }^0 \Vert e^{-i\lambda A_{d+1}}2^{-\frac{|\alpha |}{2}}A^\alpha v\Vert _{{\mathcal {H}}}^2\frac{|\alpha ||\lambda |^{|\alpha |-1}}{\alpha !}\, d\lambda \\&\qquad - \sum _{\alpha \in {\mathbb N}_0^d }\int _{-\infty }^0 \sum _{i=1}^d \Vert e^{-i\lambda A_{d+1}} 2^{-\frac{|\alpha |+1}{2}}A^{\alpha + e_i }v\Vert ^2_{{{\mathcal {H}}}}\, \frac{|\lambda |^{|\alpha |}}{\alpha !}d\lambda \\&=\Vert v\Vert ^2_{{{\mathcal {H}}}}. \end{aligned}$$

To see why the two sums cancel each other out, notice that

$$\begin{aligned} \Vert e^{-i\lambda A_{d+1}} 2^{-\frac{|\alpha |+1}{2}}A^{\alpha + e_i }v\Vert ^2_{{{\mathcal {H}}}}\,&\frac{|\lambda |^{|\alpha |}}{\alpha !}\\&= \Vert e^{-i\lambda A_{d+1}} 2^{-\frac{|\alpha +e_i|}{2}}A^{\alpha + e_i }v\Vert ^2_{{{\mathcal {H}}}}\, \frac{(\alpha _i+1)|\lambda |^{|\alpha +e_i|-1}}{(\alpha +e_i)!} \end{aligned}$$

and use the combinatorial identity

$$\begin{aligned} \sum _{i=1}^d\sum _{\alpha \in {\mathbb N}_0^d } c_{\alpha +e_i} (\alpha _i+1) = \sum _{i=1}^{d}\sum _{\beta \, : \, \beta _i \ge 1 } c_\beta \beta _i = \sum _{\beta \in {\mathbb N}_0^d\backslash \{0\}} c_\beta \sum _{i\,:\, \beta _i \ge 1 } \beta _i = \sum _{\beta \in {\mathbb N}_0^d\backslash \{0\}} c_\beta |\beta |. \end{aligned}$$

We now lift the operator $S_{\gamma ,\tau }^*$ to the space ${{\mathcal {L}}}^2(\Delta )$ by tensoring with the identity. Explicitly, for $g : {\mathbb N}_0^d \rightarrow {{\mathcal {H}}}_\Delta$,

$$\begin{aligned}{}[ S_{\gamma ,\tau }^* \otimes {{\,\mathrm{Id}\,}}]g (\alpha , \tau ) = \frac{|\lambda +\tau |^{d-|\alpha |-|\gamma |}}{|\lambda |^{d-|\alpha |}} \frac{(\alpha +\gamma )!}{\alpha ! } 2^{|\gamma |} g(\alpha +\gamma , \lambda + \tau ). \end{aligned}$$

We now show that the operator $\Theta$ is an intertwining operator for the couple $S^*_{\gamma ,\tau }\otimes {{\,\mathrm{Id}\,}}$ and $e^{-i\tau A_{d+1}} A^\gamma$ where $A=(A_1,\dots ,A_d)$. For, we have

$$\begin{aligned} \Theta ( e^{-i\tau A_{d+1}} A^\gamma v ) (\alpha ,\lambda ) = \frac{|\lambda |^{|\alpha |-d}}{\alpha !2^{|\alpha |-\frac{1}{2}}} e^{-i(\tau +\lambda ) A_{d+1}} A^{\alpha +\gamma } v , \end{aligned}$$

whereas, on the other hand,

$$\begin{aligned} ( [S^*_{\gamma ,\tau }&\otimes {{\,\mathrm{Id}\,}}] \Theta v ) (\alpha ,\lambda ) = \frac{|\lambda +\tau |^{d-|\alpha |-|\gamma |}}{|\lambda |^{d-|\alpha |}} \frac{(\alpha +\gamma )!}{\alpha ! } 2^{|\gamma |} \Theta v (\alpha +\gamma , \lambda + \tau ) \\&= \frac{|\lambda +\tau |^{d-|\alpha |-|\gamma |}}{|\lambda |^{d-|\alpha |}} \frac{(\alpha +\gamma )!}{\alpha ! } 2^{|\gamma |} \frac{|\lambda +\tau |^{|\alpha |+|\gamma |-d}}{(\alpha +\gamma )! 2^{|\alpha |+|\gamma |-\frac{1}{2}}} e^{-i(\tau +\lambda ) A_{d+1}} A^{\alpha +\gamma } v \\&= \frac{|\lambda |^{|\alpha |-d}}{\alpha !2^{|\alpha |-\frac{1}{2}}} e^{-i(\tau +\lambda ) A_{d+1}} A^{\alpha +\gamma } v \\&= \Theta ( e^{-i\tau A_{d+1}} A^\gamma v ) (\alpha ,\lambda ). \end{aligned}$$

In conclusion, the diagram (1.7) commutes and (ii) is proved. $\square$

Finally, we prove our von Neumann type inequality.

Proof of Theorem 1.3

First suppose that the tuple $(A_1,\dots A_{d+1})$ is strongly Siegel-dissipative. Let $p(z)=\sum _{|\gamma |\le N} c_\gamma z^\gamma$ be a polynomial in $z=(z_1,\dots ,z_d)$. Let $(\tau _1,\dots ,\tau _d)\in {\mathbb R}_-^d$ be fixed and let $M_j$ be the operator on ${{\mathcal {H}}}$ given by $M_j=e^{-i\tau _j A_{d+1}}A_j$, $j=1,\dots ,d$. Then,

$$\begin{aligned} p(M_1,\dots ,M_d)= \sum _{|\gamma |\le N} c_\gamma e^{-i\big (\sum _{j=1}^d\gamma _j\tau _j\big )A_{d+1}}A^\gamma =: \sum _{|\gamma |\le N} c_\gamma e^{-i\tau _\gamma A_{d+1}} A^\gamma , \end{aligned}$$

so that

$$\begin{aligned} \Theta p(M_1,\dots ,M_d)&= \sum _{|\gamma |\le N} c_\gamma \Theta e^{-i\tau _\gamma A_{d+1}}A^{\gamma }\\&= \sum _{|\gamma |\le N} c_\gamma [S_{\gamma ,\tau _\gamma }^*\otimes {{\,\mathrm{Id}\,}}]\Theta \\&= \Big (\Big [ \sum _{|\gamma |\le N} c_\gamma S_{\gamma ,\tau _\gamma }^* \Big ] \otimes {{\,\mathrm{Id}\,}}\Big )\Theta . \end{aligned}$$

Letting $m_j$ be the multiplier on DA given by $m_j(\zeta ,\zeta _{d+1})= \zeta _je^{-i\tau _j\zeta _{d+1}}$, $j=1,\dots ,d$, we have

$$\begin{aligned} \big \Vert p(M_1,\dots ,M_d)(v) \big \Vert _{{\mathcal {H}}}&= \big \Vert \Theta p(M_1,\dots ,M_d) (v)\big \Vert _{{{\mathcal {L}}}^2(\Delta )} \\&= \big \Vert \Big (\Big [ \sum _{|\gamma |\le N} c_\gamma S_{\gamma ,\tau _\gamma }^* \Big ] \otimes {{\,\mathrm{Id}\,}}\Big )\Theta (v)\big \Vert _{{{\mathcal {L}}}^2(\Delta )} \\&\le \Big \Vert \Big [ \sum _{|\gamma |\le N} c_\gamma S_{\gamma ,\tau _\gamma }^* \Big ] \otimes {{\,\mathrm{Id}\,}}\Big \Vert _{{{\mathcal {B}}}({{\mathcal {L}}}^2(\Delta ))} \Vert \Theta (v)\Vert _{{{\mathcal {L}}}^2(\Delta )} \\&= \Big \Vert \sum _{|\gamma |\le N} c_\gamma S_{\gamma ,\tau _\gamma }^* \Big \Vert _{{{\mathcal {B}}}(L^2({\mathbb N}_0\times {\mathbb R}_-,d\mu ))} \Vert v\Vert _{{\mathcal {H}}}, \end{aligned}$$

so that

$$\begin{aligned} \big \Vert p(M_1,\dots ,M_d) \big \Vert _{{{\mathcal {B}}}({{\mathcal {H}}})}&\le \Big \Vert \sum _{|\gamma |\le N} c_\gamma S_{\gamma ,\tau _\gamma }^* \Big \Vert _{{{\mathcal {B}}}(L^2({\mathbb N}_0\times {\mathbb R}_-,d\mu ))}\\&= \Big \Vert \sum _{|\gamma |\le N} \overline{c_\gamma } S_{\gamma ,\tau _\gamma } \Big \Vert _{{{\mathcal {B}}}(L^2({\mathbb N}_0\times {\mathbb R}_-,d\mu ))}\\&= \Big \Vert \sum _{|\gamma |\le N} c_\gamma \zeta ^{\gamma } e^{-i\tau _\gamma \zeta _{d+1} } \Big \Vert _{{{\mathcal {M}}}(DA)} \\&=\big \Vert p(m_1,\dots ,m_d)\big \Vert _ {{{\mathcal {M}}}(DA)}. \end{aligned}$$

In the general case let $(A_1, \dots A_{d+1})$ be Siegel-dissipative. Then, if we replace $A_{d+1}$ by $A_{d+1}+i\varepsilon {{\,\mathrm{Id}\,}}$ we get a strongly Siegel-dissipative tuple of operators. Applying the von Neumann type inequality we have

$$\begin{aligned} \Vert p( e^{\varepsilon \tau _1} M_1 , \dots , e^{\varepsilon \tau _k}M_d ) \Vert _{{{\mathcal {B}}}({{\mathcal {H}}})}\le \Vert p(m_1,\dots , m_d) \Vert _{{{\mathcal {M}}}(DA)}, \end{aligned}$$

However, the right hand side of the inequality does not depend on $\varepsilon$ and the left hand side converges in the operator norm as $\varepsilon \rightarrow 0 ^+$. In fact, it suffices to prove the convergence for each term of the polynomial separately; we have

$$\begin{aligned} \Vert e^{-i\tau A_{d+1}}e^{\tau \varepsilon } - e^{-i\tau A_{d+1}} \Vert = \Vert e^{-i\tau A_{d+1}} \Vert (1-e^{\tau \varepsilon } ) \le (1-e^{\tau \varepsilon }) \overset{\tau \nearrow 0}{\longrightarrow } 0. \end{aligned}$$

Therefore, we can pass to the limit and obtain the desired inequality. $\square$