A Subnormal Completion Problem for Weighted Shifts on Directed Trees, II

Abstract

The subnormal completion problem on a directed tree is to determine, given a collection of weights on a subtree, whether the weights may be completed to the weights of a subnormal weighted shift on the directed tree. We study this problem on a directed tree with a single branching point, $\eta$ branches and the trunk of length 1 and its subtree which is the “truncation” of the full tree to vertices of generation not exceeding 2. We provide necessary and sufficient conditions written in terms of two parameter sequences for the existence of a subnormal completion in which the resulting measures are 2-atomic. As a consequence, we obtain a solution of the subnormal completion problem for this pair of directed trees when $\eta < \infty$. If $\eta =2$, we present a solution written explicitly in terms of initial data.

1 Introduction

The class of unilateral weighted shifts on Hilbert space has been a standard and important source of examples with which to study the properties of bounded linear operators on Hilbert space, including especially the investigation of subnormality (see [18] and [5]). A recently introduced class of weighted shifts on directed trees provides a more extensive collection of objects for study (see e.g., [1,2,3, 14, 15]). In [10], we initiated the study of a subnormal completion problem for weighted shift operators on directed trees. For a classical weighted shift, the subnormal completion problem is to be given an initial finite sequence of positive weights and to determine whether or not they may be extended to the weights of an injective, bounded, subnormal unilateral weighted shift; such a shift is called a subnormal completion of the initial weight sequence. It should be emphasized that the subnormal completion problem was initiated and solved explicitly for four initial weights by Stampfli in [19]. Almost three decades later the problem was abstractly solved by Curto and Fialkow in [7, 8] (see also [6, 9]). Relatively recently an explicit solution for five initial weights was given in [16].

In the present paper we continue the study of the subnormal completion problem for weighted shifts on directed trees. As in [10], we restrict our attention to the directed tree ${\mathscr {T}}_{\eta ,\kappa }$ with a single branching point, $\eta$ branches and the trunk of length $\kappa$, and we consider the subnormal completion problem with respect to the subtree ${\mathscr {T}}_{\eta ,\kappa ,p}$, which is the “truncation” of ${\mathscr {T}}_{\eta ,\kappa }$ to vertices of generation not exceeding p. If $\eta$ is finite and the p-generation subnormal completion problem on ${\mathscr {T}}_{\eta ,\kappa }$ has a solution for given initial data $\varvec{\lambda }$, then we can always find a subnormal completion $S_{\hat{\varvec{\lambda }}}$ such that the measures $\mu _{i,1}^{\hat{\varvec{\lambda }}}$, which are canonically associated with $S_{\hat{\varvec{\lambda }}}$ at vertices of the first generation, are at most $\lfloor \frac{\kappa +p+2}{2}\rfloor$-atomic (see Theorem 2.2). So far as we know, there is no solution of the p-generation subnormal completion problem on ${\mathscr {T}}_{\eta ,\kappa }$ written in terms of initial data for $p\geqslant 2$. The only explicit solution is that for the 1-generation subnormal completion problem on ${\mathscr {T}}_{\eta ,1}$ (see [10, Theorem 5.1]). In view of the above discussion, if the 2-generation subnormal completion problem on ${\mathscr {T}}_{\eta ,1}$ has a solution for given initial data $\varvec{\lambda }$, then we can always find a subnormal completion $S_{\hat{\varvec{\lambda }}}$ of $\varvec{\lambda }$ on ${\mathscr {T}}_{\eta ,1}$ with the property that each measure $\mu _{i,1}^{\hat{\varvec{\lambda }}}$ is 1- or 2-atomic. In this paper we provide necessary and sufficient conditions written in terms of two parameter sequences for $\varvec{\lambda }$ to admit a subnormal completion $S_{\hat{\varvec{\lambda }}}$ on ${\mathscr {T}}_{\eta ,1}$ with 2-atomic measures $\mu _{i,1}^{\hat{\varvec{\lambda }}}$. As a consequence, we solve the 2-generation subnormal completion problem on ${\mathscr {T}}_{\eta ,1}$ for $\eta <\infty$. The results, taken as a whole, suggest that a complete answer to the subnormal completion problem even for this class of directed trees is at present out of reach.

The paper is organized as follows. In Sect. 2, we provide notation, terminology and results that are needed in this paper. In Sect. 3 we carry out an in-depth analysis of the first two “negative” moments of the Berger measure associated with the Stampfli completion of three increasing weights to the weight sequence for a subnormal unilateral weighted shift (see Lemma 3.6). In Sect. 4 we state and prove the solutions of the 2-generation subnormal completion problem on ${\mathscr {T}}_{\eta ,1}$ with 2-atomic measures (the case $\eta =\infty$ is included, see Theorem 4.1) and without any restrictions on supports of the associated measures (only for $\eta < \infty$; see Theorem 4.2). In view of Proposition 4.4(iii), to solve the problem with 2-atomic measures we have to compute the infimum of a quadratic form in $\eta$ variables subject to some constraints. In Sect. 5 we give a solution of the 2-generation subnormal completion problem on ${\mathscr {T}}_{2,1}$ with 2-atomic measures written entirely in terms of the initial data (see Theorem 5.2). This confirms the scale of the complexity of this problem.

2 Preliminaries

In this section we sketch briefly the notation and results necessary for the present discussion, but the reader is encouraged to consult [10] for a considerably more complete presentation.

Given a complex Hilbert space $\mathcal {H}$, we denote by ${\varvec{B} (\mathcal {H})}$ the $C^*$-algebra of all bounded linear operators on $\mathcal {H}$. Recall that an operator $T\in {\varvec{B} (\mathcal {H})}$ is said to be subnormal if there exists a complex Hilbert space $\mathcal {K}$ containing $\mathcal {H}$ and a normal operator $N\in {\varvec{B} (\mathcal {K})}$ such that $Th = Nh$ for all $h\in \mathcal {H}$. We refer the reader to [4, 5, 12] for the foundations of the theory of subnormal operators.

Denote by $\mathbb {Z}_+$, $\mathbb {N}$, $\mathbb {R}$, $\mathbb {R}_+$ and $\mathbb {C}$ the sets of nonnegative integers, positive integers, real numbers, nonnegative real numbers and complex numbers, respectively. Set $\mathbb {N}_2 = \{2,3,4, \ldots \}$ and $\bar{\mathbb {N}}_{2}=\mathbb {N}_2 \cup \{\infty \}$. Define $J_{\iota }$ by

$$\begin{aligned} J_{\iota }=\{k\in \mathbb {N}:k\leqslant \iota \} \text { for } \iota \in \mathbb {Z}_+ \cup \{\infty \}, \end{aligned}$$

using the convention that $J_0=\varnothing$. We write $\mathrm {card}(X)$ for the cardinality of a set X. In what follows, $\delta _x$ stands for the Dirac Borel measure on $\mathbb {R}_+$ at the point $x\in \mathbb {R}_+$. The closed support of a Borel probability measure $\mu$ on $\mathbb {R}_+$ is denoted by $\mathrm {supp}\,\mu$.

A pair $\mathscr {G}=(V,E)$ is a directed graph if V is a nonempty set and E is a subset of $V\times V$. A member of V is a vertex of $\mathscr {G}$, and an element of E is called an edge of $\mathscr {G}$. For $u\in V$, we set ${{\,\mathrm{{\mathsf {Chi}}}\,}}(u)=\{v\in V:(u,v)\in E\}$. A member of ${{\,\mathrm{{\mathsf {Chi}}}\,}}(u)$ is called a child of u. A vertex v of $\mathscr {G}$ is called a root of $\mathscr {G}$, which we may also write as $v\in \mathrm {Root}(\mathscr {G})$, if there is no vertex u of $\mathscr {G}$ such that (u, v) is an edge of $\mathscr {G}$. We set $V^{\circ }=V\setminus \mathrm {Root}(\mathscr {G})$. We say that ${\mathscr {T}}=(V,E)$ is a directed tree if ${\mathscr {T}}$ is a directed graph, which is connected, has no circuits and has the property that for each vertex $u \in V$ there exists at most one vertex $v\in V$, called the parent of u and denoted here by $\mathrm {par}(u)$, such that $(v,u)\in E$. The reader is referred to [15, 17] for more information on directed trees needed in this paper.

Fig. 1

An illustration of the directed tree ${\mathscr {T}}_{\eta ,\kappa }$

We will consider a certain class of directed trees with a single branching point obtained as follows: given $\eta \in \bar{\mathbb {N}}_{2}$ and $\kappa \in \mathbb {N}$, we define the directed tree ${\mathscr {T}}_{\eta ,\kappa }=(V_{\eta ,\kappa }, E_{\eta ,\kappa })$ by (see Fig. 1):

$$\begin{aligned} V_{\eta ,\kappa }&=\{-k:k\in J_{\kappa }\}\sqcup \{0\}\sqcup \{(i,j):i\in J_{\eta },j\in \mathbb {N}\},\\ E_{\eta ,\kappa }&=E_{\kappa }\sqcup \{(0,(i,1)):i\in J_{\eta }\}\sqcup \{((i,j),(i,j+1)):i\in J_{\eta },j\in \mathbb {N}\},\\ E_{\kappa }&=\{(-k,-k+1):k\in J_{\kappa }\}. \end{aligned}$$

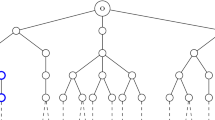
Define as well a subtree of ${\mathscr {T}}_{\eta , \kappa }$ on which we may be given “some of” the weights of a proposed shift as initial data: for $\eta \in \bar{\mathbb {N}}_{2}$, $\kappa \in \mathbb {N}$ and $p \in \mathbb {N}$, let the directed tree ${\mathscr {T}}_{\eta , \kappa , p}=(V_{\eta , \kappa , p},E_{\eta ,\kappa ,p})$ be defined by (see Fig. 2)

$$\begin{aligned} V_{\eta ,\kappa ,p}&=\{-k:k\in J_{\kappa }\}\sqcup \{0\}\sqcup \{(i,j):i\in J_{\eta },j\in J_{p}\},\\ E_{\eta ,\kappa ,p}&=E_{\kappa }\sqcup \{(0,(i,1)):i\in J_{\eta }\}\sqcup \{((i,j),(i,j+1)):i\in J_{\eta },j\in J_{p-1}\}. \end{aligned}$$

Fig. 2

An illustration of the directed tree ${\mathscr {T}}_{\eta ,\kappa ,p}$

Given a directed tree ${\mathscr {T}}=(V,E)$, let $\ell ^2(V)$ be the Hilbert space of all square summable complex functions on V equipped with the usual inner product. The family $\{e_u\}_{u\in V}$ defined by

$$\begin{aligned} e_u(v) = {\left\{ \begin{array}{ll} 1 &{} \text {if } v = u, \\ 0 &{} \text {otherwise,} \end{array}\right. } \quad v\in V, \end{aligned}$$

is clearly an orthonormal basis of $\ell ^2(V)$. Given a system $\varvec{\lambda }= \{\lambda _v\}_{v\in V^{\circ }} \subseteq \mathbb {C}$, we define the operator ${S_{\varvec{\lambda }}}$ in $\ell ^2(V)$ by ${S_{\varvec{\lambda }}}f = \varLambda _{\mathscr {T}}f$ for $f \in \ell ^2(V)$ such that $\varLambda _{\mathscr {T}}f \in \ell ^2(V)$, where $\varLambda _{\mathscr {T}}$ acts on functions $f:V \rightarrow \mathbb {C}$ via

$$\begin{aligned} (\varLambda _{\mathscr {T}}f)(v) = {\left\{ \begin{array}{ll} \lambda _v \cdot f(\mathrm {par}(v)) &{} \text {if } v \in V^\circ ,\\ 0 &{} \text {if } v \text { is a root of } {\mathscr {T}}. \end{array}\right. } \end{aligned}$$

We call ${S_{\varvec{\lambda }}}$ the weighted shift on the directed tree ${\mathscr {T}}$ with weights $\{\lambda _v\}_{v \in V^\circ }$. Throughout this paper it is assumed that the resulting operator ${S_{\varvec{\lambda }}}$ is bounded (see [10] or more generally [15] for an approach suitable even for unbounded shifts, and for discussions of when ${S_{\varvec{\lambda }}}$ is indeed bounded). If ${S_{\varvec{\lambda }}}\in {\varvec{B} (\ell ^2(V))}$, in view of [15, (3.1.4)], one may more easily express ${S_{\varvec{\lambda }}}$ by

$$\begin{aligned} {S_{\varvec{\lambda }}}e_u = \sum _{v \in {{\,\mathrm{{\mathsf {Chi}}}\,}}(u)} \lambda _v e_v. \end{aligned}$$

(We adopt the convention that $\sum _{v\in \varnothing } x_v = 0$.) The weighted shifts desired are those which are subnormal operators. According to [15, Theorem 6.1.3 and Notation 6.1.9], the following assertion holds.

(2.1)

The characterizations of subnormality of ${S_{\varvec{\lambda }}}$ on the directed tree ${\mathscr {T}}_{\eta , \kappa }$ can be found in [15, Corollary 6.2.2].

Matters are in hand for the statement of the fundamental problem considered. Let ${\mathscr {T}}=(V,E)$ be a subtree of a directed tree $\hat{{\mathscr {T}}}=(\hat{V},\hat{E})$ and let $\varvec{\lambda }=\{\lambda _v\}_{v\in V^{\circ }}$ be a system of positive real numbers. We say that a weighted shift $S_{\hat{\varvec{\lambda }}}$ on $\hat{\mathscr {T}}$ with weights $\hat{\varvec{\lambda }}=\{\hat{\lambda }_v\}_{v\in \hat{V}^{\circ }} \subseteq (0,\infty )$ is a subnormal completion of $\varvec{\lambda }$ on $\hat{\mathscr {T}}$ if $S_{\hat{\varvec{\lambda }}}\in {\varvec{B} (\ell ^2(\hat{V}))}$, $\varvec{\lambda }\subseteq \hat{\varvec{\lambda }}$, i.e., $\lambda _v=\hat{\lambda }_v$ for all $v\in V^{\circ }$, and $S_{\hat{\varvec{\lambda }}}$ is subnormal. If such a completion exists, we may sometimes say $\varvec{\lambda }$ admits a subnormal completion on $\hat{\mathscr {T}}$. The subnormal completion problem for $({\mathscr {T}},\hat{\mathscr {T}})$ consists of seeking necessary and sufficient conditions for a system $\varvec{\lambda }=\{\lambda _v\}_{v\in V^{\circ }} \subseteq (0,\infty )$ to have a subnormal completion on $\hat{\mathscr {T}}$.

Following [10], the subnormal completion problem for $({\mathscr {T}}_{\eta ,\kappa ,p}, {\mathscr {T}}_{\eta ,\kappa })$, where $p\in \mathbb {N}$, is called the p-generation subnormal completion problem on ${\mathscr {T}}_{\eta ,\kappa }$ (sometimes abbreviated to p-generation SCP on ${\mathscr {T}}_{\eta ,\kappa }$). In this particular case, our initial data takes the form

$$\begin{aligned} \varvec{\lambda }= \{\lambda _v\}_{v\in V_{\eta , \kappa ,p}^{\circ }} = \{\lambda _{-\kappa +1}, \ldots , \lambda _0\} \cup \{\lambda _{i,1}\}_{i\in J_{\eta }} \cup \cdots \cup \{\lambda _{i,p}\}_{i\in J_{\eta }}. \end{aligned}$$

The following result, which gives the measure-theoretic way of solving the p-generation subnormal completion problem on ${\mathscr {T}}_{\eta ,\kappa }$, is a consequence of [10, Lemma 4.7 and Theorem 4.9].

Lemma 2.1

Suppose $\eta \in \bar{\mathbb {N}}_{2}$, $\kappa , p \in \mathbb {N}$ and $\varvec{\lambda }= \{\lambda _v\}_{v\in V_{\eta ,\kappa ,p}^{\circ }} \subseteq (0,\infty )$ are given. Then the following conditions are equivalent:

• (i) $\varvec{\lambda }$ admits a subnormal completion on ${\mathscr {T}}_{\eta ,\kappa }$,

• (ii) there exist Borel probability measures $\{\mu _{i}\}_{i=1}^{\eta }$ on $\mathbb {R}_+$ which satisfy the following conditions:

  $$\begin{aligned}&\int _{\mathbb {R}_+} s^{n} d\mu _{i}(s) = \prod _{j=2}^{n+1}\lambda _{i,j}^{2}, \quad n\in J_{p-1},\ i\in J_{\eta },\end{aligned}$$

  (2.2)
  $$\begin{aligned}&\sum _{i=1}^{\eta } \lambda _{i,1}^{2} \int _{\mathbb {R}_+} \frac{1}{s} d \mu _{i}(s) =1,\nonumber \\&\sum _{i=1}^{\eta }\lambda _{i,1}^{2} \int _{\mathbb {R}_+} \frac{1}{s^{k+1}} d\mu _{i}(s) = \frac{1}{\prod _{j=0}^{k-1}\lambda _{-j}^{2}}, \quad k\in J_{\kappa -1},\end{aligned}$$

  (2.3)
  $$\begin{aligned}&\sum _{i=1}^{\eta } \lambda _{i,1}^{2} \int _{\mathbb {R}_+} \frac{1}{s^{\kappa +1}} d \mu _{i}(s) \leqslant \frac{1}{\prod _{j=0}^{\kappa -1} \lambda _{-j}^{2}},\end{aligned}$$

  (2.4)
  $$\begin{aligned}&\sup _{i\in J_{\eta }} \sup \mathrm {supp}\,\mu _{i} < \infty . \end{aligned}$$

  (2.5)

Moreover, if $\{\mu _{i}\}_{i=1}^{\eta }$ are as in (ii), then there exists a subnormal completion $S_{\hat{\varvec{\lambda }}}$ of $\varvec{\lambda }$ on ${\mathscr {T}}_{\eta ,\kappa }$ such that $\mu _{i,1}^{\hat{\varvec{\lambda }}}=\mu _{i}$ for all $i\in J_{\eta }$.

In [10, Theorem 5.1] we gave an explicit solution of the 1-generation subnormal completion problem on ${\mathscr {T}}_{\eta ,1}$ written in terms of initial data. As shown in [10, Theorem 6.2], the 1-generation subnormal completion problem on ${\mathscr {T}}_{\eta ,\kappa }$, where $\kappa \in \mathbb {N}$, reduces to seeking necessary and sufficient conditions for a system $\varvec{\lambda }=\{\lambda _v\}_{v\in V_{\eta ,\kappa ,1}^{\circ }} \subseteq (0,\infty )$ to have a 2-generation flat subnormal completion on ${\mathscr {T}}_{\eta , \kappa }$. It was also proved in [10, Theorem 8.3] that the problem of finding a p-generation flat subnormal completion on ${\mathscr {T}}_{\eta ,\kappa }$ can be solved by using the well-known solutions of the subnormal completion problem for unilateral weighted shifts given in [6,7,8,9, 16, 19]. However, in most cases these solutions are not written explicitly in terms of initial data. This means that we have no explicit (i.e., written in terms of initial data) solution of the p-generation subnormal completion problem on ${\mathscr {T}}_{\eta ,\kappa }$ for $p\geqslant 2$, even when $\kappa =1$. It is the right moment to make the following important observation which is implicitly contained in the proof of [10, Theorem 7.1].

Theorem 2.2

Suppose $\eta \in \mathbb {N}_2$, $\kappa , p \in \mathbb {N}$ and $\varvec{\lambda }= \{\lambda _v\}_{v\in V_{\eta ,\kappa ,p}^{\circ }} \subseteq (0,\infty )$ are given. If $\varvec{\lambda }$ admits a subnormal completion on ${\mathscr {T}}_{\eta ,\kappa }$, then it admits a subnormal completion $S_{\hat{\varvec{\lambda }}}$ on ${\mathscr {T}}_{\eta ,\kappa }$ such that

$$\begin{aligned} \mathrm {card}(\mathrm {supp}\,\mu _{i,1}^{\hat{\varvec{\lambda }}}) \leqslant \Big \lfloor \frac{\kappa +p+2}{2}\Big \rfloor , \quad i\in J_{\eta }, \end{aligned}$$

where $\lfloor x \rfloor = \min \big \{n\in \mathbb {Z}_+:n \leqslant x < n+1\big \}$ for $x\in \mathbb {R}_+$.

Proof

Applying [6, Theorems 5.1(iii) and 5.3(iii)] and arguing as in the proof of the implication (iii)$\Rightarrow$(iv) of [10, Theorem 7.1], we may assume without loss of generality that for every $i\in J_{\eta }$, the measure $\rho _i$ appearing in the proof of the implication (iv)$\Rightarrow$(v) of [10, Theorem 7.1] satisfies the following condition:

$$\begin{aligned} \mathrm {card}(\mathrm {supp}\,\rho _i) \leqslant \Big \lfloor \frac{\kappa +p+2}{2}\Big \rfloor \text { and } \mathrm {supp}\,\rho _i \subseteq (0,\infty ). \end{aligned}$$

Next, by arguing as in the proof of the implication (iv)$\Rightarrow$(v) of [10, Theorem 7.1], we get a subnormal completion with the desired property. $\square$

It follows from Theorem 2.2 that if $\eta \in \mathbb {N}_2$ and the 2-generation subnormal completion problem on ${\mathscr {T}}_{\eta ,1}$ has a solution for a given data $\varvec{\lambda }= \{\lambda _v\}_{v\in V_{\eta ,1,2}^{\circ }} \subseteq (0,\infty )$, then one can always find a subnormal completion $S_{\hat{\varvec{\lambda }}}$ of $\varvec{\lambda }$ on ${\mathscr {T}}_{\eta ,1}$ with the property that each measure $\mu _{i,1}^{\hat{\varvec{\lambda }}}$ is 1- or 2-atomic.

3 Preparatory Lemmas

One of the goals of this paper is to explore when initial data $\varvec{\lambda }=\{\lambda _v\}_{v\in V_{\eta ,1,2}^{\circ }}$ on ${\mathscr {T}}_{\eta ,1,2}$ admits a subnormal completion $S_{\hat{\varvec{\lambda }}}$ on ${\mathscr {T}}_{\eta ,1}$ such that each of the measures $\mu _{i,1}^{\hat{\varvec{\lambda }}}$ (see (2.1)) is 2-atomic (under present circumstances, the measures $\mu _{i,1}^{\hat{\varvec{\lambda }}}$ may be taken to be 1- or 2-atomic due to Theorem 2.2). We first require some background on the Stampfli completion of three increasing weights to the weight sequence for a subnormal unilateral weighted shift (cf. [19]).

In [19] the author gives an explicit construction of the completion of an initial finite sequence of three weights x, y, z satisfying $0< x< y < z$ to the sequence of positive weights $\{\alpha _n\}_{n=0}^{\infty }$ for a (bounded, injective) subnormal unilateral weighted shift $W_{\alpha }$. This includes a construction of the associated Berger measure of $W_{\alpha }$ (i.e., a unique Borel probability measure $\xi$ on $\mathbb {R}_+$ such that for any $n\in \mathbb {N}$, $\gamma _n := \alpha _{0}^2 \ldots \alpha _{n-1}^2 = \int _{\mathbb {R}_+} t^n d \xi (t)$), which turns out to be 2-atomic. The completion sequence $\{\alpha _n\}_{n=0}^{\infty }$, which is called the Stampfli completion of (x, y, z), is customarily denoted by $(x,y,z)^{\wedge }$; it is known that the moment sequence $\{\gamma _n\}_{n=0}^{\infty }$ (with $\gamma _{0}=1$) for $W_{\alpha }$ satisfies a recursion.

Definition 3.1

The Berger measure of $W_{\alpha }$ will be called the Berger measure associated with the Stampfli completion $(x,y,z)^{\wedge }$ of (x, y, z) and denoted by $\xi _{x,y,z}$.

One may see [6,7,8] for an alternative approach to these same results. We note also that one may consider the cases $0< x < y = z$ (yielding a 2-atomic measure with an atom at zero) and $0 < x = y = z$, and this last case yields a completion whose Berger measure is 1-atomic.

Our technique will be to try to choose $y_i$ and $z_i$, which will become respectively $\hat{\lambda }_{i,3}$ and $\hat{\lambda }_{i,4}$ of the completion $S_{\hat{\varvec{\lambda }}}$, in such a way that the Berger measures associated to $(x_{i},y_{i},z_{i})^{\wedge }$ will become the $\mu _{i,1}^{\hat{\varvec{\lambda }}}$ and have good properties (and of course they will automatically be 2-atomic). Figure 3 summarizes the task and our notation.

Fig. 3

An illustration of a 2-generation SCP on ${\mathscr {T}}_{\eta ,1}$ with $\lambda _{0}$, $\{\lambda _{i,1}\}_{i\in J_{\eta }}$ and $\{\lambda _{i,2}\}_{i\in J_{\eta }}$ as given data

We begin by calculating the first two “negative” moments of the Berger measure associated with the Stampfli completion $(x,y,z)^{\wedge }$ of (x, y, z).

Lemma 3.2

Suppose that $(x,y,z)\in \mathbb {R}$ are such that $0< x< y < z$. Then

$$\begin{aligned} \int _{\mathbb {R}_+} \frac{1}{s} d\xi _{x,y,z}(s) = \frac{x^{4}-2x^{2}y^{2}+ y^{2}z^{2}}{x^{2}y^{2}(z^{2}-y^{2})} = \frac{1}{x^{2}} \left[ \frac{1-2\frac{y^{2}}{x^{2}} +\frac{y^{2}}{x^{2}}\frac{z^{2}}{x^{2}}}{\frac{y^{2}}{x^{2}} (\frac{z^{2}}{x^{2}}-\frac{y^{2}}{x^{2}})} \right] \end{aligned}$$

(3.1)

and

$$\begin{aligned} \int _{\mathbb {R}_+} \frac{1}{s^2}d\xi _{x,y,z}(s)= & {} \frac{-x^{6}+y^{2}z^{4}+x^{4}(y^{2}+2z^{2})+x^{2}(y^{4}-4y^{2}z^{2})}{x^{4}(y^{3}-yz^{2})^2}\nonumber \\= & {} \frac{1}{x^4} \left[ \frac{-1+\frac{y^2}{x^2} \cdot \frac{z^4}{x^4} +\frac{y^2}{x^2} +\frac{2z^2}{x^2}+\frac{y^4}{x^4} -\frac{4y^2}{x^2}\cdot \frac{z^2}{x^2}}{\frac{y^2}{x^2} \big (\frac{z^2}{x^2} - \frac{y^2}{x^2} \big )^2} \right] .\qquad \end{aligned}$$

(3.2)

Proof

To simplify notation, set $\xi =\xi _{x,y,z}$. By [7, Example 3.14], we have

$$\begin{aligned} \xi = \rho \delta _{s_0} + (1-\rho ) \delta _{s_1}, \end{aligned}$$

where $\rho =\frac{s_1-x^2}{s_1-s_0}$, $s_0=\frac{1}{2}(\psi _1 - \sqrt{\psi _1^2 + 4 \psi _0})$ and $s_1=\frac{1}{2}(\psi _1 + \sqrt{\psi _1^2 + 4 \psi _0})$ with $\psi _0= - x^2y^2 \frac{z^2-y^2}{y^2-x^2}$ and $\psi _1= y^2 \frac{z^2-x^2}{y^2-x^2}$. Straightforward computations now yield (3.1) and (3.2). $\square$

Next we investigate the function f which comes from the expression appearing on the right-hand side of the second equality in (3.1).

Lemma 3.3

Let f be a real function on $\varOmega =\{(u, v)\in \mathbb {R}^2:v>u>1\}$ given by

$$\begin{aligned} f(u,v) = \frac{1-2u+uv}{u (v-u)}, \quad (u, v)\in \varOmega . \end{aligned}$$

Then $f(\varOmega ) = (1, \infty )$ and for any $(u, v)\in \varOmega$ and $r\in (1,\infty )$,

$$\begin{aligned} f(u,v)=r \quad \text {if and only if} \quad v= \frac{1 - 2u + r u^2}{(r-1)u}. \end{aligned}$$

(3.3)

Further, for any $u\in (1,\infty )$, the map $\varphi _{u}:(1,\infty ) \rightarrow (u, \infty )$ defined by

$$\begin{aligned} \varphi _{u}(r) =\frac{1 - 2u + r u^2}{(r-1)u}, \quad r\in (1,\infty ), \end{aligned}$$

(3.4)

is a bijection.

Proof

It is a routine matter to verify that for any $u\in (1,\infty )$, the function $\varphi _{u}$ is a well-defined bijection from $(1,\infty )$ to $(u, \infty )$. Clearly, the function f is well defined. Since $(u,\varphi _{u}(r)) \in \varOmega$ and $f(u,\varphi _{u}(r))=r$ for all $r\in (1,\infty )$ and $u\in (1,\infty )$, we deduce that $(1, \infty ) \subseteq f(\varOmega )$. Next, a simple argument shows that $f(\varOmega ) \subseteq (1,\infty )$, so $f(\varOmega ) = (1, \infty )$. It is a computation to show that (3.3) holds.$\square$

Corollary 3.4 below provides more information on the behavior of the first “negative” moment of the Berger measure appearing in Lemma 3.2.

Corollary 3.4

Let $x, y\in \mathbb {R}$ be such that $0< x < y$. Then for any $z\in (y,\infty )$, there exists a unique $r\in (1,\infty )$ such that

$$\begin{aligned} \int _{\mathbb {R}_+} \frac{1}{s} d\xi _{x,y,z}(s)= r\frac{1}{x^2}. \end{aligned}$$

(3.5)

Conversely, for any $r \in (1,\infty )$, there exists a unique $z\in (y,\infty )$ such that (3.5) holds; the number z is determined by the formula $v=\varphi _{u}(r)$ with $u = \frac{y^2}{x^2}$ and $v = \frac{z^2}{x^2}$.

Proof

Making the substitutions $u = \frac{y^2}{x^2}$ and $v = \frac{z^2}{x^2}$, we see that $(u,v)\in \varOmega$ and

$$\begin{aligned} \frac{1}{x^{2}} \left[ \frac{1-2\frac{y^{2}}{x^{2}} + \frac{y^{2}}{x^{2}} \frac{z^{2}}{x^{2}}}{\frac{y^{2}}{x^{2}}(\frac{z^{2}}{x^{2}}-\frac{y^{2}}{x^{2}})} \right] = \frac{1}{x^{2}} f(u,v). \end{aligned}$$

Now applying Lemmas 3.2 and 3.3 completes the proof. $\square$

The expression on the right-hand side of the second equality in (3.2) leads to the function g which appears in a lemma below. The proof of this lemma follows from straightforward computations via Lemma 3.3. The details are left to the reader.

Lemma 3.5

Let $\varOmega$ be as in Lemma 3.3 and g be a real function on $\varOmega$ given by

$$\begin{aligned} g(u,v) = \frac{-1+u \cdot v^2 + u + 2v + u^2 - 4u \cdot v}{u(v-u)^2}, \quad (u,v)\in \varOmega . \end{aligned}$$

For $r \in (1,\infty )$, let $h_r$ be a real function on $(1, \infty )$ defined by¹

$$\begin{aligned} h_r(u) = g\big (u, \varphi _u(r)\big ), \quad u \in (1,\infty ), \end{aligned}$$

where $\varphi _u$ is as in (3.4). Then the following statements hold for each $r\in (1,\infty )$:

• (i) $h_r(u) = \frac{1-2r + r^2 u}{u - 1}, \quad u\in (1,\infty )$,

• (ii) $\lim _{u \rightarrow 1 +}h_r(u) = \infty$,

• (iii) $\lim _{u \rightarrow \infty } h_r(u) = r^2$,

• (iv) $h_r\big ((1,\infty )\big ) = (r^2, \infty )$ and $h_r:(1,\infty ) \rightarrow (r^2, \infty )$ is a bijection.

Putting together the last three lemmas, we obtain the following crucial lemma.

Lemma 3.6

For any $(x,y,z)\in \mathbb {R}^3$ such that $0< x< y < z$, there exist $r, \vartheta \in (1,\infty )$ such that

$$\begin{aligned} \int _{\mathbb {R}_+} \frac{1}{s}d\xi _{x,y,z}(s)= & {} r \frac{1}{x^2}, \end{aligned}$$

(3.6)

$$\begin{aligned} \int _{\mathbb {R}_+} \frac{1}{s^2}d\xi _{x,y,z}(s)= & {} \vartheta \, r^2 \frac{1}{x^4}. \end{aligned}$$

(3.7)

Moreover, for any $x\in (0,\infty )$ and any $r, \vartheta \in (1,\infty )$, there exists $(y,z)\in \mathbb {R}^2$ with $x< y < z$ satisfying (3.6) and (3.7).

Proof

Assume $(x,y,z)\in \mathbb {R}^3$ is such that $0< x< y < z$. Set $u=\frac{y^2}{x^2}$ and $v=\frac{z^2}{x^2}$. Then $(u,v)\in \varOmega$. By Lemma 3.3, $r:=f(u,v) \in (1,\infty )$ and $v=\varphi _u(r)$, so

$$\begin{aligned} \int _{\mathbb {R}_+} \frac{1}{s} d\xi _{x,y,z}(s)\overset{(3.1)}{=}\frac{1}{x^2} f(u,v) = r \frac{1}{x^2}, \end{aligned}$$

which gives (3.6). In turn, by Lemma 3.5(iv), $h_r(u) \in (r^2,\infty )$ and

$$\begin{aligned} \int _{\mathbb {R}_+} \frac{1}{s^2}d\xi _{x,y,z}(s) \overset{(3.2)}{=} \frac{1}{x^4} g(u,v) = \frac{1}{x^4} h_r(u), \end{aligned}$$

which implies that (3.7) holds for some $\vartheta \in (1,\infty )$.

Suppose now that $x\in (0,\infty )$ and $r, \vartheta \in (1,\infty )$. Since $\vartheta \, r^2 \in (r^2,\infty )$, we infer from Lemma 3.5(iv) that there exists $u\in (1,\infty )$ such that $h_r(u)=\vartheta \, r^2$. Set $v=\varphi _u(r)$. Then $(u, v) \in \varOmega$ and

$$\begin{aligned} g\big (u, v\big ) = h_r(u)=\vartheta \, r^2. \end{aligned}$$

(3.8)

Setting $y=x \sqrt{u}$ and $z=x \sqrt{v}$, we see that $0<x< y < z$ and

$$\begin{aligned} \int _{\mathbb {R}_+} \frac{1}{s^2}d\xi _{x,y,z}(s) \overset{(3.2)}{=}\frac{1}{x^4} g\big (u, v\big ) \overset{(3.8)}{=} \vartheta \, r^2 \frac{1}{x^4}, \end{aligned}$$

which gives (3.7). Since $v=\varphi _u(r)$, we have

$$\begin{aligned} \int _{\mathbb {R}_+} \frac{1}{s} d\xi _{x,y,z}(s) \overset{(3.1)}{=} \frac{1}{x^2} f(u,v) = \frac{1}{x^2} f(u,\varphi _u(r)) \overset{(3.3)}{=} r \frac{1}{x^2}, \end{aligned}$$

which implies (3.6).$\square$

4 The 2-Generation SCP on ${\mathscr {T}}_{\eta ,1}$

We begin by solving the 2-generation subnormal completion problem on ${\mathscr {T}}_{\eta ,1}$ with 2-atomic measures (the case $\eta =\infty$ is included).

Theorem 4.1

Suppose $\eta \in \bar{\mathbb {N}}_{2}$, $\kappa = 1$, $p=2$ and $\varvec{\lambda }= \{\lambda _0\} \cup \{\lambda _{i,1}\}_{i=1}^{\eta } \cup \{\lambda _{i,2}\}_{i=1}^{\eta } \subseteq (0,\infty )$ are given. Then the following statements are equivalent:

• (i) $\varvec{\lambda }$ has a subnormal completion $S_{\hat{\varvec{\lambda }}}$ on ${\mathscr {T}}_{\eta , 1}$ such that each measure $\mu _{i, 1}^{\hat{\varvec{\lambda }}}$ is 2-atomic,

• (ii) there exist sequences $\{r_i\}_{i=1}^{\eta }, \{\vartheta _i\}_{i=1}^{\eta } \subseteq (1,\infty )$ such that

  $$\begin{aligned}&\sup _{i\in J_{\eta }} \frac{\vartheta _i r_i -1}{(\vartheta _i - 1)r_i} \lambda _{i,2}^2 < \infty , \end{aligned}$$

  (4.1)
  $$\begin{aligned}&\sum _{i=1}^{\eta } r_i \frac{\lambda _{i,1}^2}{\lambda _{i,2}^2} = 1, \end{aligned}$$

  (4.2)
  $$\begin{aligned}&\sum _{i=1}^{\eta } \vartheta _i r_i^2 \frac{\lambda _{i,1}^2}{\lambda _{i,2}^4} \leqslant \frac{1}{\lambda _0^2}. \end{aligned}$$

  (4.3)

Moreover, if (i) holds, then $\mu _{i, 1}^{\hat{\varvec{\lambda }}}(\{0\})=0$ for all $i\in J_{\eta }$ and

$$\begin{aligned} \lambda _0^2< \sum _{i=1}^{\eta } \lambda _{i,1}^2, \quad \sum _{i=1}^{\eta } \frac{\lambda _{i,1}^2}{\lambda _{i,2}^4}< \frac{1}{\lambda _0^2}, \quad \sum _{i=1}^{\eta } \frac{\lambda _{i,1}^2}{\lambda _{i,2}^2}< 1, \quad \sum _{i=1}^{\eta } \lambda _{i,1}^2 < \sup _{i\in J_{\eta }} \lambda _{i,2}^2.\qquad \end{aligned}$$

(4.4)

Proof

We concentrate on proving the case when $\eta =\infty$. If $\eta < \infty$, the proof simplifies. In particular, the statement (4.1) can be dropped.

(i)$\Rightarrow$(ii) Let $S_{\hat{\varvec{\lambda }}}$ be a subnormal completion of $\varvec{\lambda }$ on ${\mathscr {T}}_{\infty , 1}$ such that each measure $\mu _i:=\mu _{i, 1}^{\hat{\varvec{\lambda }}}$ is 2-atomic. It follows from [15, Corollary 6.2.2(ii)] that

$$\begin{aligned} \sum _{i=1}^{\infty }\lambda _{i,1}^{2}\int _{\mathbb {R}_+} \frac{1}{s}d\mu _{i}(s)= & {} 1, \end{aligned}$$

(4.5)

$$\begin{aligned} \sum _{i=1}^{\infty }\lambda _{i,1}^{2}\int _{\mathbb {R}_+} \frac{1}{s^2} d\mu _{i}(s)\leqslant & {} \frac{1}{\lambda _0^{2}}. \end{aligned}$$

(4.6)

Applying (2.1) to $u=e_{i,1}$ and using the Berger–Gellar–Wallen theorem (see [11, 13]), we deduce that for every $i\in \mathbb {N}$, the unilateral weighted shift $W_{\alpha ^{(i)}}$ with weights $\alpha ^{(i)}=\{\hat{\lambda }_{i,n+2}\}_{n=0}^{\infty }$ is subnormal and $\mu _i$ is the Berger measure of $W_{\alpha ^{(i)}}$. It follows from (4.5) that $\mu _i$ cannot have an atom at zero. Hence each $\mu _i$ has two atoms in $(0,\infty )$. As a consequence, $\lambda _{i,2}< \hat{\lambda }_{i,3} < \hat{\lambda }_{i,4}$ and $\mu _i=\xi _{\lambda _{i,2},\hat{\lambda }_{i,3}, \hat{\lambda }_{i,4}}$ for every $i \in \mathbb {N}$ (see [10, Lemma 2.3] and [7, Example 3.14, Theorem 3.9(iii)], respectively). Applying Lemma  3.6 to $x=x_i:=\lambda _{i,2}$, $y=y_i:=\hat{\lambda }_{i,3}$ and $z=z_i:=\hat{\lambda }_{i,4}$, we deduce that there exist sequences $\{r_i\}_{i=1}^{\infty } \subseteq (1,\infty )$ and $\{\vartheta _i\}_{i=1}^{\infty } \subseteq (1,\infty )$ such that

$$\begin{aligned} \int _{\mathbb {R}_+} \frac{1}{s}d\mu _{i}(s)= & {} r_i \frac{1}{\lambda _{i,2}^2}, \quad i \in \mathbb {N}, \end{aligned}$$

(4.7)

$$\begin{aligned} \int _{\mathbb {R}_+} \frac{1}{s^2}d\mu _i(s)= & {} \vartheta _i \, r_i^2 \frac{1}{\lambda _{i,2}^4}, \quad i \in \mathbb {N}. \end{aligned}$$

(4.8)

According to the proof of Lemma 3.6, the sequences $\{r_i\}_{i=1}^{\infty }$ and $\{\vartheta _i\}_{i=1}^{\infty }$ are constructed via the following process:

$$\begin{aligned}&y_i=x_i\sqrt{u_i}, z_i=x_i\sqrt{v_i}, v_i=\varphi _{u_i}(r_i) \text { and } h_{r_i}(u_i)=\vartheta _i r_i^2 \text { for } i\in \mathbb {N},\nonumber \\&\qquad \qquad \text {where } 0<x_i<y_i<z_i \text { and } 1< u_i < v_i. \end{aligned}$$

(4.9)

(Recall that by Lemmas 3.3 and 3.5, the functions $\varphi _{u_i}:(1,\infty ) \rightarrow (u_i, \infty )$ and $h_{r_i}:(1,\infty ) \rightarrow (r_i^2, \infty )$ are bijections.) Combining (4.5) with (4.7), we obtain (4.2). In turn, (4.6) and (4.8) imply (4.3). To get (ii), it remains to prove (4.1).

For this, we show that under the circumstances of (4.9) the following assertion holds:

$$\begin{aligned} \varXi :=\sup _{i\in \mathbb {N}}\sup \mathrm {supp}\,\xi _{x_i,y_i,z_i}< \infty \iff \sup _{i\in \mathbb {N}} x_i^2\frac{\vartheta _i r_i -1}{(\vartheta _i-1)r_i} < \infty . \end{aligned}$$

(4.10)

Indeed, according to [7, Example 3.14], we have

$$\begin{aligned} \sup \mathrm {supp}\,\xi _{x_i,y_i,z_i} = \frac{1}{2} \bigg (\psi _{1,i} + \sqrt{\psi _{1,i}^2 + 4\psi _{0,i}}\bigg ), \quad i\in \mathbb {N}, \end{aligned}$$

(4.11)

where $\psi _{0,i}= - x_i^2y_i^2 \frac{z_i^2-y_i^2}{y_i^2-x_i^2}$ for $i\in \mathbb {N}$ and

$$\begin{aligned} \psi _{1,i}= y_i^2 \frac{z_i^2-x_i^2}{y_i^2-x_i^2} \overset{(4.9)}{=} x_i^2 u_i \frac{v_i-1}{u_i-1}, \quad i\in \mathbb {N}. \end{aligned}$$

(4.12)

Since $\psi _{0,i} < 0$ and $\psi _{1,i}^2 + 4\psi _{0,i}>0$ for every $i\in \mathbb {N}$, we deduce from (4.11) that

$$\begin{aligned} \varXi< \infty \iff \sup _{i\in \mathbb {N}} \psi _{1,i} < \infty . \end{aligned}$$

(4.13)

By (4.9), $h_{r_i}(u_i)=\vartheta _i r_i^2$ for all $i\in \mathbb {N}$, so Lemma 3.5(i) leads to

$$\begin{aligned} u_i = \frac{1-2r_i+\vartheta _i r_i^2}{(\vartheta _i-1)r_i^2}, \quad i\in \mathbb {N}. \end{aligned}$$

(4.14)

Using the identity $v_i=\varphi _{u_i}(r_i)$ and (3.4), we get

$$\begin{aligned} v_i-1 = \frac{(u_i-1)(r_i u_i -1)}{(r_i-1)u_i}, \quad i \in \mathbb {N}. \end{aligned}$$

(4.15)

Combining (4.12), (4.14) and (4.15), we see that

$$\begin{aligned} \psi _{1,i} = \frac{x_i^2}{r_i-1} (r_iu_i-1) = x_i^2\frac{\vartheta _i r_i -1}{(\vartheta _i-1)r_i}, \quad i\in \mathbb {N}. \end{aligned}$$

This together with (4.13) yields (4.10). It follows from [15, Eg. (6.3.9)] that $\varXi < \infty$. Hence, by (4.10), (4.1) is satisfied, which shows that (ii) holds.

(ii)$\Rightarrow$(i) Suppose now that (ii) holds. Applying the “moreover” part of Lemma 3.6 to $x=x_i:=\lambda _{i,2}$, $r=r_i$ and $\vartheta =\vartheta _i$, we deduce that for every $i\in \mathbb {N}$, there exists $(y_i,z_i) \in \mathbb {R}^2$ with $x_i< y_i < z_i$ such that (4.7) and (4.8) hold with $\mu _i= \xi _{x_i, y_i, z_i}$. According to the proof of Lemma 3.6, the sequences $\{y_i\}_{i=1}^{\infty }$ and $\{z_i\}_{i=1}^{\infty }$ are constructed via the procedure (4.9). It follows from (4.1) and (4.10) that

$$\begin{aligned} \sup _{i\in \mathbb {N}}\sup \mathrm {supp}\,\mu _i < \infty . \end{aligned}$$

(4.16)

Since in general $\int _{\mathbb {R}_+} s d\xi _{x,y,z}(s) = x^2$ whenever $0< x< y < z$, we get

$$\begin{aligned} \int _{\mathbb {R}_+} s d\mu _i(s) = \lambda _{i,2}^2, \quad i \in \mathbb {N}. \end{aligned}$$

(4.17)

It follows that

$$\begin{aligned}&\sum _{i=1}^{\infty } \lambda _{i,1}^{2} \int _{\mathbb {R}_+} \frac{1}{s} d\mu _{i}(s) \overset{(4.7)}{=} \sum _{i=1}^{\infty } r_i \frac{\lambda _{i,1}^{2}}{\lambda _{i,2}^2} \overset{(4.2)}{=} 1, \end{aligned}$$

(4.18)

$$\begin{aligned}&\sum _{i=1}^{\infty } \lambda _{i,1}^{2} \int _{\mathbb {R}_+} \frac{1}{s^{2}} d\mu _{i}(s) \overset{(4.8)}{=} \sum _{i=1}^{\infty } \vartheta _i r_i^2 \frac{\lambda _{i,1}^{2}}{\lambda _{i,2}^4} \overset{(4.3)}{\leqslant }\frac{1}{\lambda _{0}^{2}}. \end{aligned}$$

(4.19)

Putting together the conditions (4.16), (4.17), (4.18) and (4.19), and applying Lemma 2.1, we conclude that $\varvec{\lambda }$ has a subnormal completion $S_{\hat{\varvec{\lambda }}}$ on ${\mathscr {T}}_{\infty ,1}$ such that $\mu _{i, 1}^{\hat{\varvec{\lambda }}} = \mu _i=\xi _{x_i, y_i, z_i}$ for every $i\in \mathbb {N}$. As a consequence, each $\mu _{i, 1}^{\hat{\varvec{\lambda }}}$ is 2-atomic, which gives (i).

Now we prove the “moreover” part. Suppose (i) is satisfied. The fact that $\mu _{i, 1}^{\hat{\varvec{\lambda }}}(\{0\})=0$ for every $i\in \mathbb {N}$ is a direct consequence of [10, Theorem 3.5(i)]. Notice that the second inequality in (4.4) follows from (4.3) while the third and the fourth can be deduced from (4.2). Thus, it remains to prove the first inequality in (4.4). It follows from [10, Theorem  4.9(i)] that $\lambda _0^2\leqslant \sum _{i=1}^{\infty } \lambda _{i,1}^2$. Suppose, to the contrary, that $\lambda _0^2 = \sum _{i=1}^{\infty } \lambda _{i,1}^2$. Then, by the “moreover” part of [10, Propositon 7.6], we see that $\mu _{i,1}^{\hat{\varvec{\lambda }}} = \delta _{c}$ for every $i\in \mathbb {N}$ with $c=\sum _{i=1}^{\infty } \lambda _{i,1}^2$, which contradicts our assumption that each $\mu _{i,1}^{\hat{\varvec{\lambda }}}$ is 2-atomic.$\square$

Now we are ready to solve the 2-generation subnormal completion problem on ${\mathscr {T}}_{\eta ,1}$ for $\eta \in \mathbb {N}_2$ without any restrictions on the supports of the resulting measures $\mu _{i,1}^{\hat{\varvec{\lambda }}}$.

Theorem 4.2

Suppose $\eta \in \mathbb {N}_2$, $\kappa = 1$, $p=2$ and $\varvec{\lambda }= \{\lambda _0\} \cup \{\lambda _{i,1}\}_{i=1}^{\eta } \cup \{\lambda _{i,2}\}_{i=1}^{\eta } \subseteq (0,\infty )$ are given. Then the following statements are equivalent:

• (i) $\varvec{\lambda }$ has a subnormal completion $S_{\hat{\varvec{\lambda }}}$ on ${\mathscr {T}}_{\eta , 1}$,

• (ii) there exists a sequence $\{r_i\}_{i=1}^{\eta } \subseteq [1,\infty )$ such that

  $$\begin{aligned}&\sum _{i=1}^{\eta } r_i \frac{\lambda _{i,1}^2}{\lambda _{i,2}^2} = 1, \end{aligned}$$

  (4.20)
  $$\begin{aligned}&\sum _{i=1}^{\eta } r_i^2 \frac{\lambda _{i,1}^2}{\lambda _{i,2}^4} \; {\left\{ \begin{array}{ll} \leqslant \frac{1}{\lambda _0^2} &{} \text {if } r_i=1 \text { for every } i\in J_{\eta },\\ < \frac{1}{\lambda _0^2} &{} \text {if } r_i > 1 \text { for some } i\in J_{\eta }. \end{array}\right. } \end{aligned}$$

  (4.21)

Moreover, if $S_{\hat{\varvec{\lambda }}}$ is a subnormal completion of $\varvec{\lambda }$ on ${\mathscr {T}}_{\eta , 1}$ such that each measure $\mu _{i,1}^{\hat{\varvec{\lambda }}}$ is 1- or 2-atomic, then (4.20) and (4.21) hold for some $\{r_i\}_{i=1}^{\eta } \subseteq [1,\infty )$ such that

$$\begin{aligned} r_i=1 (\text {resp. } r_i> 1)\text { if and only if } \mu _{i, 1}^{\hat{\varvec{\lambda }}} \text { is } 1\text {-atomic }(\text {resp. } 2\text {-atomic}). \end{aligned}$$

(4.22)

Conversely, if (ii) holds, then $\varvec{\lambda }$ admits a subnormal completion $S_{\hat{\varvec{\lambda }}}$ on ${\mathscr {T}}_{\eta ,1}$ which satisfies (4.22).

Proof

In view of Theorem 2.2, the statement (i) is equivalent to the fact that $\varvec{\lambda }$ admits a subnormal completion $S_{\hat{\varvec{\lambda }}}$ on ${\mathscr {T}}_{\eta ,1}$ such that each measure $\mu _{i, 1}^{\hat{\varvec{\lambda }}}$ is 1- or 2-atomic. Hence, in the proof of the implication (i)$\Rightarrow$(ii), we can define the partition (A, B) of $J_{\eta }$ as follows

$$\begin{aligned} A=\big \{i \in J_{\eta }:\mu _{i, 1}^{\hat{\varvec{\lambda }}} \text { is } 1\text {-atomic}\big \} \text { and } B=\big \{i \in J_{\eta }:\mu _{i, 1}^{\hat{\varvec{\lambda }}} \text { is } 2\text {-atomic}\big \}. \end{aligned}$$

By [15, Corollary 6.2.2(ii)] the measures $\mu _i=\mu _{i, 1}^{\hat{\varvec{\lambda }}}$, $i\in J_{\eta }$, satisfy (2.2)–(2.4) with $\kappa =1$ and $p=2$. If $B=\varnothing$, then it is easily seen that $\mu _{i, 1}^{\hat{\varvec{\lambda }}} = \delta _{\lambda _{i,2}^2}$ for every $i\in J_{\eta }$ and so (4.20) and (4.21) hold with $r_i=1$ for all $i\in J_{\eta }$. If $B\ne \varnothing$, then by combining reasonings used above and in the proof of the implication (i)$\Rightarrow$(ii) of Theorem 4.1, we get two sequences $\{r_i\}_{i\in B}, \{\vartheta _i\}_{i\in B} \subseteq (1,\infty )$ such that

$$\begin{aligned}&\sum _{i\in A} \frac{\lambda _{i,1}^2}{\lambda _{i,2}^2} + \sum _{i\in B} r_i \frac{\lambda _{i,1}^2}{\lambda _{i,2}^2} = 1, \end{aligned}$$

(4.23)

$$\begin{aligned}&\sum _{i\in A} \frac{\lambda _{i,1}^2}{\lambda _{i,2}^4} + \sum _{i\in B} \vartheta _i r_i^2 \frac{\lambda _{i,1}^2}{\lambda _{i,2}^4} \leqslant \frac{1}{\lambda _0^2}. \end{aligned}$$

(4.24)

Since $\vartheta _i > 1$ for any $i\in B$, we see that (4.23) and (4.24) imply (4.20) and (4.21) with $r_i=1$ for $i\in A$. Putting all of this together yields (ii) and (4.22).

To prove the converse implication (ii)$\Rightarrow$(i), we will define the family $\{\mu _i\}_{i\in J_{\eta }}$ of Borel probability measures on $\mathbb {R}_+$ satisfying (2.2)–(2.5) with $\kappa =1$ and $p=2$. First, we define the partition $(A',B')$ of $J_{\eta }$ by

$$\begin{aligned} A'=\{i\in J_{\eta }:r_i=1\} \text { and } B'=\{i\in J_{\eta }:r_i> 1\}. \end{aligned}$$

If $B' = \varnothing$, then the probability measures $\mu _i=\delta _{\lambda _{i,2}^2}$, $i\in J_{\eta }$, satisfy (2.2)–(2.5). If $B' \ne \varnothing$, then we proceed as follows. By (4.21) there exists $\tau \in (1,\infty )$ such that

$$\begin{aligned} \sum _{i\in A'} \frac{\lambda _{i,1}^2}{\lambda _{i,2}^4} + \tau \sum _{i\in B'} r_i^2 \frac{\lambda _{i,1}^2}{\lambda _{i,2}^4} < \frac{1}{\lambda _0^2}. \end{aligned}$$

(4.25)

If $i \in A'$, then we set $\mu _i=\delta _{\lambda _{i,2}^2}$. If $i\in B'$, then we define $\mu _i$ as in the proof of the implication (ii)$\Rightarrow$(i) of Theorem 4.1 with $\vartheta _i=\tau$. As in that proof, we verify that

$$\begin{aligned} \int _{\mathbb {R}_+} s d\mu _i(s)&= \lambda _{i,2}^2, \quad i \in J_{\eta },\\ \sum _{i=1}^{\eta } \lambda _{i,1}^{2} \int _{\mathbb {R}_+} \frac{1}{s} d\mu _{i}(s)&= \sum _{i\in A'} \frac{\lambda _{i,1}^2}{\lambda _{i,2}^2} + \sum _{i\in B'} r_i \frac{\lambda _{i,1}^2}{\lambda _{i,2}^2} \overset{(4.20)}{=} 1,\\ \sum _{i=1}^{\eta } \lambda _{i,1}^{2} \int _{\mathbb {R}_+} \frac{1}{s^{2}} d\mu _{i}(s)&= \sum _{i\in A'} \frac{\lambda _{i,1}^2}{\lambda _{i,2}^4} + \sum _{i\in B'} \vartheta _i r_i^2 \frac{\lambda _{i,1}^{2}}{\lambda _{i,2}^4} \overset{(4.25)}{<} \frac{1}{\lambda _{0}^{2}}. \end{aligned}$$

Hence (2.2)–(2.5) hold. Now, by applying Lemma  2.1, we conclude that $\varvec{\lambda }$ has a subnormal completion $S_{\hat{\varvec{\lambda }}}$ on ${\mathscr {T}}_{\eta ,1}$ such that $\mu _{i, 1}^{\hat{\varvec{\lambda }}} = \mu _i$ for every $i\in J_{\eta }$, which gives (i). Clearly, the measures $\{\mu _{i, 1}^{\hat{\varvec{\lambda }}}:i\in A'\}$ are 1-atomic while the measures $\{\mu _{i, 1}^{\hat{\varvec{\lambda }}}:i \in B'\}$ are 2-atomic. This completes the proof of the “moreover” part and the proof of the theorem. $\square$

It follows from Theorem 4.2 that the 2-generation subnormal completion problem on ${\mathscr {T}}_{\eta ,1}$ may have a solution admitting simultaneously 1- and 2-atomic measures. Below we give an example showing that the problem on ${\mathscr {T}}_{2,1}$ may have a solution of this kind with distinct atoms.

Fig. 4

Mixed completions discussed in Example 4.3

Example 4.3

Consider the 2-generation subnormal completion problem on ${\mathscr {T}}_{2,1}$ with the initial data $\varvec{\lambda }= \{\lambda _0\} \cup \{\lambda _{i,1}\}_{i=1}^{2} \cup \{\lambda _{i,2}\}_{i=1}^{2} \subseteq (0,\infty )$, where $\lambda _0 \in (0,\infty )$ is arbitrary and the remaining weights are given by (see Fig. 4)

$$\begin{aligned} \lambda _{1,1}=\lambda _{2,1}=1, \lambda _{1,2}=\sqrt{2} \text { and } \lambda _{2,2}=\sqrt{3}. \end{aligned}$$

We are looking for $\lambda _0$ for which $\varvec{\lambda }$ admits a subnormal completion $S_{\hat{\varvec{\lambda }}}$ on ${\mathscr {T}}_{2,1}$ such that $\mu _{1,1}^{\hat{\varvec{\lambda }}}$ is 1-atomic while $\mu _{2,1}^{\hat{\varvec{\lambda }}}$ is 2-atomic, and all these atoms are different. In view of [10, Theorem 4.9], any subnormal completion $S_{\hat{\varvec{\lambda }}}$ of the above $\varvec{\lambda }$ on ${\mathscr {T}}_{2,1}$ comes from compactly supported Borel probability measures $\mu _1$ and $\mu _2$ on $\mathbb {R}_+$ which satisfy the following conditions

$$\begin{aligned}&\int _{\mathbb {R}_+} s d\mu _{i}(s) \overset{}{=} \lambda _{i,2}^2 = {\left\{ \begin{array}{ll} 2 &{} \text {if } i=1,\\ 3 &{} \text {if } i=2, \end{array}\right. } \end{aligned}$$

(4.26)

$$\begin{aligned}&\int _{\mathbb {R}_+} \frac{1}{s}d\mu _{1}(s) + \int _{\mathbb {R}_+} \frac{1}{s}d\mu _{2}(s) =1,\end{aligned}$$

(4.27)

$$\begin{aligned}&\int _{\mathbb {R}_+} \frac{1}{s^{2}} d\mu _{1}(s) + \int _{\mathbb {R}_+} \frac{1}{s^{2}} d\mu _{2}(s) \leqslant \frac{1}{\lambda _{0}^{2}}. \end{aligned}$$

(4.28)

Let $\mu _1$ and $\mu _2$ be Borel probability measures on $\mathbb {R}_+$ given by

$$\begin{aligned} \mu _1=\delta _x \quad \text {and} \quad \mu _2 = \frac{1}{2} \delta _y + \frac{1}{2} \delta _z. \end{aligned}$$

It is a matter of routine to verify that $\mu _1$ and $\mu _2$ with $x=2$, $y=3-\sqrt{3}$ and $z=3+\sqrt{3}$ satisfy (4.26) and (4.27). Hence (4.28) holds if and only if $\lambda _0^2 \leqslant \frac{12}{7}$, meaning that for such $\lambda _0$’s the corresponding $\varvec{\lambda }$ admits a subnormal completion on ${\mathscr {T}}_{2,1}$ with the desired properties.

If $\eta \in \mathbb {N}_2$, Theorem 4.1 takes a much simpler form which is a direct consequence of Theorem  4.2.

Proposition 4.4

Suppose $\eta \in \mathbb {N}_2$, $\kappa = 1$, $p=2$ and $\varvec{\lambda }= \{\lambda _0\} \cup \{\lambda _{i,1}\}_{i=1}^{\eta } \cup \{\lambda _{i,2}\}_{i=1}^{\eta } \subseteq (0,\infty )$ are given. Then the following statements are equivalent:

• (i) $\varvec{\lambda }$ has a subnormal completion $S_{\hat{\varvec{\lambda }}}$ on ${\mathscr {T}}_{\eta , 1}$ such that each measure $\mu _{i, 1}^{\hat{\varvec{\lambda }}}$ is 2-atomic,

• (ii) there exists a sequence $\{r_i\}_{i=1}^{\eta } \subseteq (1,\infty )$ such that

  $$\begin{aligned} \sum _{i=1}^\eta r_i \frac{\lambda _{i,1}^2}{\lambda _{i,2}^2}= & {} 1, \end{aligned}$$

  (4.29)
  $$\begin{aligned} \sum _{i=1}^\eta r_i^2 \frac{\lambda _{i,1}^2}{\lambda _{i,2}^4}< & {} \frac{1}{\lambda _0^2}, \end{aligned}$$

  (4.30)

• (iii) $-\infty< \beta (\eta ) < \frac{1}{\lambda _0^2}$, where²

  $$\begin{aligned} \beta (\eta ):=\inf \left\{ \sum _{i=1}^\eta r_i^2 \frac{\lambda _{i,1}^2}{\lambda _{i,2}^4} :\{r_i\}_{i=1}^{\eta } \subseteq (1,\infty ) \text { and } \sum _{i=1}^\eta r_i \frac{\lambda _{i,1}^2}{\lambda _{i,2}^2} = 1\right\} .\quad \end{aligned}$$

  (4.31)

Below we discuss the 2-generation SCP on ${\mathscr {T}}_{\eta ,1}$ with 2-atomic measures under some constraints. Let us suppose temporarily that $\eta \in \mathbb {N}_2$. According to the “moreover” part of Theorem 4.1, if $S_{\hat{\varvec{\lambda }}}$ is a subnormal completion of $\varvec{\lambda }$ on ${\mathscr {T}}_{\eta ,1}$ such that each measure $\mu _{i, 1}^{\hat{\varvec{\lambda }}}$ is 2-atomic, then there exists $i\in J_{\eta }$ such that $\sum _{j=1}^\eta \lambda _{j,1}^2 < \lambda _{i,2}^2$ (use the fourth inequality in (4.4)). If the last inequality holds for all $i\in J_{\eta }$, then the solution of the 2-generation subnormal completion problem on ${\mathscr {T}}_{\eta ,1}$ with 2-atomic measures takes a simple form. Namely, the first inequality in (4.4), which is a necessary condition for solving the 2-generation subnormal completion problem on ${\mathscr {T}}_{\eta ,1}$, now becomes sufficient (see Corollary 4.5(ii) below). It is worth pointing out that in general the inequality $\lambda _0^2 \leqslant \sum _{i=1}^{\eta } \lambda _{i,1}^2$ holds whenever the p-generation subnormal completion problem on ${\mathscr {T}}_{\eta ,\kappa }$ has a solution (see [10, Theorem  4.9(i)]).

Corollary 4.5

Suppose $\eta \in \mathbb {N}_2$, $\kappa = 1$, $p=2$ and $\varvec{\lambda }= \{\lambda _0\} \cup \{\lambda _{i,1}\}_{i=1}^{\eta } \cup \{\lambda _{i,2}\}_{i=1}^{\eta } \subseteq (0,\infty )$ are given. Assume that

$$\begin{aligned} \sum _{j=1}^\eta \lambda _{j,1}^2 < \lambda _{i,2}^2, \quad i\in J_{\eta }. \end{aligned}$$

(4.32)

Then the following statements are equivalent:

• (i) $\varvec{\lambda }$ has a subnormal completion $S_{\hat{\varvec{\lambda }}}$ on ${\mathscr {T}}_{\eta , 1}$ such that each measure $\mu _{i, 1}^{\hat{\varvec{\lambda }}}$ is 2-atomic,

• (ii) $\lambda _0^2 < \sum _{i=1}^{\eta } \lambda _{i,1}^2$.

Proof

(i)$\Rightarrow$(ii) This is a direct consequence of the first inequality in (4.4).

(ii)$\Rightarrow$(i) Define $\{r_i\}_{i=1}^{\eta } \subseteq (1,\infty )$ by

$$\begin{aligned} r_i= \frac{\lambda _{i,2}^2}{\sum _{j=1}^\eta \lambda _{j,1}^2}, \quad i\in J_{\eta }. \end{aligned}$$

(4.33)

It is easily seen that with this choice of $\{r_i\}_{i=1}^{\eta }$ the Eq. (4.29) holds. Since

$$\begin{aligned} \sum _{i=1}^\eta r_i^2 \frac{\lambda _{i,1}^2}{\lambda _{i,2}^4} \overset{(4.33)}{=} \frac{1}{\sum _{i=1}^{\eta } \, \lambda _{i,1}^2} \overset{\mathrm {(ii)}}{<} \frac{1}{\lambda _0^2}, \end{aligned}$$

we obtain (4.30). Applying Proposition 4.4 completes the proof. $\square$

Remark 4.6

In view of Proposition 4.4(iii), if $\eta \in \mathbb {N}_2$ one may create many sufficient conditions for solving the 2-generation subnormal completion problem on ${\mathscr {T}}_{\eta ,1}$ with 2-atomic measures. The procedure goes as follows. First, we look for a sequence $\{r_i\}_{i\in J_{\eta }} \subseteq (1,\infty )$ satisfying the Eq. (4.29). Second, we substitute this particular choice of $\{r_i\}_{i\in J_{\eta }}$ into the expression $\sum _{i=1}^\eta r_i^2 \frac{\lambda _{i,1}^2}{\lambda _{i,2}^4}$ appearing in (4.30). Finally, we require the value so obtained to be strictly less than $\frac{1}{\lambda _0^2}$.

It is worth mentioning that the procedure described in Remark  4.6 has been applied in the proof of Corollary 4.5 (see (4.33)). Below we give a few more examples illustrating this procedure.

Corollary 4.7

Suppose $\eta \in \mathbb {N}_2$, $\kappa = 1$, $p=2$ and $\varvec{\lambda }= \{\lambda _0\} \cup \{\lambda _{i,1}\}_{i=1}^{\eta } \cup \{\lambda _{i,2}\}_{i=1}^{\eta } \subseteq (0,\infty )$ are given. Then $\varvec{\lambda }$ has a subnormal completion $S_{\hat{\varvec{\lambda }}}$ on ${\mathscr {T}}_{\eta , 1}$ such that each measure $\mu _{i, 1}^{\hat{\varvec{\lambda }}}$ is 2-atomic provided any of the following conditions holds:

• (i) $\sum _{i=1}^\eta \frac{\lambda _{i,1}^2}{\lambda _{i,2}^2} < 1$ and $\lambda _0^2 \, \sum _{i=1}^\eta \frac{\lambda _{i,1}^2}{\lambda _{i,2}^4} < \Big (\sum _{i=1}^\eta \frac{\lambda _{i,1}^2}{\lambda _{i,2}^2}\Big )^2$,

• (ii) $\eta \lambda _{i,1}^2 < \lambda _{i,2}^2$ for each $i\in J_{\eta }$ and $\lambda _0^2 \, \sum _{i=1}^\eta \frac{1}{\lambda _{i,1}^2} < \eta ^2$,

• (iii) $\lambda _{i,1}^2 \sum _{j=1}^{\eta } \frac{1}{\lambda _{j,2}^2} < 1$ for each $i\in J_{\eta }$ and $\lambda _0^2 \sum _{i=1}^{\eta } \frac{1}{\lambda _{i,1}^2\lambda _{i,2}^4} < \Big (\sum _{i=1}^{\eta } \frac{1}{\lambda _{i,2}^2}\Big )^2$.

Proof

Apply Remark 4.6 to

$$\begin{aligned} r_i = \frac{1}{\sum _{j=1}^{\eta } \frac{\lambda _{j,1}^2}{\lambda _{j,2}^2}}, \quad r_i= \frac{1}{\eta } \, \frac{\lambda _{i,2}^2}{\lambda _{i,1}^2} \quad \text { and } \quad r_i = \frac{1}{\lambda _{i,1}^2 \sum _{j=1}^{\eta } \frac{1}{\lambda _{j,2}^2}} \end{aligned}$$

in the cases (i), (ii) and (iii), respectively. $\square$

The above discussion can be applied to solve the 1-generation subnormal completion problem on ${\mathscr {T}}_{\eta ,1}$ with 2-atomic measures.

Corollary 4.8

Suppose $\eta \in \mathbb {N}_2$, $\kappa = 1$, $p=1$ and $\varvec{\lambda }= \{\lambda _0\} \cup \{\lambda _{i,1}\}_{i=1}^{\eta } \subseteq (0,\infty )$ are given. Then the following statements are equivalent:

• (i) $\varvec{\lambda }$ has a subnormal completion $S_{\hat{\varvec{\lambda }}}$ on ${\mathscr {T}}_{\eta , 1}$ such that each measure $\mu _{i, 1}^{\hat{\varvec{\lambda }}}$ is 2-atomic,

• (ii) $\lambda _0^2 < \sum _{i=1}^{\eta } \lambda _{i,1}^2$.

Proof

(i)$\Rightarrow$(ii) Let $S_{\hat{\varvec{\lambda }}}$ be a subnormal completion of $\varvec{\lambda }$ on ${\mathscr {T}}_{\eta , 1}$ such that each measure $\mu _{i, 1}^{\hat{\varvec{\lambda }}}$ is 2-atomic. Then clearly this $S_{\hat{\varvec{\lambda }}}$ is a subnormal completion of $\varvec{\lambda }\cup \{\hat{\lambda }_{i,2}\}_{i\in J_{\eta }}$ on ${\mathscr {T}}_{\eta , 1}$. Hence, by the condition (4.4), (ii) is valid.

(ii)$\Rightarrow$(i) Choose any sequence $\{\lambda _{i,2}\}_{i=1}^{\eta } \subseteq (0,\infty )$ that satisfies (4.32). By Corollary 4.5, $\varvec{\lambda }\cup \{\lambda _{i,2}\}_{i\in J_{\eta }}$ has a subnormal completion $S_{\hat{\varvec{\lambda }}}$ on ${\mathscr {T}}_{\eta , 1}$ such that each measure $\mu _{i, 1}^{\hat{\varvec{\lambda }}}$ is 2-atomic. As a consequence, this $S_{\hat{\varvec{\lambda }}}$ is a subnormal completion of $\varvec{\lambda }$ on ${\mathscr {T}}_{\eta ,1}$ as well. $\square$

In concluding this section, we consider the 2-generation subnormal completion problem on ${\mathscr {T}}_{\eta ,1}$ from the point of view of the condition (4.32).

Remark 4.9

Suppose that $\eta \in \mathbb {N}_2$. Let us consider the situation in which we are given initial data $\varvec{\lambda }= \{\lambda _0\} \cup \{\lambda _{i,1}\}_{i=1}^{\eta } \cup \{\lambda _{i,2}\}_{i=1}^{\eta } \subseteq (0,\infty )$ on ${\mathscr {T}}_{\eta , 1, 2}$ satisfying the equations

$$\begin{aligned} \lambda _{i,2} = \lambda _{1,2}, \quad i \in J_\eta . \end{aligned}$$

Notice that under the above assumption, if $\varvec{\lambda }$ admits a subnormal completion on ${\mathscr {T}}_{\eta ,1}$, then it admits a 2-generation flat subnormal completion on ${\mathscr {T}}_{\eta ,1}$ (see [10, Theorem 8.3]), and any 2-generation flat subnormal completion $S_{\hat{\varvec{\lambda }}}$ of $\varvec{\lambda }$ on ${\mathscr {T}}_{\eta ,1}$ has the property that $\mu _{i,1}^{\hat{\varvec{\lambda }}}=\mu _{1,1}^{\hat{\varvec{\lambda }}}$ for all $i\in J_{\eta }$ (apply (2.1) to $u=e_{i,1}$). Below, we discuss a few cases related to the condition (4.32).

$1^{\circ }$:

If $\lambda _{1,2}^2 < \sum _{i=1}^\eta \lambda _{i,1}^2$, then there is no completion of the sequence

$$\begin{aligned} \alpha = \left( \lambda _0, \sqrt{\sum _{i=1}^{\eta } \lambda _{i,1}^2}, \lambda _{1,2} \right) \end{aligned}$$

to a subnormal unilateral weighted shift, because it is well known that a subnormal unilateral weighted shift is hyponormal and so its weights must be monotonically increasing. Therefore, by [10, Theorem 8.3(iii)] there is no subnormal completion of $\varvec{\lambda }$ on ${\mathscr {T}}_{\eta , 1}$.

$2^{\circ }$:

If $\lambda _{1,2}^2 = \sum _{i=1}^\eta \lambda _{i,1}^2$, then the “moreover” part of Theorem 4.1 shows that there is no subnormal completion $S_{\hat{\varvec{\lambda }}}$ of $\varvec{\lambda }$ on ${\mathscr {T}}_{\eta ,1}$ with 2-atomic measures $\mu _{i,1}^{\hat{\varvec{\lambda }}}$ since we lack the third inequality in (4.4). Alternatively, we may use the “moreover” part of [10, Proposition 7.6].

$3^{\circ }$:

If $\lambda _{1,2}^2 > \sum _{i=1}^\eta \lambda _{i,1}^2$ and $\lambda _0^2 < \sum _{i=1}^\eta \lambda _{i,1}^2$ we may apply Corollary 4.5 to deduce that there is a subnormal completion $S_{\hat{\varvec{\lambda }}}$ of $\varvec{\lambda }$ on ${\mathscr {T}}_{\eta ,1}$ with 2-atomic measures $\mu _{i,1}^{\hat{\varvec{\lambda }}}$.

$4^{\circ }$:

If $\lambda _{1,2}^2 > \sum _{i=1}^\eta \lambda _{i,1}^2$ and $\lambda _0^2 = \sum _{i=1}^\eta \lambda _{i,1}^2$ we may apply the condition (4.4) of Theorem 4.1 to deduce that there is no subnormal completion $S_{\hat{\varvec{\lambda }}}$ of $\varvec{\lambda }$ on ${\mathscr {T}}_{\eta ,1}$ with the $\mu _{i,1}^{\hat{\varvec{\lambda }}}$ 2-atomic. Alternatively, again using the “moreover” part of [10, Proposition 7.6] we may deduce that the measures $\mu _{i,1}^{\hat{\varvec{\lambda }}}$ for any subnormal completion $S_{\hat{\varvec{\lambda }}}$ of $\varvec{\lambda }$ on ${\mathscr {T}}_{\eta ,1}$ (provided it exists) must be 1-atomic.

5 An Explicit Solution of the 2-Generation SCP on ${\mathscr {T}}_{2,1}$

In this section we give necessary and sufficient conditions for solving the 2-generation subnormal completion problem on ${\mathscr {T}}_{2,1}$ with 2-atomic measures explicitly in terms of the initial data. In view of Proposition 4.4(iii), the solution of the 2-generation subnormal completion problem on ${\mathscr {T}}_{\eta ,1}$ with 2-atomic measures reduces to computing the infimum $\beta (\eta )$ of the quadratic form $\sum _{i=1}^\eta r_i^2 \frac{\lambda _{i,1}^2}{\lambda _{i,2}^4}$ subject to the constraints that $\{r_i\}_{i=1}^{\eta } \subseteq (1,\infty )$ and

$$\begin{aligned} \sum _{i=1}^\eta r_i \frac{\lambda _{i,1}^2}{\lambda _{i,2}^2} = 1. \end{aligned}$$

This task is complicated. The main difficulty comes from the requirement that the numbers $r_i$ should belong to the open interval $(1,\infty )$. Even in the case of $\eta =2$, there are three different formulas for the infimum depending on weights in question (see Theorem 5.2 below). However under some additional restrictive assumptions, the infimum of the above quadratic form can be computed explicitly.

Proposition 5.1

Let $\eta \in {\mathbb N}_{2}$, $\{a_{i}\}_{i=1}^{\eta } \subseteq (0,\infty )$ and $\{b_{i}\}_{i=1}^{\eta } \subseteq (0,\infty )$. Then

$$\begin{aligned} \min \bigg \{\sum _{i=1}^\eta b_{i} r_i^2 :\{r_i\}_{i=1}^{\eta } \subseteq (0,\infty ) \text { and } \sum _{i=1}^\eta a_{i} r_i =1\bigg \} = \frac{1}{\sum _{i=1}^\eta \frac{a_{i}^2}{b_i}}. \end{aligned}$$

(5.1)

Moreover, if $\sum _{j=1}^\eta \frac{a_{j}^2}{b_j} < \frac{a_i}{b_i}$ for every $i\in J_{\eta }$, then

$$\begin{aligned} \min \bigg \{\sum _{i=1}^\eta b_{i} r_i^2 :\{r_i\}_{i=1}^{\eta } \subseteq (1,\infty ) \text { and } \sum _{i=1}^\eta a_{i} r_i =1\bigg \} = \frac{1}{\sum _{i=1}^\eta \frac{a_{i}^2}{b_i}}. \end{aligned}$$

(5.2)

In both cases the minimum is attained for

$$\begin{aligned} r_i= \frac{1}{\frac{b_i}{a_i} \sum _{j=1}^\eta \frac{a_{j}^2}{b_j}}, \quad i\in J_{\eta }. \end{aligned}$$

(5.3)

Proof

Suppose $\{r_i\}_{i=1}^{\eta } \subseteq (0,\infty )$ and $\sum _{i=1}^\eta a_{i} r_i =1$. It follows from the Cauchy–Schwarz inequality that

$$\begin{aligned} 1 = \sum _{i=1}^\eta a_{i} r_i = \sum _{i=1}^\eta \frac{a_{i}}{\sqrt{b_i}} \cdot \sqrt{b_i} \, r_i \leqslant \bigg (\sum _{i=1}^\eta \frac{a_{i}^2}{b_i}\bigg )^{1/2} \bigg (\sum _{i=1}^\eta b_{i} r_i^2\bigg )^{1/2}. \end{aligned}$$

Therefore, we have

$$\begin{aligned} \sum _{i=1}^\eta b_{i} r_i^2 \geqslant \frac{1}{\sum _{i=1}^\eta \frac{a_{i}^2}{b_i}}. \end{aligned}$$

(5.4)

Substituting $\{r_i\}_{i=1}^{\eta }$ as in (5.3) shows that the inequality in (5.4) becomes equality. This proves (5.1). The condition (5.2) is a consequence of (5.1). $\square$

As shown below, a solution of the 2-generation subnormal completion problem on ${\mathscr {T}}_{2,1}$ with 2-atomic measures can be written entirely in terms of the initial data. This is done by computing the infimum $\beta (2)$.

Theorem 5.2

Suppose $\eta =2$, $\kappa = 1$, $p=2$ and $\varvec{\lambda }= \{\lambda _0\} \cup \{\lambda _{i,1}\}_{i=1}^{2} \cup \{\lambda _{i,2}\}_{i=1}^{2} \subseteq (0,\infty )$ are given. Then $\varvec{\lambda }$ has a subnormal completion $S_{\hat{\varvec{\lambda }}}$ on ${\mathscr {T}}_{2, 1}$ with 2-atomic measures $\mu _{1, 1}^{\hat{\varvec{\lambda }}}$ and $\mu _{2, 1}^{\hat{\varvec{\lambda }}}$ if and only if $\beta (2) < \frac{1}{\lambda _0^2}$ and $1< \tau$, where

$$\begin{aligned} \beta (2) = {\left\{ \begin{array}{ll} \frac{(a_1-a_2)^2+a_1b_1}{a_{2}^{2}b_{1}} &{} \text {if } \sigma \leqslant 1,\\ \frac{1}{a_1+b_1} &{} \text {if } 1< \sigma < \tau ,\\ \frac{(b_2-b_1)^2+a_1b_1}{a_{1}b_{2}^2} &{} \text {if } \tau \leqslant \sigma , \end{array}\right. } \end{aligned}$$

with $\sigma =\frac{a_2}{a_1+b_1}$, $\tau = \frac{a_2(b_{2}-b_{1})}{a_{1}b_2}$, $a_j=\lambda _{1,j}^2$ and $b_j=\lambda _{2,j}^2$ for $j=1,2$.

Proof

In view of Proposition 4.4, it is enough to compute $\beta (2)$. If we replace $r_1$ and $r_2$ by x and y, respectively, then (4.31) with $\eta =2$ takes the form

$$\begin{aligned} \beta (2)=\inf \Big \{\Theta (x,y) :x, y \in (1,\infty ) \text { and } \phi (x,y) = 1\Big \}, \end{aligned}$$

where

$$\begin{aligned} \Theta (x,y) = x^{2} \frac{a_{1}}{a_{2}^{2}} + y^{2} \frac{b_{1}}{b_{2}^{2}} \quad \text {and} \quad \phi (x,y) = x\frac{a_{1}}{a_{2}}+y\frac{b_{1}}{b_{2}} \quad \text {for} \quad x,y\in (1,\infty ). \end{aligned}$$

If $x,y\in (1,\infty )$ are such that $\phi (x,y) = 1$, then

$$\begin{aligned} y = \frac{b_2}{b_1} \Big (1-\frac{a_{1}}{a_{2}}x\Big ) >1, \end{aligned}$$

(5.5)

so $1< x < \tau$. As a consequence, we see that $-\infty <\beta (2)$ if and only if $1 < \tau$. Substituting y as in (5.5) into $\Theta (x,y)$, we obtain

$$\begin{aligned} \Theta (x,y) = Ax^{2}-2Bx+C, \quad 1< x < \tau , \end{aligned}$$

where

$$\begin{aligned} A=\frac{a_1}{a_2^2}\left( 1 + \frac{a_{1}}{b_{1}} \right) , B=\frac{a_{1}}{a_{2}b_{1}} \text { and } C=\frac{1}{b_{1}}. \end{aligned}$$

Note that $A,B,C>0$. The quadratic polynomial $\Omega (x):=Ax^{2}-2Bx+C$ regarded as a function on $\mathbb {R}$ has a minimum at $x=\frac{B}{A}$. Observe that

$$\begin{aligned} \frac{B}{A}=\sigma \quad \text {and} \quad \Omega (\sigma ) =\frac{1}{a_1+b_1}>0. \end{aligned}$$

It is now a routine matter to compute $\beta (2)$ by considering three possible disjoint cases $\sigma \leqslant 1$, $1< \sigma < \tau$ and $\tau \leqslant \sigma$. What we get is $\beta (2)=\varOmega (1)$ in the first case, $\beta (2)=\varOmega (\sigma )$ in the second and $\beta (2)=\varOmega (\tau )$ in the third one, where

$$\begin{aligned} \varOmega (1) = \frac{(a_1-a_2)^2+a_1b_1}{a_{2}^{2}b_{1}} \quad \text {and} \quad \varOmega (\tau ) = \frac{(b_2-b_1)^2+a_1b_1}{a_{1}b_{2}^2}. \end{aligned}$$

$\square$