1 Introduction

The geometry of blowups of weighted projective spaces at a general nonsingular point has been studied in many articles. Most recently, in [4], the authors find negative curves on such blowups by finding certain Newton polygons, while in [11], the authors compute lower bounds for the effective threshold of an ample divisor \({\mathbb {P}}(a,b,c)\), which is equivalent to finding pseudo effective curves on the blowups. In [6], Hausen, Keicher, and Laface give a criterion for a blowup of a weighted projective plane to be a Mori dream space, that is, whether there exists an orthogonal pair on the blowup.

There is also extensive research on justifying whether certain families \(X(a,b,c)\) are Mori dream spaces. In [2, 4, 6, 9], the authors give examples of X(a, b, c) that are Mori dream spaces. In [3, 5], there are examples of X(a, b, c) that are not Mori dream spaces.

In this article, instead of studying the associated Rees algebras as in [2, 6], or studying certain Newton polygons as in [4], we reduce the question of finding negative curves on X(a, b, c) to applying the orbifold Riemann-Roch formula on X. We give a sufficient condition in Theorem 4.1 for a curve C to be a negative curve. This will enable us to find the effective cone for many X(a, b, c)s. As an application, we confirm in Theorem 6.2 the Mori dreamness of certain weighted projective spaces (one of them is from the table in [6, Theorem 1.3]).

2 The weighted projective plane and its blow up

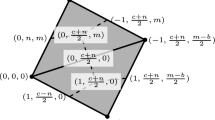
Let a, b, c be three positive integers, and assume that a, b, c are coprime. The weighted projective plane \({\mathbb {P}}(a,b,c)\) is given by the quotient of \({\mathbb {C}}^3{\backslash } \{0\}\) under the \({\mathbb {C}}^*\) action

$$\begin{aligned} \lambda : (x_1,x_2,x_3)\rightarrow (\lambda ^a x_1, \lambda ^b x_2,\lambda ^c x_3), \,\,\lambda \in {\mathbb {C}}^*. \end{aligned}$$

We see that on \({\mathbb {P}}(a,b,c)\) there are three possible singular points \(P_1=(1,0,0), P_2=(0,1,0), P_3=(0, 0, 1)\), and they are cyclic quotient singularities of type \(\frac{1}{a}(b,c), \frac{1}{b}(a,c),\frac{1}{c}(a,b)\) respectively.

Here by saying that a point is a cyclic quotient singularity of type \(\frac{1}{a}(b,c)\), we mean that there is a neighborhood around the point which is locally analytically isomorphic to the quotient \({\mathbb {C}}^2/\!\!/ \mu _a\), where \(\mu _a\) is the group of the a-th roots of unity and the action of \(\mu _a\) on \({\mathbb {C}}^2\) is given by \(\varepsilon :(x,y)\rightarrow (\varepsilon ^bx,\varepsilon ^cy)\) for \(\varepsilon \in \mu _a\) (see [12]). By considering the affine patches of \({\mathbb {P}}(a,b,c)\), we can find the singularity type of \(P_1,P_2\), and \(P_3\) as claimed.

Let X(a, b, c) be the blow up of \({\mathbb {P}}(a,b,c)\) at a general nonsingular point P. We know that X(a, b, c) is isomorphic to \({\mathbb {P}}(a,b,c)\) outside the point P, so X(a, b, c) has the same singularities as \({\mathbb {P}}(a,b,c)\).

Let \(f: X(a,b,c)\rightarrow {\mathbb {P}}(a,b,c)\) be the morphism of the blow up. Let H be the pullback of \({\mathcal {O}}(1)\), and E be the exceptional curve. Then H and E generate the Picard group of X(a, b, c). The relation between the canonical divisor \(K_X\) on X(a, b, c) and the canonical divisor \(K_{{\mathbb {P}}}\) on \({\mathbb {P}}(a,b,c)\) is given by

$$\begin{aligned} K_X=f^*K_{{\mathbb {P}}} +E\sim _{\mathbb {Q}}-(a+b+c)H+E, \end{aligned}$$

where \(\sim _{\mathbb {Q}}\) represents \({\mathbb {Q}}-\)linear equivalence. In addition, we know that

$$\begin{aligned} H^2=\frac{1}{abc},\,\, E^2=-1, \,\, H\cdot E=0. \end{aligned}$$

3 A criterion for X(a, b, c) to be a Mori dream space

According to [7], X is a Mori dream space (MDS) if and only if the semiample cone and the nef cone are equal and they are polyhedral in \(\text {Cl}_{\mathbb {Q}}(X)\). In the article [6], Hausen et. al give a criterion to determine whether X is a MDS via the Rees algebra associated with the blow up. Here we want to translate [6, Proposition 2.4] to a claim on divisors.

Lemma 3.1

Let H and E be as above. Let C be a divisor on X and \(C\sim nH-\mu E\) with \(n,\mu \) positive integers. Assume that \(h^0(C)=1\) and \(C^2<0\), and in addition assume that

  1. 1.

    \(h^0(C-k E)=0\) for any positive integer k, and

  2. 2.

    there is no positive integer \(n'<n\) such that \(h^0(n' H-\mu ' E)=1\) and \((n' H-\mu ' E)^2<0\) for any positive integer \(\mu '\).

Then C is a reduced irreducible curve.

Proof

Assume C is not a reduced irreducible curve, i.e., there exist \(C_1>0\) and \(C_2>0\) such that \(C=C_1+C_2\). Assume \(C_i\sim n_i H- \mu _i E\).

If \(n_i\) are positive integers, then we have \(C_i^2\ge 0\) and \(\mu _i>0\) since otherwise it will contradict the minimality of n. We have also \(C_1\cdot C_2\ge 0\) because otherwise \(C_1\) and \(C_2\) have a common component \(C_0\sim n_0H-\mu _0 E\) with \(C_0^2<0\). Then \(n_0 \ge 0\) is impossible under the assumption of minimality of n; if \(n_0=0\), then \(C_0\sim kE\) for some positive integer k, but this would contradict with assumption 1. But if \(C_i^2\ge 0\) and \(C_1\cdot C_2\ge 0\), then \(C^2=(C_1+C_2)^2\ge 0\) which contradicts \(C^2<0\).

Then one of the \(n_i\) has to be zero. Assume that \(C_1 \sim n_1 H- \mu _1 E\) and \(C_2\sim \mu _2 E\), where \(\mu _i\) are positive integers. In this case \(\mu _1>\mu \), contradicting assumption 1. Therefore C is a reduced irreducible curve. \(\square \)

Proposition 3.2

([1, Lemma 5.1]). Assume that a, b, c are coprime and \(\sqrt{abc}\notin {\mathbb {Z}}\). Let H and E be as before. Then X(a, b, c) is a MDS if and only if there exist a divisor C as in Lemma 3.1 and a divisor \(D>0\) such that \(D\cdot C=0\) and C is not a fixed component of |D|.

Proof

When \(\sqrt{abc}\notin {\mathbb {Z}}\), there will be no \(C>0\) such that \(C^2=\frac{n^2}{abc}-\mu ^2=0\). The proof here is similar to the proof of [6, Proposition 2.4].

\(\implies \) If X is a MDS, the effective cone of X is polyhedral, which is generated by E and an irreducible curve C, where \(C^2<0\). Then \(h^0(C)=1\). Assume \(C\sim n H-\mu E\). Suppose there is another divisor \(F \sim l H -m E\) such that \(h^0(F)=1\) and \(F^0<0\). Then

$$\begin{aligned} C^2<0,\, C\cdot F<0,\, F^2<0. \end{aligned}$$

So C is a component of F. This gives \(l>n\). This gives condition 2 in Lemma 3.1. Since C is the boundary of the effective cone, \(C-kE\), for any positive integer k, will lie outside the effective cone. This gives condition 1 in Lemma 3.1.

If X is a MDS, then its nef cone equals its semiample cone. Since the nef cone is the dual of the effective cone, there exists a divisor \(D>0\) such that \(D\cdot C=0\) and D is a generator of the nef cone. D is in addition semiample and therefore C is not a fixed component of |D|.

\(\Longleftarrow \) If there exists a curve \(C\sim n H-\mu E\) such that \(h^0(C)=1\) and \(C^2<0\) satisfying the conditions in Lemma 3.1, then C is irreducible by Lemma 3.1. According to [8, Lemma 1.22], C is in the extremal ray of the effective cone of X. That means C and E generate the effective cone. Since \(D\cdot C=0\), D and H generate the nef cone of X. We just need to check that D is also semiample. Under the condition \(C^2<0\), we have that D cannot lie in the extremal ray generated by C. Suppose \(D\sim n_2 H-\mu _2 E\), then \(\frac{\mu }{n}>\frac{\mu _2}{n_2}\), i.e., \(\mu \cdot n_2>n\cdot \mu _2\). We can then find some multiple kD such that \(kD=C+B\), where \(B\sim (kn_2-n)H-(k\mu _2-\mu )E\) is an ample divisor since \(\frac{\mu _2}{n_2}>\frac{k\mu _2-\mu }{kn_2-n}\) and \((k\mu _2-\mu )>0\) . In fact, any k satisfying \(kn_2>n\) and \(k\mu _2>\mu \) will do. Since C is not a base component of D, kD is a divisor with at most finite point base locus. This gives that D is semiample ([14, Theorem 6.2]). Therefore the nef cone is also the semiample cone, and X is a MDS. \(\square \)

We conclude from the proposition above that to check whether X(a, b, c), where a, b, c are coprime and \(\sqrt{abc}\notin {\mathbb {Z}}\), is a MDS, we just need to check the following:

  1. 1.

    Find \(C\sim n H-\mu E\) such that \(h^0(C)=1\) and \(C^2<0\), and n is minimal for this property as stated in Lemma 3.1.

  2. 2.

    Find \(D>0\) such that \(D\cdot C=0\) and \(h^0(D)\ne h^0(D-C)\).

4 Effective cone

In general, it is difficult to find \(C\sim nH-\mu E\) such that \(h^0({\mathcal {O}}_X(D))=1\) and \(C^2<0\) as in Lemma 3.1. The following theorem gives a sufficient condition.

Theorem 4.1

Let H and E be as before. Let \(C\sim nH-\mu E\) be a divisor on X(a, b, c) with \(n, \mu \) positive integers. If C is the minimal divisor that satisfies \(\chi ({\mathcal {O}}_X(C))=1\) and \(C^2< 0\) (the minimality of C means that there is no \(l<n\) such that \(\chi ({\mathcal {O}}_X(lH-kE))=1\) and \((lH-kE)^2<0\) for any positive integer k), then C is a divisor that satisfies the assumptions in Lemma 3.1.

Proof

By the Serre duality, we have

$$\begin{aligned} H^2({\mathcal {O}}_X(C))=H^0({\mathcal {O}}_X(K_X-C))=H^0({\mathcal {O}}_X(-(a+b+c+n)H+(1+\mu ) E)). \end{aligned}$$

But for positive integers \(n, \mu \), we have \(H^0({\mathcal {O}}_X(-(a+b+c+n)H+(1+\mu ) E))=0\). Therefore \(\chi ({\mathcal {O}}_X(C))=1\), together with \(C^2<0\), implies \(h^0({\mathcal {O}}_X(C))=1\) and \(h^1({\mathcal {O}}_X(C))=0\). Consider the short exact sequence

$$\begin{aligned} 0\rightarrow {\mathcal {O}}_X\rightarrow {\mathcal {O}}_X(C)\rightarrow {\mathcal {O}}_C(C)\rightarrow 0 \end{aligned}$$

and the associated long exact sequence. The fact \(h^0({\mathcal {O}}_X)=h^0({\mathcal {O}}_X(C))=1\) and \(h^1({\mathcal {O}}_X)=0\) then imply \( h^0({\mathcal {O}}_C(C))=0\). Thus \(h^0({\mathcal {O}}_C(C-kE))=0\) for any \(k>0\) since \(C\cdot E=\mu >0\). Then considering the short exact sequence

$$\begin{aligned} 0\rightarrow {\mathcal {O}}_X(-kE)\rightarrow {\mathcal {O}}_X(C-kE)\rightarrow {\mathcal {O}}_C(C-kE)\rightarrow 0 \end{aligned}$$

and the assosiated long exact sequence, we have \(h^0({\mathcal {O}}_X(C-kE))=0\) for any positive integer k. This gives condition 1 in Lemma 3.1.

Next we need to show that there are no divisors \(C'\sim n' H -\mu ' E\) such that \(h^0(C')=1\), \(C'^2<0\), and \(n'<n\). Assume there is such a \(C'\) and assume in addition \(n'\) is minimal for such divisors and \(\mu '\) is the highest possible multiple of E such a \(C'\) with given \(n'\) can have. We know \(C'\) is irreducible by Lemma 3.1, and then \(C'\) generates the extremal ray of the effective cone X. Since \(C^2<0,C'^2<0\), we have \(C\cdot C'<0\). This indicates that \(C'\) is a component of C. Assume \(C\sim C'+C'''\). If \(C' \cdot C''<0 \), \(C'\) is also a component of \(C''\). We can therefore assume \(C\sim kC'+C''\), where \(C'\cdot C''\ge 0\). We want to show that \(C''=0\) and \(k=1\).

Suppose \(C''>0\). Since \(C''\cdot E\ge 0\) (since \(H^0({\mathcal {O}}_X(C-kE))=0\) for \(k>0\)) and \(C''\cdot C'\ge 0\), we have that \(C''\) is a nef divisor and therefore \(C''\cdot C\ge 0\). Then \(h^0({\mathcal {O}}_C(C-C''))=0\). Together with the exact sequence

$$\begin{aligned} 0\rightarrow {\mathcal {O}}_X(-C'')\rightarrow {\mathcal {O}}_X(kC') \rightarrow {\mathcal {O}}_C(C-C'')\rightarrow 0, \end{aligned}$$

this will imply \(h^0({\mathcal {O}}_X(kC'))=0\), which is absurd. Therefore \(C''=0\), and \(C\sim kC'\).

The following exact sequence

$$\begin{aligned} 0\rightarrow {\mathcal {O}}_X((k-1)C') \rightarrow {\mathcal {O}}_X(kC')\rightarrow {\mathcal {O}}_{C'}(kC')\rightarrow 0 \end{aligned}$$

gives \(1=\chi ({\mathcal {O}}_X(C))=\chi ({\mathcal {O}}_X(kC'))\le \chi ({\mathcal {O}}_X(C'))\le 1\), we have \(1=\chi ({\mathcal {O}}_X(C))=\chi ({\mathcal {O}}_X(kC')\le \chi ({\mathcal {O}}_X((k-1)C'))\). By induction, \(1=\chi ({\mathcal {O}}_X(C))=\chi ({\mathcal {O}}_X(kC'))\le \chi ({\mathcal {O}}_X(C'))\le 1\). This implies \(\chi ({\mathcal {O}}_X(C'))=1\). This gives \(C\sim C'\), that is, C has to be the minimal divisor in the sense of Lemma 3.1. \(\square \)

Once we have the above theorem, we can reduce the question of finding a negative curve on X(a, b, c) to applying the orbifold Riemann-Roch formula on X(a, b, c). One remark here is that we are aware that the conditions in the above theorem are not necessary conditions, i.e., we do not always have \(\chi ({\mathcal {O}}_X(C))=1\) for a negative curve satisfying conditions Lemma 3.1. For example, X(5, 33, 49) has a negative curve \(C\sim 1617H-18E\) and \(\chi ({\mathcal {O}}_X(C))=0\); X(8, 15, 43) has a negative curve \(C\sim 645H-9E\) and \(\chi ({\mathcal {O}}_X(C))=0\) (see [9]).

5 Riemann-Roch on blowups of weighted projective planes

In this section, we want to prepare ourselves to use the Riemann-Roch formula to find curves C that satisfy the conditions in Theorem 4.1. We first introduce some notations.

For a cyclic quotient singularity of type \(\frac{1}{r}(a_1,a_2)\), we denote

$$\begin{aligned} \delta _n (\frac{1}{r}(a_1, a_2))=\frac{1}{r}\sum _{\varepsilon \in \mu _r, \varepsilon \ne 1}\frac{\varepsilon ^{-n}-1}{(1-\varepsilon ^{a_1})(1-\varepsilon ^{a_2})}, \end{aligned}$$
(5.1)

and

$$\begin{aligned} \sigma _n (\frac{1}{r}(a_1, a_2))=\frac{1}{r}\sum _{\varepsilon \in \mu _r, \varepsilon \ne 1}\frac{\varepsilon ^{-n}}{(1-\varepsilon ^{a_1})(1-\varepsilon ^{a_2})}. \end{aligned}$$
(5.2)

There are, as mentioned earlier, three possible singular points on X, which are given by \(f^{-1}(P_1)\), \(f^{-1}(P_2)\), and \(f^{-1}(P_3)\), and they are cyclic quotient singularities of type \(\frac{1}{a}(b,c), \frac{1}{b}(a,c), \frac{1}{c}(a,b)\) respectively. Given a divisor \(C=nH-\mu E\) on X(a, b, c), we can apply the orbifold Riemann-Roch formula ([13, Section 8]) and get

$$\begin{aligned} \chi ({\mathcal {O}}_X(C)) = \chi ({\mathcal {O}}_X)+\frac{1}{2}D(D-K_X)+\delta _n (\frac{1}{a}(b,c))+\delta _n(\frac{1}{b}(a,c))+\delta _n (\frac{1}{c}(a,b)). \end{aligned}$$

Taking into consideration the intersection matrix of H and E, the RR formula for D can be written as

$$\begin{aligned} \chi ({\mathcal {O}}_X(nH-\mu E))= & {} \chi ({\mathcal {O}}_X)+\frac{1}{2}\bigg (\frac{n^2+n(a+b+c)}{abc}-(\mu ^2+\mu )\bigg )\nonumber \\&+ \delta _n (\frac{1}{a}(b,c))+\delta _n (\frac{1}{b}(a,c))+\delta _n (\frac{1}{c}(a,b)). \end{aligned}$$
(5.3)

The contributions from the singularities are given by Dedekind sums. To have some control over these sums, we first recall a formula for \(\delta _n(\frac{1}{r}(a))\) and \(\sigma _n (\frac{1}{r}(a))\) for r, a coprime integers ([15, Lemma 3.2.1]). Here \(\delta _n(\frac{1}{r}(a))\) and \(\sigma _n (\frac{1}{r}(a))\) are given by

$$\begin{aligned} \delta _n (\frac{1}{r}(a))=\frac{1}{r}\sum _{\varepsilon \in \mu _r, \varepsilon \ne 1}\frac{\varepsilon ^{-n}-1}{(1-\varepsilon ^{a})} \,\text {and} \,\,\sigma _n (\frac{1}{r}(a))=\frac{1}{r}\sum _{\varepsilon \in \mu _r, \varepsilon \ne 1}\frac{\varepsilon ^{-n}}{(1-\varepsilon ^{a})}. \end{aligned}$$
(5.4)

Lemma 5.1

Given two coprime integers a and r,

$$\begin{aligned} \delta _n(\frac{1}{r}(a))=-\frac{\overline{\alpha n}}{r}, \end{aligned}$$

where \(\alpha \) is the inverse of a mod r, i.e., \(a\cdot \alpha \equiv 1\) mod r, for all \(n \in {\mathbb {Z}}\). In particular, this gives

$$\begin{aligned} \sigma _0(\frac{1}{r}(a))=\frac{r-1}{2r}. \end{aligned}$$

Lemma 5.2

Given \(\delta _n(\frac{1}{r}(a_1,a_2))\) as in 5.1, assume \(r, a_1, a_2\) are coprime, we have

$$\begin{aligned} -\frac{r}{8}\le \delta _n(\frac{1}{r}(a_1,a_2))< \frac{r}{8}. \end{aligned}$$

Proof

As \(r,a_1\) are coprime, there exists \(k>0 \in {\mathbb {Z}}\) such that \(a_1\cdot k \equiv 1 \text { mod } r\). Then

$$\begin{aligned} \delta _n(a_1, a_2)&=\frac{1}{r}\sum _{\varepsilon \in \mu _r, \varepsilon \ne 1}\frac{\varepsilon ^{-n}-1}{(1-\varepsilon ^{a_1})(1-\varepsilon ^{a_2})}\\&=\frac{1}{r}\sum _{\varepsilon \in \mu _r, \varepsilon \ne 1}\frac{(\varepsilon ^{a_1})^{r-{\overline{kn}}}-1}{(1-\varepsilon ^{a_1})(1-\varepsilon ^{a_2})}\\&=-\frac{1}{r}\sum _{\varepsilon \in \mu _r, \varepsilon \ne 1}\frac{(\varepsilon ^{a_1})^{r-{\overline{kn}}-1}+\cdots +\varepsilon ^{a_1}+1}{(1-\varepsilon ^{a_2})}\\&=-\frac{1}{r}\sum _{\varepsilon \in \mu _r, \varepsilon \ne 1}\frac{\varepsilon ^{r-{\overline{kn}}-1}+\cdots +\varepsilon +1}{(1-\varepsilon ^{ka_2})}\\&=-\frac{1}{r}\sum _{\varepsilon \in \mu _r, \varepsilon \ne 1}\frac{\varepsilon ^{-({\overline{kn}}+1)}+\cdots +\varepsilon ^{-({\overline{kn}}+r-{\overline{kn}}-1)}+\varepsilon ^{-({\overline{kn}}+r-{\overline{kn}})}}{(1-\varepsilon ^{ka_2})}. \end{aligned}$$

Since \(r, ka_2\) are coprime, there exists \(q>0 \in {\mathbb {Z}}\) such that \(q\cdot ka_2 \equiv 1 \text { mod } r\). By Lemma 5.1, we can further write the above expression as

$$\begin{aligned} \delta _n(a_1, a_2)&=\sum _{i=1}^{r-{\overline{kn}}}(\frac{\overline{q({\overline{kn}}+i)}}{r}-\frac{r-1}{2r})\\&\le \frac{({\overline{kn}}+1+r-1)(r-{\overline{kn}}-1)}{2r}-(r-{\overline{kn}})\cdot \frac{r-1}{2r}\\&=\frac{1}{2r}(-{\overline{kn}}^2+(r-2){\overline{kn}}) \\&\le \frac{r}{8}+\frac{1}{2r}-\frac{1}{2}\\&< \frac{r}{8}. \end{aligned}$$

When \(q=1\), the first inequality above becomes an equality, and when \({\overline{kn}}=\frac{r-2}{2}\), the second equality becomes an equality. The final inequality is strict as long as \(r>1\). We also have the lower bound as follows:

$$\begin{aligned} \delta _n(a_1, a_2)&=\sum _{i=1}^{r-{\overline{kn}}}(\frac{\overline{q({\overline{kn}}+i)}}{r}-\frac{r-1}{2r})\\&\ge \frac{(r-{\overline{kn}}-1+1)(r-{\overline{kn}}-1)}{2r}-(r-{\overline{kn}})\cdot \frac{r-1}{2r}\\&=\frac{1}{2r}({\overline{kn}}^2-r{\overline{kn}})\\&\ge -\frac{r}{8}. \end{aligned}$$

One sufficient condition for the first inequality to be an equality is that \(q=r-1\). The last inequality is equal when \({\overline{kn}}=\frac{r}{2}\). \(\square \)

Example

An example where \(\delta _n(\frac{1}{r}(a_1,a_2))\) takes maximal value: \(\delta _{11}(\frac{1}{24}(1,1))=\frac{24}{8}-\frac{1}{2}+\frac{1}{2\cdot 24}=\frac{121}{48}\); and an example where \(\delta _n(\frac{1}{r}(a_1,a_2))\) takes minimum value: \(\delta _{12}(\frac{1}{24}(23,1))=-\frac{24}{8}=-3.\)

Remark 5.3

It is possible to find all the contributions from cyclic quotient singularities of type \(\frac{1}{r}(a_1,a_2)\), see [15, Section 3.2]. We gave there a Magma program Contribution\((r,[a_1,a_2])\) to calculate \(\sigma _n(\frac{1}{r}(a_1,a_2))\).

6 Mori dreamness of some blowups X(a, b, c)

We start with finding a negative curve \(C\sim nH-\mu E\) that satisfies the conditions in Theorem 4.1. To reduce the searching time, we have the following proposition.

Proposition 6.1

Given \(\mu >0\), for a curve \(C\sim nH-\mu E\) to satisfy \(\chi ({\mathcal {O}}_X(C))=1\) and \(C^2<0\), one must have

$$\begin{aligned} m_-<n\le \text {min}\{ \mu \sqrt{abc}, m_+\} \end{aligned}$$

where

$$\begin{aligned} m_{-,+}=\frac{-(a+b+c)+\sqrt{((a+b+c)^2+4abc(\mu ^2+\mu ) \mp abc(a+b+c)}}{2}. \end{aligned}$$

Proof

We use the Riemann-Roch formula 5.3 and the bounds in Lemma 5.2 for the \(\delta _n\)’s. \(\square \)

This proposition says that for a given \(\mu \), we only need to check n in a certain range to search for \(C\sim nH-\mu E\) such that \(\chi ({\mathcal {O}}_X(C))=1\) and \(C^2<0\). We then increase \(\mu \) gradually to find such a C that satisfies the conditions in Theorem 4.1. We use the Magma program [10] to help us with the search. See the algorithms here [16].

In the remark after [6, Theorem 1.3], the authors suspect that the blowups of the weighted projective spaces \({\mathbb {P}}(7,10,19)\), \({\mathbb {P}}(7,19,22)\), \({\mathbb {P}}(7,23,27)\), and \({\mathbb {P}}(7,26,29)\) are Mori dream spaces. As an application of our theorem, we can show that \({\mathbb {P}}(7,10,19)\) is a Mori dream space and this rests heavily on the Kawamata-Viehweg vanishing theorem. We can not do the same for \({\mathbb {P}}(7,19,22)\), \({\mathbb {P}}(7,23,27)\), and \({\mathbb {P}}(7,26,29)\). But we could also confirm the Mori dreamness of the blow up of \({\mathbb {P}}(7,19,60)\) and \({\mathbb {P}}(7,23,59)\), which as far as we are aware of are new.

Theorem 6.2

The blowups of the weigthed projective spaces \({\mathbb {P}}(7,10,19)\), \({\mathbb {P}}(7,19,60)\), and \({\mathbb {P}}(7,23,59)\) are Mori dream spaces, and the generators of the effective cones and the generators of the semiample cones are given in the following table.

X

Effective cone

Nef and SAmp cone

X(7, 10, 19)

\((E, 437H-12E)\)

\((H, 840H-23E)\)

X(7, 19, 60)

\((E,266H-3E)\)

\((H, 90H-E)\)

X(7, 23, 59)

\((E, 184H-2E)\)

\((H, 413H-4E)\)

Proof

We use the algorithm [16] to search for the negative curves. We can easily check that the given divisors generate the corresponding effective cones according to Theorem 4.1 and Lemma 3.1. We then find the corresponding dual cone in each case, which gives the nef cone respectively. What is remaining is to check whether each nef cone is also the semiample cone.

We see this case by case.

  1. 1.

    In the case of X(7, 10, 19), we see that H and \(D\sim 840H-23E\) generate the nef cone. It remains to check whether the divisor \(D\sim 840H-23\) is also semiample. To justify that, we need to prove that the negative curve \(C\sim 437H-12E\) is not a fixed component of D. We see that \(\chi ({\mathcal {O}}_X(D))=1\) by Riemann-Roch, and this implies \(h^0({\mathcal {O}}_X(D))\ge 1\). And the divisor \(D-C\sim 403H-11E\) can be written as \(D-C\sim 403H-11E= K_X+(403+7+10+19)H-12E\). We can check that the divisor \(D-C-K_X\) is ample since

    $$\begin{aligned} (D-C-K_X)\cdot C=\frac{17}{70}, (D-C-K_X)\cdot E=12, (D-C-K_X)^2=\frac{1201}{1330}. \end{aligned}$$

    Therefore, by the Kawamata-Viehweg vanishing theorem, \(H^1({\mathcal {O}}_X(D-C))=0\). Then \(h^0({\mathcal {O}}_X(D-C))=\chi ({\mathcal {O}}_X(D-C))=0\) by Riemann-Roch. So C is not a fixed component of D. This gives the condition in Proposition 3.2. Therefore mD is semiample for some \(m>>0\) and X(7, 10, 19) is a MDS.

  2. 2.

    In the case of X(7, 19, 60), we see that H and \(D\sim 90H-E\) generate the nef cone. We claim that \(C\sim 266H-3E\) is not a fixed component of 4D. To see this, we have first \(\chi ({\mathcal {O}}_X(2D))=1\) and therefore \(h^0({\mathcal {O}}_X(4D))\ge h^0({\mathcal {O}}_X(2D))\ge 1\). Further we have \(4D-C-K_X\sim 180H-2E\), which is on the extremal ray of the nef cone. We also check \(D^2>0\), and therefore \(4D-C-K_X\) is nef and big. By the Kawamata-Viehweg vanishing theorem, we have \(H^1({\mathcal {O}}_X(4D-C))=0\). Since \(h^0({\mathcal {O}}_X(4D-C))=\chi ({\mathcal {O}}_X(4D-C))=0\), we know that C is not a base component of 4D. Again, by Proposition 3.2, X(7, 19, 20) is a MDS.

  3. 3.

    In the case of X(7, 23, 59), we see that H and \(D\sim 413H-4E\) generate the nef cone. We claim that \(C\sim 184H-2E\) is not a fixed component of D. As in the first case, we can prove \(D-C-K_X\) is ample, then \(H^1({\mathcal {O}}_X(D-C))\) vanishes. Riemann-Roch tells us \(h^0({\mathcal {O}}_X(D-C))=\chi ({\mathcal {O}}_X(D-C))=0\). But \(h^0({\mathcal {O}}_X(D))\ge \chi ({\mathcal {O}}_X(D))=1\), and therefore C is not a fixed component of D. We are done. \(\square \)

Remark 6.3

The above proof rests on the fact that \(kD-C-K_X\) is nef and big for some \(k\ge 1\). This enable us to use the Kawamata-Viehweg vanishing theorem.

Remark 6.4

We can (and should) use our algorithm to do some systematic search for more examples as above. We expect that the same method can also be extended to quasismooth del Pezzo surfaces and K3 surfaces of Picard rank 1 inside weighted projective spaces. We will try this out in our further work.