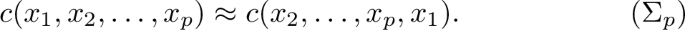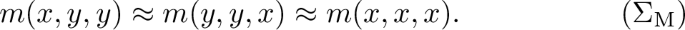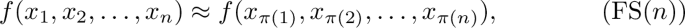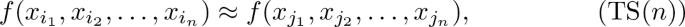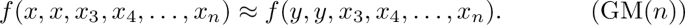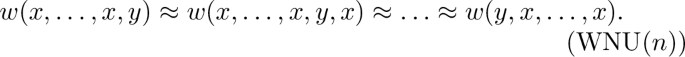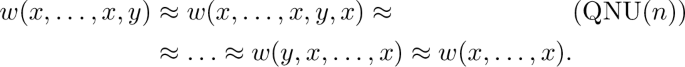Submaximal clones over a three-element set up to minor-equivalence

Abstract

We study clones modulo minor homomorphisms, which are mappings from one clone to another preserving arities of operations and respecting permutation and identification of variables. Minor-equivalent clones satisfy the same sets of identities of the form $f(x_1,\dots ,x_n)\approx g(y_1,\dots ,y_m)$, also known as minor identities, and therefore share many algebraic properties. Moreover, it was proved that the complexity of the ${\text {CSP}}$ of a finite structure $\mathbb {A}$ only depends on the set of minor identities satisfied by the polymorphism clone of $\mathbb {A}$. In this article we consider the poset that arises by considering all clones over a three-element set with the following order: we write $\mathcal {C}\ {\preceq _{\textrm{m}}}\ \mathcal {D}$ if there exists a minor homomorphism from $\mathcal {C}$ to $\mathcal {D}$. We show that the aforementioned poset has only three submaximal elements.

1 Introduction

In 1959 Janov and Mučnik [18] proved that there exists a continuum of clones over a k-element set, for every $k \ge 3$. Thus, the goal to achieve a classification à la Post [23] for clones over a three-element set seemed to falter. Subsequently, researchers in universal algebra focused on understanding particular aspects of clone lattices on finite domains. As far as concerns clones over $\{0,1,2\}$, remarkable results in this direction are the description of all maximal clones [17] and of all minimal clones [12]. Moreover, it turned out that all the aforementioned maximal clones, with the sole exception of the clone of all linear operations, contain a continuum of subclones [13, 20]. More recently, a complete description of all clones of self-dual operations over a three-element set was provided [25]. Note that this is a remarkable result since the clone of all self-dual operations, which we denote by $\mathcal {C}_3$, is one of the maximal clones over $\{0,1,2\}$; thus $\mathcal {C}_3$ is the first maximal clone besides the clone of all linear operations that has such description. In particular, $\mathcal {C}_3$ is the only maximal clone which has a full description of all its subclones, despite having continuum many of them. Another result that seems to be a setback in the research-line aimed at describing the entire lattice of clones over $\{0,1,2\}$ is the following: it is undecidable whether a given clone over a finite domain is finitely related [21].

One might still hope to classify all operation clones over finite sets up to some equivalence relation so that equivalent clones share many of the properties that are of interest in universal algebra. Recently, Barto, Opršal, and Pinsker [3] introduced a weakening of the notion of clone homomorphism on the class of clones over a finite set, known in the literature as minor homomorphism. We write $\mathcal {C}\ {\preceq _{\textrm{m}}}\ \mathcal {D}$ if there exist a minor homomorphism from $\mathcal {C}$ to $\mathcal {D}$, that is, a map preserving arities and taking minors, where a minor of an operation f is an operation obtain from f by permuting its variables, identifying variables, or by adding dummy variables (see Definitions 2.5 and 2.6). Moreover, we write $\mathcal {C}\ {\equiv _{\textrm{m}}}\ \mathcal {D}$ if $\mathcal {C}\ {\preceq _{\textrm{m}}}\ \mathcal {D}$ and $\mathcal {D}\ {\preceq _{\textrm{m}}}\ \mathcal {C}$ and say that $\mathcal {C}$ and $\mathcal {D}$ are minor-equivalent; by $\overline{\mathcal {C}}$ we denote the ${\equiv _{\textrm{m}}}$-class of $\mathcal {C}$, i.e., the class of all clones over some finite set which are minor-equivalent to $\mathcal {C}$. The relation ${\preceq _{\textrm{m}}}$ is a reflexive and transitive relation on the class of clones over a finite set, hence ${\equiv _{\textrm{m}}}$ is indeed an equivalence relation, thereby making the use of these suggestive symbols justified. Minor-equivalent clones satisfy the same sets of identities of a particular form, known as minor conditions (see Section 2.2). In a recent turn of events, it turned out that the complexity of the Constraint Satisfaction Problem of ${\mathbb A}$ (${{\,\textrm{CSP}\,}}({\mathbb A})$), where ${\mathbb A}$ is a finite relational structure with finite signature, only depends on the set of minor identities satisfied by ${{\,\textrm{Pol}\,}}({\mathbb A})$, i.e., by the polymorphism clone of ${\mathbb A}$. Moreover, the relation ${\preceq _{\textrm{m}}}$ preserves the complexity CSPs, for short: if ${{\,\textrm{Pol}\,}}({\mathbb A})\ {\preceq _{\textrm{m}}}\ {{\,\textrm{Pol}\,}}({\mathbb B})$ then there exists a log-space reduction from ${{\,\textrm{CSP}\,}}({\mathbb B})$ to ${{\,\textrm{CSP}\,}}({\mathbb A})$ [3].

In this article we focus on the set of all clones over $\{0,1,2\}$ ordered with respect to ${\preceq _{\textrm{m}}}$. More precisely, we describe the submaximal elements of the poset $\mathfrak {P}_3 {:}{=}(\{\overline{\mathcal {C}} \mid \mathcal C\text { is a clone over } \{0,1,2\}\};{\preceq _{\textrm{m}}})$. A full description of the subposet ${\downarrow \!\overline{\mathcal {C}_3}}$ which contains all the elements of $\mathfrak P_{3}$ which are smaller than $\overline{\mathcal {C}_3}$, with respect to ${\preceq _{\textrm{m}}}$, was provided in [7]. From the latter description it follows that ${\downarrow \!\overline{\mathcal {C}_3}}$ is a countably infinite lattice. In the same article [7, Conjecture 6.2] it was conjectured that $\mathfrak P_{3}$ has exactly three submaximal elements, namely the ${\equiv _{\textrm{m}}}$-classes of the following three clones:

$$\begin{aligned} \mathcal {C}_2&{:}{=}{{\,\textrm{Pol}\,}}\big ((\{0,1\};\{(0,1),(1,0)\})\big ), \\\mathcal {C}_3&{:}{=}{{\,\textrm{Pol}\,}}\big ((\{0,1,2\};\{(0,1),(1,2),(2,0)\})\big ), \\\mathcal {B}_2&{:}{=}{{\,\textrm{Pol}\,}}\big ((\{0,1\};\{0\},\{1\},\{(0,1),(1,0),(1,1)\})\big ). \end{aligned}$$

Note that $\mathcal {C}_2$ and $\mathcal {B}_2$ are clones over $\{0,1\}$; we could equivalently consider the ${\equiv _{\textrm{m}}}$-classes of the following clones: $\mathcal {C}'_2{:}{=}{{\,\textrm{Pol}\,}}\big ((E_3;\{(0,1),(1,0)\})\big )$ and $\mathcal {B}'_2{:}{=}{{\,\textrm{Pol}\,}}\big ((E_3;\{0\},\{1\},\{(0,1),(1,0),(1,1)\})\big )$, where $E_3{:}{=}\{0,1,2\}$.

1.1 Contributions

We give a positive answer to the aforementioned conjecture: we show that $\mathfrak P_{3}$ has exactly three submaximal elements, namely $\overline{\mathcal {C}_2}$, $\overline{\mathcal {C}_3}$, and $\overline{\mathcal {B}_2}$ (see Corollary 3.13). Our proof is of syntactic nature: we prove several statements that entail the existence of operations satisfying suitable identities in some clone $\mathcal {C}$, provided that $\mathcal {C}$ has certain operations. For example, we prove that if $\mathcal {C}$ is an idempotent clone over an n-element set, for some $n\ge 2$, such that $\mathcal {C}$ has a Mal’cev operation and a cyclic operation of arity p, for every prime $p\le n$, then $\mathcal {C}$ has a majority operation (see Lemma 3.4). Statements of this form constitute results of independent interest in universal algebra.

2 Preliminaries

In this section we present notation, definitions, and some basic results from the literature which we are going to use throughout the article.

2.1 A Galois connection for clones

We denote the set $\{0,\dots ,k-1\}$ by $E_k$. For $n \in {\mathbb N}$, we define

$$\begin{aligned} \mathcal {O}^{(n)}_k \,\, {:}{=}\,\, \{f\mid f:E_k^n\rightarrow E_k\}{} & {} \text {and}{} & {} \mathcal {O}_k {:}{=}\bigcup _{n \in {\mathbb N}} \mathcal {O}^{(n)}_k. \end{aligned}$$

A clone over $E_k$ is a subset $\mathcal {C}$ of $\mathcal {O}_k$ which is closed under composition of operations and which contains all projections, where a projection is any operation of the form ${{\,\textrm{pr}\,}}^{n}_{i}:(a_1,\dots ,a_n)\mapsto a_i$, for all $a_1,\dots ,a_n\in E_k$. If $F \subseteq \mathcal {O}_k$, then $\langle F\rangle$ denotes the clone generated by F, i.e., the smallest clone that contains F.

An alternative way of describing a clone of operations is to specify the clone as the set all operations preserving a given set of relations. We say that an n-ary operation f preserves a relation R on a finite set A if, for every $a_1,\dots ,a_n \in R$, it holds that $f (a_1,\dots ,a_n) \in R$. In this case we also say that R is invariant under f. If f preserves all the relations in $\Gamma$, we say that f is a polymorphism of $\Gamma$.

Let $\Gamma$ be a set of relations over $E_k$, for some $k\in {\mathbb N}$. We define the set

$$\begin{aligned} {{\,\textrm{Pol}\,}}(\Gamma ) \,\, {:}{=}\,\, \bigcup _{n\in {\mathbb N}}\Big \{f:E_k^n\rightarrow E_k \mid f \text { preserves all the relations in } \Gamma \Big \}. \end{aligned}$$

We call the set ${{\,\textrm{Pol}\,}}(\Gamma )$ the polymorphism clone of $\Gamma$.

Analogously, for every set of operations F over $E_k$, we define

$$\begin{aligned} {{\,\textrm{Inv}\,}}(F) \,\, {:}{=}\,\, \bigcup _{n\in {\mathbb N}}\Big \{R\subseteq E_k^n \mid R \text { is invariant under every operation in } F\Big \}. \end{aligned}$$

Theorem 2.1

[8, 14]. Let F be a set of operations over a finite set. It holds that ${{\,\textrm{Pol}\,}}({{\,\textrm{Inv}\,}}(F)) = \langle F \rangle$.

Let $\tau$ be a relational signature. A $\tau$-structure is a relational structure over the signature $\tau$. Let ${\mathbb A}$ and ${\mathbb B}$ be two relational $\tau$-structures. A map $h:A\rightarrow B$ is a homomorphism if for every $R\in \tau$

$$\begin{aligned} \text {if } (a_1,\dots ,a_n)\in R^{\mathbb A}, \text { then } (h(a_1),\dots ,h(a_n))\in R^{\mathbb B}. \end{aligned}$$

We denote by ${\text {Hom}}({\mathbb A},{\mathbb B})$ the set of all homomorphisms from ${\mathbb A}$ to ${\mathbb B}$. We also write ${\mathbb A}\rightarrow {\mathbb B}$ if there exists a homomorphism from ${\mathbb A}$ to ${\mathbb B}$, and we say that ${\mathbb A}$ and ${\mathbb B}$ are homomorphically equivalent if ${\mathbb A}\rightarrow {\mathbb B}$ and ${\mathbb B}\rightarrow {\mathbb A}$. An endomorphism of ${\mathbb A}$ is a homomorphism from ${\mathbb A}$ to ${\mathbb A}$. An isomorphism between ${\mathbb A}$ and ${\mathbb B}$ is a bijective homomorphism h such that the mapping $h^{-1}:B \rightarrow A$ that sends h(x) to x is a homomorphism, too. An automorphism of ${\mathbb A}$ is an isomorphism between ${\mathbb A}$ and itself. A finite structure ${\mathbb A}$ is called a core if every endomorphism of ${\mathbb A}$ is an automorphism. We say that ${\mathbb C}$ is a core of ${\mathbb A}$ if ${\mathbb C}$ is a core and ${\mathbb C}$ is homomorphically equivalent to ${\mathbb A}$. It is well known that every finite relational structure has a core which is unique up to isomorphism, thus it makes sense to speak about the core of a relational structure.

In this article, we are going to consider polymorphism clones of relational structures in addition to polymorphism clones of a set of relations: we define ${{\,\textrm{Pol}\,}}(A;\Gamma ){:}{=}{{\,\textrm{Pol}\,}}(\Gamma )$. For $n\ge 1$, we denote by ${\mathbb A}^n$ the structure with the same signature $\tau$ as ${\mathbb A}$ whose domain is $A^n$ such that for every k-ary $R\in \tau$, it holds that $(\varvec{a}_1,\dots ,\varvec{a}_k)$ is contained in $R^{{\mathbb A}^n}$ if and only if it is contained in $R^{\mathbb A}$ componentwise, i.e., $(a_{1j},\dots ,a_{kj})\in R^{\mathbb A}$ for every $1\le j\le n$. Note that, equivalently, ${{\,\textrm{Pol}\,}}({\mathbb A})=\bigcup _{n\in \mathbb {N}}{\text {Hom}}({\mathbb A}^n,{\mathbb A})$.

A primitive positive formula over $\tau$ is a first-order formula which only uses relation symbols in $\tau$, equality, conjunction and existential quantification. If ${\mathbb A}$ is a $\tau$-structure and $\phi (x_1,\dots ,x_n)$ is a $\tau$-formula with free-variables $x_1,\dots ,x_n$, then $\{(a_1,\dots ,a_n)\mid {\mathbb A}\models \phi (a_1,\dots ,a_n)\}$ is called the relation defined by $\phi$ in ${\mathbb A}$. In particular, if $\phi$ is primitive positive, then this relation is said to be pp-definable in ${\mathbb A}$. Given two relational structures ${\mathbb A}$ and $\mathbb B$ on the same domain – but with possibly different signatures – we say that ${\mathbb A}$ pp-defines ${\mathbb B}$ if every relation in ${\mathbb B}$ is pp-definable in ${\mathbb A}$.

Theorem 2.2

[8, 14]. Let ${\mathbb A}$ be a finite relational structure. A relation R has a pp-definition in ${\mathbb A}$ if and only if $R\in {{\,\textrm{Inv}\,}}({{\,\textrm{Pol}\,}}({\mathbb A}))$.

It is well known that all clones of operations over a fixed set $E_n$ form an algebraic lattice $\mathfrak {L}_n$ under set inclusion. The lattice operations are defined as follows: $\mathcal {C}\wedge \mathcal {D}{:}{=}\mathcal {C}\cap \mathcal {D}$ and $\mathcal {C}\vee \mathcal {D}{:}{=}\langle \mathcal {C}\cup \mathcal {D}\rangle$. The top-element of $\mathfrak {L}_n$ is the clone $\mathcal {O}_{n}$, its bottom-element is the clone of all projections over $E_n$, which we denote by $\mathcal {P}_n$. A celebrated result, due to Post [23], is the full description of $\mathfrak {L}_2$. Janov and Mučnik [18] proved that $\mathfrak {L}_n$ has a continuum of elements, for every $n \ge 3$.

Moreover, Theorem 2.2 underlines that pp-definability among relational structures translates to inclusion of the correspondent polymorphism clones.

Theorem 2.3

[8, 14]. Let ${\mathbb A}$ and ${\mathbb B}$ be structures on the same finite set A. Then ${\mathbb A}$ pp-defines ${\mathbb B}$ if and only if ${{\,\textrm{Pol}\,}}({\mathbb A})\subseteq {{\,\textrm{Pol}\,}}({\mathbb B})$.

2.2 The pp-constructability poset

In this section we briefly introduce the pp-constructability poset – the main object of study in this article. For this purpose, we first define the notions of pp-constructability and minor homomorphism.

Let ${\mathbb A}$ and ${\mathbb B}$ be finite relational structures. We say that ${\mathbb B}$ is a pp-power of ${\mathbb A}$ if it is isomorphic to a structure with domain $A^n$, for some $n\ge 1$, whose relations are pp-definable from ${\mathbb A}$. Notice that a k-ary relation on $A^n$ is regarded as a kn-ary relation on A.

Definition 2.4

Let ${\mathbb A}$ and ${\mathbb B}$ be finite relational structures. We say that ${\mathbb A}$ pp-constructs ${\mathbb B}$, and write ${\mathbb A}\ {\le _{\textrm{Con}}}\ {\mathbb B}$, if ${\mathbb B}$ is homomorphically equivalent to a pp-power of ${\mathbb A}$. We also write ${\mathbb A}\equiv _{\textrm{Con}}{\mathbb B}$ if ${\mathbb A}\ {\le _{\textrm{Con}}}\ {\mathbb B}$ and ${\mathbb B}\ {\le _{\textrm{Con}}}\ {\mathbb A}$.

The question that naturally arises now is how pp-constructability among relational structures translates in terms of the correspondent polymorphism clones: in particular, whether there is a Galois connection that would lead us to a result of the same flavour of Corollary 2.3.

Definition 2.5

Let f be any n-ary operation, and let $\sigma$ be a map from $E_n$ to $E_r$. We denote by $f_\sigma$ the following r-ary operation

$$\begin{aligned} f_\sigma (x_0,\dots ,x_{r-1}) {:}{=}f(x_{\sigma (0)},\dots ,x_{\sigma (n-1)}). \end{aligned}$$

Any operation of the form $f_\sigma$, for some $\sigma :E_m\rightarrow E_n$, is called a minor of f.

A minor identity is a formal expression of the form

$$\begin{aligned} \forall x_1,\dots ,x_r (f(x_{\sigma (0)},\dots ,x_{\sigma (n-1)}) = g(x_{\pi (0)},\dots ,x_{\pi (m-1)})), \end{aligned}$$

where f and g are function symbols and $\sigma :E_n \rightarrow E_r$ and $\pi :E_m \rightarrow E_r$ are some maps; in this case we write $f_\sigma \approx g_\pi$. A minor condition is a finite set of minor identities.

Definition 2.6

Let $\mathcal {A}$ and $\mathcal {B}$ be clones and let $\xi :\mathcal {A}\rightarrow \mathcal {B}$ be a mapping that preserves arities. We say that $\xi$ is a minor homomorphism if

$$\begin{aligned} \xi (f_\sigma ) = \xi (f)_\sigma \end{aligned}$$

for any n-ary operation $f \in \mathcal {A}$ and $\sigma :E_n \rightarrow E_r$.

We say that a set of operations F satisfies a minor condition $\Sigma$, and write $F \models \Sigma$, if every function symbol in $\Sigma$ can be mapped to an operation in F such that, for every $f_{\sigma }\approx g_{\pi }$ in $\Sigma$, the equality $f_{\sigma }^F = g_{\pi }^F$ holds for every evaluation of the variables. Moreover, we say that an operation f satisfies a minor condition $\Sigma$ if $\{f\}\models \Sigma$.

Next we are going to define some examples of minor conditions, which we will use in Section 3.

Definition 2.7

We define the following minor conditions:

• We call cyclic identity of arity p, for some $p\ge 2$, the following identity

  

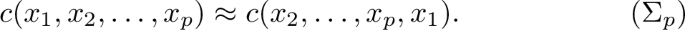
• We call quasi minority the following minor condition:

  $$\begin{aligned}m(x,y,y)\approx m(y,x,y)\approx m(y,y,x)\approx m(x,x,x).\end{aligned}$$

• We call quasi Mal’cev the following minor condition:

  

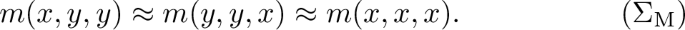
• We call quasi majority the following minor condition:

  $$\begin{aligned}m(x,y,y)\approx m(y,x,y)\approx m(y,y,x)\approx m(y,y,y).\end{aligned}$$

• We call n-ary symmetric condition the minor condition that consists of all identities of the form

  

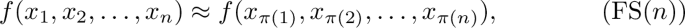
  where $\pi$ is a permutation of the set $\{1,2,\dots ,n\}$.

• We call n-ary totally symmetric condition the minor condition that consists of all identities of the form

  

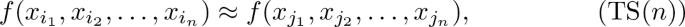
  whenever $\{i_1, i_2,\dots ,i_n\} = \{j_1,j_2,\dots ,j_n\}$.

• We call n-ary generalized minority condition, where $n\ge 3$ is odd, the minor condition that consists of all the identities from ${\text {FS}}(n)$ and

  

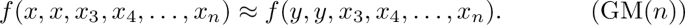
• We call weak near-unanimity condition of arity $n\ge 3$ the following minor condition

  

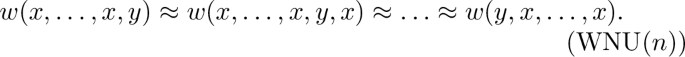
• We call quasi near-unanimity condition of arity $n\ge 3$ the following minor condition

  

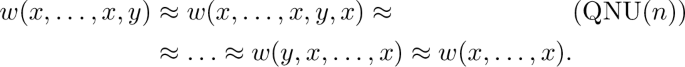
A k-ary operation f is a quasi Mal’cev operation if it satisfies the minor condition $\Sigma _{{\text {M}}}$; we adopt an analogous convention for all other conditions introduced so far. A Mal’cev operation is an idempotent quasi Mal’cev operation; we adopt a similar convention in defining a minority operation, a generalized minority operation, a majority operation, and a near-unanimity operation. If f is a totally symmetric operation of arity n we also write $f(\{x_1, x_2,\dots ,x_n\})$ instead of $f(x_1, x_2,\dots ,x_n)$. Note that every totally symmetric operation is symmetric. The other implication does not hold: the majority operation over $\{0,1\}$ is symmetric but not totally symmetric. The multiplicity of variables plays a role in the definition of a symmetric operation: as a matter of fact, f(x, x, y) need not be equal to f(x, y, y).

In Remark 2.8 we show an example of a minor condition that is not satisfied by the polymorphisms of a certain structure: the polymorphism clone of a directed cycle of length p does not satisfy the cyclic identity of arity p. This is an easy observation that will nevertheless come in handy later in this article, more precisely, in the proof of Theorem 2.14.

Remark 2.8

Consider the relational structure ${\mathbb C}_p = (E_p;R^{{\mathbb C}_p})$, where

$$\begin{aligned} R^{{\mathbb C}_p}{:}{=}\{(0,1),\dots ,(p-2,p-1),(p-1,0)\}. \end{aligned}$$

It is easy to see that, for every prime p, it holds that ${{\,\textrm{Pol}\,}}({\mathbb C}_p)$ does not satisfy the cyclic identity of arity p, i.e., ${{\,\textrm{Pol}\,}}({\mathbb C}_p)\not \models \Sigma _p$. Indeed, suppose that there exists a polymorphism f of ${\mathbb C}_p$ satisfying $\Sigma _p$, then

$$\begin{aligned} f(0,\dots ,p-1) = f(1,\dots ,p-1,0) = a, \text { for some } a\in E_p. \end{aligned}$$

It would follow that $(a,a)\in R^{{\mathbb C}_p}$, a contradiction.

The connection between pp-constructability and minor homomorphisms is given by the following theorem.

Theorem 2.9

[3]. Let ${\mathbb A}$, ${\mathbb B}$ be finite relational structures and $\mathcal {A}={{\,\textrm{Pol}\,}}({\mathbb A})$, $\mathcal {B}={{\,\textrm{Pol}\,}}({\mathbb B})$. The following are equivalent:

• (1) There exists a minor homomorphism from $\mathcal {A}$ to $\mathcal {B}$;

• (2) ${\mathbb A}$ pp-constructs ${\mathbb B}$;

• (3) if $\mathcal {A}$ satisfies a minor condition $\Sigma$, then $\mathcal {B}\models \Sigma$.

We would like to remark that, unfortunately, the latter theorem does not yield a Galois connection for clones: Barto, Opršal, and Pinsker also provide a semantic characterization of minor homomorphisms, by introducing a new operator called reflection [3]. However, a reflection of a clone need not contain projections or be closed under composition; thus, the reflection of a clone is, in general, not a clone. What we obtain by taking a reflection of a clone is known in the literature as minion; they play a crucial role in Promise Constraint Satisfaction Problems [2].

Corollary 2.10

[3]. Let ${\mathbb A}$ be a finite relational structure, let ${\mathbb C}$ be the core of ${\mathbb A}$ and let ${\mathbb C}^c$ be the expansion of ${\mathbb C}$ by all unary relations $\{a\}_{a\in C}$. Then:

• (1) ${\mathbb A}\equiv _{\textrm{Con}}{\mathbb C}\equiv _{\textrm{Con}}{\mathbb C}^c$;

• (2) for every minor condition $\Sigma$, ${{\,\textrm{Pol}\,}}({\mathbb A})\models \Sigma$ if and only if ${{\,\textrm{Pol}\,}}({\mathbb C}^c)\models \Sigma$.

We write $\mathcal {A}\ {\preceq _{\textrm{m}}}\ \mathcal {B}$ if there exists a minor homomorphism $\xi :\mathcal {A}\rightarrow \mathcal {B}$, and we denote by ${\equiv _{\textrm{m}}}$ the equivalence relation where $\mathcal {A}\ {\equiv _{\textrm{m}}}\ \mathcal {B}$ if $\mathcal {A}\ {\preceq _{\textrm{m}}}\ \mathcal {B}$ and $\mathcal {B}\ {\preceq _{\textrm{m}}}\ \mathcal {A}$. Note that $\mathcal {A}\ \subseteq \ \mathcal {B}$ implies $\mathcal {A}\ {\preceq _{\textrm{m}}}\ \mathcal {B}$. Moreover, we denote by $\overline{\mathcal {A}}$ the ${\equiv _{\textrm{m}}}$-class of $\mathcal {A}$, that is

$$\begin{aligned} \overline{\mathcal {A}}\,\, {:}{=}\,\, \{\mathcal {C}\mid \mathcal {C}\text { is a clone over some finite set and } \mathcal {C}\ {\equiv _{\textrm{m}}}\ \mathcal {A}\} \end{aligned}$$

and we write $\overline{\mathcal {A}}\ {\preceq _{\textrm{m}}}\ \overline{\mathcal {B}}$ if and only if $\mathcal {A}\ {\preceq _{\textrm{m}}}\ \mathcal {B}$.

We finally define the following posets:

$$\begin{aligned} \mathfrak P_{\textrm{fin}}&\,\, {:}{=}\,\, (\{\overline{\mathcal {C}} \mid \mathcal C\text { is a clone over a finite set}\};{\preceq _{\textrm{m}}}); \\\mathfrak {P}_n&\,\, {:}{=}\,\, (\{\overline{\mathcal {C}} \mid \mathcal C\text { is a clone over } E_n\};{\preceq _{\textrm{m}}}) \end{aligned}$$

and call them the pp-constructability poset and the pp-constructability poset restricted to clones over an n-element set, respectively. Note that a full description of $\mathfrak {P}_2$ was presented in [6], and this article entirely focuses on $\mathfrak {P}_3$.

A constant operation of arity n is an operation $c^{(n)}$ defined as follows

$$\begin{aligned} c^{(n)}(x_1,\dots ,x_n) \,\, {:}{=}\, \, c \end{aligned}$$

where $c\in E_m$, for some $n,m\ge 1$; if $n=1$, we simply write c to denote the unary constant operation $c^{(1)}$. We want to remark that if $\mathcal {C}$ has a constant operation $c^{(n)}$, for some n, then it has a constant operation for every arity. It is easy to show that $\overline{\langle 0\rangle }$ is the top-element of $\mathfrak P_{3}$. Indeed, for every clone over $\{0,1,2\}$ the map that sends every n-ary operation to $0^{(n)}$ is minor-preserving.

2.3 The unique coatom

In this section we prove that both the posets $\mathfrak P_{\textrm{fin}}$ and $\mathfrak P_{3}$ have exactly one coatom, – i.e., a unique maximal element – namely $\overline{\mathcal {I}_2}$, that is, the ${\equiv _{\textrm{m}}}$-class of the clone of all idempotent operations over $\{0,1\}$.

Let us define the following relational structures

$$\begin{aligned} {\mathbb C}_1&\,\, {:}{=}\,\, (\{0\};\{(0,0)\}); \\\mathbb {I}_n&\,\, {:}{=}\, \, (E_n;\{0\},\dots ,\{n-1\}), \text { for every } n\ge 2. \end{aligned}$$

Proposition 2.11

For every finite relational structure ${\mathbb A}$ exactly one of the following holds: either ${\mathbb C}_1\ {\le _{\textrm{Con}}}\ {\mathbb A}$ or ${\mathbb A}\ {\le _{\textrm{Con}}}\ \mathbb {I}_2$.

Proof

Let ${\mathbb A}$ be a relational structure and let ${\mathbb B}$ be its core expanded by all unary relations. By Corollary 2.10 it holds that ${\mathbb C}_1$ pp-constructs ${\mathbb A}$ if and only if ${\mathbb C}_1$ pp-constructs ${\mathbb B}$ and ${\mathbb A}$ pp-constructs $\mathbb {I}_2$ if and only if ${\mathbb B}$ pp-constructs $\mathbb {I}_2$. Thus, we are going to prove the claim for ${\mathbb B}$. Let $B=\{b_0,\dots ,b_{n-1}\}$ be the domain of ${\mathbb B}$. If $n=1$, then it is straightforward to see that ${\mathbb C}_1\ {\le _{\textrm{Con}}}\ {\mathbb B}$. Let us assume that $n>1$, we need to show that ${\mathbb B}\ {\le _{\textrm{Con}}}\ \mathbb {I}_2$. Consider the pp-power ${\mathbb S}{:}{=}(\{b_0,\dots ,b_{n-1}\};O,I)$ of ${\mathbb B}$, where O and I are the unary relations defined by the formulae $O(x){:}{=}(x=b_0)$ and $I(x){:}{=}(x=b_1)$, respectively. Let us define the maps $g:{\mathbb S}\rightarrow \mathbb {I}_2$ that maps $b_0$ to 0 and every other element to 1 and $h:\mathbb {I}_2\rightarrow {\mathbb S}$ that maps 0 to $b_0$ and 1 to $b_1$. It is straightforward to check that g and h are homomorphisms. Thus $\mathbb {I}_2$ and ${\mathbb S}$ are homomorphically equivalent and ${\mathbb B}$ pp-constructs $\mathbb {I}_2$. $\square$

Note that, for every $n\ge 2$, ${{\,\textrm{Pol}\,}}({\mathbb C}_1)\ {\npreceq _{\textrm{m}}}\ {{\,\textrm{Pol}\,}}(\mathbb {I}_n)$, since ${{\,\textrm{Pol}\,}}({\mathbb C}_1)$ satisfies the minor identity $f(x)\approx f(y)$, while ${{\,\textrm{Pol}\,}}(\mathbb {I}_n)$ does not. Therefore, for every $n\ge 2$, the structure ${\mathbb C}_1$ does not pp-construct $\mathbb {I}_n$.

Proposition 2.12

For every $n \ge 2$ it holds that $\mathbb {I}_2 \equiv _{\textrm{Con}} \mathbb {I}_n$.

Proof

First, we show that $\mathbb {I}_2\ {\le _{\textrm{Con}}}\ \mathbb {I}_n$. Consider the relational structure ${\mathbb S}{:}{=}(\{0,1\}^n;\Phi _0,\dots ,\Phi _{n-1})$ where each $\Phi _i$ is defined as follows:

$$\begin{aligned} \Phi _i \,\, {:}{=}\left\{ (x_0,\dots ,x_{n-1})\mid (x_i = 1) \wedge \bigwedge _{j \in E_n{\setminus }\{i\}} (x_j = 0)\right\} . \end{aligned}$$

Let us denote by $\varvec{e}_i\in \{0,1\}^n$ the tuple that has a 1 in the i-th coordinate and 0 s elsewhere. The maps

$$\begin{aligned} g:i\mapsto \varvec{e}_i{} & {} h:\varvec{x}\mapsto {\left\{ \begin{array}{ll} i &{} \text{ if } \varvec{x} = \varvec{e}_i, \\ 0 &{} \text{ otherwise }. \end{array}\right. } \end{aligned}$$

are respectively homomorphisms from $\mathbb {I}_n$ to ${\mathbb S}$ and from ${\mathbb S}$ to $\mathbb {I}_n$. This proves that $\mathbb {I}_2\ {\le _{\textrm{Con}}}\ \mathbb {I}_n$. The other inclusion follows from Proposition 2.11 and the fact that ${\mathbb C}_1$ does not pp-construct $\mathbb {I}_n$, which is observed in the paragraph preceding Proposition 2.12. $\square$

Let us denote ${{\,\textrm{Pol}\,}}(\mathbb {I}_n)$ by $\mathcal {I}_n$, for every $n\ge 2$. It follows from Proposition 2.12 and Theorem 2.9 that $\mathcal {I}_2\ {\equiv _{\textrm{m}}}\ \mathcal {I}_3$. Thus, $\overline{\mathcal {I}_2}$ is the unique coatom in $\mathfrak P_{3}$. In Section 3 we classify all elements covered by $\overline{\mathcal {I}_2}$ in $\mathfrak P_{3}$.

2.4 Auxiliary theorems

Here, we present two results that are going to serve as auxiliary statements in Section 3. We would like to point out that both of the statements we present in this section are known in the literature. However, in its original form, Theorem 2.13 is not formulated in terms of pp-constructability. Similarly, although it is not found with this formulation anywhere in the literature, Theorem 2.14 can be obtained with a little work from Lemma 6.8 in [5]. We therefore prefer to include two relatively simple and self-contained proofs with the aim of helping the reader. We define the structure: ${\mathbb B}_2{:}{=}(\{0,1\};\{0\},\{1\},\{(0,1),(1,0),(1,1)\})$.

Theorem 2.13

[22, Proposition 7.7]. Let ${\mathbb A}$ be a finite structure. Then ${\mathbb A}$ pp-constructs ${\mathbb B}_2$ if and only if ${{\,\textrm{Pol}\,}}({\mathbb A})$ does not satisfy $\Sigma _{{\text {M}}}$.

Proof

Note that by Corollary 2.10 it is sufficient to prove the claim for a core expanded by all unary relations; we therefore assume ${\mathbb A}$ to be such a structure. Suppose that ${\mathbb A}$ pp-constructs ${\mathbb B}_2$ and that ${{\,\textrm{Pol}\,}}({\mathbb A})$ satisfies $\Sigma _{{\text {M}}}$. By Theorem 2.9 it follows that ${{\,\textrm{Pol}\,}}({\mathbb B}_2)\models \Sigma _{{\text {M}}}$. Hence, there exists a ternary operation $m\in {{\,\textrm{Pol}\,}}({\mathbb B}_2)$ such that $m(0,1,1)=m(1,1,0)=m(0,0,0)=0$ (note that m must preserve $\{0\}$). Since m is a polymorphism of ${\mathbb B}_2$, we obtain that (0, 0) is a tuple in a relation of ${\mathbb B}_2$, a contradiction. For the other direction, assume that ${{\,\textrm{Pol}\,}}({\mathbb A})$ does not satisfy $\Sigma _{{\text {M}}}$. Our goal is to build a pp-power ${\mathbb C}$ of ${\mathbb A}$ that is homomorphically equivalent to ${\mathbb B}_2$. The domain of ${\mathbb C}$ is $A^{|A|^{2}}$ and the elements of ${\mathbb C}$ can be interpreted as operations $A^{2}\rightarrow A$. The structure ${\mathbb C}$ has a binary relation $R^{{\mathbb C}}$ and two unary relations $\{{{\,\textrm{pr}\,}}^2_2\}$ and $\{{{\,\textrm{pr}\,}}^2_1\}$; the relation $R^{{\mathbb C}}$ is defined as the set of all pairs (f, g) such that there exists a ternary operation $w\in {{\,\textrm{Pol}\,}}({\mathbb A})$ such that $w(x,x,y) = f(x,y)$ and $w(y,x,x) = g(x,y)$.

Let us show that any s-ary operation $u\in {{\,\textrm{Pol}\,}}({\mathbb A})$ preserves $R^{{\mathbb C}}$. Consider some tuples $(f_1,g_1),\dots ,(f_s,g_s)$ from $R^{{\mathbb C}}$. By definition, for every i, there exists $w_i\in {{\,\textrm{Pol}\,}}({\mathbb A})$ such that $w_i(x,x,y) = f_i(x,y)$ and $w_i(y,x,x) = g_i(x,y)$. The operation u applied to the considered tuples gives us the tuple (f, g) where

$$\begin{aligned} f(x,y)&= u(f_1(x,y),\dots ,f_s(x,y)), \text {and} \\g(x,y)&= u(g_1(x,y),\dots ,g_s(x,y)). \end{aligned}$$

Since $f(x,y) = w(x,x,y)$ and $g(x,y) = w(y,x,x)$ for

$$\begin{aligned} w(x,y,z) \,\, {:}{=}\,\, u(w_1(x,y,z),\dots ,w_s(x,y,z)), \end{aligned}$$

we obtain that (f, g) is in $R^{{\mathbb C}}$. By Theorem 2.3, $R^{{\mathbb C}}$ is pp-definable over ${\mathbb A}$. Since every $u\in {{\,\textrm{Pol}\,}}({\mathbb A})$ is idempotent, u preserves two unary relations $\{{{\,\textrm{pr}\,}}^2_2\}$ and $\{{{\,\textrm{pr}\,}}^2_1\}$; thus both $\{{{\,\textrm{pr}\,}}^2_2\}$ and $\{{{\,\textrm{pr}\,}}^2_1\}$ are pp-definable over ${\mathbb A}$.

It remains to define homomorphisms from ${\mathbb B}_2$ to ${\mathbb C}$ and back. The homomorphism $h:{\mathbb B}_2\rightarrow {\mathbb C}$ maps 0 to ${{\,\textrm{pr}\,}}^2_2$ and maps 1 to the first projection ${{\,\textrm{pr}\,}}^2_1$. Since all projections are in ${{\,\textrm{Pol}\,}}({\mathbb A})$ we have the tuples $({{\,\textrm{pr}\,}}^2_1,{{\,\textrm{pr}\,}}^2_2)$, $({{\,\textrm{pr}\,}}^2_1,{{\,\textrm{pr}\,}}^2_1)$, and $({{\,\textrm{pr}\,}}^2_2,{{\,\textrm{pr}\,}}^2_1)$ in $R^{{\mathbb C}}$. Hence h is a homomorphism. The homomorphism $h':{\mathbb C}\rightarrow {\mathbb B}_2$ maps ${{\,\textrm{pr}\,}}^2_2$ to 0 and all the remaining values to 1. Note that the tuple $({{\,\textrm{pr}\,}}^2_2,{{\,\textrm{pr}\,}}^2_2)$ is not in $R^{{\mathbb C}}$, otherwise there would exist an operation $w\in {{\,\textrm{Pol}\,}}({\mathbb A})$ such that ${{\,\textrm{pr}\,}}^2_2(x,y) = w(x,x,y) = w(y,x,x)={{\,\textrm{pr}\,}}^2_2(y,y)=w(y,y,y)$; this cannot hold since we assumed that ${{\,\textrm{Pol}\,}}({\mathbb A})$ does not satisfy $\Sigma _{{\text {M}}}$. This proves that $h'$ is a homomorphism. Thus, ${\mathbb A}\ {\le _{\textrm{Con}}}\ {\mathbb B}_2$ as desired.$\square$

Recall the relational structure ${\mathbb C}_p$ introduced in Remark 2.8.

Theorem 2.14

[5, 27]. Let ${\mathbb A}$ be a finite structure. Then, for every prime p, ${\mathbb A}$ pp-constructs ${\mathbb C}_p$ if and only if ${{\,\textrm{Pol}\,}}({\mathbb A})$ does not satisfy $\Sigma _p$.

Proof

Suppose that ${\mathbb A}$ pp-constructs ${\mathbb C}_p$, for some prime p, and that ${{\,\textrm{Pol}\,}}({\mathbb A})$ satisfies $\Sigma _p$; by Theorem 2.9 we obtain that ${{\,\textrm{Pol}\,}}({\mathbb C}_p)$ satisfies $\Sigma _p$, too. This would lead to a contradiction, as shown in Remark 2.8. For the other direction, assume that ${{\,\textrm{Pol}\,}}({\mathbb A})$ does not satisfy the cyclic identity $\Sigma _p$. Let us build a pp-power ${\mathbb B}$ of ${\mathbb A}$ which is homomorphically equivalent to ${\mathbb C}_p$. The domain of ${\mathbb B}$ is $A^{|A|^{p}}$ and every element of the domain can be viewed as an operation $A^{p}\rightarrow A$. The structure ${\mathbb B}$ has only one binary relation $R^{{\mathbb B}}$ which is defined as follows: it consists of all pairs (f, g) such that $f,g\in {{\,\textrm{Pol}\,}}({\mathbb A})$ and $g(x_1,\dots ,x_p) = f(x_2,\dots ,x_{p},x_1)$ (here we interpret operations as tuples).

Let us partition all the operations of ${{\,\textrm{Pol}\,}}({\mathbb A})$ of arity p into equivalence classes such that two operations are equivalent if one can be obtained from another by a cyclic shift of the variables. Choose one representative from each class and denote the obtained set of operations by $F_{0}$. Let us define

$$F_{i}=\{g\mid \exists f\in F_0:g(x_1,\dots ,x_p) = f(x_i,\dots ,x_p,x_1,\dots ,x_{i-1})\}.$$

Thus, operations from $F_{i}$ are obtained from operations from $F_{0}$ by the corresponding cyclic shift of the variables. If $F_{i}\cap F_{j}\ne \varnothing$ for some $i\ne j$, then there is an operation that stays the same after some cyclic shift of the variables. Since p is prime, we derive that this operation is cyclic, which contradicts our assumption.

Thus, we assume that $F_{i}\cap F_{j}=\varnothing$ whenever $i\ne j$. Let us show that any operation $w\in {{\,\textrm{Pol}\,}}({\mathbb A})$ preserves $R^{{\mathbb B}}$. Consider tuples $(f_1,g_1),\dots ,(f_s,g_s)$ from $R^{{\mathbb B}}$. Then w applied to these tuples gives us the pair (f, g), where

$$\begin{aligned} f(x_1,\dots ,x_p)&= w(f_1(x_1,\dots ,x_p),\dots ,f_s(x_1,\dots ,x_p)), \text {and} \\g(x_1,\dots ,x_p)&= w(g_1(x_1,\dots ,x_p),\dots ,g_s(x_1,\dots ,x_p)). \end{aligned}$$

Hence, f and g are from ${{\,\textrm{Pol}\,}}({\mathbb A})$. Moreover, it holds that $g(x_1,\dots ,x_p) = f(x_2,\dots ,x_p,x_1)$. Thus, we showed that w preserves $R^{{\mathbb B}}$. By Theorem 2.3, $R^{{\mathbb B}}$ is pp-definable over ${\mathbb A}$. Thus, we proved that ${\mathbb B}$ is a pp-power of ${\mathbb A}$.

It remains to show that ${\mathbb B}$ and ${\mathbb C}_p$ are homomorphically equivalent. The homomorphism $h:{\mathbb B}\rightarrow {\mathbb C}_p$ just sends operations from $F_{i}$ to i, for every i. To define the homomorphism $h':{\mathbb C}_p\rightarrow {\mathbb B}$ we just choose some operation $f_0\in F_{0}$, then consider all its cyclic shifts $f_{i}\in F_{i}$. Then $h'$ sends each i to $f_{i}$. Thus, ${\mathbb A}$ pp-constructs ${\mathbb C}_p$. $\square$

We would like to mention that the proofs in this section can be considered rather standard, since in the literature the auxiliary structures that we define in Theorems 2.13 and 2.14 – denoted by ${\mathbb C}$ and ${\mathbb B}$, respectively – are known as the free structure of ${{\,\textrm{Pol}\,}}({\mathbb A})$ generated by ${\mathbb B}_2$ and the free structure of ${{\,\textrm{Pol}\,}}({\mathbb A})$ generated by ${\mathbb C}_p$, respectively. To keep the proofs simple and self-contained we refrain from defining free structures and refer the interested reader to [2].

3 Submaximal elements of $\mathfrak P_3$

In this section we prove that $\overline{\mathcal {C}_2}$, $\overline{\mathcal {C}_3}$, and $\overline{\mathcal {B}_2}$ are the only submaximal elements of $\mathfrak {P}_3$. In particular, we show that if $\mathcal {S}$ is an idempotent clone over $\{0,1,2\}$ such that

then there exists a minor homomorphism from $\mathcal {I}_2$ to $\mathcal {S}$, i.e., $\mathcal {I}_2\ {\preceq _{\textrm{m}}}\ \mathcal {S}$. In order to prove this, we show that every idempotent clone over $E_3$ satisfying ($\spadesuit$) has a generalized minority of arity k, for every odd $k\ge 3$ – we are going to define such operations in Section 3.1 – and a totally symmetric operation of arity n, for every $n\ge 2$. Recall that we say that an n-ary operation f is totally symmetric if it satisfies the condition ${\text {TS}}(n)$ from Definition 2.7. Also, note that we can reduce to the case where we only consider idempotent clones: in fact, every clone $\mathcal {S}={{\,\textrm{Pol}\,}}({\mathbb S})$ is minor-equivalent to some idempotent clone, that is, $\mathcal {S}\ {\equiv _{\textrm{m}}}\ {{\,\textrm{Pol}\,}}({\mathbb S}')$ where ${\mathbb S}'$ is the core of ${\mathbb S}$ expanded by all unary relations (see Corollary 2.10). As a first step, we want to prove that every idempotent clone $\mathcal {S}$ over $E_3$ satisfying ($\spadesuit$) has a majority operation. For this purpose, we introduce some more notions and terminology concerning relations. In particular, we are going to consider essential and critical relations.

Definition 3.1

Let R be an n-ary relation on a finite set A. We say that

• R is an essential relation if it cannot be represented by a quantifier-free conjunctive formula over relations of smaller arities. Moreover, a tuple $(a_1,\dots ,a_n)\in A^n{\setminus } R$ is essential for R if for every $i\in \{1,\dots ,n\}$ there exists b such that

  $$(a_1,\dots ,a_{i-1},b,a_{i+1},\dots ,a_n)\in R.$$

  We denote by ${\text {Ess}}(R)$ the set of all essential tuples for R. It is not hard to see that a relation has an essential tuple if and only if it is essential [24, 25].

• R is critical if it is essential and there do not exist relations $R_1,\dots ,R_m$ pp-definable from R and different from R such that $R = R_1\cap \dots \cap R_m$.

Notice that originally in [19] a critical relation was defined to be a directly indecomposable and completely $\cap$-irreducible relation in a relational clone; our definition of critical relation relates to the original one as follows: a relation is critical if and only if it is critical – in the sense of [19] – in the relational clone generated by the relation. As it was shown in [26], every critical relation has internal symmetries, and relations having these symmetries are called key relations. Thus, every critical relation is a key relation (see [26], Lemma 2.4). In this section we will use a classification of key relations preserved by a weak unanimity operation from [26] but to avoid additional notations we formulate it for critical relations.

To formulate the classification we will need the notion of block of a relation R over a finite domain A. We denote by $\tilde{R}$ the relation $R\cup {\text {Ess}}(R)$. Again following [26], we define a graph $\mathbb {G}_{\tilde{R}}{:}{=}(\tilde{R};E)$ as follows: if $\varvec{a}$, $\varvec{b}\in \tilde{R}\subseteq A^n$, then we have $(\varvec{a},\varvec{b})\in E$ if and only if $\varvec{a}$ and $\varvec{b}$ differ just in one element, i.e., there exists a unique $i\in \{1,\dots ,n\}$ such that $a_i\ne b_i$. A block of R is a connected component of $\mathbb {G}_{\tilde{R}}$. A block is called trivial if it only contains tuples from R.

Theorem 3.2

(c.f. [26, Theorem 3.11]). Let R be a critical relation of arity $n\ge 3$, preserved by a Mal’cev operation. Then

• Every block of R equals $B_1 \times \cdots \times B_n$, for some $B_1,\dots ,B_n\subseteq A$.

• For every nontrivial block ${\textbf {B}}{:}{=}B_1 \times \cdots \times B_n$ of R, the intersection $R\cap {\textbf {B}}$ can be defined as follows: there exists an abelian group $(G;+,-,0)$ whose order is a power of a prime, and surjective mappings $\phi _i:B_i\rightarrow G$, for $i=1,2,\dots ,n$ such that

  $$\begin{aligned} R\cap {\textbf {B}} = \{(x_1,\dots ,x_n)\mid \phi _1(x_1) + \phi _2(x_2) +\ldots +\phi _n(x_n) = 0\}. \end{aligned}$$

Theorem 3.3

[1]. Let $\mathcal {C}$ be an idempotent clone over a finite set. Then, for every $k\ge 2$, the following are equivalent:

• $\mathcal {C}$ has a near-unanimity operation of arity $k+1$;

• every $(k+1)$-ary relation in ${{\,\textrm{Inv}\,}}(\mathcal {C})$ can be obtained as a conjunction of relations of arity k in ${{\,\textrm{Inv}\,}}(\mathcal {C})$.

We want to remark that, if an idempotent clone $\mathcal {C}$ does not have a near-unanimity operation of arity k, then ${{\,\textrm{Inv}\,}}(\mathcal {C})$ has an essential relation R of arity k. Furthermore, this essential relation can be represented as a conjunction of critical relations and the arity of at least one of them should also be k. Thus, every clone $\mathcal {C}$ not having a near-unanimity operation of arity k preserves a critical relation of arity k.

Lemma 3.4

Let $\mathcal {C}$ be an idempotent clone over $E_n$, for some $n\ge 2$, such that

• (1) $\mathcal {C}\models \Sigma _p$, for every prime $p\le n$, and

• (2) $\mathcal {C}\models \Sigma _{\textrm{M}}$, i.e., $\mathcal {C}$ has a Mal’cev operation.

Then $\mathcal {C}$ has a majority operation.

Proof

Let $\mathcal {C}$ be a clone satisfying all the hypotheses and suppose that $\mathcal {C}$ does not have a ternary near-unanimity operation, i.e., a majority operation. Then by Theorem 3.3 we have that ${{\,\textrm{Inv}\,}}(\mathcal {C})$ has a critical relation R of arity $k\ge 3$. Therefore, by Theorem 3.2, for every nontrivial block ${\textbf {B}}$ of R, there exists an abelian group $\textbf{G}=(G,+,-,0)$ whose order $\ell \le n$ is the power of some prime and surjective mappings $\phi _i:B_i\rightarrow G$, for $i=1,2,\dots ,k$ such that $R\cap {\textbf {B}} = \{(x_1,\dots ,x_k)\mid \phi _1(x_1) + \phi _2(x_2) +\ldots +\phi _k(x_k) = 0\}$.

Let us show that the relation R cannot be preserved by a cyclic operation $c_{p}$ of arity p, where p divides $\ell$. Choose a mapping $\psi _{i}:G\rightarrow B_{i}$, for every i, such that $\phi _{i}(\psi _{i}(x)) = x$, for every $x\in G$. Let a be an element in G of order p. Notice, that

$$\begin{aligned} B_{1}(x_1) = \exists x_2 \dots \exists x_k\; \bigwedge _{i=2}^{k} R(x_1,\psi _{2}(0),\dots ,\psi _{i-1}(0),x_i,\psi _{i+1}(0),\dots ,\psi _{k}(0)), \end{aligned}$$

which means that $B_{1}$ is pp-definable from R and constants. Combining this with the idempotency of $\mathcal {C}$ we derive that the cyclic operation $c_p$ preserves $B_{1}$. Similarly, we show that $c_{p}$ preserves $B_{i}$, for every i. Applying $c_{p}$ to the rows of the matrices

$$\begin{pmatrix} \psi _{1}(0) &{} \quad \psi _1(a)&{}\quad \psi _{1}(2a)&{}\quad \dots &{}\quad \psi _{1}((p-1)a)\\ \psi _{2}(0) &{}\quad \psi _2(-a)&{}\quad \psi _{2}(-2a)&{}\quad \dots &{}\quad \psi _{2}(-(p-1)a)\\ \psi _{3}(0) &{}\quad \psi _3(0)&{}\quad \psi _{3}(0)&{}\quad \dots &{}\quad \psi _{3}(0)\\ \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ \psi _{k}(0) &{}\quad \psi _k(0)&{}\quad \psi _{k}(0)&{}\quad \dots &{}\quad \psi _{k}(0) \end{pmatrix}$$

$$\begin{pmatrix} \psi _{1}(0) &{}\quad \psi _1(a)&{}\quad \dots &{}\quad \psi _{1}((p-2)a)&{}\quad \psi _{1}((p-1)a)\\ \psi _{2}(-a) &{}\quad \psi _2(-2a)&{}\quad \dots &{}\quad \psi _{2}(-(p-1)a)&{}\quad \psi _{2}(0)\\ \psi _{3}(a) &{}\quad \psi _3(a)&{}\quad \dots &{}\quad \psi _{3}(a)&{}\quad \psi _{3}(a)\\ \psi _{4}(0) &{}\quad \psi _4(0)&{}\quad \dots &{}\quad \psi _{4}(0)&{}\quad \psi _{4}(0)\\ \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots \\ \psi _{k}(0) &{}\quad \psi _k(0)&{}\quad \dots &{}\quad \psi _{k}(0)&{}\quad \psi _{k}(0) \end{pmatrix}$$

we get respectively the tuples

$$\begin{aligned}&(c,d,\psi _{3}(0),\psi _{4}(0),\dots ,\psi _{k}(0)), \text { and } \\ {}&(c,d,\psi _{3}(a),\psi _{4}(0),\dots ,\psi _{k}(0)) \end{aligned}$$

from $R\cap {\textbf {B}}$, which contradicts the definition of $R\cap {\textbf {B}}$. This contradiction proves that such a relation R cannot exist in ${{\,\textrm{Inv}\,}}(\mathcal {C})$, thus $\mathcal {C}$ has a majority operation. $\square$

Remark 3.5

The result presented in Lemma 3.4 can be alternatively proved using an argument coming from Tame Congruence Theory (see [16]). One can show that, assuming the same hypotheses as in Lemma 3.4, a sufficient condition for the existence of a majority operation provided in [15] holds.

Corollary 3.6

Let $\mathcal {S}$ be an idempotent clone over $E_3$ such that $\mathcal {S}\ {\npreceq _{\textrm{m}}}\ \mathcal {C}_2$, $\mathcal {S}\ {\npreceq _{\textrm{m}}}\ \mathcal {C}_3$, and $\mathcal {S}\ {\npreceq _{\textrm{m}}}\ \mathcal {B}_2$. Then $\mathcal {S}$ has a symmetric majority operation.

Proof

From Theorem 2.13 it follows that $\mathcal {S}$ has a Mal’cev operation, and from Theorem 2.14 it follows that there exist $c_2,c_3\in \mathcal {C}$ such that $c_2\models \Sigma _2$ and $c_3\models \Sigma _3$. Thus, it follows from Lemma 3.4 that $\mathcal {S}$ has a majority operation $M'$. We define the operation M as follows:

It is easy to check that M is a symmetric majority operation. $\square$

Lemma 3.7

Let $\mathcal {S}$ be an idempotent clone over $E_3$ such that $\mathcal {S}\ {\npreceq _{\textrm{m}}}\ \mathcal {C}_2$, $\mathcal {S}\ {\npreceq _{\textrm{m}}}\ \mathcal {C}_3$, and $\mathcal {S}\ {\npreceq _{\textrm{m}}}\ \mathcal {B}_2$. Then $\mathcal {S}$ has a symmetric minority operation.

Proof

Let $\mathcal {S}$ be as in the hypothesis. It follows from Theorem 2.13 that $\mathcal {S}$ has a Mal’cev operation d. Also, from Corollary 3.6 we know that $\mathcal {S}$ has a majority operation M. We define $m'_3$ as follows:

$$\begin{aligned} m'_3(x,y,z){:}{=}\,\, M(d(x,y,z),d(y,z,x),d(z,x,y)). \end{aligned}$$

It is easy to check that $m'_3$ is indeed a minority operation: note that, since d is a Mal’cev operation, whenever we identify two variables in $m'_3$ at least two of the values among d(x, y, z), d(y, z, x), and d(z, x, y) are equal to the variable that occurs only once. Hence, applying M we obtain this variable, again. Furthermore, it follows from Theorem 2.14 that $\mathcal {S}$ has a binary cyclic operation $c_2$ and a ternary cyclic operation $c_3$. We then define a symmetric minority $m_3$ in the same way we obtained a symmetric majority in Corollary 3.6: we simply replace every occurrence of M in ($\heartsuit$) by $m_3$. $\square$

Remark 3.8

Note that the value of a symmetric minority $m_3(x,y,z)$ has to be a constant $c\in \{0,1,2\}$ whenever the three values in the scope of $m_3$ are all distinct, i.e.,

$$\begin{aligned} m_3(0,1,2)&=m_3(0,2,1)=m_3(1,0,2)=\\ {}&=m_3(1,2,0)=m_3(2,0,1)=\\ {}&=m_3(2,1,0)= c. \end{aligned}$$

In this case we also denote the symmetric minority operation by $m_3^c$. We follow the same convention for symmetric majority operations.

3.1 Generalized minority operations

Recall that a generalized minority of arity n is an n-ary operation satisfying the minor condition ${\text {GM}}(n)$ from Definition 2.7. If a generalized minority $m_{n}$ is idempotent and only $a_{i}$ occurs an odd number of times in the tuple $(a_1,\dots ,a_n)$, then $m_{n}(a_1,\dots ,a_n)=a_i$. Moreover, if $m_n$ is a generalized minority on $E_3$, then $m_n(a_1,\dots ,a_n)$ returns a constant $c\in E_3$ on all the other tuples, that is on the tuples containing an odd number of each element from $E_{3}$.

Note that the minority operation $m_3(x,y,z)= x \oplus y \oplus z$ on the set $E_2=\{0,1\}$ is indeed a generalized minority of arity 3. Also note that if a clone $\mathcal {C}$ over $\{0,1\}$ contains the minority operation $m_3(x,y,z)$ then, for every $n\ge 2$, the generalized minority

$$\begin{aligned} m_{2n+1}(x_1,\dots ,x_{2n+1})&\,\, {:}{=}\, \, m_3(m_{2n-1}(x_1,\dots ,x_{2n-1}),x_{2n},x_{2n+1}) \\ {}&= x_1 \oplus x_2 \oplus \ldots \oplus x_{2n+1} \end{aligned}$$

is also in $\mathcal {C}$. We prove an analogous result for the three-element case: we show that every clone $\mathcal {S}$ over $E_3$ satisfying condition ($\spadesuit$) has a generalized minority of every odd arity. Recall that Theorem 3.7 implies that $\mathcal {S}$ has a symmetric minority operation $m_3^c$ where $c\in \{0,1,2\}$ is some constant value that $m_3^c(x,y,z)$ returns whenever $|\{x,y,z\}|=3$, see Remark 3.8. We denote by $+_3$ the addition of the group of integers modulo 3 and define the following auxiliary operation

Note that $D^c(x,y,z) = m_3^c(m_3^c(x,y,z),y,z)$, hence $D^c(x,y,z)\in \mathcal {S}$.

Theorem 3.9

Let $\mathcal {S}$ be an idempotent clone over $E_3$ such that $\mathcal {S}\ {\npreceq _{\textrm{m}}}\ \mathcal {C}_2$, $\mathcal {S}\ {\npreceq _{\textrm{m}}}\ \mathcal {C}_3$, and $\mathcal {S}\ {\npreceq _{\textrm{m}}}\ \mathcal {B}_2$. Then $\mathcal {S}$ has generalized minorities of arity k for every odd $k\ge 3$.

Proof

From Lemma 3.7 we know that $\mathcal {S}$ has a symmetric minority operation $m_3^c$; let $D^c$ the operation defined as in ($\diamondsuit$). For every $n\ge 2$, we define the operation

$$\begin{aligned} m_{2n+1}^c(x_1,\dots ,x_{2n+1}) \,\,{:}{=}\, \,m_3^c(&t_{2n+1}(x_1,x_2,x_3,x_4,\dots ,x_{2n+1}), \\ {}&t_{2n+1}(x_2,x_1,x_3,x_4,\dots ,x_{2n+1}), \\ {}&t_{2n+1}(x_3,x_1,x_2,x_4,\dots ,x_{2n+1})) \end{aligned}$$

where

$$\begin{aligned} t_{2n+1}(x_1,\dots ,x_{2n+1}) \,\,{:}{=}\, \, m_3^c(&D^c(m_{2n-1}^c(x_1,x_4,x_5,\dots ,x_{2n+1}),x_1,x_1), \\ {}&D^c(m_{2n-1}^c(x_1,x_4,x_5,\dots ,x_{2n+1}),x_1,x_2), \\ {}&D^c(m_{2n-1}^c(x_1,x_4,x_5,\dots ,x_{2n+1}),x_1,x_3)). \end{aligned}$$

Note that the first argument of $m_3^c$ in the latter formula is always equal to $m_{2n-1}^c(x_1,x_4,x_5,\dots ,x_{2n+1})$ however, for the sake of symmetry, we instead prefer to write $D^c(m_{2n-1}^c(x_1,x_4,x_5,\dots ,x_{2n+1}),x_1,x_1)$ in the definition.

We are going to prove the claim of the theorem by induction over n. Let us first make a few remarks on the symmetries of $m^c_{2n+1}$ in order to make the formula more digestible for the reader. As an inductive hypothesis we assume that $m^{c}_{2n-1}$ is a generalized minority. It follows from the symmetry of $m^{c}_{2n-1}$ that $t_{2n+1}$ is invariant under any permutation of the variables $x_4,\dots ,x_{2n+1}$. Hence $m_{2n+1}^{c}$ is also invariant under any permutation of the variables $x_4,\dots ,x_{2n+1}$. Since $m_3^c$ is symmetric, $t_{2n+1}$ is invariant under permutation of $x_2$ and $x_3$ and therefore $m_{2n+1}^{c}$ is invariant under any permutation of the variables $x_1$, $x_2$, and $x_3$. Notice that $m_1^c(x):=x$. Moreover, since $m_{2n-1}^c$ is a generalized minority, it holds

$$m_{2n-1}^c(x_1,x_2,\dots ,x_{2n-3},x,x) = m_{2n-3}^c(x_1,x_2,\dots ,x_{2n-3}),$$

thus, we obtain that

$$t_{2n+1}(x_1,x_2,\dots ,x_{2n-1},x,x) = t_{2n-1}(x_1,x_2,\dots ,x_{2n-1}),$$

and therefore $m_{2n+1}^c(x_1,x_2,\dots ,x_{2n-1},x,x) = m_{2n-1}^c(x_1,x_2,\dots ,x_{2n-1})$.

Combining this with the symmetry of $m_{2n+1}^c$ over permutation of the last $2n-2$ coordinates, we obtain that $m_{2n+1}^{c}$ behaves as a generalized minority for all the tuples having repetitive elements in $x_{4},\dots ,x_{2n+1}$. Thus, if $n\ge 3$ then $2n+1-3>3$ and $m_{2n+1}^{c}$ is a generalized minority.

Let us check how the identification of variables transforms $m_{5}^{c}$.

This proves that $m_{5}^{c}$ behaves well on all the tuples having repetitive elements in the first 3 coordinates. It only remains to consider the case when there are no repeated elements in the first three components and no repeated elements in the last two components of $m^c_5$. By making use of the known symmetries, it suffices to verify that $m^c_5(x_1, x_2, x_3, x_1, x_2 ) = x_3$.

$$\begin{aligned} t_{5}(x_1,x_2,x_3,x_1,x_2)= m_3^c\big (&D^c(m_{3}^c(x_1,x_1,x_2),x_1,x_1), \\ {}&D^c(m_{3}^c(x_1,x_1,x_2),x_1,x_2), \\ {}&D^c(m_{3}^c(x_1,x_1,x_2),x_1,x_3)\big ) \\ = m_3^c(&x_2,x_2,D^c(x_2,x_1,x_3))=D^c(x_2,x_1,x_3);\\ t_{5}(x_1,x_2,x_3,x_2,x_3)= m_3^c(&D^c(m_{3}^c(x_1,x_2,x_3),x_1,x_1), \\ {}&D^c(m_{3}^c(x_1,x_2,x_3),x_1,x_2), \\ {}&D^c(m_{3}^c(x_1,x_2,x_3),x_1,x_3))=m_3^c(x_1,x_2,x_3). \end{aligned}$$

We check the last equality as follows. If $|\{x,y,z\}|<3$, then $D^{c}(x,y,z) = x$. Hence if $|\{x_1,x_2,x_3\}|<3$, then $D^c(m_{3}^c(x_1,x_2,x_3),x_1,x_3) = m_{3}^c(x_1,x_2,x_3)$. Otherwise, if $|\{x_1,x_2,x_3\}|=3$, then $m_{3}^c(x_1,x_2,x_3)=c$ and, since $D^{c}$ returns c whenever the first coordinate is c, we get the equality.

Finally, we obtain the following equation

The equation ($\star _2$) above can be checked manually. If $\{x_1,x_2,x_3\}\ne \{0,1,2\}$, then it again follows from the fact that $m_{3}^{c}$ is the minority and $D^{c}$ is the first projection on every 2-element subset.

If $\{x_1,x_2,x_3\}=\{0,1,2\}$ and $x_{3} = c$, then

$$m_3^c(D^{c}(x_2,x_1,x_3),D^{c}(x_1,x_2,x_3),m_{3}^{c}(x_1,x_2,x_3))= m_3^c(x_1,x_2,c)=c.$$

If $\{x_1,x_2,x_3\}=\{0,1,2\}$ and $x_{1} = c$, then

$$m_3^c(D^{c}(x_2,x_1,x_3),D^{c}(x_1,x_2,x_3),m_{3}^{c}(x_1,x_2,x_3))= m_3^c(x_3,c,c)=x_3.$$

Similarly, if $\{x_1,x_2,x_3\}=\{0,1,2\}$ and $x_{2} = c$, then

$$m_3^c(D^{c}(x_2,x_1,x_3),D^{c}(x_1,x_2,x_3),m_{3}^{c}(x_1,x_2,x_3))= m_3^c(c,x_3,c)=x_3.$$

The equations ($\star _1$) and ($\star _2$) imply that $m_{5}^{c}$ is a generalized minority. $\square$

3.2 Totally symmetric operations of every arity

Here we prove that every idempotent clone $\mathcal {S}$ over $E_3$ satisfying the condition ($\spadesuit$) has totally symmetric operations of every arity $n\ge 2$ (see Definition 2.7).

Theorem 3.10

Let $\mathcal {S}$ be an idempotent clone over $E_3$ such that $\mathcal {S}\ {\npreceq _{\textrm{m}}}\ \mathcal {C}_2$, $\mathcal {S}\ {\npreceq _{\textrm{m}}}\ \mathcal {C}_3$, and $\mathcal {S}\ {\npreceq _{\textrm{m}}}\ \mathcal {B}_2$. Then $\mathcal {S}$ has a totally symmetric operation $s_n$ of arity n, for every $n\ge 2$.

Proof

From Corollary 3.6 and Lemma 3.7 it follows that $\mathcal {S}$ has a symmetric majority operation $M^c$ and a symmetric minority operation m, respectively. Also, from Theorem 2.14 it follows that there exists a binary cyclic operation $s_2\in \mathcal {S}$, thus $\mathcal {S}\models {\text {TS}}(2)$. For every $n\ge 3$ we define:

$$\begin{aligned} s_n(x_1,\dots ,x_n) \,\, {:}{=}\,\, m(&s_{n-1}(x_1,M^c(x_1,x_2,x_3),x_4,\dots ,x_n), \\ {}&s_{n-1}(x_2,M^c(x_1,x_2,x_3),x_4,\dots ,x_n), \\ {}&s_{n-1}(x_3,M^c(x_1,x_2,x_3),x_4,\dots ,x_n)). \end{aligned}$$

We will prove by induction on $n\ge 2$ that

• (i) if $\{x_1,\dots ,x_n\}=\{a,b\}\subset \{0,1,2\}$, then $s_n(x_1,\dots ,x_n)=s_2(a,b)$;

• (ii) if $\{x_1,\dots ,x_n\}=\{0,1,2\}$, then

  $$s_n(x_1,\dots ,x_n)= m(s_2(0,c),s_2(1,c),s_2(2,c)).$$

For $n=2$ this is obvious. Notice that, for every $n\ge 3$,

$$\begin{aligned} s_n(x,x,x_3,x_4,\dots ,x_n) \,\, {:}{=}\,\, m(&s_{n-1}(x,M^c(x,x,x_3),x_4,\dots ,x_n), \\ {}&s_{n-1}(x,M^c(x,x,x_3),x_4,\dots ,x_n), \\ {}&s_{n-1}(x_3,M^c(x,x,x_3),x_4,\dots ,x_n))\\&\;\;\;=s_{n-1}(x_3,x,x_4,\dots ,x_n) \end{aligned}$$

Hence, by the inductive assumption we have the required properties (i) and (ii) on all tuples whose first two elements are equal. Since the operations $M^{c}$ and m are symmetric, $s_{n}$ is symmetric under any permutation of the first 3 variables. Therefore, the property (i) always holds and the property (ii) holds on all tuples such that the first three elements are not different.

Let us prove the property (ii) on all tuples $(x_1,x_2,\dots ,x_n)$ such that $\{x_1,x_2,x_3\} = \{0,1,2\}$. For $s_3$ it immediately follows from the definition. To prove this for $n>3$ consider 3 cases.

Case 1. If $\{x_4,\dots ,x_n\}=\{a\}\subset \{0,1,2\}$ then

The equality ${\mathop {=}\limits ^{\star }}$ holds because m is symmetric. In case $a=c$, we obtain, by the induction hypothesis, that

$$\begin{aligned} s_n(x_1,\dots ,x_n)=m(s_2(0,c),s_2(1,c),s_2(2,c)). \end{aligned}$$

If $a\ne c$, then in ($\bullet _1$) we have an argument of the form $s_{n-1}(a,c,a,\dots ,a)$, one of the form $s_{n-1}(c,c,a,\dots ,a)$, and one where 0,1, and 2 occur. Therefore, by property (i) of the induction hypothesis we get $s_{n-1}(a,c,a,\dots ,a)=s_2(a,c)$ and $s_{n-1}(c,c,a,\dots ,a)=s_2(a,c)$. Moreover, by properties of m, we get

$$\begin{aligned} s_n(x_1,\dots ,x_n)=m(s_2(a,c),s_2(a,c),s_3(0,1,2))=s_3(0,1,2). \end{aligned}$$

Case 2. If $\{x_4,\dots ,x_n\}=\{a,b\}\subset \{0,1,2\}$ then, by using the fact that $s_{n-1}$ and m are symmetric, we get

If $c\notin \{a,b\}$ then each argument of m in the latter formula is equal to $s_3(0,1,2)$, by the induction hypothesis. Otherwise, if $c\in \{a,b\}$ then in ($\bullet _2$) we have an argument of the form $s_{n-1}(a,\dots ,a,b,\dots ,b)$, one of the form $s_{n-1}(b,a,\dots ,a,b\dots ,b)$, and one where 0, 1, and 2 occur. By the induction hypothesis, we get

$$\begin{aligned} s_n(x_1,\dots ,x_n)=m(s_2(a,b),s_2(a,b),s_3(0,1,2)). \end{aligned}$$

Case 3. If $\{x_4,\dots ,x_n\}=\{0,1,2\}$, then, by the symmetry of m and $s_{n-1}$, we have

It follows, by the the induction hypothesis, that each argument of m in ($\bullet _3$) is equal to $s_3(0,1,2)$; hence, we obtain $s_n(x_1,\dots ,x_n)=s_3(0,1,2)$. This concludes the proof. $\square$

3.3 The main result

In Section 2.3 we proved that $\overline{\mathcal {I}_2}$ is the unique coatom in $\mathfrak P_{3}$. Here we prove that, whenever a clone has totally symmetric operations and generalized minorities of an arbitrary large arity, there exists a minor homomorphism from $\mathcal I_2$ to this clone. Combining this with the results of the previous sections we derive the main result of our paper: $\overline{\mathcal {C}_2}$, $\overline{\mathcal {C}_3}$, and $\overline{\mathcal {B}_2}$ are the only submaximal elements in $\mathfrak P_{3}$.

It is well known that every operation over $\{0,1\}$ has a unique polynomial representation if we forbid repetitive monomials and disrespect the order of monomials. Applying this fact to idempotent operations from $\mathcal {I}_2$ we obtain the following lemma, in which operations $\oplus$ and $\wedge$ denote the usual sum and multiplication modulo 2, respectively.

Lemma 3.11

For every operation $f\in \mathcal {I}_2$ there exists an up to the order of monomials unique representation of the form $f(x_1,\dots ,x_n){:}{=}\bigoplus _{i=1}^\ell \bigwedge W_i$, where $\ell$ is odd and the sets $W_1,\dots ,W_l\subseteq \{x_1,\dots ,x_n\}$ are different and nonempty.

Proof

It is sufficient to check that every polynomial preserving $\{0\}$ does not have the constant 1 as a monomial, and that every polynomial preserving $\{1\}$ has an odd number of monomials. $\square$

Theorem 3.12

Let $\mathcal {S}$ be a clone over $E_k$, for some $k\ge 2$, such that

• $\mathcal {S}\models {\text {TS}}(n)$, for every $n\ge 2$, and

• $\mathcal {S}\models {{\,\textrm{GM}\,}}(n)$, for every odd $n\ge 3$.

Then there exists a minor homomorphism from $\mathcal {I}_2$ to $\mathcal {S}$.

Proof

Let f be any operation in $\mathcal {I}_2$. Notice that the identification of two variables of a totally symmetric operation of arity n gives a totally symmetric operation of a smaller arity. Similarly, the identification of three variables of a generalized minority gives a generalized minority of a smaller arity. Then by König’s lemma there exist an infinite sequence of totally symmetric operations $s_{2},s_{3},s_{4},\dots ,$ and an infinite sequence of generalized minorities $m_{3},m_5,m_7,\dots ,$ such that $s_{n}$ and $m_n$ are of arity n for every n, and they are compatible in the following sense. The identification of two variables of $s_{n}$ gives $s_{n-1}$ and the identification of three variables of $m_{2k+1}$ gives $m_{2k-1}$.

By Lemma 3.11 there exists an up to permutation of monomials unique representation $f(x_1,\dots ,x_k)=\bigoplus _{i=1}^\ell \bigwedge W_i$, where $\ell$ is odd and the sets $W_1,\dots ,W_l\subseteq \{x_1,\dots ,x_n\}$ are different. Notice that, for every $i\ge 2$, the operation $s_i$ only depends on the set of variables occurring in it, i.e., the order of the variables and their multiplicity can be ignored. Thus, we write $s_{|W_i|}(W_i)$ to stress this fact; moreover, we set $s_1(\{x\}){:}{=}x$, for every $x\in \{x_1,\dots ,x_k\}$. We define the map $\xi :\mathcal {I}_2\rightarrow \mathcal {S}$ as follows

$$\begin{aligned} \xi :\Bigg (\bigoplus _{i=1}^\ell \bigwedge W_i\Bigg )\mapsto m_\ell \big (s_{|W_1|}(W_1),\dots ,s_{|W_\ell |}(W_\ell )\big ). \end{aligned}$$

Since $m_{\ell }$ is symmetric, the map $\xi$ is well defined.

Note that both the operation $\oplus$ and $m_\ell$ only depend on the parity of the elements occurring among their arguments.

Let $\pi :\{1,\dots ,k\}\rightarrow \{1,\dots ,r\}$ be a map. By first applying $\xi$ we obtain $m_\ell \big (s_{|W_1|}(W_1),\dots ,s_{|W_\ell |}(W_\ell )\big )$ and then, via $\pi$, we obtain

$$\begin{aligned} m_\ell \big (s_{|W^\pi _1|}(W^\pi _1),\dots ,s_{|W^\pi _{\ell }|}(W^\pi _{\ell })\big ), \text{ where } W^\pi _{i}{:}{=}\{x_{\pi (j)}\mid x_j\in W_i\}. \end{aligned}$$

Let $\{U_1,\dots ,U_{t}\}$ be the set of all different subsets in $\{W^\pi _1,\dots ,W^\pi _\ell \}$. Without loss of generality we assume that $U_{i}$ appears an odd number of times in $W^\pi _1,\dots ,W^\pi _\ell$ for $i\in \{1,2\dots ,d\}$ and $U_{i}$ appears an even number of times in $W^\pi _1,\dots ,W^\pi _\ell$ for $i\in \{d+1,d+2\dots ,t\}$. Then using properties of $m_{\ell }$ we have

$$m_\ell \big (s_{|W^\pi _1|}(W^\pi _1),\dots ,s_{|W^\pi _{\ell }|}(W^\pi _{\ell })\big ) = m_d\big (s_{|U_1|}(U_1),\dots ,s_{|U_{d}|}(U_{d})\big ). $$

On the other side, if we first apply $\pi$, we get $\bigoplus _{i=1}^\ell \bigwedge W^\pi _{i} = \bigoplus _{i=1}^d \bigwedge U_{i}$. Since all the monomials in $\bigoplus _{i=1}^d \bigwedge U_{i}$ are different, $\xi$ applied to it gives us $m_d\big (s_{|U_1|}(U_1),\dots ,s_{|U_{d}|}(U_{d})\big )$, which is exactly what we need. $\square$

Corollary 3.13

Let $\mathcal {S}$ be an idempotent clone over $E_3$ such that $\mathcal {S}\ {\npreceq _{\textrm{m}}}\ \mathcal {C}_2$, $\mathcal {S}\ {\npreceq _{\textrm{m}}}\ \mathcal {C}_3$, and $\mathcal {S}\ {\npreceq _{\textrm{m}}}\ \mathcal {B}_2$. There is a minor homomorphism from $\mathcal {I}_2$ to $\mathcal {S}$.

Proof

From Theorem 3.9 we know that $\mathcal {S}$ has a generalized minority $m_\ell$, for every odd number $\ell \ge 3$. Moreover, from Theorem 3.10 it follows that $\mathcal {S}$ has a totally symmetric operation $s_n$ of arity n, for every $n\ge 2$. Thus, the claim follow from Theorem 3.12. $\square$

4 Conclusion

The results presented in this article together with the work from [7] give hope that a complete description of $\mathfrak P_{3}$ might be achievable. We conclude this article by stating three open problems, with the aim of suggesting a path leading to a full description of $\mathfrak P_{3}$.

Problem 4.1

Find all the atoms of $\mathfrak P_{3}$. Is every atom of $\mathfrak P_{3}$ of the form $\overline{\mathcal {C}}$, for some finitely related clone $\mathcal {C}$?

Note that a positive solution to Problem 4.1 would provide a concrete list of the hardest tractable CSPs over $\{0,1,2\}$, refining [10].

By Corollary 3.13 it immediately follows that $\overline{\mathcal {C}_2}$, $\overline{\mathcal {C}_3}$, and $\overline{\mathcal {B}_2}$ are exactly the submaximal elements of $\mathfrak P_{3}$. Furthermore, in order to prove that $\mathfrak P_{3}$ has at most countably infinite many elements, we can even focus only on those clones for which there exists a minor homomorphism to $\mathcal {B}_2$. Indeed, we prove that every clone $\mathcal {C}$ over a finite set has a Mal’cev operation (Theorem 2.13) if and only if there is no minor homomorphism from $\mathcal {C}$ to $\mathcal {B}_2$ and Bulatov [9] proved that there are only finitely many clones over $\{0,1,2\}$ containing a Mal’cev operation.

Problem 4.2

Find all elements of $\mathfrak P_{3}$ that are below $\overline{\mathcal {C}_2}$.

It follows from Theorems 3.13 and 2.13 that all clones over $\{0,1,2\}$ with a Mal’cev operation are below $\overline{\mathcal {C}_2}$ or $\overline{\mathcal {C}_3}$ in $\mathfrak P_{3}$. Since all the elements of $\mathfrak P_{3}$ which are below $\overline{\mathcal {C}_3}$ were found in [7], in order to solve Problem 4.2, we have to consider all clones over $\{0,1,2\}$ with a Mal’cev operation and a cyclic operation of arity 3, and order them with respect to ${\preceq _{\textrm{m}}}$.

Problem 4.3

Find all elements of $\mathfrak P_{3}$ that are below $\overline{\mathcal {B}_2}$.

We would like to emphasise that, out of the three problems proposed in this section, Problem 4.3 is the more challenging one as, a priori, there might exist continuum many elements below $\overline{\mathcal {B}_2}$.

An alternative direction that this research strand can take is to investigate whether Corollary 3.13 can be generalized to domains strictly larger than three. More precisely, one could ask if the following holds: for every $n>3$, if $\mathcal {S}$ is an idempotent clone over $E_n$ such that, for every prime $p\le n$, it holds that $\mathcal {S}\ {\npreceq _{\textrm{m}}}\ \mathcal {C}_p$ and $\mathcal {S}\ {\npreceq _{\textrm{m}}}\ \mathcal {B}_2$, then there exists a minor homomorphism from $\mathcal {I}_2$ to $\mathcal {S}$. The latter statement was proved to be true if we only consider polymorphism clones of finite directed graphs [4].

However, there is a structure in the literature that proves the statement to be false in general. Carvalho and Krokhin [11] – for different purposes – presented a structure $\mathbb {K}$ with 21 elements that has cyclic polymorphisms of all arities, a Mal’cev polymorphism, and that does not have any symmetric polymorphism of arity 5. Note that, from Theorem 2.14 and ${{\,\textrm{Pol}\,}}(\mathbb {K})\models \Sigma _p$ for every prime p, it follows that ${{\,\textrm{Pol}\,}}(\mathbb {K})\ {\npreceq _{\textrm{m}}}\ \mathcal {C}_p$. Moreover, it follows from ${{\,\textrm{Pol}\,}}(\mathbb {K})\models \Sigma _{{\text {M}}}$ and Theorem 2.13 that ${{\,\textrm{Pol}\,}}(\mathbb {K})\ {\npreceq _{\textrm{m}}}\ \mathcal {B}_2$. However, we have that $\mathcal {I}_2\ {\npreceq _{\textrm{m}}}\ {{\,\textrm{Pol}\,}}(\mathbb {K})$, since $\mathcal {I}_2\models {\text {FS}}(5)$ while ${{\,\textrm{Pol}\,}}(\mathbb {K})\not \models {\text {FS}}(5)$.

For the sake of full disclosure, the structure $\mathbb {K}$ is defined as follows: $\mathbb {K}{:}{=}(K; R, S)$, where $K = \{0,1,2,\dots ,9,10,a,b,c,d,e,f,g,h,i,j\}$, and R and S are binary relations that are the graphs of the following permutations r and s, respectively (see Figure 1),

$$\begin{aligned} r&= (0\ 1\ 2)(5\ 6\ 7)(8\ 9\ 10)(e\ b\ a)(d\ g\ i)(f\ h\ c), \\s&= (1\ 4)(2\ 3)(5\ 6)(7\ 8)(j\ e)(b\ c)(a\ d)(i\ f). \end{aligned}$$

Fig. 1

The structure

In the light of this, we conclude this article with the following conjecture.

Conjecture 4.4

Let $\mathcal {S}$ be a clone over $E_k$, for some $k\ge 2$, such that

• $\mathcal {S}$ satisfies ${\text {TS}}(n)$, for every $n\ge 2$, and

• $\mathcal {S}$ satisfies $\Sigma _{{\text {M}}}$.

Then there exists a minor homomorphism from $\mathcal {I}_2$ to $\mathcal {S}$.

Note that Conjecture 4.4 implies Theorem 3.12: indeed, the assumption of having a quasi Mal’cev operation is a strictly weaker assumption than that of requiring the existence of a generalized minority of every odd arity.