Generalized quasiorders and the Galois connection ${\textbf {End}}$–$\varvec{{{\,\textrm{gQuord}\,}}}$

Abstract

Equivalence relations or, more general, quasiorders (i.e., reflexive and transitive binary relations) $\varrho$ have the property that an n-ary operation f preserves $\varrho ,$ i.e., f is a polymorphism of $\varrho ,$ if and only if each translation (i.e., unary polynomial function obtained from f by substituting constants) preserves $\varrho ,$ i.e., it is an endomorphism of $\varrho .$ We introduce a wider class of relations—called generalized quasiorders—of arbitrary arities with the same property. With these generalized quasiorders we can characterize all algebras whose clone of term operations is determined by its translations by the above property, what generalizes affine complete algebras. The results are based on the characterization of so-called u-closed monoids (i.e., the unary parts of clones with the above property) as Galois closures of the Galois connection ${\textrm{End}}$–${{\,\textrm{gQuord}\,}},$ i.e., as endomorphism monoids of generalized quasiorders. The minimal u-closed monoids are described explicitly.

1 Introduction

Equivalence relations $\varrho$ have the remarkable well-known property that an n-ary operation f preserves $\varrho$ (i.e., f is a polymorphism of $\varrho$) if and only if each translation, i.e., unary polynomial function obtained from f by substituting constants, preserves $\varrho$ (i.e., is an endomorphism of $\varrho$). Checking the proof one sees that symmetry is not necessary, thus the same property, called $\Xi$ in this paper (see Definition 2.2), also holds for quasiorders, i.e., reflexive and transitive relations.

No further relations with property $\Xi$ were known and once we came up with the interesting (for us) question, if there are other relations (than quasiorders) which satisfy $\Xi ,$ we hoped to prove that $\Xi (\varrho )$ implies that $\varrho$ has to be a quasiorder (or at least to be “constructible” from quasiorders). This attempt failed, but a new notion was born: transitivity of a relation with higher arity. The next step was to investigate reflexive and transitive m-ary relations which naturally are called generalized quasiorders for $m\ge 3$ (for $m=2$ they coincide with usual (binary) quasiorders) and which all have the property $\Xi$ (Theorem 3.8). Moreover, these generalized quasiorders are more powerful than quasiorders or equivalence relations (see Remark 5.4) and therefore allow finer investigations of the structure of algebras (A, F).

The next challenging question was: are there further relations with property $\Xi ,$ other than generalized quasiorders? The answer is “yes, but not really”: there are relations $\varrho$ with $\Xi (\varrho ),$ i.e., satisfying $\Xi ,$ and not being a generalized quasiorder (see Example in Remark 4.5), but each such relation $\varrho$ is “constructively equivalent” to generalized quasiorders in the sense that they generate the same relational clone and therefore can be expressed mutually by primitive positive formulas (Proposition 4.4).

With the property $\Xi$ the clone ${{\,\textrm{Pol}\,}}\varrho$ of polymorphisms is completely determined by the endomorphism monoid $M={\textrm{End}}\varrho .$ Changing the point of view and starting with an arbitrary monoid M of unary mappings on a set A (notation $M\le A^{A}$), one can ask for the set $M^{*}$ of all operations whose translations belong to M. Then $\Xi (\varrho )$ means ${{\,\textrm{Pol}\,}}\varrho =({\textrm{End}}\varrho )^{*}$ (for details see Section 2), in particular, $M^{*}$ is a clone. But in general, $M^{*}$ is only a so-called preclone (counterexample 2.4). This leads to the question When $M^{*}$ is a clone? and to the notion of a u-closed monoid (namely if $M^{*}$ is a clone).

These u-closed monoids play a crucial role in this paper. Their characterization via generalized quasiorders, namely as Galois closed monoids (of the Galois connection ${\textrm{End}}$–${{\,\textrm{gQuord}\,}}$ introduced in Section 4), is one of the main results (Theorem 4.2) from which the answer to all above questions more or less follows.

The paper is organized as follows. All needed notions and notation are introduced in Section 1. Section 2 deals with the property $\Xi$ and the u-closure and clarifies the preclone structure of $M^{*}.$ Section 3 is the stage for the main player of this paper: the generalized quasiorders. In particular, Theorem 3.8 proves the property $\Xi$ for them. As already mentioned, in Section 4 the Galois connection ${\textrm{End}}$–${{\,\textrm{gQuord}\,}}$ and the crucial role of u-closed monoids is considered. Moreover, the behavior of the u-closure under taking products and substructures is clarified. In Section 5 we consider the u-closure of concrete monoids $M\le A^{A},$ in particular all minimal u-closed monoids are determined (Theorem 5.3). In Section 6 we collect some facts and problems for further research. In particular we show how the notion of an affine complete algebra can be generalized via generalized quasiorders.

2 Preliminaries

In this section we introduce (or recall) all needed notions and notation together with some results. Throughout the paper, A is a finite, nonempty set. $\mathbb {N}{:}{=}\{0,1,2,\ldots \}$ $(\mathbb {N}_{+}{:}{=}\mathbb {N}{\setminus }\{0\})$ denotes the set of (positive) natural numbers.

Operations and Relations 1.1

Let ${{\,\textrm{Op}\,}}^{(n)}(A)$ and ${{\,\textrm{Rel}\,}}^{(n)}(A)$ denote the set of all n-ary operations $f:A^{n}\rightarrow A$ and n-ary relations $\varrho \subseteq A^{n},$ $n\in \mathbb {N}_{+},$ respectively. Further, let ${{\,\textrm{Op}\,}}(A)=\bigcup _{n\in \mathbb {N}_{+}}{{\,\textrm{Op}\,}}^{(n)}(A)$ and ${{\,\textrm{Rel}\,}}(A)=\bigcup _{n\in \mathbb {N}_{+}}{{\,\textrm{Rel}\,}}^{(n)}(A).$

The so-called projections $e^{n}_{i}\in {{\,\textrm{Op}\,}}^{(n)}(A)$ are defined by $e^{n}_{i}(x_{1},\ldots ,x_{n}){:}{=}x_{i}$ $(i\in \{1,\ldots ,n\},$ $n\in \mathbb {N}_{+}).$ The identity mapping is denoted by $\textsf{id}_{A}$ $(=e^{1}_{1}).$

$C{:}{=}\{\varvec{c}_{a}\,\,|\,\, a\in A\}$ is the set of all constants, considered as unary operations given by $\varvec{c}_{a}(x){:}{=}a$ for $a\in A.$

Special subsets of ${{\,\textrm{Rel}\,}}^{(2)}(A)$ are ${{\,\textrm{Eq}\,}}(A)$ and ${{\,\textrm{Quord}\,}}(A),$ i.e., all equivalence relations (binary, reflexive, symmetric and transitive) and quasiorder relations (binary, reflexive and transitive), respectively, on the set A.

For $f\in {{\,\textrm{Op}\,}}^{(n)}(A)$ and $r_{1},\ldots ,r_{n}\in A^{m},$ $r_{j}=(r_{j}(1), \ldots , r_{j}(m)),$ $(n,m\in \mathbb {N}_{+},$ $j\in \{1,\ldots ,n\}),$ let $f(r_{1},\ldots ,r_{n})$ denote the m-tuple obtained from componentwise application of f,  i.e., the m-tuple

$(f(r_{1}(1),\ldots ,r_{n}(1)),\ldots ,f(r_{1}(m),\ldots ,r_{n}(m))).$

For $f\in {{\,\textrm{Op}\,}}^{(n)}(A)$ and unary operations $g_{1},\ldots ,g_{n}\in {{\,\textrm{Op}\,}}^{(1)}(A),$ the composition $f[g_{1},\ldots ,g_{n}]$ is the unary operation given by $f[g_{1},\ldots ,g_{n}](x){:}{=}f(g_{1}(x),\ldots ,g_{n}(x)),$ $x\in A.$

The Galois connection Pol–Inv 1.2

An operation $f\in {{\,\textrm{Op}\,}}^{(n)}(A)$ preserves a relation $\varrho \in {{\,\textrm{Rel}\,}}^{(m)}(A)$ $(n,m\in \mathbb {N}_{+})$ if for all $r_{1},\ldots ,r_{n}\in \varrho$ we have $f(r_{1},\ldots ,r_{n})\in \varrho ,$ notation $f{\triangleright }\varrho .$

The Galois connection induced by ${\triangleright }$ gives rise to several operators as follows. For $Q\subseteq {{\,\textrm{Rel}\,}}(A)$ and $F\subseteq {{\,\textrm{Op}\,}}(A)$ let

$$\begin{aligned} {{\,\textrm{Pol}\,}}Q&{:}{=}\{f\in {{\,\textrm{Op}\,}}(A) \,\,|\,\, \forall \varrho \in Q: f{\triangleright }\varrho \}&\text { (polymorphisms ),}\\ {{\,\textrm{Inv}\,}}F&{:}{=}\{\varrho \in {{\,\textrm{Rel}\,}}(A) \,\,|\,\, \forall f\in F: f{\triangleright }\varrho \}&\text { (invariant relations ),}\\ {\textrm{End}}Q&{:}{=}\{f\in {{\,\textrm{Op}\,}}^{(1)}(A) \,\,|\,\, \forall \varrho \in Q: f{\triangleright }\varrho \}&\text { (endomorphisms ),}\\ {{\,\textrm{Con}\,}}F&{:}{=}{{\,\textrm{Con}\,}}(A,F){:}{=}{{\,\textrm{Inv}\,}}F\cap {{\,\textrm{Eq}\,}}(A)&\text { (congruence relations ),}\\ {{\,\textrm{Quord}\,}}F&{:}{=}{{\,\textrm{Quord}\,}}(A,F){:}{=}{{\,\textrm{Inv}\,}}F\cap {{\,\textrm{Quord}\,}}(A)&\text { (compatible quasiorders ).} \end{aligned}$$

The Galois closures for ${{\,\textrm{Pol}\,}}$–${{\,\textrm{Inv}\,}}$ and ${\textrm{End}}$–${{\,\textrm{Inv}\,}}$ are known and can be characterized as follows: ${{\,\textrm{Pol}\,}}{{\,\textrm{Inv}\,}}F=\langle F \rangle _{}$ (clone generated by F), ${{\,\textrm{Inv}\,}}{{\,\textrm{Pol}\,}}Q=[Q]_{\exists ,\wedge ,=}$ (relational clone, generated by Q,  equivalently characterizable as closure with respect to primitive positive formulas, i.e., formulas containing variable and relational symbols and only $\exists ,\wedge ,=$), ${\textrm{End}}{{\,\textrm{Inv}\,}}M=\langle M \rangle _{}$ ((sub)monoid generated by $M\subseteq A^{A}$), ${{\,\textrm{Inv}\,}}{\textrm{End}}Q=[Q]_{\exists ,\wedge ,\vee ,=}$ (weak Krasner algebra generated by Q,  equivalently characterizable as closure with respect to positive formulas, i.e., formulas containing variable and relational symbols and $\exists ,\wedge ,\vee , =$). We refer to, e.g., [22, 1.2.1, 1.2.3, 2.1.3], [2, 15, 21].

Definition 1.3

A set $F \subseteq {{\,\textrm{Op}\,}}(A)$ is called a preclone if it contains $\textsf{id}_{A}$ and is closed under the operations $\zeta ,$ $\tau$ and $\circ$ that are defined as follows. Let $f\in {{\,\textrm{Op}\,}}^{(n)}(A)$ and $g \in {{\,\textrm{Op}\,}}^{(m)}(A),$ $n,m\in \mathbb {N}_{+}.$ Then

• (1) $\textsf{id}_A(x){:}{=}x$ (identity operation);

• (2) $(\zeta f)(x_{1},x_{2},\ldots ,x_{n}) {:}{=} f(x_{2},\ldots ,x_{n},x_{1})$ (cyclic shift),if $n = 1$ then $\zeta f {:}{=} f;$

• (3) $(\tau f)(x_{1},x_{2},x_{3},\ldots ,x_{n}) {:}{=} f(x_{2},x_{1},x_{3},\ldots ,x_{n})$ (permuting the first two arguments), if $n = 1$ then $\tau f {:}{=} f;$

• (4) $(f\circ g)(x_{1},\ldots ,x_{m},x_{m+1},\ldots ,x_{m+n-1})$${:}{=}f(g(x_{1},\ldots ,x_{m}),x_{m+1},\ldots ,x_{m+n-1})$ (composition).

For later use we introduce here also the operations $\nabla$ (adding a fictitious argument at first place) and $\Delta$ (identification of the first two arguments):

• (5) $(\nabla f)(x_{1},x_{2},\ldots ,x_{n+1}) {:}{=}f(x_{2},\ldots ,x_{n+1}),$

• (6) $(\Delta f)(x_{1},\ldots ,x_{n-1}){:}{=}f(x_{1},x_{1},\ldots ,x_{n-1})$ if $n\ge 2,$ and $\Delta f=f$ for $n=1.$

Remarks

Clearly, because of (1) and (4), the unary part $F\cap {{\,\textrm{Op}\,}}^{(1)}(A)$ of a preclone F is a monoid. The $(m+n-1)$-ary function $f \circ g$ (defined in (4)) sometimes is called linearized composition (or superposition), because this is a special case of the general linearized composition, linearization or superposition mentioned in [3, 2.1], [6, page 2] or [17, Section 2.1], respectively.

Preclones, also known as operads, can be thought as “clones where identification of variables is not allowed” (cf. Remark 1.4). The term preclone was introduced by Ésik and Weil [4] in a study of the syntactic properties of recognizable sets of trees. A general characterization of preclones as Galois closures via so-called matrix collections can be found in [17]. The notion of operad originates from the work in algebraic topology by May [20] and Boardman and Vogt [1]. For general background and basic properties of operads, we refer the reader to the survey article by Markl [19].

Remark 1.4

Clones are special preclones. There are many (equivalent) definitions of a clone. One of these definitions is that a clone is a set $F\subseteq {{\,\textrm{Op}\,}}(A)$ closed under the operations 1.3(1)–(6), [22, 1.1.2]. Therefore we have:

A preclone is a clone if and only if it is also closed under $\nabla$ (adding fictitious variables) and $\Delta$ (identification of variables).

For $F\subseteq {{\,\textrm{Op}\,}}(A),$ the clone generated by F is denoted by $\langle F \rangle _{}$ or $\langle F \rangle _{A}.$

3 The property ${\varvec{\Xi }}$ and u-closed monoids

Equivalence relations or, more general, quasiorder relations $\varrho$ have the remarkable property $\Xi$ (see Definition 2.2 below) that for an operation f the property of being a polymorphism, i.e., $f\in {{\,\textrm{Pol}\,}}\varrho ,$ is completely determined by its translations $\textsf{trl}(f)$ defined as follows:

Definitions 2.1

For an n-ary operation $f:A^{n}\rightarrow A,$ $i\in \{1,\ldots ,n\}$ and a tuple $\textbf{a}=(a_{1},\ldots ,a_{i-1},a_{i+1},\ldots ,a_{n})\in A^{n-1},$ let $f_{\textbf{a},i}$ be the unary polynomial function

$$\begin{aligned} f_{\textbf{a},i}(x){:}{=}f(a_{1},\ldots ,a_{i-1},x,a_{i+1},\ldots ,a_{n}), \end{aligned}$$

(1)

called translation (see, e.g., [7, 1.4.7], 1-translation in [5, p. 375] or basic translation in [18]) and let $\textsf{trl}(f)$ be the set of all such translations $f_{\textbf{a},i}.$ For constants (as well as for arbitrary unary functions) f we put $\textsf{trl}(f){:}{=}\{f\}.$ For $F\subseteq {{\,\textrm{Op}\,}}(A)$ let

$$\begin{aligned} \textsf{trl}(F){:}{=}\bigcup _{f\in F}\textsf{trl}(f)\subseteq A^{A}. \end{aligned}$$

(2)

Given a set $M\subseteq A^{A}$ we define

$$\begin{aligned} M^{*}{:}{=}\{f\in {{\,\textrm{Op}\,}}(A) \,\,|\,\, \textsf{trl}(f)\subseteq M\}. \end{aligned}$$

(3)

Remark

Because of (3) we have $\textsf{trl}(M^{*})\subseteq M$ and $M\subseteq M^{*}.$ Moreover $M=\textsf{trl}(M)$ (since $\textsf{trl}(f)=\{f\}$ for unary functions), thus $M=\textsf{trl}(M)\subseteq \textsf{trl}(M^{*})\subseteq M,$ i.e., $\textsf{trl}(M^{*})=M$ for every $M\subseteq A^{A}.$

Definition 2.2

(The property ${{\Xi }}$). For a relation $\varrho \in {{\,\textrm{Rel}\,}}(A)$ we consider the following property $\Xi$ in three equivalent formulations:

$$\begin{aligned} \Xi (\varrho ):&\iff \quad \forall f\in {{\,\textrm{Op}\,}}(A):\; f{\triangleright }\varrho \iff \textsf{trl}(f){\triangleright }\varrho \end{aligned}$$

(*)

$$\begin{aligned}&\iff \quad \forall f\in {{\,\textrm{Op}\,}}(A):\; f\in {{\,\textrm{Pol}\,}}\varrho \iff \textsf{trl}(f)\subseteq {\textrm{End}}\varrho \end{aligned}$$

(**)

$$\begin{aligned}&\iff \quad {{\,\textrm{Pol}\,}}\varrho =({\textrm{End}}\varrho )^{*}. \end{aligned}$$

(***)

This can be extended to sets $Q\subseteq {{\,\textrm{Rel}\,}}(A)$ just by substituting Q for $\varrho$ in the above definition, e.g., $\Xi (Q)\iff {{\,\textrm{Pol}\,}}Q=({\textrm{End}}Q)^{*}.$

Remark 2.3

As noticed above, it is well-known that $\Xi (\varrho )$ holds for $\varrho \in {{\,\textrm{Eq}\,}}(A)$ or, more general, for $\varrho \in {{\,\textrm{Quord}\,}}(A)$. Equivalently, expressed with the usual notions of congruence or quasiorder lattices, this means

$$\begin{aligned} {{\,\textrm{Con}\,}}(A,F)={{\,\textrm{Con}\,}}(A,\textsf{trl}(F))\text { and }{{\,\textrm{Quord}\,}}(A,F)={{\,\textrm{Quord}\,}}(A,\textsf{trl}(F)) \end{aligned}$$

for each algebra (A, F) $(F\subseteq {{\,\textrm{Op}\,}}(A)).$

Clearly, there arises the question already mentioned in the Introduction:

Do there exist other relations $\varrho$ with the property $\Xi (\varrho )$?

$\Xi (\varrho )$ implies that $({\textrm{End}}\varrho )^{*}$ is a clone and therefore $({\textrm{End}}\varrho )^{*}$ is closed under $\nabla$ (cf. Remark 1.4). As we shall see in Proposition 2.5 below this also implies $C\subseteq {\textrm{End}}\varrho ,$ what expresses the fact that $\varrho$ is reflexive (see Definition 3.2). However, the converse is not true: not each reflexive relation satisfies $\Xi (\varrho )$ as the following example shows.

Example 2.4

Let $A=\{0,1,2\}$ and $M{:}{=}{\textrm{End}}\varrho$ for the binary relation $\varrho =\{(0,0),(1,1), (2,2), (0,1), (1,2)\}.$ Note that $\varrho$ is reflexive but not transitive. Define $f:A^{2}\rightarrow A$ by the following table:

$$\begin{aligned}{}\begin{array}{|r|rcc|} \hline { f}({ x},\,{ y}) &{} { y}= 0&{}1&{}2\\ \hline { x}= 0 &{} 0&{}0&{}1\\ 1 &{} 0&{}0&{}1\\ 2 &{} 1&{}1&{}2\\ \hline \end{array} \end{aligned}$$

One can immediately check that each unary polynomial $f_{\textbf{a},i}$ preserves $\varrho ,$ i.e., $\textsf{trl}(f)\subseteq M,$ but $g{:}{=}\Delta f$ (i.e., $g(x)=f(x,x)$) is the mapping $0\mapsto 0,$ $1\mapsto 0,$ $2\mapsto 2$ which does not belong to M (since g does not preserve $\varrho$ because g maps $(1,2)\in \varrho$ to $(0,2)\notin \varrho$). Thus $f\in M^{*}$ but $g\notin M^{*}.$ Hence $M^{*}$ is not a clone.

Since $M^{*}$ is not always a clone, there also arises the question: what is the algebraic nature of the sets $M^{*}$? The answer gives the following proposition.

Proposition 2.5

Let $M\le A^{A}$ be a monoid. Then $M^{*}$ is a preclone (cf. Definition 1.3). Moreover,  $M^{*}$ is closed under $\nabla$ (cf. Definition 1.3(5)) if and only if $C\subseteq M.$

Proof

Clearly $\textsf{id}_{A}\in M\subseteq M^{*}.$ It is straightforward to check that for $f,g\in M^{*}$ also $\zeta f, \tau f$ and $f\circ g$ belong to $M^{*}$ (notation see Definition 1.3). We show it for the operation 1.3(4): if all variables $x_{1},\ldots ,x_{m},\ldots ,x_{m+n-1},$ with exception of $x_{i},$ are constant, say $\textbf{a}=(a_{1},\ldots ,a_{m},\ldots ,a_{m+n-1}),$ then, for $i\ge m+1,$ we have $(f\circ g)_{\textbf{a},i}(x_{i})=f(b,a_{m+1},\ldots ,x_{i},\ldots ,a_{m+n-1})$ with $b{:}{=}g(a_{1},\ldots ,a_{m}),$ what obviously belongs to $\textsf{trl}(f)\subseteq M.$ If $i\le m,$ then we have $g_{{\mathbf {a'}},i}\in M$ (because $g\in M^{*}$) for ${\mathbf {a'}}{:}{=}(a_{1},\ldots ,a_{m})$ (without the i-th component) and $f_{{\mathbf {a''}},1}(x)=f(x,a_{m+1},\ldots ,a_{m+n-1})$ belongs to M (because $f\in M^{*}$), where ${\mathbf {a''}}{:}{=}(a_{m+1},\ldots ,a_{m+n-1}),$ consequently $(f\circ g)_{\textbf{a},i}(x)=f_{{\mathbf {a''}},1}(g_{{\mathbf {a'}},i}(x))$ also belongs to the monoid M. Thus $\textsf{trl}(f\circ g)\subseteq M,$ i.e., $f\circ g\in M^{*}.$

Further we observe $\nabla f=f\circ e^{2}_{2}$ and $e^{2}_{2}=\nabla \textsf{id}_{A}$ where $e^{2}_{2}$ is the binary projection $e^{2}_{2}(x_{1},x_{2})=x_{2}.$ Thus the preclone $M^{*}$ is closed under $\nabla$ if and only if $e^{2}_{2}\in M^{*}.$ But $\textsf{trl}(e^{2}_{2})=\{\textsf{id}_{A}\}\cup C$ (since $e^{2}_{2}(a,x)=\textsf{id}_{A}(x)$ and $e^{2}_{2}(x,a)=\varvec{c}_{a}$ for $a\in A$), therefore $e^{2}_{2}\in M^{*}\iff \textsf{trl}(e^{2}_{2})\subseteq M\iff C\subseteq M,$ and we are done. $\square$

Remark 2.6

$M^{*}$ is a preclone for a monoid M by Proposition 2.5. Conversely, for a preclone P the translations $\textsf{trl}(P)$ form a monoid (because of Definition 1.3(1) and (4)). Thus we can consider the following two mappings between monoids and preclones:

$$\begin{aligned} \varphi&: P\mapsto \textsf{trl}(P),\text { where { P} is a preclone on { A}.}\\ \psi&: M\mapsto M^{*}, \text {where }\,\,M\le A^{A}\,\, \text { is a monoid on}\,\, A. \end{aligned}$$

Then $(\varphi ,\psi )$ is a residuated pair of mappings (covariant Galois connection) between the lattice of submonoids of $A^{A}$ and the lattice of preclones on A. We have $\varphi (P)\subseteq M\iff P\subseteq \psi (M).$ Moreover, the corresponding kernel operator $\varphi (\psi (M))=\textsf{trl}(M^{*})=M$ is trivial (cf. remark in Definition 2.1). However, the corresponding closure operator $P\mapsto \psi (\varphi (P))$ is nontrivial and it is an open problem which preclones are closed, i.e., when do we have $P=\psi (\varphi (P))=(\textsf{trl}(P))^{*}$?

Lemma 2.7

Let $M_{i}\le A^{A},$ $i\in I.$ Then $(\bigcap _{i\in I} M_{i})^{*}=\bigcap _{i\in I}M_{i}^{*}.$

Proof

Since, for a residuated pair $(\varphi ,\psi ),$ the residual $\psi$ is meet-preserving, the Lemma immediately follows from Remark 2.6. We add a direct proof just using the definitions:

$$\begin{aligned} f\in (\textstyle \bigcap _{i\in I} M_{i})^{*}&\iff \textsf{trl}(f)\subseteq \textstyle \bigcap _{i\in I}M_{i} \iff \forall i\in I: \textsf{trl}(f)\subseteq M_{i}\\&\iff \forall i\in I: f\in M_{i}^{*} \iff f\in \textstyle \bigcap _{i\in I}M_{i}^{*}. \end{aligned}$$

$\square$

Since $M^{*}$ is not always a clone, the question arises: For which monoids $M\le A^{A}$ the preclone $M^{*}$ is a clone? To attack this problem we introduce the u-closure $\overline{M}$ what shall lead to the equivalent problem (cf. Remark 2.9(iii)) of characterizing u-closed monoids.

Definition 2.8

For $M\subseteq A^{A}$ let

$$\begin{aligned} \overline{M}{:}{=}\bigcap \{N \,\,|\,\, M\subseteq N \le A^{A},\text { and} \,\, N^{*}\,\, \text { is a clone}\}. \end{aligned}$$

A set $M\subseteq A^{A}$ is called u-closed if $\overline{M}=M.$

Remarks 2.9

Let $M\subseteq A^{A}.$

• (i) The operator $M\mapsto \overline{M}$ is a closure operator (in fact, due to Lemma 2.7, $\overline{M}$ is the least monoid N containing M such that $N^{*}$ is a clone, thus the operator is monoton and $\overline{\overline{M}}=\overline{M}$).

• (ii) $\overline{M}$ is a monoid containing C and $(\overline{M})^{*}$ is a clone (the latter follows from Lemma 2.7 because, by definition, $\overline{M}$ is the intersection of monoids N with $N^{*}$ being a clone; thus from Proposition 2.5 follows $C\subseteq \overline{M},$ too). In particular we have $\overline{\langle M \rangle _{}}=\overline{M}=\langle \overline{M} \rangle _{}.$

• (iii) M is u-closed (i.e. $\overline{M}=M$) if and only if $M^{*}$ is a clone (in fact, “$\Rightarrow$” follows from (ii), “$\Leftarrow$” follows from Definition 2.8).

A characterization of u-closed monoids M will be given in the next sections (Proposition 3.10, Theorem 4.2 and Corollary 4.3).

4 Generalized quasiorders

Notation 3.1

Let $A=\{a_{1},\ldots ,a_{k}\}$ and $M\le A^{A}.$ We define the following |A|-ary relation:

$$\begin{aligned} \Gamma _{M}{:}{=}\{(ga_{1},\ldots ,ga_{k}) \,\,|\,\, g\in M\}. \end{aligned}$$

Thus $\Gamma _{M}$ consists of all “function tables” $\textbf{r}_{g}{:}{=}(ga_{1},\ldots ,ga_{k})$ (considered as elements (columns) of a relation) of the unary functions g in M.

In particular, we have

$$\begin{aligned} M={\textrm{End}}\Gamma _{M}. \end{aligned}$$

In fact, $h\in {\textrm{End}}\Gamma _{M},$ i.e., $h{\triangleright }\Gamma _{M},$ implies $h(\textbf{r}_{\textsf{id}})\in \Gamma _{M},$ i.e., $\exists g\in M: h(\textbf{r}_{id})=\textbf{r}_{g}$ what gives $h=g\in M.$ Conversely , if $h\in M,$ then $h(\textbf{r}_{g})=\textbf{r}_{h\circ g}\in \Gamma _{M}$ for all $\textbf{r}_{g}\in \Gamma _{M},$ i.e., $h{\triangleright }\Gamma _{M}.$

Moreover, it is known that ${{\,\textrm{Pol}\,}}\Gamma _{M}$ coincides with the so-called stabilizer ${\textrm{Sta}}(M)$ of M and it is the largest element in the monoidal interval defined by M (all clones with unary part M form an interval in the clone lattice, called monoidal interval, cf., e.g., [23, 3.1]). If F is a clone with $F^{(1)}=M,$ then $\Gamma _{M}$ is the so-called first graphic of F denoted by $\Gamma _{F}(\chi _{1})$ in [22].

Definition 3.2

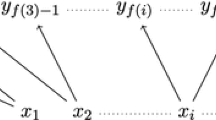
(Generalized quasiorder). An m-ary relation $\varrho \subseteq A^{m}$ is called reflexive if $(a,\ldots ,a)\in \varrho$ for all $a\in A,$ and it is called (generalized) transitive if for every $m\times m$-matrix $(a_{ij})\in A^{m\times m}$ we have: if every row and every column belongs to $\varrho$ — for this property we write $\varrho \models (a_{ij})$ — then also the diagonal $(a_{11},\ldots ,a_{mm})$ belongs to $\varrho ,$ cf. Figure 1.

Fig. 1

Transitivity for an m-ary relation $\varrho$

A reflexive and transitive m-ary relation is called generalized quasiorder. The set of all generalized quasiorders on the base set A shall be denoted by ${{\,\textrm{gQuord}\,}}(A),$ and ${{\,\textrm{gQuord}\,}}^{(m)}(A){:}{=}{{\,\textrm{Rel}\,}}^{(m)}(A)\cap {{\,\textrm{gQuord}\,}}(A)$ will denote the m-ary generalized quasiorders.

Examples 3.3

From the definitions easily follows:

• (i) Each quasiorder (i.e., binary reflexive and transitive relation) is also a generalized quasiorder. The converse is also true: Each binary generalized quasiorder is a usual quasiorder relation, consequently we have ${{\,\textrm{gQuord}\,}}^{(2)}(A)={{\,\textrm{Quord}\,}}(A).$

• (ii) Each diagonal relation is a generalized quasiorder where an m-ary relation $\delta \in {{\,\textrm{Rel}\,}}(A)$ ($m\in \mathbb {N}_{+}$) is called diagonal relation if there exists an equivalence relation $\varepsilon$ on the set $\{1,\ldots ,m\}$ of indices such that $\delta =\{(a_{1},\ldots ,a_{m})\in A^{m} \,\,|\,\, \forall i,j\in \{1,\ldots ,m\}: (i,j)\in \varepsilon \implies a_{i}=a_{j}\}.$

We generalize the notation $\varrho \models (a_{ij})$ to n-dimensional “$m\times \ldots \times m$-matrices” (tensors) $(a_{i_{1},\ldots , i_{n}})\in A^{m\times \cdots \times m}$ where $i_{1},\ldots ,i_{n}\in \{1,\ldots ,m\}$): $\varrho \models (a_{i_{1},\ldots , i_{n}})$ denotes the fact that every “row” in each dimension belongs to $\varrho ,$ i.e., for each index $j\in \{1,\ldots ,n\}$ and any fixed $i_{1},\ldots ,i_{j-1},i_{j+1},\ldots ,i_{n}$ the m-tuple $a_{i_{1},\ldots ,[j],\ldots ,i_{n}}{:}{=} (a_{i_{1},\ldots ,1,\ldots ,i_{n}},\ldots ,a_{i_{1},\ldots ,m,\ldots ,i_{n}})$ (the indices $1,\ldots ,m$ are on the j-th place in the index sequence) belongs to $\varrho .$

Example: For $n=3,$ $\varrho \models (a_{i_{1},i_{2},i_{3}})$ means that for all indices $i_{1},i_{2},i_{3}\in \{1,\ldots ,m\}$ we have $(a_{1,i_{2},i_{3}},\ldots ,a_{m,i_{2},i_{3}})\in \varrho ,$ $(a_{i_{1},1,i_{3}},\ldots ,a_{i_{1},m,i_{3}})\in \varrho$ and $(a_{i_{1},i_{2},1},\ldots ,a_{i_{1},i_{2},m})\in \varrho .$ The (main) diagonal of $(a_{i_{1},i_{2},i_{3}})$ is the m-tuple $(a_{1,1,1},\ldots ,a_{m,m,m}).$

Remark 3.4

Let $A=\{1,\ldots ,k\}.$ We mention that for an n-ary function $f:A^{n}\rightarrow A$ and a monoid $M\le A^{A}$ we have $f\in M^{*}\iff \Gamma _{M}\models (a_{i_{1},\ldots ,i_{n}})$ where $a_{i_{1},\ldots ,i_{n}}{:}{=}f({i_{1}},\ldots ,{i_{n}}),$ $i_{1},\ldots ,i_{n}\in \{1,\ldots ,k\}.$

Definitions 3.5

For $\varrho \subseteq A^{m}$ let $\varrho ^{\textsf{tra}}$ denote the transitive closure of $\varrho ,$ i.e., $\varrho ^{\textsf{tra}}=\bigcap \{\sigma \subseteq A^{m} \,\,|\,\, \sigma \text { is transitive and }\varrho \subseteq \sigma \}$ is the least transitive relation containing $\varrho$ (it is easy to check that the intersection of transitive relations is again transitive). Analogously, the generalized quasiorder closure $\varrho ^{\textsf{gqu}}$ is the least generalized quasiorder containing $\varrho .$ The reflexive closure is naturally defined as $\varrho ^{\textsf{ref}}{:}{=}\varrho \cup \{(c,\ldots ,c)\in A^{m} \,\,|\,\, c\in A\}.$

These closures can be constructed (inductively) as follows.

Proposition 3.6

For $\varrho \in {{\,\textrm{Rel}\,}}^{(m)}(A)$ define $\partial (\varrho ){:}{=}\{(a_{11},\ldots ,a_{mm})\in A^{m} \,\,|\,\, \exists (a_{ij})\in A^{m\times m}: \varrho \models (a_{ij})\}$ and let $\varrho ^{(0)}{:}{=}\varrho ,$ $\varrho ^{(n+1)}{:}{=}\varrho ^{(n)}\cup \partial (\varrho ^{(n)})$ for $n\in \mathbb {N}.$ Then we have

$$\begin{aligned} \varrho ^{\textsf{tra}}=\bigcup _{n\in \mathbb {N}}\varrho ^{(n)} \quad \text { and }\quad \varrho ^{\textsf{gqu}}=\varrho ^{\textsf{ref}\,\textsf{tra}}. \end{aligned}$$

Remark

If $\varrho$ is reflexive, then $\varrho \subseteq \partial (\varrho ).$ For binary relations $\varrho$ the operator $\partial$ is just the relational product: $\partial (\varrho )=\varrho \circ \varrho .$ Note that $\partial (\varrho )$ is always pp-definable from $\varrho ,$ i.e., $\partial (\varrho )\in [\varrho ]_{\exists ,\wedge ,=}.$

Lemma 3.7

Let $\varrho \in {{\,\textrm{gQuord}\,}}^{(m)}(A).$ For every n-dimensional $m\times \cdots \times m$-matrix $(a_{i_{1},\ldots , i_{n}})_{i_{1},\ldots ,i_{n}\in \{1,\ldots ,m\}}$ we have

$$\begin{aligned} \varrho \models (a_{i_{1},\ldots , i_{n}})\implies (a_{1,\ldots ,1},\ldots ,a_{m,\ldots , m})\in \varrho . \end{aligned}$$

Proof

For $n=2$ the condition follows from the definition of a generalized quasiorder. Thus we can assume $n\ge 3.$ Let $M_{k}=(b^{k}_{i_{1},\ldots ,i_{n-k}})$ denote the $(n-k)$-dimensional $m\times \cdots \times m$-matrix with $b^{k}_{i_{1},\ldots ,i_{n-k}}{:}{=}a_{i_{1},\ldots ,i_{1},i_{2},\ldots ,i_{n-k}}$ (the first k coordinates are equal $i_{1}$). . Thus $M_{0}=(a_{i_{1}\dots ,i_{n}})$ and $M_{n-1}=(b^{1}_{i})=(a_{i,\ldots ,i})_{i\in \{1,\ldots ,m\}}= (a_{1,\ldots ,1},\ldots ,a_{m,\ldots , m}).$ We have to show $M_{n-1}\in \varrho$ (formally $\varrho \models M_{n-1}$). This can be done by induction on k. By assumption we have $\varrho \models M_{k}$ for $k=0.$ Assume $\varrho \models M_{k}$ for some $k\in \{0,1,\ldots ,n-2\}.$ We are going to show $\varrho \models M_{k+1}$ what will finish the proof.

Let $i_{1},\ldots ,i_{n-k}\in \{1,\ldots ,m\}.$ We fix $i_{3},\ldots ,i_{n-k}$ and consider the 2-dimensional $m\times m$-matrix $M'_{k}{:}{=}(b^{k}_{i,j,i_{3},\ldots ,i_{n-k}})_{i,j\in \{1,\ldots ,m\}}.$ Clearly, $\varrho \models M_{k}$ implies $\varrho \models M'_{k}.$ Therefore $(b^{k}_{1,1,i_{3},\ldots ,i_{n-k}},\ldots ,b^{k}_{m,m,i_{3},\ldots ,i_{n-k}})\in \varrho$ because $\varrho$ is a generalized quasiorder. Since $i_{3},\ldots ,i_{n-k}$ were chosen arbitrarily, this implies (together with $\varrho \models M_{k}$) that we have $\varrho \models M_{k+1}$ (note $b^{k+1}_{i_{1},i_{3},\ldots ,i_{n-k}}=b^{k}_{i_{1},i_{1},i_{3},\ldots ,i_{n-k}}$). $\square$

One of the crucial properties of generalized quasiorders is that preservation of a relation only depends on the translations, i.e., it extends the property $\Xi$ (see Definition 2.2(*)) from (usual) quasiorders to generalized quasiorders.

Theorem 3.8

For $f\in {{\,\textrm{Op}\,}}(A)$ and $\varrho \in {{\,\textrm{gQuord}\,}}(A)$ we have : 

$$\begin{aligned} f{\triangleright }\varrho \iff \textsf{trl}(f){\triangleright }\varrho . \end{aligned}$$

Thus $\Xi (\varrho )$ holds.

Proof

“$\Rightarrow$”: Since each $g\in \textsf{trl}(f)$ is a composition of f and constants $c\in C$ and since constants preserve $\varrho$ because of reflexivity, we have $\textsf{trl}(f)\subseteq \langle \{f\}\cup C \rangle _{}{\triangleright }\varrho .$

“$\Leftarrow$”: Let ${{\,\textrm{ar}\,}}(f)=n,$ ${{\,\textrm{ar}\,}}(\varrho )=m,$ $\textsf{trl}(f){\triangleright }\varrho$ and let $r_{1},\ldots ,r_{n}\in \varrho .$ We are going to show $f(r_{1},\ldots ,r_{n})\in \varrho$ what implies $f{\triangleright }\varrho$ and will finish the proof. Define $a_{i_{1},\ldots ,i_{n}}{:}{=}f(r_{1}(i_{1}),\ldots ,r_{n}(i_{n})).$ Then $a_{i_{1},\ldots ,[j],\ldots ,i_{n}}=f_{\textbf{b},j}(r_{j})\in \varrho$ for $\textbf{b}=(r_{1}(i_{1}),\ldots ,r_{j-1}(i_{j-1}),r_{j+1}(i_{j+1}),\ldots ,r_{n}(i_{n}))$ (notation see Definition 2.1(1)) because $f_{\textbf{b},j}\in \textsf{trl}(f){\triangleright }\varrho ,$ $j\in \{1,\ldots ,n\}.$ Thus $\varrho \models (a_{i_{1},\ldots ,i_{n}})$ and we have

$$\begin{aligned} f(r_{1},\ldots ,r_{n})&=(f(r_{1}(1),\ldots ,r_{n}(1)),\ldots ,f(r_{1}(m),\ldots ,r_{n}(m)))\\&=(a_{1,\ldots ,1},\ldots ,a_{m,\ldots ,m})\in \varrho \end{aligned}$$

by Lemma 3.7, and we are done. $\square$

Corollary 3.9

Let $F\subseteq {{\,\textrm{Op}\,}}(A)$ and $Q\subseteq {{\,\textrm{gQuord}\,}}(A).$ Then

• (i) ${{\,\textrm{gQuord}\,}}(A,F)={{\,\textrm{gQuord}\,}}(A,\textsf{trl}(F))$ (cf. Remark 2.3)

• (ii) $\Xi (Q)$ holds,  i.e.,  ${{\,\textrm{Pol}\,}}Q=({\textrm{End}}Q)^{*},$ in particular,  $({\textrm{End}}Q)^{*}$ is a clone and ${\textrm{End}}Q$ is u-closed.

Proof

(i) directly follows from Theorem 3.8. Concerning (ii), we have

${{\,\textrm{Pol}\,}}Q=\bigcap _{\varrho \in Q}{{\,\textrm{Pol}\,}}\varrho =_{3.8,2.2(***)}\bigcap _{\varrho \in Q}({\textrm{End}}\varrho )^{*} =_{2.7}(\bigcap _{\varrho \in Q}{\textrm{End}}\varrho )^{*}=({\textrm{End}}Q)^{*},$ i.e., $\Xi (Q).$ $\square$

Now we characterize the u-closed monoids $M\le A^{A}$ (i.e., $\overline{M}=M$) by various properties. The condition (iii) Proposition 3.10 will show that the situation as in Example 2.4 is characteristic for being not u-closed.

Proposition 3.10

For a monoid $M\le A^{A}$ the following are equivalent : 

• (i) M is u-closed (equivalently,  $M^{*}$ is a clone), 

• (ii) $M^{*}={{\,\textrm{Pol}\,}}\Gamma _{M},$

• (iii) $C\subseteq M$ and for every binary $f\in M^{*}$ we have $\Delta f\in M,$

• (iv) $\Gamma _{M}$ is a generalized quasiorder.

Proof

Each of the conditions (i), (ii) and (iv) implies $C\subseteq M$ (cf. Proposition 2.5 for (i), (ii) and note that $\Gamma _{M}$ is reflexive if and only if $C\subseteq M$). Thus we can assume $C\subseteq M$ in the following.

(ii)$\implies$(i)$\implies$(iii) is clear (each set of the form ${{\,\textrm{Pol}\,}}Q$ is a clone, and any clone is closed under $\Delta$).

(i)$\implies$(ii): M is just the unary part $F^{(1)}$ of the clone $F{:}{=}M^{*}.$ It is well-known (cf., e.g., [23, 3.1]) that ${{\,\textrm{Pol}\,}}\Gamma _{M}$ is the largest clone F with unary part $F^{(1)}=M,$ thus $M^{*}=F\subseteq {{\,\textrm{Pol}\,}}\Gamma _{M}.$

Conversely, let $f\in {{\,\textrm{Pol}\,}}\Gamma _{M},$ i.e., $f{\triangleright }\Gamma _{M}.$ Remember that the elements of $\Gamma _{M}$ are of the form $\textbf{r}_{g}$ for some $g\in M$ (notation see Notation 3.1). Thus $f{\triangleright }\Gamma _{M}$ means $f(\textbf{r}_{g_{1}},\ldots ,\textbf{r}_{g_{n}})\in \Gamma _{M}$ whenever $g_{1},\ldots ,g_{n}\in M.$ Since $f(\textbf{r}_{g_{1}},\ldots ,\textbf{r}_{g_{n}})=\textbf{r}_{f[g_{1},\ldots ,g_{n}]},$ this equivalently can be expressed by the condition that the composition $f[g_{1},\ldots ,g_{n}]$ belongs to M whenever $g_{1},\ldots ,g_{n}\in M.$ Consequently, any translation $g{:}{=}f_{\textbf{a},i}$ derived from f (w.l.o.g. we take $i=1$), say $g(x){:}{=}f(x,a_{2},\ldots ,a_{n})$ for some $a_{2},\ldots ,a_{n}\in A,$ must belong to M,  since $g=f[\textsf{id}_{A},\varvec{c}_{a_{2}},\ldots ,\varvec{c}_{a_{n}}]$ and M contains the identity $\textsf{id}_{A}$ and the constant functions. Thus $\textsf{trl}(f)\subseteq M,$ hence $f\in M^{*},$ and we get ${{\,\textrm{Pol}\,}}\Gamma _{M}\subseteq M^{*}.$

(iii)$\implies$(i): Assume (iii) and assume on the contrary that $M^{*}$ is not a clone. We lead this to a contradiction. Since $M^{*}$ is a preclone by Proposition 2.5, $M^{*}$ cannot be closed under $\Delta$ and there must exist a function $f\in M^{*},$ say n-ary, such that $h{:}{=}\Delta f\notin M^{*}$ (clearly $n\ge 3,$ otherwise we have a contradiction to (iii)). Thus some translation $g{:}{=}h_{\textbf{a},i}$ derived from h cannot belong to M. If $i\not = 1,$ then $g(x)=h(c_{1},\ldots ,c_{i-1},x,c_{i+1}\dots ,c_{n-1})=f(c_{1},c_{1},c_{i-1},x,c_{i+1}\dots ,c_{n-1})$ would belong to M since $f\in M^{*}.$ Therefore $i=1$ and $g(x)=h(x,c_{2},\ldots ,c_{n-1})=f(x,x,c_{2},\ldots ,c_{n-1})$ does not belong to M. Consider the binary function $f'(x_{1},x_{2}){:}{=}f(x_{1},x_{2},c_{2},\ldots ,c_{n-1}).$ We have $f'\in M^{*}$ (since $f\in M^{*}$) and $\Delta f'\notin M$ (since $g=\Delta f'$ by definition), in contradiction to (iii).

(iii)$\iff$(iv): Let $A=\{1,\ldots ,k\}.$ There is a bijection between binary operations $f:A^{2}\rightarrow A$ and $(k\times k)$-matrices $(a_{ij})$ via $a_{ij}=f(i,j)$ for $i,j\in \{1,\ldots ,k\}.$ Note that rows and columns of $(a_{ij})$ are just the function tables $(f(i,1),\ldots ,f(i,k))$ and $(f(1,j),\ldots ,f(k,j))$ of the translations f(i, x) and f(x, j). Therefore $f\in M^{*}$ (i.e., $\textsf{trl}(f)\subseteq M$ by definition) is equivalent to the property that all rows and columns of $(a_{ij})$ belong to $\Gamma _{M}$ (since the columns of $\Gamma _{M}$ are just the function tables of the unary functions in M), i.e., $\Gamma _{M}\models (a_{ij}).$ Further, $\Delta f\in M$ is equivalent to the property that the diagonal $(a_{11},\ldots ,a_{kk})$ of $(a_{ij})$ belongs to $\Gamma _{M}.$ Thus condition (iii) is equivalent to the reflexivity (because $C\subseteq M$) and transitivity of $\Gamma _{M}$ (according to Definition 3.2), and therefore to $\Gamma _{M}$ being a generalized quasiorder. $\square$

The following corollary is a simple tool to construct functions in the u-closure of a monoid.

Corollary 3.11

Let $A=\{1,\ldots ,k\}$ and $M\le A^{A}.$ If,  for a binary operation $h:A^{2}\rightarrow A,$ we have $h\in (\overline{M})^{*},$ in particular if $h\in M^{*},$ then $\Delta h\in \overline{M}.$

Proof

The statement is just Proposition 3.10(iii) for the u-closed monoid $\overline{M}.$ $\square$

Note that (according to Remark 3.4) for a binary operation h we have $h\in (\overline{M})^{*}$ if and only if $\Gamma _{\overline{M}}\models V$ for the matrix $V{:}{=}(h(i,j))_{i,j\in A}.$

5 The Galois connection ${{\textbf {End}}}$–${\varvec{{{\,\textrm{gQuord}\,}}}}$

The Galois connection End–gQuord 4.1

The preservation property ${\triangleright }$ induces a Galois connection between unary mappings and generalized quasiorders given by the operators

$$\begin{aligned} {\textrm{End}}Q&{:}{=}\{h\in A^{A} \,\,|\,\, \forall \varrho \in Q: h{\triangleright }\varrho \} \text { (endomorphisms) and}\\ {{\,\textrm{gQuord}\,}}M&{:}{=}\{\varrho \in {{\,\textrm{gQuord}\,}}(A) \,\,|\,\, \forall h\in M: h{\triangleright }\varrho \} \text { (generalized quasiorders)} \end{aligned}$$

for $M\subseteq A^{A}$ and $Q\subseteq {{\,\textrm{gQuord}\,}}(A).$ The corresponding Galois closures are ${\textrm{End}}{{\,\textrm{gQuord}\,}}M$ and ${{\,\textrm{gQuord}\,}}{\textrm{End}}Q.$

Now we can show one of our main results, namely that the u-closed monoids are just the Galois closures with respect to the Galois connection ${\textrm{End}}$–${{\,\textrm{gQuord}\,}}.$ As a consequence (as shown in Corollary 4.3 and Proposition 4.4) we can answer the questions raised in the Introduction.

Theorem 4.2

Let $M\subseteq A^{A}.$ Then we have : 

$$\begin{aligned} \overline{M}={\textrm{End}}{{\,\textrm{gQuord}\,}}M. \end{aligned}$$

Proof

At first we observe $M\subseteq {\textrm{End}}{{\,\textrm{gQuord}\,}}M$ (this holds for every Galois connection), $M\subseteq \overline{M}={\textrm{End}}\Gamma _{\overline{M}},$ in particular $M{\triangleright }\Gamma _{\overline{M}},$ and by Proposition 3.10(iv) we know $\Gamma _{\overline{M}}\in {{\,\textrm{gQuord}\,}}(A).$ Thus $\Gamma _{\overline{M}}\in {{\,\textrm{gQuord}\,}}M.$ Consequently we get $\overline{M}\subseteq \overline{{\textrm{End}}{{\,\textrm{gQuord}\,}}M}=_{3.9(ii)}{\textrm{End}}{{\,\textrm{gQuord}\,}}M\subseteq {\textrm{End}}\Gamma _{\overline{M}}=\overline{M},$ and we are done. $\square$

In addition to the characterization in Proposition 3.10 we give some further consequences of Theorem 4.2, characterizing $M^{*}$ (4.3(a)) and u-closed monoids M (4.3(b)). Since every monoid can be given as endomorphism monoid of invariant relations, $M={\textrm{End}}Q,$ we also look for the characterization of those Q with u-closed endomorphism monoid (4.3(c)):

Corollary 4.3

• (a) $(\overline{M})^{*}={{\,\textrm{Pol}\,}}{{\,\textrm{gQuord}\,}}M$ for $M\subseteq A^{A}.$

• (b) The following are equivalent for $M\le A^{A}{:}$

  • (i) M is u-closed,  (i)$'$ $M^{*}$ is a clone,  (i)$''$ $\Gamma _{M}\in {{\,\textrm{gQuord}\,}}(A),$

  • (ii) $M={\textrm{End}}Q$ for some $Q\subseteq {{\,\textrm{gQuord}\,}}(A),$

  • (iii) $M^{*}={{\,\textrm{Pol}\,}}Q$ for some $Q\subseteq {{\,\textrm{gQuord}\,}}(A),$

  where the same Q can be taken in (ii) and (iii).

• (c) The following are equivalent for $Q\subseteq {{\,\textrm{Rel}\,}}(A){:}$

  • (i) ${\textrm{End}}Q$ is u-closed,  (i)$'$$({\textrm{End}}Q)^{*}$ is a clone,  (i)$''$$\Gamma _{{\textrm{End}}Q}{\in }{{\,\textrm{gQuord}\,}}(A),$

  • (ii) $\exists Q'\subseteq {{\,\textrm{gQuord}\,}}(A): {\textrm{End}}Q={\textrm{End}}Q',$

  • (ii)’ $\exists Q'\subseteq {{\,\textrm{gQuord}\,}}(A): [Q]_{\exists ,\wedge ,\vee ,=}=[Q']_{\exists ,\wedge ,\vee ,=}$ (closure under positive formulas)

  • (iii) $\exists Q'\subseteq {{\,\textrm{gQuord}\,}}(A): ({\textrm{End}}Q)^{*}={{\,\textrm{Pol}\,}}Q',$

  where the same $Q'$ can be taken in (ii) and (iii). Instead of “$\exists Q'\subseteq {{\,\textrm{gQuord}\,}}(A)$” one can take “$\exists \varrho \in {{\,\textrm{gQuord}\,}}(A)$” and $Q'=\{\varrho \}.$

Proof

(a): Let $Q{:}{=}{{\,\textrm{gQuord}\,}}M.$ Then $\Xi (Q)$ by Theorem 3.8, i.e., ${{\,\textrm{Pol}\,}}Q=({\textrm{End}}Q)^{*}$ (cf. Definition 2.2(*)). Thus ${{\,\textrm{Pol}\,}}Q=({\textrm{End}}{{\,\textrm{gQuord}\,}}M)^{*}=(\overline{M})^{*}$ by Theorem 4.2.

 (b): For (i)$\iff$(i)$'$ $\iff$(i)$''$ see Remark 2.9(iii) and Proposition 3.10(iv).

(i)$\implies$(ii): Take $Q{:}{=}{{\,\textrm{gQuord}\,}}M.$ If M is u-closed, then $M=\overline{M}=_{4.2}{\textrm{End}}Q.$

(ii)$\implies$(iii): $({\textrm{End}}Q)^{*}={{\,\textrm{Pol}\,}}Q$ directly follows from Corollary 3.9(ii).

(iii)$\implies$(i)$'$ is obvious, because $M^{*}={{\,\textrm{Pol}\,}}Q$ is a clone.

 (c) is just (b) for $M={\textrm{End}}Q.$ (ii)$\iff$(ii)$'$ follows from the properties of the Galois connection ${\textrm{End}}$–${{\,\textrm{Inv}\,}}$ (in particular $[Q]_{\exists ,\wedge ,\vee ,=}={{\,\textrm{Inv}\,}}{\textrm{End}}Q,$ cf. 1.2). Further note, that $Q'=\{\Gamma _{{\textrm{End}}Q}\}$ also will do the job (instead of arbitrary $Q'$) since ${\textrm{End}}Q={\textrm{End}}\Gamma _{{\textrm{End}}Q}.$ $\square$

Now we are also able to answer the question which (sets of) relations satisfy the property $\Xi$ (cf. Definition 2.2):

Proposition 4.4

The following are equivalent for $Q\subseteq {{\,\textrm{Rel}\,}}(A){:}$

• (i) $\Xi (Q)$ holds,  i.e.,  ${{\,\textrm{Pol}\,}}Q=({\textrm{End}}Q)^{*},$

• (ii) $\exists Q'\subseteq {{\,\textrm{gQuord}\,}}(A): {{\,\textrm{Pol}\,}}Q={{\,\textrm{Pol}\,}}Q',$

• (ii)’ $\exists Q'\subseteq {{\,\textrm{gQuord}\,}}(A): [Q]_{\exists ,\wedge ,=}=[Q']_{\exists ,\wedge ,=}$ (closure under primitive positive formulas), 

• (ii)” $[Q]_{\exists ,\wedge ,=}=[[Q]_{\exists ,\wedge ,=}\cap {{\,\textrm{gQuord}\,}}(A)]_{\exists ,\wedge ,=}.$

Proof

(i)$\implies$(ii): Assume ${{\,\textrm{Pol}\,}}Q=({\textrm{End}}Q)^{*}$ and let $M{:}{=}{\textrm{End}}Q$ and $Q'{:}{=}{{\,\textrm{gQuord}\,}}M.$ M is u-closed (since $M^{*}$ is a clone), therefore ${{\,\textrm{Pol}\,}}Q=M^{*}=(\overline{M})^{*}=_4.3(\textrm{a}){{\,\textrm{Pol}\,}}Q'.$

(ii)$\implies$(i): Assume ${{\,\textrm{Pol}\,}}Q={{\,\textrm{Pol}\,}}Q'$ ($Q'\subseteq {{\,\textrm{gQuord}\,}}(A)$). Then ${\textrm{End}}Q={\textrm{End}}Q'$ and we have ${{\,\textrm{Pol}\,}}Q={{\,\textrm{Pol}\,}}Q'=_{3.9(ii)}({\textrm{End}}Q')^{*}=({\textrm{End}}Q)^{*},$ consequently $\Xi (Q)$ by Definition 2.2.

(ii)$\iff$(ii)$'$ follows from the properties of the classical Galois connection ${{\,\textrm{Pol}\,}}$–${{\,\textrm{Inv}\,}}$ (in particular $[Q]_{\exists ,\wedge ,=}={{\,\textrm{Inv}\,}}{{\,\textrm{Pol}\,}}Q,$ cf. 1.2). (ii)$'$ $\iff$(ii)$''$ is obvious. $\square$

Remark 4.5

We know from Theorem 3.8 that $\varrho \in {{\,\textrm{gQuord}\,}}(A)$ implies $\Xi (\varrho ).$ The converse is not true: $\Xi (\varrho )$ does not imply $\varrho \in {{\,\textrm{gQuord}\,}}(A)$ in general! A counterexample is the binary relation $\varrho =\{(i,j) \,\,|\,\, 1\le i,j\le n,\; j\le i+1,\; j\ne i-1\}$ in [16, 3.5] on an at least 5-element set $A=\{1,\ldots ,n\}.$ This relation is strongly C-rigid (what means ${{\,\textrm{Pol}\,}}\varrho =\langle \{\textsf{id}_{A}\}\cup C \rangle _{}$) and reflexive, but not transitive, i.e., $\varrho \notin {{\,\textrm{gQuord}\,}}(A).$ Nevertheless $\Xi (\varrho )$ holds. To see this we have to show ${{\,\textrm{Pol}\,}}\varrho =M^{*},$ where $M{:}{=}{\textrm{End}}\varrho ,$ i.e., $M=\{\textsf{id}_{A}\}\cup C=T.$ M is u-closed (what we shall prove in Proposition 5.1), thus $M^{*}={{\,\textrm{Pol}\,}}\Gamma _{M}$ by Proposition 3.10(ii). By [16, 2.2.], for a clone F,  if its unary part $F^{(1)}$ equals $\{\textsf{id}_{A}\}\cup C,$ then $F=\langle \{\textsf{id}_{A}\}\cup C \rangle _{}.$ Consequently, for $F=M^{*}$ we have $F^{(1)}=M=\{\textsf{id}_{A}\}\cup C$ and therefore we get $M^{*}=\langle \{\textsf{id}_{A}\}\cup C \rangle _{}={{\,\textrm{Pol}\,}}\varrho .$

For $n=5$ we get the relation $\varrho$ shown in Figure 2 (this is a so-called tournament).

Fig. 2

A reflexive but not transitive relation $\varrho$ with $\Xi (\varrho )$

Nevertheless, by Proposition 4.4, $\varrho$ must be “constructively equivalent” to some $Q'\subseteq {{\,\textrm{gQuord}\,}}(A),$ i.e., $[\varrho ]_{\exists ,\wedge ,=}=[Q']_{\exists ,\wedge ,=}.$ In this concrete case we can take $Q'=\{\Gamma _{M}\},$ i.e., we have $[\varrho ]_{\exists ,\wedge ,=}=[\Gamma _{M}]_{\exists ,\wedge ,=},$ since ${{\,\textrm{Pol}\,}}\varrho ={{\,\textrm{Pol}\,}}\Gamma _{M}.$

Before we investigate the u-closure for concrete monoids we show how this closure behaves under taking products and substructures. For this we need some notation.

Definition 4.6

Let $g_{i}\in A_{i}^{A_{i}}$ ($i\in \{1,2\}$) and $A=A_{1}\times A_{2}.$ Then $g{:}{=}g_{1}\otimes g_{2}$ denotes the unary operation $g\in A^{A}$ defined componentwise by $g(a_{1},a_{2}){:}{=}(g_{1}a_{1},g_{2}a_{2}).$ For $M_{i}\subseteq A_{1}^{A_{i}}$ we put $M_{1}\otimes M_{2}{:}{=}\{g_{1}\otimes g_{2} \,\,|\,\, g_{1}\in M_{1}\text { and }g_{2}\in M_{2}\}.$

Further, for $\varrho _{i}\in {{\,\textrm{Rel}\,}}^{(m)}(A_{i})$ and $Q_{i}\subseteq {{\,\textrm{Rel}\,}}(A_{i}),$ $i\in \{1,2\},$ let

$$\begin{aligned} \varrho _{1}\otimes \varrho _{2}&{:}{=}\{((a_{1},b_{1}),\ldots ,(a_{m},b_{m})) \,\,|\,\, (a_{1},\ldots ,a_{m})\in \varrho _{1}\wedge (b_{1},\ldots ,b_{m})\in \varrho _{2}\},\\ Q_{1}\otimes Q_{2}&{:}{=}\{\varrho _{1}\otimes \varrho _{2} \,\,|\,\, \varrho _{1}\in Q^{(m)}_{1}\wedge \varrho _{2}\in Q^{(m)}_{2},\, m\in \mathbb {N}_{+}\}. \end{aligned}$$

Remarks

For monoids $M_{1}, M_{2},$ the product $M_{1}\otimes M_{2}$ is isomorphic (as monoid) to the direct product $M_{1}\times M_{2}.$ In the proof of Proposition 4.7(ii) below, the notation $g_{1}\otimes g_{2}$ is used also for n-ary operations. This is a straightforward generalization of the above definition, given explicitly in [22, 2.3.6]; there also $F_{1}\otimes F_{2}{:}{=} \{f_{1}\otimes f_{2} \,\,|\,\, f_{1}\in F_{1}^{(n)}, f_{2}\in F_{2}^{(n)}, n\in \mathbb {N}_{+}\}$ is defined for clones $F_{1}\subseteq {{\,\textrm{Op}\,}}(A_{1})$ and $F_{2}\subseteq {{\,\textrm{Op}\,}}(A_{2}).$

Proposition 4.7

Let $\textsf{id}_{A_{i}}\in M_{i}\subseteq A_{i}^{A_{i}},$ $i\in \{1,2\}$ and $A=A_{1}\times A_{2}.$ Then we have

• (i) ${{\,\textrm{gQuord}\,}}_{A}(M_{1}\otimes M_{2})=({{\,\textrm{gQuord}\,}}_{A_{1}}M_{1})\otimes ({{\,\textrm{gQuord}\,}}_{A_{2}}M_{2}).$

• (ii) $\overline{M_{1}\otimes M_{2}}=\overline{M_{1}}\otimes \overline{M_{2}}.$

Proof

(i): According to [22, 2.3.7] and because the identity map belongs to $M_{i},$ we have ${{\,\textrm{Inv}\,}}_{A}(M_{1}\otimes M_{2})=({{\,\textrm{Inv}\,}}_{A_{1}}M_{1})\otimes ({{\,\textrm{Inv}\,}}_{A_{2}}M_{2})$ for the invariant relations. Thus, in order to prove (i), it only remains to show that

$$\begin{aligned} \varrho _{1}\otimes \varrho _{2}\in {{\,\textrm{gQuord}\,}}(A) \iff \varrho _{1}\in {{\,\textrm{gQuord}\,}}(A_{1}) \text { and }\varrho _{2}\in {{\,\textrm{gQuord}\,}}(A_{2}) \end{aligned}$$

for $\varrho _{1}\in {{\,\textrm{Rel}\,}}^{(m)}(A_{1})$ and $\varrho _{2}\in {{\,\textrm{Rel}\,}}^{(m)}(A_{2}).$ But this follows from (notation see Definition 3.2)

$$\begin{aligned} \varrho _{1}\models (a_{ij})\text { and } \varrho _{2}\models (b_{ij})&\iff (\varrho _{1}\otimes \varrho _{2})\models ((a_{ij},b_{ij})),\text { and}\\ (a_{11},\ldots ,a_{mm})\in \varrho _{1}\text { and }&(b_{11},\ldots ,b_{mm})\in \varrho _{2}\\ {}&\iff ((a_{11},b_{11}),\ldots ,(a_{mm},b_{mm}))\in \varrho _{1}\otimes \varrho _{2}, \end{aligned}$$

what is clear from the definitions in 4.6.

(ii): The trivial equivalence relations $\Delta _{A_{i}}$ and $\nabla _{A_{i}}$ are (generalized) quasiorders and thus belong to ${{\,\textrm{gQuord}\,}}_{A_{i}}M_{i}$ ($i\in \{1,2\}$). Therefore we can apply $({{\,\textrm{Pol}\,}}_{A_{1}}Q_{1})\otimes ({{\,\textrm{Pol}\,}}_{A_{2}}Q_{2})={{\,\textrm{Pol}\,}}_{A}(Q_{1}\otimes Q_{2})$ from [22, Satz 2.3.7(vi) and Üb 2.4, p.73] (restricting to unary mappings, i.e., taking ${\textrm{End}}$ instead of ${{\,\textrm{Pol}\,}}$ and $Q_{i}={{\,\textrm{gQuord}\,}}M_{i}$) in order to get the second equality in the following conclusions:

$$\begin{aligned} \overline{M_{1}}\otimes \overline{M_{2}}&{\mathop {=}\limits ^{(4.2)}}({\textrm{End}}{{\,\textrm{gQuord}\,}}M_{1})\otimes ({\textrm{End}}{{\,\textrm{gQuord}\,}}M_{2})\\&={\textrm{End}}(({{\,\textrm{gQuord}\,}}M_{1})\otimes ({{\,\textrm{gQuord}\,}}M_{2}))\\&{\mathop {=}\limits ^{(i)}}{\textrm{End}}{{\,\textrm{gQuord}\,}}(M_{1}\otimes M_{2})\\&{\mathop {=}\limits ^{(4.2)}}\overline{M_{1}\otimes M_{2}}. \end{aligned}$$

$\square$

Proposition 4.8

Let $M\subseteq A^{A}$ and $B\in {{\,\textrm{Inv}\,}}M$ for some $\emptyset \ne B\subset A.$ Then

$$\begin{aligned} {{\,\textrm{gQuord}\,}}_{B}(M\mathclose \restriction _{B})=({{\,\textrm{gQuord}\,}}_{A}M)\mathclose \restriction _{B}. \end{aligned}$$

Proof

“$\subseteq$”: Let $\sigma \in {{\,\textrm{gQuord}\,}}^{(m)}(M\mathclose \restriction _{B})$ and $\varrho {:}{=}\sigma \cup \{(a,\ldots ,a)\in A^{m} \,\,|\,\, a\in A{\setminus } B\}.$ Then $\sigma =\varrho \mathclose \restriction _{B}.$ We are going to show $\varrho \in {{\,\textrm{gQuord}\,}}_{A}M.$ Clearly, $\varrho$ is reflexive by construction. To show transitivity, let $\varrho \models (a_{ij})\in A^{m\times m}.$ If $(a_{ij})\in B^{m\times m},$ then $\sigma \models (a_{ij})$ and we get $(a_{11},\ldots ,a_{mm})\in \sigma \subseteq \varrho$ (since $\sigma$ is transitive). If some row or column of $(a_{ij})$ contains an element $a\in A{\setminus } B,$ then by definition of $\varrho$ this row or column must be $(a,\ldots ,a).$ Thus $a_{ij}=a$ for all i, j,  and the diagonal obviously belongs to $\varrho .$ Thus $\varrho$ is transitive, i.e., $\varrho \in {{\,\textrm{gQuord}\,}}(A).$ It remains to show $M{\triangleright }\varrho .$ Let $f\in M$ and $(a_{1},\ldots ,a_{m})\in \varrho .$ Let $g{:}{=}f\mathclose \restriction _{B}\in M\mathclose \restriction _{B}$ and note $g{\triangleright }\sigma$ by assumption. If $(a_{1},\ldots ,a_{m})=(a,\ldots ,a)$ for some $a\in A{\setminus } B,$ then obviously $(fa,\ldots ,fa)\in \varrho .$ Otherwise $(a_{1},\ldots ,a_{m})\in \sigma \subseteq B^{m}$ and we have $(fa_{1},\ldots ,fa_{m})=(ga_{1},\ldots ,ga_{m})\in \sigma \subseteq \varrho ,$ i.e., $f{\triangleright }\varrho .$ Consequently, $\sigma =\varrho \mathclose \restriction _{M}\in ({{\,\textrm{gQuord}\,}}_{A}M)\mathclose \restriction _{B}.$

“$\supseteq$”: Let $\sigma \in ({{\,\textrm{gQuord}\,}}_{A}M)\mathclose \restriction _{B},$ i.e., there is some $\varrho \in {{\,\textrm{gQuord}\,}}_{A}M$ such that $\sigma =\varrho \mathclose \restriction _{B}.$ Then obviously $\sigma$ is reflexive (on B) and also transitive (since each matrix $(b_{ij})\in B^{m\times m}$ can be considered as a matrix in $A^{m\times m}$). Thus $\sigma \in {{\,\textrm{gQuord}\,}}(B).$ It remains to prove $M\mathclose \restriction _{B}{\triangleright }\sigma .$ Take $g=f\mathclose \restriction _{B}\in M\mathclose \restriction _{B}$ (for some $f\in M$) and $(b_{1},\ldots ,b_{m})\in \sigma .$ Since $f{\triangleright }\varrho$ and $f{\triangleright }B$ we also have that f preserves $\varrho \cap B^{m}=\sigma .$ Thus $(gb_{1},\ldots ,gb_{m})=(fb_{1},\ldots ,fb_{m})\in \sigma ,$ i.e., $g{\triangleright }\sigma .$ Consequently, $\sigma \in {{\,\textrm{gQuord}\,}}(M\mathclose \restriction _{B}).$ $\square$

Remark 4.9

We do not consider here the other side of the Galois connection, i.e., the Galois closures of the form ${{\,\textrm{gQuord}\,}}{\textrm{End}}Q$ for $Q\subseteq {{\,\textrm{gQuord}\,}}(A).$ In general, they are not relational clones (contrary to the Galois connection ${\textrm{End}}-{{\,\textrm{Inv}\,}}$). In particular, ${{\,\textrm{Quord}\,}}(A)$ is not a relational clone. It contains all diagonal relations and is closed under several relational clone operations, but, e.g., not under ${{\,\textrm{pr}\,}}$ (i.e., deleting of coordinates). For example, the relation $\varrho {:}{=}\{(0,0,0),(1,1,1),(2,2,2),(2,0,1),(1,1,2)\}$ on $A=\{0,1,2\}$ is a generalized quasiorder (this is easy to check), but ${{\,\textrm{pr}\,}}_{2,3}(\varrho )=\{(x,y) \,\,|\,\, \exists a:(a,x,y)\in \varrho \}=\{(0,0),(1,1),(2,2),(0,1),(1,2)\}$ is not (because it is not transitive).

6 Minimal u-closed monoids

In this section we investigate some special monoids and their u-closure. For a unary function $f\in A^{A}$ let $M_{f}{:}{=}\langle f \rangle _{}\cup C.$ This is the least monoid containing f and all constants. What can be said about the u-closure of such monoids $M_{f}$?

In the following we have to deal much with the relation $\Gamma _{M}$ for a monoid $M=M_{f}$ and with the situation that $\Gamma _{M}\models V$ for some $k\times k$-matrix $V=(v_{ij}),$ $k{:}{=}|A|.$ Therefore it is convenient to identify a $g\in M$ with the vector $\textbf{r}_{g}=(ga_{1},\ldots ,ga_{k})$ (cf. Notation 3.1, here we assume $A=\{a_{1},\ldots ,a_{k}\}$ where A is implicitly ordered by the indices of $a_{i}$). Thus we can say that a row or column $\textbf{r}$ of V equals some “vector” (k-tuple) $g\in M$ and write $\textbf{r}=g$ meaning $\textbf{r}=(ga_{1},\ldots ,ga_{k}).$ This will be used very often in the proofs (in great detail in the proof of Proposition 5.1). Furthermore, let $\varvec{v}_{i,*}{:}{=}(v_{i1},\ldots ,v_{ik})$ and $\varvec{v}_{*,i}{:}{=}(v_{1i},\ldots ,v_{ki})$ denote the i-th row and the i-th column of $V=(v_{ij}),$ respectively ($i\in \{1,\ldots ,k\}$). Note that $\Gamma _{M_{f}}$ is reflexive since $M_{f}$ contains all constants.

For the trivial monoid $T{:}{=}M_{\textsf{id}_{A}}=\{\textsf{id}_{A}\}\cup C$ we have:

Proposition 5.1

The monoid $T=\{\textsf{id}_{A}\}\cup C$ is u-closed.

Proof

Let $A=\{a_{1},\ldots ,a_{k}\}.$ We show that $\Gamma _{T}$ is a generalized quasiorder (then we are done due to Proposition 3.10(iv)). $\Gamma _{T}$ is reflexive, thus it remains to show that $\Gamma _{T}$ is transitive. Let $V=(v_{ij})_{i,j\in \{1,\ldots ,k\}}$ be a $k\times k$-matrix such that $\Gamma _{T}\models V,$ i.e., each row and each column is one of the “vectors” $g\in T,$ namely $\textsf{id}_{A}=(a_{1},\ldots ,a_{k})$ or one of the constants $\varvec{c}_{1}=(a_{1},\ldots ,a_{1}),$..., $\varvec{c}_{k}=(a_{k},\ldots ,a_{k})$ ($\varvec{c}_{i}$ denotes the constant mapping $\varvec{c}_{i}(x)=a_{i}$). If $v_{jj}=a_{i}$ for some $i\ne j,$ then $\Gamma _{T}\models V$ can hold only if all rows and columns are equal to the constant $\varvec{c}_{i}$ (since $\varvec{c}_{i}$ is the only vector where $a_{i}$ is on the j-th place), in particular, the main diagonal of V also equals $\varvec{c}_{i}$ and therefore belongs to $\Gamma _{T}.$ It remains the case $v_{ii}=a_{i}$ for all $i\in \{1,\ldots ,k\}.$ Then the diagonal of V is $\textsf{id}_{A},$ also belonging to $\Gamma _{T}.$ Consequently, $\Gamma _{T}$ is transitive. $\square$

For $|A|=2$ there exist only two monoids containing all constants, namely T and $A^{A},$ both are u-closed (the first by Proposition 5.1, the second trivially). Therefore, in the following, we always can assume $|A|\ge 3.$

We are going to characterize the minimal u-closed monoids, i.e., u-closed monoids $M\le A^{A}$ which properly contain no other u-closed monoid except the trivial monoid $T=\{\textsf{id}_{A}\}\cup C.$ Such minimal u-closed monoids must be generated by a single function, i.e., they must be of the form $\overline{M_{f}}$ for some unary f,  moreover, $M_{f}$ can be assumed to be C-minimal, i.e., minimal among all monoids properly containing T (otherwise $M_{f'}< M_{f}$ would imply $\overline{M_{f'}}\le \overline{M_{f}}$ and $\overline{M_{f}}$ could be canceled in the list of minimal u-closed monoids).

It is well-known which unary functions f generate a C-minimal monoid $M_{f}\le A^{A}$ (it follows, e.g., from [22, 4.1.4]), namely if and only if $f\in A^{A}$ is a nontrivial (i.e., $f\notin T$) function satisfying one of the following conditions:

• (i) $f^{2}=f,$

• (ii) $f^{2}$ is constant,

• (iii) f is a permutation, such that $f^{p}=\textsf{id}_{A}$ for some prime number p.

As shown in [10, Theorem 3.1], among these functions are those for which the quasiorder lattice ${{\,\textrm{Quord}\,}}f$ is maximal among all quasiorder lattices (on A), equivalently, for which ${\textrm{End}}{{\,\textrm{Quord}\,}}f$ is minimal (among all endomorphism monoids of quasiorders). These functions are of so-called type I, II or III, defined as follows:

• (I) $f^{2}=f,$

• (II) $f^{2}$ is constant, say v,  and $|\{x\in A \,\,|\,\, fx=v\}|\ge 3,$

• (III) f is a permutation with at least two cycles of length p,  such that $f^{p}=\textsf{id}_{A}$ for some prime number p.

Note that $\langle f \rangle _{}=\{\textsf{id}_{A},f\}$ for f of type I and II, while for f of type III, $\langle f \rangle _{}=\{\textsf{id}_{A},f,f^{2},\ldots ,f^{p-1}\}$ is a cyclic group of prime order.

Surprisingly it turns out (see Theorem 5.3) that for each candidate $M_{f}$ with f satisfying (i)–(iii), the u-closure $\overline{M_{f}}$ is either not a minimal u-closed monoid or $M_{f}$ itself is already u-closed. Thus the minimal u-closed monoids coincide with the u-closed C-minimal monoids. We start with the functions of type I, II and III.

Proposition 5.2

Let f be a function of type I,  II or III. Then $M_{f}$ is a minimal u-closed monoid,  in particular $M_{f}=\overline{M_{f}}.$ Moreover,  for these monoids we have ${\textrm{End}}{{\,\textrm{gQuord}\,}}M_{f}={\textrm{End}}{{\,\textrm{Quord}\,}}M_{f}.$

Proof

Clearly, $\langle f \rangle _{}\cup C=M_{f}\subseteq {\textrm{End}}{{\,\textrm{gQuord}\,}}M_{f}\subseteq {\textrm{End}}{{\,\textrm{Quord}\,}}M_{f}.$ But we have ${\textrm{End}}{{\,\textrm{Quord}\,}}M_{f}=\langle f \rangle _{}\cup C$ as it was explicitly stated in [13, Theorem 2.1(B)] (but it already follows from the results in [8, 9] and also from [11, 4.8]). Thus we have equality instead of the above inclusions and $M_{f}$ is u-closed (by Theorem 4.2). Since $M_{f}$ has no proper submonoids except T because f satisfies one of the above conditions (i)–(iii), it is a minimal u-closed monoid. $\square$

Theorem 5.3

Let $3\le |A|<\infty .$ The minimal u-closed monoids $M\le A^{A}$ are exactly those of the form $M_{f}=\langle f \rangle _{}\cup C$ where $f\in A^A$ is nontrivial and satisfies

• (I) $f^2=f,$ or

• (II$')$ $f^2$ is a constant and $|A|\ge 4,$ or

• (III$')$ $f^p=\textsf{id}_A$ for some prime p such that f has at least two fixed points or f is of type III.

In particular,  each minimal u-closed monoid is C-minimal,  too.

Proof

Part 1: At first we show that $M_{f}$ is u-closed for all functions of type I, and of the new type II$'$ or III$'.$ Because of Proposition 5.2, it remains to check only those functions which are of type II$'$ or III$',$ but not of type II or III, respectively.

Case 1: f is of type II$'$ but not of type II, i.e., $f^{2}$ is constant, denoted by 1,  $|\{x\in A \,\,|\,\, fx=1\}|=2$ and $|A|\ge 4.$

For simplicity we denote the elements of A by natural numbers, $A=\{1,2,\ldots ,k\},$ where $f1=1$ and $f2=1$ (otherwise $fx=2$), $k\ge 4.$ Thus f has the form as given in Figure 3(a). Observe that $M_{f}=\{\textsf{id}_{A},f,\varvec{c}_{1},\ldots ,\varvec{c}_{k}\}$ ($\varvec{c}_{i}$ denotes the constant function i).

Fig. 3

The function f for Case 1 and Case 2 in the proof of Theorem 5.3

As in the proof of Proposition 5.1 it is enough to show that $\Gamma _{M_{f}}$ is transitive. Assume $\Gamma _{M_{f}}\models V$ for a matrix $V=(v_{ij})_{i,j\in A},$ i.e., the rows and columns of V all are of the form $\textsf{id}_{A}=(1,2,3,\ldots ,k),$ $f=(1,1,2,\ldots ,2)$ or $\varvec{c}_{i}=(i,i,i,\ldots ,i)$ ($i\in \{1,\ldots ,k\}$). We have to show that the diagonal $d_{V}{:}{=}(v_{11},\ldots ,v_{mm})$ belongs to $\Gamma _{M_{f}}.$ Step by step we reduce the cases to be checked.

(a) We start with $v_{11}=i\ne 1$ for some $i\in \{2,\ldots ,k\}.$ Then $\varvec{v}_{1,*}=\varvec{c}_{i}$ (otherwise $\varvec{v}_{1,*}\notin \Gamma _{M_{f}}$), thus, for each $j\in \{2,\ldots ,k\}$ we have $v_{1j}=i$ what implies $\varvec{v}_{*,j}=\varvec{c}_{i}.$ Consequently $d_{V}=\varvec{c}_{i}\in \Gamma _{M_{f}}$ and we are done.

(b) Now we can assume $v_{11}=1.$ Then $\varvec{v}_{1,*}, \varvec{v}_{*,1}\in \{\textsf{id}_{A},f,\varvec{c}_{1}\}$ what implies $\varvec{v}_{2,*}\in \{\textsf{id}_{A},f,\varvec{c}_{1}\}$ and therefore we have $v_{12},v_{21},v_{22}\in \{1,2\}.$

Let $\boxed {v_{22}=1}$. Then $\varvec{v}_{*,2},\varvec{v}_{2,*}\in \{f,\varvec{c}_{1}\}$ (because f and $\varvec{c}_{1}$ are the only elements of $\Gamma _{M_{f}}$ with value 1 in the second component), in particular $v_{2i}\in \{1,2\}$ for all i.

If $\varvec{v}_{*,i}=\varvec{c}_{j}$ is constant for some $i\ge 3,$ then $j\in \{1,2\}$ (because $v_{2i}\in \{1,2\}$) and all rows $\varvec{v}_{\ell ,*}$ must be equal to $\varvec{c}_{j}$ for all $\ell \ge 3,$ consequently $d_{V}=(1,1,j,\ldots ,j)\in \Gamma _{M_{f}}$ for $j\in \{1,2\}.$ The same argument applies for the cases where $\varvec{v}_{i,*}=\varvec{c}_{j}$ for some $i\ge 3$ (change the role of rows and columns).

If $\varvec{v}_{*,i}=f$ for some $i\ge 3,$ then all rows $\varvec{v}_{\ell ,*}$ must be equal to f for all $\ell \ge 3$ (in no other element of $\Gamma _{M_{f}}$ appears 2 at the i-th place; the constant $\varvec{c}_{2}$ can be excluded because this case already was considered above), consequently $d_{V}=(1,1,2,\ldots ,2)\in \Gamma _{M_{f}}.$ As above (changing the role of rows and columns), the same argument applies for the cases where $\varvec{v}_{i,*}=f$ for some $i\ge 3.$

Thus it remains to consider the case that all $\varvec{v}_{*,i}$ and $\varvec{v}_{i,*}$ ($i\ge 3$) are neither f nor some $\varvec{c}_{j}.$ However then all these columns and rows were equal to $\textsf{id}_{A},$ but this cannot appear because, e.g., $\varvec{v}_{3,*}=\textsf{id}_{A}$ and $\varvec{v}_{*,4}=\textsf{id}_{A}$ would give $v_{34}=4$ and $v_{34}=3,$ respectively, a contradiction. Note that here is used the fact $k\ge 4.$

Now let $\boxed {v_{22}=2}$. Then $\varvec{v}_{2,*}\in \{\textsf{id}_{A},\varvec{c}_{2}\}.$

If $\varvec{v}_{2,*}=\textsf{id}_{A},$ then we must have $\varvec{v}_{*,j}=\varvec{c}_{j}$ for $j\ge 3,$ thus $d_{V}=(1,2,3,\ldots ,k)\in \Gamma _{M_{f}}.$ If $\varvec{v}_{2,*}=\varvec{c}_{2},$ then we must have $\varvec{v}_{*,1}=\textsf{id}_{A}$ (recall $v_{11}=1$). Consequently, $\varvec{v}_{j,*}=\varvec{c}_{j}$ for $j\ge 3$ and we also get $d_{V}=(1,2,3\dots ,k)\in \Gamma _{M_{f}}.$

Case 2: f is of type III$'$ but not of type III, i.e., $f^{p}=\textsf{id}_{A}$ for some prime p and the permutation f has only one cycle of length p but m fixed points $z_{1},\ldots ,z_{m}$ where $m\ge 2.$

For simplicity let $A=\{0,1,\ldots ,p-1,z_{1},\ldots ,z_{m}\}$ where $0,1,\ldots ,p-1$ denote the elements of the cycle, i.e., $f=(0\,1\,\dots \, p-1)(z_{1})\ldots (z_{m}),$ moreover let $k{:}{=}p+m=|A|,$ cf. Figure 3(b). Thus $\Gamma _{M_{f}}$ consists of the n-tuples $f^{i}=(i,i+1,\ldots ,i+p-1,z_{1},\ldots ,z_{m})$ ($i\in \mathbb {Z}_{p}=\{0,1,\ldots ,p-1\},$ all counting in $\mathbb {Z}_{p}$ is done modulo p) and all constants $\varvec{c}_{a}=(a,a,\ldots ,a),$ $a\in A.$

We have to show that $\Gamma _{M_{f}}$ is transitive. Thus let $\Gamma _{M_{f}}\models V$ where V is an $(k\times k)$-matrix $V=(v_{ij})_{i,j\in A}$ (here we enumerate the rows and columns by the elements of A).

If $v_{00}=z$ is a fixed point $z\in \{z_{1},\ldots ,z_{m}\}$ then all columns and rows of V (as elements of $\Gamma _{M_{f}}$) must be equal to $\varvec{c}_{z},$ thus $d_{V}=(z,\ldots ,z)\in \Gamma _{M_{f}}.$

Let $v_{00}=i$ for some $i\in \mathbb {Z}_{p}.$ Then $\varvec{v}_{*,0}\in \{\varvec{c}_{i},f^{i}\}.$

Assume $\varvec{v}_{*,0}=\varvec{c}_{i}.$ If there exists some row $\varvec{v}_{j,*}=f^{i}$ (for some $j\in \mathbb {Z}_{p}$), then $v_{j,z}=z$ and therefore $\varvec{v}_{*,z}=z$ for each $z\in \{z_{1},\ldots ,z_{m}\}.$ Thus the last m columns are all different, what implies $\varvec{v}_{a,*}=f^{i}$ for all $a\in A$ (here we need $m\ge 2$). Consequently, $d_{V}=(i,i+1,\ldots ,i+p-1,z_{1},\ldots ,z_{m})\in \Gamma _{M_{f}}.$

Otherwise (if such a row $\varvec{v}_{j,*}=f^{i}$ does not exist), all rows $\varvec{v}_{j,*}$ ($j\in \mathbb {Z}_{p}$) must be equal to $\varvec{c}_{i},$ what implies $\varvec{v}_{*,z}=\varvec{c}_{i}$ for $z\in \{z_{1},\ldots ,z_{m}\},$ consequently $d_{V}=(i,\ldots ,i,\ldots ,i)\in \Gamma _{M_{f}}.$ The same arguments apply to the case $\varvec{v}_{0,*}=\varvec{c}_{i}$ resulting in $d_{V}\in \Gamma _{M_{f}}.$

Thus it remains to consider the case $\varvec{v}_{*,0}=f^{i}$ and $\varvec{v}_{0,*}=f^{i}.$ However, this case cannot occur since then $\varvec{v}_{z_{1},*}=\varvec{c}_{z_{1}}$ and $\varvec{v}_{*,z_{2}}=\varvec{c}_{z_{2}}$ leads to the contradiction $v_{z_{1},z_{2}}=z_{1}$ and $v_{z_{1},z_{2}}=z_{2}$ (note $m\ge 2$).

Part 2: Now we show that there are no more minimal u-closed monoids than those of type I, II$'$ and III$'.$ There are only the following two cases (A) and (B) for functions f to be considered for which $M_{f}$ is C-minimal (i.e., satisfies (i)–(iii)) but which are not of type I, II$'$ or III$'.$ We are going to show that for these f the u-closure $\overline{M_{f}}$ is not minimal what will finish the proof of the Theorem.

Case (A): $f^{2}$ is constant and $|A|=3.$

There is only one (up to isomorphism) such function f on a 3-element set and we use the notation from Figure 4(A). Then $M_{f}=\{\textsf{id}_{A},f,\varvec{c}_{0},\varvec{c}_{1},\varvec{c}_{2}\}.$ Consider the binary mapping h defined by the following table:

$$\begin{aligned}{}\begin{array}{c|ccc||c} h &{} \quad 0&{}\quad 1&{}\quad 2&{}\quad \in \Gamma _{M_{f}}\\ \hline 0 &{}\quad 0&{}\quad 0&{}\quad 0&{}\quad \varvec{c}_{0}\\ 1 &{}\quad 0&{}\quad 0&{}\quad 1&{}\quad f\\ 2 &{}\quad 0&{}\quad 1&{}\quad 2&{}\quad \textsf{id}_{A}\\ \hline \end{array} \end{aligned}$$

Clearly $h\in M_{f}^{*}$ (as indicated in the last column). Therefore (cf. Corollary 3.11) $g{:}{=}\Delta h\in \overline{M_{f}}$ where g is a function of type I. Thus, by Proposition 5.2, we get $\overline{M_{g}}=M_{g}\subset \overline{M_{f}},$ i.e., $\overline{M_{f}}$ is not minimal u-closed.

Fig. 4

The remaining functions of type (ii) and (iii) in the proof of Theorem 5.3

Case (B): $f^{p}=\textsf{id}_{A},$ f consists of a single p-cycle and has at most one fixed point.

For f we use the notation as in Figure 4(B), $A=\{0,1,\ldots ,p-1,z\}.$ All computation in $\mathbb {Z}_{p}=\{0,1,\ldots ,p-1\}$ is done modulo p. If f has no fixed point, z can be ignored in all what follows. We have

$M_{f}=\{\textsf{id},f,f^{2},\ldots ,f^{p-1},\varvec{c}_{0},\varvec{c}_{1},\ldots ,\varvec{c}_{p-1},\varvec{c}_{z}\}.$

Consider the binary mapping h defined by the following table:

Clearly $h\in M^{*}$ (indicated in the last column). Therefore (cf. Corollary 3.11) $g{:}{=}\Delta h\in \overline{M_{f}}$ and g is the permutation $g:x\mapsto 2x$ for $x\in Z_{p}$ and $gz=z.$ Note that 0 is an additional fixed point. First we consider the case that $p\ge 5.$ In the group generated by g there must exist an element $g'$ of prime order q with $q<p.$ Since $p\ge 5,$ g has either more than one q-cycle or at least two fixed points, i.e., $g'$ is of type III$'.$ Since $g'\in \langle g \rangle _{}\subseteq \overline{M_{f}}$ we get (with Proposition 5.2) $\overline{M_{g'}}=M_{g'}\subset \overline{M_{f}},$ i.e., $\overline{M_{f}}$ is not minimal u-closed.

It remains to consider the cases $p=2$ and $p=3.$ For $p=3,$ we get $g=(0)(12)(z)$ (in cycle notation) if there exists a fixed point z what is a function of type III$',$ and we can continue as above with $g'.$ Otherwise we have $g=(0)(12).$ For $p=2$ there must exist the fixed point z (since $|A|\ge 3$), i.e., we have $f=(01)(z),$ what is a function of the same form as g in case $p=3$ (up to isomorphism). Thus we can continue with g. Take the function $h'$ given by the table

$$\begin{aligned}{}\begin{array}{c|ccc||c} h'&{}\quad 0&{}\quad 1&{}\quad 2&{}\quad \in \Gamma _{M_{g}}\\ \hline 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad \varvec{c}_{0}\\ 1&{}\quad 0&{}\quad 1&{}\quad 2&{}\quad \textsf{id}_{A}\\ 2&{}\quad 0&{}\quad 2&{}\quad 1&{}\quad g\\ \hline \end{array} \end{aligned}$$

Then $h'\in M_{g}^{*}$ (as indicated in the last column) and therefore $g''{:}{=}\Delta h'$ belongs to $\overline{M_{g}}\subseteq \overline{M_{f}}.$ But $g''$ is a function of type I ($g'0=0,$ $g'2=g'1=1$). Thus, as above, $\overline{M_{g''}}=M_{g''}\subset \overline{M_{f}},$ i.e., $\overline{M_{f}}$ is not minimal u-closed. $\square$

Remark 5.4

Comparing Theorem 5.3 with the above mentioned results from [10], we can conclude that there are monoids $M\le A^{A}$ which are characterizable by generalized quasiorders but not by quasiorders, i.e., we have $M={\textrm{End}}{{\,\textrm{gQuord}\,}}M$ but $M\subsetneqq {\textrm{End}}{{\,\textrm{Quord}\,}}M$ (namely those $M_{f}$ with f of type II$'$ or III$'$ but not of type II or III). With other words, generalized quasiorders are really more powerful than quasiorders (or congruences).

For $|A|=3,$ M. Behrisch (personal communication) computed all monoids of the form ${\textrm{End}}Q$ for $Q\subseteq {{\,\textrm{gQuord}\,}}(A)$ and of the form ${\textrm{End}}Q$ for $Q\subseteq {{\,\textrm{Quord}\,}}(A),$ their number is 89 and 71, respectively, among all 699 monoids $M\le A^{A}.$

Remark 5.5

Let $A=\mathbb {Z}_{k}=\{0,1,\ldots ,k-1\},$ $k\ge 2,$ and let $\gamma _{k}\in A^{A}$ be the full cycle $\gamma _{k}=(01\dots k{-}1),$ i.e., $\gamma _{k}(x)=x+1$ (all computation is done modulo k). Consider the monoid $M_{\gamma _{k}}=\langle \gamma _{k} \rangle _{{\textrm{Sym}}(A)}\cup C$ where $\langle \gamma _{k} \rangle _{{\textrm{Sym}}(A)}$ denotes the subgroup (of the full symmetric group ${\textrm{Sym}}(A)$ of all permutations on A) generated by $\gamma _{k}.$ It can be shown (unpublished result) that for the u-closure $\overline{M_{\gamma _{k}}}=\overline{\langle \gamma _{k} \rangle _{{\textrm{Sym}}(A)}}$ we need only congruence relations instead of all generalized quasiorders (cf. Theorem 4.2), i.e., we have $\overline{M_{\gamma _{k}}}={\textrm{End}}{{\,\textrm{Con}\,}}M_{\gamma _{k}}.$ This closure contains much more elements than $M_{\gamma _{k}}$ (namely, if $k=p_{1}^{m_{1}}\cdot \ldots \cdot p_{n}^{m_{n}}$ is the decomposition of k into powers of different primes, then we have $|\overline{M_{\gamma _{k}}}|= \sum _{i=1}^{n}p_{i}^{\,p_{i}+p_{i}^{2}+\ldots +p_{i}^{m_{i}}}$). In particular, $M_{\gamma _{k}}$ is not u-closed (what was proved, at least for prime $k=p,$ already with Part II, Case (B), in the proof of Theorem 5.3).

The lattices ${\mathcal {K}}^{(m)}_{A}$ 5.6

For fixed base set A and fixed arity $m\in \mathbb {N}_{+},$ the set ${{\,\textrm{gQuord}\,}}^{(m)}(A,F)$ of all m-ary generalized quasiorders of an algebra (A, F) forms a lattice with respect to inclusion (where one can restrict F to unary mappings because of Theorem 3.8). All these lattices together also form a lattice, namely

$$\begin{aligned} {\mathcal {K}}^{(m)}_{A}{:}{=}\{{{\,\textrm{gQuord}\,}}^{(m)}(A,F) \,\,|\,\, F\subseteq A^{A}\}. \end{aligned}$$

For $m=2$ this lattice was investigated in [10] (note that ${{\,\textrm{Quord}\,}}(A,F)={{\,\textrm{gQuord}\,}}^{(2)}(A,F)$). Due to the Galois connection ${\textrm{End}}$–${{\,\textrm{gQuord}\,}}$ the lattice ${\mathcal {K}}^{(m)}_{A}$ is dually isomorphic to the lattice of all those u-closed monoids $M\le A^{A}$ which are endomorphism monoids of m-ary generalized quasiorders.

The “largest” lattice ${\mathcal {K}}^{(k)}_{A}$ with $k{:}{=}|A|$ is isomorphic to the lattice of all u-closed monoids. With Theorem 5.3 we also determined the maximal elements of this lattice ${\mathcal {K}}^{(k)}_{A},$ which are of the form ${{\,\textrm{gQuord}\,}}M_{f}$ with f satisfying one of the conditions I, II$'$ or III$'.$

This ${\mathcal {K}}^{(k)}_{A}$ contains all ${\mathcal {K}}^{(m)}_{A}$ for $m<k$ via an order embedding. In fact, for $m<n,$ there is an order embedding $\varphi ^{m}_{n}:{\mathcal {K}}^{(m)}_{A}\hookrightarrow {\mathcal {K}}^{(n)}_{A}$ given by $\varphi ^{m}_{n}({{\,\textrm{gQuord}\,}}^{(m)}(A,F)){:}{=}{{\,\textrm{gQuord}\,}}^{(n)}(A,\widehat{F})$ with $\widehat{F}{:}{=}{\textrm{End}}{{\,\textrm{gQuord}\,}}^{(m)}(A,F).$

Conversely, there is a surjective order preserving map $\psi ^{n}_{m}:{\mathcal {K}}^{(n)}_{A}\rightarrow {\mathcal {K}}^{(m)}_{A}$ given by $\psi ^{n}_{m}({{\,\textrm{gQuord}\,}}^{(n)}(A,F)){:}{=}{{\,\textrm{gQuord}\,}}^{(m)}(A,F).$ This mapping is well-defined because ${{\,\textrm{gQuord}\,}}^{(m)}(A,F)$ is “contained” in ${{\,\textrm{gQuord}\,}}^{(n)}(A,F))$ since ${{\,\textrm{gQuord}\,}}^{(m)}(A,F)=\{\varrho \in {{\,\textrm{Rel}\,}}^{(m)}(A) \,\,|\,\, A^{n-m}\times \varrho \in {{\,\textrm{gQuord}\,}}^{(n)}(A,F)\}$ where $A^{n-m}\times \varrho =\{(a_{1},\ldots ,a_{n-m},b_{1},\ldots ,b_{m}) \,\,|\,\, a_{1},\ldots ,a_{m}\in A, (b_{1},\ldots ,b_{m})\in \varrho \}$ (it is easy to see that $A^{n-m}\times \varrho$ is a generalized quasiorder if and only if $\varrho$ is). Thus $\varrho \mapsto A^{n-m}\times \varrho$ is an order embedding from ${{\,\textrm{gQuord}\,}}^{(m)}(A,F)$ into ${{\,\textrm{gQuord}\,}}^{(n)}(A,F).$

7 Concluding remarks

An algebra (A, F) is called affine complete if every function compatible with all congruence relations of (A, F) is a polynomial function, equivalently (for finite A), if ${{\,\textrm{Pol}\,}}{{\,\textrm{Con}\,}}(A,F)$ is the clone $\langle F\cup C \rangle _{A}$ generated by F and the constants C. With the notation introduced in Definition 2.1(3) (and due to Remark 2.3) we have:

$$\begin{aligned} (A,F)\text { affine complete}&\iff \langle F\cup C \rangle _{A}={{\,\textrm{Pol}\,}}{{\,\textrm{Con}\,}}(A,F),\\&\iff \exists Q\subseteq {{{\,\textrm{Eq}\,}}(A)}:\\&\langle F\cup C \rangle _{A}=M^{*} \text { for } M{:}{=}{\textrm{End}}Q. \end{aligned}$$

Instead of equivalence relations we may now consider other relations which also satisfy the property $\Xi$ (cf. Definition 2.2). This leads to the notion generalized quasiorder complete, or ${{\,\textrm{gQuord}\,}}$-complete for short, which can be defined and characterized as follows:

$$\begin{aligned} (A,F) {{\,\textrm{gQuord}\,}}-\text {complete}:&\iff \langle F\cup C \rangle _{A}={{\,\textrm{Pol}\,}}{{\,\textrm{gQuord}\,}}(A,F)\\&\iff \exists Q\subseteq {{{\,\textrm{gQuord}\,}}(A)}:\\&\langle F\cup C \rangle _{A}=M^{*} \text { for } M{:}{=}{\textrm{End}}Q\\&\iff \exists \text { u-closed } M\le A^{A}: \langle F\cup C \rangle _{A}=M^{*}. \end{aligned}$$

As an intermediate step one might introduce ${{\,\textrm{Quord}\,}}$-complete algebras (replacing ${{\,\textrm{gQuord}\,}}$ by ${{\,\textrm{Quord}\,}}$ above).

Clearly, affine completeness implies ${{\,\textrm{gQuord}\,}}$-completeness (but not conversely). Thus it is natural to ask which algebraic properties of affine complete algebras remain valid for ${{\,\textrm{gQuord}\,}}$-complete algebras. Moreover, what can be said about varieties generated by ${{\,\textrm{gQuord}\,}}$-complete algebras?

We recall that a variety ${\mathcal {V}}$ is called affine complete, if all algebras $A\in {\mathcal {V}}$ are affine complete. Similarly, we can define a ${{\,\textrm{gQuord}\,}}$-complete variety by the property that all its algebras $A\in {\mathcal {V}}$ are ${{\,\textrm{gQuord}\,}}$-complete. Hence, by our definition, ${{\,\textrm{gQuord}\,}}$-complete varieties can be considered a generalization of the affine complete varieties. It is known that any affine complete variety is congruence distributive (see e.g. [14]). There arises the question what are the properties of ${{\,\textrm{gQuord}\,}}$-complete varieties, could they be still congruence distributive? In the paper [14] also a characterization of affine complete arithmetical varieties is established (A variety is called arithmetical, if any algebra in it is congruence distributive and congruence permutable.) Therefore, it is meaningful to ask if there exists any characterization for ${{\,\textrm{gQuord}\,}}$-complete arithmetical algebras.

We mention some further topics for research:

• Characterize the u-closed monoids which are already given by their quasiorders or congruences (cf. Remarks 5.4, 5.5), i.e., characterize monoids M with the property $M={\textrm{End}}{{\,\textrm{gQuord}\,}}M={\textrm{End}}{{\,\textrm{Quord}\,}}M$ or $M={\textrm{End}}{{\,\textrm{gQuord}\,}}M={\textrm{End}}{{\,\textrm{Con}\,}}M,$ respectively.

• Characterize the Galois closures ${{\,\textrm{gQuord}\,}}{\textrm{End}}Q,$ cf. Remark 4.9.

• Investigate the lattices ${\mathcal {K}}^{(m)}_{A}$ (Remark 5) and their interrelations.

8 Remarks by two of the coauthors

In June 2022, a Honorary colloquium on the occasion of Reinhard Pöschel’s 75th birthday was held in Dresden. There R. Pöschel presented a talk containing the basics of this article [12]. The colloquium was organized by M. Bodirsky and M. Schneider, who at the same time informed about a forthcoming topical collection of Algebra Universalis, which will be dedicated to R. Pöschel. At that time, the full version of the presented results was not yet written.

We, the coauthors of the results, also wanted to contribute to this honorary commemoration and therefore here — because with Reinhard as coauthor we cannot submit it to the topical collection — we use the presentation of our common results as an opportunity to express our deep respect and gratitude to Reinhard, for his inventiveness, creativity, energy, and for his kindness. For more than 16 years we both have been working successfully together with Reinhard who was the initiator of many of our joint works. Our thanks also go to Martin Schneider for his helpful hints.

June 2023 Danica Jakubíková-Studenovská and Sándor Radeleczki