On a generalized notion of metrics

Abstract

In these notes we generalize the notion of a (pseudo) metric measuring the distance of two points, to a (pseudo) n-metric which assigns a value to a tuple of $n \ge 2$ points. Some elementary properties of pseudo n-metrics are provided and their construction via exterior products is investigated. We discuss some examples from the geometry of Euclidean vector spaces leading to pseudo n-metrics on the unit sphere, on the Stiefel manifold, and on the Grassmann manifold. Further, we construct a pseudo n-metric on hypergraphs and discuss the problem of generalizing the Hausdorff metric for closed sets to a pseudo n-metric.

1 Introduction

The classical notion of a (pseudo) metric or distance on a set X is a map which assigns to any two points in X a real value such that d is (semi-)definite, symmetric, and satisfies the triangle inequality. Since the subject is vast we just mention [13] as an elementary and [7] as an advanced monograph. The purpose of this contribution is to investigate an n-dimensional ($n \ge 2$) generalization of this notion. To be precise, we call a map

$$\begin{aligned} d:X^n=\prod _{i=1}^n X \rightarrow {\mathbb {R}}\end{aligned}$$

a pseudo n-metric on X if it has the following properties:

• (i) (Semidefiniteness) If $x=(x_1,\ldots ,x_n)\in X^n$ satisfies $x_i=x_j$ for some $i\ne j$, then $d(x_1,\ldots ,x_n)=0$.

• (ii) (Symmetry) For all $x=(x_1,\ldots ,x_n)\in X^n$ and all $\pi \in \mathcal {P}_n$

  $$\begin{aligned} d(x_{\pi (1)},\ldots ,x_{\pi (n)})= d(x_1,\ldots ,x_n). \end{aligned}$$

  (1)

  Here $\mathcal {P}_n$ denotes the group of permutations of $\{1,\ldots ,n\}$.

• (iii) (Simplicial inequality) For all $x=(x_1,\ldots ,x_n)\in X^n$ and $y \in X$

  $$\begin{aligned} d(x_1,\ldots ,x_n) \le \sum _{i=1}^n d(x_1,\ldots ,x_{i-1},y,x_{i+1},\ldots ,x_n). \end{aligned}$$

  (2)

Clearly, a pseudo 2-metric agrees with the notion of an ordinary pseudo metric. If we sharpen condition (i) to definiteness, i.e. $d(x_1,\ldots ,x_n) = 0$ implies $x_i=x_j \text { for some } i\ne j$, then we call d an n-metric. Most of our examples below with $n \ge 3$ will not have this stronger property. So we consider definiteness to be an exceptional case.

The most important example of a pseudo n-metric occurs in Eudlidean vector spaces when $d(x_1,\ldots , x_n)$ is taken as the volume of the simplex $\mathcal {S}(x_1,\ldots ,x_n)$ spanned by $x_1,\ldots ,x_n$ or (up to a factor of $(n-1)!$) as the volume of the parallelepiped spanned by $x_2-x_1,\ldots ,x_n-x_1$ (see Theorem 1). While semidefiniteness and symmetry are obvious in this case, the simplicial inequality reflects the fact that $\mathcal {S}(x_1,\ldots ,x_n)$ is covered by the union of the simplices $\mathcal {S}(x_1,\ldots ,x_{i-1},y,x_{i+1},\ldots ,x_n)$, $i=1,\ldots ,n$ (with equality in case $y\in \mathcal {S}(x_1,\ldots ,x_n)$).

In differential geometry, the metric tensor of a Riemannian manifold is defined as a 2-tensor on the tangent bundle. In principle, this is a local definition using charts which does not yet allow us to compare arbitrary points on the manifold. This is then achieved by the Riemannian distance (or the metric in the sense of this paper) which employs geodesics, i.e. paths of shortest length connecting the two points, or more general metric structures; see e.g. [7, Ch.2,5].

In [15, 16] the authors consider area-metrics on Riemannian manifolds which are metric 4-tensors and which are more general than the canonical area metric induced by the metric 2-tensor. Using this concept, some interesting implications for gravity dynamics and electrodynamics are discussed. However, there seems to be no attempt to define a pseudo 3-metric in our sense, i.e. an area metric which is defined for any triple of points on the manifold and which satisfies the three properties above. Other generalizations of the metric notion, such as the polymetrics in [14] or the multi-metrics in [8] aim at spaces where several 2-metrics are given, sometimes with different multiplicities.

In Sect. 4 we construct a specific pseudo n-metric on the unit ball of a Hilbert space, and derive from this suitable pseudo n-metrics on manifolds of matrices such as the Stiefel and the Grassmann manifold (see [4] for a recent overview). In Sect. 5 we turn to metrics on discrete spaces and show how to extend the standard shortest path distance in an undirected graph to a pseudo n-metric on a connected hypergraph. Finally, in Sect. 6 we discuss two open problems. The first one is concerned with the search for a pseudo n-metric on the Grassmann manifold which is a canonical extension of the classical 2-metric ( [10, Ch.6.4]). The second one concerns a generalization of the Hausdorff metric for closed sets where we show that an obvious definition fails to produce a pseudo n-metric.

Due to its various areas of application, we think that the axiomatic notion of a pseudo n-metric deserves to be studied in its own right.

2 Elementary properties and a first example

This section deals with few statements about pseudo n-metrics in the general setting of Sect. 1.

Proposition 1

• (i) If the mapping $d:X^n \rightarrow {\mathbb {R}}$ is semidefinite, symmetric, and satisfies (2) for all $y \notin \{x_1,\ldots ,x_n\}$, then d is a pseudo n-metric.

• (ii) A pseudo n-metric on X satisfies $d(x) \ge 0$ for all $x \in X^n$.

Proof

For (i) it suffices to show (2) for the case $y\in \{x_1,\ldots ,x_n\}$, i.e. $y = x_j$ for some $j \in \{1,\ldots ,n\}$. Then we have by the semidefiniteness of d

$$\begin{aligned} d(x_1,\ldots ,x_n)&=d(x_1,\ldots ,x_{j-1},y,x_{j+1}, \ldots , x_n)\\&= \sum _{i=1}^n d(x_1,\ldots ,x_{i-1},y,x_{i+1},\ldots ,x_n). \end{aligned}$$

To prove (ii) we apply (2) with $y=x_1$ and obtain from the semidefiniteness and the symmetry

$$\begin{aligned} 0&= d(x_2,x_2,x_3,\ldots ,x_n) \le d(x_1,x_2,\ldots ,x_n)+ d(x_2,x_1,\ldots ,x_n) \\&\quad + \sum _{i=3}^n d(x_2,x_2,x_3,\ldots ,x_{i-1},x_1,x_{i+1},\ldots ,x_n) \\&= d(x_1,x_2,\ldots ,x_n)+ d(x_2,x_1,\ldots ,x_n) = 2 d(x_1,\ldots ,x_n). \end{aligned}$$

$\square$

The proof of the following proposition is elementary. For the notion of a monotone norm we refer to [11, Ch.5.4].

Proposition 2

Let $d_X$ be a pseudo n-metric on a set X.

• (i) For any subset $Y\subset X$, $d_Y=(d_X)_{|Y^n}$ defines a pseudo n-metric on Y.

• (ii) If $d_Y$ is a pseudo n-metric an a set Y, then

  $$\begin{aligned} d_{X \times Y}\Big ( \begin{pmatrix} x_1 \\ y_1 \end{pmatrix}, \ldots , \begin{pmatrix} x_n \\ y_n \end{pmatrix} \Big ):= \Big \Vert \begin{pmatrix} d_X(x_1,\ldots ,x_n) \\ d_Y(y_1, \ldots ,y_n) \end{pmatrix} \Big \Vert \end{aligned}$$

  defines a pseudo n-metric on $X \times Y$ for any monotone norm $\Vert \cdot \Vert$ in ${\mathbb {R}}^2$.

The following is a kind of minimal choice for a pseudo n-metric satisfying the axioms (i)–(iii) in $X={\mathbb {R}}$.

Example 1

(Vandermonde pseudo n-metric) The function

$$\begin{aligned} d(x_1,\ldots ,x_n) = \prod _{1\le i<j \le n} |x_i -x_j|, \quad x=(x_1,\ldots ,x_n) \in {\mathbb {R}}^n \end{aligned}$$

(3)

defines an n-metric on ${\mathbb {R}}$.

Note that $d(x_1,\ldots ,x_n)=|V(x_1,\ldots ,x_n)|$ holds with the Vandermonde determinant

$$\begin{aligned} V(x_1,\ldots ,x_n) = \det \begin{pmatrix} x_1^{n-1} &{} \cdots &{} x_n^{n-1} \\ \vdots &{} \cdots &{} \vdots \\ 1 &{} \cdots &{} 1 \end{pmatrix}= \prod _{1 \le i < j \le n} (x_i-x_j). \end{aligned}$$

The semidefiniteness follows from the definition (3). For the symmetry, observe that for $\pi \in S_n$

$$\begin{aligned} d(x_1,\ldots ,x_n)^2 = \prod _{i \ne j}|x_i -x_j| = \prod _{\pi (i) \ne \pi (j)}|x_{\pi (i)} -x_{\pi (j)}|= d(x_{\pi (1)},\ldots ,x_{\pi (n)})^2, \end{aligned}$$

since $(i,j) \mapsto (\pi (i),\pi (j))$ is a bijection of the set $\{(i,j): i,j \in \{1,\ldots ,n\}, i \ne j \}$. For the proof of the simplicial inequality we can assume the values $x_i$ to be pairwise distinct. For a given $y \in {\mathbb {R}}$ let the vector $(a_1,\ldots ,a_n)^{\top }$ solve the linear system

$$\begin{aligned} \begin{pmatrix} x_1^{n-1} &{} \cdots &{} x_n^{n-1} \\ \vdots &{} \cdots &{} \vdots \\ 1 &{} \cdots &{} 1 \end{pmatrix} \begin{pmatrix}a_1 \\ \vdots \\ a_n \end{pmatrix} = \begin{pmatrix} y^{n-1} \\ \vdots \\ 1 \end{pmatrix}. \end{aligned}$$

(4)

By Cramer’s rule we have

$$\begin{aligned} a_i = \frac{V(x_1,\ldots ,x_{i-1},y,x_{i+1},\ldots ,x_n)}{V(x_1,\ldots ,x_n)}, \quad i=1,\ldots ,n. \end{aligned}$$

Hence the last line of (4) leads to

$$\begin{aligned} 1&= \sum _{i=1}^n a_i \le \sum _{i=1}^n |a_i| = \sum _{i=1}^n \frac{|V(x_1,\ldots ,x_{i-1},y,x_{i+1},\ldots ,x_n)|}{|V(x_1,\ldots ,x_n)|}\\ {}&= \frac{1}{d(x_1,\ldots ,x_n)}\sum _{i=1}^n d(x_1,\ldots ,x_{i-1},y,x_{i+1},\ldots ,x_n), \end{aligned}$$

which proves the simplicial inequality. For an extension of this example we refer to [5].

3 Examples in linear spaces

3.1 Pseudo n-norms

In vector spaces it is natural to first define a pseudo n-norm and then define a pseudo n-metric by taking the n-norm of differences.

Definition 1

Let X be a vector space. A map $\Vert \cdot \Vert :X^n \rightarrow {\mathbb {R}}$ is called a pseudo n-norm if it has the following properties:

• (i) (Semidefiniteness) If $x_i$, $i\in \{1,\ldots ,n\}$ are linearly dependent then $\Vert (x_1, \ldots , x_n)\Vert =0$.

• (ii) (Symmetry) For all $x=(x_1,\ldots ,x_n) \in X^n$ and for all $\pi \in \mathcal {P}_n$

  $$\begin{aligned} \Vert (x_1,\ldots ,x_n)\Vert = \Vert (x_{\pi (1)},\ldots ,x_{\pi (n)}) \Vert . \end{aligned}$$

  (5)

• (iii) (Positive homogeneity) For all $x=(x_1,\ldots ,x_n) \in X^n$ and for all $\lambda \in {\mathbb {R}}$

  $$\begin{aligned} \Vert (\lambda x_1,\ldots ,x_n)\Vert = |\lambda | \, \Vert (x_{1},\ldots ,x_{n}) \Vert . \end{aligned}$$

  (6)

• (iv) (Multi-sublinearity) For all $x=(x_1,\ldots ,x_n) \in X^n$ and $y \in X$,

  $$\begin{aligned} \Vert (x_1+y,\ldots ,x_n)\Vert \le \Vert (x_1,x_2,\ldots ,x_n)\Vert + \Vert (y,x_2,\ldots ,x_n)\Vert . \end{aligned}$$

  (7)

A pseudo n-norm is called an n-norm if $\Vert (x_1,\ldots ,x_n)\Vert =0$ holds if and only if $x_i,i=1,\ldots ,n$ are linearly dependent.

Clearly, a pseudo 1-norm is a semi-norm in the usual sense. Also note that the positive homogeneity (6) and the sublinearity (7) transfers from the first component to all other components via (5).

Next consider a matrix $A\in {\mathbb {R}}^{n,n}$ and the induced linear map $A_X:=A^{\top }\otimes I_X$ on $X^n$ given by

$$\begin{aligned} \begin{aligned} A_X \begin{pmatrix} x_1 \\ \vdots \\ x_n \end{pmatrix}&= \begin{pmatrix} A_{11}I_X &{}{} \cdots &{}{} A_{n1} I_X \\ \vdots &{}{} &{}{} \vdots \\ A_{1n}I_X &{}{} \cdots &{}{} A_{nn} I_X \end{pmatrix} \begin{pmatrix} x_1 \\ \vdots \\ x_n \end{pmatrix} \in X^n \\ ( A_X (x_1,\ldots ,x_n))_j&= \sum _{i=1}^n A_{ij}x_i, \quad j=1,\ldots ,n. \end{aligned} \end{aligned}$$

(8)

Lemma 1

Let $\Vert \cdot \Vert$ be a pseudo n-norm on X and $A \in {\mathbb {R}}^{n,n}$. Then the map (8) satisfies

$$\begin{aligned} \Vert A_X(x_1,\ldots ,x_n)\Vert = |\det (A)|\, \Vert (x_1,\ldots ,x_n)\Vert \quad \forall (x_1,\ldots ,x_n) \in X^n. \end{aligned}$$

(9)

Remark 1

The result shows that the pseudo n-norm is a volume form on $X^n$.

Proof

If A is singular then the vectors $(A_X(x_1,\ldots ,x_n))_j$, $j=1,\ldots ,n$ are linearly dependent, hence formula (9) is trivially satisfied. Otherwise there exists a decomposition $A=P L D U$ where P is an $n\times n$ permutation matrix, $L\in {\mathbb {R}}^{n,n}$ resp. U is a lower resp. upper triangular $n \times n$-matrix with ones on the diagonal and $D\in {\mathbb {R}}^{n,n}$ is diagonal. Since $A_X =U_X D_X L_X P_X$ it suffices to show that all 4 types of matrices satisfy the formula (9). For $P_X$ this follows from (5) and for $D_X$ from (6). For $L_X$ note that $L_X(x_1,\ldots ,x_n)$ is of the form

$$\begin{aligned} L_X(x_1,\ldots ,x_n) = ( \star , x_{n-1}+L_{n,n-1}x_n,x_n). \end{aligned}$$

With (7) and Definition 1(i) we obtain

$$\begin{aligned} \Vert ( \star , x_{n-1}+L_{n,n-1}x_n,x_n)\Vert&\le \Vert ( \star , x_{n-1},x_n)\Vert +\Vert ( \star , L_{n,n-1} x_n,x_n)\Vert \\&=\Vert ( \star , x_{n-1},x_n)\Vert . \end{aligned}$$

Similarly,

$$\begin{aligned} \Vert ( \star , x_{n-1},x_n)\Vert&\le \Vert ( \star , x_{n-1}+L_{n,n-1}x_n,x_n)\Vert +\Vert ( \star ,- L_{n,n-1} x_n,x_n)\Vert \\&= \Vert ( \star , x_{n-1}+L_{n,n-1}x_n,x_n)\Vert , \end{aligned}$$

hence we have

$$\begin{aligned} \Vert ( \star , x_{n-1},x_n)\Vert =\Vert ( \star , x_{n-1}+L_{n,n-1}x_n,x_n)\Vert . \end{aligned}$$

By induction one eliminates all terms $L_{i,j}x_i,i>j$ from the pseudo n-norm. Since $\det (L)=1$ this proves (9) for L. In a similar manner, one shows

$$\begin{aligned} \Vert R_X(x_1,\ldots ,x_n)\Vert&= \Vert (x_1,x_2 + R_{12}x_1,\star )\Vert = \Vert (x_1,x_2,\star )\Vert \end{aligned}$$

and finds that (9) is also satisfied for the map $R_X$.

$\square$

Proposition 3

Let $\Vert \cdot \Vert$ be a pseudo $(n-1)$-norm on a vector space X. Then

$$\begin{aligned} d(x_1,\ldots ,x_n)= \Vert (x_2-x_1,\ldots ,x_n-x_1)\Vert \end{aligned}$$

defines a pseudo n-metric on X.

Proof

Let $x_i=x_j$ for some $i,j \in \{1,\ldots ,n\}$, $i \ne j$. Then the vectors $x_{\nu }-x_1,\nu =2,\ldots ,n$ are linearly dependent, hence $d(x_1,\ldots ,x_n)=0$ follows from condition (i) of Definition 1. Since $\mathcal {P}_n$ can be generated by transpositions, it is enough to show (1) when transposing $x_1$ with some $x_j$, $j \in \{2,\ldots ,n\}$. For this purpose consider the matrix with $-1$ in the j-th row

$$\begin{aligned} A= \begin{pmatrix} 1&{} 0 &{} \cdots &{} \cdots &{} 0 \\ \vdots &{} \ddots &{} &{} &{}\vdots \\ -1&{} -1 &{} -1 &{} -1 &{} -1 \\ \vdots &{} &{} &{} \ddots &{} \vdots \\ 0 &{} \cdots &{} \cdots &{} 0 &{} 1 \end{pmatrix} \in {\mathbb {R}}^{n-1,n-1}, \end{aligned}$$

which satisfies $\det (A)=-1$ and

$$\begin{aligned}&A_X (x_2-x_1, \ldots , x_n-x_1)\\&= (x_2-x_j, \ldots , x_{j-1}-x_j,x_1-x_j, x_{j+1}-x_j, \ldots ,x_n -x_j). \end{aligned}$$

Taking norms and using (5) and (9) leads to

$$\begin{aligned} d(x_1,\ldots ,x_n)=d(x_j,x_1,x_2,\ldots ,x_{j-1},x_{j+1},\ldots ,x_n). \end{aligned}$$

For the simplicial inequality (2) we use the multi-sublinearity (7)

$$\begin{aligned} d(x_1,\ldots ,x_n)&= \Vert (x_2-y+y-x_1,\ldots , x_n-x_1) \Vert \\&\le \Vert (x_2-y,x_3-x_1,\ldots ,x_n-x_1)\Vert \\ {}&\quad + \Vert (y-x_1,x_3-x_1,\ldots ,x_n -x_1)\Vert \\&= \Vert (x_2-y,x_3-x_1,\ldots ,x_n-x_1)\Vert \\ {}&\quad + \Vert (y-x_1,x_3-y,\ldots ,x_n -y)\Vert \end{aligned}$$

For the last term we employed (9) and

$$\begin{aligned} (y-x_1,x_3-y,\ldots ,x_n - y)&= U_X (y-x_1,x_3-x_1,\ldots ,x_n-x_1) \end{aligned}$$

for the upper triangular matrix

$$\begin{aligned} U= \begin{pmatrix} 1 &{} -1 &{} \cdots &{} -1 \\ 0 &{} 1 &{}0 &{} 0 \\ \vdots &{} &{} \ddots &{} \vdots \\ 0 &{} &{} \cdots &{} 1 \end{pmatrix}. \end{aligned}$$

Thus we have proved for $j=2$ the following assertion

$$\begin{aligned} \begin{aligned} d(x_1,\ldots ,x_n)&\le \sum _{i=2}^j d(y,x_1,\ldots ,x_{i-1},x_{i+1},\ldots ,x_n) \\&+ \Vert (x_2-y,\ldots ,x_j-y,x_{j+1}-x_1,\ldots ,x_n -x_1)\Vert . \end{aligned} \end{aligned}$$

(10)

In the induction step we split $x_{j+1}-x_1 =x_{j+1}-y + y -x_1$ in the last term:

$$\begin{aligned}&\Vert (x_2-y,\ldots ,x_j-y,x_{j+1}-x_1,\ldots ,x_n -x_1)\Vert \\&\le \Vert (x_2-y,\ldots ,x_j-y,x_{j+1}-y,x_{j+2}-x_1,\ldots ,x_n -x_1)\Vert \\&+\Vert (x_2-y,\ldots ,x_j-y,y-x_1,x_{j+2}-x_1,\ldots ,x_n -x_1)\Vert \end{aligned}$$

As in the first step we can replace all vectors $x_i-x_1$, $i \ge j+2$ in the last term by $x_i-y$ and then move $y-x_1$ to the front position. This proves that (10) holds for $j+1$. For $j=n$ equation (10) reads

$$\begin{aligned} d(x_1,\ldots ,x_n)&\le \sum _{i=2}^n d(y,x_1,\ldots ,x_{i-1},x_{i+1},\ldots ,x_n) \\&+ \Vert (x_2-y,\ldots ,x_n -y)\Vert = \sum _{i=1}^n d(y,x_1,\ldots ,x_{i-1},x_{i+1},\ldots ,x_n). \end{aligned}$$

$\square$

3.2 Construction via exterior products

The previous results suggest to use exterior products in defining appropriate pseudo n-norms. For this purpose recall the following calculus for a separable reflexive Banach space X; see [17, Ch.V], [1, Section 6], [2, Ch.3.2.3]. The linear space $\bigwedge ^n(X)$ is the set of continuous alternating n-linear forms on the dual $X^{\star }$, using the identification of X and its bidual $X^{\star \star }$. $\bigwedge ^nX$ is called the n-fold exterior product of X. Elements of $\bigwedge ^n(X)$ are exterior products $x_1 \wedge \ldots \wedge x_n$ defined for $x_1,\ldots ,x_n\in X$ by the dual pairing

$$\begin{aligned} \langle x_1 \wedge \ldots \wedge x_n, (f_1,\ldots ,f_n) \rangle = \det \left( \langle f_i , x_j \rangle _{i,j=1}^n \right) \end{aligned}$$

where $f_1,\ldots ,f_n \in X^{\star }$ and $\langle \cdot , \cdot \rangle$ is the dual pairing of $X^{\star }$ and X. As usual we write in the following

$$\begin{aligned} \bigwedge _{i=1}^n x_i = x_1\wedge \ldots \wedge x_n. \end{aligned}$$

By linearity one can extend exterior products to sums

$$\begin{aligned} \sum _{j=1}^J c_j (x_1^j\wedge \ldots \wedge x_n^j), \quad c_j \in {\mathbb {R}}, x_i^j \in X,i=1,\ldots ,n, j=1,\ldots ,J \in {\mathbb {N}}. \end{aligned}$$

Closing the linear hull with respect to the norm

$$\begin{aligned} \Vert \Phi \Vert _{\wedge }{=} \sup \{ | \Phi (f_1,\ldots ,f_n)|: f_j \in X^{\star }, \Vert f_j\Vert _{X^{\star }}{=}1,j{=}1,\ldots ,n \}, \quad \Phi \in {\bigwedge } ^n(X) \end{aligned}$$

turns $\bigwedge ^n(X)$ into a Banach space.

Some standard properties are collected in the following lemma; see [17, Ch.V], [2, Lemma 3.2.6]:

Lemma 2

Let $\bigwedge ^n X$ be the n-fold exterior product of a separable reflexive Banach space space X with $n\le \dim (X)$. Then the following holds

• (i) If X is $m \ge n$-dimensional and $e_1,\ldots ,e_m$ is a basis of X then

  $$\begin{aligned} \{e_{i_1}\wedge \ldots \wedge e_{i_n}: 1 \le i_1< i_2 \ldots < i_n \le m\} \end{aligned}$$

  is a basis of $\bigwedge ^n X$. In particular $\bigwedge ^n X$ has dimension $m \atopwithdelims ()n$.

• (ii) One has $x_1\wedge \ldots \wedge x_n=0$ if and only if $x_1,\ldots ,x_n$ are linearly dependent.

• (iii) If X is a Hilbert space with inner product $\langle \cdot , \cdot \rangle$ then the bilinear and continuous extension of

  $$\begin{aligned} \langle x_1\wedge \ldots \wedge x_n,y_1\wedge \ldots \wedge y_n \rangle = \det \big ( \langle x_i,y_j \rangle _{i,j=1}^n\big ) \end{aligned}$$

  (11)

  defines an inner product on the Hilbert space $\bigwedge ^n X$. In particular, the corresponding norm

  $$\begin{aligned} \Vert x_1 \wedge \ldots \wedge x_n \Vert _{\wedge } = \big (\det ( \langle x_i,x_j \rangle _{i,j=1}^n) \big )^{1/2} \end{aligned}$$

  (12)

  is the volume of the n-dimensional parallelepiped spanned by $x_1,\ldots ,x_n$. Further, the generalized Hadamard inequality holds for $j=1,\ldots ,n$

  $$\begin{aligned} \Vert x_1 \wedge \ldots \wedge x_n\Vert _{\wedge } \le \Vert x_1 \wedge \ldots \wedge x_j\Vert _{\wedge } \Vert x_{j+1} \wedge \ldots \wedge x_n\Vert _{\wedge }. \end{aligned}$$

  (13)

Theorem 1

Let X be a separable reflexive Banach space.

• (i) Let $n \in {\mathbb {N}}$ and $\Vert \cdot \Vert$ be a norm in $\bigwedge ^nX$. Then

  $$\begin{aligned} \Vert (x_1,\ldots ,x_n)\Vert = \big \Vert \bigwedge _{i=1}^n x_i \big \Vert , \quad x=(x_1,\ldots ,x_n) \in X^n \end{aligned}$$

  (14)

  defines an n-norm on X.

• (ii) Let $\Vert \cdot \Vert$ be a norm in $\bigwedge ^{n-1} X$ for some $n \ge 2$. Then

  $$\begin{aligned} d(x_1,\ldots ,x_n)=\big \Vert \bigwedge _{i=2}^{n}(x_i-x_1)\big \Vert , \quad x=(x_1,\ldots ,x_n) \in X^n \end{aligned}$$

  (15)

  defines a pseudo n-metric on X. Moreover, $d(x_1,\ldots ,x_n)=0$ holds if and only if $x_i-x_1, i=2,\ldots ,n$ are linearly dependent.

Proof

By Proposition 3 it suffices to show that (14) defines an n-norm on X. Condition (i) in Definition 1 follows from Lemma 2 (ii), and (5) is a consequence the alternating property of the exterior product. Further, the positive homogeneity (6) follows from the homogeneity of the exterior product and the positive homogeneity of the norm in $\bigwedge ^nX$. Finally, inequality (7) is implied by taking norms of the multilinear relation

$$\begin{aligned} (x_1+y)\wedge \bigwedge _{i=2}^n x_i = y \wedge \bigwedge _{i=2}^n x_i +\bigwedge _{i=1}^n x_i. \end{aligned}$$

$\square$

Example 2

Let $(H,\langle \cdot ,\cdot ,\rangle _H,\Vert \cdot \Vert _H)$ be a separable Hilbert space. Then a 2-norm on H is given by

$$\begin{aligned} \begin{aligned} \Vert (u,v)\Vert&= \left[ \det \begin{pmatrix} \Vert u\Vert _H^2 &{} \langle u,v\rangle _H \\ \langle u,v \rangle _H &{} \Vert v\Vert _H^2 \end{pmatrix} \right] ^{1/2}\\&= \left[ \Vert u\Vert _H^2 \Vert v\Vert _H^2 - \langle u,v \rangle _H^2 \right] ^{1/2}\\&= \Vert u\Vert _H \Vert v\Vert _H(1 - \cos ^2 \measuredangle (u,v))^{1/2}= \Vert u\Vert _H \Vert v\Vert _H | \sin \measuredangle (u,v) |. \end{aligned} \end{aligned}$$

(16)

The corresponding pseudo 3-metric on H is

$$\begin{aligned} \begin{aligned} d(u,v,w)&=\left[ \det \begin{pmatrix} \Vert v-u\Vert _H^2 &{} \langle v-u, w-u \rangle _H \\ \langle v-u, w-u \rangle _H &{} \Vert w-u\Vert _H^2 \end{pmatrix}\right] ^{1/2}\\&=\left[ \Vert v-u\Vert _H^2\Vert w-u\Vert _H^2- \langle v-u, w-u \rangle _H^2\right] ^{1/2}\\&= \Vert v-u\Vert _H \Vert w-u\Vert _H | \sin \measuredangle (v-u,w-u) |. \end{aligned} \end{aligned}$$

4 Some pseudo n-metrics on manifolds

We use the results from the previous section to set up a pseudo n-metric on the unit sphere of a separable Hilbert space.

Proposition 4

Let $(H,\langle \cdot ,\cdot ,\rangle _H,\Vert \cdot \Vert _H)$ be a separable Hilbert space and consider the unit sphere

$$\begin{aligned} S_H=\{ x \in H: \Vert x\Vert _H = 1 \}. \end{aligned}$$

Then the n-norm defined by (14) and (12) generates a pseudo n-metric on $S_H$:

$$\begin{aligned} d(x_1,\ldots ,x_n)= \big \Vert \bigwedge _{i=1}^n x_i \big \Vert _{\wedge } = \big (\det ( \langle x_i,x_j \rangle _H )_{i,j=1}^n \big )^{1/2}, \quad x_i \in S_H,i=1,\ldots ,n. \end{aligned}$$

Proof

The semidefiniteness and the symmetry are consequences of Proposition 1. It remains to prove the simplicial inequality. For given $x_i \in S_H$, $i=1,\ldots ,n$ we write $y \in S_H$ with suitable coefficients $c,c_i(i=1,\ldots ,n)$ as

$$\begin{aligned} y = \sum _{j=1}^n c_j x_j+ c y^{\perp }, \quad \langle x_i, y^{\perp }\rangle _H=0 \ (i=1,\ldots ,n), \quad \Vert y^{\perp }\Vert _H = 1. \end{aligned}$$

(17)

Then we have the equality

$$\begin{aligned} 1 = \langle y, y \rangle _H = \sum _{i,j=1}^n c_i c_j \langle x_i, x_j \rangle _H +c^2. \end{aligned}$$

Using $|\langle x_i,x_j \rangle _H| \le 1$ we obtain

$$\begin{aligned} 1 \le \sum _{i,j=1}^n|c_i| |c_j|+ c^2 = \Big ( \sum _{i=1}^n |c_i| \Big )^2 + c^2. \end{aligned}$$

(18)

From (17) and the properties of the exterior product we have for $i=1,\ldots ,n$

$$\begin{aligned}&x_1 \wedge \ldots \wedge x_{i-1} \wedge y \wedge x_{i+1} \wedge \ldots \wedge x_n \\ {}&= x_1 \wedge \ldots \wedge x_{i-1} \wedge (c_i x_i + cy^{\perp }) \wedge x_{i+1} \ldots \wedge x_n. \end{aligned}$$

Further, the orthogonality in (17) implies via (11)

$$\begin{aligned} \big \langle x_1 \wedge \ldots \wedge x_n, x_1 \wedge \ldots \wedge x_{i-1} \wedge y^{\perp } \wedge x_{i+1} \ldots \wedge x_n \big \rangle =0, \end{aligned}$$

hence by (17)

$$\begin{aligned} \Vert x_1\wedge \ldots \wedge x_{i-1} \wedge y \wedge x_{i+1} \wedge \ldots \wedge x_n\Vert _{\wedge }^2 = c_i^2 d_n^2 + c^2 d_{i,n-1}^2, \end{aligned}$$

(19)

where we use the abbreviations $d_{i,n-1}=\Vert x_1\wedge \ldots \wedge x_{i-1} \wedge x_{i+1}\wedge \ldots \wedge x_n \Vert _{\wedge }$ and $d_n = \Vert x_1 \wedge \ldots \wedge x_n\Vert _{\wedge }$..

Note that Hadamard’s inequality (13) implies $d_n \le d_{i,n-1}$ for $i=1,\ldots ,n$. With (18), (19) and the triangle inequality in ${\mathbb {R}}^2$ we find

$$\begin{aligned} d_n&\le d_n \Big \Vert \begin{pmatrix} \sum _{i=1}^n |c_i| \\ |c| \end{pmatrix}\Big \Vert _2 \le d_n \Big \Vert \begin{pmatrix} \sum _{i=1}^n |c_i| \\ n |c| \end{pmatrix}\Big \Vert _2 \le d_n \sum _{i=1}^n \Big \Vert \begin{pmatrix} |c_i| \\ |c| \end{pmatrix}\Big \Vert _2 \\&\le \sum _{i=1}^n \big ( c_i^2 d_n^2 + c^2 d_{i,n-1}^2 \big )^{1/2} = \sum _{i=1}^n d(x_1,\ldots ,x_{i-1},y,x_{i+1},\ldots ,x_n). \end{aligned}$$

$\square$

Example 3

As examples we list the induced pseudo 2-metric (compare (16)) and the pseudo 3-metric on $S_H$:

$$\begin{aligned} \begin{aligned} d(u,v)&= |\sin \measuredangle (u,v) |, \quad u,v \in S_H, \end{aligned} \end{aligned}$$

$$\begin{aligned} \begin{aligned} d(u,v,w)^2&= \det \begin{pmatrix} 1 &{} \langle u,v\rangle _H &{} \langle u,w \rangle _H \\ \langle u,v \rangle _H &{} 1 &{} \langle v,w \rangle _H \\ \langle u,w \rangle _H &{} \langle v,w \rangle _H &{} 1 \end{pmatrix} \\&= \det \begin{pmatrix} 1 &{} \cos \measuredangle ( u,v) &{} \cos \measuredangle ( u,w ) \\ \cos \measuredangle ( u,v ) &{} 1 &{} \cos \measuredangle ( v,w ) \\ \cos \measuredangle ( u,w ) &{} \cos \measuredangle ( v,w ) &{} 1 \end{pmatrix} \\&= 1 - \cos ^2 \measuredangle ( u,v ) - \cos ^2 \measuredangle ( u,w )- \cos ^2 \measuredangle ( v,w ) \\ {}&+ 2 \cos \measuredangle ( u,v ) \cos \measuredangle ( u,w ) \cos \measuredangle ( v,w ), \quad u,v,w \in S_H. \end{aligned} \end{aligned}$$

(20)

Remark 2

The value d(u, v, w) in (20) agrees with the three-dimensional polar sine ${}^{3}{}{\textrm{polsin}} (O,u\ v \ w)$, already defined by Euler; see [9, Sect.6]. The work [9] discusses various ways of measuring n-dimensional angles and its history in spherical geometry. The main result is a simple derivation of the law of sines for the n-dimensional sine ${}^{n}{}\sin$ and the n-dimensional polar sine ${}^{n}{}{\textrm{polsin}}$ defined by

$$\begin{aligned} \begin{aligned} {}^{n}{}\sin (O,x_1\cdots x_n)&= \frac{\Vert x_1 \wedge \ldots \wedge x_n\Vert ^{n-1}}{\prod _{i=1}^n \Vert x_1 \wedge \ldots \wedge x_{i-1} \wedge x_{i+1}\wedge x_n||},\\ {}^{n}{}{\textrm{polsin}}(O,x_1\cdots x_n)&= \frac{\Vert x_1 \wedge \ldots \wedge x_n\Vert }{\prod _{i=1}^n \Vert x_i\Vert }. \end{aligned}\nonumber \\ \end{aligned}$$

(21)

However, the simplicial inequality in Proposition 4 seems not to have been observed.

Next we consider the separable Hilbert space $H=L({\mathbb {R}}^k,{\mathbb {R}}^m)$ of linear mappings from ${\mathbb {R}}^k$ to ${\mathbb {R}}^m$ endowed with the Hilbert-Schmidt inner product and norm

$$\begin{aligned} \begin{aligned} \langle A, B \rangle _H&= \frac{1}{k}\sum _{j=1}^k \langle A e_j, Be_j\rangle _2, \quad A,B \in H, \\ \Vert A\Vert _H^2&= \frac{1}{k}\sum _{j=1}^k \Vert Ae_j\Vert _2^2, \quad A \in H. \end{aligned} \end{aligned}$$

(22)

Here the vectors $e_j,j=1,\ldots ,k$ form an orthonormal basis of ${\mathbb {R}}^k$ and the prefactor $\frac{1}{k}$ is used for convenience, so that an orthogonal map $A\in H$, i.e. $A^{\star }A=I_k$, satisfies $\Vert A\Vert _H=1$. It is well known that the Hilbert-Schmidt inner product and norm are independent of the choice of orthonormal basis $(e_j)_{j=1}^k$. By Proposition 4 the unit sphere $S_H$ in H carries a pseudo n-metric defined by

$$\begin{aligned} d_H(A_1,\ldots ,A_n)= \big (\det ( \langle A_i,A_j \rangle _H )_{i,j=1}^n \big )^{1/2}. \end{aligned}$$

(23)

By Proposition 2(i) we thus obtain the following corollary.

Corollary 1

For $k \le m$ equation (23) defines a pseudo n-metric on the Stiefel manifold

$$\begin{aligned} \textrm{St}(k,m) = \{ A \in L({\mathbb {R}}^k,{\mathbb {R}}^m): A^{\star }A = I_k \}. \end{aligned}$$

Example 4

In case $n=2$ we obtain

$$\begin{aligned} d_H(A_1,A_2) = (1 - \langle A_1,A_2 \rangle _H^2)^{1/2}, \quad A_1,A_2 \in \textrm{St}(k,m). \end{aligned}$$

(24)

For the Grassmannian ${{\mathcal {G}}}(k,m)$ of k-dimensional subspaces of ${\mathbb {R}}^m$, $k \le m$, the situation is not so simple. One can identify ${{\mathcal {G}}}(k,m)$ with the quotient space

$$\begin{aligned} \textrm{St}(k,m)/\sim , \quad \text {where} \; A \sim B \Longleftrightarrow \exists Q \in O(k): A=BQ \end{aligned}$$

(25)

by setting $V=\textrm{range}(A)$ for $[A]_{\sim }\in \textrm{St}(k,m)/\sim$. Then the Hilbert Schmidt norm is invariant w.r.t. the equivalence class, but the inner product (22) is not, since we obtain terms $\langle A Q_1e_j, BQ_2 e_j\rangle _2$ for which the orthogonal maps $Q_1,Q_2$ differ, in general.

Therefore, we associate with every element $V \in {{\mathcal {G}}}(k,m)$ the orthogonal projection P onto V, given by $P=A A^{\star }$ where $V=\textrm{range}(A)$ for $A\in \textrm{St}(k,m)$ (cf. [4]). The projection is an invariant for the equivalence classes in (25) It is appropriate to measure orthogonal projections of rank k by the scaled Hilbert-Schmidt inner product and norm

$$\begin{aligned} \begin{aligned} \langle A, B \rangle _{k,H}&= \frac{1}{k}\sum _{j=1}^m \langle A e_j, Be_j\rangle _2, \quad A,B \in L({\mathbb {R}}^m,{\mathbb {R}}^m), \\ \Vert A\Vert _{k,H}^2&= \frac{1}{k}\sum _{j=1}^m \Vert Ae_j\Vert _2^2, \quad A \in L({\mathbb {R}}^m,{\mathbb {R}}^m), \end{aligned} \end{aligned}$$

where $(e_j)_{j=1,\ldots ,m}$ form an orthonormal basis of ${\mathbb {R}}^m$. We claim that the orthogonal projection P belongs to the unit ball

$$\begin{aligned} S_{k,H}= \{ B \in L({\mathbb {R}}^m,{\mathbb {R}}^m): \Vert B\Vert _{k,H}=1 \}. \end{aligned}$$

To see this, choose a special orthonormal basis of ${\mathbb {R}}^m$ where $e_1,\ldots ,e_k$ are the columns of A and $e_{k+1},\ldots ,e_m$ form a basis of the orthogonal complement $V^{\perp }$. Since the norm is invariant and $AA^* e_j=e_j$ for $j=1,\ldots ,k$, $AA^{\star }e_j=0$ for $j >k$ we obtain $\Vert P\Vert _{k,H}=1$. Thus we can proceed as before and invoke Propositions 4 and 2(i) to obtain the following result.

Proposition 5

For $V_i\in {{\mathcal {G}}}(k,m)$ let $P_i\in L({\mathbb {R}}^m,{\mathbb {R}}^m)$, $i=1,\ldots ,n$ be the corresponding orthogonal projections. Then the setting

$$\begin{aligned} d_{{{\mathcal {G}}}}(V_1,\ldots ,V_n)= \big (\det ( \langle P_i,P_j \rangle _{k,H} )_{i,j=1}^n \big )^{1/2}. \end{aligned}$$

(26)

defines a pseudo n-metric on ${{\mathcal {G}}}(k,m)$.

For an interpretation of (26) let us compute the inner product of two orthogonal projections.

Lemma 3

For $A_j \in \textrm{St}(k,m)$, $j=1,2$ let $P_j=A_j A_j^{\star }$ be the corresponding orthogonal projections in ${\mathbb {R}}^m$. Then the following holds

$$\begin{aligned} \langle P_1,P_2 \rangle _{k,H} = \frac{1}{k}\sum _{j=1}^k \sigma _j^2, \end{aligned}$$

where $\sigma _1\ge \ldots \ge \sigma _k \ge 0$ are the singular values of $A_1^{\star }A_2$.

Proof

Consider the SVD $A_1^{\star } A_2 = Y \Sigma Z^{\star }$ with $\Sigma = {{\,\textrm{diag}\,}}(\sigma _1,\ldots ,\sigma _k)$ and $Y,Z\in O(k)$. Further, choose $A_j^c \in \textrm{St}(m-k,m)$ such that $\begin{pmatrix} A_j&A_j^c \end{pmatrix}$, $j=1,2$ are orthogonal. Then we conclude

$$\begin{aligned} k \langle P_1, P_2 \rangle _{k,H}&= \textrm{tr}(A_1 A_1^{\star }A_2 A_2^{\star }) = \textrm{tr}\Big ( \begin{pmatrix} A_1&A_1^c \end{pmatrix} \begin{pmatrix} A_1^{\star } A_2 &{} 0 \\ 0 &{} 0 \end{pmatrix} \begin{pmatrix} A_2^{\star } \\ A_2^{c \star } \end{pmatrix} \Big )\\&= \textrm{tr}\Big ( \begin{pmatrix} A_1^{\star } A_2 &{} 0 \\ 0 &{} 0 \end{pmatrix} \begin{pmatrix} A_2^{\star } \\ A_2^{c \star } \end{pmatrix} \begin{pmatrix} A_1&A_1^c \end{pmatrix} \Big )\\&=\textrm{tr} \begin{pmatrix} A_1^{\star }A_2 A_2^{\star }A_1 &{} A_1^{\star }A_2 A_2^{\star } A_1^c \\ 0 &{} 0 \end{pmatrix}= \textrm{tr} \big (A_1^{\star }A_2 A_2^{\star }A_1 \big ) \\&= \textrm{tr}(Y \Sigma Z^{\star } Z \Sigma Y^{\star }) = \textrm{tr} \Sigma ^2 = \sum _{j=1}^k \sigma _j^2. \end{aligned}$$

$\square$

Recall from [10, Ch.6.4] that the singular values $\sigma _1 \ge \ldots \ge \sigma _k$ of $A_1^{\star }A_2$ define the principal angles $0 \le \theta _1 \le \ldots \le \theta _k \le \frac{\pi }{2}$ between $V_1$ and $V_2$ by $\sigma _j=\cos (\theta _j)$, $j=1,\ldots ,k$.

For $n=2$ this leads to an explicit expression of (26).

Proposition 6

In case $n=2$ equation (26) defines a 2-metric on ${{\mathcal {G}}}(k,m)$ by

$$\begin{aligned} d_{{{\mathcal {G}}}}(V_1,V_2)= (1-\frac{1}{k^2} \big (\sum _{j=1}^k \sigma _j^2)^2 \big )^{1/2} = \frac{1}{k} \Big ( k^2 - \big ( \sum _{j=1}^k \cos ^2(\theta _j) \big )^2 \Big )^{1/2}, \end{aligned}$$

(27)

where $0\le \theta _1\le \cdots \le \theta _k \le \frac{\pi }{2}$ are the principal angles of the subspaces $V_1$ and $V_2$.

Proof

From Lemma 3 and (26) we find

$$\begin{aligned} d_{{{\mathcal {G}}}}(V_1,V_2)&= (1-\frac{1}{k^2} \big (\sum _{j=1}^k \sigma _j^2)^2 \big )^{1/2} = \frac{1}{k} \Big ( k^2 - \big ( \sum _{j=1}^k \cos ^2(\theta _j) \big )^2 \Big )^{1/2}. \end{aligned}$$

$\square$

In Sect. 6.1 we continue the discussion of pseudo n-metrics on the Grassmannian and its relation to known 2-metrics.

5 A pseudo n-metric for hypergraphs

The notion of hypergraph allows edges which connect more than two vertices; see [6].

Definition 2

A pair (V, E) is called a hypergraph if V is a finite set and E is a subset of the power set $\mathcal {P}(V)$ of V. An element $e \in E$ is called a hyperedge. In particular, it is called an n-hyperedge if $\#e=n$. The hypergraph is called n-uniform if all its hyperedges are n-hyperedges

Obviously, a 2-uniform hypergraph is an ordinary (undirected) graph. The following definition generalizes the standard notion of connectedness.

Definition 3

Let (V, E) be an n-uniform hypergraph.

• (i) A subset $P \subset E$ is called a connected component of (V, E) if for any two $e_0,e_{\infty } \in P$ there exist finitely many $e_1,\ldots ,e_k \in P$ such that $e_{i-1}\cap e_{i} \ne \emptyset$ for $i=1,\ldots , k+1$ where $e_{k+1}:=e_{\infty }$. Any subset $W \subset \bigcup _{e \in P}e$ is said to be connected by P.

• (ii) The hypergraph is called connected if E is a connected component of (V, E) and $V=\bigcup _{e \in E}e$.

In case $n=2$ this agrees with the usual notion of connected components. For a connected hypergraph one can connect any subset of V by the (maximal) connected component E.

Definition 4

Let (V, E) be an n-uniform and connected hypergraph. For any tuple $(v_1,\ldots ,v_n)\in V^n$ define $d(v_1,\ldots ,v_n)=0$ if there exist $i,j \in \{1,\ldots ,n\}$ with $i \ne j$ and $v_i=v_j$. Otherwise set $W=\{v_1,\ldots ,v_n\}$ and

$$\begin{aligned} d(v_1,\ldots ,v_n) = \min \{\#P: P \text { connected component of ({ V},\,{ E}) connecting} \; W \}. \end{aligned}$$

Example 5

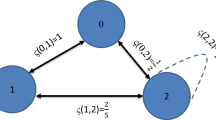
Let $V=\{1,2,3,4\}$ and

$$\begin{aligned} E=\big \{\{1,2,4\},\{2,3,4\},\{1,3,4\} \big \}. \end{aligned}$$

This is a 3-uniform hypergraph satisfying $d(1,2,4)=1$, $d(2,3,4)=1$, $d(1,3,4) =1$. Moreover, we have $d(1,2,3)=2$ since $\{1,2,3\}$ is not a hyperedge and $P=\big \{\{1,2,4\},\{2,3,4\}\big \}$ is a connected component of (V, E) which has cardinality 2 and connects $\{1,2,3\}$. Another connected component with this property and of the same cardinality is $P'=\big \{\{1,2,4\},\{1,3,4\}\big \}$.

Proposition 7

Let (V, E) be an n-uniform and connected hypergraph. Then the map $d:V^n \rightarrow {\mathbb {R}}$ from Definition 4 is a pseudo n-metric on V.

Proof

The semidefiniteness and the symmetry are obvious by Definition 4. Now consider $(v_1,\ldots ,v_n) \in V^n$. If two components agree then (2) is trivially satisfied. Otherwise $W=\{v_1,\ldots ,v_n\}$ is a subset of V with $\#W=n$. Let $y \in V$ be arbitrary. By Lemma 1 it suffices to prove the simplicial inequality for $y \notin W$. Let $P_1$ resp. $P_2$ be connected components of minimal cardinality $p_1=d(y,v_2,\ldots ,v_n)$ resp. $p_2=d(v_1,y,\ldots ,v_n)$ which connect $W_1=\{y,v_2,\ldots ,v_n\}$ resp. $W_2=\{v_1,y,\ldots ,v_n\}$. Then $P=P_1 \cup P_2$ is a connected component which connects $\{v_1,\ldots ,v_n\}$. To see this, note first that

$$\begin{aligned} W \subset W_1 \cup W_2 \subset \bigcup _{e \in P_1}e \cup \bigcup _{e \in P_2}e =\bigcup _{e \in P} e. \end{aligned}$$

Let $e_0,e_{\infty }\in P$. If both are in $P_1$ or in $P_2$ then they can be connected as in Definition 3 (i). So assume w.l.o.g. $e_0 \in P_1$, $e_{\infty } \in P_2$. Since $P_1$ connects $W_1$ there exists a hyperedge $e_+ \in P_1$ such that $y \in e_+$ and a hyperedge $e_- \in P_2$ such that $y \in e_-$. Further, there are sequences of hyperedges $e_1,\ldots ,e_k\in P_1$ such that $e_{i-1}\cap e_i \ne \emptyset$ for $i=1,\ldots ,k+1$ with $e_{k+1}=e_+$. Similarly, there exist hyperedges $e_-=e_0',e_1',\ldots ,e_{k'}'$ such that $e'_{i-1}\cap e'_i \ne \emptyset$ for $i=1,\ldots ,k'+1$ with $e'_{k'+1}= e_{\infty }$. Since $y \in e_{k+1}\cap e'_0$ we obtain that the sequence $e_0,\ldots ,e_k,e_+,e_-,e'_1,\ldots ,e'_{k'},e_{\infty }$ lies in P and has nonempty intersections of successive hyperedges. Therefore,

$$\begin{aligned} d(v_1,\ldots ,v_n) \le p_1 + p_2 =d(y,v_2,\ldots ,v_n)+d(v_1,y,\ldots ,v_n), \end{aligned}$$

which proves (2). $\square$

The proof shows that we have a sharper inequality than (2)

$$\begin{aligned} d(x_1,\ldots ,x_n) \le \max _{1\le i < j \le n}&\big ( d(x_1,\ldots ,x_{i-1},y,x_{i+1},\ldots ,x_n)\\&+ d(x_1,\ldots ,x_{j-1},y,x_{j+1},\ldots ,x_n)\big ). \end{aligned}$$

6 Further examples, problems, and conjectures

6.1 The Grassmannian ${{\mathcal {G}}}(k,m)$

The pseudo n-metric (26) on ${{\mathcal {G}}}(k,m)$ is not completely satisfactory for several reasons. First, one expects a suitable pseudo n-metric on ${{\mathcal {G}}}(k,m)$ to be a canonical generalization of the standard 2-metric given by

$$\begin{aligned} d(V_1,V_2)= \Vert P_1 - P_2\Vert _2, \quad V_1,V_2 \in {{\mathcal {G}}}(k,m), \end{aligned}$$

where $P_1,P_2$ denote the orthogonal projections onto $V_1,V_2$ respectively, and $\Vert \cdot \Vert _2$ denotes the Euclidean operator norm (spectral norm) in ${\mathbb {R}}^m$; see [10, Ch.6.4.3]. This 2-metric may be expressed equivalently as

$$\begin{aligned} d(V_1,V_2)= \sin (\measuredangle (V_1,V_2)) = \sin (\theta _k), \end{aligned}$$

(28)

where $\theta _k$ is the largest principal angle between $V_1$ and $V_2$; see [10, Ch.2.5, Ch.6.4] and Proposition 6. Note that the 2-metric (28) differs from the 2-metric in (27). An alternative to (26) is to measure the exterior product $\bigwedge _{j=1}^n P_j$ of orthogonal projections by a norm different from the Hilbert-Schmidt norm (cf. (21)):

$$\begin{aligned} \max _{0 \ne F_{\ell }\in {\mathbb {R}}^{m,m},\ell =1,\ldots ,n}\frac{ |\Big (\bigwedge _{j=1}^n P_j\Big )(F_1,\ldots ,F_n)|}{\prod _{j=1}^n \Vert F_j\Vert _*}, \end{aligned}$$

where $\Vert \cdot \Vert _*$ is either the spectral norm $\Vert \cdot \Vert _2$ or its dual $\Vert \cdot \Vert ^D$ given by the sum of singular values; see [11, Ch.5.6]. However, neither were we able to prove the simplicial inequality for this setting, nor did we find an explicit expression for the associated 2-metric comparable to (28).

The fact that the Grassmannian may be viewed as a quotient space of $\textrm{St}(k,m)$ (see (25)) suggests another construction of a 2-metric on ${{\mathcal {G}}}(k,m)$ by setting

$$\begin{aligned} d_{{{\mathcal {G}}},H}(V_1,V_2) = \min _{Q_1,Q_2\in O(k)}d_H(A_1Q_1,A_2Q_2)= \min _{Q \in O(k)}d_H(A_1,A_2Q), \nonumber \\ \end{aligned}$$

(29)

for $V_j=\textrm{range}(A_j)$, $A_j \in \textrm{St}(k,m)$ and $d_H$ from (23), (24). The symmetry and definiteness of $d_{{{\mathcal {G}}},H}$ are obvious. The triangle inequality is also easily seen: for $A_j \in \textrm{St}(k,m)$ and $V_j=\textrm{range}(A_j)$, $j=1,2,3$ select $Q_1,Q_2 \in O(k)$ with

$$\begin{aligned} d_H(A_1,A_3Q_1)=d_{{{\mathcal {G}}},H}(V_1,V_3), \quad d_{H}(A_3,A_2Q_2)= d_{{{\mathcal {G}}},H}(V_3,V_2). \end{aligned}$$

Then we obtain

$$\begin{aligned} d_{{{\mathcal {G}}},H}(V_1,V_2)&\le d_H(A_1,A_2 Q_2Q_1) \le d_{H}(A_1,A_3Q_1)+d_{H}(A_3Q_1,A_2Q_2Q_1) \\&=d_{H}(A_1,A_3Q_1)+d_{H}(A_3,A_2Q_2)=d_{{{\mathcal {G}}},H}(V_1,V_3)+ d_{{{\mathcal {G}}},H}(V_3,V_2). \end{aligned}$$

The next proposition gives an explicit expression of the 2-metric (29) in terms of the principal angles $\theta _j$, $j=1,\ldots ,k$ between the subspaces $V_1$ and $V_2$.

Proposition 8

The expression (29) defines a 2-metric on the Grassmannian ${{\mathcal {G}}}(k,m)$. The metric satisfies

$$\begin{aligned} d_{{{\mathcal {G}}},H}(V_1,V_2) = \Big (1 - k^{-2}\big (\sum _{j=1}^k \sigma _j \big )^2\Big )^{1/2}, \end{aligned}$$

(30)

where $\sigma _1=\cos (\theta _1)\ge \cdots \ge \sigma _k=\cos (\theta _k)>0$ denote the singular values of $A_1^{\star }A_2$.

Proof

Consider the singular value decomposition $A_1^{\star }A_2= Y \Sigma Z^{\star }$ where $Y,Z \in O(k)$ and $\Sigma = \textrm{diag}(\sigma _1,\ldots ,\sigma _k)$. By (24) the minimum in (29) is achieved when maximizing

$$\begin{aligned} \langle A_1Q_1, A_2Q_2\rangle _H^2&= k^{-2} \textrm{tr}^2(Q_1^{\star }A_1^{\star }A_2 Q_2) = k^{-2}\textrm{tr}^2(Q_1^{\star }Y \Sigma Z^{\star } Q_2) \\&= k^{-2}\textrm{tr}^2(\Sigma Z^{\star } Q_2Q^{\star }_1 Y) \quad \text {w.r.t.} \quad Q_1,Q_2 \in O(k). \end{aligned}$$

Setting $Q=Z^{\star } Q_2Q^{\star }_1 Y \in O(k)$ this is equivalent to maximizing $\textrm{tr}^2(\Sigma Q)$ with respect to $Q \in O(k)$. Since the diagonal elements of $Q\in O(k)$ satisfy $|Q_{jj}| \le 1$ we obtain

$$\begin{aligned} \textrm{tr}^2(\Sigma Q)&= \big |\sum _{j=1}^k \sigma _j Q_{jj} \big |^2 \le \big ( \sum _{j=1}^k \sigma _j |Q_{jj}|)^2 \le \big ( \sum _{j=1}^k \sigma _j \big )^2= \textrm{tr}^2(\Sigma I_k). \end{aligned}$$

This proves our assertion. $\square$

Note that (30) differs from both expressions (28) and (27). Still another metric on the Grassmannian is given by the angle $\theta =\theta (V_1,V_2)$ defined in [12, Section 3]. It is related to the principal angles in (30) through $\cos (\theta )=\cos (\theta _1) \cdots \cos (\theta _k)$; see [12, Theorem 5].

Let us further note that we did not succeed to prove the simplicial inequality for the natural generalization of (29)

$$\begin{aligned} d_{{{\mathcal {G}}},H}(V_1,\ldots ,V_n) = \min _{Q_j\in O(k),j=1,\ldots ,n}d_H(A_1Q_1,\ldots , A_nQ_n) \end{aligned}$$

with $V_j=\textrm{range}(A_j)$, $A_j \in \textrm{St}(k,m)$. We rather conjecture that this is false which is suggested by analogy to a counterexample from the next subsection.

Finally, we discuss the special case $k=1$, when we can identify $V\in {{\mathcal {G}}}(1,m)$ with a unit vector $v \in S_{{\mathbb {R}}^m}$ such that $V = \textrm{span}\{v\}$. Proposition 4 then shows that a suitable pseudo n-metric on ${{\mathcal {G}}}(1,m)$ is given by

$$\begin{aligned} d(V_1,\ldots ,V_n)= \big (\det (\langle v_i, v_j \rangle _2)_{i,j=1}^n \big )^{1/2}, \end{aligned}$$

where $V_i=\textrm{span}\{v_i\}$, $\Vert v_i\Vert _2=1$ for $i=1,\ldots ,n$. In particular, in case $n=2$ we obtain

$$\begin{aligned} d(V_1,V_2)=\big ( 1 -\langle v_1,v_2\rangle ^2\big )^{1/2} = \big ( 1 -\cos \measuredangle (v_1,v_2)^2\big )^{1/2}= \sin \measuredangle (v_1,v_2), \end{aligned}$$

which is consistent with (28). On the other hand the pseudo n-metric (26) leads to

$$\begin{aligned} d_{{{\mathcal {G}}}}(V_1,\ldots ,V_n)= \big (\det (\langle v_i,v_j \rangle _2^2 )_{i,j=1}^n \big )^{1/2} \end{aligned}$$

which in case $n=2$ differs from (28). Therefore, we still consider it an open problem to construct a pseudo n-metric on the Grassmannian which is a natural generalization of the 2-metric (28).

6.2 Pseudo n-metric for subsets

It is natural to ask whether the classical Hausdorff distance for closed sets of a metric space (see e.g. [3, Chapter 1.5], [13, Ch.1.2.4]) has an extension to a pseudo n-metric.

Definition 5

Let $d:X^n \rightarrow {\mathbb {R}}$ be a pseudo n-metric on a set X. Then we define for nonempty subsets $A_j \subseteq X$, $j=1,\ldots ,n$ the following quantities

$$\begin{aligned} \begin{aligned} \textrm{dist}(x_1;A_2,\ldots ,A_n)&= \inf \{d(x_1,x_2,\ldots ,x_n): x_j \in A_j, j=2,\ldots ,n \}, \\ \textrm{dist}(A_1;A_2,\ldots ,A_n)&= \sup \{ \textrm{dist}(x_1;A_2,\ldots ,A_n): x _1 \in A_1 \}, \\ d_H(A_1,\ldots ,A_n)&= \max _{j=1,\ldots ,n} \textrm{dist}(A_j;A_1,\ldots , A_{j-1},A_{j+1},\ldots ,A_n). \end{aligned} \end{aligned}$$

(31)

For an ordinary 2-metric the construction (31) leads to the familiar Hausdorff distance

$$\begin{aligned} d_H(A_1,A_2)&= \max (\textrm{dist}(A_1;A_2),\textrm{dist}(A_2;A_1)) \end{aligned}$$

where $\textrm{dist}(A_1;A_2)$ is the Hausdorff semidistance defined by

$$\begin{aligned} \textrm{dist}(A_1;A_2)&= \sup _{x_1 \in A_1} \inf _{x_2 \in A_2} d(x_1,x_2). \end{aligned}$$

It is well known that $d_H$ is a metric on the set of all closed subsets of X where ’closedness’ is defined with respect to the given metric in X; see e.g. [3, Ch.9.4].

It is not difficult to see that the map $d_H$ defined in (31) is semidefinite and symmetric. While the simplicial inequality is true for $n=2$, i.e. the Hausdorff distance, we claim that it is generally false for $n \ge 3$.

Example 6

(Counterexample for the simplicial inequality)

Consider the case $n=3$ and four finite sets $A_1=\{w_1\}$, $A_2= \{x_1,\ldots ,x_{N}\}$, $A_3=\{y_1,\ldots ,y_{N}\}$, $A_4= \{z_1,\ldots ,z_{N} \}$ where $N \ge 2$. The set X is defined as $X=A_1 \cup A_2 \cup A_3 \cup A_4$. For convenience we introduce the following abbreviations for $i=1$ and $j,k,\ell =1,\ldots ,N$:

$$\begin{aligned} d_{0jk\ell }&= d(x_j,y_k,z_{\ell }),\quad d_{i0k\ell } = d(w_i,y_k,z_{\ell }),\\ d_{ij0\ell }&= d(w_i,x_j,z_{\ell }),\quad d_{ijk0} = d(w_i,x_j,y_k). \end{aligned}$$

The values of the 3-metric with three arguments from different sets $A_{\nu }$ in X are defined as follows:

$$\begin{aligned} d_{0jk\ell }&= {\left\{ \begin{array}{ll} 0, &{} j =k = \ell , \\ 1, &{} \text {otherwise}, \end{array}\right. }\\ d_{i0k\ell }&= {\left\{ \begin{array}{ll} 1, &{} k = \ell , \\ 0, &{} \text {otherwise}, \end{array}\right. }\\ d_{ij0\ell }&= {\left\{ \begin{array}{ll} 1, &{} j = \ell ,\\ 0, &{} \text {otherwise}, \end{array}\right. }\\ d_{ijk0}&= 1. \end{aligned}$$

Our first observation is

$$\begin{aligned} 1= \min _{\ell =1,\ldots ,N}(d_{ij0\ell }+d_{i0k\ell }+ d_{0jk\ell }), \end{aligned}$$

which implies $d_{ijk0}\le d_{ij0\ell }+d_{i0k\ell }+ d_{0jk\ell }=:D_{\ell }$ for all $i,j, k, \ell$. In fact, we find

$$\begin{aligned} D_{\ell }= {\left\{ \begin{array}{ll} 1+1 + 0, &{} k =j = \ell , \\ 0+0 + 1, &{} k =j \ne \ell ,\\ 1+0 + 1, &{} k \ne j = \ell ,\\ 0+1 + 1, &{} j \ne \ell =k ,\\ 0+0+1, &{} k \ne j \ne \ell \ne k . \end{array}\right. } \end{aligned}$$

Further, the simplicial inequalities

$$\begin{aligned} \begin{aligned} d_{ij0\ell }&\le d_{ijk0}+d_{i0k\ell } + d_{0jk\ell },\\ d_{i0k\ell }&\le d_{ijk0}+ d_{ij0\ell }+ d_{0jk\ell }. \\ d_{0jk\ell }&\le d_{ijk0}+d_{ij0\ell }+ d_{i0k\ell }, \end{aligned} \end{aligned}$$

(32)

hold, because $d_{ijk0}=1$ and all metric values lie in $\{0,1\}$.

By the definition of $d_{ijk\ell }$ and $N\ge 2$ we also obtain

$$\begin{aligned} \forall i \quad \exists j,\ell&: d_{ij0\ell }=0;\quad \forall j \quad \exists i,\ell : d_{ij0\ell }=0; \quad \forall \ell \quad \exists i,j : d_{ij0\ell }=0;\\ \forall i \quad \exists k,\ell&: d_{i0k\ell }=0; \quad \forall k \quad \exists i,\ell : d_{i0k\ell }=0; \quad \forall \ell \quad \exists i,k : d_{i0k\ell }=0;\\ \forall j \quad \exists k,\ell&: d_{0jk\ell }=0; \quad \forall k \quad \exists j,\ell : d_{0jk\ell }=0; \quad \forall \ell \quad \exists j, k : d_{0jk\ell }=0. \end{aligned}$$

Following the definition of $d_H$ in (31) this implies

$$\begin{aligned} d_H(A_1,A_2,A_4)&= \max \big (\max _i \min _{j,\ell }d_{ij0\ell }, \max _j \min _{i,\ell }d_{ij0\ell },\max _\ell \min _{i,j}d_{ij0\ell }\big )=0,\\ d_H(A_1,A_3,A_4)&= \max \big (\max _i \min _{k,\ell }d_{i0k\ell }, \max _k \min _{i,\ell }d_{i0k\ell },\max _\ell \min _{i,k}d_{i0k\ell }\big )=0,\\ d_H(A_2,A_3,A_4)&= \max \big (\max _j \min _{k,\ell }d_{0jk\ell }, \max _k \min _{j,\ell }d_{0jk\ell },\max _\ell \min _{j,k}d_{0jk\ell }\big )=0. \end{aligned}$$

On the other hand, we have

$$\begin{aligned} 1=\max \big ( \max _i(\min _{j,k} d_{ijk0}),\max _j(\min _{i,k} d_{ijk0}), \max _k(\min _{i,j} d_{ijk0})\big )=d_H(A_1,A_2,A_3), \end{aligned}$$

which contradicts the simplicial inequality (2).

In the following we define d for all triples where at least two elements lie in the same set, so that the axioms of a 3-metric are satisfied. Without loss of generality we define $d(\xi _1,\xi _2,\xi _3)$ when $\xi _1,\xi _2,\xi _3$ lie in sets $A_1$, $A_2$, $A_3$, $A_4$ with increasing lower index. All other values are then given by the permutation symmetry (1). Further, we set $d(\xi _1,\xi _2,\xi _3)=0$ if two of the arguments agree (semidefiniteness) or if all three arguments $\xi _1,\xi _2,\xi _3$ lie in the same set $A_\nu$. It remains to define the following quantities

$$\begin{aligned} d_{i,j \iota ,00}=d(w_i,x_j,x_{\iota })&= 0, \\ d_{i0,k \kappa ,0}=d(w_i,y_k,y_{\kappa })&=0 ,\\ d_{i00,\ell \lambda }=d(w_i,z_{\ell },z_{\lambda })&= 0,\\ d_{0,j \iota ,0 \ell }=d(x_j,x_{\iota },z_{\ell })&= {\left\{ \begin{array}{ll} 1, &{} (\iota = \ell ) \vee (j = \ell ), \\ 0, &{} \text {otherwise}, \end{array}\right. } \\ d_{0j0,\ell \lambda }= d(x_j,z_{\ell },z_{\lambda })&= {\left\{ \begin{array}{ll} 1, &{} (j = \ell ) \vee (j = \lambda ), \\ 0, &{} \text {otherwise}, \end{array}\right. }\\ d_{00,k \kappa ,\ell }=d(y_k,y_{\kappa },z_{\ell })&= {\left\{ \begin{array}{ll} 1, &{} (k = \ell ) \vee (\kappa = \ell ), \\ 0, &{} \text {otherwise}, \end{array}\right. }\\ d_{00k,\ell \lambda }=d(y_k,z_{\ell },z_{\lambda })&= {\left\{ \begin{array}{ll} 1, &{} (k=\ell ) \vee (k= \lambda ),\\ 0,&{} \text {otherwise}, \end{array}\right. }\\ d_{0,j \iota ,k0}=d(x_j,x_{\iota },y_k)&=1 , \\ d_{0j,k \kappa ,0}= d(x_j,y_k,y_{\kappa })&= 1. \end{aligned}$$

We have to check all simplicial inequalities involving two arguments from the same set and for which the d-value on the lefthand side is 1. We use the symbol $*$ to denote values which are either 0 or 1 and $(* + 1)$ to denote a sum which is $\ge 1$:

$$\begin{aligned} 1&= d_{0jk\ell }, \quad \text {if}\; (j \ne k) \vee (k \ne \ell ),\\&\le d_{0,j \iota ,k0}+d_{0\iota k \ell }+ d_{0,j \iota ,0\ell }=1+*+*,\\&\le d_{0j,k \kappa ,0}+d_{0j \kappa \ell }+d_{00,k \kappa ,\ell }= 1+* +*,\\&\le d_{0j0, \ell \lambda }+d_{00k,\ell \lambda }+d_{0jk \lambda }=* + (* + 1). \end{aligned}$$

For the last line note that either $d_{0jk \lambda }=1$ or ($d_{0jk \lambda }=0$, $j=k=\lambda$, $d_{00k,\ell \lambda }=1$).

$$\begin{aligned} 1&= d_{ij0 \ell }, \quad \text {if}\; (j =\ell ),\\&\le d_{i,j \iota ,00}+d_{i\iota 0 \ell }+ d_{0,j \iota ,0\ell }=*+*+1,\\&\le d_{0j0, \ell \lambda }+d_{i00,\ell \lambda }+d_{ij \lambda }=1 + * + *. \end{aligned}$$

$$\begin{aligned} 1&= d_{i0k\ell }, \quad \text {if}\; (k =\ell ),\\&\le d_{i,0,k \kappa ,0}+d_{i 0 \kappa \ell }+ d_{00,k \kappa ,\ell }=*+*+1,\\&\le d_{i00, \ell \lambda }+d_{i0k \lambda }+d_{00k,\ell \lambda }=*+* + 1 . \end{aligned}$$

$$\begin{aligned} 1&= d_{ijk0},\\&\le d_{i,j \iota ,00}+d_{i\iota k 0}+ d_{0,j \iota ,k0}=*+1+*,\\&\le d_{i0,k \kappa ,0}+d_{ij \kappa 0}+d_{0j,k \kappa ,0}= *+1 +*. \end{aligned}$$

In each of these three cases we test only two inequalities since the remaining three are satisfied by (32).

It remains to discuss d-values where either $j\iota$, $k \kappa$ or $\ell \lambda$ appears on the lefthand side.

$$\begin{aligned} 1&= d_{0,j \iota , k0}, \\&\le d_{ijk0} + d_{i \iota k 0} + d_{i,j \iota ,00}= 1 + 1 + *, \\&\le d_{0j,k \kappa , 0}+ d_{0 \iota ,k \kappa , 0}+ d_{0,j \iota , \kappa ,0} = * + * + 1, \\&\le d_{0jk \ell } + d_{0,j \iota ,0 \ell } + d_{0 \iota k \ell } = (1+ *) + *. \end{aligned}$$

For the last line note that either $d_{0jk \ell }=1$ or ( $d_{0jk \ell }=0$, $j=k=\ell$, $d_{0, j \iota ,0 \ell }=1$).

$$\begin{aligned} 1&= d_{0j ,k \kappa , 0}, \\&\le d_{ijk0} + d_{i j \kappa 0} + d_{i0, k \kappa ,0 }= 1 + 1 + *, \\&\le d_{0,j \iota ,k 0}+ d_{0,j \iota , \kappa , 0}+ d_{0\iota ,k \kappa ,0} = * + * + 1, \\&\le d_{00,k \kappa , \ell }+ d_{0j k \ell } + d_{0 j \kappa \ell } = (1+*) + *. \end{aligned}$$

For the last line note that either $d_{0jk \ell }=1$ or ($d_{0jk \ell }=0$, $j=k=\ell$, $d_{00,k \kappa , \ell }=1$).

For the final four cases the indices of the metric value on the left satisfy an extra condition

$$\begin{aligned} 1&= d_{0,j \iota , 0 \ell }, \quad \text {if}\; (j= \ell ) \vee (\iota = \ell ), \\&\le d_{ij0 \ell } + d_{i \iota 0 \ell } + d_{i,j \iota ,00}= (1 + *) + *, \\&\le d_{0,j \iota ,k 0}+ d_{0 j k \ell }+ d_{0 \iota k \ell } = 1 + * + *, \\&\le d_{0j0, \ell \lambda } + d_{0\iota 0, \ell \lambda } + d_{0,j \iota , 0 \lambda } = (1+ *) + *. \end{aligned}$$

For last line note that $d_{0j0, \ell \lambda }=1$ if $j = \ell$ and $d_{0\iota 0, \ell \lambda }=1$ if $\iota =\ell$.

$$\begin{aligned} 1&= d_{00,k \kappa , \ell }, \quad \text {if} \; (k=\ell )\vee (\kappa =\ell ),\\&\le d_{i0k\ell } + d_{i 0 \kappa \ell } + d_{i0, k \kappa ,0 }= (1 + *) + *, \\&\le d_{0,j k \ell }+ d_{0 j \kappa \ell }+ d_{0j,k \kappa ,0} = * + * + 1, \\&\le d_{00k , \ell \lambda }+ d_{00 \kappa , \ell \lambda } + d_{0 , k \kappa , \lambda } = (1+*) + *. \end{aligned}$$

For the last line note that $d_{00k, \ell \lambda }=1$ if $k = \ell$ and $d_{00 \kappa , \ell \lambda }=1$ if $\kappa =\ell$.

$$\begin{aligned} 1&= d_{0j 0, \ell \lambda }, \quad \text {if}\; (j= \ell ) \vee (j = \lambda ), \\&\le d_{ij0 \ell } + d_{i j 0 \lambda } + d_{i00,\ell \lambda }= (1 + *) + *, \\&\le d_{0,j \iota ,0 \ell }+ d_{0 ,j \iota ,0 \lambda }+ d_{0 \iota 0, \ell \lambda } = (1 + *) + *, \\&\le d_{0jk \ell } + d_{0jk\lambda } + d_{00k, \ell \lambda } = *+ (1+ *). \end{aligned}$$

For the last line note that either $d_{0jk \lambda }=1$ or ($d_{0jk \lambda }=0$, $j=k=\lambda$, $d_{00k, \ell \lambda }=1$).

$$\begin{aligned} 1&= d_{00k, \ell \lambda }, \quad \text {if}\; (k= \ell ) \vee (k = \lambda ), \\&\le d_{i0k \ell } + d_{i 0 k \lambda } + d_{i00,\ell \lambda }= (1 + *) + *, \\&\le d_{0j k \ell }+ d_{0 j k \lambda }+ d_{0 j 0, \ell \lambda } = * + (1+*), \\&\le d_{00,k \kappa , \ell } + d_{00,k \kappa , \lambda } + d_{00 \kappa , \ell \lambda } = (1+*)+ *. \end{aligned}$$

For the last line note that $d_{00,k \kappa , \ell }=1$ if $k = \ell$ and $d_{00,k \kappa , \lambda }=1$ if $k = \lambda$.

Finally, in case $N \ge 3$ we have to test the last six blocks of simplicial inequalities when a double pair $j \iota$ resp. $k \kappa$ resp. $\ell \lambda$ is prolonged by another index $j'$ resp. $k'$ resp. $\ell '$. For example, two characteristic cases are the following:

$$\begin{aligned} 1&= d_{0,j \iota , k0}, \\&\le d_{0,j \iota j',00}+d_{0,j j',k0}+ d_{0, \iota j',k0}=0+1+1, \\ 1&= d_{0,j \iota , 0 \ell }, \quad \text {if}\; (j= \ell ) \vee (\iota = \ell ), \\&\le d_{0,j \iota j',00}+ d_{0,j j',0 \ell }+d_{0, \iota j', 0 \ell }=0 +(1+ *). \end{aligned}$$

For the last line note that $d_{0,j j',0 \ell }=1$ if $j=\ell$ and $d_{0, \iota j', 0 \ell }=1$ if $\iota =\ell$. By inspection one finds that the remaining four cases can be handled in the same way.

While this example shows that the definition (31) with an arbitrary pseudo n-metric does not necessarily define a pseudo n-metric on subsets, it is still open whether some of the special n-metrics from Sect. 3 have this property.