Ruled Surfaces in 3-Dimensional Riemannian Manifolds

Abstract

In this work, ruled surfaces in 3-dimensional Riemannian manifolds are studied. We determine the expressions for the extrinsic and sectional curvatures of a parametrized ruled surface, where the former one is shown to be non-positive. We also quantify the set of ruling vector fields along a given base curve which allows us to define a relevant reference frame that we refer to as Sannia frame. The fundamental theorem of existence and equivalence of Sannia ruled surfaces in terms of a system of invariants is given. The second part of the article tackles the concept of the striction curve, which is proven to be the set of points where the so-called Jacobi evolution function vanishes on a ruled surface. This characterisation of striction curves provides independent proof for their existence and uniqueness in space forms and disproves their existence or uniqueness in some other cases.

1 Introduction

Ruled surfaces constitute a distinguished family of submanifolds in the area of differential geometry with a long history and a rich collection of works in the literature. Even though their original framework in the Euclidean space is still an active field of research (just to mention one, the reader may have a look at the study of non-developable ruled surfaces in Ref. [14]), ruled surfaces are also a prominent object in other Riemannian manifolds. For example, in the case of the Heisenberg group, where parts of planes, helicoids and hyperbolic paraboloids are proven to be the only minimal ruled surfaces (see Ref. [20]), or the minimal (resp. maximal) ruled surfaces in the Bianchi–Cartan–Vranceanu spaces $\mathbb {E}(\kappa ,\tau )$ (resp. in their Lorentzian counterparts), see Ref. [1]. In Ref. [4], several results for ruled surfaces in 3-dimensional Riemannian manifolds are established, where formulas for the striction curve, the distribution parameter and the first and second fundamental forms of ruled surfaces in space forms are obtained. The authors also find a model-independent proof for the well-known fact that surfaces in 3-dimensional space forms with vanishing (extrinsic) Gauss curvature are necessarily ruled. In addition, a necessary and sufficient condition on the Riemann tensor of a generic 3-dimensional Riemannian manifold is derived for an extrinsically flat surface to be ruled. Specifically, if Z and X are independent vector fields tangent to the surface where Z generates the rulings and N stands for the normal vector field, such requirement is given by $\textrm{Riem}(X,Z,Z,N)=0$. Ruled surfaces have also been studied in Lorentzian contexts as in Ref. [5], where all Weingarten surfaces are characterised in the 3-dimensional Minkowski space. Other results concerning ruled surfaces in the 3-dimensional Minkowski space $\mathbb {R}^3_1$ have been established in Refs. [3, 10, 11]. In Ref. [3], Choi classifies the ruled surfaces satisfying relation $\triangle \xi =A\xi$, where $\xi$ is the Gauss map of non-degenerate surfaces and $A\in \textrm{mat}(3,\mathbb {R})$ are real $3\times 3$ matrices. The only surfaces that solve the problem are planes (Riemannian and Lorentzian) and cylinders (Lorentzian, hyperbolic and circular of index 1). In Ref. [10], the authors classify the so-called surfaces of pointwise 1-type Gauss map in the 3-dimensional Minkowski space, which are the ones satisfying $\triangle \xi =f\xi$, where f is a smooth function on the surface. The authors conclude that the only cylindrical ones are non-degenerate planes and cylinders (Lorentzian, hyperbolic and circular of index 1), the non-cylindrical ones are helicoids (1st, 2nd and 3rd kind) and conjugate of Enneper surfaces of the 2nd kind, and the null scrolls are Minkowskian planes and B-scrolls (flat and non-flat). Finally, in Ref. [11], the authors provide a classification of non-flat ruled surfaces in $\mathbb {R}^3_1$ whose second Gaussian curvature, mean curvature and Gaussian curvature satisfy suitable linear combinations along their rulings (helicoids of 1st, 2nd and 3rd kind, conjugate of Enneper surfaces of the 2nd kind, surfaces with vanishing second Gaussian curvature and null scrolls). Lightlike ruled hypersurfaces have also been of great utility to address the problem of some geometric inequalities as in Ref. [15], where some cases of the so-called null Penrose inequality for the Bondi energy of a spacetime are proven.

All Euclidean ruled surfaces except cylinders admit a unique special curve called striction curve, which is made up of the so-called central points of each generator [18, 23]. In the case of the cylinder, the uniqueness property is not fulfilled, for every curve in it is a striction one. On the other hand, striction curves can degenerate to a single point, as occurs with the cone, where it is made up exclusively of its vertex. A central point in a geodesic generator of the surface furnishes a critical point to the distance from points on that generator to neighbouring geodesics. The family of generators along the striction curve is parallel with respect to the induced connection on the corresponding surface along it. Striction curves are important, among other reasons, because they contain the singular points of the ruled surface in case they exist [6]. The determination of the striction curve has sometimes been achieved, as in the case of Ref. [4], where the authors determine its position on ruled surfaces in ambients of constant curvature. In addition, in Ref. [9], the authors find the position of striction curves on the ruled surfaces in $\mathbb {S}^3$. Although the terminology “striction curve” is not considered in their work, the solutions $\theta _0$ of Eq. (4.5) parametrise such curves (see also Remark 2 of Ref. [4]). However, to the best of our knowledge, there are no results in the literature involving a method to determine the striction curve of ruled surfaces in generic Riemannian manifolds. In this work, we present a new strategy to determine the existence of striction curves in such context based on a function referred to as Jacobi evolution function, which vanishes at this type of curves in case they lie on the surface. Even though the presence of striction curves is addressed in Ref. [4] for ruled surfaces in $\mathbb {S}^3(r)$ and $\mathbb {H}^3(r)$, no results are found in the literature where either the existence or uniqueness of the striction curve is violated in such contexts. In fact, in this work, the aforementioned Jacobi evolution function is applied to prove that there exists at most one striction curve on ruled surfaces in the 3-dimensional hyperbolic space $\mathbb {H}^3$, with examples of surfaces with no striction curve.

In case that the striction curve of a ruled surface in a 3-dimensional Riemannian manifold is regular, it is possible to define a specific reference frame called Sannia after the Italian mathematician who first proposed it (see Refs. [18, 19]), and which is characterised for having the generating vector of the rulings as the first element of the basis. The evolution of the Sannia frame provides two Euclidean invariants associated with the surface referred to as curvature and torsion, which together with the (striction) angle enclosed, determine a complete system of Euclidean invariants for the ruled surface. A fundamental problem in Riemannian Geometry is that of equivalence of objects in a determined class, namely to provide a criterion to know whether two given objects in this class are congruent under isometries or not. In Ref. [2], the problem of curves with values in an arbitrary dimensional Riemannian manifold is solved with respect to the Frenet curvatures. However, spaces with non-constant curvature require additional invariants to establish such result. The classical Sannia problem of reconstructing suitable surfaces provided a set of associated invariant functions is known and is presented in Theorem 5.3.8 in Ref. [18]. In this work, we establish an analogous result of local existence and uniqueness of ruled surfaces in generic 3-dimensional Riemannian manifolds. In our main theorem, we prove that four functions of suitable regularity and the Sannia frame at a given point $p_0\in M$ determine uniquely a (local) ruled surface passing through $p_0$. Moreover, we do not require the base to be a striction curve. This is a great advantage since, as we shall see, certain ruled surfaces lack this sort of curves.

The paper is structured as follows. In Sect. 2, we introduce the concept of parametrized ruled surface, which is the most practical way to present ruled surfaces for the purposes of this work. As a first result, we obtain the expression for the sectional curvature of any ruled surface in a 3-dimensional Riemannian manifold in terms of the ambient geometry and its second fundamental form. We also define the extended distribution parameter function that generalises the distribution parameter for ruled surfaces in the Euclidean space. At the end of the section, we introduce the concept of Sannia ruled surface, which we define as the ones admitting a ruling vector field which is linearly independent with its covariant derivative along it. In particular, this means that a Sannia frame can be defined along the base curve. An idea of the size of the set of vectors satisfying such a property is put forward in Proposition 2.14. Deriving the evolution equations for the vectors of a Sannia frame along a given base curve gives rise to a set of two invariant functions associated with the Sannia ruled surface which, together with two additional angle functions, provide the fundamental theorem of ruled surfaces (see Theorem 2.22 below). In addition to the local existence of the ruled surface in generic Riemannian manifolds, its uniqueness up to local isometries holds exclusively in constant curvature backgrounds. In Sect. 3, we focus our interest on the existence and uniqueness of striction curves. We define a new function on the ruled surface that we refer to as Jacobi evolution function, which vanishes on the striction curves in case of existence. This makes such a function a useful tool for proving the presence of striction curves on ruled surfaces. In the case of constant curvature k, we compute its expression explicitly in the three possible cases of sign of k. In particular, for $k<0$, the striction curve may not exist (in contrast to Ref. [4]). Furthermore, some extra examples of ruled surfaces in certain product manifolds are put forward to disprove the uniqueness of the striction curve in such backgrounds. In the text, Einstein’s summation convention will be assumed.

2 Ruled Surfaces in 3-Dimensional Riemannian Manifolds

2.1 Definitions and Properties

Let (M, g) be a 3-dimensional Riemannian manifold and let $\psi :\Sigma \rightarrow (M,g)$ be an immersed surface in (M, g). We recall some basic concepts of the geometry of hypersurfaces (see for instance, Ref. [12]). We denote by $\nabla$ and $\nabla ^\Sigma$ the Levi-Civita connections of (M, g) and $(\Sigma , \psi ^* g=g_\Sigma )$, respectively. Locally, we can assume $\Sigma$ to be embedded in (M, g). Let us choose a unit normal vector $\xi$ in a neighbourhood U of a point $p\in \Sigma$. Recall that the second fundamental form of $\Sigma$ is defined as

$$\begin{aligned}&\textbf{h}:T_p\Sigma \times T_p\Sigma \rightarrow T^\perp _p \Sigma \\&(U,V) \mapsto (\nabla _{U}V)_{p}^{\perp }=h(U,V)\xi , \end{aligned}$$

where $T^\perp _p \Sigma$ is the subspace of normal vectors on $\Sigma$, and $h:T_{p}\Sigma \times T_{p}\Sigma \rightarrow \mathbb {R}$ is the associated second fundamental form tensor of $\Sigma$ defined as

$$\begin{aligned} h(U,V)=-g(\nabla _{U}\xi ,V). \end{aligned}$$

Given any vectors fields $X,Y,Z,T\in \mathfrak {X}(M)$, we consider the curvature tensor of (M, g) as

$$\begin{aligned} R(X,Y)Z=\nabla _X \nabla _Y Z-\nabla _Y \nabla _X Z-\nabla _{[X,Y]} Z, \end{aligned}$$

and the Riemann tensor is $\textrm{Riem}(X,Y,Z,T)=-g(R(X,Y)Z,T)$. The induced curvature tensor and Riemann tensor on $\Sigma$ will be denoted by $R^\Sigma$ and $\textrm{Riem}^\Sigma$, respectively. Given any $p\in M$ and two linearly independent vectors $X,Y\in T_p M$ generating a plane $T_p \Sigma \subset T_p M$, the sectional curvature $K(T_p\Sigma )$ in (M, g) is defined by

$$\begin{aligned} K(T_p\Sigma )=\frac{\textrm{Riem}(X,Y,X,Y)}{g(X,X)g(Y,Y)-g(X,Y)^2}, \end{aligned}$$

and the sectional curvature of $\Sigma$ will be denoted by $K^\Sigma$. The sectional curvatures $K(T_p\Sigma )$ in (M, g) and $K^\Sigma _p$ in $(\Sigma ,g_\Sigma )$ are related by

$$\begin{aligned} K^\Sigma _p = K(T_p\Sigma ) + K^\Sigma _\mathrm {{ext}}, \end{aligned}$$

(2.1)

where $K^\Sigma _\mathrm{{ext}}$ is the extrinsic or Gauss curvature (the determinant of the second fundamental form endomorphism).

Ruled surfaces are a remarkable family of surfaces in 3-dimensional Riemannian manifolds. They are generally defined as follows.

Definition 2.1

We say that the immersed surface $\psi :\Sigma \rightarrow (M,g)$ in (M, g) is ruled if there exists a foliation of $\Sigma$ by curves which are geodesics in the ambient space (M, g).

However, in the following, we are going to work with a notion, closer to the classical constructions in the Euclidean space, of ruled surface defined by base curves and ruling directions.

Definition 2.2

Let (M, g) be a complete 3-dimensional Riemannian manifold. Let $\alpha :I\rightarrow (M,g)$ be a smooth regular curve and Z a non-vanishing smooth vector field along $\alpha$, i.e. a curve in TM such that $Z(u)\in T_{\alpha (u)}M$, $\forall u\in I$. The parametrized ruled surface defined by $\alpha$ and Z is the differentiable map

$$\begin{aligned}{} & {} \textbf{X}:I\times \mathbb {R} \rightarrow (M,g) \nonumber \\{} & {} (u,v) \mapsto \gamma _{Z(u)}(v)=\exp _{\alpha (u)}(vZ(u)), \end{aligned}$$

(2.2)

where $\gamma _{Z(u)}:\mathbb {R}\rightarrow (M,g)$ is the geodesic satisfying

$$\begin{aligned} \gamma _{Z(u)}(0)&=\alpha (u),\\ \gamma _{Z(u)}^{\prime }(0)&=Z(u). \end{aligned}$$

Remark 2.3

Obviously, the image of the map $\textbf{X}$ is not necessarily an embedded surface in (M, g). But if we require the rank of $d\textbf{X}$ to be 2, it will be an immersed surface. On the other hand, if (M, g) is not complete, the definition above is still valid by restricting the domain of $\textbf{X}$.

Note that the partial derivative $\textbf{X}_v=\partial \textbf{X}/\partial v$ is a geodesic vector field, that is

$$\begin{aligned} \nabla _{\textbf{X}_v}\textbf{X}_v=0. \end{aligned}$$

In addition, $\textbf{X}_v(u,0)=Z(u)$. The other partial derivative $\textbf{X}_u= \partial \textbf{X}/\partial u$ is a Jacobi vector field along the geodesic $\gamma _{Z(u)}$ since it is a geodesic variation. Hence, it satisfies the Jacobi equation

$$\begin{aligned} \nabla _{\textbf{X}_v}\nabla _{\textbf{X}_v}\textbf{X}_u+R(\textbf{X}_u,\textbf{X}_v)\textbf{X}_v=0. \end{aligned}$$

(2.3)

In the following result, we derive the expression for the (intrinsic) curvature $K_p^\Sigma$ of a ruled surface $\Sigma$ in (M, g).

Proposition 2.4

Let $\Sigma$ be a parametrized ruled surface in (M, g) defined by $\textbf{X}:I\times \mathbb {R}\rightarrow (M,g)$, where $d\textbf{X}$ is of rank 2. Then, we have

$$\begin{aligned} K_p^{\Sigma }=\frac{-g(\nabla _{\textbf{X}_v} \nabla _{\textbf{X}_v} \textbf{X}_u,\textbf{X}_u)}{\vert \vert \textbf{X}_u\vert \vert ^2 \vert \vert \textbf{X}_v\vert \vert ^2-g(\textbf{X}_u,\textbf{X}_v)^2}-\frac{\textrm{vol}_g(\textbf{X}_u,\textbf{X}_v,\nabla _{\textbf{X}_u}\textbf{X}_v)^2}{(\vert \vert \textbf{X}_u\vert \vert ^2 \vert \vert \textbf{X}_v\vert \vert ^2-g(\textbf{X}_u,\textbf{X}_v)^2)^2}.\nonumber \\ \end{aligned}$$

(2.4)

Proof

Taking into account the Gauss equation (see Ref. [12, Volume II, Chapter VII, Proposition 4.1]), the sectional curvature for $T_{p}\Sigma$ is written as follows:

$$\begin{aligned} K_p^\Sigma&=\frac{\textrm{Riem}^\Sigma (\textbf{X}_u,\textbf{X}_v,\textbf{X}_u,\textbf{X}_v)}{\vert \vert \textbf{X}_u\vert \vert ^2 \vert \vert \textbf{X}_v\vert \vert ^2-g(\textbf{X}_u,\textbf{X}_v)^2}\\&=\frac{\textrm{Riem}(\textbf{X}_u,\textbf{X}_v,\textbf{X}_u,\textbf{X}_v)+g(\textbf{h}(\textbf{X}_u,\textbf{X}_u),\textbf{h} (\textbf{X}_v,\textbf{X}_v))}{\vert \vert \textbf{X}_u\vert \vert ^2 \vert \vert \textbf{X}_v\vert \vert ^2-g(\textbf{X}_u,\textbf{X}_v)^2} \\&\hspace{0.5cm}-\frac{g(\textbf{h}(\textbf{X}_u,\textbf{X}_v),\textbf{h}(\textbf{X}_u,\textbf{X}_v))}{\vert \vert \textbf{X}_u\vert \vert ^2 \vert \vert \textbf{X}_v\vert \vert ^2-g(\textbf{X}_u,\textbf{X}_v)^2}. \end{aligned}$$

Since $\textbf{X}_v$ is geodesic and $[\textbf{X}_u,\textbf{X}_v]=0$, we have

$$\begin{aligned} K_p^\Sigma =\frac{-g(\nabla _{\textbf{X}_v}\nabla _{\textbf{X}_v}\textbf{X}_u,\textbf{X}_u)-h(\textbf{X}_u,\textbf{X}_v)^2}{\vert \vert \textbf{X}_u\vert \vert ^2 \vert \vert \textbf{X}_v\vert \vert ^2-g(\textbf{X}_u,\textbf{X}_v)^2}. \end{aligned}$$

The proof is complete by taking into account

$$\begin{aligned} |h(\textbf{X}_u,\textbf{X}_v)|=|g(\xi ,\nabla _{\textbf{X}_u}\textbf{X}_v)|=\frac{|\textrm{vol}_g(\textbf{X}_u,\textbf{X}_v,\nabla _{\textbf{X}_u}\textbf{X}_v)|}{\sqrt{\vert \vert \textbf{X}_u\vert \vert ^2 \vert \vert \textbf{X}_v\vert \vert ^2-g(\textbf{X}_u,\textbf{X}_v)^2}}. \end{aligned}$$

$\square$

Remark 2.5

Considering (2.1) and (2.4), it follows that

$$\begin{aligned} K(T_{p}\Sigma )= & {} \frac{-g(\nabla _{\textbf{X}_v} \nabla _{\textbf{X}_v} \textbf{X}_u,\textbf{X}_u)}{\vert \vert \textbf{X}_u\vert \vert ^2 \vert \vert \textbf{X}_v\vert \vert ^2-g(\textbf{X}_u,\textbf{X}_v)^2}, \nonumber \\ K_{\textrm{ext}}^{\Sigma }= & {} -\frac{\textrm{vol}_g(\textbf{X}_u,\textbf{X}_v,\nabla _{\textbf{X}_u}\textbf{X}_v)^2}{(\vert \vert \textbf{X}_u\vert \vert ^2 \vert \vert \textbf{X}_v\vert \vert ^2-g(\textbf{X}_u,\textbf{X}_v)^2)^2}. \end{aligned}$$

(2.5)

Note that the extrinsic curvature $K^\Sigma _\mathrm{{ext}}$ of a parametrized ruled surface in a generic Riemannian background is non-positive, as (2.5) shows. In particular, the (intrinsic) curvature of a ruled surface is always less or equal than the ambient sectional curvature. Also notice that the extrinsic curvature relation $K_{\textrm{ext}}^{\Sigma }$ in (2.5) is still valid for any other basis of $T_p\Sigma$ since it is a tensorial expression.

Remark 2.6

If the manifold (M, g) has constant sectional curvature k, we have that $\textrm{vol}_{g}(X_{u},X_{v},\nabla _{\textbf{X}_{u}}X_{v})$ is constant along the ruling geodesics. Indeed,

$$\begin{aligned}{} & {} \frac{\textrm{d}}{\textrm{d}v}\textrm{vol}_{g}(\textbf{X}_u,\textbf{X}_v,\nabla _{\textbf{X}_u}\textbf{X}_v) \\{} & {} \quad =\textrm{vol}_{g}(\nabla _{\textbf{X}_v}\textbf{X}_u,\textbf{X}_v,\nabla _{\textbf{X}_u}\textbf{X}_v) +\textrm{vol}_{g}(\textbf{X}_u,\nabla _{\textbf{X}_v}\textbf{X}_v,\nabla _{\textbf{X}_u}\textbf{X}_v) \\{} & {} \qquad +\textrm{vol}_{g}(\textbf{X}_u,\textbf{X}_v,\nabla _{\textbf{X}_v}\nabla _{\textbf{X}_u}\textbf{X}_v)\\{} & {} \quad =\textrm{vol}_{g}(\textbf{X}_{u},\textbf{X}_{v}, R(\textbf{X}_v,\textbf{X}_u)\textbf{X}_v)\\{} & {} \quad =\textrm{vol}_{g}(\textbf{X}_u,\textbf{X}_v,k(g(\textbf{X}_u,\textbf{X}_v)\textbf{X}_v-g(\textbf{X}_v,\textbf{X}_v)\textbf{X}_u))=0, \end{aligned}$$

where we have taken into account that the Riemannian volume form is parallel with respect to $\nabla$, as well as $\nabla _{\textbf{X}_v}\textbf{X}_u-\nabla _{\textbf{X}_u}\textbf{X}_v=[\textbf{X}_v,\textbf{X}_u]=0=\nabla _{\textbf{X}_v}\textbf{X}_v$. In particular, in this case we have that $K_\mathrm{{ext}}=0$ if and only if $K_\mathrm{{ext}}|_{\alpha }=0$. Note that the fact that

$$\begin{aligned} \textrm{vol}_{g}(\textbf{X}_{u},\textbf{X}_{v},\nabla _{\textbf{X}_{u}}\textbf{X}_{v})(u,v)=\textrm{vol}_{g}(\textbf{X} _{u},\textbf{X}_{v},\nabla _{\textbf{X}_{u}}\textbf{X}_{v})(u,0) \end{aligned}$$

disagrees with Ref. [4]. We feel that this discrepancy comes from a slight misinterpretation of formula

$$\begin{aligned} Z^{\prime }=DZ-\frac{1}{r^{2}}\langle \alpha ^{\prime },Z\rangle \psi (u,v), \end{aligned}$$

after formula 15 of Ref. [4]. As Z is only defined along $\psi (u,0)$, the previous formula should be

$$\begin{aligned} Z^{\prime }=DZ-\frac{1}{r^{2}}\langle \alpha ^{\prime },Z\rangle \psi (u,0)=DZ-\frac{1}{r^{2}}\langle \alpha ^{\prime },Z\rangle \alpha (u). \end{aligned}$$

With this expression, one also proves that $\textrm{vol}_{g}(\textbf{X}_{u},\textbf{X}_{v} ,\nabla _{\textbf{X}_{u}}\textbf{X}_{v})(u,v)=\textrm{vol}_{g}(\textbf{X} _{u},\textbf{X}_{v},\nabla _{\textbf{X}_{u}}\textbf{X}_{v})(u,0)$. Notice that having considered this correction, the fact that $K_{\textrm{ext}}=0$ if and only if $K_{\textrm{ext}}|_\alpha =0$ still holds, which makes it much easier to establish a classification of extrinsically flat surfaces in space forms.

The expression of the extrinsic curvature that we have obtained above is connected with a classical invariant in the theory of ruled surfaces, the distribution parameter $\lambda$ of ruled surfaces in the Euclidean space (see Refs. [6, 8, 18, 21] for more details). We next define a function defined on a parametrized ruled surface motivated by the classical concept of distribution parameter:

Definition 2.7

(Extended distribution parameter) Let $\textbf{X}:I\times \mathbb {R}\rightarrow (M,g)$ be a parametrized ruled surface as in (2.2) in a Riemmanian 3-manifold (M, g) with $d\textbf{X}$ of rank 2. We define the extended distribution parameter function of $\textbf{X}:I\times \mathbb {R}\rightarrow (M,g)$ as

$$\begin{aligned} \lambda (u,v)=\frac{\textrm{vol}_g(\textbf{X}_u,\textbf{X}_v,\nabla _{\textbf{X}_u}\textbf{X}_v)}{\Vert \nabla _{\textbf{X}_u}\textbf{X}_v\Vert ^2}. \end{aligned}$$

(2.6)

Remark 2.8

As we will illustrate in Sect. 3, for $v=0$ the above formula reduces to the classical distribution parameter $\lambda (u,0)=\lambda (u)$ provided $\alpha :I\rightarrow \textbf{X}(I\times \mathbb {R})$ is a striction base curve.

Definition 2.9

Let $\textbf{X}:I\times \mathbb {R}\rightarrow (M,g)$ a parametrized ruled surface in (M, g) as in (2.2). The function $\sigma :I\rightarrow \mathbb {R}$ satisfying

$$\begin{aligned} \cos \sigma _{\alpha (u)}=\frac{g(\alpha ^{\prime }(u),Z(u))}{\Vert \alpha ^\prime (u)\Vert } \end{aligned}$$

is called base angle along the curve $\alpha$.

It is a well-known fact that given a one-parameter family of geodesics parametrized by arc-length on a Riemannian manifold, the product of their velocity by the associated Jacobi vector field is constant along each one (see for instance, Ref. [8]). For the sake of completeness of this work, we include a proof of this result adapted to the setting we are considering, which in turn allows us to find an expression for the angle $\sigma$ between $\textbf{X}_u$ and $\textbf{X}_v$ at any point q of a ruled surface in terms of the geometry of its base curve and the norm of the Jacobi field $\textbf{X}_u$ at q:

Proposition 2.10

Let $\textbf{X}:I\times \mathbb {R}\rightarrow (M,g)$ be a parametrized ruled surface as in (2.2), being Z a unit vector field. Then $g(\textbf{X}_u,\textbf{X}_v)$ is constant along its rulings. Moreover, the angle $\sigma$ between $\textbf{X}_u$ and $\textbf{X}_v$ at any point q of the ruling containing $p=\alpha (u)$ is given by

$$\begin{aligned} \cos {\sigma }_q=\frac{\Vert \alpha ^\prime (u)\Vert }{\Vert \textbf{X}_u\Vert _q}\cos {\sigma _p}. \end{aligned}$$

(2.7)

Proof

Differentiating the function $g(\textbf{X}_u,\textbf{X}_v)$ along the vector field $\textbf{X}_v$ gives

$$\begin{aligned} \textbf{X}_v(g(\textbf{X}_u,\textbf{X}_v))=g(\nabla _{\textbf{X}_v}\textbf{X}_u,\textbf{X}_v)+g(\textbf{X}_u,\nabla _{\textbf{X}_v}\textbf{X}_v)=g(\nabla _{\textbf{X}_u} \textbf{X}_v,\textbf{X}_v)=0, \end{aligned}$$

where we have taken into account that $[\textbf{X}_u,\textbf{X}_v]=0$ and $\textbf{X}_v$ is geodesic. This means that $g(\textbf{X}_u,\textbf{X}_v)=\Vert \textbf{X}_u\Vert \cos {\sigma }$ is constant along the rulings. This value can be obtained by evaluating it at the point $p=\alpha (u)$. Indeed, given any q of the ruling at $p=\alpha (u)$,

$$\begin{aligned} g(\textbf{X}_u,\textbf{X}_v)|_q=\Vert \textbf{X}_u\Vert _q\cos {\sigma _q}=\Vert \textbf{X}_u\Vert _p\cos {\sigma }_p=\Vert \alpha ^\prime (u)\Vert \cos {\sigma _p}, \end{aligned}$$

from where relation (2.7) follows. $\square$

Remark 2.11

Relation (2.7) shows that whenever the vectors $\textbf{X}_u(u,0)=\alpha ^\prime (u)$ and $Z_p=\textbf{X}_v(u,0)$ are orthogonal at the base curve, they remain orthogonal along the ruling $\gamma _{Z(u)}(v)={\textbf {X}}_v(u,v)$. Nevertheless, the coordinate basis $(\textbf{X}_u,\textbf{X}_v)$ associated with the parametrization (2.2) with $d\textbf{X}$ of rank 2 is not necessarily orthogonal.

As already mentioned, $\textbf{X}_u$ is a Jacobi vector field on every parametrized ruled surface, not necessarily orthogonal to its rulings. However, it is sometimes useful to consider the orthogonal component to the surface generators, which turns out to be a Jacobi field too. In the following proposition, we compute the decomposition of $\textbf{X}_u$ into its tangent and normal components to the rulings.

Proposition 2.12

Let $\textbf{X}:I\times \mathbb {R}\rightarrow (M,g)$ be a parametrized ruled surface in (M, g) as in (2.2), being Z a unit vector field. Then the decomposition of the Jacobi field $\textbf{X}_u$ into its tangential and normal part with respect to the ruling is

$$\begin{aligned} \textbf{X}_u=\Vert \alpha ^\prime (u)\Vert (\cos {\sigma _p})\textbf{X}_v+\textbf{X}_u^{\bot }, \end{aligned}$$

where $\textbf{X}_u^{\bot }$ is a Jacobi field along the ruling $\gamma _{Z(u)}$ and orthogonal to it, and $\sigma _p$ is the base angle at $p=\alpha (u)$.

Proof

It is a well-known fact that any Jacobi vector field along a geodesic curve $\gamma (v)$ parametrized by its arc-length decomposes as

$$\begin{aligned} J(v)=(a+bv)\gamma '(v)+J^{\bot }(v), \end{aligned}$$

where $a=g(J(0),\gamma '(0))$, $b=g((\nabla _{\gamma '} J)_p, \gamma '(0))$ and $J^{\bot }$ is an orthogonal Jacobi field along $\gamma$. In this background, the Jacobi field $\textbf{X}_u$ evaluated at p reads $\textbf{X}_u|_p=\alpha ^\prime (u)$, so

$$\begin{aligned} a=g(\alpha ^\prime (u),Z_p)=\Vert \alpha ^\prime (u)\Vert \cos {\sigma _p}, \end{aligned}$$

and

$$\begin{aligned} b=g((\nabla _{\textbf{X}_v} \textbf{X}_u)|_p,Z_p)=\frac{1}{2}\textbf{X}_u(g(\textbf{X}_v,\textbf{X}_v))|_p=0, \end{aligned}$$

since $\Vert \textbf{X}_v\Vert =1$. Decomposition (2.8) follows from such values. $\square$

2.2 Sannia Invariants and the Fundamental Theorem of Ruled Surfaces

Orthonormal frames along curves are often considered in Geometry and Physics to address problems in relation to the geometry of manifolds and submanifolds. In this work, we consider frames whose first vector is determined by the geodesics defining the ruled surface. Under suitable regularity hypothesis, a possible way of constructing the rest of the vectors in the frame is by considering successive derivatives of the first one along the tangent direction to the curve (see for example, Ref. [2]). However, it may occur that some of the derivatives are linearly dependent with some other vector in the frame, which would prevent such a set of vectors to become a basis. With the following results, we first intend to give an idea of the size of the set of ruled surfaces admitting such a relevant frame, and then we prove the main result of this work, the fundamental theorem of ruled surfaces, in which we state that certain ruled surfaces are uniquely determined from certain invariants.

Definition 2.13

A vector field $Z\in \mathfrak {X}(\alpha )$ along a smooth curve $\alpha :I\rightarrow M$ taking values into a manifold M endowed with a linear connection $\nabla$ is said to be in general position at $u_{0}\in I$ if the vector fields Z and $\nabla _{\alpha ^{\prime }}Z$ along $\alpha$ are linearly independent at $u_{0}$. The vector field $Z\in \mathfrak {X}(\alpha )$ is in general position if it is in general position for every $u\in (a,b)$.

The following result quantifies the set of vectors in general position along a curve on a manifold endowed with a linear connection. To this purpose it will be necessary to make use of the so-called jet bundles. We refer the reader to Ref. [13, section 41] for more details on this topic.

Proposition 2.14

Let M be a 3-dimensional manifold endowed with a linear connection $\nabla$ and let $\alpha :I\rightarrow M$ be a smooth curve on M. The set of vector fields $Z\in \mathfrak {X}(\alpha )$ along $\alpha$ that are in general position is a dense set on $\mathfrak {X}(\alpha )$ with respect to the strong topology.

Proof

The sections of the bundle $E=\alpha ^{*}TM\rightarrow I$ are vector fields along $\alpha$. Let consider the 1-jet bundle of E. The morphism on $J^{1}E$ given by

$$\begin{aligned} \varrho :J^{1}E&\longrightarrow E\oplus E\\ j_{u}^{1}Z&\mapsto \left( Z(u),(\nabla _{\alpha ^{\prime }}Z)(u)\right) \end{aligned}$$

is an isomorphism. We define the singular set

$$\begin{aligned} S=\{(Z_{1},Z_{2})\in E\oplus E:Z_{1}\wedge Z_{2}=0\}, \end{aligned}$$

which can written as the (non-disjoint) union $S=S_{1}\cup S_{2}$, with

$$\begin{aligned} S_{1}&=\{(Z_{1},Z_{2})\in E\oplus E:Z_{2}=fZ_{1}\}\simeq E\times \mathbb {R},\\ S_{2}&=\{(Z_{1},0)\in E\oplus E\}\simeq E. \end{aligned}$$

Both $S_{1}$ and $S_{2}$ are closed submanifolds of $E\oplus E$, of dimensions $3+1$ (resp. codimension $2-1$) and 3 (resp. codimension 3), respectively. The same properties apply to $T_{1}=\varrho ^{-1}(S_{1})$ and $T_{2} =\varrho ^{-1}(S_{2})$. According to Thom’s transversality Theorem (cf. [22, VII, Théorème 4.2]), the set of curves $Z(u)\in \Gamma (E)$ such that $j^{1}Z$ is transversal to both $T_{1}$ and $T_{2}$ is open and dense in $\Gamma (E)$ with the strong topology. For these curves Z(u), the codimension of $(j^{1}Z)^{-1}(T_{1})$ is 2 and the codimension of $(j^{1}Z)^{-1}(T_{2})$ is 3. Since these are set in $I\subset \mathbb {R}$, they must be empty. Therefore, for this dense set of curves Z(u), we have that $j^{1}Z\cap S=\varnothing$, and the proof is complete. $\square$

Definition 2.15

Let (M, g) be a Riemannian 3-manifold. A parametrized ruled surface $\textbf{X}:I\times \mathbb {R}\rightarrow (M,g)$ is said to be a Sannia ruled surface if $Z\in \mathfrak {X}(\alpha )$ is in general position with respect to the Levi-Civita connection of g.

Proposition 2.16

Let (M, g) be an oriented 3-dimensional Riemannian manifold and let $\textbf{X}:I\times \mathbb {R}\rightarrow (M,g)$ be a Sannia ruled surface defined by a vector field Z along a smooth curve $\alpha :I\rightarrow (M,g)$. Then, there exist unique vector fields $X_{i}$, $1\le i\le 3$, defined along $\alpha$ and smooth functions $\kappa _{i}:I\rightarrow \mathbb {R}$, $\,0\le i\le 2$, with $\kappa _{0}>0$ and $\kappa _{1}>0$, such that

• 1. $( X_{1}(u),X_{2}(u),X_{3}(u) )$ is a positively oriented orthonormal linear frame of $T_{\alpha (u)}M$ for $u\in I$.

• 2. The following formulas hold:

  • (a) $Z=\kappa _{0}X_{1}$,

  • (b) $\nabla _{\alpha ^{\prime }}X_{1}=\kappa _{1}X_{2} ,$

  • (c) $\nabla _{\alpha ^{\prime }}X_{2}=-\kappa _{1} X_{1}+\kappa _{2}X_{3},$

  • (d) $\nabla _{\alpha ^{\prime }}X_{3}=-\kappa _{2} X_{2}.$

Proof

We define

$$\begin{aligned} X_{1}= & {} (\kappa _{0})^{-1}Z,\\ X_{2}= & {} (\kappa _{1})^{-1}\nabla _{\alpha ^{\prime }} X_{1}, \end{aligned}$$

where $\kappa _{0}=\left\| Z \right\|$, $\kappa _{1}=\left\| \nabla _{\alpha ^{\prime }}X_{1}\right\|$. For $X_3$ we consider the unique vector field defining a positive orthonormal basis with $X_1$ and $X_2$. Differentiating $g(X_i,X_j)$ with respect to u we get the formulas (2a)–(2d) in the statement. $\square$

Remark 2.17

Note that the relation $\nabla _{\alpha '}X_1=\kappa _1 X_2$ defines the Sannia invariant $\kappa _1$, which is nothing but the relative curvature of $\alpha$ with respect to $X_1$, or courbure inclinée (see Ref. [21]).

Definition 2.18

The frame $( X_{1},X_{2},X_{3} )$ along $\alpha$ determined in the above Proposition is called Sannia frame along $\alpha$, and the functions $\kappa _{0},\kappa _{1},\kappa _{2}$ are the Sannia invariants of the ruled surface $\textbf{X}:I\times \mathbb {R}\rightarrow (M,g)$.

Let $\theta , \varphi$ denote the spherical angles of $\alpha '$ with respect to $(X_{1},X_{2},X_{3})$; that is,

$$\begin{aligned} \frac{\alpha ^\prime }{\Vert \alpha '\Vert }=\cos {\varphi }\cos {\theta }\, X_1+\sin {\varphi }\,X_2+\cos {\varphi }\sin {\theta }\,X_3. \end{aligned}$$

(2.8)

If $\varphi =0$, then $\theta$ is the base angle $\sigma$ (see Definition 2.9). We will show in Sect. 3 that this case corresponds to the base curve being a striction one.

Remark 2.19

It would be more accurate to collect the angle invariants $\theta$ and $\varphi$ into a single smooth function $\varsigma :I\rightarrow \mathbb {S}^2\subset \mathbb {R}^3$ assigning the coordinates of $\alpha '$ with respect to the Sannia basis. However, in order to be close to the classical results in the Euclidean space, we will keep track of the angles $\theta$ and $\varphi$ instead of $\varsigma$.

In Definition 2.7, we have presented a function that extends the traditional Euclidean distribution parameter to the whole surface in generic 3-dimensional Riemannian backgrounds. With a view to recovering the distribution parameter in the classical sense, we next give the value of this function in terms of the invariants $\kappa _0$, $\kappa _1$, $\kappa _2$, $\theta$ and $\varphi$ of the Sannia frame associated with a base curve which does not have to be necessarily a striction curve.

Proposition 2.20

If $( X_{1},X_{2},X_{3} )$ is the Sannia frame of a Sannia ruled surface $\textbf{X}:I\times \mathbb {R}\rightarrow (M,g)$, then the value of the distribution parameter function $\lambda$ on the base curve $\alpha$ is

$$\begin{aligned} \lambda (u,0)= \frac{\Vert \alpha ^\prime (u) \Vert \kappa _{0}^{2}(u)\kappa _1(u) \cos {\varphi }_{\alpha (u)}\sin {\theta }_{\alpha (u)}}{\left( \frac{\textrm{d}\kappa _0(u)}{\textrm{d}u}\right) ^2+\kappa _0^{2}(u)\kappa _1^{2}(u)}. \end{aligned}$$

Proof

The result follows directly when (2.8) and relations (2a)–(2d) in Proposition 2.16 are inserted into expression (2.6), evaluated at $v=0$. $\square$

Remark 2.21

Note that it is always possible to consider a unit ruling Z along an arc-length parametrized curve $\alpha$, i.e. $\kappa _0=1$ and $\Vert \alpha ^\prime \Vert =1$. In such case the value of the distribution parameter function along $\alpha$ reduces to

$$\begin{aligned} \lambda (u,0)=\frac{\cos {\varphi }_{\alpha (u)}\sin {\theta }_{\alpha (u)}}{\kappa _1(u)}. \end{aligned}$$

(2.9)

We next state and prove the local existence and uniqueness theorem of ruled surfaces in general 3-dimensional Riemannian manifolds:

Theorem 2.22

(Fundamental theorem of ruled surfaces) Let (M, g) be a 3-dimensional oriented Riemannian manifold and let $(e_{1},e_{2},e_{3})$ be a positively oriented orthonormal basis of $T_{p_{0}}M$, $p_0\in M$. Given smooth functions $\overline{\kappa }_{i}:(u_{0}-\varepsilon ,u_{0}+\varepsilon )\rightarrow \mathbb {R}$, $0\le i\le 2$, $\overline{\theta } :(u_{0}-\varepsilon ,u_{0}+\varepsilon )\rightarrow \mathbb {R}$, $\overline{\varphi }:(u_{0}-\varepsilon ,u_{0}+\varepsilon )\rightarrow \mathbb {R}$ with $\overline{\kappa }_{0},\overline{\kappa }_1 >0$, there exists $\delta <\varepsilon$, a curve $\alpha :(u_{0}-\delta ,u_{0}+\delta )\rightarrow (M,g)$, parametrized by its arc-length, and a vector field $Z\in \mathfrak {X}(\alpha )$ such that the Sannia ruled surface $\textbf{X}:I\times \mathbb {R}\rightarrow (M,g)$, $\textbf{X}(u,v)=\exp _{\alpha (u)}(vZ(u))$ satisfies

• 1. $\alpha (u_{0})=p_{0}$,

• 2. $X_{i}(u_{0})=e_{i}$ for $1\le i\le 3$,

• 3. $\kappa _{i}=\overline{\kappa }_{i}$ for $0\le i\le 2$, $\overline{\theta }= \theta$, $\overline{\varphi }=\varphi$,

where $\kappa _{i}$, $0\le i\le 2$, $\theta$ and $\varphi$ are the invariants of Definition 2.18 and $X_{i}(u_{0})$ for $1\le i\le 3$ is the Sannia frame. In addition, given any two points $p_{0},p_{0}^{\prime }\in M$ and two oriented orthonormal bases $(e_i)_{i=1}^3$, $(e'_i)_{i=1}^3$ of $T_{p_{0}}M$ and $T_{p_{0}^{\prime }}M$, respectively, there always exists a local isometry around $p_{0}$ and $p_{0}^{\prime }$ sending one ruled surface to the other if and only if (M, g) is of constant curvature.

Proof

We consider the vector bundle $p_{M}:\oplus ^{3}TM\rightarrow M$ and a normal coordinate system $(U,(x_{i})_{i=1}^{3})$ centred at $p_{0}$ associated with the orthonormal basis $(e_i)_{i=1}^3$. We define the natural coordinate system $(x^{i},y_{k}^{j})$, $i,j,k=1,2,3$ in $p_{M}^{-1}(U)$ such that

$$\begin{aligned} w_{j}=y_{j}^{i}(w)\left. \frac{\partial }{\partial x^{i}}\right| _{p},\qquad \forall w=\left( w_{1},w_{2},w_{3}\right) \in \oplus ^{3} T_{x}M,\quad p\in U. \end{aligned}$$

Let $X:I \rightarrow \oplus ^{3}TM$, $a<u_{0}<b$, be the curve given by

$$\begin{aligned} X(u)=\left( X_{1}(u),X_{2}(u),X_{3}(u)\right) . \end{aligned}$$

Without loss of generality, the ruling can be considered to be of unit length, i.e. $\overline{\kappa }_0=1$ in Proposition 2.16. This condition together with the formulas (2a)–(2d) can be expressed as follows:

(2.10)

with $1\le i\le 3$ and where $\Gamma _{jk}^{i}$ are the components of the Levi-Civita connection $\nabla$ of g with respect to the coordinate system $(x_{i})_{i=1}^{3}$. From the general theory of ODE’s, the system (2.10) has unique solutions $x^{i}\circ \alpha ,y_{k}^{j}\circ X$, $i,j,k=1,2,3$, satisfying the initial conditions $\left( x^{i}\circ \alpha \right) (u_{0})=x^{i}(x_{0})$, $\left( y_{k}^{j}\circ X\right) (u_{0} )={\hat{\delta }}_{k}^{j}$, $i,j,k=1,2,3$, where ${\hat{\delta }}$ is the Kronecker delta. We consider the ruled surface $\textbf{X}:I\times \mathbb {R}\rightarrow (M,g)$, $\textbf{X}(u,v)=\exp _{\alpha (u)}(vZ(u))$ with

$$\begin{aligned} \alpha (u)=(x^{1}(u),x^{2}(u),x^{3}(u)),\qquad Z(u)=y_{1}^{i}(u)\left( \frac{\partial }{\partial x^{i}}\right) _{\alpha (u)}. \end{aligned}$$

We first prove that

$$\begin{aligned} X_{k}(u)=y_{k}^{i}(u)\left( \frac{\partial }{\partial x^{i}}\right) _{\alpha (u)},\qquad 1\le k\le 3, \end{aligned}$$

define an orthonormal basis. To this end, consider the functions

$$\begin{aligned} \phi _{ij}(u)=g_{\alpha (u)}(X_{i}(u),X_{j}(u)),\qquad 1\le i\le j\le 3. \end{aligned}$$

As a consequence of the system (2.10), it is straightforward to check that $\phi _{ij}$ satisfy the following equations:

$$\begin{aligned} \left\{ \begin{array}{llll} \dfrac{\textrm{d}\phi _{11}}{\textrm{d}u}=2\overline{\kappa }_{1}\phi _{12},\\ \dfrac{\textrm{d}\phi _{12}}{\textrm{d}u}=\overline{\kappa }_{1}\phi _{22}-\overline{\kappa }_{1} \phi _{11}+\overline{\kappa }_{2}\phi _{13},\\ \dfrac{\textrm{d}\phi _{13}}{\textrm{d}u}=\overline{\kappa }_{1}\phi _{23}-\overline{\kappa }_{2} \phi _{12},\\ \dfrac{\textrm{d}\phi _{22}}{\textrm{d}u}=-2\overline{\kappa }_{1}\phi _{12}+2\overline{\kappa }_{2} \phi _{23},\\ \dfrac{\textrm{d}\phi _{23}}{\textrm{d}u}=-\overline{\kappa }_{1}\phi _{13}+\overline{\kappa }_{2} \phi _{33}-\overline{\kappa }_{2}\phi _{22},\\ \dfrac{\textrm{d}\phi _{33}}{\textrm{d}u}=-2\overline{\kappa }_{2}\phi _{23}, \end{array} \right. \end{aligned}$$

with initial conditions $\phi _{ij}(u_{0})={\hat{\delta }}_{j}^{i}$. But the constant function ${\hat{\phi }}_{ij}(u)={\hat{\delta }}_{j}^{i}$ also satisfies this system of differential equations with these initial conditions. By the uniqueness theorem of EDOs, it follows that $\phi _{ij}(u)={\hat{\delta }}_{j}^{i}$, for all u. In addition, since $( X_{1}(u_{0}),X_{2}(u_{0}),X_{3} (u_{0}))$ is an oriented positive basis, by continuity, so it is $(X_{1}(u),X_{2}(u),X_{3}(u))$ for any u. The frame determined by X verifies that $X_{1}=Z$ and $\nabla _{\alpha ^{\prime }}X_{1}=\overline{\kappa }_1 X_{2}$, so since $( X_{1},X_{2},X_{3})$ is positive, it is the Sannia basis of the ruled surface $\textbf{X}:I\times \mathbb {R}\rightarrow (M,g)$. Finally, again from (2.10), it follows that $\overline{\kappa }_{1}$ and $\overline{\kappa }_{2}$ are the Sannia invariants.

We now prove the uniqueness of the ruled surface up to isometries. First, if (M, g) is of constant curvature, given $p_{0},p_{0}^{\prime }\in M$ and $( e_{i})_{i=1}^3$, $(e'_{i})_{i=1}^3$ oriented orthonormal bases at $T_{p_{0}}M$ and $T_{p_{0}^{\prime }}M$, respectively, we consider a local isometry $\phi$ sending $p_{0}$ to $p_{0}^{\prime }$ and $( e_{i} )_{i=1}^3$ to $(e'_{i})_{i=1}^3$. Since $\phi$ preserves the Levi-Civita connection, the image $\phi \circ \textbf{X}$ of the ruled surface defined by $p_{0}$ and $( e_{i} )_{i=1}^3$ is a ruled surface with the same parameters $\overline{\kappa }_{1}$, $\overline{\kappa }_{2}$. By the uniqueness of the system of differential equations (2.10), we have $\textbf{X}^{\prime }=\phi \circ \textbf{X}$. Conversely, if given $p_{0}$, $p_{0}^{\prime }\in M$ and orthonormal bases $( e_{i} )_{i=1}^3$, $(e'_{i})_{i=1}^3$ at $T_{p_{0}}M$ and $T_{p_{0}^{\prime }}M$, respectively, there is a local isometry sending one to the other, the space is locally isotropic, and hence of constant curvature (cf. [12]). $\square$

3 Central Points and Striction Curves

Euclidean ruled surfaces contain a special curve called striction curve which is the locus of the points whose distance with respect to neighbouring geodesics is extremal. In particular striction curves are divided into expanding–contracting and contracting–expanding curves depending on whether this distance corresponds to a maximum or a minimum value, respectively. In general, the striction curve of a family of Euclidean curves is the locus for the points where the geodesic curvature of the corresponding orthogonal set of curves vanishes (read Refs. [16, 17] for more details). The striction curve of any Euclidean ruled surface is also characterised by the fact that the generators along it are parallel in the Levi-Civita sense. The following relation is necessarily satisfied on striction curves in generic 3-dimensional Riemannian manifolds, as Eq. (16) in Ref. [23] illustrates. In our work, we delve deeper into the causes of this fact, and we define on this basis the so-called Jacobi evolution function, which will play a fundamental role in the study of existence and uniqueness of striction curves on ruled surfaces.

Definition 3.1

Let $\textbf{X}:I\times \mathbb {R}\rightarrow (M,g)$ be a parametrized ruled surface. A curve $s:I \rightarrow \textbf{X}(I\times \mathbb {R})$ is said to be a striction curve if

$$\begin{aligned} g(s^{\prime },\nabla _{s^{\prime }}\textbf{X}_v)=0. \end{aligned}$$

As already mentioned, whenever the striction curve $s:I \rightarrow \textbf{X}(I\times \mathbb {R})$ exists, it can be taken as the base curve of the ruled surface so that it can be reparametrised as $\textbf{X}(u,v)=\textrm{exp}_{s(u)}(vZ(u))$.

Proposition 3.2

Let $\textbf{X}:I\times \mathbb {R}\rightarrow (M,g)$ be a Sannia ruled surface in a 3-dimensional Riemannian manifold $\left( M,g\right)$ admitting a striction curve $s:I \rightarrow \textbf{X}(I\times \mathbb {R})$ and chosen to be its base curve. For any $p=\textbf{X}(u,0)$, the vectors $\{X_{1},X_{3}\}$ of the associated Sannia frame constitute an orthonormal basis of $T_{p}\,(\textbf{X}(I\times \mathbb {R}))$ and the angle $\varphi$ defined by (2.8) vanishes identically. Therefore

$$\begin{aligned} s^{\prime }(u)=\cos \sigma _{s(u)}\,X_{1}+\sin \sigma _{s(u)}\,X_{3} \quad \hbox { for all}\ u\in I. \end{aligned}$$

Proof

The above relation holds since the tangent plane to $\textbf{X}:I\times \mathbb {R}\rightarrow (M,g)$ along s is spanned by $s^{\prime }$ and Z, and the second vector $X_2=\nabla _{s'}Z/\vert \vert \nabla _{s'}Z \vert \vert$ of the corresponding Sannia frame is perpendicular to both of them. $\square$

As mentioned above, in the Euclidean setting, the ruling vector field of a ruled surface is parallel along the striction curve with respect to its induced Levi-Civita connection. This property also holds in a general Riemannian background as shown in the following result.

Corollary 3.3

Under the hypotheses of Proposition 3.2, the ruling vector field Z is parallel along the striction curve with respect to the induced connection on the Sannia ruled surface.

Proof

The Gauss identity on the striction curve reads

$$\begin{aligned} \nabla _{s'}Z =\nabla ^{\Sigma }_{s'}Z+\textbf{h}(s',Z), \end{aligned}$$

where $\nabla ^{\Sigma }$ stands for the induced connection on the ruled surface $\Sigma \equiv \textbf{X}(I\times \mathbb {R})$. By Proposition 3.2, $\nabla _{s'}Z$ is orthogonal to $\Sigma$, which means that $\nabla ^{\Sigma }_{s'}Z=0$. $\square$

Remark 3.4

In the classical statement of the fundamental theorem of ruled surfaces in the Euclidean space $(\mathbb {R}^3,\delta )$, a striction curve can always be taken as the base curve in the parametrization for it always exists. By virtue of the above proposition, in such a context $\varphi =0$ and $\theta =\sigma$, i.e. the base angle on the striction curve. In particular, the distribution parameter formula (2.9) on a general base curve reduces to

$$\begin{aligned} \lambda (u,0)=\frac{\sin {\sigma _{s(u)}}}{\kappa _1(u)}, \end{aligned}$$

which is the classical expression for the Euclidean distribution parameter (on a striction curve) [18, Lemma 5.3.7].

In the following result, we obtain a characterisation of striction curves in terms of the coordinate basis $(\textbf{X}_u,\textbf{X}_v)$.

Proposition 3.5

Let $\textbf{X}:I\times \mathbb {R}\rightarrow (M,g)$ be a parametrized ruled surface $\textbf{X}:I\times \mathbb {R}\rightarrow (M,g)$ with $\alpha :I \rightarrow \textbf{X}(I\times \mathbb {R})$ an associated base curve, and with a unit ruling vector field $Z\in \mathfrak {X}(\alpha )$. A curve $s:I \rightarrow \textbf{X}(I\times \mathbb {R})$ on such a surface is a striction curve if and only if the squared norm of the vector field $\textbf{X}_u$ along each generator $\gamma _{Z(u)}(v)$ is critical at the corresponding point s(u), i.e.

$$\begin{aligned} \textbf{X}_v(\Vert \textbf{X}_u\Vert ^{2})|_{p}=0,\quad \hbox { for all}\ p=s(u). \end{aligned}$$

(3.1)

Proof

Given any curve of the form $s:I\rightarrow \textbf{X}(I\times \mathbb {R})$, $s(u)=\textbf{X}(u,v(u))$, where $v:I \rightarrow \mathbb {R}$ is smooth, we have $s^{\prime }=\textbf{X}_u+v^{\prime }\textbf{X}_v$. Then

$$\begin{aligned} g(s^{\prime },\nabla _{s^{\prime }}\textbf{X}_v)= & {} g (\textbf{X}_u+v^{\prime }\textbf{X}_v, \nabla _{\textbf{X}_u+v^{\prime }\textbf{X}_v} \textbf{X}_v)= g (\textbf{X}_u+v^{\prime }\textbf{X}_v, \nabla _{\textbf{X}_u} \textbf{X}_v)\\= & {} g (\textbf{X}_u, \nabla _{\textbf{X}_u} \textbf{X}_v) = g (\textbf{X}_u, \nabla _{\textbf{X}_v} \textbf{X}_u) = \tfrac{1}{2}\textbf{X}_v(\Vert \textbf{X}_u\Vert ^{2}), \end{aligned}$$

where we have taken into account that $g(\textbf{X}_v,\textbf{X}_v)$ is constantly 1, and that $\nabla _{\textbf{X}_u}\textbf{X}_v-\nabla _{\textbf{X}_v}\textbf{X}_u=[\textbf{X}_u,\textbf{X}_v]=0$. The proof is complete by the definition of striction curve. $\square$

Remark 3.6

Since the length of the Jacobi vector field $\textbf{X}_u$ gives a local idea of the deviation of a congruence of geodesics, relation (3.1) is in accordance with the definition of striction curve established in a Euclidean sense, where any point in these curves has a critical distance with respect to neighbouring geodesics, as mentioned before.

The previous result motivates the following definition.

Definition 3.7

Let $\textbf{X}:I\times \mathbb {R}\rightarrow (M,g)$ be a parametrized ruled surface in a 3-dimensional Riemannian manifold (M, g). The function that describes the derivative of the squared norm of the Jacobi field

$$\begin{aligned} F:\textbf{X}(I\times \mathbb {R}) \rightarrow \mathbb {R}, \quad F(p)=\tfrac{1}{2}(\textbf{X}_v\Vert \textbf{X}_u\Vert ^2)|_p \end{aligned}$$

(3.2)

will be referred to as the Jacobi evolution function of the ruled surface. The points of the parametrized ruled surface where F vanishes are called central points.

Remark 3.8

Therefore, striction curves lie on the vanishing set of the function F. Furthermore, the function F describes the evolution of the norm of the Jacobi variational field $\textbf{X}_u$ along each ruling. The study of the sign of F provides relevant information with regard to the behaviour of the rulings in a local manner. If F is strictly positive at a point, the norm of the Jacobi is increasing and hence the rulings are locally spreading apart. Just the opposite happens in case that F is strictly negative at some point. Since (u, v) is a system of coordinates associated with the parametrization (2.2) of the ruled surface, we will simply refer to $(F\circ \textbf{X})(u,v)$ as F(u, v) for the sake of simplicity.

We next explore the behaviour of the first and second derivatives of the function F.

Theorem 3.9

Let $\textbf{X}:I\times \mathbb {R}\rightarrow (M,g)$ be a parametrized ruled surface in a Riemannian 3-manifold (M, g). The first and second derivatives of the Jacobi evolution function F are

$$\begin{aligned}{} & {} \frac{\partial F}{\partial v}=-\textrm{Riem}(\textbf{X}_v,\textbf{X}_u,\textbf{X}_v,\textbf{X}_u)+\Vert \nabla _{\textbf{X}_v} \textbf{X}_u\Vert ^2, \end{aligned}$$

(3.3)

$$\begin{aligned}{} & {} \frac{\partial ^2 F}{\partial \, v^2}= g\left( \left( \nabla _{\textbf{X}_v}R\right) (\textbf{X}_v,\textbf{X}_u,\textbf{X}_v),\textbf{X}_u\right) -4\textrm{Riem}(\textbf{X}_v,\textbf{X}_u,\textbf{X}_v,\nabla _{\textbf{X}_v}\textbf{X}_u). \nonumber \\ \end{aligned}$$

(3.4)

Proof

If we differentiate F along the $\textbf{X}_v$-direction, we obtain

$$\begin{aligned} \frac{\partial F}{\partial v}=\nabla _{\textbf{X}_v}g(\nabla _{\textbf{X}_v}\textbf{X}_u,\textbf{X}_u)= g(\nabla _{\textbf{X}_v}\nabla _{\textbf{X}_v}\textbf{X}_u,\textbf{X}_u)+g(\nabla _{\textbf{X}_v}\textbf{X}_u,\nabla _{\textbf{X}_v}\textbf{X}_u). \end{aligned}$$

As $\textbf{X}_u$ is a Jacobi vector field along the rulings, it satisfies (2.3) so that

$$\begin{aligned} \frac{\partial F}{\partial v}= & {} -g(R(\textbf{X}_u,\textbf{X}_v)\textbf{X}_v,\textbf{X}_u)+\Vert \nabla _{\textbf{X}_v}\textbf{X}_u\Vert ^2 \nonumber \\= & {} -\textrm{Riem}(\textbf{X}_v,\textbf{X}_u,\textbf{X}_v,\textbf{X}_u)+\Vert \nabla _{\textbf{X}_v} \textbf{X}_u\Vert ^2, \end{aligned}$$

and

$$\begin{aligned} \frac{\partial ^2 F}{\partial \, v^2}= & {} g\left( \nabla _{\textbf{X}_v}(R(\textbf{X}_v,\textbf{X}_u)\textbf{X}_v),\textbf{X}_u\right) +g(R(\textbf{X}_v,\textbf{X}_u)\textbf{X}_v),\nabla _{\textbf{X}_v}\textbf{X}_u) \nonumber \\{} & {} +2g(\nabla _{\textbf{X}_v}\nabla _{\textbf{X}_v}\textbf{X}_u,\nabla _{\textbf{X}_v}\textbf{X}_u) \nonumber \\= & {} g\left( \nabla _{\textbf{X}_v}(R(\textbf{X}_v,\textbf{X}_u)\textbf{X}_v),\textbf{X}_u\right) +3g(R(\textbf{X}_v,\textbf{X}_u)\textbf{X}_v,\nabla _{\textbf{X}_v}\textbf{X}_u). \nonumber \\ \end{aligned}$$

(3.5)

On the other hand, taking into account the symmetries of the Riemann tensor and the fact that $\textbf{X}_v$ is a geodesic vector field, we obtain

$$\begin{aligned} g(\nabla _{\textbf{X}_v}(R(\textbf{X}_v,\textbf{X}_u)\textbf{X}_v),\textbf{X}_u)= & {} g((\nabla _{\textbf{X}_v}R)(\textbf{X}_v,\textbf{X}_u,\textbf{X}_v),\textbf{X}_u) \nonumber \\{} & {} +g(R(\textbf{X}_v,\textbf{X}_u)\textbf{X}_v,\nabla _{\textbf{X}_v}\textbf{X}_u). \end{aligned}$$

(3.6)

Plugging (3.6) into (3.5) finally gives (3.4), which finally concludes the proof of the theorem. $\square$

As a consequence, in the special case where the ambient manifold has constant curvature, the above derivatives of F read as follows.

Corollary 3.10

Let (M(k), g) be a Riemannian 3-manifold of constant sectional curvature k and $\textbf{X}:I\times \mathbb {R}\rightarrow (M,g)$ be a parametrized ruled surface with Z a unit vector field. Then the first and second derivatives of the Jacobi evolution function F read

$$\begin{aligned} \frac{\partial F}{\partial v}= & {} -k(\Vert \textbf{X}_u\Vert ^2-\Vert \alpha ^\prime (u)\Vert ^2\cos ^2\sigma _p)+\Vert \nabla _{\textbf{X}_v}\textbf{X}_u\Vert ^2 \end{aligned}$$

(3.7)

and

$$\begin{aligned} \frac{\partial ^2 F}{\partial \, v^2}= & {} (-2k)\textbf{X}_v(\Vert \textbf{X}_u\Vert ^2)=-4kF(u,v), \end{aligned}$$

(3.8)

where $p=\alpha (u)=\textbf{X}(u,0)$ and $\sigma _p$ is the base angle between $\alpha ^\prime (u)$ and Z at p.

Proof

By the sectional curvature relation for a space form, we have

$$\begin{aligned} \textrm{Riem}(\textbf{X}_v,\textbf{X}_u,\textbf{X}_v,\textbf{X}_u)=k\left( \Vert \textbf{X}_u\Vert ^2-g(\textbf{X}_u,\textbf{X}_v)^2 \right) , \end{aligned}$$

(3.9)

since $\textbf{X}_v$ is a unit vector field. On the other hand, we know by Proposition 2.10 that $g(\textbf{X}_u,\textbf{X}_v)=\Vert \alpha ^\prime (u)\Vert \cos {\sigma _p}$ is constant along the associated ruling. Hence, (3.9) can be rewritten as

$$\begin{aligned} \textrm{Riem}(\textbf{X}_v,\textbf{X}_u,\textbf{X}_v,\textbf{X}_u)=k\left( \Vert \textbf{X}_u\Vert ^2-\Vert \alpha ^\prime (u)\Vert ^2 \cos ^2 \sigma _p \right) , \end{aligned}$$

(3.10)

so (3.3) becomes (3.7) when relation (3.10) is inserted. Let us derive now relation (3.8). By virtue of formula (3.4), the second derivative of the Jacobi evolution function F in a space form becomes

$$\begin{aligned} \frac{\partial ^2 F}{\partial \, v^2}=-4\,\textrm{Riem}(\textbf{X}_v,\textbf{X}_u,\textbf{X}_v,\nabla _{\textbf{X}_v}\textbf{X}_u)=4\,g(R(\textbf{X}_v,\textbf{X}_u)\textbf{X}_v,\nabla _{\textbf{X}_v}\textbf{X}_u), \end{aligned}$$

for $\nabla R=0$ holds. Since

$$\begin{aligned} R(\textbf{X}_v,\textbf{X}_u)\textbf{X}_v=R(\textbf{X}_v,\textbf{X}_u^{\bot })\textbf{X}_v=-k \textbf{X}_u^{\bot }, \end{aligned}$$

where the last equality is fulfilled as a consequence of the ambient manifold being a space form, we have

$$\begin{aligned} \frac{\partial ^2 F(u,v)}{\partial v^2}=(-4k) g(\textbf{X}_u^{\bot },\nabla _{\textbf{X}_v}\textbf{X}_u). \end{aligned}$$

(3.11)

Using the splitting given in Proposition 2.12 for the Jacobi field $\textbf{X}_u$, we obtain

$$\begin{aligned} g(\textbf{X}_u^{\bot },\nabla _{\textbf{X}_v}\textbf{X}_u)= & {} g(\textbf{X}_u,\nabla _{\textbf{X}_v}\textbf{X}_u)-\Vert \alpha ^\prime (u)\Vert (\cos {\sigma _p})g(\textbf{X}_v,\nabla _{\textbf{X}_v}\textbf{X}_u)\nonumber \\ {}= & {} \frac{1}{2}\textbf{X}_v(\Vert \textbf{X}_u\Vert ^2), \end{aligned}$$

(3.12)

with $\sigma _p$ the base angle at $p=\alpha (u)$, where $[\textbf{X}_u,\textbf{X}_v]=0$ has been applied in combination with the fact that $\textbf{X}_v$ is geodesic. Inserting (3.12) into (3.11) finally gives (3.8). $\square$

In the next result, we integrate the differential equation (3.8) in the different models for positive, zero or negative k.

Theorem 3.11

Let $\textbf{X}:I\times \mathbb {R}\rightarrow (M,g)$ be a parametrized ruled surface in a complete manifold (M, g) of constant sectional curvature k, with Z a unit ruling vector field. Then the expression of the Jacobi evolution function F is

$$\begin{aligned} F(u,v)= & {} C_1 \cos {(\sqrt{4k}v)}+C_2 \sin {(\sqrt{4k}v)}, \quad \hbox { if}\ k>0, \end{aligned}$$

(3.13)

$$\begin{aligned} F(u,v)= & {} C_1 + C_2 v, \quad \hbox { if}\ k=0 \end{aligned}$$

(3.14)

$$\begin{aligned} F(u,v)= & {} C_1 \cosh {(\sqrt{-4k}v)}+C_2\sinh {(\sqrt{-4k}v)}, \quad \hbox { if}\ k<0 \end{aligned}$$

(3.15)

where

$$\begin{aligned} C_1=g_p(\nabla _{\alpha ^\prime }Z,\alpha ^\prime ), \end{aligned}$$

(3.16)

and

$$\begin{aligned} C_2= & {} {} \tfrac{1}{\sqrt{|4k|}}\left( -k\Vert \alpha ^\prime \Vert _p^2\sin ^2{\sigma _p}+\Vert \nabla _{\alpha ^\prime }Z\Vert _p^2\right) , \quad \text{ if } \quad k>0 \quad \text{ or } \quad k<0, \nonumber \\ \end{aligned}$$

(3.17)

$$\begin{aligned} C_2= & {} \Vert \nabla _{\alpha ^\prime }Z\Vert ^2_p, \quad \hbox { if}\ k=0. \end{aligned}$$

(3.18)

Proof

Evaluating the Jacobi evolution function F(u, v) at $v=0$ gives

$$\begin{aligned} F(u,0)= & {} \tfrac{1}{2}\textbf{X}_v(\Vert \textbf{X}_u\Vert ^2)|_p=g_p(\nabla _{\textbf{X}_v}\textbf{X}_u,\textbf{X}_u)=g_p(\nabla _{\textbf{X}_u}\textbf{X}_v,\textbf{X}_u) \\= & {} g_p(\nabla _{\alpha ^\prime }Z,\alpha ^\prime ), \end{aligned}$$

which implies (3.16), after evaluating (3.13), (3.14) and (3.15), at $v=0$. To compute $C_2$, we use the Jacobi first derivative relation (3.7), which becomes

$$\begin{aligned} \frac{\partial F}{\partial v}(u,0)=-k\Vert \alpha ^\prime (u)\Vert _p^2\sin ^2{\sigma _p}+\Vert \nabla _{\alpha ^\prime } Z\Vert ^2_p \end{aligned}$$

(3.19)

since $\textbf{X}_u(u,0)=\alpha ^\prime (u)$. Differentiating (3.13) at $v=0$, from (3.19), we obtain

$$\begin{aligned} C_2 \sqrt{4k}=-k\Vert \alpha ^\prime (u)\Vert ^2\sin ^2{\sigma _p}+\Vert \nabla _{\alpha ^\prime } Z\Vert ^2_p, \end{aligned}$$

which is none other than $C_2$ in (3.17) for $k>0$. The respective value of $C_2$ for $k<0$ is obtained in an analogous way differentiating (3.15) at $v=0$. Likewise, in the Euclidean context $k=0$, $(\partial F/\partial v)(0)=\Vert \nabla _{\alpha ^\prime } Z\Vert ^2_p$, which implies the value of $C_2$ in (3.18) for the Jacobi evolution function is $F(u,v)=C_1+C_2 v$ in the flat case. $\square$

Theorem 3.12

Let $\textbf{X}:I\times \mathbb {R}\rightarrow (M,g)$ be a Sannia ruled surface $\textbf{X}:I\times \mathbb {R}\rightarrow (M,g)$ in a complete manifold (M, g) of constant sectional curvature k, where $\alpha :I \rightarrow \textbf{X}(I\times \mathbb {R})$ is an associated base curve, and with a unit ruling vector field $Z\in \mathfrak {X}(\alpha )$. If $s:I \rightarrow \textbf{X}(I\times \mathbb {R})$, $s(u)=\textbf{X}(u,v(u))$ is an striction curve, then

$$\begin{aligned} v(u)= & {} \frac{1}{\sqrt{4k}}\arctan {\left( \frac{-\sqrt{4k}\,g_p(\nabla _{\alpha ^\prime }Z,\alpha ^\prime )}{-k\Vert \alpha ^\prime \Vert _p^2\sin ^2{\sigma _p}+\Vert \nabla _{\alpha ^\prime } Z\Vert ^2_p}\right) } \quad \hbox { if}\ k>0, \end{aligned}$$

(3.20)

$$\begin{aligned} v(u)= & {} -\frac{g_p(\nabla _{\alpha ^\prime }Z,\alpha ^\prime )}{\Vert \nabla _{\alpha ^\prime }Z\Vert ^2_p} \quad \hbox { if}\ k=0, \end{aligned}$$

(3.21)

$$\begin{aligned} v(u)= & {} \frac{1}{\sqrt{-4k}}\textrm{arctanh}{\left( \frac{-\sqrt{-4k}\,g_p(\nabla _{\alpha ^\prime }Z,\alpha ^\prime )}{-k\Vert \alpha ^\prime \Vert _p^2\sin ^2{\sigma _p}+\Vert \nabla _{\alpha ^\prime } Z\Vert ^2_p}\right) } \quad \hbox { if}\ k<0, \nonumber \\{} & {} \end{aligned}$$

(3.22)

where $\sigma _p$ is the angle between the vectors $\alpha ^\prime$ and Z at $p=\alpha (u)$. In addition, if M is simply connected (that is, $M=\mathbb {S}^3$ for $k>0$, $M=\mathbb {R}^3$ for $k=0$ or $M=\mathbb {H}^3$ for $k<0$ with their standard metrics scaled by $1/\sqrt{|k|}$ when $k\ne 0$), then for $k\ge 0$, every Sannia surface has a unique striction curve. For $k<0$, every Sannia surface has at most one striction curve.

Proof

As already noted in Remark 3.8, a necessary condition for a point p to lie on the striction curve is that the Jacobi evolution function verifies $F(p)=0$. Then the expressions for v(u) are directly obtained from (3.13), (3.14) and (3.15), respectively, taking into account (3.17) or (3.18). For $k>0$, the expression must be understood to provide $v(u)=\pm \pi /(4\sqrt{k})$ if $-k\Vert \alpha ^\prime \Vert _p^2\sin ^2{\sigma _p}+\Vert \nabla _{\alpha ^\prime } Z\Vert ^2_p=0$. In any case, the value of v(u) is periodic with period $2\pi /\sqrt{k}$, which is exactly the period of the geodesics in $\mathbb {S}^3$, so that the striction curve is geometrically unique. The uniqueness holds trivially true for $k=0$. For $k<0$, the injectivity of the function $\textrm{arctanh}$ implies that there is at most a solution for v(u). $\square$

Remark 3.13

Formula (3.21) is the classical formula for the striction curve in the Euclidean space. Formulas (3.20) in $\mathbb {S}^3$ and (3.22) in $\mathbb {H}^3$ were given in Ref. [4], where the uniqueness of striction curves is also addressed. However, they obtain the results by working with the sphere or the hyperbolic space as submanifolds of $\mathbb {R}^4$ with the standard Euclidean or Lorentzian metric, respectively, that is, in a less intrinsic fashion. Our approach involves a differential equation that, in principle, could be analysed in arbitrary Riemannian manifolds. Note that in such a case, the equation will involve the curvature of the ambient space. Finally, the authors also claim in Ref. [4] that the striction curve always exists for $k<0$, a fact that is wrong as the following example illustrates.

Remark 3.14

Note that the function $v:I\rightarrow \mathbb {R}$ can determine a degenerate striction curve (single point). This would be for example the case of the Euclidean cone. The study of cones in generic 3-dimensional Riemannian manifolds will require special attention and further research.

Example 1: A ruled surface in the hyperbolic space without striction curve. We consider in $(\mathbb {H}^3,g=\frac{1}{z^2}(dx^2+dy^2+dz^2))$ the ruled surface with base curve $\alpha :[0,2\pi )\rightarrow (\mathbb {H}^3,g)$ determined by $\alpha (u)=(\cos {u},\sin {u},1)$ and the unit ruling vector $Z(u)=(\cos {u},\sin {u},0)$ defined along $\alpha$. A straightforward computation shows that

$$\begin{aligned} \nabla _{\alpha ^\prime }Z=-\sin {u}\,\partial _x+\cos {u}\,\partial _y. \end{aligned}$$

The form for the Jacobi evolution function F is described by relation (3.15) for negative constant sectional curvature. The coefficients $C_1$ and $C_2$ read this time $C_1=g_p(\alpha ^\prime ,\nabla _{\alpha ^\prime }Z)=1$ and $C_2=\frac{1}{2}\left( \Vert \alpha ^\prime \Vert _p^2\sin ^2{\sigma _p}+\Vert \nabla _{\alpha ^\prime }Z\Vert _p^2\right) =1$, since $\sigma _p=\pi /2$. Therefore, the Jacobi evolution function associated with such a ruled surface is

$$\begin{aligned} F(u,v)=\cosh {2v}+\sinh {2v}. \end{aligned}$$

Condition $F=0$ holds on the striction curve in case of existence, which is equivalent to

$$\begin{aligned} 1+\tanh {2v}=0, \end{aligned}$$

which clearly does not have any solution.

Actually, we can characterise when a (complete) Sannia ruled surface in $\mathbb {H}^3(k)$ never admits a striction curve in terms of its extrinsic curvature and first Sannia invariant. For that, first note that in a ruled surfaces defined by an arc-parametrized curve $\alpha$ and a unit vector field $Z(u)=\pm \alpha '(u)$ (that is, tangent ruled surfaces), the curve $\alpha$ is already a striction curve. On the other hand, if $\alpha '(u)$ and Z(u) are linearly independent, the curve ${\bar{\alpha }}(u)=\textbf{X}(u,f(u))$ where f satisfies the ODE $f'(u)=-g(\textbf{X}_u,\textbf{X}_v)_{\textbf{X}(u,f(u))}$, defines a new parametrization of the same surface such that ${\bar{\alpha }}'(u)$ and $\bar{Z}(u)=\textbf{X}_v(u,f(u))$ are always orthogonal.

Proposition 3.15

Let $\textbf{X}(u,v)=\exp _{\alpha (u)}(vZ(u))$ a Sannia ruled surface in $\mathbb {H}^{3}(k)$ defined by an arc-parametrized curve $\alpha$ and a unit ruling vector field $Z\in \mathfrak {X}(\alpha )$ such that $g(\alpha ^{\prime },Z)=0$. Then the surface does not admit a striction curve if and only if its extrinsic curvature $K_\mathrm{{ext}}$ vanishes and the first Sannia curvature satisfies $\kappa _{1}=\sqrt{-k}$.

Proof

According to (3.22), the non-existence of the striction curve is equivalent to the condition

$$\begin{aligned} \frac{2\sqrt{-k}\left| g(\alpha ^{\prime },\nabla _{\alpha ^{\prime }}Z)\right| }{-k+\left\| \nabla _{\alpha ^{\prime }}Z\right\| ^{2}} =\frac{2\sqrt{-k}\left\| \nabla _{\alpha ^{\prime }}Z\right\| \left| \cos \psi \right| }{-k+\left\| \nabla _{\alpha ^{\prime }}Z\right\| ^{2}}\ge 1, \end{aligned}$$

where $\psi =\widehat{\alpha ^{\prime },\nabla _{\alpha ^{\prime }}Z}$. On the other hand, we always have

$$\begin{aligned} \frac{2\sqrt{-k}\left\| \nabla _{\alpha ^{\prime }}Z\right\| \left| \cos \psi \right| }{-k+\left\| \nabla _{\alpha ^{\prime }}Z\right\| ^{2}}\le \frac{2\sqrt{-k}\left\| \nabla _{\alpha ^{\prime }}Z\right\| }{-k+\left\| \nabla _{\alpha ^{\prime }}Z\right\| ^{2}} \le 1, \end{aligned}$$

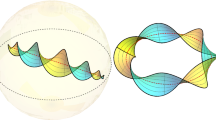
where last step is the arithmetic–geometric mean inequality. Then, we have that expression (2) is never bigger than 1 and it is 1 if and only if $\cos \psi =\pm 1$ and $\left\| \nabla _{\alpha ^{\prime }}Z\right\| =\sqrt{-k}$. The proof is now complete by taking into account that, on one hand $Z=X_{1}$ and $\kappa _{1}=\left\| \nabla _{\alpha ^{\prime }}X_{1}\right\|$, and on the other hand noting that $vol(\alpha ^{\prime },Z,\nabla _{\alpha ^{\prime }}Z)$ vanishes (which is equivalent to the vanishing of $K_\mathrm{{ext}}$) if and only if $\psi =0$ or $\pi$ (that is, $\alpha ^{^{\prime }}$ is parallel to $\nabla _{\alpha ^{\prime }}Z$), since $\alpha ^{\prime }\perp Z$, and $Z\perp \nabla _{\alpha ^{\prime }}Z$ (Fig. 1). $\square$

Fig. 1

Ruled surface in $\mathbb {H}^3$ with no striction curve. The figure corresponds to the ruled surface described in Example 1, i.e. an ideal cylinder in the Poincaré half-model $\mathbb {R}^3_{+}$ of $\mathbb {H}^3$ in the sense of Ref. [7].

We end the article in ambient manifolds of non-constant curvature, where we see that the uniqueness of the striction curve cannot be guaranteed.

Example 2: A ruled surface in a product manifold equipped with different striction curves. We consider the surface of revolution in the Euclidean space generated by the rotation of the curve $(t,2+\sin {t},0)$ in the xy-plane about the x-axis. Such a surface admits the following parametrization:

$$\begin{aligned}{} & {} \textbf{Y}:[0,2\pi )\times \mathbb {R}\rightarrow (\mathbb {R}^3,\delta ) \nonumber \\{} & {} \textbf{Y}(u,v)=(v, (2+\sin {v})\cos {u}, (2+\sin {v})\sin {u}), \end{aligned}$$

(3.23)

from which, the expression of the induced metric is

$$\begin{aligned} g_\Sigma =(2+\sin {v})^2 \textrm{d}u^2+(1+\cos ^2{v})\textrm{d}v^2, \end{aligned}$$

in the local coordinates associated with the parametrization (3.23). Recall that the generating curves of a surface of revolution are pregeodesics of the surface. We now consider $M=\mathbb {R}\times (0,2\pi )\times \mathbb {R}$ equipped with the product metric $g=\textrm{d}t^2+g_\Sigma$. We define the ruled surface

$$\begin{aligned} \textbf{X}(u,v)=(0,u,f(v))\in M, \end{aligned}$$

where f satisfies $f(0)=0$ and $f'(v)=1/\sqrt{1+\cos ^2 v}$ so that $(0,u_0,f(v))$ are geodesics with unit velocity. That is, we have a parametrized ruled surface with $\alpha (u)=(0,u,0)$ and ruling vector field $Z(u)=(0,0,1/\sqrt{2})$. Some easy computations give

$$\begin{aligned} \textbf{X}_u=\partial _u,\quad \textbf{X}_{v}=\frac{1}{\sqrt{1+\cos ^2 v}}\partial _v,\qquad \nabla _{\textbf{X}_u}\textbf{X}_v=\frac{\cos v}{\sqrt{1+\cos ^2 v}(2+\sin v)}\partial _u. \end{aligned}$$

Then the Sannia basis along $\alpha$ is

$$\begin{aligned} X_1=\frac{1}{\sqrt{2}}\partial _v, \quad X_2=\frac{1}{2}\partial _u,\quad X_3=\partial _t, \end{aligned}$$

and the Sannia curvatures are

$$\begin{aligned} \kappa _0 =1,\quad \kappa _1 = \frac{1}{\sqrt{2}},\quad \kappa _2 =0. \end{aligned}$$

Finally,

$$\begin{aligned} F(u,v)=g(\textbf{X}_u,\nabla _{\textbf{X}_u}\textbf{X}_v)=\frac{\cos {v}(2+\sin {v})}{\sqrt{1+\cos ^2{v}}}. \end{aligned}$$

Since the striction curves are given by the solution of $F=0$, each curve $\alpha _{v_k}(u)=\textbf{X}(u,\pi /2+k\pi )$ with $k\in \mathbb {Z}$ is a striction curve.

Example 3: A ruled surface in a warped product manifold with an arbitrary number of striction curves. Given an open interval $I\subset \mathbb {R}$ and a 2-dimensional Riemannian manifold $(F,g_F)$, consider the product 3-manifold $I\times F$ endowed with the metric $g=\textrm{d}t^2+f^2(t)g_F$, where $f:I\rightarrow \mathbb {R}$ is a smooth positive function. We will refer to the warped product manifold $(I\times F,g)$ as $I\times _f F$. Consider a closed unit curve $\alpha ^F:[a,b)\rightarrow (F,g_F)$ in the fibre of $I\times _f F$. Given any $t_0\in I$, $\alpha ^F$ can be lifted in a natural way to the slice $\{t=t_0\}$ as the curve $\alpha _{t_0}:[a,b)\rightarrow I\times _f F$ defined by $\alpha _{t_0}(u)=(t_0,\alpha ^F(u))$, with $Z=\partial _{t}|_{\alpha _{t_0}}$ as ruling unit vector field along $\alpha _{t_0}$. A straightforward computation shows that the Sannia basis along $\alpha _{t_0}$ is

$$\begin{aligned} X_1=\partial _t, \quad X_2=\frac{\alpha '_{t_0}}{f(t_0)},\quad X_3=\frac{\nabla ^F_{\alpha '_{t_0}}\alpha '_{t_0}}{\Vert \nabla ^F_{\alpha '_{t_0}}\alpha '_{t_0}\Vert _{g_F}}, \end{aligned}$$

where $\nabla ^F$ and $\Vert \cdot \Vert _{g_F}$ stand for the Levi-Civita connection and the norm of $g_F$, respectively. The Sannia curvatures read

$$\begin{aligned} \kappa _0 =1,\quad \kappa _1 = (\partial _{t}f)(t_0),\quad \kappa _2 =\frac{\Vert \nabla ^F_{\alpha '_{t_0}}\alpha '_{t_0}\Vert _{g_F}}{f(t_0)}. \end{aligned}$$

As usual, the initial value of the Jacobi field $\textbf{X}_u$ on $\alpha _{t_0}$ is $\textbf{X}_u|_{\alpha _{t_0}}=\alpha ^\prime _{t_0}$. Since $Z=\partial _t|_{\alpha _{t_0}}$ is orthogonal to the base curve, $\textbf{X}_u$ will remain orthogonal to the ruling by virtue of Proposition 2.10. Thus $\textbf{X}_u$ is tangent to the fibre in $I\times _f F$ and $\textbf{X}_v=\partial _t$ is orthogonal to it, so

$$\begin{aligned} \nabla _{\textbf{X}_u} \textbf{X}_v=(\partial _t\log f) \textbf{X}_u\end{aligned}$$

and the corresponding Jacobi evolution function reads

$$\begin{aligned} F(u,v)=g(\textbf{X}_u,\nabla _{\textbf{X}_u} \textbf{X}_v)=(\partial _t\log f)(v)\Vert \textbf{X}_u\Vert ^2. \end{aligned}$$

The solution to the equation $F=0$ which determines the striction curves is given in this case by $f'(v)=0$. Hence, there will be as many striction curves as there are values at which the function $f'$ vanishes in I. For instance, if we consider $I=\mathbb {R}$ and $(F,g_F)$ isometric to the two-dimensional Euclidean space $(\mathbb {R}^2,\delta )$, for the choice $f(t)=2+\sin {t}$, every curve of the form $\alpha _{t_k}(u)=(\pi /2+k\pi ,\cos {u},\sin {u})$ with $k\in \mathbb {Z}$ is a striction curve in the ruled surface determined by it and $\textbf{X}_v=\partial _t$.

Note that the extrinsic curvature of the ruled surfaces in the two last examples vanishes. A study of more general examples deserves further investigation.