1 Introduction

The integro-differential equations (IDEs), which combine differential and integral equations, have attracted more attention in recent years. Applications in mathematics, physics, biology, and engineering all heavily rely on IDEs.

The equations known as the Volterra equations were studied in the early years of the 20th century by Italian mathematician Vito Volterra. In the 1930 s, Volterra showed that mathematical models for some seasonal diseases, e.g., influenza, are formulated as integral and differential equations. The use of VIDEs is widespread in the fields of biology, ecology, medicine, physics, and other sciences. To the best of our knowledge, it has been observed in a variety of physical applications, including the glass-forming process, heat transfer, the diffusion process generally, neutron diffusion, the coexistence of biological species with varying generation rates, and wind ripple in the desert.

One of the most crucial methods for researching the qualitative characteristics of solutions to ordinary, functional, and IDEs is Lyapunov’s second method because this method is widely recognized as an excellent tool in the study of differential equations. Theoretically, this method is quite significant, and it is used in many different applications, see [24]. Lyapunov’s second method is a sufficient condition to show the stability of systems, which means the system may still be stable even if one cannot find a Lyapunov-Krasovskii functional (LKF) candidate to conclude the system stability property.

There are many interesting results have been obtained in the literature to study the behaviour of solutions for DDE by Lyapunov’s theory, see for example [4, 10, 15, 16, 22, 25].

Besides, it is worth mentioning, that according to our observation from the literature, recently we found many exciting papers on the kind of VIDEs, for example [2, 3, 9,10,11,12,13, 15,16,17,18,19,20,21,22].

In 2000, Zhang [25] investigated the uniform asymptotic stability for the linear scaler VIDE

$$\begin{aligned} {\dot{x}}(t)= A x(t) +\int _{0}^{t}{C(t-s)x(s)\textrm{d}s}, \end{aligned}$$

where A ia a constant and \(C:\mathbb {R}^{+} \rightarrow \mathbb {R}\) is a continuous function.

In 2015, Tunç [14] studied the stability and the boundedness of the zero solution of the non-linear VIDE with delay of the form

$$\begin{aligned} {\dot{x}}(t)= -\,a(t)f(x(t))+\int _{t-\tau }^{t}{B(t,s)g(x(s))\textrm{d}s}+p(t). \end{aligned}$$

Recently, in 2022, Appleby and Reynold [1] studied the asymptotic stability of the scalar linear VIDE

$$\begin{aligned} {\dot{x}}(t)= -\,a x(t) +\int _{0}^{t}{k(t-s)x(s)\textrm{d}s}, ~ t>0,~~ x(0)=x_0. \end{aligned}$$

Our goal for this paper is to create the sufficient conditions for the UAS of second and third-order VIDEs with delay for the following equations

$$\begin{aligned} \ddot{x} + f_1(x){\dot{x}}+ \int _{0}^{t}{h_1(t-s_1)v_1(x(s_1))\textrm{d}s_1} = 0, \end{aligned}$$
(1.1)

and

$$\begin{aligned} \dddot{x} + f_2({\dot{x}})\ddot{x}+\alpha {\dot{x}}+ \int _{0}^{t}{h_2(t-s_2)v_2 \left( {\dot{x}}(s_2)\right) \textrm{d}s_2} = 0, \end{aligned}$$
(1.2)

where \( h_1,h_2:[0,\infty )\rightarrow (-\infty ,\infty )\) are continuous functions depend on the differences \( t-s_1, t-s_2\), respectively, and \(L^{1}(0,\infty )\), \(L^{1}\) is the space of integrable Lebesgue functions, \(s_1, s_2\) are time delays with \(s_1, s_2 \le t\), also there exist two functions \(H_1,H_2: [0,\infty )\rightarrow [0,\infty )\) such that \({\dot{H}}_1(t-s_1)=\frac{\textrm{d}}{\textrm{d}t}(H_1(t-s_1))=-h_1(t-s_1)\), \({\dot{H}}_2(t-s_2)=\frac{\textrm{d}}{\textrm{d}t}(H_2(t-s_2))=-h_2(t-s_2)\) with \(\int _{0}^{\infty }{|h_1 (u)|\textrm{d}u }, \int _{0}^{\infty }{|h_2 (u)|du} \in L^{1}[0,\infty ) \) and \( \int _{t}^{\infty }{|H_2 (u)|\textrm{d}u}, \int _{t}^{\infty }{|H_2 (u)|\textrm{d}u} \in L^{1}[0,\infty ) \). The functions \(f_1(x),f_2(y), v_1(x)\) and \( v_2(y)\) are continuous scalar functions defined on \(\mathbb {R}\) with \(f_1(0)=f_2(0)=v_1(0)= v_2(0)=0\).

Remark 1.1

We will give the following remarks:

1.:

Whenever, \(\ddot{x}\) replaced by \({\dot{x}}\), \(f_1(x) {\dot{x}}\) replaced by Ax(t) , and let \(v_1(x)=x(t),\) in the integral term then (1.1) reduces to the equation that is considered in [25]. Thus, the stability and results obtained in (1.1) include and extend the previous results.

2.:

In [1], If we replaced the term \(\ddot{x}\) by \({\dot{x}}\), \(f_1(x) {\dot{x}}\) by ax(t) , and let \(v_1(x)=x(t)\) in the integral term, then (1.1) reduces to the equation that considered in [1]. Then the stability results of this paper include and improve the stability result obtained in [1]. Then (1.1) and (1.2) generalize and improve the results obtained in [1, 25].

3.:

As an application in physics, many models can be modeled by IDEs. For example, first, by the Kirchhoffs second law, the net voltage drop across a closed loop equals the voltage impressed E(t). Thus, the standard closed electric RLC circuit can be governed IDE [5], second, an Abel-type Volterra integral equation describes the temperature distribution along the surface when the heat transfer to it is balanced by radiation from it. Finally, also, Abel-type Volterra integral equation determines the temperature in a semi-infinite solid, whose surface can dissipate heat by nonlinear radiation [23].

2 Main Results

Consider the general functional differential system

$$\begin{aligned} {\dot{x}} = F(t,x_{t}), \end{aligned}$$
(2.1)

where, \(x_t\) represents a function from \([\alpha ,t]\rightarrow \mathbb {R}^{n}, \, \, -\infty \le \alpha \le t_0\). For any \(t\ge t_0\), by \((X(t),\Vert .\Vert ),\) we shall mean the space of continuous functions \(\phi : [\alpha ,t]\rightarrow \mathbb {R}^{n}, \alpha >0, \, \text {with} \Vert \phi \Vert =\sup _{\alpha \le s \le t}|\phi (s)|, ~s \in R\) and |.| is any norm on \( \mathbb {R}^n\). The symbol \(X_H(t)\) denotes those \(\phi \in X(t) \) with \(\Vert \phi \Vert \le H\) for some \(H>0\).

Here, F is a continuous function of t for \(t_0\le t\le \infty , \) whenever \(x_t\in X_H(t) \) for \(t_0\le t\le \infty , \) and takes closed bounded sets of \(\mathbb {R}\times X(t)\) into bounded sets of \(\mathbb {R}^n\).

Theorem 2.1

[7] Let \(V(t,x_t)\) be continuous functional and locally Lipschitz for

\( t_{0} \le t < \infty \text {and} \,\, x_t\in X_H(t) \). Suppose there is a continuous function \( \Phi : [0,\infty ) \rightarrow [0,\infty )\) which is \( L^{1}[0,\infty )\) and satisfies

(i):

\(W_{1}(|x|)\le V(t,x_{t})\le W_{2}(|x|)+ W_{3}\bigg {(}\int _{\alpha }^{t}{\Phi (t-s)W_{4}(|x(s)|)\textrm{d}s} \bigg {)},\) where \(W_{i}; \big {(}i=1,2,3,4\big {)}\) are wedges;

(ii):

\( {\dot{V}}_{(2.1)}(t,x_{t})\le -W_{5}(|x|)\).

Then, the zero solution of (2.1) is uniformly asymptotically stable (UAS).

The following two theorems will be our main results for (1.1) and (1.2).

Theorem 2.2

In addition to the basic assumptions given on the functions \(f_1\), \(H_1\) and \(v_1\) for (1.1), we suppose that there are the non-negative constants \( a_{1},\; a_{2},\;b_{1},\;b_{2}, \) \(L_{1}, \, L, \, c_{1}\), \(\beta _1,\,\beta _2\) and \(c_{2}, \) such that

(i):

\( a_{2}\le f_1(x)\le a_{1}, \,\, |f_1'(x)|\le c_{1}\,\,\) and \(\, \,b_{2}\le v_1(x)\le b_{1},\,\,\) \(|v_1'(x)|\le c_{2}.\)

(ii):

\(\int _{0}^{\infty }{|H_1(u)|\textrm{d}u}=L<1\) and \(\int _{t}^{\infty }{|H_1(u)|\textrm{d}u} \in L^{1}[0,\infty )\).

(iii):

\(0<\beta _{1}\le |H_1(0)| \le \beta _{2}.\)

(iv):

\(\int _{0}^{t}{|H_1(t-s_1)|\textrm{d}s_1}+ \int _{t}^{\infty }{|H_1(u-t)|\textrm{d}u}=L_{1}\).

Then, the zero solution of (1.1) is UAS, provided that

$$\begin{aligned} \beta _{1}b_{2}c_{1}+ 2 \beta _{1}c_{2}^{2}L_{1} \ge c_{1}b_{1} L \, \, \, and \, \,\,2 a_{2}\ge c_{1} b_{1}L. \end{aligned}$$

Theorem 2.3

Together with the fundamental conditions given on the functions \(f_2, H_2\) and \( v_2\) for (1.2), we assume that there exist the positive constants \( \alpha _1, \alpha _2, \alpha _3, \alpha _4,\) \( d_1, d_2, L, \theta _1,\theta _2\) and \(\theta _3\), so that the following assumptions are true

(i):

\(\alpha _{1} \le f_2(y)\le \alpha _2 \), \( |f'_2(y)|\le d_1\) and \(\alpha _3 \le v_2(y)\le \alpha _4\), \( |v'_2(y)|\le d_2\).

(ii):

\(\int _{0}^{\infty }{|H_2(u)|\textrm{d}u}=L<1\) and \(\int _{t}^{\infty }{|H_2(u)|\textrm{d}u} \in L^{1}[0,\infty )\).

(iii):

\( 0<\theta _1\le |H_2(0)|\le \theta _2. \)

(iv):

\( \int _{0}^{t}{|H_2(t-s_2)|\textrm{d}s_2}+\int _{t}^{\infty }{|H_2(u-t)|\textrm{d}u}\le \frac{\theta _1\theta _3}{\theta _2}\).

Then, the zero solution of (1.2) is UAS, provided that

$$\begin{aligned} (1+\alpha +2\alpha _1) \ge d_2 \theta _3. \end{aligned}$$

3 Proof of Theorem 2.2.

Rewrite (1.1) as the following

$$\begin{aligned} \begin{aligned}&{\dot{x}}=y, \\ {}&{\dot{y}}=-f_1(x)y-H_1(0)v_1(x)+\frac{\textrm{d}}{\textrm{d}t}\int _{0}^{t}{H_1(t-s_1) v_1(x(s_1))\textrm{d}s_1}. \end{aligned} \end{aligned}$$
(3.1)

Define the LKF \( V_1(t,x_t,y_t)\) as

$$\begin{aligned} \begin{aligned} V_1(t,x_{t},y_{t})=&\bigg {(}y-\int _{0}^{t}{H_1(t-s_1) v_1(x(s_1))ds_1}\bigg {)}^{2} +4H_1(0)\int _{0}^{x}{ v_1(\xi )d\xi }\\ {}&+\bigg {(}y+\int _{0}^{x}{ f_1(\xi )d\xi }-\int _{0}^{t}{H_1(t-s_1) v_1(x(s_1))\textrm{d}s_1}\bigg {)}^{2}\\ {}&+ 2H_1(0)\int ^{t}_{0}{\int ^{\infty }_{t}{|H_1(u-s_1)|\textrm{d}u \, v_1^{2}(x(s_1))\textrm{d}s_1}}. \end{aligned}\nonumber \\ \end{aligned}$$
(3.2)

It can be written as

$$\begin{aligned} V_1= & {} \, 2y^{2}+ 2\bigg {(}\int _{0}^{t}{H_1(t-s_1) v_1(x(s_1))\textrm{d}s_1}\bigg {)}^{2}-4y\int _{0}^{t}{H_1(t-s_1) v_1(x(s_1))\textrm{d}s_1}\nonumber \\{} & {} +4H_1(0)\int _{0}^{x}{v_1(\xi ))\textrm{d}\xi }+\bigg {(}\int _{0}^{x}{f_1(\xi )\textrm{d}\xi }\bigg {)}^{2}+2y\int _{0}^{x}{f_1(\xi )\textrm{d}\xi }\nonumber \\{} & {} -2\int _{0}^{x}{f_1(\xi )\textrm{d}\xi } \int _{0}^{t}{H_1(t-s_1)v_1(x(s_1))\textrm{d}s_1}\nonumber \\{} & {} +2H_1(0) \int ^{t}_{0}{\int ^{\infty }_{t}{|H_1(u-s_1)|\textrm{d}u\, v_1^{2}(x(s_1))\textrm{d}s_1}}. \end{aligned}$$
(3.3)

Using the Schwarz inequality [8], we get

$$\begin{aligned} \begin{aligned} \bigg {(}\int _{0}^{t}{H_1(t-s_1) v_1(x(s_1))\textrm{d}s_1}\bigg {)}^{2}&=\bigg {(}\int _{0}^{t}{|H_1(t-s_1)|^{\frac{1}{2}}|H_1(t-s_1)|^{\frac{1}{2}}v_1(x(s_1))\textrm{d}s_1}\bigg {)}^{2} \\ {}&\le \int _{0}^{t}{|H_1(t-s_1)|\textrm{d}s_1}\int _{0}^{t}{|H_1(t-s_1)|v_1^{2}(x(s_1))\textrm{d}s_1}. \end{aligned}\nonumber \\ \end{aligned}$$

By using the inequality \(|mn|\le \frac{1}{2}(m^{2}+n^{2})\), and the previous inequality, we can write (3.3) as the following form

$$\begin{aligned} \begin{aligned} V_1 \le&\, 2y^{2}+ 2\int _{0}^{t}{|H_1(t-s_1)|\textrm{d}s_1}\int _{0}^{t}{|H_1(t-s_1)|v_1^{2}(x(s_1))\textrm{d}s_1}\\ {}&+2\int _{0}^{t}{H_1(t-s_1)\big {(} v_1^{2}(x(s_1))+y^{2}(t)\big {)}\textrm{d}s_1} +4H_1(0)\int _{0}^{x}{v_1(\xi )\textrm{d}\xi }\\ {}&+\bigg {(}\int _{0}^{x}{f_1(\xi )d\xi }\bigg {)}^{2}+2y\int _{0}^{x}{f_1(s_1)\textrm{d}s_1}\\&-2\int _{0}^{x}{f_1(s_1)\textrm{d}s_1} \int _{0}^{t}{H_1(t-s_1)v_1(x(s_1))\textrm{d}s_1}\\ {}&+2H_1(0)\int ^{t}_{0}{\int ^{\infty }_{t}{|H_1(u-s_1)|\textrm{d}u\, v_1^{2}(x(s_1))\textrm{d}s_1}}. \end{aligned} \end{aligned}$$

By the assumptions of Theorem 2.2, we have

where W is a wedge function.

Therefore, we have

$$\begin{aligned} (2+a_{2}+2L)c_2^2|H_1(t-s_1)|+2c_2^2\beta _{2}\int _{t-s_1}^{\infty }{H_1(u)\textrm{d}u}=\Phi (t-s_1). \end{aligned}$$

Therefore, one can conclude that

$$\begin{aligned} V_1\le \gamma _{1}(x^{2}+y^{2})+W\bigg {(}\int _{0}^{t}{\Phi (t-s_1)(x^{2}(s_1)+y^{2}(s_1))\textrm{d}s_1}\bigg {)}, \,\, \gamma _{1}> 0.\nonumber \\ \end{aligned}$$
(3.4)

On the other hand

$$\begin{aligned} \begin{aligned} V_1&\ge \bigg {(}y-\int _{0}^{t}{H_1(t-s_1) v_1(x(s_1))\textrm{d}s_1}\bigg {)}^{2}\\ {}&\,\,\,\,\,\,+\bigg {(}y+\int _{0}^{x}{ f_1(\xi )\textrm{d}\xi }-\int _{0}^{t}{H_1(t-s_1) v_1(x(s_1))\textrm{d}s_1}\bigg {)}^{2} \\ {}&\ge \bigg {(}|y|-\int _{0}^{t}{|H_1(t-s_1)|| v_1(x(s_1))|\textrm{d}s_1}\bigg {)}^{2} \\ {}&\,\,\,\,\,\,+\bigg {(}|y+\int _{0}^{x}{ f_1(\xi )\textrm{d}\xi }|-\int _{0}^{t}{|H_1(t-s_1)|| v_1(x(s_1))|\textrm{d}s_1}\bigg {)}^{2}. \end{aligned} \end{aligned}$$

Since \(\int _{0}^{\infty }{|H_1(u)|\textrm{d}u}=L<1\) and by the assumption (i) of Theorem 2.2, we conclude

(3.5)

Thus, from (3.4) and (3.5), we conclude that the condition (i) of Theorem 2.1 is satisfied.

Now, by differentiating Eq. (3.2), we obtain

$$\begin{aligned} \begin{aligned} \frac{\textrm{d}V_1}{\textrm{d}t}=&\, 2\bigg {(}y-\int _{0}^{t}{H_1(t-s_1)v_1(x(s_1))\textrm{d}s_1}\bigg {)}\bigg {(}-f_1(x)y-H_1(0)v_1(x) \bigg {)} \\ {}&+2\bigg {(}y+\int _{0}^{t}{f_1(\xi )\textrm{d}\xi }-\int _{0}^{t}{H_1(t-s_1)v_1(x(s_1))\textrm{d}s_1}\bigg {)} \bigg {(}-H_1(0)v_1(x) \bigg {)}\\ {}&+ 4H_1(0) v_1(x)y +2H_1(0)\frac{\textrm{d}}{\textrm{d}t}\int ^{t}_{0}{\int ^{\infty }_{t}{|H_1(u-s_1)|\textrm{d}u\, v_1^{2}(x(s_1))\textrm{d}s_1}}. \end{aligned} \end{aligned}$$

From Leibnitz rule [23] Pg. 17 and the identity [23] Pg. 17 and [6] Pg. 41, we have

then, we get

From the condition (i) and the inequality \( |mn|\le \frac{1}{2}(m^{2}+n^{2})\), we obtain

Therefore, we conclude

Consider the conditions (i)–(iv) and \(|H_1(0)|\ge \beta _1\), we have

Therefore, we conclude for \(D_1>0\), that

$$\begin{aligned} \frac{\textrm{d}V_1}{\textrm{d}t}\le -D_1(|x|^{2}+|y|^{2}), \,\, \text {for all} \, D_1>0, \end{aligned}$$
(3.6)

where, \(D_1=\min {\{\beta _{1}b_{2}c_{1}+2\beta _{1}c_{2}-c_{1}b_{1}L, 2a_{2}-c_{1}b_{1}}\}.\)

Thus, from (3.4), (3.5) and (3.6) all the assumptions of Theorem 2.1 are satisfied. Therefore the zero solution of (1.1) is UAS. Hence, the proof of Theorem 2.2 is now complete.

4 Proof of Theorem 2.3.

We can rewrite (1.2) as the following equivalent system

$$\begin{aligned} \begin{aligned}&{\dot{x}}=y, \\ {}&{\dot{y}}=z,\\ {}&{\dot{z}}=-f_2(y)z-\alpha y-H_2(0)v_2(y)+\frac{\textrm{d}}{\textrm{d}t}\int _{0}^{t}{H_2(t-s_2) v_2(y(s_2))\textrm{d}s_2}. \end{aligned} \end{aligned}$$
(4.1)

Define the LKF \(V_2(t,x_t,y_t,z_t)\) as

$$\begin{aligned} \begin{aligned} V_2(t,x_t,y_t,z_t)=&\bigg {(} z+\alpha x+ \int _0^y{f_2(\xi )\textrm{d}\xi }-\int _0^t{H_2(t-s_2)v_2(y(s_2))\textrm{d}s_2}\bigg {)}^{2} \\ {}&+H_2(0)\int ^{t}_{0}{\int ^{\infty }_{t}{|H_2(u-s_2)|\textrm{d}u \, v_2^2(y(s_2))\textrm{d}s_2}}. \end{aligned} \end{aligned}$$
(4.2)

From Eq. (4.2), we get

$$\begin{aligned} \begin{aligned} V_2=&\bigg {(} z+\alpha x+ \int _0^y{f_2(\xi )\textrm{d}\xi }\bigg {)}^2+\bigg {(}\int _0^t{H_2(t-s_2)v_2(y(s_2))\textrm{d}s_2}\bigg {)}^{2} \\ {}&-2\bigg {(}z+\alpha x+ \int _0^y{f_2(\xi )\textrm{d}\xi }\bigg {)}\bigg {(}\int _0^t{H_2(t-s_2)v_2(y(s_2))\textrm{d}s_2}\bigg {)}\\ {}&+H_2(0)\int ^{t}_{0}{\int ^{\infty }_{t}{|H_2(u-s_2)|\textrm{d}u\, v_2^2(y(s_2))\textrm{d}s_2}}. \end{aligned} \end{aligned}$$

Applying the condition (i) and the inequality \(|mn|\le \frac{1}{2}(m^2+n^2)\), we obtain

Since \(\int _0^\infty {H_2(u)}\textrm{d}u=L\) and from condition (i), then we get

$$\begin{aligned} \begin{aligned} V_2\le&(1+\alpha +\alpha _2+L)\bigg {(} \alpha x^2(t)+\alpha _2 y^2(t)+z^2(t)\bigg {)}\\ {}&+ \bigg {(}\int _0^t{H_2(t-s_2)v_2(y(s_2))\textrm{d}s_2}\bigg {)}^{2} \\ {}&+d_2^2(1+\alpha +\alpha _1)\int _0^t{|H_2(t-s_2)|y^2(s_2)\textrm{d}s_2}\\ {}&+H_2(0)\int ^{t}_{0}{\int ^{\infty }_{t}{|H_2(u-s_2)|\textrm{d}u\, v_2^2(y(s_2))\textrm{d}s_2}}. \end{aligned}\nonumber \\ \end{aligned}$$
(4.3)

By the Schwarz inequality [8], we have

$$\begin{aligned} \begin{aligned} \bigg {(}\int _{0}^{t}{H_2(t-s_2) v_2(x(s_2))\textrm{d}s_2}\bigg {)}^{2}&=\bigg {(}\int _{0}^{t}{|H_2(t-s_2)|^{\frac{1}{2}}|H_2(t-s_2)|^{\frac{1}{2}}v_2(x(s_2))\textrm{d}s_2}\bigg {)}^{2} \\ {}&\le \int _{0}^{t}{|H_2(t-s_2)|\textrm{d}s_2}\int _{0}^{t}{|H_2(t-s)2)|v_2^{2}(x(s_2))\textrm{d}s_2}. \end{aligned} \end{aligned}$$

Applying the conditions of Theorem 2.3, we obtain

$$\begin{aligned} \begin{aligned} V_2\le&(1+\alpha +\alpha _2+L)\bigg {(}\alpha x^2(t)+\alpha _2 y^2(t)+z^2(t)\bigg {)}\\ {}&+ \int _{0}^{t}{|H_2(t-s_2)|\textrm{d}s_2}\int _{0}^{t}{|H_2(t-s_2)|v_2^{2}(x(s_2))\textrm{d}s_2} \\ {}&+d_2^2(1+\alpha +\alpha _1)\int _0^t{|H_2(t-s_2)|y^2(s_2)\textrm{d}s_2}\\ {}&+\theta _2d_2^2\int ^{t}_{0}{\int ^{\infty }_{t}{|H_2(u-s_2)|\textrm{d}u y^2(s_2)\textrm{d}s_2}}. \end{aligned} \end{aligned}$$

It follows that

If we let

$$\begin{aligned} d_2(1+\alpha +\alpha _1)|H_2(t-s_2)|+d^2_2 \theta _{2}\int _{t-s_2}^{\infty }{H_2(u)\textrm{d}u}=\Phi (t-s_2), \end{aligned}$$

then, we get

$$\begin{aligned} \begin{aligned} V_2\,&\le (1+\alpha +\alpha _2+L)\bigg {(}\alpha x^2+\alpha _2 y^2+z^2\bigg {)} \\ {}&\quad +W\bigg {(}\int ^{t}_{0}{\Phi (t-s_2)y^2(s_2)\textrm{d}s_2}\bigg {)}. \end{aligned} \end{aligned}$$

Since \(1+\alpha +\alpha _2+L>0\), then we have a positive constant \(\gamma _2\), such that

$$\begin{aligned} \begin{aligned} V_2\le&\gamma _2\,\bigg {(}\alpha x^2+\alpha _2 y^2+z^2\bigg {)} \\ {}&+W\bigg {(}\int ^{t}_{0}{\Phi (t-s_2)\big {(}x^2(s_2)+y^2(s_2)+z^2(s_2)\big {)}}\bigg {)}. \end{aligned} \end{aligned}$$
(4.4)

Now, (4.2) becomes

$$\begin{aligned} \begin{aligned} V_2&\ge \bigg {(} z+\alpha x+ \int _0^y{f_2(\xi )\textrm{d}\xi }-\int _0^t{H_2(t-s_2)v_2(y(s_2))\textrm{d}s_2}\bigg {)}^{2} \\ {}&\ge \bigg {(} |z+\alpha x+ \int _0^y{f_2(\xi )\textrm{d}\xi }|-\int _0^t{\left| H_2(t-s_2)v_2(y(s_2))\right| \textrm{d}s_2}\bigg {)}^{2}. \end{aligned} \end{aligned}$$

By (ii), we have \(\int _{0}^{\infty }{|H_2(u)|\textrm{d}u}=L<1\) and by the assumption (i) of Theorem 2.3, we conclude that

$$\begin{aligned} \begin{aligned} V_2\ \ge \bigg {(}|z|+\alpha | x|+ \alpha _1 |y|-d_2 |y|\bigg {)}^{2}. \end{aligned} \end{aligned}$$
(4.5)

Differentiating the LKF \(V_2(t,x_t,y_t,z_t)\) with respect to t

From Leibnitz rule [23] Pg. 17 and the identity [6] Pg. 41, we get

By using the equivalent system (4.1), we obtain

$$\begin{aligned} \begin{aligned} \frac{\textrm{d}V_2}{\textrm{d}t}=&\, 2\bigg {(} z+\alpha x+ \int _0^y{f_2(\xi )\textrm{d}\xi }-\int _0^t{H_2(t-s_2)v_2(y(s_2))\textrm{d}s_2}\bigg {)} \\ {}&\,\,\,\times \bigg {(} -H(0)v(y)+\frac{\textrm{d}}{\textrm{d}t}\int _0^t{H_2(t-s_2)v_2(y(s_2))\textrm{d}s_2}\\ {}&-\frac{\textrm{d}}{\textrm{d}t}\int _0^t{H_2(t-s_2)v_2(y(s_2))\textrm{d}s_2}\bigg {)} +H_2(0)\int ^{\infty }_{t}{|H_2(u-t)|\textrm{d}u}\,v_2^{2}(y(t))\\ {}&-H_2(0)\int _{0}^{t}{|H_2(t-s_2)|v_2^{2}(y(s_2))\textrm{d}s_2}. \end{aligned} \end{aligned}$$

From condition (i), we get

$$\begin{aligned} \begin{aligned} \frac{\textrm{d}V_2}{\textrm{d}t}\le&-2H_{2}(0)d_2yz -2\alpha H_{2}(0) d_2xy -2H_2(0) d_2\alpha _1y^2\\ {}&+H_2(0)\bigg {(}\int _{0}^{t}{|H_2(t-s_2)|\textrm{d}s_2}+\int ^{\infty }_{t}{|H_2(u-t)|\textrm{d}u} \bigg {)}d_2^{2}y^2. \end{aligned} \end{aligned}$$

It follows from condition (iv) and the inequality \(|mn|\le \frac{1}{2}(m^2+n^2)\) that

Thus, one can conclude for a positive constant \(D_2>0\) that

$$\begin{aligned} \frac{\textrm{d}V_2}{\textrm{d}t}\le -D_2 \left( x^2+y^2+z^2 \right) , \end{aligned}$$
(4.6)

where \(D_2=\theta _1 \min {\{ d_2+ \alpha d_2 +2\alpha _1 d_2 -\theta _3d_2^2,\alpha d_2,d_2\}}.\) From the results (4.4), (4.5) and (4.6), we note that all assumptions of Theorem 2.1 are satisfied, then the zero solution of (1.2) is UAS.

Thus, the proof of Theorem 2.3 is now complete.

5 Illustrative Examples

Example 5.1

Consider the following VIDE with delay

$$\begin{aligned} \ddot{x} + (10x^\frac{1}{2}-5\sin (x)){\dot{x}}+ \int _{0}^{t}{e^{t-s_1-1} \big {(}6\sin ^2(x(s_1))+5 \sin ^3(x(s_1))\big {)}\textrm{d}s_1} = 0.\nonumber \\ \end{aligned}$$
(5.1)

Note that

$$\begin{aligned} f_1(x)=10x^\frac{1}{2}-5\sin (x), \,\, f_1(0)=0. \end{aligned}$$

So, we find

$$\begin{aligned} 10 \le 10x^\frac{1}{2}-5\sin (x) \le 46, \,\, \text {so}\, \,\, a_1=46 \,\, \text {and} \,\, a_2=10, \end{aligned}$$

and

$$\begin{aligned} f'_1(x)=5x^{-\frac{1}{2}}-5\cos x, \,\, |f'_1(x)|\le 10=c_{1}. \end{aligned}$$
Fig. 1
figure 1

Trajectories of the functions \(f_1(x)\) and \(f_1'(x)\)

Full size image

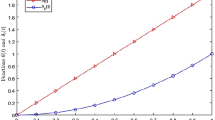
Figure 1, shows the behaviour of \(f_1(x)\) and \(f_1'(x)\) on the interval \(t\in [2,20] \) and \(t\in [0,90]\), respectively.

Moreover, we have

$$\begin{aligned} v_1(x)=6\sin ^2x+5 \sin ^3x, \,\, \text {so}, \,\, 1\le v_1(x)\le 5 \,\,\text {then,\, we\, get} \, \,\, b_1=5, \,\, b_2=1, \end{aligned}$$

and

$$\begin{aligned} v'_1(x)=12\sin x \cos x+15\sin ^2 x \cos x, \,\,\, \text {therefore} \,\,\,\, |v'_1(x)|\le 12=c_2. \end{aligned}$$
Fig. 2
figure 2

Trajectories of the functions \(v_1(x)\) and \(v_1'(x)\)

Full size image

Figure 2, illustrates the behaviour of \(v_1(x)\) and \(v_1'(x)\) through the interval \(t\in [0,90]\).

Also, we have

$$\begin{aligned} \int _{0}^{\infty }{|H_1(u)|\textrm{d}u} = \frac{1}{e}=L, \end{aligned}$$

and

$$\begin{aligned} L_{1}=\int _{t}^{\infty }{e^{t-s_1-1} \textrm{d}s_1} +\int _{0}^{t}{e^{t-s_1-1}\textrm{d}s_1}=\frac{1}{e}. \end{aligned}$$

Then, we get

$$\begin{aligned} H_1(0)=\frac{1}{e}, \,\, \,\, \frac{1}{2e}\le H_1(0)\le \frac{2}{e}, \end{aligned}$$

and

$$\begin{aligned} \beta _{1} b_{2}c_{1} + 2 \beta _{1}L_{1}c_{2}^{2}= 21.3 \,\, \text {and} \,\, c_{1}b_{1} L =18.4. \end{aligned}$$

So, it is clear that

$$\begin{aligned} \beta _{1} b_{2}c_{1} + 2 \beta _{1}L_{1}c_{2}^{2}> c_{1}b_{1} L, \,\,\, 2a_{2}=20 >c_1b_{1} L. \end{aligned}$$

We can see that the behaviour of the solutions (x(t), y(t)) with the initial values \((x_0=0, y_0=1)\) for (5.1) by Fig. 3.

Fig. 3
figure 3

Trajectories of the solutions for Example 5.1

Full size image

Thus, all the hypotheses of Theorem 2.2 are satisfied.

Then, the zero solution of (5.1) is UAS.

Example 5.2

Consider the following VIDE with delay

$$\begin{aligned} \dddot{x}+3 \sin ({\dot{x}}) \ddot{x}+8{\dot{x}}+\int _{0}^t{2e^{t-s_2-1} (2 \sin {^{2} s_2})\textrm{d}s_2}=0. \end{aligned}$$
(5.2)

It follows that

$$\begin{aligned} f_2(y)=3\sin y, \, \text {then} \, \,\,f_2(0)=0. \end{aligned}$$

So, we get

$$\begin{aligned} 1 \le f_2(y)\le 3, \, \text {then} \,\,\, \alpha _1=1, \, \alpha _2=3, \end{aligned}$$

and

$$\begin{aligned} f'_2(y)=3\cos {y}, \, \text {then} \,\,\, |3\cos {y} |\le 3 =d_1. \end{aligned}$$
Fig. 4
figure 4

Trajectories of the functions \(f_2(y)\) and \(f'_2(y)\)

Full size image

Figure 4, shows the behaviour of \(f_2(x)\) and \(f_2'(x)\) on the interval \(t\in [0,50]\).

Moreover

$$\begin{aligned} v_2(y)=2\sin ^2 y,\,\, \text {then} \,\,\,\, v_2(0)=0. \end{aligned}$$

So, we get

$$\begin{aligned} 0 \le v_2(y)\le 2, \,\, \text {then} \,\,\, \alpha _3=0, \, \alpha _4=2, \end{aligned}$$

and

$$\begin{aligned} v'_2(y)=4\sin y \cos y, \, \text {then} \,\, |4\sin y\cos y|\le 2 =d_2. \end{aligned}$$

Figure 5, illustrates the path of \(v_2(x)\) and \(v_2'(x)\) on the interval \(t \in [0,50]\).

Also, we have

$$\begin{aligned} \int _{0}^{\infty }{|H_2(u)|du} = \frac{1}{e}=L, \end{aligned}$$
Fig. 5
figure 5

Trajectories of the functions \(v_2(y)\) and \({v'_2}(y)\)

Full size image

and

$$\begin{aligned} \int _{t}^{\infty }{2e^{t-s_2-1} \textrm{d}s_2} +\int _{0}^{t}{2e^{t-s_2-1}\textrm{d}s_1}=\frac{2}{e}=\theta _3. \end{aligned}$$

Also, we have

$$\begin{aligned} H_2(0)=\frac{2}{e}, \,\, \,\, \frac{e}{4}\le H(0)\le \frac{1}{e}. \end{aligned}$$

and

$$\begin{aligned} \int _{t}^{\infty }{2e^{t-s_2-1} \textrm{d}s_2} +\int _{0}^{t}{2e^{t-s_2-1}\textrm{d}s_2}=\frac{2}{e}<\frac{\theta _1\theta _3}{\theta _2}. \end{aligned}$$

So, it is clear that

$$\begin{aligned} 1+\alpha +2\alpha _1> d_2\theta _3, \end{aligned}$$

Figure 6, shows the behaviour of the solutions (x(t), y(t), z(t)) with the initial values \((x_0=0, y_0=1, z_0=1)\) for (5.2).

Fig. 6
figure 6

Path of the solutions for Example 5.2

Full size image

Thus, all the hypotheses of Theorem 2.3 are verified.

Then, the zero solution of (5.2) is UAS.

6 Conclusion

This work emphasizes the stability of solutions to certain nonlinear second-order and third-order VIDE with delay.

By employing Lyapunov’s second method, a suitable LKF was constructed and used to establish the sufficient conditions of Theorems 2.2 and 2.3.

Two numerical examples were given and all functions were drawn to prove the sufficient conditions of Theorems 2.2 and 2.3, and also orbits of the numerical solutions were drawn with assigned initial conditions to demonstrate the effectiveness of the obtained results.

The results obtained in this paper extend many existing and exciting results on nonlinear VIDE.