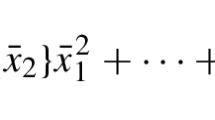Abstract
In this note, we provide a formula for the Tjurina number of a join of isolated hypersurface singularities in separated variables. From this, we are able to provide a characterization of isolated hypersurface singularities whose difference between the Milnor and Tjurina numbers is less or equal than two arising as the join of isolated hypersurface singularities in separated variables. Also, we are able to provide new upper bounds for the quotient of Milnor and Tjurina numbers of certain join of isolated hypersurface singularities. Finally, we deduce an upper bound for the quotient of Milnor and Tjurina numbers in terms of the singularity index of any isolated hypersurface singularity, not necessarily a join of singularities.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let \(f\in \mathbb {C}\{x_0,\dots ,x_n\}\) be a germ of holmorphic function defining an isolated hypersurface singularity and let us denote by \(J_f=(\partial f/\partial x_0,\dots ,\partial f/\partial x_n)\) the Jacobian ideal. The Tjurina number
is one of the most important analytic invariants of an hypersurface singularity. Being certainly not the finer analytic invariant of an isolated singularity, the deepening on its natural comparison with the Milnor number, \(\mu _f:=\dim _{\mathbb {C}}\mathbb {C}\{x_0,\dots ,x_n\}/J_f\), and its generalizations have provided several interesting results in Singularity Theory during the last 50 years.
In this note, we will focus on the comparison of these two invariants in the particular case of the join of two isolated hypersurface singularities in separated variables, i.e. an isolated hypersurface singularity defined by \(f+g\in \mathbb {C}\{\textbf{x};\textbf{y}\}=\mathbb {C}\{x_0,\dots ,x_n;y_0,\dots ,y_m\}\) with \(f\in \mathbb {C}\{\textbf{x}\}\) and \(g\in \mathbb {C}\{\textbf{y}\}.\) In this case, it is then easy to see that \(\mu _{f+g}=\mu _f\mu _g.\) Moreover, in 1971, Sebastiani and Thom [21] proved that the local monodromy of \(f+g\) is equivalent to the tensor product of the local monodromies of \(f\) and \(g.\) Thus, after 1971, it has been frequent in the literature to call a Sebastiani–Thom type isolated hypersurface singularity to a join of two isolated hypersurface singularities in separated variables.
While the original Sebastiani–Thom Theorem is of topological nature, it is also natural to study up to what extent one can compute the main analytic invariants of a Sebastiani–Thom type singularity \(f+g\) from the analytic invariants of \(f\) and \(g.\) In this direction, the main results concern the mixed Hodge structure on the cohomology of the Milnor fiber [20] and its related invariants, such as the spectrum of the singularity [15, 20, 23]. Also, there are several Sebastiani–Thom type theorems for other objects of analytic nature related to a hypersurface singularity such as the kappa invariant, multiplier ideals and Hodge ideals, see [6, 12, 13].
From this point of view, with an eye on the nice expression of the Milnor number of a Sebastiani–Thom type singularity, it is natural to ask for an expression of \(\tau _{f+g}\) in terms of the Tjurina numbers \(\tau _f\) and \(\tau _g.\) Surprisingly, as far as the author knows, it does not exist any explicit result concerning a formula for the Tjurina number in the Sebastiani–Thom case. Our main result provides the following formula for the Tjurina number of a Sebastiani–Thom type singularity.
Theorem 1
Let \(f_1(\textbf{x})\in \mathbb {C}\{\textbf{x}\}=\mathbb {C}\{x_0,\dots ,x_n\}\) and \(f_2(\textbf{y})\in \mathbb {C}\{\textbf{y}\}=\mathbb {C} \{y_0,\dots ,y_n\}\) be germs of isolated hypersurface singularities in different variables. Then, we have
In particular,
Here, the numbers \(\nu _1^{(f_1)},\nu _1^{(f_2)},b_{f_1+f_2},u_{f_1+f_2}\) are nonnegative integers associated to certain dimensions of \(\mathbb {C}\)–vector spaces, which will be defined in Sect. 2. It is important to remark that the numbers \(\nu _1^{(f_1)},\nu _1^{(f_2)},b_{f_1+f_2},u_{f_1+f_2}\) are in general difficult to manage, moreover, as we will see in the proof of Theorem 1 the numbers \(b_{f_1+f_2},u_{f_1+f_2}\) seems to strongly depend on \(f_1+f_2\) rather than the separated \(f_1,f_2.\)
In contrast with the formula, the bounds provided by Theorem 1 are quite simple and also they are sharp. For that reason, we think that the important part of Theorem 1 is precisely the lower and upper bounds; and more specifically the upper bound. That estimates will allow us to characterize Sebastiani–Thom type singularities with \(\mu -\tau \le 2\) (Corollary 1 and Corollary 3). Also, from Theorem 1, we can deduce that we cannot expect a “nice”expression for the Tjurina subspectrum for this family of singularities (see Sect. 2).
The motivation to tackle the problem of finding a formula for the Tjurina number of a Sebastiani–Thom type singularity is to provide new particular cases of the following problem proposed by the author in [2].
Problem 1
[2, Problem 1] Let \((X,0)\subset (\mathbb {C}^N,0)\) be an isolated complete intersection singularity of dimension \(n\) and codimension \(k=N-n\). Is there an optimal \(\frac{b}{a}\in \mathbb {Q}\) with \(b<a\) such that
Here, optimal means that there exist a family of singularities such that \(\mu /\tau \) tends to \(\frac{a}{a-b}\) when the multiplicity at the origin tends to infinity.
Problem 1 was originated as an extension of a question posed by Dimca and Greuel about the quotient of the Milnor and Tjurina numbers of a plane curve singularity [4]. In [2], we showed the following solutions for k=1: in the case of plane curve singularities, we have \((a,b)=(1,4)\) and in the case of surface singularities satisfying Durfee’s conjecture, we have \((a,b)=(1,3).\) Combining those result together with Theorem 1, we are able to give a solution to Problem 1 in the case of a join of surface singularities or plane curves with quasi-homogeneous functions (Proposition 3). Also, in the case of the join of a plane curve singularity with a surface singularity (Proposition 4), we will provide an upper bound for \(b/a\) (Proposition 4). In another vein, we will use a result of Varchenko, in order to show an upper bound for \(\mu /\tau \) of an hypersurface singularity, not necessarily of Sebastiani–Thom type, in terms of the embedding dimension and the minimal spectral value (Proposition 1).
The paper is organized as follows: in Sect. 2, we will prove the formula for the Tjurina number of a Sebastiani–Thom type singularity and we will show some of its consequences. In Sect. 3, we will study the quotient \(\mu /\tau \) for any isolated hypersurface singularity, not necessarily of Sebastiani–Thom type; we will present an upper bound in terms of the minimal spectral value (Proposition 1). Finally, we will discuss the new cases of Problem 1 that can be obtained as a consequence of our formula for the Tjurina number of a Sebastiani–Thom type singularity.
2 Tjurina Number in the Sebastiani–Thom Case
Let \(f\in \mathbb {C}\{x_0,\dots ,x_n\}\) be a germ of isolated hypersurface singularity. Let us denote by
the Milnor and Tjurina algebras respectively. Recall that, since multiplication by \(f\) in \(M_f\) is a \(\mathbb {C}\)–linear map, we can see the Tjurina algebra as the cokernel of this map, i.e.
In the case of a Sebastiani–Thom type singularity \(f_1+f_2\) with \(f_1(\textbf{x})\in \mathbb {C}\{\textbf{x}\}=\mathbb {C}\{x_0,\dots ,x_n\}\) and \(f_2(\textbf{y})\in \mathbb {C}\{\textbf{y}\}=\mathbb {C}\{y_0,\dots ,y_n\},\) the Milnor algebra \(M_{f_1+f_2}\) decomposes as the tensor product of the Milnor algebras \(M_{f_1}\) and \(M_{f_2}.\) Therefore, we have the following exact sequence
In order to simplify notation, for two \(\mathbb {C}\)–vector spaces \(V\subset W\), we will denote \(W{\setminus } V\) to the complement of \(V\) in \(W,\) i.e \(V\oplus (W{\setminus } V)=W;\) which means that \(\{0\}= (W{\setminus } V)\cap V.\) Also, we will denote \(\dim :=\dim _{\mathbb {C}}\) since all vector spaces to be considered are over \(\mathbb {C}.\)
Let us denote by \(A_i:=M_{f_i}{\setminus }({\text {Ker}}(f_i)+{\text {Im}}(f_i))\) and \(B_i:={\text {Im}}(f_i){\setminus }({\text {Im}}(f_i) \cap {\text {Ker}}(f_i)).\) Then we have the following decomposition of the Milnor algebra \(M_{f_i}={\text {Ker}}(f_i)\oplus B_{i}\oplus A_i.\) Using the decomposition in direct sum of the Milnor algebras, we are able to provide the proof of Theorem 1
Proof of Theorem 1
In order to simplify notation, let us denote by \(\mu _i:=\mu _{f_i}\) and \(\tau _{i}:=\tau _{f_i}.\) Also let us denote by
Our aim is to describe \({\text {Im}}(f_1+f_2).\) To do so observe that
where
and
Before to continue, observe that we have the following equality
In order to check Eq. (2.2), we will show that the obvious inclusions
are in fact equalities by a dimension argument. Since by definition \((B_1\oplus A_1)\cap {\text {Ker}}(f_1)=\{0\},\) then it is straightforward to check
Thus, we have \(\dim (f_1(B_1\oplus A_1)\otimes {\text {Ker}}(f_2))=(\mu _1-\tau _1)\tau _2\) and in this way, we obtain the following equality
A similar argument shows that \(({\text{ Ker }}(f_1)\otimes f_2(B_2))\oplus ({\text{ Ker }}(f_1)\otimes f_2(A_2))={\text{ Ker }}(f_1)\otimes {\text{ Im }}(f_2)\). Therefore, \(U=U'.\) Moreover, we can easily compute its dimension as
since \(\dim (({\text {Ker}}(f_1)\cap {\text {Im}}(f_1))\otimes ({\text {Ker}}(f_2)\cap {\text {Im}}(f_2)))=\nu _1^{(f_1)}\nu _1^{(f_2)}.\)
We can now rewrite Eq. (2.1) as follows
At this point, we are going to show that the previous sum has the following decomposition as direct sum:
In order to do that, let us consider a basis \(\mathcal {B}_i=\{b^{i}_1,\dots ,b^{i}_{\mu _i}\}\) of \(M_{f_i}\) such that \(\{b_1^i,\dots ,b^i_{\tau _i}\}\) is a basis of \(\ker (f_i),\) \(\{b^{i}_{\tau _i+1},\dots ,b^{i}_{\mu _i-\nu _1^{(f_i)}}\}\) is a basis of \(B_i\) and \(\{b^{i}_{\mu _i-\nu _1^{(f_i)}+1},\dots ,b^{i}_{\mu _i}\}\) is a basis of \(A_i.\) We start with \(U\cap (f_1+f_2)(A_1\otimes B_2)=\{0\},\) and similar arguments work for \(U\cap (f_1+f_2)(A_1\otimes A_2)=\{0\}\) and \(U\cap (f_1+f_2)(B_1\otimes A_2)=\{0\}.\) Assume that there exist \(0\ne u\in U\cap (f_1+f_2)(A_1\otimes B_2)\), then
Thus,
Since \(1\otimes f_2\) is an injective linear map on \(A_1\otimes B_2\) then Eq. (2.4) implies that \(\alpha _{j,k}=0\) for all \(j,k\). Therefore, it provides a contradiction with the fact that \(u\ne 0.\)
Finally, we check \((f_1+f_2)(A_1\otimes A_2)\cap (f_1+f_2)(B_1\otimes A_2)=\{0\},\) and similar arguments work for the rest of intersections that remain to check. Assume that there exists \(0\ne u\in (f_1+f_2)(A_1\otimes A_2)\cap (f_1+f_2)(B_1\otimes A_2)\), then
Thus,
As \(1\otimes f_2\) is an injective linear map on \(A_1\otimes A_2\) then \(\alpha _{j,k}=0\) for all \(j,k\). Therefore it provides a contradiction with the fact that \(u\ne 0.\)
To finish, we only need to compute the dimension of each summand as follows
Let us denote by \(b_{f_1+f_2}:=\dim ((f_1+f_2)(B_1\otimes B_2))\) and by \(u_{f_1+f_2}:=\dim (U\cap (f_1+f_2(B_1\otimes B_2)))\). Then, combining Eqs. (2.3) and (2.5), we have
Then,
as claimed. Let us finally show the “in particular ”statement. First, observe that
Then,
where the last inequality follows from the fact that \(\nu _1^{(f_1)}\ge 0\) and \(u_{f_1+f_2}\ge 0.\)
In order to show the upper bound, we recall that \(\nu _1^{(f_i)}\le (\mu _i-\tau _i)\) and \(u_{f_1+f_2}\le b_{f_1+f_2}.\) Therefore,
from which the desire bound follows. \(\square \)
Remark 1
Our proof provides not only a formula for the Tjurina number for the Sebastiani–Thom type singularities but also provides an explicit expression of the structure of \({\text {Im}}(f_1+f_2).\) In particular, by means of the good basis considered by Scherk [19], Saito [17] and Hertling [7, 8] one can describe a basis of \({\text {Im}}(f_1+f_2)\) which behaves well with respect to the \(V\)–filtration associated to \(J_{f_1+f_2}+(f_1+f_2).\)
Remark 2
A point of interest in this setting is the Tjurina subspectrum. In [9], Jung et al. defined the Tjurina subspectrum \(\{\alpha _i^{Tj}\}_{i\in A}\) of \(f\). This subspectrum is a subset of the spectrum of \(f\) such that \(|A|=\tau \) where the indexes are chosen carefully with respect to certain properties of the Hodge ideal \(V\)–filtration associated to \(J_f+f.\) Recall that if \(\{\alpha _1,\dots ,\alpha _{\mu _f}\}\) and \(\{\beta _1,\dots ,\beta _{\mu _g}\}\) are the spectral numbers of \(f\) and \(g\), respectively, then
are the spectral numbers of \(f+g.\) However, Theorem 1 shows that the Tjurina subspectrum does not behave so well with respect to the Sebastiani–Thom property since otherwise \(\tau _{f+g}\) would be the product of \(\tau _f\) and \(\tau _g\). Being obvious one of the implications, we wonder whether the Sebastiani–Thom property on the Tjurina subspectrum is equivalent to the fact that \(\tau _{f+g}=\tau _f\tau _g;\) where by the Sebastiani–Thom property on the Tjurina subspectrum we mean that if \(\{\alpha _i^{Tj}\}_{i\in A_f}\) and \(\{\beta _k^{Tj}\}_{i\in A_g}\) are the Tjurina subspectrum of \(f\) and \(g\) respectively then
is the Tjurina spectrum of \(f+g.\)
A first consequence of Theorem 1 is the following characterization of quasi-homogeneous singularities arising as the join of two functions.
Corollary 1
Let \(F=f+g\in \mathbb {C}\{x_0,\dots ,x_n;y_0,\dots ,y_m\}\) be a germ of isolated hypersurface singularity defined as the join of \(f(\textbf{x})\in \mathbb {C}\{\textbf{x}\}=\mathbb {C}\{x_0,\dots ,x_n\}\) and \(g(\textbf{y})\in \mathbb {C}\{\textbf{y}\}=\mathbb {C}\{y_0,\dots ,y_n\}\). Then, the following are equivalent
-
1.
\(F\) is quasi-homogeneous,
-
2.
\(f\) and \(g\) are quasi-homogeneous.
-
3.
\(\tau _{F}=\mu _f\mu _g.\)
Proof
(1) \(\Rightarrow \) (2), we assume \(F\) to be a quasi-homogeneous function. Let us suppose \(f\) being quasi-homogeneous and \(g\) not quasi-homogeneous. By Theorem 1 and K. Saito’s Theorem [14], we have
Now, assume \(F\) to be a quasi-homogeneous function and \(f\) and \(g\) not quasi-homogeneous. By Theorem 1
where the last inequality is strict because by Saito’s Theorem [14] \((\tau _f-\mu _f)\tau _g+(\tau _g-\mu _g)\tau _f\lvertneqq 0.\) Therefore, in both cases, we have a contradiction since by Saito’s Theorem \(\mu _F=\tau _F.\)
\((2)\Rightarrow (3)\) is a direct consequence of Theorem 1 and K. Saito’s Theorem [14].
\((3)\Leftrightarrow (1)\) follows from Saito’s Theorem [14].
\(\square \)
If we denote by \(e^{BS}(f):=\min \{k\in \mathbb {N}\;|\;f^k\in (\partial f/\partial x_0,\dots ,\partial f/\partial x_n)\},\) the case where one of the singularities has \(e^{BS}(f)=2\) is of special interest since in that case \(\nu _1=\mu -\tau .\) A particular example of this situation is a join where one of the functions defines a plane curve singularity. In those cases, we have the following simplified expression of the Tjurina number.
Corollary 2
Let \(f_1(\textbf{x})\in \mathbb {C}\{\textbf{x}\}=\mathbb {C}\{x_0,\dots ,x_n\}\) and \(f_2(\textbf{y})\in \mathbb {C}\{\textbf{y}\}= \mathbb {C}\{y_0,\dots ,y_n\}\) be germs of isolated hypersurface singularities in separated variables. Assume that \(e^{BS}(f_1)=2\) or \(e^{BS}(f_2)=2.\) Then,
Proof
Assume that \(e^{BS}(f_1)=2,\) and the case \(e^{BS}(f_2) =2\) follows from similar arguments. Observe that if \(e^{BS}(f_1)=2\) then \(\nu _1^{(f_1)}=\mu _{f_1}-\tau _{f_1},\) which in particular implies \(B_1={\text {Im}}(f_1){\setminus }({\text {Im}}(f_1)\cap {\text {Ker}}(f_1))=\{0\}.\) Thus, the claim follows from Theorem 1. \(\square \)
Example 1
Let us consider the isolated hypersurface singularity in \(\mathbb {C}\{x_1,x_2,x_3,x_4,x_5,x_6\}\) defined by
which is the join of three irreducible plane curve singularities of the form \(G(x,y)=y^4-x^5+x^3y^2.\)
We can compute the Milnor and Tjurina numbers of \(G,\) \(\mu (G)=12\) and \(\tau (G)=11.\) By Corollary 2, if we consider the hypersurface in \(\mathbb {C}\{x_1,x_2,x_3,x_4\}\) defined by \(H=G(x_1,x_2)+G(x_3,x_4),\) we have that
With the help of SINGULAR [3], we can compute \(\nu _1^{(H)}=21.\) Therefore, by Corollary 2, we can compute
To finish, we can provide a characterization of Sebastiani–Thom type singularities with \(\mu -\tau \le 2.\)
Corollary 3
Let \(f_1(\textbf{x})\in \mathbb {C}\{\textbf{x}\}=\mathbb {C}\{x_0,\dots ,x_n\}\) and \(f_2(\textbf{y})\in \mathbb {C}\{\textbf{y}\}= \mathbb {C}\{y_0,\dots ,y_n\}\) be germs of isolated hypersurface singularities in separated variables. Then,
-
(1)
\(\tau _{f_1+f_2}=\mu _{f_1+f_2}-1\) if and only if \(\mu _{f_1}=\tau _{f_1}=1\) and \(\mu _{f_2}-1=\tau _{f_2}\) or \(\mu _{f_2}=\tau _{f_2}=1\) and \(\mu _{f_1}-1=\tau _{f_1}.\)
-
(2)
\(\tau _{f_1+f_2}=\mu _{f_1+f_2}-2\) if and only if \(f_1,f_2\) are in one of the following cases:
-
(a)
\(\mu _{f_1}=\tau _{f_1}=1\) and \(\mu _{f_2}-2=\tau _{f_2}\).
-
(b)
\(\mu _{f_2}=\tau _{f_2}=1\) and \(\mu _{f_1}-2=\tau _{f_1}.\)
-
(c)
\(\mu _{f_1}=\mu _{f_2}=2\) and \(\tau _{f_1}=\tau _{f_2}=1.\)
-
(d)
\(\mu _{f_1}=\tau _{f_1}=2\) and \(\mu _{f_2}-1=\tau _{f_2}.\)
-
(e)
\(\mu _{f_2}=\tau _{f_2}=2\) and \(\mu _{f_1}-1=\tau _{f_1}.\)
-
(a)
Proof
Let us start with (1). By Theorem 1, we have the following inequality
Therefore, we have
Since \(\tau _{f_i}(\tau _{f_i}-\mu _{f_i})\) are integers numbers, then the inequality is satisfied if at least one of the \(f_i\) is a quasi-homogeneous singularity. Observe that by Corollary 1 both cannot be quasi-homogeneous since we are assuming \(\tau _{f_1+f_2}\ne \mu _{f_1+f_2}.\) Also, at least one of the \(f_i\) must be quasi-homogeneous since otherwise \(\tau _{f_1}(\tau _{f_2}-\mu _{f_2})+\tau _{f_2}(\tau _{f_1}-\mu _{f_1})\le -2.\) Let us assume \(f_1\) is quasi-homogeneous, the case \(f_2\) will follow mutatis mutandis. In that case, since \(\mu _{f_2}\ne \tau _{f_2}\) we have
which implies \(\tau _{f_1}=1=\tau _{f_2}-\mu _{f_2}.\) The converse implication is obviously trivial.
Let us move to the case (2). As before, by Theorem 1, we have the following inequality
As in the proof of part (1), we have the following subcases: \(\tau _{f_1}(\tau _{f_2}-\mu _{f_2})=-2\) and \(\tau _{f_1}=\mu _{f_1},\) \(\tau _{f_2}(\tau _{f_1}-\mu _{f_1})=-2\) and \(\tau _{f_2}=\mu _{f_2},\) \(\tau _{f_2}(\tau _{f_1}-\mu _{f_1})=\tau _{f_1}(\tau _{f_2}-\mu _{f_2})=-1\). The claim now easily follows from the casuistic of each subcase. \(\square \)
3 The Quotient of Milnor and Tjurina Numbers
In 2017, Liu [11] showed that for any isolated hypersurface singularity defined by \(f:\mathbb {C}^{n+1}\rightarrow \mathbb {C}\) one has \(\mu /\tau \le n+1\). However, following his proof, we are going to show that we can actually be more precise about this upper bound. Recall that the Briançon–Skoda exponent of \(f\) is defined by
According to the Briançon–Skoda Theorem [18], we know that \(e^{BS}(f)\le n+1.\) However, one can slightly improve that bound by using the spectrum of \(f.\) Recall that the spectrum is a discrete invariant formed by \(\mu \) rational spectral numbers (see [10, II.8.1])
They are certain logarithms of the eigenvalues of the monodromy on the middle cohomology of the Milnor fibre which correspond to the equivariant Hodge numbers of Steenbrink’s mixed Hodge structure. From this set of invariants, Varchenko [23, Theorem 1.3] proved the following result.
Theorem 2
Let \(f\in \mathbb {C}\{x_0,\dots ,x_n\}\) be a germ of holmorphic function defining an isolated hypersurface singularity. Let \(\alpha _{min}\) be the minimal spectral number, then
Remark 3
Our definition of spectral numbers follows K. Saito and M. Saito’s definition [15, 16] in contrast with Steenbrink and Varchenko’s definition [22, 23]. This means that \(\alpha '\) is a spectral number with Steenbrink and Varchenko’s definition if and only if \(\alpha '+1\) is a spectral number with Saito’s definition.
Therefore, Varchenko’s Theorem 2 allows to slightly improve the general upper bound provided by Liu in [11].
Proposition 1
Let \(f\) be a holomorphic function in \(\mathbb {C}\{x_0,\dots ,x_n\}\). Let \(\alpha _{min}\) be the minimal spectral number of \(f\). Then,
In particular, \(\mu /\tau <\lfloor n+1-2\alpha _{min}\rfloor +1.\)
Proof
If we denote by \((f^{i})\) the ideal of \(M_f\) generated by \((f^{i}),\) those ideals define a decreasing filtration
Then, one can consider the following long exact sequence:
where the middle map is the multiplication by \(f\). Then,
Therefore,
Applying Varchenko’s Theorem 2, we obtain \(\mu /\tau <\lfloor n+1-2\alpha _{min}\rfloor +1.\) \(\square \)
Remark 4
Since \(\alpha _{min}>0\) then \(n+1-2\alpha _{min}<n+1\) from which we have \(\lfloor n+1-2\alpha _{min}\rfloor \le n.\) Therefore, in the worst case, we have Liu’s result. In the case where \(\alpha _{min}>1/2,\) as for example rational singularities, then \(\lfloor n+1-2\alpha _{min}\rfloor \le n-1\) and we obtain a strictly better upper bound than the one coming from Briançon–Skoda Theorem.
After Proposition 1, one can then estimate the \(b/a\) of Problem 1. Unfortunately, it is easy to check that the bound provided by Proposition 1 is not sharp. In [2], we showed that for any plane curve singularity \(\mu /\tau <4/3\) and moreover, it is asymptotically sharp. This result provided a full answer to a question posed by Dimca and Greuel in [4]. The techniques used to prove that bound were based on the theory of surface singularities. More concretely, we showed the relation of Problem 1 with the long standing Durfee’s conjecture [5] and its generalization [15], which claims that if \(f\in \mathbb {C}\{x_0,\dots ,x_n\}\) defines an isolated hypersurface singularity then \((n+1)!p_g<\mu ,\) where \(p_g\) is the geometric genus. With the help of Durfee’s conjecture, we were also able to show an asymptotically sharp upper bound in the case of surface singularities in \(\mathbb {C}^{3}.\) Those results are collected in the following
Proposition 2
[2, Theorem 6 and Proposition 3]
-
(1)
If \(f(x,y)\) is a plane curve then \(\mu /\tau <4/3.\)
-
(2)
If \(f(x,y,z)\) is a surface singularity satisfying Durfee’s conjecture then \(\mu /\tau <3/2.\)
Therefore, the combination of Theorem 1 and Proposition 2 allow us to generalize our previous results to the following Sebastiani–Thom type singularities.
Proposition 3
Let \(g(z_0,\dots ,z_n)\) be a quasi-homogeneous function. Then,
-
(1)
If \(f(x,y)\) is an isolated plane curve singularity, then
$$\begin{aligned}\frac{\mu _{f+g}}{\tau _{f+g}}<\frac{4}{3}.\end{aligned}$$ -
(2)
If \(f(x_1,x_2,x_3)\) is an isolated surface singularity in \(\mathbb {C}^3\) satisfying Durfee’s conjecture, then
$$\begin{aligned}\frac{\mu _{f+g}}{\tau _{f+g}}<\frac{3}{2}.\end{aligned}$$
Proof
Since \(g\) is quasi-homogeneous then \(\tau _g=\mu _g\) and \(\tau _{f+g}=\tau _f\mu _g.\) Then, in both cases, we have \(\mu _{f+g}/\tau _{f+g}=\mu _f/\tau _f.\) Therefore, the claim follows from Proposition 2. \(\square \)
Moreover, it is easy to find families for which the bounds of Proposition 3 are asymptotically sharp. In the case of plane curve singularities, consider \(f(x,y)=y^{n}-x^{n+1}+g(x,y)\) with \( \deg _w(f) < \deg _w(g) \) with respect to the weights \(w=(n,n+1).\) Moreover, choose \(g\) such that \(\tau _f=\tau _{min},\) i.e. the Tjurina number of \(f\) is minimal over all possible Tjurina numbers in a \(\mu \)–constant deformation of \(y^{n}-x^{n+1}.\) Then, [1],
Therefore, the join of \(f\) with any quasi-homogeneous function \(h\) in separated variables gives
In [2, Example 3], we showed a family of surface singularities in \(\mathbb {C}^{3}\) with \(\mu /\tau \rightarrow 3/2.\) Using that example, the same reasoning as before allows to construct an example where the bound of Proposition 3 (2) is asymptotically sharp.
To finish, the following Proposition also follows from a direct application of Theorem 1 and Proposition 2.
Proposition 4
Let \(f(x_1,x_2,x_3)\) be an isolated surface singularity in \(\mathbb {C}^3\) satisfying Durfee’s conjecture and \(g(z_1,z_2)\) be a plane curve singularity. Then,
Proof
By Theorem 1, we have \(\tau _{f+g}\ge \tau _f\tau _g.\) Then, \(\mu _{f+g}/\tau _{f+g}\le (\mu _f\mu _g)/(\tau _f\tau _g) <2\) where the last inequality follows by Proposition 2. \(\square \)
In the case of Proposition 4, since \(g\) is a plane curve singularity, Corollary 2 shows that in fact we have
In order to find a family where the bound of Proposition 4 is asymptotically sharp one should deal with the uncomfortable term \(\nu _1^{(f)}(\mu _g-\tau _g).\) Moreover, it is reasonable to think that the bound of Proposition 4 should not be asymptotically sharp.
Data Availability
All data generated or analyzed during this study are included in this published article.
References
Alberich-Carramiñana, M., Almirón, P., Blanco, G., Melle-Hernández, A.: The minimal Tjurina number of irreducible germs of plane curve singularities. Indiana Univ. Math. J. 70(4), 1211–1220 (2021)
Almirón, P.: On the quotient of Milnor and Tjurina numbers for two-dimensional isolated hypersurface singularities. Math. Nachr. 295(7), 1254–1263 (2022)
Decker, W., Greuel, G.-M., Pfister, G., Schönemann, H.: SINGULAR 4-2-1-A computer algebra system for polynomial computations. http://www.singular.uni-kl. (2021)
Dimca, A., Greuel, G.-M.: On 1-forms on isolated complete intersection curve singularities. J. Singul. 18, 114–118 (2018)
Durfee, A.H.: The signature of smoothings of complex surface singularities. Math. Ann. 232(1), 85–98 (1978)
Greuel, G.-M.: Ergänzung und Berichtigung zu: “Die Zahl der Spitzen und die Jacobi-Algebra einer isolierten Hyperflächensingularität (Manuscripta Math. 21 (1977), no. 3, 227-241)”. Manuscr. Math. 25(2), 205–208 (1978)
Hertling, C.: Classifying spaces for polarizedmixedHodge structures and for Brieskorn lattices. Compos. Math. 116(1), 1–37 (1999)
Claus Hertling and Colin Stahlke: Bernstein polynomial and Tjurina number. Geom. Dedicata. 75(2), 137–176 (1999)
Jung, S.-J., Kim, I.-K., Saito, M., Yoon, Y.: Hodge ideals and spectrumof isolated hypersurface singularities. Ann. Inst. Fourier (Grenoble) 72(2), 465–510 (2022)
Kulikov, V.S.: Mixed Hodge structures and singularities. Vol. 132. Cambridge Tracts in Mathematics. Cambridge University Press, Cambridge, pp. xxii+186 (1998)
Liu, Y.: Milnor and Tjurina numbers for a hypersurface germ with isolated singularity. C. R. Math. Acad. Sci. Paris 356(9), 963–966 (2018)
Maxim, L., Saito, M., Schürmann, J.: Thom–Sebastiani theorems for filtered D-modules and for multiplier ideals. Int. Math. Res. Not. IMRN 1, 91–111 (2020)
Mustaţǎ, M.: The multiplier ideals of a sum of ideals. Trans. Am. Math. Soc. 354(1), 205–217 (2002)
Saito, K.: Quasihomogene isolierte Singularitäten von Hyperflächen. Invent. Math. 14, 123–142 (1971)
Saito, K.: The zeroes of characteristic function c f for the exponents of a hypersurface isolated singular point. In: Algebraic varieties and analytic varieties (Tokyo, 1981). Vol. 1. Adv. Stud. Pure Math. North-Holland, Amsterdam, pp. 195–217 (1983)
Saito, M.: On the exponents and the geometric genus of an isolated hypersurface singularity. In: Singularities, Part 2 (Arcata, Calif., 1981). Vol. 40. Proc. Sympos. Pure Math. Amer. Math. Soc., Providence, RI, pp. 465–472 (1983)
Saito, M.: On the structure of Brieskorn lattice. Ann. Inst. Fourier (Grenoble) 39(1), 27–72 (1989)
Skoda, H., Briançon, J.: Sur la clôture intégrale d’un idéal de germes de fonctions holomorphes en un point de Cn. C. R. Acad. Sci. Paris Sér. A 278, 949–951 (1974)
Scherk, J.: On the Gauss–Manin connection of an isolated hypersurface singularity. Math. Ann. 238(1), 23–32 (1978)
Scherk, J., Steenbrink, J.H.M.: On the mixed Hodge structure on the cohomology of the Milnor fibre. Math. Ann. 271(4), 641–665 (1985)
Sebastiani, M., Thom, R.: Un résultat sur la monodromie. Invent. Math. 13, 90–96 (1971)
Steenbrink, J. H. M.: Mixed Hodge structure on the vanishing cohomology. In: Real and complex singularities (Proc. Ninth Nordic Summer School/NAVF Sympos. Math., Oslo, 1976). pp. 525–563 (1977)
Varčenko, A. N.: AsymptoticHodge structure on vanishing cohomology. Izv. Akad. Nauk SSSR Ser. Mat. 45(3), 540–591 (1981)
Acknowledgements
I would like to thank J.J. Moyano-Fernández, P.D. González-Pérez and J. Viu-Sos for the useful comments and suggestions during the preparation of this work. I would also like to thank the anonymous referee for the careful reading of the manuscript. Funding for open access publishing: Universidad de Granada/CBUA
Funding
Funding for open access publishing: Universidad de Granada/CBUA The author is supported by Spanish Ministerio de Ciencia, Innovación y Universidades PID2020-114750GB-C32 and by the IMAG-Maria de Maeztu grant CEX2020-001105-M / AEI / 10.13039/501100011033, through a postdoctoral contract in the ‘Maria de Maeztu Programme for Centres of Excellence’.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
The authors declare no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The author is supported by Spanish Ministerio de Ciencia, Innovación y Universidades PID2020-114750GB-C32 and by the IMAG-Maria de Maeztu grant CEX2020-001105-M/AEI /10.13039/501100011033, through a postdoctoral contract in the ‘Maria de Maeztu Programme for Centres of Excellence’.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Almirón, P. The Tjurina Number for Sebastiani–Thom Type Isolated Hypersurface Singularities. Mediterr. J. Math. 20, 258 (2023). https://doi.org/10.1007/s00009-023-02458-3
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00009-023-02458-3