Catalan Generating Functions for Generators of Uni-parametric Families of Operators

Abstract

In this paper we study solutions of the quadratic equation $AY^2-Y+I=0$ where A is the generator of a one parameter family of operator ($C_0$-semigroup or cosine functions) on a Banach space X with growth bound $w_0 \le \frac{1}{4}$. In the case of $C_0$-semigroups, we show that a solution, which we call Catalan generating function of A, C(A), is given by the following Bochner integral,

$$\begin{aligned} C(A)x := \int _{0}^\infty c(t) T(t)x \; \mathrm{d}t, \quad x\in X, \end{aligned}$$

where c is the Catalan kernel,

$$\begin{aligned} c(t) := \frac{1}{2\pi } \int _{\frac{1}{4}}^\infty e^{-\lambda t} \frac{\sqrt{4\lambda -1}}{\lambda } \; \mathrm{d}\lambda , \quad t>0. \end{aligned}$$

Similar (and more complicated) results hold for cosine functions. We study algebraic properties of the Catalan kernel c as an element in Banach algebras $L^1_{\omega }(\mathbb R^+)$, endowed with the usual convolution product, $*$ and with the cosine convolution product, $*_c$. The Hille–Phillips functional calculus allows to transfer these properties to $C_0$-semigroups and cosine functions. In particular, we obtain a spectral mapping theorem for C(A). Finally, we present some examples, applications and conjectures to illustrate our results.

1 Introduction

The Catalan numbers $(C_n)_{n \ge 0}$ given by,

$$\begin{aligned} C_n = \frac{1}{n+1} \left( {\begin{array}{c}2n\\ n\end{array}}\right) , \quad n \ge 0, \end{aligned}$$

form an integer sequence deeply studied in number theory and combinatorics. Historically, one of the first interpretation given to the Catalan number $C_n$ was through the number of ways to triangulate a regular $n+2$-sided polygon, known as Euler problem. Another example where this sequence appears is counting the ways of constructing binary trees. Specifically, $C_n$ represents the number of ways to construct a binary tree with n nodes. In fact, a large amount of applications and interpretations of $(C_n)_{n \ge 0}$, more than 200, may be found in [19].

The generating function of the Catalan numbers is given by

$$\begin{aligned} C(z):= \sum _{n=0}^\infty C_n z^n = \frac{1-\sqrt{1-4z}}{2z}, \quad z \in D\left( 0,\frac{1}{4}\right) := \left\{ z \in \mathbb C\, | \, \left| z\right| \le \frac{1}{4} \right\} , \end{aligned}$$

which is one of the solution for y in the quadratic equation,

$$\begin{aligned} z y^2 - y + 1 = 0. \end{aligned}$$

In this context, one may wonder what happens when we replace the complex values y and z by operators or elements in a general Banach algebra. Recently, this point of view has been explored in [14] for bounded operators in a Banach space X, obtaining a way to solve the equation presented above.

To extend these results to a wider family of operators, mainly non-bounded operators, we consider generators of $C_0$-semigroups and cosine operators. A family of bounded operators $(T(t))_{t \ge 0}$ on a Banach space X is called a strongly continuous semigroup (or $C_0$-semigroup) if it satisfies the functional equation,

$$\begin{aligned} \left\{ \begin{aligned}&T(t+s) = T(t)T(s), \quad \text {for all } t,s \ge 0 \\&T(0) = I, \end{aligned} \right. \end{aligned}$$

and $\lim _{t \rightarrow 0^+} T(t)x = x$ for all $x \in X$. The linear operator (A, D(A)) defined as,

$$\begin{aligned} Ax:= \lim _{h \rightarrow 0}\frac{T(h)x-x}{h}, \quad x \in D(A):=\{ x \in X \, | \, Ax \text { exists on }X \} \end{aligned}$$

is the infinitesimal generator of the semigroup $(T(t))_{t \ge 0}$ with closed and densely defined domain D(A). The solution of the Cauchy problem,

$$\begin{aligned} \left\{ \begin{aligned}&u'(t)x = Au(t), \quad \text {for } t \ge 0, \\&u(0)x = x\in D(A), \end{aligned} \right. \end{aligned}$$

is given by the orbit $u(t)=T(t)x$. In the case that $A \in \mathcal {B}(X)$, the set of linear and bounded operators on X, the $C_0$-semigroup is expressed by the vector-valued exponential function,

$$\begin{aligned} T(t)x=e^{tA}x=\sum _{n=0}^{\infty } \frac{t^n}{n!} A^n(x), \quad x\in X, \end{aligned}$$

see more details in [2, Theorem 1.4].

A family of bounded operators $({{\,\mathrm{Cos}\,}}(t))_{t \ge 0}$ on a Banach space X is called a strongly continuous cosine function if it satisfies the functional equation,

$$\begin{aligned} \left\{ \begin{aligned}&{{\,\mathrm{Cos}\,}}(t+s) +{{\,\mathrm{Cos}\,}}(t-s)= 2{{\,\mathrm{Cos}\,}}(t){{\,\mathrm{Cos}\,}}(s), \quad \text {for } t \ge s\ge 0, \\&{{\,\mathrm{Cos}\,}}(0) = I, \end{aligned} \right. \end{aligned}$$

and $\lim _{t \rightarrow 0^+} {{\,\mathrm{Cos}\,}}(t)x = x$ for all $x \in X$. The linear operator (A, D(A)) defined as,

$$\begin{aligned} Ax:= 2\lim _{h \rightarrow 0}\frac{{{\,\mathrm{Cos}\,}}(h)x-x}{h^2}, \quad x \in D(A):=\{ x \in X \, | \, Ax \text { exists on }X \} \end{aligned}$$

is the generator of the cosine function $({{\,\mathrm{Cos}\,}}(t))_{t \ge 0}$ with closed and densely defined domain D(A). The solution of the wave problem,

$$\begin{aligned} \left\{ \begin{aligned}&v''(t)x = Av(t), \quad \text {for all } t \ge 0, \\&v(0)x = x\in D(A), \\&v'(0)x = 0, \end{aligned} \right. \end{aligned}$$

is given by the orbit $v(t)={{\,\mathrm{Cos}\,}}(t)x$. In the case that $A \in \mathcal {B}(X)$ the cosine function is expressed by the vector-valued hyperbolic cosine function,

$$\begin{aligned} {{\,\mathrm{Cos}\,}}(t)x=\sum _{n=0}^{\infty } \frac{t^{2n}}{(2n)!} A^{2n}(x), \quad x\in X, \end{aligned}$$

see more details in [1, Section 3.14].

In this work we show that

$$\begin{aligned} C(A)x:= \int _{0}^\infty c(t) T(t)x\, \mathrm{d}t, \quad x\in X, \end{aligned}$$

is a solution of the equation,

$$\begin{aligned} A Y^2 - Y + I = 0, \end{aligned}$$

(1.1)

where A is the generator of a $C_0$-semigroup $(T(t))_{t \ge 0}$ bounded by $\left\| T(t)\right\| \le M e^{w_0 t}$, with $w_0\le \frac{1}{4}$, see Theorem 4.2. The function c, called Catalan kernel, is defined by

$$\begin{aligned} c(t) := \frac{1}{2\pi } \int _{\frac{1}{4}}^\infty e^{-\lambda t} \frac{\sqrt{4\lambda -1}}{\lambda } \; \mathrm{d}\lambda , \quad t>0. \end{aligned}$$

(1.2)

Similarly, when A generates a cosine function $({{\,\mathrm{Cos}\,}}(t))_{t \ge 0}$, $\left\| {{\,\mathrm{Cos}\,}}(t)\right\| \le M e^{w_0 t}$, with $M \ge 1$ and $w_0\le \frac{1}{4}$, the operator

$$\begin{aligned} {\mathcal {C}}(A)x= \int _{0}^\infty c(t){{\,\mathrm{Cos}\,}}(t)x \, \mathrm{d}t, \quad x\in X, \end{aligned}$$

is a solution of the biquadratic equation

$$\begin{aligned} 4A Y^4 - Y^2 + I = 0, \end{aligned}$$

(1.3)

see Theorem 4.4.

The Catalan kernel c has already appeared in the literature and its integral expression (1.2), see for example [16, formula 15]. The key point is that the moments of this function are the Catalan numbers,

$$\begin{aligned} C_n= \int _0^\infty \frac{t^n}{n!}\, c(t) \; \mathrm{d}t, \quad n\ge 0. \end{aligned}$$

(1.4)

Other integral representations of Catalan numbers may be found in [17, 19].

However, other notable properties of this function have not yet been considered. In Sect. 2, the following algebraic properties are shown,

$$\begin{aligned} (c*c)'(t)= & {} -c(t),\\ (c*_c c)(t)= & {} \int _0^\infty \frac{1}{ \sqrt{4 \pi s}} e^{-\frac{t^2}{16s}}c(s)\mathrm{d}s,\\ 4(c*_c c *_c c *_c c)''(t)= & {} (c*_c c)(t), \end{aligned}$$

for $t>0$, see Theorem 2.4, Lemma 2.7 and Theorem 2.8. Here we denote by $*$ and $*_c$ the usual convolution product and the cosine convolution product defined in the weighted Lebesgue space $L^1_\omega (\mathbb R^+)$, see Sects. 2.1, and 2.2.

The main idea in this paper is to obtain new information about the Catalan kernel c in the algebras $(L^1_\omega (\mathbb R^+), *)$ and $(L^1_\omega (\mathbb R^+), *_c)$ (Sect. 2) to transfer later to $C_0$-semigroups (Sect. 3) and cosine functions (Sect. 4).

The Laplace transform and the cosine transform are useful tools to obtain those properties for the Catalan kernel c. Also, spectra of the element c are identified and represented in both convolution algebras in Sect. 2.

For $C_0$-semigroups, we define the Catalan operator in Sect. 3. We show a spectral mapping theorem for this operator and the connection with the square root in Theorem 3.2. In the case that A generates a $C_0$-group, then $4A^2$ generates a $C_0$-semigroup and

$$\begin{aligned} C(4A^2)=\left( \frac{C(A)+C(-A)}{2}\right) ^2, \end{aligned}$$

see Theorem 3.5.

For cosine operators, we define the Catalan operator in Sect. 4. We also show a spectral mapping theorem for this operator and the connection with the square root in Theorem 4.4. As A also generates a $C_0$-semigroup, $C(4A)=({\mathcal {C}}(A))^2$ where C(4A) is given in Definition 3.1.

Finally, in the last section we present some concrete examples of operators A which generates $C_0$-semigroups and cosine functions. We calculate the Catalan operator C(A) for these operators. We also give some conjectures and ideas to extend our results presented in a future research. For $\alpha$-times integrated semigroup, resolvent estimates or fractional powers of infinitesimal generators of bounded $C_0$-semigroups, the Catalan operator C(A) may be interesting to consider in further research.

2 Algebraic Properties of the Catalan Kernel

The Catalan numbers $(C_n)_{n \ge 0}$ form a sequence of integers defined by the recurrence relation

$$\begin{aligned} C_n = \sum _{i=0}^{n-1} C_i C_{n-1 -i}, \quad n \ge 1, \end{aligned}$$

and $C_0 = 1$. They can also be expressed by the following explicit formula using binomial numbers,

$$\begin{aligned} C_n=\frac{1}{n+1}\left( {\begin{array}{c}2n\\ n\end{array}}\right) , \quad n \ge 0, \end{aligned}$$

see [19, Section 1.4]. The generating function of this sequence is,

$$\begin{aligned} C(z):= \sum _{n=0}^\infty C_n z^n = \frac{1-\sqrt{1-4z}}{2z}, \quad z \in D\left( 0,\frac{1}{4}\right) := \left\{ z \in \mathbb C\, | \, \left| z\right| \le \frac{1}{4}\right\} , \end{aligned}$$

(2.1)

and it satisfies the following quadratic equation,

$$\begin{aligned} zC^2(z)-C(z)+1=0, \quad z \in D\left( 0,\frac{1}{4}\right) , \end{aligned}$$

(2.2)

see [19, Section 1.3]. Moreover, the function $\frac{1}{zC(z)} = \frac{1+\sqrt{1-4z}}{2z}$ also satisfies this equation,

$$\begin{aligned} z\left( \frac{1}{zC(z)}\right) ^2-\frac{1}{zC(z)}+1=0, \quad z \in D\left( 0,\frac{1}{4}\right) {\setminus } \{0\}. \end{aligned}$$

Lastly, it’s worth mentioning that the Catalan numbers admit the following integral representation,

$$\begin{aligned} C_n = \frac{1}{2\pi } \int _0^4 x^n \sqrt{\frac{4-x}{x}} \; \mathrm{d}x, \end{aligned}$$

(2.3)

see [16, Equation 10].

Remind that a measurable function f belongs to this weighted Lebesgue space $L^1_\omega (\mathbb R^+)$ if the following norm,

$$\begin{aligned} \left\| f\right\| _{L^1_\omega (\mathbb R^+)} := \int _0^\infty \left| f(t)\right| e^{\omega t} \; \mathrm{d}t, \end{aligned}$$

is finite where $\omega \in \mathbb R$. In fact, the space $L^1_{\omega }(\mathbb R^+)$ may be embedded with different convolution products.

2.1 The Catalan Kernel in the Algebra $(L^1_\omega (\mathbb R^+), *)$

The usual convolution product $*$ is defined by,

$$\begin{aligned} (f *g)(t) = \int _0^t f(u)g(t-u) \; \mathrm{d}u, \quad t>0, \end{aligned}$$

for $f,g \in L^1_\omega (\mathbb R^+)$. We write $(f*g)(0):=\lim _{t\rightarrow 0^+} (f*g)(t)$ whenever this limit exists.

The convolution product $*$ is commutative, associative, with bounded approximate identity and

$$\begin{aligned} \left\| f*g\right\| _{L^1_\omega (\mathbb R^+)}\le \left\| f\right\| _{L^1_\omega (\mathbb R^+)}\left\| g\right\| _{L^1_\omega (\mathbb R^+)}, \quad f, g\in L^1_\omega (\mathbb R^+). \end{aligned}$$

Then the space $(L^1_\omega (\mathbb R^+), *)$ is, in fact, a Banach algebra whose spectrum $\sigma (L^1_\omega (\mathbb R^+), *)=\{z\in \mathbb C\, | \, \Re z\ge -\omega \}$ and its Gelfand transform is the Laplace transform given by

$$\begin{aligned} {\mathcal {L}}(f)(z)=\int _0^\infty f(s) e^{-zs}\mathrm{d}s, \quad \Re z>-\omega , \end{aligned}$$

for $f \in L^1_\omega (\mathbb R^+)$. As it is known, the Laplace transform verifies ${\mathcal {L}}(f*g) = {\mathcal {L}}(f) {\mathcal {L}}(g)$ and

$$\begin{aligned} \sup _{\Re z> - \omega }\vert {\mathcal {L}}(f)(z)\vert \le \left\| f\right\| _{L^1_\omega (\mathbb R^+)}, \quad f\in {L^1_\omega (\mathbb R^+)}. \end{aligned}$$

Definition 2.1

The Catalan kernel is the positive function $c : (0,\infty ) \rightarrow (0,\infty )$ defined as,

$$\begin{aligned} c(t) := \frac{1}{2\pi } \int _{\frac{1}{4}}^\infty e^{-\lambda t} \frac{\sqrt{4\lambda -1}}{\lambda } \; \mathrm{d}\lambda , \quad t>0. \end{aligned}$$

(2.4)

In the following theorem, we recollect some basic results about the Catalan kernel c. We also present an alternate definition for c using the complementary error function ${{\,\mathrm{erfc}\,}}$ defined by

$$\begin{aligned} {{\,\mathrm{erfc}\,}}(z) := 1-{{\,\mathrm{erf}\,}}(z) = 1 - \frac{2}{\sqrt{\pi }} \int _{[0,z]} e^{-t^2} \; \mathrm{d}t, \quad z\in \mathbb C. \end{aligned}$$

Since the following asymptotic behavior holds

$$\begin{aligned} \frac{1}{2} {{\,\mathrm{erfc}\,}}\left( \frac{\sqrt{t}}{2}\right) \sim \frac{e^{-\frac{t}{4}}}{\sqrt{\pi } \sqrt{t}} \left( 1 - \frac{2}{t} + \frac{12}{t^2} - \cdots \right) ,\quad t\rightarrow \infty , \end{aligned}$$

([15, formula 40:6:3]), the ${{\,\mathrm{erfc}\,}}$ function belongs to $L^1_\omega (\mathbb R^+)$ for $\omega <\frac{1}{4}$, see its graphic in fig. 1.

Fig. 1

The Catalan kernel defined at Definition 2.1

Theorem 2.2

Let the Catalan kernel c be defined by (2.4). Then the following properties hold.

• (i) $\lim _{t\rightarrow 0^+}c(t)=\infty$, $\lim _{t\rightarrow \infty } c(t)=0$, $c'(t)<0$ for $t>0$ and c is a decreasing function.

• (ii) For $\omega \le \frac{1}{4}$, $c \in L^1_\omega (\mathbb R^+)$ and

  $$\begin{aligned} \left\| c\right\| _{L^1_\omega (\mathbb R^+)} = \frac{1-\sqrt{1-4\omega }}{2\omega }\le 2. \end{aligned}$$

• (iii) The Laplace transform of c is

  $$\begin{aligned} \mathcal {L}(c)(z) = \frac{\sqrt{1+4z}-1}{2z}= \frac{2}{\sqrt{1+4z}+1}, \quad \Re z \ge -\frac{1}{4}. \end{aligned}$$

• (iv) An alternative expression of c is given by

  $$\begin{aligned} c(t) = \frac{e^{-\frac{t}{4}}}{\sqrt{\pi }\sqrt{t}} - \frac{1}{2}{{\,\mathrm{erfc}\,}}\left( \frac{\sqrt{t}}{2}\right) , \quad t > 0. \end{aligned}$$

Proof

The item (i) is an exercise of elemental calculus. To prove (ii), as $\omega \le \frac{1}{4}$ then,

$$\begin{aligned} \begin{aligned}&\int _0^\infty \left| c(t)\right| e^{\omega t} \; \mathrm{d}t\\&\quad = \frac{1}{2\pi } \int _{\frac{1}{4}}^\infty \frac{\sqrt{4\lambda -1}}{\lambda } \int _0^\infty e^{-(\lambda -\omega )} \; \mathrm{d}t \; \mathrm{d}\lambda = \frac{2}{\pi } \int _{0}^1 \frac{\sqrt{1-u}}{\sqrt{u}} \frac{\mathrm{d}u}{(1-4 \omega u)}\\&\quad = \frac{2}{\pi } \left( \frac{1}{4\omega } \int _{0}^1 \frac{\mathrm{d}u}{\sqrt{u}\sqrt{1-u}} + \left( 1-\frac{1}{4\omega } \right) \int _{0}^1 \frac{\mathrm{d}u}{\sqrt{u}\sqrt{1-u}(1-4 \omega u)} \right) \\&\quad = \frac{2}{\pi } \left( \frac{1}{4\omega } \beta \left( \frac{1}{2},\frac{1}{2}\right) + \left( 1-\frac{1}{4\omega } \right) \frac{\pi }{\sqrt{1-4\omega }} \right) = \frac{1-\sqrt{1-4\omega }}{2\omega }, \end{aligned} \end{aligned}$$

where $\beta$ is the Euler beta function, and we have used [4, formula 3.121(2)]. As the Catalan kernel is a positive function, the Laplace transform of the function c is also checked in (ii) and

$$\begin{aligned} \mathcal {L}(c)(z) = \frac{\sqrt{1+4z}-1}{2z}, \quad \Re z\ge -\frac{1}{4}. \end{aligned}$$

Finally, to check (iv), we split the Laplace transform of c in the following way:

$$\begin{aligned} \mathcal {L}(c)(z) = \frac{2}{\sqrt{4z+1}} + \frac{1-\sqrt{4z+1}}{2z\sqrt{4z+1}} = \frac{1}{\sqrt{z+\frac{1}{4}}} + \frac{1}{4z\sqrt{z+\frac{1}{4}}} - \frac{1}{2z}. \end{aligned}$$

As

$$\begin{aligned} \begin{aligned} \mathcal {L}\left( \frac{e^{-\frac{t}{4}}}{\sqrt{\pi }\sqrt{t}}\right) (z)&= \frac{1}{\sqrt{z+\frac{1}{4}}}, \quad \mathcal {L}\left( -\frac{1}{2}\right) (z) = -\frac{1}{2z}, \\ \mathcal {L}\left( \frac{1}{2}{{\,\mathrm{erf}\,}}\left( \frac{\sqrt{t}}{2}\right) \right) (z)&= \mathcal {L}\left( \int _0^t \frac{e^{-\frac{u}{4}}}{4\sqrt{\pi }\sqrt{u}} \; \mathrm{d}u \right) (z) = \frac{1}{4z\sqrt{z+\frac{1}{4}}}, \end{aligned} \end{aligned}$$

and the Laplace transform is injective in $L^1(\mathbb R^+)$, we conclude the desired equality in $L^1 (\mathbb R^+)$ and then in $L^1_\omega (\mathbb R^+)$ for $\omega \le \frac{1}{4}$. $\square$

Remark 2.3

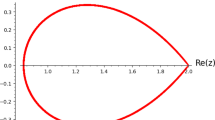
Since $\sigma _{(L^1_\omega (\mathbb R^+), *)}(c)={\mathcal {L}}(c)(\sigma (L^1_\omega (\mathbb R^+), *))\cup \{0\}$ ([8, Theorem 3.4.1(ii)]), we may identify the boundary of $\sigma _{(L^1_\omega (\mathbb R^+), *)}(c)$, i.e.,

$$\begin{aligned} \partial \left( \sigma _{(L^1_\omega (\mathbb R^+), *)}(c) \right) ={\mathcal {L}}(c)(-\omega +i \mathbb R)=\left\{ \frac{2}{\sqrt{1-4\omega +4ti}+1}\, \, :\, t\in \mathbb R\right\} , \end{aligned}$$

and we plot $\partial \left( \sigma _{(L^1_\omega (\mathbb R^+), *)}(c)\right)$ in Fig. 2 for several values of $\omega$.

Let the Catalan kernel

Fig. 2

The boundary of the spectrum of c in the algebra $(L^1_\omega (\mathbb R^+), *)$

Notice that the Laplace transform of the Catalan kernel c is in fact the generating function of the Catalan numbers evaluated at $-z$, Eq. 2.1, that is,

$$\begin{aligned} \mathcal {L}(c)(z) = C(-z) = \frac{\sqrt{1+4z}-1}{2z}. \end{aligned}$$

Using that the generating function C(z) satisfies the quadratic Catalan equation (2.2), we have that $\mathcal {L}(c)$ is a solution of the quadratic equation

$$\begin{aligned} -zY^2 -Y + 1 = 0, \end{aligned}$$

(2.5)

which motivates the study of the function $c *c$, with property $(c *c)' = -c$ that will be useful in the next section.

Theorem 2.4

The function $c *c$ satisfies the following properties:

• (i) It is a strictly positive function for $t>0$.

• (ii) The Laplace transform of $c*c$ is

  $$\begin{aligned} \mathcal {L}(c *c)(z) = \left( \frac{\sqrt{1+4z}-1}{2z}\right) ^2, \quad z \ge -\frac{1}{4}. \end{aligned}$$

• (iii) For $\omega \le \frac{1}{4}$, $c *c \in L^1_\omega (\mathbb R^+)$ and

  $$\begin{aligned} \left\| c *c\right\| _{L^1_\omega (\mathbb R^+)} = \left( \frac{1-\sqrt{1-4\omega }}{2\omega }\right) ^2. \end{aligned}$$

• (iv) It admits the following representation in terms of the Catalan kernel,

  $$\begin{aligned} (c *c)(t) = 1 - \int _0^t c(u) \; \mathrm{d}u, \quad t > 0. \end{aligned}$$

• (v) The function $c*c$ is bounded, decreasing, $(c *c)' = -c$ and $(c *c)(0)=1$.

• (vi) An alternative expression of $c *c$ is given by,

  $$\begin{aligned} (c *c)(t) = - \frac{ e^{-\frac{t}{4}} \sqrt{t} }{\sqrt{\pi }} + \left( 1+\frac{t}{2} \right) {{\,\mathrm{erfc}\,}}\left( \frac{\sqrt{t}}{2} \right) , \quad t > 0. \end{aligned}$$

Proof

The third first properties are direct consequences of Theorem 2.2. To show (iv), notice that

$$\begin{aligned} \mathcal {L}(c *c)(z)= & {} \frac{1-\sqrt{1+4z}}{2z^2} + \frac{1}{z}\\= & {} -\frac{\mathcal {L}(c)(z)}{z} + \mathcal {L}(1)(z)= \mathcal {L}\left( - \int _0^t c(u) \; \mathrm{d}u + 1\right) (z) \end{aligned}$$

for $\Re z \ge -\frac{1}{4}$. As the Laplace transform is injective, we conclude the equality. Note that item (v) is a consequence of item (iv)

To show item (vi), we apply Theorem 2.2 (4), and get

$$\begin{aligned} \begin{aligned} 1 - \int _0^t c(u) \; \mathrm{d}u&= 1 - \int _0^t \frac{e^{-\frac{u}{4}}}{\sqrt{\pi }\sqrt{u}} - \frac{1}{2}{{\,\mathrm{erfc}\,}}\left( \frac{\sqrt{u}}{2}\right) \; \mathrm{d}u \\&= - 2 {{\,\mathrm{erf}\,}}\left( \frac{\sqrt{t}}{2}\right) + 1 + \frac{1}{2} \int _0^t {{\,\mathrm{erfc}\,}}\left( \frac{\sqrt{u}}{2}\right) \; \mathrm{d}u \\&= - 2 {{\,\mathrm{erf}\,}}\left( \frac{\sqrt{t}}{2}\right) + 1 + \frac{1}{2} \mathcal {I}(t) \\ \end{aligned} \end{aligned}$$

where $\mathcal {I}(t):={\int _0^t {{\,\mathrm{erfc}\,}}\left( \frac{\sqrt{u}}{2}\right) \; \mathrm{d}u }$. As ${\int {{\,\mathrm{erf}\,}}(x) \; \mathrm{d}x}= x {{\,\mathrm{erf}\,}}(x) + \frac{e^{-x^2}}{\sqrt{\pi }} + C$ ([4, formula 5.41]), we integrate by parts twice to compute $\mathcal {I}(t)$, i.e.,

$$\begin{aligned} \begin{aligned} \mathcal {I}(t)&= \int _0^t {{\,\mathrm{erfc}\,}}\left( \frac{\sqrt{u}}{2}\right) \; \mathrm{d}u = t - 8 \int _0^{\frac{\sqrt{t}}{2}} x{{\,\mathrm{erf}\,}}(x) \; \mathrm{d}x\\&= t - t {{\,\mathrm{erf}\,}}\left( \frac{\sqrt{t}}{2} \right) + 8 \int _0^{\frac{\sqrt{t}}{2}} \frac{x^2 e^{-x^2}}{\sqrt{\pi }} \; \mathrm{d}x\\&= t {{\,\mathrm{erfc}\,}}\left( \frac{\sqrt{t}}{2} \right) - \frac{2 e^{-\frac{t}{4}} \sqrt{t} }{\sqrt{\pi }} + 2 \frac{2}{\sqrt{\pi }} \int _0^{\frac{\sqrt{t}}{2}} e^{-x^2} \; \mathrm{d}x. \end{aligned} \end{aligned}$$

By item (4), we conclude the following equality

$$\begin{aligned} (c*c)(t) = - \frac{e^{-\frac{t}{4}} \sqrt{t}}{\sqrt{\pi }} + \left( 1+\frac{t}{2} \right) {{\,\mathrm{erfc}\,}}\left( \frac{\sqrt{t}}{2} \right) , \end{aligned}$$

for $t>0$. $\square$

Remark 2.5

Note that the function $c*c$ is a positive, decreasing function and $\lim _{t\rightarrow 0^+}(c *c)(t)=1$. We plot $c*c$ in Fig. 3.

Fig. 3

The function $c *c$

2.2 The Catalan Kernel in the Algebra $(L^1_\omega (\mathbb R^+), *_c)$

For $\omega \ge 0$, a second convolution product is introduced in the Lebesgue space $L^1_\omega (\mathbb R^+)$, the cosine convolution product $*_c$. Given $f,g\in L^1_\omega (\mathbb R^+)$, we define $f*_c g$ by

$$\begin{aligned} (f*_c g)(t):=\frac{1}{2}\left( (f*g) (t)+(f\circ g)(t)+(g\circ f)(t)\right) , \quad t>0, \end{aligned}$$

where ${f\circ g(t):=\int _t^\infty f(s-t)g(s)\mathrm{d}s}$ for $t>0$. This product is also commutative, associative, with bounded approximate identity and

$$\begin{aligned} \left\| f*_c g\right\| _{L^1_\omega (\mathbb R^+)}\le \left\| f\right\| _{L^1_\omega (\mathbb R^+)}\left\| g\right\| _{L^1_\omega (\mathbb R^+)}, \quad f, g\in L^1_\omega (\mathbb R^+), \end{aligned}$$

see for example [13, Theorem 1.1]. Then the space $(L^1_\omega (\mathbb R^+), *_c)$ is a Banach algebra whose Gelfand transform is the cosine transform given by

$$\begin{aligned} {\mathcal {C}}(f)(z)=\int _0^\infty f(s) \cosh (zs)\mathrm{d}s, \quad f \in L^1_\omega (\mathbb R^+), \quad z\in \overline{\Pi ^+_\omega }, \end{aligned}$$

where $\overline{\Pi ^+_\omega }:\{z\in \mathbb C:\, -\omega \le \Re z\le \omega ;\, \Im z\ge 0\}=\sigma _{(L^1_\omega (\mathbb R^+), *_c)}$. The cosine transform is injective and verifies ${\mathcal {C}}(f*_c g) = {\mathcal {C}}(f) {\mathcal {C}}(g)$ and

$$\begin{aligned} \sup _{z\in \overline{\Pi ^+_\omega } }\vert {\mathcal {C}}(f)(z)\vert \le \left\| f\right\| _{L^1_\omega (\mathbb R^+)}, \quad f\in {L^1_\omega (\mathbb R^+)}, \end{aligned}$$

see [11, Theorem 1.5].

In the next lemma we present two technical results about $f^{*_c2}$ and $f^{*_c3}$, where $f^{*_c2}:= f*_c f$ and $f^{*_c3}:=f^{*_c2}*_c f$.

Lemma 2.6

Let $f\in L^1_\omega (\mathbb R^+)$ with $\omega \ge 0$. Then

• (i) ${f^{*_c2}=\frac{1}{2}(f*f) + (f\circ f)}$.

• (ii) $f^{*_c3}=\frac{1}{4}(f*f*f) + \frac{3}{4}(f*f)\circ f+\frac{3}{4}f\circ (f*f)= \frac{3}{2}(f*f)*_c f- \frac{1}{2}(f*f*f)$.

Proof

The first item is a direct consequence of the definition of cosine convolution product. To show (ii), note that

$$\begin{aligned} f^{*_c3}= & {} \frac{1}{2}(f*f)*_c f + (f\circ f)*_c f= \frac{1}{4}(f*f*f)+ \frac{1}{4}(f*f)\circ f\\&+\frac{1}{4}(f\circ (f*f))+\frac{1}{2}((f\circ f)*f)+ \frac{1}{2}(f\circ f)\circ f+ \frac{1}{2}(f\circ (f\circ f)). \end{aligned}$$

As $f\circ (f\circ f)=(f*f)\circ f$ and $(f\circ f)\circ f= (f*f)\circ f-f\circ (f*f)$, see for example [12, Theorem 3.2 and 4.1], we conclude that

$$\begin{aligned} f^{*_c3}=\frac{1}{4}(f*f*f) + \frac{3}{4}(f*f)\circ f+\frac{3}{4}f\circ (f*f), \end{aligned}$$

for $f\in L^1_\omega (\mathbb R^+)$. $\square$

In the following lemma, we present some interesting algebraic properties about the Catalan kernel and the cosine convolution product $*_c$.

Lemma 2.7

Let c be the Catalan kernel given in Definition 2.1 and $0\le \omega \le \frac{1}{4}$. Then

• (i) ${(c\circ c)(t)=\frac{1}{\pi }\int _\frac{1}{4}^{\infty } \frac{\sqrt{4\lambda -1}}{\lambda (\sqrt{4\lambda +1}+1)}e^{-\lambda t}\mathrm{d}\lambda }$ for $t>0$ and $(c\circ c)'\not \in L^1_\omega (\mathbb R^+)$.

• (ii) ${(c*_c c)'(t)=-\frac{1}{4\pi }\int _\frac{1}{4}^{\infty } \frac{\sqrt{16\lambda ^2-1}}{\lambda } e^{-\lambda t}\mathrm{d}\lambda }$ for $t>0$ and $(c*_c c)'\not \in L^1_\omega (\mathbb R^+)$.

• (iii) ${ (c*_c c)(t)=\int _0^\infty \frac{1}{ \sqrt{4 \pi s}} e^{-\frac{t^2}{16s}}c(s)\mathrm{d}s,}$ for $t>0$.

• (iv) ${(c^{*_c 3})'= -\frac{1}{2}c -\frac{1}{4}{c*c}}$ and $(c^{*_c 3})'\in L^1_\omega (\mathbb R^+)$.

• (v) ${(c^{*_c 4})'= -\frac{1}{4}(c*c) -\frac{1}{8}{c*c*c}}- \frac{1}{2}(c^{*_c 3})\circ c+\frac{1}{2}c\circ (c^{*_c 3})$ and $(c^{*_c 4})'\in L^1_\omega (\mathbb R^+)$.

• (vi) ${(c^{*_c 4})'(0)= -\frac{1}{4}}.$

Proof

(i) Take $t>0$, and

$$\begin{aligned} (c\circ c)(t)=\frac{1}{4\pi ^2}\int _\frac{1}{4}^\infty \frac{\sqrt{4\lambda -1}}{\lambda } e ^{-\lambda t}\left( \int _\frac{1}{4}^\infty \frac{\sqrt{4\mu -1}}{\mu }\frac{1}{\lambda +\mu } \mathrm{d}\mu \right) \mathrm{d}\lambda . \end{aligned}$$

As an elemental exercise of calculus, we have that

$$\begin{aligned} \int _\frac{1}{4}^\infty \frac{\sqrt{4\mu -1}}{\mu }\frac{1}{\lambda +\mu }\mathrm{d}\mu =\frac{\pi }{\lambda }\left( \sqrt{4\lambda +1}-1\right) =\frac{4\pi }{\sqrt{4\lambda +1}+1}, \quad \lambda >0, \end{aligned}$$

and we conclude the result. As $(c*_c c)'(t)= \frac{1}{2}(c*c)'+ (c\circ c)'$, we apply (i) and Theorem 2.4(v) to have

$$\begin{aligned} (c*_c c)'(t)= & {} -\frac{1}{2}c(t)- \frac{1}{4\pi }\int _\frac{1}{4}^\infty \frac{\sqrt{4\lambda -1}}{\lambda }\left( \sqrt{4\lambda +1}-1\right) e ^{-\lambda t}\mathrm{d}\lambda \\= & {} - \frac{1}{4\pi }\int _\frac{1}{4}^\infty \frac{\sqrt{16\lambda ^2-1}}{\lambda }e^{-\lambda t}\mathrm{d}\lambda , \end{aligned}$$

and we finish the proof of item (ii).

Now we define ${F(t):=\int _0^\infty \frac{1}{ \sqrt{4 \pi s}} e^{-\frac{t^2}{16s}}c(s)\mathrm{d}s,}$ for $t>0$. Then,

$$\begin{aligned} F'(t)= & {} -\int _0^\infty \frac{1}{\sqrt{ \pi s}} \frac{t}{16s} e^{-\frac{t^2}{16s}} c(s)\mathrm{d}s\\= & {} -\frac{t}{32 \pi ^{\frac{3}{2}}}\int _\frac{1}{4}^\infty \frac{\sqrt{4\lambda -1}}{\lambda }\int _0^\infty \frac{1}{s^\frac{3}{2}} e^{-\frac{t^2}{16s}}e^{-\lambda s}\mathrm{d}s\mathrm{d}\lambda \\= & {} -\frac{t}{32 \pi ^{\frac{3}{2}}}\int _\frac{1}{4}^\infty \frac{\sqrt{4\lambda -1}}{\lambda }\frac{4\sqrt{\pi }}{t}e^{-\frac{t\sqrt{\lambda }}{2}}\mathrm{d}\lambda \\= & {} -\frac{1}{4 \pi }\int _\frac{1}{4}^\infty \frac{\sqrt{16\mu ^2-1}}{\mu }e^{-t\mu }\mathrm{d}\mu = (c*_c c)'(t), \end{aligned}$$

where we have applied [4, Formula 3.471, 15] and we have done the change of variable $\mu =\frac{\lambda }{2}$. Since $\lim _{t\rightarrow \infty } F(t)= \lim _{t\rightarrow \infty } (c*_c c)(t)=0$, we conclude $F= c*_c c$.

To show item (iv), we apply Lemma 2.6 (ii)

$$\begin{aligned} \begin{aligned} (c^{*_c 3})'(t)&= \frac{1}{4}(c*c*c)'(t) + \frac{3}{4}((c*c)\circ c)'(t)+\frac{3}{4}(c\circ (c*c))'(t)\\&= \frac{1}{4}(c*c)(0)c(t)+\frac{1}{4}((c*c)'*c)(t) \\&\quad -\frac{3}{4}(c*c)(0)c(t)-\frac{3}{4}((c*c)'\circ c)(t)+\frac{3}{4}(c\circ (c*c)')(t) \\&= -\frac{1}{2}c(t)-\frac{1}{4}(c*c)(t), \end{aligned} \end{aligned}$$

and we use that $c*c(0)=1$ and $(c*c)'=-c$, see Theorem 2.4 (iv).

To show (v), note that $(c^{*_c 4})'= (c^{*_c 3}*_c c)'$ and

$$\begin{aligned} \begin{aligned} (c^{*_c 3}*_c c)'&= \frac{1}{2}\left( (c^{*_c 3})'*c-(c^{*_c 3})'\circ c+ c\circ (c^{*_c 3})' \right) \\&= -\frac{1}{4}(c*c)-\frac{1}{8}(c*c*c)-\frac{1}{2}(c^{*_c 3})'\circ c+\frac{1}{2} (c\circ (c^{*_c 3})' ), \end{aligned} \end{aligned}$$

where we have applied item (iv). Finally, the equality ${(c^{*_c 4})'(0)= -\frac{1}{4}}$ follows from (v) and $(c*c)(0)=1$. $\square$

Finally, we present the main result of this section.

Theorem 2.8

Let c be the Catalan kernel given in Definition 2.1 and $0\le \omega \le \frac{1}{4}$.

• (i) The cosine transform of c, ${\mathcal {C}}(c)$, is given by

  $$\begin{aligned} {\mathcal {C}}(c)(z)=\frac{2}{\sqrt{1+4z}+\sqrt{1-4z}}, \quad -\omega<\Re z<\omega . \end{aligned}$$

• (ii) $({\mathcal {C}}(c))^2(z)= C(4z)$ for $-\omega<\Re z<\omega .$

• (iii) The function ${\mathcal {C}}(c)(z)$ is a solution of the biquadratic equation $4z^2 Y^4-Y^2+ I=0$.

• (iv) The Catalan kernel satisfies the algebraic-differential equation

  $$\begin{aligned} 4 (c*_c c*_c c *_c c)''=c*_c c. \end{aligned}$$

Proof

• (i) Note that

  $$\begin{aligned} {\mathcal {C}}(c)(z)= & {} \frac{1}{2}\left( {\mathcal {L}}(c)(z)+{\mathcal {L}}(c)(-z))\right) = \frac{1}{2}\left( \frac{\sqrt{1+4z}-1}{2z}-\frac{\sqrt{1-4z}-1}{2z}\right) \\= & {} \frac{2}{\sqrt{1+4z}+\sqrt{1-4z}},\\\end{aligned}$$

  for $-\omega<\Re z<\omega .$

• (ii) Take $-\omega<\Re z<\omega$ and then

  $$\begin{aligned} ({\mathcal {C}}(c))^2(z)= \left( \frac{2}{\sqrt{1+4z}+\sqrt{1-4z}}\right) ^2=\frac{2}{1+\sqrt{1-(4z)^2}}=C(4z). \end{aligned}$$

• (iii) As ${\mathcal {L}}(c)(z)$ satisfies the Eq. (2.5) and similarly ${\mathcal {L}}(c)(-z)$, we apply [14, Theorem 2.1] to conclude that ${\mathcal {C}}(c)$ is a solution of $4z^2 Y^4-Y^2+ I=0$.

• (iv) As ${\mathcal {C}}(f'')(z)=-f'(0)+z^2{\mathcal {C}}(f)(z)$, for $f \in L^1_\omega (\mathbb R+)$ with $f''\in L^1_\omega (\mathbb R+)$, we have, for $-\omega<\Re z<\omega$, that

  $$\begin{aligned} {\mathcal {C}}(4(c^{*_c 4})'')(z)= & {} -4(c^{*_c 4})'(0)+4z^2{\mathcal {C}}((c^{*_c 4}))(z)=1+4z^2({\mathcal {C}}(c)(z))^4\\= & {} {\mathcal {C}}(c)(z))^2={\mathcal {C}}(c*_c c)(z), \end{aligned}$$

  where we have applied Lemma 2.7 (v) and the map ${\mathcal {C}}$ is an algebra homomorphism in $(L^1_\omega (\mathbb R^+), *_c)$. Since ${\mathcal {C}}$ is injective, we conclude that $4 (c*_c c*_c c *_c c)''=c*_c c.$ $\square$

Remark 2.9

Since $\sigma _{(L^1_\omega (\mathbb R^+), *_c)}(c)={\mathcal {C}}(c)(\sigma (L^1_\omega (\mathbb R^+), *_c))\cup \{0\}$ ([8, Theorem 3.4.1(ii)]), we may identify the boundary of $\sigma _{(L^1_\omega (\mathbb R^+), *_c)}(c)$, i.e.,

$$\begin{aligned} \partial \left( \sigma _{(L^1_\omega (\mathbb R^+), *_c)}(c)\right)= & {} {\mathcal {C}}(c)(-\omega +i \mathbb R)\\ {}= & {} \left\{ \frac{2}{\sqrt{1-4\omega +4ti}+\sqrt{1+4\omega -4ti}}\, \, :\, t\in \mathbb R\right\} , \end{aligned}$$

and plot $\partial \left( \sigma _{(L^1_\omega (\mathbb R^+), *_c)}(c)\right)$ in Fig. 4 for several values of $\omega$.

Fig. 4

The boundary of spectrum of c in the algebra $(L^1_\omega (\mathbb R^+), *_c)$

3 The Catalan Operator for $C_0$-Semigroups

In this section we solve the general quadratic Eq. (1.1) in the case that A generates a $C_0$-semigroup with growth bound less than $\frac{1}{4}$. To accomplish this we apply the Hille–Phillips functional calculus to the Catalan kernel c.

A $C_0$-semigroup $(T(t))_{t \ge 0}$ is always exponentially bounded, i.e. there exists constants $M \ge 1$ and $\omega \in \mathbb R$ such that, $\left\| T(t)\right\| \le Me^{\omega t}$ with $t\ge 0$. The infimum of these values $\omega$ is called the growth bound of $(T(t))_{t\ge 0}$, see for example [2, Definition I.5.6]. For $\omega =0$, it is said that $(T(t))_{t\ge 0}$ is bounded.

As usual, the complex set where the operator $\lambda I - A$ is invertible in $\mathcal {B}(X)$ is called the resolvent set of A, and it’s denoted by $\rho (A)$. The complement $\mathbb C{\setminus } \rho (A)$ it’s the spectrum of A, and it’s denoted by $\sigma (A)$. The set $\rho (A)$ is open in $\mathbb C$, thus $\sigma (A)$ is closed. If $\lambda \in \rho (A)$ then the operator $(\lambda -A)^{-1}$ is the resolvent of A at $\lambda$, and denoted by $R(\lambda ,A)$. Moreover, if $\lambda \in \mathbb C$ with $\Re \lambda > \omega$, then $\lambda \in \rho (A)$ and,

$$\begin{aligned} R(\lambda ,A)x = \int _0^\infty e^{-\lambda t} T(t)x \; \mathrm{d}t,\quad x \in X, \end{aligned}$$

(3.1)

where this integral has to be understood in the Bochner sense.

Now we consider the Hille–Phillips functional calculus $\Theta : (L^1_\omega (\mathbb R^+),*) \!\rightarrow \mathcal {B}(X)$,

$$\begin{aligned} \Theta (f) x = \int _0^\infty f(t)T(t)x \; \mathrm{d}t, \quad f \in L^1_\omega (\mathbb R^+), \, x \in X. \end{aligned}$$

The application $\Theta$ is an algebra homomorphism, i.e., $\Theta (f*g)=\Theta (f)\Theta ( g)$, $\Vert \Theta (f)\Vert \le C \Vert f\Vert _{L^1_\omega (\mathbb R^+)}$, and $\Theta (e_\lambda )=R(\lambda ,A)$ where $e_\lambda (t):=e^{-\lambda t}$ for $\Re \lambda >\omega$, see for example [6, Section 3.3].

As $\sigma (A)\subset \{z\in \mathbb C\, \, : \Re z<\omega \}$, a holomorphic function calculus (sometimes called Dunford–Schwartz calculus) is defined for holomorphic functions in a neighborhood of $\sigma (A)$. This functional calculus is defined by the integral Cauchy-formula,

$$\begin{aligned} f(A)x:=\int _{\Gamma }f(z)(z-A)^{-1}x\mathrm{d}z, \quad x\in X. \end{aligned}$$

As usual, the path $\Gamma$ rounds the spectrum set $\sigma (A)$. Both homomorphism, $\Theta (f)$ and f(A) coincides under common conditions $\Theta (f)={\mathcal {L}}(f)(-A)$, for “enough good functions” see for example [6].

In this section, we consider a $C_0$-semigroup $(T(t))_{t \ge 0}$ with growth bound less than $\frac{1}{4}$. We start to give a formal definition for the Catalan operator for $C_0$-semigroups.

Definition 3.1

Let (A, D(A)) be the generator of the $C_0$-semigroup $(T(t))_{t \ge 0}$ such that $\left\| T(t)\right\| \le Me^{\omega t}$ with $M \ge 1$ and $\omega \le \frac{1}{4}$ for all $t > 0$. Then we define the Catalan operator $C(A)\in {\mathcal {B}}(X)$ as,

$$\begin{aligned} C(A) x :=\Theta (c)x= \int _{0}^\infty c(t)T(t) x \; \mathrm{d}t, \quad x \in X, \end{aligned}$$

where c is the Catalan kernel seen in Definition 2.1.

Recall, that if $(T(t))_{t\le 0}$ is a uniformly bounded $C_0$-semigroup with generator (A, D(A)) we have the following definition for the fractional power of the generator,

$$\begin{aligned} (-A)^\alpha x := \frac{1}{\Gamma (-\alpha )} \int _0^\infty \frac{(T(t)-I)x}{t^{1+\alpha }} \; \mathrm{d}t, \quad x \in D(A), \end{aligned}$$

see [20, section IX.11]. In the next theorem, we prove the main properties of the Catalan operator C(A) defined by $C_0$-semigroups.

Theorem 3.2

Let A be the generator of the $C_0$-semigroup $(T(t))_{t \ge 0}$ as in Definition 3.1.

• (i) The Cataln operator C(A) is well-defined and

  $$\begin{aligned} \Vert C(A)\Vert \le M\frac{1-\sqrt{1-4\omega }}{2\omega }. \end{aligned}$$

• (ii) The Catalan operator C(A) satisfies the quadratic Catalan Eq. (1.1), i.e.,

  $$\begin{aligned} A C(A)^2 - C(A) + I = 0. \end{aligned}$$

• (iii) The Catalan operator C(A) has the following integral representation

  $$\begin{aligned} C(A)x = \frac{1}{2\pi } \int _{\frac{1}{4}}^\infty \frac{\sqrt{4\lambda -1}}{\lambda } R(\lambda ,A)x \; \mathrm{d}\lambda , \quad x\in X. \end{aligned}$$

• (iv) The following representation holds,

  $$\begin{aligned} AC(A)x = \frac{1}{2}x - \sqrt{\frac{1}{4} - A}(x), \quad x\in D(A). \end{aligned}$$

• (v) The spectral mapping theorem holds for C(A), i.e.,

  $$\begin{aligned} \sigma (C(A)) = {\left\{ \begin{array}{ll} C(\sigma (A)), &{} A \in {\mathcal {B}}(X) \\ C(\sigma (A)) \cup \{0\}, &{} A \notin {\mathcal {B}}(X). \end{array}\right. } \end{aligned}$$

Proof

The proof of item (i) is a consequence of Theorem 2.2 (i). To show (ii), note that $A\Theta (f)=-f(0)-\Theta (f')$ for $f, f'\in L_\omega ^1(\mathbb R^+)$ and then,

$$\begin{aligned} A C(A)^2=A\Theta ( c*c)=-(c*c)(0)-\Theta ((c*c)')=-1+\Theta (c)=-1+C(A), \end{aligned}$$

where we have applied Theorem 2.4 (v).

To show the item (iii), we have that

$$\begin{aligned} \frac{1}{2\pi } \int _{\frac{1}{4}}^\infty \frac{\sqrt{4\lambda -1}}{\lambda } R(\lambda ,A)x \; \mathrm{d}\lambda= & {} \frac{1}{2\pi } \int _{\frac{1}{4}}^\infty \frac{\sqrt{4\lambda -1}}{\lambda } \int _0^\infty e^{-\lambda t} T(t)x\,\mathrm{d}t\,\mathrm{d}\lambda \\ {}= & {} C(A)x, \end{aligned}$$

for $x\in X$.

(iv) Now take $x\in D(A)$. Then we have that

$$\begin{aligned} AC(A)x= & {} \frac{1}{2\pi } \int _{\frac{1}{4}}^\infty \frac{\sqrt{4\lambda -1}}{\lambda } A R(\lambda ,A) x\; \mathrm{d}\lambda \\= & {} \frac{1}{2\pi } \int _{\frac{1}{4}}^\infty \frac{\sqrt{4\lambda -1}}{\lambda } (\lambda R(\lambda ,A)-I)x \; \mathrm{d}\lambda \\= & {} \frac{1}{2\pi } \int _{\frac{1}{4}}^\infty \sqrt{4\lambda -1} \left( \int _0^\infty e^{-\lambda t} (T(t)-I)x \; \mathrm{d}t \right) \mathrm{d}\lambda \\= & {} \frac{1}{2\sqrt{\pi }} \int _{0}^\infty \frac{(T(t)-I)x}{t^{\frac{3}{2}}} e^{-\frac{t}{4}}\; \mathrm{d}t. \end{aligned}$$

Therefore,

$$\begin{aligned} \begin{aligned} AC(A)x&= \frac{1}{2\sqrt{\pi }} \int _{0}^\infty \frac{(T(t)-I)x}{t^{\frac{3}{2}}} e^{-\frac{t}{4}}\; \mathrm{d}t\\&= \frac{1}{2\sqrt{\pi }} \left( \int _{0}^\infty \frac{(e^{-\frac{t}{4}}T(t)-I)x}{t^{\frac{3}{2}}} \; \mathrm{d}t - \int _{0}^\infty \frac{(e^{-\frac{1}{4}t}-I)x}{t^{\frac{3}{2}}} \; \mathrm{d}t \right) \\ {}&= \frac{1}{2}x - \sqrt{\frac{1}{4} - A}(x) \end{aligned} \end{aligned}$$

Finally, to show item (v), we write $A_\omega = A-\omega$, and the function $g_\omega$ defined by

$$\begin{aligned} g_\omega (z)= \frac{\sqrt{1+4(z-\omega )}-1}{2(z-\omega )} =\mathcal {L}(e^{\omega t}c(t))(z) , \quad \Re z > \omega -\frac{1}{4}. \end{aligned}$$

Note that $C(A)=g_{\omega }(-A_\omega )$ and the function

$$\begin{aligned} g_\omega \in \mathcal {H}^{\infty }(\mathbb C^+) :=\{f: \mathbb C^+ \rightarrow \mathbb C\, | \, f \text { is holomorphic and bounded}\}. \end{aligned}$$

Observe that we can extend holomorphically the function $g_{\omega }$ to the set $\mathbb C{\setminus } (-\infty ,\omega -\frac{1}{4})$. In addition, note that $g_{\omega }(0)= \frac{1-\sqrt{1-4\omega }}{2\omega }$ which is well-defined for $\omega \le \frac{1}{4}$ and then $g_{\omega }$ has finite polynomial limit at 0. Also, $\lim _{\left| z\right| \rightarrow \infty }$ $g_{\omega }(z) = 0$ with $z \in \mathbb C{\setminus } (-\infty ,\omega -\frac{1}{4})$ so $g_{\omega }$ has polynomial limit at $\infty$. Using [6, Lemma 2.2.3] we have that the function $g_{\omega } \in \mathcal {E}_{\varphi _0}$, the extended Dunford–Riesz class, for $\varphi _0 \in [\frac{\pi }{2},\pi )$. Note that $-A_{\omega }$ is a sectorial operator of angle $\frac{\pi }{2}$ because $(e^{-\omega t}T(t))_{t\ge 0}$ is a uniformly bounded $C_0$-semigroup. Therefore, we can apply the spectral mapping theorem [6, Theorem 2.7.8] to obtain,

$$\begin{aligned} \sigma (C(A)) \!=\! \sigma ( (g_{\omega }(-A_{\omega }) ) \!=\! {\left\{ \begin{array}{ll} g_{\omega }(\sigma (-A_\omega ))\!=\! C(\sigma (A)), &{} A \!\in \! {\mathcal {B}}(X), \\ g_{\omega }(\sigma (-A_\omega )) \!\cup \! \{0\}\!=\! C(\sigma (A)) \!\cup \! \{0\}, &{} A \!\notin \! {\mathcal {B}}(X), \end{array}\right. } \end{aligned}$$

and we conclude the proof. $\square$

In the case that $A \in \mathcal {B}(X)$ with 4A of power-bounded, we check that the definition of C(A) given in Definition 3.1 coincides with the power series presented in [14, Section 5].

Corollary 3.3

Let $A \!\in \! \mathcal {B}(X)$ with 4A of power-bounded, i.e., $\sup _{n\ge 0}\Vert 4^nA^n\Vert \!<\infty$. Then

$$\begin{aligned} C(A)=\sum _{n\ge 0} C_nA^n. \end{aligned}$$

Proof

Note that A generates a $C_0$-semigroup, $T(t)=:e^{tA}$ and

$$\begin{aligned} \left\| T(t)\right\| = \left\| \sum _{n\ge 0}\frac{t^n A^n}{n!}\right\| \le \sup _{n\ge 0}\left\| 4^nA^n\right\| \sum _{n\ge 0}\frac{t^n }{4^n n!}=\sup _{n\ge 0}\left\| 4^nA^n\right\| e^{\frac{t}{4}}, \end{aligned}$$

for $t\ge 0$. Then

$$\begin{aligned} C(A)x\!=\!\int _{0}^\infty c(t)e^{tA} (x) \; \mathrm{d}t\!=\! \sum _{n\ge 0} A^n(x)\int _0^\infty \frac{t^n}{n!}c(t)\mathrm{d}t\!=\! \sum _{n\ge 0} C_nA^n(x), \quad x \!\in \! X, \end{aligned}$$

where we have applied formula (1.4). $\square$

Remark 3.4

An alternative approach to Catalan operator C(A) may be followed using fractional powers of sectorial operators. As it is commented in the proof of Theorem 3.2 (v), $-( A-\omega )$ is a sectorial operator of angle $\pi /2$. Then $B:=I-4A$ is also a sectorial operator of angle (at most) $\pi /2$, the fractional power $\sqrt{B}$ is sectorial of angle $\pi /4$, and its square is B. Using standard properties of fractional powers (see, for example [10]) one may establish that

$$\begin{aligned} C(A) = 2 (I+\sqrt{B})^{-1}. \end{aligned}$$

However this approach hides the rich algebraic properties of function c which are commented in Sect. 2.

Even in the case that $\hbox {dim}(X)=2$, the quadratic equation (1.1) may have one, two, infinite or no solutions, see [14, Section 6.1]. In the case that $(AC(A))^{-1}\in {\mathcal {B}}(X)$, then this operator provides a second solution of (1.1). Note that

$$\begin{aligned} (AC(A))^{-1}= \left( \frac{1}{2} + \sqrt{\frac{1}{4} - A}\right) A^{-1} \end{aligned}$$

which might give a way to apply the natural functional calculus treated in [6].

In the case that A and $-A$ generates $C_0$-semigroups, $(T_+(t))_{t\ge 0}$ and $(T_{-}(t))_{t\ge 0}$ it is said that A generates a $C_0$-group $(T(t))_{t\in \mathbb R}$ given by

$$\begin{aligned} T(t)= \left\{ \begin{aligned}&T_+(t) , \quad \text {for } t \ge 0, \\&T_-(t) , \quad \text {for } t \le 0. \\ \end{aligned} \right. \end{aligned}$$

Note that an algebra homomorphism $\Phi$, which extends the map $\Theta$, is defined by

$$\begin{aligned} \Phi (F)x= \int _{-\infty }^\infty F(t)T(t) x \; \mathrm{d}t, \quad x \in X,\quad F\in L^1_\omega (\mathbb R), \end{aligned}$$

and $\Phi (F\star G)=\Phi (F)\Phi (G)$, where $F\star G(t)=\int _{-\infty }^\infty F(t-s)G(s)\mathrm{d}s$ for $F,G\in L^1_\omega (\mathbb R)$.

When A generates a bounded $C_0$-group, $(T(t))_{t\in \mathbb R}$, then $A^2$ generates a bounded $C_0$-semigroup $(T_{A^2}(t))_{t>0}$ given by

$$\begin{aligned} T_{A^2}(t)x:=\frac{1}{\sqrt{4 \pi t}}\int _{-\infty }^\infty e^{- \frac{s^2}{4 t}}T(s)x \; \mathrm{d}s, \quad t\ge 0, \end{aligned}$$

(3.2)

see [1, Corollary 3.7.15].

Theorem 3.5

Let A be the generator of a bounded $C_0$-group, $(T(t))_{t\in \mathbb R}$. Then

$$\begin{aligned} C(4A^2)=\left( \frac{C(A)+C(-A)}{2}\right) ^2. \end{aligned}$$

Proof

As the operator $A^2$ generates a $C_0$-semigroup, $(T_{A^2}(t))_{t\ge 0}$ given by (3.2), then $4A^2$ also generates a bounded $C_0$-semigroup, $(T_{4A^2}(t))_{t\ge 0}$ and $T_{4A^2}(t)=T_{A^2}(4t)$ for $t\ge 0$. By Definition 3.1, we have

$$\begin{aligned} \begin{aligned}&C(4A^2)x \\&\quad = \int _0^\infty c(t)T_{A^2}(4t)x \; \mathrm{d}t= \int _0^\infty c(t)\frac{1}{\sqrt{16\pi t}}\int _{-\infty }^\infty e^{-\frac{s^2}{16t}}T(s)x \; \mathrm{d}s \; \mathrm{d}t \\&\quad = \frac{1}{2}\int _{-\infty }^\infty T(s)x\int _0^\infty \frac{1}{\sqrt{4\pi t}}e^{-\frac{s^2}{16t}}c(t) \;\mathrm{d}t \;\mathrm{d}s = \frac{1}{2}\int _{-\infty }^\infty ( c*_c c)( \vert s\vert ) T(s)x \; \mathrm{d}s \\&\quad = \frac{1}{4}\int _{-\infty }^\infty (\tilde{c}\star \tilde{c})( s) T(s)x \; \mathrm{d}s= \frac{1}{4}(\Phi (\tilde{c}))^2 x = \left( \frac{C(A)+C(-A)}{2}\right) ^2 x, \end{aligned} \end{aligned}$$

where we have applied Lemma 2.7 (iii) and we have defined $\tilde{c}(s):=c(\vert s\vert )$ for $s\in \mathbb R$. $\square$

4 The Catalan Operator for Cosine Functions

In this section we consider the general quartic Eq. (1.3) in the case that A generates a cosine operator with growth bound less than $\frac{1}{4}$. We follow similar (and more complicated) ideas than in the case of $C_0$-semigroups.

A cosine function $({{\,\mathrm{Cos}\,}}(t))_{t \ge 0}$ is always exponentially bounded, i.e. there exists constants $M\ge 1$ and $\omega \ge 0$ such that, $\left\| {{\,\mathrm{Cos}\,}}(t)\right\| \le Me^{\omega t}$ with $t\ge 0$. Moreover, if $\lambda \in \mathbb C$ with $\Re \lambda > \omega$, then $\lambda ^2 \in \rho (A)$ and,

$$\begin{aligned} \lambda R(\lambda ^2,A)x = \int _0^\infty e^{-\lambda t} {{\,\mathrm{Cos}\,}}(t)x \; \mathrm{d}t,\quad x \in X, \end{aligned}$$

(4.1)

where this integral has to be understood in the Bochner sense, see [1, Section 3.14]. The spectrum $\sigma (A)$ of A is contained in the parabola $\{\xi +i\eta \,:\eta \in \mathbb R, \xi \le \omega ^2-\eta ^2/4 \omega ^2\}$, see for example [1, Proposition 3.14.18].

Now we consider the vector-valued cosine transform $\Theta : (L^1_\omega (\mathbb R^+),*_c) \rightarrow \mathcal {B}(X)$,

$$\begin{aligned} \Psi (f) x = \int _0^\infty f(t){{\,\mathrm{Cos}\,}}(t)x \; \mathrm{d}t, \quad f \in L^1_\omega (\mathbb R^+), \, x \in X. \end{aligned}$$

The application $\Psi$ is an algebra homomorphism, i.e., $\Psi (f*_cg)=\Psi (f)\Psi ( g)$, $\Vert \Psi (f)\Vert \le C \Vert f\Vert _{L^1_\omega (\mathbb R^+)}$ for $f\in L^1_\omega (\mathbb R^+)$, and $\Psi (e_\lambda )=\lambda R(\lambda ^2,A)$ for $\Re \lambda >\omega$, see [13].

As $\sigma (A)$ is contained in the parabola $\{\xi +i\eta \,:\eta \in \mathbb R, \xi \le \omega ^2-\eta ^2/4 \omega ^2\}$, a (holomorphic) Dunford-Schwartz calculus is defined for holomorphic functions in a neighborhood of $\sigma (A)$. This functional calculus is also defined by the integral Cauchy-formula,

$$\begin{aligned} g(A)x:=\int _{\Gamma }g(z)(z-A)^{-1}x \; \mathrm{d}z, \quad x\in X, \end{aligned}$$

see [5, Section 3.2]. The path $\Gamma$ rounds the spectrum set $\sigma (A)$. Both homomorphism, $\Psi (f)$ and g(A) coincides when $g(z):={\mathcal {C}}(f)(\sqrt{z})$ for $z \in \overline{\Pi ^+_\omega }$, see [5, Theorem 4.3].

We give formal definition for the Catalan operator for generators of cosine functions.

Definition 4.1

Let (A, D(A)) be the generator of a cosine function $({{\,\mathrm{Cos}\,}}(t))_{t \ge 0}$ such that $\left\| {{\,\mathrm{Cos}\,}}(t)\right\| \le Me^{\omega t}$ with $M \ge 1$ and $\omega \le \frac{1}{4}$ for all $t > 0$. Then we define the Catalan operator ${\mathcal {C}}(A)\in {\mathcal {B}}(X)$ as,

$$\begin{aligned} {\mathcal {C}}(A) x :=\Psi (c)x= \int _{0}^\infty c(t){{\,\mathrm{Cos}\,}}(t) x \; \mathrm{d}t, \quad x \in X, \end{aligned}$$

where c is the Catalan kernel given in Definition 2.1.

Theorem 4.2

Let A be the generator of a cosine function $({{\,\mathrm{Cos}\,}}(t))_{t \ge 0}$ as in Definition 4.1.

• (i) The Catalan operator ${\mathcal {C}}(A)$ is well-defined and

  $$\begin{aligned} \Vert {\mathcal {C}}(A)\Vert \le M\frac{1-\sqrt{1-4\omega }}{2\omega }. \end{aligned}$$

• (ii) The Catalan operator ${\mathcal {C}}(A)$ satisfies the biquadratic Catalan Eq. 1.1, i.e.,

  $$\begin{aligned} 4 A {\mathcal {C}}(A)^4 - {\mathcal {C}}(A)^2 + I = 0. \end{aligned}$$

• (iii) The Catalan operator ${\mathcal {C}}(A)$ has the following integral representation

  $$\begin{aligned} {\mathcal {C}}(A)x = \frac{1}{2\pi } \int _{\frac{1}{4}}^\infty {\sqrt{4\lambda -1}}R(\lambda ^2,A)x \; \mathrm{d}\lambda , \quad x\in X. \end{aligned}$$

Proof

The proof of item (i) is a consequence of Theorem 2.2 (i). To show (ii), note that $A\Psi (f)=f'(0)+\Psi (f'')$ for $f, f''\in L_\omega ^1(\mathbb R^+)$ and then

$$\begin{aligned} 4A {\mathcal {C}}(A)^4= & {} 4A\Psi (c^{*_c 4} )=4(c^{*_c 4})'(0)+4\Psi ((c^{*_c 4})'' )=-1+\Psi (c*_c c)\\ {}= & {} -1+ {\mathcal {C}}(A)^2, \end{aligned}$$

where we have applied Lemma 2.7 (vi) and Theorem 2.8 (iv).

Finally, to show the item (iii), we have that

$$\begin{aligned} \frac{1}{2\pi } \int _{\frac{1}{4}}^\infty {\sqrt{4\lambda -1}} R(\lambda ^2,A)x \; \mathrm{d}\lambda= & {} \frac{1}{2\pi } \int _{\frac{1}{4}}^\infty \frac{\sqrt{4\lambda -1}}{\lambda } \int _0^\infty e^{-\lambda t} {{\,\mathrm{Cos}\,}}(t)x\,\mathrm{d}t\,\mathrm{d}\lambda \\= & {} {\mathcal {C}}(A)x, \end{aligned}$$

for $x\in X$. $\square$

Remark 4.3

In the case that $A \in \mathcal {B}(X)$ then ${{\,\mathrm{Cos}\,}}(t)= \sum _{n\ge 0} \frac{t^{2n}}{(2n)!} A^n$. If 4A is of power-bounded, then

$$\begin{aligned} {\mathcal {C}}(A)x= & {} \int _{0}^\infty c(t){{\,\mathrm{Cos}\,}}(t)x \; \mathrm{d}t= \sum _{n\ge 0} A^n(x)\int _0^\infty \frac{t^{2n}}{(2n)!}c(t)\mathrm{d}t\\ {}= & {} \sum _{n\ge 0} C_{2n}A^n(x), \quad x \in X, \end{aligned}$$

where we have applied formula (1.4).

Now we suppose that A generates a $C_0$-group $(T(t))_{t\in \mathbb R}$ such that $\Vert T(t)\Vert \le Me^{\omega }\vert t\vert$ for $t\in \mathbb R$ and $M\ge 1$ and $\omega \ge 0$. Then $A^2$ generates a cosine function $(C(t))_{t\ge 0}$ where

$$\begin{aligned} {{\,\mathrm{Cos}\,}}(t):=\frac{T(t)+T(-t)}{2},\quad t\ge 0, \end{aligned}$$

[1, Example 3.14.15]. If $\omega \le \frac{1}{4}$, we obtain that

$$\begin{aligned} {\mathcal {C}}(A^2)=\frac{C(A)+C(-A)}{2}, \end{aligned}$$

(4.2)

where the Catalan generating functions ${\mathcal {C}}(A^2)$, C(A) and $C(-A)$ are defined by the uni-parametric families $({{\,\mathrm{Cos}\,}}(t))_{t\ge 0}$, $(T(t))_{t\ge 0}$ and $(T(-t))_{t\ge 0}$, respectively.

A converse result holds in UMD-spaces for bounded cosine functions. Let A a bounded cosine function on a UMD-space. Then $i(-A)^\frac{1}{2}$ generates a bounded $C_0$-group $(T_\frac{1}{2}(t))_{t\in \mathbb R}$ [7, Theorem 1.1] and

$$\begin{aligned} {\mathcal {C}}(A)=\frac{C(i(-A)^\frac{1}{2})+C(-i(-A)^\frac{1}{2})}{2}. \end{aligned}$$

Suppose that A is the generator of a cosine function $({{\,\mathrm{Cos}\,}}(t))_{t \ge 0}$ such that $\Vert {{\,\mathrm{Cos}\,}}(t) \Vert \le M e^{\omega t}$ for $t\ge 0,$ $M\ge 1$ and $\omega >0$. Then A is the generator of a $C_0$-semigroup $(T(t))_{t>0}$ where

$$\begin{aligned} T(t)x=\frac{1}{\sqrt{\pi t}}\int _0^\infty e^{-\frac{s^2}{4t}}{{\,\mathrm{Cos}\,}}(s)x \; \mathrm{d}s, \quad x\in X, \end{aligned}$$

(4.3)

with $\Vert T(t)\Vert \le M e^{\omega ^2 t}$ for $t>0$, see [1, Theorem 3.14.17].

Theorem 4.4

Let A be the generator of a cosine function $({{\,\mathrm{Cos}\,}}(t))_{t \ge 0}$ as in Definition 4.1.

• (i) $C(4A)=( {\mathcal {C}}(A))^2$ where C(4A) is given in Definition 3.1 and ${\mathcal {C}}(A)$ in Definition 4.1.

• (ii)
  $$\begin{aligned} A( {\mathcal {C}}(A))^2x = \frac{1}{2}\left( \frac{1}{4}x - \sqrt{\frac{1}{16} - A}(x)\right) , \quad x\in D(A). \end{aligned}$$

• (iii) The spectral mapping theorem holds for ${\mathcal {C}}(A)$, i.e.,

  $$\begin{aligned} \sigma ( {\mathcal {C}}(A)) = {\left\{ \begin{array}{ll} {\mathcal {C}}(c)(\sqrt{\sigma (A)}), &{} A \in {\mathcal {B}}(X) \\ {\mathcal {C}}(c)(\sqrt{\sigma (A)} \cup \{0\}, &{} A \notin {\mathcal {B}}(X). \end{array}\right. } \end{aligned}$$

Proof

(i) As the operator A generates a $C_0$-semigroup, $(T(t))_{t>0}$ given by (4.3), then 4A also generates a $C_0$-semigroup, $(T_{4A}(t))_{t\ge 0}$ and $T_{4A}(t)=T(4t)$ with $\Vert T_{4A}(t)\Vert \le M e^{4\omega ^2 t}$, for $t\ge 0$. By Definition 3.1, we have

$$\begin{aligned} \begin{aligned} C(4A)x&= \int _0^\infty c(t)T(4t)x \; \mathrm{d}t = \int _0^\infty c(t)\frac{1}{\sqrt{4\pi t}}\int _0^\infty e^{-\frac{s^2}{16t}}{{\,\mathrm{Cos}\,}}(s)x \; \mathrm{d}s \; \mathrm{d}t \\&= \int _0^\infty {{\,\mathrm{Cos}\,}}(s)x\int _0^\infty \frac{1}{\sqrt{4\pi t}}e^{-\frac{s^2}{16t}}c(t) \; \mathrm{d}t \; \mathrm{d}s\\ {}&= \int _0^\infty (c*_c c)(s) {{\,\mathrm{Cos}\,}}(s)x \; \mathrm{d}s \\&= ( {\mathcal {C}}(A))^2 x, \end{aligned} \end{aligned}$$

where we have applied Lemma 2.7 (iii).

We apply Theorem 3.2 (iv) to get that

$$\begin{aligned} 4 A( {\mathcal {C}}(A))^2x= 4AC(4A)= \frac{1}{2}x - 2\sqrt{\frac{1}{16} - 4A}(x), \quad x\in D(A). \end{aligned}$$

Finally, we suppose that $A\in {\mathcal {B}}(X)$. As C(4A) and ${\mathcal {C}}(A)$ are bounded operators, $\sigma ( {\mathcal {C}}(A))=\sqrt{\sigma (C(4A))}$. We apply Theorem 3.2 (v) to get

$$\begin{aligned} \sigma ( {\mathcal {C}}(A))= & {} \{\sqrt{C(z)}\, | \, z\in \sigma (4A)\}= \left\{ {\mathcal {C}}(c)\left( \sqrt{\frac{z}{4}} \right) \, \left| \right. \, z\in \sigma (4A) \right\} \\= & {} \{{\mathcal {C}}(c)(\sqrt{z})\, \, ;\,\,z\in \sigma (A)\}. \end{aligned}$$

Similarly, the equality holds for $A\not \in {\mathcal {B}}(X)$. $\square$

5 Examples, Applications and Conjectures

In this section we illustrate our results with different examples of operators A and the correspondent solution of the quadratic Catalan Eq. (1.1). Finally, we present some conjectures and ideas to continue this research in future projects in Sect. 5.2.

5.1 Examples and Applications

Here we discuss the Catalan generating functions for generators of translation, multiplication and composition semigroups on the space $L^p(\mathbb R)$ and in $\ell ^p(\mathbb Z)$ for A a finite difference operator.

Catalan operator for generators of translation semigroups Consider in the Banach space $L^p(\mathbb R^+)$ for $1\le p < \infty$ the left-translation semigroup

$$\begin{aligned} T_l(t)f(s):= f(s+t), \quad t,s \in \mathbb R^+, \end{aligned}$$

which defines a strongly continuous $C_0$-semigroup uniformly bounded. As seen in [2, Section II.2.10] the generator of the left translation semigroup $(T_l(t))_{t \ge 0}$ on $L^p(\mathbb R^+)$ is given by

$$\begin{aligned} Af := f', \end{aligned}$$

with domain $D(A) = \{f \in L^p(\mathbb R^+): f \text { absolutely continuous and } f' \in L^p(\mathbb R^+)\}$. Then we can define the Catalan operator for A as follows,

$$\begin{aligned} C(A)f(s) \!=\! \int _0^\infty T_l(t)f(s)c(t) \; \mathrm{d}t \!=\! \int _s^\infty f(s)c(u-s) \; \mathrm{d}s\!=\! (c\circ f)(s), \quad s\in \mathbb R^+. \end{aligned}$$

In $L^p(\mathbb R)$ for $1 \le p < \infty$, the right-translation semigroup

$$\begin{aligned} T_r(t)f(s):= f(s-t), \quad s,t \in \mathbb R, \end{aligned}$$

defines a strongly continuous $C_0$-group uniformly bounded whose generator is given by

$$\begin{aligned} Af := -f', \end{aligned}$$

with domain $D(A) = \{f \in L^p(\mathbb R): f \text { absolutely continuous and } f' \in L^p(\mathbb R)\}$. Then we can define the Catalan operator for A as follows,

$$\begin{aligned} C(A)f(s) = \int _0^\infty T_r(t)f(s)c(t) \; \mathrm{d}t = \int _0^\infty f(s-t)c(t) \; \mathrm{d}t = (c\star f)(s), \quad s\in \mathbb R. \end{aligned}$$

Note that $A^2f= f''$ defines a bounded cosine function and

$$\begin{aligned} {\mathcal {C}}(A^2)f(s)= \frac{1}{2}(\tilde{c}\star f)(s), \quad s\in \mathbb R, \end{aligned}$$

where we have used formula (4.2) and $\tilde{c}(s):=c(\vert s\vert )$ for $s\in \mathbb R$.

Catalan operator for generators of multiplication semigroups Consider in the Banach space $L^p(\mathbb R)$ for $1 \le p < \infty$, the multiplication semigroup

$$\begin{aligned} T_m(t)f(s):= e^{tm(s)} f(s), \quad s \in \mathbb R, t \in \mathbb R^+, \end{aligned}$$

and $m \in L^\infty (\mathbb R)$ with $\left\| m\right\| _\infty \le 1/4$. Then $(T_m(t))_{t\ge 0}$ is a strongly continuous $C_0$-semigroup with growth bound $\left\| m\right\| _\infty$. The generator of the multiplication semigroup $(T_m(t))_{t \ge 0}$ on $L^p(\mathbb R)$ is given by the multiplication operator $M_mf := m f,$ with domain $D(M_m) = \{f \in L^p(\mathbb R): m f \in L^p(\mathbb R)\}$, see [2, Section II.2.9]. Then we can define the Catalan operator for $M_m$, $C(M_m)$, given by

$$\begin{aligned} C(M_m)f(s) = \int _0^\infty e^{tm(s)} f(s) c(t) \; \mathrm{d}t = \mathcal {L}(c)(-m(s)) f(s)= C(m(s)) f(s),\quad s\in \mathbb R^+, \end{aligned}$$

where we have used Theorem 2.2 (iii) in the last equality and C(m(s))f(s) denotes the usual product of C(m(s)) and f(s). Therefore, the Catalan operator $C(M_m)$ is a multiplication operator.

Catalan operator for generators of composition semigroups For this subsection we consider the following family of operators

$$\begin{aligned} T_p(t)f(s):= e^{-\frac{t}{p}} f(e^{-t}s), \quad s \in \mathbb R^+, t \in \mathbb R, \end{aligned}$$

in the Banach space $L^p(\mathbb R^+)$ for $1 \le p < \infty$. This family has been studied recently in [9] due to its connection with the generalized Cesàro operator. In particular, we have that the family of operators $(T_p(t))_{t\in \mathbb R}$ is a $C_0$-group of isometries on $L^p(\mathbb R^+)$ whose infinitesimal generator $\Lambda$ is given by

$$\begin{aligned} \Lambda f(s) := -sf'(s)-\frac{1}{p}f(s), \quad s\in \mathbb R^+, \end{aligned}$$

with domain $D(\Lambda ) = \{f \in L^p(\mathbb R^+): f' \in L^p(\mathbb R^+)\}$. Thus, we can define the Catalan operator for $\Lambda$,

$$\begin{aligned} C(\Lambda ) f(s) = \int _0^\infty e^{-\frac{t}{p}} f(e^{-t}s) c(t) \; \mathrm{d}t = \frac{1}{s} \int _0^s \left( \frac{u}{s}\right) ^{\frac{1}{p}-1} c\left( \log \left( \frac{s}{u}\right) \right) f(u) \; \mathrm{d}u, \quad s\in \mathbb R^+. \end{aligned}$$

To simplify this expression we introduce the incomplete Gamma function $\Gamma (z,\alpha ) := \int _\alpha ^\infty t^{z-1}e^{-t} \; \mathrm{d}t$ for $\left| \arg (\alpha )\right| < \pi$. In particular, we are interested in the following recursion formula,

$$\begin{aligned} \Gamma (z+1,\alpha ) = z\Gamma (z,\alpha ) + \alpha ^ze^{-\alpha }, \end{aligned}$$

and its relation with the complementary error function,

$$\begin{aligned} {{\,\mathrm{erfc}\,}}(z) = \frac{1}{\sqrt{\pi }} \Gamma \left( \frac{1}{2},z^2\right) , \end{aligned}$$

(5.1)

see [18, pages 10 and 11].

Let $\beta (u,s) = \log \left( \left( \frac{u}{s}\right) ^\frac{1}{4}\right)$. From Theorem 2.2 (iv) and (5.1) we have that,

$$\begin{aligned} c\left( \log (\frac{s}{u})\right) = \left( \frac{u}{s}\right) ^{\frac{1}{4}} \frac{1}{\sqrt{2\pi }\sqrt{-\beta (u,s)}} - \frac{1}{2\sqrt{\pi }} \Gamma \left( \frac{1}{2}, -\beta (u,s) \right) , \end{aligned}$$

and using the recursion formula for the incomplete gamma function, we get,

$$\begin{aligned} \Gamma \left( \frac{1}{2}, -\beta (u,s) \right) = -\frac{1}{2} \Gamma \left( -\frac{1}{2}, -\beta (u,s) \right) + \frac{1}{\sqrt{-\beta (u,s)}} \left( \frac{u}{s}\right) ^{\frac{1}{4}}. \end{aligned}$$

Thus,

$$\begin{aligned} c\left( \log \frac{s}{u}\right) = \frac{1}{4\sqrt{\pi }} \Gamma \left( -\frac{1}{2},- \log \left( \left( \frac{u}{s}\right) ^\frac{1}{4}\right) \right) . \end{aligned}$$

Finally, we can express the Catalan operator as,

$$\begin{aligned} C(\Lambda ) f(s) = \frac{1}{4\sqrt{\pi }s} \int _0^s \left( \frac{u}{s}\right) ^{\frac{1}{p}-1} \Gamma \left( -\frac{1}{2},- \log \left( \left( \frac{u}{s}\right) ^\frac{1}{4}\right) \right) f(u) \; \mathrm{d}u, \quad s\in \mathbb R^+. \end{aligned}$$

Catalan operators on the sequence space Consider the Banach space of complex sequences $\ell ^p(\mathbb Z)$, formed by sequences of the form $a = (a_n)_{n \in \mathbb Z} \subset \mathbb C$ where the following norm,

$$\begin{aligned} \left\| a\right\| _p := \left( \sum _{n \in \mathbb Z} \left| a_n\right| ^p \right) ^{\frac{1}{p}}, \quad 1 \le p < \infty , \end{aligned}$$

is finite. In this space the usual product to consider is the discrete convolution $*$ given by,

$$\begin{aligned} (a *b) (n) := \sum _{j \in \mathbb Z} a(j)b(n-j), \quad a,b \in \ell ^p(\mathbb Z). \end{aligned}$$

Consider the element $a = \delta _1 - \delta _0$ where $\delta _j(i) = 1$ if $j=i$ and 0 in other case. The element $-a$ defines the classical backward difference operator

$$\begin{aligned} \nabla (f)(n) := f(n)-f(n-1) = -a *f (n), \quad f \in \ell ^p(\mathbb Z), \, n \in \mathbb Z. \end{aligned}$$

The norm of the operator is $\left\| \nabla \right\| = 2$, and we have that $-\nabla$ generates the following $C_0$-group,

$$\begin{aligned} T(t)f(n) = (e^{at}*f)(n), \quad f \in \ell ^p(\mathbb Z), t \in \mathbb R, n \in \mathbb Z, \end{aligned}$$

with $e^{at}(n):=e^{-t} \frac{t^n}{n!}$ if $n \ge 0$ and 0 in other case. In addition, we have that $\left\| T(t)\right\| = 1$ for $t>0$, see [3, Theorem 3.3]. Therefore, we can define the Catalan operator as in Definition 3.1 as,

$$\begin{aligned} C(-\nabla )f(n) = \int _{0}^\infty (e^{at}*f)(n) c(t) \; \mathrm{d}t = \sum _{j=0}^\infty \left( \int _{0}^\infty e^{-t}\frac{t^j}{j!} c(t) \; \mathrm{d}t \right) f(n-j), \quad n \in \mathbb Z. \end{aligned}$$

Now, we calculate the value of the integral ${\int _{0}^\infty e^{-t}\frac{t^j}{j!} c(t) \; \mathrm{d}t}$ for $j \in \mathbb Z^+ \cup \{0\}$. By Definition 2.1,

$$\begin{aligned} \begin{aligned} \int _{0}^\infty e^{-t}\frac{t^j}{j!} c(t) \; \mathrm{d}t&= \frac{1}{2\pi } \int _{\frac{1}{4}}^\infty \frac{\sqrt{4\lambda -1}}{\lambda } \int _{0}^\infty e^{-(\lambda + 1)t} \frac{t^j}{j!} \; \mathrm{d}t \; \mathrm{d}\lambda \\&= \frac{1}{2\pi } \int _{\frac{1}{4}}^\infty \frac{\sqrt{4\lambda -1}}{\lambda (\lambda +1)^{j+1}} \; \mathrm{d}\lambda \\&= \frac{4^{j+1}}{2\pi } \int _0^\infty \frac{\sqrt{u}}{(u+1)(u+5)^{j+1}} \; \mathrm{d}u= \frac{1}{\sqrt{5}} \sum _{k=j}^\infty \frac{C_k}{5^k}, \end{aligned} \end{aligned}$$

where we have applied [14, Theorem 2.4] for $z=5$ and $C_k$ is the kth Catalan number. Finally, we conclude

$$\begin{aligned} C(-\nabla )f(n) = \sum _{j=0}^\infty \left( \frac{1}{\sqrt{5}} \sum _{k=j}^\infty \frac{C_k}{5^k} \right) f(n-j), \quad n \in \mathbb Z. \end{aligned}$$

The associated cosine function, generated by a, is given by

$$\begin{aligned} {{\,\mathrm{Cos}\,}}(z)(n)=\frac{\sqrt{\pi }}{n!}\left( \frac{z}{2}\right) ^{n+\frac{1}{2}}J_{n-\frac{1}{2}}(z)\chi _{\mathbb N_0}(n), \quad n\in \mathbb N_0, \end{aligned}$$

where $J_{n-\frac{1}{2}}(z)$ is the Bessel function and $z\in \mathbb C$ ([3, Theorem 3.3]). We calculate ${\mathcal {C}}(a)$ using Definition 4.1

$$\begin{aligned} {\mathcal {C}}(a)(n)= & {} \int _0^\infty c(t){{\,\mathrm{Cos}\,}}(t)(n)\mathrm{d}t=\frac{1}{2\pi }\frac{\sqrt{\pi }}{n!}\int _\frac{1}{4}^\infty \frac{4\lambda -1}{\lambda }\int _0^\infty \left( \frac{t}{2}\right) ^{n+\frac{1}{2}}J_{n-\frac{1}{2}}(t)\mathrm{d}t\mathrm{d}\lambda \\= & {} \frac{1}{2\pi }\int _\frac{1}{4}^\infty \frac{4\lambda -1}{\lambda (\lambda ^2+1)^{n+1}}\mathrm{d}\lambda , \end{aligned}$$

where we have applied [4, Formula 6.623] for $n\ge 0$ and equal to 0 for $n<0$.

A similar result holds for the forward difference operator defined by $\Delta f(n) := f(n+1)-f(n)$, see [3, Theorem 3.2].

5.2 Conjectures and Future Research

In this section we present some conjectures and ideas to continue the research which we have developed in this article.

$\alpha$-times integrated semigroups and cosine functions A generalization of $C_0$-semigroups are called $\alpha$-times integrated semigroups, $(T_\alpha (t))_{t\ge 0}$ for $\alpha >0$ ([1, Section 3.2]). Similarly, a generator (A, D(A)) for $\alpha$-times integrated semigroups is defined and

$$\begin{aligned} R(\lambda ,A)x=\lambda ^\alpha \int _0^\infty e^{-\alpha t}T_\alpha (t)x\mathrm{d}t, \quad x\in X, \lambda >\omega . \end{aligned}$$

A Catalan generating function may be defined by

$$\begin{aligned} C(A)x:=\int _0^\infty W^\alpha c(t) T_\alpha (t)x\mathrm{d}t, \quad x\in X, \end{aligned}$$

where ${W^\alpha c(t)=\frac{1}{2\pi }\int _\frac{1}{4}^\infty \sqrt{4\lambda -1}\lambda ^{\alpha -1}e^{-\lambda t}\mathrm{d}\lambda }$, for $t>0$. Here we denote by $W^\alpha c$ the Weyl fractional derivative of Catalan kernel c. Algebraic properties and the Hille–Phillips functional calculus, similar to $\Theta$, for $\alpha$-times integrated semigroups may allow to check that C(A) is solution of the quadratic Eq. (1.1) and extend other interesting results for these operators.

$\alpha$-Times integrated cosine functions, $(C_\alpha (t))_{t\ge 0}$, extend the notion of cosine functions. A generator (A, D(A)) is defined and, in this case,

$$\begin{aligned} R(\lambda ^2,A)x=\lambda ^{\alpha -1}\int _0^\infty e^{-\alpha t}C_\alpha (t)x\mathrm{d}t, \quad x\in X, \lambda >\omega . \end{aligned}$$

A Catalan generating function may be defined by

$$\begin{aligned} {\mathcal {C}}(A)x:=\int _0^\infty W^\alpha c(t) C_\alpha (t)x\mathrm{d}t, \quad x\in X. \end{aligned}$$

Using again algebraic properties and a homomorphism similar to $\Psi$ (see [11]) for $\alpha$-times integrated cosine might allow to check that ${\mathcal {C}}(A)$ is solution of the biquadratic Eq. (1.3).

Resolvent estimates Suppose that (A, D(A)) is a closed operator on a Banach space X such that $\left( \frac{1}{4},\infty \right) \subset \rho (A)$ and

$$\begin{aligned} \Vert R(\lambda ,A)\Vert \le \frac{C}{(4\lambda -1)^\varepsilon }, \quad \lambda > \frac{1}{4}, \end{aligned}$$

for $\varepsilon >\frac{1}{2}$. Then the following integral

$$\begin{aligned} \frac{1}{2\pi } \int _{\frac{1}{4}}^\infty \frac{\sqrt{4\lambda -1}}{\lambda } R(\lambda ,A)x \; \mathrm{d}\lambda , \quad x\in X \end{aligned}$$

converges and defines a bounded operator which we may call the Catalan operator of A, C(A), compare with Theorem 3.2 (iii).

Catalan generating functions for fractional powers Suppose that $(T(t))_{t\ge 0}$ is a uniformly bounded $C_0$-semigroup with generator (A, D(A)). Then the fractional power $-(-A)^\alpha$ for $0<\alpha <1$ also defines a uniformly bounded $C_0$-semigroup see [20, section IX.11]. It is natural to ask about the connection between C(A) and $C(-(-A)^\alpha )$ given by Definition 3.1.

New identities for Catalan numbers In this paper we have presented interesting formulae for the Catalan kernel c, see for example Lemma 2.7 and Theorem 2.8 (iv). The similar nature of Catalan kernel c and the Catalan numbers $(C_n)_{n\ge 0}$ allows to conjecture that new formulae for Catalan numbers hold. Some of them may involve a discrete cosine convolution product.