Catalan generating functions for bounded operators

Abstract

In this paper, we study the solution of the quadratic equation $TY^2-Y+I=0$ where T is a linear and bounded operator on a Banach space X. We describe the spectrum set and the resolvent operator of Y in terms of the ones of T. In the case that 4T is a power-bounded operator, we show that a solution (named Catalan generating function) of the above equation is given by the Taylor series

$$\begin{aligned} C(T):=\sum _{n=0}^\infty C_nT^n, \end{aligned}$$

where the sequence $(C_n)_{n\ge 0}$ is the well-known Catalan numbers sequence. We express C(T) by means of an integral representation which involves the resolvent operator $(\lambda T)^{-1}$. Some particular examples to illustrate our results are given, in particular an iterative method defined for square matrices T which involves Catalan numbers.

1 Introduction

The well-known Catalan numbers $(C_n)_{n\ge 0}$ given by the formula

$$\begin{aligned} C_n={1\over n+1}{2n\atopwithdelims ()n},\quad \ n\ge 0, \end{aligned}$$

appear in a wide range of problems. For instance, the Catalan number $C_n$ counts the number of ways to triangulate a regular polygon with $n +2$ sides, or the number of ways that 2n people seat around a circular table are simultaneously shaking hands with another person at the table in such a way that none of the arms cross each other, see for example [24, 25]. They have been studied in depth in many papers and monographs (see for example [3, 18, 23, 25]) and the Catalan sequence is probably the most frequently encountered sequence.

The generating function of the Catalan sequence $c=(C_n)_{n\ge 0}$ is defined by

$$\begin{aligned} C(z):=\sum _{n=0}^\infty C_nz^n= {1- \sqrt{1-4z}\over 2z}, \quad z\in D\left( 0,{1\over 4}\right) :=\left\{ z\in {\mathbb {C}}\,\,|\,\, \vert z\vert <{1\over 4}\right\} ,\nonumber \\ \end{aligned}$$

(1.1)

see, for example, [25, Section 1.3]. This function satisfies the quadratic equation $zy^2-y+1=0.$ The main object of this paper is to consider this quadratic equation in the set of linear and bounded operators, ${{\mathcal {B}}}(X)$ on a Banach space X, i.e.,

$$\begin{aligned} TY^2-Y+I=0, \end{aligned}$$

(1.2)

where I is the identity on the Banach space, and $T, Y \in {{\mathcal {B}}}(X)$. Formally, some solutions of this vector-valued quadratic equations are expressed by

$$\begin{aligned} Y={1\pm \sqrt{1-4T}\over 2T}, \end{aligned}$$

which involves the (non-trivial) problems of the square root of operator $1-4T$ and the inverse of operator T.

In general, the Eq. (1.2) may have no solution, one, several or infinite solutions, see examples in Sect. 6. Note that the study of quadratic equations in Banach space X with $\hbox {dim}(X)\ge 2$ is more complicated than in the scalar case. For example, there are infinite symmetric square roots of $I_2 \in {\mathbb {R}}^{2\times 2}$ given by

$$\begin{aligned} \begin{pmatrix} 1 &{} 0\\ 0 &{} 1 \end{pmatrix}, \quad \begin{pmatrix} -1 &{} 0\\ 0 &{} -1 \end{pmatrix}, \quad \begin{pmatrix} a &{} \pm \sqrt{1-a^2}\\ \pm \sqrt{1-a^2} &{} -a \end{pmatrix} \end{aligned}$$

with $a\in [-1,1]$.

As far as we are aware, no useful necessary and sufficient conditions for the existence of solutions of quadratic equations in Banach spaces are known, even in the classical case of square roots in finite-dimensional spaces. To find some easily applicable conditions is of interest, in part because these equations are frequently used in the study of, for example, physical or biological phenomena, see for instance [4, 5, 13, 21].

In 1952, Newton’s method was generalized to Banach spaces by Kantorovich. Kantorovich’s theorem asserts that the iterative method of Newton, applied to a most general system of nonlinear equations $P(x) =0$, converges to a solution $x^*$ near some given point $x_0$, provided the Jacobian of the system satisfies a Lipschitz condition near $x_0$ and its inverse at $x_0$ satisfies certain boundedness conditions. The theorem also gives computable error bounds for the iterates. From here, a large theory has been developed to obtain sharp iterative methods to approximate solutions of non-linear equations (see for example [11, 14, 17]) and in particular quadratic matrix equations [10, 13].

The paper is organized as follows—in Sect. 2, we show new results about the well-known Catalan numbers sequence $(C_n)_{n\ge 0}$. In Theorem 2.4, we prove that the following technical identity holds

$$\begin{aligned} \int _0^\infty {\sqrt{t}\over (t+1)(t+z)^{j+1}}{\textrm{d}}t={\pi \over 2\sqrt{z}(z-1)^{j}}\sum _{k=j}^{\infty }C_k\left( {z-1\over 4z}\right) ^k, \quad \Re (z)\ge {1\over 2}, \end{aligned}$$

for $j\ge 1$. A nice result about solutions of quadratic equations

$$\begin{aligned} xy^2-y+1=0, \quad -xz^2-z+1=0, \end{aligned}$$

is given in Theorem 2.1: the arithmetic mean ${y+z\over 2}$ is solution of the biquadratic equation $4x^2w^4-w^2+1=0$.

We consider the sequence $c=(C_n)_{n\ge 0}$ as an element in the Banach algebra $\ell ^1({\mathbb {N}}^0, {1\over 4^n})$ in Sect. 3. We describe the spectrum set $\sigma (c)$ in Proposition 3.2 and the resolvent element $(\lambda -c)^{-1}$ in Theorem 3.4.

In Sect. 4, we study spectral properties of the solution of quadratic equation (1.2) with $T\in {{\mathcal {B}}}(X)$. We prove several results connecting $\sigma (T)$ and $\sigma (Y)$ where $\sigma (\cdot )$ denotes the spectrum set of a given bounded operator T. Moreover, we express $(\lambda -Y)^{-1}$ in terms of the resolvent of operator T in Theorem 4.4.

For operators T which 4T are power-bounded, we define the generating Catalan function

$$\begin{aligned} C(T):=\sum _{n\ge 0}C_nT^n. \end{aligned}$$

This operator solves the quadratic equation (1.2) and has interesting properties connected with T, see Theorem 5.1; in particular the following integral representation holds,

$$\begin{aligned} C(T)x={1\over \pi }\int _{1\over 4}^\infty {\sqrt{\lambda -{1\over 4}}\over \lambda }(\lambda T)^{-1}x {\textrm{d}}\lambda , \quad x\in X. \end{aligned}$$

In the last section, we illustrate our results with some examples of operators T in the Eq. (1.2). We consider the Euclidean space ${\mathbb {C}}^2$ and matrices

$$\begin{aligned} T=\lambda I_2, \,\, \begin{pmatrix} 0 &{} \lambda \\ \lambda &{} 0 \end{pmatrix}, \,\, \begin{pmatrix} 0 &{} \lambda \\ 0 &{} 0 \end{pmatrix}. \end{aligned}$$

We solve the Eq. (1.2) and calculate C(T) for these matrices. We also check C(a) for some particular values of $a\in \ell ^1({\mathbb {N}}^0, {1\over 4^n})$. Finally, we present an iterative method for matrices ${\mathbb {R}}^{n\times n }$ which are defined using Catalan numbers.

2 Some news results about Catalan numbers

The Catalan numbers may be defined recursively by $C_0=1$ and

$$\begin{aligned} C_n= \sum _{i=0}^{n-1} C_i C_{n-1-i}, \quad n\ge 1, \end{aligned}$$

(2.1)

and first terms in this sequence are $1,\,\,1,\,\,2,\,\,5,\,\,14, \,\,42, \,\,132, \ldots .$ The generating function of the Catalan sequence $c=(C_n)_{n\ge 0}$ is given in (1.1). This function satisfies the quadratic equation

$$\begin{aligned} zC(z)^2-C(z)+1=0, \quad z\in D\left( 0,{1\over 4}\right) , \end{aligned}$$

(2.2)

see for example [25, Section 1.3]. The second solution of this quadratic equation is given by

$$\begin{aligned} {1\over zC(z)}={1+ \sqrt{1-4z}\over 2z}, \quad z\in D\left( 0,{1\over 4}\right) \backslash \{0\}. \end{aligned}$$

The following theorem shows that the arithmetic mean of two solutions of these quadratic equations is also solution of a biquadratic equation, closer to the previous ones.

Theorem 2.1

Let A be a commutative algebra over ${\mathbb {R}}$ or ${\mathbb {C}}$ with $x\in A$. If y and z are solutions of the quadratic equations

$$\begin{aligned} xy^2-y+1=0, \quad -xz^2-z+1=0, \end{aligned}$$

then $w={y+z\over 2}$ is a solution of the biquadratic equation $4x^2w^4-w^2+1=0$.

Proof

Note that it is enough to show $x^2(y+z)^4-(y+z)^2+4=0$. We write for a while

$$\begin{aligned} P&:= (xy^2-y+1)(xy^2+4xyz+3xz^2),\\ Q&:=(-xz^2-z+1)(-xz^2-4xyz-3xy^2),\\ P+Q&=x^2(y+z)^4-xy^3-xy^2z-2xy^2+xz^3+xz^2y+2xz^2\\&=x^2(y+z)^4-xy^2(y+z+2)+xz^2(z+y+2)\\ {}&=x^2(y+z)^4+(y+z+2)(xz^2- xy^2). \end{aligned}$$

Since y and z are solutions of these quadratic equations, we have $xz^2- xy^2=2-(y+z)$ and

$$\begin{aligned} 0=P+Q= x^2(y+z)^4+(y+z+2)(2-(y+z))=x^2(y+z)^4-(y+z)^2+4, \end{aligned}$$

and we conclude the proof.$\square$

Remark 2.2

The sum of both equations $xy^2-y+1=0$ and $-xz^2-z+1=0$ gives

$$\begin{aligned} {y+z\over 2}-1={1\over 2} x(y^2-z^2)=2x\left( {y-z\over 2}\right) \left( {y+z\over 2}\right) , \end{aligned}$$

and we may obtain ${y-z\over 2}$ in terms of ${y+z\over 2}$ whenever the inverse of ${2x {y+z\over 2}}$ exists in the algebra A, i.e.,

$$\begin{aligned} {y-z\over 2}=\left( {y+z\over 2}-1\right) \left( 2x {y+z\over 2}\right) ^{-1}. \end{aligned}$$

As a direct application of Abel’s theorem to (1.1), we obtain

$$\begin{aligned} \sum _{n=0}^\infty {C_n\over 4^n}=\lim _{z\rightarrow {1\over 4}}C(z)=2, \quad \sum _{n=0}^\infty {C_n\over (-4)^n}=\lim _{z\rightarrow -{1\over 4}}C(z)=2(\sqrt{2}-1), \end{aligned}$$

(2.3)

[25, Exercise A.66]. In fact, one has

$$\begin{aligned} C_n\sim {4^n\over \sqrt{\pi }n^{3\over 2}}, \quad n\rightarrow \infty , \end{aligned}$$

[25, Exercise A.64].

A straightforward consequence of the generating formula (1.1) and Theorem 2.1 is the following proposition, where we consider the odd and even parts of function C(z),

$$\begin{aligned} C_o(z):={C(z)+C(-z)\over 2}, \quad C_e(z):= {C(z)-C(-z)\over 2}, \quad \vert z\vert <{1\over 4}. \end{aligned}$$

The proof is left to the reader.

Proposition 2.3

Let $c=(C_n)_{n\ge 0}$ be the Catalan sequence. Then

$$\begin{aligned} C_e(z):=\sum _{n=0}^\infty C_{2n}z^{2n}= & {} {\sqrt{1+4z}-\sqrt{1-4z}\over 4z},\\ C_o(z):=\sum _{n=0}^\infty C_{2n+1}z^{2n+1}= & {} {2-\sqrt{1+4z}-\sqrt{1-4z}\over 4z},\\ \end{aligned}$$

for $\vert z\vert \le {1\over 4}$. In particular,  $4z^2C_e(z)^4-C_e(z)^2+1=0,$ $C_e(z)^2=C(4z^2),$ ${C_o(z)}={C_e(z)-1\over 2zC_e(z)}$ for $\vert z\vert \le {1\over 4}$ and

$$\begin{aligned} \sum _{n=0}^\infty {C_{2n}\over 4^{2n}}=\sqrt{2},\quad \sum _{n=0}^\infty {C_{2n+1}\over 4^{2n+1}}=2-\sqrt{2}. \end{aligned}$$

Catalan numbers have several integral representations, for example,

$$\begin{aligned} C_n={1\over 2\pi }\int _0^4t^n{\sqrt{4-t\over t}}{\textrm{d}}t={2^{2n+1}\over \pi }\beta \left( {3\over 2}, n+{1\over 2}\right) , \end{aligned}$$

where the function $\beta$ is the well-known Euler Beta function, $\beta (u,v):=\int _0^1t^{u-1}(1-t)^{v-1}{\textrm{d}}t$ for $u,v>0$, see the monography [25] and the survey [20]. In the next theorem, we present a new result which involves the Taylor polynomials of the Catalan generating function C(z).

Theorem 2.4

Given $1\not =z\in {\mathbb {C}}^{+}:=\{z\in {\mathbb {C}};\,\,\Re z>0\},$ then

$$\begin{aligned} \int _0^\infty {\sqrt{t}\over (t+1)(t+z)}{\textrm{d}}t= & {} {\pi \over z-1}\left( {\sqrt{z}}-{1}\right) ,\\ \int _0^\infty {\sqrt{t}\over (t+1)(t+z)^{j+1}}{\textrm{d}}t= & {} {\pi \over (z-1)^{j+1}}\left( {\sqrt{z}}-{1}-{z-1\over 2\sqrt{z}}\sum _{k=0}^{j-1}C_k\left( {z-1\over 4z}\right) ^k\right) \\= & {} {\pi \over 2\sqrt{z}(z-1)^{j}}\sum _{k=j}^{\infty }C_k\left( {z-1\over 4z}\right) ^k, \end{aligned}$$

for $j\ge 1$ and where the last equality holds for $\Re (z)\ge {1\over 2}$.

Proof

The first integral is a easy exercise of elemental calculus. To do the second one, note

$$\begin{aligned} {\sqrt{t}\over (t+1)(t+z)^{j+1}}={1\over z-1}\left( {\sqrt{t}\over (t+1)(t+z)^{j}}- {\sqrt{t}\over (t+z)^{j+1}}\right) , \end{aligned}$$

and then

$$\begin{aligned} \int _0^\infty {\sqrt{t}\over (t+1)(t+z)^{j+1}}{\textrm{d}}t= & {} {1\over z-1}\left( \int _0^\infty {\sqrt{t}\over (t+1)(t+z)^{j}}{\textrm{d}}t- {\beta ({3\over 2}, j-{1\over 2})\over z^{j-{1\over 2}}}\right) \\= & {} {1\over z-1}\left( \int _0^\infty {\sqrt{t}\over (t+1)(t+z)^{j}}{\textrm{d}}t- {\pi C_{j-1}\over 2\sqrt{z}(4z)^{j-1}}\right) , \end{aligned}$$

for $j\ge 1$. We iterate this formula to get the final expression. $\square$

Remark 2.5

By holomorphicity, Theorem 2.4 holds for $z\in {\mathbb {C}}\backslash (-\infty , 0]$. Moreover for $z=1,$

$$\begin{aligned} \int _0^\infty {\sqrt{t}\over (t+1)^{j+2}}={\pi C_{j}\over 2^{2j+1}}=\pi \lim _{z\rightarrow 1}\left( {\sqrt{z}-{1}-{z-1\over 2\sqrt{z}}\sum _{k=0}^{j-1}C_k\left( {z-1\over 4z}\right) ^k\over (z-1)^{j+1}}\right) , \end{aligned}$$

for $j\ge 1$. Finally, when $j\rightarrow \infty$, we recover the generating formula

$$\begin{aligned} \sum _{k=0}^\infty C_k\left( {z-1\over 4z}\right) ^k= {2\sqrt{z}\over \sqrt{z}+1}, \quad \Bigg | {{z-1}\over z}\Bigg | \le 1. \end{aligned}$$

3 The sequence of Catalan numbers

We may interpret the equality (2.3) in terms of norm in the weight Banach algebra $\ell ^1({\mathbb {N}}^0, {1\over 4^n}).$ This algebra is formed by sequences $a=(a_n)_{n\ge 0}$ such that

$$\begin{aligned} \Vert a\Vert _{1, {1\over 4^n}}:=\sum _{n=0}^\infty {\vert a_n\vert \over 4^n}<\infty , \end{aligned}$$

and the product is the usual convolution $*$ defined by

$$\begin{aligned} (a*b)_n=\sum _{j=0}^na_{n-j}b_j, \quad a,b \in \ell ^1\left( {\mathbb {N}}^0, {1\over 4^n}\right) . \end{aligned}$$

The canonical base $\{\delta _j\}_{j\ge 0}$ is formed by sequences such that $(\delta _j)_n=\delta _{j,n}$ is the known delta Kronecker. Note that $\delta _1^{*n}= \delta _1\dots ^{n}\delta _1=\delta _n$ for $n\in {\mathbb {N}}$. This Banach algebra has identity element, $\delta _0$, its spectrum set is the closed disk $\overline{D(0,{1\over 4})}$ and its Gelfand transform is given by the Z-transform

$$\begin{aligned} Z(a)(z):= \sum _{n=0}^\infty {a_n}z^n, \quad z\in \overline{D\left( 0,{1\over 4}\right) }. \end{aligned}$$

It is straightforward to check $Z(\delta _n)(z)=z^n$ for $n\ge 0$ (see, for example, [15]).

In the next proposition, we collect some properties of the Catalan sequence c in the language of the Banach algebra $\ell ^1({\mathbb {N}}^0, {1\over 4^n})$. In particular, identities (2.1) and (2.2) are both equivalent to the item (iii).

Proposition 3.1

Take $c=(C_n)_{n\ge 0}$. Then

• (i) $\Vert c\Vert _{1, {1\over 4^n}}=2.$

• (ii) $C(z)=Z(c)(z)$ for $z\in D(0,{1\over 4}).$

• (iii) $\delta _1* c^{*2}-c+\delta _0=0.$

We recall that the resolvent set of $a\in \ell ^1({\mathbb {N}}^*, {1\over 4^n})$, denoted as $\rho (a)$, is defined by

$$\begin{aligned} \rho (a):=\left\{ \lambda \in {\mathbb {C}}\, \,: \,\, (\lambda \delta _0-a)^{-1}\in \ell ^1\left( {\mathbb {N}}^0, {1\over 4^n}\right) \right\} , \end{aligned}$$

and the spectrum set of a is denoted by $\sigma (a)$ and given by $\sigma (a):={\mathbb {C}}\backslash \rho (a)$.

Proposition 3.2

The spectrum of the Catalan sequence $c=(C_n)_{n\ge 0}$ is given by $\sigma (c)=C(\overline{D(0,{1\over 4})})$ and its boundary by

$$\begin{aligned} \partial (\sigma (c))=\left\{ 2{\textrm{e}}^{-i\theta }\left( 1-\sqrt{2\Bigg \vert \sin \left( {\theta \over 2}\right) }\Bigg \vert {\textrm{e}}^{i(\pi -\theta )\over 4}\right) \,\,:\,\,\theta \in (-\pi , \pi ]\right\} . \end{aligned}$$

Proof

As the algebra $\ell ^1({\mathbb {N}}^0, {1\over 4^n})$ has identity, we apply [15, Theorem 3.4.1] to get the equality set $\sigma (c)=C(\overline{D(0,{1\over 4})})$.

We write ${\mathbb {T}}:= \{{\textrm{e}}^{i\theta }\,:\,\, \theta \in (-\pi , \pi ]\}$. Since the function $C(\cdot )$ is univalent on $\overline{D(0,{1\over 4})},$ then $\partial (\sigma (c))= C({1\over 4}{\mathbb {T}})$. Take $z\in \partial (\sigma (c))$ and

$$\begin{aligned} z=2{\textrm{e}}^{-i\theta } \left( 1-\sqrt{2i \sin \left( {\theta \over 2}\right) {\textrm{e}}^{-i\theta \over 2}}\right) = 2{\textrm{e}}^{-i\theta }\left( 1-\sqrt{2\vert \sin \left( {\theta \over 2}\right) }\vert {\textrm{e}}^{i(\pi -\theta )\over 4}\right) , \end{aligned}$$

for $\theta \in (-\pi , \pi ].$ $\square$

Remark 3.3

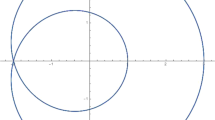
In the Fig. 1, we plot the set $\partial (\sigma (c)).$

Fig. 1

The set $\partial (\sigma (c))$

Given $\lambda \in {\mathbb {C}}$, we consider the geometric progression $p_{\lambda }:= ({1 \over \lambda ^n})_{n\ge 0}.$ Note $p_{\lambda } \in \ell ^1({\mathbb {N}}^0, {1\over 4^n})$ if and only if $\vert \lambda \vert >{1\over 4}$. Moreover,

$$\begin{aligned} (\lambda -\delta _1)^{-1}={1\over \lambda }p_{\lambda }, \quad \vert \lambda \vert > {1\over 4}, \end{aligned}$$

and $Z((\lambda -\delta _1)^{-1})(z)=(\lambda z)^{-1}$ for $z \in D(0,{1\over 4})$ and $\vert \lambda \vert > {1\over 4}.$ Note

$$\begin{aligned} C_n={1\over \pi }\int _{1\over 4}^\infty {\sqrt{\lambda -{1\over 4}}\over \lambda ^{2+n}}{\textrm{d}}\lambda ={1\over \pi }\int _{1\over 4}^\infty {\sqrt{\lambda -{1\over 4}}\over \lambda ^{2}}p_\lambda (n){\textrm{d}}\lambda , \quad n \ge 0, \end{aligned}$$

(3.1)

see, for example [20, Section 4.7].

In the next theorem, we express $(\lambda -c)^{-1}$ in terms of $p_\lambda$ and c for $0\not =\lambda \in {\mathbb {C}}\backslash \sigma (c)$.

Theorem 3.4

The inverse of the Catalan sequence c is given by $c^{-1}= \delta _0-\delta _1*c$ and

$$\begin{aligned} (\lambda -c)^{-1}={\delta _0\over \lambda }+{1\over \lambda (\lambda -1)}p_{\lambda -1\over \lambda ^2}+{1\over \lambda ^2 } c-{1\over \lambda ^2}c*p_{\lambda -1\over \lambda ^2}, \quad 0\not =\lambda \in {\mathbb {C}}\backslash \sigma (c). \end{aligned}$$

Proof

By Proposition 3.1(iii), $(\delta _0- \delta _1*c)*c= \delta _0$ and we conclude $c^{-1}= \delta _0-\delta _1*c$.

Now we introduce the following open set,

$$\begin{aligned} \Omega :=\left\{ \lambda \in {\mathbb {C}}\, :\,\,\left| { \lambda -1\over \lambda ^2}\right| >{1\over 4}\right\} . \end{aligned}$$

For $\lambda \in \Omega$, we apply the Zeta transform to get

$$\begin{aligned}{} & {} Z\left( {\delta _0\over \lambda }+{1\over \lambda (\lambda -1)}p_{\lambda -1\over \lambda ^2}\right) (z)={1\over \lambda }\left( 1+{1\over \lambda -1-z\lambda ^2}\right) ={z\lambda -1\over z\lambda ^2-\lambda +1},\\{} & {} Z\left( {1\over \lambda ^2 } c-{1\over \lambda ^2}c*p_{\lambda -1\over \lambda ^2}\right) (z)={C(z)\over \lambda ^2}\left( 1-{\lambda -1\over \lambda -1-z\lambda ^2}\right) ={zC(z)\over z\lambda ^2-\lambda +1}, \end{aligned}$$

for $z\in D(0,{1\over 4})$. To conclude the equality, we check

$$\begin{aligned} (\lambda C(z))\left( {z\lambda -1+zC(z)\over z\lambda ^2-\lambda +1}\right) = {z\lambda ^2-\lambda +C(z)-zC(z)^2\over z\lambda ^2-\lambda +1}=1, \end{aligned}$$

where we have applied the quadratic identity (2.2).

Since $\rho (c)={\mathbb {C}}\backslash \sigma (c)$ is connected (see Fig. 2) and the mapping $\lambda \mapsto (\lambda -c)^{-1}$ is holomorphic in $\rho (c)$, it follows by the uniqueness of analytic continuation that the resolvent of c is given by

$$\begin{aligned} (\lambda -c)^{-1}={\delta _0\over \lambda }+{1\over \lambda (\lambda -1)}p_{\lambda -1\over \lambda ^2}+{1\over \lambda ^2 } c-{1\over \lambda ^2}c*p_{\lambda -1\over \lambda ^2}, \quad 0\not =\lambda \in {\mathbb {C}}\backslash \sigma (c), \end{aligned}$$

and we conclude the proof. $\square$

Remark 3.5

Note that the set $\Omega$ is strictly contained in $\rho (c)$ and the boundary of $\sigma (c)$ is contained in the boundary of $\Omega$, i.e., $\partial (\sigma (c))\subset \partial (\Omega )=\{\lambda \in {\mathbb {C}}\, :\,\,\left| { \lambda -1\over \lambda ^2}\right| ={1\over 4}\}$. In the Fig. 2, we plot both sets, $\partial (\Omega )$ in blue and $\partial (\sigma (c))$ in red.

A nice consequence of Theorem 3.4 is that the sequence

$$\begin{aligned} \left( {1\over \lambda -1}\delta _0-{1\over \lambda }c\right) *p_{\lambda -1\over \lambda ^2} \end{aligned}$$

belongs to $\ell ^1({\mathbb {N}}^0, {1\over 4^n})$ for all $0\not =\lambda \in \rho (c)$, even though $p_{\lambda -1\over \lambda ^2}\not \in \ell ^1({\mathbb {N}}^0, {1\over 4^n})$ for $\lambda \not \in \Omega$.

Fig. 2

The set $\partial (\Omega )$ in blue and $\partial (\sigma (c))$ in red (color figure online)

4 Inverse spectral mapping theorem of the quadratic Catalan equation

Now we consider $(X, \Vert \quad \Vert )$ a Banach space and ${{\mathcal {B}}}(X)$ the set of linear and bounded operators on X. Given $T\in {{\mathcal {B}}}(X)$, as usual we write $\rho (T)$ the resolvent set given $\lambda \in {\mathbb {C}}$ such that $(\lambda T)^{-1}\in {{\mathcal {B}}}(X)$ and $\sigma (T):={\mathbb {C}}\backslash \rho (T)$. The spectrum of an operator is a non-empty closed set such that $\sigma (T)\subset \overline{D(0, \Vert T\Vert )}$ [22].

In this section, we study spectral properties of the solution of quadratic equation (1.2) with $T\in {{\mathcal {B}}}(X)$. We say that $Y\in {{\mathcal {B}}}(X)$ is a solution of (1.2) when the equality holds. Depending on T, the Eq. (1.2), has no solution, one, two or infinite solutions, see Sect. 6.1.

The proof of the following lemma is a direct consequence of the equality (1.2).

Lemma 4.1

Given $T\in {{\mathcal {B}}}(X)$ and Y a solution of (1.2). Then Y has left-inverse and $Y^{-1}_l=I-TY$.

Theorem 4.2

Given $T\in {{\mathcal {B}}}(X)$ and Y a solution of (1.2). Then the following are equivalent—

• (i) $0\in \rho (Y).$

• (ii) $T=Y^{-1}-Y^{-2}.$

• (iii) T and Y commute.

• (iv) $TY^2=YTY.$

Proof

(i) As $0 \in \rho (Y)$, we obtain item (ii) from (1.2). The expression of T in (ii) implies that T and Y commute. Now, if T and Y commute, then the equality $TY^2-YTY=0$ holds. Finally, we show that item (iv) implies (i). By Lemma 4.1, we have that $I-TY$ is a left-inverse of Y and it is enough to check if is a right-inverse

$$\begin{aligned} Y(I-TY)=Y-YTY=Y-TY^2=I, \end{aligned}$$

where we have applied (iv) and the Eq. (1.2). $\square$

In the case that $\text {dim}(X)<\infty$, to be left-invertible implies to be invertible and the conditions of Theorem 4.2 hold.

Corollary 4.3

Let X be a Banach space with ${\textrm{dim}}(X)<\infty ,$ $T\in {{\mathcal {B}}}(X)$ and Y a solution of (1.2). Then Y is invertible,  T and Y commute and $T=Y^{-1}-Y^{-2}.$

In the next theorem, we give the expression of $(\lambda -Y)^{-1}$ which extends the equality $Y^{-1}=I-TY$ given in Lemma 4.1.

Theorem 4.4

Given $T\in {{\mathcal {B}}}(X)$ and Y a solution of (1.2) such that $0\in \rho (Y)$.

• (i) Given $\lambda \in {\mathbb {C}}$ such that ${\lambda -1\over \lambda ^2}\in \rho (T)$ then $\lambda \in \rho (Y)$ and

  $$\begin{aligned} (\lambda -Y)^{-1}= & {} {1\over \lambda }+{1\over \lambda ^3}\left( {\lambda -1\over \lambda ^2}-T\right) ^{-1}+{Y\over \lambda ^2}- {(\lambda -1)Y\over \lambda ^4}\left( {\lambda -1\over \lambda ^2}-T\right) ^{-1}, \\ {}= & {} {\lambda T-1-YT\over \lambda ^2T-\lambda +1}. \end{aligned}$$

• (ii) Given $\lambda \in \rho (Y)$ such that ${\lambda \over \lambda -1}\in \rho (Y)$ then ${\lambda -1\over \lambda ^2}\in \rho (T)$ and

  $$\begin{aligned} \left( {\lambda -1\over \lambda ^2}-T\right) ^{-1}= & {} {\lambda ^4\over \lambda -1}\left( {\lambda \over \lambda -1}-Y\right) ^{-1}\left( (\lambda -Y)^{-1}-{\lambda +Y\over \lambda ^2}\right) ,\\ {}= & {} {(\lambda -1) Y^2-\lambda ^2 TY^2\over \left( \lambda -(\lambda -1)Y\right) (\lambda -Y)}. \end{aligned}$$

Proof

By Theorem 4.2, operators T and Y commute and we check that their inverse operators are right-inverse.

(i) For ${\lambda -1\over \lambda ^2}\in \rho (T)$, we have

$$\begin{aligned}{} & {} {1\over \lambda }+{1\over \lambda ^3}\left( {\lambda -1\over \lambda ^2}-T\right) ^{-1}={1\over \lambda }\left( 1+{1\over \lambda -1-\lambda ^2T}\right) ={\lambda T-1\over \lambda ^2 T-\lambda +1},\\{} & {} {Y\over \lambda ^2}- {(\lambda -1)Y\over \lambda ^4}\left( {\lambda -1\over \lambda ^2}-T\right) ^{-1}={Y\over \lambda ^2}\left( 1-{\lambda -1\over \lambda -1-\lambda ^2T}\right) ={YT\over \lambda ^2 T-\lambda +1}. \end{aligned}$$

To conclude the equality, we check

$$\begin{aligned} (\lambda -Y)\left( {\lambda T-1+YT\over \lambda ^2T-\lambda +1}\right) = {\lambda ^2T-\lambda +Y-TY^2\over \lambda ^2 T-\lambda +1}=1, \end{aligned}$$

where we have applied the quadratic equation (1.2).

(ii) Take $\lambda \in \rho (Y)$ such that ${\lambda -1\over \lambda }\in \rho (Y)$.

$$\begin{aligned} {\lambda ^4\over \lambda -1}({\lambda \over \lambda -1}-Y)^{-1}\left( (\lambda -Y)^{-1}-{\lambda +Y\over \lambda ^2}\right) ={\lambda ^2 Y^2\over (\lambda -(\lambda -1)Y)(\lambda -Y)}. \end{aligned}$$

Now we check

$$\begin{aligned} \left( {\lambda -1\over \lambda ^2}-T\right) {\lambda ^2 Y^2\over (\lambda -(\lambda -1)Y)(\lambda -Y)}={(\lambda -1) Y^2-\lambda ^2 TY^2\over (\lambda -(\lambda -1)Y)(\lambda -Y)}=1, \end{aligned}$$

where we have applied the quadratic equation (1.2) in the last equality. $\square$

Remark 4.5

The part (i) of Theorem 4.4 may be considered as an inverse spectral mapping theorem: given $\lambda \in \sigma (Y)$ then ${\lambda -1\over \lambda ^2}\in \sigma (T)$, in fact, $T={Y-1\over Y^2}$, see Theorem 4.2(ii).

5 Catalan generating functions for bounded operators

In this section, we consider the particular case that T is a linear and bounded operator on the Banach space X, $T\in {\mathcal B}(X)$, such that

$$\begin{aligned} \sup _{n\ge 0} {\Vert 4^n T^n\Vert }:=M<\infty , \end{aligned}$$

(5.1)

i.e., 4T is a power-bounded operator. In this case, $\sigma (T)\subset \overline{D(0,{1\over 4})}$. Under the condition (5.1), we may define the following bounded operator,

$$\begin{aligned} C(T):=\sum _{n\ge 0}C_nT^n, \end{aligned}$$

(5.2)

as a direct consequence of (2.3). Moreover, the bounded operator C(T) may be considered as the image of the Catalan sequence $c=(C_n)_{n\ge 0}$ in the algebra homomorphism $\Phi : \ell ^1({\mathbb {N}}^0, {1\over 4^n}) \rightarrow {{\mathcal {B}}}(X)$ where

$$\begin{aligned} \Phi (a)x:=\sum _{n\ge 0} a_nT^n(x), \qquad a=(a_n)_{n\ge 0}\in \ell ^1\left( {\mathbb {N}}^0, {1\over 4^n}\right) , \quad x\in X, \end{aligned}$$

i.e., $\Phi (c)=C(T)$. The $\Phi$ algebra homomorphism (also called functional calculus) has been considered in several papers, two of them are [7, Section 2] and more recently [8, Section 5.2]. In particular, the map $\Phi$ allows to define the following operators

$$\begin{aligned} \Phi (\delta _n)= & {} T^n, \quad n\ge 0,\\ \Phi \left( {1\over \lambda }{ p_\lambda }\right)= & {} (\lambda T)^{-1}, \quad \vert \lambda \vert >{1\over 4},\\ {\sqrt{{1}-{4T}}}= & {} \sum _{n\ge 0} {(-4)^n}{ {1\over 2}\atopwithdelims ()n} T^n,\\ \end{aligned}$$

where we have applied the “generalized binomial formula”, $(1+z)^\alpha =\sum _{n\ge 0}{\alpha \atopwithdelims ()n}z^n$, for $\vert z\vert <1$ and ${\alpha \atopwithdelims ()n}={\alpha (\alpha -1)\cdots (\alpha -n+1)\over n!}$ for $\alpha >0$. Remind that ${\alpha \atopwithdelims ()n}\sim {1\over n^{1+\alpha }}$ when $n\rightarrow \infty$ and $\alpha \not \in {\mathbb {N}}$.

Theorem 5.1

Given $T\in {{\mathcal {B}}}(X)$ such that 4T is power-bounded and $c=(C_n)_{n\ge 0}$ the Catalan sequence. Then

• (i) The operator C(T) defined by (5.2) is well-defined,  T and C(T) commute,  and C(T) is a solution of the quadratic equation (1.2).

• (ii) The following integral representation holds

  $$\begin{aligned} C(T)x={1\over \pi }\int _{1\over 4}^\infty {\sqrt{\lambda -{1\over 4}}\over \lambda }(\lambda T)^{-1}x {\textrm{d}}\lambda , \quad x\in X. \end{aligned}$$

• (iii) The following equality holds

  $$\begin{aligned} TC(T)={I\over 2}-{\sqrt{{1\over 4}-T}}. \end{aligned}$$

• (iv) The spectral mapping theorem holds for C(T),  i.e.,  $\sigma (C(T))=C(\sigma (T))$ and

  $$\begin{aligned} \sigma (C(T))\subset C\left( \overline{D\left( 0,{1\over 4}\right) }\right) = \sigma (c). \end{aligned}$$

• (v) Given $\lambda \in {\mathbb {C}}$ such that ${\lambda -1\over \lambda ^2}\in \rho (T)$, then $\lambda \in \rho (C(T))$ and

  $$\begin{aligned} (\lambda C(T))^{-1}={1\over \lambda }+{1\over \lambda ^3}\left( {\lambda -1\over \lambda ^2}-T\right) ^{-1}+{C(T)\over \lambda ^2}- {(\lambda -1)C(T)\over \lambda ^4}\left( {\lambda -1\over \lambda ^2}-T\right) ^{-1}. \end{aligned}$$

Proof

(i) From (2.3), $C(T)\in {{\mathcal {B}}}(X)$ as we have commented. It is clear that T and C(T) commute. We apply the algebra homomorphism to the equality given in Proposition 3.1(iii) to get

$$\begin{aligned} 0=\Phi (\delta _1* c^{*2}-c+\delta _0)=\Phi (\delta _1)(\Phi ( c))^{2}-\Phi (c)+\Phi (\delta _0)=T(C(T))^2-C(T)+I. \end{aligned}$$

(ii) As the homomorphism $\Phi$ is continuous, we apply the formula (3.1) to get

$$\begin{aligned} C(T)x= \Phi \left( {1\over \pi }\int _{1\over 4}^\infty {\sqrt{\lambda -{1\over 4}}\over \lambda ^{2}}p_\lambda {\textrm{d}}\lambda \right) x={1\over \pi }\int _{1\over 4}^\infty {\sqrt{\lambda -{1\over 4}}\over \lambda }(\lambda T)^{-1}x {\textrm{d}}\lambda , \end{aligned}$$

for $x\in X$.

(iii) Note

$$\begin{aligned} {I\over 2}-{\sqrt{{1\over 4}-T}}=-{1\over 2}\sum _{n\ge 0} {(-4)^{n+1}}{ {1\over 2}\atopwithdelims ()n+1} T^{n+1}=TC(T), \end{aligned}$$

since ${C_{n}= -{1\over 2} {(-4)^{n+1}}{ {1\over 2}\atopwithdelims ()n+1}}$ for $n\ge 0$.

(iv) Since 4T is power-bounded, the spectral mapping theorem for C(T) may be found in [7, Theorem 2.1]. As $\sigma (T)\subset \overline{D(0,{1\over 4})}$, we apply Proposition 3.2 to conclude $\sigma (C(T))\subset C(\overline{D(0,{1\over 4})})= \sigma (c).$

(v) As C(T) is a solution of (1.2) such that $0\in \rho (C(T))$, the item (v) is a particular case of Theorem 4.4(i). An alternative proof may be obtained using Theorem 3.4 and the algebra homomorphism $\Phi$ for $\lambda \in \Omega \backslash \{0\}.$ $\square$

Remark 5.2

In the case that $\sigma (T)\subset D(0,{1\over 4})$, the generating function C(z) given in (1.1) is a holomorphic function in a neighborhood of $\sigma (T)$. Then the Dunford functional calculus, defined by the integral Cauchy formula,

$$\begin{aligned} f(T)x:=\int _{\Gamma }f(z)(z-T)^{-1}x{\textrm{d}}z, \quad x\in X, \end{aligned}$$

allows to defined C(T), [26, Section VIII.7] which, of course, coincides with the expression gives in (5.2). As usual, the path $\Gamma$ rounds the spectrum set $\sigma (T)$.

6 Examples, applications, and final comments

In this section, we present some particular examples of operators T for which we solve the Eq. (1.2). In the Sect. 6.1, we consider the Euclidean space ${\mathbb {C}}^2$ and matrices $T=\lambda I_2, \,\lambda \begin{pmatrix} 0 &{} 1\\ 1 &{} 0 \end{pmatrix}, \lambda \begin{pmatrix} 0 &{} 1\\ 0 &{} 0 \end{pmatrix}$ where $\lambda \in {\mathbb {C}}$. Note that we have to solve a system of four quadratic equations. We also calculate C(T) for these matrices. In Sect. 6.2, we check C(a) for some $a\in \ell ^1({\mathbb {N}}^0, {1\over 4^n})$. Finally, we present an iterative method for matrices ${\mathbb {R}}^{n\times n }$ which are defined using Catalan numbers in Sect. 6.3.

6.1 Matrices on ${\mathbb {C}}^2$

We consider the Euclidean space ${\mathbb {C}}^2$ and the operator $T=\lambda I_2$ with $0\not =\lambda \in {\mathbb {C}}$. Then all solutions of (1.2) are given by

$$\begin{aligned} Y=\begin{pmatrix} {1\pm \sqrt{1-4\lambda (1+\lambda bc)}\over 2\lambda } &{} b\\ c &{} {1\mp \sqrt{1-4\lambda (1+\lambda bc)}\over 2\lambda } \end{pmatrix}, \end{aligned}$$

for $\vert c\vert +\vert b\vert >0$ where the allowed signs are $(-, +)$ and $(+,-)$. For $c=b=0$, the solutions are given by

$$\begin{aligned} Y=\begin{pmatrix} {1\pm \sqrt{1-4\lambda }\over 2\lambda } &{} 0\\ 0 &{} {1\pm \sqrt{1-4\lambda }\over 2\lambda } \end{pmatrix}, \end{aligned}$$

where the allowed signs are all four combinations. In both cases, note that $\sigma (Y)\subset \{C(\lambda ), {1\over \lambda C(\lambda )}\}$ and $\sigma (T)=\{\lambda \}$, compare with Theorem 4.4. In the case that $\vert \lambda \vert \le {1\over 4}$.

$$\begin{aligned} C(T)=\begin{pmatrix} C(\lambda ) &{} 0\\ 0 &{} C(\lambda ) \end{pmatrix}. \end{aligned}$$

Now we study the case $T=\begin{pmatrix} 0 &{} \lambda \\ \lambda &{} 0 \end{pmatrix}$ with $\lambda \in {\mathbb {C}}\backslash \{0\}$. All the solutions of (1.2) are given by

$$\begin{aligned} Y=\begin{pmatrix} {a} &{} {a-1\over 2\lambda a}\\ {a-1\over 2\lambda a} &{} a \end{pmatrix}, \end{aligned}$$

where a is a solution of the biquadratic equation $4\lambda ^2a^4-a^2+1=0$. In the case that $\vert \lambda \vert \le {1\over 4}$, we get

$$\begin{aligned} C(T)=\begin{pmatrix} C_e(\lambda ) &{} C_o(\lambda )\\ C_o(\lambda ) &{} C_e(\lambda ) \end{pmatrix}, \end{aligned}$$

where functions $C_e$ and $C_o$ are defined in Proposition 2.3

Finally, take now $T=\begin{pmatrix} 0 &{} \lambda \\ 0 &{} 0 \end{pmatrix}$ with $\lambda \in {\mathbb {C}}$. The only solution of (1.2) is given by $Y= \begin{pmatrix} 1 &{} \lambda \\ 0 &{} 1 \end{pmatrix}=C_0I_2+C_1T$; note that $T^n=0$ for $n\ge 2$.

6.2 Catalan operators on $\ell ^p$

We consider the space of sequences $\ell ^p({\mathbb {N}}^0, {1\over 4^n})$ where

$$\begin{aligned} \Vert a\Vert _{p, {1\over 4^n}}:=\left( \sum _{n=0}^\infty {\vert a_n\vert ^p\over 4^{np}}\right) ^{1\over p}<\infty , \end{aligned}$$

for $1\le p<\infty$ and $\ell ^\infty ({\mathbb {N}}^0, {1\over 4^n})$ the space of sequences endowed with the norm

$$\begin{aligned} \Vert a\Vert _{\infty , {1\over 4^n}}:=\sup _{n\ge 0}{\vert a_n\vert \over 4^{n}}<\infty . \end{aligned}$$

Note that $\ell ^1({\mathbb {N}}^0, {1\over 4^n})\hookrightarrow \ell ^p({\mathbb {N}}^0, {1\over 4^n})\hookrightarrow \ell ^\infty ({\mathbb {N}}^0, {1\over 4^n})$.

Now we consider $c=(C_n)_{n\ge 0}$ the Catalan sequence and the convolution operator $C(f):= c*f$ for $f\in \ell ^p({\mathbb {N}}^0, {1\over 4^n})$ with $1\le p\le \infty$. Since $C(f)=\sum _{n\ge 0} c_n\delta _n(f)=\sum _{n\ge 0} c_n(\delta _1)^n(f)$, we apply Theorem 5.1(iv) to get

$$\begin{aligned} \sigma (C)=C(\sigma (\delta _1))=C\left( \overline{D\left( 0,{1\over 4}\right) }\right) , \end{aligned}$$

i.e., it is independent on p and coincides with the spectrum of the Catalan sequence c in $\ell ^1({\mathbb {N}}^0, {1\over 4^n})$ (Proposition 3.2).

We consider the spaces $\ell ^p({\mathbb {Z}})$ for $1\le p\le \infty$ defined in the usual way. The element $a=\delta _1-\delta _0$ defines the classical backward difference operator

$$\begin{aligned} (a*f)(n):= f(n-1)-f(n), \quad f\in \ell ^p({\mathbb {Z}}), \end{aligned}$$

for $n\in {\mathbb {Z}}$. Note that $\Vert a\Vert =2$, and

$$\begin{aligned} (\lambda \delta _0+a)^{-1}=\sum _{j\ge 0}{\delta _j\over (1+\lambda )^{j+1}}, \quad 1<\vert 1+\lambda \vert , \end{aligned}$$

see [9, Theorem 3.3 (4)]. Now we need to consider ${a\over 8}$ and the associated Catalan generating operator defined by (5.2). By Theorem 5.1(ii), we get

$$\begin{aligned} C\left( {a\over 8}\right)= & {} {8\over \pi }\int _{1\over 4}^\infty {\sqrt{\lambda -{1\over 4}}\over \lambda }(8\lambda \delta _0+a)^{-1} {\textrm{d}}\lambda \\ {}= & {} {4\over \pi }\sum _{j\ge 0}{\delta _j\over 2^{j+1}}\int _0^\infty {\sqrt{t}\over (t+1)(t+{3\over 2})^{j+1}}{\textrm{d}}t\\= & {} (2\sqrt{6}-4)\delta _0+\sum _{j=1}^\infty \left( {\sqrt{6}\over 3}\sum _{k=j}^{\infty }{C_k\over 12^k}\right) \delta _j, \end{aligned}$$

where we have applied Fubini’s Theorem and Theorem 2.4 for $z={3\over 2}$.

Similar results hold for the forward difference operator defined by $\Delta f (n):=f(n+1)-f(n)$, [9, Theorem 3.2],

$$\begin{aligned} C\left( {\Delta \over 8}\right) = (2\sqrt{6}-4)\delta _0+\sum _{j=1}^\infty \left( {\sqrt{6}\over 3}\sum _{k=j}^{\infty }{C_k\over 12^k}\right) \delta _{-j}. \end{aligned}$$

6.3 Iterative methods on ${\mathbb {R}}^{m\times m}$ applied to quasi-birth–death processes

The quadratic matrix equation:

$$\begin{aligned} {\mathcal {Q}}(Y):= TY^2- Y+I=0, \end{aligned}$$

(6.1)

is related to the particular Markov chain characterized by its transition matrix P, which is an infinite block tridiagonal matrix of the form:

$$\begin{aligned} P= \left( \begin{array}{ccccc } D_1&{} D_2&{} &{} &{}0 \\ I&{} 0&{}T&{}&{} \\ &{}I&{} 0&{}T&{}\\ 0&{}&{} \ddots &{}\ddots &{}\ddots \end{array}\right) , \end{aligned}$$

where I is the identity matrix and the blocks $D_1$, $D_2$, T are $m\times m$ nonnegative matrices such that $D_1+D_2$ and $I+T$ are row stochastic. A discrete-time Markov chain represent a quasi-birth-death stochastic process. In fact, a quasi-birth–death stochastic process is a Discrete-time Markov chain having infinitely states [16]. Thus, a nonnegative solution of quadratic matrix equation (6.1) is necessary to describe probabilistically the behavior of that Markov chain.

In [4, 5, 12], the author demonstrated the usefulness of Newton’s method for solving the quadratic matrix equation. There are many papers containing algorithmic methodologies and acceleration techniques related to quadratic matrix equations, see for instance [4, 5, 11, 13, 21].

Our purpose in this section is to show experimentally the benefits of a higher-order iterative method to approximate the nonnegative solution of Eq. (6.1) which uses the Catalan numbers, $C_j$:

$$\begin{aligned} \left\{ \begin{array}{ll} Y_0\ \text {given},\\[1ex] Y_{n+1}= Y_n +\sum _{j\ge 0}H_j(Y_n), \quad n\ge 0, \end{array} \right. \end{aligned}$$

(6.2)

where

$$\begin{aligned} H_j(Y)=-\frac{C_j}{2^j}L_Q (Y)^j[{\mathcal {Q}}'(Y)]^{-1}{\mathcal {Q}}(Y), \quad L_Q (Y)= [{\mathcal {Q}}'(Y)]^{-1}{\mathcal {Q}}''(Y)[{\mathcal {Q}}'(Y)]^{-1}{\mathcal {Q}}(Y) \end{aligned}$$

and $L_Q (Y)^j$ denotes the composition of $L_Q (Y)$, j times.

Notice that, the first Fréchet derivative at a matrix Y is a linear map ${\mathcal {Q}}'(Y): {\mathbb {R}}^{m\times m} \rightarrow {\mathbb {R}}^{m\times m}$ such that

$$\begin{aligned} {\mathcal {Q}}'(Y) E= (TY- I) E+ TEY, \end{aligned}$$

(6.3)

and the second derivative at Y, ${\mathcal {Q}}''(Y): {\mathbb {R}}^{m\times m}\times {\mathbb {R}}^{m\times m} \rightarrow {\mathbb {R}}^{m\times m}$ is given by

$$\begin{aligned} {\mathcal {Q}}''(Y) E_1 E_2= T(E_1E_2+ E_2E_1), \end{aligned}$$

(6.4)

is a bilinear constant operator.

Method (6.2) has infinite convergence order (or equivalently infinite convergence speed) to approximate a solution of Eq. (6.1), see [10]. That is, the solution is obtained using one iteration. However, to apply this method carries on computing the square root of the matrix $(I-4T)$. To avoid this, we can truncate the series, thus obtaining a high-order method of convergence. High-order iterative schemes require more computational cost than other simpler iterative schemes, which makes them unfavorable. However, the use of the high-order iterative schemes in the case of quadratic equations is justified in terms of efficiency [6]. Therefore, this type of iterative schemes is of great interest.

As shown below, to approximate a solution of Eq. (6.1) by truncating the series of (6.2) is reduced to solve Sylvester equations. The standard Sylvester equation has the form:

$$\begin{aligned} AY + YB =D, \end{aligned}$$

(6.5)

where $A\in {\mathbb {R}}^{m\times m}$, $B \in {\mathbb {R}}^{m\times m}$, $D \in {\mathbb {R}}^{m\times m}$, and $X\in {\mathbb {R}}^{m\times m}$ is the sought after solution. The existence and the uniqueness of the solution X of (6.5) are determined by $\Lambda (A)$ and $\Lambda (B)$, the spectra of the corresponding matrices. Sylvester equations have numerous applications in control theory, signal processing, filtering, model reduction, image restoration, decoupling techniques for ordinary and partial differential equations, implementation of implicit numerical methods for ordinary differential equations, and block diagonalization of matrices (see, e.g., [1, 2, 13, 19]).

In fact, fixed $j=q$, $q\in {\mathbb {N}}$, iterative method (6.2) is reduced to solve $q+1$ Sylvester equations with the same matrix system and different independent terms,

$$\begin{aligned} \left\{ \begin{array}{l} Y_0\ \text {given},\\[1ex] ( TY_n-I)H_0(Y_n) + TH_0(Y_n) Y_n = -(TY_n ^2- Y_n+I), \\ (T Y_n-I)H_1(Y_n) + TH_1(Y_n) Y_n = -\frac{ C_1}{ C_{0}}T( H_0(Y_n) H_{0}(Y_n) ),\\ \vdots \qquad \qquad \qquad =\qquad \qquad \qquad \vdots \\ (T Y_n-I)H_q(Y_n) + TH_q(Y_n) Y_n = -\frac{C_j}{2C_{j-1}}T(H_0(Y_n) H_{q-1}(Y_n) \\ \quad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad +H_{q-1}(Y_n) H_0(Y_n) ),\\ Y_{n+1} = Y_n+ \sum _{j=0}^{q} H_j(Y_n), \end{array} \right. \end{aligned}$$

(6.6)

which greatly reduces the operational cost. The Bartels–Stewart algorithm is ideally suited to the sequential solution of Sylvester equation (6.5) with the same matrix system ( [1]).

Notice that, the most commonly used iterative method, Newton’s method, is obtained fixed $j=0$:

$$\begin{aligned} \left\{ \begin{array}{l} Y_0\ \text {given},\\[1ex] ( TY_n-I)H_0(Y_n) + T H_0(Y_n) Y_n = -(T Y_n^2-Y_n+I), \\[1ex] Y_{n+1} = Y_n +H_0(Y_n) \end{array} \right. \end{aligned}$$

or equivalently:

$$\begin{aligned} (TY_n-I) Y_{n+1}+T Y_{n+1} Y_n = TY_n^2-I, \end{aligned}$$

which has a quadratic convergence speed ( [4, 5]). Moreover, fixed $j=1$, method (6.2) has forth order of converge:

$$\begin{aligned} \left\{ \begin{array}{l} Y_0\ \text {given},\\[1ex] ( TY_n-I)H_0(Y_n) + T H_0(Y_n) Y_n = -(T Y_n^2-Y_n+I), \\[1ex] (TY_n-I) H_1(Y_n) +T H_1(Y_n) Y_n = -T H_0(Y_n)H_0(Y_n),\\[1ex] Y_{n+1} = Y_n+ H_0(Y_n)+H_1(Y_n). \end{array} \right. \end{aligned}$$

(6.7)

Taking into account that we double the convergence speed of Newton’s method, just by adding one single Sylvester equation, method (6.7) is a good alternative to approximate a solution of quadratic equation (6.1) as shown numerically in the following example—

We choose T as an ill-conditioned matrix and we approximate numerically the nonnegative solution of Eq. (6.1) using the method (6.7) with high accuracy. To do that, we take $T=(t_{ii})$ a diagonal matrix $100\times 100$ with entries $t_{ii}= 10^{-1}, i=1\ldots , 99$ and $t_{100,100}= 10^{-10}$. Method (6.7) is implemented in Mathematica Version 10.0, with stopping criterion $\Vert \ {\mathcal {Q}}(Y_n)\Vert _\infty <10^{-20}$. We choose the starting matrix $Y_0= T.$ We show the number of iterations necessary to achieve the required precision. The numerical results are reported in Table 1.

Table 1 Residuals for Newton’s method and method (6.7), with stopping criteria $\Vert \ {\mathcal {Q}}(Y_n)\Vert _\infty < 10^{-20}$