Weak-Type Lower Bounds for High-Dimensional Hardy–Littlewood Maximal Operators on Certain Measures via Averaging Operators

Abstract

Consider $\mathbb {R}^d$ with the euclidean distance, and let $0<\alpha <1$. We study the behavior of the averaging operators given by the radial density $d\mu (x)=|x|^{-\alpha d}dx$. When $1\le p<\infty$ is such that $(1-2\alpha )p<1-\alpha$, we show that the weak (p, p) bounds grow exponentially with the dimension d. As a consequence, the corresponding results follow for the centered Hardy–Littlewood maximal operator. The lower bounds obtained here are new for averaging operators, and when $0<\alpha \le 1/2$ and $p>1$, they are also new for the maximal operator.

1 Introduction

Consider the metric space $\mathbb {R}^d$ with the euclidean distance, and let $\mu$ be a Borel measure on $\mathbb {R}^d$ such that all balls (with strictly positive and finite radii) have strictly positive and finite measure. For a fixed $r>0$, the averaging operator acting on a locally integrable function f is defined by

$$\begin{aligned} A_{r,\mu }f(x):=\frac{1}{\mu (B(x,r))}\int _{B(x,r)}f(y)d\mu (y). \end{aligned}$$

(1)

This operator is obviously related to the centered Hardy–Littlewood maximal operator $M_\mu$, which is given by

$$\begin{aligned} M_\mu f (x):=\sup _{r>0}\frac{1}{\mu (B(x,r))}\int _{B(x,r)}|f(y)|d\mu (y). \end{aligned}$$

(2)

It is clear that $M_\mu f(x)=\sup _{r>0}A_{r,\mu }|f|(x)$ and thus, averaging operators are bounded by the Hardy–Littlewood maximal operator.

Let us note that since $\mu$ assigns finite measure to all balls (with finite radii), then it does not matter whether one uses open or closed balls in the definition of $M_\mu$.

The Hardy–Littlewood maximal operator admits many variants: Instead of averaging |f| over balls centered at x (the centered operator) as in (2), it is possible to consider all balls containing x (the uncentered operator) or average over convex bodies more general than euclidean balls, or averages over spheres, etc.

The Hardy–Littlewood maximal operator is an often used tool in Real and Harmonic Analysis, mainly (but not exclusively) due to the fact that while $|f|\le M_\mu f$ a.e., $M_\mu f$ is not too large (in a $L^p$ sense) since for every locally finite Borel measure $\mu$ defined on $\mathbb {R}^d$, it satisfies the following strong-type (p, p) inequality: $\Vert M_\mu f\Vert _p\le C_{p}\Vert f\Vert _p$, for $1<p\le \infty$. Thus, $M_\mu f$ is often used to replace f, or some average of f, in chains of inequalities, without leaving $L^p$ ($p>1$).

The situation when $p=1$ is different. It follows from the Besicovitch Covering Theorem that $M_\mu$ satisfies the weak (1, 1) inequality $\sup _{\lambda >0} \lambda \mu (\{M_\mu f \ge \lambda \})\le c_1\Vert f\Vert _1$ for every locally finite Borel measure $\mu$ on $\mathbb {R}^d$. This is a very important fact, as it implies the $L^p$ bounds for $1<p<\infty$ via interpolation (the Marcinkiewicz Interpolation Theorem generalizes this result). From now on, we shall use $c_{p,d,\mu }$ to denote the lowest possible constant in the weak (p, p) inequality when the measure in $\mathbb {R}^d$ is $\mu$, and likewise, $C_{p,d,\mu }$ will denote the lowest possible strong (p, p) constant.

Let us take into account that for other maximal operators, the situation for $L^p$ bounds can be different. E.M. Stein showed that for $d\ge 3$ the (Stein’s) spherical maximal operator (where averages are taken over spheres) was bounded in $L^p$ if and only if $p>d/(d-1)$, cf. [29]. Some years later, Bourgain extended Stein’s result to $d=2$, cf. [11].

The study of the constants $c_{1,d,\mu }$ and $C_{p,d,\mu }$ has attracted considerable interest. For instance, if $d=1$, given any Borel measure in $\mathbb {R}$, a simple covering argument yields for the uncentered operator $c_{1,1,\mu }\le 2$ (cf. [1]), and often $c_{1,1,\mu }=2$ is sharp, for instance, for $\mu =m$, the Lebesgue measure. However, the same question for the centered operator is difficult, even for the Lebesgue measure. Of course, since the centered operator is bounded by the uncentered operator, it is clear that $c_{1,1,m}\le 2$. In [2] the commonly accepted conjecture $c_{1,1,m}=3/2$ was refuted. The exact value $c_{1,1,m}=(11+\sqrt{61})/12$ was obtained by Melas by a rather involved argument, in the two papers [24, 25]. Thus, it seems that, even for the Lebesgue measure $m_d$ in $\mathbb {R}^d$, obtaining a precise formula for $c_{1,d,m_d}$ is a very difficult task.

Considerable efforts have gone into determining how changing the dimension on $\mathbb {R}^d$ modifies the best constants $C_{p,d,m_d}$ and $c_{1,d,m_d}$ in the case of Lebesgue measure. When $p=\infty$, we can take $C_{\infty ,d,m_d}=1$ in every dimension, since averages never exceed a supremum. At the other endpoint $p=1$, the first boundedness arguments used the Vitali covering lemma, which leads to exponential bounds of the type $c_{1,d,m_d}\le 3^d$, and by interpolation, to exponential bounds for $C_{p,d,m_d}$. So, it is natural to try to improve on these bounds, and in particular, to seek bounds independent on the dimension, with a view towards infinite dimensional generalizations of Harmonic Analysis.

Quite remarkably, E.M. Stein showed that for $M_{m_d}$, there exists bounds for $C_{p,d,m_d}$ that are independent of d ([30, 31, 33], see also [32]). Stein’s result was generalized to the maximal function defined using an arbitrary norm by Bourgain [12,13,14] and Carbery [16] when $p>3/2$. For $\ell _q$ balls, $1\le q<\infty$, Müller [27] showed that uniform bounds again hold for every $p>1$. For the case of $\ell _\infty$ balls (cubes) it took decades to fill the gap $1<p\le 3/2$. Bourgain showed the existence of uniform bounds also in this case (see [14]).

Regarding weak-type (1, 1) inequalities, in [33], Stein and Strömberg proved that the smallest constants in the weak-type (1, 1) inequality satisfied by $M_{m_d}$ grow at most like O(d) for euclidean balls, and at most like $O(d\log d)$ for more general balls. They also asked if uniform bounds could be found, a question still open for euclidean balls.

In 2008, Aldaz (cf. [4]) proved that if one considers cubes with sides parallel to the coordinate axes (that is, $\ell _\infty$ balls) instead of euclidean balls, then the best constants $c_{1,d,m_d}$ must diverge to infinity with d, and thus the answer to the Stein-Strömberg question is negative for cubes. This result was posted in 2008 in the Math ArXiv, but it was published in 2011. In the meantime, G. Aubrun refined Aldaz’s result and showed that $c_{1,d,m_d} \ge \Theta (\log ^{1 -\varepsilon }d)$, where $\Theta$ denotes the exact order and $\varepsilon > 0$ is arbitrary, cf. [10]. Later, Iakovlev and Strömberg proved $c_{1,d,m_d} \ge \Theta (d^{1/4})$, cf. [20].

For a thorough survey about the results cited in the three previous paragraphs, we refer the reader to [19].

A different line of research studies if the previous results can be extended to more general settings than $\mathbb {R}^d$ and Lebesgue measure. In this sense, a remarkable extension of the Stein and Strömberg $O(d\log d)$ theorem has been obtained by Naor and Tao (cf. [28]) who consider separable metric spaces equipped with a Radon measure finite over balls of finite radius. It is assumed also a microdoubling condition on the measure. They bound localized maximal operators by averaging operators and use this microdoubling condition. Other interesting results are the O(d) upper bound of the weak (1, 1) inequality in the Heisenberg groups (cf. [22]) or the $O(d\log d)$ upper bound in hyperbolic spaces with the Riemannian volume (which does not satisfy a doubling condition) (cf. [23]).

Till now, we have mentioned O(d) or $O(d\log d)$ upper bounds for the weak (1, 1) inequality and bounds independent on the dimension for the strong (p, p) inequality. However, as we will see later, it is known that even in $\mathbb {R}^d$ with the euclidean distance, the situation can be quite different for arbitrary locally finite Borel measures. Let us recall that by the Besicovitch covering theorem for $\mathbb {R}^d$, one can obtain upper bounds exponential in the dimension for $c_{1,d,\mu }$ and, by interpolation, for $C_{p,d,\mu }$. These bounds are independent on the Radon measure chosen. The structure of the metric space is important in order to get this kind of bounds. For instance, Aldaz proved in [6] that a geometrically bounded condition of the metric space assures boundedness of averaging operators in $L^p$ for any $1\le p<\infty$, with bounds independent on the measure.

From now on, we always refer to the centered Hardy–Littlewood maximal function defined by euclidean balls. We only deal with some special classes of functions (something that of course, simplifies the arguments and lower the constants). It is shown in [26, Theorem 3] that considering only radial functions (with Lebesgue measure) leads to $c_{1,d,m_d}\le 4$ in all dimensions, and the same happens if Lebesgue measure is replaced by a radial, radially increasing measure, cf. [21, Theorem 2.1]. Besides, for Lebesgue measure and radial decreasing functions, it is shown in [7, Theorem 2.7] that the sharp constant is $c_{1,d,m_d}=1$.

If instead of radial, radially increasing measures, one considers radial, radially decreasing measures, the situation changes radically. Typically, one has exponential increase in the dimension for $c_{1,d,\mu }$, and some times even for the strong-type constants $C_{p,d,\mu }$. Furthermore, it is enough to consider characteristic functions of balls centered at zero (hence, radial and decreasing) to prove exponential increase. The weak-type (1, 1) case for integrable radial densities defined via bounded decreasing functions was studied in [3]. It was shown there that the best constants $c_{1,d,\mu }$ satisfy $c_{1,d,\mu } \ge \Theta \left( 1\right) \left( 2/\sqrt{3}\right) ^{d/6}$, in strong contrast with the linear O(d) upper bounds known for Lebesgue measure. Exponential increase was also shown for the same measures and small values of $p > 1$ in [17]; shortly after (and independently) these results were improved in [8], as they applied to larger exponents p and to a wider class of measures. It was also shown in [8] that exponential increase could occur for arbitrarily large values of p and suitably chosen doubling measures. Together with the results for hyperbolic spaces mentioned before, this shows that the doubling condition is neither necessary nor sufficient to have “good bounds” for maximal inequalities in terms of the dimension. Finally, it is proven in [18] that for the standard Gaussian measure in $\mathbb {R}^d$, one has exponential increase in the constants for all $p \in (1,\infty )$ (cf. [5] for a related result, dealing with averaging operators).

In the previous paragraphs, we have seen that, acting only on radial functions, the maximal operator has $c_{1,d,\mu }$ upper bounds independent on the dimension if $\mu$ is a radially increasing density or the Lebesgue measure. We have seen also that for some $\mu$ defined by radial decreasing densities, we have exponential increase of $c_{1,d,\mu }$, exponential increase of $c_{p,d,\mu }$ for some sufficiently small values of $p>1$, and in some special cases, for every $p>1$. So, it is natural to ask whether Lebesgue measure is the borderline case which separates uniform from non-uniform behavior in the constants. The answer to this question is negative. In [9, Theorem 3.1(3)] it is proved that for the homogeneous measures $d\mu (x)=dx/|x|^{\alpha _d}$ if $\alpha _d\le K$ (with K that does not depend on d), acting on radial functions, $c_{1,d,\mu }$ are bounded uniformly in d and, by interpolation, the same happens for $C_{p,d,\mu }$.

When $d\rightarrow \infty$, the behavior of $c_{1,d,\mu }$ depends on whether $\alpha _d$ is bounded or not. For $\alpha _d\le d/2$ we have that $c_{1,d,\mu }\ge \Theta ((5^{1/2}/2)^{\alpha _d})$ (cf. Theorem 3.1(2) of [9]). Thus, if $\alpha _d\le d/2$ and $\limsup _{d\rightarrow \infty }\alpha _d=\infty$, then $\limsup _{d\rightarrow \infty }c_{1,d,\mu }=\infty$.

In the case of radial densities that decrease faster than the previous ones, such as $\alpha _d=\alpha \cdot d$ for $1/2<\alpha <1$ we not only have exponential increase of $c_{1,d,\mu }$ but also for all $p<\infty$. That is, there exist $b(\alpha ,p)>1$ such that $c_{p,d,\mu }\ge \Theta (b^d)$ (cf. [9]).

Here, we consider the homogeneous densities $d\mu (x)=dx/|x|^{\alpha d}$. In Corollary 2.2, we prove that for any $0<\alpha <1$ and $1\le p<\infty$ such that $(1-2\alpha )p<1-\alpha$ we have a lower bound for $c_{p,d,\mu }$ which is exponential with d. This implies that if $\alpha \in [1/2,1)$ and $1\le p<\infty$, $c_{p,d,\mu }$ grows exponentially in d. Besides, if $0<\alpha <1/2$ and $1\le p< (1-\alpha )/(1-2\alpha )$, $c_{p,d,\mu }$ also grows exponentially in d.

Let us note that for $0<\alpha \le 1/2$, as we have written in the previous paragraphs, the result was known for $p=1$. For small $p>1$, it was not known whether the constants $c_{p,d,\mu }$ are bounded with the dimension or not, even when we restrict the operator to radial functions (let us note that the results in [8] for small $p>1$ do not apply for these measures). In Corollary 2.2, we obtain exponential growth for $\alpha =1/2$ and $p\in [1,\infty )$ and for $0<\alpha <1/2$ and $p\in [1,(1-\alpha )/(1-2\alpha ))$.

Theorem 2.1 below deals with averaging operators. Since $A_{r,\mu }f\le M_\mu f$ it is clear that $A_{r,\mu }$ satisfies weak (1, 1) and strong (p, p) inequalities. Furthermore, for some measures $\mu$, the operator $A_{r,\mu }$ can be substantially smaller than $M_\mu$. This is the case with the Lebesgue measure, since $A_{r,m^d}$ satisfies a strong (1, 1) inequality with constant 1. If we denote by $\zeta _{p,d,\mu }$ the best constant of the operator $A_r$ in the weak (p, p) inequality we trivially have $\zeta _{p,d,\mu }\le c_{p,d,\mu }$. One can see (cf. Lemma 3.1) that for the measures considered in this paper $\zeta _{p,d,\mu }$ does not depend on the radius r of the operator $A_{r,\mu }$ considered. In Theorem 2.1, under the conditions on $\alpha$ and p mentioned previously, exponential growth for $\zeta _{p,d,\mu }$ is obtained. As a consequence Corollary 2.2 immediately follows.

I am indebted to Prof. J.M. Aldaz for some suggestions that improved the presentation of this note.

2 Notation and Results

Recall that for any $x\in \mathbb {R}^d$, we denote by $|x|=(x_1^2+x_2^2+\ldots +x_d^2)^{1/2}$ its euclidean norm. Given $r>0$, denote by $B(x,r)=\{y\in \mathbb {R}^d:|x-y|<r\}$ the euclidean open ball. A function $f:\mathbb {R}^d\longrightarrow \mathbb {R}$ is radial if there exists a $g:[0,\infty )\longrightarrow \mathbb {R}$ such that $f(x)=g(|x|)$ for all $x\in \mathbb {R}^d$, i.e., f depends only on one parameter (the distance to the origin), and thus, f is rotation invariant.

Let $0<\alpha <1$ be fixed. For any A Borel subset of $\mathbb {R}^d$, we define the radial measures

$$\begin{aligned} \mu (A)=\int _A\frac{dx}{|x|^{\alpha d}}. \end{aligned}$$

Since $\alpha <1$, the measures are locally finite. For these measures we define the centered Hardy–Littlewood maximal operator $M_\mu$ as in (2), and for any $r>0$ we define the averaging operator $A_{r,\mu }$ as in (1).

Since $A_{r,\mu }|f|\le M_\mu f$, by Besicovitch covering Lemma both operators satisfy weak (p, p) inequalities for $1\le p<\infty$. Let us denote by $\zeta _{p,d,\mu }$ the best constant in the weak (p, p) inequality for $A_{r,\mu }$ in $\mathbb {R}^d$. By homogeneity one can check (see Lemma 3.1 below) that $\zeta _{p,d,\mu }$ does not depend on the $r>0$ chosen.

The following theorem shows exponential growth of $\zeta _{p,d,\mu }$ with the dimension.

Theorem 2.1

Fix $0<\alpha <1$ and $1\le p<\infty$ satisfying $(1-2\alpha )p\le 1-\alpha$. Let $\mu$ be the measure on $\mathbb {R}^d$ defined by $d\mu (x)=dx/|x|^{\alpha d}$. Let $\zeta _{p,d,\mu }$ be the best constant for the weak (p, p) inequality satisfied by all averaging operators in this measure space.

Then, there exist $c(\alpha ,p)>0$ and $K(\alpha ,p)>1$, independent of d, such that

$$\begin{aligned} \zeta _{p,d,\mu }\ge \frac{c(\alpha ,p)}{d} K(\alpha ,p)^{d-1} \quad \text {for all }d\ge 3. \end{aligned}$$

From this theorem, the following corollary is obtained.

Corollary 2.2

Fix $0<\alpha <1$ and $1\le p<\infty$ satisfying $(1-2\alpha )p\le 1-\alpha$. Let $\mu$ be the measure on $\mathbb {R}^d$ defined by $d\mu (x)=dx/|x|^{\alpha d}$. Let $c_{p,d,\mu }$ be the best constant for the weak (p, p) inequality for $M_\mu$.

Then, there exist $c(\alpha ,p)>0$ and $K(\alpha ,p)>1$, independent of d, such that

$$\begin{aligned} c_{p,d,\mu }\ge \frac{c(\alpha ,p)}{d} K(\alpha ,p)^{d-1} ,\quad \text {for all }d\ge 3. \end{aligned}$$

3 Preliminary Lemmas

The next lemma shows that for a measure $dx/|x|^{\alpha d}$, the best constants for the weak (p, p) inequality are the same for all the averaging operators and they do not depend on the radius chosen.

Lemma 3.1

Let $0<\alpha <1$ and let $d\mu (x)=dx/|x|^{\alpha d}$ be a measure on $\mathbb {R}^d$. Let $1\le p<\infty$. For every $r>0$ and $A_{r,\mu }$ (the averaging operator with radius r) denote by $\zeta _{p,d,\mu }(r)$ the best constant for the weak (p, p) inequality satisfied by $A_{r,\mu }$. Then, $\zeta _{p,d,\mu }(r)=\zeta _{p,d,\mu }(1)$.

Proof

Let A be a measurable subset of $\mathbb {R}^d$. For any $r>0$, denote by $rA:=\{ra:a\in A\}$. By a change of variable, it is easy to see that

$$\begin{aligned} \mu (rA)=r^{(1-\alpha )d}\mu (A). \end{aligned}$$

(3)

Let us note also that

$$\begin{aligned} B(rx,r)=rB(x,1),\quad x\in \mathbb {R}^d. \end{aligned}$$

(4)

Besides, for any measurable function f on $\mathbb {R}^d$ and any $r>0$, denote by $f_r(x):=f(r^{-1}x)$. By (3), (4) and a change of variable, it can be proved that

$$\begin{aligned} A_r(f_r)(rx)=A_1(f)(x),\quad x\in \mathbb {R}^d, \end{aligned}$$

(5)

and

$$\begin{aligned} \Vert f_r\Vert _{p,\mu }=r^{(1-\alpha )d/p} \Vert f\Vert _{p,\mu }. \end{aligned}$$

Now, for any $\lambda >0$ and any f measurable function on $\mathbb {R}^d$, (5) implies that $x\in \{A_{1,\mu }(f)>\lambda \}$ if and only if $rx\in \{A_{r,\mu }(f_r)>\lambda \}$. Thus, if f is not equivalent to the null function, we have

$$\begin{aligned} \lambda \frac{\left( \mu (\{A_{r,\mu }(f_r)>\lambda \})\right) ^{1/p}}{\Vert f_r\Vert _{p,\mu }}=\lambda \frac{\left( \mu (\{A_{1,\mu }(f)>\lambda \})\right) ^{1/p}}{\Vert f\Vert _{p,\mu }}. \end{aligned}$$

From here, a routine argument shows that $\zeta _{p,d,\mu }(r)=\zeta _{p,d,\mu }(1)$. $\square$

Lemma 3.2

For $0<a<2$, let us define

$$\begin{aligned} h_a(R)=\frac{1-a}{2-a}(1+R^2)+\frac{1}{2-a}\sqrt{1+2[1-2a(2-a)]R^2+R^4},\quad -1<R<1. \end{aligned}$$

(6)

For every $0<a<1$, set

$$\begin{aligned} H_a(R)=\frac{1+R^2-h_a(R)}{2a}h_a(R)^{1-a},\quad -1<R<1. \end{aligned}$$

(7)

Then, for every $0<a,b<1$ such that $2a+b-1>0$, there exists $0<R_{a,b}<1/2$ such that

$$\begin{aligned} \frac{H_{a+b}(R_{a,b})}{H_a(R_{a,b})}>1. \end{aligned}$$

Proof

First, note that $h(a,R)\in \mathbb {R}$. Now, for fixed $0<a<2$, it is easy to prove that the McLaurin expansion of $h_a(R)$ is:

$$\begin{aligned} h_a(R)=1+(1-2a)R^2+2a(1-a)^2R^4+o(R^4). \end{aligned}$$

Thus,

$$\begin{aligned} H_a(R)&=R^2[1-(1-a)^2R^2+o(R^2)]h_a(R)^{1-a} \\&=R^2[1-(1-a)^2R^2+o(R^2)][1+(1-a)(1-2a)R^2+o(R^2)]\\&=R^2[1-a(1-a)R^2+o(R^2)]. \end{aligned}$$

Then, for every $0<a,b<1$ and $R\ne 0$, we have

$$\begin{aligned} \frac{H_{a+b}(R)}{H_a(R)}=\frac{1-(a+b)(1-a-b)R^2+o(R^2)}{1-a(1-a)R^2+o(R^2)}=1+b(2a+b-1)R^2+o(R^2). \end{aligned}$$

In consequence, the lemma holds since $b(2a+b-1)+o(R^2)/R^2>0$ at least for $R_{a,b}$ sufficiently close to 0. $\square$

Lemma 3.3

For every $0<a<1$ and $0<R<1$ we set

$$\begin{aligned} F_{a,R}(t)=\frac{4t-(t+1-R^2)^2}{4t^a},\quad t\in \left[ (1-R)^2,(1+R)^2\right] , \end{aligned}$$

(8)

and

$$\begin{aligned} t_{a,R}=\frac{1-a}{2-a}(1+R^2)+\frac{1}{2-a}\sqrt{1+2[1-2a(2-a)]R^2+R^4}. \end{aligned}$$

(9)

Then,

$$\begin{aligned} \max _{t\in [(1-R)^2,(1+R)^2]}F_{a,R}(t)=F_{a,R}(t_{a,R})=H_a(R), \end{aligned}$$

(10)

where $H_a(R)$ is defined as in Lemma 3.2. Besides, if

$$\begin{aligned} \frac{1-R^2}{1+3R^2}\le \gamma \le 1, \end{aligned}$$

(11)

we have

$$\begin{aligned} F_{a,R}(\gamma t_{a,R})\ge \gamma ^{2-a} F_{a,R}(t_{a,R}). \end{aligned}$$

(12)

Proof

It is easy to see that

$$\begin{aligned} F_{a,R}(t)=\frac{-t^2+2(1+R^2)t-(1-R^2)^2}{4t^a}. \end{aligned}$$

(13)

Thus, $F_{a,R}((1-R)^2)=F_{a,R}((1+R)^2)=0$. Besides, the derivative is

$$\begin{aligned} F'_{a,R}(t)=\frac{-(2-a)t^2+2(1-a)(1+R^2)t+a(1-R^2)^2}{4t^{a+1}}. \end{aligned}$$

It is easy to check that the equation

$$\begin{aligned} -(2-a)t^2+2(1-a)(1+R^2)t+a(1-R^2)^2=0 \end{aligned}$$

(14)

has one root less than $(1-R)^2$ and the other root, $t_{a,R}$, satisfies (9). With routine calculations one can check that

$$\begin{aligned} (1-R)^2<1-R^2<t_{a,R}<1+R^2<(1+R)^2. \end{aligned}$$

(15)

Thus, $F_{a,R}$ increases from $(1-R)^2$ to $t_{a,R}$ and decreases from $t_{a,R}$ to $(1+R)^2$, so the left equality in (10) holds.

Now, by (13) and (14) with $t_{a,R}$ instead of t, it follows that

$$\begin{aligned} F_{a,R}(t_{a,R})=\frac{(1+R^2-t_{a,R})t_{a,R}^{1-a}}{2a}. \end{aligned}$$

(16)

Comparing (16) and (7), and taking into account that $t_{a,R}$ has the same expression as $h_a(R)$ in (6) we obtain the right hand side equality in (10).

By (15) and (11) we have that $(1-R)^2\le \gamma t_{a,R}\le t_{a,R}$. Thus, $\gamma t_{a,R}$ is in the domain of $F_{a,R}$. Using (13), it is easy to check that inequality (12) is equivalent to

$$\begin{aligned} 2(1+R^2)\gamma t_{a,R}\ge (1-R^2)^2(1+\gamma ), \end{aligned}$$

which easily follows from (15) and (11). $\square$

Remark 3.4

Denote by $\mathbb {S}^{d-1}=\{x\in \mathbb {R}^d: |x|=1\}$ the unit $(d-1)$-dimensional sphere in $\mathbb {R}^d$, and by $\omega _{d-1}=|\mathbb {S}^{d-1}|_{d-1}$, its $(d-1)$-dimensional Hausdorff measure.

Since we deal with radial measures $dx/|x|^{\alpha d}$ and we will use radial measurable functions g(|x|), $x\in \mathbb {R}^d$, it will be natural to use a spherical change of coordinates. Thus, it is easy to see that

$$\begin{aligned} \int _{B(0,R)}g(|x|)\frac{dx}{|x|^{\alpha d}}=\omega _{d-1}\int _0^Rg(\rho )\rho ^{d(1-\alpha )}\frac{d\rho }{\rho }. \end{aligned}$$

(17)

When the ball is not centered at the origin, things are not so straightforward. To simplify the proof of the theorem, in the next Lemma, we integrate over a ball that does not touch the origin. These computations appeared in [9, 18]. We include them here for the reader’s convenience. $\square$

Lemma 3.5

Let $0<\alpha <1$, $0<R<1/2$ and let $g(|\cdot |)$ be a measurable radial function on $\mathbb {R}^d$. Let $e_1\in \mathbb {R}^d$ be the first vector in the standard basis. Then,

$$\begin{aligned} \frac{\omega _{d-2}}{d-1}\int _{1-R}^{1+R}F_{\alpha ,R}(\rho ^2)^\frac{d-1}{2}g(\rho )\frac{d\rho }{\rho ^\alpha }\le & {} \int _{B(e_1,R)}g(|x|)\frac{dx}{|x|^{\alpha d}}\\\le & {} \frac{2}{\sqrt{3}} \frac{\omega _{d-2}}{d-1}\int _{1-R}^{1+R}F_{\alpha ,R}(\rho ^2)^\frac{d-1}{2}g(\rho )\frac{d\rho }{\rho ^\alpha }, \end{aligned}$$

where $F_{\alpha ,R}$ is defined in (8).

Proof

By changing to spherical coordinates, we have

$$\begin{aligned} \int _{B(e_1,R)}g(|x|)\frac{dx}{|x|^{\alpha d}}=\int _{1-R}^{1+R}|\partial B(0,\rho )\cap B(e_1,R)|_{d-1}g(\rho )\frac{d\rho }{\rho ^{\alpha d}}, \end{aligned}$$

where $|\cdot |_{d-1}$ denotes the $(d-1)$-dimensional Hausdorff measure. Call $\beta _\rho$ the angle determined by the segment that joins the origin with $e_1$ and the one that connects the origin to any point of the intersection of $\partial B(0,\rho )$ with $\partial B(e_1,R)$. Then $0\le \beta _\rho <\pi /6$ since $R<1/2$. Thus,

$$\begin{aligned} |\partial B(0,\rho )\cap B(e_1,R)|_{d-1}= & {} \int _0^{\beta _\rho }\omega _{d-2}(\rho \sin \theta )^{d-2}\rho d\theta \nonumber \\= & {} \omega _{d-2}\rho ^{d-1}\int _0^{\beta _\rho }(\sin \theta )^{d-2} d\theta . \end{aligned}$$

(18)

By the cosine law, applied to the triangle $T(1,\rho ,R)$ with side lengths 1, $\rho$, and R, and the angle $\beta _\rho$ facing the R-side, we have

$$\begin{aligned} \cos \beta _\rho =\frac{1+\rho ^2-R^2}{2\rho }, \end{aligned}$$

(19)

so

$$\begin{aligned} \sin \beta _\rho =\left[ 1-\left( \frac{1+\rho ^2-R^2}{2\rho }\right) ^2\right] ^{1/2}. \end{aligned}$$

(20)

Note that the minimum value of $\cos \beta _\rho$ occurs when $\beta _\rho$ attains its maximum value. And this happens when the ray starting at 0 is tangent to $B(e_1,R)$, so the triangle $T(1,\rho ,R)$ has a right angle and hence $\rho =\sqrt{1-R^2}$. Thus, by (19) we have that for every $\rho \in [1-R,1+R]$,

$$\begin{aligned} \cos \beta _\rho \ge \frac{1+(\sqrt{1-R^2})^2-R^2}{2\sqrt{1-R^2}}=\sqrt{1-R^2}. \end{aligned}$$

Now, with this inequality and (18), we obtain

$$\begin{aligned} \omega _{d-2}\rho ^{d-1}\int _0^{\beta _\rho }\cos \theta (\sin \theta )^{d-2} d\theta\le & {} |\partial B(0,\rho )\cap B(e_1,R)|_{d-1}\\\le & {} \frac{\omega _{d-2}\rho ^{d-1}}{\sqrt{1-R^2}}\int _0^{\beta _\rho }\cos \theta (\sin \theta )^{d-2} d\theta . \end{aligned}$$

In consequence,

$$\begin{aligned} \frac{\omega _{d-2}}{d-1}\rho ^{d-1}(\sin \beta _\rho )^{d-1}\le & {} |\partial B(0,\rho )\cap B(e_1,R)|_{d-1}\\\le & {} \frac{1}{\sqrt{1-R^2}}\frac{\omega _{d-2}}{d-1}\rho ^{d-1}(\sin \beta _\rho )^{d-1}. \end{aligned}$$

Using this inequality and (20), the lemma is proved. $\square$

4 Proof of the Theorem

Proof of Theorem 2.1

First, fix $0<\alpha <1$ and $p\ge 1$ such that $(1-2\alpha )p\le 1-\alpha$. Now we apply Lemma 3.2 with $a=\alpha$ and $b=(1-\alpha )/p$. Then, since $2a+b>1$, there exists $0<R_{\alpha ,\alpha +(1-\alpha )/p}<1/2$ depending on $\alpha$ and p such that

$$\begin{aligned} \frac{H_{\alpha +(1-\alpha )/p}(R_{\alpha ,\alpha +(1-\alpha )/p})}{H_\alpha (R_{\alpha ,\alpha +(1-\alpha )/p})}>1. \end{aligned}$$

We denote the previous quotient by $K(\alpha ,p)^2>1$. Let us fix this $R_{\alpha ,\alpha +(1-\alpha )/p}$; for simplicity we write $R\equiv R_{\alpha ,\alpha +(1-\alpha )/p}$. Now, for these values of R and $\alpha$, we set $t_{\alpha ,R}$ as in (9).

Define $T:=\sqrt{t_{\alpha +(1-\alpha )/p,R}}$. Since $t_{\alpha +(1-\alpha )/p,R}\in [(1-R)^2,(1+R)^2]$, it follows that $T\in (1-R,1+R)$. Moreover, since (15) and $R<1/2$ we have

$$\begin{aligned} T\ge \sqrt{1-R^2}\ge \frac{\sqrt{3}}{2}. \end{aligned}$$

Let us define

$$\begin{aligned} f(x)= & {} g(|x|)=\frac{1}{\left( (1-1/d\right) T)^{\frac{1-\alpha }{p}d}} \chi _{[0,(1-1/d)T)}(|x|)\\&+\frac{1}{|x|^{\frac{1-\alpha }{p}d}}\chi _{[(1-1/d)T,T]}(|x|),\quad x\in \mathbb {R}^d. \end{aligned}$$

Note that f is radially decreasing. Furthermore, from (17) we obtain

$$\begin{aligned} \Vert f\Vert _{p,\mu }^p&=\frac{1}{\left( \left( 1-1/d\right) T\right) ^{(1-\alpha )d}}\int _{B(0,(1-1/d)T)}\frac{dx}{|x|^{\alpha d}}\\&\quad +\int _{B(0,T)\setminus B(0,(1-1/d)T)}\frac{dx}{|x|^{d}} \\&=\frac{\omega _{d-1}}{\left( \left( 1-1/d\right) T\right) ^{(1-\alpha )d}}\int _0^{(1-1/d)T}\rho ^{d(1-\alpha )}\frac{d\rho }{\rho }\\&\quad +\omega _{d-1}\int _{(1-1/d)T}^T \frac{d\rho }{\rho } \\&=\omega _{d-1}\left( \frac{1}{d(1-\alpha )}-\log (1-1/d)\right) \\&=\frac{\omega _{d-1}}{d}\left( \frac{1}{1-\alpha }+\log \left( (1-1/d)^{-d}\right) \right) . \end{aligned}$$

Since $(1-1/d)^{-d}$ decreases in d and $d\ge 3$, we have

$$\begin{aligned} \Vert f\Vert _{p,\mu }^p\le \frac{\omega _{d-1}}{d}\left( \frac{1}{1-\alpha }+3\log (3/2)\right) . \end{aligned}$$

(21)

Utilizing again (17), we compute

$$\begin{aligned}&\mu \left( B(0,1)\setminus B(0,1-1/d)\right) =\omega _{d-1}\int _{1-1/d}^1 \rho ^{d(1-\alpha )}\frac{d\rho }{\rho } \nonumber \\&\quad =\frac{\omega _{d-1}}{d(1-\alpha )}\left( 1-(1-1/d)^{d(1-\alpha )}\right) \nonumber \\&\quad \ge \frac{\omega _{d-1}}{d(1-\alpha )}\left( 1-e^{-(1-\alpha )}\right) \ge \frac{\omega _{d-1}}{d}(1-e^{-1}). \end{aligned}$$

(22)

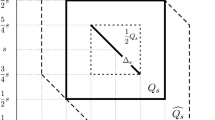
Next, given $x\in B(0,1)\setminus B(0,1-1/d)$, we present a lower bound for its averaging function

$$\begin{aligned} A_{R,\mu }f(x)=\frac{\int _{B(x,R)}f(y)\frac{dy}{|y|^{\alpha d}}}{\int _{B(x,R)}\frac{dy}{|y|^{\alpha d}}}. \end{aligned}$$

(23)

Let us note that radial functions are invariant with respect rotations at the origin, while a ball remains a ball after any rigid motion. Thus,

$$\begin{aligned} \int _{B(x,R)}f(y)\frac{dy}{|y|^{\alpha d}}= & {} \int _{B(|x|e_1,R)}f(y)\frac{dy}{|y|^{\alpha d}}\quad \text {and}\quad \int _{B(x,R)}\frac{dy}{|y|^{\alpha d}}\nonumber \\= & {} \int _{B(|x|e_1,R)}\frac{dy}{|y|^{\alpha d}}. \end{aligned}$$

(24)

Besides, since f is radially decreasing, we have

$$\begin{aligned} \int _{B(|x|e_1,R)}f(y)\frac{dy}{|y|^{\alpha d}}\ge & {} \int _{B(e_1,R)}f(y)\frac{dy}{|y|^{\alpha d}}\quad \text {and}\quad \int _{B(|x|e_1,R)}\frac{dy}{|y|^{\alpha d}}\nonumber \\\le & {} \int _{B((1-1/d)e_1,R)}\frac{dy}{|y|^{\alpha d}}. \end{aligned}$$

(25)

Moreover,

$$\begin{aligned} \int _{B((1-1/d)e_1,R)}\frac{dy}{|y|^{\alpha d}}= & {} \int _{B(e_1,R)}\frac{dy}{|y-e_1/d|^{\alpha d}} \nonumber \\= & {} \int _{B(e_1,R)}\frac{|y|^{\alpha d}}{|y-e_1/d|^{\alpha d}}\frac{dy}{|y|^{\alpha d}}\nonumber \\\le & {} \int _{B(e_1,R)}\left( \frac{|y|}{|y|-1/d}\right) ^{\alpha d}\frac{dy}{|y|^{\alpha d}} \nonumber \\= & {} \int _{B(e_1,R)}\left( \frac{1}{1-1/(d|y|)}\right) ^{\alpha d}\frac{dy}{|y|^{\alpha d}} \nonumber \\\le & {} \left( \frac{1}{1-\frac{1}{d(1-R)}}\right) ^{\alpha d}\int _{B(e_1,R)}\frac{dy}{|y|^{\alpha d}} \nonumber \\\le & {} 3^{3\alpha }\int _{B(e_1,R)}\frac{dy}{|y|^{\alpha d}}. \end{aligned}$$

(26)

By (23), (24), (25) and (26) we get

$$\begin{aligned} A_{R,\mu }f(x)\ge \frac{\int _{B(e_1,R)}f(y)\frac{dy}{|y|^{\alpha d}}}{27\int _{B(e_1,R)}\frac{dy}{|y|^{\alpha d}}},\quad x\in B(0,1)\setminus B(0,1-1/d). \end{aligned}$$

(27)

Now, using Lemma 3.5, we estimate the integrals from (27). For the integral in the denominator, Lemma 3.5 together with (10) leads to

$$\begin{aligned} \int _{B(e_1,R)}\frac{dy}{|y|^{\alpha d}}\le & {} \frac{2}{\sqrt{3}}\frac{\omega _{d-2}}{d-1}\int _{1-R}^{1+R}F_{\alpha ,R}(\rho ^2)^\frac{d-1}{2}\frac{d\rho }{\rho ^\alpha } \nonumber \\\le & {} \frac{2}{\sqrt{3}}\frac{\omega _{d-2}}{d-1}H_\alpha (R)^\frac{d-1}{2}\int _{1-R}^{1+R}\frac{d\rho }{\rho ^\alpha } \nonumber \\\le & {} \frac{4}{\sqrt{3}}\frac{\omega _{d-2}}{d-1}H_\alpha (R)^\frac{d-1}{2}. \end{aligned}$$

(28)

For the integral in the numerator,

$$\begin{aligned} \int _{B(e_1,R)}f(y)\frac{dy}{|y|^{\alpha d}}&\ge \frac{\omega _{d-2}}{d-1}\int _{1-R}^{1+R}F_{\alpha ,R}(\rho ^2)^\frac{d-1}{2}g(\rho )\frac{d\rho }{\rho ^\alpha }\\&\ge \frac{\omega _{d-2}}{d-1}\int _{(1-1/d)T}^{T}F_{\alpha ,R}(\rho ^2)^\frac{d-1}{2}g(\rho )\frac{d\rho }{\rho ^\alpha }= \\&= \frac{\omega _{d-2}}{d-1}\int _{(1-1/d)T}^{T}F_{\alpha +\frac{1-\alpha }{p},R}(\rho ^2)^\frac{d-1}{2}\frac{d\rho }{\rho ^{\alpha +\frac{1-\alpha }{p}}}. \end{aligned}$$

We choose $\gamma =\max \{(1-1/d)^2,(1-R^2)/(1+3R^2)\}$. From this last inequality and (12) we get

$$\begin{aligned} \int _{B(e_1,R)}f(y)\frac{dy}{|y|^{\alpha d}}\ge & {} \frac{\omega _{d-2}}{d-1}\int _{T\sqrt{\gamma }}^{T}\frac{d\rho }{\rho ^{\alpha +\frac{1-\alpha }{p}}}\min _{t\in [\gamma t_{a,R},t_{a,R}]}F_{\alpha +\frac{1-\alpha }{p},R}(t)^\frac{d-1}{2}\nonumber \\\ge & {} \frac{\omega _{d-2}}{d-1}\left( T\right) ^{1-\alpha -(1-\alpha )/p}(1-\sqrt{\gamma })H_{\alpha +\frac{1-\alpha }{p}}(R)^\frac{d-1}{2}\gamma ^{d-1}\nonumber \\\ge & {} \frac{\sqrt{3}\,\omega _{d-2}}{2(d-1)}(1-\sqrt{\gamma })H_{\alpha +\frac{1-\alpha }{p}}(R)^\frac{d-1}{2}\gamma ^{d-1}. \end{aligned}$$

(29)

Now, since

$$\begin{aligned} \gamma ^{d-1}\ge \gamma ^d\ge \left( 1-\frac{1}{d}\right) ^{2d}\ge (2/3)^6, \end{aligned}$$

and

$$\begin{aligned} 1-\sqrt{\gamma }= \min \left\{ \frac{1}{d},1-\sqrt{\frac{1-R^2}{1+3R^2}}\right\} \ge \min \left\{ \frac{1}{d},R^2\right\} , \end{aligned}$$

we can bound (29) and get

$$\begin{aligned} \int _{B(e_1,R)}f(y)\frac{dy}{|y|^{\alpha d}}\ge \frac{2^5}{3^{11/2}} \min \left\{ \frac{1}{d},R^2\right\} \frac{\,\omega _{d-2}}{d-1}H_{\alpha +\frac{1-\alpha }{p}}(R)^\frac{d-1}{2}. \end{aligned}$$

(30)

In conclusion, from (27), (28) and (30) it follows that

$$\begin{aligned} A_Rf(x)\ge & {} \frac{2^3}{3^{8}}\min \left\{ \frac{1}{d},R^2\right\} \left( \frac{H_{\alpha +(1-\alpha )/p}(R)}{H_\alpha (R)}\right) ^{(d-1)/2}\\= & {} \frac{2^3}{3^{8}}\min \left\{ \frac{1}{d},R^2\right\} \left( K(\alpha ,p) \right) ^{d-1}, \end{aligned}$$

for all $x\in B(0,1)\setminus B(0,1-1/d)$. Now, we choose $\lambda =\frac{2^3}{3^{8}}\min \left\{ \frac{1}{d},R^2\right\} \left( K(\alpha ,p)\right) ^{d-1}$. Then, by (21) and (22)

$$\begin{aligned} \zeta _{p,d,\mu }&\ge \frac{\lambda \mu (\{x\in \mathbb {R}^d:A_{R,\mu }f(x)\ge \lambda \})^{1/p}}{\Vert f\Vert _{p,\mu }}\ge \lambda \frac{ \mu (B(0,1)\setminus B(0,1-1/d))^{1/p}}{\Vert f\Vert _{p,\mu }}\\&\ge \frac{2^3}{3^{8}} \left( \frac{1-e^{-1}}{\frac{1}{1-\alpha }+3\log (3/2)}\right) ^{1/p}\min \left\{ \frac{ 1}{d},R^2\right\} \left( K(\alpha ,p)\right) ^{d-1}. \end{aligned}$$