On Narrow Operators from $L_p$ into Operator Ideals

Abstract

It is well known that every $l_2$-strictly singular operator from $L_p$, $1<p<\infty$ to any Banach space X with an unconditional basis is narrow. In this article, we extend this result to the setting of Banach spaces without an unconditional basis. We show that if $1 \le p,r <\infty$, then every $\ell _2$-strictly singular operator T from $L_p$ into the Schatten–von Neumann r-class $C_r$ is narrow. This is a noncommutative complement to results in Mykhaylyuk et al. (in Israel J Math 203:81–108, 2014).

1 Introduction

Let F(0, 1) be a separable symmetric function space of (classes of equivalent) Lebesgue measurable functions on (0, 1). Suppose that A is a measurable subset of (0, 1). By a sign on A we mean an element $x\in L_{\infty }(0,1)$ with $\text {supp}\,x=A$ which takes values in $\{-1,0,1\}$. We say that $x\in F(0,1)$ is a mean zero sign on A if x is a sign on A and $\int _0^1 x d\mu =0$. Let X be a Banach space and L(F(0, 1), X) be the space of all bounded linear operators from F(0, 1) into X. We say that a linear operator $T\in L(F(0,1),X)$ is narrow if for every $\varepsilon >0$ and every measurable set $A\subset (0,1)$, there exists a mean zero sign x on A, such that $\left\Vert {Tx}\right\Vert _X <\varepsilon$. The notion of narrow operators was formally introduced by Plichko and Popov [18] for operators acting on symmetric function spaces (in fact, the study of operators of this type goes back to Bourgain, Ghoussoub and Rosenthal, see [18, 19, 22] and references therein).

In 1990, Plichko and Popov [18] asked whether every $\ell _2$-strictly singular operator $T:L_p\rightarrow X$ is necessarily narrow (see also [19] and [20, Problem 1.6]). Here, an operator T is said to be $\ell _2$-strictly singular if it is not an isomorphism when restricted to any isomorphic copy of $\ell _2$ in $L_p$.

When $1\le p<2$ and $p<r$, it is proved in [13, Theorem 5] that every operator $T:L_p \rightarrow \ell _r$ is narrow. It is also known that when $1\le r<2$ and $1\le p<\infty$, every operator $T:L_p \rightarrow \ell _r$ is narrow [18, Proposition 2]. The remaining cases were settled in [16]. Precisely, [16, Theorem A] shows that every $T:L_p\rightarrow \ell _r$ is narrow when $1\le p<\infty$ and $1\le r\ne 2<\infty$ or $1\le p<2$ and $r=2$. Moreover, when $p>2$ and $r=2$, there exists a non-narrow operator $T:L_p\rightarrow \ell _2$ [16, Example 1.1]. Finally, [16, Theorem B] asserts that every $\ell _2$-strictly singular operator $T:L_p\rightarrow X$ is necessarily narrow provided that X has an unconditional basis.

The main objective of this paper is to establish a noncommutative generalization of [16, Theorems A and B] for the situation where we deal with $\ell _2$-strictly singular operators $T:L_p\rightarrow X$ if the space X does not possess an unconditional basis. For all unexplained notions and notations we refer the reader to [1, 11, 12].

Let E be a separable symmetric sequence space [2, 14], that is, a Banach space of sequences such that the standard unit vectors $e_n$’s, $n=1,2,3,\ldots$, (defined by $e_n(j)=\delta _{n,j}$) form a normalized, 1-symmetric basis of E. Let $C_E$ be the ideal in $B(\ell _2 )$ corresponding to E (see [2, 14]), i.e., the Banach space of all compact operators x on $\ell _2$ for which $s(x)\in E$, normed by

$$\begin{aligned} \left\| x \right\| _{C_E}=\Vert s(x)\Vert _{E}. \end{aligned}$$

Here, $s(x)=\{s_n(x)\}_{n=1}^\infty$ is the sequence of s-numbers of x, i.e., the eigenvalues of $|x|=(x^*x)^{\frac{1}{2}}$ arranged in a non-increasing ordering, counting multiplicity. In the case when $E=\ell _p$, the ideal $C_{\ell _p}$ is denoted simply by $C_p$.

Let $\{e_{ij}\}_{i,j\ge 1}$ be the matrix unit of $C_E$. Let $T_E$ be the upper triangular part of $C_E$, i.e., $x\in T_E$ if and only if $x:= (x_{ij})\in C_E$ with $x_{ij }=0$ when ${i>j}$.

Note that all preceding results in this area are established only for spaces X either with unconditional bases or for Banach lattices [19], whereas the spaces $C_E$ do not even possess the local unconditional structure [7]. In particular, it follows from [10] that the ideal $C_E$ has an unconditional basis if and only if it coincides with the Hilbert–Schmidt ideal.

Our approach to the study of narrow operators $T:L_p\rightarrow X$ when $X=T_E$ or $X=C_E$ is based on a fundamental fact that the spaces $T_E$ admit the finite-dimensional unconditional (Schauder) decomposition (UFDD) given by elements $\{\mathrm{span}\{e_{ij}\}_{1\le i\le j} \}_{j\ge 1}$ (see for details [2, Proposition 4.9]). Recall also that $T_E$ is isomorphic to $C_E$ when E has non-trivial Boyd indices [2, Theorem 4.7] (see also [3, Proposition 2] and [15]).

This setting has been already explored in [8], where assuming the so-called 2-co-lacunary property (see [25]), the authors of the present article obtained a noncommutative version of [18, Proposition 2]. Precisely, since $C_r$, $r\le 2$, is 2-co-lacunary, it follows from [8, Theorem 4.3 and Remark 4.4] that every $\ell _2$-strictly singular operator $T:L_p \rightarrow C_r$ is narrow when $1\le p <\infty$ and $1\le r\le 2$. However, the case of $r>2$ remains unresolved and this case cannot be treated by methods from [8].

The following theorem is a noncommutative analogue of [16, Theorem A], which answers Plichko and Popov’s question for Banach spaces $C_r$, $r>2$ and resolves the unanswered cases in [8]. Our proof is motivated by an extended version of reproducibility hatched within noncommutative analysis in [4]. Based on a careful analysis of approach used in [16], we obtain a slight extension of [16, Proposition 3.1] concerning on the reproducibility (with respect to non-narrow operators) of the Haar basis in $L_p$ (see Proposition 2.2 below). Our approach is applicable to a much wider class of operator ideals than the class of (Schatten–von Neumann ideals) $C_r$, $2<r<\infty$. The main result of the present paper, Theorem 1.1 below, is stated for ideals $C_E$, for which the symmetric space E is satisfying an upper r-estimate (see, e.g. [12]), which extends and complements results in [6, 8, 13, 16, 18].

Theorem 1.1

Let $2<r<\infty$ and let F(0, 1) be a separable symmetric function space having the Khintchine property. If E is a separable symmetric sequence space satisfying an upper r-estimate, then every $\ell _2$-strictly singular operator $T:F(0,1)\rightarrow T_E$ is narrow.

Recall that $T_p: =T_{C_p}$ is isomorphic to $C_p$ when $p>1$ [2, Theorem 4.7] (see also [3, Proposition 2] and [15]) and $L_p$ has the Khintchine property when $p\in [1,\infty )$ (see, e.g. [12] or [21]). Combining Theorem 1.1 with [8, Theorem 4.3], we obtain the following corollary. Note that [16, Theorem A] does not hold if we replace $\ell _r$ with $C_r$ (i.e., there exist operators $T: L_p \rightarrow C_2$, $p>2$, which are not narrow, see e.g. Remark 3.4 below or [16, Theorem A and Example 1.1]).

Corollary 1.2

Let $1\le p,r<\infty$. Every $\ell _2$-strictly singular operator $T:L_p \rightarrow C_r$ is narrow.

The authors thank Professor Popov for discussion concerning results presented in [16] and [19]. We also thank the anonymous reviewer for his/her careful reading and helpful comments.

2 Proof of Theorem 1.1

Let S(0, 1) be the space of all Lebesgue measurable functions on (0, 1) equipped with Lebesgue measure m i.e. functions which coincide almost everywhere are considered identical.

For $x\in S(0,1)$, we denote by $x^*$ the decreasing rearrangement of the function |x|. That is,

$$\begin{aligned} x^*(t)=\inf \left\{ s\ge 0:\ m(\{|x|>s\})\le t \right\} ,\quad t>0. \end{aligned}$$

Definition 2.1

Let $E(0,1)\subset S(0,1)$ be a Banach space. We say that $(E(0,1),\left\| \cdot \right\| _E)$ is a symmetric function space on (0, 1) if whenever $x\in E(0,1)$ and $y\in S(0,1)$ are such that $y^*\le x^*,$ then $y\in E(0,1)$ and $\left\| y\right\| _E\le \left\| x\right\| _E$.

We recall some basic terminology concerning Schauder decomposition [11, Chapter 1, Section g]. Let X be a Banach space. A sequence $\{X_n\}_{n=1}^\infty$ of closed subspaces of X is called a Schauder decomposition of X if every $x\in X$ has a unique representation of the form

$$\begin{aligned} x=\sum _{n=1}^\infty x_n \end{aligned}$$

with $x_n \in X_n$ for every $n \ge 1$.

If $\{X_n\}_{n=1}^\infty$ is a Schauder decomposition of X and if for any $x=\sum _{n=1}^\infty x_n\in X$ and any sequence $\epsilon =\{\epsilon _n=\pm 1 \}_{n=1}^\infty$, the series

$$\begin{aligned} \sum _{n=1}^\infty \epsilon _n x_n \end{aligned}$$

converges in X [1, Lemma 2.4.2], then the sequence $\{X_n\}_{n=1}^\infty$ is said to form an unconditional Schauder decomposition of X. Moreover, the operator $M_{\epsilon }x:=\sum _{i=1}^\infty \epsilon _n x_n$ is bounded and $\sup _\epsilon \left\Vert {M_\epsilon }\right\Vert <\infty$ (see e.g. [4] or [1, Proposition 3.1.3]).

Recall that a Schauder basis $\{x_n\}_{n=1}^\infty$ of a Banach space X is said to be K-reproducible for some $K\ge 1$, if for every isometric embedding of X into a space Y with a basis $\{y_k\}_{k=1}^\infty$ and every $\varepsilon >0$, there exists a block basis $\{z_n\}_{n=1}^\infty$ of $\{y_k\}_{k=1}^\infty$ which is $K+\varepsilon$-equivalent to $\{x_n\}_{n\ge 1}$. When $K=1$, the basis is said to be precisely reproducible. It is well-known that the Haar system in an arbitrary separable symmetric function space on (0, 1) is precisely reproducible [12, Theorem 2.c.8] (see also [17]).

In noncommutative analysis, there is a more useful notion of reproducibility. A Schauder basis $\{x_n\}_{n=1}^\infty$ of a Banach space X is said to be precisely finite-dimensional decomposition (FDD)-reproducible, if for every isometric embedding of X into a space Y with a finite-dimensional decomposition $\{Y_n\}_{n \ge 1}$ and every $\varepsilon >0$, there exists an increasing sequence $\{q_n\}_{n =1}^\infty$ of positive integers and a basic sequence of elements $z_n = \sum _{q_n \le k\le q_{n+1} -1}\lambda _k y_k$ ($y_k\in Y_k, \lambda _k \in \mathbb {R}$), which is $(1+\varepsilon )$-equivalent to $\{x_n\}$. It was observed in [4, Theorem 5.2] that [12, Theorem 2.c.8] can be improved, that is, the Haar system in an arbitrary separable symmetric function space is precisely FDD-reproducible.

In [16, Proposition 3.1], Mykhaylyuk et al. considered the reproducibility of the ($L_p$-normalized) Haar system $\{h_n\}_{n\ge 1}$ with respect to non-narrow operators. Note that [16, Proposition 3.1] can be easily generalized from the case of $L_p$-space, $1\le p<\infty$, to the case where F(0, 1) is an arbitrary separable symmetric space on (0, 1). The following proposition is a slight generalization of [16, Proposition 3.1] with respect to the FDD-reproducibility.

Proposition 2.2

[16, Proposition 3.1] Suppose that F(0, 1) is an arbitrary separable symmetric function space, X is a Banach space with a basis $(e_n)$, $T\in L (F(0,1), X)$ satisfies $\left\Vert {Tx}\right\Vert _X \ge 2\delta$ for each mean zero sign $x\in F(0,1)$ on (0, 1) and some $\delta >0$. Let $\{X_n=\mathrm{span}\{e_k\}_{k= q_n}^{q_{n+1}-1}\}_{n=1}^\infty$ be a finite-dimensional decomposition of X, where $\{q_n\}_{n\ge 1}$ is an arbitrary increasing sequence of positive integers.

Then, for each $\varepsilon >0$, there exist an operator $S\in L(F(0,1), X)$, an increasing sequence $\{p_n\}_{n\ge 1}$ of positive integers, a normalized basis $(u_n )$ such that $u_n = \sum _{p_n \le k\le p_{n+1} -1}\lambda _k x_k$ ($x_k\in X_k, \lambda _k \in \mathbb {R}$), and real numbers $(a_n)$ such that

• (1) $Sh_n =a_n u_n$ for each $n \in \mathbb {N}$ with $a_1 =0$;

• (2) $\left\Vert {Sx}\right\Vert _X \ge \delta$ for each mean zero sign $x\in F(0,1)$ on (0, 1);

• (3) there exists a linear isometry $V:F(0,1) \rightarrow _{into} F(0,1)$, which sends signs to signs, so that $\left\Vert {Sx}\right\Vert _X \le \left\Vert {TVx}\right\Vert _X +\varepsilon$ for every $x\in F(0,1)$ with $\left\Vert {x}\right\Vert _{F(0,1) }=1$;

• (4) there are finite codimensional subspaces $X_n$’s of F(0, 1) such that $\left\Vert {Sx}\right\Vert _X\le \left\Vert {TVx}\right\Vert _X +\frac{1}{n}$ for every $x\in X_n$ with $\left\Vert {x}\right\Vert _{F(0,1) } =1$.

If, moreover, $\left\Vert {Tx}\right\Vert _X \ge 2\delta \left\Vert {x}\right\Vert _{F(0,1) }$ for every sign x, then $|a_n|\ge \delta$ for each $n \ge 2$.

Proof

The proof is almost a verbatim repetition of that in [16, Proposition 3.1]. The only difference is that we need to consider a subsequence of the basis projections in the Banach space X while the proof in [16, Proposition 3.1] simply proceeded with the set of all basis projections.

More precisely, let $(P_n)_{n=1}^\infty$ be the basis projections in X with respect to the basis $\{e_k\}_{k\ge 1}$ and $P_0=0$. Recall that $X_n=\mathrm{span}\{e_k\}_{k= q_n}^{q_{n+1}-1}$ for every $n\ge 1$. Let

$$\begin{aligned} Q_n =P_{q_{n+1}-1} \text{ and } Q_0=0. \end{aligned}$$

In particular, $Q_n$ is the projection onto $\mathrm{clm} \{ X_k\}_{k=1}^n$. Now, the claim of Proposition 2.2 can be obtained from the proof of [16, Proposition 3.1] (see also [19, Proposition 9.10]) by simply replacing $P_n$ with $Q_n$ throughout. Since our other arguments repeat [16, Proposition 3.1] we omit further details. $\square$

The following proposition is well known to experts [16, 19]. We include a proof below for completeness.

Proposition 2.3

Let T and S be as in Proposition 2.2. If T is $\ell _2$-strictly singular, then S is also $\ell _2$-strictly singular.

Proof

Assume by contradiction that S is not $\ell _2$-strictly singular. That is, there exists a sequence $(x_n)_{n=1}^\infty$ in F(0, 1) which is equivalent to the natural basis of $\ell _2$, and a constant $c>0$ such that

$$\begin{aligned} c^{-1} \left\Vert {(\lambda _n)}\right\Vert _{\ell _2} \le \left\Vert {\sum _{n=1}^\infty \lambda _n x_n}\right\Vert _{F(0,1)}\le c \left\Vert {(\lambda _n)}\right\Vert _{\ell _2}, ~\forall (\lambda _n)\in \ell _2 \end{aligned}$$

(2.1)

and a constant $C>0$ such that

$$\begin{aligned} C^{-1} \left\Vert {(\lambda _n)}\right\Vert _{\ell _2} \le \left\Vert {S\left( \sum _{n=1}^\infty \lambda _n x_n\right) }\right\Vert _X\le C \left\Vert {(\lambda _n)}\right\Vert _{\ell _2}, ~\forall (\lambda _n)\in \ell _2. \end{aligned}$$

(2.2)

Let $k\in \mathbb {N}$ be so large that $\frac{1}{k}(1+\frac{1}{k})^2 \le \frac{1}{2} c^{-1}C^{-1 }$. By (4) of Proposition 2.2, there is a finite codimensional subspace $X_k$ of F(0, 1) such that

$$\begin{aligned} \left\Vert {Sx}\right\Vert \le \left\Vert {TVx}\right\Vert +\frac{1}{k}, \end{aligned}$$

(2.3)

for every $x\in X_k$ with $\left\Vert {x}\right\Vert =1$.

Since every subspace with finite codimension in a Banach space is complemented [23, Lemma 4.21], it follows that there exists a bounded projection P from F(0, 1) onto $X_k$. Since $(x_n)$ is weakly null, it follows that $(1-P)x_n$ is weakly null. Since $X_k$ is finite-codimensional, it follows that $(1-P)x_n\rightarrow 0$ in $\left\Vert {\cdot }\right\Vert _{F(0,1)}$. Therefore, passing to a subsequence if necessary, we may assume that the sequence

$$\begin{aligned} \{y_n:=P(x_n )\}_{n\ge 1} \subset X_k \end{aligned}$$

is $(1+\frac{1}{k})$-equivalent to the basic sequence $\{x_n\}$ and is $c (1+\frac{1}{k})$-equivalent to the natural basis of $\ell _2$. By (2.1) and (2.2), we have

$$\begin{aligned} c^{-1}(1+ \frac{1}{k})^{-1} \left\Vert {(\lambda _n)}\right\Vert _{\ell _2} \le \left\Vert {\sum _{n=1}^\infty \lambda _n y_n}\right\Vert _{F(0,1)}\le c (1+\frac{1}{k}) \left\Vert {(\lambda _n)}\right\Vert _{\ell _2}, ~\forall (\lambda _n)\in \ell _2.\nonumber \\ \end{aligned}$$

(2.4)

Passing to a subsequence if necessary, we may assume that

$$\begin{aligned} C^{-1} (1+ \frac{1}{k})^{-1} \left\Vert {(\lambda _n)}\right\Vert _{\ell _2} \le \left\Vert {S(\sum _{n=1}^\infty \lambda _n y _n)}\right\Vert _X\le C (1+ \frac{1}{k}) \left\Vert {(\lambda _n)}\right\Vert _{\ell _2}, \forall (\lambda _n)\in \ell _2.\nonumber \\ \end{aligned}$$

(2.5)

For any $\sum _{n=1}^\infty \lambda _n y_n \in F(0,1)$ such that $\left\Vert { \sum _{n=1}^\infty \lambda _n y_n }\right\Vert _{F(0,1)}=1$, we have

$$\begin{aligned} c^{-1} C^{-1 } \left\Vert {\sum _{n=1}^\infty \lambda _n y _n}\right\Vert _{F(0,1)}&{\mathop {\le }\limits ^{(2.4)}} (1+ \frac{1}{k}) C^{-1 } \left\Vert {(\lambda _n)}\right\Vert _2 \nonumber \\&{\mathop {\le }\limits ^{(2.5)}} (1+ \frac{1}{k})^2 \left\Vert {S (\sum _{n=1}^\infty \lambda _n y_n)}\right\Vert _X \nonumber \\&{\mathop {\le }\limits ^{(2.3)}} (1+ \frac{1}{k}) ^2 \left\Vert {TV (\sum _{n=1}^\infty \lambda _n y_n)}\right\Vert _X +\frac{1}{k} (1+ \frac{1}{k}) ^2.\nonumber \\ \end{aligned}$$

(2.6)

Recall that $\frac{1}{k}(1+\frac{1}{k})^2 \le \frac{1}{2} c^{-1}C^{-1 }$. For any $\sum _{n=1}^\infty \lambda _n y_n \in F(0,1)$ such that $\left\Vert { \sum _{n=1}^\infty \lambda _n y_n }\right\Vert _{F(0,1)}=1$, we have

$$\begin{aligned} \frac{1}{2} c^{-1}C^{-1 } \left\Vert {\sum _{n=1}^\infty \lambda _n y_n }\right\Vert _{F(0,1)}&= c^{-1}C^{-1 } \left\Vert {\sum _{n=1}^\infty \lambda _n y_n }\right\Vert _{F(0,1)}\\&\quad - \frac{1}{2} c^{-1}C^{-1 } \left\Vert {\sum _{n=1}^\infty \lambda _n y_n }\right\Vert _{F(0,1)} \\&= c^{-1}C^{-1 } \left\Vert {\sum _{n=1}^\infty \lambda _n y_n }\right\Vert _{F(0,1)}- \frac{1}{2} c^{-1}C^{-1 } \\&\le c^{-1}C^{-1 } \left\Vert {\sum _{n=1}^\infty \lambda _n y_n }\right\Vert _{F(0,1)}- \frac{1}{k} (1+ \frac{1}{k})^2 \\&{\mathop {\le }\limits ^{(2.6)}} (1+ \frac{1}{k})^2 \left\Vert {TV (\sum _{n=1}^\infty \lambda _n y_n)}\right\Vert _X, \end{aligned}$$

and, therefore,

$$\begin{aligned} \frac{1}{2} c^{-1}C^{-1 } \left\Vert {V\left( \sum _{n=1}^\infty \lambda _n y_n\right) }\right\Vert _{F(0,1)}&= \frac{1}{2} c^{-1}C^{-1 } \left\Vert {\sum _{n=1}^\infty \lambda _n y_n }\right\Vert _{F(0,1)} \\&\le \Big (1+ \frac{1}{k}\Big )^2 \left\Vert {TV \left( \sum _{n=1}^\infty \lambda _n y_n\right) }\right\Vert _X \\&\le \Big (1+ \frac{1}{k}\Big )^2 \left\Vert {T}\right\Vert \left\Vert { V\left( \sum _{n=1}^\infty \lambda _n y_n \right) }\right\Vert _{F(0,1)}. \end{aligned}$$

Hence, T is an isomorphism on $\overline{\mathrm{span}\{V y_n\}}^{\left\Vert {\cdot }\right\Vert _{F(0,1)}}$. However, by (2.4) and the fact that V is an isometry, $\overline{\mathrm{span}\{V y_n\}}^{\left\Vert {\cdot }\right\Vert _{F(0,1)}}$ is isomorphic to $\ell _2$, which contracts the assumption that T is $\ell _2$-strictly singular. $\square$

Throughout this section by $(\overline{h}_n)_{n=1}^\infty$ is denoted the $L_\infty$-normalized Haar system. Let

$$\begin{aligned} r_m: =\sum _{k=1}^{2^m }\overline{h}_{2^m +k },\quad m=0, 1,\ldots \end{aligned}$$

be mth Rademacher function.

We say that a symmetric function space E(0, 1) has the Khintchine property if the Rademacher system in E(0, 1) is equivalent to the natural basis of $\ell _2$. In particular, $L_p(0,1)$, $p\ge 1$, has the Khintchine property (see e.g. [12, 21]).

2.1 Proof of Theorem 1.1

Before proceeding to the proof of Theorem 1.1, we need one more auxiliary result.

Proposition 2.4

Let F(0, 1) be a separable symmetric function space having the Khintchine property and E be a separable symmetric sequence space. Let $T_E$ be the upper triangular part of the separable symmetric ideal $C_E$ corresponding to E. Let $S:F(0,1) \rightarrow T_E$ be defined as in Proposition 2.2 by taking $X=T_E$ with FDD $X_n:= \mathrm{span}\{e_{in}\}_{i\le n}$.

Assume, in addition, that S is an $\ell _2$-strictly singular operator. There exists a subsequence $(n_m)_{m\ge 1}$ of $\mathbb {N}$ such that

$$\begin{aligned} \left\Vert {Sr_{n_m} - y_m}\right\Vert _{T_E}\le \frac{\delta }{2^m }, \end{aligned}$$

where $(y_m)$ is a sequence of elements in $T_E$ which are disjointly supported from the left and the right.¹

Proof

Let

$$\begin{aligned} P_{N } = \sum _{i=1}^N e_{ii}. \end{aligned}$$

(2.7)

By Proposition 2.2, $(Sr_n)$ is a sequence in $T_E$, which are disjointly supported from the right. Indeed, every non-zero element in $X_n$ has its right support equal to $e_{nn}$. By Proposition 2.2, $r(Sh_n) \le \sum _{k=p_n}^{p_{n+1}-1}e_{ii}$. for some strictly increasing sequence $\{p_n\}_{n\ge 1}$ Therefore, $Sr_n$’s are disjointly supported from the right.

Let $n_1=1$ and let $y_1=Sr_{1}$. By Proposition 2.2, there exists a positive integer $N_1$ large enough such that

$$\begin{aligned} P_{N_1 } Sr_1 P_{N_1} =Sr_1. \end{aligned}$$

We claim that $P_{N_1} Sr_n\rightarrow 0$ in $T_E$ as $n\rightarrow \infty$. Otherwise, if

$$\begin{aligned} \liminf _{n\rightarrow \infty }\left\Vert {P_{N_1}Sr_n }\right\Vert _{T_E}>\delta '>0, \end{aligned}$$

then, passing to a subsequence of $(r_n)$ if necessary, we obtain the existence of an integer m with $m\le {N_1}$ such that

$$\begin{aligned} \liminf _{n\rightarrow \infty }\left\Vert {(P_m-P_{m-1})Sr_n }\right\Vert _{T_E} \ge \frac{\delta '}{N_1}>0. \end{aligned}$$

Indeed, if $\liminf _{n\rightarrow \infty }\left\Vert {(P_m-P_{m-1})Sr_n }\right\Vert _{T_E} < \frac{\delta '}{N_1}$ for all $m\le N_1$, then by the triangle inequality, we have $\liminf _{n\rightarrow \infty } \left\Vert {P_m Sr_n }\right\Vert _{T_E} <\delta$, which is a contradiction. Passing to a subsequence, we may assume that $\left\Vert {(P_m-P_{m-1})Sr_n }\right\Vert _{T_E} \ge \frac{\delta '}{N_1}$ for all n. Denoting $e_{mm}(Sr_n) (e_{mm}(Sr_n))^*= e_{mm}(Sr_n)(Sr_n)^*e_{mm}= ae_{mm}$ for some $a\ge 0$, we have

$$\begin{aligned} \frac{\delta '}{N_1}&\le \left\Vert {(P_m-P_{m-1})Sr_n}\right\Vert _{T_E}= \left\Vert {e_{mm}Sr_n}\right\Vert _{T_E}\\&= \left\Vert {s(e_{mm}Sr_n)}\right\Vert _{E} = \left\Vert {s(e_{mm}Sr_n(e_{mm} Sr_n)^*)^{1/2}}\right\Vert _{E}\\&= \left\Vert { s (a e_{mm} )^{1/2}}\right\Vert _{ E} = a^{1/2 }. \end{aligned}$$

Hence, $e_{mm}(Sr_n)(Sr_n)^*e_{mm}= ae_{mm} \ge (\frac{\delta '}{N_1})^2 e_{mm}$. Moreover, since $Sr_n$’s are disjointly supported from the right, it follows that for any $(\alpha _n)\in \ell _2$, we have

$$\begin{aligned} s\left( (P_m-P_{m-1}) \sum _{n=1}^\infty \alpha _n Sr_n\right)&{\mathop {=}\limits ^{(2.7)}} s\left( e_{mm} \sum _{n=1}^\infty \alpha _n Sr_n\right) \nonumber \\&= s\!\left( \!\left( e_{mm} \sum _{n=1}^\infty \alpha _n Sr_ n (e_{mm} \sum _{n=1}^\infty \alpha _n Sr_ n)^* \!\right) ^{1/2}\right) \nonumber \\&= s\left( e_{mm}\left( \sum _{n=1}^\infty |\alpha _n|^2 (Sr_ n)(Sr_n)^* \right) e_{mm} \right) ^{1/2}\nonumber \\&\ge s\left( \sum _{n=1}^\infty |\alpha _n|^2 (\frac{\delta '}{N_1})^2 e_{mm}\right) ^{1/2} \nonumber \\&= \left( \frac{\delta '}{N_1} \left\Vert {(\alpha _n)}\right\Vert _{\ell _2},0,0,0,\cdots \right) . \end{aligned}$$

(2.8)

Hence, for any $(\alpha _n)\in \ell _2$, we have

$$\begin{aligned} \frac{\delta '}{N_1}\left\Vert { ( \alpha _n) }\right\Vert _{\ell _2}&{\mathop {\le }\limits ^{(2.8)}} \left\Vert {(P_m-P_{m-1}) \sum _{n=1}^\infty \alpha _n Sr_n}\right\Vert _{T_E} \le \left\Vert {P_{N_1 }\sum _{n=1}^\infty \alpha _n Sr_n}\right\Vert _{T_E}\\&\le \left\Vert {\sum _{n=1}^\infty \alpha _n Sr_n}\right\Vert _{T_E} \le \left\Vert {S}\right\Vert \left\Vert {\sum _{n=1}^\infty \alpha _n r_n}\right\Vert _{F(0,1)} \le c(p) \left\Vert {( \alpha _n) }\right\Vert _{\ell _2}, \end{aligned}$$

where c(p) is a positive constant depending on p. This contradicts the fact that S is $\ell _2$-strictly singular. Hence,

$$\begin{aligned} P_{N_1} Sr_n\rightarrow 0, \end{aligned}$$

in $T_E$ as $n\rightarrow \infty$. There exists a positive integer $n_2$ such that

$$\begin{aligned} \left\Vert {P_{N_1} Sr_{n_2}}\right\Vert _{T_E} \le \frac{\delta }{4}. \end{aligned}$$

By Proposition 2.2, there exists a positive integer $N_2$ sufficiently large such that

$$\begin{aligned} Sr_{n_2}= P_{ N_2} Sr_{n_2}. \end{aligned}$$

We have

$$\begin{aligned} \left\Vert {Sr_{n_2} - (P_{ N_2}- P_{N_1}) Sr_{n_2} }\right\Vert _{T_E}=\left\Vert { P_{N_1} Sr_{n_2} }\right\Vert _{T_E}\le \frac{\delta }{4}. \end{aligned}$$

Observe that $(P_{ N_2}- P_{N_1}) Sr_{n_2}$ and $y_1$ are disjointly supported from the left and the right. We define $y_2:= (P_{ N_2}-P_{N_1}) Sr_{n_2}$.

Continuing the procedure, we construct a sequence of integers $(n_m)$ and a sequence $(y_m)$ of elements in $C_E$ which are disjointly supported from the left and the right such that

$$\begin{aligned} \left\Vert {Sr_{n_m} - y_m}\right\Vert _{T_E}\le \frac{\delta }{2^m }. \end{aligned}$$

This completes the proof. $\square$

Now, we are ready to prove Theorem 1.1.

Proof of Theorem 1.1

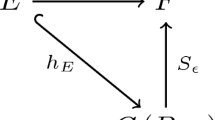
Let $r>2$. Let $\{e_{ij}\}_{j\ge i}$ be the natural Schauder basis of $T_E$ (e.g. in the induced rectangular ordering [15]). Suppose that $T\in L(F(0,1), T_E)$ is not narrow. Without loss of generality, we may assume that there exists a positive number $\delta$ such that $\left\Vert {Tx }\right\Vert _{T_E} \ge 2\delta$ for any mean zero sign x on (0, 1). Applying Proposition 2.2 by taking $\varepsilon <\left\Vert {T}\right\Vert$, $X=T_E$ and $X_n=\mathrm{span} \{e_{i,n}\}_{1\le i\le n}$, we can choose an operator $S\in L(F(0,1), T_E)$ such that

$$\begin{aligned} \left\Vert {S}\right\Vert \le 2\left\Vert {T}\right\Vert , \end{aligned}$$

(2.9)

and for which conditions (1)–(4) in Proposition 2.2 hold. By Proposition 2.3, S is $\ell _2$-strictly singular. By Proposition 2.4, we may assume that there exists a subsequence $(n(m))_{m\ge 1}$ of $\mathbb {N}$ such that n(m)’s are odd numbers and $(Sr_{n(m)})$ is equivalent to a basic sequence of elements in $T_E$ which are disjointly supported from the left and the right. We consider

$$\begin{aligned} \{ h_{2^{n(m)} +i }\}_{m \ge 1, 1\le i\le 2^{n(m) } }. \end{aligned}$$

Let $C>0$ and $N \in \mathbb {N}$. We denote

$$\begin{aligned} I_m^k:= \mathrm{supp }~ h_{2^m+k } = \left[ \frac{k-1}{2^m}, \frac{k}{2^m } \right) . \end{aligned}$$

We define

$$\begin{aligned} f:= \frac{C}{\sqrt{N}} \sum _{m=1}^{2^{N+1}} \sum _{k=1}^{2^{n(m) }} \overline{h}_{2^{n(m)}+k} =\frac{C}{\sqrt{N}} \sum _{m=1}^{2^{N+1}} r_{n(m) }. \end{aligned}$$

Since $Sr_{n(m)}$ is equivalent to a sequence of elements in $T_r$ which are disjointly supported from the left and the right and E satisfies an upper r-estimate with $r>2$, we have

$$\begin{aligned} \left\Vert {Sf}\right\Vert _{T_E}&= \left\Vert {\frac{C}{\sqrt{N}} \sum _{m=1}^{2^{N+1}} S (r_{n(m) })}\right\Vert _{T_E} \le \frac{C}{\sqrt{N}}\left( \sum _{m=1}^{2^{N+1}} \left\Vert { S (r_{n(m) })}\right\Vert _{T_E}^r \right) ^{1/r}\\&\le \frac{C}{\sqrt{N}} \left\Vert {S}\right\Vert \left( \sum _{m=0}^N \left\Vert {r_{n(m)}}\right\Vert _{F(0,1)} ^r \right) ^{1/r}{\mathop {\le }\limits ^{(2.9)}} 2 C \left\Vert {T}\right\Vert (N+1)^{1/r}N^{-\frac{1}{2}}. \end{aligned}$$

Since $r>0$, it follows that

$$\begin{aligned} \left\Vert {Sf}\right\Vert _{T_E} \rightarrow 0, \text{ as } N \rightarrow \infty . \end{aligned}$$

Our goal is to select a subset J of $\{2^{n(m)} +k\}_{m \ge 1, 0\le i \le 2^{n(m)}-1}$ such that $g = \frac{C}{\sqrt{N}}\sum _{n \in J}\overline{h}_n$ is close enough to a sign.

Set

$$\begin{aligned} A:= \left\{ \omega \in [0,1]: \max _{j\in \{2^{n(m) }+k\}_{m\ge 1,1\le k\le 2^{n(m)} }} \left| \frac{C}{\sqrt{N} } \sum _{i=2^{n(m)}+k \le j} \overline{h}_i(\omega ) \right| >1 \right\} , \end{aligned}$$

and

$$\begin{aligned} \tau (\omega )\! =\! {\left\{ \begin{array}{ll} \min \left\{ {j\in \{2^{n(m) }+k\}_{m\ge 1, 1\le k\le 2^{n(m) } }}: \left| \frac{C}{\sqrt{N}}\sum _{ i=2^{n(m)}+k \le j} \overline{h}_i(\omega )\right| >1 \right\} , \text{ if } ~\omega \in A, \\ 2^{n(N)} +k, ~ \text{ if } ~\omega \notin A \text{ and } \omega \in I_{n(N)}^k \end{array}\right. }. \end{aligned}$$

Observe that if $\tau (\omega ) =2^{n(m)}+k$, then $\omega \in I_{n(m)}^k$ (see, e.g. the argument in [16, p.94] and [19]). Further, if there exists $\omega \in I_{n(m)}^k$ with $\tau (\omega ) \ge 2^{n(m)} +k$, then we have

$$\begin{aligned} \tau (\xi )\ge 2^{n(m)} +k \end{aligned}$$

(2.10)

for every $\xi \in I_{n(m)}^k$. Indeed, since $\omega \in I_{n(m)}^k$, for every $z<2^{n(m)}+k$ and every $\xi \in I_{n(m)}^k$, we have $\overline{h}_z(\omega ) =\overline{h}_z (\xi )$. Thus,

$$\begin{aligned} \left| \frac{C}{\sqrt{N}} \sum _{ p=2^{n_i}+j \le 2^{n(m)} +k-1} \overline{h}_p(\xi )\right| = \left| \frac{C}{\sqrt{N}} \sum _{ p=2^{n_i}+j \le 2^{n(m)} +k-1} \overline{h}_p(\omega )\right| \le 1. \end{aligned}$$

Hence, $\tau (\xi )\ge 2^{n(m)} +k$.

Now, we define a set

$$\begin{aligned} J:&=\{ j =2^{n(m)}+k \le 2^{n(N)+1}: \exists \omega \in I_{n(m)}^k \text{ with } \tau (\omega )\ge j\}\\&=\{ j =2^{n(m)}+k \le 2^{n(N) +1}: \forall \xi \in I_{n(m)}^k \text{ with } \tau (\xi )\ge j\}. \end{aligned}$$

Let $g:[0,1]\rightarrow \mathbb {R}$ be defined as

$$\begin{aligned} g(\omega ) = \frac{C}{\sqrt{N}} \sum _{2^{n(m)}+k \le \tau (\omega )} \overline{h}_{2^{n(m)}+k } (\omega ). \end{aligned}$$

Observe that for every $\omega \in [0,1]$, we have

$$\begin{aligned}&\left\{ j=2^{n(m)} +k:~\omega \in I_{n(m)}^k\right\} \cap J\\&\quad = \left\{ j=2^{n(m)} +k:~\omega \in I_{n(m)}^k \right\} \cap \\&\qquad \times \left( \cup _{\omega _1 \in [0,1]} \{ j=2^{n(m)} +k \le \tau (\omega _1 ):~ \omega _1 \in I_{n(m)}^k\} \right) \\&\quad = \cup _{\omega _1 \in [0,1]} \{ j=2^{n(m)} +k \le \tau (\omega _1 ):~ \omega _1, \omega \in I_{n(m)}^k\}\\&\quad {\mathop {=}\limits ^{(2.10)}} \left\{ j=2^{n(m)} +k \le \tau (\omega ):~ \omega \in I_{n(m)}^k \right\} . \end{aligned}$$

Since

$$\begin{aligned} \overline{h}_{2^{n(m)} +k}(\omega ) =0, \end{aligned}$$

(2.11)

for any $\omega \notin I_{n(m) }^k,$ it follows that for any $\omega \in [0,1]$, we have

$$\begin{aligned} g(\omega )= & {} \frac{C}{\sqrt{N}} \sum \limits _{j\in \{ j=2^{n(m)} +k \le \tau (\omega ): \omega \in I_{n(m)}^k\} } \overline{h}_j (\omega )\nonumber \\= & {} \frac{C}{\sqrt{N}} \sum \limits _{j\in \left\{ j=2^{n(m)} +k:~\omega \in I_{n(m)}^k\right\} \cap J } \overline{h}_j (\omega )\nonumber \\&{\mathop {=}\limits ^{(2.11)}}&\frac{C}{\sqrt{N}} \sum \limits _{j\in \left\{ j=2^{n(m)} +k:~\omega \in I_{n(m)}^k\right\} \cap J } \overline{h}_j (\omega ) \nonumber \\&+ \frac{C}{\sqrt{N}} \sum \limits _{j\in \left\{ j=2^{n(m)} +k:~\omega \notin I_{n(m)}^k\right\} \cap J } \overline{h}_j (\omega )=\frac{C}{\sqrt{N}}\sum \limits _{j\in J} \overline{h}_j (\omega ). \end{aligned}$$

(2.12)

By the unconditionality of the decomposition $\{X_n =\mathrm{span} \{e_{i,n}\}\}_{1\le i\le n}$ of $T_E$ [2, Lemma 4.5], we have

$$\begin{aligned} \left\Vert {Sg}\right\Vert _{T_E} {\mathop {=}\limits ^{(2.12)}}\left\Vert { \frac{C}{\sqrt{N}}\sum _{j\in J} S \overline{h}_j }\right\Vert _{T_E}\le & {} c_E \left\Vert {\frac{C}{\sqrt{N}} \sum _{m=1}^{2^{N+1}} \left( \sum _{k=1}^{2^{n(m) }} S \overline{h}_{2^{n(m)}+k} \right) }\right\Vert \nonumber \\= & {} c_E \left\Vert {Sf}\right\Vert _{T_E} \le c_E \cdot 2C\left\Vert {T}\right\Vert (N+1)^{1/r} N^{-1/2},\nonumber \\ \end{aligned}$$

(2.13)

where $c_E>0$ depends on E only.

Assume that N is an odd number. By the definition of $\tau (\omega )$ and $g(\omega )$, for every $\omega \in A$, we have

$$\begin{aligned} 1<|g(\omega )| <1 +\frac{C}{\sqrt{N}}, \end{aligned}$$

(2.14)

and for every $\omega \in [0,1]\setminus A$,

$$\begin{aligned} g(\omega )\ne 0. \end{aligned}$$

(2.15)

Indeed, since N is odd (that is, $N-1$ is even), it follows that $\sum _{j=1}^ {N-1} r_{n_j} \ne \pm 1$ everywhere, and therefore, for $\omega \in I_{n(N)}^k$, we have

$$\begin{aligned} g(\omega )&=\frac{C}{\sqrt{N}} \sum _{\begin{array}{c} 2^{n(m)}+k_1 \le \tau (\omega )\\ 1\le k_1\le 2^{n(m)} \end{array}} \overline{h}_{2^{n(m)}+k_1 } (\omega ) \\&=\frac{C}{\sqrt{N}} \sum _{\begin{array}{c} 2^{n(m)} + k_1 \le 2^{n(N)}+k \\ 1\le k_1\le 2^{n(m)} \end{array}} \overline{h}_{2^{n(m)}+k_1 } (\omega ) \\&=\frac{C}{\sqrt{N}} \sum _{\begin{array}{c} 2^{n(m)} + k_1 \le 2^{n(N)} \\ 1\le k_1\le 2^{n(m)} \end{array}} \overline{h}_{2^{n(m)}+k_1} (\omega ) +\frac{C}{\sqrt{N}} \sum _{ 2^{n(N)}+1 \le j \le 2^{n(N)} +k } \overline{h}_{j } (\omega ) \\&=\frac{C}{\sqrt{N}} \sum _{j=1}^ {N-1} r_{n_j} (\omega ) +\frac{C}{\sqrt{N}} \sum _{2^{n(N) }+1 \le j \le 2^{n(N) }+k} \overline{h}_j (\omega ) \ne 0. \end{aligned}$$

Now, we define a function g by setting

$$\begin{aligned} \widetilde{g}(\omega ) = \mathrm{sgn}(g(\omega )). \end{aligned}$$

By (2.14), we have

$$\begin{aligned} \left\Vert {g -\tilde{g}}\right\Vert _{F(0,1) } \le \left\Vert {\frac{C}{\sqrt{N}}\chi _A + \chi _{[0,1]\setminus A} }\right\Vert _{F(0,1) }. \end{aligned}$$

By the Central Limit Theorem, for a sufficiently large odd number N, we have

$$\begin{aligned} \mu ([0,1]\setminus A)&= \mu \left\{ \omega : \left| \frac{1}{\sqrt{N}}\sum _{m=1}^{N} \sum _{k=1}^{2^{n(m)}} \overline{h}_{2^{n(m)} +k} \right| \le \frac{1}{C}\right\} \\&\le \frac{1}{\sqrt{2\pi }} \int _{-\frac{1}{C}}^{\frac{1}{C}} e^{-{\frac{\omega ^2}{2}}}d\omega +\frac{1}{10C} <\frac{1}{C}. \end{aligned}$$

Thus,

$$\begin{aligned} \left\Vert {\chi _{[0,1]\setminus A}}\right\Vert _{F(0,1)} \le \left\Vert {\chi _{(0,\frac{1}{C})}}\right\Vert _{F(0,1)}. \end{aligned}$$

Hence, we have

$$\begin{aligned} \left\Vert {g-\tilde{g}}\right\Vert _{F(0,1) } \le \frac{C}{\sqrt{N}} +\left\Vert {\chi _{(0,\frac{1}{C})}}\right\Vert _{F(0,1)}. \end{aligned}$$

Thus, by (2.9) and (2.13), we have

$$\begin{aligned} \left\Vert {S\tilde{g}}\right\Vert _{T_E}&\le \left\Vert {Sg}\right\Vert _{T_E } +\left\Vert {S}\right\Vert \left\Vert {g-\tilde{g}}\right\Vert _{F(0,1)} \\&\le c_E \cdot 2C\left\Vert {T}\right\Vert (N+1)^{1/r}N^{-1/2}+2\left\Vert {T}\right\Vert \left( \frac{C}{\sqrt{N}} +\left\Vert {\chi _{(0,\frac{1}{C})}}\right\Vert _{F(0,1)}\right) . \end{aligned}$$

Since $r>2$, it follows that for every $\delta >0$, there exists a sufficiently large positive number C and a sufficiently large odd number N such that

$$\begin{aligned} \left\Vert {S\tilde{g}}\right\Vert _{T_E } \le \delta . \end{aligned}$$

It remains to observe that $\tilde{g}$ is a mean zero sign on [0, 1]. Indeed, since N is an odd number, it follows from (2.14) and (2.15) that the support of $\tilde{g}$ is equal to [0, 1]. Observe that for every $\omega \in [0,1]$ and every $2^{n(m)} +k \le 2^{n(N)+1 }$, $k \le 2^{n(m) }$, we have

$$\begin{aligned} \overline{h}_{2^{n(m)} +k }(\omega ) = - \overline{h}_{2^{n(m)} + (2^{n(m)} -k ) +1} (1-\omega ). \end{aligned}$$

Thus, $g(\omega ) =-g(1-\omega )$ for every $\omega \in [0,1]$, and

$$\begin{aligned} \mu (\{\omega \in [0,1]:g(\omega )>0\}) = \mu (\{ \omega \in [0,1]:g(\omega )<0\}). \end{aligned}$$

Thus, $\tilde{g}$ is a mean zero sign on [0, 1], which contradicts (2) of Proposition2.2. $\square$

3 Remarks

It is shown in [6, Theorem 1.1] that if T is a regular operator from $L_p$ into an order continuous Banach lattice F, then “T is $\ell _2$-strictly singularity” $\Rightarrow$ “T is narrow”. Note that [16, Theorem B] is stated for $\ell _2$-strictly singular operator $T:L_p \rightarrow X$ when $1<p<\infty$ and X has an unconditional basis. However, a careful analysis of its proof shows that it still holds for any $p\in [1,\infty )$ (see also [19, p.110]). By a verbatim repetition of the proof in [16, Theorem B] by replacing [16, Proposition 3.1] with Proposition 2.2, we obtain the following result for general Banach spaces, which provides an alternative proof for Theorem 1.1.

Theorem 3.1

Let F(0, 1) be a separable symmetric function space having the Khintchine property and let X be a Banach space having an unconditional finite-dimensional decomposition. Then every $\ell _2$-strictly singular operator $T:F(0,1) \rightarrow X$ is narrow.

The class of Banach spaces having unconditional finite-dimensional decompositions is very wide. For example, the operator ideal $C_E$ has an UFDD when E has non-trivial Boyd indices [2, Corollary 4.6]. Let E(0, 1) be a symmetric function space on the unit interval (0, 1) and let $E(\mathcal {R})$ be the noncommutative operator space [14] affiliated with the hyperfinite $II_1$-factor $\mathcal {R}$. Then, $E(\mathcal {R})$ has an UFDD [4, 24]. This opens an avenue for further extensions of Theorem 1.1.

Definition 3.2

Let $E(\mathcal {M},\tau )$ be a noncommutative symmetric space and Y be an F-space. We call $T:E(\mathcal {M},\tau )\rightarrow Y$ a narrow operator if for each projection $p\in \mathcal {M}$ and $\varepsilon >0$, there exists a self-adjoint element $x\in E(\mathcal {M},\tau )$ such that $x^2 =p$, $\tau (x) =0$ and $\left\Vert {T(x)}\right\Vert _Y <\varepsilon$.

Assume that E(0, 1) is a symmetric function and X is a Banach space. It is clear (see e.g. the proof of [8, Corollary 4.5]) that if all elements of L(E(0, 1), X) are narrow, then every element of $L(E(\mathcal {M}),X)$ is narrow for an arbitrary atomless finite von Neumann algebra $\mathcal {M}$ equipped with a faithful normal tracial state $\tau$. The following result is a direct consequence of Corollary 1.2.

Corollary 3.3

Let $\mathcal {M}$ be an atomless finite von Neumann algebra equipped with a faithful normal tracial state $\tau _1$. Let $1\le p,r<\infty$. Every $\ell _2$-strictly singular operator $T:L_p(\mathcal {M}) \rightarrow C_r$ is narrow.

Recall that a Banach space X is said to have infratype $q>1$ [19, p.216] if there exists a constant $C>0$ such that for each $n\in \mathbb {N}$ and $x_1,\ldots , x_n\in X$, we have

$$\begin{aligned} \min _{\theta _k =\pm 1} \left\Vert {\sum _{k=1}^n \theta _k x_k}\right\Vert \le C\left( \sum _{k=1}^n \left\Vert {x_k}\right\Vert ^q \right) ^{1/q}. \end{aligned}$$

It is clear that if a Banach space has type q then it has infratype q. Note that if $q<2$, then the notions of type and infratype coincide [26].

Remark 3.4

Assume that $1\le p<2$ and $r>p$. Recall that $C_r$ has type $\min \{r,2\}$ (see, e.g. [5]), and therefore, has infratype $\min \{r,2\}$. By [19, Theorem 9.8], we obtain that all operators from $L_p$ into $C_r$ are narrow.

Assume that $p\ge 2$. Note that there exists a non-narrow operator $T:L_p\rightarrow \ell _2$ [16, Example 1.1]. Since $\ell _2$ is a complemented subspace of $C_r$, it follows that there exists a non-narrow operator from $L_p$ into $C_r$.

When $p=r=1$, it is shown in [9] that all operators from $L_1$ into $C_1$ are Dunford–Pettis, and therefore, narrow.

The case for $1<p <2$ and $1\le r\le p$ seems to be open, i.e., we do not know whether there exists a non-narrow operator from $L_p$ into $C_r$ when $1<p <2$ and $1\le r\le p$.