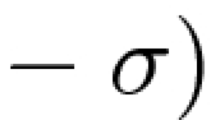Abstract
In the paper, we study some new criteria for the oscillation of the nonlinear second-order delay difference equations of the form \(\varDelta (r\left( t \right) ({\varDelta x\left( t \right) )}^{\alpha })+q\left( t \right) x^{\beta }\left( t-m+1 \right) =0\), via comparison with a second-order linear difference equation or a first-order linear delay difference equation whose oscillatory behavior is discussed intensively in the literature. The presented results essentially improve existing ones.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this paper, we shall study the oscillatory behavior of the solutions of nonlinear second-order delay difference equations of the form
We shall assume that
-
(i)
\(\{q(t)\}\) and \(\{r(t)\}\) are positive real sequences,
-
(ii)
\({\upalpha }\, \mathrm {and}\, {\upbeta }\) are ratios of positive odd integers,
-
(iii)
\(m {\ge } 1\) is a positive integer.
Moreover, it is assumed that
Recall that a solution of (1.1) is a nontrivial real-valued sequence \(\{x(t)\}\) satisfying (1.1) for \(t \ge \, t_{0}-m+1\).
Solutions vanishing identically in some neighborhood of infinity will be excluded from our consideration. A solution x of (1.1) is said to be oscillatory if it is neither eventually positive nor eventually negative; otherwise, it is called nonoscillatory. An equation itself is said to be oscillatory if all its solutions are oscillatory.
The problem of investigating oscillation criteria for various types of difference equations has been a very active research area over the past several decades. A large number of papers and monographs have been devoted to this problem; for a few examples, see [1,2,3,4,5,6,7,8,9,10,11, 13,14,15] and the references contained therein.
The main goal of this paper was to provide some new oscillation criteria for Eq. (1.1) via comparison with a second-order linear difference equation or a first-order linear delay difference equation whose oscillatory behavior is discussed intensively in the literature. We will demonstrate the usefulness of our main results via some applications to neutral difference equations and some examples.
2 Comparison Theorems
To obtain our result, we need the following two lemmas:
Lemma 2.1
Let \(\{q (t)\}\) be a sequence of positive real numbers; m is a positive real number and f: R\(\rightarrow \) R is a continuous nondecreasing function, and \(x\, f(x) > 0\) for \(x\ne 0.\) If the first-order delay differential inequality
has an eventually positive solution, so does the delay equation
This Lemma is an extension of the discrete analogue of known results. See Lemma 6.2.2 in [2] and also in [11]. The proof is immediate.
Lemma 2.2
Let \(\{x(t)\}\) be an eventually increasing solution of Eq. (1.1). Then \(x^{\beta -\alpha }(t)\ge \varphi (t)\), where \(\varphi \left( t \right) \) is given by
where a and b are positive constants and all large \(t\ge t_{1}\ge t_{0.}\)
Proof
Since \(\{x(t)\}\) is a positive increasing solution of Eq. (1.1), there exists a constant \(c > 0\) such that x(t) \(\ge c\, for\, all\, t\ge t_{1\, }for\, some\, t_{1}\ge t_{0}\). Now, one can easily find that
Since \(r(t)\left( \varDelta x(t) \right) ^{\alpha }\) is positive and non-increasing on\(\, [t_{1},\infty )\), there exists a constant \(C > 0\) such that
Summing this inequality from \(t_{1}\) to t-1, we have
and for some constant \(C>\, 0\) and so,
where \( a = \quad c^{\beta -\alpha }\, and\, b=C^{\beta -\alpha }\). This proves the Lemma.
For t\(\, \ge t_{1}\ge t_{0}\) , we let
and
Now, we present our first oscillation result for Eq. (1.1) via comparison with second-order linear difference equation.
Theorem 2.1
Let \({\alpha \ge 1}\),the conditions (i)–(iii) and (1.2) hold. If the second-order linear difference equation
is oscillatory for all large \(t\ge t_{1,\, }\, \) then Eq. (1.1) is oscillatory.
Proof
Let \(\{x(t)\}\) be a nonoscillatory solution of Eq. (1.1), say \(x(t) > 0\), and \(x(t - m + 1)) > 0\) for \(t\ge t_{1}\mathrm {\, for\, some\, }\mathrm {t}_{1}\ge t_{0}.\) The proof if x(t) is eventually negative is similar, so we omit the details of that case here as well as in the remaining proofs in this paper. Then, it follows from Eq. (1.1) that
It is easy to see that there exists a \(\mathrm {t}_{2}\ge t_{1}\) such that
By using (2.1) in (2.4) we have
Inequality (2.4) can be written in the following form:
\(\varDelta -\)derivative yields
or,
Using (2.2), there exists\(\, t_{3} \ge t_{2}\) such that
using the fact that \(r^{\frac{1}{\alpha }}\left( t \right) \varDelta x\left( t \right) \)is a nonincreasing sequence, we see that
and using (2.6) in (2.7) we get
Substituting this inequality in (2.5) and using the fact that \({\upalpha }\ge \mathrm {1,\, we\, see\, that}\)
or,
From (2.2) It follows that
i.e. \(\frac{x(t)}{R(t,\mathrm {t}_{\mathrm {1}})}\) is eventually nonincreasing for \(t\ge t_{2}.\) Thus, we have
and so,
or,
But by Lemma 1 of [14], the corresponding Eq. (2.3) has a positive solution. We derive a contradiction which completes the proof.
By Applying Theorem 3.5 in [8] to Eq. (2.3), we have the following oscillation result;
Corollary 2.1
Let \({\upalpha \ge 1,the}\), conditions (i)–(iii) and (1.2) hold. If there exists a nondecreasing positive sequence \(\{\pi (t)\}\) such that for any \(t\ge t_{0}\)
then Eq. (1.1) is oscillatory.
Next, we present our second oscillation result for Eq. (1.1) via comparison with first-order delay difference equation.
Theorem 2.2
Let \(0<{\upalpha }\le 1\), the conditions (i)–(iii) and (1.2) hold. If the first-order linear delay difference equation
is oscillatory for all large \(t\ge t_{1\, }\, \), then Eq. (1.1) is oscillatory.
Proof
Let x(t) be a nonoscillatory solution of Eq. (1.1), say \(x(t) > 0\) and x (\(\tau (t)) > 0\) for \(t\ge t_{1}\mathrm {\, for\, some\, }\mathrm {t}_{1}\ge t_{0}.\) The proof if x(t) is eventually negative is similar, so we omit the details of that case here as well as in the remaining proofs in this paper. Proceeding as in the proof of Theorem 2.1, we obtain the inequalities (2.5)–(2.7). Using (2.6) into (2.5), we have
or,
or,
where, \(w(t) = r^{\frac{1}{\alpha }}(t)\varDelta x\left( t \right) >0.\) Summing inequality (2.10) from \(t \ge t_{3} \)to u and letting u \(\rightarrow \quad \infty \), we obtain
The function w(t) is strictly decreasing on [\(t_{3}\), \(\infty )\). It follows from Lemma 2.1 that the corresponding difference Eq. (2.9) also has a positive solution. We arrive at a contradiction which completes the proof.
By summing Eq. (2.9) from t - m\(+\)1 to t -1, we have the following result:
Corollary 2.2
Let \(0<{\upalpha }\le 1\),the conditions (i)–(iii), and (1.2) hold. If for all large \(t\ge t_{1\, }\)
then Eq. (1.1) is oscillatory.
Example 2.1
Consider the second order difference equation
Here,\(\, \alpha =3,\) and \({\upbeta >0\, }\)and \(q\left( t \right) \, \)is a positive of real sequence, r\((t) =\)1, R(t,\(\, t_{0}) = t-t_{0}\).
If the second-order linear difference equation
is oscillatory for all large \(t\ge t_{1\, }and\, any\, constant\, C\in (0\, ,1]\) .All condition of Theorem 2.1 are satisfied and hence we see that Eq. (2.12) is oscillatory.
3 Applications
In this section we apply our previous results to neutral second-order difference equations of the form
where \((I) y(t) = x(t) + \mathrm {p}_{\mathrm {1}}\left( \mathrm {t} \right) \mathrm {x}^{{\upgamma }}\left( \mathrm {t-}k_{1} \right) \mathrm {+}\mathrm {p}_{\mathrm {2}}\left( \mathrm {t} \right) \mathrm {x}^{{\updelta }}\left( \mathrm {t-}k_{2} \right) \) or, (II) y(t) = x(t) \(+\) p(t) \(\mathrm {x}^{{\upgamma }}\left( \mathrm {t-k} \right) ,\)
\({\upgamma \, \text {and}\, \updelta \, \text {are}\, \text {ratios}\, \text {of}\, \text {positive}\, \text {odd}\, \text {integers}\, \text {with}\, 0<\, \upgamma \le 1\, \text {and}\, \updelta \ge 1}\) , k,\({\, }k_{1}\) and \(k_{2\, }\)are positive integers and \(\{p(t)\}, \{\mathrm {p}_{\mathrm {1}}\left( \mathrm {t} \right) \}\) and \(\{\mathrm {p}_{\mathrm {2}}\left( \mathrm {t} \right) \}\) are positive sequences of real numbers.
To obtain our results we need the following lemma:
Lemma 3.1
[12]. If X and Y are nonnegative, then
where equality holds if and only if X \(=\) Y.
Now, we present our oscillation result for Eq. (3.1) with (I),
i.e., second-order equation with sublinear and superlinear neutral terms.
Theorem 3.1
Let the conditions (i)–(iii), and (1.2) hold and let
Equation (3.1) is oscillatory if one of the following conditions holds for all large:
-
(I)
The second-order linear difference equation
$$\begin{aligned} \varDelta \left( r^{\frac{1}{\alpha }}(t)\varDelta x\left( t \right) \right) +C \, Q_{1}\left( t,t_{1} \right) x\left( t+1 \right) =0, \end{aligned}$$(3.4)with \({\upalpha \ge 1,}\) is oscillatory.
-
(II)
Let \({\upalpha \ge 1\, and\, assume\, that\, }\)there exists a nondecreasing positive sequence \(\{\pi (t)\}\) such that for any \(t\ge t_{1}\ge t_{0}\)
$$\begin{aligned} \mathop {\text{ lim } \text{ sup }}\limits _{t \rightarrow \infty } \sum \limits _{t_{0}}^{t-1} {\left[ \, C\pi \left( s \right) \, Q_{1}\left( t,t_{1} \right) \, -\frac{r^{\frac{1}{\alpha }}\left( s \right) }{4}\left( \frac{\varDelta \pi \left( s \right) }{\pi \left( s \right) } \right) ^{2}\, \right] =\infty } ,\, \end{aligned}$$(3.5) -
(III)
The first-order linear delay difference equation
$$\begin{aligned} \varDelta \, w(t)+ C Q_{2}\left( t,t_{1} \right) \, w\left( t-m+1 \right) =0 \end{aligned}$$(3.6)with \({\upalpha >0}\) is oscillatory.
-
(IV)
Let \(0<{\upalpha }\le 1\, \)and condition (2.11).
Proof
Let \(\{x(t)\}\) be a nonoscillatory solution of Eq. (1.1), say \(x(t)> 0, x (\mathrm {t-}k_{1})> 0, x (\mathrm {t-}k_{2}) > 0\), and \(x(t-m+1) > 0\) and \(y(t) > 0\) for \(t\ge t_{1}\mathrm {\, for\, some\, }\mathrm {t}_{1}\ge t_{0}.\) The proof if x(t) is eventually negative is similar, so we omit the details of that case here as well as in the remaining proofs in this paper. Then, it follows from (3.1) that
Since x(t) \(\le \) y(t), it follows from the definition of y(t) that
By applying (3.2) with
we obtain
Substituting (3.9) into (3.8) we find
Since \(y(t) > 0\) and \(\varDelta y(t) > 0\) on [\(\mathrm {t}_{2}\), \(\infty )\), there exists a constant \(c_{1} > 0\) such that
Since \(r(t)\left( \varDelta y(t) \right) ^{\alpha }\) is positive and non-increasing on\(\, [t_{1},\infty )\), there exist a constant \(C > 0\) and a \(\mathrm {t}_{3}\ge t_{2}\)such that
Summing the inequality (3.12) from \(t_{3}\) to t-1 we have
for some \(t_{4}{\ge \, }t_{3}\) and for some constant \(C>\, 0\).
Using (3.11) and (3.13) in (3.10) gives
where B \(=\) max \(\{\mathrm {1}+\frac{\left( 1-\gamma \right) \gamma ^{\frac{\gamma }{1-\gamma }}\, }{c_{1}},\, C^{\delta -1}\}\).
Now, in view of (3.3), for any \(\rho \in \) (0, 1) there exists \(t_{\rho }\ge t_{4}\) such that
Fix \(\rho \in \) (0, 1) and choose \(t_{\rho }\)by (3.15). Since \(\lim _{t\rightarrow \infty }{\tau (t)} = \infty \), we can choose \(t_{5} \ge t_{\rho }\) such that \(\tau \) (t) \(\ge t_{\rho }\) for all t \(\ge t_{5}\). Thus, from (3.15) we have
Using this inequality in Eq. (3.1) we find
The rest of the proof is similar to that of Theorem 2.1 and hence is omitted.
Example 3.1
Consider the second-order neutral difference equation
and the second-order difference equation with a sublinear neutral term of the form
Here,\(\, \upalpha =3, {\upgamma =}\frac{\mathrm {1}}{\mathrm {3}}{,\, \updelta =3}\) and \({\upbeta >0}\) , k,\({\, }k_{1}\, \)and \(k_{2\, }\)are positive integers and p(t)\(=\)1/t\(={\mathrm {\, p}}_{\mathrm {1}}\left( \mathrm {t} \right) \) ,
\(\mathrm {p}_{\mathrm {2}}\left( \mathrm {t} \right) = \frac{1}{t^{3}}\, ,\, q\left( t \right) \, \)are positive sequences of real numbers. \(r(t) =1, R(t,\, t_{0}) = t-1-t_{0}\).
If the second-order linear difference equation
is oscillatory for all large \(t\ge t_{1\, }and\, any\, constant\, C\in (0\, ,1]\) .Applying Theorems 2.1 and 3.2 we see that both Eqs. (3.18) and (3.19) are oscillatory.
Next, we present the following oscillation result for Eq. (3.1) with (II),
i.e., second-order equation with a sublinear neutral term.
Theorem 3.2
Let the conditions (i)–(iii), and (1.2) hold and let \({\mathrm {lim}}_{t\rightarrow \infty }p_{1}\left( t \right) =\, 0\, .\)
Then the conclusions of Theorem 3.1 hold.
Proof
Let \(\{x(t)\}\) be a nonoscillatory solution of Eq. (1.1), say \(x(t)> 0, x (\mathrm {t-k}))> 0 \text {and} x(t-m+1) > 0\) and \(y(t) > 0\) for \(t\ge t_{1}\mathrm {\, for\, some\, }\mathrm {t}_{1}\ge t_{0}.\) The proof if x(t) is eventually negative is similar, so we omit the details of that case here as well as in the remaining proofs in this paper. Then, it follows from (3.1) that
Since x(t) \(\le \) y(t), it follows from the definition of y(t) with y(t) is a nondecreasing sequence that
Using (3.11), there exists a constant b \(\in (0\, ,1]\) such that
The rest of the proof is similar to that of Theorem 2.1 and hence is omitted.
Example 3.1. Consider the second-order neutral difference equation
and the second-order difference equation with a sublinear neutral term of the form
Here,\(\, \alpha =1/3, {\upgamma =}\frac{\mathrm {1}}{\mathrm {3}}{,\, \updelta =3}\) and \({\upbeta >0}\) , k,\({\, }k_{1}\, \)and \(k_{2\, }\)are positive integers and p(t)\(=\)1/t\(={\mathrm {\, p}}_{\mathrm {1}}\left( \mathrm {t} \right) \),
\(\mathrm {p}_{\mathrm {2}}\left( \mathrm {t} \right) = \frac{1}{t^{3}}\, ,\, q\left( t \right) \, \)are positive of real numbers. r(t) \(=\)1, R(t,\(\, t_{0}) =\) t-1-\(t_{0}\).
If the first-order linear delay difference equation
is oscillatory for all large \(t\ge t_{2\, }and\, any\, constant\, C\in (0\, ,1]\) , then Eqs. (3.21) and (3.22) are oscillatory.
4 General Remarks
The results of this paper are presented in a new form and of high degree of generality.
Our main task here is to reduce the oscillation of half-linear delay difference equations and/or nonlinear delay difference equations to the oscillation of linear or first-order difference equations whose oscillatory behavior is known and literature is filled with all types of criteria.
References
Agarwal, R.P.: Difference Equations and Inequalities. Dekker, New York (2000)
Agarwal, R.P., Bohner, M., Grace, S.R., O’Regan, D.: Discrete Oscillation Theory. Hindawi, New York (2005)
Agarwal, R.P., Grace, S.R., O’Regan, D.: Oscillation Theory for Difference and Functional Difference Equations. Kluwer, Dordrecht (2000)
Benekas, V., Kashkynbayev, A., Ioannis, Stavroulakis, P.: A sharp oscillation criterion for a difference equation with constant delay. Adv. Differ. Equ. 2020, 566 (2020)
El-Morshedy, H.A.: Oscillation and nonoscillation criteria for half-linear second order difference equations. Dyn. Syst. Appl. 15, 429–450 (2006)
El-Morshedy, H.A.: New oscillation criteria for second order linear difference equations with positive and negative coeffcients. Comput. Math. Appl. 58, 1988–1997 (2009)
Grace, S.R., Agarwal, R.P., Bohner, M., O’Regan, D.: Oscillation of second-order strongly superlinear and strongly sublinear dynamic equations. Commun. Nonlinear Sci. Numer. Simul. 14, 3463–3471 (2009)
Grace, S.R., Bohner, M., Agarwal, R.P.: On the oscillation of second-order half-linear dynamic equations. J. Differ. Equ. Appl. 15, 451–460 (2009)
Grace, S.R., El-Morshedy, H.A.: Oscillation criteria of comparison type for second order difference equations. J. Appl. Anal. 6, 87–103 (2000)
Grace, S.R., Graef, J.R.: Oscillatory behavior of second order nonlinear differential equations with a sublinear neutral term. Math. Model. Anal. 23, 217–226 (2018)
Gyori, I., Ladas, G.: Oscillation Theory of Delay Differential Equations with Applications. Clarendon Press, Oxford (1991)
Hardy, G.H., Littlewood, J.E., Polya’, G.: Inequalities, 1952nd edn. Cambridge University Press, Cambridge (1988)
Thandapani, E., Ravi, K.: Oscillation of second order half-linear difference equations. Appl. Math. Lett. 13, 43–49 (2000)
Thandapani, E., Ravi, K., Graef, J.R.: Oscillation and comparison theorem for halflinear second order difference equations. Comput. Math. Appl. 42, 953–960 (2001)
Yan, J., Qian, C.: Oscillation and comparison results for delay difference equations. J. Math. Anal. Appl. 165, 346–360 (1992)
Acknowledgements
I would like to extend my sincere thanks and appreciation to the reviewers for the effort they made to make this manuscript in appropriate form.
Funding
Open access funding provided by The Science, Technology & Innovation Funding Authority (STDF) in cooperation with The Egyptian Knowledge Bank (EKB).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Grace, S.R. New Oscillation Criteria of Nonlinear Second Order Delay Difference Equations. Mediterr. J. Math. 19, 166 (2022). https://doi.org/10.1007/s00009-022-02072-9
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00009-022-02072-9