Abstract
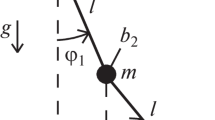
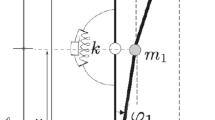
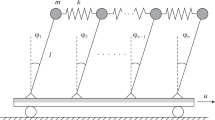
We investigate nonlinear stability for equilibrium of a pendulum with viscoelastic components. The tracking force is chosen so that the matrix of the linearized part of the perturbed motion has two purely imaginary roots or one zero and one negative root. The other two roots are complex with negative real part. The boundary of the domain of stability is divided into “dangerous” and “safe” (in the sense of Bautin) zones.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
V. I. Arnol'd, “Lectures on bifurcation in versal families,”Usp. Mat. Nauk,27, 119–184 (1972).
N. N. Bautin,The Behavior of Dynamic Systems Close to the Boundary of the Domain of Stability [in Russian], Nauka, Moscow (1984).
I. G. Boruk and L. G. Lobas, “On the motion of an inverted two-link mathematical pendulum with tracking force,”Prikl. Mekh.,35, No. 7, 108–112 (1999).
Yu. P. Varkhalev and G. V. Gorr, “Asymptotic pendulum motion of Hesse-Appelroth gyroscopes,”Prikl. Mat. Mekh.,48, No. 3, 490–493 (1984).
V. I. Gulyaev, A. L. Zubritskaya, and V. L. Koshkin, “On doubling the period of oscillation of a variable-length pendulum,”Prikl. Mekh.,26, No. 6, 74–80 (1990).
A. A. Zevin and B. I. Moroz, “Qualitative investigation of the stability of forced oscillation of two connected pendulums,”Prikl. Mekh.,21, No. 6, 89–94 (1985).
A. A. Zevin and L. A. Filonenko, “Periodic oscillation of a pendulum with horizontal vibration of pivot points,”Prikl. Mekh.,24, No. 8, 103–107 (1988).
A. Yu. Ishlinskii, V. A. Storozhenko, and M. E. Temchenko, “Quasiparadoxical motion of a rigid body,”Prikl. Mekh.,28, No. 9, 3–17 (1992).
T. S. Krasnopol'skaya and A. Yu. Shvets, “Chaotic oscillation of a spherical pendulum as an effect of interaction with an energy source,”Prikl. Mekh.,28, No. 10, 61–68 (1992).
L. G. Lobas, “Nonlinear stability and Y-shaped bifurcation in dynamic systems with simple symmetry,”Prikl. Mat. Mekh.,60, No. 2, 327–332 (1996).
L. G. Lobas, “Invariant manifolds and behavior of dynamic systems with symmetries close to the boundary of the domain of stability,”Prikl. Mat. Mekh.,32, No. 5, 81–88 (1996).
A. M. Lyapunov,Collected Works, in Three Volumes [in Russian], Vol. 2, Izd. Akad. Nauk SSSR, Moscow-Leningrad (1956).
A. N. Maryuta, “The dynamics of an inverted pendulum with vibrating pivot,”Prikl. Mekh.,29, No. 12, 78–86 (1993).
T. G. Strizhak,Methods for Investigating Dynamic Systems of Pendulum Type [in Russian], Izd. Nauka Kaz. SSR, Alma-Ata (1981).
K. N. Shevchenko, “On the motion of a pendulum,”Prikl. Mekh.,32, No. 6, 90–94 (1996).
P. Hagedorn, “On the destabilizing effect of nonlinear damping in nonconservative systems with follower forces,”Int. J. Nonlinear Mechanics,5, No. 2, 341–358 (1970).
H. Troger, and K. Zeman, “Zur Korrekten Modellbildung in der Dynamik Diskreter Systeme,”Ing. Arch.,51, No. 1/2, 13–43 (1981).
H. Troger, and A. Steindl,Nonlinear Stability and Bifurcation Theory, Springer-Verlag, Vienna-New York (1991).
H. Ziegler, “Die Stabilitatskriterien der Elastomechanik,”Ing. Arch. 20, No. 1 49–56 (1952).
Author information
Authors and Affiliations
Additional information
Translated from Prikladnaya Mekhanika, Vol. 35, No. 9, pp. 100–105, September, 1999.
Rights and permissions
About this article
Cite this article
Boruk, I.G., Lobas, L.G. Stability of equilibrium for an inverted two-link mathematical pendulum with critical tracking forces. Int Appl Mech 35, 962–967 (1999). https://doi.org/10.1007/BF02682293
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF02682293