Stabilization of the Double-inverted Pendulum with an Elastic Joint

Abstract

Background

Stabilization of unstable systems is an important problem in the field of nonlinear dynamics with rich applications in engineering and applied sciences.

Purpose

In this article we propose algorithms for stabilizing a double pendulum with an elastic joint. The stability zones in the parameter space of the model are obtained within the analytical approach.

Methods

Feedback principle, software stabilization, as well as the Routh-Hurwitz stability criterion.

Results

The critical value of the elastic coupling coefficient between the arms of the double inverted pendulum is found. This value allows to achieve the stabilization of the considered system in a small neighborhood of an unstable equilibrium.

Conclusion

The obtained results open up new perspectives for stabilizing unstable systems in the field of the applied problems.

Appendices

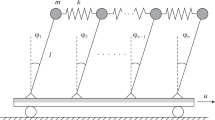
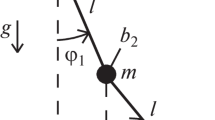
Appendix A Analytical Determination for the Stiffness Coefficient

$$\begin{aligned}&\alpha _{3}>0 \wedge \\&\left( \left( \alpha _{3}+\alpha _{4}<0 \wedge \alpha _{1}>\frac{g\left( m_{1}+m_{2}\right) }{m_{1}+2 m_{2}}\wedge \right. \right. \\&\quad \left. \left. \frac{g m_{2} \alpha _{3}+\left( -g\left( m_{1}+m_{2}\right) +\left( m_{1}+2 m_{2}\right) \alpha _{1}\right) \alpha _{4}}{\left( m_{1}+2 m_{2}\right) \alpha _{3}}<\alpha _{2}\right. \right. \wedge \\&\alpha _{1}+\alpha _{2}<g \wedge \\&\quad \frac{m_{2}\left( \left( g m_{2}+m_{1} \alpha _{2}\right) \alpha _{3}^{2}-m_{1} \alpha _{1} \alpha _{3} \alpha _{4}-g\left( m_{1}+m_{2}\right) \alpha _{4}^{2}\right) }{l\left( \alpha _{3}+\alpha _{4}\right) \left( 2 m_{2} \alpha _{3}-\left( m_{1}+2 m_{2}\right) \alpha _{4}\right) }< k \wedge \\&\left. k<\frac{g m_{2}\left( m_{1}+m_{2}\right) }{2\left( m_{1}+2 m_{2}\right) }\right) \vee \left( -\alpha _{3}<\alpha _{4}<\frac{2 m_{2} \alpha _{3}}{m_{1}+2 m_{2}} \wedge \right. \\&\quad \left. \left( \left( \alpha _{1}<\frac{g\left( m_{1}+m_{2}\right) }{m_{1}+2 m_{2}}\right. \right. \right. \wedge \\&\left. \alpha _{1}+\alpha _{2}>g \wedge \right. \\&\quad \left. k>\frac{m_{2}\left( \left( g m_{2}+m_{1} \alpha _{2}\right) \alpha _{3}^{2}-m_{1} \alpha _{1} \alpha _{3} \alpha _{4}-g\left( m_{1}+m_{2}\right) \alpha _{4}^{2}\right) }{l\left( \alpha _{3}+\alpha _{4}\right) \left( 2 m_{2} \alpha _{3}-\left( m_{1}+2 m_{2}\right) \alpha _{4}\right) }\right) \vee \\&\left( \frac{g\left( m_{1}+m_{2}\right) }{m_{1}+2 m_{2}}=\alpha _{1} \wedge \alpha _{2}>\right. \\&\left. \quad \frac{g m_{2} \alpha _{3}+\left( -g\left( m_{1}+m_{2}\right) +\left( m_{1}+2 m_{2}\right) \alpha _{1}\right) \alpha _{4}}{\left( m_{1}+2 m_{2}\right) \alpha _{3}}\right. \wedge \\&\left. k>\frac{m_{2}\left( \left( g m_{2}+m_{1} \alpha _{2}\right) \alpha _{3}^{2}-m_{1} \alpha _{1} \alpha _{3} \alpha _{4}-g\left( m_{1}+m_{2}\right) \alpha _{4}^{2}\right) }{l\left( \alpha _{3}+\alpha _{4}\right) \left( 2 m_{2} \alpha _{3}-\left( m_{1}+2 m_{2}\right) \alpha _{4}\right) }\right) \vee \\&\left( \alpha _{1}>\frac{g\left( m_{1}+m_{2}\right) }{m_{1}+2 m_{2}} \wedge \left( \left( k>\frac{g m_{2}\left( m_{1}+m_{2}\right) }{l\left( m_{1}+2 m_{2}\right) } \wedge g<\alpha _{1}+\alpha _{2}\right. \right. \right. \wedge \\&\left. \alpha _{2}<\frac{g m_{2} \alpha _{3}+\left( -g\left( m_{1}+m_{2}\right) +\left( m_{1}+2 m_{2}\right) \alpha _{1}\right) \alpha _{4}}{\left( m_{1}+2 m_{2}\right) \alpha _{3}}\right) \vee \\&\left( k>\frac{m_{2}\left( \left( g m_{2}+m_{1} \alpha _{2}\right) \alpha _{3}^{2}-m_{1} \alpha _{1} \alpha _{3} \alpha _{4}-g\left( m_{1}+m_{2}\right) \alpha _{4}^{2}\right) }{2\left( \alpha _{3}+\alpha _{4}\right) \left( 2 m_{2} \alpha _{3}-\left( m_{1}+2 m_{2}\right) \alpha _{4}\right) }\right. \wedge \\&\left. \left. \left. \left. \alpha _{2} \ge \frac{g m_{2} \alpha _{3}+\left( -g\left( m_{1}+m_{2}\right) +\left( m_{1}+2 m_{2}\right) \alpha _{1}\right) \alpha _{4}}{\left( m_{1}+2 m_{2}\right) \alpha _{3}}\right) \right) \right) \right) \vee \\&\left( \frac{2 m_{2} \alpha _{3}}{m_{1}+2 m_{2}}=\alpha _{4} \wedge \alpha _{1}>\frac{g\left( m_{1}+m_{2}\right) }{m_{1}+2 m_{2}} \wedge g<\alpha _{1}+\alpha _{2}\right. \wedge \\&\alpha _{2}<\frac{g m_{2} \alpha _{3}+\left( -g\left( m_{1}+m_{2}\right) +\left( m_{1}+2 m_{2}\right) \alpha _{1}\right) \alpha _{4}}{\left( m_{1}+2 m_{2}\right) \alpha _{3}} \wedge \\&\left. k>\frac{g m_{2}\left( m_{1}+m_{2}\right) }{2\left( m_{1}+2 m_{2}\right) }\right) \vee \\&\left( \alpha _{4}>\frac{2 m_{2} \alpha _{3}}{m_{1}+2 m_{2}} \wedge \alpha _{1}>\frac{g\left( m_{1}+m_{2}\right) }{m_{1}+2 m_{2}} \wedge g<\alpha _{1}+\alpha _{2}\right. \wedge \\&\alpha _{2}<\frac{g m_{2} \alpha _{3}+\left( -g\left( m_{1}+m_{2}\right) +\left( m_{1}+2 m_{2}\right) \alpha _{1}\right) \alpha _{4}}{\left( m_{1}+2 m_{2}\right) \alpha _{3}} \wedge \\&\frac{g m_{2}\left( m_{1}+m_{2}\right) }{2\left( m_{1}+2 m_{2}\right) }<k \wedge \\&\left. \left. k<\frac{m_{2}\left( \left( g m_{2}+m_{1} \alpha _{2}\right) \alpha _{3}^{2}-m_{1} \alpha _{1} \alpha _{3} \alpha _{4}-g\left( m_{1}+m_{2}\right) \alpha _{4}^{2}\right) }{l\left( \alpha _{3}+\alpha _{4}\right) \left( l m_{2} \alpha _{3}-\left( m_{1}+2 m_{2}\right) \alpha _{4}\right) }\right) \right) . \end{aligned}$$

Appendix B The Fundamental Matrix of Solutions

The fundamental matrix of solutions (22)

$$\begin{aligned} \Phi _1(t) = \begin{pmatrix} \beta _{00} &{} \beta _{01} &{} \beta _{02} &{} \beta _{03} \\ \beta _{10} &{} \beta _{11} &{} \beta _{12} &{} \beta _{13} \\ \beta _{20} &{} \beta _{21} &{} \beta _{22} &{} \beta _{23} \\ \beta _{30} &{} \beta _{31} &{} \beta _{32} &{} \beta _{33} \end{pmatrix}, \end{aligned}$$

where

$$\begin{aligned} \begin{array}{lcl} \beta _{00} = \frac{\sqrt{- 2 y_{1} + 4 y_{2}} \left( - \frac{x_{1}}{2} - \frac{x_{2}}{2} + \frac{y_{1}}{4} - \frac{y_{2}}{2}\right) e^{- \frac{\sqrt{2} t \sqrt{- y_{1} + 2 y_{2}}}{2}}}{x_{1} x_{3}}, \\ \beta _{01} = \frac{\sqrt{- 2 y_{1} + 4 y_{2}} \left( \frac{x_{1}}{2} + \frac{x_{2}}{2} - \frac{y_{1}}{4} + \frac{y_{2}}{2}\right) e^{\frac{\sqrt{2} t \sqrt{- y_{1} + 2 y_{2}}}{2}}}{x_{1} x_{3}}, \\ \beta _{02} = - \frac{\sqrt{2 y_{1} + 4 y_{2}} \left( \frac{x_{1}}{2} + \frac{x_{2}}{2} + \frac{y_{1}}{4} + \frac{y_{2}}{2}\right) e^{- \frac{\sqrt{2} t \sqrt{y_{1} + 2 y_{2}}}{2}}}{x_{1} x_{3}}, \\ \beta _{03} = \frac{\sqrt{2 y_{1} + 4 y_{2}} \left( \frac{x_{1}}{2} + \frac{x_{2}}{2} + \frac{y_{1}}{4} + \frac{y_{2}}{2}\right) e^{\frac{\sqrt{2} t \sqrt{y_{1} + 2 y_{2}}}{2}}}{x_{1} x_{3}}, \\ \beta _{10} = \frac{\left( x_{1} - \frac{y_{1}}{2} + y_{2}\right) e^{- \frac{\sqrt{2} t \sqrt{- y_{1} + 2 y_{2}}}{2}}}{x_{1}}, \\ \beta _{11} = \frac{\left( x_{1} - \frac{y_{1}}{2} + y_{2}\right) e^{\frac{\sqrt{2} t \sqrt{- y_{1} + 2 y_{2}}}{2}}}{x_{1}}, \\ \beta _{12} = \frac{\left( x_{1} + \frac{y_{1}}{2} + y_{2}\right) e^{- \frac{\sqrt{2} t \sqrt{y_{1} + 2 y_{2}}}{2}}}{x_{1}}, \\ \beta _{13} = \frac{\left( x_{1} + \frac{y_{1}}{2} + y_{2}\right) e^{\frac{\sqrt{2} t \sqrt{y_{1} + 2 y_{2}}}{2}}}{x_{1}}, \\ \beta _{20} = \frac{\sqrt{- 2 y_{1} + 4 y_{2}} \left( - \frac{x_{1}}{2} - \frac{x_{2}}{2} + \frac{x_{3}}{2} + \frac{y_{1}}{4} - \frac{y_{2}}{2}\right) e^{- \frac{\sqrt{2} t \sqrt{- y_{1} + 2 y_{2}}}{2}}}{x_{1} x_{3}} ,\\ \beta _{21} = \frac{\sqrt{- 2 y_{1} + 4 y_{2}} \left( \frac{x_{1}}{2} + \frac{x_{2}}{2} - \frac{x_{3}}{2} - \frac{y_{1}}{4} + \frac{y_{2}}{2}\right) e^{\frac{\sqrt{2} t \sqrt{- y_{1} + 2 y_{2}}}{2}}}{x_{1} x_{3}}, \\ \beta _{22} = \frac{\sqrt{2 y_{1} + 4 y_{2}} \left( - \frac{x_{1}}{2} - \frac{x_{2}}{2} + \frac{x_{3}}{2} - \frac{y_{1}}{4} - \frac{y_{2}}{2}\right) e^{- \frac{\sqrt{2} t \sqrt{y_{1} + 2 y_{2}}}{2}}}{x_{1} x_{3}} ,\\ \beta _{23} = \frac{\sqrt{2 y_{1} + 4 y_{2}} \left( \frac{x_{1}}{2} + \frac{x_{2}}{2} - \frac{x_{3}}{2} + \frac{y_{1}}{4} + \frac{y_{2}}{2}\right) e^{\frac{\sqrt{2} t \sqrt{y_{1} + 2 y_{2}}}{2}}}{x_{1} x_{3}}, \\ \beta _{30} = e^{- \frac{\sqrt{2} t \sqrt{- y_{1} + 2 y_{2}}}{2}}, \; \beta _{31} = e^{\frac{\sqrt{2} t \sqrt{- y_{1} + 2 y_{2}}}{2}} \\ \beta _{32} = e^{- \frac{\sqrt{2} t \sqrt{y_{1} + 2 y_{2}}}{2}} , \; \beta _{33} = e^{\frac{\sqrt{2} t \sqrt{y_{1} + 2 y_{2}}}{2}}, \\ y_1 = \sqrt{x_{1}^{2} + 2 x_{1} x_{2} + 2 x_{1} x_{3} + x_{2}^{2} - 2 x_{2} x_{3} + x_{3}^{2}},\\ y_2 = - \frac{x_{1}}{2} - \frac{x_{2}}{2} + \frac{x_{3}}{2}. \end{array} \end{aligned}$$

Appendix C The Fundamental Matrix of Ssolutions

The fundamental matrix of solutions (23)

$$\begin{aligned} \Phi _2(t) = \begin{pmatrix} \gamma _{00} &{} \gamma _{01} &{} \gamma _{02} &{} \gamma _{03} \\ \gamma _{10} &{} \gamma _{11} &{} \gamma _{12} &{} \gamma _{13} \\ \gamma _{20} &{} \gamma _{21} &{} \gamma _{22} &{} \gamma _{23} \\ \gamma _{30} &{} \gamma _{31} &{} \gamma _{32} &{} \gamma _{33}, \end{pmatrix} \end{aligned}$$

where

$$\begin{aligned} \begin{array}{lcl} \gamma _{00} = \frac{\sqrt{- 2 y_{3} + 4 y_{4}} \left( - \frac{x_{4}}{2} - \frac{x_{5}}{2} + \frac{y_{3}}{4} - \frac{y_{4}}{2}\right) e^{- \frac{\sqrt{2} t \sqrt{- y_{3} + 2 y_{4}}}{2}}}{x_{4} x_{6}}, \\ \gamma _{01} = \frac{\sqrt{- 2 y_{3} + 4 y_{4}} \left( \frac{x_{4}}{2} + \frac{x_{5}}{2} - \frac{y_{3}}{4} + \frac{y_{4}}{2}\right) e^{\frac{\sqrt{2} t \sqrt{- y_{3} + 2 y_{4}}}{2}}}{x_{4} x_{6}}, \\ \gamma _{02} = - \frac{\sqrt{2 y_{3} + 4 y_{4}} \left( \frac{x_{4}}{2} + \frac{x_{5}}{2} + \frac{y_{3}}{4} + \frac{y_{4}}{2}\right) e^{- \frac{\sqrt{2} t \sqrt{y_{3} + 2 y_{4}}}{2}}}{x_{4} x_{6}}, \\ \gamma _{03} = \frac{\sqrt{2 y_{3} + 4 y_{4}} \left( \frac{x_{4}}{2} + \frac{x_{5}}{2} + \frac{y_{3}}{4} + \frac{y_{4}}{2}\right) e^{\frac{\sqrt{2} t \sqrt{y_{3} + 2 y_{4}}}{2}}}{x_{4} x_{6}}, \\ \gamma _{10} = \frac{\left( x_{4} - \frac{y_{3}}{2} + y_{4}\right) e^{- \frac{\sqrt{2} t \sqrt{- y_{3} + 2 y_{4}}}{2}}}{x_{4}}, \\ \gamma _{11} = \frac{\left( x_{4} - \frac{y_{3}}{2} + y_{4}\right) e^{\frac{\sqrt{2} t \sqrt{- y_{3} + 2 y_{4}}}{2}}}{x_{4}}, \\ \gamma _{12} = \frac{\left( x_{4} + \frac{y_{3}}{2} + y_{4}\right) e^{- \frac{\sqrt{2} t \sqrt{y_{3} + 2 y_{4}}}{2}}}{x_{4}}, \\ \gamma _{13} = \frac{\left( x_{4} + \frac{y_{3}}{2} + y_{4}\right) e^{\frac{\sqrt{2} t \sqrt{y_{3} + 2 y_{4}}}{2}}}{x_{4}}, \\ \gamma _{20} = \frac{\sqrt{- 2 y_{3} + 4 y_{4}} \left( - \frac{x_{4}}{2} - \frac{x_{5}}{2} + \frac{x_{6}}{2} + \frac{y_{3}}{4} - \frac{y_{4}}{2}\right) e^{- \frac{\sqrt{2} t \sqrt{- y_{3} + 2 y_{4}}}{2}}}{x_{4} x_{6}} ,\\ \gamma _{21} = \frac{\sqrt{- 2 y_{3} + 4 y_{4}} \left( \frac{x_{4}}{2} + \frac{x_{5}}{2} - \frac{x_{6}}{2} - \frac{y_{3}}{4} + \frac{y_{4}}{2}\right) e^{\frac{\sqrt{2} t \sqrt{- y_{3} + 2 y_{4}}}{2}}}{x_{4} x_{6}}, \\ \gamma _{22} = \frac{\sqrt{2 y_{3} + 4 y_{4}} \left( - \frac{x_{4}}{2} - \frac{x_{5}}{2} + \frac{x_{6}}{2} - \frac{y_{3}}{4} - \frac{y_{4}}{2}\right) e^{- \frac{\sqrt{2} t \sqrt{y_{3} + 2 y_{4}}}{2}}}{x_{4} x_{6}}, \\ \gamma _{23} = \frac{\sqrt{2 y_{3} + 4 y_{4}} \left( \frac{x_{4}}{2} + \frac{x_{5}}{2} - \frac{x_{6}}{2} + \frac{y_{3}}{4} + \frac{y_{4}}{2}\right) e^{\frac{\sqrt{2} t \sqrt{y_{3} + 2 y_{4}}}{2}}}{x_{4} x_{6}}, \\ \gamma _{30} = e^{- \frac{\sqrt{2} t \sqrt{- y_{3} + 2 y_{4}}}{2}} ,\; \gamma _{31} = e^{\frac{\sqrt{2} t \sqrt{- y_{3} + 2 y_{4}}}{2}} \\ \gamma _{32} = e^{- \frac{\sqrt{2} t \sqrt{y_{3} + 2 y_{4}}}{2}} ,\; \gamma _{33} = e^{\frac{\sqrt{2} t \sqrt{y_{3} + 2 y_{4}}}{2}} \\ y_3 = \sqrt{x_{4}^{2} + 2 x_{4} x_{5} + 2 x_{4} x_{6} + x_{5}^{2} - 2 x_{5} x_{6} + x_{6}^{2}}, \\ y_4 =- \frac{x_{4}}{2} - \frac{x_{5}}{2} + \frac{x_{6}}{2}. \end{array} \end{aligned}$$

Appendix D The Monodromy Matrix

The monodromy matrix of (20)

$$\begin{aligned} M = \begin{pmatrix} \theta _{00} &{} \theta _{01} &{} \theta _{02} &{} \theta _{03} \\ \theta _{10} &{} \theta _{11} &{} \theta _{12} &{} \theta _{13} \\ \theta _{20} &{} \theta _{21} &{} \theta _{22} &{} \theta _{23} \\ \theta _{30} &{} \theta _{31} &{} \theta _{32} &{} \theta _{33}. \end{pmatrix} \end{aligned}$$

(27)

$$\begin{aligned} \theta _{00}= & {} \left( 1+\frac{-\frac{y_{3}}{2}+y_{4}}{x_{4}}\right) \left( \frac{\left( x_{1}+x_{2}\right) \sqrt{-\frac{y_{1}}{2}+y_{2}}}{x_{1} x_{3}}\right. \\&\quad \left. +\frac{\left( -\frac{y_{1}}{2}+y_{2}\right) ^{\frac{3}{2}}}{x_{1} x_{3}}\right) \\&\quad e^{\pi \sqrt{-\frac{y_{1}}{2}+y_{2}}} e^{-\pi \sqrt{-\frac{y_{3}}{2}+y_{4}}} \\&\quad +\left( -\frac{\left( -\frac{y_{3}}{2}+y_{4}\right) ^{\frac{3}{2}}}{x_{4} x_{6}}-\frac{\sqrt{-\frac{y_{3}}{2}+y_{4}}\left( x_{4}+x_{5}-x_{6}\right) }{x_{4} x_{6}}\right) \\&\quad \left( -\frac{\left( x_{1}+x_{2}\right) \sqrt{\frac{y_{1}}{2}+y_{2}}}{x_{1} x_{3}}-\frac{\left( \frac{y_{1}}{2}+y_{2}\right) ^{\frac{3}{2}}}{x_{1} x_{3}}\right) \\&\quad \cdot e^{-\pi \sqrt{\frac{y_{1}}{2}+y_{2}}} e^{-\pi \sqrt{-\frac{y_{3}}{2}+y_{4}}} \\&\quad +\left( -\frac{\left( x_{1}+x_{2}\right) \sqrt{-\frac{y_{1}}{2}+y_{2}}}{x_{1} x_{3}}-\frac{\left( -\frac{y_{1}}{2}+y_{2}\right) ^{\frac{3}{2}}}{x_{1} x_{3}}\right) \\&\quad \left( -\frac{\left( x_{4}+x_{5}\right) \sqrt{-\frac{y_{3}}{2}+y_{4}}}{x_{4} x_{6}}-\frac{\left( -\frac{y_{3}}{2}+y_{4}\right) ^{\frac{3}{2}}}{x_{4} x_{6}}\right) \\&\quad \cdot e^{-\pi \sqrt{-\frac{y_{1}}{2}+y_{2}}} e^{-\pi \sqrt{-\frac{y_{3}}{2}+y_{4}}} \\&\quad +\left( \frac{\left( x_{1}+x_{2}\right) \sqrt{\frac{y_{1}}{2}+y_{2}}}{x_{1} x_{3}}+\frac{\left( \frac{y_{1}}{2}+y_{2}\right) ^{\frac{3}{2}}}{x_{1} x_{3}}\right) \\ &\quad e^{\pi \sqrt{\frac{y_{1}}{2}+y_{2}}} e^{-\pi \sqrt{-\frac{y_{3}}{2}+y_{4}}}, \\ \theta _{10}= & {} \left( 1+\frac{-\frac{y_{1}}{2}+y_{2}}{x_{1}}\right) \left( 1+\frac{-\frac{y_{3}}{2}+y_{4}}{x_{4}}\right) \\&\quad e^{\pi \sqrt{-\frac{y_{1}}{2}+y_{2}}} e^{-\pi \sqrt{-\frac{y_{3}}{2}+y_{4}}} \\&\quad +\left( 1+\frac{-\frac{y_{1}}{2}+y_{2}}{x_{1}}\right) \left( -\frac{\left( x_{4}+x_{5}\right) \sqrt{-\frac{y_{3}}{2}+y_{4}}}{x_{4} x_{6}}\right. \\&\quad \left. -\frac{\left( -\frac{y_{3}}{2}+y_{4}\right) ^{\frac{3}{2}}}{x_{4} x_{6}}\right) \\&\quad e^{-\pi \sqrt{-\frac{y_{1}}{2}+y_{2}}} e^{-\pi \sqrt{-\frac{y_{3}}{2}+y_{4}}} \\&\quad +\left( 1+\frac{\frac{y_{1}}{2}+y_{2}}{x_{1}}\right) \left( -\frac{\left( -\frac{y_{3}}{2}+y_{4}\right) ^{\frac{3}{2}}}{x_{4} x_{6}}\right. \\&\quad \left. -\frac{\sqrt{-\frac{y_{3}}{2}+y_{4}}\left( x_{4}+x_{5}-x_{6}\right) }{x_{4} x_{6}}\right) \\&\quad e^{-\pi \sqrt{\frac{y_{1}}{2}+y_{2}}} e^{-\pi \sqrt{-\frac{y_{3}}{2}+y_{4}}} \\&\quad +\left( 1+\frac{\frac{y_{1}}{2}+y_{2}}{x_{1}}\right) \cdot e^{\pi \sqrt{\frac{y_{1}}{2}+y_{2}}} e^{-\pi \sqrt{-\frac{y_{3}}{2}+y_{4}}} \\ \theta _{20}= & {} \left( 1+\frac{-\frac{y_{3}}{2}+y_{4}}{x_{4}}\right) \left( \frac{\left( -\frac{y_{1}}{2}+y_{2}\right) ^{\frac{3}{2}}}{x_{1} x_{3}}\right. \\&\quad \left. +\frac{\sqrt{-\frac{y_{1}}{2}+y_{2}}\left( x_{1}+x_{2}-x_{3}\right) }{x_{1} x_{3}}\right) \\&\quad e^{\pi \sqrt{-\frac{y_{1}}{2}+y_{2}}} e^{-\pi \sqrt{-\frac{y_{3}}{2}+y_{4}}} \\&\quad +\left( -\frac{\left( -\frac{y_{1}}{2}+y_{2}\right) ^{\frac{3}{2}}}{x_{1} x_{3}}-\frac{\sqrt{-\frac{y_{1}}{2}+y_{2}}\left( x_{1}+x_{2}-x_{3}\right) }{x_{1} x_{3}}\right) \\&\quad \left( -\frac{\left( x_{4}+x_{5}\right) \sqrt{-\frac{y_{3}}{2}+y_{4}}}{x_{4} x_{6}}-\frac{\left( -\frac{y_{3}}{2}+y_{4}\right) ^{\frac{3}{2}}}{x_{4} x_{6}}\right) \\&\quad \cdot e^{-\pi \sqrt{-\frac{y_{1}}{2}+y_{2}}} e^{-\pi \sqrt{-\frac{y_{3}}{2}+y_{4}}} \\&\quad +\left( -\frac{\left( \frac{y_{1}}{2}+y_{2}\right) ^{\frac{3}{2}}}{x_{1} x_{3}}-\frac{\sqrt{\frac{y_{1}}{2}+y_{2}}\left( x_{1}+x_{2}-x_{3}\right) }{x_{1} x_{3}}\right) \\ &\quad \left( -\frac{\left( -\frac{y_{3}}{2}+y_{4}\right) ^{\frac{3}{2}}}{x_{4} x_{6}}-\frac{\sqrt{-\frac{y_{3}}{2}+y_{4}}\left( x_{4}+x_{5}-x_{6}\right) }{x_{4} x_{6}}\right) \\&\quad \cdot e^{-\pi \sqrt{\frac{y_{1}}{2}+y_{2}}} e^{-\pi \sqrt{-\frac{y_{3}}{2}+y_{4}}} \\&\quad +\left( \frac{\left( \frac{y_{1}}{2}+y_{2}\right) ^{\frac{3}{2}}}{x_{1} x_{3}}+\frac{\sqrt{\frac{y_{1}}{2}+y_{2}}\left( x_{1}+x_{2}-x_{3}\right) }{x_{1} x_{3}}\right) \\&\quad e^{\pi \sqrt{\frac{y_{1}}{2}+y_{2}}} e^{-\pi \sqrt{-\frac{y_{3}}{2}+y_{4}}} ,\\ \theta _{30}= & {} \left( 1+\frac{-\frac{y_{3}}{2}+y_{4}}{x_{4}}\right) e^{\pi \sqrt{-\frac{y_{1}}{2}+y_{2}}} \\&\quad e^{-\pi \sqrt{-\frac{y_{3}}{2}+y_{4}}}+\left( -\frac{\left( -\frac{y_{3}}{2}+y_{4}\right) ^{\frac{3}{2}}}{x_{4} x_{6}}\right. \\&\quad \left. -\frac{\sqrt{-\frac{y_{3}}{2}+y_{4}}\left( x_{4}+x_{5}-x_{6}\right) }{x_{4} x_{6}}\right) \\&\quad \cdot e^{-\pi \sqrt{\frac{y_{1}}{2}+y_{2}}} e^{-\pi \sqrt{-\frac{y_{3}}{2}+y_{4}}} \\&\quad +\left( -\frac{\left( x_{4}+x_{5}\right) \sqrt{-\frac{y_{3}}{2}+y_{4}}}{x_{4} x_{6}}-\frac{\left( -\frac{y_{3}}{2}+y_{4}\right) ^{\frac{3}{2}}}{x_{4} x_{6}}\right) \\&\quad e^{-\pi \sqrt{-\frac{y_{1}}{2}+y_{2}}} \\&\quad e^{-\pi \sqrt{-\frac{y_{3}}{2}+y_{4}}}+e^{\pi \sqrt{\frac{y_{1}}{2}+y_{2}}} e^{-\pi \sqrt{-\frac{y_{3}}{2}+y_{4}}}, \\ \theta _{01}= & {} \left( 1+\frac{-\frac{y_{3}}{2}+y_{4}}{x_{4}}\right) \left( \frac{\left( x_{1}+x_{2}\right) \sqrt{-\frac{y_{1}}{2}+y_{2}}}{x_{1} x_{3}}\right. \\&\quad \left. +\frac{\left( -\frac{y_{1}}{2}+y_{2}\right) ^{\frac{3}{2}}}{x_{1} x_{3}}\right) \\&\quad e^{\pi \sqrt{-\frac{y_{1}}{2}+y_{2}}} e^{\pi \sqrt{-\frac{y_{3}}{2}+y_{4}}} \\&\quad +\left( \frac{\left( -\frac{y_{3}}{2}+y_{4}\right) ^{\frac{3}{2}}}{x_{4} x_{6}}+\frac{\sqrt{-\frac{y_{3}}{2}+y_{4}}\left( x_{4}+x_{5}-x_{6}\right) }{x_{4} x_{6}}\right) \\&\quad \left( -\frac{\left( x_{1}+x_{2}\right) \sqrt{\frac{y_{1}}{2}+y_{2}}}{x_{1} x_{3}}-\frac{\left( \frac{y_{1}}{2}+y_{2}\right) ^{\frac{3}{2}}}{x_{1} x_{3}}\right) \\&\quad \cdot e^{-\pi \sqrt{\frac{y_{1}}{2}+y_{2}}} e^{\pi \sqrt{-\frac{y_{3}}{2}+y_{4}}} \\&\quad +\left( -\frac{\left( x_{1}+x_{2}\right) \sqrt{-\frac{y_{1}}{2}+y_{2}}}{x_{1} x_{3}}-\frac{\left( -\frac{y_{1}}{2}+y_{2}\right) ^{\frac{3}{2}}}{x_{1} x_{3}}\right) \\&\quad \left( \frac{\left( x_{4}+x_{5}\right) \sqrt{-\frac{y_{3}}{2}+y_{4}}}{x_{4} x_{6}}+\frac{\left( -\frac{y_{3}}{2}+y_{4}\right) ^{\frac{3}{2}}}{x_{4} x_{6}}\right) \\&\quad \cdot e^{-\pi \sqrt{-\frac{y_{1}}{2}+y_{2}}} e^{\pi \sqrt{-\frac{y_{3}}{2}+y_{4}}} \\&\quad +\left( \frac{\left( x_{1}+x_{2}\right) \sqrt{\frac{y_{1}}{2}+y_{2}}}{x_{1} x_{3}}+\frac{\left( \frac{y_{1}}{2}+y_{2}\right) ^{\frac{3}{2}}}{x_{1} x_{3}}\right) \\&\quad e^{\pi \sqrt{\frac{y_{1}}{2}+y_{2}}} e^{\pi \sqrt{-\frac{y_{3}}{2}+y_{4}}}, \\\end{aligned}$$

$$\begin{aligned} \theta _{11}= & {} \left( 1+\frac{-\frac{y_{1}}{2}+y_{2}}{x_{1}}\right) \left( 1+\frac{-\frac{y_{3}}{2}+y_{4}}{x_{4}}\right) e^{\pi \sqrt{-\frac{y_{1}+y_{2}}{2}}}\\&\quad e^{\pi \sqrt{-\frac{y_{3}}{2}+y_{4}}} \\&\quad +\left( 1+\frac{-\frac{y_{1}}{2}+y_{2}}{x_{1}}\right) \left( \frac{\left( x_{4}+x_{5}\right) \sqrt{-\frac{y_{3}}{2}+y_{4}}}{x_{4} x_{6}}\right. \\&\quad \left. +\frac{\left( -\frac{y_{3}}{2}+y_{4}\right) ^{\frac{3}{2}}}{x_{4} x_{6}}\right) \\&\quad e^{-\pi \sqrt{-\frac{y_{1}}{2}+y_{2}}} e^{\pi \sqrt{-\frac{y_{3}}{2}+y_{4}}} \\&\quad +\left( 1+\frac{\frac{y_{1}}{2}+y_{2}}{x_{1}}\right) \left( \frac{\left( -\frac{y_{3}}{2}+y_{4}\right) ^{\frac{3}{2}}}{x_{4} x_{6}}\right. \\&\quad \left. +\frac{\sqrt{-\frac{y_{3}}{2}+y_{4}}\left( x_{4}+x_{5}-x_{6}\right) }{x_{4} x_{6}}\right) \\&\quad e^{-\pi \sqrt{\frac{y_{1}}{2}+y_{2}}} e^{\pi \sqrt{-\frac{y_{3}}{2}+y_{4}}}\\&\quad +\left( 1+\frac{\frac{y_{1}}{2}+y_{2}}{x_{1}}\right) \cdot e^{\pi \sqrt{\frac{y_{1}}{2}+y_{2}}} e^{\pi \sqrt{-\frac{y_{3}}{2}+y_{4}}} ,\\ \theta _{21}= & {} \left( 1+\frac{-\frac{y_{3}}{2}+y_{4}}{x_{4}}\right) \left( \frac{\left( -\frac{y_{1}}{2}+y_{2}\right) ^{\frac{3}{2}}}{x_{1} x_{3}}\right. \\&\quad \left. +\frac{\sqrt{-\frac{y_{1}}{2}+y_{2}}\left( x_{1}+x_{2}-x_{3}\right) }{x_{1} x_{3}}\right) \\&\quad e^{\pi \sqrt{-\frac{y_{1}}{2}+y_{2}}} e^{\pi \sqrt{-\frac{y_{3}}{2}+y_{4}}} \\&\quad +\left( -\frac{\left( -\frac{y_{1}}{2}+y_{2}\right) ^{\frac{3}{2}}}{x_{1} x_{3}}-\frac{\sqrt{-\frac{y_{1}}{2}+y_{2}}\left( x_{1}+x_{2}-x_{3}\right) }{x_{1} x_{3}}\right) \\ &\quad \left( \frac{\left( x_{4}+x_{5}\right) \sqrt{-\frac{y_{3}}{2}+y_{4}}}{x_{4} x_{6}}+\frac{\left( -\frac{y_{3}}{2}+y_{4}\right) ^{\frac{3}{2}}}{x_{4} x_{6}}\right) \\&\quad \cdot e^{-\pi \sqrt{-\frac{y_{1}}{2}+y_{2}}} e^{\pi \sqrt{-\frac{y_{3}}{2}+y_{4}}} \\&\quad +\left( -\frac{\left( \frac{y_{1}}{2}+y_{2}\right) ^{\frac{3}{2}}}{x_{1} x_{3}}-\frac{\sqrt{\frac{y_{1}}{2}+y_{2}}\left( x_{1}+x_{2}-x_{3}\right) }{x_{1} x_{3}}\right) \\&\quad \left( \frac{\left( -\frac{y_{3}}{2}+y_{4}\right) ^{\frac{3}{2}}}{x_{4} x_{6}}+\frac{\sqrt{-\frac{y_{3}}{2}+y_{4}}\left( x_{4}+x_{5}-x_{6}\right) }{x_{4} x_{6}}\right) \\&\quad \cdot e^{-\pi \sqrt{\frac{y_{1}}{2}+y_{2}}} e^{\pi \sqrt{-\frac{y_{3}}{2}+y_{4}}} \\&\quad +\left( \frac{\left( \frac{y_{1}}{2}+y_{2}\right) ^{\frac{3}{2}}}{x_{1} x_{3}}+\frac{\sqrt{\frac{y_{1}}{2}+y_{2}}\left( x_{1}+x_{2}-x_{3}\right) }{x_{1} x_{3}}\right) \\&\quad e^{\pi \sqrt{\frac{y_{1}}{2}+y_{2}}} e^{\pi \sqrt{-\frac{y_{3}}{2}+y_{4}}}, \\ \theta _{31}= & {} \left( 1+\frac{-\frac{y_{3}}{2}+y_{4}}{x_{4}}\right) e^{\pi \sqrt{-\frac{y_{1}}{2}+y_{2}}} e^{\pi \sqrt{-\frac{y_{3}}{2}+y_{4}}}\\&\quad +\left( \frac{\left( -\frac{y_{3}}{2}+y_{4}\right) ^{\frac{3}{2}}}{x_{4} x_{6}}+\frac{\sqrt{-\frac{y_{3}}{2}+y_{4}}\left( x_{4}+x_{5}-x_{6}\right) }{x_{4} x_{6}}\right) \\&\quad \cdot e^{-\pi \sqrt{\frac{y_{1}}{2}+y_{2}}} e^{\pi \sqrt{-\frac{y_{3}}{2}+y_{4}}} \\&\quad +\left( \frac{\left( x_{4}+x_{5}\right) \sqrt{-\frac{y_{3}}{2}+y_{4}}}{x_{4} x_{6}}+\frac{\left( -\frac{y_{3}}{2}+y_{4}\right) ^{\frac{3}{2}}}{x_{4} x_{6}}\right) \\&\quad e^{-\pi \sqrt{-\frac{y_{1}}{2}+y_{2}}} e^{\pi \sqrt{-\frac{y_{3}}{2}+y_{4}}}+e^{\pi \sqrt{\frac{y_{1}}{2}+y_{2}}} e^{\pi \sqrt{-\frac{y_{3}}{2}+y_{4}}},\\ \end{aligned}$$

$$ \begin{aligned} \theta _{02}= & {} \left( 1+\frac{\frac{y_{3}}{2}+y_{4}}{x_{4}}\right) \left( \frac{\left( x_{1}+x_{2}\right) \sqrt{-\frac{y_{1}}{2}+y_{2}}}{x_{1} x_{3}}\right. \\&\quad \left. +\frac{\left( -\frac{y_{1}}{2}+y_{2}\right) ^{\frac{3}{2}}}{x_{1} x_{3}}\right) \\&\quad e^{\pi \sqrt{-\frac{y_{1}}{2}+y_{2}}} e^{-\pi \sqrt{\frac{\sqrt{3}{2}}{+} y_{4}}} \\&\quad +\left( -\frac{\left( \frac{y_{3}}{2}+y_{4}\right) ^{\frac{3}{2}}}{x_{4} x_{6}}-\frac{\sqrt{\frac{y_{3}}{2}+y_{4}}\left( x_{4}+x_{5}-x_{6}\right) }{x_{4} x_{6}}\right) \\&\quad \left( -\frac{\left( x_{1}+x_{2}\right) \sqrt{\frac{y_{1}}{2}+y_{2}}}{x_{1} x_{3}}-\frac{\left( \frac{y_{1}}{2}+y_{2}\right) ^{\frac{3}{2}}}{x_{1} x_{3}}\right) \\&\quad \cdot e^{-\pi \sqrt{\frac{y_{1}}{2}+y_{2}}} e^{-\pi \sqrt{\frac{y_{3}}{2}+y_{4}}} \\&\quad +\left( -\frac{\left( x_{1}+x_{2}\right) \sqrt{-\frac{y_{1}}{2}+y_{2}}}{x_{1} x_{3}}-\frac{\left( -\frac{y_{1}}{2}+y_{2}\right) ^{\frac{3}{2}}}{x_{1} x_{3}}\right) \\&\quad \left( -\frac{\left( x_{4}+x_{5}\right) \sqrt{\frac{y_{3}}{2}+y_{4}}}{x_{4} x_{6}}-\frac{\left( \frac{y_{3}}{2}+y_{4}\right) ^{\frac{3}{2}}}{x_{4} x_{6}}\right) \\&\quad \cdot e^{-\pi \sqrt{-\frac{y_{1}}{2}+y_{2}}} e^{-\pi \sqrt{\frac{y_{3}}{2}+y_{4}}} \\&\quad +\left( \frac{\left( x_{1}+x_{2}\right) \sqrt{\frac{y_{1}}{2}+y_{2}}}{x_{1} x_{3}}+\frac{\left( \frac{y_{1}}{2}+y_{2}\right) ^{\frac{3}{2}}}{x_{1} x_{3}}\right) \\&\quad e^{\pi \sqrt{\frac{y_{1}}{2}+y_{2}}} e^{-\pi \sqrt{\frac{y_{3}}{2}+y_{4}}} ,\\ \theta _{12}= & {} \left( 1+\frac{-\frac{y_{1}}{2}+y_{2}}{x_{1}}\right) \left( 1+\frac{\frac{y_{3}}{2}+y_{4}}{x_{4}}\right) \\&\quad e^{\pi \sqrt{-\frac{y_{1}}{2}+y_{2}}} e^{-\pi \sqrt{\frac{y_{3}}{2}+y_{4}}} \\&\quad +\left( 1+\frac{-\frac{y_{1}}{2}+y_{2}}{x_{1}}\right) \left( -\frac{\left( x_{4}+x_{5}\right) \sqrt{\frac{y_{3}}{2}+y_{4}}}{x_{4} x_{6}}\right. \\&\quad \left. -\frac{\left( \frac{y_{3}}{2}+y_{4}\right) ^{\frac{3}{2}}}{x_{4} x_{6}}\right) \\&\quad e^{-\pi \sqrt{-\frac{y_{1}}{2}+y_{2}}} e^{-\pi \sqrt{\frac{y_{3}}{2}+y_{4}}} \\&\quad +\left( 1+\frac{\frac{y_{1}}{2}+y_{2}}{x_{1}}\right) \left( -\frac{\left( \frac{y_{3}}{2}+y_{4}\right) ^{\frac{3}{2}}}{x_{4} x_{6}}\right. \\&\quad \left. -\frac{\sqrt{\frac{y_{3}}{2}+y_{4}}\left( x_{4}+x_{5}-x_{6}\right) }{x_{4} x_{6}}\right) \\&\quad e^{-\pi \sqrt{\frac{y_{1}}{2}+y_{2}}} e^{-\pi \sqrt{\frac{v_{3}}{2}+y_{4}}} \\&\quad +\left( 1+\frac{\frac{y_{1}}{2}+y_{2}}{x_{1}}\right) e^{\pi \sqrt{\frac{y_{1}}{2}+y_{2}}} e^{-\pi \sqrt{\frac{v_{3}}{2}+y_{4}}}, \\ \theta _{22}= & {} \left( 1+\frac{\frac{y_{3}}{2}+y_{4}}{x_{4}}\right) \left( \frac{\left( -\frac{y_{1}}{2}+y_{2}\right) ^{\frac{3}{2}}}{x_{1} x_{3}}\right. \\&\quad \left. +\frac{\sqrt{-\frac{y_{1}}{2}+y_{2}}\left( x_{1}+x_{2}-x_{3}\right) }{x_{1} x_{3}}\right) \\&\quad e^{\pi \sqrt{-\frac{y_{1}}{2}+y_{2}}} e^{-\pi \sqrt{\frac{y_{3}}{2}+y_{4}}} \\ &\quad +\left( -\frac{\left( -\frac{y_{1}}{2}+y_{2}\right) ^{\frac{3}{2}}}{x_{1} x_{3}}-\frac{\sqrt{-\frac{y_{1}}{2}+y_{2}}\left( x_{1}+x_{2}-x_{3}\right) }{x_{1} x_{3}}\right) \\&\quad \left( -\frac{\left( x_{4}+x_{5}\right) \sqrt{\frac{y_{3}}{2}+y_{4}}}{x_{4} x_{6}}-\frac{\left( \frac{y_{3}}{2}+y_{4}\right) ^{\frac{3}{2}}}{x_{4} x_{6}}\right) \\&\quad \cdot e^{-\pi \sqrt{-\frac{y_{1}}{2}+y_{2}}} e^{-\pi \sqrt{\frac{y_{3}}{2}+y_{4}}} \\&\quad +\left( -\frac{\left( \frac{y_{1}}{2}+y_{2}\right) ^{\frac{3}{2}}}{x_{1} x_{3}}-\frac{\sqrt{\frac{y_{1}}{2}+y_{2}}\left( x_{1}+x_{2}-x_{3}\right) }{x_{1} x_{3}}\right) \\&\quad \left( -\frac{\left( \frac{y_{3}}{2}+y_{4}\right) ^{\frac{3}{2}}}{x_{4} x_{6}}-\frac{\sqrt{\frac{y_{3}}{2}+y_{4}}\left( x_{4}+x_{5}-x_{6}\right) }{x_{4} x_{6}}\right) \\&\quad \cdot e^{-\pi \sqrt{\frac{y_{1}}{2}+y_{2}}} e^{-\pi \sqrt{\frac{y_{3}}{2}+y_{4}}} \\&\quad +\left( \frac{\left( \frac{y_{1}}{2}+y_{2}\right) ^{\frac{3}{2}}}{x_{1} x_{3}}+\frac{\sqrt{\frac{y_{1}}{2}+y_{2}}\left( x_{1}+x_{2}-x_{3}\right) }{x_{1} x_{3}}\right) \\&\quad e^{\pi \sqrt{\frac{y_{1}}{2}+y_{2}}} e^{-\pi \sqrt{\frac{y_{3}}{2}+y_{4}}}. \\ \end{aligned}$$

$$ \begin{aligned} \theta _{32}= & {} \left( 1+\frac{\frac{y_{3}}{2}+y_{4}}{x_{4}}\right) e^{\pi \sqrt{-\frac{y_{1}}{2}+y_{2}}} e^{-\pi \sqrt{\frac{y_{3}}{2}+y_{4}}} \\&\quad +\left( -\frac{\left( \frac{y_{3}}{2}+y_{4}\right) ^{\frac{3}{2}}}{x_{4} x_{6}}-\frac{\sqrt{\frac{y_{3}}{2}+y_{4}}\left( x_{4}+x_{5}-x_{6}\right) }{x_{4} x_{6}}\right) \\&\quad e^{-\pi \sqrt{\frac{y_{1}}{2}+y_{2}}} e^{-\pi \sqrt{\frac{y_{3}}{2}+y_{4}}} \\&\quad +\left( -\frac{\left( x_{4}+x_{5}\right) \sqrt{\frac{y_{3}}{2}+y_{4}}}{x_{4} x_{6}}-\frac{\left( \frac{y_{3}}{2}+y_{4}\right) ^{\frac{3}{2}}}{x_{4} x_{6}}\right) \\&\quad e^{-\pi \sqrt{-\frac{y_{1}}{2}+y_{2}}} e^{-\pi \sqrt{\frac{y_{3}}{2}+y_{4}}}+e^{\pi \sqrt{\frac{y_{1}}{2}+y_{2}}} e^{-\pi \sqrt{\frac{y_{3}}{2}+y_{4}}},\\ \theta _{03}= & {} \left( 1+\frac{\frac{y_{3}}{2}+y_{4}}{x_{4}}\right) \left( \frac{\left( x_{1}+x_{2}\right) \sqrt{-\frac{y_{1}}{2}+y_{2}}}{x_{1} x_{3}}\right. \\&\quad \left. +\frac{\left( -\frac{y_{1}}{2}+y_{2}\right) ^{\frac{3}{2}}}{x_{1} x_{3}}\right) \\&\quad e^{\pi \sqrt{-\frac{y_{1}}{2}+y_{2}}} e^{\pi \sqrt{\frac{y_{3}}{2}+y_{4}}} \\&\quad +\left( \frac{\left( \frac{y_{3}}{2}+y_{4}\right) ^{\frac{3}{2}}}{x_{4} x_{6}}+\frac{\sqrt{\frac{y_{3}}{2}+y_{4}}\left( x_{4}+x_{5}-x_{6}\right) }{x_{4} x_{6}}\right) \\&\quad \left( -\frac{\left( x_{1}+x_{2}\right) \sqrt{\frac{y_{1}}{2}+y_{2}}}{x_{1} x_{3}}-\frac{\left( \frac{y_{1}}{2}+y_{2}\right) ^{\frac{3}{2}}}{x_{1} x_{3}}\right) \\&\quad \cdot e^{-\pi \sqrt{\frac{y_{1}}{2}+y_{2}}} e^{\pi \sqrt{\frac{y_{3}}{2}+y_{4}}} \\&\quad +\left( -\frac{\left( x_{1}+x_{2}\right) \sqrt{-\frac{y_{1}}{2}+y_{2}}}{x_{1} x_{3}}-\frac{\left( -\frac{y_{1}}{2}+y_{2}\right) ^{\frac{3}{2}}}{x_{1} x_{3}}\right) \\&\quad \left( \frac{\left( x_{4}+x_{5}\right) \sqrt{\frac{y_{3}}{2}+y_{4}}}{x_{4} x_{6}}+\frac{\left( \frac{y_{3}}{2}+y_{4}\right) ^{\frac{3}{2}}}{x_{4} x_{6}}\right) \\&\quad \cdot e^{-\pi \sqrt{-\frac{y_{1}}{2}+y_{2}}} e^{\pi \sqrt{\frac{y_{3}}{2}+y_{4}}} \\&\quad +\left( \frac{\left( x_{1}+x_{2}\right) \sqrt{\frac{y_{1}}{2}+y_{2}}}{x_{1} x_{3}}+\frac{\left( \frac{y_{1}}{2}+y_{2}\right) ^{\frac{3}{2}}}{x_{1} x_{3}}\right) \\&\quad e^{\pi \sqrt{\frac{y_{1}}{2}+y_{2}}} e^{\pi \sqrt{\frac{y_{3}}{2}+y_{4}}} , \\ \theta _{13}= & {} \left( 1+\frac{-\frac{y_{1}}{2}+y_{2}}{x_{1}}\right) \left( 1+\frac{\frac{y_{3}}{2}+y_{4}}{x_{4}}\right) \\&\quad e^{\pi \sqrt{-\frac{y_{1}}{2}+y_{2}}} e^{\pi \sqrt{\frac{y_{3}}{2}+y_{4}}} \\&\quad +\left( 1+\frac{-\frac{y_{1}}{2}+y_{2}}{x_{1}}\right) \left( \frac{\left( x_{4}+x_{5}\right) \sqrt{\frac{y_{3}}{2}+y_{4}}}{x_{4}x_{6}}\right. \\&\quad + \left. \frac{\left( \frac{y_{3}}{2}+y_{4}\right) ^{\frac{3}{2}}}{x_{4}x_{6}}\right) e^{-\pi \sqrt{-\frac{y_{1}}{2}+y_{2}}} e^{\pi \sqrt{\frac{y_{3}}{2}+y_{4}}} \\&\quad +\left( 1+\frac{\frac{y_{1}}{2}+y_{2}}{x_{1}}\right) \left( \frac{\left( \frac{y_{3}}{2}+y_{4}\right) ^{\frac{3}{2}}}{x_{4}x_{6}}\right. \\&\quad \left. +\frac{\sqrt{\frac{y_{3}}{2}+y_{4}}\left( x_{4}+x_{5}-x_{6}\right) }{x_{4}x_{6}}\right) \\&\quad e^{-\pi \sqrt{\frac{y_{1}}{2}+y_{2}}} e^{\pi \sqrt{\frac{3_{3}}{2}+y_{4}}} \\&\quad +\left( 1+\frac{\frac{y_{1}}{2}+y_{2}}{x_{1}}\right) e^{\pi \sqrt{\frac{y_{1}}{2}+y_{2}}} e^{\pi \sqrt{\frac{y_3}{2}+y_{4}}} ,\\ \theta _{23}= & {} \left( 1+\frac{\frac{y_{3}}{2}+y_{4}}{x_{4}}\right) \left( \frac{\left( -\frac{y_{1}}{2}+y_{2}\right) ^{\frac{3}{2}}}{x_{1} x_{3}}\right. \\&\quad \left. +\frac{\sqrt{-\frac{y_{1}}{2}+y_{2}}\left( x_{1}+x_{2}-x_{3}\right) }{x_{1} x_{3}}\right) \\&\quad e^{\pi \sqrt{-\frac{y_{1}}{2}+y_{2}}} e^{\pi \sqrt{\frac{\not 3}{2}+y_{4}}} \\&\quad +\left( -\frac{\left( -\frac{y_{1}}{2}+y_{2}\right) ^{\frac{3}{2}}}{x_{1} x_{3}}-\frac{\sqrt{-\frac{y_{1}}{2}+y_{2}}\left( x_{1}+x_{2}-x_{3}\right) }{x_{1} x_{3}}\right) \\&\quad \left( \frac{\left( x_{4}+x_{5}\right) \sqrt{\frac{y_{3}}{2}+y_{4}}}{x_{4} x_{6}}+\frac{\left( \frac{y_{3}}{2}+y_{4}\right) ^{\frac{3}{2}}}{x_{4} x_{6}}\right) \\&\quad \cdot e^{-\pi \sqrt{-\frac{y_{1}}{2}+y_{2}}} e^{\pi \sqrt{\frac{y_{3}}{2}+y_{4}}} \\&\quad +\left( -\frac{\left( \frac{y_{1}}{2}+y_{2}\right) ^{\frac{3}{2}}}{x_{1} x_{3}}-\frac{\sqrt{\frac{y_{1}}{2}+y_{2}}\left( x_{1}+x_{2}-x_{3}\right) }{x_{1} x_{3}}\right) \\&\quad \left( \frac{\left( \frac{y_{3}}{2}+y_{4}\right) ^{\frac{3}{2}}}{x_{4} x_{6}}+\frac{\sqrt{\frac{y_{3}}{2}+y_{4}}\left( x_{4}+x_{5}-x_{6}\right) }{x_{4} x_{6}}\right) \\&\quad \cdot e^{-\pi \sqrt{\frac{y_{1}}{2}+y_{2}}} e^{\pi \sqrt{\frac{y_3}{2}+y_{4}}} \\&\quad +\left( \frac{\left( \frac{y_{1}}{2}+y_{2}\right) ^{\frac{3}{2}}}{x_{1} x_{3}}+\frac{\sqrt{\frac{y_{1}}{2}+y_{2}}\left( x_{1}+x_{2}-x_{3}\right) }{x_{1} x_{3}}\right) \\&\quad e^{\pi \sqrt{\frac{y_{1}}{2}+y_{2}}} e^{\pi \sqrt{\frac{y_{3}}{2}+y_{4}}}, \\ \theta _{33}= & {} \left( 1+\frac{\frac{y_{3}}{2}+y_{4}}{x_{4}}\right) e^{\pi \sqrt{-\frac{y_{1}}{2}+y_{2}}} \\&\quad e^{\pi \sqrt{\frac{y_{3}}{2}+y_{4}}}+\left( \frac{\left( \frac{y_{3}}{2}+y_{4}\right) ^{\frac{3}{2}}}{x_{4} x_{6}}\right. \\&\quad \left. +\frac{\sqrt{\frac{y_{3}}{2}+y_{4}}\left( x_{4}+x_{5}-x_{6}\right) }{x_{4} x_{6}}\right) \\&\quad \cdot e^{-\pi \sqrt{\frac{y_{1}}{2}+y_{2}}} e^{\pi \sqrt{\frac{y_{3}}{2}+y_{4}}} \\&\quad +\left( \frac{\left( x_{4}+x_{5}\right) \sqrt{\frac{y_{3}}{2}+y_{4}}}{x_{4} x_{6}}+\frac{\left( \frac{y_{3}}{2}+y_{4}\right) ^{\frac{3}{2}}}{x_{4} x_{6}}\right) \\&\quad e^{-\pi \sqrt{-\frac{y_{1}}{2}+y_{2}}} e^{\pi \sqrt{\frac{y_{3}}{2}+y_{4}}}\\&\quad +e^{\pi \sqrt{\frac{y_{1}}{2}+y_{2}}} e^{\pi \sqrt{\frac{y_{3}}{2}+y_{4}}}. \end{aligned}$$