Abstract
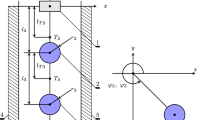
The paper discusses the dynamic behavior of a double mathematical pendulum with identical parameters of links and end loads, which is under the influence of viscous friction at both of its hinges with generally different dissipative coefficients. A linear mathematical model of system motion for small deviations is given, and a characteristic equation containing two dimensionless dissipative parameters is derived. For the case of low damping, approximate analytical expressions are derived that make it possible to evaluate and compare with each other the damping factors during motion of the system in each of the vibration modes. A diagram of dissipative motion regimes is constructed, which arises when the plane of dimensionless parameters is divided by discriminant curves into regions with a qualitatively different character of system motion. It is noted that a dissipative internal resonance can occur in the system under consideration; the conditions for its existence are established in an analytical form, and a graphic illustration of these conditions are also displayed. This publication is the first part of the study of the dynamics of a dissipative double pendulum, the continuation of which will be presented as a separate publication “Dynamics of a Double Pendulum with Viscous Friction at the Hinges. II. Dissipative Vibration Modes and Optimization of the Damping Parameters.”




Similar content being viewed by others
REFERENCES
A. M. Formal’skii, Stabilisation and Motion Control of Unstable Objects (Fizmatlit, Moscow, 2014; de Gruyter GmbH, Berlin, 2016).
O. A. Peregudova and D. S. Makarov, “Control synthesis for three-link manipulator,” Avtom. Protsessov Upr., No. 2, 109–113 (2015).
N. V. Anokhin, “Bringing a multilink pendulum to the equilibrium position using a single control torque,” J. Comput. Syst. Sci. Int. 52, 717–725 (2013).
B. A. Smol’nikov and E. I. Yurevich, “About the problem of biomorphic robot motion control,” Robototekh. Tekh. Kibern., No. 1, 17–20 (2015).
A. A. Tyazhelov, N. N. Kizilova, V. A. Fishchenko, S. Yu. Yaremin, M. Yu. Karpinskii, and E. D. Karpinskaya, “Analysis of posturography based on mathematical model of human body as multilink system,” Travma 13 (4), 17–25 (2012).
K. R. Sawant and V. Shrikanth, “Energy dissipation and behavioral regimes in an autonomous double pendulum subjected to viscous and dry friction damping,” Eur. J. Phys. 42, 055008 (2021).
S. Bendersky and B. Sandler, “Investigation of a spatial double pendulum: An engineering approach,” Discrete Dyn. Nat. Soc. 2006, 25193 (2006).
A. S. Smirnov and B. A. Smolnikov, “Dissipative model of double mathematical pendulum with noncollinear joints,” in Advances in Mechanical Engineering: Proc. Conf. “Modern Engineering: Science and Education”, St. Petersburg, Russia, June 2021 (Springer-Verlag, Cham, 2022), in Ser.: Lecture Notes in Mechanical Engineering, pp. 38–47.
V. L. Biderman, Theory of Mechanical Vibrations (Vysshaya Shkola, Moscow, 1980) [in Russian].
S. P. Timoshenko, Vibration Problems in Engineering (Nauka, Moscow, 1967; Van Nostrand, Toronto, 1955).
K. Magnus, Schwingungen. Eine Einführung in die theoretische Behandlung von Schwingungsproblemen (Teubner, Stuttgart, 1961; Mir, Moscow, 1982).
Vibrations in Technology. Directory, Vol. 1: Oscillations of Linear Systems, Ed. by V. V. Bolotin (Mashinostroenie, Moscow, 1978) [in Russian].
Strength, Stability, Oscillations, Ed. by I. A. Birger and Ya. G. Panovko (Mashinostroenie, Moscow, 1968), Vol. 3 [in Russian].
V. A. Leont’ev, A. S. Smirnov, and B. A. Smol’nikov, “Optimal damping of two-link manipulator oscillations,” Robototekh. Tekh. Kibern., No. 2, 52–59 (2018).
A. S. Smirnov and B. A. Smol’nikov, “Optimization of Oscillation Damping Modes of a Spatial Double Pendulum: 1. Formulation of the Problem,” Vestn. St. Petersburg Univ.: Math. 55, 243–248 (2022). https://doi.org/10.1134/S1063454122020133
A. S. Smirnov and B. A. Smol’nikov, “Optimization of Oscillation Damping Modes of a Spatial Double Pendulum: 2. Solution of the Problem and Analysis of the Results,” Vestn. St. Petersburg Univ.: Math. 56, 93–106 (2023). https://doi.org/10.1134/S1063454123010132
N. N. Bolotnik, Optimization of Amortization Systems (Nauka, Moscow, 1983) [in Russian].
B. A. Smol’nikov, Problems of Mechanics and Robot Optimization (Nauka, Moscow, 1991) [in Russian].
T. von Kármán and M. A. Biot, Mathematical Methods in Engineering (McGraw-Hill, New York, 1940; GITTL, Moscow, 1946).
I. I. Blekhman, A. D. Myshkis, and Ya. G. Panovko, Mechanics and Applied Mathematics. Logic and Features of Applications of Mathematics (Nauka, Moscow, 1983) (in Russian).
A. H. Nayfeh, Introduction to Perturbation Techniques (Wiley, New York, 1981; Mir, Moscow, 1984).
Funding
This work was supported by ongoing institutional funding. No additional grants to carry out or direct this particular research were obtained.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
The authors of this work declare that they have no conflicts of interest.
Additional information
Publisher’s Note.
Pleiades Publishing remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
About this article
Cite this article
Smirnov, A.S., Kravchinskiy, I.A. Dynamics of a Double Pendulum with Viscous Friction at the Hinges. I. Mathematical Model of Motion and Construction of the Regime Diagram. Vestnik St.Petersb. Univ.Math. 57, 254–262 (2024). https://doi.org/10.1134/S1063454124700109
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S1063454124700109