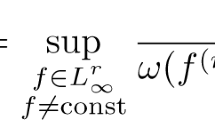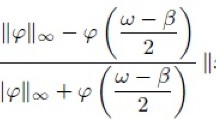Skip to main content
SpringerLink
Log in

The best one-sided approximation of the classes WrHω

  • Published:
Mathematical notes of the Academy of Sciences of the USSR Aims and scope Submit manuscript

Abstract

In this paper we calculate the upper bounds of the best one-sided approximations, by trigonometric polynomials and splines of minimal defect in the metric of the space L, of the classes WrHω (r = 2, 4, 6, ...) of all 2π-periodic functions f(x) that are continuous together with their r-th derivative fr(x) and such that for any points x′ and x″ we have ¦f r (x′) fr (x″) ¦⩽ ω (x′−x″¦), where ω(t) is a modulus of continuity that is convex upwards.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Literature cited

  1. G. Hardy, J. Littlewood, and G. Polya, Inequalities, Cambridge Univ. Press (1934).

  2. V. G. Doronin and A. A. Ligun, “On the best one-sided approximation of one class of functions by another,” Mat. Zametki,14, No. 5, 627–632 (1973).

    Google Scholar 

  3. V. G. Doronin and A. A. Ligun, “On exact values of the best one-sided approximations by splines,” International Conference on the Theory of Approximation of Functions, Abstracts, 44–45, Kaluga (1975).

  4. N. P. Korneichuk, “On the extremal properties of periodic functions,” Dokl. Akad. Nauk Ukr.SSR, No. 8, 993–998 (1962).

    Google Scholar 

  5. N. P. Korneichuk, “Extremal values of functionals and best approximation on classes of periodic functions,” Izv. Akad. Nauk SSSR, Ser. Mat.,35, No. 1, 93–124 (1971).

    Google Scholar 

  6. N. P. Korneichuk, “Inequalities for differentiable periodic functions and best approximation of one class of functions by another,” Izv. Akad. Nauk SSSR, Ser. Mat.,36, No. 2, 423–434 (1972).

    Google Scholar 

  7. E. G. Gol'shtein, Duality Theory in Mathematical Programming and Its Applications [in Russian], Nauka, Moscow (1971).

    Google Scholar 

  8. L. Hörmander, “A new proof and generalization of an inequality of Bohr,” Math. Scand.,2, No.1, 33–45 (1954).

    Google Scholar 

  9. N. I. Akhiezer, Lectures on Approximation Theory [in Russian], Nauka, Moscow (1965).

    Google Scholar 

  10. V. G. Doronin and A. A. Ligun, “Upper bounds for the best one-sided approximations of the classes WrL1 by splines,” Mat. Zametki,19, No. 1, 11–17 (1976).

    Google Scholar 

  11. V. G. Doronin and A. A. Ligun, “On the best one-sided approximation by splines,” in: Problems of Approximation Theory and Its Applications, Institut Matematiki Akad. Nauk Ukr. SSR, Kiev (1976), pp. 97–109.

    Google Scholar 

  12. V. G. Doronin, “Bounds for the best one-sided approximation of a class of differentiable periodic functions,” Nauchnye Zapiski, Collection of Papers by Post-Graduates of Dnepropetrovsk State Univ., Dnepropetrovsk (1970), pp. 72–87.

Download references

Author information

Authors and Affiliations

  1. Dneprodzerzhinsk Industrial Institute, USSR

    V. G. Doronin & A. A. Ligun

Authors
  1. V. G. Doronin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. A. Ligun
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Translated from Matematicheskie Zametki, Vol. 21, No. 3, 313–327, March, 1977.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Doronin, V.G., Ligun, A.A. The best one-sided approximation of the classes WrHω . Mathematical Notes of the Academy of Sciences of the USSR 21, 174–182 (1977). https://doi.org/10.1007/BF01106740

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF01106740

Keywords

Search

Navigation