Almost all undergraduate students take at least one mathematics course in college, and, for many, mathematics course requirements have a strong influence on their choice of majors and, ultimately, their careers. Science, Technology, Engineering, and Mathematics (STEM) disciplines continue to experience a “pipeline problem”: less than 40% of US students who enter university with an interest in STEM finish with a STEM-related degree (President’s Council of Advisors on Science and Technology 2012). Since success in mathematics courses often plays a decisive role in admission to STEM majors, improving the quality of undergraduate mathematics instruction is a key ingredient to address the pipeline problem (Bressoud et al. 2015).

Instructors’ selection of mathematical concepts, as well as the methods they use to teach students about these concepts, can significantly affect student learning (Bergqvist and Lithner 2012; Nardi et al. 2005). Although there is a general call in education for data-driven-decisions, there is a critical need for reliable measures of classroom practice with robust validity arguments in order to produce the data needed to make such decisions about classroom teaching. Therefore, robust measures for observing and improving undergraduate mathematics teaching are incredibly important (Belnap and Allred 2009). Observations of mathematics instruction have been common in K-12 settings (Bostic et al. 2018; Boston et al. 2015), but corresponding techniques in collegiate contexts are rare (e.g., Beisiegel et al. 2016; Hayward et al. 2018).

To address the need for high-quality observation data to inform undergraduate mathematics teaching, we have developed an observation protocol that focuses on instructors’ and students’ actions and interactions during undergraduate mathematics instruction that provide opportunities for students to engage in mathematical meaning making. Specifically, we present an analysis of data collected using this observation protocol on novice graduate student instructors at two universities in their first academic year as instructors of record.

Aligned with the Standards for Educational and Psychological Testing (American Educational Research Association (AERA), American Psychological Association (APA), & National Council on Measurement in Education (NCME) 2014), we include validity evidence based on content and internal structure of the Graduate Student Instructor Observation Protocol (GSIOP, Appendix). First, we describe existing STEM- or mathematics-focused observation protocols and discuss the need for our instrument focused on novice mathematics instructors’ use of lesson design practices that engage students in mathematical meaning making. Then, we describe the process for developing the GSIOP, methods of collecting and analyzing the data, and results from the validation and reliability study. We conclude the paper by discussing appropriate uses for the GSIOP.

Theoretical Background

Because the mathematics instructors in this study were novices in their first semester of teaching undergraduate mathematics courses, we first describe what, if anything, existing literature discusses about typical professional development practices for working with this population of instructors. In relation to this population of instructors and the need for robust measures of classroom instruction, we include our definition of effective mathematics teaching in relation to the Mathematical Association of America’s (MAA) Instructional Practices Guide (MAA 2018). Finally, we explain how the GSIOP is situated in relation to other observation protocols, especially STEM- or mathematics-focused protocols.

Background on Systems of Support for Novice Mathematics Graduate Student Instructors

We observed undergraduate mathematics classroom teaching when it was being taught by mathematics graduate student instructors (GSIs).Footnote 1 This population of instructors, GSIs, teach hundreds of thousands of undergraduate mathematics students each semester, yet often lack guidance and support to teach undergraduate students effectively (Rogers and Steele 2016; Speer and Murphy 2009). GSIs’ initial teaching experiences often set the stage for how they will teach in the short term in graduate school and in the long term as future faculty members (Lortie 1975). Moreover, GSIs often participate in professional development (PD) concurrent with their first semesters as instructors of record. Thus, GSIs are uniquely positioned as a population of instructors who are simultaneously receiving and applying strategies and theories learned in PD seminars, courses, and other such opportunities. As researchers have documented (Belnap and Allred 2009; Bressoud et al. 2015; Ellis et al. 2016a, b), PD opportunities and teaching assignments for GSIs vary significantly in mathematics departments and universities across the US. GSI PD ranges from help with mundane teaching tasks to teaching skills and techniques. The extent and depth of GSI PD also ranges from a few workshops to semester-long seminars. This current variance makes it challenging to determine what and how GSI PD can be the most impactful and effective for improving student learning outcomes in undergraduate mathematics courses. Therefore, there is a critical need for consistent, research-based, GSI PD that incorporates basic teaching techniques and also prepares GSIs to develop into effective, student-focused mathematics instructors while they are in graduate school and for their potential future faculty careers.

Our Conception of Effective Teaching: Facilitating Undergraduate Mathematics Students’ Opportunities to Engage in Meaning Making

Drawing from the MAA’s Instructional Practices Guide (2018), we focus on lesson design practices, teacher facilitation, and classroom practices that promote student engagement when conceptualizing effective mathematics instructional practices that we aim to help GSIs develop. First, “we define design practices to be the plans and choices instructors make before they teach and what they do after they teach to modify and revise for the future. Design practices inform the construction of the learning environment and curriculum and support instructors in implementing pedagogies that maximize student learning” (MAA 2018, p. 118). To help GSIs focus on ways to plan and structure their lessons to engage students in high-level thinking and reasoning, we specifically consider some basic lesson design practices including, lesson planning around explicit, measurable, learning goals; designing mathematical activities aligned with the learning goals; and communicating instructional decisions and mathematical connections effectively to students. Second, when GSIs have created lessons with activities intended to engage students in mathematical meaning making, they also need to effectively implement the lesson, which involves teacher facilitation. We agree with Gleason et al.(2017, p. 114) when they explain that

current research and reform efforts call for a teacher who can facilitate high-quality tasks, interactions, and student reasoning (Barker et al. 2004; NCTM 1991, 2006, 2011; NGACBP and CCSSO 2010; NRC 2002; Stein et al. 2008, 2009). Key elements to consider with teacher facilitation of a task include the amount of scaffolding (Anghileri 2006), productive struggle (Hiebert and Grouws 2007), the level of questioning (Reys et al. 2015; Schoenfeld 1998; Winne 1979), and peer-to-peer discourse (Cobb et al. 1993; Nathan and Knuth 2003) that occur with a mathematical task, while keeping in mind the complexity that occurs between teachers’ decisions and students’ responses (Brophy and Good 1986).

Therefore, we believe that an observation protocol designed to support GSIs’ facilitation of mathematics tasks should document these aspects of teacher facilitation that Gleason et al. (2017) described. Third, GSIs can help students retain information by engaging students in meaning making during class. Specifically,

student engagement can be enhanced by activities that require sense-making, analysis, or synthesis of ideas during class. These strategies may be ‘anything course-related that all students in a class session are called upon to do other than simply watching, listening, and taking notes’ (Felder and Brent 2009, p. 2). . . . Students need to actively engage in the process of learning mathematical ideas, developing strong conceptual understanding, and using these ideas to develop procedural fluency. (MAA 2018, pp. 10 & 63)

Thus, when observing GSIs teaching students in undergraduate mathematics classrooms, we consider student engagement by focusing on whether or not students engage with mathematical ideas, different strategies, their peers, and formative assessment strategies. We endeavor to both facilitate the development of GSIs’ abilities to effectively design and implement mathematics lessons in order to provide opportunities for undergraduate students to engage in, and with, mathematics, and to develop a method for observing and documenting this growth.

Situating Our Observation Protocol in Relation to Other Instruments and Theory

Within this context, where we are observing GSIs teaching in order to help them develop into more effective instructors who focus on student-engagement, we designed the GSIOP. To unpack the features and purposes of the GSIOP, we describe the need for observation protocols in general, some important considerations when measuring the quality of mathematics instruction, and how the GSIOP relates to other existing STEM- or mathematics-focused protocols.

Classroom Observations and Student Learning

To connect teachers’ perception of learning outcomes and the student’s actual learning outcomes, it is vital to measure classroom practices. The quality of teaching and learning cannot be determined solely with checklists or student grades—contexts matter (e.g., Smith 2012), as do issues of equity (e.g., Gutiérrez and Gutiérrez 2012). Teachers’ instructional practices are directly linked with student outcomes in a wide variety of research studies (e.g., Allen et al. 2011; Blazar 2015; Bressoud et al. 2015; Bressoud and Rasmussen 2015; Freeman et al. 2014; Kersting et al. 2012; Koellner and Jacobs 2015; Rasmussen et al. 2014). Although the connections between teaching and learning are not disputed, the improvement of undergraduate student outcomes via improved instructional practices is not as clearly understood (Ellis et al. 2016b). Many researchers depend on self-reported instructional practices (e.g., Desimone et al. 2013; Garet et al. 2011), yet even the most well-intentioned teachers tend to overestimate their teaching effectiveness and their uses of evidence-based instructional practices (National Research Council 2012). For instance, Desimone et al. (2010) used National Assessment of Education Progress (NAEP) data and found very low correlations between K-12 student and teacher perceptions of classroom activities. The National Center for Educational Statistics (NCES) conducted a careful validity and reliability study comparing data from K-12 observations, self-reported survey data, and self-reported daily teaching logs (US Department of Education, NCES 1999). On one hand, items about specific content and instructional structures (e.g., amount of time students spent copying notes) showed fairly high agreement, meaning that the frequency to which observers noted classroom practices occurring closely matched the self-reported data. Items about the quality of instruction (e.g., the extent to which a whole class discussion engaged all students in mathematical reasoning and communicating), on the other hand, had very low agreement where teachers consistently rated themselves much higher than observers did. Therefore, the aforementioned need to measure classroom practices to align the teacher’s perception and student learning suggests the use of a recorded observation and an observation protocol that identifies concrete interactions and engagement of students. Since the “design for student-centered learning must be in sync with evidence-based practices,” (MAA 2018, p. 90), we designed the GSIOP with this in mind. And a systematic examination of student performance as related to GSIOP data is an area for future investigation.

Considerations for Measuring Quality of Instruction

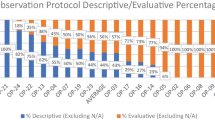
A key aspect of the validation argument for a measure of instruction is the alignment of the protocol’s purpose with the purpose of the data collection (AERA, APA, and NCME 2014; Kane 2012). One component of the purpose of a protocol is whether its authors intend it to be used as a descriptive or evaluative instrument. A descriptive protocol’s principal aim is to capture and describe what is happening in a class, whereas evaluative protocols measure (with ordinal, cardinal, or scalar measurements) the quality of a class against a theory of instructional quality.

Moreover, observation protocols may also be holistic (encompassing the whole lesson) or segmented (separately rating shorter segments of the lesson). Segmented protocols usually capture structure, while holistic views can be more appropriate for capturing quality (Tatto et al. 2018a, b). For example, a lengthy whole-class discussion may span several segments that are treated separately. A holistic protocol, on the other hand, might focus on how an error made early in a lesson is featured in the lesson closing, clearing up students’ misconceptions.

Additionally, protocols may focus on the instructor or students, may or may not take subject matter into account, may require high or low inference by the observer, and may vary in the degree of structure. Although much can be learned from a content-general observation protocol (e.g., Classroom Assessment Scoring System, Mikami et al. 2011), specific indicators of mathematics teaching and learning are important for capturing quality of mathematics instruction. Both the National Council of Teachers of Mathematics (NCTM 2014) and the Mathematical Association of America (MAA 2018) cite numerous indicators of quality in mathematics lessons which are particular to mathematics, including precise language and addressing mathematical errors. Thus, the GSIOP is a mathematics-specific observation protocol that is based on another mathematics-specific protocol (Mathematical Classroom Observation Protocol for Practices (MCOP2), Gleason et al. 2017, pp. 113–119) focused on the extent to which an instructor facilitates active-learning and student engagement during teaching.

Measures of Instruction

For K-12 measures of instruction, multiple research projects (e.g., Joe et al. 2013; Mihaly et al. 2013) and reviews (Bostic et al. in press, 2015) synthesize the major mathematics observation protocols. This provides the field with syntheses of measures for K-12 mathematics teaching, but currently there are no overarching synthesis of protocols for measuring the quality of undergraduate mathematics instruction. To explain the way the GSIOP developed from a particular K-16 mathematics-focused observation protocol, therefore, we first characterize the main features of several existing STEM-related observation protocols at both the K-12 and undergraduate levels (Table 1). The purpose of this categorization, which builds off of existing characterizations (Hayward et al. 2018), is to recognize that the existing STEM-related observation protocols used in collegiate settings are diverse and that this diversity is not always made explicit. Moreover, individual items within a protocol may fall into another category. For example, some individual items on the MCOP2 (and, by extension, the GSIOP) are more descriptive than evaluative. Therefore, in Table 1 we used the term “mostly” to indicate the type of items that made up the majority of that listed protocol.

Table 1 Structure and purposes of some existing STEM-related protocols
Full size table

The Mathematical Classroom Observation Protocol for Practices (MCOP2)

Because it is important to help novice collegiate mathematics instructors consistently engage undergraduate students in their mathematics learning, we chose to modify an existing protocol (the MCOP2, Gleason et al. 2015) that was mathematics-specific and attended to strategies for engaging students (i.e., active learning techniques). Gleason et al.’s (2017) validation study indicated that the MCOP2 is a reliable protocol for assessing K-16 mathematics classrooms, explicitly explaining,

MCOP2 . . . measures the actions of both the teacher and students. By capturing both sets of actions, the MCOP2 differentiates between teacher implementation of a lesson and the students’ engagement. This makes the MCOP2 a holistic assessment of the classroom environment not found in [other well-known] observation protocols . . . . Another benefit of this instrument for research, in comparison to other observation tools, is that the MCOP2 is more manageable. Extensive training or professional development is not necessarily required, beyond reviewing the detailed user guide (Gleason et al. 2015) with the assumption that the user understands the terminology in the rubrics. (pp. 118-119)

When using observation protocols, two crucial considerations are training observers and calibrating observations (e.g., Ho and Kane 2013; Tatto et al. 2018b). For observations to help improve teachers’ practices and student outcomes, observers need to be trained in the uses and applications of the protocol selected. Further, observers need to interpret the protocol in the same ways, so that scores are reliable. Therefore, since the GSIOP builds on the MCOP2extensive training is also not required, but that does not mean there is no training involved. Currently, training for using the GSIOP takes place during two-three 90 min seminar meetings where we rate and discuss GSIOP scores of training videos to help GSIs understand the GSIOP.Footnote 2

Ultimately, we focused on modifying the MCOP2 because it measures how mathematics instructors use practices “for teaching lessons that are goal-oriented toward conceptual understanding as described by standards documents put forth by national organizations” (Gleason et al. 2017, p. 113). Because we wanted novice GSIs to learn to design and facilitate lessons that focus on student engagement, we began pilot testing the use of the MCOP2 by having upper-level graduate students use the MCOP2 when observing other GSIs as they taught undergraduate courses at two public universities in the US. Based on these pilot tests, we modified the MCOP2 to incorporate basic lesson design practices, explicit formative assessment strategies, and a further emphasis promoting undergraduate student engagement.

Method: Graduate Student Instructor Observation Protocol Development and Theory

The MCOP2 provided a foundation for our project, which was to develop an observation protocol to inform quality feedback given to GSIs that could then positively affect their growth and development as instructors who regularly engage students in mathematical meaning making. Our intention was to develop an observation protocol that could be used by experienced GSIs or by faculty members to provide meaningful, critical feedback to novices about their teaching practices. We wanted to use the protocol to generate observation data that would provide useful feedback about the kinds of challenges faced by first-time instructors while also encouraging them to reflect on and incorporate student-centered strategies into their classroom practices.

To develop the GSIOP, we used pilot tests where experienced graduate students were first trained to use the MCOP2 to observe GSIs teaching undergraduate courses at two US public universities. Based on these pilot tests, two of the authors on this paper (Author 1 & Author 3) created the GSIOP to: (1) better align terminology for mathematics graduate students; (2) restructure it for ease of use according to student-focused, teacher-focused, and lesson-focused items; (3) incorporate lesson design practice items of specific concern to GSIs (including international GSIs); and (4) collapse some items together while expanding others to streamline the observation process and help the observer focus on student engagement.

Pilot Tests and Graduate Student Instructor Observation Protocol Creation

As Gleason et al. (2017) noted, terminology used in the rubrics could be a barrier to some observers’ use, and there were a few rubric items that could be reworded to clarify what the language/practices meant to allow GSIs (esp., those who are less familiar with National Standards documents) to more easily apply the protocol. For instance, we reworded the rubric descriptions for the sixth item on the MCOP2 (The lesson involved fundamental concepts of the subject to promote relational/conceptual understanding, IV.B in the GSIOP, Appendix) because it mentioned “as described by the appropriate standards.” This clause in the rubric was confusing to GSIs where national standards for undergraduate-level instruction are either non-existent or not well-known. Similarly, the seventh item stated the lesson promoted modeling with mathematics with a score of 3 indicating “students engaged in the modeling cycle (as described in the Common Core Standards).” This was reworded to describe modeling in a fashion that was clearer to GSIs who had never heard of the Common Core Standards (NGSA 2010). Also, the tenth item was worded as the lesson promoted precision of mathematical language but the language in the rubric focused on things the teacher did or did not do, and occasionally mentioned the students as well. We worded the overarching phrase to focus on “The teacher promoted…” rather than the lesson.

Next, the MCOP2 includes 16 items that we reordered based on the primary focus of the items. We noted that eight of the items were primarily student-focused, four were primarily teacher-focused, and four were focused on the lesson design or structure. Since the GSIs had never used an observation protocol before, we reordered the items so they could pay attention to the student, teacher, or lesson for the related items, thereby reducing the observers’ cognitive load when filling out the protocol. Ten GSIs and two mathematics education researchers practiced using this reordered, slightly reworded version of the MCOP2 by observing one or more class sessions taught by mathematics graduate student instructors. Then, they discussed any additional modifications or areas needing clarification.

Following a second round of pilot testing, we realized that GSI observers were also overwhelmed with the number of student-focused items, considered some items to be consistently less applicable in foundational undergraduate mathematics courses, and suggested adding other items that clarified the nature of student-centered instruction being observed and attended more directly to this population of instructors. More specifically, we pared the number of student-focused items down to four, we removed two lesson-focused items while adding one new one, and we added a teacher-focused item about the use of formative assessments, since that was an area of emphasis in our work with GSIs that we wanted to capture. This restructuring was done carefully to reduce the cognitive load for the GSI observers while maintaining the focus on basic lesson design practices, teacher facilitation, and student engagement. First, for the student-focused items there were subtle differences among the eight original items that allowed us to often collapse two or three items from the MCOP2 into a single item in the GSIOP. Second, the two lesson-focused items we removed were about “modeling with mathematics” and “tasks that have multiple paths…or multiple solutions”. Since the student-focused items still include one that addresses whether or not students evaluated solution strategies, and there are still two items on the GSIOP about multiple representations being used, we removed these two lesson-focused items to allow some space for new items.

Finally, through this process, we added new items to the instrument: a lesson-focused item, a teacher-focused item, and a Cover Page. The lesson-focused item added to the GSIOP focuses the observer’s attention on the learning goals of the lesson and provides a subjective summary of the observation and the perceived effectiveness at meeting learning goals. This item serves two primary purposes: (1) to help highlight whether the instructor made the learning goals explicit for an observer (and students) to understand and be able to answer such an item; and (2) to provide a holistic category for the observer to fill out where they consider all the earlier aspects of the GSIOP and what evidence they observed to answer this last item. The teacher-focused item that we added specifically asks the observer to note whether or not the instructor incorporated formative assessments into the lesson (and if so, to note what they were). Adding this item allows observers tangible things to highlight and recommend an instructor continue doing or consider trying to incorporate in their future lessons. Finally, in response to GSI observers’ comments about the need to add explicit categories that address general, basic teaching mechanics that are especially important for novices to quickly address fundamental issues early in their teaching, we added a Cover Page to the entire instrument. These basic teaching mechanics related to the basic lesson design practices we described in Our Conception of Effective Teaching section, focusing on aspects of planning and communicating the lesson content effectively. Furthermore, the MCOP2 did not explicitly ask observers to record some basic information about the class and instructor that could inform feedback. Hence, the Cover Page was added that addressed these two concerns (Appendix). In addition to the initial textbox-entry items, such as who and what was being observed, we added five design practice items to the cover page, specifically, Preparation and Organization, Verbal Articulation, General Presentation Clarity, Enthusiasm, and Clearly Communicated Lesson Context. Especially when working with novices who have never taught before, the experienced GSIs considered these five items to be important principles that would likely need to be addressed prior to discussing changes that might relate to teacher facilitation or student engagement more directly. After adding this cover page, the GSI observers conducted another round of observations, ultimately resulting in the current form of the GSIOP, which is included in the Appendix.

These changes to the MCOP2 resulted in the GSIOP that is structured around components that relate basic lesson design practices, teacher facilitation, and classroom practices focused on student engagement, related to national undergraduate mathematics teaching and learning recommendations (MAA 2018; National Research Council 2002). Thus, we investigated the following research question: Does the GSIOP demonstrate validity and reliability across its 17 items?

Data Collection

The GSIOP was used for two years in a project which implemented a peer-mentoring process at two universities (Yee and Rogers 2017a; Rogers and Yee 2018). During that time, 291 observations were completed by thirteen peer-mentors who had been trained to use the GSIOP during semester-long PD seminars. This training incorporated the use of the GSIOP by watching multiple videos and live observations. In Table 2 we describe the courses that the mentors observed, the number of GSIOP scores recorded, and some notable features of the GSIOP scores from these observations.

Table 2 Participant data from two years of GSIOP data collection during peer mentoring
Full size table

Since Gleason et al. (2017) suggested that the MCOP2 should be used to capture more than one classroom episode for the same instructor, most novices were observed by their mentor three times during a single semester. In some cases, only one or two observations could be arranged. Overall, 79 classes were observed three times, 23 were observed twice, and 8 were observed only once (Table 2). The novices taught a variety of courses, based on the needs of the department and course schedules. The number of undergraduates enrolled in these courses taught by novices ranged from 14 to 40. When observing a novice, mentors collected video data, took observation notes, took digital images of any handouts or major assignments from the lesson, completed the GSIOP, and then conducted a follow up, one-on-one conversation with the novice to provide focused feedback regarding areas where the novice was and was not effectively supporting student engagement. Our analysis focused on the mentor’s GSIOP data as well as the video observation data for interrater reliability analysis.

Prototypical Examples from the Data

To familiarize the reader with some of the 17 items on the GSIOP, we provide a set of prototypical examples from the data. To select which items to provide examples of within the manuscript, we refer back to our focus on class design practices, teacher facilitation, and classroom practices that promote student engagement as key aspects of effective teaching (see Our Conception of Effective Teaching section). Aligned with this background, GSIOP items are either primarily lesson-focused, teacher-focused, or student-focused.

Specifically, we consider a GSIOP item to be lesson-focused if the subject of the item is the lesson structure, goals, or mathematical content. GSIOP items that are teacher-focused attend to the teacher’s classroom actions, decisions, utterances, and movements. GSIOP items that are student-focused guide the observer to look for evidence in student(s) actions, talk, or interactions with one another. We provide prototypical scenarios of classroom observations for one or two items within each of these foci in Table 3.

Table 3 Scenarios where an observer would select 0, 1, 2, or 3 ratings for some GSIOP items
Full size table

In the hyperlink to the entire GSIOP (see footnote in the Appendix) one can refer to the rubric descriptions for each item, but we also detail prototypical situations for four different items from the GSIOP (Table 3). That is, for the Lesson-focused item, one could imagine an instructor was being observed when they wanted students to complete word problems whose solutions required them to calculate derivatives, and Table 3 includes classroom scenario in which an observer would select a 0, 1, 2, or 3 rating in that context. Similarly, Table 3 contains four rating scenarios in a different Calc I context for the Teacher-focused item, an Introduction to Statistics context for one Student-focused item (B) and a Calculus II context for another student-focused item (C). By providing different situations for each of the four selected criteria, the reader can compare how each rating may be observed for a single item in a class observation.

Data Analysis: The Validation Process

In his often-cited article on validity, Messick (1995) frames the concept of validity as a study of the fitness of an instrument for a particular use: “Validity is not a property of the test or assessment as such, but rather of the meaning of the test scores” (p. 741). In the context of this study, we assessed the fitness of the GSIOP for use in the undergraduate mathematics classroom, and in particular, for assessing teaching, and helping mentors organize feedback for novices.

Gleason et al.’s (2017) validation study of the MCOP2 provided a helpful starting point for the present analysis because the GSIOP is adapted from the MCOP2. Data from 291 observations (Table 2) was used for the internal consistency and factor analyses described in sections that follow. In addition, another trained graduate student researcher watched video data from 39 of the observations and scored the GSIOP based on the video. These 39 ratings were paired with the ratings the peer-mentors completed when they observed the live teaching and used to assess interrater reliability; described in the Interrater Reliability section.

Results of the Validation Study

This study addressed three aspects of the GSIOP’s fitness for use as an assessment of undergraduate mathematics classroom practice. First, the internal consistency of the instrument addressed how the items being measured contributed to the instrument’s overall measurement of effective mathematics classrooms as we defined them. Second, interrater reliability addressed whether different raters obtained the same results. Finally, a factor analysis addressed the question of what major underlying constructs are measured by the instrument.

Internal Consistency

The internal consistency of an instrument is an indication of its items’ correlations with one another, and indicates the degree to which the items measure the same general construct. In the present case, the GSIOP is intended to measure effective teaching within mathematics classrooms, as defined by the Instructional Practices Guide (MAA 2018). Specifically, we took into account lesson design practices, teacher facilitation practices, assessment practices, and classroom practices identifiable through classroom observations with an emphasis that “effective teaching and deep learning require student engagement with mathematics both inside and outside the classroom” (p. x). A lesson that accomplishes this should have better scores on all items, compared to a lesson that is less successful in doing so.

Internal consistency is often measured using Cronbach’s alpha, which uses the pairwise correlations between all items, and yields an alpha statistic that can range from negative infinity to one. A rule of thumb is that an alpha of 0.7 to 0.8 or higher indicates adequate internal consistency of the measured variables (Bland and Altman 1997). Using the 291 observations completed by the mentors, a Cronbach’s alpha of 0.868 was computed for the 17 GSIOP items. Tavakol and Dennick (2011) explain that if the instrument measures more than one construct, alpha should be computed for each one. Consistent with Gleason et al.’s (2017) findings in their analysis of the MCOP2, the factor analysis we report found three such constructs, student engagement, lesson design practice, and teacher facilitation and computed alphas of 0.824, 0.663, and 0.816 respectively.

Cronbach’s alphas in this range indicate that the internal consistency of the instrument supports the assumption that its items measure the underlying constructs. Although the alpha for lesson design practice was on the low end of the range (0.663), we assume that this is due to the range of teacher behaviors being measured. The development of the instrument allows us to assume that its general construct is that the actions of teachers and students in the classroom facilitate students’ conceptual understanding, and it measures the factors of student engagement, design practice, and teacher facilitation.

Interrater Reliability

Interrater reliability measures the extent to which different trained raters using the instrument to score the same observations yield similar scores. It is expected that a reliable instrument producing ordinal or continuous data would have a high percentage of ratings of the same observation that were the same or with only small differences.

In the case of the GSIOP, all observations were originally scored by the mentors who carried out the observations during a live observation. In addition, a sample of 39 of the observations completed in the first year (21 at one university, and 18 at the other) were scored by a second rater who viewed the videos made at the time of the observation. To select the sample, observations were first organized by instructor, mentor, and time in the semester, then selected at random from within these categories to ensure that the sample was broadly representative.

The 17 GSIOP items (see Appendix) are given scores ranging from 0 to 3, based on rubric descriptions of performance at each of the four levels. The scores are ordered, in the sense that higher scores indicate higher levels of performance. The individual item data is ordinal, but not interval, since the “distance” from one score to the next is not necessarily an equal measurement. In addition, summary variables on the four categories of variables (cover page, student-focused, teacher-focused, and lesson-focused items) were computed by averaging the scores given on each of the related variables. In this study, interrater reliability was measured in two ways: (1) ratings by two independent raters were cross-tabulated to determine the percentages of ratings that were the same (different by 1 position in the numerical rating, or different by more than 1 numerical position); and (2), correlation statistics for each variable’s paired observations were computed.

A consistently scored, reliable instrument would find few cases of large differences in scores between the two raters. Therefore, there would be a large proportion of ratings that were the same or close. We used Spearman-correlations and looked for Spearman correlation with a confidence level of 95% (alpha = 5%).

Crosstabulations assess interrater reliability, and provide an immediate, intuitive understanding of the data. We analyzed our dataset (N = 39) by creating crosstabulations in which ratings by one rater were compared to the ratings by the second rater. The first three data columns of Table 4 show the results of the crosstabs. The first column shows the percentage of times the raters agreed exactly, and the second shows the proportion of times the ratings were no more than 1 position apart (e.g., rater 1 scored the item as 2 and rater 2 scored it 3). The third column shows the percentage of cases in which the raters were farther apart than 1 position. To account for crosstabular error (if the two raters’ scores were independent, the scores would be the same about 25% of the time by chance alone), we also used a correlation analysis.

Table 4 Study of interrater reliability
Full size table

The Spearman’s rho and its p value were computed for each pair of variables (i.e. rater one’s rating vs. rater two’s ratings for each of the 39 paired ratings). Spearman’s was used because the individual variables’ values are ordinal. They are not interval data because their four possible values are not quantitative measures equidistant from each other. This also means that they do not meet the criterion of being normally distributed, which would be necessary for Pearson’s r. However, Pearson’s r was appropriate for the summary variables, which met the requirements of being continuous and normally distributed. Regarding both individual items and summary variables, we looked for a confidence level of 95% (alpha = 5%), and only one variable failed to meet this criterion. We display the results of these analyses in Table 4.

Each of the individual variables is assigned a rubric position (score) of 0, 1, 2, or 3. For all variables, there was agreement within one rubric position in 85% or more of the cases (e.g., if rater 1 scored the variable a 2, rater 2 would need to score the variable 1, 2, or 3 to meet this criterion), and for all but five variables the agreement was greater than 95%. The other analyses were consistent with the expected results (i.e. a correlation significance of less than .05) except in the case of variable E (rho = 0.26, p = 0.055), which we interpret as indicating that this variable’s rubric level definitions may need refinement. Overall, these crosstabulations and correlations indicate that there is a high level of interrater reliability on all but one item when the raters are trained to score classroom observations using this instrument.

Factor Analysis

Exploratory factor analysis (principal components analysis) is used to identify underlying components, usually referred to as factors, within a number of variables in a dataset (Garson 2018). The process analyzes the variance in a correlation matrix of the variables and yields a set of factor loadings that can be used to group statistically-related variables together. The grouping indicates that the variables are likely to measure an underlying construct that they have in common. The explanatory strength of each factor is indicated by its eigenvalue, which is the ratio of the amount of variance explained by the factor versus the total variance in the dataset. Results of the factor analysis may be confirmed by running the procedure twice on two different random subsets of the data.

Exploratory factor analysis assumes that the variables being examined are at least interval-level and that they use the same distributions. In the case of this dataset, all responses had integer values between 0 and 3. Although a number of different scholars have proposed different rules of thumb regarding the required number of cases (Garson 2018), our dataset included 291 unique observations, and this meets most of the recommended criteria in this regard. According to the Central Limit Theorem and the number of groupings we looked at in our factor analysis, we meet the sample size necessary to assume a normal distribution, which is necessary for this test. A final criterion is Bartlett’s test of Sphericity, which determines whether the variables are independent of one another, in which case there could not be any underlying factors. Bartlett’s p value (N = 291) was less than 0.001, satisfying this assumption.

Factors with low eigenvalues are typically eliminated from consideration using a combination of three common criteria: comprehensibility; the Kaiser criterion (K1 rule); and the Scree plot. Comprehensibility has been met by the appropriateness of the factors. The Kaiser rule (which is the default setting in SPSS) indicates that factors with eigenvalues less than 1 should be eliminated from consideration. Finally, the Cattell scree test is a plot of the components resulting from the factor analysis in descending order of eigenvalues. This plot usually begins with a steep decline ending with a bend toward a lower rate of decline. According to this criterion, factors to the right of this bend should be dropped (Garson 2018).

Using the 291 original observation scores, a factor analysis was performed. Using the K1 rule to drop all factors with eigenvalues less than one, three factors were identified, explaining a cumulative 51.1% of the variance in the data. Gleason et al. (2017) identified two of these three factors, which they labeled student engagement (SE) and teacher facilitation (TF). Our analysis added a third factor, which loaded mostly on the basic classroom organization and presentation items we had added to the cover page, and which we labeled design practice (DP). These results were consistent with the comprehensibility, Kaiser, and scree plot (see Fig. 1) criteria.

Fig. 1
figure 1

Scree plot of factor analysis

Full size image

We include the results of the three-factor solution in Table 5 as well as the Cronbach’s alphas calculated for the factors. According to Garson (2018), ideally, factor loadings shown in the rotated component matrix should be strong, in the range of 0.7 and above. However, especially for exploratory factor analysis in the social sciences, this is a very high bar, and loadings as moderate as 0.4 are often accepted; we follow this approach.

Table 5 Factor analysis rotated component matrix
Full size table

This factor matrix (Table 5) resulted in six items for the first factor (SE), five items for the second factor (DP), and nine items for the third factor (TF). There was very little overlap between the factors because only three items had loadings higher than 0.40 for two different factors. The SE items, aligned with the first factor, were identified and labeled as such since they all depend on the actions, interactions, and responses of students. For instance, although the teacher is the one incorporating formative assessments in item III.I, it is with a focus on eliciting student responses and it loaded onto this SE factor. The DP items, associated with the second factor, focus on teachers’ actions that are related to the basic lesson design practices that we previously described, including: planning and implementing student-learning-oriented mathematics lessons (I.G.1 and III.G) and effectively communicating instructional decisions and mathematical connections to students (I.G.2, I.G.3, and I.G.4). The third factor contained TF items where the items depend on teachers’ actions during class that facilitate or encourage students to engage with the mathematics. When considering the three items that had overlap between two factors, there are interactions between teachers’ and students’ actions that are being highlighted. For III.F, there is an interaction between the types of questions the teacher asks and the extent to which students’ thinking is made visible, and this item loads slightly more strongly with the TF factor. Considering item II.B, the primary focus is on how students use different means to represent concepts, but a teacher’s facilitation may also encourage or discourage students from engaging in those types of opportunities during the lesson. Finally, item I.G.1 focuses on a teacher’s actions for planning and implementing a cohesive lesson, which falls more under the DP factor but is still associated with the TF factor.

The factor analysis indicates that there is alignment between the two foci of the MCOP2 instrument (SE and TF) underlying the variables of the GSIOP and how these variables relate to the factors in this analysis (Table 5). The additional factor (DP) measures items that are particularly important to consider when providing feedback for novice instructors. We conclude that Gleason et al. (2017) identified two significant constructs of the instrument on which the GSIOP was based, and that the GSIOP shares those constructs while adding a third construct that measures lesson design practice issues that “inform the construction of the learning environment and curriculum and support instructors in implementing pedagogies that maximize student learning” (MAA 2018, p. 118).

Discussion

When assessing validity of the GSIOP we built on Gleason et al.’s (2017) work and their expert assessment of individual observation items. We looked at three kinds of evidence to determine validity. First, we examined internal consistency of the instrument’s items, addressing the question “did all of its items taken together measure a particular construct?” The measure of internal consistency indicates whether the items appear to measure an underlying construct, but not what that construct might be. In this instance, this piece of evidence indicated that the GSIOP appeared to measure an underlying construct. Second, we considered interrater reliability, addressing the question “does the instrument yield similar results when an observation is scored by more than one trained rater?” We found that there was an acceptable (or better) level of interrater reliability for all but one item (Teacher-Focused Item E), and modifications of this item are currently being tested. We note with interest that this level of interrater reliability was achieved despite the fact that the first ratings were based on in-person observations, and the second used video recordings of the class sessions. Third, we conducted a factor analysis identifying three components, or underlying constructs; two of these constructs were consistent with those found in the MCOP2 study. Taken together, these results provide strong support for our contention that the GSIOP provides a useful and accurate measure of the conduct of an undergraduate mathematics lesson. We also note that our results were based on both video and live observations of classrooms, so we emphasize that the validity results are indicative of the applicability of the protocol to both settings, providing opportunities for use in PD programs and research settings that use either method for data collection.

Implications for Practice

Most college instructors, including GSIs, receive end-of-semester evaluations from students. Although it is possible that these evaluations can provide helpful comments about teaching, they are almost always seen by instructors after the course has ended and grades have been submitted to the university, limiting an instructor’s ability to implement any changes based on comments they received. Doing so, though, is almost entirely dependent upon the instructor being motivated enough to seek out the information from the evaluations, determine what changes to make, and remember to implement such changes in subsequent courses. In addition, researchers consistently find that student evaluations of instruction are biased (e.g. Basow and Silberg 1987; Miller and Chamberlin 2000; Mitchell and Martin 2018) and unreliable measures of effective teaching (see Uttl et al. 2017 for a meta-analysis review). However, recent research suggests that student evaluations are still the primary way that mathematics departments evaluate their GSIs and GSI PD programs (Speer et al. 2017).

Given our determination of reliability in measuring what is happening in GSIs’ undergraduate mathematics classrooms and the fact that mathematics GSIs are typically required to participate in some form of PD at their institutions (Speer et al. 2017), we see potential use of the GSIOP for practitioners interested in helping GSIs develop student-centered classrooms earlier in their teaching careers and in finding more meaningful ways to evaluate the instruction of GSI, and, more importantly, the growth of GSIs as effective instructors.

The GSIOP provides a framework for providing feedback to novice instructors about observations of their teaching. In fact, preparing peer-mentors to use the GSIOP for this purpose is a significant part of the agenda of a semester-long mentor PD process that experienced GSIs undergo before stepping into their roles as peer-mentors (Yee and Rogers 2017b). The primary role of a peer-mentor (in our study, but potentially applicable to any observer using this protocol) is to support their novices (the instructors they are observing) as they learn to teach undergraduate mathematics students, not to evaluate the instructor.

Although a few of the items in the GSIOP are normative, indicating that we take an evaluative stance regarding what can be regarded as effective classroom practices for promoting students’ conceptual understanding, these evaluative components are the least emphasized aspect of the GSIOP. That is, we suggest using the GSIOP as a lens for observing instructional practices (especially regarding student engagement and teacher facilitation) and not as a means to rate or score classroom practices or performance.

Implications for Research

The field of research on novice college mathematics instructors is a relatively young one but growing, partially due to the large numbers of undergraduate students that interact with these instructors. Although other observation protocols (e.g., Table 1) could be used when examining classrooms of GSIs, the GSIOP fills a need as a mathematics-focused observation protocol capturing both instructional activities and student engagement in the classroom but was also specifically developed for observing mathematics GSIs. We developed the instrument (based on the MCOP2) with the assistance of GSIs specifically taking into consideration (a) GSIs’ familiarity (or lack thereof) with national standards for teaching mathematics put forth by US professional societies, and (b) some basic teaching mechanics that must also be mastered by novice instructors of collegiate mathematics. Given the findings in this study that the GSIOP is useful and accurate in measuring student engagement and teaching practices in undergraduate mathematics classrooms (taught by GSIs), we envision many applications of the protocol in research settings. Such research settings can include evaluation researchers examining mathematics GSI PD programs, educational researchers investigating classroom practices, and educational researchers comparing student perceptions to observed practices. The relatively small amount of time needed for training an observer to use the GSIOP and the ability to use it in a live classroom or with video recordings provide many opportunities for researchers to better collect accurate data on mathematics GSI classroom practices.

Moreover, the authors of this manuscript have used the protocol as part of a feedback cycle for novice GSIs. Through that research, we have found that the information collected with the GSIOP combined with a structured feedback process results in varying levels of changes in instructional practices (Yee et al. 2019a, b). We found that among the novice GSIs, we saw more increases in student engagement and student-centered instructional practices when the feedback provided by the mentor was specific and accompanied by suggestions on how to improve it. Not all mentors were proficient in providing this type of feedback, so in addition to providing research results, we see potential for reforming feedback processes that can results in observable improvement in teaching.

Limitations

A primary limitation of this instrument is its intentional focus. Specifically, the GSIOP has been used for two years by dozens of more experienced GSIs who were trained to observe novices in two mathematics departments in the US. Propagation of the instrument to additional departments is ongoing and may lead to additional insight into the instrument and its potential uses. We also note that the GSIOP has not been used in non-mathematics undergraduate classrooms nor has it been used to observe instructors who are not graduate students, and these other populations could be a focus of future studies. We conjecture, though, that this observation protocol could provide a helpful lens for generating feedback for novice STEM instructors or experienced mathematics instructors who may be teaching a course for the first or second time or using different methods to teach a course that is familiar to them.

Conclusion

Teaching undergraduate mathematics students necessitates the instructor designing their lesson with student-engagement strategies and teaching facilitation techniques that encourage and invite student exploration and involvement (MAA 2018). This protocol provides a way to guide an observer to note ways an individual lesson includes teaching practices relevant to these aspects and has demonstrated viable fitness with respect to internal consistency, interrater reliability, and factor analysis. The GSIOP offers a consistent, reliable, and needed protocol for observing novice mathematics GSIs’ classroom practices.