Abstract
In this paper, a novel model is presented to estimate the thermophysical properties of superheated steam (SHS) in dual-tubing wells (DTW). Firstly, a mathematical model comprised of the mass conservation equation, momentum balance equation and energy balance equation in the integral joint tubing (IJT) and annuli is proposed for concentric dual-tubing wells (CDTW), and in the main tubing (MT) and auxiliary tubing (AT) for parallel dual-tubing wells (PDTW). Secondly, the distribution of temperature, pressure and superheat degree along the wellbores are obtained by finite difference method on space and solved with iteration technique. Finally, based upon the validated model, sensitivity analysis of injection temperature is conducted. The results show that: (1) effect of injection temperature difference between MT and AT on temperature profiles is weak compared with that between the IJT and annuli. (2) Temperature gradient in IJT and annuli near wellhead is larger than that in MT and AT. (3) Superheat degree in both CDTW and PDTW increases with the increase in injection temperature in IJT and MT, respectively. (4) Superheat degree in IJT and MT decreases rapidly near wellhead, but the superheat degree in annuli and AT has an increase. (5) Thermal radiation and convection are the main ways of heat exchange between MT and AT. This paper gives engineers a novel insight into what is the flow and heat transfer characteristics of SHS in DTW, and provides an optimization method of injection parameters for oilfield.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Thermal methods, such as steam-assisted gravity drainage (SAGD) (Butler 1991; Vander et al. 2007; Al-Bahlani and Babadagli 2009; Miura and Wang 2012; Yang et al. 2016) and steam huff-puff (Marx and Langenheim 1959; Willman and Valleroy 1961; Boberg and Lanz 1966; Hou and Chen 1997; Sandler et al. 2014; Sun et al. 2017a) have been proved successful for heavy oil recovery. Precisely predicting thermophysical parameters of thermal fluid along wellbores is the first important task for oilfield engineers. However, the prediction of thermophysical properties of thermal fluid in wellbores is never easy due to the complexity of thermal fluid flow in wellbores (Sun et al. 2017b, c, d).
In 1960s, conventional oil resources are relatively abundant and the development of heavy oil was subjected to many restrictions (Ramey 1962; Holst and Flock 1966; Willhite 1967; Orkiszewski 1967; Beggs and Brill 1973). However, with the change of energy demand and with the progress of technology, the recovery of heavy oil has come more into focus. Predicting thermal parameters of thermal fluid along the wellbores is significant for optimizing heavy oil recovery (Cheng et al. 2011, 2012, 2013, 2014; Dong et al. 2014; Gu et al. 2014, 2015a, b; Wei et al. 2015; Fan et al. 2016).
Based upon the energy balance equation, Satter (1965) gave a model for predicting steam quality in wellbores. Pacheco and Ali (1972) proposed a comprehensive mathematical model for predicting pressure in wellbores taking friction losses into consideration. Farouq Ali (1981) developed a model to analyze the pressure profiles for both upward and downward flow. Adopting iteration technique, Durrant and Thambynayagam (1986) gave an improved model for quick estimation of transient heat transfer rate along the wellbores, which laid a solid foundation for follow-up studies (Ejiogu and Fiori 1987; Tortike and Ali 1989; Sagar et al. 1991; Alves et al. 1992; Bahonar et al. 2010, 2011).
Several studies have been done by Hasan and Kabir (1991, 1994, 2007, 2009, 2012), Hasan (1995) and Hasan et al. (2007a, b, 2010) on the flow and heat transfer characteristics of wet steam in wellbores, which serve as the foundation for later studies (Chiu and Thakur 1991; Cheng et al. 2011, 2012, 2013, 2014). However, all of these previous studies were focused upon the simple-structured single-tubing wells.
Field tests have shown that the application of single-tubing wells is easier to cause non-uniform steam suction (Hight et al. 1992; Griston and Willhite 1987; Liu 2009; Gu et al. 2014). Therefore, DTW was proposed to alleviate these shortcomings, and fortunately, it has been proved to be effective (Barua 1991; Hight et al. 1992).
Caetano (1985)developed an early model for predicting pressure drop in annuli, which presented a basic reference for follow-up studies (Brill 1987; Hasan and Kabir 1992; Brill and Mukherjee 1999; Lage and Time 2000, 2002; Yu et al. 2010; Wu et al. 2011). Based on the new concept of equivalent radius, Griston and Willhite (1987) presented an improved model for predicting pressure drop in annuli, which was proved reliable later by Kaya et al. (2001). In recent years, Gu et al. (2014) presented an improved model to estimate the pressure drop in annuli. It their work, a new radius calculation method for steam flow in annuli was proposed.
However, all of these studies were focused on saturated steam flow and they did not cover the subject of SHS flow in DTW. Zhou et al. (2010), Xu et al. (2013), Gu et al. (2015a, b), Fan et al. (2016) and Sun et al. (2017e, f) presented basic models for predicting thermophysical properties of SHS in conventional single-tubing wells for both onshore and offshore conditions. But the heat transfer characteristics in single-tubing wells are very different from that in DTW (Sun et al. 2017g). Sun et al. (2017g) presented a numerical model for SHS flow in CDTW. However, their model cannot be used directly to PDTW. Besides, an essential comparison between CDTW and PDTW is needed. More researches are needed to reveal the flow characteristics of SHS in DTW.
In this paper, a new model is developed for predicting thermophysical properties of SHS in DTW. The thermophysical properties of SHS along the wellbores are obtained by finite difference method on space and solved with iteration technique. Moreover, thermal radiation and convection between MT and AT is also accounted for in the model. The effect of injection temperature in each tubing on the profiles of thermophysical properties of SHS in wellbores is analyzed. This study unravels some intrinsic flow characteristics of SHS in DTW, which has a significant impact on the optimization of SHS injection parameters and analysis of heat transfer law in DTW.
Model description
Basic assumptions
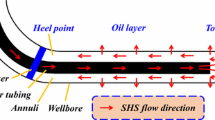
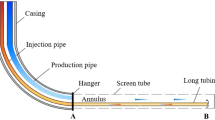
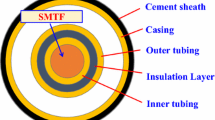
A schematic of the DTW is shown in detail in Fig. 1. In order to study the flow characteristics of SHS in DTW, some basic assumptions are made as follows:
-
1.
The injection parameters at wellhead are assumed to be constant.
-
2.
SHS flow in DTW is assumed to be steady state.
-
3.
The momentum balance of the SHS flow process is assumed to be steady state.
-
4.
Heat transfer rate inside the wellbores is assumed to be steady state.
-
5.
Heat transfer rate in formation is assumed to be transient (Sun et al. 2017h).
-
6.
Thermophysical properties of formation are assumed to be independent of well depth (Sun et al. 2017h).
Mathematical modeling of SHS flow in IJT and MT
Firstly, based on the mass conservation law in the IJT (Sun et al. 2017g) and MT, the mass balance equation of SHS flow in IJT (Sun et al. 2017g) and MT can be given as:
where \(w_{\text{ij,MT}}\) denotes the mass flow rate of SHS in IJT or MT, kg/s; \(z\) denotes the vertical depth of the wellbore, m; \(r_{\text{ij,MTi}}\) denotes the inner radius of the IJT or MT, m; \(\rho_{\text{ij,MT}}\) denotes the SHS density in IJT or MT, kg/m3; \(v_{\text{ij,MT}}\) denotes the flow velocity of SHS in IJT or AT, m/s.
Secondly, the energy balance equation of SHS in the IJT (Sun et al. 2017g) can be expressed as:
where \(Q_{\text{ij}}\) denotes the heat exchange rate between IJT and annuli, J/s; \(h_{\text{ij}}\) denotes the enthalpy of SHS in IJT, J/kg; \(\theta\) denotes the included angle between wellbore and the vertical line, rad.
The energy balance equation of SHS in MT can be expressed as:
where \(Q_{\text{MTout}}\) denotes heat loss rate of the MT (Wei. 2015), J/s; \(Q_{\text{MTin}}\) denotes the heat absorption rate of the MT (Wei. 2015), J/s; \(h_{\text{MT}}\) denotes the enthalpy of SHS in MT, J/kg.
Finally, the steady-state momentum balance equation of SHS in the IJT (Sun et al. 2017g) and MT can be expressed as:
where \(p_{\text{ij,MT}}\) denotes the SHS pressure in IJT and MT, Pa; \(\tau_{\text{f}}\) denotes the shear stress in IJT and MT, N.
Thus, the governing hydrodynamic equations of SHS flow in IJT and MT are established.
Mathematical modeling of SHS flow in annuli and AT
Firstly, based on the mass conservation law in annuli, the mass balance equation of SHS flow in the IJT can be given as (Sun et al. 2017g):
where \(w_{\text{an}}\) denotes the mass flow rate in annuli in CDTW, kg/s; \(r_{\text{ai}}\) denotes the inner radius of the inner tubing, m; \(r_{\text{ijo}}\) denotes the outer radius of the IJT, m; \(\rho_{\text{an}}\) denotes the SHS density in annuli, kg/m3; \(v_{\text{an}}\) denotes the flow velocity of SHS in annuli, m/s.
The mass balance equation of SHS flow in AT can be expressed as:
where \(w_{\text{AT}}\) denotes the mass flow rate of SHS in AT, kg/s; \(r_{\text{ATi}}\) denotes the inner radius of the AT, m; \(\rho_{\text{AT}}\) denotes the SHS density in AT, kg/m3; \(v_{\text{AT}}\) denotes the flow velocity of SHS in AT, m/s.
Secondly, based on the energy conservation law in annuli, the energy balance equation of SHS in annuli can be expressed as (Sun et al. 2017g):
where \(Q_{\text{an}}\) denotes the heat transfer rate from annuli to formation, J/s; \(w_{\text{an}}\) denotes the mass flow rate of SHS in annuli, kg/m3; \(h_{\text{an}}\) denotes the SHS enthalpy in annuli, J/s; \(v_{\text{an}}\) denotes the flow velocity of SHS in annuli, m/s.
The energy balance equation of SHS flow in AT can be expressed as:
where \(Q_{\text{ATout}}\) denotes the AT heat loss rate (Wei. 2015), J/s; \(Q_{\text{ATin}}\) denotes the AT heat absorption rate (Wei. 2015), J/s; \(w_{\text{AT}}\) denotes the mass flow rate of SHS in AT, kg/m3; \(h_{\text{AT}}\) denotes the SHS enthalpy in AT, J/kg; \(v_{\text{AT}}\) denotes the flow velocity of SHS in AT, m/s.
Finally, the momentum balance equation of SHS flow in annuli can be expressed as (Sun et al. 2017g):
where \(p_{\text{an}}\) denotes the SHS pressure in annuli, Pa.
The momentum balance equation of SHS flow in AT can be expressed as:
where \(p_{\text{AT}}\) denotes the SHS pressure in AT, Pa.
The above equation models SHS flow in annuli.
Numerical solution of the model
The proposed model is solved with finite difference method on space. Both IJT and annuli or MT and AT are evenly divided into equal segments. Then, the temperature and pressure at the interface between the neighboring segments can be obtained in DTW. The pressure and temperature in the IJT and annuli or in the MT and AT are solved sequentially. Based on Eq. (5), the difference equation can be expressed as:
Similarly, based on Eq. (9), the difference equation for pressure solving in annuli can be obtained:
The difference equation for pressure solving in AT can be obtained:
In order to solve Eqs. (11–13), we must assume a pair of the outlet temperature. Taking CDTW as an example, this will leave two unknown numbers (\(p_{\text{ij,out}}\) and \(p_{\text{an,out}}\)) with two equations, and the outlet pressure of the studied segment can be calculated. In this paper, function zero method is adopted, as shown below:
Similarly, we can solve for temperature, which can be derived from Eqs. (2, 3, 7, 8).
In order to get accurate results of the outlet values of the studied segment, iteration method is then adopted.
Finally, the accurate values of pressure and temperature at outlet of the ith segment are used as inputs for the inlet of the (i + 1)th segment. Then, another iteration begins. Finally, the pressure and temperature along the wellbores can be obtained. The detailed mathematical model solving process is shown as a flowchart in Fig. 2.
Results and discussion
Validation of the model
In order to verify the accuracy of the proposed model, the model was validated by testing it against field data. Basic tubing parameters used for calculation can be found in Table 1. And the simulated results for SHS flow in CDTW are presented in Fig. 3. Besides, simulated results for SHS flow in PDTW are also added for comparison.
Figure 3 shows the temperature and pressure profiles in DTW. For CDTW, the injection pressure, temperature and mass flow rate at wellhead in IJT and annuli are 4.5 MPa, 650 K, 293 t/d, and 3.5 MPa, 600 K, 259 t/d, respectively. It is observed that the predicted results from our model are in good agreement with field data. What is to stress that some additional factors (pipe contact, formation heterogeneity, etc.) that are neglected in the mathematical model causes more temperature drop (Fig. 3b). This is the main reason why the predicted temperature is a little higher than field data. However, the maximum relative error for both pressure and temperature predictions is still smaller than 5%.
Characteristic analysis of SHS flow in CDTW
From Fig. 3a, it is observed that: (1) SHS pressure in IJT and annuli or in MT and AT decreases with well depth; (2) pressure gradient in the IJT is larger than in annuli. This is because the relatively larger injection rate in the IJT, which causes more friction loss; (3) pressure gradient in MT is larger than in AT. This is because the flow radius of SHS in MT is smaller and the mass flow rate of SHS in MT is larger, which causes more friction loss.
It can be observed from Fig. 3b that: (1) Temperature in the IJT decreases rapidly from wellhead to the depth of 50 m; after 50 m, the temperature decrease is gradual; (2) Temperature in annuli has an increase from wellhead to the depth of 50 m, after which it gradually decreases. This is because \(U_{\text{ijo}}\) is much higher than \(U_{\text{ao}}\). For our particular case, \(U_{ijo}\) has a value of 1560 W/(m2 K). Thus, the heat exchange rate between IJT and annuli is large even if there exists a small temperature difference between IJT and annuli; (3) Temperature gradient in IJT and annuli tends to be equal from the depth of 50 m to well bottom; (4) the heat exchange rate between MT and AT is much smaller compared with that between IJT and annuli. This is because the MT and AT are not contact to each other. The channels of heat transfer between MT and AT are thermal radiation and convection. As a result, SHS with a higher temperature in MT decreases slowly compared with that in IJT. And the SHS with a lower temperature in AT increases slowly compared with that in annuli.
Figure 4a shows the profiles of heat transfer rate in CDTW. It can be observed that (1) heat transfer rate from IJT to annuli has a decrease of 79% from wellhead to the depth of 50 m; (2) the net heat loss rate in annuli increases rapidly from −132,298 to −2751 W/m from wellhead to the depth of 50 m, and turns positive at the depth of 165 m. SHS in IJT begins to absorb heat from SHS in annuli. This is because the SHS temperature in IJT drops faster than SHS temperature in annuli.
From Fig. 4b, we can find that the temperature in annuli is much higher than the temperature at the interface of the cement sheath and formation, and of course, much higher than the initial formation temperature. Consequently, CDTW heat losses cannot be avoided due to this temperature difference.
Figure 4c shows the profiles of superheat degree in the IJT and annuli and in the MT and AT. It is observed that (1) superheat degree in annuli increases at first and then begins to decrease with well depth. (2) Superheat degree in the IJT decreases rapidly from wellhead to the depth of 100 m, and then, the superheat degree decrease is gradual. In fact, in the case of CDTW, superheat degree in IJT and annuli is influenced not only by the injection conditions at wellhead, but also by the heat transfer between the IJT and annuli. For example, when the SHS in annuli absorbs heat from SHS in the IJT, the latter is just like a heat resource that can transfer heat to annuli, causing the superheat degree in annuli to increase with well depth. (3) The decrease rate of superheat degree in MT from wellhead to the depth of 100 m is smaller than that in IJT. This is because the heat transfer rate from MT to AT is smaller than that from IJT to annuli. As a result, superheat degree in AT has a small increase from wellhead to the depth of 50 m compared with that in annuli.
Effect analysis of the injection temperature in IJT and MT
In this section, effect of injection temperature in IJT on the profiles of thermophysical properties of SHS in wellbores is studied. Temperatures were tested (550, 570, 590, 610, 630, 650 K) with no change in values of injection pressure and rate. Besides, injection temperatures in MT with same values were tested for comparison. The predicted results are presented in Fig. 5.
Figure 5a shows that (1) when \(T_{\text{ij}}\) and \(T_{\text{MT}}\) are relatively small, SHS temperature in IJT and MT increases from wellhead to the depth of 50 and 150 m, respectively, and then turns to decrease. This is because when \(T_{\text{ij}}\) and \(T_{\text{MT}}\) are smaller than \(T_{\text{an}}\) and \(T_{\text{AT}}\), SHS in IJT and MT absorbs heat from SHS in annuli and AT, which causes the increase in SHS temperature near wellhead. (2) SHS temperature starts to decrease when \(T_{\text{ij}}\) reaches 600 K, and the temperature starts to decrease when \(T_{\text{MT}}\) reaches 600 K. The reason is that when \(T_{\text{ij}}\) and \(T_{\text{MT}}\) are smaller than \(T_{\text{an}}\) and \(T_{\text{AT}}\), respectively, SHS in IJT and MT absorbs heat from SHS in annuli and AT, respectively. (3) From wellhead to the depth of 50 m, temperature in the IJT changes drastically due to the fact that there exists a large temperature difference between the IJT and annuli. Similarly, from wellhead to 150 m, temperature in MT changes rapidly with a large temperature difference between MT and AT. For depths greater than 50 m in CDTW, temperature in IJT and annuli decreases at a same rate. This is because the temperature difference between IJT and annuli is very small after 50 m. For depths greater than 150 m in PDTW, temperature in MT and AT decreases with a same rate. This is because the temperature difference between MT and AT becomes small when it is deeper than 150 m.
Figures 5b shows that: (1) When SHS injection temperature in IJT and MT is smaller than 600 K, SHS temperature in annuli and AT decreases from wellhead to the depth of 50 and 150 m, respectively. This is because when \(T_{\text{ij}}\) and \(T_{\text{MT}}\) are smaller than \(T_{\text{an}}\) and \(T_{\text{AT}}\), respectively, SHS in annuli and AT transfers heat to SHS in IJT and MT, respectively. (2) When SHS injection temperature in IJT and MT is larger than 600 K, SHS in annuli and AT begins to absorb heat from SHS in IJT and MT. As a result, SHS temperature in annuli and AT increases from wellhead to the depth of 50 and 150 m, respectively.
Figure 5c, d is important from an engineering point of view as they show the superheat degree at well bottom. It is observed that (1) the superheat degree in both CDTW and PDTW increases with the increase in \(T_{\text{ij}}\) and \(T_{\text{MT}}\), respectively. But the practicing engineers are suggested to take the boiler capacity into consideration in order to achieve maximum economic benefits. (2) Gradient of the superheat degree in IJT with depth greater than 50 m is larger than that in MT. This is because the MT and AT are not contacted to each other. There exists thermal radiation and convection between MT and AT. Therefore, the effect of injection temperature in MT on AT is weaker compared with the effect of IJT on annuli.
Figure 5e shows heat transfer rate from IJT to annuli. It is observed that for depths greater than 100 m, heat transfer rate inside the wellbore gradually becomes zero. Figure 5f shows the profiles of net heat loss rate in annuli (CDTW heat loss rate) under various injection temperatures in IJT; it can be observed that the net heat loss rate is large when there exists a large temperature difference between IJT and annuli, but the curve becomes smooth with the increase in \(T_{\text{ij}}\) and turns negative when \(T_{\text{ij}}\) reaches 600 K.
Analysis of the injection temperature in annuli
In the following section, we will study the effect of the injection temperature in annuli on temperature profiles, degree of superheat and heat transfer rate in CDTW. Different injection temperatures in annuli were tested (550, 570, 590, 610, 630, 650 K) with no change in values of injection pressure and rate. The results are presented in Fig. 6.
Figure 6a shows the influence of injection temperature in annuli and AT on temperature profiles in IJT and AT, respectively. It is observed that (1) the SHS temperature at well bottom in both IJT and MT increases with the increase in injection temperature in annuli and AT, respectively. (2) SHS temperature in IJT and MT decreases rapidly from wellhead to the depth of 100 m when injection temperature in annuli and AT is smaller than that in IJT and MT, respectively. This is because the heat transfer rate between the IJT and annuli or between MT and AT wells is large when there exists a large temperature difference between the IJT and annuli or between MT and AT, as shown in Fig. 6e. Moreover, Fig. 6f also illustrates the characteristics of heat transfer in CDTW, and we can observe that the net heat loss rate in annuli increases rapidly with the increase in \(T_{\text{an}}\). (3) Temperature gradient in IJT is larger than that in MT. This is because the effect of heat transfer in PDTW on temperature profiles in MT and AT is weak compared with that in CDTW.
Figure 6b shows the effect of injection temperature in annuli and AT on the profiles of temperature in annuli and AT. Firstly, we can find that the temperature near wellhead in both annuli and AT increases when the injection temperature in annuli and AT is smaller than that in IJT and MT. This is because SHS in annuli and AT absorbs heat from SHS in IJT and AT due to temperature difference between IJT and annuli or between MT and AT. Secondly, the increase in temperature near wellhead in annuli and AT gradually becomes smaller with the increase in injection temperature in annuli and AT, respectively. This is because the heat transfer rate inside the wellbore decreases and the net heat loss rate in annuli increases with the increase in \(T_{\text{an}}\), as shown in Fig. 6e, f.
Figure 6c shows the effect of injection temperature in annuli and AT on the profiles of superheat degree in IJT and AT. It is observed that (1) superheat degree in both IJT and MT at a certain place in wellbores increases with the increase in injection temperature in annuli and AT. (2) Superheat degree decreases rapidly near wellhead when injection temperature in annuli and AT is smaller than that in IJT and MT, respectively.
Figure 6d shows the effect of injection temperature in annuli and AT on the profiles of superheat degree in annuli and AT. Firstly, it is observed that the superheat degree increases near wellhead when the injection temperature in annuli and AT is smaller than that in IJT and MT, respectively. Secondly, the increase in temperature near wellhead in annuli and AT gradually decreases with the increase in injection temperature in annuli and AT, respectively. In conclusion, in order to obtain a satisfactory oil recovery rate, a higher injection rate in annuli and AT is recommended. Besides, the effect of injection temperature on superheat degree profiles becomes weak when PDTW is selected.
Conclusions
In this paper, a novel model is proposed to analyze the flow and heat transfer characteristics of SHS in DTW. The model was validated using field data. We can conclude:
-
1.
In CDTW, temperature difference between IJT and annuli has a strong influence on the profiles of temperature and superheat degree in both IJT and annuli. A relatively small difference in temperature at wellhead is able to cause a large amount of heat to flow between IJT and annuli. Besides, the effect of injection temperature on superheat degree profiles becomes weak when PDTW is selected.
-
2.
For depth less than 50 m, SHS temperature in IJT decreases rapidly near wellhead, while SHS temperature in annuli increases rapidly. For depth greater than 50 m, the heat exchange rate between IJT and annuli is small. For depth less than 150 m, SHS temperature in MT decreases rapidly near wellhead, while SHS temperature in AT increases rapidly. For depth greater than 150 m, the heat exchange rate between MT and AT is small.
-
3.
Superheat degree in IJT and annuli or in MT and AT increases with the increase in injection temperature in IJT and MT, respectively.
-
4.
Gradient of superheat degree near wellhead in IJT is larger than that in MT. This is because the MT and AT are not contacted to each other. Thermal radiation and convection are the main ways of heat exchange between MT and AT.
-
5.
In order to obtain a satisfactory oil recovery rate, a higher injection temperature for both CDTW and PDTW is recommended. However, practicing engineers are suggested to take the boiler capacity into consideration.
Abbreviations
- w :
-
Mass flow rate of SHS in each tubing (kg/s)
- \(\rho\) :
-
SHS density (Zhang and Zhao 1997; Gu et al. 2015a, b) (kg/m3)
- \(v\) :
-
Flow velocity of SHS in the tubing (m/s)
- r :
-
Radius of tubing (m)
- z :
-
Well depth from the surface (m)
- \(Q_{\text{ij}}\) :
-
The heat exchange rate between the IJT and annuli (W)
- \(Q_{\text{an}}\) :
-
The heat loss rate from annuli to formation (W)
- \(Q_{\text{MTout}}\) :
-
The heat loss rate of MT (W)
- \(Q_{\text{MTin}}\) :
-
The heat absorption rate of MT (W)
- \(Q_{\text{ATout}}\) :
-
The heat loss rate of AT (W)
- \(Q_{\text{ATin}}\) :
-
The heat absorption rate of AT (W)
- \(h\) :
-
Specific enthalpy of SHS (J/kg)
- g :
-
The gravitational acceleration (9.81 m/s2)
- \(\theta\) :
-
Well angle from vertical (rad)
- \(U_{\text{ijo}}\) :
-
Comprehensive heat transfer coefficient between the IJT and annuli [W/(m2 K)]
- \(T\) :
-
SHS temperature in the tubing (K)
- \(p\) :
-
SHS pressure (Pa)
- \(\lambda\) :
-
Wellbore thermal conductivity [W/(m K)]
- \(\lambda_{\text{e}}\) :
-
Formation thermal conductivity [W/(m K)]
- \(T_{\text{ei}}\) :
-
Formation temperature (K)
- \(h_{\text{c}}\) :
-
The convective heat transfer coefficient [W/(m2 K)]
- \(h_{\text{r}}\) :
-
The radiative heat transfer coefficient [W/(m2 K)]
- \(\tau_{\text{f}}\) :
-
The shear stress (N)
- \(\mu_{\text{ij}}\) :
-
SHS viscosity (Pa s)
- \(T_{ 0}\) :
-
The ground temperature (K)
- \(a\) :
-
The geothermal gradient (K/m)
- \({\text{ij}}\) :
-
The integral joint tubing
- \({\text{an}}\) :
-
The annuli
- \({\text{MT}}\) :
-
Main tubing
- \({\text{AT}}\) :
-
Auxiliary tubing
- \({\text{i}}\) :
-
Inner radius
- \({\text{o}}\) :
-
Outer radius
- \({\text{in}}\) :
-
Inlet of the segment
- \({\text{out}}\) :
-
Outlet of the segment
- \({\text{a}}\) :
-
Inner tubing
- \({\text{b}}\) :
-
Outer tubing
- \({\text{c}}\) :
-
The casing
- \({\text{tub}}\) :
-
The metallic tubing
- \({\text{ins}}\) :
-
Insulation materials
- \({\text{cas}}\) :
-
The casing
- \({\text{cem}}\) :
-
The cement sheath
References
Al-Bahlani A, Babadagli T (2009) SAGD laboratory experimental and numerical simulation studies: a review of current status and future issues. J Pet Sci Eng 68(3–4):135–150
Alves IN, Alhanati FJS, Shoham Ovadia (1992) A unified model for predicting flowing temperature distribution in wellbores and pipelines. SPE Prod Eng 7:363–367
Bahonar M, Azaiez J, Chen Z (2010) A semi-unsteady-state wellbore steam/water flow model for prediction of sandface conditions in steam injection wells. J Can Pet Technol 49(9):13–21
Bahonar M, Azaiez J, Chen Z (2011) Two issues in wellbore heat flow modelling along with the prediction of casing temperature in steam injection wells. J Can Pet Technol 50:43–63
Barua S (1991) Computation of heat transfer in wellbores with single and dual completions. In: Proceedings of the 66th annual technical conference and exhibition, Dallas, TX: SPE22868, pp 487–502
Beggs DH, Brill JP (1973) A study of two-phase flow in inclined pipes. J Pet Technol 25:607–617
Boberg TC, Lanz RB (1966) Calculation of the production rate of a thermally stimulated well. JPT 18:1613–1623
Brill JP (1987) Multiphase flow in wells. J Pet Technol 39:15–21
Brill JP, Mukherjee H (1999) Multiphase flow in wells, 1st edn. Society of Petroleum Engineers, Richardson
Butler Roger M (1991) Thermal recovery of oil and bitumen. Prentice Hall, New Jersey
Caetano EF (1985) Upward two-phase flow through an annulus. Dissertation, University of Tulsa
Cheng WL, Huang YH, Lu DT et al (2011) A novel analytical transient heat-conduction time function for heat transfer in steam injection wells considering the wellbore heat capacity. Energy 36:4080–4088
Cheng WL, Huang YH, Liu N et al (2012) Estimation of geological formation thermal conductivity by using stochastic approximation method based on well-log temperature data. Energy 38:21–30
Cheng WL, Li TT, Nian YL et al (2013) Studies on geothermal power generation using abandoned oil wells. Energy 59:248–254
Cheng WL, Nian YL, Li TT et al (2014) A novel method for predicting spatial distribution of thermal properties and oil saturation of steam injection well from temperature logs. Energy 66:898–906
Chiu K, Thakur SC (1991) Modeling of wellbore heat losses in directional wells under changing injection conditions. In: Proceedings of the 66th annual technical conference and exhibition, Dallas, TX: SPE22870, pp 517–528
Dong XH, Liu HQ, Zhang ZX et al (2014) The flow and heat transfer characteristics of multi-thermal fluid in horizontal wellbore coupled with flow in heavy oil reservoirs. J Pet Sci Eng 122:56–68
Durrant AJ, Thambynayagam RKM (1986) Wellbore heat transmission and pressure drop for steam/water injection and geothermal production: a simple solution technique. SPE Reserv Eng 1:148–162
Ejiogu GC, Fiori M (1987) High-pressure saturated steam correlations. J Pet Technol 39:1585–1590
Fan ZF, He CG, Xu AZ (2016) Calculation model for on-way parameters of horizontal wellbore in the superheated steam injection. Pet Explor Dev 43(5):798–805
Farouq Ali SM (1981) A comprehensive wellbore steam/water flow model for steam injection and geothermal applications. SPE J 21:527–534
Griston S, Willhite GP (1987) Numerical model for evaluating concentric steam injection wells. In: Proceedings of the SPE California region meeting. Ventura, California: SPE, pp 127–39
Gu H, Cheng LS, Huang SJ, Du BJ, Hu CH (2014) Prediction of thermophysical properties of saturated steam and wellbore heat losses in concentric dual-tubing steam injection wells. Energy 75:419–429
Gu H, Cheng LS, Huang SJ et al (2015a) Thermophysical properties estimation and performance analysis of superheated-steam injection in horizontal wells considering phase change. Energy Convers Manag 99:119–131
Gu H, Cheng LS, Huang SJ et al (2015b) Steam injection for heavy oil recovery: modeling of wellbore heat efficiency and analysis of steam injection performance. Energy Convers Manag 97:166–177
Hasan AR (1995) Void fraction in bubbly and slug flow in downward vertical and inclined systems. SPE Prod Facil 10:172–176
Hasan AR, Kabir CS (1991) Heat transfer during two-phase flow in wellbores: part I-formation temperature. In: Proceedings of the 66th annual technical conference and exhibition, Dallas, TX: SPE22866, pp 469–478
Hasan AR, Kabir CS (1992) Two-phase flow in vertical and inclined annuli. Int J Multiph Flow 18(2):279–293
Hasan AR, Kabir CS (1994) Aspects of wellbore heat transfer during two-phase flow. SPE Prod Facil 9:211–216
Hasan AR, Kabir CS (2007) A simple model for annular two-phase flow in wellbores. SPE Prod Oper 22:168–175
Hasan AR, Kabir CS (2009) Modeling two-phase fluid and heat flows in geothermal wells. In: Proceedings of the 2009 SPE western regional meeting, San Jose, California, USA: SPE121351, pp 1–13
Hasan AR, Kabir CS (2012) Wellbore heat-transfer modeling and applications. J Pet Sci Eng 86–87:127–136
Hasan AR, Kabir CS, Sayarpour M (2007a) A basic approach to wellbore two-phase flow modeling. In: Proceedings of the 2007 SPE annual technical conference and exhibition, Anaheim, California, USA: SPE109868, pp 1–9
Hasan AR, Kabir CS, Wang X (2007b) A robust steady-state model for flowing-fluid temperature in complex wells. In: Proceedings of the 2007 SPE annual technical conference and exhibition, Anaheim, California, USA: SPE109765, pp 1–9
Hasan AR, Kabir CS, Sayarpour M (2010) Simplified two-phase flow modeling in wellbores. J Pet Sci Eng 72:42–49
Hight MA, Redus CL, Lehrmann JK (1992) Evaluation of dual-injection methods for multiple-zone steamflooding. SPE Reserv Eng 7:45–51
Holst PH, Flock DL (1966) Wellbore behaviour during saturated steam injection. J Can Pet Technol 5:184–193
Hou J, Chen YM (1997) An improved steam soak predictive model. Pet Explor Dev 24(3):53–56
Kaya AS, Sarica C, Brill JP (2001) Mechanistic modeling of two-phase flow in deviated wells. SPE Prod Facil 16:156–165
Lage ACVM, Time RW (2000) Mechanistic model for upward two-phase flow in annuli. In: Proceedings of the 2000 SPE annual technical conference and exhibition, Dallas, Texas: SPE63127, pp 1–11
Lage ACVM, Time RW (2002) An experimental and theoretical investigation of upward two-phase flow in annuli. SPE J 7:325–336
Liu HQ (2009) Optimized design and research on technology parameters of dualstring steam injection in horizontal well. Master thesis, China University of Petroleum, East China
Marx JW, Langenheim RH (1959) Reservoir heating by hot fluid injection petroleum transactions. AIME 216:312–315
Miura K, Wang J (2012) An analytical model to predict cumulative steam/oil ratio (CSOR) in thermal recovery SAGD process. J Can Pet Technol 51(4):268–275
Orkiszewski J (1967) Predicting two-phase flow pressure drops in vertical pipe. J Pet Technol 19:829–838
Pacheco EF, Farouq Ali SM (1972) Wellbore heat losses and pressure drop in steam injection. J Pet Technol 24:139–144
Ramey HJ (1962) Wellbore heat transmission. J Pet Technol 14:427–435
Sagar R, Doty DR, Schmidt Z (1991) Predicting temperature profiles in a flowing well. SPE Prod Eng 6:441–448
Sandler J, Fowler G, Cheng K, Kovscek AR (2014) Solar-generated steam for oil recovery: reservoir simulation, economic analysis, and life cycle assessment. Energy Convers Manag 77:721–732
Satter A (1965) Heat losses during flow of steam down a wellbore. J Pet Technol 17:845–851
Sun FR, Li CL, Cheng LS, Huang SJ, Zou M, Sun Q, Wu XJ (2017a) Production performance analysis of heavy oil recovery by cyclic superheated steam stimulation. Energy 121:356–371
Sun FR, Yao YD, Li XF, Yu PL, Ding GY, Zou M (2017b) The flow and heat transfer characteristics of superheated steam in offshore wells and analysis of superheated steam performance. Comput Chem Eng 100:80–93
Sun FR, Yao YD, Li XF, Yu PL, Zhao L, Zhang Y (2017c) A numerical approach for obtaining type curves of superheated multi-component thermal fluid flow in concentric dual-tubing wells. Int J Heat Mass Transf 111:41–53
Sun FR, Yao YD, Li XF, Zhao L, Ding GY, Zhang XJ (2017d) The mass and heat transfer characteristics of superheated steam coupled with non-condensing gases in perforated horizontal wellbores. J Pet Sci Eng 156:460–467
Sun FR, Yao YD, Chen MQ, Li XF, Zhao L, Meng Y, Sun Z, Zhang T, Feng D (2017e) Performance analysis of superheated steam injection for heavy oil recovery and modeling of wellbore heat efficiency. Energy 125:795–804
Sun FR, Yao YD, Li XF, Zhao L (2017f) Type curve analysis of superheated steam flow in offshore horizontal wells. Int J Heat Mass Transf 113:850–860
Sun FR, Yao YD, Li XF, Tian J, Zhu GJ, Chen ZM (2017g) The flow and heat transfer characteristics of superheated steam in concentric dual-tubing wells. Int J Heat Mass Transf 115:1099–1108
Sun FR, Yao, Li XF, Li H, Chen G, Sun Z (2017h) A numerical study on the non-isothermal flow characteristics of superheated steam in ground pipelines and vertical wellbores. J Pet Sci Eng 159:68–75
Tortike WS, Farouq Ali SM (1989) Saturated-steam-properties functional correlations for fully implicit thermal reservoir simulation. SPE Reserv Eng 4:471–474
Vander Valk PA, Yang P (2007) Investigation of key parameters in SAGD wellbore design and operation. J Can Pet Technol 46(6):49–56
Wei SL (2015) Flow mechanism and production practice for the integral process of SAGD using horizontal well pairs. Ph.D. thesis, China University of Petroleum, Beijing
Wei SL, Cheng LS, Huang WJ et al (2015) Flow behavior and heat transmission for steam injection wells considering the tubing buckling effect. Energy Technol 3:935–945
Willhite GP (1967) Over-all heat transfer coefficients in steam and hot water injection wells. J Pet Technol 19:607–615
Willman BT, Valleroy VV (1961) Laboratory studies of oil recovery by steam injection. JPT 222:681–696
Wu H, Wu XD, Wang Q, Zhu M, Fang Y (2011) A wellbore flow model of CO2 separate injection with concentric dual tubes and its affecting factors. Acta Pet Sin 32(4):722–727
Xu AZ, Mu LX, Fan ZF, Zhao L (2013) New findings on heatloss of superheated steam transmitted along the wellbore and heating enhancement in heavy oil reservoirs. In: The international petroleum technology conference held in Beijing, China, 26–28 Mar
Yang Y, Huang SJ, Yang L et al (2016) A multistage theoretical model to characterize the liquid level during steam-assisted-gravity-drainage process. SPE J 22:1–12
Yu TT, Zhang HQ, Li MX et al (2010) A mechanistic model for gas/liquid flow in upward vertical annuli. SPE Prod Oper 25:285–295
Zhang JR, Zhao YY (1997) Manual for thermophysical properties of commonly-used materials in engineering, 1st edn. National Denfense Industry Press, Beijing
Zhou TY, Cheng LS, He CB, Pang ZX, Zhou FJ (2010) Calculation model of on-way parameters and heating radius in a superheated steam injection wellbore. Pet Explor Dev 37(1):83–88
Acknowledgements
The authors wish to thank the State Key Laboratory of efficient development of offshore oil (2015-YXKJ-001). This work was also supported in part by a grant from National Science and Technology Major Projects of China (2011ZX05030-005-04). The authors recognize the support of the China University of Petroleum (Beijing) for the permission to publish this paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Sun, F., Yao, Y. & Li, X. Numerical simulation of superheated steam flow in dual-tubing wells. J Petrol Explor Prod Technol 8, 925–937 (2018). https://doi.org/10.1007/s13202-017-0390-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13202-017-0390-7